Study on the Effect of Cracks in Diaphragm Couplings on the Dynamic Characteristics of Shaft System ^†

Abstract

Diaphragm couplings are prone to developing diaphragm cracks under prolonged high-speed operating conditions, which can lead to degradation in the performance of the transmission system and affect the dynamics of the shafting system. To investigate the effects of diaphragm cracks on the dynamics of couplings and the shafting system, a finite element model of a diaphragm coupling with a crack failure is established using ANSYS finite element software to analyze the time-varying characteristics of the diaphragm coupling’s angular and radial stiffness. A shaft dynamics model of the diaphragm coupling with a crack is developed using Timoshenko beam elements to analyze the impact of different crack lengths and locations on the dynamics of the shafting system. The validity of the dynamic model for a diaphragm coupling with a crack is verified through a constant speed experiment conducted on a rotor test bench. The results indicate that diaphragm crack failure causes a change in the periodicity of the time-varying stiffness of the diaphragm coupling, leading to a distinct 2× component appearing in the frequency domain of the transmission shaft system.

1. Introduction

Diaphragm couplings are one of the most important components of mechanical transmission systems, which are used to connect and transmit torque. However, under long-term high-speed and high-torque operating conditions of diaphragm couplings, diaphragm cracks may occur, directly affecting the coupling performance and thus the stability of the shaft system during operation. Therefore, it is extremely important to study the dynamic behavior of diaphragm cracks on the transmission shaft system.

So far, scholars at home and abroad have carried out extensive work regarding the impact of diaphragm coupling misalignment on the dynamic characteristics of the rotor system, as well as the implications of rotor system crack failure on the overall system. Ganesan et al. [1] investigated the dynamic characteristics of the system of a rotor in the parallel misalignment state of the coupling and concluded that the parallel misalignment state introduces time-varying stiffness, and the responses obtained clearly indicated the effect of parametric excitation at one-fourth, one-third, and one-half of the principal parametric resonance. Gupta T C et al. [2] developed the dynamic equations of a two-span rotor by considering the coupling stiffness, coupled loads, and nonlinearities in bearings and found that misalignment will produce 2× frequency response. Patel [3] experimentally investigated rotor misalignment faults and found that the rotor exhibits a strong 2× frequency response under misalignment faults at one-half the critical speed, and at one-third of the critical rotational speed, the rotor exhibits strong 2× and 3× frequency responses.

Shentu et al. [4] studied the nonlinear dynamic behavior of the stacked plate coupling system under the parallel misalignment fault and established a simplified system parallel misalignment dynamics model. They concluded that as the speed continues to increase, a series of bifurcation phenomena occur in the system, leading to the emergence of a two-times cycle resonance phenomenon. Cui et al. [5] used an experimental method for rotor misalignment faults and found that frequency-doubling vibration occurs in the rotor at one-half critical speed and dual and triple frequency vibration components at one-third critical speed. Desouki et al. [6] analyzed the effect of unbalance and misalignment on the rotor system in the presence of both and found that parallel misalignment mainly affects the 2× frequency response of rotor vibration, while angular misalignment affects the 2× and 4× frequency responses. Lees [7] carried out a dynamic analysis of the rotor system misalignment under rigid connection and derived the equations of motion of a machine with coupled alignment faults using an idealized linear model and explained that the harmonics are caused by the interaction of torsional and bending effects. Pennacchi and Huang [8,9] investigated the misalignment dynamics behavior of the system under touch-and-go faults with rigid couplings. Fu [10] and others used the Lagrangian method to establish an unbalanced one-unaligned one-touch fault coupling system in a hydraulic turbine and found that there are multiple harmonic components based on 1× and 2× frequency responses in the rotor system. Khorrami et al. [11] developed a dynamic model of a rotor containing a crack and analyzed the effects of cracks’ characteristics such as depth and location on the dynamic characteristics. Guo et al. [12] used the Hilbert–Huang transform to analyze the dynamic characteristics of a transversely cracked rotor and investigated the effect of the crack on the rotational speeds’ 1×, 2×, and 3× frequency responses. Li et al. [13] analyzed the dynamic characteristics of a rotor with a transverse crack using the stress intensity factor method to solve for stiffness and developed a new dynamic model with a slant crack based on fractional damping. Parbhakar et al. [14] used a continuous wavelet transform method to analyze the vibration characteristics of the rotor–coupling–bearing system under crack and coupling misalignment force faults, and the results showed that the method can effectively distinguish between crack and misalignment faults in the rotor system. Lu et al. [15] investigated the dynamic characteristics of hollow-shaft rotor systems with breathing cracks. The results indicate that when a transverse crack appears, resonance peaks can be observed at the second, third, and even fourth critical whirling speeds of the two rotors. In addition, numerical validation was performed using the Newmark—β method. Sinou et al. [16] used Fourier series expansion to derive the stiffness change within one cycle of cracked rotor rotation to describe the change rule of crack depth and crack location. Through the harmonic balance method, it was found that the subcritical resonance phenomenon occurs within the rotation cycle of the cracked rotor with 2× and 3× ultraharmonics components. With the expansion of surface cracks, the 2× component is more sensitive to changes in crack depth, and the 2× component amplitude increases significantly. On the basis of previous research, Sinou et al. [17] utilized the ultraharmonics components of the rotor when a crack fault occurs to diagnose the crack fault, which provides insights into the subsequent crack fault diagnosis. Huang and Tan et al. [18] established a dynamic model of the helicopter tail rotor transmission system and analyzed the impact of angular and radial misalignment errors of diaphragm coupling on the system’s dynamic characteristics. Yu and Ding et al. [19] established a dynamic bent–wobble–axial coupling model of diaphragm coupling, taking into account the coupling stiffness matrix and the axial nonlinear stiffness of the coupling, and studied the influence of helicopter maneuvering flight status on its coupling vibration characteristics. Mutra et al. [20] analyzed the rotor response, orbital pattern, and response FFTs during operation to determine the presence of cracks in the rotor bearing system. Open-wedge cracks (OWC) and breathing-wedge cracks (BWCs) were modeled, and their behavior was studied.

During the literature survey, it was found that domestic and foreign scholars have conducted extensive research in the area of shaft system dynamics modeling with diaphragm coupling and the damage analysis of cracked shaft rotor systems, but few studies exist that investigate the shaft system dynamics behavior with diaphragm cracks. To fill the research gap in this area, in this paper, we establish a kinetic model of a transmission shaft system with a cracked diaphragm, analyze the influence of the diaphragm crack on the dynamic characteristics of the system, and provide a technical basis for the identification of diaphragm crack faults in the transmission shaft system.

2. Dynamic Modeling

The shaft system, shown in Figure 1, mainly consists of an input shaft, an output shaft, an intermediate shaft, a diaphragm coupling, and a deep groove ball bearing. The structure of the diaphragm coupling, shown in Figure 2, is mainly composed of a diaphragm group, bolt, nut, bushing, and input and output flange. The diaphragm group includes multilayer diaphragms, gaskets, and flanged bushings. During operation, the power is mainly transmitted to the driven flange through the active flange at one end via the bolt and diaphragm group.

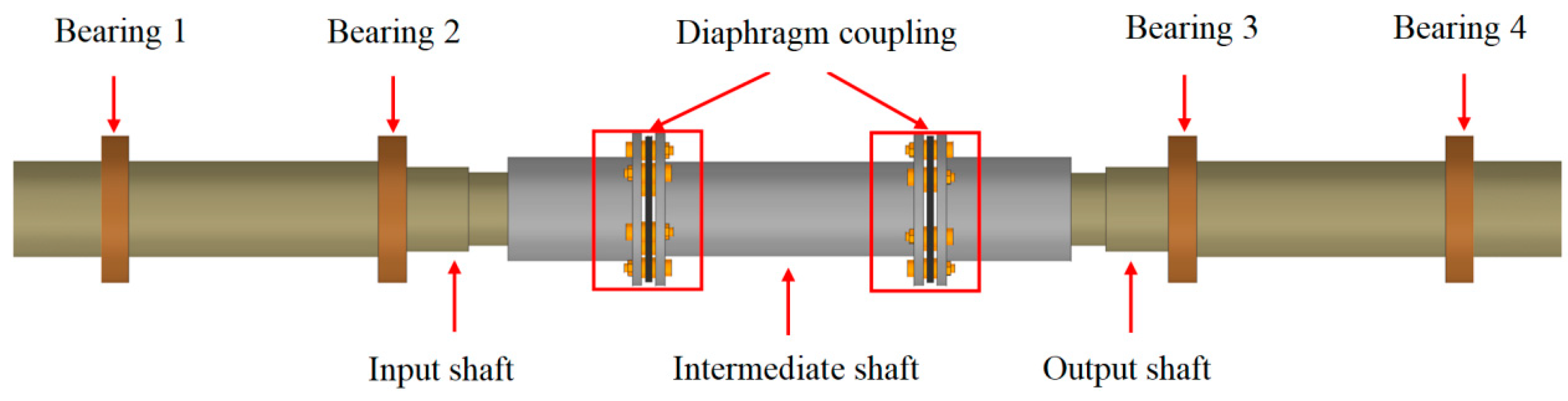
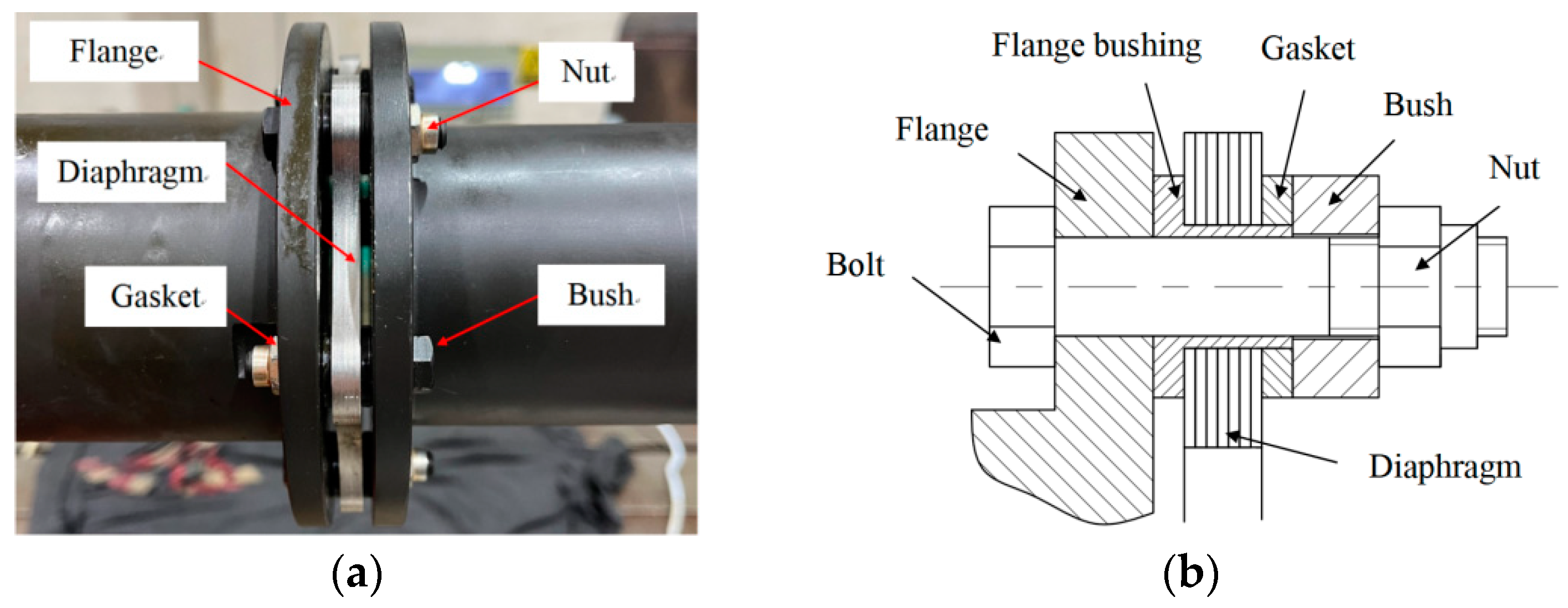
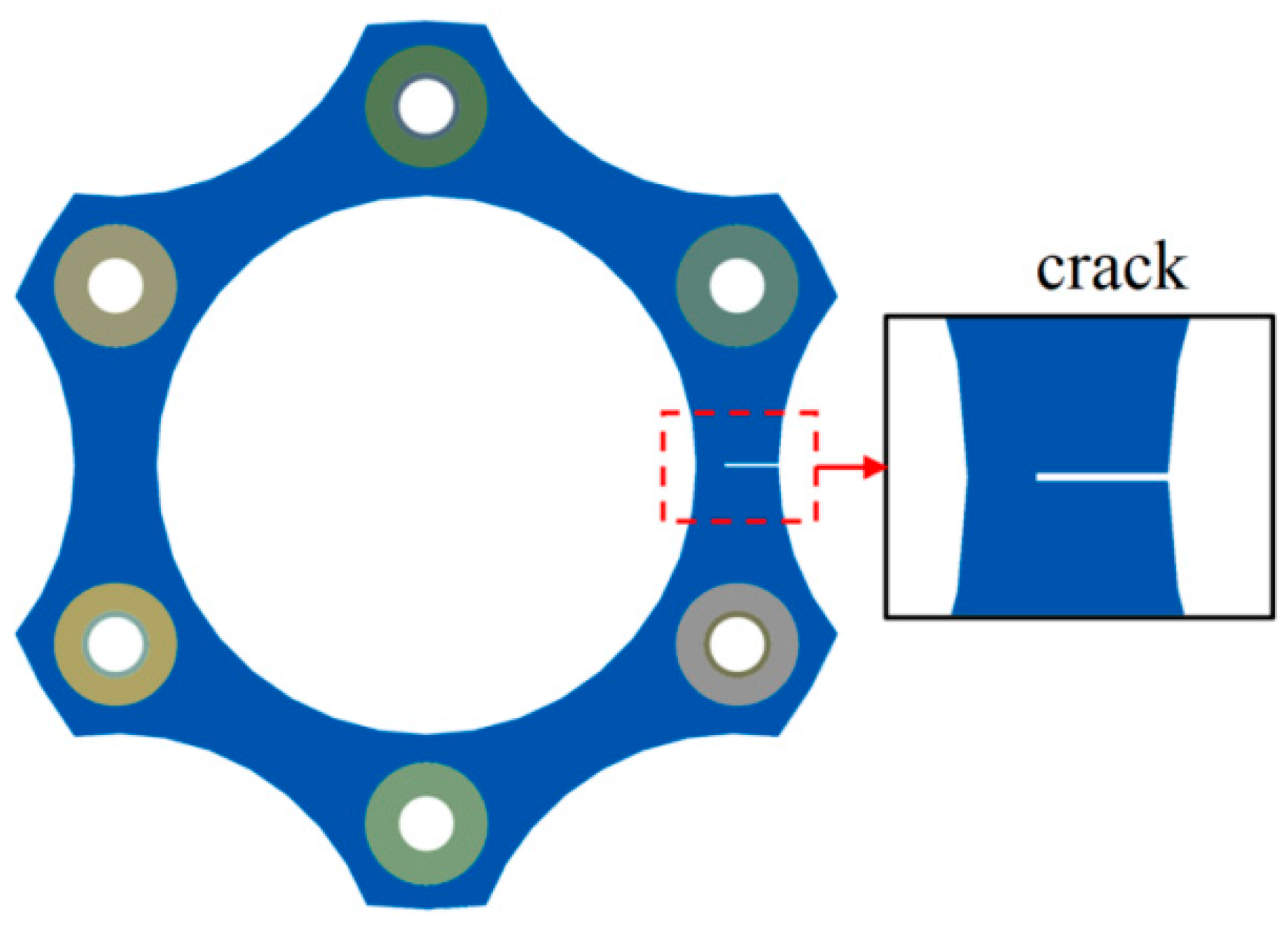
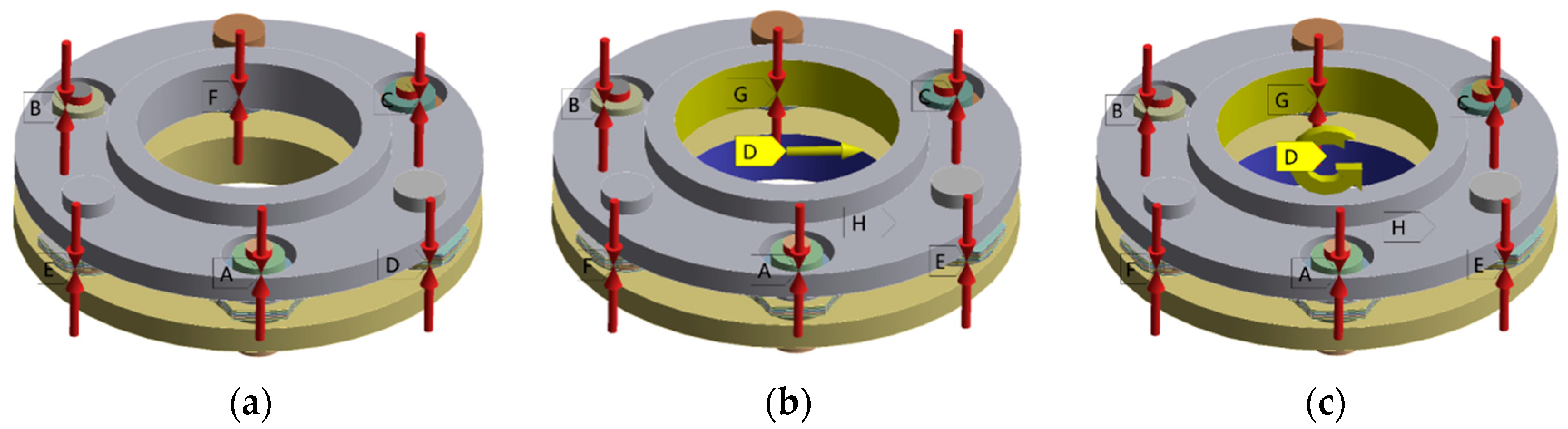
2.1. The Finite Element Model of the Diaphragm Coupling with Crack

When the diaphragm coupling is in operation, the stress concentration phenomenon occurs at the diaphragm girdle, and fatigue crack (fracture) is prone to occur. The crack at the diaphragm girdle is at the minimum width of the diaphragm girdle and extends along the inner ring of the diaphragm. To study the effect of a cracked diaphragm on the dynamics of the shaft system, a diaphragm model with crack failure was established, as shown in Figure 3. Since the minimum width of the diaphragm is 12 mm, five sets of data were selected for testing in order to find a general pattern, so the crack lengths were incremented at 2 mm intervals. Healthy diaphragms and four types of diaphragms with crack widths of 0.5 mm and lengths of 2 mm, 4 mm, 6 mm, and 8 mm were selected for stiffness simulation.

To establish the simulation model of the coupling with diaphragm cracks, the ANSYS software (2022R1) was used, which comes with a multi-area meshing tool comprising multizone for meshing and a grid type for three-dimensional solid cells. The finite element model and meshing are shown in Figure 4.

The contact type and parameter settings of each part of the diaphragm coupling are shown in Figure 5. The assembly relationship between the flanged bushing and the washer was an interference fit, while the nut and bolt connection was a self-locking nut, so the contact surfaces mentioned above were set as bound contacts. Because bolts and nuts are usually connected by a large tightening torque, non-separating contact was used for the flanged bushing–flange contact surfaces involved in tightening, the washer–bushing contact surfaces, and the bushing–bolt contact surfaces. Considering the nonlinear contact of the diaphragm with other parts and the nonlinear contact of the cylindrical surface of the bolt with other parts, these contacts were set as frictional or frictionless contacts. Since the diaphragm contact surfaces were coated with a low friction coefficient coating to reduce friction and wear, the coefficient of friction between the diaphragm and the diaphragm was set to 0.12, while the coefficient of friction of the other contact surfaces was set to 0.15.

Since the diaphragm coupling is a six-hole diaphragm, its radial stiffness and angular stiffness have time-varying characteristics in one rotation cycle. To calculate the time-varying stiffness value of the diaphragm coupling, a fixed constraint was used on the surface of the bore of the flange at the active end, and a remote point was set up on the surface of the bore of the flange at the driven end to apply the remote displacement. Two analysis steps were used for the load application. In the first analysis step, ta bolt preload force of 10 kN was applied on the axes of six bolts, as shown in Figure 6a. In the second analysis step, the bolt preload force was set to lock. When solving the radial stiffness, radial displacement was applied at the remote control point, and multiple sub-steps were used to simulate and solve the radial stiffness values under different radial directions in one rotation cycle using the force loading method, as shown in Figure 6b. When solving the angular stiffness, angular displacement was applied at the remote control point, and multiple sub-steps were set to simulate and solve the angular stiffness values under different angular directions in one rotation cycle. The angular stiffness values in different angular directions were simulated, and the force loading method is shown in Figure 6c.

Simulations were performed to obtain different crack lengths, the diaphragm coupling radial stiffness, and angular stiffness with the rotor in a rotational cycle of the stiffness change law, as shown in Figure 7 and Figure 8. In a rotational cycle, no crack diaphragm coupling exhibits radial stiffness and angular stiffness with time-varying characteristics; radial stiffness presents three periodic time-varying changes, and angular stiffness presents six periodic time-varying changes. With the increase in the diaphragm’s crack length, the overall amplitude of radial stiffness and angular stiffness shows a nonlinear downward trend, and the time-varying periodicity of stiffness changes greatly. Since the rotor system in this study rotates at a constant angular velocity, the effect of different crack lengths on the stiffness and rotor system is reflected in the change rule of stiffness with the rotation angle.

Considering that the time-varying angular and radial stiffness of the diaphragm coupling has a similar trend to that of the sine or cosine wave, the stiffness was fitted using a Fourier function composed of Fourier series. The fitted time-varying angular and radial stiffness can be expressed as follows [16]:

$$\begin{array}{l}{k}_{rx}(t)=a_{r0}+{\displaystyle \sum _{i=1}^n\left[a_{ri}\cos (n\mathrm{\Omega }t)+b_{ri}\sin (n\mathrm{\Omega }t)\right]}\\ k_{ry}(t)=a_{r0}+{\displaystyle \sum _{i=1}^n\left[a_{ri}\cos (n\mathrm{\Omega }t+\pi /2)+b_{ri}\sin (n\mathrm{\Omega }t+\pi /2)\right]}\\ k_{\theta x}(t)=a_{\alpha 0}+{\displaystyle \sum _{i=1}^n\left[a_{\alpha i}\cos (n\mathrm{\Omega }t)+b_{\alpha i}\sin (n\mathrm{\Omega }t)\right]}\\ k_{\theta y}(t)=a_{\alpha 0}+{\displaystyle \sum _{i=1}^n\left[a_{\alpha i}\cos (n\mathrm{\Omega }t+\pi /2)+b_{\alpha i}\sin (n\mathrm{\Omega }t+\pi /2)\right]}\end{array}$$

(1)

where $k_{\theta }$ and $k_r$ are the average values of angular and radial time-varying stiffness; $n$ is the order of the harmonic term of the Fourier function; ${\alpha }_{\alpha i}$, ${\alpha }_{ri}$, $b_{\alpha i}$, and $b_{ri}$ are the angular and radial stiffness amplitudes of the harmonic components; $w_m$ is the rotational frequency; and $t$ is the time of the axial system dynamics simulation solution. The intercepted Fourier expansion order in this section is the 18th order. The fitted angular and radial stiffnesses change with the rotational angle every moment in the dynamic simulation.

2.2. The System Dynamic Equation

The crack-containing diaphragm coupling–shaft system was divided into 14 shaft segments with a total of 15 nodes, and four degrees of freedom were considered for each node, i.e., degrees of freedom to move along the X and Y directions and degrees of freedom to rotate around the X and Y directions. The whole system had a total of 60 degrees of freedom, and the finite element model of the shaft system with a diaphragm coupling was established (Figure 9). The drive shaft was discretized into a Timoshenko beam unit with eight degrees of freedom [21]. The nodes ranging from 1 to 6 correspond to the input shaft unit, whereas nodes 7 through 9 are associated with the intermediate shaft unit. Nodes 10 to 15, on the other hand, pertain to the unit linked with the output shaft.

The bearing was simplified to a centralized parametric model by disregarding the time-varying, nonlinear, and touch friction of the rolling bearing stiffness, retaining only the main stiffness term, and assembling the bearing stiffness and damping to the corresponding support nodes 1, 6, 25, and 30. The stiffness and damping matrix expression for the bearing is as follows [22]:

$${\mathbf{K}}_b=\left[\begin{array}{cccc}{k}_{brx}& & & \\ & k_{bry}& & \\ & & k_{b\theta x}& \\ & & & k_{b\theta y}\end{array}\right]$$

(2)

$${\mathbf{C}}_b=\left[\begin{array}{cccc}{c}_{brx}& & & \\ & c_{bry}& & \\ & & c_{b\theta x}& \\ & & & c_{b\theta y}\end{array}\right]$$

(3)

where $k_{brx}$, $k_{bry}$ is the radial stiffness of the bearing; $k_{b\theta x}$, $k_{b\theta y}$ is the angular stiffness of the bearing; $c_{brx}$, $c_{bry}$ is the radial damping of the bearing; and $c_{b\theta x}$, $c_{b\theta y}$ is the angular damping of the bearing.

To investigate the coupling effect of bending and radial deformation in the diaphragm coupling, the stiffness matrix is established, which is assembled to nodes 12, 13, 18, and 19. The diaphragm coupling’s stiffness matrix $\mathrm{Kc}$ is as follows:

$$\mathbf{Kc}=\left[\begin{array}{cc}{\mathbf{K}}_1& -{\mathbf{K}}_1\\ -{\mathbf{K}}_1& {\mathbf{K}}_1\end{array}\right]$$

(4)

$${\mathbf{K}}_1=\left[\begin{array}{cccc}{k}_{rx}& & & \\ & k_{ry}& & \\ & & k_{\alpha x}& \\ & & & k_{\alpha y}\end{array}\right]$$

(5)

where the radial stiffness $k_{rx}$, $k_{ry}$ and angular stiffness $k_{\alpha x}$, $k_{\alpha y}$ of the diaphragm coupling are substituted into the angular and radial stiffness fitted by Equation (1).

The elements are assembled according to the finite element method to obtain the finite element dynamics equation of the shaft system with diaphragm coupling as follows:

$$\mathit{M}\ddot{\mathit{X}}+(\mathit{C}+\mathrm{\Omega }\mathit{G})\dot{\mathit{X}}+\mathit{K}(t)\mathit{X}={\mathit{F}}_g+{\mathit{F}}_u$$

(6)

where M and G denote the mass and gyroscopic matrices of the system, which are obtained by assembling the two-section diaphragm coupling, the shaft unit, and the bearing unit. C is the damping matrix of the system, which is damped by Rayleigh damping, and $\mathrm{\Omega }$ is the system’s rotational speed. K denotes the stiffness matrix of the shaft system, obtained by assembling the diaphragm coupling stiffness, the shaft unit stiffness, and the bearing stiffnesses. $\mathit{X}$, $\dot{\mathit{X}}$, and $\ddot{\mathit{X}}$ are the displacement, velocity, and acceleration vectors of the system, respectively. ${\mathit{F}}_g$ is the gravity vector applied to the system, and ${\mathit{F}}_u$ is the unbalanced excitation vector applied to the system. In this study, an unbalanced excitation with an unbalance of 1 × 10⁻⁴ kgm was added at node 6. The matrix and vector expressions of typical Timoshenko beam elements can be seen in Appendix A.

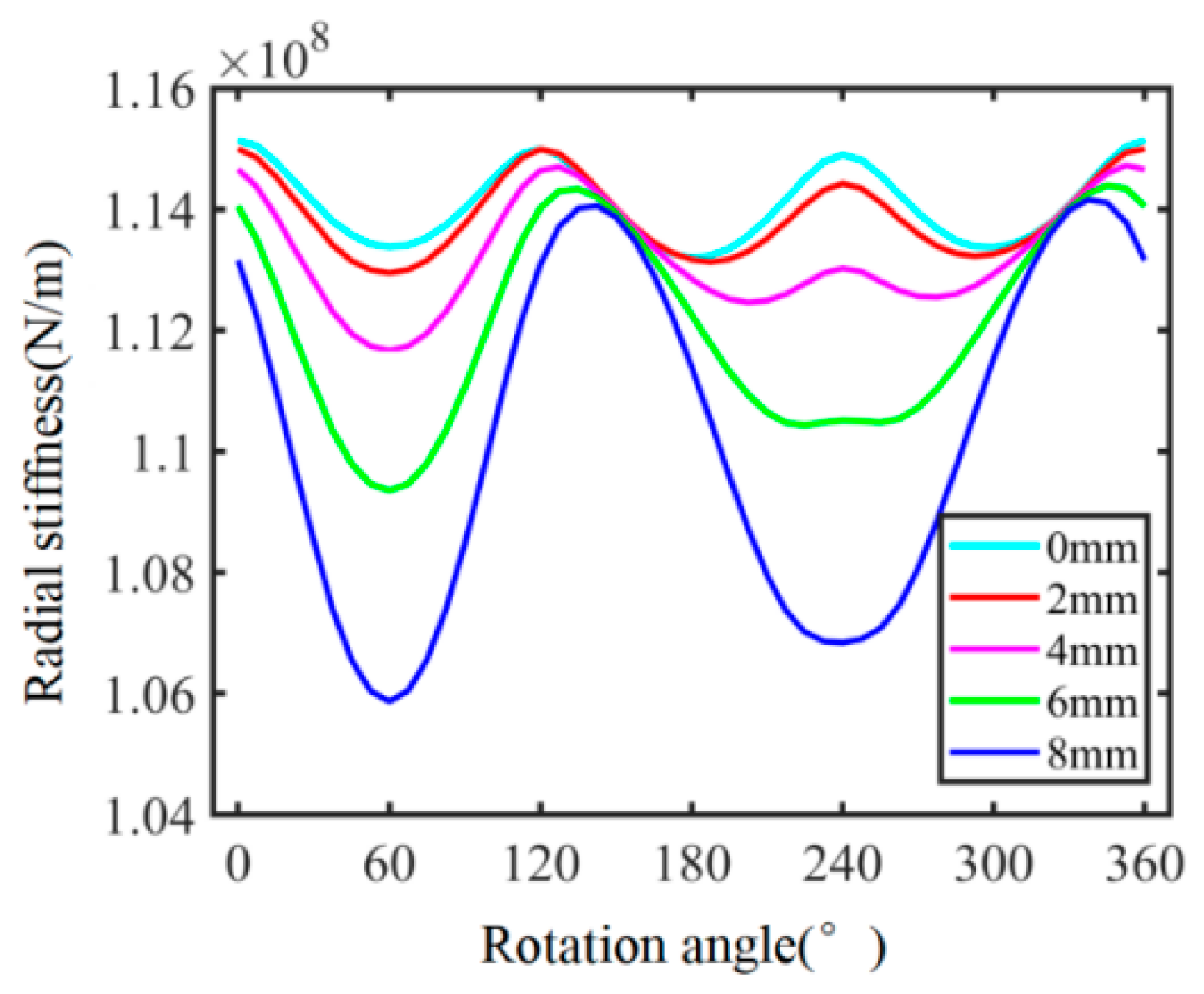
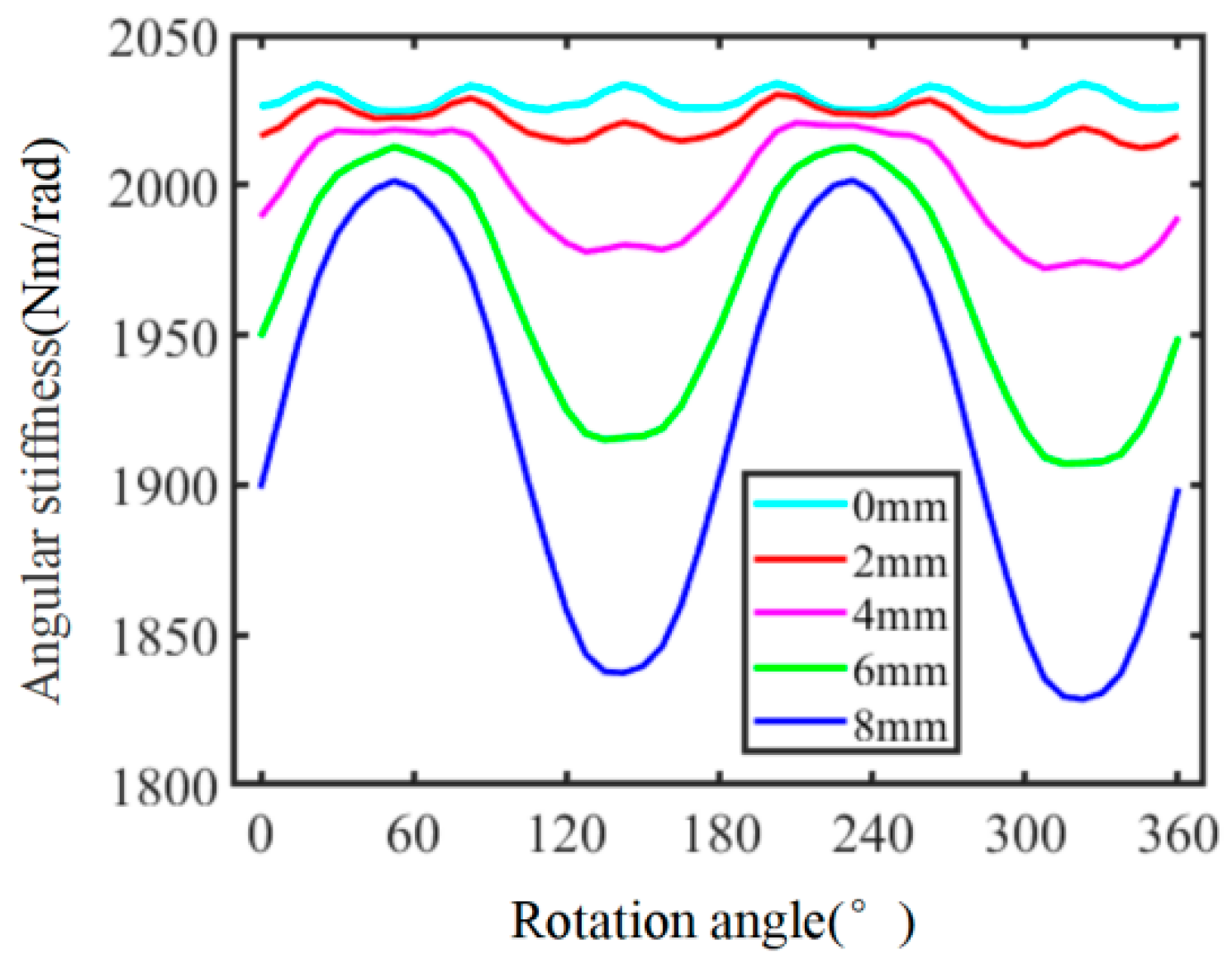
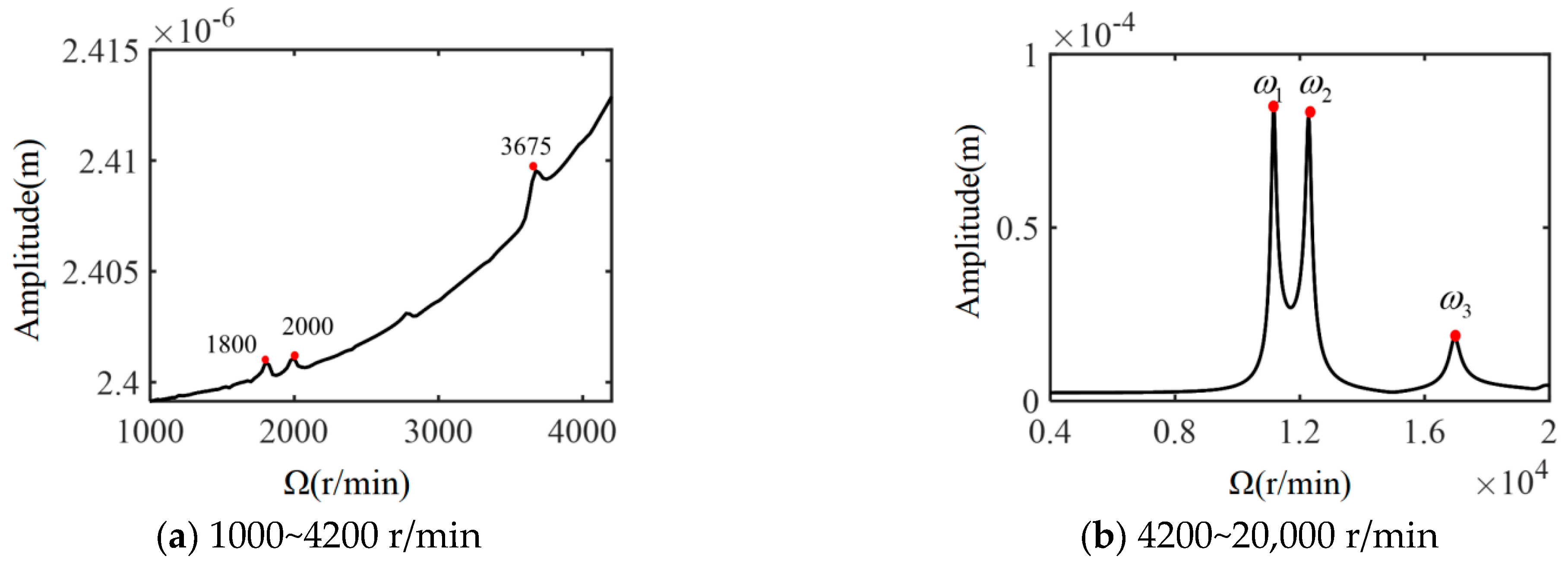
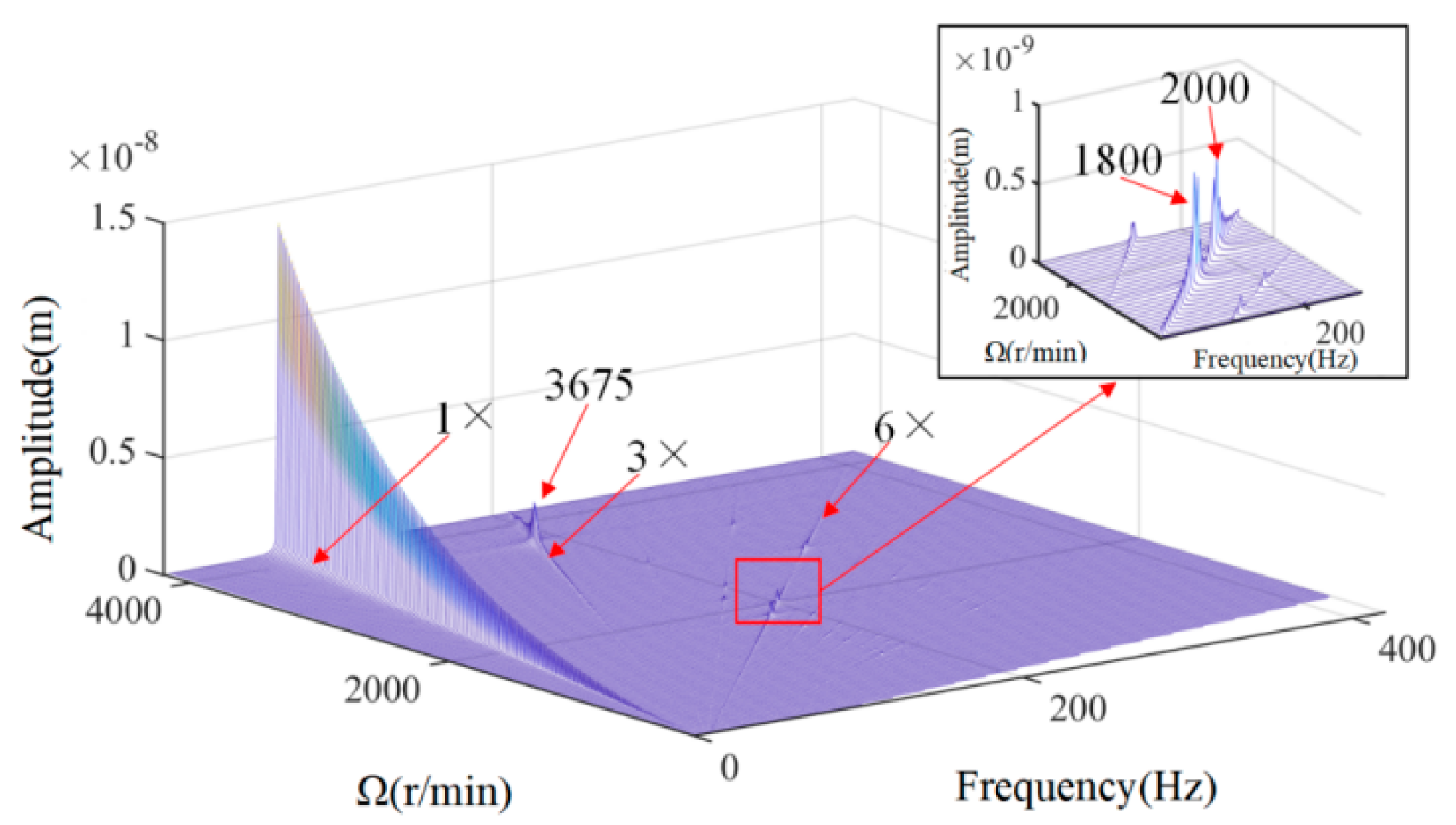
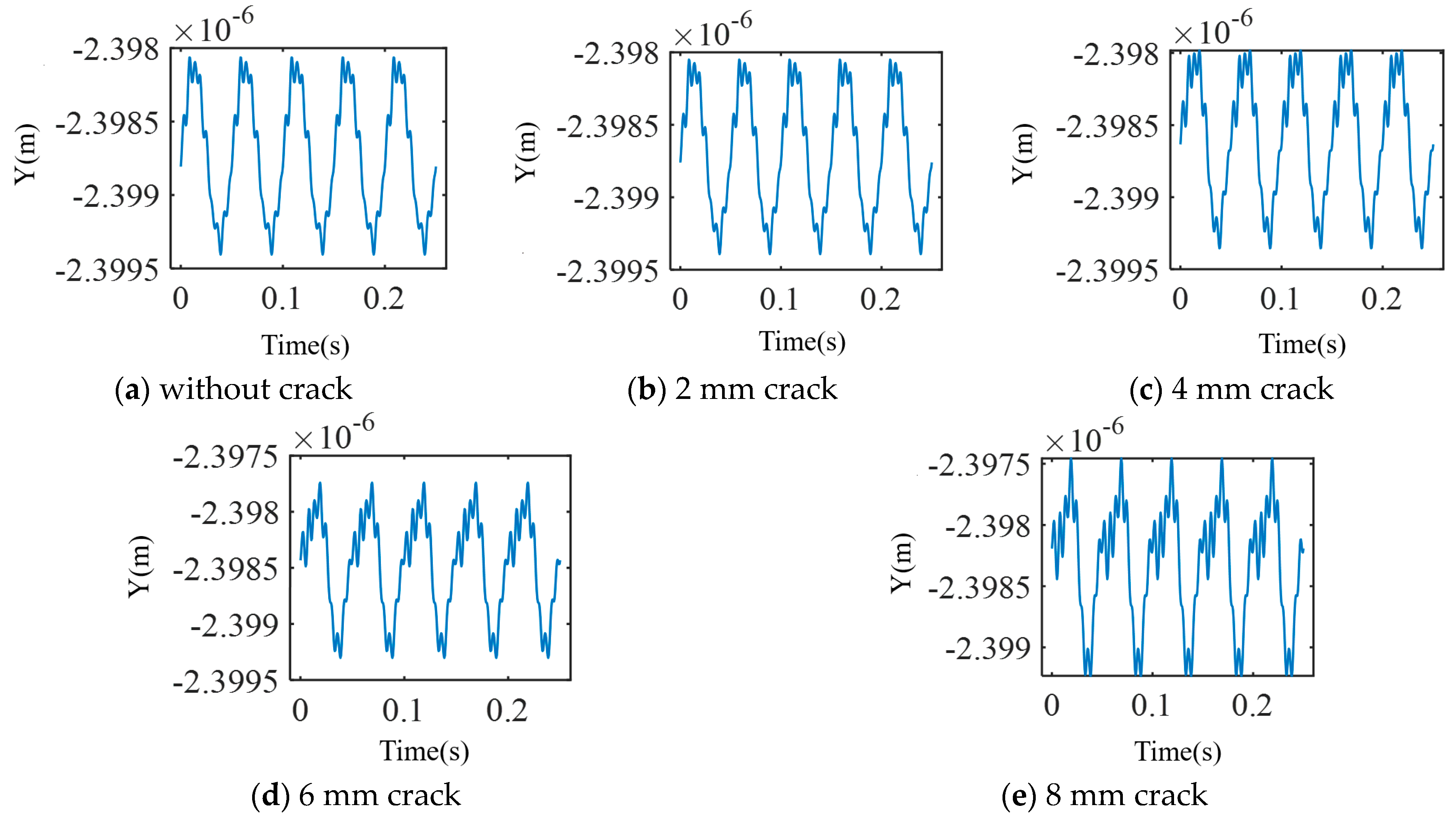
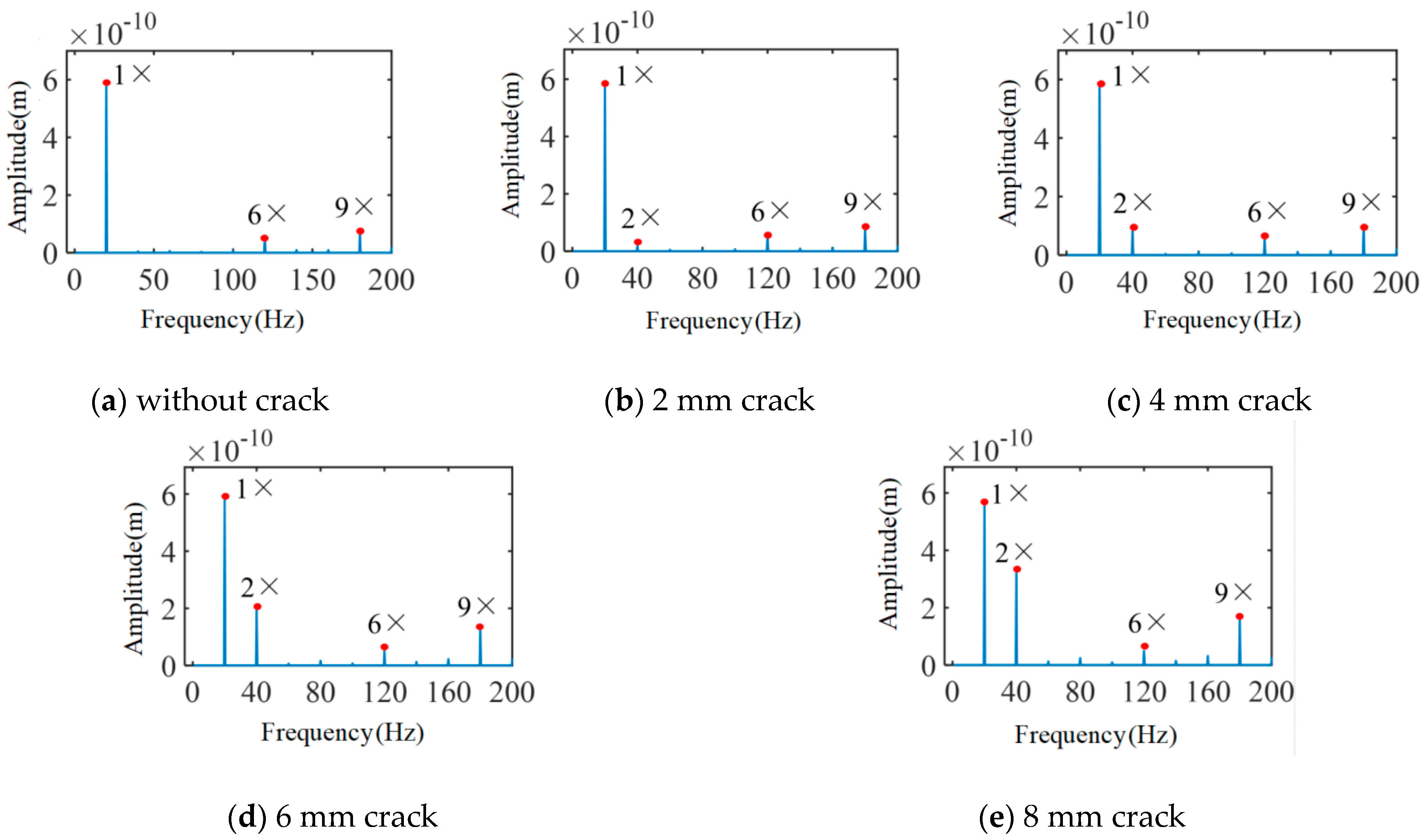
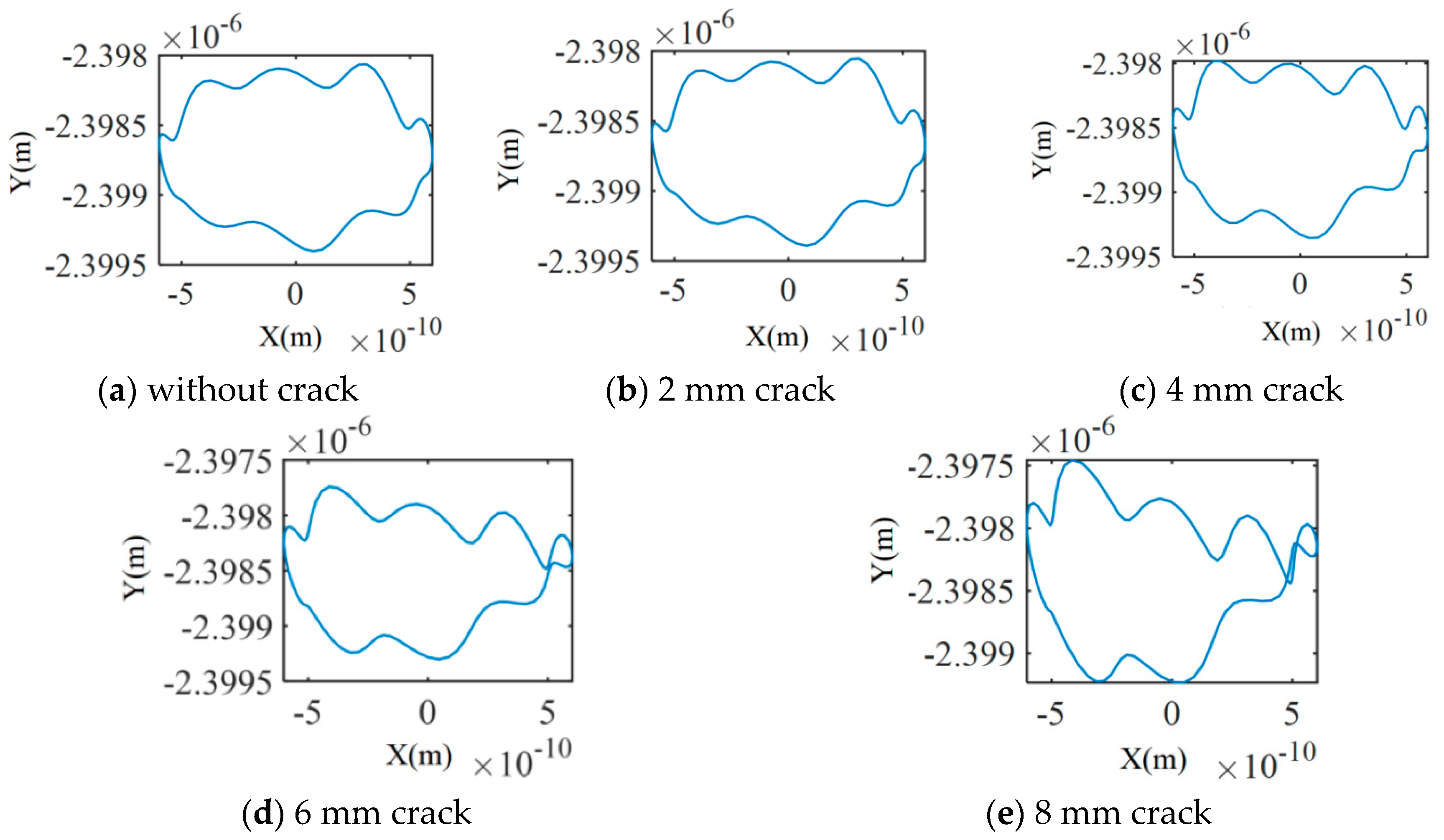
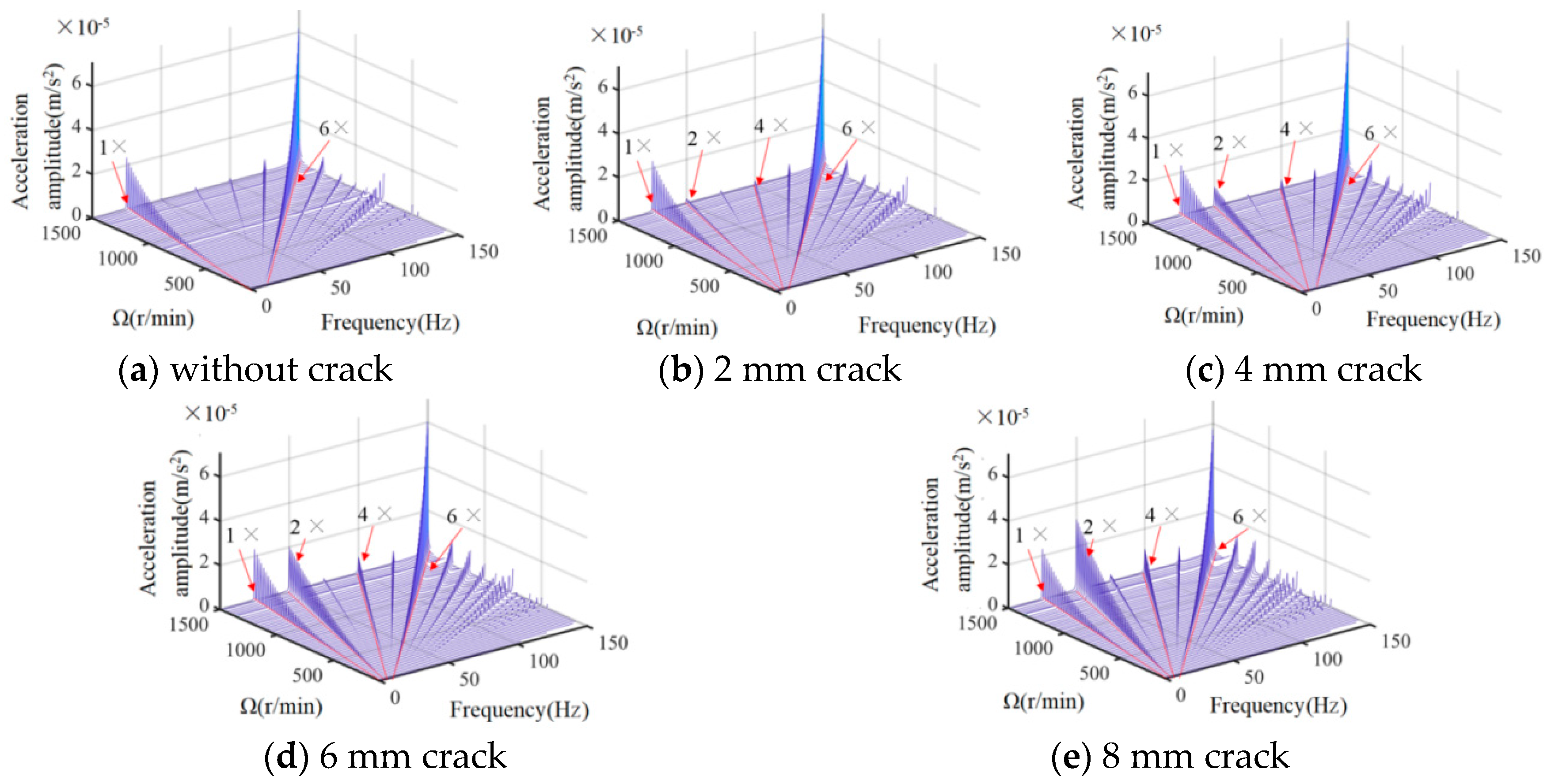
3. Results and Discussion

The system parameters used to analyze the effect of different diaphragm crack sizes on the dynamic characteristics of the diaphragm coupling shaft system are shown in

Table 1. The specific parameters of the system.

Parameters	Value
The density of the shaft, $\rho s$	7850 kg/m3
The elastic modulus of the shaft, $E$	200 Gpa
The Poisson’s ratio of the shaft, $\mu$	0.3
Bearing angular stiffness, $k_{b\theta x}$	7.1 × 104 N/m
Bearing radial stiffness, $k_{brx}$	1.15 × 108 N·m/rad
Bearing angular damping, $c_{b\theta x}$	800 N·s/rad
Bearing radial damping, $c_{brx}$	1000 N·s/m
Mass unbalance, $m_e$	1 × 10−4 kgm

. The diaphragm coupling stiffness was obtained using the finite element simulation solution, and the bearing stiffness and damping were obtained based on the KISSsoft software (2022) calculation. In this study, the stiffness of the whole system was updated before each computational step when solving the dynamic response of the shaft system using the Newmark—β method.

The amplitude–frequency characteristic plot of node 13 in the absence of crack failure is given in Figure 10. From Figure 10a, it can be seen that node 13 resonates near $\omega 1$ = 11,150 r/min, $\omega 2$ = 12,280 r/min, and $\omega 3$ = 16,980 r/min, and $\omega 1$, $\omega 2$ and $\omega 3$ are the first, second, and third critical speeds, respectively. The value of the amplitude of the shaft system is small when it is far from the critical speed, and the amplitude increases rapidly when it is close to the critical speed. Figure 10b shows the resonance phenomenon that occurs before reaching the critical speed. The first peak response speed is 1800r/min, which is about one-sixth of the first-order critical speed where resonance occurs; the second peak response speed is 2000 r/min, which is about one-sixth of the second-order critical speed where resonance occurs; and the third peak response value speed is 3675 r/min, which is about one-third of the first critical speed where resonance occurs.

The rotational speed–frequency–displacement amplitude waterfall plot in the Y-axis direction of the analyzed node 13 in the rotational speed range of 100~4200 r/min is shown in Figure 11. The displacement response spectrum mainly shows 1× rotational frequency response and a small amount of 3× and 6× rotational frequency responses. With the increase in rotational speed, the 1× rotational frequency component increases significantly, which is because the size of the unbalanced excitation applied on the rotor is proportional to the square of the rotational speed, and with the increase in rotational speed, the unbalanced excitation increases, which is reflected in the increase in the 1× rotational frequency response in the displacement spectrum. Near 3675 r/min, the 3× rpm component of the displacement spectrum rises rapidly, and the response peak occurs. At 1800 r/min and 2000 r/min, the 6× component of the displacement spectrum rises rapidly, and the response peak occurs. Combined with the results in Figure 10b, it is illustrated that the subcritical resonance phenomenon in the amplitude–frequency characteristic curves is mainly due to the rotational frequency components. Thus, 3× and 6× rotational frequency responses appear because the angular stiffness and radial stiffness of the six-hole diaphragm coupling are time-varying, with the radial stiffness presenting a three-cycle variation in one rotational cycle and the angular stiffness presenting a six-cycle variation, which introduces the 3× and 6× rotational frequency responses into the dynamic response of the shaft system.

The steady-state response of different crack lengths at the girdle waist at node 13 was obtained by taking the non-cracked diaphragm as well as the diaphragm with crack lengths at the girdle waist of 2 mm, 4 mm, 6 mm, and 8 mm at the given rotational speed of 1200 r/min, as shown in Figure 12 and Figure 13. The appearance of the crack at the girdle leads to the emergence of 2× rotational frequency responses in the displacement spectrum, and with an increase in the length of the crack at the girdle, the high rotational frequency components, such as 2× and 9× rotational frequency responses, increase significantly, making the displacement vibration time domain waveform and the axial trajectory more complex, and thus the stability of the axial system deteriorates, as shown in Figure 14. This is because the crack failure at the diaphragm girdle makes the time-varying periodicity of the angular stiffness and radial stiffness of the diaphragm coupling change, which introduces high rotational frequency components.

The waterfall plot of the rotational speed–frequency–acceleration amplitude in the Y-axis direction for node 13 is shown in Figure 15. Comparing the waterfall plots for different crack lengths at the girdle, it is found that with an increase in the crack length at the diaphragm girdle, the 2× and 4× turn-frequency responses in the spectrum increase, and the change in the 2× turn-frequency response is particularly significant. Therefore, the increase in the 2× turn-frequency responses in the acceleration spectral response can be considered an indicator of a diaphragm crack fault.

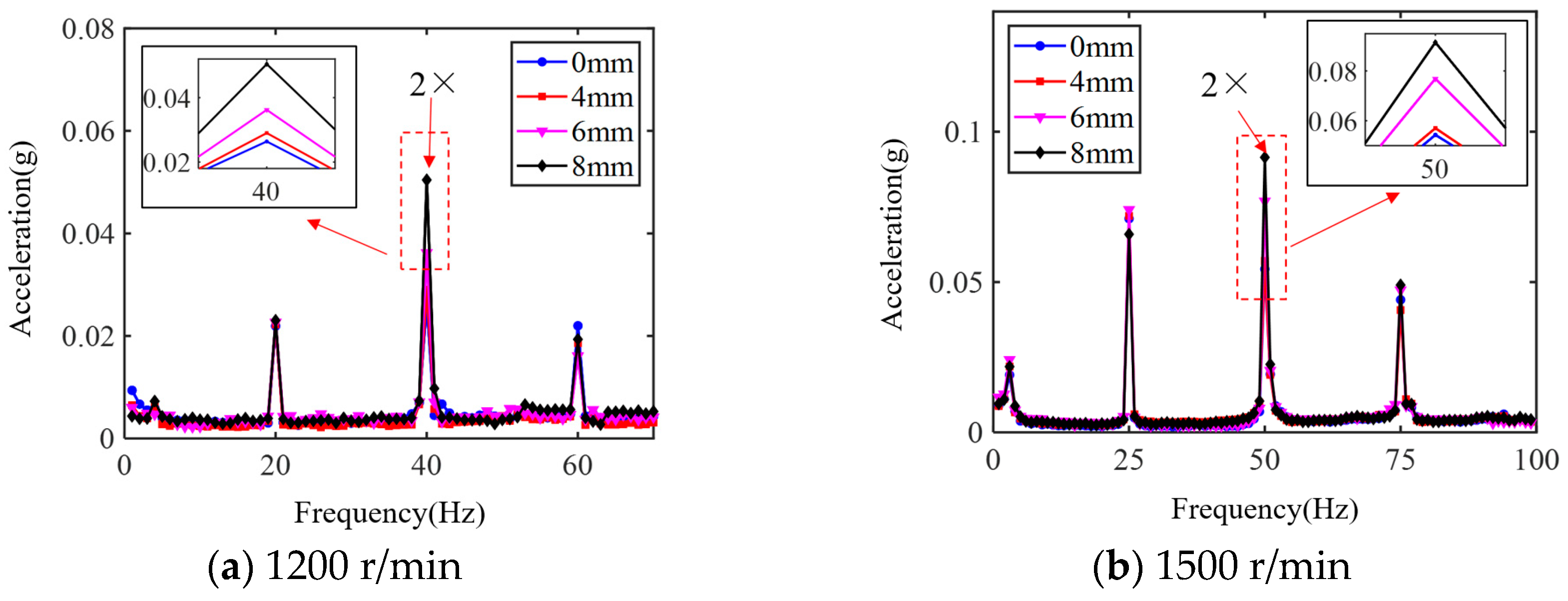
4. Experimental Verification

To simulate the diaphragm coupling cracking faults, an electrical discharge machining (EDM) cutting processing method was used to prefabricate the cracking faults at the position of the diaphragm girdle. Three kinds of diaphragm group test pieces were designed: no cracked diaphragm group, 4 mm cracked diaphragm group, and 8 mm cracked diaphragm group. The three kinds of test pieces are shown in Figure 16.

To verify the accuracy of the established shaft system dynamics model, a shaft system test rig with a diaphragm coupling was constructed, and force hammer tapping experiments were carried out on a test rig of the diaphragm coupling shaft section without cracking faults, as shown in Figure 17. To ensure the reproducibility of the results, the tests and simulations were repeated three times to obtain the results. A comparison of the first three orders of theoretical and experimental inherent frequencies is shown in

Table 2. Comparison between experimental and theoretical natural frequencies.

Order	Test Natural Frequency	Theoretical Natural Frequency	Relative Error
1	177 Hz	183 Hz	4.5%
2	201 Hz	201 Hz	5.5%
3	278 Hz	282 Hz	1.1%
4	344 Hz	328 Hz	5.4%

, in which the maximum error is 5.5%, verifying the accuracy of the established shaft system dynamic model.

To verify the effectiveness of the crack fault identification method, the diaphragm coupling shaft section was installed on the rotor test bed, and the rotor test bed and the acquisition system are shown in Figure 18. A three-way acceleration sensor was arranged on the bearing seat, and the torque was set to 400 Nm to carry out the vibration signal acquisition test at 1200 r/min and 1500 r/min rotational speeds, respectively. The sampling frequency was set to 512 Hz, and the acquisition time was set to 30 s. For the double-section diaphragm coupling in the test bench, the left end was replaced with a different diaphragm test piece, and the right end was kept unchanged with a healthy diaphragm. The acceleration signal acquisition test of different diaphragm test pieces under different test conditions was carried out separately.

The acceleration frequency domain components of the acceleration signal were determined for each second for a total of 30 s, and the values were averaged to obtain the trend of the average rotor frequency components in the acceleration spectrum with the crack length at 1200 r/min and 1500 r/min rotational speeds, as shown in Figure 19. From Figure 19a,b and Figure 20, it can be seen that the amplitude of the 2× frequency response of the acceleration response in the rotor system increases with the increase in the diaphragm crack length. This proves the effectiveness of the diaphragm crack fault identification method of the shaft system dynamics model established in this paper.

5. Conclusions

To solve the lack of a dynamic model of the diaphragm coupling with cracks, the modeling and analysis of a diaphragm coupling with cracks were carried out, and the time-varying radial and angular stiffness rates were determined. The dynamic model of the shaft system of the diaphragm coupling with cracks was further established to analyze the influence of the diaphragm crack failure on the dynamic characteristics of the shaft system, and finally, tests were carried out to verify the results. The specific conclusions and outlook drawn are as follows:

• The radial and angular stiffness rates of the diaphragm coupling have time-varying characteristics within one rotation cycle, with the radial stiffness showing 3× periodic changes and the angular stiffness showing 6× periodic changes. After the introduction of cracks at the girdle, the overall amplitude of radial and angular stiffness decreases, and the time-varying period of stiffness changes.
• The emergence of crack faults at the diaphragm girdle introduces a high transconductance component in the displacement spectrum, which makes the displacement axial trajectory complex; with the increase in crack length at the diaphragm girdle, the 2× transconductance component in the acceleration spectrum shows an obvious monotonous increasing trend, and the crack faults can be recognized by the change in the 2× transconductance component.
• This study is an exceptional starting point for further research in the field of crack failures in rotating machinery. The study of nonlinear dynamics of rotor systems with cracked diaphragm couplings is of great importance for the early detection of crack failures and for ensuring the safe operation of large rotating machinery.
• In this paper, the effect of diaphragm crack length on diaphragm coupling stiffness was only investigated for penetration cracks, but in fact, the forms of diaphragm coupling crack failures are diverse; they may be single diaphragm cracks, diagonal cracks, composite cracks, and other crack failures. Thus, the effect of different diaphragm crack failures on the stiffness value of the diaphragm couplings needs to be further investigated.
• In this paper, the effect of diaphragm cracks on the dynamic characteristics of the shaft system was investigated, but in practice, crack failures of the shaft system may also occur at the rotor shaft, bearings, and the connecting bolts of the diaphragm coupling. Thus, further research is needed to study the effects of single-crack failures and compound-crack failures on the dynamic response of the shaft system.
• When analyzing the effect of diaphragm crack faults on the dynamics of the shaft system with misalignment error, the dynamics of the shaft system at low rotational speeds was mainly studied, and the mechanism at high rotational speeds was less studied, which requires further research.