Efficient Nonlinear Model Predictive Path Tracking Control for Autonomous Vehicle: Investigating the Effects of Vehicle Dynamics Stiffness

Abstract

Motion control is one of the three core modules of autonomous driving, and nonlinear model predictive control (NMPC) has recently attracted widespread attention in the field of motion control. Vehicle dynamics equations, as a widely used model, have a significant impact on the solution efficiency of NMPC due to their stiffness. This paper first theoretically analyzes the limitations on the discretized time step caused by the stiffness of the vehicle dynamics model equations when using existing common numerical methods to solve NMPC, thereby revealing the reasons for the low computational efficiency of NMPC. Then, an A-stable controller based on the finite element orthogonal collocation method is proposed, which greatly expands the stable domain range of the numerical solution process of NMPC, thus achieving the purpose of relaxing the discretized time step restrictions and improving the real-time performance of NMPC. Finally, through CarSim 8.0/Simulink 2021a co-simulation, it is verified that the vehicle dynamics model equations are with great stiffness when the vehicle speed is low, and the proposed controller can enhance the real-time performance of NMPC. As the vehicle speed increases, the stiffness of the vehicle dynamics model equation decreases. In addition to the superior capability in addressing the integration stability issues arising from the stiffness nature of the vehicle dynamics equations, the proposed NMPC controller also demonstrates higher accuracy across a broad range of vehicle speeds.

1. Introduction

Since industry pioneers such as Google, Baidu, and Tesla launched their research projects in self-driving car technologies [1,2], autonomous driving has gained escalating interest from both academia and industry during past few years.

Motion control is one of the core technologies in autonomous driving, which is responsible for stably and precisely tracking the reference trajectories. A variety of vehicle motion control techniques have been proposed over recent years, such as Proportional-Integral-Derivative (PID) control [3], the Stanley method [4], sliding mode control [5], Linear Quadratic Regulator (LQR) [6], Model Predictive Control (MPC) [7], and data-driven methodologies [8], etc. Due to the ability to take into account system constraints in an explicit fashion and address multivariable and multi-objective challenges, MPC is extensively utilized among these methods.

Linear model predictive control (LMPC) remains mainstream in existing commercial solutions. However, it encounters inherent limitations such as an inability to incorporate nonlinear constraints [9]. The impact of nonlinear tire dynamics on trajectory tracking control for autonomous vehicles was studied in [10]. The nonlinear dynamic characteristics of vehicle drift motion was analyzed in [11] and a feedback controller was designed to ensure stable and agile vehicle behavior during sharp turns on low adhesion surfaces. A Particle Swarm Optimization-Back Propagation neural network was developed in [12] to enhance Adaptive Model Predictive Controller for autonomous vehicles, focusing on optimizing trajectory tracking under diverse road conditions through real-time adjustments of the controller parameters and tire lateral stiffness. In [13], tire-road contact state estimation methods were reviewed and constructive strategies for intelligent tire sensing systems for autonomous vehicles were proposed, focusing on real-time tire-road contact monitoring to improve vehicle dynamics control and advance autonomous driving safety.

Recently, nonlinear model predictive control (NMPC) has gained popularity in the realm of autonomous vehicle motion control due to its proficiency in precisely predicting the dynamics of nonlinear systems. Compared with LMPC, stability and efficiency are primary obstacles impeding the adoption of NMPC in autonomous vehicle systems. This manuscript is dedicated to tackling these two challenges to align with the prerequisites for the operational deployment of NMPC on actual systems [14].

Both indirect and direct approaches for NMPC involve the transformation of a continuous system into a discrete-time one. The discretization of continuous system is in essence the process of integration. Consequently, numerical integration techniques designed for Ordinary Differential Equations (ODEs) could be utilized in the discretization of continuous systems.

The explicit Euler approach has been extensively employed in MPC-based vehicle motion control studies due to its simple formulation. Falcone et al. [7] introduced an MPC strategy based on the Euler discretization for controlling vehicular active front steering systems. Similarly, Peng et al. [15] proposed a hierarchical MPC control scheme for the dynamic wheel torque management in Four-Motor In-Wheel Drive Electric Vehicles (4MIDEV) steering systems, in which the Euler method is engaged for system discretization. Zhao and Xu et al. [16] implemented the Euler technique for the discretization of their Linear Model Predictive Control (LMPC) scheme, taking into account the energy dissipation due to slippage. Satzger [17] employed an identical approach within an integrated wheel-slip management and torque blending regulatory strategy. Although the Euler method has simple form, its precision for integration is insufficient. Furthermore, the region within which the Euler method maintains integration stability is rather confined.

The zero-order hold (ZOH) method, as referenced in [9], is the most attractive discretization method in the context of linear MPC-based studies. It could attain an accurate discretization and ensures stability throughout the discretization process, which means that the outcomes of its integration are in exact correspondence with the state of the continuous system at the discrete temporal intervals. Because of these exceptional properties, the ZOH method finds broad application in vehicle motion control [18] and is similarly instrumental in the domain of stability control [19,20,21]. However, the ZOH method does not demonstrate equivalent efficacy when applied to nonlinear systems.

The fourth-order Runge–Kutta (RK4) method serves as an alternative discretization technique that is commonly utilized in the context of NMPC-based control strategies. A real-time implementation of NMPC that utilizes the RK4 method for stabilizing a vehicle at its performance limits has been put forward in [22]. Allamaa and Listov have also incorporated the RK4 method within their Nonlinear Model Predictive Control (NMPC)-based motion control framework for autonomous vehicles [23]. The torque-vectoring control system proposed by Parra also utilizes the fourth-order Runge–Kutta (RK4) method for discretization within its framework [24]. While the RK4 method enhances the precision of integration, the enlargement of the stability region is limited.

The stiffness of the ordinary differential equations that correlate to the nonlinear dynamics of vehicles will lead to integration stability problems for vehicle motion control. A common strategy to address the challenge is to utilize a kinematic model as predictive model. Numerous kinematic-based Nonlinear Model Predictive Controls (NMPCs) have been confirmed effective through validation on actual vehicles [25,26,27,28]. However, relying solely on kinematics within these systems encounters emerging challenges, since kinematics fall short in precisely capturing vehicle dynamics at high speed. When utilizing the dynamics model as the predictive model in motion control systems based on NMPC, a smaller step size was adopted in [22,24] during the discretization phase to circumvent the problem of integration stability. However, this approach may introduce the issue of real-time performance. Stability control, due to its shorter prediction horizon, is less affected by real-time issues. Conversely, path following problems in motion control require a much longer prediction horizon and thus the necessity to use a small-time step for discretization inevitably poses challenges to real-time issues. The Runge–Kutta–Chebyshev technique, as employed in [29], is leveraged to deal with the integration stability problem by broadening the region of stability in the direction of the negative real axis, yet the stable zone remains restricted.

It is evident from the existing literature that the main challenge for vehicle motion control based on NMPC lies in the delicate balance between efficiency and stability. To address this challenge, it is imperative to utilize a smaller step size during the discretization of continuous systems within the NMPC problem-solving process. Moreover, path following control necessitates the adoption of a long prediction horizon. Consequently, this leads to an escalation in the dimension of the resulting optimization problem, which in turn increases the computational burden. This paper aims to develop an NMPC controller tailored for autonomous vehicle motion control, enabling the efficient tackling of the integration stability problem while maintaining the computational efficiency.

The main contributions of this paper are as follows: (1) the stability condition and corresponding stability region for both the Euler method and the explicit RK4 method were analyzed in theory to reveal the existing integration stability issue for autonomous vehicle motion control systems that utilize NMPC. (2) The stability region of the orthogonal collocation method was evaluated in comparison with those of the Euler method and the explicit RK4 method. Furthermore, an NMPC controller based on the orthogonal collocation method was designed. (3) The proposed NMPC controller was compared with controllers based on the explicit Euler method and RK4 method to demonstrate its superior effectiveness in addressing the integration stability problem without compromising computational efficiency.

2. Vehicle Dynamics

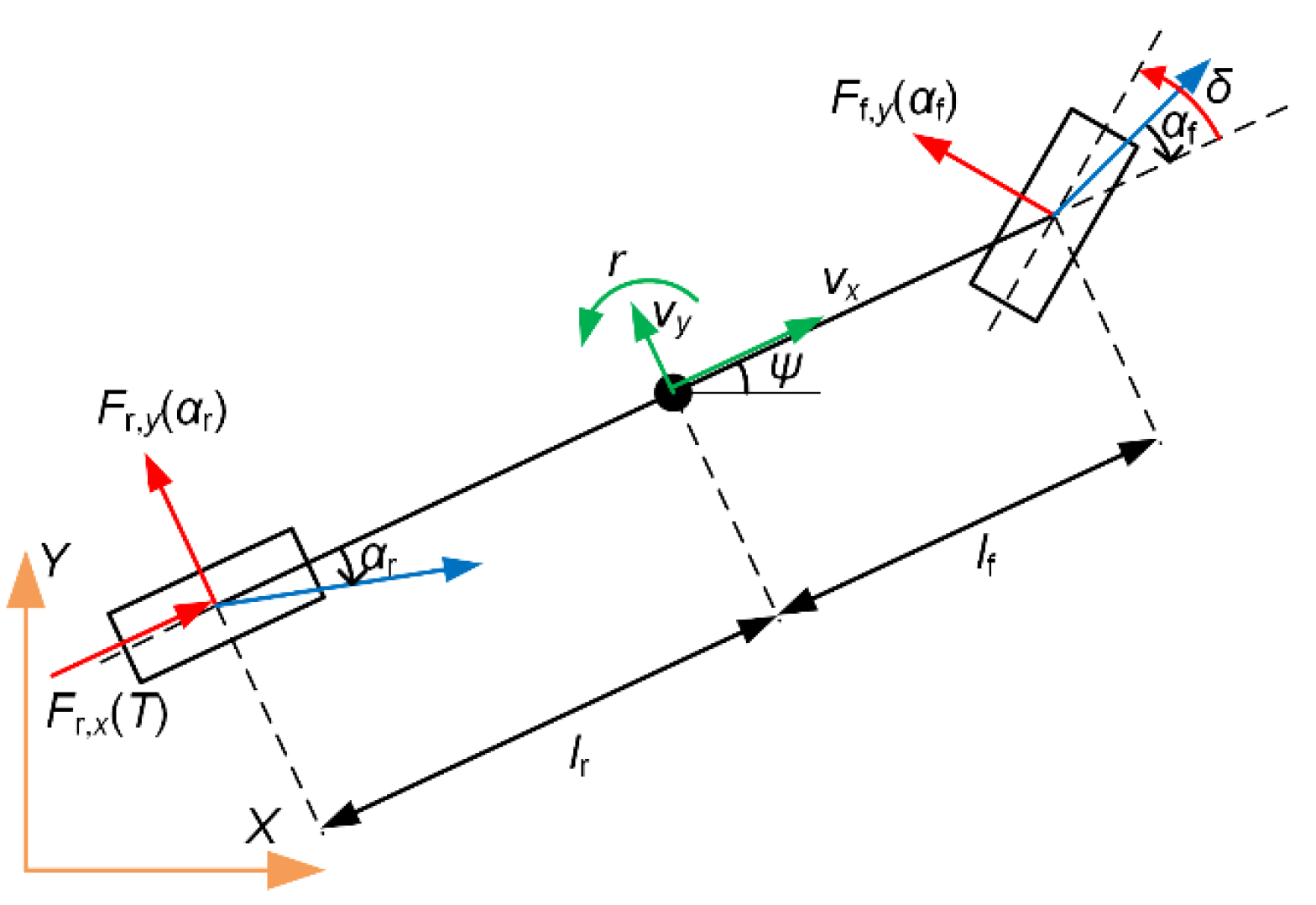
In this section, vehicle dynamics and the characteristics of the tires are described in detail to facilitate the simulation and the formulation of control strategies. As depicted in Figure 1, a simplified bicycle model for vehicle dynamics comprising five system states was established, which was achieved by aggregating the two front and two rear wheels at the geometric center of their respective axles. This model primarily considers lateral and yaw movements, with the assumption that the velocity in the longitudinal direction remains unchanged. The model utilized was formulated based on the following hypotheses: (i) the vehicle travels on a uniformly flat surface, (ii) the Ackermann steering relation is ignored and the difference in wheel angles between the left and right sides is not taken into account, (iii) the load transfer due to pitching and compliance of the suspension can be negligible. The resulting model was characterized by a set of differential equations, which are formulated as follows:

$$\begin{array}{l}\dot{X}=v_x\cos \left(\psi \right)-v_y\sin \left(\psi \right),\\ \dot{Y}=v_x\sin \left(\psi \right)+v_y\cos \left(\psi \right),\\ \dot{\psi }=r,\\ {\dot{v}}_y={\displaystyle \frac{1}{m}}\left(F_{r,y}+F_{f,y}\cos \delta -m{v}_{x}r\right),\\ \dot{r}={\displaystyle \frac{1}{I_z}}\left(F_{f,y}{l}_f\cos \delta -F_{r,y}{l}_r\right),\end{array}$$

(1)

where $m$ denotes the mass of the vehicle, $I_z$ signifies the moment of inertia around the vertical $\left(Z\right)$ axis, and $l_f$ and $l_r$ are the distances from the center of gravity (CoG) to the front and rear wheels, respectively. The state vector x $={\left[v_y r \psi Y X\right]}^T$ is composed of the coordinates of the center of gravity (COG), denoted as X and Y, the orientation angle of the vehicle with respect to the inertial reference frame $\psi$, the lateral velocity of the vehicle at the COG $v_y$, and the yaw rate r. The control input, denoted as $u=\delta$, is the steering angle of the front wheels. As a result, the dynamics of the continuous-time vehicle system can be expressed in a condensed form $\dot{\mathit{x}}=f\left(\mathit{x},\mathit{u}\right)$.

The tire forces play a pivotal role in the interaction between the automobile and the pavement, acting as the primary external influences on the vehicle’s maneuverability with the exception of aerodynamic forces. The pronounced nonlinear characteristics in vehicle dynamics, particularly at high speeds, are predominantly manifested through the complex behavior of tire forces. In this study, the Dugoff tire model [30] was employed to characterize the tire-road contact forces and the lateral tire forces could be expressed as:

$$F_y=\left\{\begin{array}{c}-C_{\alpha }\mathit{tan}\alpha ,\left|\mathit{tan}\alpha \right|<\mu F_z^N/\left(2C_{\alpha }\right)\\ sign\left(\alpha \right)\mu F_z^N\left[1-\mu F_z^N/\left(4C_{\alpha }\left|\mathit{tan}\alpha \right|\right)\right],else\end{array}\right.,$$

(2)

where $F_z^N$ signifies the nominal vertical load exerted on the tire (3), $\alpha$ represents the tire sideslip angle (4), $C_{\alpha }$ denotes the lateral stiffness coefficient (5), and $\mu$ symbolizes the friction coefficient between tire and the road surface.

$$F_{zf}={\displaystyle \frac{l_{r}mg}{2\left(l_f+l_r\right)}},F_{zr}={\displaystyle \frac{l_{f}mg}{2\left(l_f+l_r\right)}},$$

(3)

$$\begin{array}{l}{\alpha }_f=\arctan \left({\displaystyle \frac{\dot{\psi }{l}_f+v_y}{v_x}}\right)-\delta \approx {\displaystyle \frac{\dot{\psi }{l}_f+v_y}{v_x}}-\delta \\ {\alpha }_r=\arctan \left({\displaystyle \frac{\dot{\psi }{l}_r-v_y}{v_x}}\right)\approx {\displaystyle \frac{\dot{\psi }{l}_r-v_y}{v_x}}\end{array},$$

(4)

$$C_{\alpha }\left(F_z\right)={\displaystyle \frac{F_z}{F_z^N}}\left\{2C_{\alpha }\left(F_z^N\right)-{\displaystyle \frac{1}{2}}{C}_{\alpha }\left(2F_z^N\right)-\left[2C_{\alpha }\left(F_z^N\right)-{\displaystyle \frac{1}{2}}{C}_{\alpha }\left(2F_z^N\right)\right]{\displaystyle \frac{F_z}{F_z^N}}\right\}.$$

(5)

The related vehicle and tire parameters are shown in

Table 1. Vehicle parameters.

Symbol	Definition	Value (Unit)
m	Vehicle total mass	1650 (kg)
$I_z$	Vehicle yaw inertial	3234 (kg·m2)
$l_f$	Distance from CG to front axle	1.4 (m)
$l_r$	Distance from CG to rear axle	1.65 (m)
$C_f$	Cornering stiffness of front tires	$66,900\times 2$ (N/rad)
$C_r$	Cornering stiffness of rear tires	$62,700\times 2$ (N/rad)

, which will be used in the subsequent sections.

3. NMPC Formulation

This section begins with a detailed description of the general formulation for an optimal control problem. Subsequently, the specific design methodology for autonomous driving trajectory tracking based on nonlinear model predictive control (NMPC) is introduced. Finally, this section provides a theoretical analysis of the integral stability issues inherent in motion control problems based on NMPC.

3.1. Nonlinear Optimal Control Problem Formulation

Nonlinear Model Predictive Control (NMPC) involves the iterative solution of an online Nonlinear Optimal Control Problem (NOCP), taking into account the predicted future dynamics of the system. This prediction is facilitated by a high-fidelity model, which is essential for maintaining the system output in accordance with reference trajectories. The NMPC approach yields a feasible control law by minimizing a pre-designed cost function, subject to a suite of constraints. The general formulation of an NOCP can be articulated as follows:

$$\begin{array}{l}Obj:\min :J=E\left(x(t_f)\right)+{\displaystyle {\int }_{t_0}^{t_f}L\left(x\left(t\right),u\left(t\right),t\right)dt}\\ s.t.\left.\begin{array}{l}\dot{x}\left(t\right)=f\left(x\left(t\right),u\left(t\right),t\right)\\ x\left(t_0\right)=x_0\\ g\left(x\left(t\right),u\left(t\right),t\right)\le 0\\ x_{\min }\le x\left(t\right)\le x_{\max }\\ u_{\min }\le u\left(t\right)\le u_{\max }\end{array}\right\}\end{array},$$

(6)

where, t denotes time, with t₀ and t_f representing the initial and final time instances, respectively. The state variable vector is represented by $x\left(t\right)\in {\mathrm{R}}^{N_x}$, the control variable vector by $u\left(t\right)\in {\mathrm{R}}^{N_u}$ and the initial state vector by $x_o$. The performance index, denoted by J, encompasses both the Mayer term $E(·):{\mathrm{R}}^{{\mathrm{N}}_{\mathrm{x}}}\to \mathrm{R}$ and the Lagrange term $L(·):{\mathrm{R}}^{{\mathrm{N}}_{\mathrm{x}}}\times {\mathrm{R}}^{{\mathrm{N}}_{\mathrm{u}}}\times [t_0,t_{\mathrm{f}}]\to \mathrm{R}$. Additionally, $g(·)$ signifies the state constraints, and $x_{\min },u_{\min ,}{x}_{\max },u_{\max }$ represent the lower and upper bounds on the control variables, respectively.

3.2. Path Tracking Control Strategy

The objective of path tracking control for autonomous vehicles is to ensure that the vehicle adheres precisely to a predefined reference trajectory, characterized by the heading angle $\psi$ and the lateral displacement Y. In Section 2, state variables are defined as $\mathit{x}={\left[v_y r \psi Y X\right]}^{\mathrm{T}}$ and control variable is designated as the front steering angle $u=\delta$. The output map, represented by p, serves as the functional relationship that projects the state vector x onto the observable outputs.

$$\mathit{\eta }=p\left(\mathit{x}\right)=\left[\begin{array}{l}\begin{array}{ccccc}0& 0& 0& 1& 0\end{array}\\ \begin{array}{ccccc}0& 0& 1& 0& 0\end{array}\end{array}\right]\mathit{x},$$

(7)

where $\mathit{\eta }={\left[\begin{array}{cc}Y& \psi \end{array}\right]}^T$, encapsulating lateral displacement Y and the yaw angle $\psi$.

Then, the objective function, which takes into account the reference signal ${\eta }_{ref}={\left[\begin{array}{cc}{Y}_{ref}& {\psi }_{ref}\end{array}\right]}^{\mathrm{T}}$ could be expressed as follows.

$$J={‖\begin{array}{c}Y-Y_{ref}\\ \phi -{\phi }_{ref}\end{array}‖}_{\mathrm{Q}}^2+{‖\mathit{\Delta }\mathit{u}‖}_{\mathrm{R}}^2+\rho {\epsilon }^2,$$

(8)

where $\mathit{Q}=\mathrm{diag}(Q_1,Q_2)$ are weights assigned to lateral error. The matrix R signifies the weight attributed to the control increment, the term $\epsilon$ denotes the relaxation factor, which is crucial for the optimization process and $\rho$ serves as the weight factor for the slack variable, ensuring the robustness of the solution.

The objective function is composed of several terms, each serving a distinct purpose. The first term encapsulates the sum of the squares of the lateral displacement error and the heading error, quantifying the system’s deviation from the reference path during tracking. The second term, which is the sum of the squares of the control increment quantities, emphasizes the need to minimize control increments under normal conditions to prevent abrupt maneuvers. The third term introduces slack variables to ensure that the solvability of the optimization problem.

Within the domain of vehicular control systems, it is essential to impose constraints on the control quantities to guarantee the operational integrity and safety of the vehicle. As previously discussed, the control input for the vehicle is selected to be the front wheel steering angle, denoted by $\delta$. Taking into account the mechanical properties of the steering system, it is imperative that the variation in the front wheel steering angle is kept within reasonable limits. Consequently, the permissible range of the front wheel steering angle and the increment of this angle are both subject to constraints.

$$\begin{gathered} u_{min}\le u\le u_{max}, \\ {\mathit{\Delta }u}_{min}\le \mathit{\Delta }u\le {\mathit{\Delta }u}_{max}, \end{gathered}$$

(9)

3.3. Integration Stability Analysis

Whether employing direct or indirect optimal control techniques, the process of discretizing a dynamic system relies heavily on the application of integrators. Consequently, the stability of these integrators is critical for guaranteeing the reliability and precision of the resulting control strategies. An integrator that exhibits instability is incapable of providing accurate predictions regarding the system’s future state, thereby compromising the tracking accuracy. Furthermore, the stability of the entire closed-loop system is also jeopardized. Drawing upon the principles of integration stability theory, this analysis delves into the integration stability issues encountered in the lateral motion control of vehicles.

As previously outlined, vehicle dynamics represented by ordinary differential equations (ODEs) are included in NMPC-based vehicle motion control problems. The stiffness inherent in these ODE-formulated vehicle dynamics equations exerts a significant influence on the integration stability of the control system when solving NMPC problems. To further the understanding of this stiffness, a rigorous analysis leveraging the Dahlquist test equation [31] is hereby presented.

$$\dot{y}=\lambda y,y\left(0\right)=y_0,$$

(10)

when any single-step integrator is substituted into the above equation, the resulting discrete relationship is derived as follows,

$$y_{k+1}=R\left(h\lambda \right)y_k,$$

(11)

where h denotes the integration step size. Set $z=h\lambda$, the stability function could be represented by $R\left(z\right)$. While the Dahlquist test equations are inherently formulated as linear systems, their significance extends to the analysis of general nonlinear systems as well. This is because nonlinear systems $\dot{x}=f\left(x\right)$ could be linearized around specific state $x=x_0$. The Jacobian matrix for resulting linearized systems could be further converted to diagonal or Jordan form. Consequently, the parameters $\lambda$ in Dahlquist test equations correspond directly to the eigenvalues of the system’s characteristic matrix, which in turn determine the stability properties of the numerical integration method.

Subsequently, the integration stability condition for the numerical integration methods is introduced.

Theorem 1

([31]). The numerical integration method is stable if any eigenvalue of Jacobian matrix of the system satisfies |R(z)| ≤ 1.

In conjunction with Equation (11), the following relationship needs to be satisfied in order to avoid $y_k$ divergence.

$$\left|R\left(h\lambda \right)\right|\le 1,$$

(12)

When employing the explicit Euler method to discretize continuous systems which utilizes the forward difference to approximate the derivative, the following equation can be derived.

$$y_{k+1}=\left(1+h\lambda \right)y_k=\left(1+z\right)y_k,$$

(13)

Thus, the stability function associated with the explicit Euler method is given by $R_e\left(z\right)=1+z$.

While explicit Runge–Kutta methods of the same order may exhibit variations in their specific computational procedures, they are characterized by having identical stability functions. The stability function for the explicit Runge–Kutta method of order $p$ is presented as follows:

$$R_{\mathit{rk}}\left(z\right)=1+z+{\displaystyle \frac{z^2}{2!}}+{\displaystyle \frac{z^3}{3!}}+\mathit{\cdots }+{\displaystyle \frac{z^p}{p!}},$$

(14)

As demonstrated in proceeding analyses, stability functions of numerical integrators are related to both the eigenvalues of systems’ Jacobian Matrices and the integration step size.

For specific vehicle motion control problem based on NMPC, the Jacobian matrix corresponding to vehicle dynamics state equations is,

$$\mathrm{A}=\left[\begin{array}{ccccc}{\displaystyle \frac{\sum {\tilde{C}}_{\alpha i}\frac{\partial {\alpha }_i}{\partial v_y}}{m}}& {\displaystyle \frac{\sum {\tilde{C}}_{\alpha i}\frac{\partial {\alpha }_i}{\partial r}}{m}}-v_x& 0& 0& 0\\ {\displaystyle \frac{\sum l_i{\tilde{C}}_{\alpha i}\frac{\partial {\alpha }_i}{\partial v_y}}{I_z}}& {\displaystyle \frac{\sum l_i{\tilde{C}}_{\alpha i}\frac{\partial {\alpha }_i}{\partial r}}{I_z}}& 0& 0& 0\\ 0& 1& 0& 0& 0\\ \mathit{cos}\phi & 0& v_x\mathit{cos}\phi -v_y\mathit{sin}\phi & 0& 0\\ -\mathit{sin}\phi & 0& -v_x\mathit{sin}\phi -v_{\mathrm{y}}\mathit{cos}\phi & 0& 0\end{array}\right],$$

(15)

where $\mathrm{i}=\mathrm{f},\mathrm{r}$, ${\displaystyle \frac{\partial {\mathsf{\alpha }}_{\mathrm{i}}}{\partial {\mathrm{v}}_{\mathrm{y}}}}={\displaystyle \frac{1}{{\mathrm{v}}_{\mathrm{x}}}}$, ${\displaystyle \frac{\partial {\mathsf{\alpha }}_{\mathrm{f}}}{\partial \mathrm{r}}}={\displaystyle \frac{{\mathrm{l}}_{\mathrm{f}}}{{\mathrm{v}}_{\mathrm{x}}}}$, ${\displaystyle \frac{\partial {\mathsf{\alpha }}_{\mathrm{r}}}{\partial \mathrm{r}}}=-{\displaystyle \frac{{\mathrm{l}}_{\mathrm{r}}}{{\mathrm{v}}_{\mathrm{x}}}}$, ${\stackrel{\mathrm{~}}{\mathrm{C}}}_{\mathsf{\alpha }\mathrm{i}}={\displaystyle \frac{\partial {\mathrm{F}}_{\mathrm{yi}}}{\partial \tan {\mathsf{\alpha }}_{\mathrm{i}}}}{\displaystyle \frac{\partial \tan {\mathsf{\alpha }}_{\mathrm{i}}}{\partial {\mathsf{\alpha }}_{\mathrm{i}}}}=\left\{\begin{array}{c}-{\mathrm{C}}_{\mathsf{\alpha }},\left|\tan \mathsf{\alpha }\right|<\mathsf{\mu }{\mathrm{F}}_{\mathrm{z}}^{\mathrm{N}}/\left(2{\mathrm{C}}_{\mathsf{\alpha }}\right)\\ {\displaystyle \frac{\mathrm{sign}\left(\mathsf{\alpha }\right){\left(\mathsf{\mu }{\mathrm{F}}_{\mathrm{z}}^{\mathrm{N}}\right)}^2}{4{\mathrm{C}}_{\mathsf{\alpha }}{\left(\tan \mathsf{\alpha }\right)}^2}},\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right.$.

The Jacobian matrix of the state equations possesses two distinct nonzero eigenvalues, which are

$$\begin{gathered} {\lambda }_1={\displaystyle \frac{\left(A_{11}+A_{22}\right)-{\left[{\left(A_{11}-A_{22}\right)}^2+4A_{12}{A}_{21}\right]}^{1/2}}{2}}, \\ {\lambda }_2={\displaystyle \frac{\left(A_{11}+A_{22}\right)+{\left[{\left(A_{11}-A_{22}\right)}^2+4A_{12}{A}_{21}\right]}^{1/2}}{2}}, \end{gathered}$$

(16)

Further analysis of Equation (16) indicates that the eigenvalues are correlated with the vehicle’s speed and the cornering stiffness of the tires. The eigenvalues, as indicated by their relationship, increase with lower vehicle speeds and higher tire stiffnesses. Figure 2 illustrates the spectral Radii of the vehicle dynamics model at a vehicle speed of 1 m/s and 0.2 m/s, indicating the maximum eigenvalue magnitude of the Jacobian matrix associated with the state equation. This spectral radius is an indication of change rates for the corresponding system states, which confers a stiff nature upon the system.

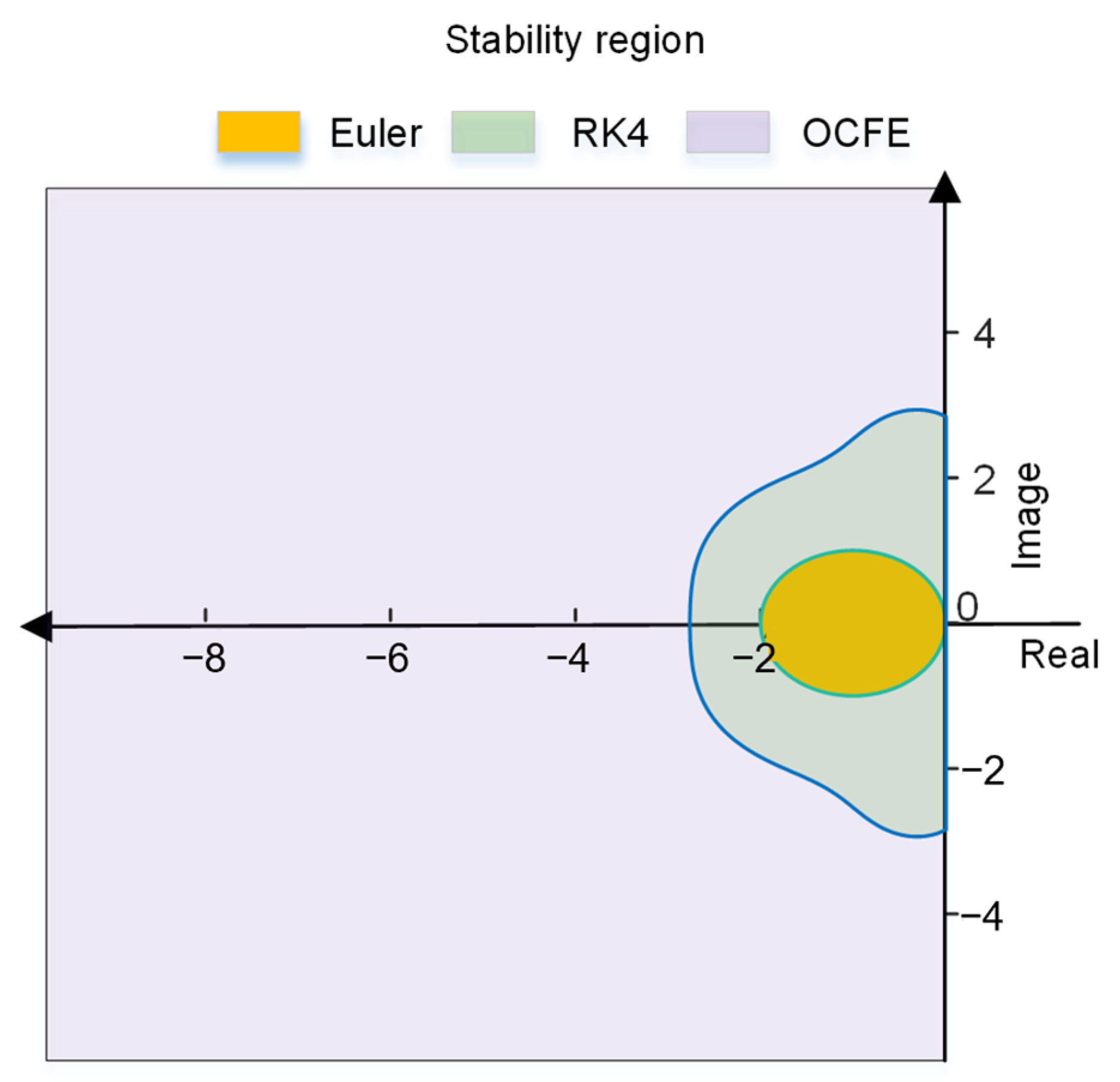
To maintain integration stability, it is necessary to set limits on the length of integration step size referring to the stability condition and the limits vary for different integration method. As depicted in Figure 2, the spectral radius exceeds 180 at a vehicle speed of 1 m/s when the tire stiffness exceeds 150,000 N/m. When employing the explicit Euler method, the integration step size must be constrained to a maximum of 11 milliseconds to ensure that the stability function of the method complies with the criteria established in Equation (12). Similarly, when utilizing the explicit fourth-order Runge–Kutta method, the step size must not surpass 16 milliseconds to maintain the method’s stability criteria. That is, a relatively small integration step size is imperative to ensure the stability of the numerical integration process, which inevitably increase the online computing burden and can degrade the system’s real-time performance.

4. Orthogonal Collocation on Finite Elements Method

Integration stability necessitates the adoption of a small step size when employing both the Euler discretization method and the explicit fourth-order Runge–Kutta method. However, to ensure the stability of the integrator as a prerequisite, a comparatively larger step size is typically favored in the implementation of NMPC integration because it can enhance computational efficiency which is critical for the performance of NMPC. In this section, orthogonal collocation method is introduced, which is an A-stable method [32] and allows for a relaxation of the constraints on integration step size.

Orthogonal collocation method is a member of the weighted residual methods, which approximate the solutions of differential equations through a linear combination of trial functions [33]. When integrated with the finite element approach, the entire horizon is segmented, and the orthogonal collocation technique is applied within each individual element.

4.1. The Discretization of State Variables

As illustrated in Figure 3, the time domain is partitioned into $N_{NTE}$ elements. Within the i-th time element, defined by the interval $\left[t^{i-1},t^i\right]$, the state is approximated using the nodal approximation given by Equation (9). This approximation employs Lagrange interpolation polynomials, as described by Equation (8), based on a dimensionless time coordinate $\tau$.

According to the principles outlined in orthogonal collocation [34], the discrete points within the method can be categorized into two distinct groups: collocated points and non-collocated points. The collocated points coincide with the zeros of the orthogonal polynomials, whereas the non-collocated points are typically situated at the endpoints of the time subintervals. Let $N_t$ denote the number of collocation points for state variables within each time element. Considering the i-th time subinterval $\left[t^{i-1},t^i\right]$ as an exemplar, the set comprises $N_t+1$ discrete points, which include a non-collocated point at $t^i$ and $N_t$ collocated points. This configuration is adopted when employing Legendre–Gauss–Radau (LGR) collocation points.

$$\tau ={\displaystyle \frac{t-t^{i-1}}{t^i-t^{i-1}}},t\in [t^{i-1},t^i],$$

(17)

$$l_j\left(\tau \right)={\prod }_{k=0,k\ne j}^{N_t}{\displaystyle \frac{\tau -{\tau }_k}{{\tau }_j-{\tau }_k}},$$

(18)

$${\mathit{x}}^{\mathit{i}}\left(t\right)={\sum }_{j=0}^{N_t}{l}_j\left(\tau \right)·{\mathit{x}}^{i,j}\left(t\right),$$

(19)

where, $t^{NTE}=t_f$; $l_j$ represents the Lagrange basis polynomial. The set ${\left\{{\tau }_k\right\}}_{k=1}^{N_t}$ consists of orthogonal collocation points, with ${\tau }_0$ being the initial point. The state vector ${\mathit{x}}^{i,j}\left(t\right)$ is defined at the collocation point ${\tau }_j$ within the i-th time subinterval. Here, $j$ ranges from 0 to $N_t$ and $i$ ranges from 1 to NTE.

4.2. The Discretization of Control Variables

Control variables are discretized within the time domain in a manner analogous to that of state variables. Let $N_u$ denote the number of collocation points allocated for control variables within each time element. It is important to note that, due to the potential discontinuity of control actions at the boundaries of these elements, the inclusion of a non-collocated point is typically precluded

$$l_m\left(\tau \right)={\prod }_{k=1,k\ne m}^{N_u}{\displaystyle \frac{\tau -{\tau }_k}{{\tau }_j-{\tau }_k}},$$

(20)

$${\mathit{u}}^{\mathit{n}}\left(t\right)={\sum }_{m=0}^{N_u}{l}_m\left(\tau \right)·{\mathit{u}}^{n,m}\left(t\right),$$

(21)

where $n=1,2,\cdots ,NTE$.

More specifically, a piecewise-constant control strategy can be realized by setting $N_u=1$, whereas a piecewise-linear control approach is achieved when $N_u=2$.

4.3. Orthogonal Collocation Equations

The first-order derivatives of the Lagrange interpolating polynomials, commonly referred to as differential matrices, are presented in Equation (20). This expression illustrates that the differential matrices are solely dependent on the positions of the discrete points ${\left\{{\tau }_k\right\}}_{k=1}^{N_t}$, suggesting that these matrices can be precomputed offline, thereby reducing the computational load during the online phase.

$$a_{r,s}={\left.{\displaystyle \frac{d{l}_s\left(\tau \right)}{d\tau }}\right|}_{\tau ={\tau }_r},r,s=0,1,\cdots ,N,$$

(22)

Consequently, the first-order derivatives of the state variables, as detailed in Equation (21), are computed by differentiating the trial function presented in Equation (19).

$${\left.{\displaystyle \frac{d{x}^i}{dt}}\right|}_{t=t^j}={\displaystyle \frac{1}{\Delta t^i}}{\displaystyle \sum _{k=0}^{N_t}{a}_{j,k}{\mathit{x}}^{i,k}\left({\tau }_k\right)},i=1,2,\cdots ,NTE;j=0,1,\cdots N_t,$$

(23)

where $a_{j.k}$ represents the differential matrix computed at the discrete temporal point ${\tau }_j$ and ${\mathit{\Delta }t}^i=t^i-t^{i-1}$.

Hence, the original constraints of the ordinary differential equations (ODEs) can be discretized into a sequence of algebraic equations derived from the orthogonal collocation method, which are denoted by

$$F\left({\mathit{x}}^{i,j},u_m^i,t_j^i\right)=0,$$

(24)

where $i=1,2\cdots NTE,j=0,1,\cdots N_t,m=0,1,\cdots N_u$.

4.4. Initial Conditions and Continuity Conditions

Assuming that ${\mathit{x}}_0$ represents the state value at initial time $t_0$, then the initial condition is defined as follows:

$${\mathit{x}}^{0,0}={\mathit{x}}_0,$$

(25)

Furthermore, to ensure the attachment of time elements, appropriate continuity conditions must be imposed. With the selection of Legendre–Gauss–Radau (LGR) points, the final collocation point is precisely positioned at the right endpoint, which results in

$${\mathit{x}}^{i+1,0}={\mathit{x}}^{i,N_t},i=1,2,\cdots ,NTE,$$

(26)

4.5. Stability Region

As mentioned at the beginning, orthogonal collocation method is A-stable, whose stability domain satisfies $S\supset C^{-}=\left\{z;\mathrm{R}\mathrm{E}\left(z\right)\le 0\right\}$ referring to [31]. If the Legendre-Gauss–Radau (LGR) collocation points are selected and the number of collocation points is specified as three, the stability function of the orthogonal collocation method can also be articulated as follows by linearizing the nonlinear system and applying to the Dahlquist equation:

$$R\left(z\right)={\displaystyle \frac{1+2z/5+z^2/20}{1-3z/5+3z^2/20-z^3/60}},$$

(27)

Substituting Equation (25) into (12) to satisfy the stability condition, the stable region for orthogonal collocation method is illustrated in Figure 4, alongside the stability regions for the explicit Euler method and the fourth-order Runge–Kutta (RK4) method. The x-y plane in the figure represents the complex plane of variable z.

The stable region of each method encompasses those areas within the complex plane where the method yields solutions that are both stable and accurate. It is evident that the stability region of the orthogonal collocation method is significantly expanded relative to that of the explicit Euler method and RK4 method. Furthermore, the orthogonal collocation method imposes no restrictions on the integration step size h, attributable to the entire left half-plane comprising its stability region. This characteristic renders the orthogonal collocation method particularly advantageous for addressing integration stability issues in stiff systems, as opposed to the explicit Euler and fourth-order Runge–Kutta (RK4) methods, which typically necessitate smaller step sizes to maintain stability.

5. Simulation and Discussions

In this section, the efficacy of the proposed control algorithm is rigorously evaluated within the CarSim/Simulink co-simulation environment, under the U-Turn maneuvers at different vehicle speeds. The open-source optimization framework CasADi is utilized to address the optimization problem [35]. For the sake of clarity in illustration, controllers that implement the control algorithm introduced in this study are designated as OCFE controllers. Controllers discretized based on the Euler discretization method are categorized as Euler controllers, while those founded on the fourth-order Runge–Kutta method are identified as RK4 controllers.

5.1. Simulation of Low-Speed U-Turn Maneuver

The U-turn reference path is defined by the following equations:

$$\begin{array}{c}{X}_{ref}\left(Y\right)=50+\sqrt{2R_{road}Y-Y^2},\\ {\phi }_{ref}=\left\{\begin{array}{c}{cot}^{-1}{\displaystyle \frac{R_{road}-Y}{50+\sqrt{2R_{road}Y-Y^2}}},\mathrm{if}Y\le R_{road}\\ \pi -{cot}^{-1}{\displaystyle \frac{{Y-R}_{road}}{50+\sqrt{2R_{road}Y-Y^2}}},ifY\ge R_{road}\end{array}\right.,\end{array}$$

(28)

where $X_{ref}$, $Y_{ref}$, ${\phi }_{ref}$ represent the position and heading angle of the reference path in global coordinate frame, respectively.

Under the low-speed condition specified, the vehicle’s longitudinal driving speed is set to $v_x=1.0\mathrm{m}/\mathrm{s}$. The road surface adhesion coefficient is denoted by $\mu =0.85$. Initially, the vehicle travels in a straight line for a distance of 5 m before commencing a U-Turn maneuver with a designated turning radius $R_{\mathrm{road}}=6\mathrm{m}$.

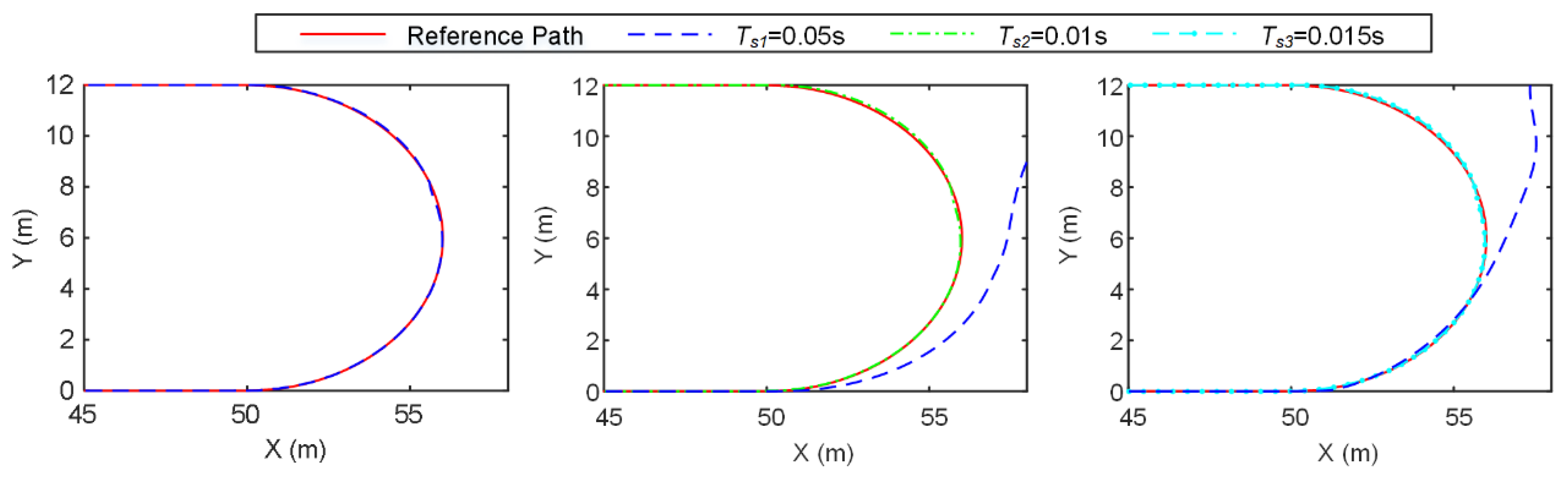
Figure 5 shows the trajectory tracking results of the OCFE controller, Euler controller, and RK controller. Specifically, OCFE-T1 denotes the trajectory traced by the controller employing the OCFE discretization method at a discrete time step of $T_1=0.05\mathrm{s}$. The trajectories Euler-T1 and Euler-T2 correspond to the tracking performance of the controller utilizing the forward Euler discretization method at discrete time steps $T_1$ and $T_2$, respectively, where $T_2=0.01\mathrm{s}$. Moreover, RK4-T3 signifies the tracking result of the controller based on the fourth-order Runge–Kutta discretization method with a discrete time step of $T_3=0.015\mathrm{s}$.

It can be seen from the figure that when the discrete time step is large ($T_1=0.05\mathrm{s}$), the controller Euler-T1 based on the forward Euler discrete method fails to completely track the given reference trajectory. Upon entering the turning part, the Euler-T1 controller struggles due to the problem of low-speed integral stability. Specifically, the state variations of the vehicle’s lateral and yaw speed of the vehicle characterized by large integral stiffness are ignored under large discrete time steps, leading to an inability to effectively manage the vehicle’s steering. Consequently, the tracking error accumulates, ultimately resulting in a complete divergence from the reference trajectory. In contrast, when the discrete time step is reduced to $T_2=0.01\mathrm{s}$, the Euler-T2 controller demonstrates the capacity to guide the vehicle in accurately following the reference trajectory. This simulation-based validation further verified the theoretical discrete stability analysis detailed in Section 3. Specifically, under the predefined vehicle parameter conditions, a vehicle speed of 1 m/s requires a discrete time step of 0.01 s or smaller to guarantee the discrete stability when employing the Euler discretization method.

The fourth-order Runge–Kutta discretization method also faces a comparable challenge. When subjected to large discrete time steps, it is unable to accurately capture the state changes in vehicle lateral speed and yaw velocity, thereby hindering the vehicle’s ability to track the prescribed U-shaped reference trajectory. By reducing the discrete time step to $T_3=0.015\mathrm{s}$, the RK4-T3 controller is capable of executing the vehicle trajectory tracking task effectively while circumventing the integral stability issues during the discretization process with a smaller time step.

In contrast to the traditional Euler discretization method and the fourth-order Runge–Kutta (RK4) discretization method, the OCFE-T1 controller demonstrates the ability to effectively track the reference trajectory even when the discrete time step is $T_1=0.05\mathrm{s}$. This indicates that the NMPC trajectory tracking control algorithm based on the OCFE discretization proposed in this study exhibits resilience against the challenges posed by low-speed integral stability. The stability remains preserved even under the condition of employing a large discrete time step.

From the foregoing analysis, it is evident that the OCFE-T1, Euler-T2, and RK4-T3 control methods are capable of ensuring integral stability within the numerical solutions of NMPC. The computational time required for their single-step iterative processes is depicted in Figure 6. This depiction illustrates the performance of the entire computation process, which was conducted on a personal laptop equipped with an Intel Core i5-9400 processor running at 2.9 GHz.

As illustrated in the Figure 6, the OCFE-T1 controller demonstrates a significant reduction in calculation, which is attributed to the increase in the discretization step length. The average computation time for the OCFE-T1 controller is recorded at 0.013 s, marking a reduction of 23.5% and 35% relative to the Euler-T2 controller’s 0.017 s and the RK4-T3 controller’s 0.02 s, respectively. This enhancement in computation time consequently bolsters the real-time performance.

Due to the vehicle’s low longitudinal speed, all three controllers are capable of guiding the vehicle to more accurately track the reference trajectory when an appropriate discrete time step is selected. The quantization results for lateral tacking errors are presented in

Table 2. Lateral tracking error of three controllers.

	Orthogonal-Ts1 Controller	Euler-Ts2 Controller	RK-Ts3 Controller
$e_{y\mathrm{m}\mathrm{a}\mathrm{x}}$ (m)	0.0985	0.1058	0.0995
$e_{y\mathrm{R}\mathrm{S}\mathrm{M}\mathrm{E}}$ (m)	0.0118	0.0218	0.0214

. It is observed that selecting a larger integration step does not adversely affect the tracking performance of the orthogonal collocation controller. The maximum lateral tracking error for the three controllers is less than 0.11 m, indicating high tracking accuracy. Among them, the orthogonal collocation controller demonstrates the highest level of control precision.

5.2. Simulation of High-Speed U-Turn Maneuver

The conditions for high-speed U-Turn maneuvers are defined as follows: road adhesion coefficient is $\mu =0.85$, and the vehicle’s longitudinal speed is $v_x=72\mathrm{km}/\mathrm{h}$. The geometric configuration of reference path is similar to that of the low-speed U-Turn condition, where it first travels 40 m along a straight path before initiating the U-Turn with a steering radius of $R_{\mathrm{road}}=60\mathrm{m}$. The reference track for the U-Turn under high-speed conditions is obtained by substituting the appropriate parameters of the described trajectory into Equation (26).

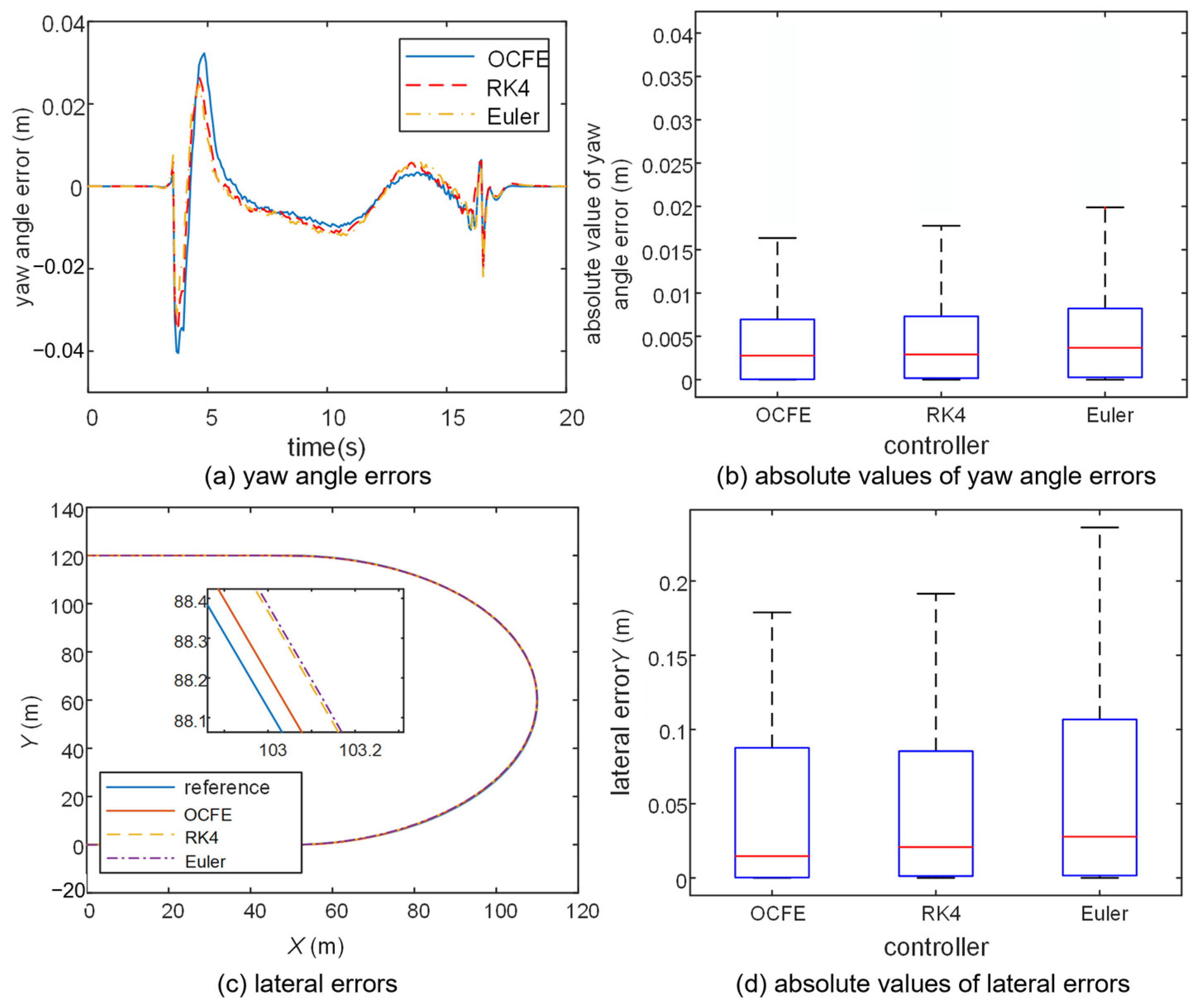
The preceding analysis in Section 3 indicates that vehicle dynamics model equations transition to a non-stiff form with the increase in the vehicle’s longitudinal driving speed. Consequently, the constraints on the discrete-time step inherent in traditional discrete-time methods within the NMPC solution process are alleviated. In this condition, Figure 7 presents the simulation results for the OCFE, RK4, and Euler controllers. As depicted in the figure, under the condition of a discrete time step of $T_1=0.05\mathrm{s}$, all three controllers are capable of successfully executing the tracking task for the reference U-shaped trajectory.

The yaw angle errors exhibited by the three controllers are closely comparable. The average course angle errors for the OCFE, RK4, and Euler controllers are recorded as 0.0051 rad, 0.0049 rad, and 0.0051 rad, respectively. Moreover, the absolute value of the maximum yaw angle error does not exceed 0.04 rad. Regarding lateral tracking error, the OCFE and RK4 controllers demonstrate average errors of 0.0451 m and 0.0479 m, respectively, with maximum errors reaching 0.1719 m and 0.1915 m, respectively. The OCFE controller exhibits enhanced precision in comparison to the RK4 controller. As depicted in the lateral error distribution Figure 7b, these two statistical indicators for the OCFE controller are significantly superior to those of the Euler discrete controller. Specifically, the average tracking error of the OCFE controller is 24.45% lower than that of the Euler controller, which is 0.0597 m. Additionally, the maximum lateral error is reduced by 27.19% in comparison to the Euler controller’s error of 0.2361 m. Therefore, the proposed OCFE-based NMPC controller shows higher accuracy compared to traditional controller while ensuring stability.

6. Conclusions

Vehicle dynamics equations, serving as a widely used model in motion control for autonomous vehicles, exert a considerable influence on computational efficiency of NMPC primarily due to its stiffness. This study first presented a theoretical analysis of the stiffness of the vehicle dynamics model equations and then derived the resulting constraints imposed on the integration time step when employing conventional numerical methods. The analysis revealed that the adoption of small-time steps leads to the increasing online computational loads. To address the issue, the finite element orthogonal collocation method (OCFE)-based NMPC controller was proposed, which could relax the discretized time step restrictions. The proposed controller was compared with the traditional NMPC controller through the CarSim/Simulink co-simulation platform. The results showed that the vehicle dynamics model equations are stiffer when the vehicle speed is low and the proposed OCFE-based NMPC controller can improve the real-time performance while ensuring the path tracking accuracy. The influence of the stiffness on the online computational time of the NMPC controller diminishes as the vehicle speed is larger. In addition to the superiority of addressing integration stability issues caused by the stiffness nature of the vehicle dynamics equations, the OCFE-based NMPC controller also showed its higher accuracy across a wide of vehicle speeds, from low to high speed. In the future work, the efficacy of the proposed strategy will be validated in both hardware-in-loop simulations and real-world vehicle testing scenarios.