The Precision Improvement of Robot Integrated Joint Module Based on a New ADRC Algorithm
Abstract
1. Introduction
- (1)
- The current measures to improve the accuracy of robots are either focused on compensating the dynamic model and optimizing the parameters of robots, or on improving the accuracy of harmonic reducers from a mechanical design perspective. The design of control theory and harmonic reducers has not been well integrated in the current research. This article incorporates the advantages of two types of precision improvement and combines control theory with the characteristics of harmonic reducers to systematically study robot joints. A precision compensation technology for robot joint modules is proposed.
- (2)
- This article expands the research topic of ADRC and studies the harmonic reducer and the PMSM as a whole control object. In robot motion control, traditional ADRC studies the dynamic performance, steady-state accuracy, and disturbance rejection ability of the PMSM output shaft. In fact, the motion angle output of the motor is converted by the harmonic reducer to obtain the motion angle of the robot. During this angle conversion process, there are important factors that affect the accuracy of robot motion, such as gear deformation, load disturbance, and mechanical vibration. Even if the PMSM achieves precise control of motor output, the accuracy transmitted to the end of the robot is greatly reduced, which is also the difficulty of robot accuracy control. This article adopts a new approach, which differs from the traditional approach of only controlling the output shaft accuracy of the PMSM. The harmonic reducer model is integrated into the PMSM control strategy to redesign the ADRC controller. By adjusting the output of the ADRC torque loop to counteract these uncertain torque disturbances, the control accuracy can be improved.
2. Mathematical Model of Robot Joint Module
2.1. PMSM-Harmonic Reducer System
2.2. Mathematical Model of Permanent Magnet Synchronous Motor
2.3. Precision Error Model of Harmonic Reducer
2.4. Mathematical Analysis of Robot Joint Model
2.4.1. Meshing Deformation of Gear
2.4.2. Harmonic Reducer Output Elastic Deformation
2.4.3. Vibration of Robot Joint Module
2.5. Harmonic Retarder Disturbance Model
3. ADRC of Robot Joint Module
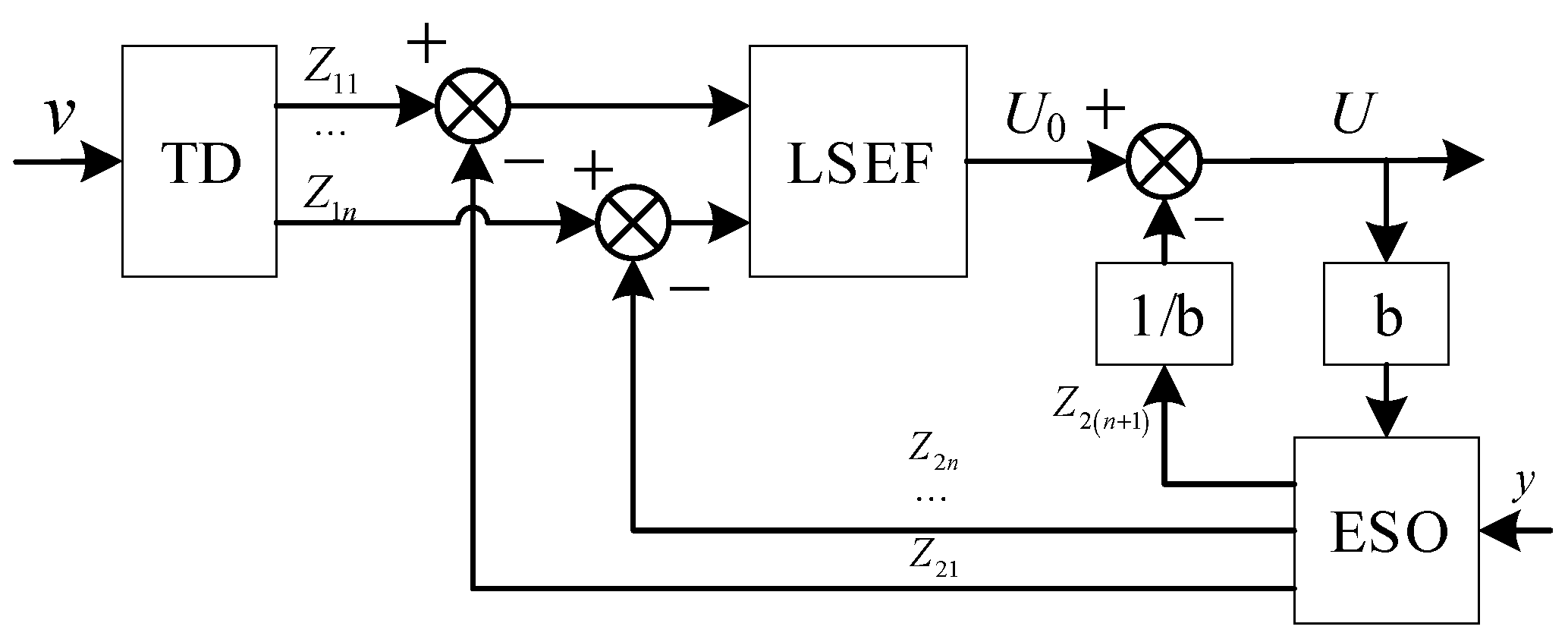
3.1. Design of Extended State Observer (ESO)
3.2. LSEF Controller Design
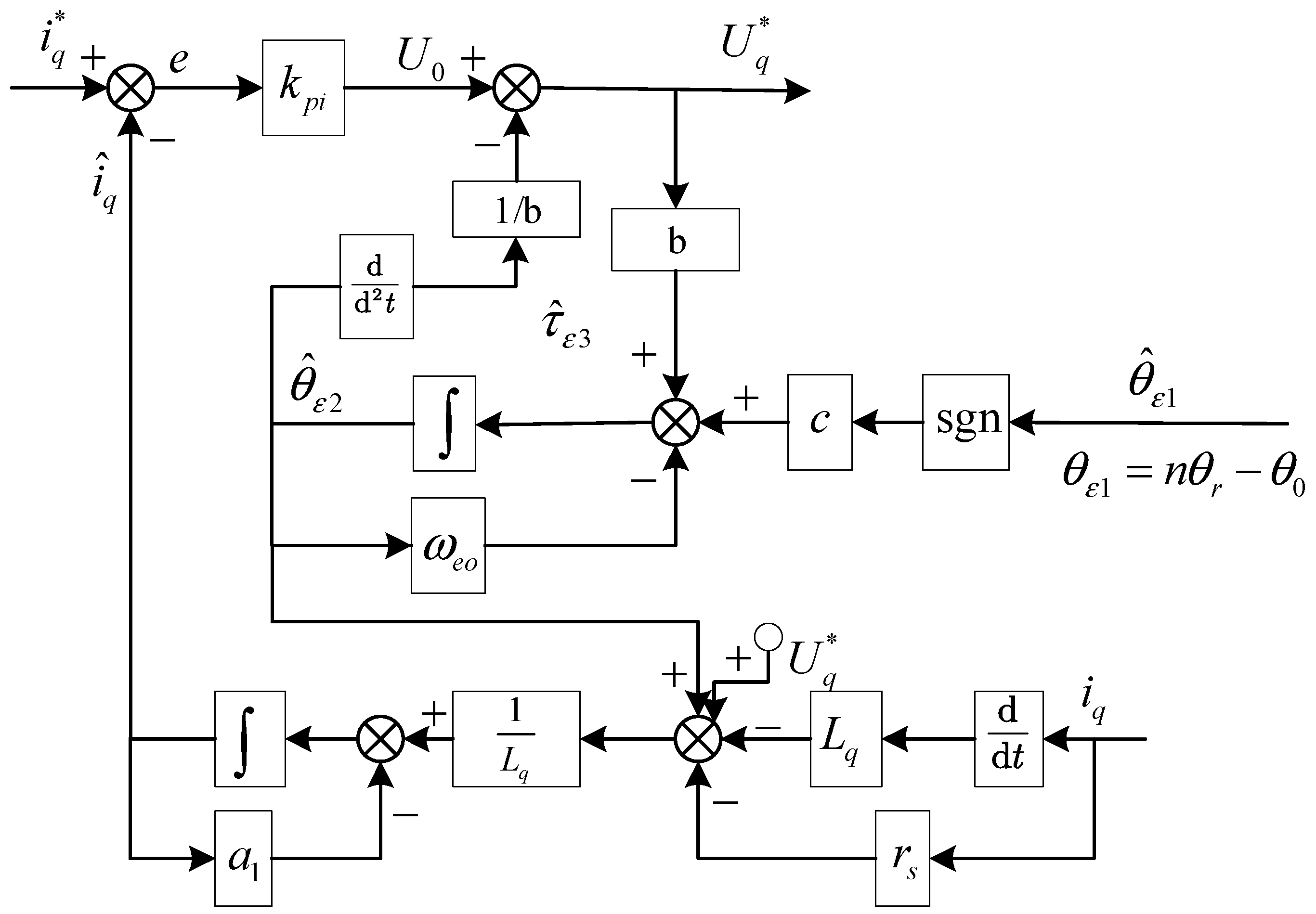
3.3. Active Disturbance Rejection Compensation Control Strategy
4. Comparison and Analysis of Experimental Results
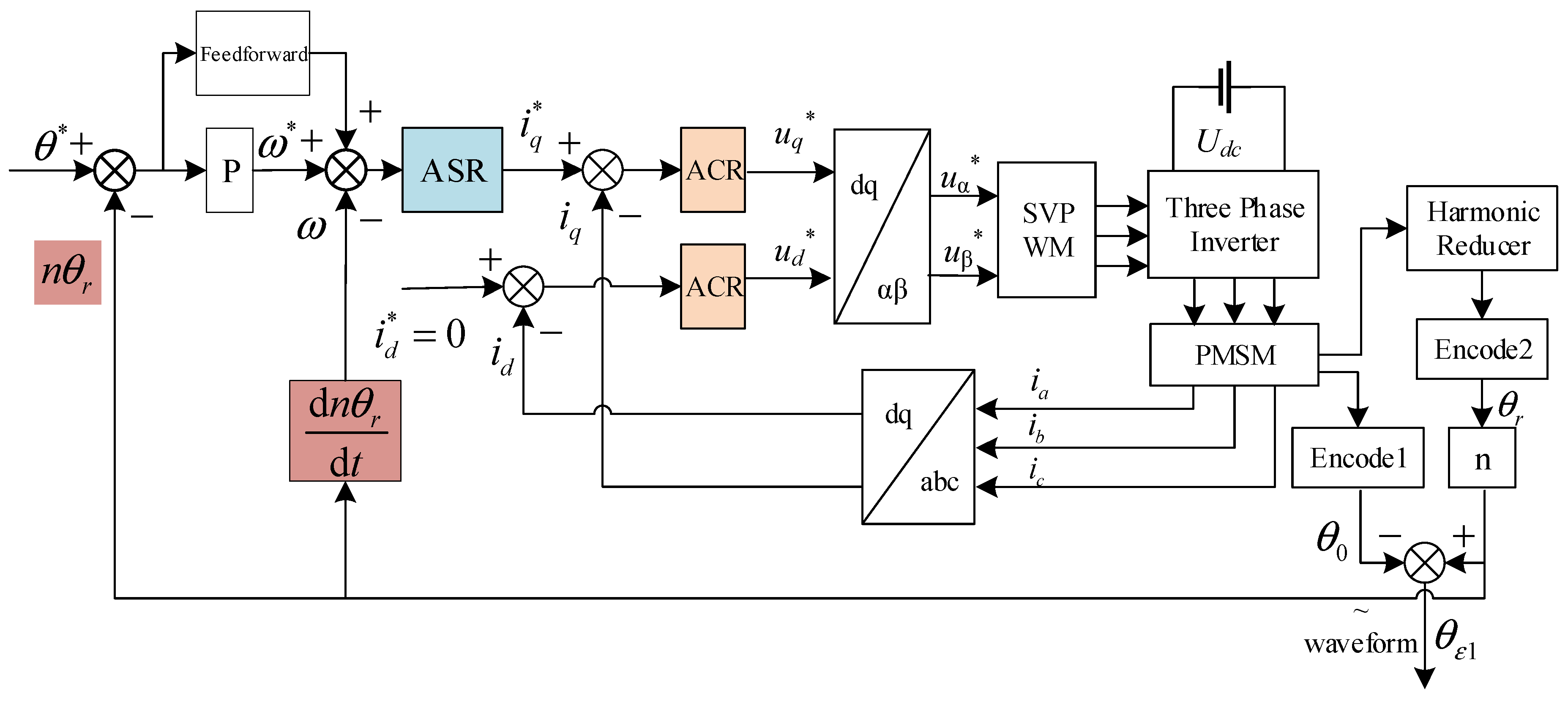
4.1. Experimental Method for Performance Test of Robot Joint Module
4.1.1. PMSM Output Bearing Position Closed-Loop Control Waveform
4.1.2. Harmonic Reducer Output Bearing Position Closed-Loop Control
4.1.3. Current-Loop ADRC
4.2. Experimental Platform
4.3. Experimental Results and Analysis
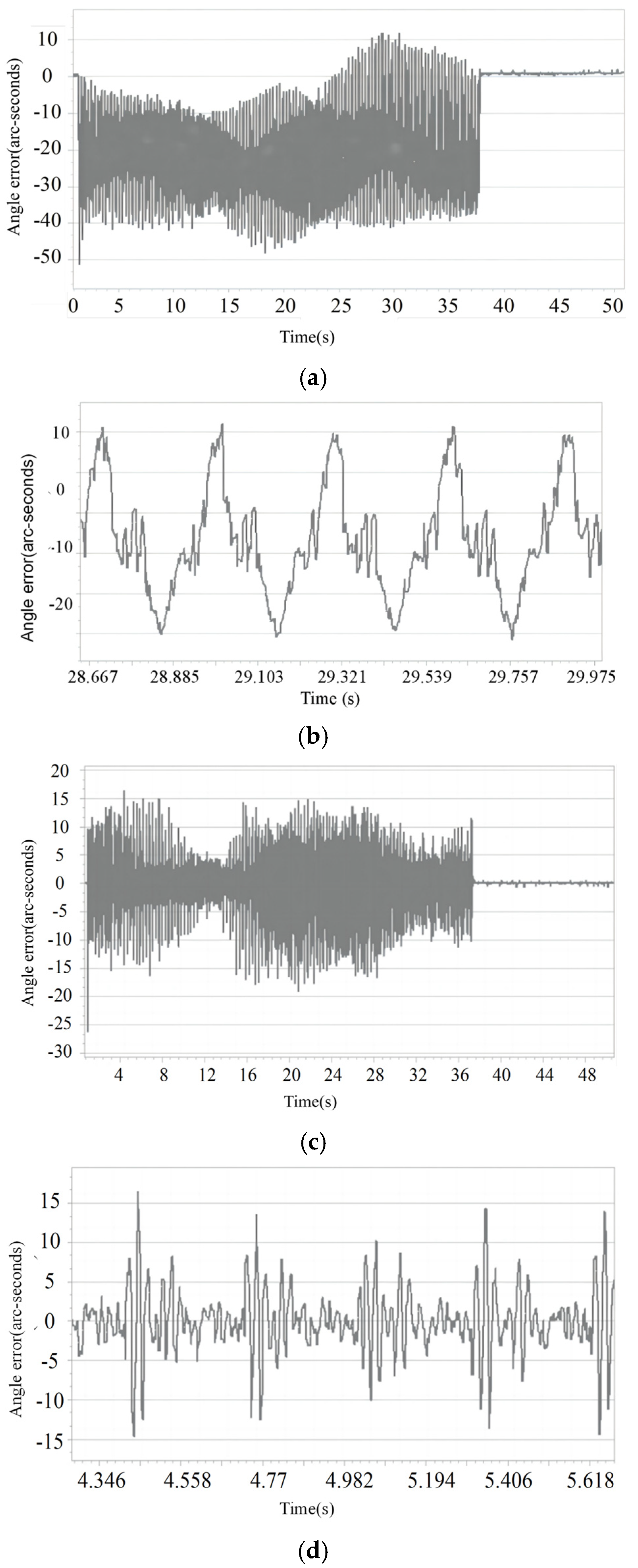
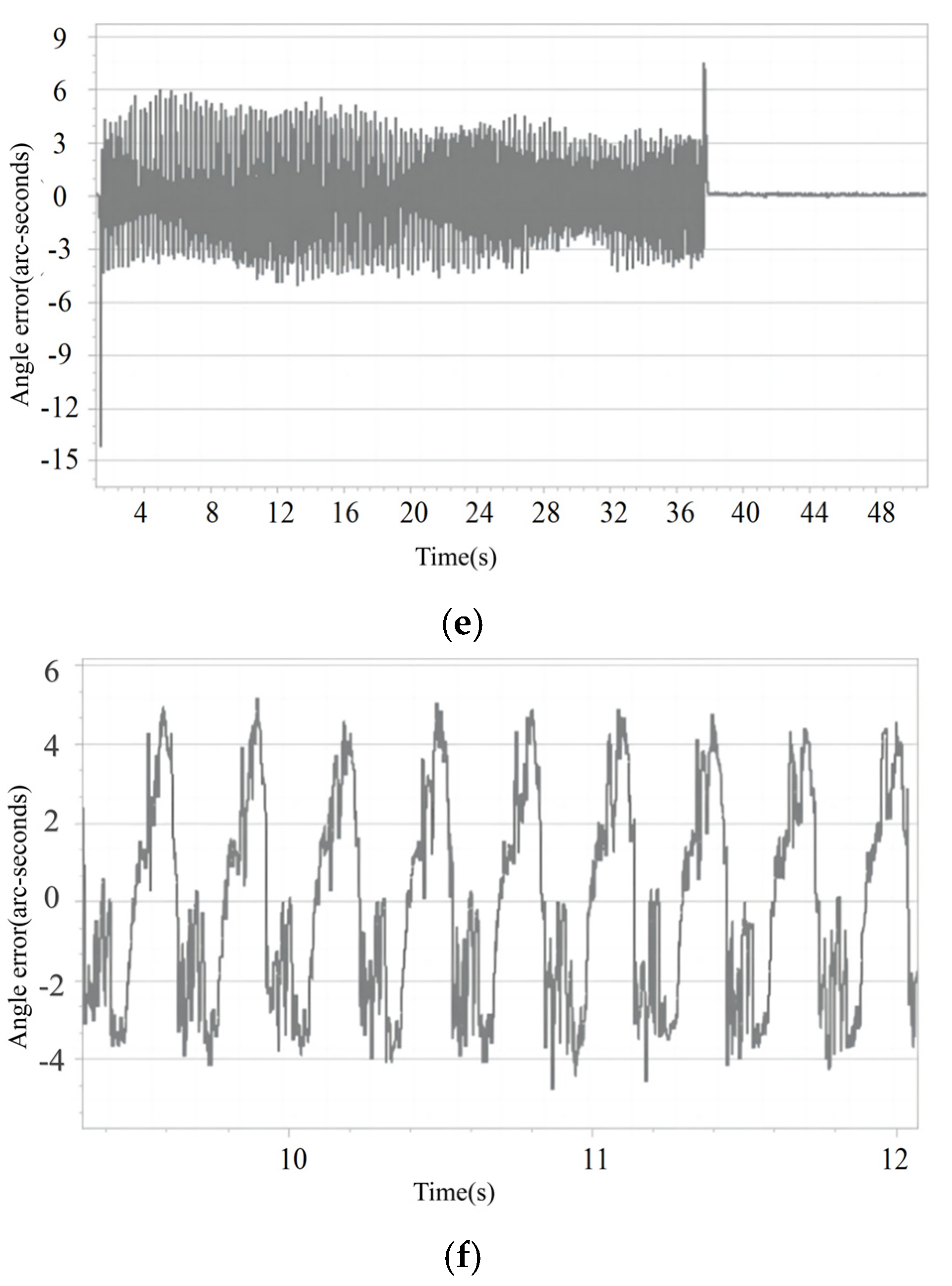
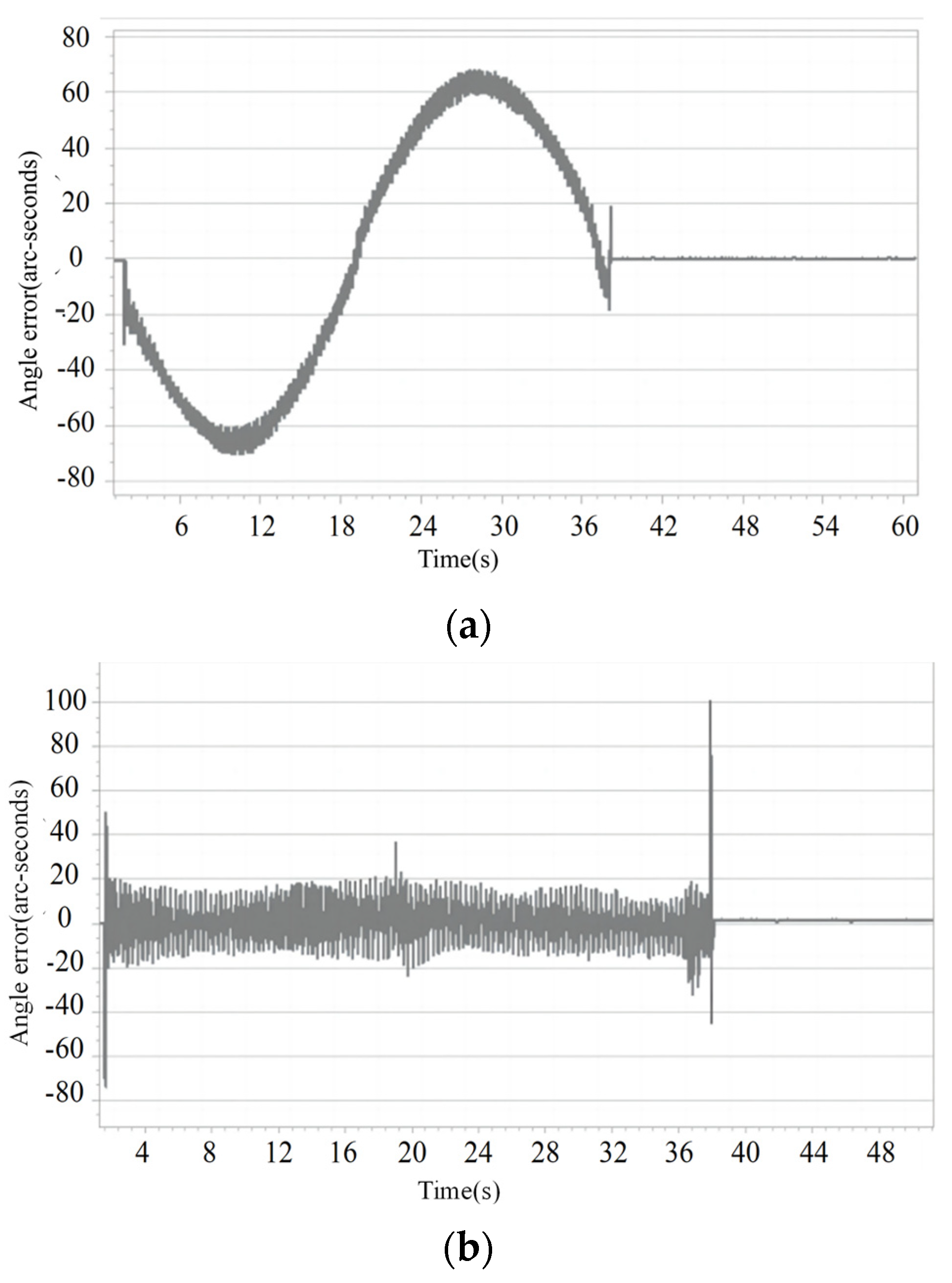
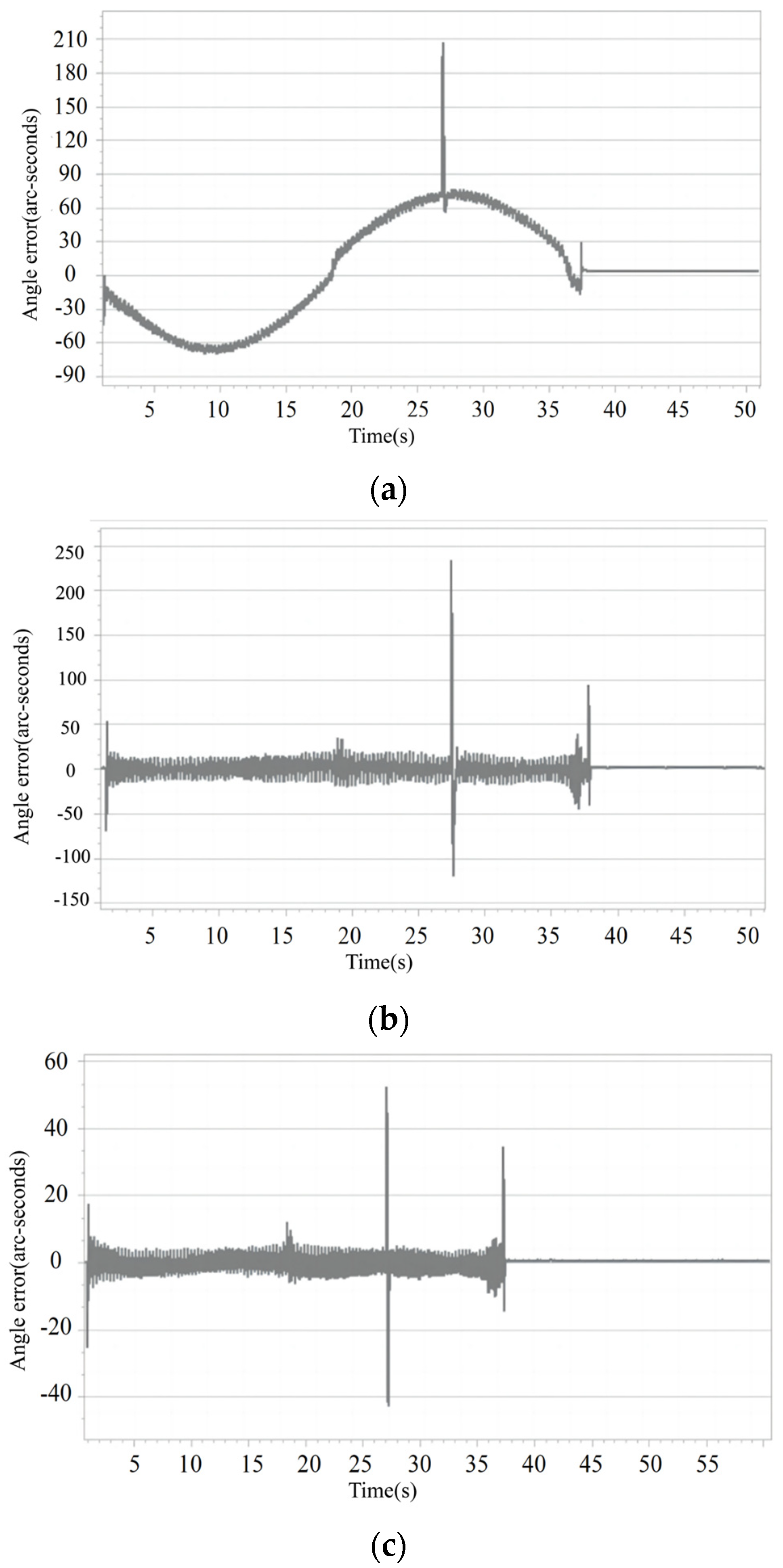
4.3.1. No-Load Experiment
4.3.2. 5 kg Load Experiment
4.3.3. Sudden Load Disturbance Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Gao, Z. Engineering cybernetics: 60 years in the making. Control Theory Technol. 2014, 12, 97–109. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, J. Active disturbance rejection trajectory tracking control of omnidirectional mobile robot. Mech. Sci. Technol. Aerosp. Eng. 2022, 41, 1869–1876. [Google Scholar]
- Chen, Z.; Ruan, X.; Li, Y. An active disturbance rejection based balance control method for cubic robot. Control Decis. 2019, 34, 1203–1210. [Google Scholar]
- Qiao, G.; Jiang, X.; Nie, X.; Gao, C. Accuracy improvement for industrial robot based on joint position sensitive virtual tool transformation fitting method. In Proceedings of the 2023 6th International Conference on Robotics, Control and Automation Engineering (RCAE), Suzhou, China, 3–5 November 2023; pp. 303–308. [Google Scholar] [CrossRef]
- Peng, T.; Zhang, T.; Sun, Z. Research on robot accuracy compensation method based on modified grey wolf algorithm. In Proceedings of the 2023 8th Asia-Pacific Conference on Intelligent Robot Systems (ACIRS), Xi’an, China, 7–9 July 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Trang, T.; Pham, T.; Yin, Q.; Wang, Q.; Hu, Y.; Li, W. Design harmonic drive for application in robot joint. In Proceedings of the 2022 International Conference on Mechanical and Electronics Engineering (ICMEE), Xi’an, China, 21–23 November 2022; pp. 106–113. [Google Scholar] [CrossRef]
- Park, M.-W. A study on conceptual design of planocentric involute reducer for modular robot. In Proceedings of the 2019 19th International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 15–18 October 2019; pp. 1412–1414. [Google Scholar] [CrossRef]
- Bekey, G.A.; Goldberg, K.Y. (Eds.) Neural Networks in Robotics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 202. [Google Scholar]
- Sun, F.; Sun, Z.; Woo, P. Neural network-based adaptive controller design of robotic manipulators with an observer. IEEE Trans. Neural Netw. 2001, 12, 54–67. [Google Scholar] [PubMed]
- Hoai-Nhan, N.; Zhou, J.; Kang, H. A calibration method for enhancing robot accuracy through integration of an extended Kalman filter algorithm and an artificial neural network. Neurocomputing 2015, 151, 996–1005. [Google Scholar]
- Bai, M.; Zhang, M.; Zhang, H.; Li, M.; Zhao, J.; Chen, Z. Calibration method based on models and least-squares support vector regression enhancing robot position accuracy. IEEE Access 2021, 9, 136060–136070. [Google Scholar] [CrossRef]
- Litvin, F.L.; Fuentes, A.; Gonzalez-Perez, I.; Carvenali, L.; Kawasaki, K.; Handschuh, R.F. Modified involute helical gears: Computerized design, simulation of meshing and stress analysis. Comput. Methods Appl. Mech. Eng. 2003, 192, 3619–3655. [Google Scholar] [CrossRef]
- Temirkhan, M.; Spitas, C.; Wei, D. A computationally robust solution to the contact problem of two rotating gear surfaces in space. Meccanica 2023, 58, 2455–2466. [Google Scholar] [CrossRef]
- Fuentes-Aznar, A.; Gonzalez-Perez, I. Mathematical definition and computerized modeling of spherical involute and octoidal bevel gears generated by crown gear. Mech. Mach. Theory 2016, 106, 94–114. [Google Scholar] [CrossRef]
- Kolivand, M.; Kahraman, A. An ease-off based method for loaded tooth contact analysis of hypoid gears having local and global surface deviations. ASME J. Mech. Des. 2010, 132, 071004. [Google Scholar] [CrossRef]
- Tariq, H.; Galym, Z.; Amrin, A.; Spitas, C. Assessment of contact forces and stresses, torque ripple and efficiency of a cycloidal gear drive and its involute kinematical equivalent. Mech. Based Des. Struct. Mach. 2022, 52, 1304–1323. [Google Scholar] [CrossRef]
- Li, J. Research on Vector Control System of Permanent Magnet Synchronous Motor Based on DSP. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2008. [Google Scholar]
- Wang, J. Structural Mechanics Analysis of Harmonic Drive Reducer. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2011. [Google Scholar]
- Tuttle, T.D. Understanding and Modeling the Behavior of a Harmonic Drive Gear Transmission. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1992. [Google Scholar]
- Ghorbel, F.H.; Gandhi, P.S.; Alpeter, F. On the kinematic error in harmonic drive gears. J. Mech. Des. 2001, 123, 90–97. [Google Scholar] [CrossRef]
- Zou, C.; Tao, T.; Jiang, G.; Mei, X.; Wu, J. A harmonic drive model considering geometry and internal interaction. Proc. Inst. Mech. Eng. Part C-J. Eng. Mech. Eng. Sci. 2017, 231, 728–743. [Google Scholar] [CrossRef]
- Dhaouadi, R.; Ghorbel, F.H. Modelling and analysis of nonlinear stiffness, hysteresis and friction in harmonic drive gears. Int. J. Model Simul. 2008, 28, 329–336. [Google Scholar] [CrossRef]
- Ma, D.; Yan, S.; Yin, Z.; Yang, Y. Investigation of the friction behavior of harmonic drive gears at low speed operation. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1382–1388. [Google Scholar]
- Routh, B. Design aspects of harmonic drive gear and performance improvement of its by problems identification: A review. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2018. [Google Scholar]
- Tuttle, T.D.; Seering, W.P. Kinematic error, compliance, and friction in a harmonic drive gear transmission. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Albuquerque, NM, USA, 19–22 September 1993; American Society of Mechanical Engineers: New York, NY, USA, 1993. [Google Scholar]
- Yamamoto, M.; Iwasaki, M.; Hirai, H.; Okitsu, Y.; Sasaki, K.; Yajima, T. Modeling and compensation for angular transmission error in harmonic drive gearings. IEEJ Trans. Electr. Electron. Eng. 2009, 4, 158–165. [Google Scholar] [CrossRef]
- Gandhi, P.S.; Ghorbel, F.H. Closed-loop compensation of kinematic error in harmonic drives for precision control applications. IEEE Trans. Control Syst. Technol. 2002, 10, 759–768. [Google Scholar] [CrossRef]
- Iwasaki, M.; Yamamoto, M.; Hirai, H.; Okitsu, Y.; Sasaki, K.; Yajima, T. Modeling and compensation for angular transmission error of harmonic drive gearings in high precision positioning. In Proceedings of the 2009 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Singapore, 14–17 July 2009; IEEE: Piscataway, NJ, USA, 2009. [Google Scholar]
- Dong, H.; Dong, B.; Zhang, C.; Wang, D. An equivalent mechanism model for kinematic accuracy analysis of harmonic drive. Mech. Mach. Theory 2022, 173, 104825. [Google Scholar] [CrossRef]
- Taghirad, H.D.; Belanger, P.R. Torque ripple and misalignment torque compensation for the built-in torque sensor of harmonic drive systems. IEEE Trans. Instrum. Meas. 1998, 47, 309–315. [Google Scholar] [CrossRef]
- Xie, J.; Wei, W.; Liao, P.; Liu, J. Design of ADRC controller for induction motor based on improved fal function. In Proceedings of the 2022 14th International Conference on Advanced Computational Intelligence (ICACI), Wuhan, China, 15–17 July 2022; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar]
- Liu, B.; Hong, J.; Wang, L. Linear inverted pendulum control based on improved ADRC. Syst. Sci. Control Eng. 2019, 7, 1–12. [Google Scholar] [CrossRef]
- Deng, F.; Guan, Y. PMSM vector control based on improved ADRC. In Proceedings of the 2018 IEEE International Conference of Intelligent Robotic and Control Engineering (IRCE), Lanzhou, China, 24–27 August 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Su, G. Fuzzy ADRC controller design for PMSM speed regulation system. Adv. Mater. Res. 2011, 201, 2405–2408. [Google Scholar] [CrossRef]
- Su, Y.; Zheng, C.; Duan, B. Automatic disturbances rejection controller for precise motion control of permanent-magnet synchronous motors. IEEE Trans. Ind. Electron. 2005, 52, 814–823. [Google Scholar] [CrossRef]
- Hezzi, A.; Ben Elghali, S.; Bensalem, Y.; Zhou, Z.; Benbouzid, M.; Abdelkrim, M.N. ADRC-based robust and resilient control of a 5-phase PMSM driven electric vehicle. Machines 2020, 8, 17. [Google Scholar] [CrossRef]
- Tian, M.; Wang, B.; Yu, Y.; Dong, Q.; Xu, D. Discrete-time repetitive control-based ADRC for current loop disturbances suppression of PMSM drives. IEEE Trans. Ind. Inform. 2021, 18, 3138–3149. [Google Scholar] [CrossRef]





| Items | Values |
|---|---|
| 0.8 | |
| 1.2 | |
| 1.8 | |
| 0.7 | |
| 1.0 | |
| 1.5 | |
| 0.5 |
| Items | Parameters |
|---|---|
| rated speed | 3000 rpm |
| rated current | 13.4 A |
| rated torque | 2.3 N.m |
| phase resistance | 0.126 ohms |
| phase inductance | 0.208 mH |
| back electromotive force | 8.3 Vrms/krpm |
| encoders | 20-bit absolute multi-turn encoder |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Fang, S. The Precision Improvement of Robot Integrated Joint Module Based on a New ADRC Algorithm. Machines 2024, 12, 712. https://doi.org/10.3390/machines12100712
Wang G, Fang S. The Precision Improvement of Robot Integrated Joint Module Based on a New ADRC Algorithm. Machines. 2024; 12(10):712. https://doi.org/10.3390/machines12100712
Chicago/Turabian StyleWang, Gang, and Shuhua Fang. 2024. "The Precision Improvement of Robot Integrated Joint Module Based on a New ADRC Algorithm" Machines 12, no. 10: 712. https://doi.org/10.3390/machines12100712
APA StyleWang, G., & Fang, S. (2024). The Precision Improvement of Robot Integrated Joint Module Based on a New ADRC Algorithm. Machines, 12(10), 712. https://doi.org/10.3390/machines12100712







