A Review of the Degradation Research on the Single-Lap Bolted Joint
Abstract
1. Introduction
- The characteristic length of components is in the order of 100 to 101 m, while the scale of connection structures is typically in the order of 10−2 m.
- The time for equipment to reach steady-state response under dynamic load is in the order of 100 to 101 s, while the time step describing the slip behavior of the joint surface is in the order of 10−9 s.
- There are a large number of bolted joints in the equipment, leading to widespread and more severe cross-scale phenomena. Therefore, the multiple cross-scale phenomena have made the numerical solution of the dynamic response of equipment challenging.
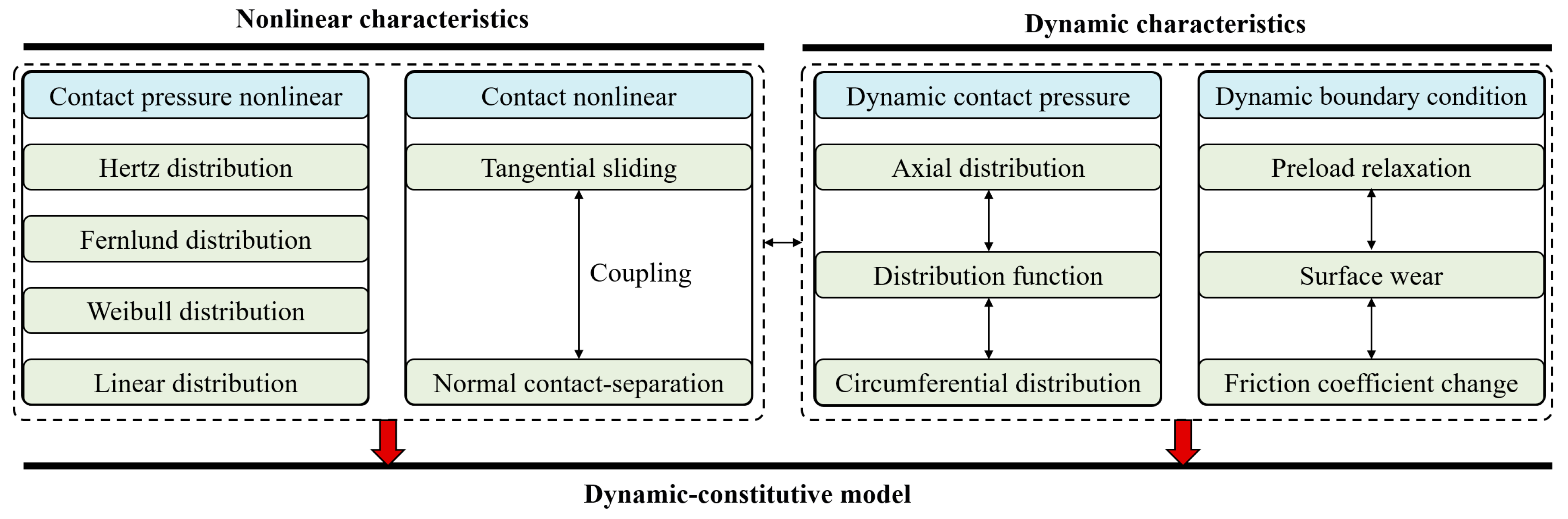
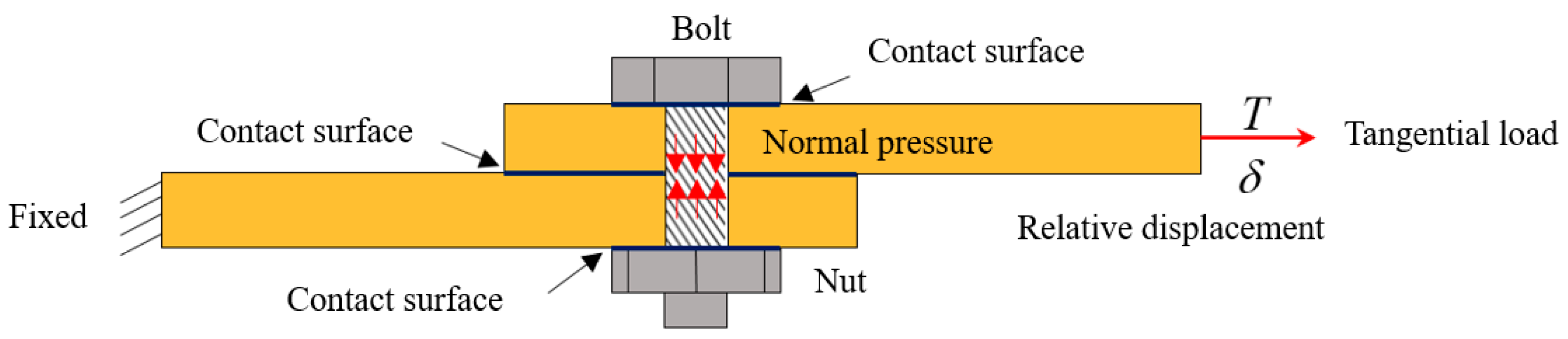
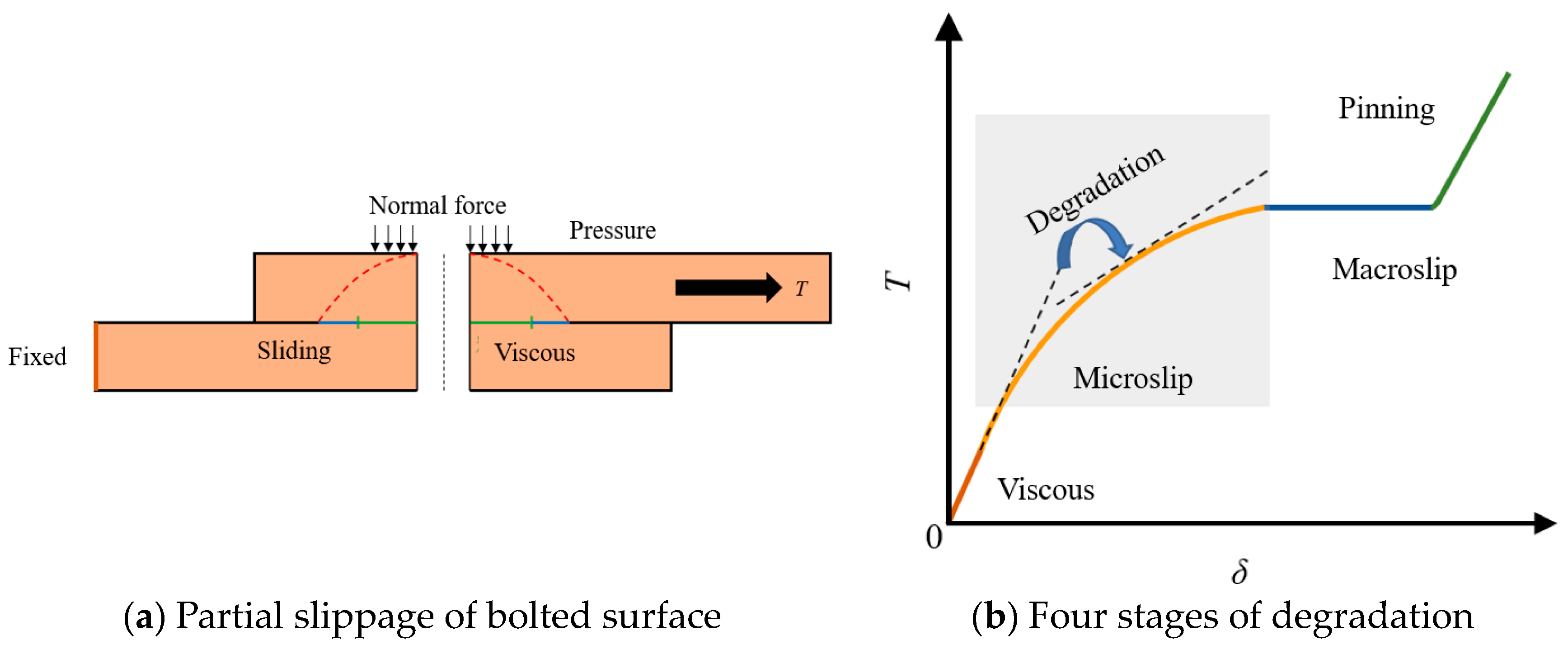
2. Nonlinear Degradation in Bolted Joints
3. Contact Models
3.1. Static-Friction Models
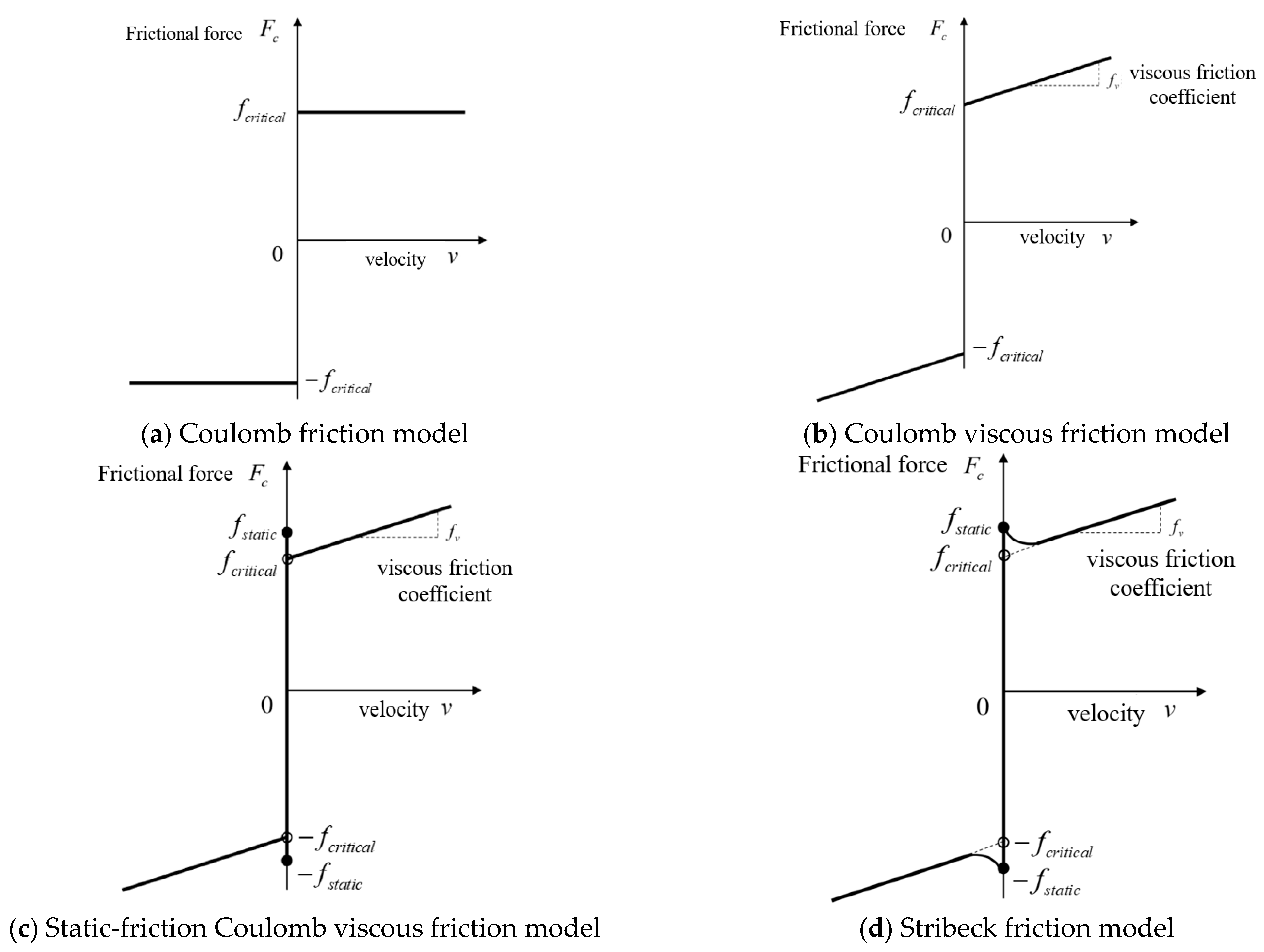
3.2. Dynamic-Friction Models
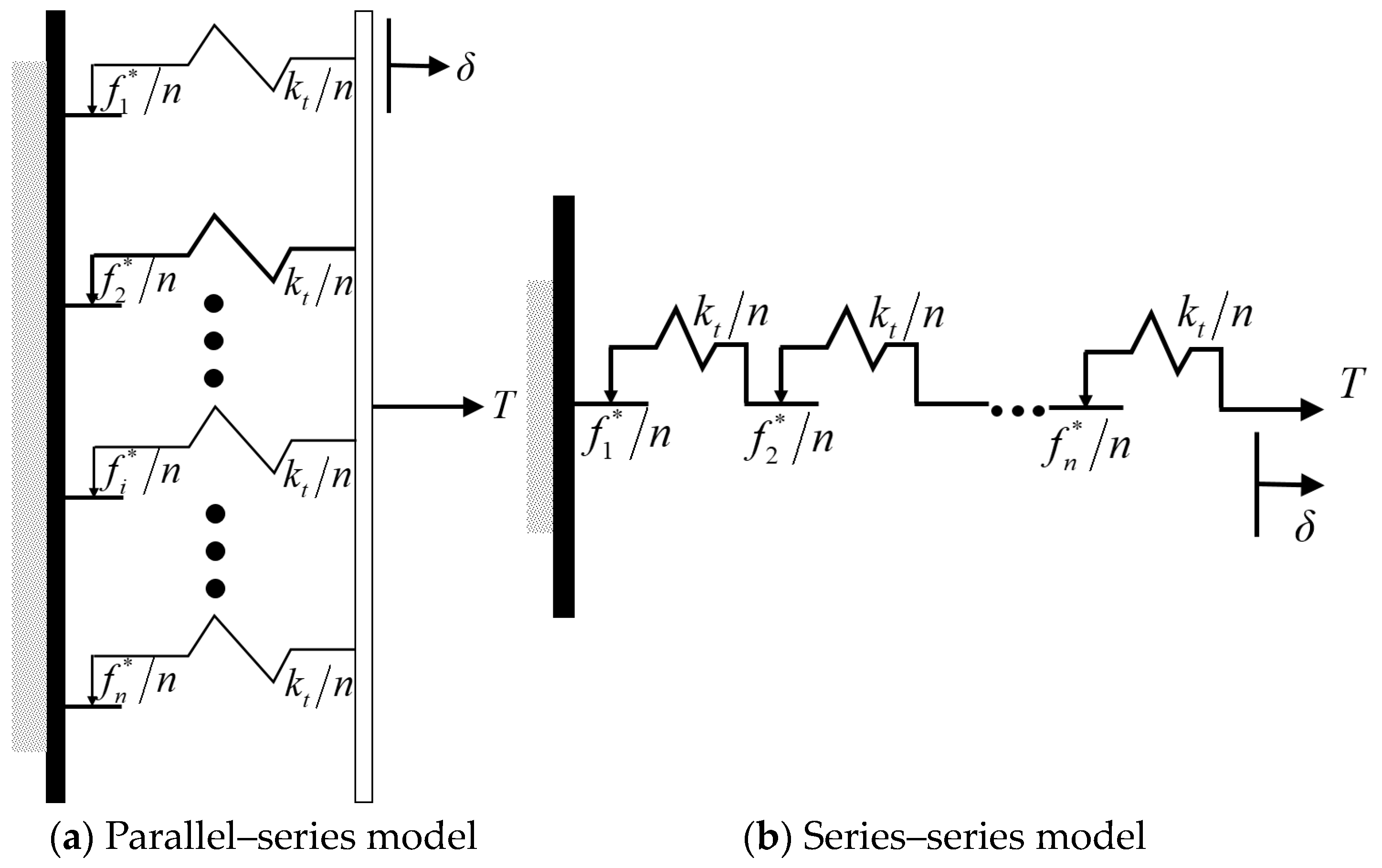
3.3. Friction-Constitutive Model
4. Experiment of Bolted Joints
4.1. Indirect Methods
4.2. Direct Methods
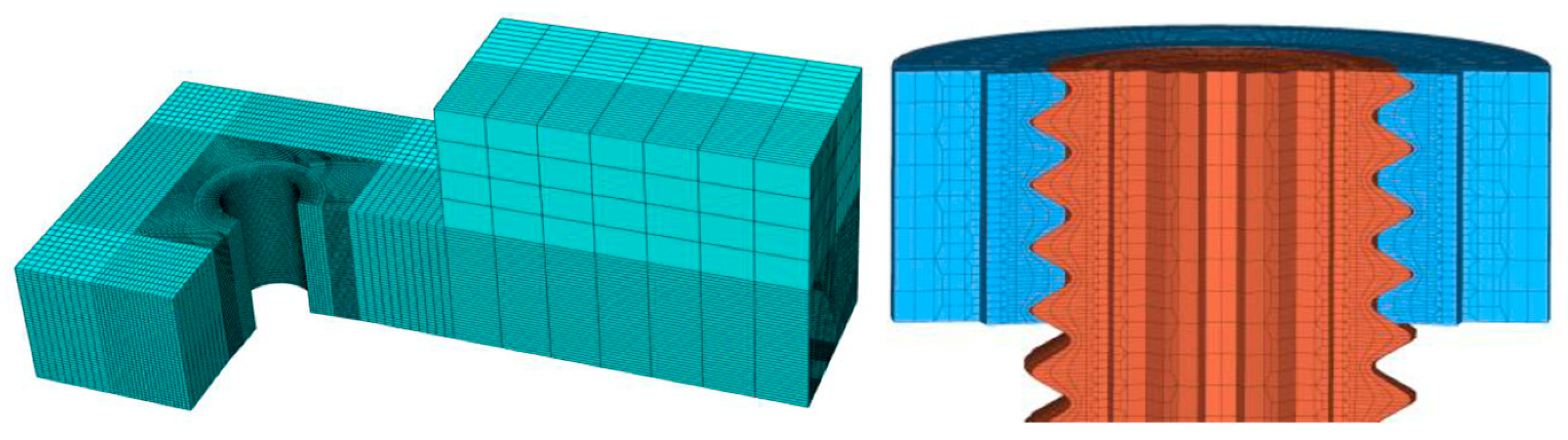
5. Numerical Analysis Methods
6. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cao, J.; Liu, Q.; Hong, J. A review of the study of microfriction to macrodynamics of bolted joints. China Mech. Eng. 2021, 32, 13. [Google Scholar]
- Qi, Y.; Wu, G. U.S. Trident 2 submarine-launched ballistic missile and its modernization improvements. Airborne Missile 2021, 11, 33–37. [Google Scholar] [CrossRef]
- Xu, C.; Zhou, B.; Liu, X.; Zhang, D. Research progress on monitoring and identification methods of mechanical bolt connection condition. Struct. Environ. Eng. 2009, 36, 28–36. [Google Scholar]
- Li, D.; Botto, D.; Xu, C.; Liu, T.; Gola, M. A micro-slip friction modeling approach and its application in underplatform damper kinematics. Int. J. Mech. Sci. 2019, 161–162, 105029. [Google Scholar] [CrossRef]
- Li, D.; Xu, C.; Botto, D.; Zhang, Z.; Gola, M. A fretting test apparatus for measuring friction hysteresis of bolted joints. Tribol. Int. 2020, 151, 106431. [Google Scholar] [CrossRef]
- Li, D.; Botto, D.; Xu, C.; Gola, M. A new approach for the determination of the Iwan density function in modeling friction contact. Int. J. Mech. Sci. 2020, 180, 105671. [Google Scholar] [CrossRef]
- Zhao, B.; Wu, F.; Sun, K.; Mu, X.; Zhang, Y.; Sun, Q. Study on tangential stiffness nonlinear softening of bolted joint in friction-sliding process. Tribol. Int. 2021, 156, 106856. [Google Scholar] [CrossRef]
- Marshall, M.B.; Lewis, R.; Dwyer-Joyce, R.S. Characterisation of Contact Pressure Distribution in Bolted Joints. Strain 2006, 42, 31–43. [Google Scholar] [CrossRef]
- Ito, Y.; Toyoda, J.; Nagata, S. Interface Pressure Distribution in a Bolt-Flange Assembly. J. Mech. Des. 1979, 101, 330–337. [Google Scholar] [CrossRef]
- Luan, Y.; Liu, S.; Guan, Z. Nonlinear characteristics of static stiffness of bolt-flange connected structures under small deformation. Struct. Environ. Eng. 2011, 38, 29–35. [Google Scholar]
- Qin, Y.; Hou, X.; He, G. Force analysis of the shell end connecting screw hole of solid rocket motor under bending load. J. Solid Rocket Technol. 2011, 34, 369–372. [Google Scholar]
- Li, C.; Qiao, R.; Miao, X.; Jiang, Y. Research on nonlinear modeling and parameter identification method of bolted connection interface. J. Mech. Eng. 2021, 57, 78–86. [Google Scholar] [CrossRef]
- Groper, M.; Hemmye, J. The dissipation of energy in high strength friction grip bolted joints. In Proceedings of the SESA Spring Conference, Cleveland, OH, USA, 15–20 May 1983. [Google Scholar]
- Groper, M.; Hemmye, J. Partial slip damping in high strength friction grip bolted joints. In Proceedings of the Fourth International Conference of Mathematical Modeling, Zurich, Switzerland, 15–17 August 1983. [Google Scholar]
- Robert, B.M. The Mechanics of Jointed Structures; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Dahl, P. Solid friction damping of spacecraft oscillations. In Proceedings of the Guidance and Control Conference, Boston, MA, USA, 20–22 August 1975; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1975. [Google Scholar] [CrossRef]
- de Wit, C.C.; Olsson, H.; Astrom, K.; Lischinsky, P. A new model for control of systems with friction. IEEE Trans. Autom. Control 1995, 40, 419–425. [Google Scholar] [CrossRef]
- Haessig, D.A.; Friedland, B. On the modeling and simulation of friction. In Proceedings of the 1990 American Control Conference, San Diego, CA, USA, 23–25 May 1990; pp. 1256–1261. [Google Scholar]
- Valanis, K. Fundamental Consequences of a New Intrinsic Time Measure. Plast. A Limit Endochronic Theory Arch. Mech. 1978, 32, 68. [Google Scholar]
- Jalali, H.; Ahmadian, H.; Pourahmadian, F. Identification of micro-vibro-impacts at boundary condition of a nonlinear beam. Mech. Syst. Signal Process. 2011, 25, 1073–1085. [Google Scholar] [CrossRef]
- Ahmadian, H.; Jalali, H.; Pourahmadian, F. Nonlinear model identification of a frictional contact support. Mech. Syst. Signal Process. 2010, 24, 2844–2854. [Google Scholar] [CrossRef]
- Do, N. Modeling of Frictional Contact Conditions in Structures. Master’s Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2005. Available online: https://repository.gatech.edu/entities/publication/b19dfeed-35eb-444d-87bf-73e6fac93057 (accessed on 19 August 2024).
- Gaul, L.; Lenz, J. Nonlinear dynamics of structures assembled by bolted joints. Acta Mech. 1997, 125, 169–181. [Google Scholar] [CrossRef]
- Iwan, W.D. A Distributed-Element Model for Hysteresis and Its Steady-State Dynamic Response. J. Appl. Mech. 1966, 33, 893–900. [Google Scholar] [CrossRef]
- Wentzel, H. Modelling of Frictional Joints in Dynamically Loaded Structrues: A Review; Technology R I O: Stockholm, Sweden, 2006. [Google Scholar]
- Argatov, I.I.; Butcher, E.A. On the Iwan models for lap-type bolted joints. Int. J. Non-Linear Mech. 2011, 46, 347–356. [Google Scholar] [CrossRef]
- Segalman, D.J.; Starr, M.J. Relationships among Certain Joint Constitutive Models; Sandia National Laboratories: Albuquerque, NM, USA, 2004.
- Segalman, D.J.; Starr, M.J. Inversion of Masing models via continuous Iwan systems. Int. J. Non-Linear Mech. 2008, 43, 74–80. [Google Scholar] [CrossRef]
- Song, Y.; Hartwigsen, C.; McFarland, D.; Vakakis, A.; Bergman, L. Simulation of dynamics of beam structures with bolted joints using adjusted Iwan beam elements. J. Sound Vib. 2004, 273, 249–276. [Google Scholar] [CrossRef]
- Goodman, L.E. A review of progress in analysis of interfacial slip damping. Struct. Damping 1959, 35–48. [Google Scholar]
- Segalman, D.J.; Gregory, D.L.; JS, M. Handbook on Dynamics of Jointed Structure; Sandia Laboratory: Albuerque, NM, USA, 2009.
- Smallwood, D.O.; Gregory, D.L.; Coleman, R.G. Damping investigations of a simplified frictional shear joint. In Proceedings of the 71st Shock and Vibration Symposium, Arlington, VA, USA, 6–9 November 2000. [Google Scholar]
- Ungar, E.E. Energy Dissipation at Structural Joints: Mechanisms and Magnitudes; Technical Documentary Report No. FDL-TDR-64-98; Wright-Patterson Air Force Base, Air Force Flight Dynamics Lab.: Wright-Patterson OH, USA, 1964. [Google Scholar]
- Han, I.; Gilmore, B.J. Multi-Body Impact Motion with Friction—Analysis, Simulation, and Experimental Validation. J. Mech. Des. 1993, 115, 412–422. [Google Scholar] [CrossRef]
- Gonthier, Y.; McPhee, J.; Lange, C.; Piedbœuf, J.-C. A Regularized Contact Model with Asymmetric Damping and Dwell-Time Dependent Friction. Multibody Syst. Dyn. 2004, 11, 209–233. [Google Scholar] [CrossRef]
- Gaul, L.; Mayer, M. Modeling of Contact Interfaces in Built-up Structures by Zero-thickness Elements. In Schwingungen 2017; VDI Wissensforum GmbH: Düsseldorf, Germany, 2017; pp. 271–286. [Google Scholar] [CrossRef]
- Yang, B.D.; Chu, M.L.; Menq, C.H. Stick–slip–separation analysis and non-linear stiffness and damping characterization of friction contacts having variable normal load. J. Sound Vib. 1998, 210, 461–481. [Google Scholar] [CrossRef]
- Rajaei, M.; Ahmadian, H. Development of generalized Iwan model to simulate frictional contacts with variable normal loads. Appl. Math. Model. 2014, 38, 4006–4018. [Google Scholar] [CrossRef]
- Ouyang, H.; Oldfield, M.J.; Mottershead, J.E. Experimental and theoretical studies of a bolted joint excited by a torsional dynamic load. Int. J. Mech. Sci. 2006, 48, 1447–1455. [Google Scholar] [CrossRef]
- Oldfield, M.; Ouyang, H.; Mottershead, J.E. Simplified models of bolted joints under harmonic loading. Comput. Struct. 2005, 84, 25–33. [Google Scholar] [CrossRef]
- Mindlin, R.D. Compliance of elastic bodies in contact. J. Appl. Mech. 2021, 16, 259–268. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Mason, W.P.; Osmer, T.F.; Deresiewicz, H. Effects of an oscillating tangential force on the contact surfaces of elastic spheres. In Proceedings of the First US National Congress of Applied Mechanics, Chicago, IL, USA, 11–16 June 1989. [Google Scholar]
- Segalman, D.J. A Four-Parameter Iwan Model for Lap-Type Joints. J. Appl. Mech. 2005, 72, 752–760. [Google Scholar] [CrossRef]
- Li, Y.; Hao, Z. A six-parameter Iwan model and its application. Mech. Syst. Signal Process. 2016, 68–69, 354–365. [Google Scholar] [CrossRef]
- Wang, D.; Fan, X. Dynamic analysis of hysteretic nonlinear characteristics of connected interface. J. Vib. Eng. 2019, 32, 1060–1066. [Google Scholar]
- Liu, B.; Dong, X.; Peng, Z. Nonlinear equivalent model of bolted joint surface based on Iwan model. Noise Vib. Control 2020, 40, 7–12. [Google Scholar]
- Gong, H.; Liu, J.; Ding, X. Thorough understanding on the mechanism of vibration-induced loosening of threaded fasteners based on modified Iwan model. J. Sound Vib. 2020, 473, 115238. [Google Scholar] [CrossRef]
- Lischinsky, P.; Canudas-De-Wit, C.; Morel, G. Friction compensation for an industrial hydraulic robot. IEEE Control Syst. Mag. 1999, 19, 25–32. [Google Scholar]
- Freidovich, L.; Robertsson, A.; Shiriaev, A.; Johansson, R. LuGre-model-based friction compensation. IEEE Trans. Control Syst. Technol. 2010, 18, 194–200. [Google Scholar] [CrossRef]
- Renger, A.; Johnson, K.L. Contact Mechanics; John Wiley & Sons, Ltd.: Cambridge, UK, 1989. [Google Scholar]
- Greenwood, J.A.; Williamson, J.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. A 1966, 295, 300–319. [Google Scholar]
- Greenwood, J.A. A unified theory of surface roughness. Proc. R. Soc. Lond. A 1984, 393, 133–157. [Google Scholar]
- Chang, W.-R.; Etsion, I.; Bogy, D. An Elastic-Plastic Model for the Contact of Rough Surfaces. J. Tribol. Trans. Asme 1987, 109, 257–263. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. Elastic-Plastic Contact Analysis of a Sphere and a Rigid Flat. J. Appl. Mech. 2002, 69, 657–662. [Google Scholar] [CrossRef]
- Brizmer, V.; Kligerman, Y.; Etsion, I. Elastic–plastic spherical contact under combined normal and tangential loading in full stick. Tribol. Lett. 2007, 25, 61–70. [Google Scholar] [CrossRef]
- Zhao, Y.; Lv, Y.; Jiang, J. A new elastoplastic contact model for rough surfaces. J. Mech. Eng. 2007, 109, 95–101. [Google Scholar] [CrossRef]
- Mikic, B. Analytical studies of contact of noinally flat surfaces; Effect of previous loading. J. Lubr. Technol. 1971, 93, 451–456. [Google Scholar] [CrossRef]
- Mandelbrot, B. How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef]
- Majumdar, A.; Bhushan, B. Role of Fractal Geometry in Roughness Characterization and Contact Mechanics of Surfaces. J. Tribol. 1990, 112, 205–216. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, N.; Wen, S.; Chen, Y.; Lan, G. Elastic-plastic fractal model of tangential contact damping energy dissipation of mechanical joint surfaces. J. Mech. Eng. 2013, 49, 43–49. [Google Scholar]
- Zhang, X.; Wen, S.; Lan, G.; Ding, H.; Zhang, Z.; Wang, X.; Liu, Z. Fractal model and simulation of tangential contact damping of plane joint surface. J. Xi ‘Jiaotong Univ. 2011, 45, 74–77+136. [Google Scholar]
- Rogers, P.F.; Boothroyd, G. Damping at Metallic Interfaces Subjected to Oscillating Tangential Loads. J. Eng. Ind. 1975, 97, 1087–1093. [Google Scholar] [CrossRef]
- Padmanabhan, K.K.; Murty, A. Damping in structural joints subjected to tangential loads. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1991, 205, 121–129. [Google Scholar] [CrossRef]
- Ren, Y.; Beards, C.F. An experimental study on the dynamic response of a beam structure containing a pseudo joint. J. Mech. Eng. Sci. 1994, 208, 321–328. [Google Scholar] [CrossRef]
- Ulutan, M.; Celik, O.N.; Gasan, H.; Er, U. Effect of Different Surface Treatment Methods on the Friction and Wear Behavior of AISI 4140 Steel. J. Mater. Sci. Technol. 2010, 26, 251–257. [Google Scholar] [CrossRef]
- Eriten, M.; Polycarpou, A.; Bergman, L. Development of a Lap Joint Fretting Apparatus. Exp. Mech. 2011, 51, 1405–1419. [Google Scholar] [CrossRef]
- Eriten, M.; Polycarpou, A.A.; Bergman, L.A. Effects of surface roughness and lubrication on the early stages of fretting of mechanical lap joints. Wear 2011, 271, 2928–2939. [Google Scholar] [CrossRef]
- Eriten, M.; Lee, C.H.; Polycarpou, A.A. Measurements of tangential stiffness and damping of mechanical joints: Direct versus indirect contact resonance methods. Tribol. Int. 2012, 50, 35–44. [Google Scholar] [CrossRef]
- Ovcharenko, A.; Halperin, G.; Etsion, I.; Varenberg, M. A novel test rig for in situ and real time optical measurement of the contact area evolution during pre-sliding of a spherical contact. Tribol. Lett. 2006, 23, 55–63. [Google Scholar] [CrossRef]
- Varenberg, M.; Halperin, G.; Etsion, I. Different aspects of the role of wear debris in fretting wear. Wear 2002, 252, 902–910. [Google Scholar] [CrossRef]
- Abad, J.; Medel, F.J.; Franco, J.M. Determination of Valanis model parameters in a bolted lap joint: Experimental and numerical analyses of frictional dissipation. Int. J. Mech. Sci. 2014, 89, 289–298. [Google Scholar] [CrossRef]
- Kartal, M.E.; Mulvihill, D.M.; Nowell, D.; Hills, D.A. Determination of the Frictional Properties of Titanium and Nickel Alloys Using the Digital Image Correlation Method. Exp. Mech. 2011, 51, 359–371. [Google Scholar] [CrossRef]
- Schwingshackl, C.; Petrov, E.; Ewins, D. Measured and estimated friction interface parameters in a nonlinear dynamic analysis. Mech. Syst. Signal Process. 2012, 28, 574–584. [Google Scholar] [CrossRef]
- Botto, D.; Lavella, M. High temperature tribological study of cobalt-based coatings reinforced with different percentages of alumina. Wear 2014, 318, 89–97. [Google Scholar] [CrossRef]
- Mu, A.; Db, A. Measurement of contact parameters on under-platform dampers coupled with blade dynamics. Int. J. Mech. Sci. 2019, 159, 450–458. [Google Scholar]
- Botto, D.; Campagna, A.; Lavella, M.; Gola, M.M. Experimental and Numerical Investigation of Fretting Wear at High Temperature for Aeronautical Alloys. Asme Turbo Expo Power Land Sea Air 2010, 44014, 1353–1362. [Google Scholar]
- Eckhard, K.; Thomas, W.; Thomas, G.; Menning, J.D.M.; Peters, J.; Breimann, R.; Kraus, B.; Welzbacher, P.; Küchenhof, J.; Krause, D.; et al. A review on sensor-integrating machine elements. Adv. Sens. Res. 2024, 3, 2300113. [Google Scholar]
- Liu, N.; Bai, J.; Hua, J. Research on the source analysis and improvement of nonmatter understanding in higher order harmonic balance method. Chin. J. Theor. Appl. Mech. 2016, 48, 897–906. [Google Scholar]
- David, J.W.; Mitchell, L.D.; Daws, J.W. Using transfer matrices for parametric system forced response. J. Vib. Acoust. Stress 1987, 109, 356–360. [Google Scholar] [CrossRef]
- Zhou, B.; Thouverez, F.; Lenoir, D. A variable-coefficient harmonic balance method for the prediction of quasi-periodic response in nonlinear systems. Mech. Syst. Signal Process. 2015, 64–65, 233–244. [Google Scholar] [CrossRef]
- Lacayo, R.; Pesaresi, L.; Groß, J.; Fochler, D.; Armand, J.; Salles, L.; Schwingshackl, C.; Allen, M.; Brake, M. Nonlinear modeling of structures with bolted joints: A comparison of two approaches based on a time-domain and frequency-domain solver. Mech. Syst. Signal Process. 2019, 114, 413–438. [Google Scholar] [CrossRef]
- Coudeyras, N.; Sinou, J.J.; Nacivet, S. A new treatment for predicting the self-excited vibrations of nonlinear systems with frictional interfaces: The Constrained Harmonic Balance Method, with application to disc brake squeal. J. Sound Vib. 2009, 319, 1175–1199. [Google Scholar] [CrossRef]
- Moon, B.Y.; Kang, B.S. Vibration analysis of harmonically excited non-linear system using the method of multiple scales. J. Sound Vib. 2003, 263, 1–20. [Google Scholar] [CrossRef]
- Chen, Y.M.; Liu, J.K. A new method based on the harmonic balance method for nonlinear oscillators. Phys. Lett. A 2007, 368, 371–378. [Google Scholar] [CrossRef]
- Von Groll, G.; Ewins, D.J. The harmonic balance method with arc-length continuation in rotor/stator contact problems. J. Sound Vib. 2001, 241, 223–233. [Google Scholar] [CrossRef]
- Ren, Y.; Lim, T.M.; Lim, M.K. Identification of properties of nonlinear joints using dynamic test data. J. Vib. Acoust. 1998, 120, 324–330. [Google Scholar] [CrossRef]
- Petrov, E.P. A high-accuracy model reduction for analysis of nonlinear vibrations in structures with contact interfaces. J. Eng. Gas Turbines Power 2011, 133, 1025–1037. [Google Scholar] [CrossRef]
- Firrone, C.M.; Zucca, S.; Gola, M.M. The effect of underplatform dampers on the forced response of bladed disks by a coupled static/dynamic harmonic balance method. Int. J. Non-Linear Mech. 2011, 46, 363–375. [Google Scholar] [CrossRef]
- Allen, M.S.; Lacayo, R.M.; Brake, M.R. Quasi-static modal analysis based on implicit condensation for structures with nonlinear joints. In Proceedings of the International Conference on Noise and Vibration Engineering, Leuven, Belgium, 18–21 September 2016. [Google Scholar]
- Yuan, J.; Salles, L.; El Haddad, F.; Wong, C. An adaptive component mode synthesis method for dynamic analysis of jointed structure with contact friction interfaces. Comput. Struct. 2020, 229, 106177.1–106177.15. [Google Scholar] [CrossRef]
- Bai, H.; Huang, X. Study on the calculation method of Krylov-Bogoliubov for random excitation of oscillators with velocity variation of sliding friction coefficient. Mech. Sci. Technol. Aerosp. Eng. 2001, 20, 346–347. [Google Scholar]
- Li, H.; Liu, J.; He, B.; Wang, H.K.; Pei, D. A simplified method of equipment impact connector based on time domain analysis. Chin. J. Ship Res. 2018, 13, 85–89. [Google Scholar] [CrossRef]
- Subbaraj, K.; Dokainish, M.A. A survey of direct time-integration methods in computational structural dynamics—II. Implicit methods. Comput. Struct. 1989, 32, 1387–1401. [Google Scholar] [CrossRef]
- Xie, Y.M. An assessment of time intergation schemes for non-linear dynamic equations. J. Sound Vib. 1996, 192, 321–331. [Google Scholar] [CrossRef]
- Hagedorn, P.; Schramm, W. On the dynamics of large systems with localized nonlinearities. J. Appl. Mech. 1988, 55, 946–951. [Google Scholar] [CrossRef]
- Cao, J.; Liu, Q.; Hong, J. A review of microscopically to macroscopically dynamic studies of bolting. China Mech. Eng. 2020, 11, 1–14. [Google Scholar]
- Deng, J.; Cheng, G. Reduction method of structural dynamic model based on local interpolation. Chin. J. Theor. Appl. Mech. 2012, 44, 342–350. [Google Scholar]
- Wang, D.; Zhang, Z. Time-frequency domain dynamic reduction method for connecting local hysteretic nonlinearities. J. Vib. Eng. 2021, 34, 559–566. [Google Scholar]
- Miller, J.D.; Dane Quinn, D. A two-sided interface model for dissipation in structural systems with frictional joints. J. Sound Vib. 2009, 321, 201–219. [Google Scholar] [CrossRef]
- Gaul, L.; Nitsche, R. The Role of Friction in Mechanical Joints. Appl. Mech. Rev. 2001, 54, 93–106. [Google Scholar] [CrossRef]
- Wei, F. Local Nonlinear Structural Analysis Method and Its Application in Spacecraft Structural Analysis; Harbin Institute of Technology: Harbin, China, 2010. [Google Scholar]
- Wang, D.; Zhang, Z. High-efficiency nonlinear dynamic analysis for joint interfaces with Newton–Raphson iteration process. Nonlinear Dyn. 2020, 100, 543–559. [Google Scholar] [CrossRef]
- Minorsky, N. Nonlinear oscillations. Phys. Today 1962, 15, 63–65. [Google Scholar] [CrossRef]
- Ahmadian, H.; Jalali, H. Generic element formulation for modelling bolted lap joints. Mech. Syst. Signal Process. 2007, 21, 2318–2334. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, X.; Wei, H. Nonlinear vibration of dry friction vibrator with Iwan model based on harmonic balance method. J. Aerosp. Power 2013, 28, 1–9. [Google Scholar]
- Kim, T.C.; Rook, T.E.; Singh, R. Super- and sub-harmonic response calculations for a torsional system with clearance nonlinearity using the harmonic balance method. J. Sound Vib. 2005, 281, 965–993. [Google Scholar] [CrossRef]
- Khajeh Salehani, M.; Irani, N.; Nicola, L. Modeling adhesive contacts under mixed-mode loading. J. Mech. Phys. Solids 2019, 130, 320–329. [Google Scholar] [CrossRef]
- Waters, J.F.; Guduru, P.R. Mode-mixity-dependent adhesive contact of a sphere on a plane surface. Proc. R. Soc. A Math. Phys. Eng. Sci. 2009, 466, 1303–1325. [Google Scholar] [CrossRef]
- Kou, J.; Xu, F.; Xie, W.; Zhang, X.; Feng, W. A theoretical 4-stage shear model for single-lap torqued bolted-joint with clearances. Compos. Struct. 2018, 186, 1–16. [Google Scholar] [CrossRef]
- Lobitz, D.; Gregory, D.; Smallwood, D. Comparison of Finite Element Predictions to Measurements from the Sandia Microslip Experiment. In Proceedings of the IMAC XIX Conference on Structural Dynamics, Kissimmee, FL, USA, 9 November 2000. [Google Scholar]

| Method | Advantages | Disadvantages |
|---|---|---|
| Direct method | Real and reliable data | High cost, long experiment period, complex loading equipment and measuring instruments |
| Indirect method | Low cost, short experiment period | Complex data-parsing and signal-processing techniques, limited information |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Zhu, M.; Guo, M.; Wu, F. A Review of the Degradation Research on the Single-Lap Bolted Joint. Machines 2024, 12, 711. https://doi.org/10.3390/machines12100711
Wang S, Zhu M, Guo M, Wu F. A Review of the Degradation Research on the Single-Lap Bolted Joint. Machines. 2024; 12(10):711. https://doi.org/10.3390/machines12100711
Chicago/Turabian StyleWang, Sheng’ao, Min Zhu, Ming Guo, and Fei Wu. 2024. "A Review of the Degradation Research on the Single-Lap Bolted Joint" Machines 12, no. 10: 711. https://doi.org/10.3390/machines12100711
APA StyleWang, S., Zhu, M., Guo, M., & Wu, F. (2024). A Review of the Degradation Research on the Single-Lap Bolted Joint. Machines, 12(10), 711. https://doi.org/10.3390/machines12100711





