Resilient Reinforcement Learning for Voltage Control in an Islanded DC Microgrid Integrating Data-Driven Piezoelectric
Abstract
1. Introduction
2. Material Testing Machine and Piezoelectric Data
2.1. Testing System
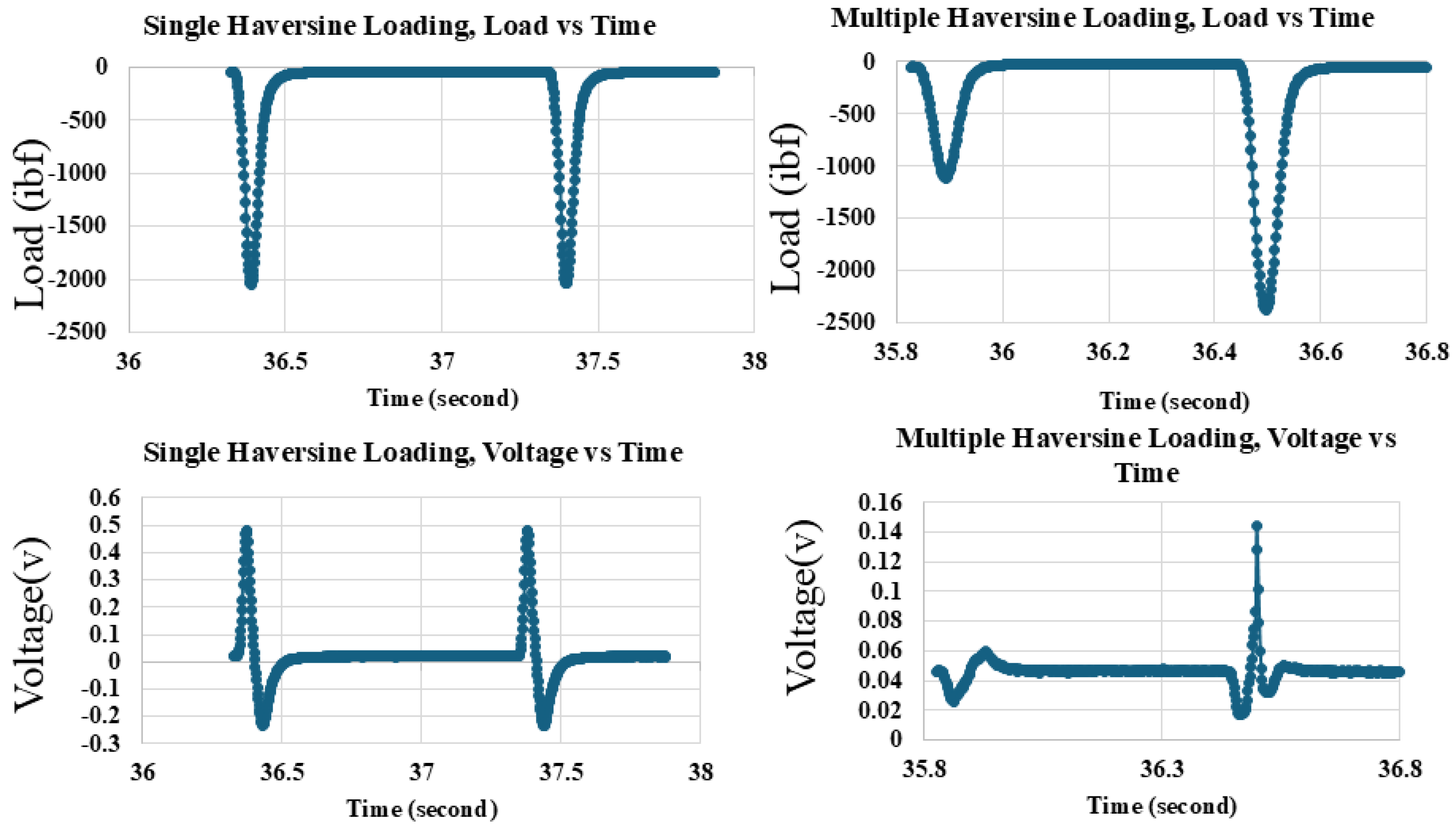
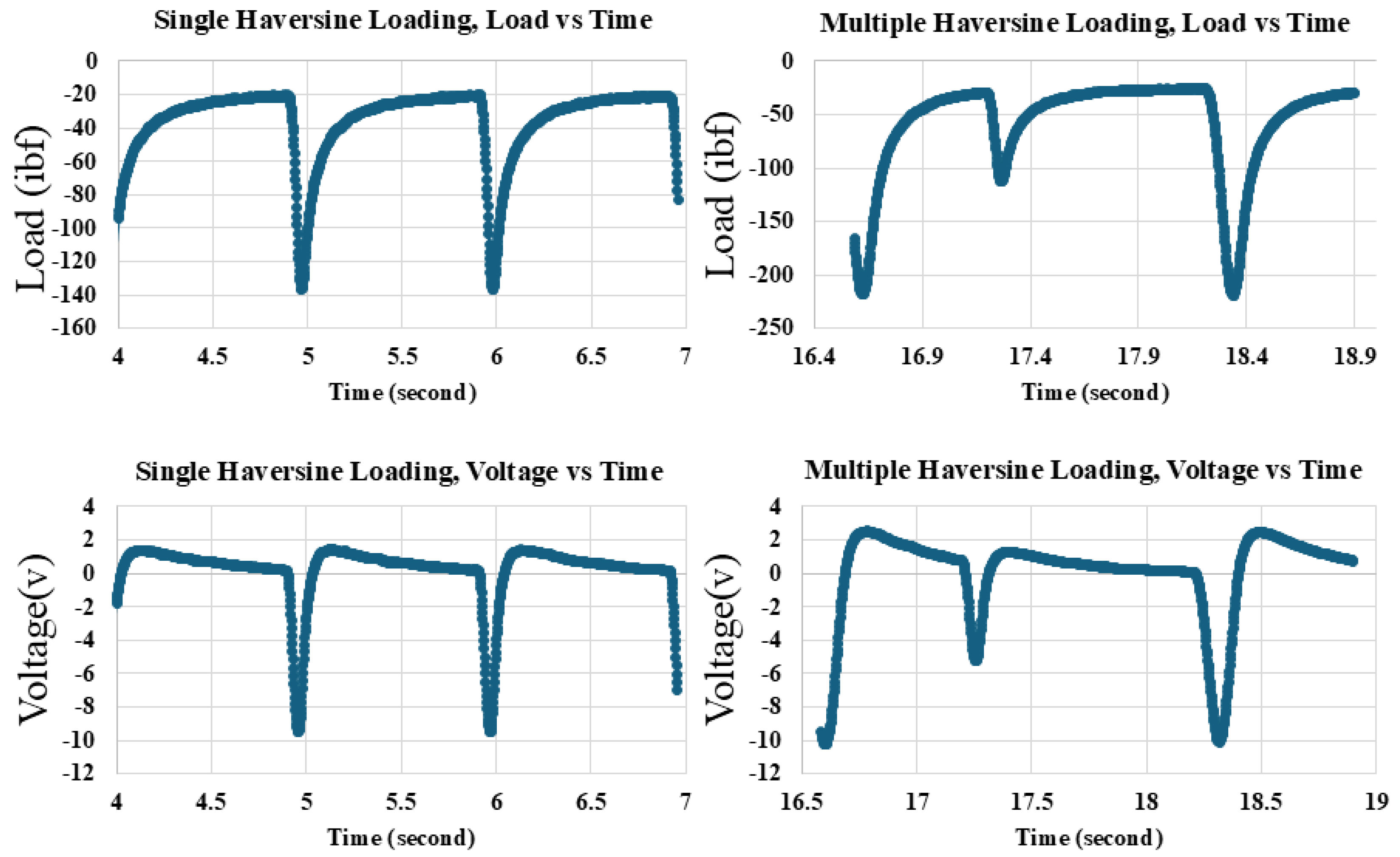
2.2. Embedment of Piezoelectric Sensors in Fiber-Reinforced Concrete Samples
2.3. Piezoelectric Sensors in Asphalt Samples
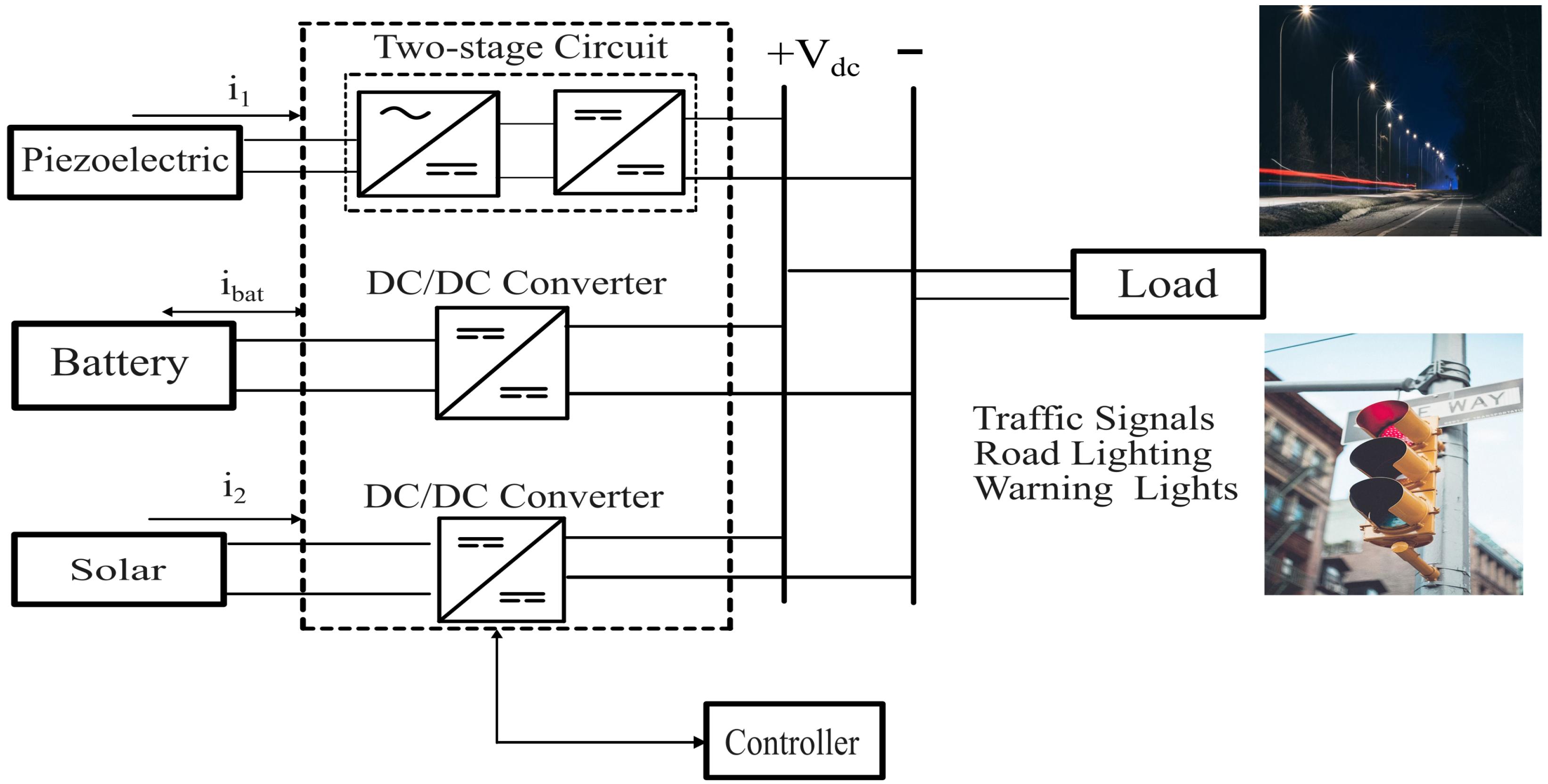
3. Islanded DC Microgrid Configurations and Setup
3.1. Piezoelectric
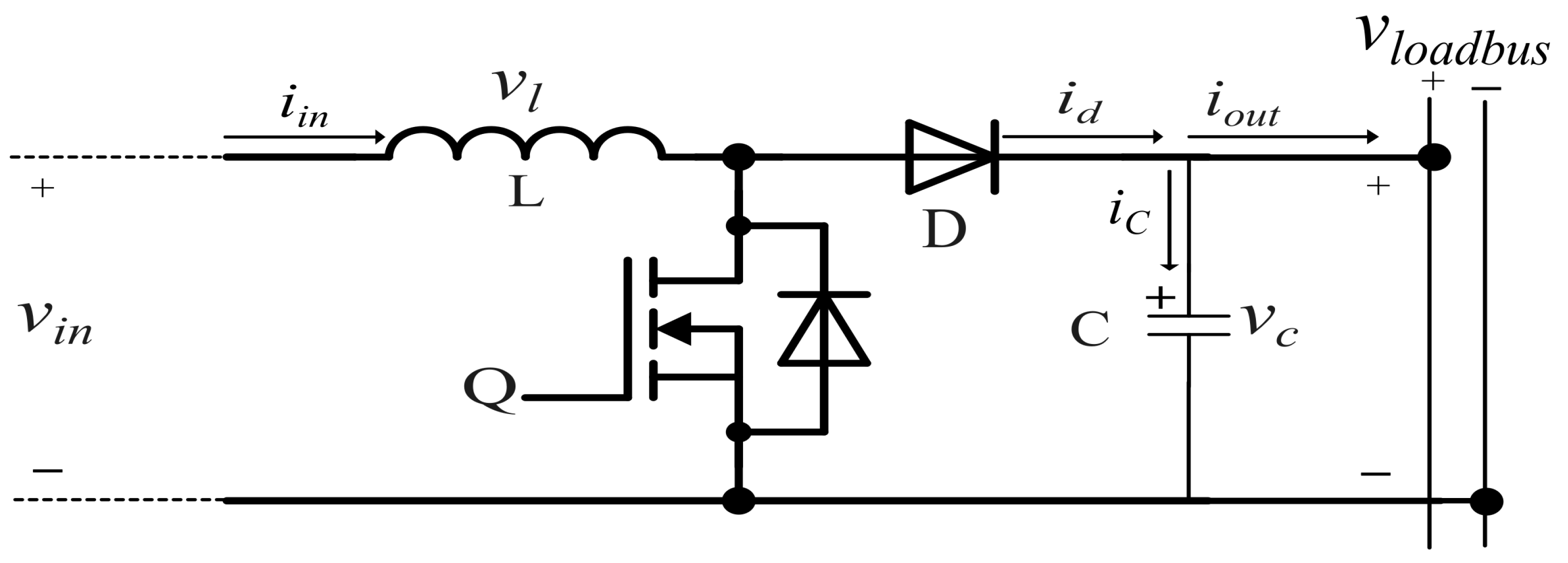
3.1.1. Rectifier
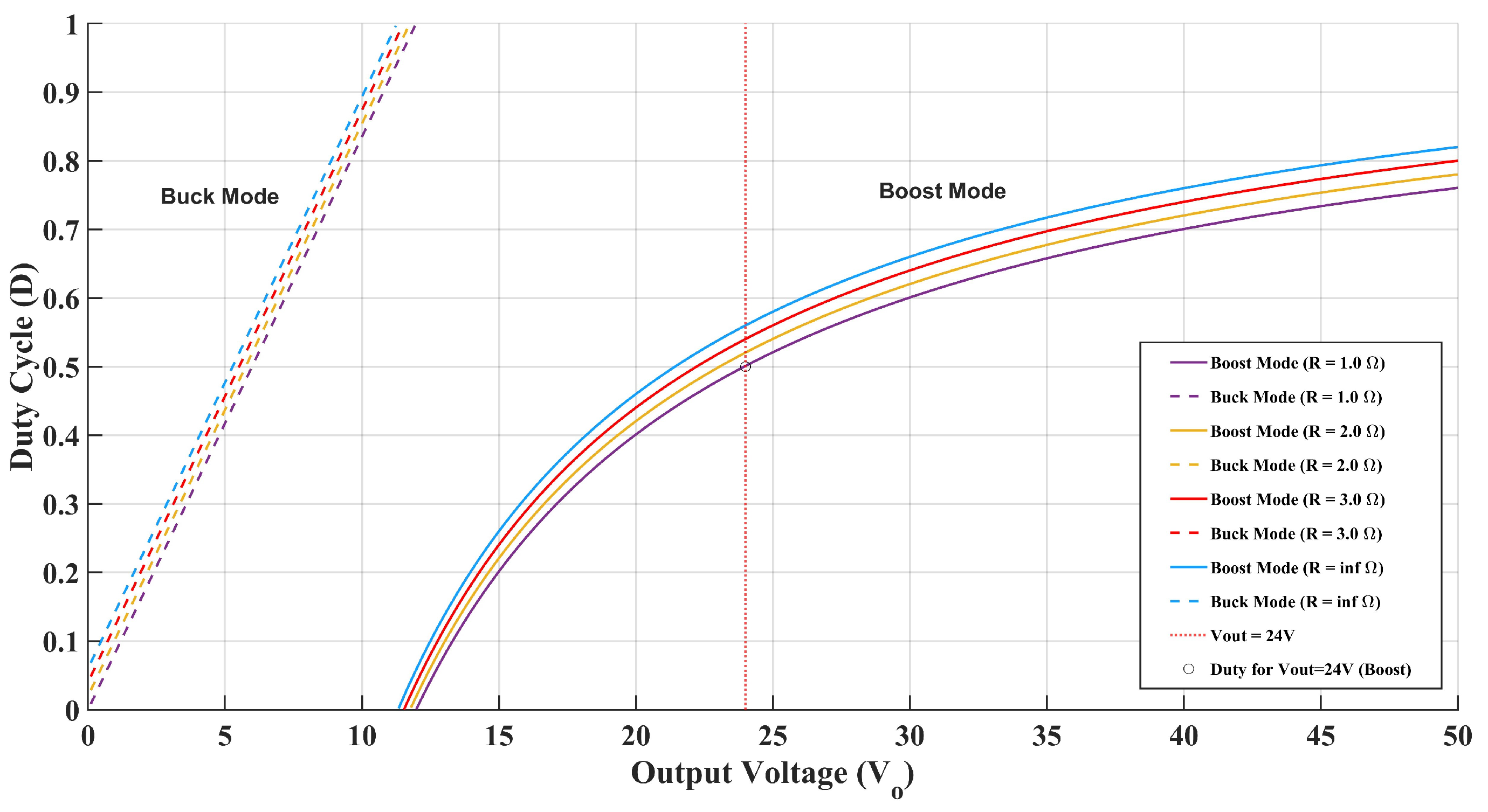
3.1.2. DC-DC Boost Converter
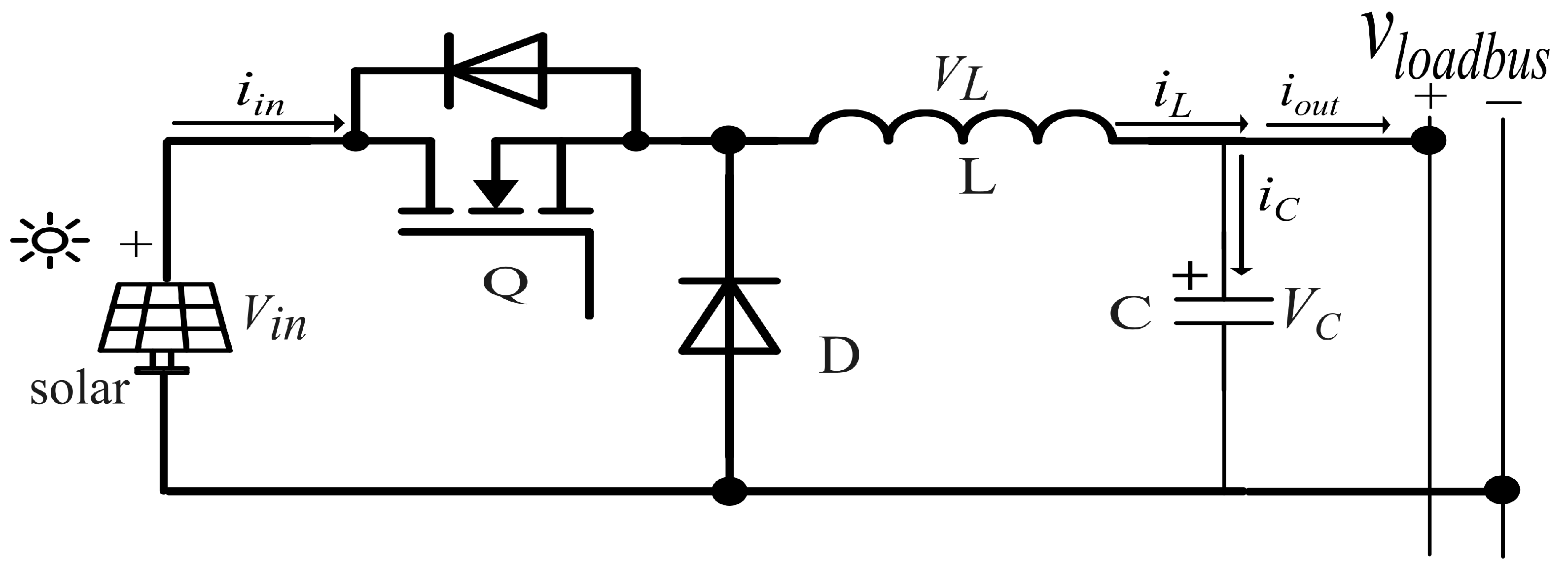
3.2. Solar
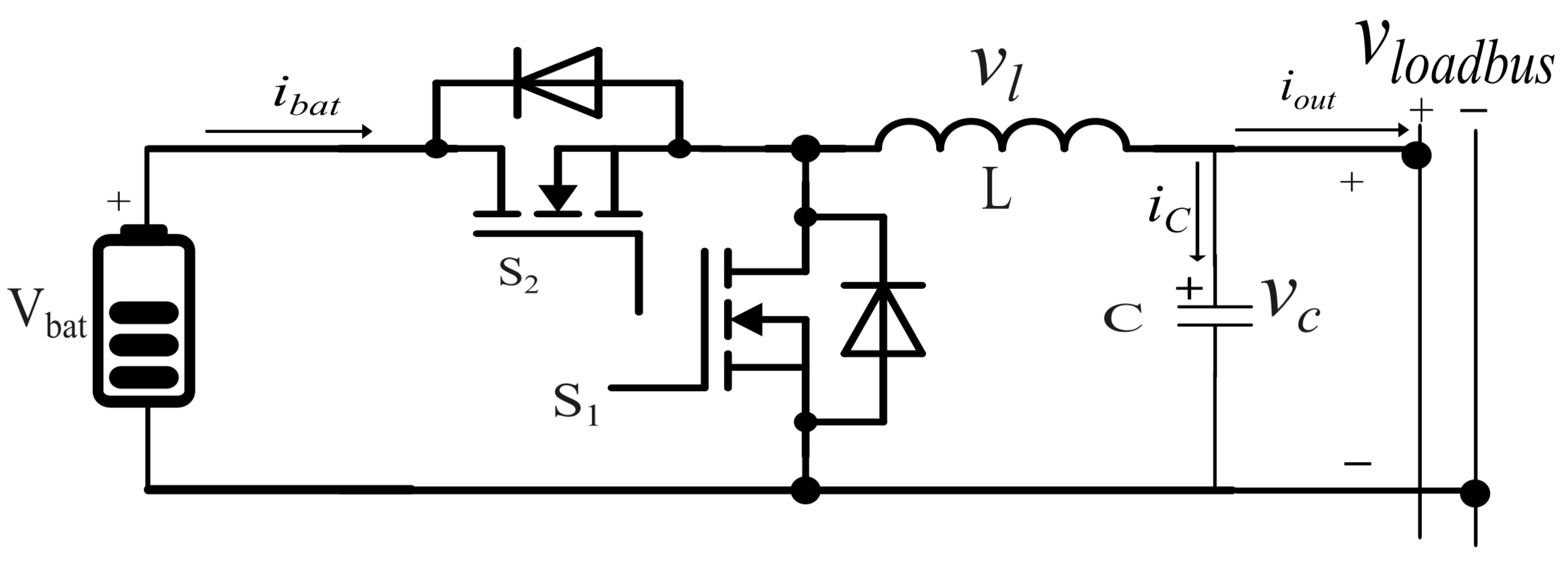
3.3. Battery
4. Methodology and Proposed Controller
4.1. Reinforcement Learning
4.1.1. Regression
4.1.2. Suggested Approach
| Algorithm 1 Policy update algorithm |
|
5. Results and Discussion
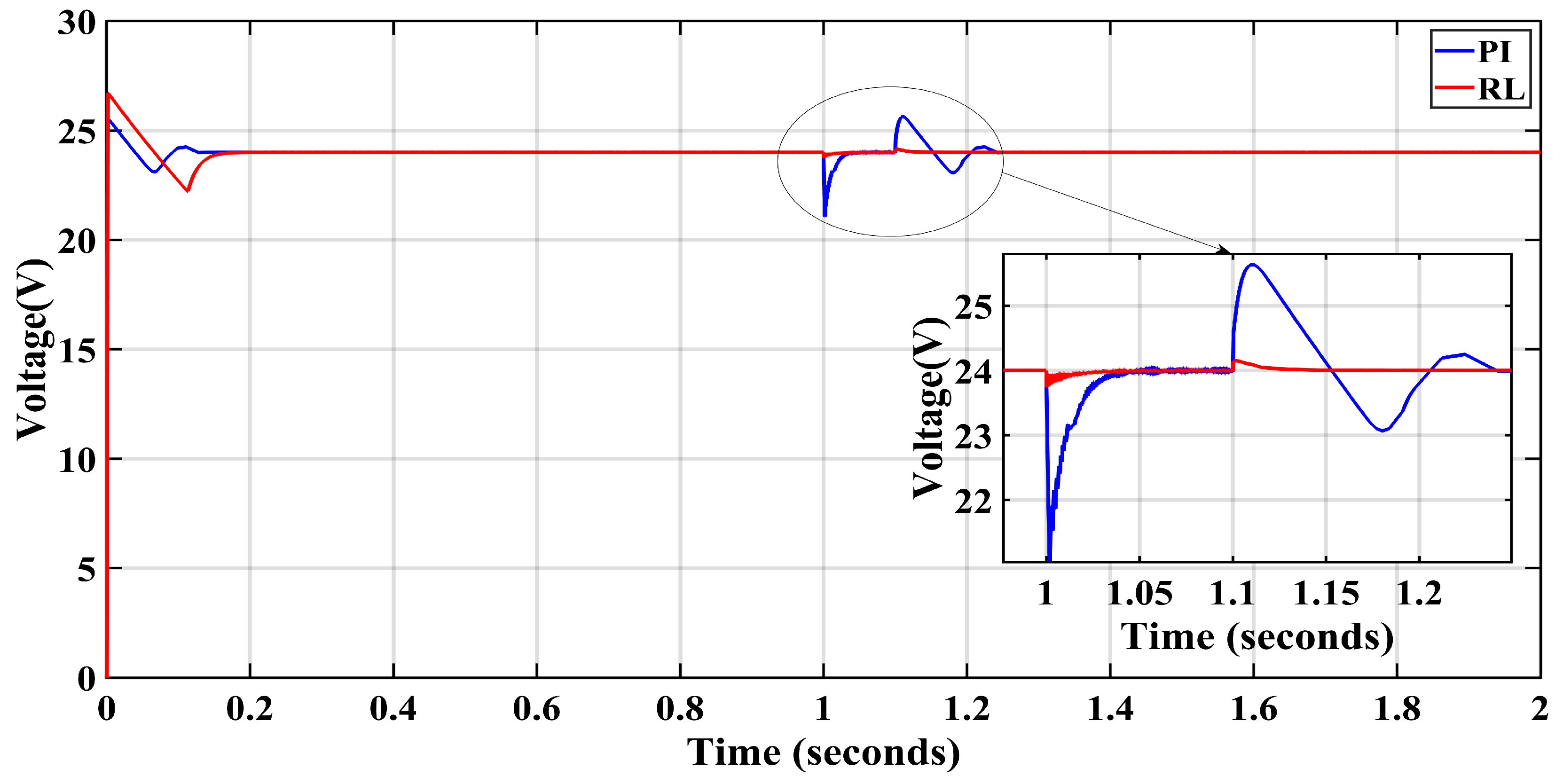
5.1. Short Circuit Across the Load
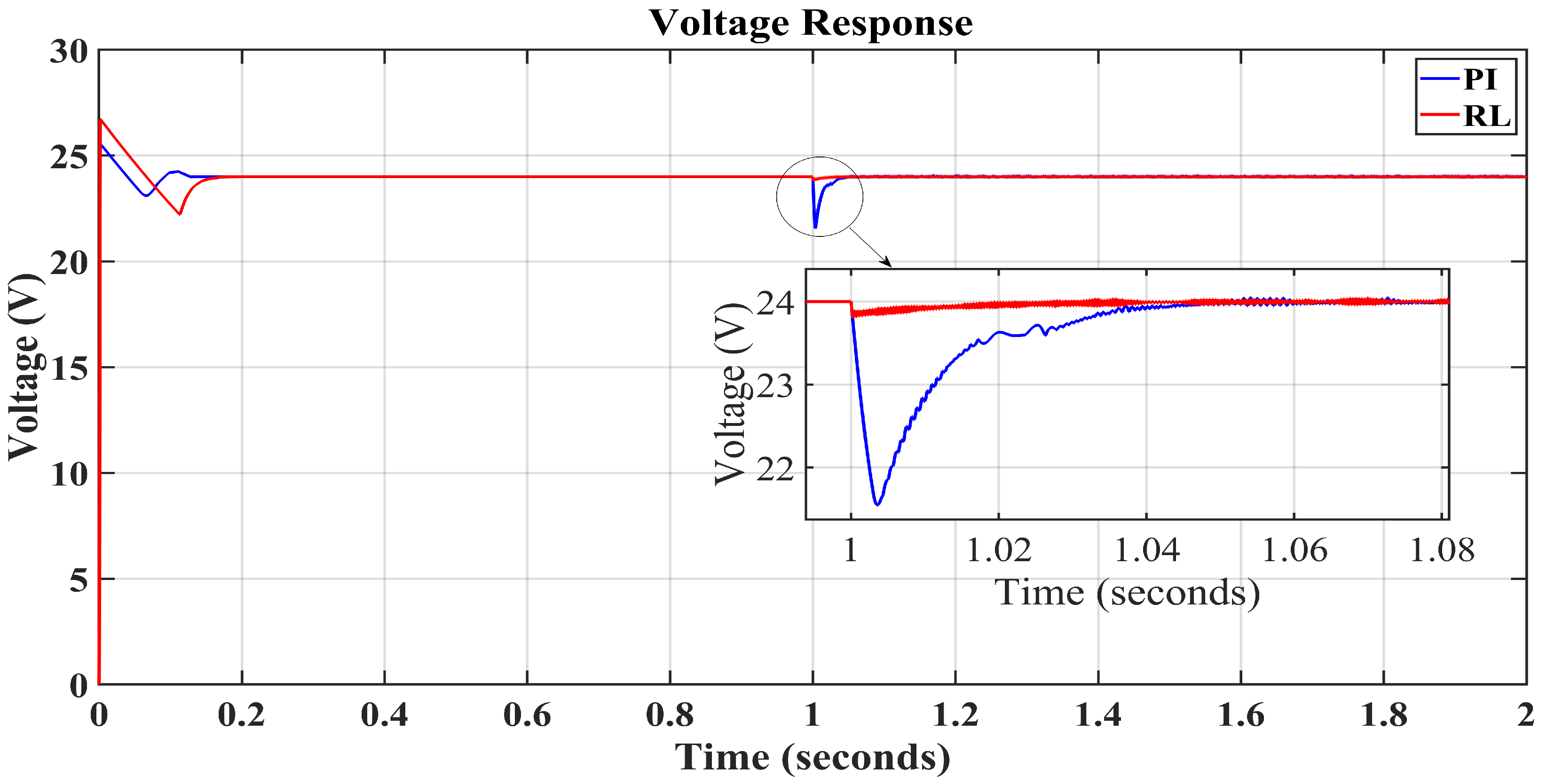
5.2. Converter Failure
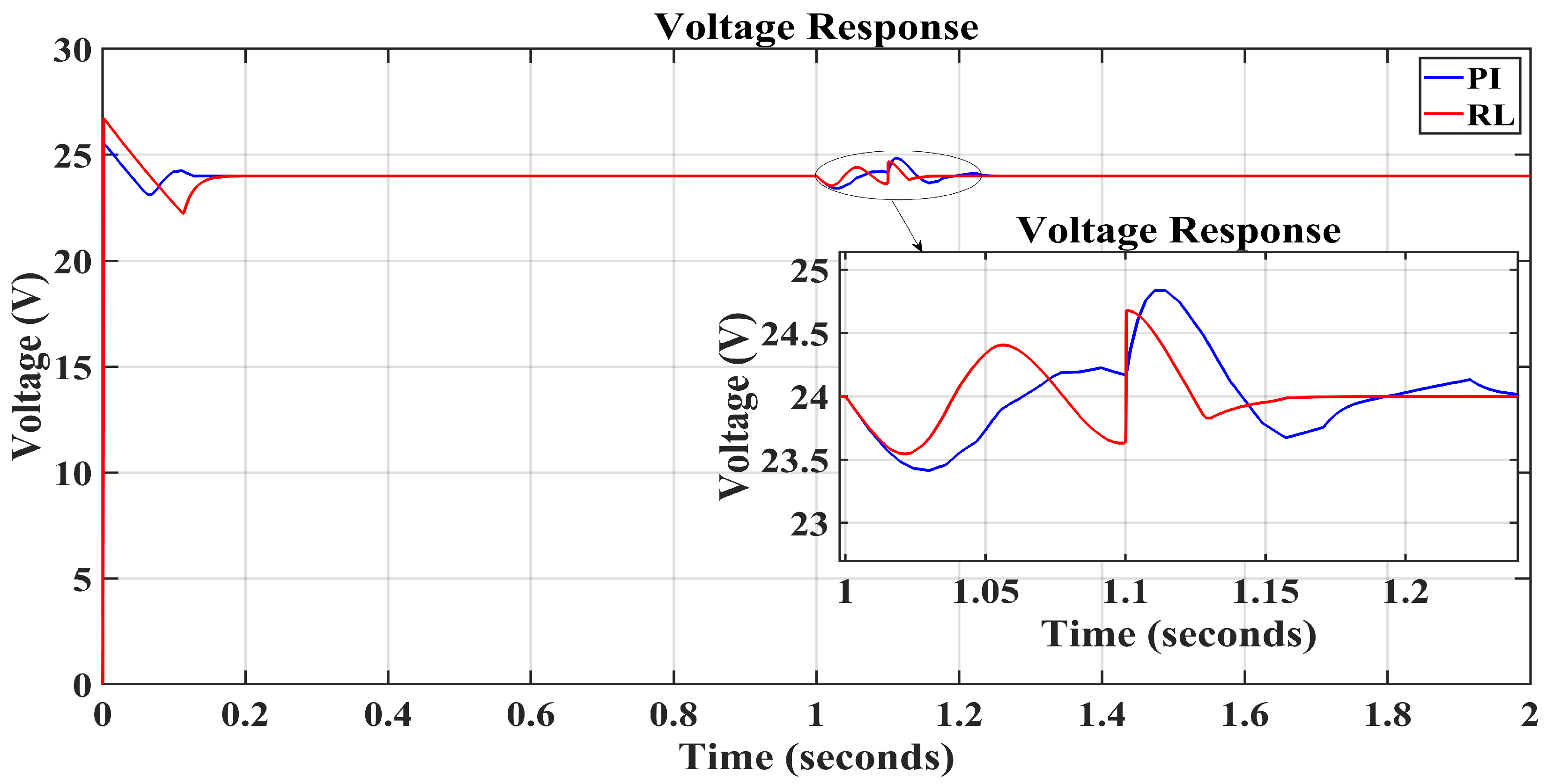
5.3. Load Variation
5.4. Open Circuit of the Load
6. What Is Next
7. Conclusions and Future Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Saeed, M.H.; Fangzong, W.; Kalwar, B.A.; Iqbal, S. A review on microgrids’ challenges & perspectives. IEEE Access 2021, 9, 166502–166517. [Google Scholar]
- Strielkowski, W.; Civín, L.; Tarkhanova, E.; Tvaronavičienė, M.; Petrenko, Y. Renewable energy in the sustainable development of electrical power sector: A review. Energies 2021, 14, 8240. [Google Scholar] [CrossRef]
- Abdelghany, M.B.; Al-Durra, A.; Gao, F. A coordinated optimal operation of a grid-connected wind-solar microgrid incorporating hybrid energy storage management systems. IEEE Trans. Sustain. Energy 2023, 15, 39–51. [Google Scholar] [CrossRef]
- Edla, M.; Lim, Y.Y.; Mikio, D.; Padilla, R.V. A Single-Stage Rectifier-Less Boost Converter Circuit for Piezoelectric Energy Harvesting Systems. IEEE Trans. Energy Convers. 2022, 37, 505–514. [Google Scholar] [CrossRef]
- Lefeuvre, E.; Audigier, D.; Richard, C.; Guyomar, D. Buck-Boost Converter for Sensorless Power Optimization of Piezoelectric Energy Harvester. IEEE Trans. Power Electron. 2007, 22, 2018–2025. [Google Scholar] [CrossRef]
- Bairagi, S.; ul Islam, S.; Shahadat, M.; Mulvihill, D.M.; Ali, W. Mechanical energy harvesting and self-powered electronic applications of textile-based piezoelectric nanogenerators: A systematic review. Nano Energy 2023, 111, 108414. [Google Scholar] [CrossRef]
- Yingyong, P.; Thainiramit, P.; Jayasvasti, S.; Thanach-Issarasak, N.; Isarakorn, D. Evaluation of harvesting energy from pedestrians using piezoelectric floor tile energy harvester. Sens. Actuators A Phys. 2021, 331, 113035. [Google Scholar] [CrossRef]
- Sun, J.-Q.; Xu, T.-B.; Yazdani, A. Ultra-High Power Density Roadway Piezoelectric Energy Harvesting System. Ph.D. Thesis, University of California, Merced, CA, USA, 2023; pp. 1–42. [Google Scholar]
- Long, S.X.; Khoo, S.Y.; Ong, Z.C.; Soong, M.F. Finite element analysis of a dual-layer substrate sandwiched bridge piezoelectric transducer for harvesting energy from asphalt pavement. In Proceedings of the 2019 IEEE International Conference on Sensors and Nanotechnology, Penang, Malaysia, 24–25 July 2019. [Google Scholar] [CrossRef]
- Rezaei-Hosseinabadi, N.; Amoorezaei, A.; Tabesh, A.; Khajehoddin, S.A.; Dehghani, R.; Moez, K. A Voltage-Feedback-Based Maximum Power Point Tracking Technique for Piezoelectric Energy Harvesting Interface Circuits. IEEE Internet Things J. 2024, 11, 20433–20442. [Google Scholar] [CrossRef]
- Feng, Y.; Liang, M.; Li, Y. Adaptive Controller with Anti-Windup Compensator for Piezoelectric Micro Actuating Systems. IEEE Trans. Nanotechnol. 2024, 23, 45–54. [Google Scholar] [CrossRef]
- Forrester, J.; Davidson, J.N.; Foster, M.P. Inductorless Step-Up Piezoelectric Resonator (SUPR) Converter: A Describing Function Analysis. IEEE Trans. Power Electron. 2023, 38, 12874–12885. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.; Law, M.K.; Du, S.; Liang, J.; Cheng, X.; Han, J.; Zeng, X.; Chen, Z. Piezoelectric Energy Harvesting Interface Using Self-Bias-Flip Rectifier and Switched-PEH DC–DC for MPPT. IEEE J. Solid-State Circuits 2024, 59, 2248–2259. [Google Scholar] [CrossRef]
- Mahmood, H.; Michaelson, D.; Jiang, J. A Power Management Strategy for PV/Battery Hybrid Systems in Islanded Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 870–882. [Google Scholar] [CrossRef]
- Yang Zhao, K.W.; Guan, M. An adaptive boost converter for low voltage piezoelectric energy harvesting. Ferroelectrics 2016, 502, 107–118. [Google Scholar] [CrossRef]
- Arunkumari, T.; Indragandhi, V. An overview of high voltage conversion ratio DC-DC converter configurations used in DC micro-grid architectures. Renew. Sustain. Energy Rev. 2017, 77, 670–687. [Google Scholar] [CrossRef]
- Cristri, A.; Iskandar, R. Analysis and Design of Dynamic Buck Converter with Change in Value of Load Impedance. Procedia Eng. 2017, 170, 398–403. [Google Scholar] [CrossRef]
- Galkin, I.A.; Saltanovs, R.; Bubovich, A.; Blinov, A.; Peftitsis, D. Considerations on Combining Unfolding Inverters with Partial Power Regulators in Battery–Grid Interface Converters. Energies 2024, 17, 893. [Google Scholar] [CrossRef]
- Kumar, R.R.; Bharatiraja, C.; Udhayakumar, K.; Devakirubakaran, S.; Sekar, K.S.; Mihet-Popa, L. Advances in Batteries, Battery Modeling, Battery Management System, Battery Thermal Management, SOC, SOH, and Charge/Discharge Characteristics in EV Applications. IEEE Access 2023, 11, 105761–105809. [Google Scholar] [CrossRef]
- Mahazabeen, M.; Abianeh, A.J.; Ebrahimi, S.; Daoud, H.; Ferdowsi, F. Enhancing EV charger resilience with reinforcement learning aided control. e-Prime Adv. Electr. Eng. Electron. Energy 2023, 5, 100276. [Google Scholar] [CrossRef]
- Seyedi, M.; Sheida, K.; Siner, S.; Ferdowsi, F. Enhanced Resilience in Battery Charging through Co-Simulation with Reinforcement Learning. Available online: https://www.techrxiv.org/doi/pdf/10.36227/techrxiv.170846720.02245839 (accessed on 30 September 2024).
- Sheida, K.; Seyedi, M.; Ferdowsi, F. Adaptive Voltage and Frequency Regulation for Secondary Control via Reinforcement Learning for Islanded Microgrids. In Proceedings of the 2024 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 12–13 February 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Zhao, S.; Blaabjerg, F.; Wang, H. An overview of artificial intelligence applications for power electronics. IEEE Trans. Power Electron. 2020, 36, 4633–4658. [Google Scholar] [CrossRef]
- Marahatta, A.; Rajbhandari, Y.; Shrestha, A.; Phuyal, S.; Thapa, A.; Korba, P. Model predictive control of DC/DC boost converter with reinforcement learning. Heliyon 2022, 8, e11416. [Google Scholar] [CrossRef]
- Saeidinia, Y.; Arabshahi, M.; Aminirad, M.; Shafie-khah, M. Enhancing DC microgrid performance through machine learning-optimized droop control. IET Gener. Transm. Distrib. 2024, 18, 1919–1934. [Google Scholar] [CrossRef]
- Yadav, N.; Tummuru, N.R. Short-Circuit Fault Detection and Isolation Using Filter Capacitor Current Signature in Low-Voltage DC Microgrid Applications. IEEE Trans. Ind. Electron. 2022, 69, 8491–8500. [Google Scholar] [CrossRef]
- Tarzamni, H.; Esmaeelnia, F.P.; Tahami, F.; Fotuhi-Firuzabad, M.; Dehghanian, P.; Lehtonen, M.; Blaabjerg, F. Reliability Assessment of Conventional Isolated PWM DC-DC Converters. IEEE Access 2021, 9, 46191–46200. [Google Scholar] [CrossRef]
- Zhou, S.; Qian, Y.; Wan, Y.; Lin, Z.; Shamash, Y.A.; Premakumar, A.V.P.; Davoudi, A. On the Resilience Analysis of DC Microgrids with Power Buffer Control. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 1–14. [Google Scholar] [CrossRef]











| Sources | Parameters | Values |
|---|---|---|
| Battery | Battery Voltage | 12 V |
| Battery Current | 3 A | |
| Converter Inductor | 4 mH | |
| Converter Capacitor | 400 µF | |
| Internal Inductor Resistance | 0.1 | |
| Load Bus Voltage | 24 V | |
| SOC | 90% | |
| Solar PV | Open Circuit Voltage | 48 V |
| Short-circuit Current | 3 A | |
| Irradiance | 1000 W/m2 | |
| Temperature | 25 °C | |
| Converter Inductor | 4.5 mH | |
| Converter Capacitor | 400 µF | |
| Internal Inductor Resistance | 0.1 | |
| Load Bus Voltage | 24 V | |
| Piezoelectric | Voltage Range | 0–13.5 V |
| Max Current/Module | 0.8 A | |
| Converter Inductor | 4 mH | |
| Internal Inductor Resistance | 0.1 | |
| Converter Capacitor | 400 µF | |
| Load Bus Voltage | 24 V |
| Controller | RL | PI | RL | PI | RL | PI | RL | PI |
|---|---|---|---|---|---|---|---|---|
| Metrics | Scenarios | |||||||
| SCL (%) | OCL (%) | CF (%) | LV (%) | |||||
| Steady-State Error | 0.07 | 0.03 | 0.078 | 0.02 | 0.06 | 0 | 1.79 | 4.12 |
| Overshoot | 0.63 | 6.82 | 0.73 | 1.51 | 2.90 | 3.48 | 0.22 | 0.34 |
| Undershoot | 1.07 | 12.28 | 2.83 | 5.33 | 1.91 | 2.44 | 0.82 | 10.22 |
| Peak-to-Peak | 40.62 | 458.3 | 85.5 | 164.12 | 115.54 | 142.16 | 25.03 | 253.69 |
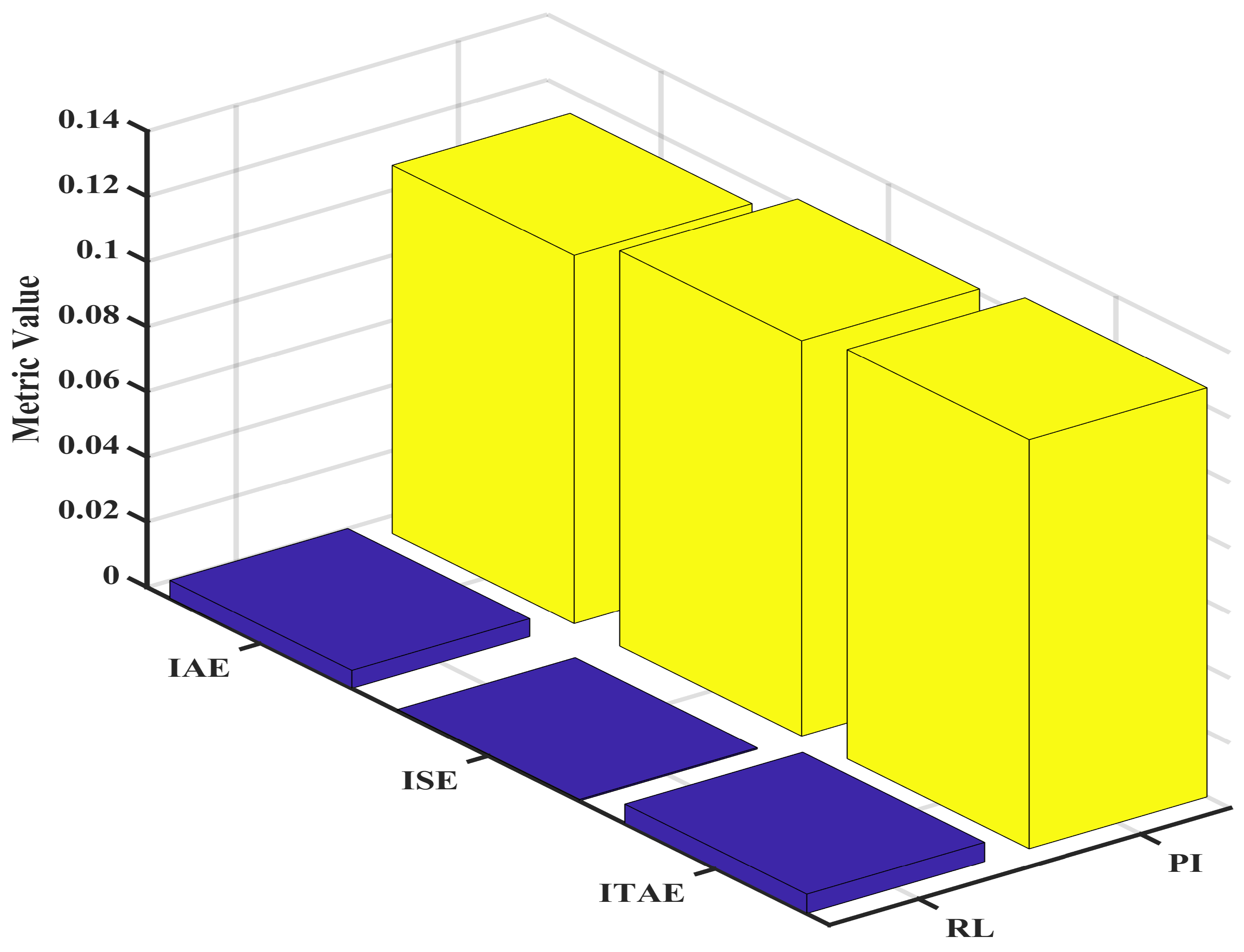
| IAE | 0.55 | 11.31 | 3.35 | 8.31 | 4.01 | 6.15 | 2.06 | 4.45 |
| ISE | 0.04 | 12.14 | 0.91 | 5.16 | 1.44 | 2.75 | 0.07 | 3.70 |
| ITAE | 0.59 | 12.57 | 3.56 | 9.25 | 4.31 | 6.74 | 3.03 | 5.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheida, K.; Seyedi, M.; Afridi, M.A.; Ferdowsi, F.; Khattak, M.J.; Gopu, V.K.; Rupnow, T. Resilient Reinforcement Learning for Voltage Control in an Islanded DC Microgrid Integrating Data-Driven Piezoelectric. Machines 2024, 12, 694. https://doi.org/10.3390/machines12100694
Sheida K, Seyedi M, Afridi MA, Ferdowsi F, Khattak MJ, Gopu VK, Rupnow T. Resilient Reinforcement Learning for Voltage Control in an Islanded DC Microgrid Integrating Data-Driven Piezoelectric. Machines. 2024; 12(10):694. https://doi.org/10.3390/machines12100694
Chicago/Turabian StyleSheida, Kouhyar, Mohammad Seyedi, Muhammad Ali Afridi, Farzad Ferdowsi, Mohammad J. Khattak, Vijaya K. Gopu, and Tyson Rupnow. 2024. "Resilient Reinforcement Learning for Voltage Control in an Islanded DC Microgrid Integrating Data-Driven Piezoelectric" Machines 12, no. 10: 694. https://doi.org/10.3390/machines12100694
APA StyleSheida, K., Seyedi, M., Afridi, M. A., Ferdowsi, F., Khattak, M. J., Gopu, V. K., & Rupnow, T. (2024). Resilient Reinforcement Learning for Voltage Control in an Islanded DC Microgrid Integrating Data-Driven Piezoelectric. Machines, 12(10), 694. https://doi.org/10.3390/machines12100694







