Analysis of Friction and Wear Properties of Friction Ring Materials for Friction Rings under Mixed Lubrication
Abstract
1. Introduction
2. Modeling and Numerical Analysis
2.1. Geometric Models
2.2. Numerical Analysis
2.2.1. Basic Assumptions for Thermal Deformation Analysis
- Neglecting the heat carried away by the leakage, the heat generated by friction is regarded as the heat source, and all of it is transferred between the sealing rings.
- The edge of the seal ring in contact with the air side is regarded as adiabatic, and convective heat transfer is generated with the flushing liquid.
- The properties of the sealing-ring material do not change with temperature, and the coefficient of friction remains unchanged.
2.2.2. Calculation of Thermodynamic Parameters
2.3. Archard Wear Model
3. Wear Test
3.1. Test Material
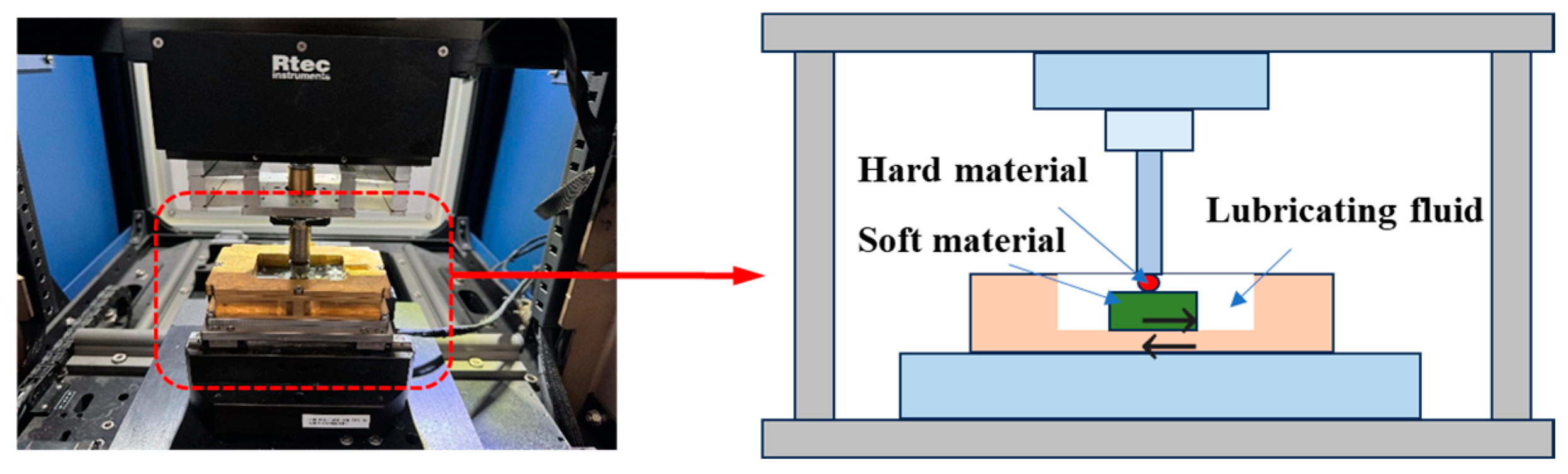
3.2. Friction Wear Test
4. Results and Discussion
4.1. Simulation Analysis Results
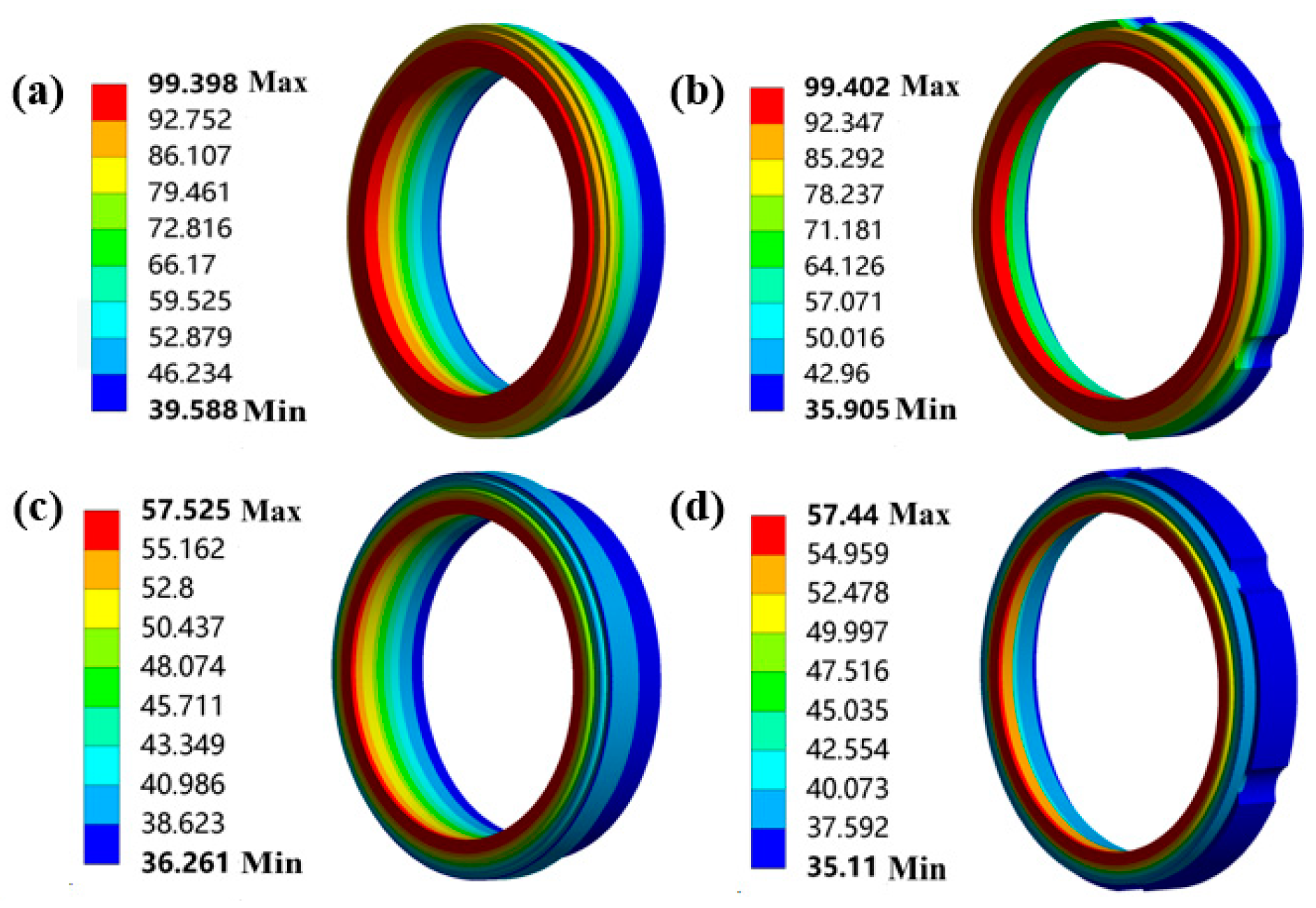
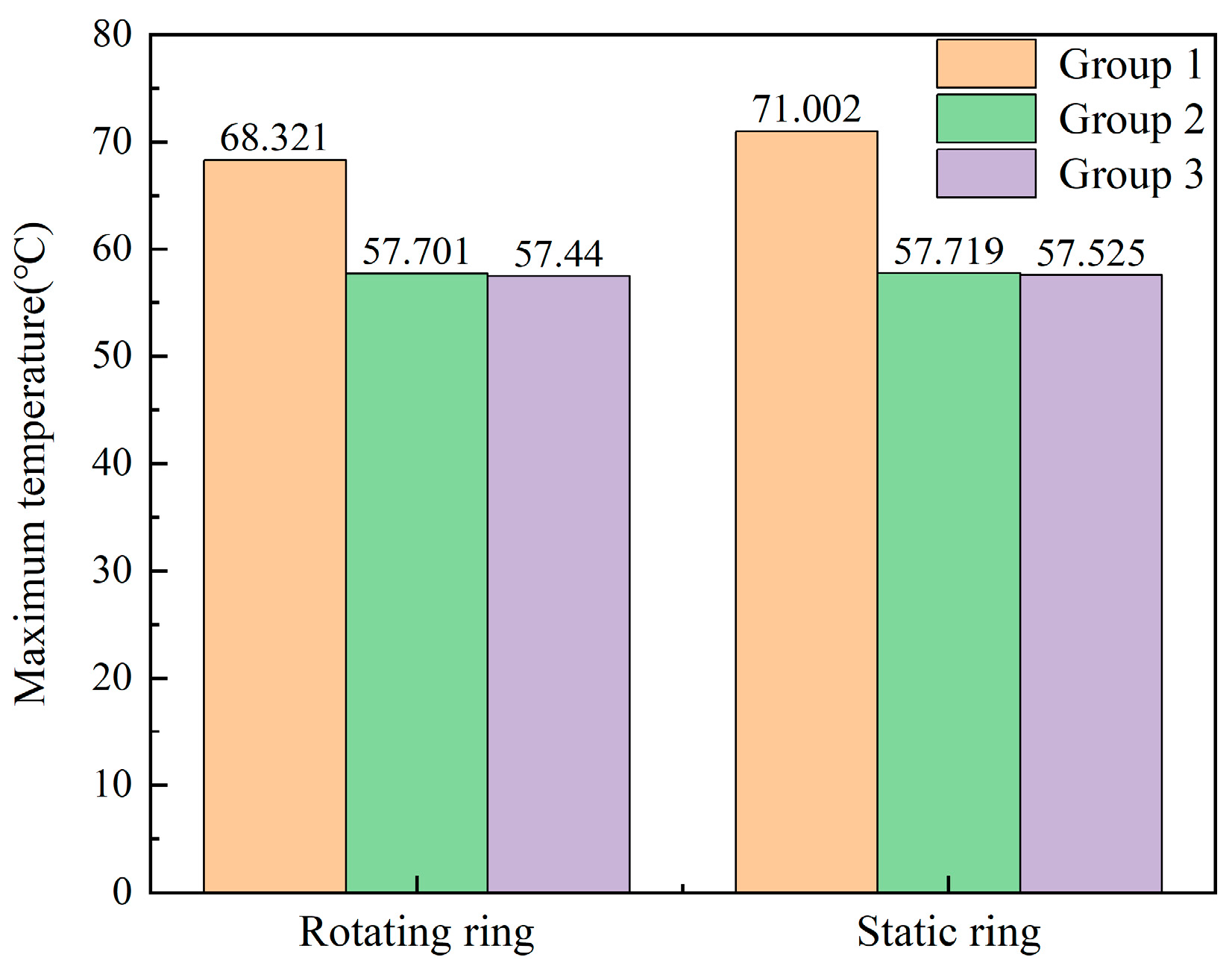
4.1.1. Temperature Field Analysis
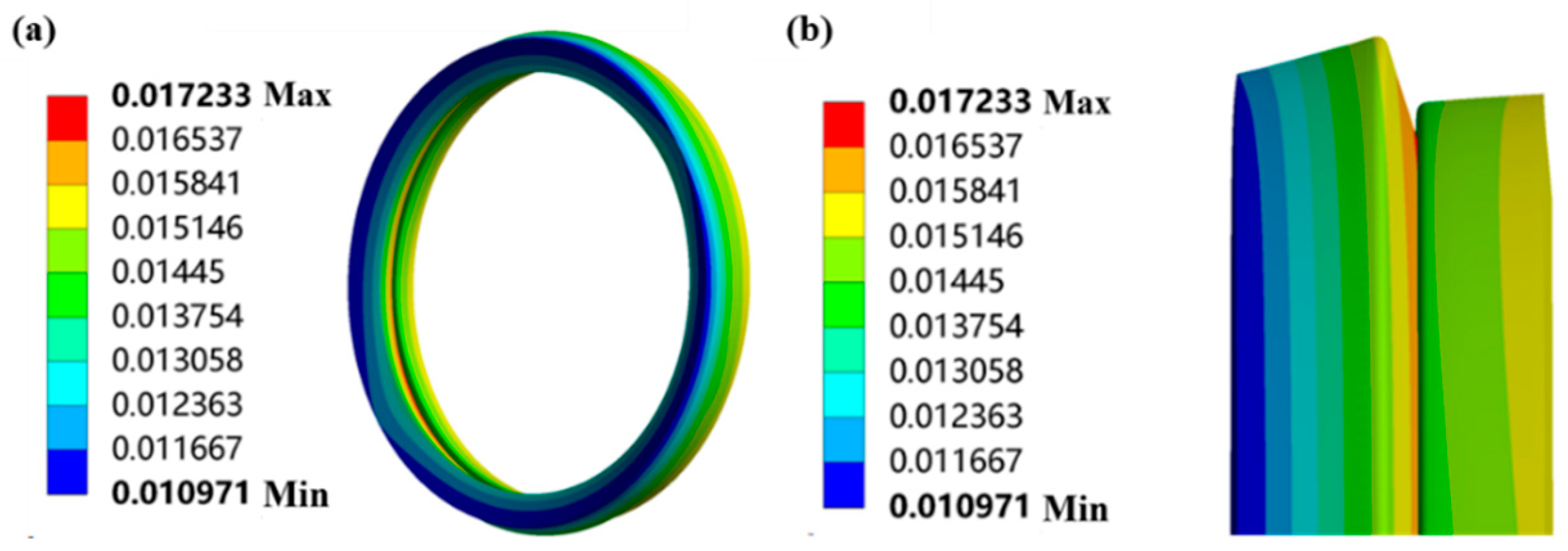
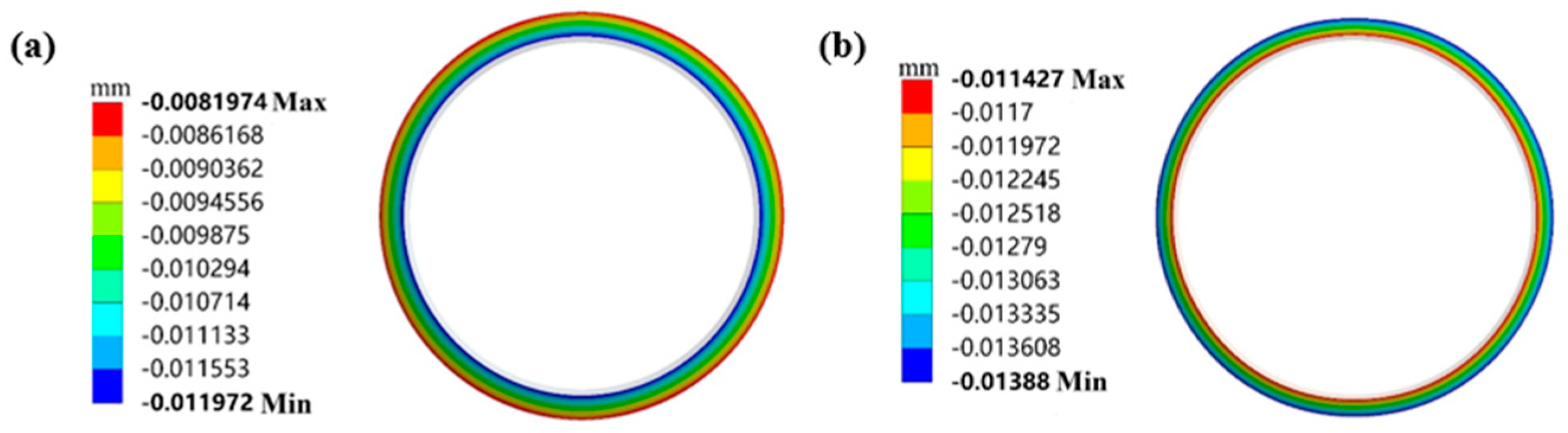
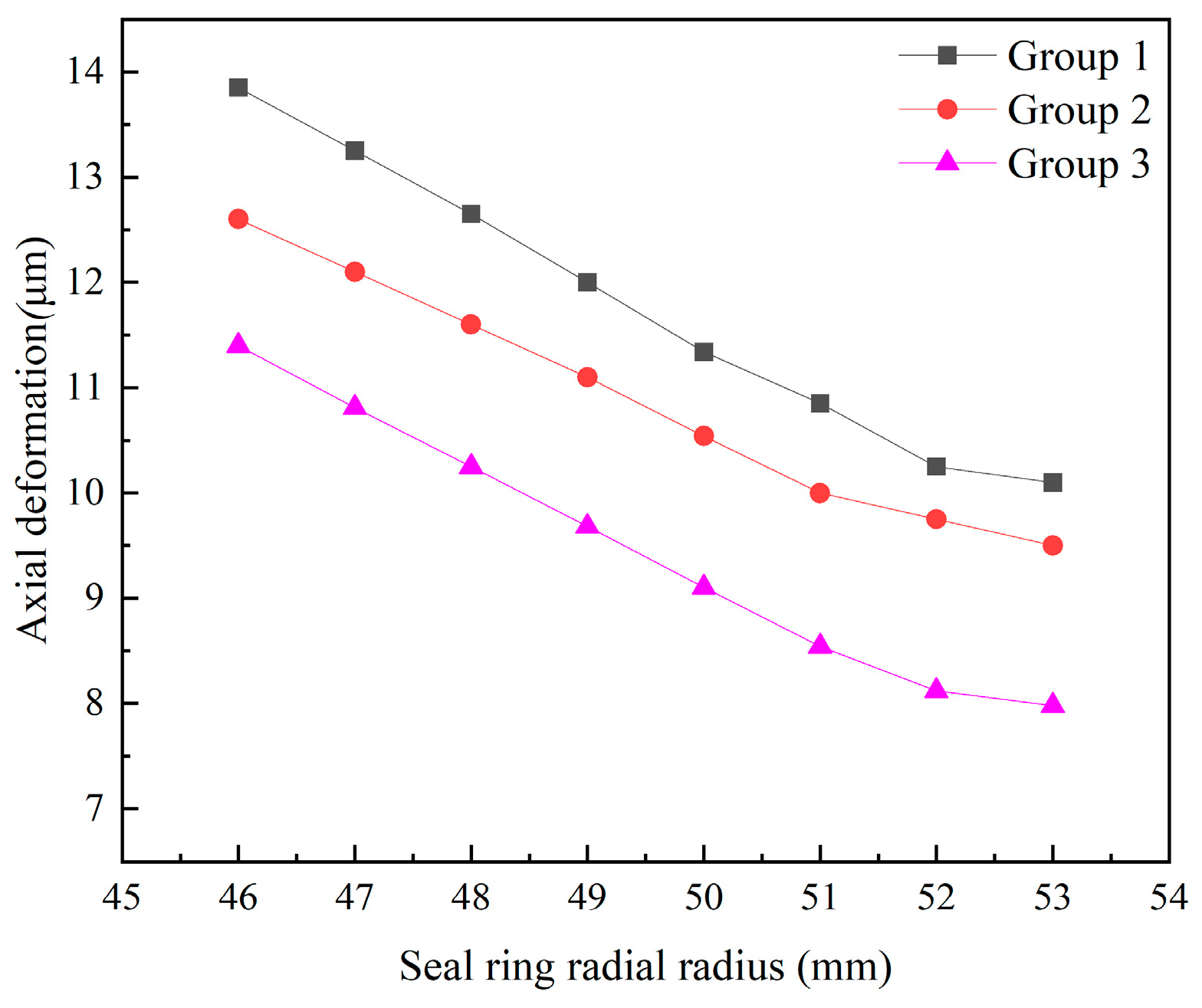
4.1.2. Thermal Deformation Analysis
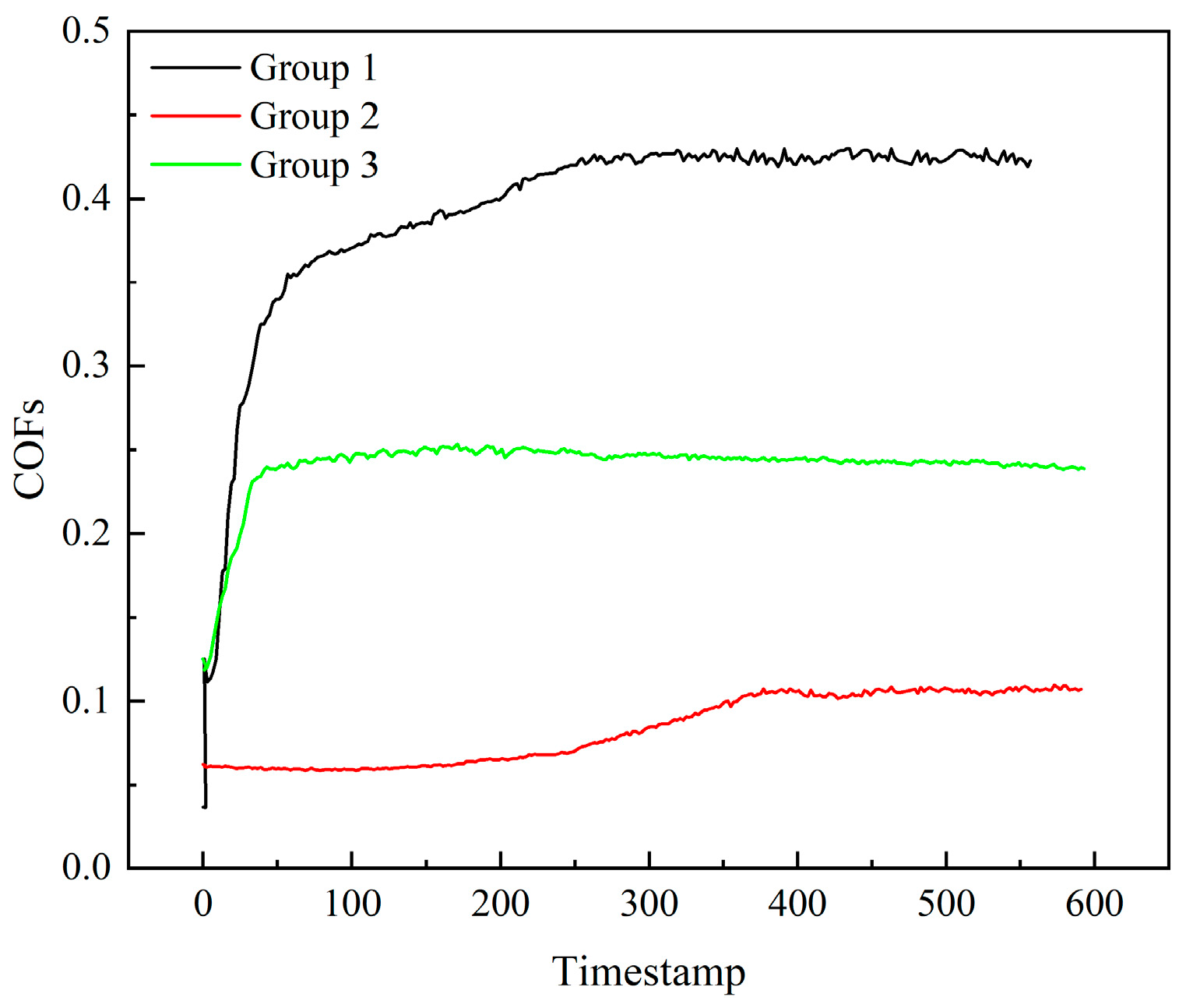
4.2. Test Results
4.3. Correction to the Wear Relation
5. Conclusions
- The friction performance is better when the soft-ring material is C. The temperature, as well as the deformation, is better when the soft-ring material is SIC, and the overall performance is better.
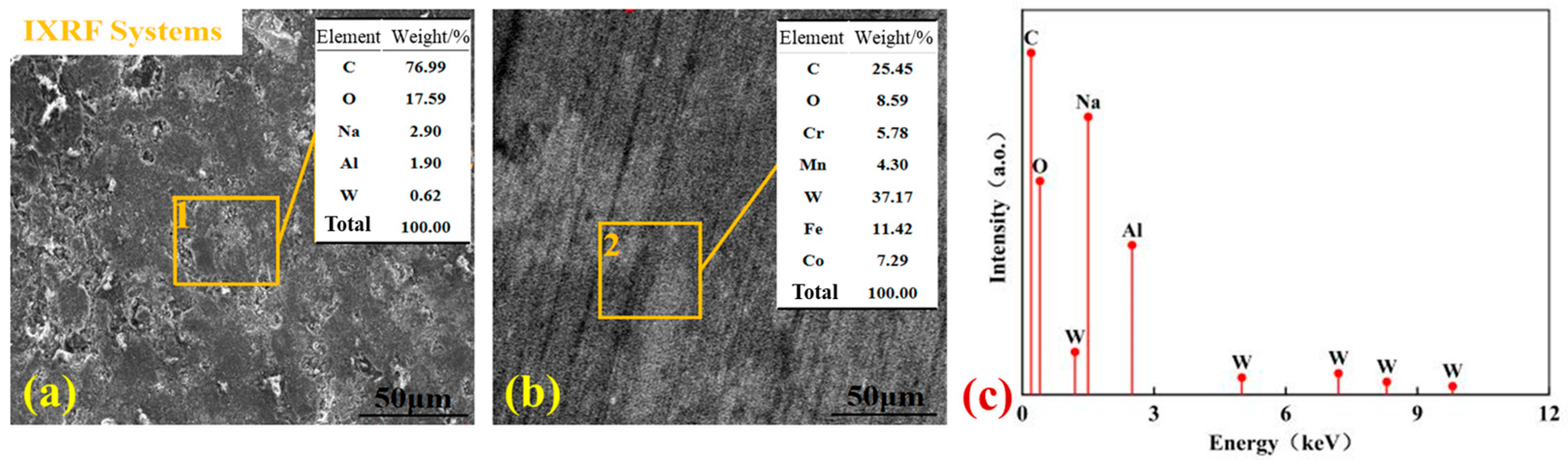
- Through SEM morphology observation of the test specimens, the main wear of the dynamic and static rings is due to adhesive wear leading to particle shedding, which in turn leads to cratering by extrusion, resulting in the wear of the sealing ring.
- The correction coefficients for several materials were calculated, and the correction coefficients were obtained to be 0.23 for SIC, 0.14 for C, and 0.31 for Ss, which can more accurately predict the service life of mechanical seal gaskets.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bi, H.-C.; Hao, M.M.; Ren, B.-J.; Sun, X.-H.; Li, Y.-F.; Li, T.-Z.; Liu, F.-Y.; Li, X.-Y. Friction E-volution of contact Mechanical seals under Mixed lubrication. Tribology 2023, 43, 1241–1253. [Google Scholar]
- Yu, M. Thermal and Structural Coupling deformation Analysis and parameter Optimization of sealing ring with outer circular groove. Lubr. Seal. 2020, 45, 66–71. [Google Scholar]
- GB/T 33509-2017; General Specification for Mechanical Seals. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration of the People’s Republic of China. China Standard Press: Beijing, China, 2017; p. 20.
- Gu, Y. Mechanical Seal Practical Technology; Machinery Industry Press: Beijing, China, 2001; pp. 66–104. [Google Scholar]
- Wei, W.; Li, S.; Zhang, J.; Yan, X.; Song, Y. Study on the effect of sealing ring Material of ship stern shaft on Sealing Performance based on thermo-solid coupling. FanTechnology 2022, 64, 5461. [Google Scholar]
- Zhao, J.; Li, Y.; Liu, Y.; Huang, W.; Xu, Y. Friction and wear performances of impregnated graphite in ring-on-ring tribological test. Tribol. Int. 2022, 174, 107715. [Google Scholar] [CrossRef]
- Wei, Q.; Ahmat, M.; Yin, Y.; He, W. Numerical analysis and relation correction of mechanical seal ring wear of slurry pump based on thermal deformation. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2023. [Google Scholar] [CrossRef]
- Hirani, H.; Goilkar, S.S. Formation of transfer layer and its effect on friction and wear of carbon–graphite face seal under dry, water and steam environments. Wear 2009, 266, 1141–1154. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, Y.; Wen, Q.; Wang, Y. Frictional performance of silicon carbide under different lubrication conditions. Friction 2014, 2, 58–63. [Google Scholar] [CrossRef]
- Cui, G.; Li, J.; Wu, G. Friction and wear behavior of bronze matrix composites for seal in antiwear hydraulic oil. Tribol. Trans. 2015, 58, 51–58. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, G.; Dong, G. Friction and wear behavior of different seal materials under water-lubricated conditions. Friction 2021, 9, 697–709. [Google Scholar] [CrossRef]
- Wang, N.; Pang, S.; Ye, C.; Fan, T.; Choi, S.-B. The friction and wear mechanism of O-rings in magnetorheological damper: Numerical and experimental study. Tribol. Int. 2021, 157, 106898. [Google Scholar] [CrossRef]
- Selech, J.; Ulbrich, D.; Romek, D.; Kowalczyk, J.; Wlodarczyk, K.; Nadolny, K. Experimental study of abrasive, mechanical and corrosion effects in ring-on-ring sliding contact. Materials 2020, 13, 4950. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.; Li, Q.; Liu, Q.; Kouediatouka, A.N.; Ji, H.; Dong, G. A friction mechanism for surface texturing under dry/mixed lubrication conditions based on the sublinear dependence of friction on load. Tribol. Int. 2024, 194, 109488. [Google Scholar] [CrossRef]
- Zhang, N.; Liu, Y.; Li, Z.; Zhan, X. Sealing performance and optimization design of squamous textured mechanical seal. Tribol. Int. 2024, 193, 109425. [Google Scholar] [CrossRef]
- Ilie, F.; Ipate, G.; Manaila, F.C. Tribological Properties Study of Solid Lubrication with TiO2 Powder Particles. Materials 2022, 15, 7145. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z. Forced Convective and Boiling Heat Transfer Characteristics of Hot Cylinder Revolving in Annular N-arrow Spaces. J. Shanghai Jiaotong Univ. 1997, 31, 10–14. [Google Scholar]
- Zhu, D.C. Experimental Study of Contact Heat Transfer Coefficients at Solid Interfaces. Master’s Thesis, Dalian University of Technology, Dalian, China, 2007. [Google Scholar]
- Archard, J.F. Contact and rubbing of flat surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Chen, R.; Zhao, B.; He, T.; Tu, L.; Xie, Z.; Zhong, N.; Zou, D. Study on coupling transient mixed lubrication and time-varying wear of main bearing in-actual operation of low-speed diesel engine. Tribol. Int. 2024, 191, 109159. [Google Scholar] [CrossRef]
- Microscopy, T.E. Analyzing Mild-and Ultra-Mild Sliding Wear of Metallic Materials. In Analytical Methods in Tribology; Springer: Berlin/Heidelberg, Germany, 2018; pp. 25–29. [Google Scholar]
- Lee, S.; Joub, L. Application of numerical simulation for wear analysis of warm forging die. J. Mater. Process Technol. 2003, 140, 43–48. [Google Scholar] [CrossRef]
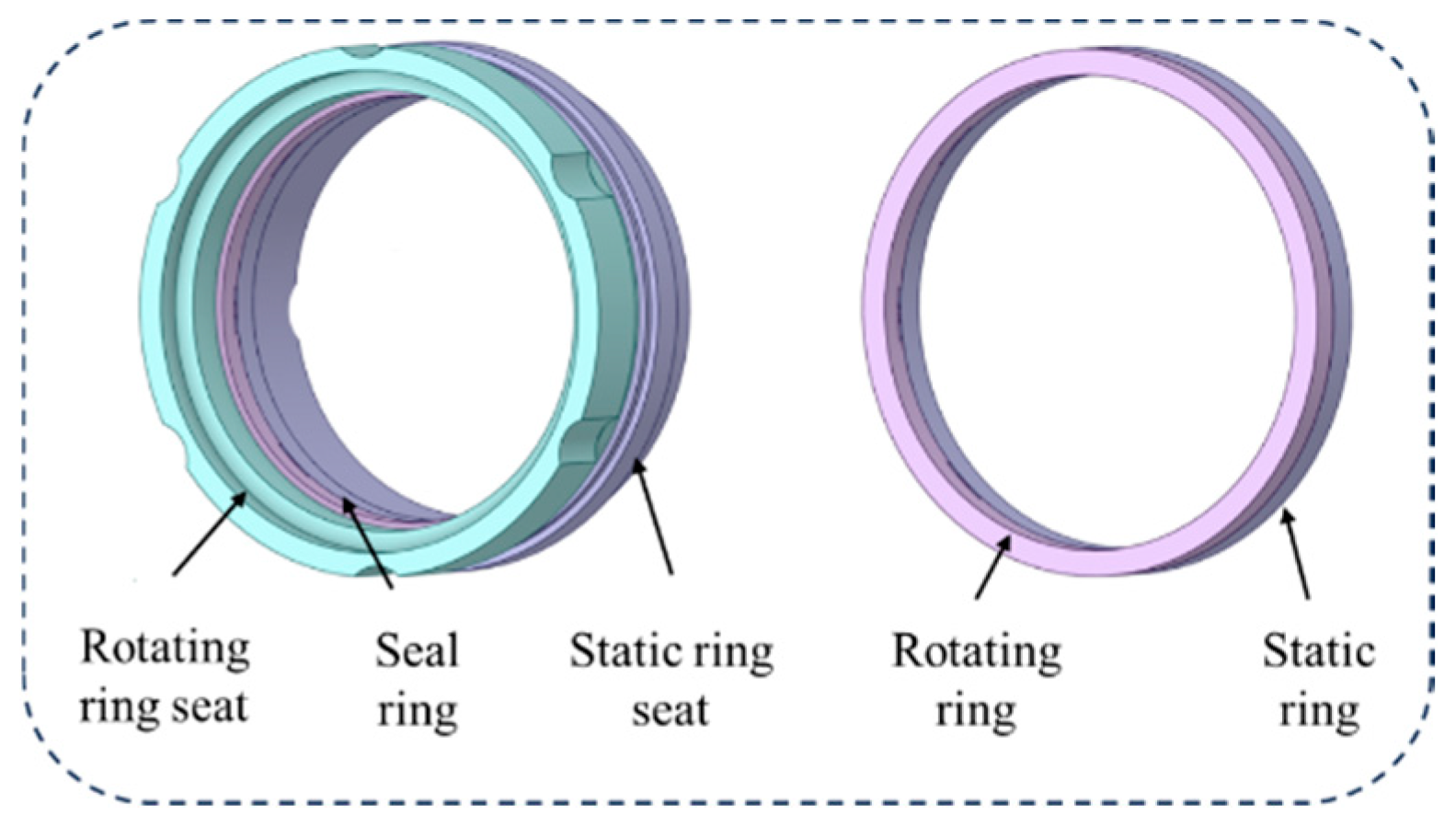



| Mechanical Seal Components | Radial Dimensions/mm | Axial Dimensions/mm |
|---|---|---|
| Dynamic-ring inner diameter | 92.5 | 6 |
| Dynamic-ring outer diameter | 102.5 | 6 |
| Dynamic-ring-seat outer diameter | 116 | 22 |
| Static-ring inner diameter | 91.5 | 7 |
| Static-ring outer diameter | 105.5 | 7 |
| Static-ring-seat outer diameter | 114.6 | 25 |
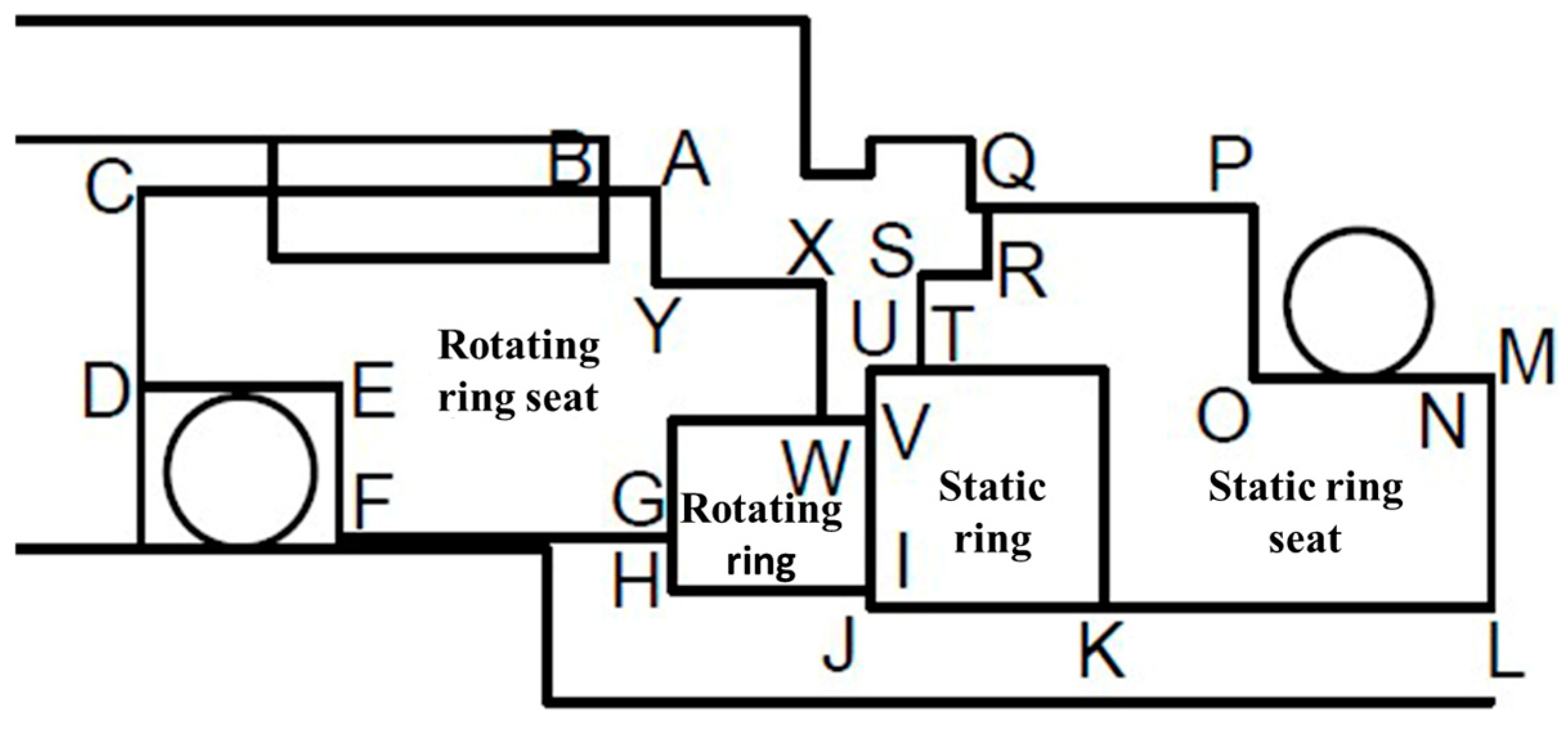
| Stress Conditions | Stress Boundary |
|---|---|
| Spring force | CD |
| Flushing fluid pressure | CD, EF, QR, RS, ST, TU, UV |
| Flushing fluid pressure | VW, WX, XY, YA, AB, BC, VI |
| Medium pressure | FG, GH, HI, IJ, JK, KL |
| Thermal Conditions | Boundary |
|---|---|
| Heating boundary | VI |
| Flushing fluid convection heat dissipation | QR, RS, ST, TU, UV, VW, WX, XY, YA, AB |
| Contact convection heat dissipation of sealing chamber | MN, PQ, BC, CD |
| Medium convection heat dissipation | LK, KJ, JI, IH, HG, GF |
| Flushing Solution (Lubrication) | Dynamic Viscosity μ/(Pa·s) | Thermal Conductivity λ/(W/(m·K)) | Densities ρ/(kg·m−3) | Specific Heat Capacity Cp/(J·kg−1·k−1) |
|---|---|---|---|---|
| Water | 1.01 × 10−3 | 0.62 | 998 | 4179 |
| Materials | Static-Ring Heat Flux Density/W·m−2 | Rotating-Ring Heat Flux Density/W·m−2 |
|---|---|---|
| Silicon carbide | 169,322 | 156,297 |
| Stainless steel | 175,834 | 149,785 |
| Graphite | 178,521 | 151,843 |
| Heat Transfer Coefficient/W·(m2·°C)−1 | Rotating Ring (Seat) | Static Ring | Static Ring Seat |
|---|---|---|---|
| Flushing fluid | 5571 | 4237 | 4150 |
| Phosphate slurry | 860 | 493 | 672 |
| Materials | Density/Kg·m−3 | Modulus of Elasticity/GPa | Poisson’s Ratio | Thermal Conductivity/(W/(m·K)) | Coefficient of Thermal Expansion/K−1 |
|---|---|---|---|---|---|
| WC-Co-cemented carbide (YG8) | 15,000 | 710 | 0.234 | 70 | 6.9 × 10−6 |
| Stainless steels (S30408) | 7920 | 204 | 0.28 | 16.3 | 1.6 × 10−5 |
| Silicon carbide (SIC) | 3190 | 380 | 0.16 | 100 | 4.2 × 10−6 |
| Plumbago (M106K) | 1700 | 130 | 0.28 | 90 | 1.2 × 10−5 |
| No. | Static-Ring Material | Dynamic-Ring Material |
|---|---|---|
| 1 | Ss | YG8 |
| 2 | C | YG8 |
| 3 | SIC | YG8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Ahmat, M.; Yin, R. Analysis of Friction and Wear Properties of Friction Ring Materials for Friction Rings under Mixed Lubrication. Machines 2024, 12, 680. https://doi.org/10.3390/machines12100680
Li T, Ahmat M, Yin R. Analysis of Friction and Wear Properties of Friction Ring Materials for Friction Rings under Mixed Lubrication. Machines. 2024; 12(10):680. https://doi.org/10.3390/machines12100680
Chicago/Turabian StyleLi, Tan, Mutellip Ahmat, and Runsheng Yin. 2024. "Analysis of Friction and Wear Properties of Friction Ring Materials for Friction Rings under Mixed Lubrication" Machines 12, no. 10: 680. https://doi.org/10.3390/machines12100680
APA StyleLi, T., Ahmat, M., & Yin, R. (2024). Analysis of Friction and Wear Properties of Friction Ring Materials for Friction Rings under Mixed Lubrication. Machines, 12(10), 680. https://doi.org/10.3390/machines12100680





