Integrated Intelligent Control of Redundant Degrees-of-Freedom Manipulators via the Fusion of Deep Reinforcement Learning and Forward Kinematics Models
Abstract
1. Introduction
2. Design of the FK-DRL Control Algorithm
2.1. Control Problem and MDP Modelling
2.2. Modelling of the FK of the Manipulator
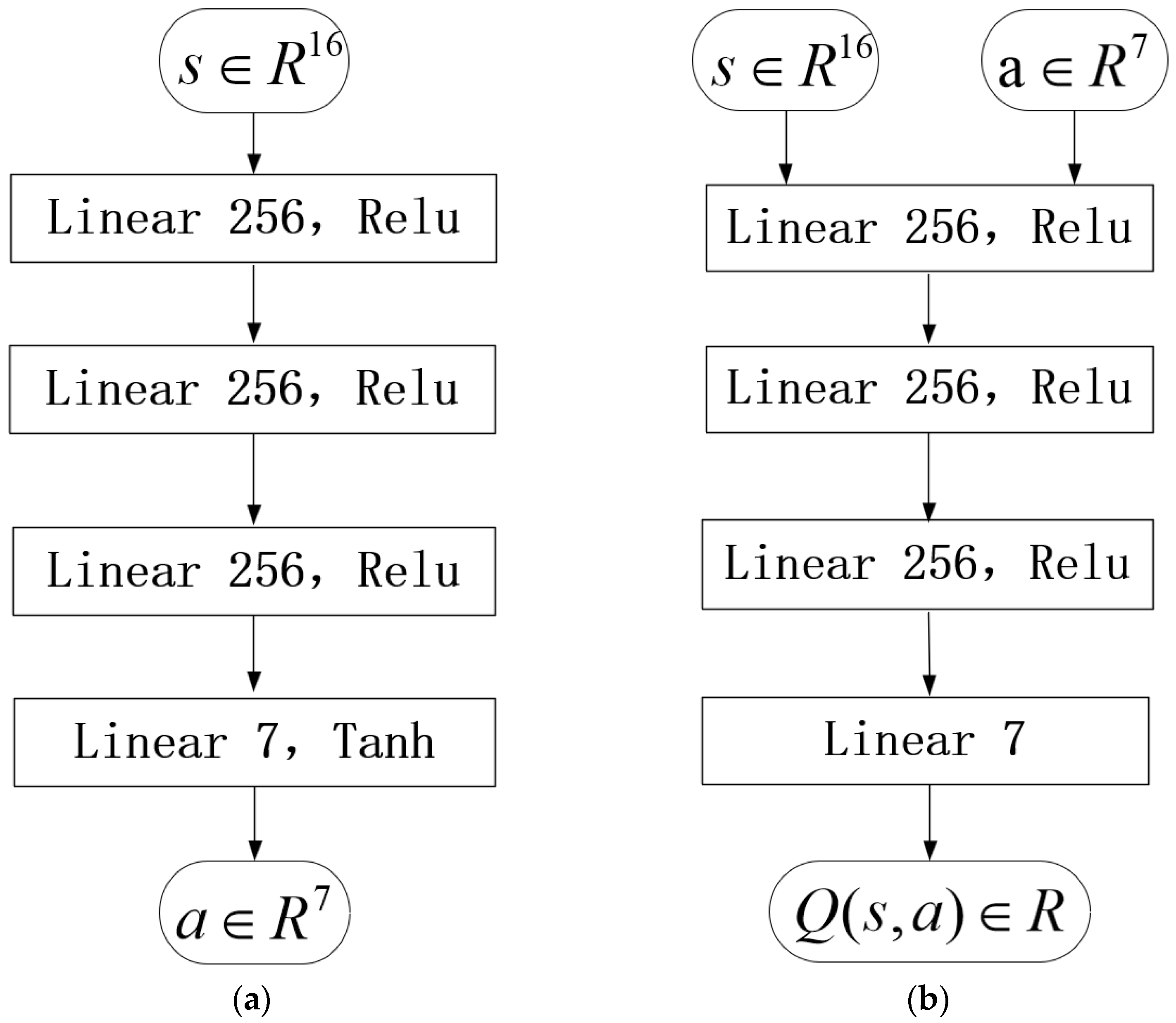
2.3. FK-DRL Algorithm
- (1)
- Take one unfinished task from the experience pool .
- (2)
- For the sake of differentiation, the state is denoted as and used as the initial state in an episode of planning. At the same time, OU (Ornstein Uhlenbeck) noise is added to the action [28] and is denoted as .
- (3)
- Inputting the action into the model M, the pose of the end-effector is obtained. The next state is obtained from the current state after the input action . The reward value is calculated to get the , which is stored in the experience pool.
- (4)
- Input into the Actor network, which then outputs an action. Add OU noise to this action to obtain action and repeat step (3) to obtain , which is then stored in the experience pool. Extract experiences from the pool to update the Actor and Critic networks.
- (5)
- Continue to interact with model M until the number of interactions reaches T2 and the Actor and Critic networks, indicating the end of this dynamic planning episode;
- (6)
- Repeat steps (1)–(5) P times.
| Algorithm 1. FK-DRL |
 |
3. Simulation
3.1. Simulation Environment
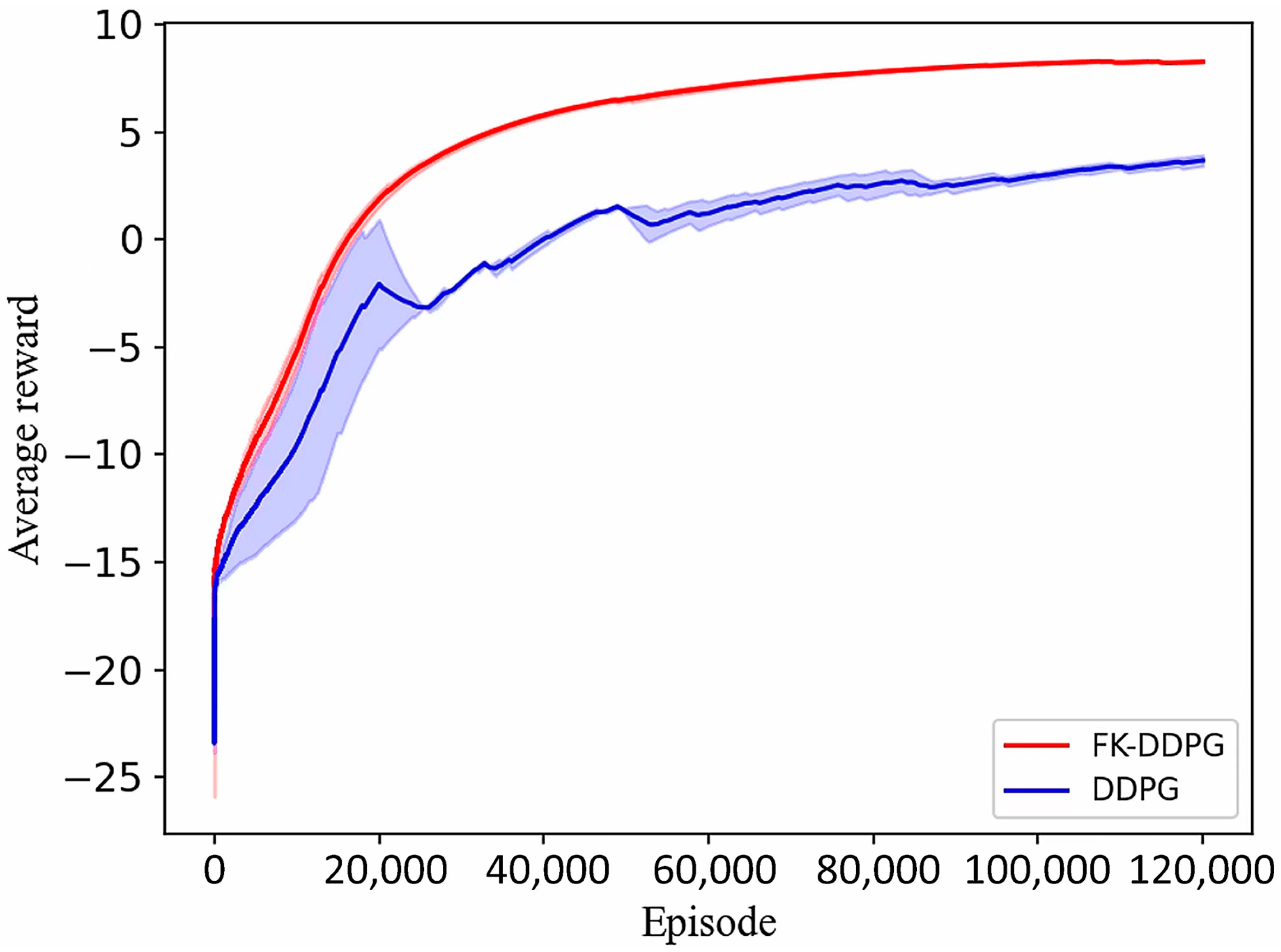
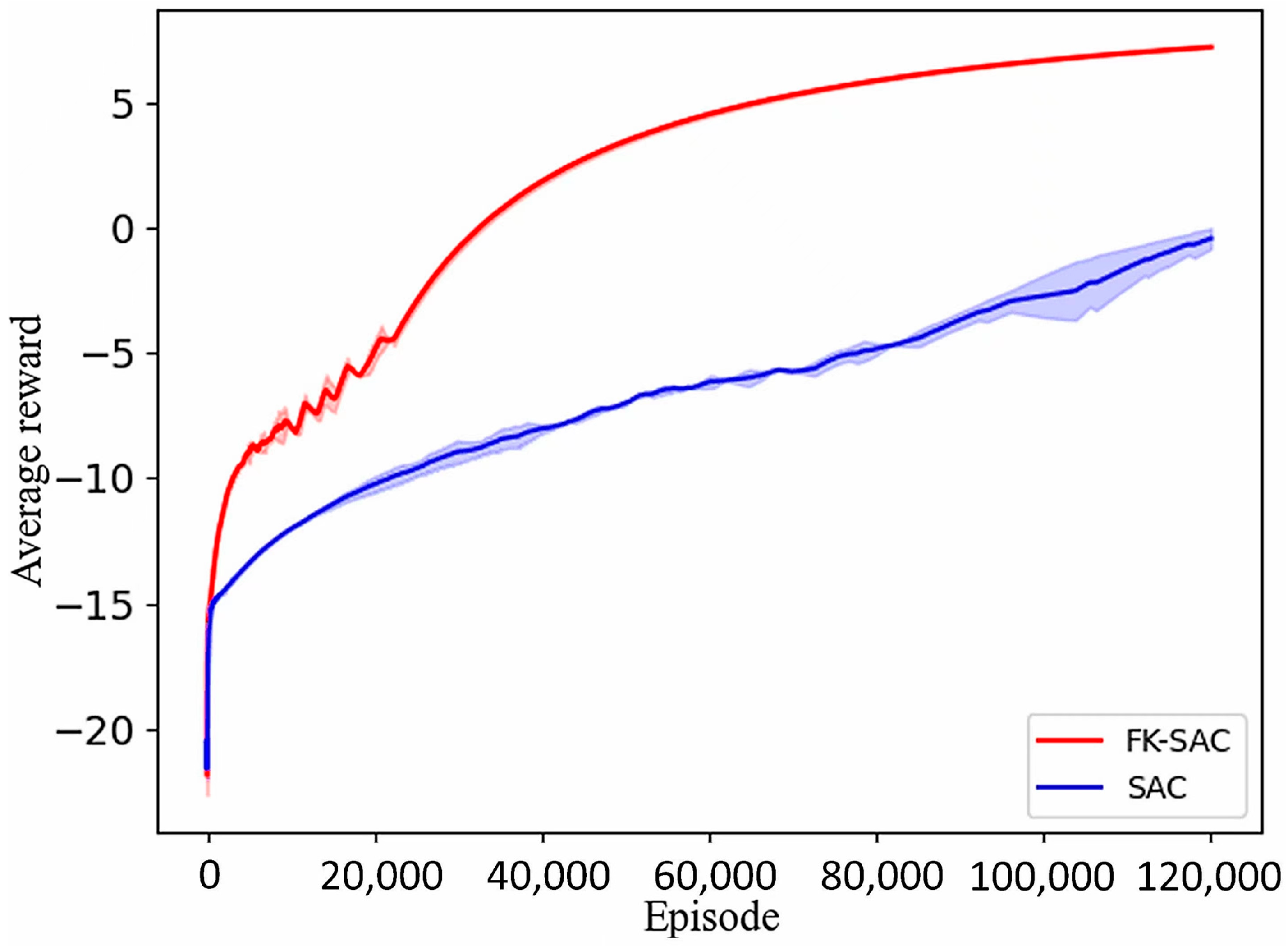
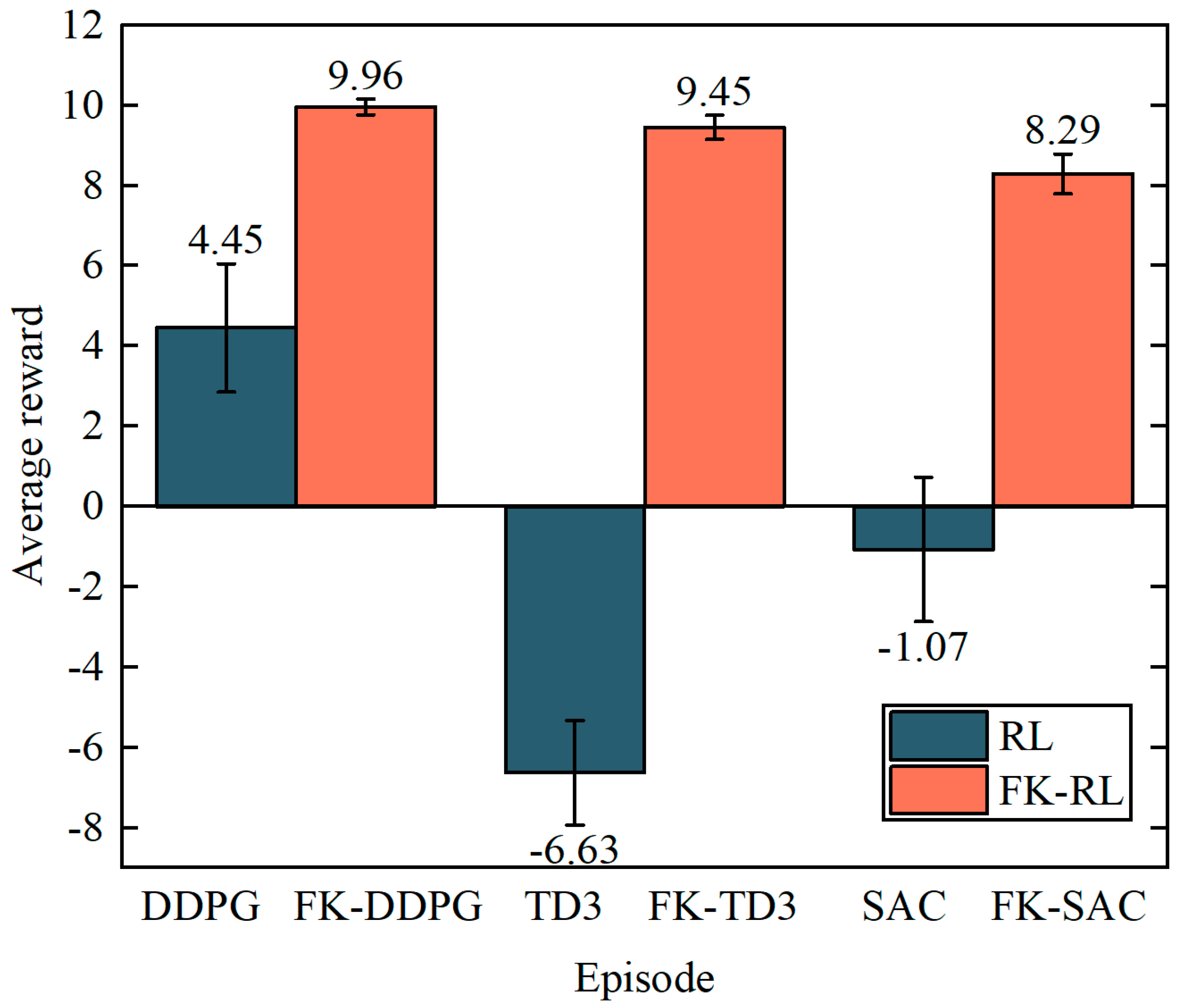
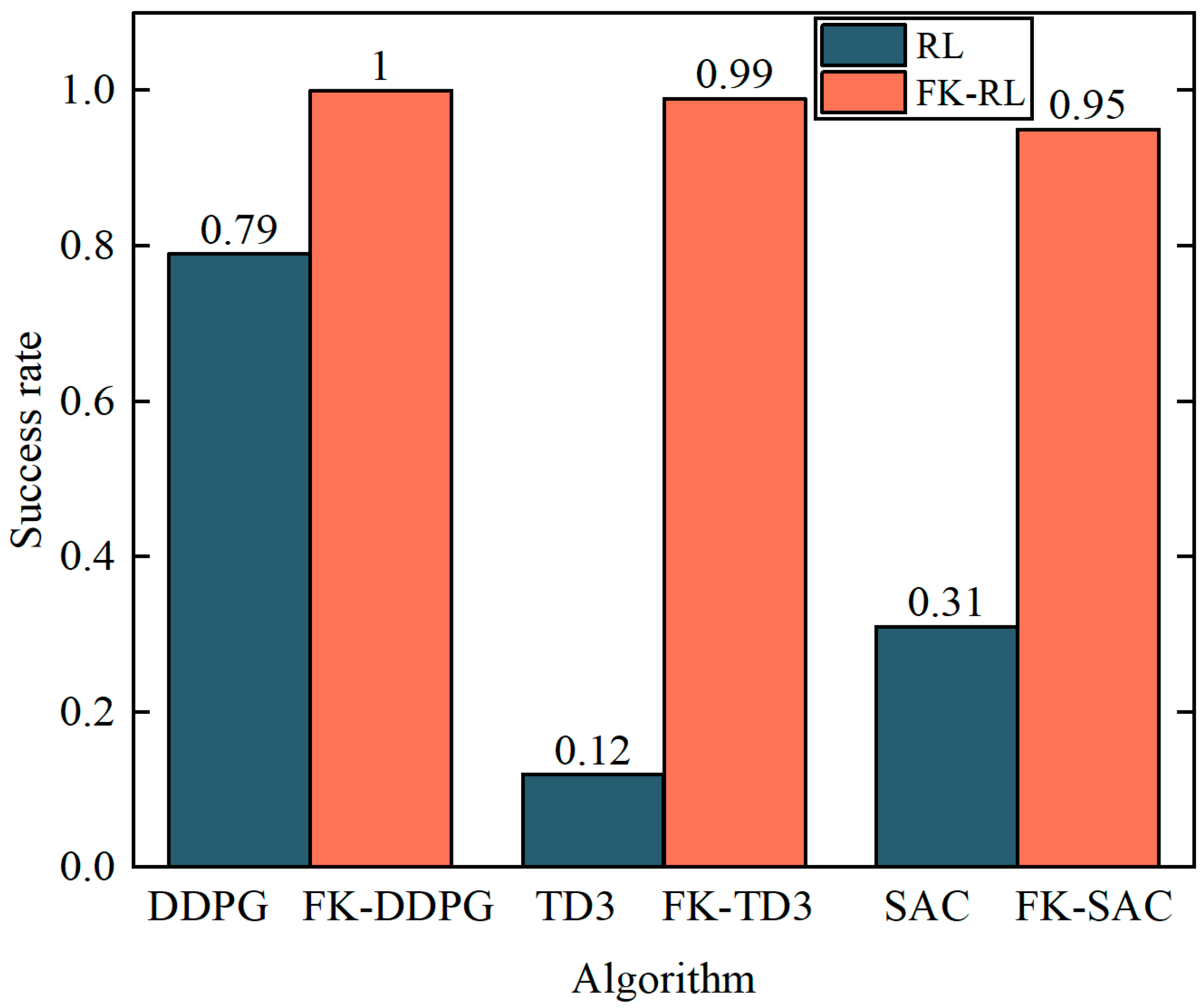
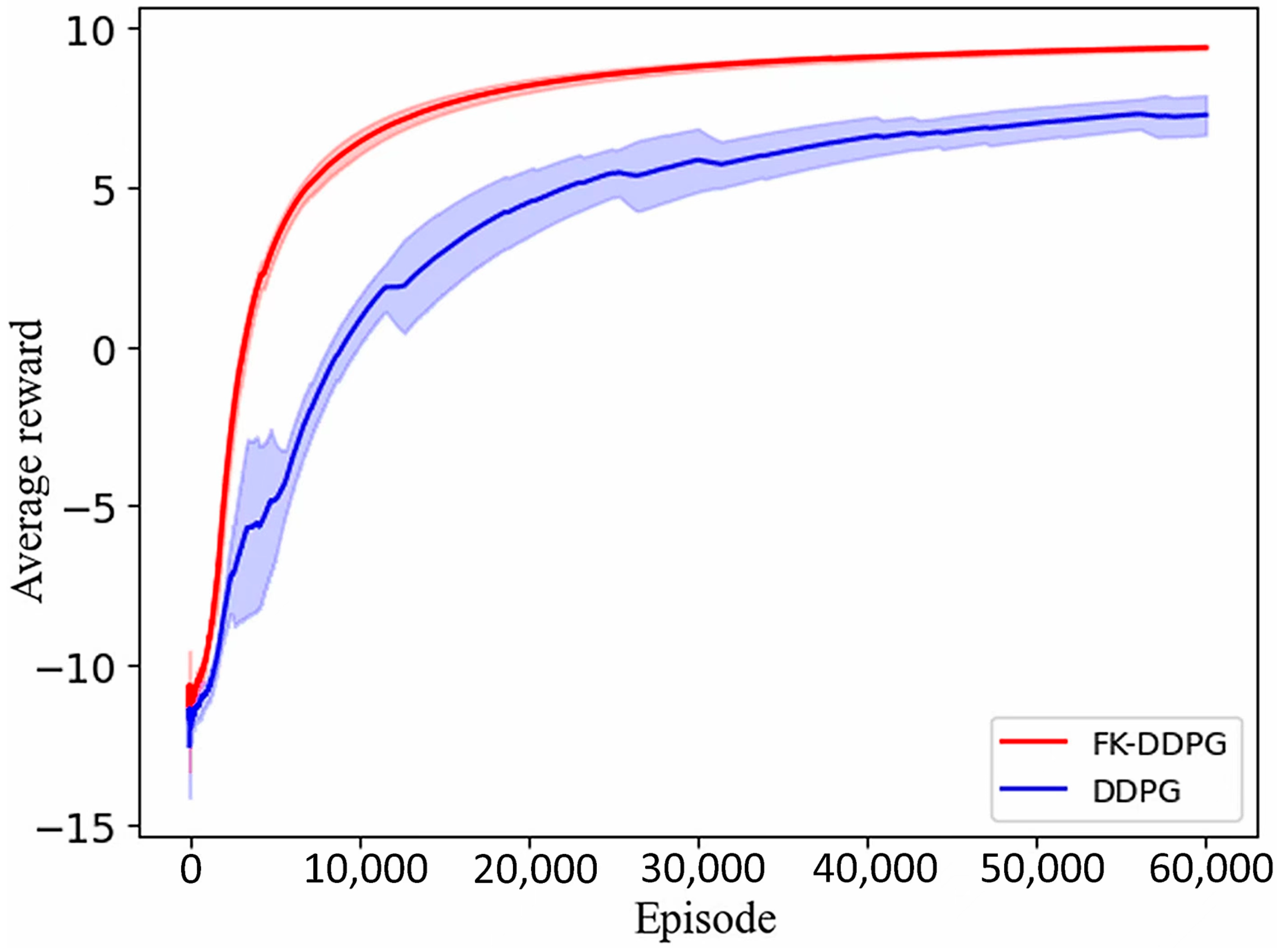
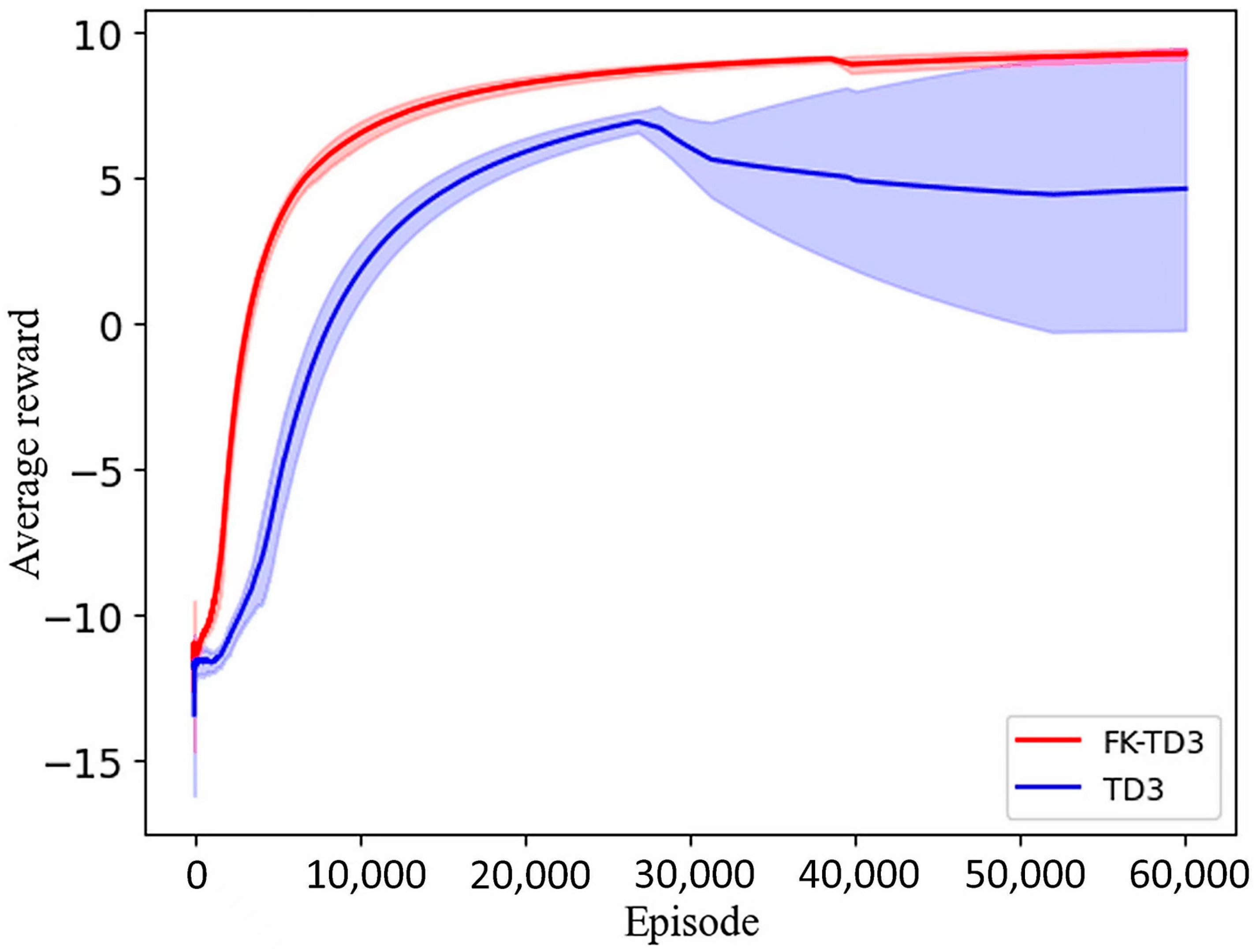
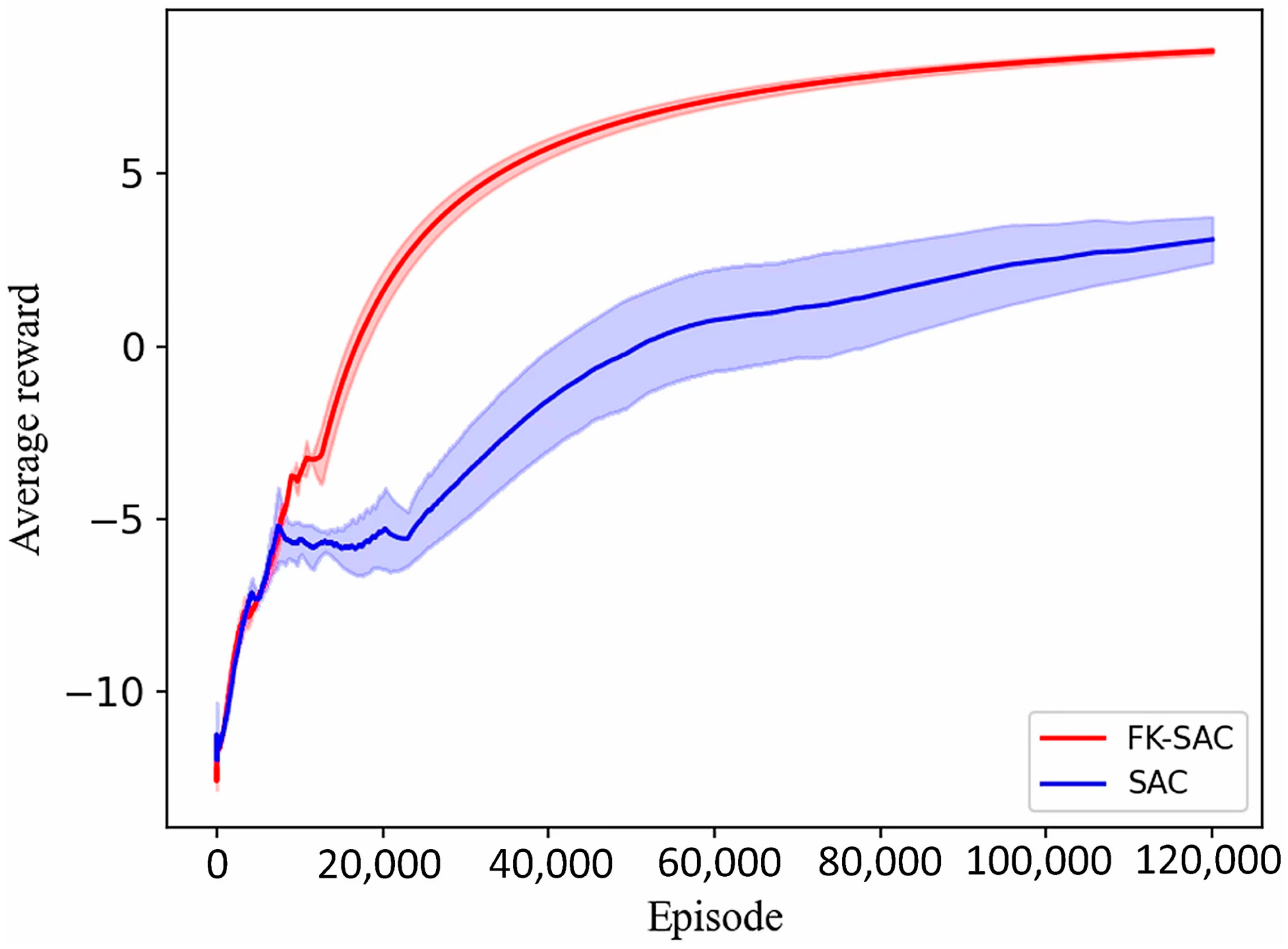
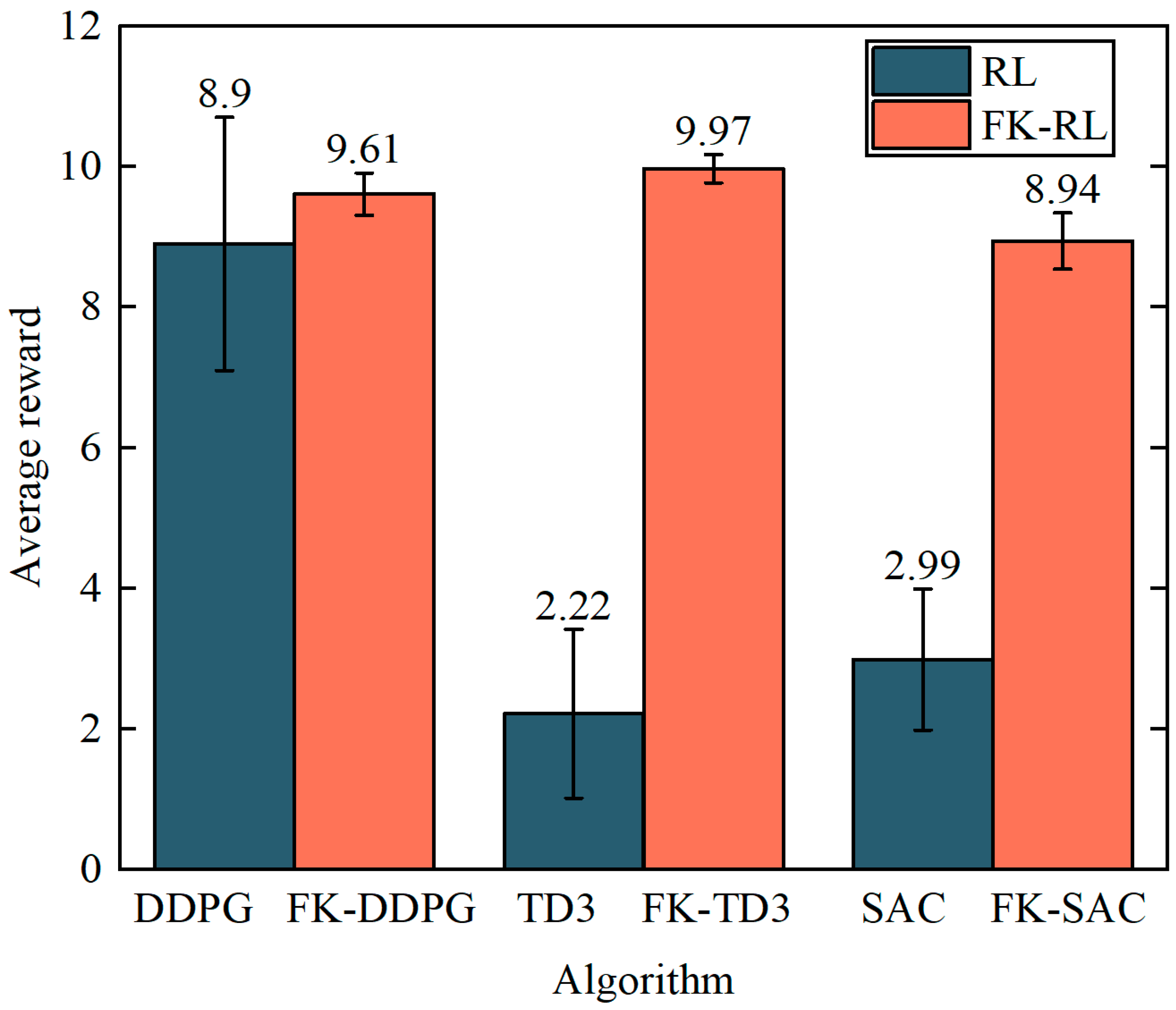
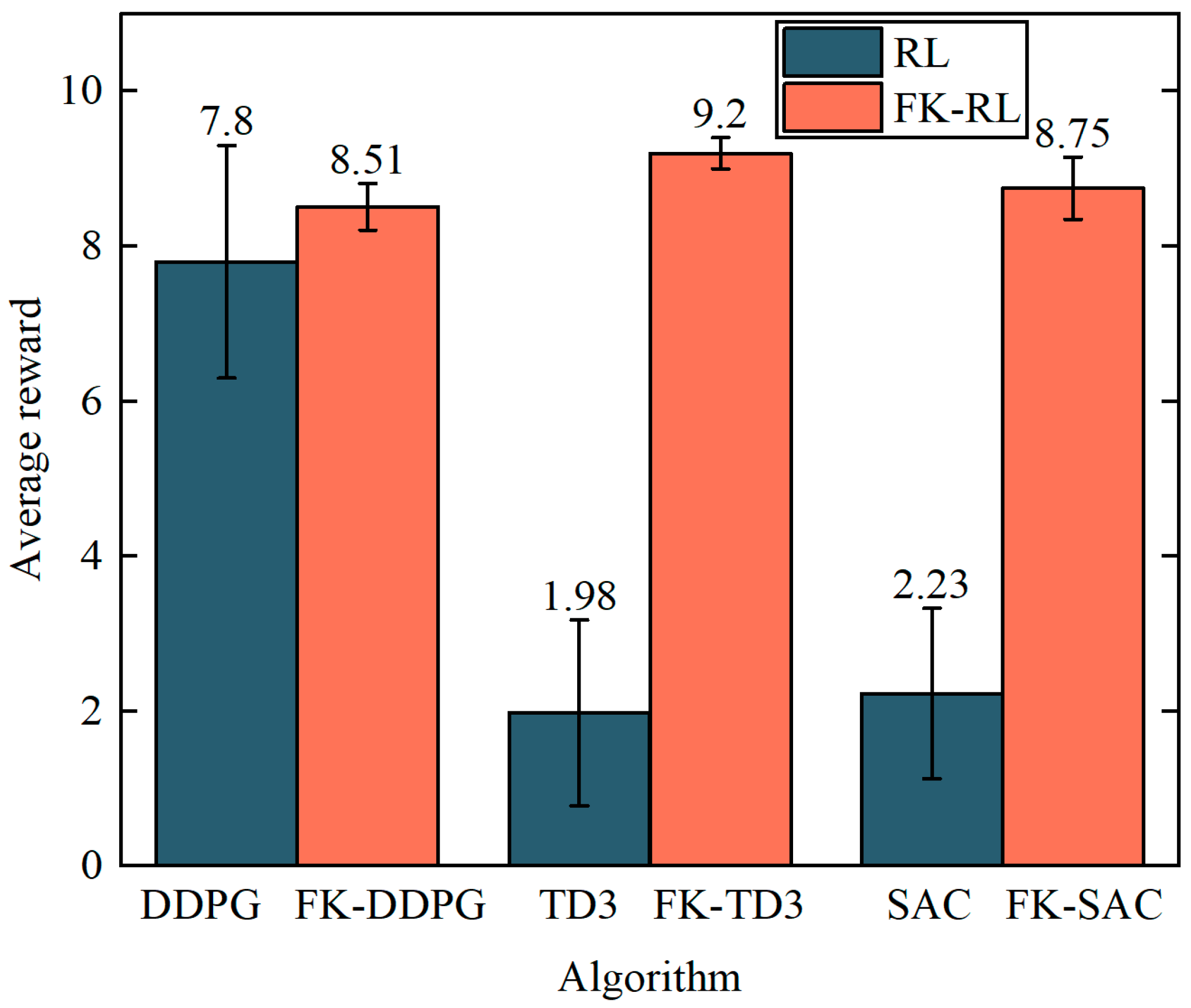
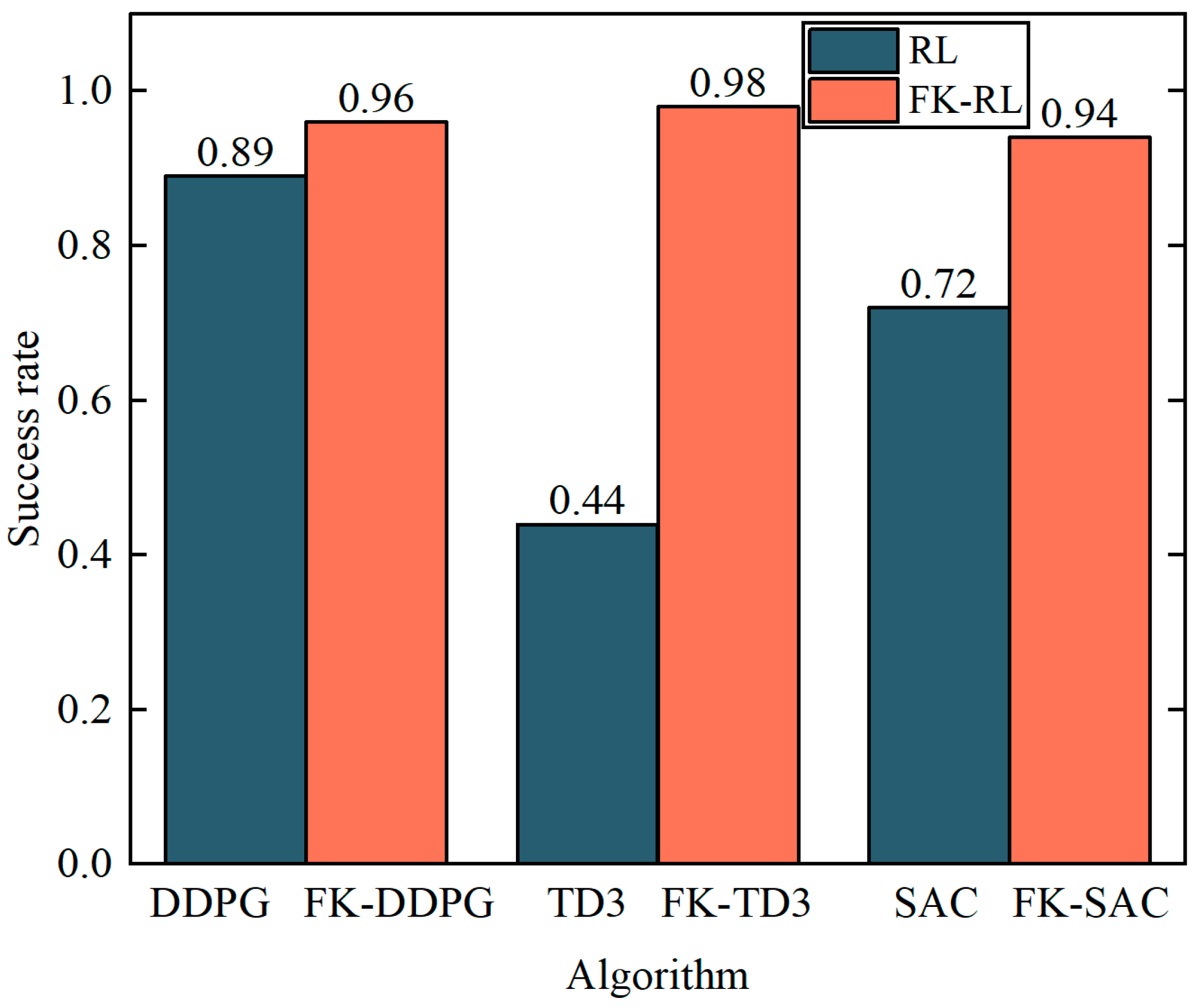
3.2. Analysis of Simulation Results of 7-DOF Manipulator
3.3. Analysis of Simulation Results of 4-DOF Manipulator
4. Experiments and Analysis
4.1. Experimental Platform
4.2. Analysis of Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tan, N.; Zhong, Z.; Yu, P.; Li, Z.; Ni, F. A Discrete Model-Free Scheme for Fault-Tolerant Tracking Control of Redundant Manipulators. IEEE Trans. Ind. Inform. 2022, 18, 8595–8606. [Google Scholar] [CrossRef]
- Tong, Y.; Liu, J.; Liu, Y.; Yuan, Y. Analytical inverse kinematic computation for 7-DOF redundant sliding manipulators. Mech. Mach. Theory 2021, 155, 104006. [Google Scholar] [CrossRef]
- Quan, Y.; Zhao, C.; Lv, C.; Wang, K.; Zhou, Y. The Dexterity Capability Map for a Seven-Degree-of-Freedom Manipulator. Machines 2022, 10, 1038–1059. [Google Scholar] [CrossRef]
- Ning, Y.; Li, T.; Du, W.; Yao, C.; Zhang, Y.; Shao, J. Inverse kinematics and planning/control co-design method of redundant manipulator for precision operation: Design and experiments. Robot. Comput.-Integr. Manuf. 2023, 80, 102457. [Google Scholar] [CrossRef]
- Sahbani, A.; El-Khoury, S.; Bidaud, P. An overview of 3D object grasp synthesis algorithms. Robot. Auton. Syst. 2012, 60, 326–336. [Google Scholar] [CrossRef]
- Crane, C.; Duffy, J.; Carnahan, T. A kinematic analysis of the space station remote manipulator system. J. Robot. Syst. 1991, 8, 637–658. [Google Scholar] [CrossRef]
- Xavier da Silva, S.; Schnitman, L.; Cesca, V. A Solution of the Inverse Kinematics Problem for a 7-Degrees-of-Freedom Serial Redundant Manipulator Using Grobner Bases Theory. Math. Probl. Eng. 2021, 2021, 6680687. [Google Scholar] [CrossRef]
- Gong, M.; Li, X.; Zhang, L. Analytical Inverse Kinematics and Self-Motion Application for 7-DOF Redundant Manipulator. IEEE Access 2019, 7, 18662–18674. [Google Scholar] [CrossRef]
- Marcos, M.; Machado, J.; Azevedo-Perdicoulis, T. Trajectory planning of redundant manipulators using genetic algorithms. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 2858–2869. [Google Scholar] [CrossRef]
- Xie, Z.; Jin, L. Hybrid Control of Orientation and Position for Redundant Manipulators Using Neural Network. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 2737–2747. [Google Scholar] [CrossRef]
- Yang, Q.; Jagannathan, S. Reinforcement Learning Controller Design for Affine Nonlinear Discrete-Time Systems using Online Approximators. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2012, 42, 377–390. [Google Scholar] [CrossRef] [PubMed]
- Perrusquia, A.; Yu, W.; Li, X. Multi-agent reinforcement learning for redundant robot control in task-space. Int. J. Mach. Learn. Cyber. 2021, 12, 231–241. [Google Scholar] [CrossRef]
- Lee, C.; An, D. AI-Based Posture Control Algorithm for a 7-DOF Robot Manipulator. Machines 2022, 10, 651. [Google Scholar] [CrossRef]
- Ramirez, J.; Yu, W. Reinforcement learning from expert demonstrations with application to redundant robot control. Eng. Appl. Artif. Intell. 2023, 119, 105753. [Google Scholar] [CrossRef]
- Xu, W.; Sen, W.; Xing, L. Deep Reinforcement Learning: A Survey. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 5064–5078. [Google Scholar]
- Li, X.; Liu, H.; Dong, M. A General Framework of Motion Planning for Redundant Robot Manipulator Based on Deep Reinforcement Learning. IEEE Trans. Ind. Inform. 2022, 18, 5253–5263. [Google Scholar] [CrossRef]
- Calderón-Cordova, C.; Sarango, R.; Castillo, D.; Lakshminarayanan, V. A Deep Reinforcement Learning Framework for Control of Robotic Manipulators in Simulated Environments. IEEE Access 2024, 12, 103133–103161. [Google Scholar] [CrossRef]
- Zheng, L.; Wang, Y.; Yang, R.; Wu, S.; Guo, R.; Dong, E. An Efficiently Convergent Deep Reinforcement Learning-Based Trajectory Planning Method for Manipulators in Dynamic Environments. J. Intell. Robot. Syst. 2023, 107, 50. [Google Scholar] [CrossRef]
- Feng, Z.; Hou, Q.; Zheng, Y.; Ren, W.; Ge, J.Y.; Li, T.; Cheng, C.; Lu, W.; Cao, S.; Zhang, J.; et al. Method of artificial intelligence algorithm to improve the automation level of Rietveld refinement. Comput. Mater. Sci. 2019, 156, 310–314. [Google Scholar] [CrossRef]
- Cammarata, A.; Maddio, P.D.; Sinatra, R.; Belfiore, N.P. Direct Kinetostatic Analysis of a Gripper with Curved Flexures. Micromachines 2022, 13, 2172. [Google Scholar] [CrossRef]
- Corke, P. A simple and systematic approach to assigning Denavit-Hartenberg parameters. IEEE Trans. Robot. 2007, 23, 590–594. [Google Scholar] [CrossRef]
- Chen, P.; Lu, W. Deep reinforcement learning based moving object grasping. Inf. Sci. 2021, 565, 62–76. [Google Scholar] [CrossRef]
- Sadeghzadeh, M.; Calvert, D.; Abdullah, H. Autonomous visual servoing of a robot manipulator using reinforcement learning. Int. J. Robot. Autom. 2016, 31, 26–38. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, C. DDPG-Based Adaptive Robust Tracking Control for Aerial Manipulators with Decoupling Approach. IEEE Trans. Cybern. 2022, 52, 8258–8271. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.; Han, D.; Park, J.; Kim, J. Motion Planning of Robot Manipulators for a Smoother Path Using a Twin Delayed Deep Deterministic Policy Gradient with Hindsight Experience Replay. Appl. Sci. 2020, 10, 575–589. [Google Scholar] [CrossRef]
- Chen, P.; Pei, J.; Lu, W.; Li, M. A deep reinforcement learning based method for real-time path planning and dynamic obstacle avoidance. Neurocomputing 2022, 497, 64–75. [Google Scholar] [CrossRef]
- Hassanpour, H.; Wang, X. A practically implementable reinforcement learning-based process controller design. Comput. Chem. Eng. 2024, 70, 108511. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Y.; Shi, P.; Wang, F. Scalable-MADDPG-Based Cooperative Target Invasion for a Multi-USV System. IEEE Trans. Neural Netw. Learn. Syst. 2023, 2023, 3309689. [Google Scholar] [CrossRef]
- Bogaerts, B.; Sels, S.; Vanlanduit, S.; Penne, R. Connecting the CoppeliaSim robotics simulator to virtual reality. SoftwareX 2020, 11, 100426. [Google Scholar] [CrossRef]
- Su, S.; Chen, Y.; Li, C.; Ni, K.; Zhang, J. Intelligent Control Strategy for Robotic Manta Via CPG and Deep Reinforcement Learning. Drones 2024, 8, 323. [Google Scholar] [CrossRef]
- Rohan, A. Enhanced Camera Calibration for Machine Vision using OpenCV. IAES Int. J. Artif. Intell. (IJ-AI) 2014, 3, 136. [Google Scholar]
- Huang, B.; Zou, S. A New Camera Calibration Technique for Serious Distortion. Processes 2022, 10, 488. [Google Scholar] [CrossRef]
- Ju, H.; Juan, R.; Gomez, R.; Nakamura, K.; Li, G. Transferring policy of deep reinforcement learning from simulation to reality for robotics. Nat. Mach. Intell. 2022, 4, 1077–1087. [Google Scholar] [CrossRef]
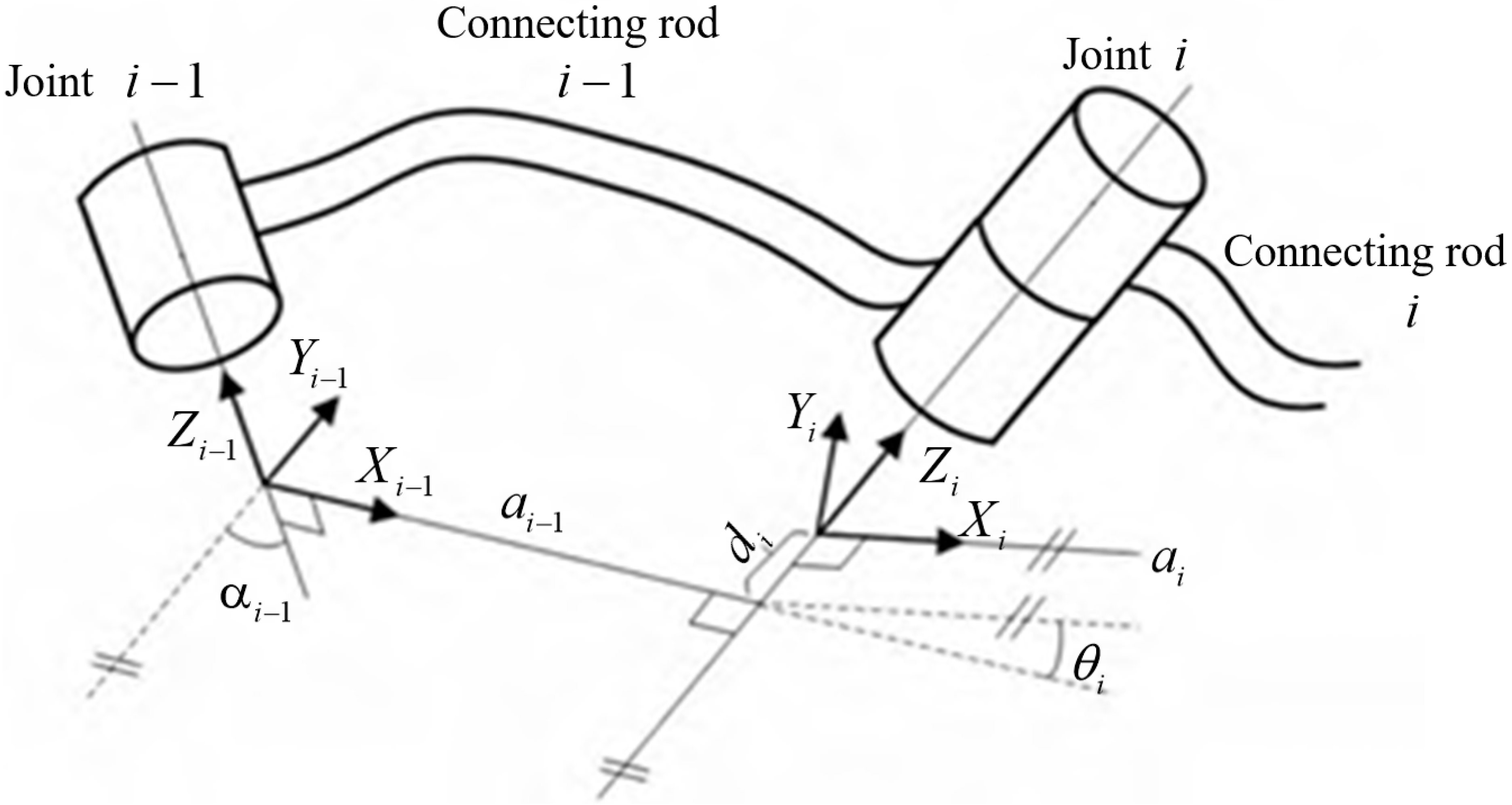

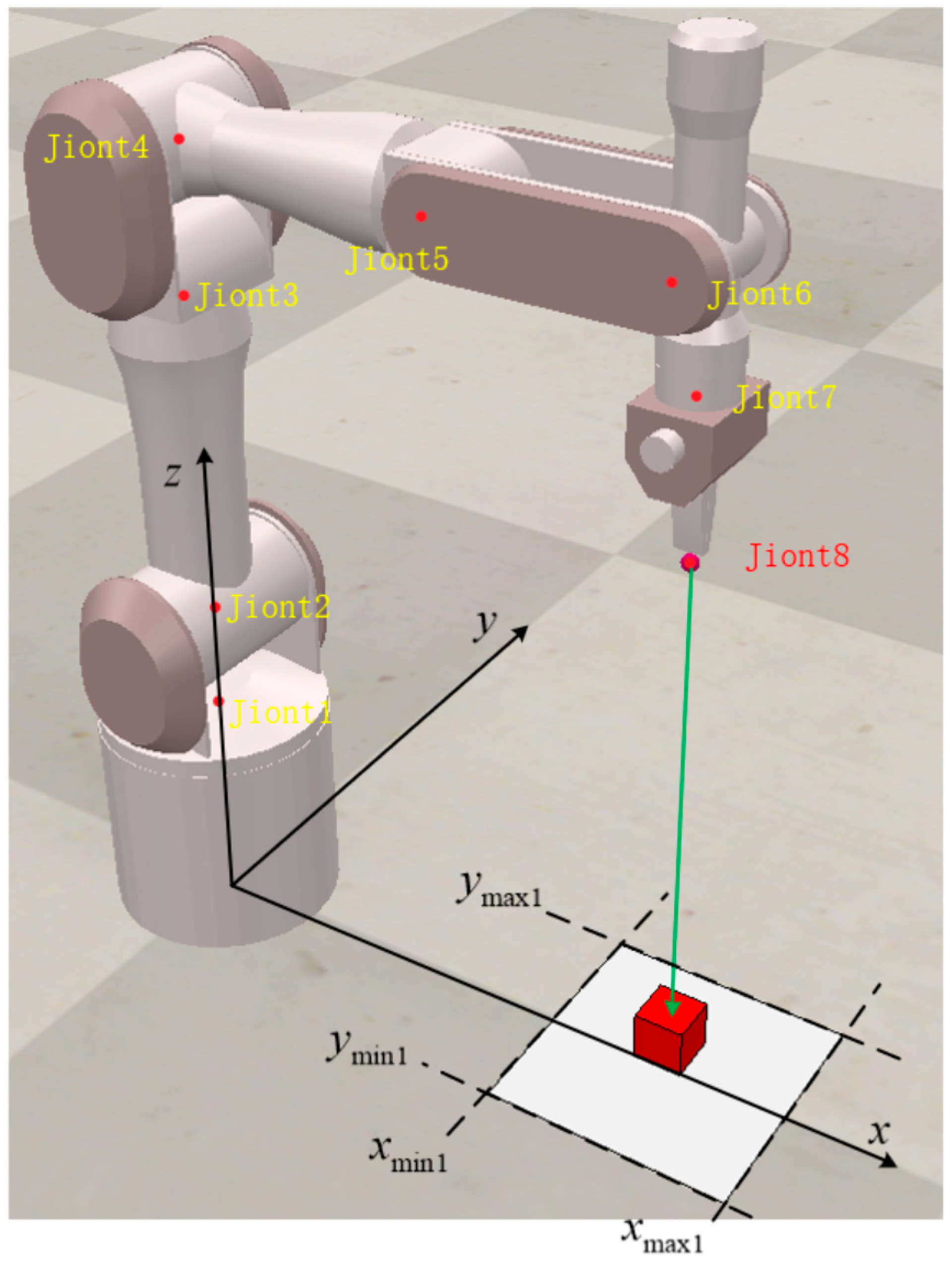
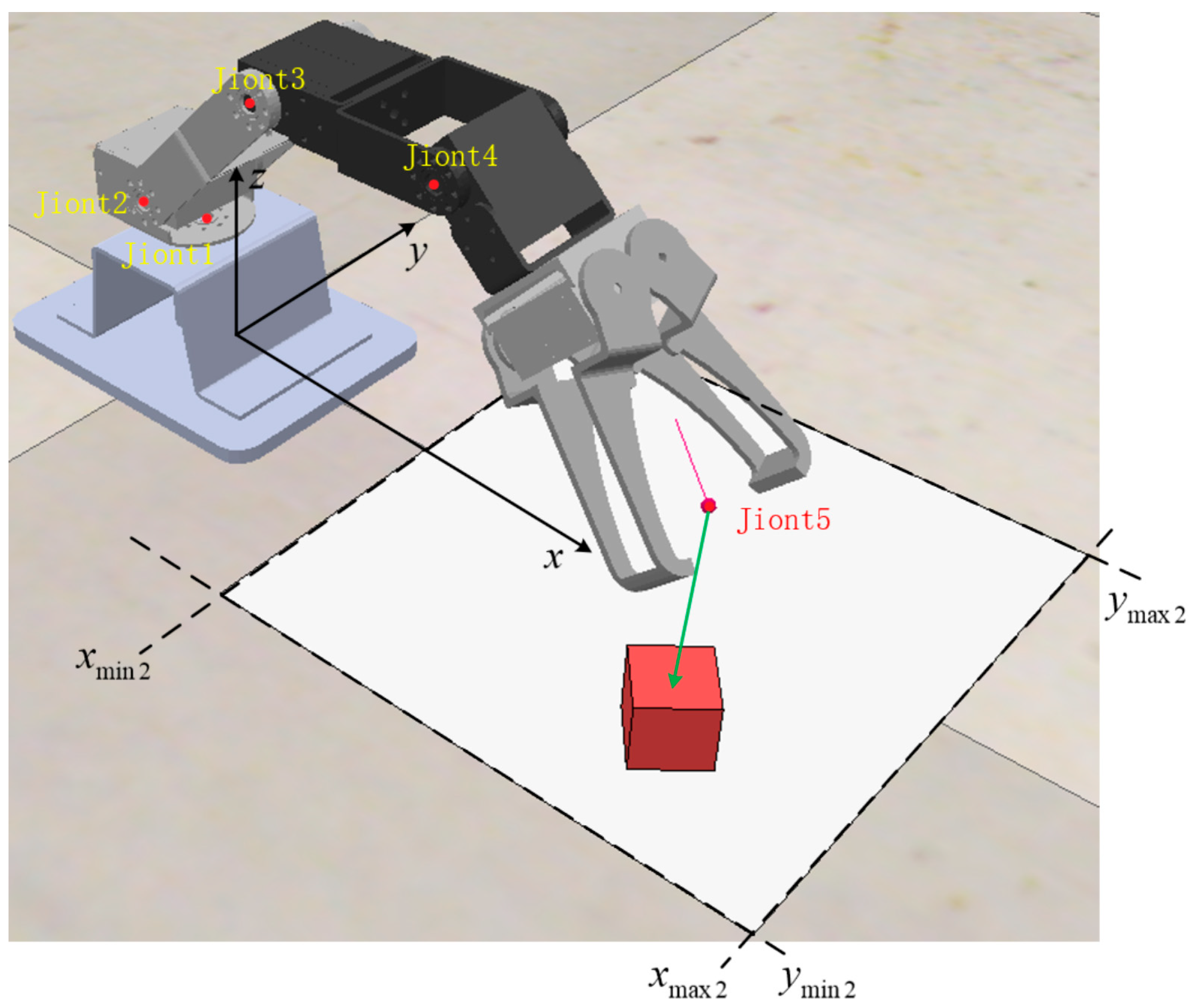






| 1 | 0 | 0 | 0.2039 | |
| 2 | 90 | 0 | 0 | |
| 3 | −90 | 0 | 0.2912 | |
| 4 | 90 | 0 | 0 | |
| 5 | −90 | 0 | 0.3236 | |
| 6 | 90 | 0 | 0 | |
| 7 | −90 | 0 | 0.0606 | |
| 8 | 0 | 0 | 0.1006 |
| 1 | 0 | 0 | 0.0445 | |
| 2 | 90 | 0.0025 | 0 | |
| 3 | 0 | 0.081 | 0 | |
| 4 | 0 | 0.0775 | 0 | |
| 5 | 0 | 0.126 | 0 |
| Parameter | Value |
|---|---|
| Learning rate of Actor network | 1 × 10−4 |
| Learning rate of Critic network | 5 × 10−4 |
| Discount rate | 0.9 |
| Size of the replay buffer capacity | 10,000 |
| Target network soft update factor | 0.005 |
| Batch size | 32 |
| Episode | 120,000 |
| Step of interactions with the environment per episode | 16 |
| Step of interactions with M in dynamic programming | 16 |
| Step of dynamic programming | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Su, S.; Ni, K.; Li, C. Integrated Intelligent Control of Redundant Degrees-of-Freedom Manipulators via the Fusion of Deep Reinforcement Learning and Forward Kinematics Models. Machines 2024, 12, 667. https://doi.org/10.3390/machines12100667
Chen Y, Su S, Ni K, Li C. Integrated Intelligent Control of Redundant Degrees-of-Freedom Manipulators via the Fusion of Deep Reinforcement Learning and Forward Kinematics Models. Machines. 2024; 12(10):667. https://doi.org/10.3390/machines12100667
Chicago/Turabian StyleChen, Yushuo, Shijie Su, Kai Ni, and Cunjun Li. 2024. "Integrated Intelligent Control of Redundant Degrees-of-Freedom Manipulators via the Fusion of Deep Reinforcement Learning and Forward Kinematics Models" Machines 12, no. 10: 667. https://doi.org/10.3390/machines12100667
APA StyleChen, Y., Su, S., Ni, K., & Li, C. (2024). Integrated Intelligent Control of Redundant Degrees-of-Freedom Manipulators via the Fusion of Deep Reinforcement Learning and Forward Kinematics Models. Machines, 12(10), 667. https://doi.org/10.3390/machines12100667






