Optimization of Occupant Restraint System Using Machine Learning for THOR-M50 and Euro NCAP
Abstract
1. Introduction
1.1. Background
1.2. Research Objectives
2. Materials and Methods
2.1. Overview
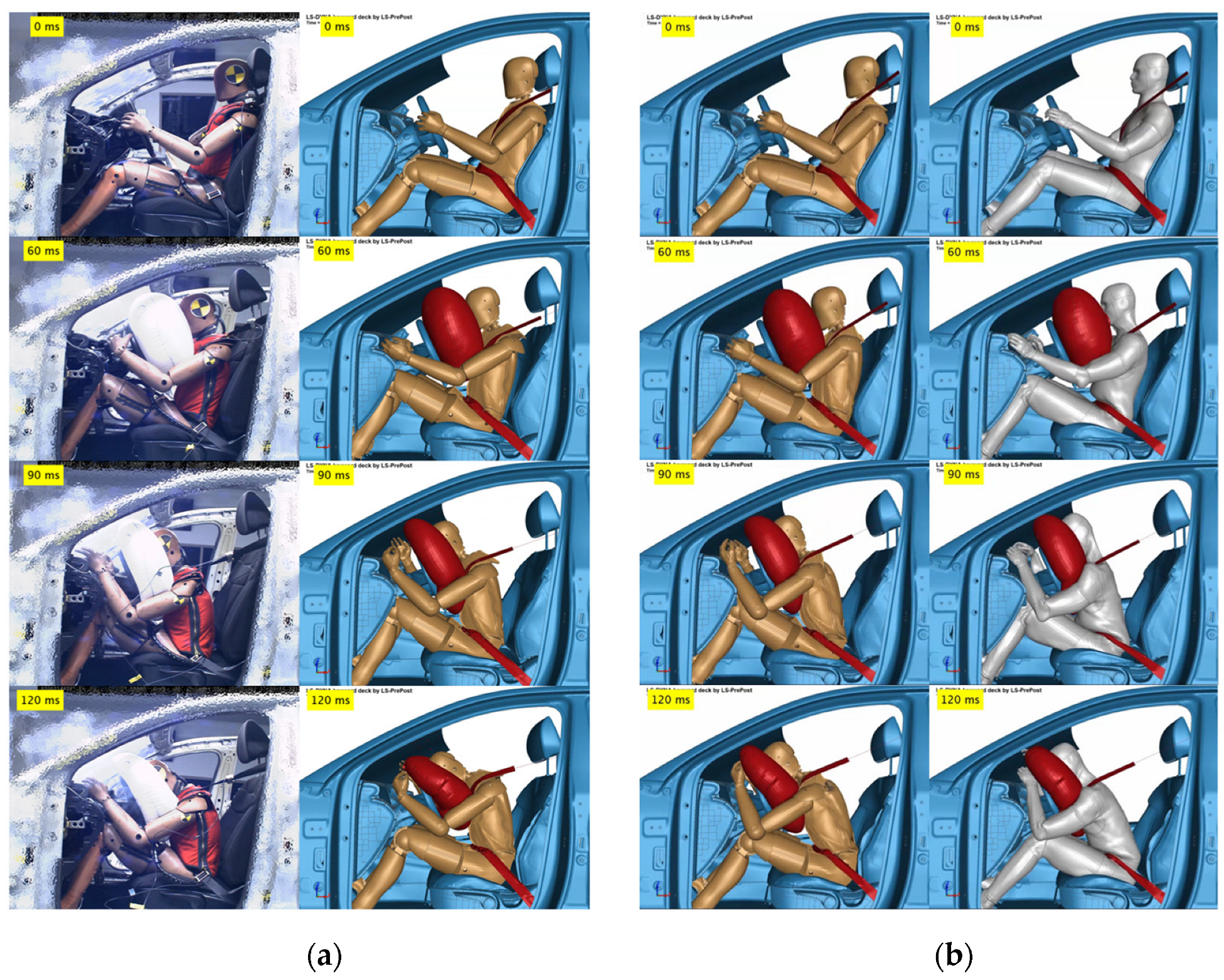
2.2. Model Validation
2.3. Parametric Simulation
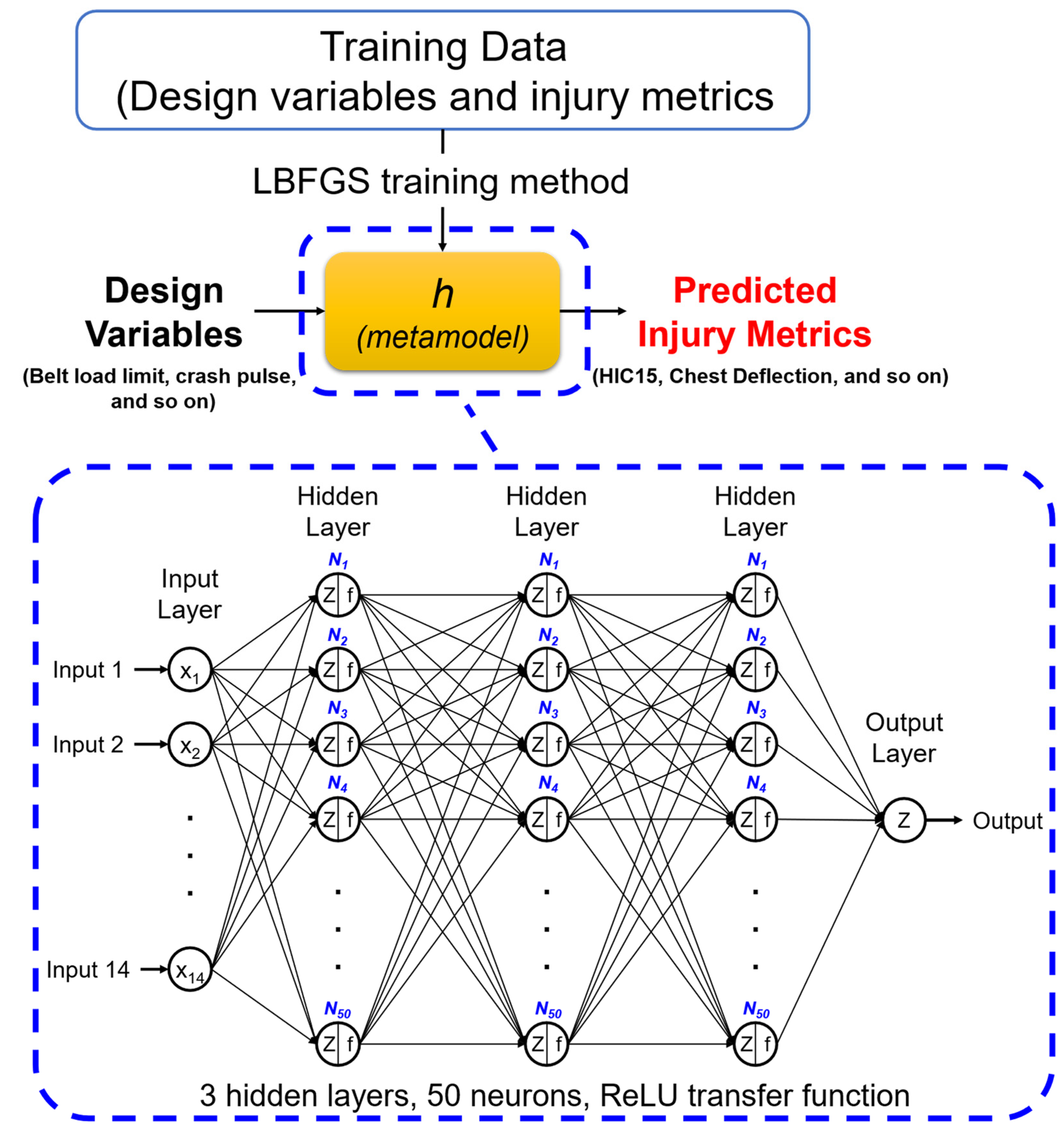
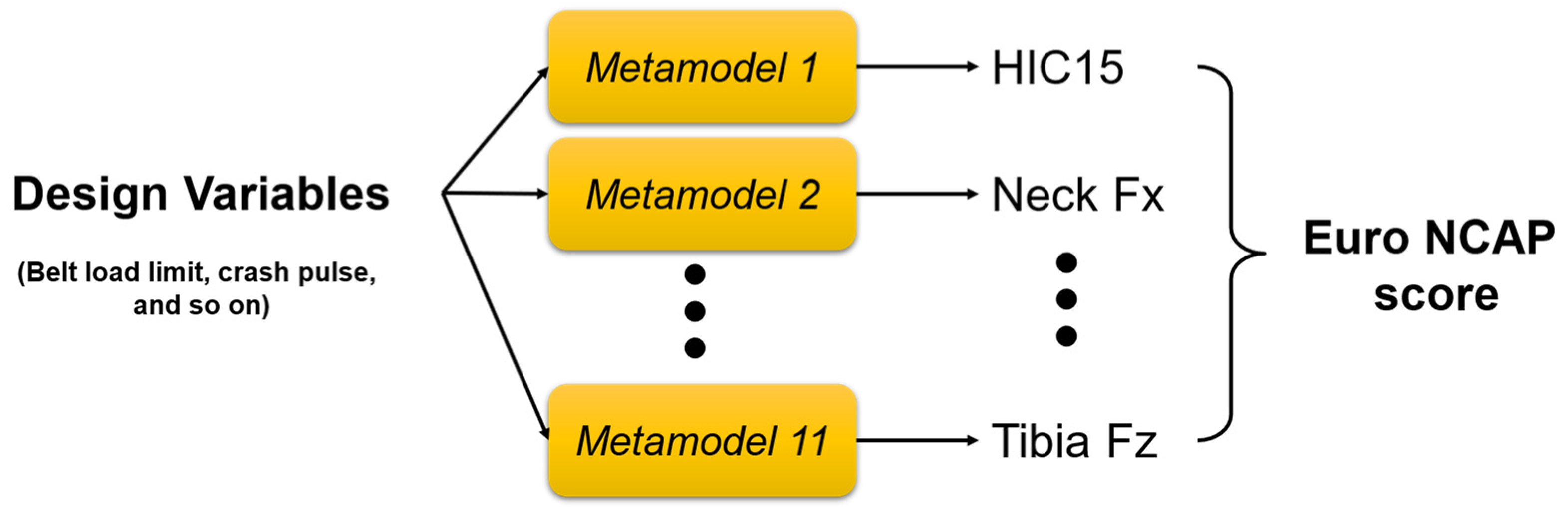
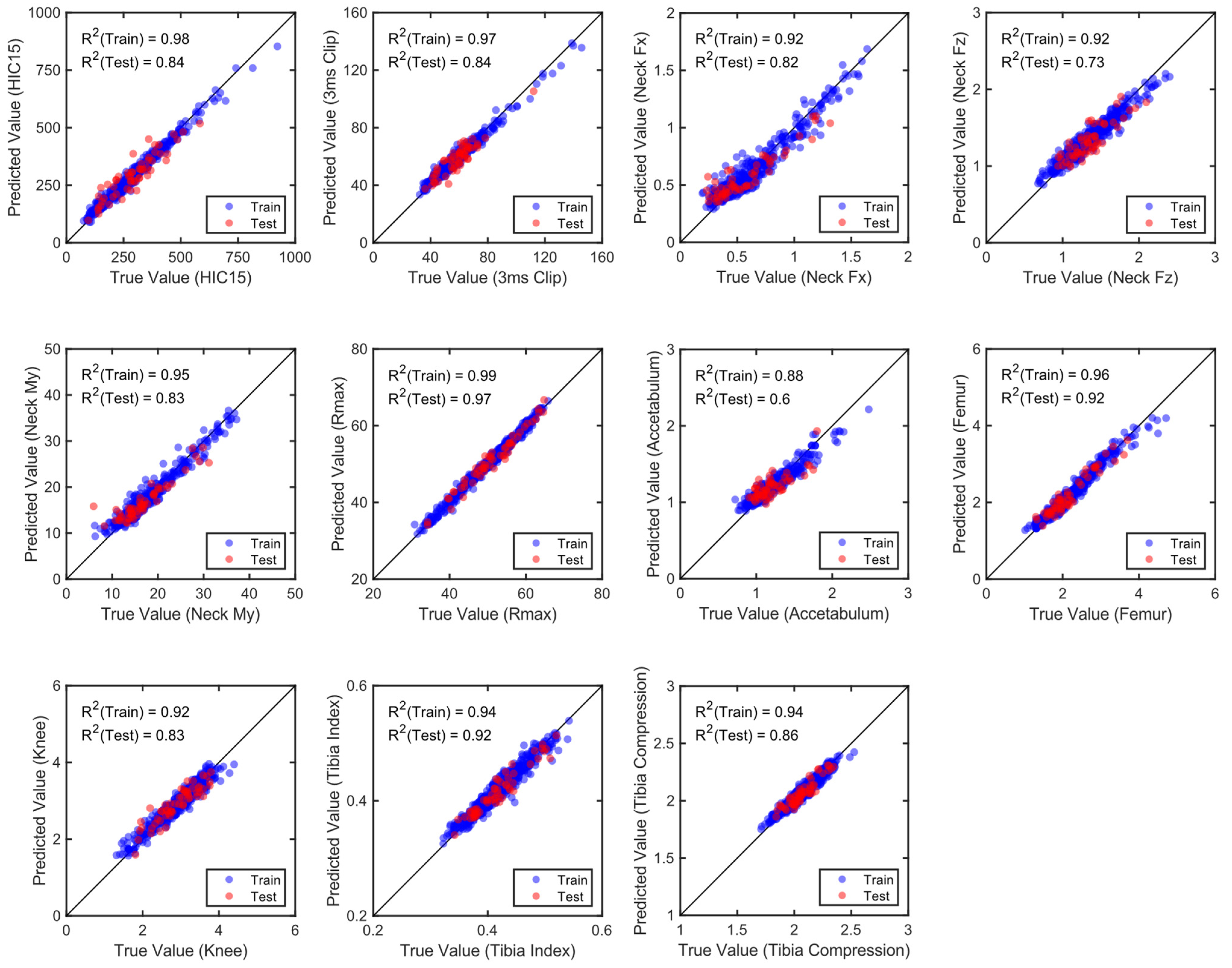
2.4. Metamodeling
2.5. Optimization
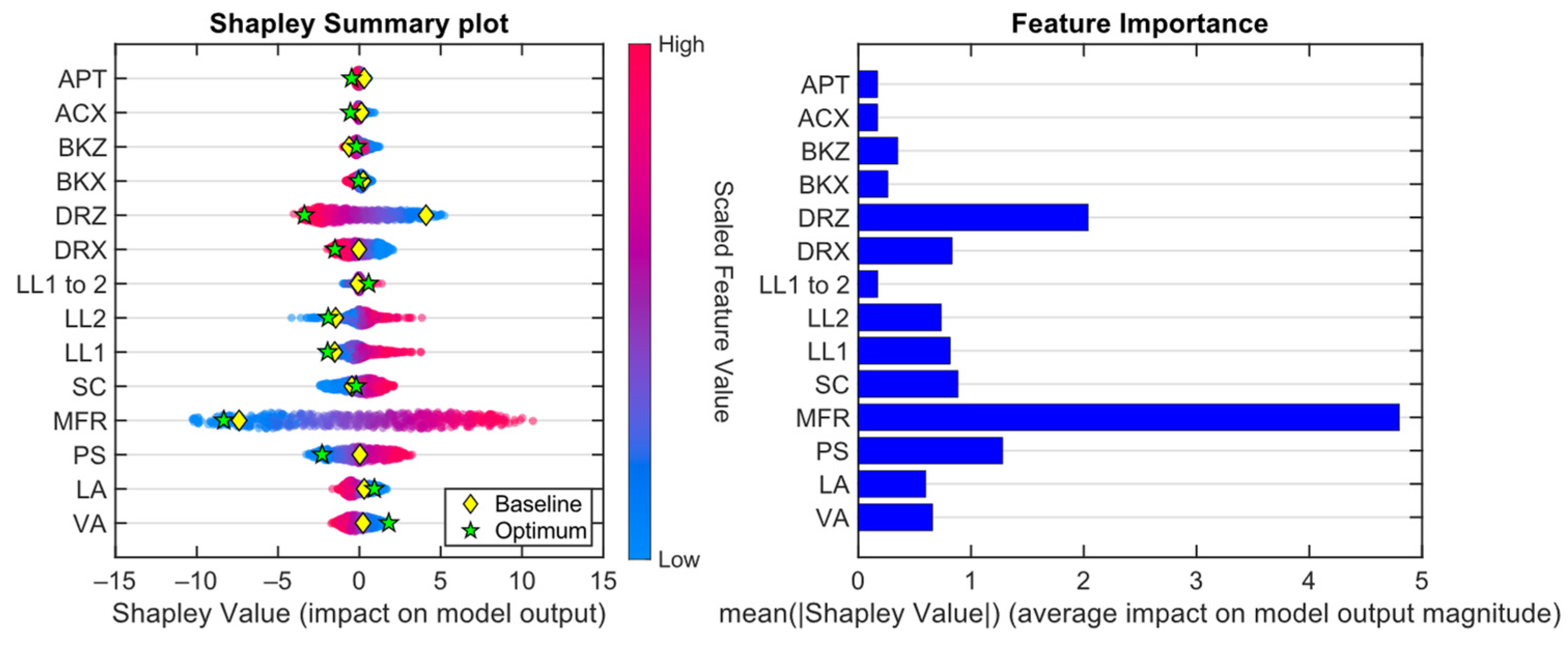
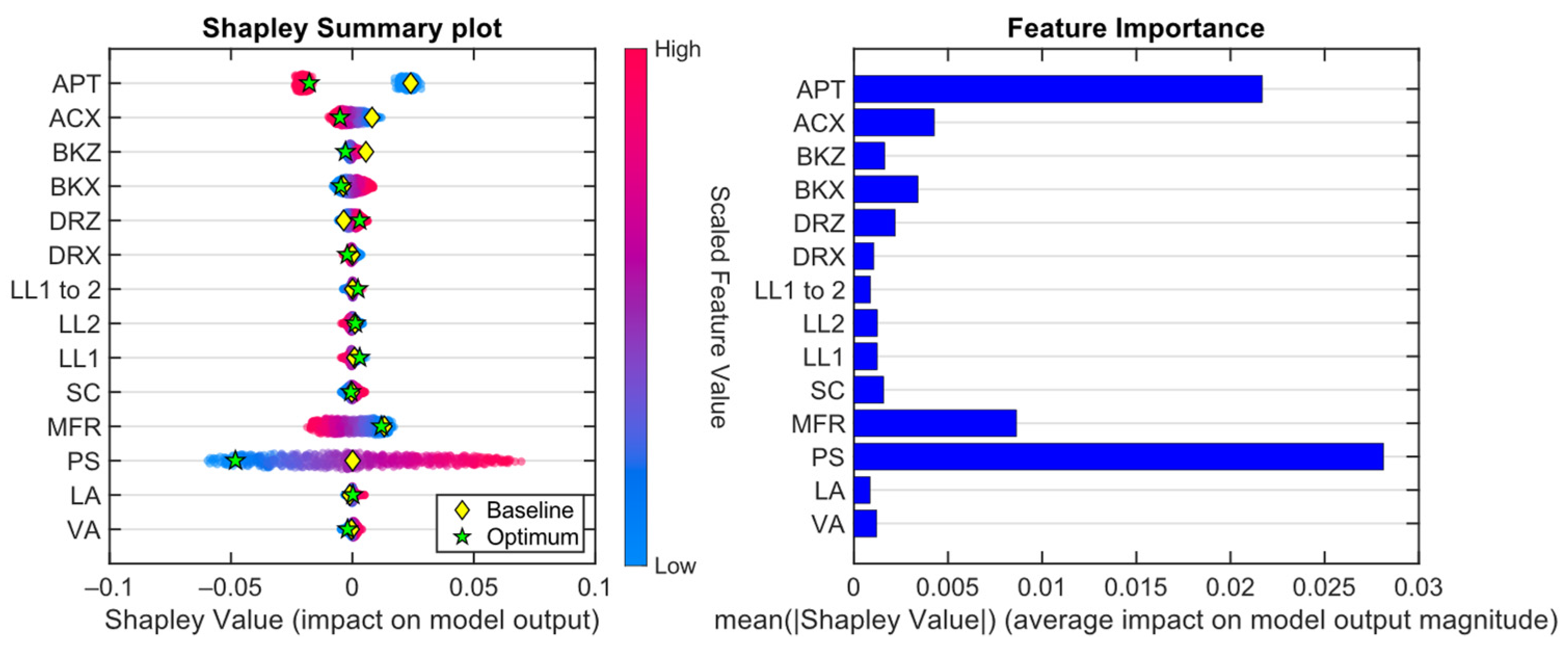
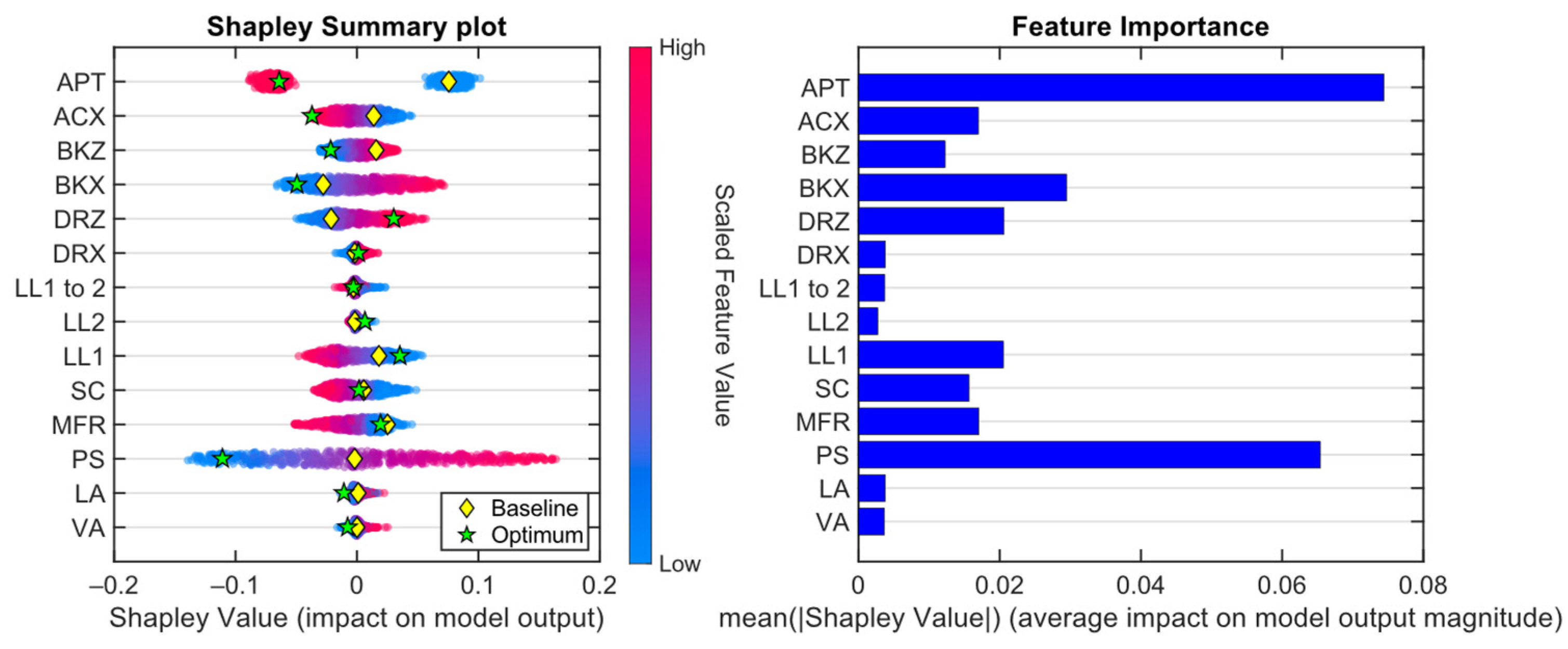
2.6. Sensitivity Analysis
3. Results
3.1. Model Validation
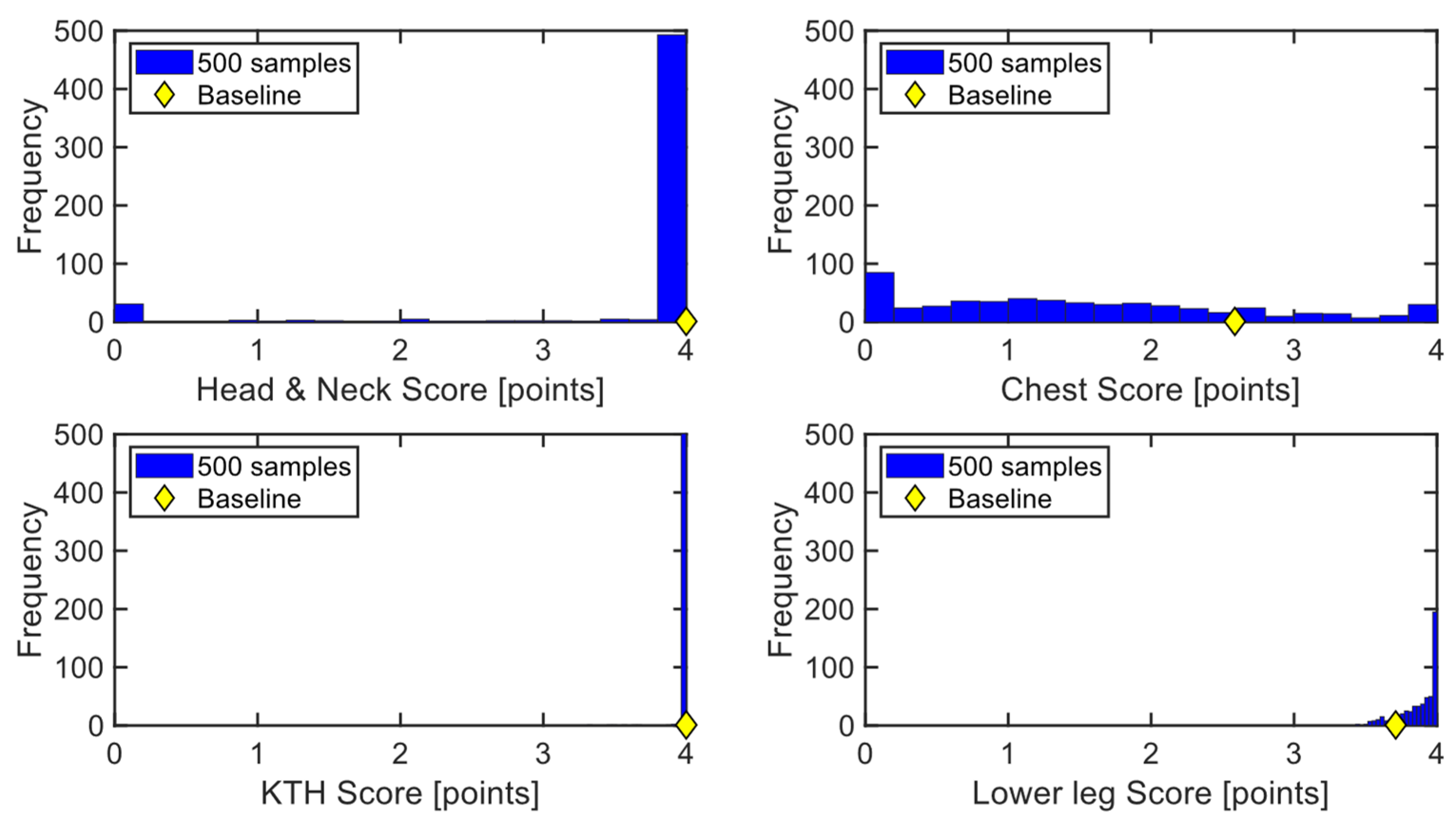
3.2. Parametric Simulations
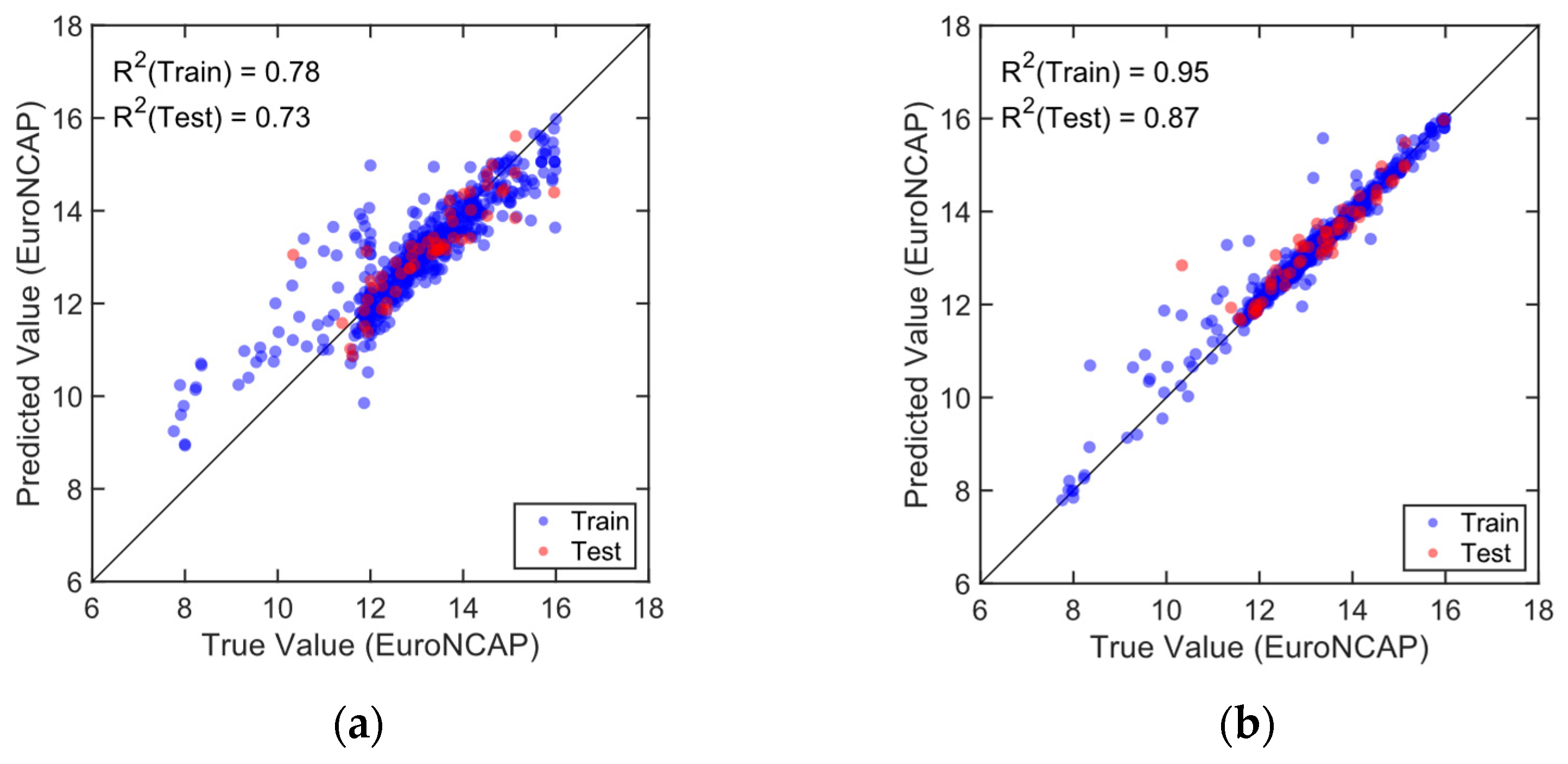
3.3. Development of Metamodels
3.4. Optimization and Verification
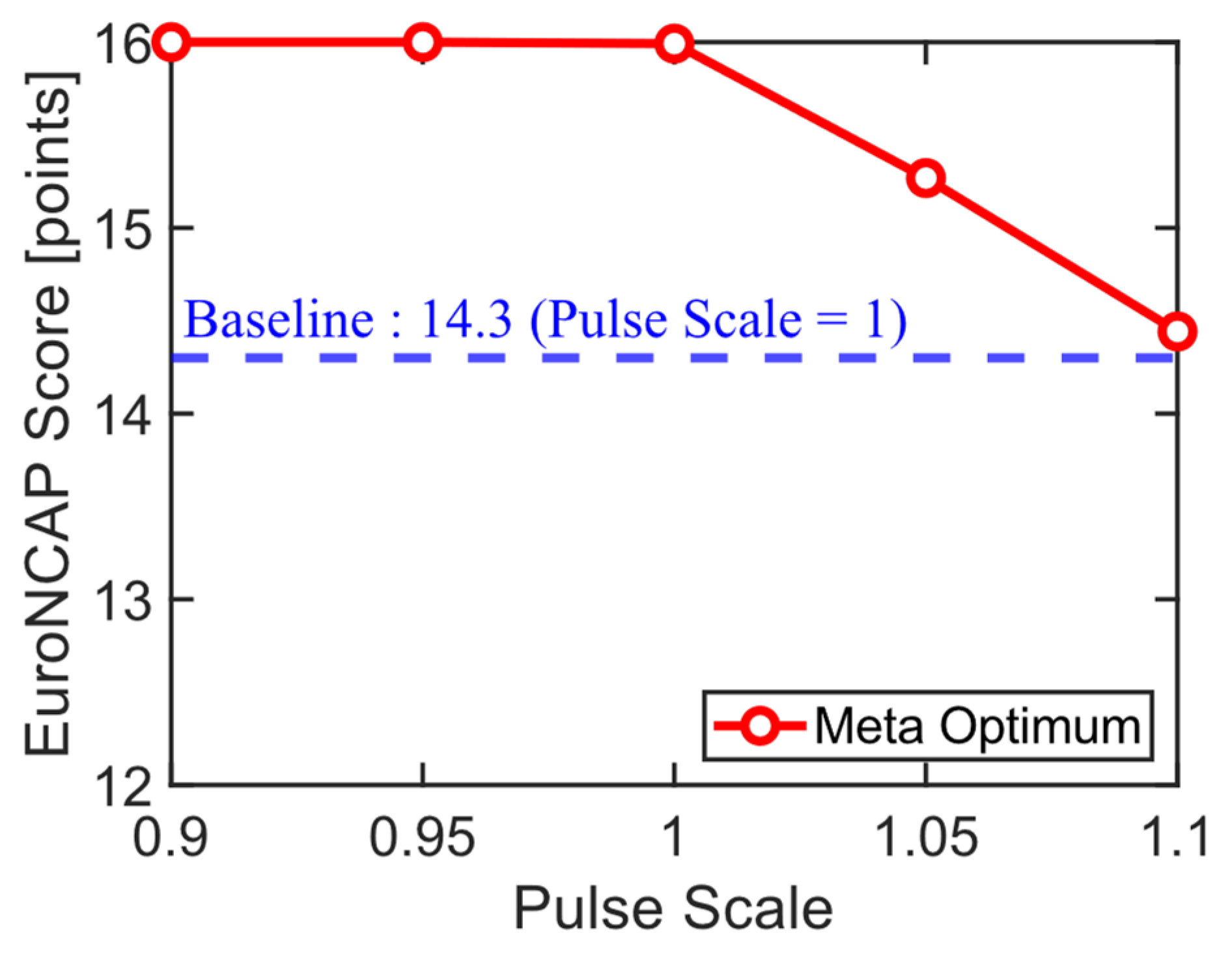
3.5. Metamodel Interpretation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miller, T.R.; Bhattacharya, S.; Zaloshnja, E. Fruits of 20 years of highway safety legislative advocacy in the United States. In Annals of Advances in Automotive Medicine/Annual Scientific Conference; Association for the Advancement of Automotive Medicine: Chicago, IL, USA, 2011; Volume 55, p. 357. [Google Scholar]
- O’Neill, B. Preventing passenger vehicle occupant injuries by vehicle design—A historical perspective from IIHS. Traffic Inj. Prev. 2009, 10, 113–126. [Google Scholar] [CrossRef]
- Fang, J.; Sun, G.; Qiu, N.; Kim, N.H.; Li, Q. On design optimization for structural crashworthiness and its state of the art. Struct. Multidiscip. Optim. 2017, 55, 1091–1119. [Google Scholar] [CrossRef]
- Bhalla, K.; Gleason, K. Effects of vehicle safety design on road traffic deaths, injuries, and public health burden in the Latin American region: A modelling study. Lancet Glob. Health 2020, 8, e819–e828. [Google Scholar] [CrossRef] [PubMed]
- Forman, J.; Poplin, G.S.; Shaw, C.G.; McMurry, T.L.; Schmidt, K.; Ash, J.; Sunnevang, C. Automobile injury trends in the contemporary fleet: Belted occupants in frontal collisions. Traffic Inj. Prev. 2019, 20, 607–612. [Google Scholar] [PubMed]
- Bai, Z.; Jiang, B.; Zhu, F.; Cao, L. Optimizing the passenger air bag of an adaptive restraint system for multiple size occupants. Traffic Inj. Prev. 2014, 15, 556–563. [Google Scholar] [PubMed]
- Sandner, V.; van Ratingen, M.; Ellway, J. Euro ncap-new frontal impact test with mobile progressive deformable barrier (mpdb). In Proceedings of the 26th International Technical Conference on the Enhanced Safety of Vehicles (ESV): Technology: Enabling a Safer Tomorrow National Highway Traffic Safety Administration, Eindhoven, The Netherlands, 10–13 June 2019. paper number. 19-0196. [Google Scholar]
- Parent, D.; Craig, M.; Moorhouse, K. Biofidelity Evaluation of the THOR and Hybrid III 50th Percentile Male Frontal Impact Anthropomorphic Test Devices (No. 2017-22-0009); SAE Technical Paper; SAE: Warrendale, PA, USA, 2017. [Google Scholar]
- Yoganandan, N.; Pintar, F.A.; Moore, J.; Maiman, D.J. Sensitivity of THOR and Hybrid III dummy lower neck loads to belt systems in frontal impact. Traffic Inj. Prev. 2011, 12, 88–95. [Google Scholar]
- McMurry, T.L.; Sherwood, C.; Poplin, G.S.; Seguí-Gómez, M.; Crandall, J. Implications of functional capacity loss and fatality for vehicle safety prioritization. Traffic Inj. Prev. 2015, 16 (Suppl. 2), S140–S145. [Google Scholar] [CrossRef]
- Sunnevång, C.; Lecuyer, E.; Hynd, D.; Carroll, J.; Kruse, D.; Boström, O. Evaluation of near-side oblique frontal impacts using THOR with SD3 shoulder. Traffic Inj. Prev. 2014, 15 (Suppl. 1), S96–S102. [Google Scholar] [CrossRef][Green Version]
- Liufu, K.; Liu, Q.; Lu, Y.; Chen, Z.; Zhang, Z.; Li, Q. Multiobjective optimization on cooperative control of autonomous emergency steering and occupant restraint system for enhancing occupant safety. Accid. Anal. Prev. 2021, 159, 106302. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, J.; Zhang, T.; Zhang, H.; Peng, Y. A Coupling Optimization Method of Vehicle Structure and Restraint System for Occupant Injury Protection in Traffic Accidents. Symmetry 2023, 15, 558. [Google Scholar]
- Zhang, J.; Wang, D.; Ni, Y.; Chen, C. A two degrees of freedom model–based optimization method for occupant restraint systems in vehicle crash. Struct. Multidiscip. Optim. 2019, 60, 2597–2614. [Google Scholar]
- Horii, H. Advancement of vehicle occupant restraint system design by integration of artificial intelligence technologies. Int. J. Transp. Dev. Integr. 2021, 5, 242–253. [Google Scholar]
- Joodaki, H.; Gepner, B.; Lee, S.H.; Katagiri, M.; Kim, T.; Kerrigan, J. Is optimized restraint system for an occupant with obesity different than that for a normal BMI occupant? Traffic Inj. Prev. 2021, 22, 623–628. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Xu, H.; Zhu, F. A data mining method for structure design with uncertainty in design variables. Comput. Struct. 2021, 244, 106457. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 1–10. [Google Scholar]
- Chen, H.; Chen, H.; Zhou, R.; Liu, Z.; Sun, X. Exploring the mechanism of crashes with autonomous vehicles using machine learning. Math. Probl. Eng. 2021, 2021, 5524356. [Google Scholar] [CrossRef]
- Dong, S.; Khattak, A.; Ullah, I.; Zhou, J.; Hussain, A. Predicting and analyzing road traffic injury severity using boosting-based ensemble learning models with SHAPley Additive exPlanations. Int. J. Environ. Res. Public Health 2022, 19, 2925. [Google Scholar]
- Guo, M.; Yuan, Z.; Janson, B.; Peng, Y.; Yang, Y.; Wang, W. Older pedestrian traffic crashes severity analysis based on an emerging machine learning XGBoost. Sustainability 2021, 13, 926. [Google Scholar]
- Helton, J.C.; Davis, F.J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- The MathWorks Inc. MATLAB, Version: 9.13.0 (R2022b); The MathWorks Inc.: Natick, MA, USA, 2022. Available online: https://www.mathworks.com (accessed on 1 November 2023).
- Chipperfield, A.J.; Fleming, P.J. The MATLAB Genetic Algorithm Toolbox. 1995. Available online: https://digital-library.theiet.org/content/conferences/10.1049/ic_19950061 (accessed on 1 November 2023).
- Joodaki, H.; Gepner, B.; Kerrigan, J. Leveraging machine learning for predicting human body model response in restraint design simulations. Comput. Methods Biomech. Biomed. Eng. 2021, 24, 597–611. [Google Scholar]
- Schneider, B.; Kofler, D.; D’Addetta, G.A.; Freienstein, H.; Wolkenstein, M.; Klug, C. Approach for machine learning based design of experiments for occupant simulation. Front. Future Transp. 2022, 3, 913852. [Google Scholar] [CrossRef]
- Joseph, V.R.; Gul, E.; Ba, S. Designing computer experiments with multiple types of factors: The MaxPro approach. J. Qual. Technol. 2020, 52, 343–354. [Google Scholar] [CrossRef]
- Eggers, A.; Eickhoff, B.; Dobberstein, J.; Zellmer, H.; Adolph, T. Effects of variations in belt geometry, double pretensioning and adaptive load limiting on advanced chest measurements of THOR and Hybrid III. In Proceedings of the IRCOBI Conference, Berlin, Germany, 10–12 September 2014. [Google Scholar]
- Hu, J.; Reed, M.P.; Rupp, J.D.; Fischer, K.; Lange, P.; Adler, A. Optimizing Seat Belt and Airbag Designs for Rear Seat Occupant Protection in Frontal Crashes (No. 2017-22-0004); SAE Technical Paper; SAE: Warrendale, PA, USA, 2017. [Google Scholar]

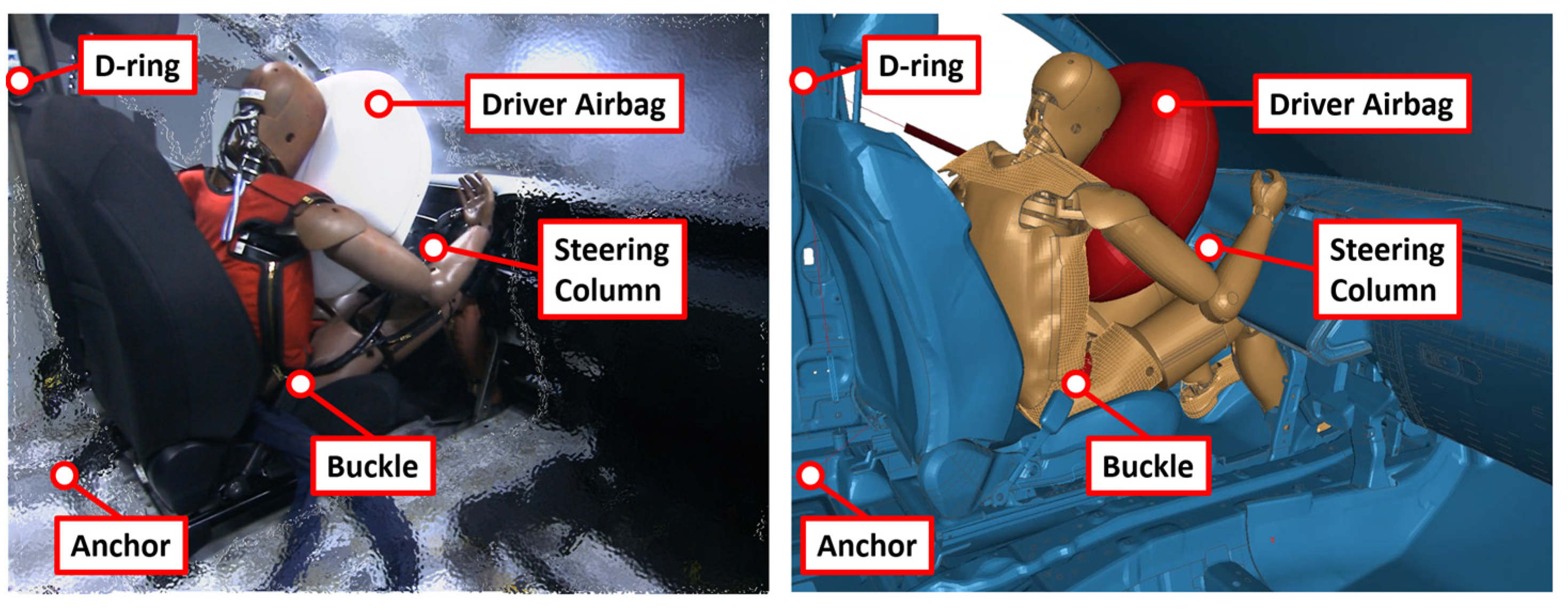



| Body Region | Injury Criterion | Unit | Upper | Lower | Scoring |
|---|---|---|---|---|---|
| Head & Neck | HIC15 | - | 700 | 500 | 4 points |
| SUFEHM | - | Monitoring | |||
| BrIC | - | Monitoring | |||
| A Resultant 3 ms | G | 80 | 72 | ||
| Fx | kN | 3.1 | 1.9 | ||
| Fz | kN | 3.3 | 2.7 | ||
| My | Nm | 57 | 42 | ||
| Chest & Abdomen | Chest Compression/Rmax | mm | 60 | 35 | 4 points |
| Abdominal Compression (ignored) | mm | 88 | N/A | ||
| Knee, Femur, Pelvis | L/R Acetabulum | kN | 4.1 | 3.28 | 4 points |
| L/R Femur Compression | kN | 9.07 | 3.8 | ||
| L/R Knee shear displacement | mm | 15 | 6 | ||
| Lower Leg | L/R Tibia index | - | 1.4 | 0.4 | 4 points |
| L/R Tibia Compression | kN | 8 | 2 | ||
| Input Parameter | Range | ||
|---|---|---|---|
| Hard Point | 1 | D-ring X-position (DRX) | 75 mm (+37.5, −37.5) (+: rearward) |
| 2 | D-ring Z-position (DRZ) | 107 mm (+107, 0) (+: upward) | |
| 3 | Buckle X-position (BKX) | 45 mm (+37.5, −7.5) (+: rearward) | |
| 4 | Buckle Z-position (BKZ) | 40 mm (0, −40) (+: upward) | |
| 5 | Anchor X-position (ACX) | 75 mm (+65, −10) (+: rearward) | |
| Belt | 6 | Anchor Pretensioner (APT) | on/off |
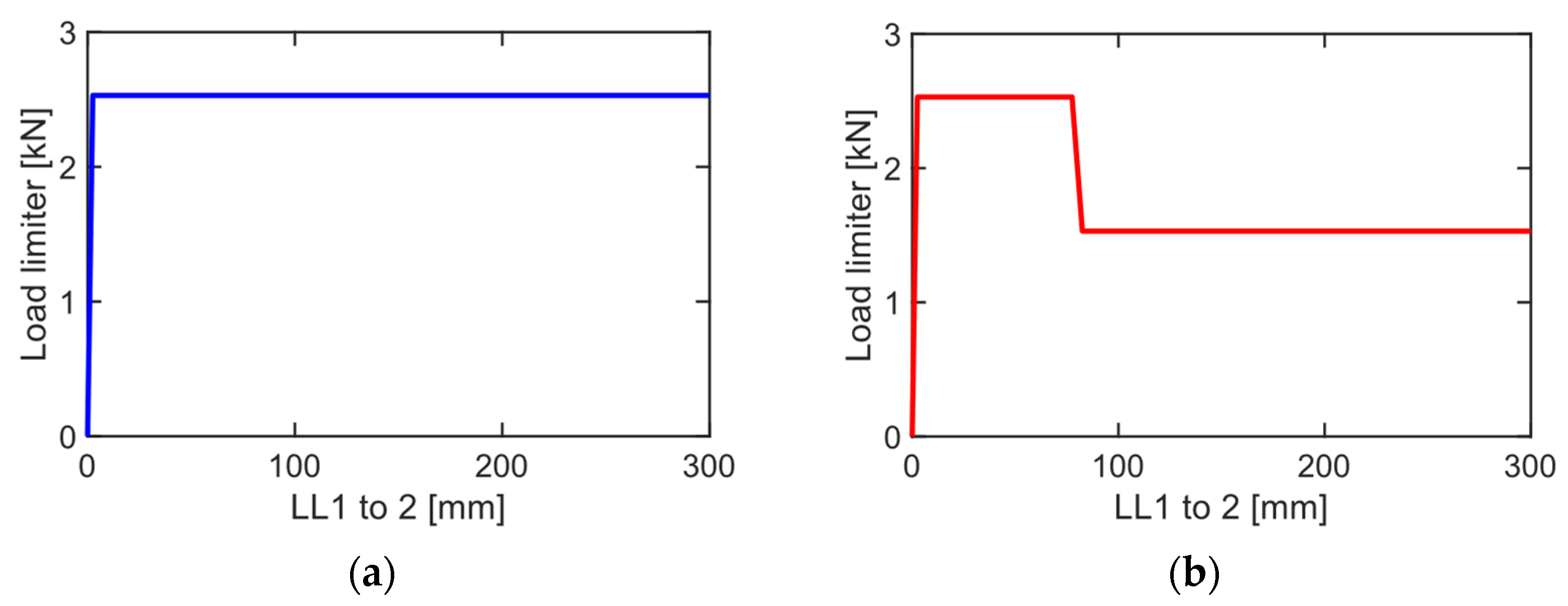
| 7 | Load limiter 1st level (LL1) | 1.5–6 kN | |
| 8 | Load limiter 2nd level (LL2) | 1.5–6 kN | |
| 9 | Load limiter 1st to 2nd (LL1 to 2) | 0–100 mm | |
| Airbag | 10 | Mass flow rate scale (MFR) | 0.7–4 |
| 11 | Vent area scale (VA) | 0.5–2 (245–980 mm2) | |
| 12 | Leakage area scale (LA) | 0.5–2 (480–1820 mm2) | |
| Steering | 13 | Steering column load scale (SC) | 0.5–2 |
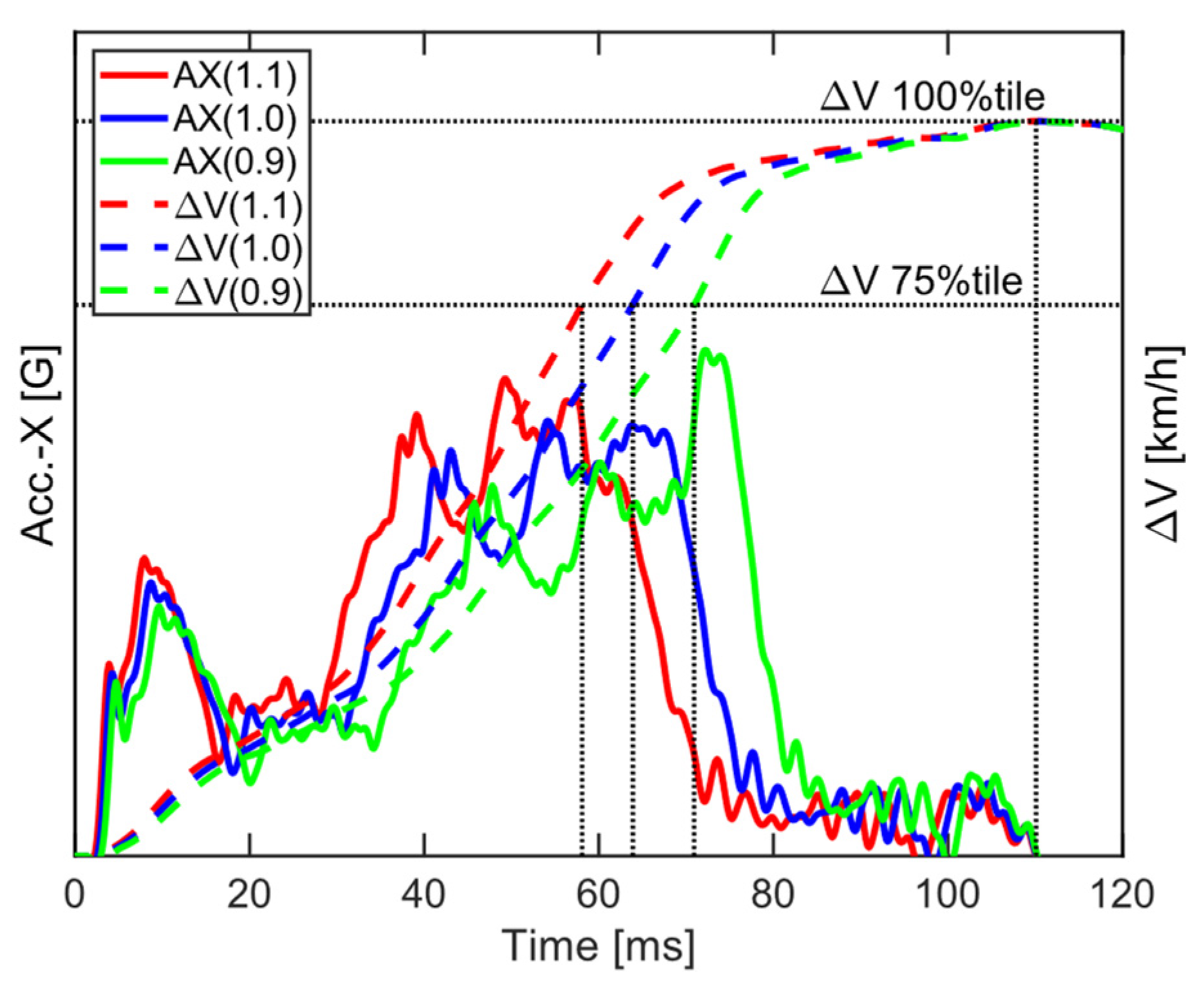
| Pulse | 14 | Pulse scale (PS) | 0.9–1.1 |
| Minimize | (Table 1) |
| with respect to | |
| subject to |
| Body Region | Criterion | Baseline (Test) | Baseline (Simulation) | |||
|---|---|---|---|---|---|---|
| Value | Score | Value | Score | Error (%) | ||
| Head | HIC15 | 122.06 | 4 | 135.75 | 4 | 0.0 |
| A Resultant 3 ms | 40.47 | 40.28 | ||||
| Neck | Fx | 0.69 | 0.80 | |||
| Fz | 0.93 | 1.01 | ||||
| My | 25.73 | 20.17 | ||||
| Chest and Abdomen | Rmax | 43.90 | 2.58 | 43.84 | 2.59 | 0.39 |
| Amax | N/A | N/A | ||||
| Acetabulum | 1.81 | 4 | 1.01 | 4 | 0.0 | |
| Knee, Femur, Pelvis | Femur Compression | 2.96 | 2.74 | |||
| Knee shear displacement | 1.68 | 3.37 | ||||
| Lower Leg | Tibia index | 0.61 | 3.18 | 0.47 | 3.71 | 17.0 |
| Tibia Compression | 1.76 | 2.18 | ||||
| Euro NCAP Score | 13.76 | 14.3 | 4.0 | |||
| Input Parameter | Baseline | Sample Best | Meta Optimum | ||
|---|---|---|---|---|---|
| Vent area scale (VA) | 1 | 1.6 | High | 0.5 | Low |
| Leakage area scale (LA) | 1 | 1.5 | High | 0.56 | Low |
| Mass flow rate scale (MFR) | 1 | 1.5 | High | 0.89 | Low |
| Pulse scale (PS) | 1 | 0.9 | Low | 0.90 | Low |
| Steering column load scale (SC) | 1 | 1.2 | High | 1.1 | High |
| Load limiter 1st level (LL1) | 2.5 | 2.6 | High | 1.7 | Low |
| Load limiter 2nd level (LL2) | 2.5 | 1.7 | Low | 1.5 | Low |
| Load limiter 1st to 2nd (LL1 to 2) | N/A | 12.0 | - | 100 | - |
| D-ring X-position (DRX) | 0 | 11.0 | High | 36.5 | High |
| D-ring Z-position (DRZ) | 0 | 18.0 | High | 107 | High |
| Buckle X-position (BKX) | 0 | 21.0 | High | −7.5 | Low |
| Buckle Z-position (BKZ) | 0 | −5.6 | Low | −40.0 | Low |
| Anchor X-position (ACX) | 0 | 6.9 | High | 65 | High |
| Anchor Pretensioner (APT) | off | on | - | on | - |
| Body Region | Criterion | Baseline (THOR) | Sample Best (THOR) | Meta Optimum (THOR) | Baseline (GHBM-O) | Meta Optimum (GHBM-O) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Value | Score | Value | Score | Value | Score | Value | Score | Value | Score | ||
| Head | HIC15 | 135.8 | 4 | 220.9 | 4 | 160.1 | 4 | 124.1 | 4 | 116.2 | 4 |
| A Resultant 3 ms | 40.3 | 69.3 | 43.6 | 38.3 | 38.7 | ||||||
| Neck | Fx | 0.8 | 0.3 | 0.4 | 0.4 | 0.7 | |||||
| Fz | 1.0 | 0.9 | 0.8 | 1.2 | 1.2 | ||||||
| My | 20.1 | 15.4 | 12.6 | 24.4 | 18.8 | ||||||
| Chest & Abdomen | Rmax | 43.8 | 2.6 | 37.8 | 3.6 | 32.8 | 4 | 34.6 | 4 | 30.9 | 4 |
| Amax | N/A | N/A | N/A | N/A | N/A | ||||||
| Acetabulum | 1.0 | 4 | 0.9 | 4 | 1.6 | 4 | 2.7 | 4 | 2.7 | 4 | |
| Knee, Femur, Pelvis | Femur Compression | 2.7 | 1.8 | 1.0 | 1.0 | 0.5 | |||||
| Knee shear displacement | 3.4 | 2.6 | 1.6 | N/A | N/A | ||||||
| Lower Leg | Tibia index | 0.5 | 3.7 | 0.4 | 4 | 0.4 | 4 | 0.5 | 3.7 | 0.5 | 3.8 |
| Tibia Compression | 2.2 | 1.9 | 1.8 | 1.2 | 1.2 | ||||||
| Euro NCAP Score | 14.3 | 15.6 | 16 | 15.7 | 15.8 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heo, J.; Cho, M.G.; Kim, T. Optimization of Occupant Restraint System Using Machine Learning for THOR-M50 and Euro NCAP. Machines 2024, 12, 74. https://doi.org/10.3390/machines12010074
Heo J, Cho MG, Kim T. Optimization of Occupant Restraint System Using Machine Learning for THOR-M50 and Euro NCAP. Machines. 2024; 12(1):74. https://doi.org/10.3390/machines12010074
Chicago/Turabian StyleHeo, Jaehyuk, Min Gi Cho, and Taewung Kim. 2024. "Optimization of Occupant Restraint System Using Machine Learning for THOR-M50 and Euro NCAP" Machines 12, no. 1: 74. https://doi.org/10.3390/machines12010074
APA StyleHeo, J., Cho, M. G., & Kim, T. (2024). Optimization of Occupant Restraint System Using Machine Learning for THOR-M50 and Euro NCAP. Machines, 12(1), 74. https://doi.org/10.3390/machines12010074





