Control Design for a Power-Assisted Mobile Trainer: Applied to Clinical Stroke Rehabilitation

Abstract

This paper presents control design and implementation for a power-assisted mobile trainer that employs neuro-developmental treatment (NDT) principles. NDT is a gait rehabilitation technique for stroke patients that provides minimum intervention at critical gait events. Traditional NDT rehabilitation is an effective post-stroke treatment but is also time consuming and labor intensive for therapists. Therefore, we designed a mobile NDT trainer to automatically repeat therapists’ intervention patterns, allowing patients to receive sufficient training without increasing therapists’ workloads. Because the trainer was self-propelled, it could cause burdens to stroke patients with limited muscle strength, thereby potentially degrading the rehabilitation effects. Hence, this paper proposes a power-assisted device that can let the mobile trainer follow the user, allowing the subject to focus on the rehabilitation training. We conducted system identification and control design for the power-assisted NDT trainer. We then implemented the designed controllers and tested the trainer. Finally, we invited 10 healthy subjects and 12 stroke patients to conduct clinical experiments. After using the power-assisted NDT trainer, most participants exhibited improvements in swing-phase symmetry, pelvic rotation, and walking speed. Based on the results, the power-assisted device was deemed effective in facilitating stroke rehabilitation.

1. Introduction

Stroke is the second leading cause of death globally [1]. Even those who survive a stroke can still experience various after-effects, such as balance issues, difficulties in walking, cognitive impairments, visual problems, language difficulties, and fatigue [2]. Because approximately half of post-stroke patients cannot walk [3], regaining independent walking is the primary goal for post-stroke rehabilitation as one’s walking ability can significantly affect their daily activities and life.

Many rehabilitation devices have been proposed to assist stroke patients in recovering their walking abilities. For example, Banala et al. [4] developed lower-limb exoskeletons to improve patients’ gait patterns and walking speeds for rehabilitation on treadmills. Pietrusinski et al. [5] developed a robotic gait rehabilitation trainer that provided practical guidance on pelvic tilt angles for stroke patients to improve their walking ability. Werner et al. [6] designed an electromechanical gait trainer to provide non-ambulatory subjects with repetitive practice of gait-like movements.

Another therapeutic approach for treating post-stroke sequelae is neuro-developmental treatment (NDT) [7,8,9], which is a way to let patients have the feeling of walking with minimal intervention. The essence of NDT is to rectify sensory perception and re-educate the processes of posture and motor functions for daily activities. Patients can intentionally impel their center of gravity (COG) forward to balance themselves during NDT training [10]. In contrast with other gait-training methods that depend on mechanical aids, NDT applies facilitated interventions to cultivate the effects of motor learning. With minimum intervention, NDT applies stimulating interventions at critical times to correct patients’ inaccurate movements, thereby enhancing their compensatory movements and daily activities. Utilizing training techniques based on the NDT theory allows patients to learn correct movement patterns through motor learning because of the human brain’s learning capability and high plasticity [11,12,13].

NDT training has shown positive effects on stroke patients, but it places heavy demands on participating therapists, and human factors influence the quality of training. For these reasons, Wang et al. [14] developed an automatic mobile NDT trainer that repeats therapeutic interventions that the therapist must typically perform every time. Their analysis of patients’ movements and therapists’ actions revealed that the therapists conducted NDT intervention primarily at the heel strike (HS) events. Hence, they applied a motion-capture system to detect the HS. Wang et al. [15] later proposed a movable NDT trainer that allowed the users to receive visual feedback during training. They attached inertial measurement units (IMUs) to the user’s legs and measured the kinematic data to identify three essential gait events: the mid-swing (MS), HS, and toe off (TO). Wang et al. [16] developed a Long Short-Term Memory (LSTM) model, which is an advanced recurrent neural network to process and predict time-series data to detect HS events effectively. They applied experimental gait data to develop a gait-detection model, which sent a triggering signal to motors to repeat NDT interventions upon detecting an HS. The experimental results showed that subjects improved their gait performance after the NDT training. In this paper, we applied the LSTM model to detect HS events based on IMU data and designed robust control to repeat NDT interventions by a motor system.

During clinical experiments, however, we found that operating the self-propelled mobile trainer could be burdensome for stroke patients, who usually exhibit a significant reduction in muscle strength in their legs, especially on the paretic side [17]. Therefore, this paper proposed a power-assisted device to let the trainer follow the user, thereby allowing stroke patients to focus on gait training without having to manually propel the trainer. We conducted system identification and control design for the power-assisted NDT trainer. We then implemented the designed controller and recruited ten healthy subjects who wore a joint restrictor to mimic stroke gaits to test the power-assisted trainer. We then invited 12 stroke patients to participate in clinical experiments. We evaluated the rehabilitation effects by the swing-phase symmetry, pelvic rotation, and walking speeds during and after receiving the NDT training with the power-assisted device.

Gait symmetry is an essential index for the gait rehabilitation of post-stroke patients and requires shifting the COG at the right moments to initiate stepping [14]. The rotation of the pelvis reduces the center of mass movement and thereby conserves energy [18]. Increasing walking speed can improve the quality of daily life of stroke patients [19]. Darcy et al. [20] suggested that improving stroke patients’ walking speed could reduce energy consumption. Reciprocal and repeated training can help patients improve their gaits by motor learning and accumulating experience from comparisons with the sound side. This study showed that the subjects’ gait performance and walking speeds improved after receiving NDT rehabilitation by using the proposed trainer.

2. Materials and Methods

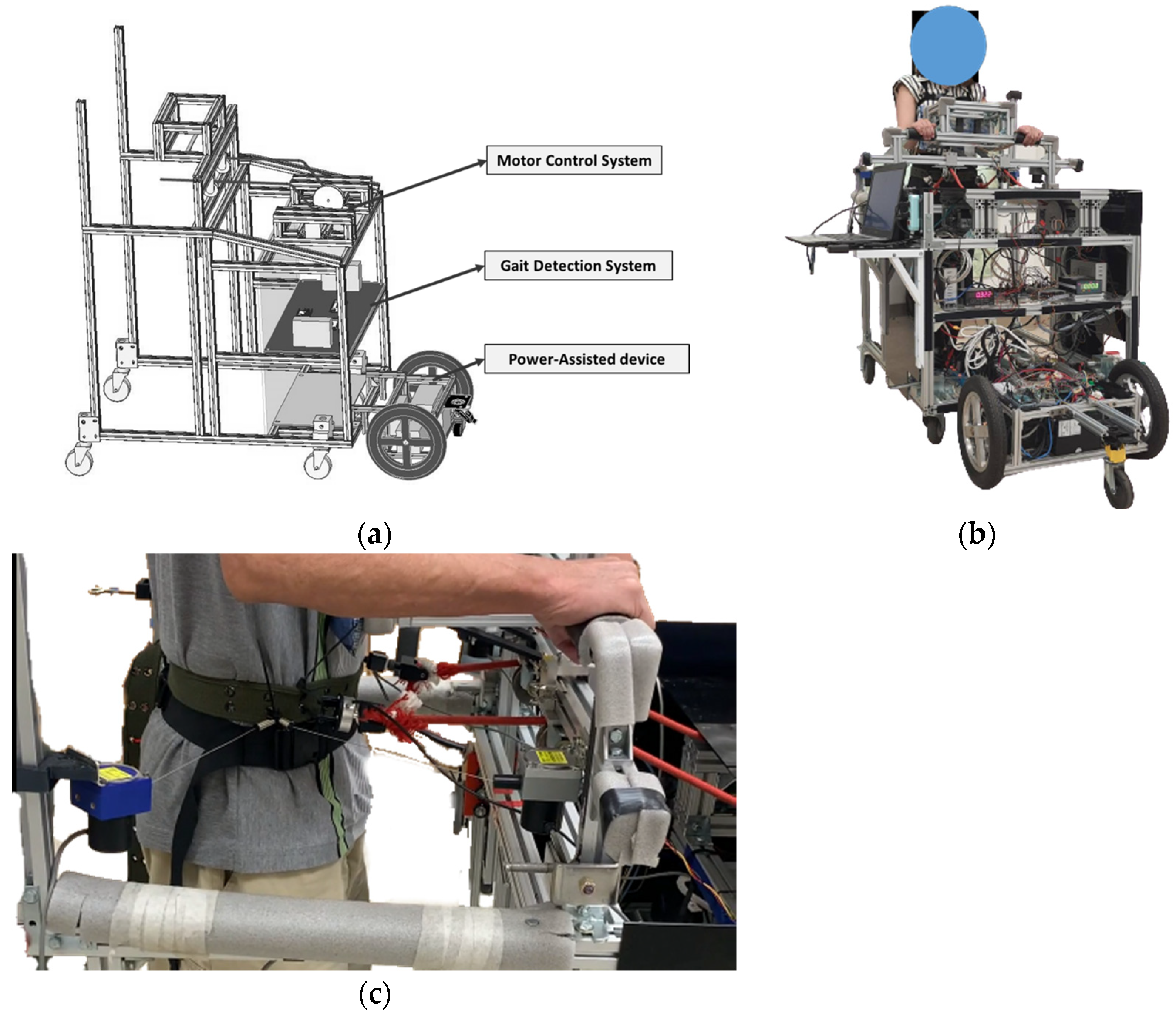
The power-assisted NDT trainer comprises a motor-control system, a gait-detection system, and a power-assisted device, as shown in Figure 1a. We conducted system identification and control designs for the intervention and power-assisted systems. Then, we recruited subjects to perform clinical experiments, as illustrated in Figure 1b.

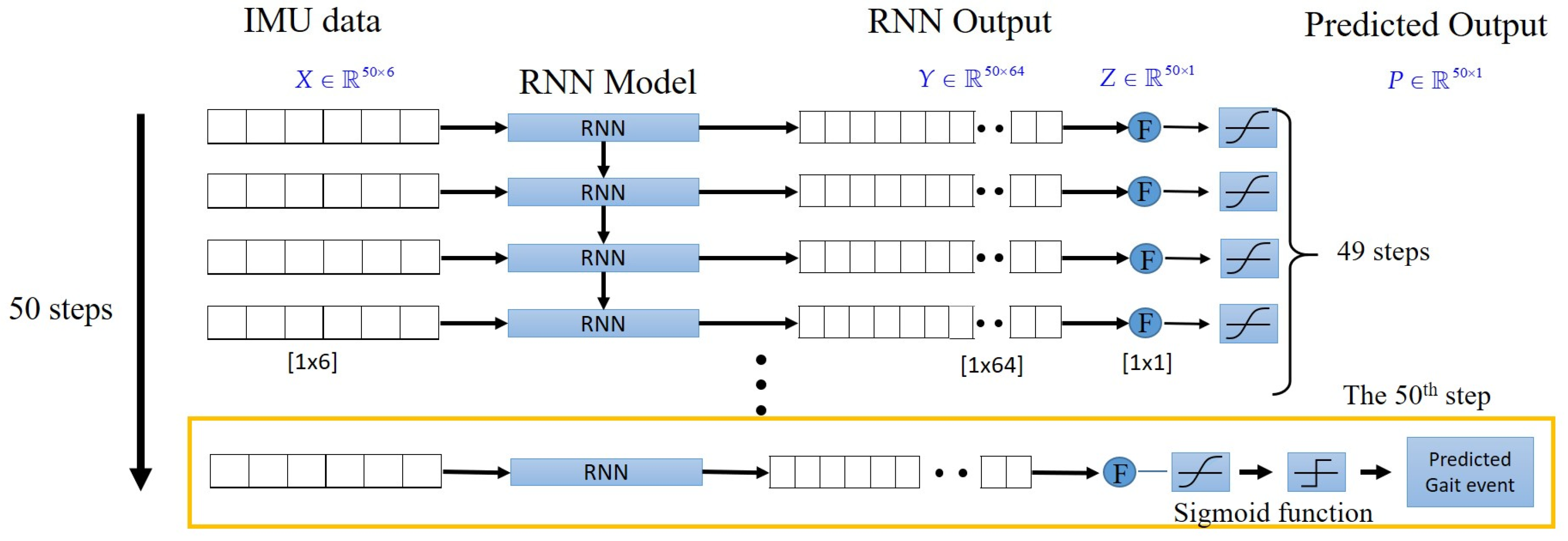
The gait-detection system applies two IMUs attached to the subjects’ lower legs to detect HS events by using the LSTM model, as Appendix A shows [16]. It sends a triggering signal to the motor-control system to perform NDT intervention upon detecting an HS. The motor-control system [20] cues the subject’s anterior superior iliac spine (ASIS) by ropes upon receiving the triggering signals from the gait-detection system, as shown in Figure 1c. ASIS is a bony prominence located at the front and upper part of the pelvis, where the subcostal nerve lies close and the tensor fasciae latae muscle attaches to its lateral. The power-assisted system comprises a laser-distance sensor and two motors, where the sensor measures the participant’s position and controls the trainer to keep the trainer at a constant distance from the subject. Therefore, the subjects can focus on receiving the NDT training without manually propelling the trainer.

2.1. NDT Intervention by the Motor-Control System

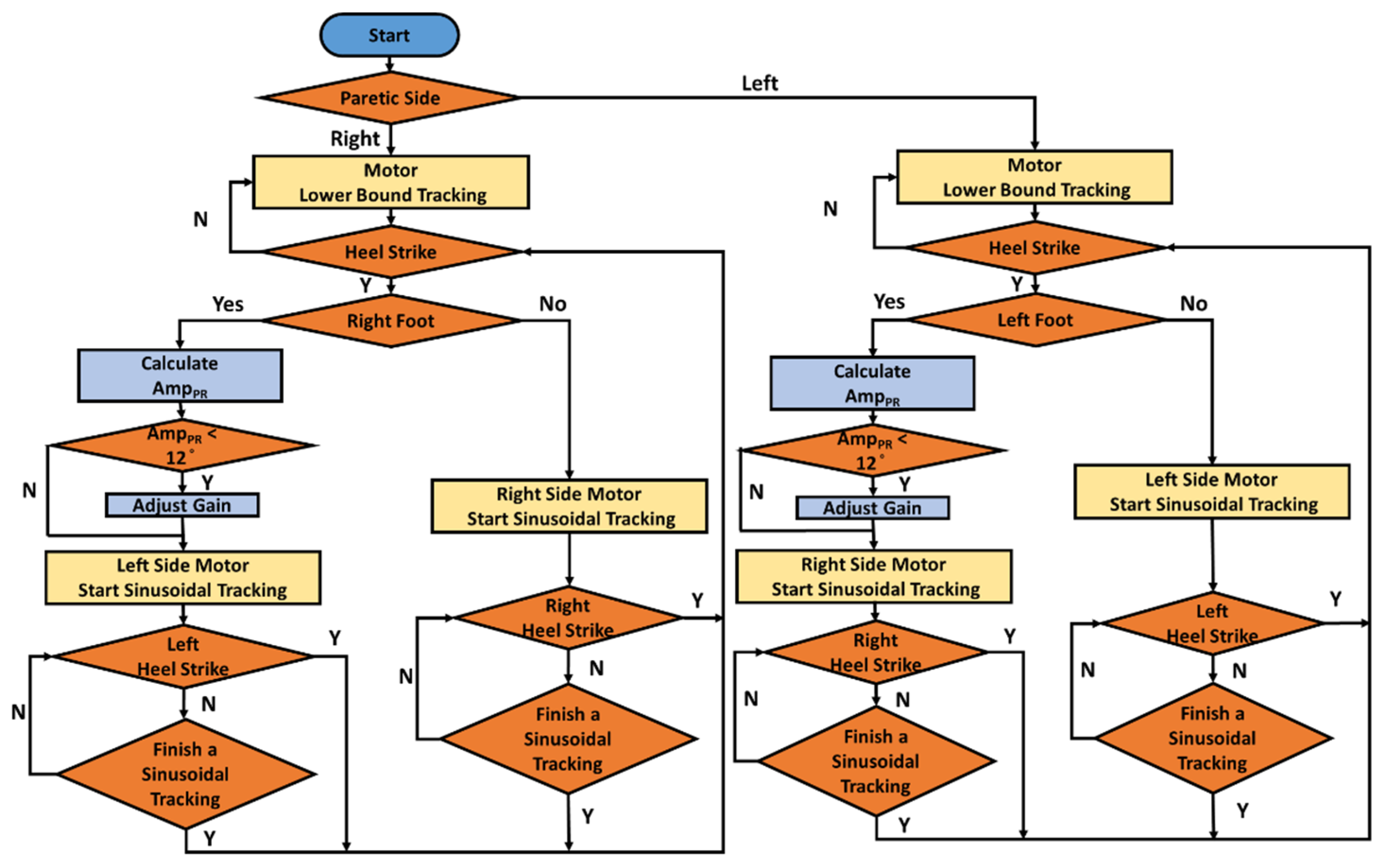
We invited therapists to conduct clinical NDT training and observed their actions. During the training, the therapists guided the subject’s motions by using the ropes attached to the subject’s ASIS. We recorded the therapists’ applied forces and the subjects’ motions to analyze the therapists’ intervention patterns [14,18]. First, the therapists applied forces to cue the subject’s opposite ASIS when they observed the subject’s HS. The intervention forces were approximately sinusoidal, as shown in Appendix A [18]. Second, the therapist increased the applied forces when they observed insufficient pelvic rotation, as illustrated in Appendix C [18]. Therefore, we implemented these intervention patterns to control the NDT motors, as shown in Figure 2, which produced the corresponding forces to cue the subjects’ ASIS through the ropes. When the gait-detection system identifies an HS, the motor-control system tracks the following command to cue the opposite ASIS [18]:

$$F\left(t\right)=\frac{\left({\overline{F}}_{\max }-{\overline{F}}_{\min }\right)}{2}\times \sin \left(2\pi ft\right)+\frac{\left({\overline{F}}_{\max }+{\overline{F}}_{\min }\right)}{2}$$

(1)

where ${\overline{F}}_{\max }$ and ${\overline{F}}_{\min }$ represent the maximum and minimum forces, respectively. f = 1 Hz. The maximum force is initially set as ${\overline{F}}_{\max }$ = 6 lb and increases to ${\overline{F}}_{\max }$ = 9 lb when the pelvic rotation $Am{p}_{PR}$ is less than ${12}^{°}$. The minimum force is set as ${\overline{F}}_{\min }$ = 1 lb to keep the rope tight.

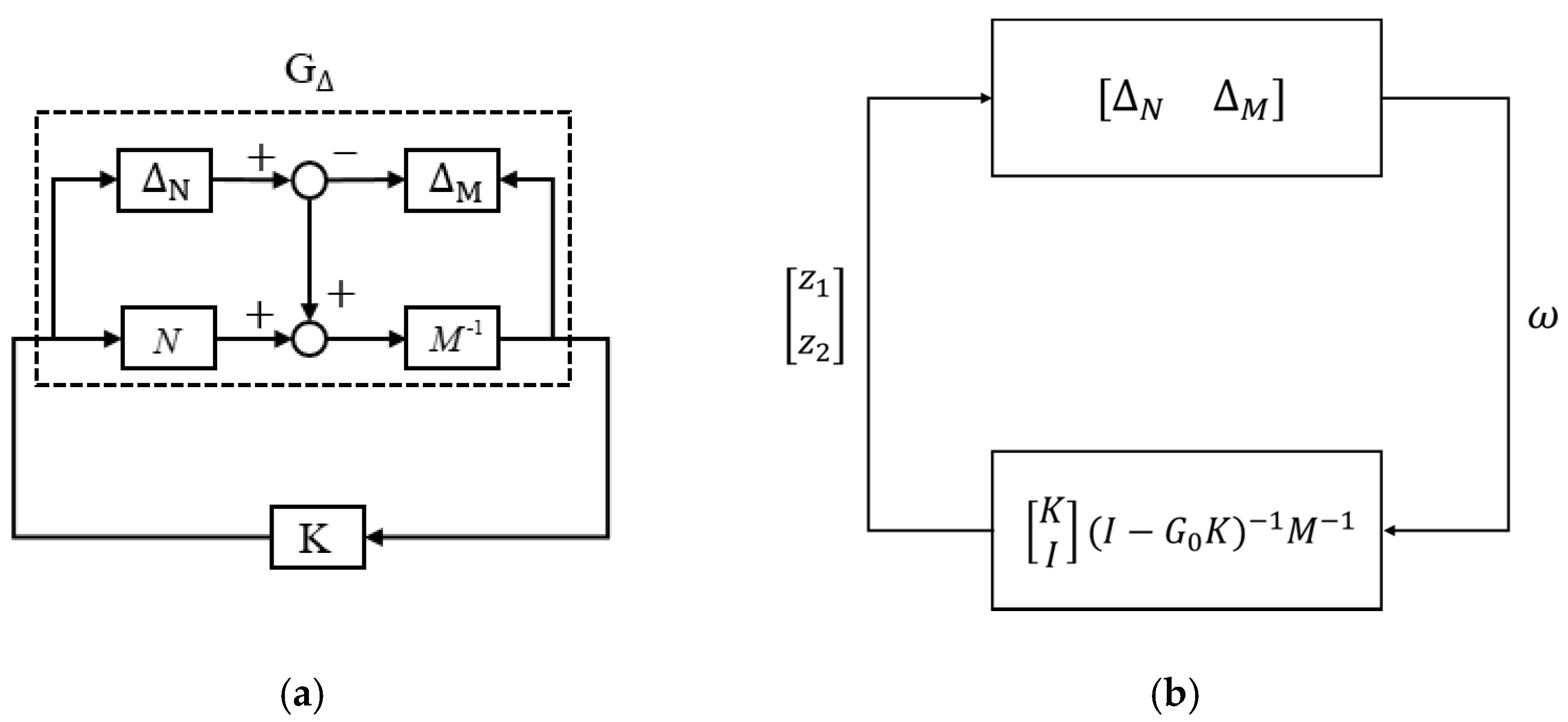
Considering the human factor in the system, we applied robust control to replicate the therapists’ rehabilitation interventions automatically in that robust control has a superior ability to cope with system uncertainty and disturbances. Before control design, we derive the system model by experiments.

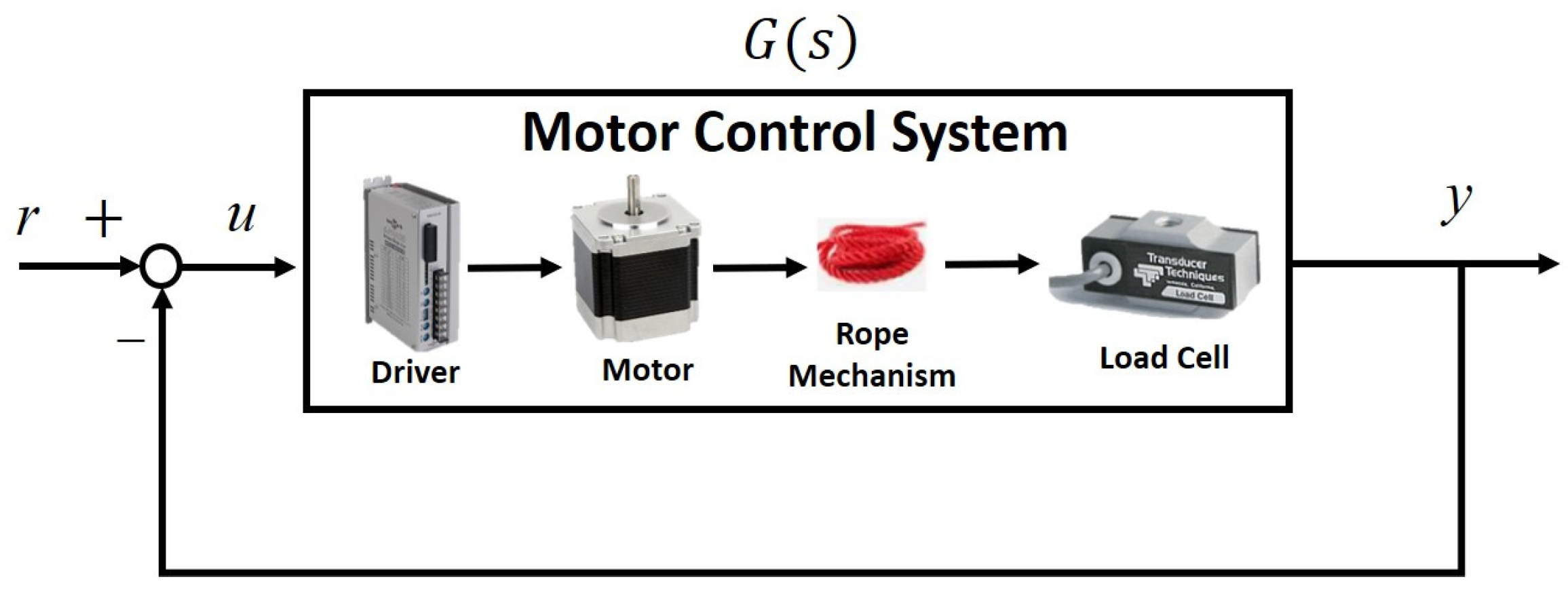
Because the rope provided only traction forces, we conducted closed-loop identification. The block diagram of the rope motor-control system is illustrated in Figure 3, where we sent the swept sinusoidal input signals r with magnitudes of 1–6 pounds and frequencies of 0.01–2 Hz. We then measured the motor drive signal u and the output force y. The system transfer functions were then derived by the Matlab command tfest by using these signals. Considering system variation and uncertainties, we repeated the experiments ten times to derive the following transfer functions:

$$\begin{array}{l}{G}_1(s)=\frac{-29.39s + 342.87}{s^2 + 46.79s + 114.27}, G_2(s)=\frac{-19.74s + 263.14}{s^2 + 31.82s + 90.71}, G_3(s)=\frac{-19.80s + 274.81}{s^2 + 33.19s + 86.43}, \\ G_4(s)=\frac{-28.87s + 355.76}{s^2 + 42.55s + 104.69}, G_5(s)=\frac{-29.91s + 348.55}{s^2 + 41.51s + 115.71}, G_6(s)=\frac{-30.76s + 366.68}{s^2 + 41.41s + 107.09}, \\ G_7(s)=\frac{-29.38s + 355.41}{s^2 + 39.68s + 102.89}, G_8(s)=\frac{-22.06s + 280.76}{s^2 + 33.74s + 93.37}, G_9(s)=\frac{-29.52s + 355.94}{s^2 + 39.44s + 103.77},\\ G_{10}(s)=\frac{-23.74s + 290.55}{s^2 + 33.95s + 99.00}.\end{array}$$

(2)

We applied a gap metric [21] to select a nominal plant from (2) to perform the robust control design. Suppose a nominal plant $G_0$ has a left coprime factorization of $G_0=M^{-1}\hspace{0.17em}N$, where $M\hspace{0.17em}{M}^{*}+N\hspace{0.17em}{N}^{*}=I, \mathrm{and} {\mathsf{\Delta }}_M, {\mathsf{\Delta }}_N\in R{H}_{\infty }$. Assume a perturbed system $G_{\mathsf{\Delta }}$ can be expressed as $G_{\mathsf{\Delta }}={(M+{\mathsf{\Delta }}_M)}^{-1}(N+{\mathsf{\Delta }}_N)$, where ${\mathsf{\Delta }}_M, {\mathsf{\Delta }}_N\in R{H}_{\infty }$. The gap between these two systems, $G_0 \mathrm{and} G_{\mathsf{\Delta }}$, is defined as the smallest ${‖[\begin{array}{cc}{\mathsf{\Delta }}_N& {\mathsf{\Delta }}_M\end{array}] ‖}_{\infty }$ that can perturb $G_0 \mathrm{to} G_{\mathsf{\Delta }}$, denoted as $\delta (G_0,\hspace{0.17em}{G}_{\mathsf{\Delta }})$ [21]. Hence, we selected $G_0=G_{10}(s)$ to represent the motor system because it minimized the maximum gap between $G_0$ and other plants $G_i \mathrm{for} i=1,2,\cdots ,10$, as follows:

$$G_0=\arg \left\{\underset{G_0}{\min }\hspace{0.33em}\underset{G_i}{\max }\hspace{0.33em}\delta (G_0,G_i)\right\}, \forall G_i,$$

(3)

with a gap of $\delta (G_0,G_i)\le 0.078, \forall G_i$.

We applied the nominal plant $G_0$ to design a robust controller. Considering a closed-loop system with a controller K (see Figure 4a), we can rearrange the system as the standard block diagram for the Small-Gain Theorem (see Figure 4b) because system stability is independent of input signals. According to the Small-Gain Theorem [21], the closed-loop system is internally stable for all perturbations $\mathsf{\Delta }=\left[\begin{array}{cc}{\mathsf{\Delta }}_N& {\mathsf{\Delta }}_M\end{array}\right]$ with ${‖\mathsf{\Delta }‖}_{\infty }<\epsilon$ if and only if [21]:

$${‖\hspace{0.33em}\left[\begin{array}{l}K\\ I\end{array}\right]{(I-G_0\hspace{0.33em}K)}^{-1}{M}^{-1}\hspace{0.33em}‖}_{\infty }={‖\hspace{0.33em}\left[\begin{array}{l}K\\ I\end{array}\right]{(I-G_0\hspace{0.33em}K)}^{-1}[\hspace{0.17em}I\hspace{1em}{G}_0\hspace{0.17em}]\hspace{0.33em}‖}_{\infty }\le 1/\epsilon$$

(4)

Therefore, we can define the system’s stability margin $b(G_0,K)$ as follows:

$$b(G_0,K)={‖\hspace{0.33em}\left[\begin{array}{l}K\\ I\end{array}\right]{(I-G_0\hspace{0.33em}K)}^{-1}[\hspace{0.17em}I\hspace{1em}{G}_0\hspace{0.17em}]\hspace{0.33em}‖}_{\infty }^{-1}.$$

So that the necessary and sufficient condition to maintain internal stability for a system $G_0$ with a perturbation of $\mathsf{\Delta }$, where ${‖\mathsf{\Delta }‖}_{\infty }<\epsilon$, is to design a controller K that provides a stability margin $b(G_0,K)\ge \epsilon$. Hence, we must design a robust controller K for the system $G_0=G_{10}(s)$ with a stability margin $b(G_0,K)\ge 0.078$.

We applied $H_{\infty }$ loop-shaping techniques [22], as shown in Figure 5. We set the weighting function

$$W\left(s\right)=\frac{2s+4}{\left(0.02s+1\right)s}$$

(5)

and applied the shaped plant $G_s(s)=G_0(s)W(s)$ to design the following robust controller:

$$K_{\infty }\left(s\right)=\frac{-3.004s^3-244.1s^2-4614s-9755}{s^3+132.3s^2+\mathrm{14,910}s+\mathrm{29,310}}.$$

(6)

The stability margin $b(G_0,W{K}_{\infty })=0.2789$ exceeded the system gap and guaranteed system stability during operations. Therefore, we applied the shaped controller $K(s)=W(s)K_{\infty }(s)$ to the original plant $G_0(s)$, as shown in Figure 5b.

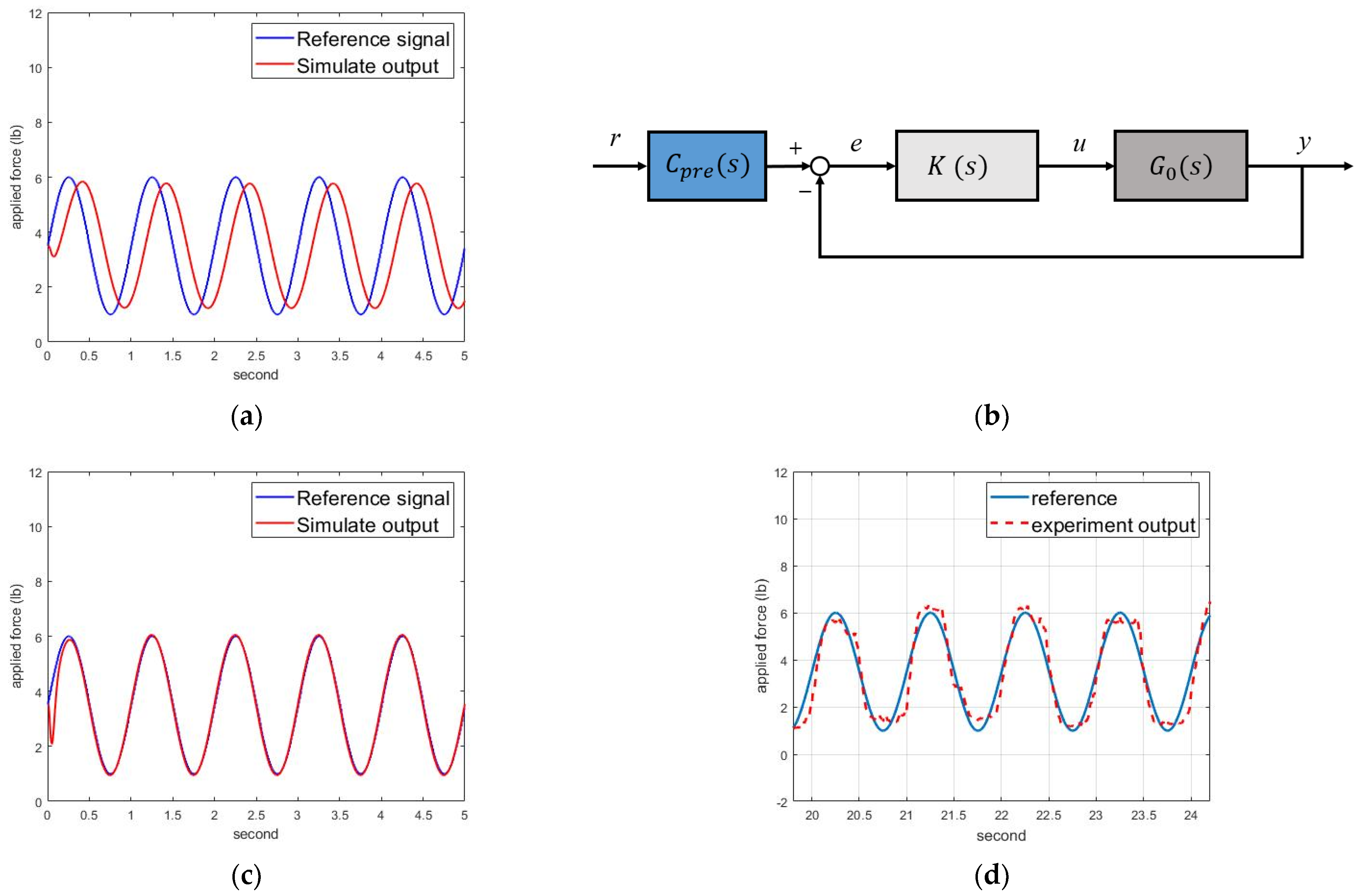
The simulation results are shown in Figure 6a, with significant phase delay and magnitude decay. Hence, we designed a pre-compensator to modify the responses, as shown in Figure 6b. Assuming the concerned frequency was 1 Hz, we designed the following pre-compensator:

$$C_{pre}\left(s\right)=\frac{0.1721s+0.4816}{0.016s+1}$$

The simulation results are shown in Figure 6c, where the motor-control system could track the intervention forces. Therefore, we implemented the motor-control system to track the intervention force commands of (1). Figure 6d shows the experimental force-tracking responses, where the motor could track the intervention force commands for NDT rehabilitation.

2.2. Control Design for the Power-Assisted System

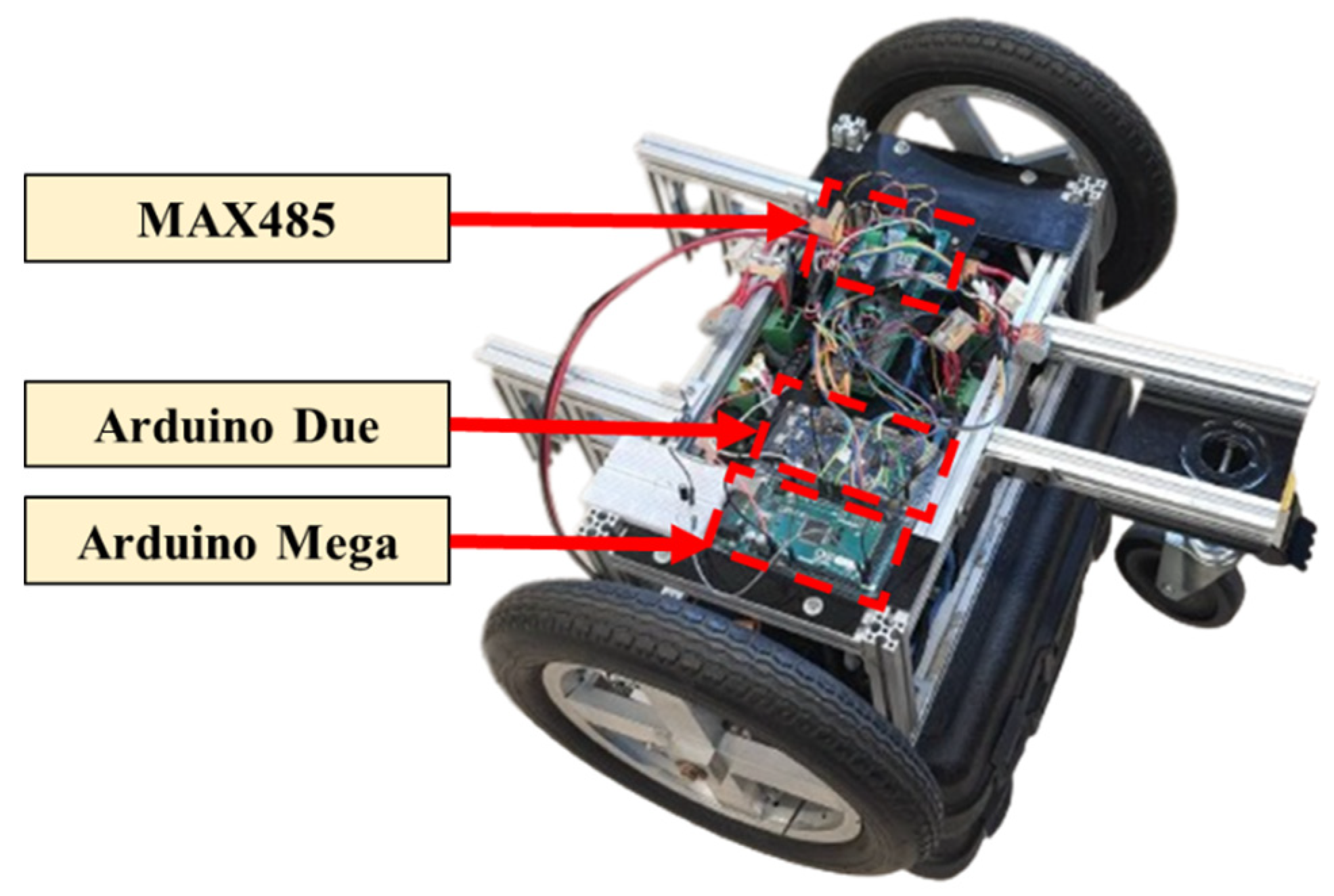
Figure 7 illustrates the power-assisted device. The main control microprocessor is an Arduino Due [23], which sends pulse-width modulation (PWM) signals to the wheel motor drivers. The second microprocessor is an Arduino Mega [24], equipped with an MAX485 communication module to receive feedback signals from the motors and the laser-distance sensor.

We connected the power-assisted device to the trainer and conducted open-loop system identification by experiments. First, we set swept sinusoidal input signals with frequencies of 0.01–2 Hz and converted the signals to the corresponding PWM signals to drive the motors. We then measured the output signals by the laser-distance sensor to derive the system’s model from these signals. We considered system variation and repeated the identification experiments to derive the following transfer functions:

$$\begin{array}{l}{\overline{G}}_1(s)=\frac{39.69}{s^2 + 6.15s}, {\overline{G}}_2(s)=\frac{39.31}{s^2 + 6.25s}, {\overline{G}}_3(s)=\frac{37.91}{s^2 + 6.03s}, {\overline{G}}_4(s)=\frac{ 38.88}{s^2 + 6.51s}, \\ {\overline{G}}_5(s)=\frac{ 34.83}{s^2 + 6.00s}, {\overline{G}}_6(s)=\frac{41.42}{s^2 + 7.14s}, {\overline{G}}_7(s)=\frac{37.75}{s^2 + 6.03s}, {\overline{G}}_8(s)=\frac{45.90}{s^2 + 6.27s}, \\ {\overline{G}}_9(s)=\frac{43.79}{s^2 + 6.93s}, {\overline{G}}_{10}(s)=\frac{37.92}{s^2 + 5.78s}.\end{array}$$

(7)

which represented the entire power-assisted device, including the wheels and motor-reduction mechanism.

Similarly, we calculated the gaps between these transfer functions and selected the following nominal plant:

$${\overline{G}}_0(s)=\underset{i}{\min }\underset{j}{\max }\delta ({\overline{G}}_i, {\overline{G}}_j),\forall i, j=1,2, \dots 10={\overline{G}}_{10},$$

(8)

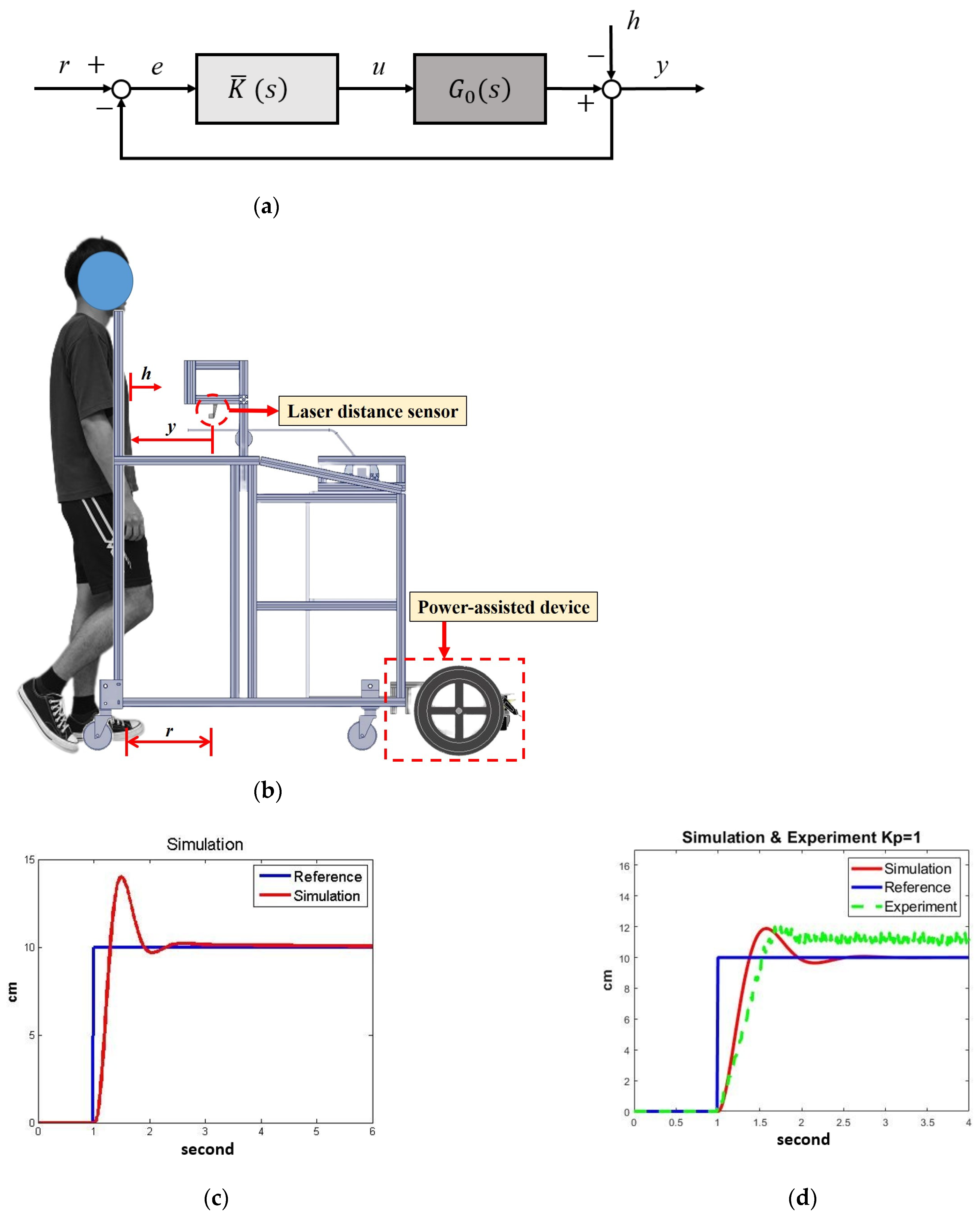
which minimized the gaps between the nominal plant and other plants, with a gap of $\delta ({\overline{G}}_0,{\overline{G}}_i)\le 0.061, \forall {\overline{G}}_i$. The power-assisted control is shown in Figure 8a, where r is the reference, h represents the disturbances from human movements, e is the position error, u is the motor-control signal, and y is the actual distance. We first applied robust loop-shaping control to design a controller $\overline{K}$ that gives a stability margin $b({\overline{G}}_0,\overline{K})\ge 0.061$.

Based on previous experimental experiences [15], we set the NDT trainer to maintain a constant distance of r = 10 cm from the participant, as shown in Figure 8b. The subject’s movement h was regarded as a disturbance to the system. The laser sensor measured the actual distance (y) between the participant and the trainer so that the feedback system could compensate for the position error e by the motors.

Referring to Figure 5, we set the weighting W as follows:

$$W\left(s\right)=\frac{10s+3}{\left(s+2\right)s}$$

(9)

and derived the following robust controller:

$$K_{\infty }\left(s\right)=-\frac{(1.02\times {10}^4)s^4+(1.02\times {10}^5)s^3+(2.79\times {10}^5)s^2+(7.29\times {10}^4)}{ s^4+(3.29\times {10}^3)s^3+(7.499\times {10}^4)s^2+(7.82\times {10}^5)s+(2.28\times {10}^5)}.$$

(10)

We then reduced the weighted controller $\overline{K}=W{K}_{\infty }$ to the fifth order, which provided a stability margin $b({\overline{G}}_0,\overline{K})=0.2823$, which exceeded the system gaps and could guarantee robust stability during operation. The simulation results are shown in Figure 8c, where the significant overshoot and the high-order controller were disfavored. Therefore, we applied gain-scheduling control for the power-assisted system.

The gain-scheduling-control design was conducted empirically because the control signal u should be large enough to overcome frictions and small enough to avoid overshoots. We tuned the controller gain $\overline{K}(s)=K_p$ and verified its effects iteratively. For example, when $\overline{K}(s)=K_p=1$, the stability margin was $b({\overline{G}}_0,\overline{K})=0.3910$ with the system response as shown in Figure 8d, where the overshoot and steady-state error were significant due to friction. On the other hand, when $\overline{K}(s)=K_p=0.8$, the stability margin was $b({\overline{G}}_0,\overline{K})=0.4259$ with the system response, as shown in Figure 8e, where the steady-state error was negative because of the low gain and friction. Therefore, we designed the following gain-scheduling control:

$$\overline{K}(s)=\left\{\begin{array}{ll}Kp=1,\hfill & \mathrm{If} \left|e\right| > 5\mathrm{cm}\hfill \\ Kp=0.8, \hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(11)

The simulation and experimental responses are shown in Figure 8f, where the system responses were satisfactory during experiments despite slight oscillations and steady-state errors. The gain-scheduling control could successfully regulate the NDT trainer, keeping it at a constant distance from the user. Therefore, we applied this controller in clinical experiments.

2.3. Performance Indexes and Evaluation

A complete gait cycle is illustrated in Figure 9, which comprises three essential gait events: the MS, HS, and TO. The swing phase of a leg is defined as the duration between the leg’s TO and its subsequent HS and accounts for about 40% of a gait cycle [25] while the stance phase takes the remaining 60%.

We evaluated the participants’ gait performance by their asymmetry of swing phase, pelvic rotation, and average walking speed.

(1)

Asymmetry of swing phase: We measured each subject’s gait response and segmented it into gait cycles based on HSs. The asymmetry of the swing phase $Asy{m}_{SP}$ is defined as follows:

$$Asy{m}_{SP}\left(\%\right)=\frac{S{P}_{paretic}-S{P}_{non-paretic}}{S{P}_{paretic}}\times 100\%,$$

(12)

where $S{P}_{paretic}$ and $S{P}_{non-paretic}$ represent the swing phases on the paretic and sound sides, respectively.

(2)

Amplitude of pelvic rotation: We attached an IMU to the subject’s waist to measure the rotation angle of the pelvis [18]. The pelvic rotation is the maximum rotational angle between two successive HS events, defined as follows:

$$Am{p}_{PR}={\theta }_{\max }^{}-{\theta }_{\min }^{},$$

(13)

where ${\theta }_{\max }^{}$ and ${\theta }_{\min }$ represent the minimum and minimum pelvic angles in a gait cycle.

(36)

Average walking speed: we estimated the subject’s average walking speed based on the encoder data from the motors on the power-assisted device, as in the following:

$$V_{ave}=\omega D\cdot R_{red},$$

(14)

where $\omega$ is the motors’ angular velocity, D is the wheel diameter, and $R_{red}$ is the motors’ reduction ratio for amplifying the motor torques to drive the trainer. In the experiments, we set D = 0.3 m and $R_{red}$ = 1/15.

2.4. Clinical Experiments

We recruited 10 healthy subjects and 12 stroke patients to participate in the experiments. The inclusion criteria were (1) stroke patients with lower-limb paralysis at Brunnstrom stage III to V, whose characteristics are described in Appendix B. The Brunnstrom stage is used to assess and describe the stages of limb-function recovery in stroke patients. (2) The ability to walk independently and follow commands. (3) Age between 18 and 80 years. Appendix C illustrates the participants’ statistical data. All participants provided written informed consent before participating in the study.

(1)

Healthy subjects: The healthy subjects wore a joint restrictor with a 2 kg block on one knee, as shown in Figure 10a; the joint restrictor constrained their knee flexion to simulate stroke patients’ gait patterns. Each participant performed the following two sets of experiments to validate the effectiveness of the power-assisted device:

(a)

Experiments without power assistance.

(b)

Experiments with power assistance.

Each set of experiments contained three stages: stage A (pre-treatment), stage B (during treatment), and stage $\overline{\mathrm{A}}$ (post-treatment). First, the subject walked approximately 25 m without intervention at the A stage. Then, the subject walked approximately 50 m with the NDT intervention at the B stage. Finally, the subject walked approximately 25 m without intervention at the $\overline{\mathrm{A}}$ stage. There were no breaks between the stages, but the subject could rest if necessary.

(2)

Stroke patients: The experiments were conducted within a hospital approved by the Cheng Hsin General Hospital. Twelve stroke patients participated in the experiments, walking in a straight line with the NDT trainer at their most comfortable pace, as shown in Figure 10b.

The stroke patients’ experiments also consisted of three stages. First, each subject walked approximately 44 m without intervention at stage A. Then, the subject walked approximately 88 m with the trainer’s intervention at stage B. Finally, the subject walked approximately 44 m without intervention at stage $\overline{\mathrm{A}}$. Participants completed the procedures consecutively, with the option to rest if necessary during the experiments. Considering the stroke patients’ physical stamina and walking ability, they only conducted one set of experiments with the power-assisted device.

3. Results

The participants’ data are illustrated in Appendix C. The average age (±standard deviation, SD) was 24.3 ± 2.4 years for the healthy subjects and 51.5 ± 7.8 years for the stroke patients. Among the stroke patients, 10 (83%) were males and 2 (17%) were females. The mean duration (±SD) from stroke onset was 21.1 ± 28.0 months. The number of patients at the Brunnstrom recovery stages III, IV, and V were 7, 4, and 1, respectively. Because the participants had different physical conditions, we compared each subject’s performance before, during, and after the NDT training.

The healthy subjects wore a joint restrictor to simulate the stroke gait. Their gait performance indexes are illustrated in Appendix D.

Table 1. Improved ratio in experiments (healthy subjects).

	Power-Assisted	Stage B	$\mathbf{Stage} \overline{\mathbf{A}}$
$Asy{m}_{SP}$	No	6/10	7/10
	Yes	5/10	7/10
$Am{p}_{PR}$	No	9/10	5/10
	Yes	10/10	6/10
$V_{ave}$	No
	Yes	10/10	10/10

shows the number of subjects whose performance indexes were improved after the experiments (a) and (b). The improved rates were almost identical in experiments (a) and (b) for the asymmetry of the swing phase and the pelvic rotation. In addition, all the subjects’ walking speeds increased after using the power-assisted trainer. The results indicate that the power-assisted device improved the subjects’ walking speed without compromising other rehabilitation effects.

The 12 stroke patients only conducted one set of experiments with the power-assisted device. Their gait performance indexes are illustrated in Appendix D.

Table 2. Improved ratio in experiments (stroke patients).

	Power-Assisted	Stage B	$\mathbf{Stage} \overline{\mathbf{A}}$
$Asy{m}_{SP}$	Yes	8/12	8/12
$Am{p}_{PR}$	Yes	12/12	8/12
$V_{ave}$	Yes	11/12	10/12

shows the number of subjects whose performance indexes improved after using the NDT trainer. For the swing phase, eight stroke patients showed improvement at the B and $\overline{\mathrm{A}}$ stages. For pelvic rotation, 12 and 8 stroke patients showed improvement at stage B and $\overline{\mathrm{A}}$, respectively. Finally, 11 and 10 subjects’ walking speeds increased at stage B and $\overline{\mathrm{A}}$, respectively. The results indicate that the power-assisted device relieved the subjects’ burden in pushing the trainer while slightly improving the NDT rehabilitation effects.

4. Discussion

In this study, we developed a power-assisted trainer that can automatically move with the user and perform NDT training. We conducted closed-loop identification and a robust control design for the motor-rope system so that the trainer could automatically repeat the NDT intervention based on key gait events. We then performed open-loop identification and gain-scheduling-control design for the power-assisted system, which could automatically follow the subject during NDT training and relieve the user’s burden of pushing the trainer.

We recruited 10 healthy subjects and 12 stroke patients to participate in experiments to verify the trainer’s effectiveness in improving the subjects’ gait performance. The healthy subjects conducted two experiments: without and with power assistance. On the other hand, the stroke patients participated in only one experiment with power assistance because of their limited muscle strength and endurance. Each subject walked in a straight line with the NDT trainer at their most comfortable pace. Most participants exhibited improvements in swing-phase symmetry, pelvic rotation, and walking speed.

For the healthy subjects, the improved ratio of the swing-phase symmetry was almost the same with or without power assistance: less improvement in the swing-phase symmetry at the B stage but more improvement in pelvic rotation at the B and $\overline{\mathrm{A}}$ stages. We conjectured that pushing the trainer might be a form of resistance training, which could improve the subjects’ lower-limb muscle strength and balance abilities. Flansbjer et al. [26] showed significant differences in muscle strength for stroke patients undergoing resistance training compared to a control group. Shao et al. [27] demonstrated the improvement in balance, functional capacity, and muscle strength by training the stroke patients’ paraplegic side. Noveletto et al. [28] designed a task-oriented game that enhanced lower-limb motor function and improved muscle control and gait speed. These studies highlighted the positive impact of resistance training on stroke subjects’ lower-limb strength and balance. The healthy subjects also showed slightly better improvement in pelvic rotation because they did not need to propel the trainer, which consumed part of the movement energy and limited the pelvic rotation. Similarly, the walking speeds of all the healthy subjects were increased with power assistance because no walking energy was consumed by pushing the trainer.

The stroke patients only conducted the experiments with power assistance; therefore, we cannot compare the effects of using and not using the power-assisted device. However, most subjects showed improvements in swing-phase symmetry, pelvic rotation, and walking speeds. Compared to healthy individuals, patients with stroke have paretic hemi-limb strength and impaired endurance and balance. Consequently, a power-assisted device could alleviate the physical effort required to activate the NDT trainer, thereby allowing participants to complete their intervention with less effort. Our findings had clinical significance, as utilizing a power-assisted gait trainer improved ambulatory ability in patients with stroke in the chronic phase. According to the previous literature, power-assisted devices (e.g., exoskeletons) showed alterations in stroke paretic patterns during ambulation training that were not detected during traditional gait training without a power-assisted device [29]. Another study based on a wearable, powered, lower-limb robot also revealed an improved gait speed compared to a control group that received traditional gait rehabilitation training [30]. Supportive results from a study by Pohl et al. [10] showed that patients with subacute stroke who received gait training with an electromechanical gait trainer exhibited a significantly better gait ability than patients who received conventional physical therapy only. Most stroke patients’ walking speed increased at stages B and $\overline{\mathrm{A}}$. Increasing walking speed can also reduce stroke patients’ energy consumption and let them feel less fatigued when receiving rehabilitation training [20].

Another perspective of the power-assisted NDT device involves its potential to stimulate central pattern generators (CPGs), which are neuronal circuits activated to produce rhythmic motion patterns, such as walking. This neural circuit has no sensory or descending inputs. Previous studies have identified that all forms of bipedal movement appear to be controlled by four or five CPGs [31]. A locomotion study based on spinal-cord-injury patients also suggested that a CPG pattern of ambulation is better recognized with a straighter trunk and knee alignment when partial weight bearing is provided [32]. In our study, handrails provided by the NDT trainer also provided partial weight support for the participants. The improved gait pattern observed immediately after the power-assisted NDT training is more likely attributable to neural adaptations than aerobic exercise’s muscular effects. Improvement due to the latter typically becomes evident after an intensive treadmill therapy regimen lasting three to six months [33]. Suppose NDT training can indeed induce a CPG pattern of locomotion in stroke patients. In that case, it will allow those patients to ambulate, despite the lack of supraspinal motor signals arising via interneuron pathways.

The improvements in pelvic rotation and average walking speed were particularly notable, as more than 90% of the healthy and stroke subjects achieved improvement during the intervention. These improvements might be attributed to the reduced energy consumption required to push the trainer. According to a study by Mahaki et al. [34], stride length increases with pelvic rotation. However, increasing the walking speed also shortened the training time and number of repetitions because our experiment utilized a fixed distance, which might potentially affect the subjects’ level of improvement. Nevertheless, the power-assisted NDT trainer demonstrated positive rehabilitation effects in all three indicators: asymmetry of the swing phase, amplitude of pelvic rotation, and average walking speed.

This study has some limitations. First, our participant pool was limited to a small group of individuals who had experienced strokes. Consequently, the applicability of these findings to the broader stroke-patient population undergoing gait training might be restricted. Second, our intervention period was relatively short, prompting the need for a more extensive investigation of the lasting impacts of NDT intervention. Our stroke patients also did not receive non-power-assisted NDT training due to their limited strength and endurance. We plan to conduct a large-scale controlled trial with extended intervention periods and a comprehensive assessment of functional outcomes to investigate the long-term effects of the power-assisted NDT trainer.

5. Conclusions

This study proposes a power-assisted NDT trainer that automatically follows a stroke subject while repeating NDT rehabilitation training. We conducted system identification and control designs for the motor-traction and power-assisted systems. We then invited 10 healthy subjects and 12 stroke patients to participate in clinical experiments. Their kinematic data were collected to analyze the training effects on swing-phase symmetry, pelvic rotation, and walking speed.

The preliminary validation of the power-assisted device in this study indicates that the power-assisted trainer can relieve the stroke patients’ burden of manually propelling the trainer when receiving NDT training and enable them to focus more on gait rehabilitation. Consequently, most participants’ performance indexes were improved with the power-assisted device. During the experiment, the trainer facilitated walking to expedite the training process. It raises the possibility of extending the intervention time for stroke patients undergoing treatment to enhance rehabilitation performance.