Universal Jamming Gripper: Experimental Analysis on Envelope and Granular Materials
Abstract
1. Introduction
- Data acquisition: Automated stations usually rely on RGB cameras to input data into the systems. These devices can feed deep learning models to estimate object positions [5] or contours [6] and, thus, command the robot’s movement [7]. Depth images and point clouds are a standard complement to RGB images. With this information, models can also estimate the orientation of the objects and improve versatility [8].
- Grasping point strategies: Some models rely on the power of Convolutional Neural Networks (CNNs) to determine the quality of several grasping points for an object [9]. On other occasions, the model first estimates the location and orientation of the object and then, with this information, locates the grasping point. In most cases, synthetic data generation has reached a prominent position as a tool to create and label datasets [10]. Finally, in those cases where the positioning or the complexity of the part is high, some solutions explore the coordination of two robots [11].
- Robot kinematics: For the last few decades, RL has mimicked the mammal’s brain response to positive stimuli. RL has become a popular tool to orchestrate robotic movement based on trial and error as well as adequate reward policies. Some achievements include reaching tasks, pick&place tasks, or even higher-level tasks such as opening doors [4]. Again, the experience gathered through virtual simulators has reached a prominent relevance [12], although some approaches have opted to acquire real-life experience [13]. In addition to these techniques, other projects have developed ad hoc strategies for particular picking tasks [14] or multiagent strategies for static and dynamic collision avoidance [15].
- Gripper designs: Some of the most important developments have come from the soft robotics field [16]. This technique replicates nature to reproduce soft bodies with no rigid structure [17]. The main characteristics describing these bodies are silicones as materials and air pressure as the actuation system to generate movement [18,19]. In addition, some solutions have implemented paper folding and paper cutting techniques (origami and kirigami). These techniques have provided both grippers with larger contact surfaces [20] and grippers capable of adapting their geometry and passively modulating the force they apply [3]. Finally, also inspired by nature, other projects base the gripping ability on geckos’ traction technique. Here, the gripper is a thin sheet of deformable biphase material that changes its properties by heat application. Temperature variations produce phase changes that increase Van der Waals forces, allowing this prototype to grasp different geometry objects [21].

- Primary Contribution: We provide a robust empirical foundation for material selection in applications involving elements of soft robotics, particularly those requiring lax compression, vacuum application, and traction under the jamming effect, such as in robotic grasping scenarios.
- Unique Gripping Cycle Analysis: Unlike other studies, this research closely replicates the gripping cycle of a robot, including lax compression (simulating grip deformation) and traction with an active jamming effect (representing the maximum gripping force). We test the prototypes with this optimization goal, and our methods and designs align with this goal.
- Introduction of a New Metric: We introduce an unexplored metric in this context—the energy absorbed in the grip—proposed as a quality measure for assessing grip efficacy.
- Extensive Material Combination Study: We research an extensive range of material combinations (16 in total), a significantly broader scope than most literature, examining both filler (four glass ball diameters) and enveloping materials (four different materials).
- Detailed Analysis of Filler Material Dimensions: Unlike common studies that focus on glass balls larger than 1 mm, this research delves into finer details, analyzing up to three sizes of glass beads below 1 mm, enhancing material optimization sampling.
- The Thinner the Better for Optimizing Weight Lifting: Our research suggests that envelopes with thinner walls allow the internal granulate to manifest in the external texture of the prototype, increasing its coefficient of friction. In other words, the selection of internal material not only affects the forces that can be developed during the jamming effect phenomenon (internal influence) but also has a very notable effect on what happens in the prototype piece contact (external influence) when the envelope wall is thin.
2. Related Work
- Gripper compression against the part without the jamming effect;
- Creation of a vacuum, preparing the gripper for action under the jamming effect;
- Traction while the gripper is engaged with the object, with the jamming effect active.
3. Methodology
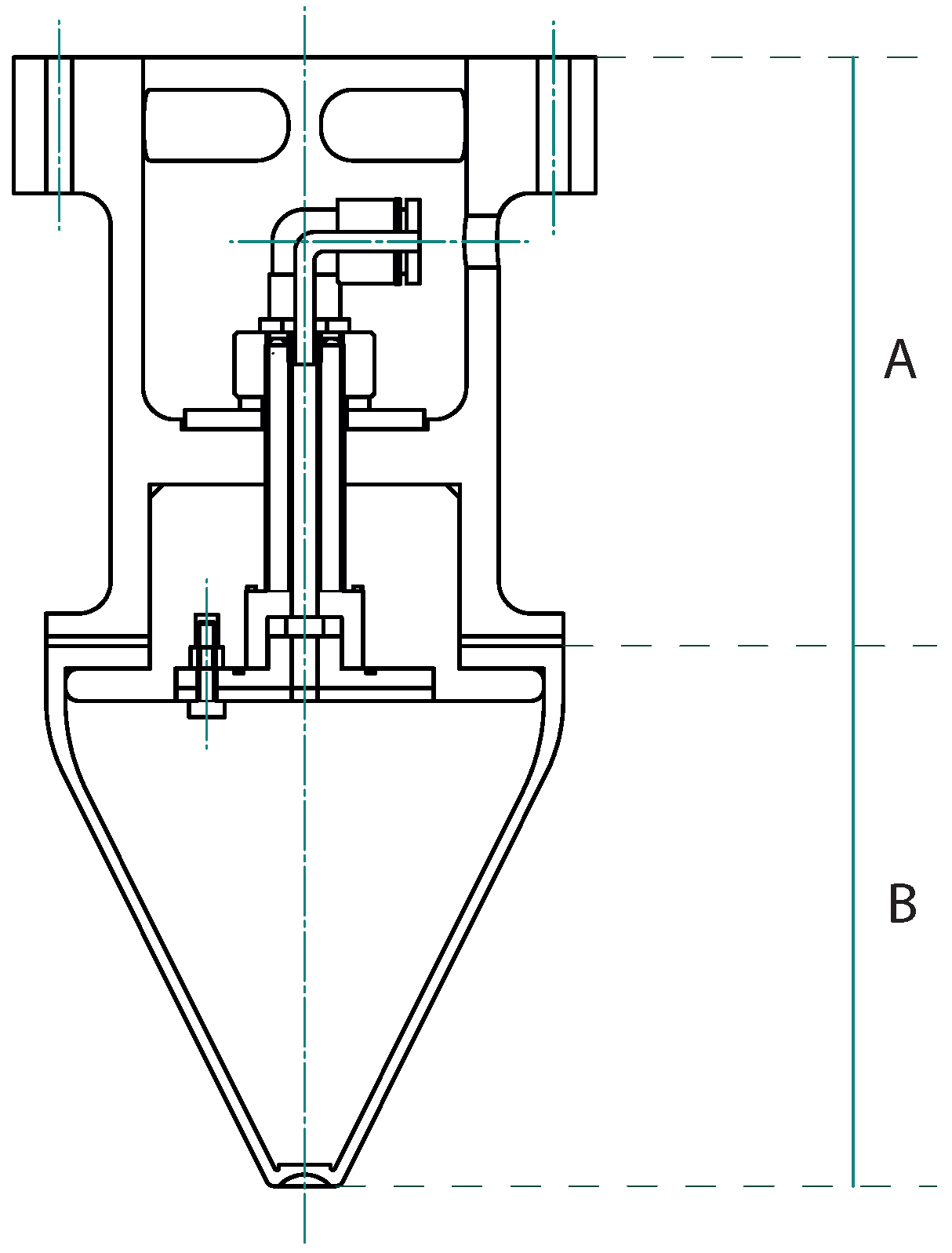
3.1. Gripper Geometry
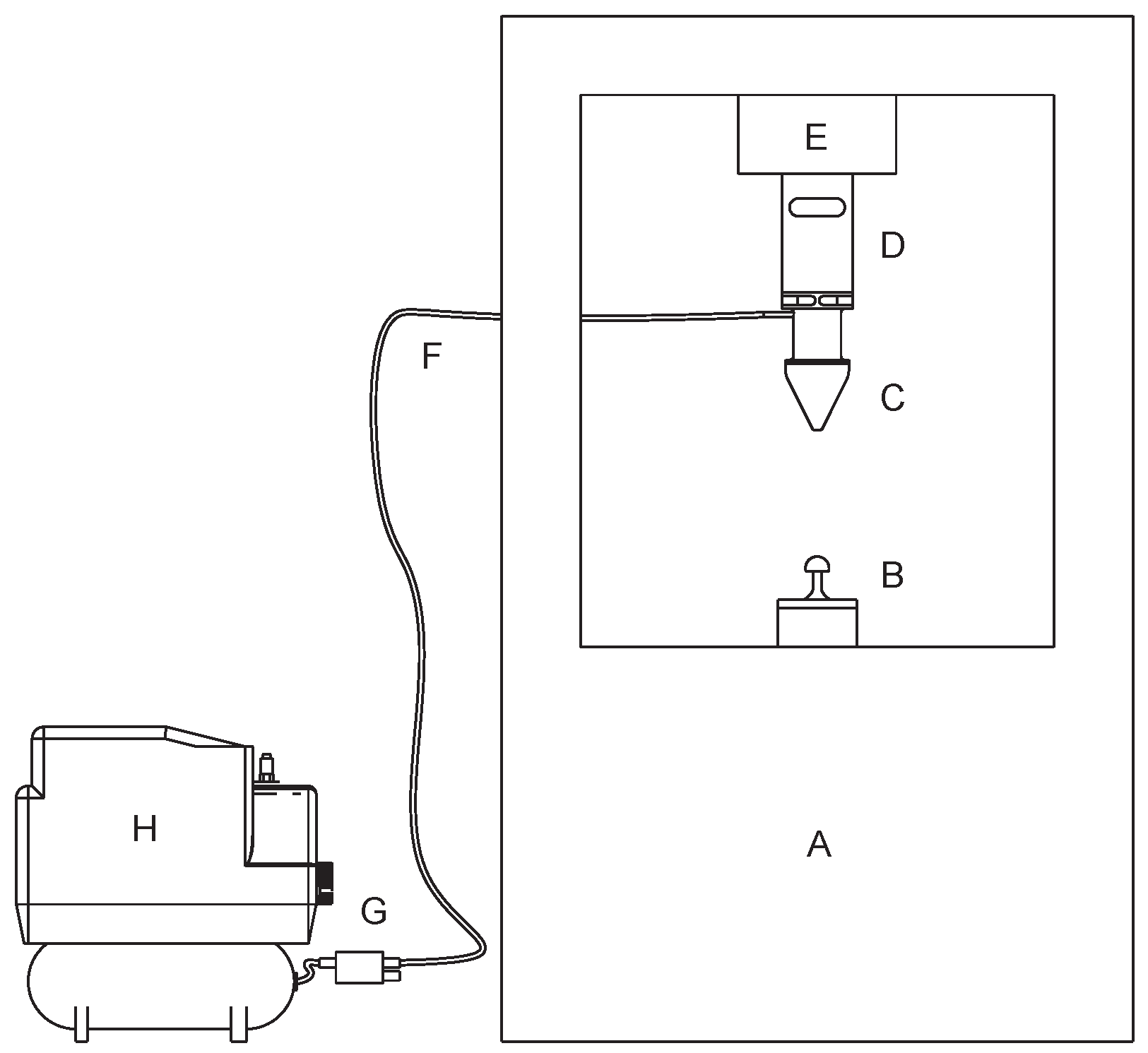
3.2. Setup Description
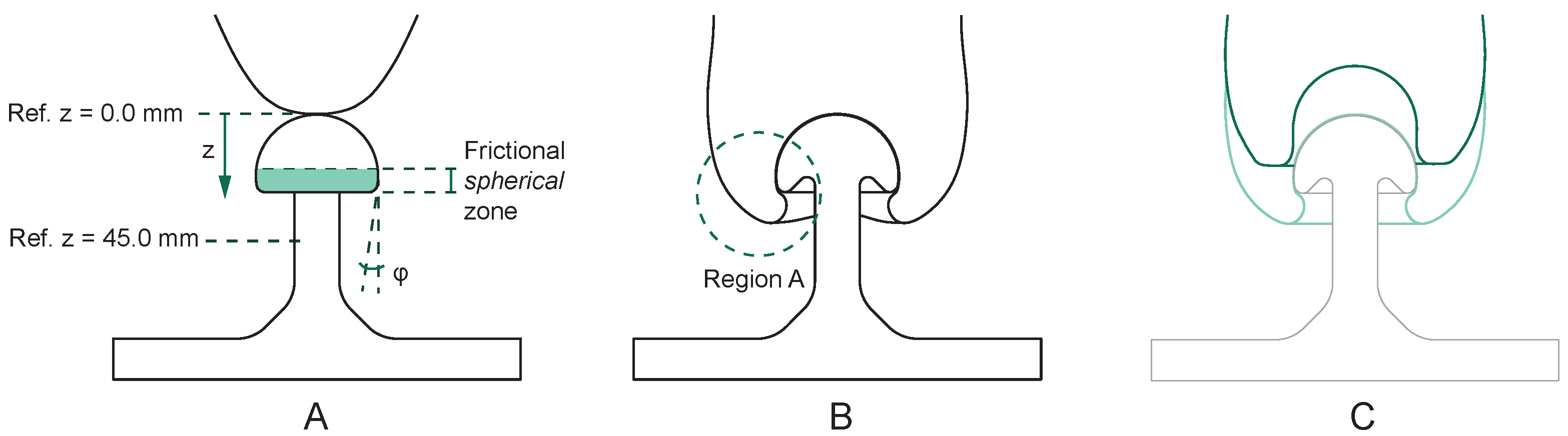
- Static friction: The machine used to manufacture the specimen is a Multi Jet Fusion 3D printer. The material used is powdered nylon PA12. The combination of the process and the material results in a linear roughness of 78 μm, providing an isotropic and uniform friction factor along the contact area. The contact zone provided by the specimen is limited to the region marked in green in Figure 7A.
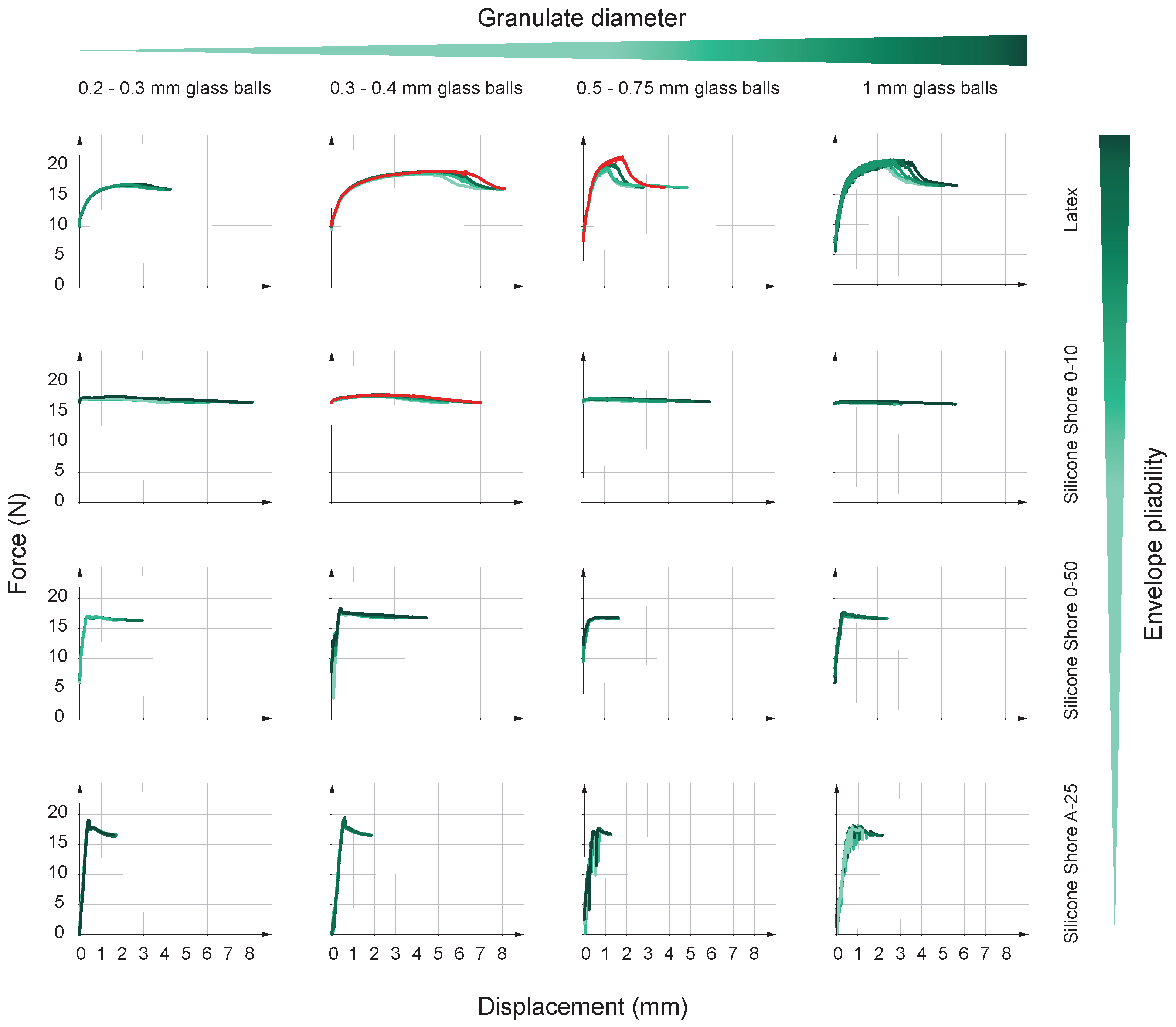
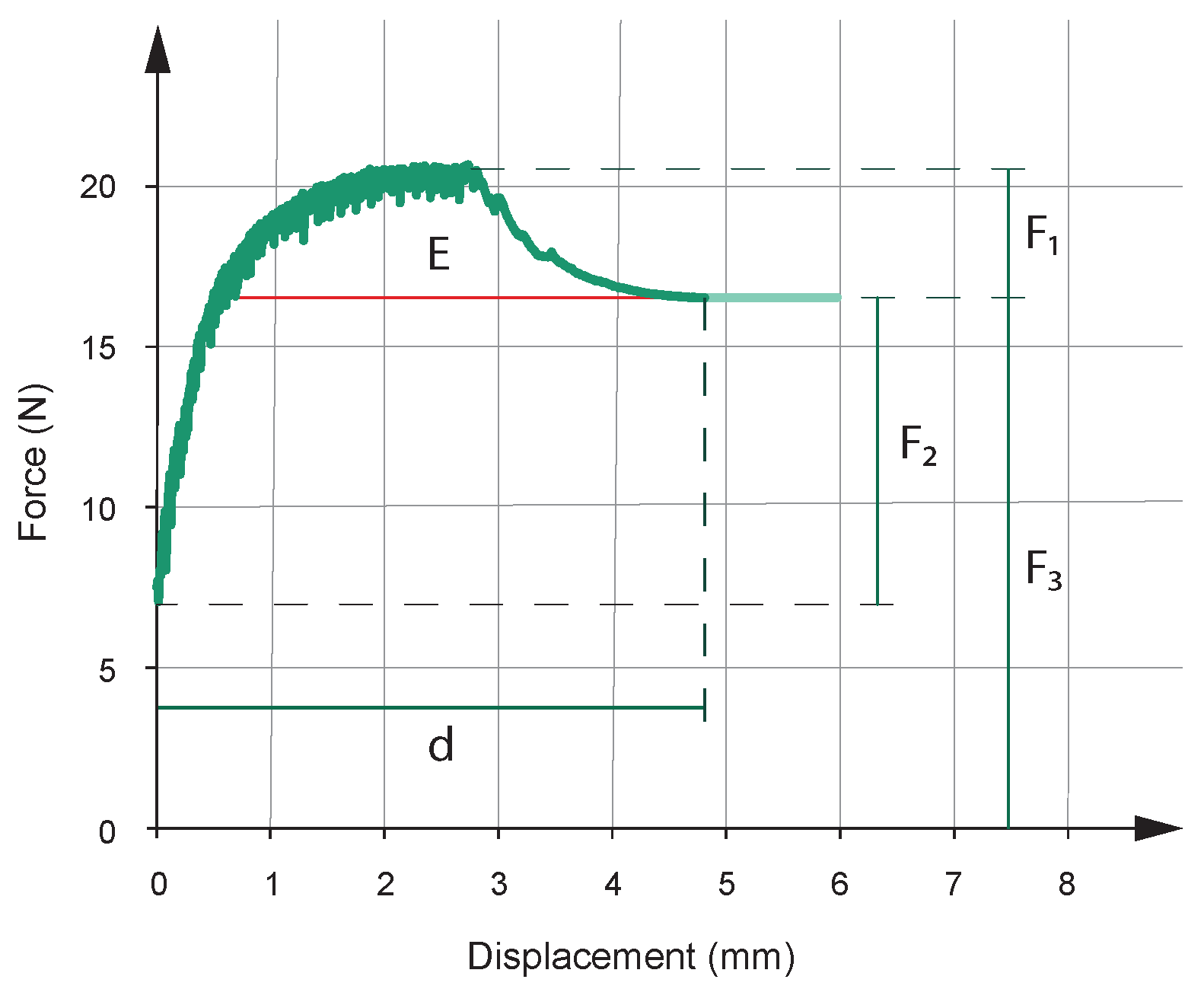
- Geometric constraints: We wanted to reward only those gripper combinations with good deformation behavior. Thus, we designed the specimen so that there are no easily reachable geometric constraints. Instead, we hid the constraint behind the convexity of the mushroom head. Figure 7A defines the angle . This parameter describes the ability of the gripper to occupy the geometric constraint provided by the specimen. Figure 7B explicitly shows how prototypes can occupy the gripper zone called Region A. Only those prototypes with adequate fluidity and pliability can reach this zone. This fact allows their performance to improve. As shown in Figure 8, prototypes manage to increase the gripping distance d and maximize the stored energy E (both parameters are defined in Figure 9).
- Vacuum chambers: We decided not to consider any vacuum chamber effect. To prevent the formation of any pressure chamber, we included a convex shape at the top of the test specimen.
3.3. Pull-Off Force Test
- Lifted weight: This variable is the maximum weight a gripper can lift. The gripper reaches this value during the tension testing phase.
- Stored energy: The second relevant parameter is the stored energy in the pull-off process. This value means the energy needed to pull off the gripper from the test specimen, i.e., the energy required to make any grasped object drop. This parameter is relevant since it expresses the quality of the grasp. In a real-life scenario, when a robotic arm attaches to the gripper, this external energy might be revealed in vibrations or inertial forces associated with linear accelerations and rotational movements. The higher the energy value is, the better the quality of the grasps.
- Deformation force: This parameter is the force a gripper needs to adapt its initial shape to the desired object. The tensile test machine obtains this value during the compression phase when the gripper is relaxed. The deformation force value is relevant since some industrial applications require robotics systems to grasp delicate parts such as brittle or deformable objects.
- First step: The volume of glass balls inside the envelope must be uniform for every test combination and equal to 153 mL. This is the theoretical interior volume (measured in CAD) that the envelope can wrap.
- Second step: The envelope must be clean every time a test starts. Cleaning it with alcohol guarantees that no particle from the surrounding environment is attached to the surface, and thus, no friction losses happen.
- Third step: Once the surface is dry, the upper part of the tensile tester machine starts its movement downwards. This movement compresses the gripper against the mushroom-shaped test specimen while the gripper is still relaxed. The movement stops when the displacement is equal to 45 mm from the reference position. Figure 7A shows the reference position ( when the gripper tip is tangent to the mushroom head). The maximum displacement any gripper can handle without entering the nonlinear compression force region is 45 mm (Figure 10 indicates the typical gripper behavior during the compression phase). The downwards velocity of the gripper at this stage is 250 mm/min.
- Fourth step: When the gripper is in position, the vacuum valve activates. Then, the gripper stands in this position for 40 s. Even though the petrification is almost immediate, the 40 s delay allows the system to reach a steady-state compression force. This compression value reveals the deformation force defined above ( in Figure 9). Vacuum pressure in our case study (robotic grasping) has an influence on two points: internal influence on the mechanical capabilities of the jamming effect and external influence on the gripper piece contact.In the first phenomenon, the higher the vacuum pressure, the more pronounced the jamming effect. This behavior can be qualitatively observed in the results of Hudson [38], where a progression of mechanical performance with increasing vacuum pressure is demonstrated. (Hudson’s results serve here to qualitatively guide the intuition of the effect of pressure, as his work studies the jamming effect only under compression and not under tension, as in our case).On the other hand, an increase in vacuum pressure in some prototypes favors an increase in the friction coefficient between the gripper and the grasped piece, as an increase in vacuum pressure causes the internal material to manifest on the external surface of the gripper, increasing its macroroughness (especially in cases of enveloping materials with lower hardness and thinner wall thickness, as shown in Figure 11).In any case, in this work, we assume that the effect of increasing vacuum pressure tends towards a limit in which both phenomena saturate. In this study, the research on the influence of pressure is beyond the scope, and we work with a uniform pressure value of 0.8 bar provided by the Venturi device.
- Fifth step: The setup is ready to start a conventional tensile force test with a 20 mm/min quasi-static speed rate.
4. Results and Discussion
- Lifted weight (). This parameter corresponds to the peak value in the tensile force curve.
- Stored energy (E). This parameter is the area between the tensile curve and the final traction value derived from the prototype’s weight ().
- Deformation force (). This value is equal to the difference between the weight () and the initial value of the tensile curve.
- Gripping distance (d). This parameter shows the distance over which the prototype can grip the mushroom-shaped specimen along its frictional spherical zone (Figure 7A).
- Total weight of the prototype (). This value includes the weight of the assembly shown in Figure 4 plus other components that attach it to the tensile tester.
- Lifted weight: Figure 12 shows the maximum lifted weight results following the guidelines stated above. Here, the three plots on the left (silicones) show the best performance for the 0.3–0.4 mm diameter balls, followed by some pick-up cases for the 1 mm balls.Nevertheless, the best behaviors appear with latex (plot on the far right), doubling the best results reached by the silicones. This plot shows a correlation between ball diameter and force output, reaching the best performance with diameters larger than 0.4 mm. Thus, the best combination to optimize the maximum weight the gripper can lift is a latex envelope in addition to the 1.0 mm diameter glass balls (if 0.5–0.75 mm outliers are discarded).Figure 12 does not show a clear trend for the influence of the granulate size on the lifted weight, at least in those prototypes manufactured with silicone. However, the opposite happens in the case of the latex envelope. If compared, envelopes are different in the material used to manufacture them but also in their wall thickness (it is relevant to remark here again that these wall thicknesses are the minimum achievable due to manufacturing restrictions; Table 1). Thus, we consider that the main reason the latex shows better results is its wall thickness (0.15 mm). This hypothesis assumes that smaller envelopes’ wall thicknesses allow the relief of the granular material to manifest more easily on the outside. Consequently, different grain sizes allow us to achieve different friction coefficients.As indicated in Figure 7A, the lifted weight is due to the frictional force established between the test specimen and the prototype. Thus, this force is directly proportional to the value of the static friction coefficient (), which can be qualitatively related to the roughness and waviness values of the prototype surface while the prototype is in the jamming phase (vacuum on).We performed waviness measurements of the prototypes for different granulate materials. In these measurements, we are only interested in the waviness values (and not in the roughness ones). This bias is because we consider the grain size sufficiently large (from 0.2 to 1.0 mm) to consider its effects on a macroscopic scale. Thus, we discard roughness values, as we consider them to reflect the influence of the envelope surface on a microscopic scale. In addition, since we want to see the influence of the granulate size on performance, it does not make sense to consider any contribution coming from the envelope side.The analysis of the prototypes showed minor waviness variations in the silicone cases (wall thicknesses of 1 and 2 mm). This result is due to the thick silicone wall’s cushioning effect, preventing the granular material’s relief from manifesting on the outside (Figure 11, diagram C). However, in the case of latex, significant waviness changes appear when analyzing the different granulate sizes (Figure 11, diagrams A and B) since the latex’s wall thickness is unable to provide any cushioning effect. Table 2 gathers the waviness results for the four different granulate and latex combinations.
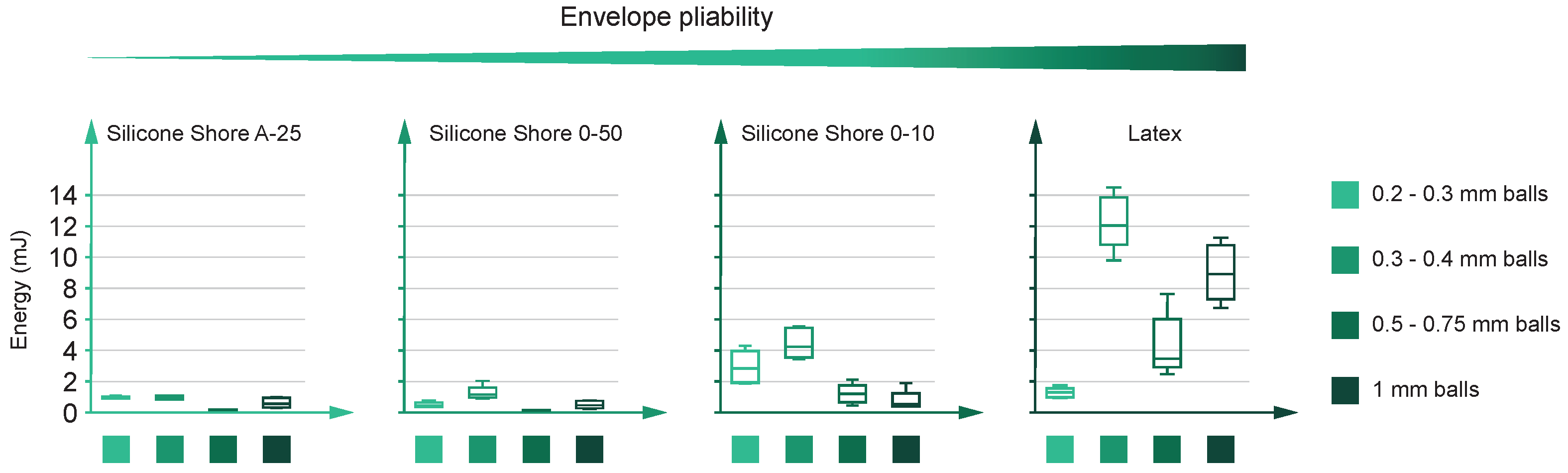
- Stored energy: Figure 13 shows the energy results of the tests. This figure follows the same format as the previous one. Again, the behavior of the silicones (three plots on the left) differ from the latex and display an inverse correlation between Shore hardness and energy absorption. The two hardest silicones (Shore 00-50 and Shore A-25) find it difficult to reach 2 mJ, but it is relevant to remark on the 0.5–0.75 mm diameter balls’ inability in both scenarios. There, the energy absorption is null.On the other hand, still analyzing silicones, the outcomes of the Shore 00-10 silicone improve the results of the hardest ones. The plot shows a properly defined maximum value for the 0.3–0.4 mm diameter one, multiplying by almost three the best results of its competitors.Figure 13 shows remarkable differences between silicones when absorbing energy. This difference lies in their plasticity. Analogously, we can refer to tensile tests on metals: more ductile metals obtain higher energy absorption values than brittle ones. Similarly, silicones with lower Shore hardness (more plastic and deformable) obtain better results than those with higher Shore hardness (more rigid).Finally, latex shows outstanding behavior compared to silicones. The results improve for every ball diameter, except for the smallest one, and the best combination (0.3–0.4 mm diameter) performs over 10 mJ in almost every case. Finally, it is also interesting that the 1.0 mm diameter balls step up after a sharp drop. This fall is due to the 0.5–0.75 mm balls, which tend to worsen the energy performance for every envelope.The simplified energy formula explains the better latex performance. In this formula, F is the lifted weight, and d is the gripping distance. Here, latex is the envelope that obtains better results because of both parameters: F and d. Lifted weight has already been explained in the previous point, and, on the other hand, latex maximizes the gripping distance d due to its ability to obtain better angle values (Figure 7A) and to take advantage of Region A (Figure 7B).
- Deformation force: Figure 14 shows deformation force results. Again, this figure follows the same format as the previous figures. As stated before, the optimum deformation force is most likely to be the one with the minimum value. The deformation force results allow for breaking off the previously seen silicone cluster, i.e., the silicones produce the best and the worst performance here. The hardest silicone (Shore A-25) suffers the most significant deformation values: in addition to 0.2–0.3 mm balls, the force goes over 20 newtons. Conversely, on the opposite side of the hardness scale, Shore 00-10 silicone results in close to zero forces. In addition, the other materials (latex and Shore 00-50 silicone) show a less attractive behavior, reaching values between 5 to 10 newtons.The parameter discussed here shows a clear correlation between the force values and the envelope plasticity. If considered a membrane, the more rigid the envelope is, the more tension appears in the deformation process. This tension restricts the movement of the inner particles, producing higher forces in those cases where the inner particles’ relocation is blocked. Thus, when the envelope adapts its form to the mushroom-shaped part, the glass balls find a limp boundary in the case of Shore 00-10 and a less permissive one in the case of Shore A-25. This difference in the boundary tension leads to particles’ movement behavior and the consequent results in Figure 14.Contrary to what happens with the envelope materials, it is not possible to extract a behavior trend for the glass balls. At first glance, the friction force between inner particles might arise as the leading cause contributing to the gripper deformation force. Since friction force is proportional to area, reducing the contact area between balls might be an interesting way to decrease the gripper deformation force. Thus, the larger the glass balls’ diameter, the lower the gripper deformation force. Even though the plot on the right in Figure 14 may confirm this hypothesis, the others discredit it. In this way, the relation between the balls’ diameter and gripper deformation force seems more complex. A new hypothesis might consider the interaction between envelope material and balls (instead of just balls). Thus, the envelopes’ roughness might enter the scene and explain the diameter influence. However, the confirmation of this hypothesis is left for future work.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
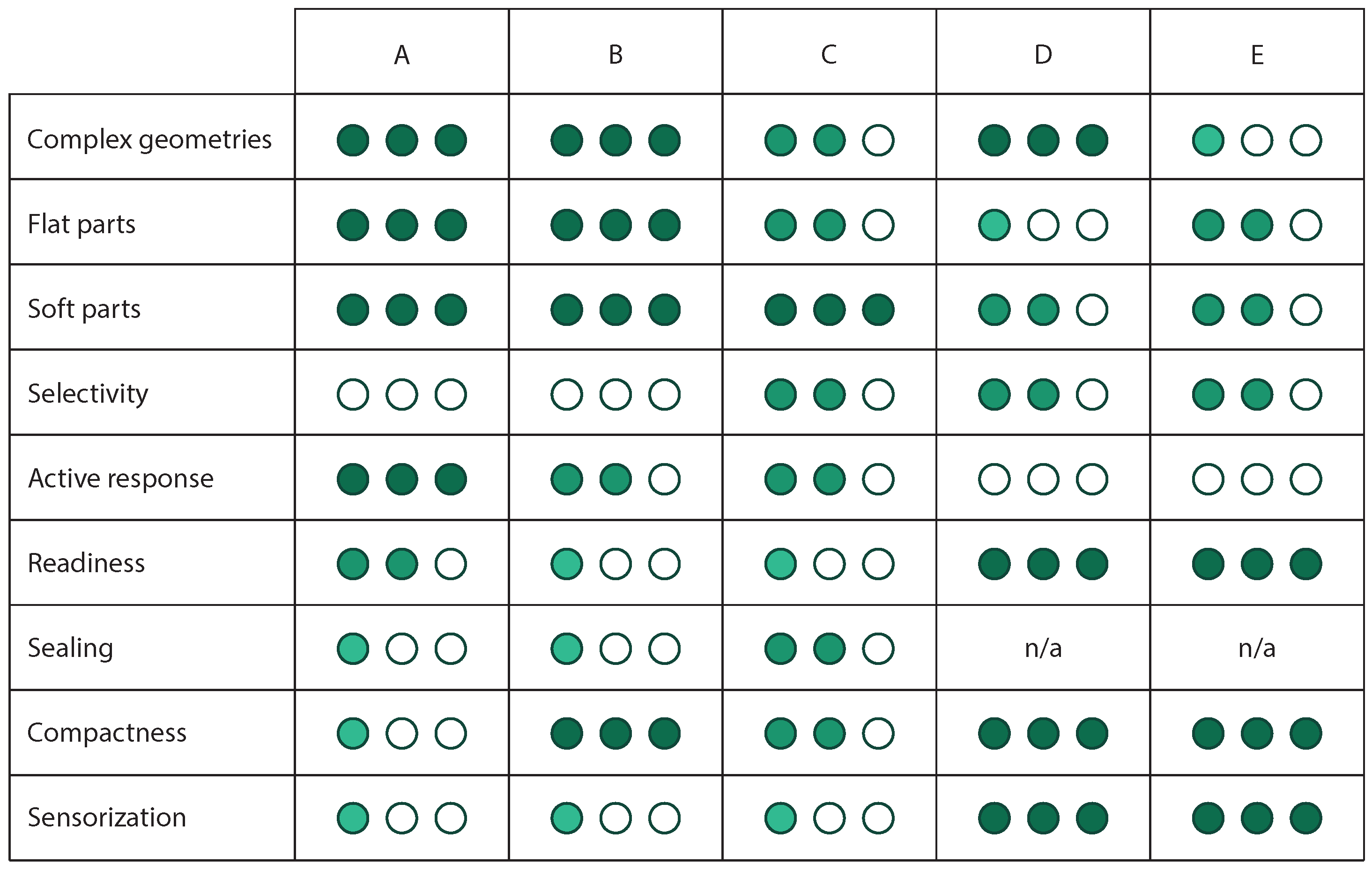
Appendix A. Alternative Gripping Techniques and Decision Matrix
- Complex geometries, flat parts, and soft parts: evaluates the ability of the grippers to grasp parts with these features.
- Selectivity: describes the ability of the gripper to grasp a unique object in a random and chaotic scene.
- Active response: indicates if the prototype includes any system to actively react or adapt its behavior depending on the object to grasp.
- Readiness: describes the ability of the prototype to grasp two completely different objects without requiring intermediate steps, i.e., this indicator punishes those grippers needing an intermediate step to adjust their performance. An intermediate step might be a tool change or any adjustment not done on the fly. On the other hand, this parameter rewards designs with few to no intermediate steps.
- Sealing: when applicable, this indicator shows the ability of the design to prevent airflow and pressure losses. This parameter often relates to selectivity since air leaks attract an undesired number of objects. Of course, as this factor is not applicable to every prototype, the scores awarded in this section are not computed to choose the final candidate.
- Compactness: evaluates the ability of the prototype to develop its actions without interfering with other objects surrounding the robot. It also rewards those alternatives with fewer components and mechanisms to trigger the grasping action.
- Sensorization: describes the potential and predisposition of the prototype to include sensors that might help enrich the system’s data acquisition.

References
- Eppner, C.; Höfer, S.; Jonschkowski, R.; MartÍn-Martín, R.; Sieverling, A.; Wall, V.; Brock, O. Lessons from the amazon picking challenge: Four aspects of building robotic systems. In Robotics: Science And Systems; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Correll, N.; Bekris, K.E.; Berenson, D.; Brock, O.; Causo, A.; Hauser, K.; Okada, K.; Rodriguez, A.; Romano, J.M.; Wurman, P.R. Analysis and observations from the first amazon picking challenge. IEEE Trans. Autom. Sci. Eng. 2016, 15, 172–188. [Google Scholar] [CrossRef]
- Yang, Y.; Vella, K.; Holmes, D.P. Grasping with kirigami shells. Sci. Robot. 2021, 6, eabd6426. [Google Scholar] [CrossRef] [PubMed]
- Gu, S.; Holly, E.; Lillicrap, T.; Levine, S. Deep reinforcement learning for robotic manipulation with asynchronous off-policy updates. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3389–3396. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 779–788. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Yan, B.; Fan, P.; Lei, X.; Liu, Z.; Yang, F. A real-time apple targets detection method for picking robot based on improved YOLOv5. Remote. Sens. 2021, 13, 1619. [Google Scholar] [CrossRef]
- Chen, K.; Cao, R.; James, S.; Li, Y.; Liu, Y.H.; Abbeel, P.; Dou, Q. Sim-to-Real 6D Object Pose Estimation via Iterative Self-training for Robotic Bin-picking. arXiv 2022, arXiv:2204.07049. [Google Scholar]
- Mahler, J.; Matl, M.; Satish, V.; Danielczuk, M.; DeRose, B.; McKinley, S.; Goldberg, K. Learning ambidextrous robot grasping policies. Sci. Robot. 2019, 4, eaau4984. [Google Scholar] [CrossRef]
- Cartucho, J.; Tukra, S.; Li, Y.S.; Elson, D.; Giannarou, S. VisionBlender: A tool to efficiently generate computer vision datasets for robotic surgery. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2021, 9, 331–338. [Google Scholar] [CrossRef]
- Kitagawa, S.; Wada, K.; Hasegawa, S.; Okada, K.; Inaba, M. Few-experiential learning system of robotic picking task with selective dual-arm grasping. Adv. Robot. 2020, 34, 1171–1189. [Google Scholar] [CrossRef]
- Todorov, E.; Erez, T.; Tassa, Y. Mujoco: A physics engine for model-based control. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Loulé, Portugal, 7–12 October 2012; pp. 5026–5033. [Google Scholar]
- Levine, S.; Pastor, P.; Krizhevsky, A.; Ibarz, J.; Quillen, D. Learning hand-eye coordination for robotic grasping with deep learning and large-scale data collection. Int. J. Robot. Res. 2018, 37, 421–436. [Google Scholar] [CrossRef]
- Xiong, Y.; Ge, Y.; From, P.J. An obstacle separation method for robotic picking of fruits in clusters. Comput. Electron. Agric. 2020, 175, 105397. [Google Scholar] [CrossRef]
- Gafur, N.; Kanagalingam, G.; Ruskowski, M. Dynamic collision avoidance for multiple robotic manipulators based on a non-cooperative multi-agent game. arXiv 2021, arXiv:2103.00583. [Google Scholar]
- Shintake, J.; Cacucciolo, V.; Floreano, D.; Shea, H. Soft robotic grippers. Adv. Mater. 2018, 30, 1707035. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Laschi, C.; Trimmer, B. Soft robotics: A bioinspired evolution in robotics. Trends Biotechnol. 2013, 31, 287–294. [Google Scholar] [CrossRef] [PubMed]
- Elsayed, Y.; Vincensi, A.; Lekakou, C.; Geng, T.; Saaj, C.; Ranzani, T.; Cianchetti, M.; Menciassi, A. Finite element analysis and design optimization of a pneumatically actuating silicone module for robotic surgery applications. Soft Robot. 2014, 1, 255–262. [Google Scholar] [CrossRef]
- Luo, Y.; Wu, K.; Spielberg, A.; Foshey, M.; Rus, D.; Palacios, T.; Matusik, W. Digital Fabrication of Pneumatic Actuators with Integrated Sensing by Machine Knitting. In Proceedings of the CHI Conference on Human Factors in Computing Systems, New Orleans, LA, USA, 29 April–5 May 2022; pp. 1–13. [Google Scholar]
- Li, S.; Stampfli, J.J.; Xu, H.J.; Malkin, E.; Diaz, E.V.; Rus, D.; Wood, R.J. A vacuum-driven origami “magic-ball” soft gripper. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 7401–7408. [Google Scholar]
- Coulson, R.; Stabile, C.J.; Turner, K.T.; Majidi, C. Versatile soft robot gripper enabled by stiffness and adhesion tuning via thermoplastic composite. Soft Robot. 2021, 9, 189–200. [Google Scholar] [CrossRef]
- Fantoni, G.; Capiferri, S.; Tilli, J. Method for supporting the selection of robot grippers. Procedia CIRP 2014, 21, 330–335. [Google Scholar] [CrossRef]
- Brown, E.; Rodenberg, N.; Amend, J.; Mozeika, A.; Steltz, E.; Zakin, M.; Lipson, H.; Jaeger, H. Universal robotic gripper based on the jamming of granular material. Proc. Natl. Acad. Sci. USA 2010, 107, 18809–18814. [Google Scholar] [CrossRef]
- Lambeta, M.; Chou, P.W.; Tian, S.; Yang, B.; Maloon, B.; Most, V.R.; Stroud, D.; Santos, R.; Byagowi, A.; Kammerer, G.; et al. DIGIT: A novel design for a low-cost compact high-resolution tactile sensor with application to in-hand manipulation. IEEE Robot. Autom. Lett. 2020, 5, 3838–3845. [Google Scholar] [CrossRef]
- Follmer, S.; Leithinger, D.; Olwal, A.; Cheng, N.; Ishii, H. Jamming user interfaces: Programmable particle stiffness and sensing for malleable and shape-changing devices. In Proceedings of the 25th Annual ACM Symposium on User Interface Software and Technology, Cambridge, MA, USA, 7–10 October 2012; pp. 519–528. [Google Scholar]
- Jaeger, H.M. Celebrating soft matter’s 10th anniversary: Toward jamming by design. Soft Matter 2015, 11, 12–27. [Google Scholar] [CrossRef]
- Dierichs, K.; Menges, A. Designing architectural materials: From granular form to functional granular material. Bioinspiration Biomimetics 2021, 16, 065010. [Google Scholar] [CrossRef]
- Fitzgerald, S.G.; Delaney, G.W.; Howard, D. A review of jamming actuation in soft robotics. Actuators 2020, 9, 104. [Google Scholar] [CrossRef]
- Amend, J.R.; Brown, E.; Rodenberg, N.; Jaeger, H.M.; Lipson, H. A positive pressure universal gripper based on the jamming of granular material. IEEE Trans. Robot. 2012, 28, 341–350. [Google Scholar] [CrossRef]
- Amend, J.; Cheng, N.; Fakhouri, S.; Culley, B. Soft robotics commercialization: Jamming grippers from research to product. Soft Robot. 2016, 3, 213–222. [Google Scholar] [CrossRef]
- Choi, Y.T.; Hartzell, C.M.; Leps, T.; Wereley, N.M. Gripping characteristics of an electromagnetically activated magnetorheological fluid-based gripper. AIP Adv. 2018, 8, 056701. [Google Scholar] [CrossRef]
- Nishida, T.; Okatani, Y.; Tadakuma, K. Development of universal robot gripper using MR α fluid. Int. J. Humanoid Robot. 2016, 13, 1650017. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Yang, Y.; Wei, Y. Passive particle jamming and its stiffening of soft robotic grippers. IEEE Trans. Robot. 2017, 33, 446–455. [Google Scholar] [CrossRef]
- Bartkowski, P.; Gawiński, F.; Pawliszak, Ł. E-Morph as a New Adaptive Actuator for Soft Robotics. IEEE Robot. Autom. Lett. 2022, 7, 8831–8836. [Google Scholar] [CrossRef]
- Götz, H.; Santarossa, A.; Sack, A.; Pöschel, T.; Müller, P. Soft particles reinforce robotic grippers: Robotic grippers based on granular jamming of soft particles. Granul. Matter 2022, 24, 31. [Google Scholar] [CrossRef]
- Loeve, A.J.; van de Ven, O.S.; Vogel, J.G.; Breedveld, P.; Dankelman, J. Vacuum packed particles as flexible endoscope guides with controllable rigidity. Granul. Matter 2010, 12, 543–554. [Google Scholar] [CrossRef]
- Miskin, M.Z.; Jaeger, H.M. Evolving design rules for the inverse granular packing problem. Soft Matter 2014, 10, 3708–3715. [Google Scholar] [CrossRef]
- Hudson, S.W. Mechanical Characterization of Jammable Granular Systems. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2012. [Google Scholar]
- Howard, D.; O’Connor, J.; Letchford, J.; Brett, J.; Joseph, T.; Lin, S.; Furby, D.; Delaney, G.W. Getting a Grip: In Materio Evolution of Membrane Morphology for Soft Robotic Jamming Grippers. In Proceedings of the 2022 IEEE 5th International Conference on Soft Robotics (RoboSoft), Edinburgh, UK, 4–8 April 2022; pp. 531–538. [Google Scholar]
- Jiang, A.; Ranzani, T.; Gerboni, G.; Lekstutyte, L.; Althoefer, K.; Dasgupta, P.; Nanayakkara, T. Robotic granular jamming: Does the membrane matter? Soft Robot. 2014, 1, 192–201. [Google Scholar] [CrossRef]
- Xiao, W.; Du, X.; Chen, W.; Yang, G.; Hu, D.; Han, X. Cooperative collapse of helical structure enables the actuation of twisting pneumatic artificial muscle. Int. J. Mech. Sci. 2021, 201, 106483. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, Y.; Ren, T.; Chen, Q.; Yan, C.; Yang, Y.; Li, Y. A novel, variable stiffness robotic gripper based on integrated soft actuating and particle jamming. Soft Robot. 2016, 3, 134–143. [Google Scholar] [CrossRef]
- Cheng, N.G.; Lobovsky, M.B.; Keating, S.J.; Setapen, A.M.; Gero, K.I.; Hosoi, A.E.; Iagnemma, K.D. Design and analysis of a robust, low-cost, highly articulated manipulator enabled by jamming of granular media. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St. Paul, MN, USA, 14–18 May 2012; pp. 4328–4333. [Google Scholar]
- Licht, S.; Collins, E.; Mendes, M.L.; Baxter, C. Stronger at depth: Jamming grippers as deep sea sampling tools. Soft Robot. 2017, 4, 305–316. [Google Scholar] [CrossRef] [PubMed]
- Cheng, N.; Amend, J.; Farrell, T.; Latour, D.; Martinez, C.; Johansson, J.; McNicoll, A.; Wartenberg, M.; Naseef, S.; Hanson, W.; et al. Prosthetic jamming terminal device: A case study of untethered soft robotics. Soft Robot. 2016, 3, 205–212. [Google Scholar] [CrossRef]
- Jiang, Y.; Amend, J.R.; Lipson, H.; Saxena, A. Learning hardware agnostic grasps for a universal jamming gripper. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St. Paul, MN, USA, 14–18 May 2012; pp. 2385–2391. [Google Scholar]
- Hermes, M.; Dijkstra, M. Jamming of polydisperse hard spheres: The effect of kinetic arrest. Europhys. Lett. 2010, 89, 38005. [Google Scholar] [CrossRef]







| S. A-25 | S. 00-50 | S. 00-10 | Latex | |
|---|---|---|---|---|
| Density [g cm−3] | 1.18 | 1.07 | 1.04 | 0.96 |
| Thickness [mm] | 1.0 | 2.0 | 2.0 | 0.15 |
| Roughness [μm] | 6.15 | 29.01 | 15.26 | 32.06 |
| 0.2–0.3 mm | 0.3–0.4 mm | 0.5–0.75 mm | 1.0 mm | |
|---|---|---|---|---|
| Waviness [μm] | 9.54 | 28.81 | 23.55 | 74.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Rodrigo, I.; Belart, J.; Lopez-Lopez, A.J. Universal Jamming Gripper: Experimental Analysis on Envelope and Granular Materials. Machines 2024, 12, 52. https://doi.org/10.3390/machines12010052
de Rodrigo I, Belart J, Lopez-Lopez AJ. Universal Jamming Gripper: Experimental Analysis on Envelope and Granular Materials. Machines. 2024; 12(1):52. https://doi.org/10.3390/machines12010052
Chicago/Turabian Stylede Rodrigo, Ignacio, Jorge Belart, and Alvaro J. Lopez-Lopez. 2024. "Universal Jamming Gripper: Experimental Analysis on Envelope and Granular Materials" Machines 12, no. 1: 52. https://doi.org/10.3390/machines12010052
APA Stylede Rodrigo, I., Belart, J., & Lopez-Lopez, A. J. (2024). Universal Jamming Gripper: Experimental Analysis on Envelope and Granular Materials. Machines, 12(1), 52. https://doi.org/10.3390/machines12010052






