Functional Electrostimulation System for a Prototype of a Human Hand Prosthesis Using Electromyography Signal Classification by Machine Learning Techniques

Abstract

Functional electrical stimulation (FES) has been proven to be a reliable rehabilitation technique that increases muscle strength, reduces spasms, and enhances neuroplasticity in the long term. However, the available electrical stimulation systems on the market produce stimulation signals with no personalized voltage–current amplitudes, which could lead to muscle fatigue or incomplete enforced therapeutic motion. This work proposes an FES system aided by machine learning strategies that could adjust the stimulating signal based on electromyography (EMG) information. The regulation of the stimulated signal according to the patient’s therapeutic requirements is proposed. The EMG signals were classified using Long Short-Term Memory (LSTM) and a least-squares boosting ensemble model with an accuracy of 91.87% and 84.7%, respectively, when a set of 1200 signals from six different patients were used. The classification outcomes were used as input to a second regression machine learning algorithm that produced the adjusted electrostimulation signal required by the user according to their own electrophysiological conditions. The output of the second network served as input to a digitally processed electrostimulator that generated the necessary signal to be injected into the extremity to be treated. The results were evaluated in both simulated and robotized human hand scenarios. These evaluations demonstrated a two percent error when replicating the required movement enforced by the collected EMG information.

1. Introduction

The human hand is recognized as the main tool people use to interact with their environment. Through it, people can communicate, innovate, create, and defend themselves from external danger. Although hand function is taken for granted in everyday life, when some pathologies affect the upper limb, the person who suffers them simultaneously loses mobility and his or her independence and quality of life [1]. Since the hands send somatosensory information and receive motor information through the nerves that make up the peripheral nervous system, any alteration in them can affect their functionality [2].

The main pathologies/accidents that can affect the upper limb are stroke and nerve damage. The former, which affects more than 800,000 people worldwide, is the main cause of disability and the third leading cause of death in the world. This pathology consists of a neurological explosion caused by the poor perfusion of blood vessels in the brain; it includes two types: ischemic (85% of cases) and hemorrhagic (15% of cases) [3]. The most prevalent type of stroke is ischemic, arising from a blockage in a blood vessel that causes a lack of oxygen and nutrients. This blockage often stems from narrowed vessels due to atherosclerosis, which are progressively obstructed. Consequently, neurons experience suffocation from reduced blood flow and are prone to necrosis. Hemorrhagic strokes occur when pressure on the brain leads to the overloading of blood vessels. This type of stroke is divided into intracerebral and subarachnoid hemorrhages. In the former, blood gathers inside the brain; in the latter, it collects in the subarachnoid space. Around 90% of survivors face some type of disability afterward, often experiencing limb weakness or paralysis [4].

The second kind of disability is nerve damage. Notice that somatosensory and motor information is transmitted through the radial, ulnar, and median nerves, which arise from the spinal column from C6 to C8. As mentioned above, these nerves’ lack of bony protection makes them susceptible to damage and wear and tear, translating into a loss of sensation and movement. The most common of these injuries are due to traffic accidents, violence, sports, or falls. Globally, the incidence ranges from 10.4 to 83 in developed countries, with 53.9% of these cases affecting the cervical spine [5]. Most people who suffer this type of injury are at a young and productive age [6]; therefore, when faced with this new disability, they also face significant economic losses due to the cost and duration of rehabilitation, as well as those caused by the disability itself.

Several strategies have been developed to face disability that involve technology, which improves safety, efficiency, and even the time involved in the rehabilitation process [7]. One of the most promising rehabilitation techniques is FES, which produces electric currents that pass through electrodes to a muscle to make a specific movement [8,9]. This technique is used to correct the execution of movements, improve muscle weakness, and promote a habit by exercising neuroplasticity [10].

The electrical discharge propagates through the electrodes, which can be either cathodes or anodes. At the same time, they can be invasive or non-invasive. In the case of invasive electrodes, the current reported in the literature is between 15 and 30 mA [11]. The signal’s shape can be monophasic, consisting of a single polarity, or biphasic, ensuring that the transmitted current can be removed from the tissue and subdivided into symmetrical and asymmetrical currents. The former stimulates the muscle under the cathode and anode. It seeks to undo the electrochemical reaction caused by the initial phase. Typically, a period pause is located between the biphasic stimulations to ensure the proper propagation of action potentials. With the asymmetrical current, the contractions happen only under the cathode [12]. Moreover, before administering electrical stimulation, it is crucial to consider the regular state of healthy patients. As the stimulation signal travels through the skin to reach the muscle, its initial condition needs assessment. The skin may be in poor condition with pressure injuries or irritation; moreover, the prolonged use of electrodes can also cause irritation [13,14,15]. One may notice that selecting an effective electrical stimulation signal depends on many factors. However, the most significant one relates to the patient’s therapy. Usually, the suggested therapy includes the performance of specific extremity motions, which could be aided by applying the electrostimulation strategy. Hence, the electrophysiological activity in the proximal muscles can be used as triggering information to choose the requested stimulation signal, which is indeed a scarcely explored operation strategy.

Electromyographic (EMG) signals represent the electrical activity of muscles. When these signals are measured, they must be amplified and filtered. The gain is selected based on the function and the desired amplification, while the signal noise is removed with a proper arrangement of filters [16]. Once the EMG signals have been properly obtained, they can be processed to determine muscle damage and therapy effectiveness. Among these processing strategies, EMG signal automatic classification could be used to determine the patient’s motion intention, which could then be used to define the adequate electrostimulation signal.

Automatic signal classification implies extracting features in each signal interval to recognize the characteristic information of each extremity motion [17]. Different strategies have been studied to classify EMG signals, such as Simple Logistic Regression, Artificial Neural Networks (ANNs), Linear Discrimination Analysis, Naive Bayes, and K-nearest neighbors. EMG classification by machine learning has been used for different purposes.

Gonzalez et al. [18] developed a hand gesture recognition model where the EMG signals were collected through the Myo Armband, which has eight channels and works with a sampling frequency of 200 Hz. Then, the features were extracted and classified according to the following gestures: fist, finger stretch, inward move, outward move, and double tap. The classification was achieved through ANNs with three layers and a total efficiency of 88.3%.

Ref. [19] also collected the EMG data through a Myo Armband; however, the authors classified stronger movements as wrist pronation, supination, and elbow flexion and extension. The data were classified through ANNs with an accuracy of 94% [19].

Gandolla et al. [20] developed a controller based on electromyographic signals for a hand-assisted robotic device that detected movement intention. The authors measured the following movements: pinching, grasping, and fist. The Porti device from Twente Medical Systems was selected to collect the signals. It has five channels and works with a sampling frequency of 2049 Hz. After the feature selection process, the data were preprocessed with a third-order Butterworth bandpass filter of 5 to 10 Hz. Then, the authors used two ANNs, and each trial was classified as input in the form of EMG signal portions corresponding to the electromechanical delay—the pattern vector. The pattern vector was provided as input to successive ANNs with one hidden layer [20]. This process demonstrated an accuracy of $76\pm 14\%$.

Espinoza et al. [21] compared decision trees and support vector machines for EMG signals. Eight EMG sensors were used to study the following movements: cylindrical grasp, tip grasp, hook grasp, open hand, palmar grasp, spherical grasp, lateral grasp, and fist. Then, the data were classified through the Extended Associative Memories (EAMs) method, which develops a relationship between the input (x) and an index $\mu$ of the class to determine class movement. Through this method, the authors achieved an accuracy of 95.83% for these strong movements [21]. Moreover, ref. [22] collected and preprocessed raw EMG signals with a cut-off frequency of 5 to 500 Hz. Then, the authors classified the data with an ANN of the Long Short-Term Memory (LSTM) type; this network represented the features of the signals in a score range and obtained an overall accuracy of 90.4% [22]. Due to this accuracy performance, we decided to develop an ANN of the LSTM type.

These results demonstrate the possibility of using an ANN as an efficient machine-learning tool to classify EMG signals, supporting the choice of an ANN in this study as the EMG classifier, which defines the signal to be electrostimulated. Nevertheless, most of the previous studies considered the application of an ANN with a static topology, which could neglect the time-dependent nature of EMG signals. This fact emphasizes the necessity of devising automatic classification algorithms based on dynamic forms of ANNs that can handle EMG signals more efficiently over time.

The motivation behind this research was multifold: enhancing rehabilitation, minimizing muscle fatigue, and enabling precision in treatment by FES. Overall, the ultimate goal of this research was to provide a more efficient and personalized rehabilitation approach for individuals with neurological injuries affecting their hand movements. Setting a base for combining functional therapy with careful stimulation adjustment (based on the automatic classification of EMG signals) aims to help these individuals regain upper limb mobility and improve their overall quality of life. The proposed automatic selection of FES signals involves the application of a recurrent ANN to consider the temporal nature of the processed information and the signals to be produced. The proposed methodology was evaluated on a prototype of a prosthetic hand that performed the motion established by the detected EMG signal. The device included a strategy that controlled the hand motion to achieve the correct position only when the produced FES signal corresponded to the expected motion defined by the classified EMG.

2. Methodology

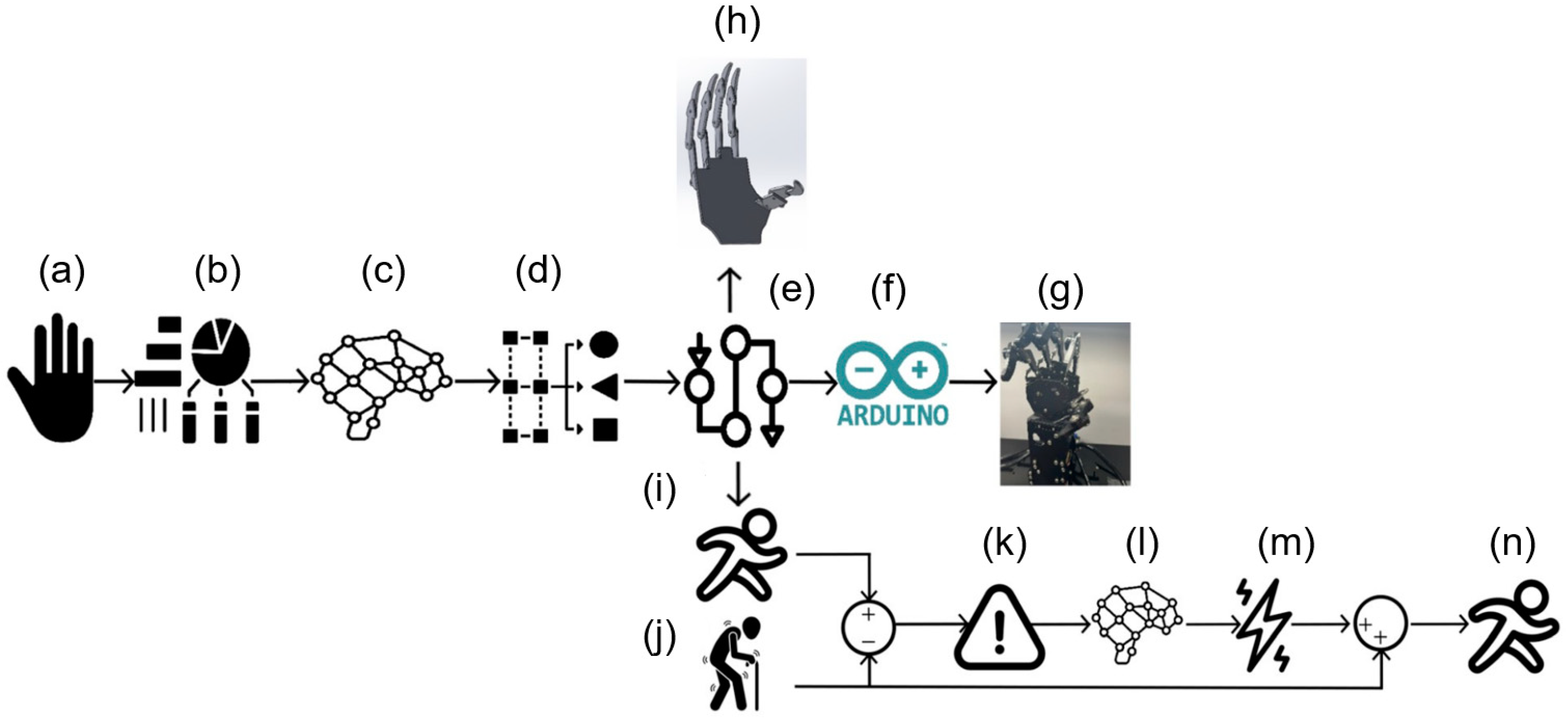
The proposed methodology comprised the following sequence of processing stages (Figure 1): (a) Initially, a dataset containing ten different human hand movements was employed, consisting of five combinations of movements and five distinct finger movements. These signals were then processed by integrating signal processing, automatic classification, bioinstrumentation, and the controlled regulation of the prosthesis prototype. (b) Key features relevant to the application were extracted from these ten movements, six subjects, two channels, and ten repetitions. (c) Subsequently, a neural network was utilized to classify these movements based on the specific hand motion being executed. (d) The neural network output a number from 1 to 10 corresponding to one of the ten movements studied. (e) A set of trajectories required to replicate the movements of a healthy hand for reference purposes was determined. (f) A digital processing board was used to regulate the electronic function of the actual prosthetic device. (g) The Hiwonder UHand 2.0 device was used as the prosthetic hand, which received control instructions from the digital processing board. (h) A digital twin of the hand prosthesis was considered to evaluate the classification and the control. (i) Based on the processed information, the trajectories corresponded to a healthy movement. Because of this, they were used as reference coordinates. (j) To simulate the effectiveness of the FES strategy, a numerically evaluated sickness motion was proposed for the prosthetic hand using a non-tuned control form. (k) To assess the deviation from the reference coordinates for a person with a medical condition, the coordinates representing the affected individual were subtracted from the reference coordinates, resulting in an error that should be related to the required control actions in the hand. (l) Using this information differential, a second dynamic neural network calculated the decoded FES signal (m) that acted on the prosthetic hand, as shown in stage (n).

2.1. Database of Hand’s EMG Signals

The EMG signals used in this research were obtained from the database presented by [23]. The authors measured ten different hand movements from six healthy men aged between 20 and 25 years. The EMG signals were acquired through two channels and were employed by the Delsys DE sensors. The first channel measured the signals from the extensor carpi ulnaris and extensor digiti minimi muscles. In contrast, the second one measured the signals from the flexor digitorum superficials and palmaris longus [23]. Ten different movements were analyzed: five individual movements (thumb, index, middle, ring, and little), and five combination movements (thumb–index, thumb–middle, thumb–ring, thumb–little, and hand close). The acquired signals were processed with an amplifier gain of 1000 and filtered using a bandpass with a bandwidth of 20 to 450 Hz and a notch filter of 50 Hz to eliminate the interference. The result of measuring six people through 2 channels, performing ten movements ten times, was a matrix of 1200 signals.

Feature Extraction and Selection

Once the signals were preprocessed, they were converted to the frequency domain through the fast Fourier transformation. Since the result matrix was a series of complex numbers, their spectrum and phases were extracted from the signals. After that, the most common statistical characteristics in the literature were extracted through the following Matlab commands: average (1), standard deviation (2), root mean square (3), shape factor (4), peak value, signal to noise ratio crest factor (5), and signal to noise and distortion ratio (6).

The average ($\overline{X}$) was the summation of all the signal components divided by the total number of signal components (N) (1).

$$\overline{X}=\frac{X_1+X_2+X_3+...+X_n}{n}$$

(1)

$\overline{X}$ was used to obtain the standard deviation $\left(S\right)$ as stipulated in Equation (2).

$$S=\sqrt{\frac{\sum {(x-\overline{x})}^2}{n-1}}$$

(2)

The root mean square $\left(RMS\right)$ was obtained by squaring each of the signal components, then adding them together and later dividing by n (1200). Finally, the square root was applied to the result (3).

$$RMS=\sqrt{\frac{X_1^2+X_2^2+X_3^2+...+X_n^2}{n}}$$

(3)

$$Shapefactor=\frac{RMS}{Average}$$

(4)

The crest factor was obtained by dividing the maximum value of the signal by the RMS.

$$Crestfactor=\frac{Peak}{RMS}$$

(5)

$$SNR=\frac{P_{Signal}}{P_{Noise}}$$

(6)

After the feature extraction, the signal matrix was confirmed by a length of 1200 signals (rows) and nine characteristics (columns), where the first characteristic was the movement the signal referred to, and the following eight were the previous characteristics.

2.2. Automatic Classifier of EMG Signals

Because EMG signals lack a specific shape, the information they yield is interpreted based on the amplitude of the signals. The smaller the amplitude, the more the muscle is at rest; the more significant the amplitude, the more active the muscle. It is possible to find patterns encompassing each muscle’s information through machine learning (ML) techniques applied as classifiers, thus characterizing which movement is being executed.

One of these ML techniques is the ANN, a computational system inspired by biological neurons [24]. ANNs have been demonstrated to successfully classify different kinds of biopotentials due to their ability to establish complex relationships between inputs and outputs. Other techniques have been tested for this task, such as the least-squares boosting ensemble. This kind of ensemble uses voting techniques to provide better predictive performance for regression problems. This work used these methods to classify the hand movement EMG signals: Long Short-Term Memory (LSTM), a kind of dynamic ANN, and a least-squares boosting ensemble.

2.2.1. LSTM Used as Automatic EMG Classifier

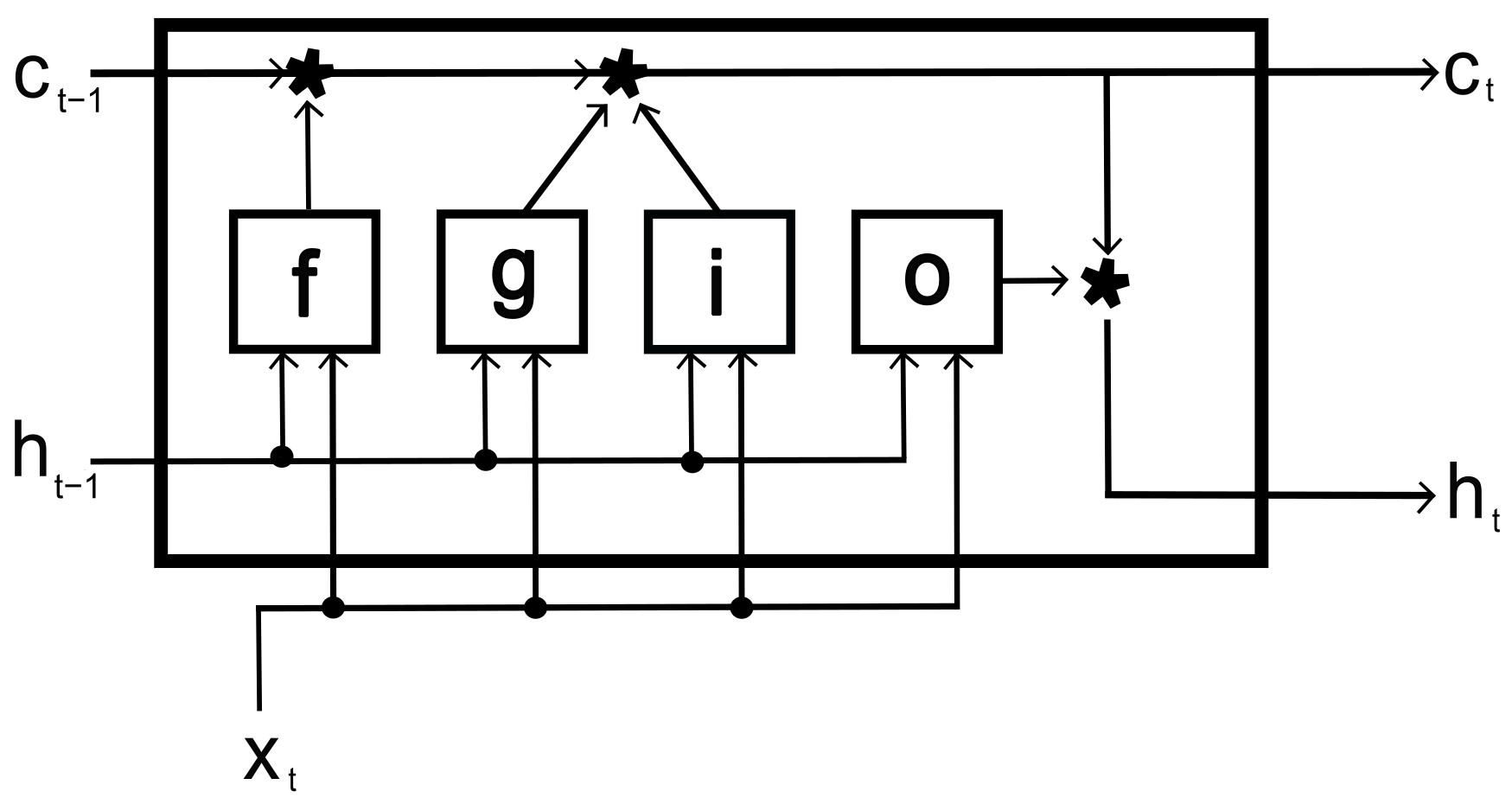
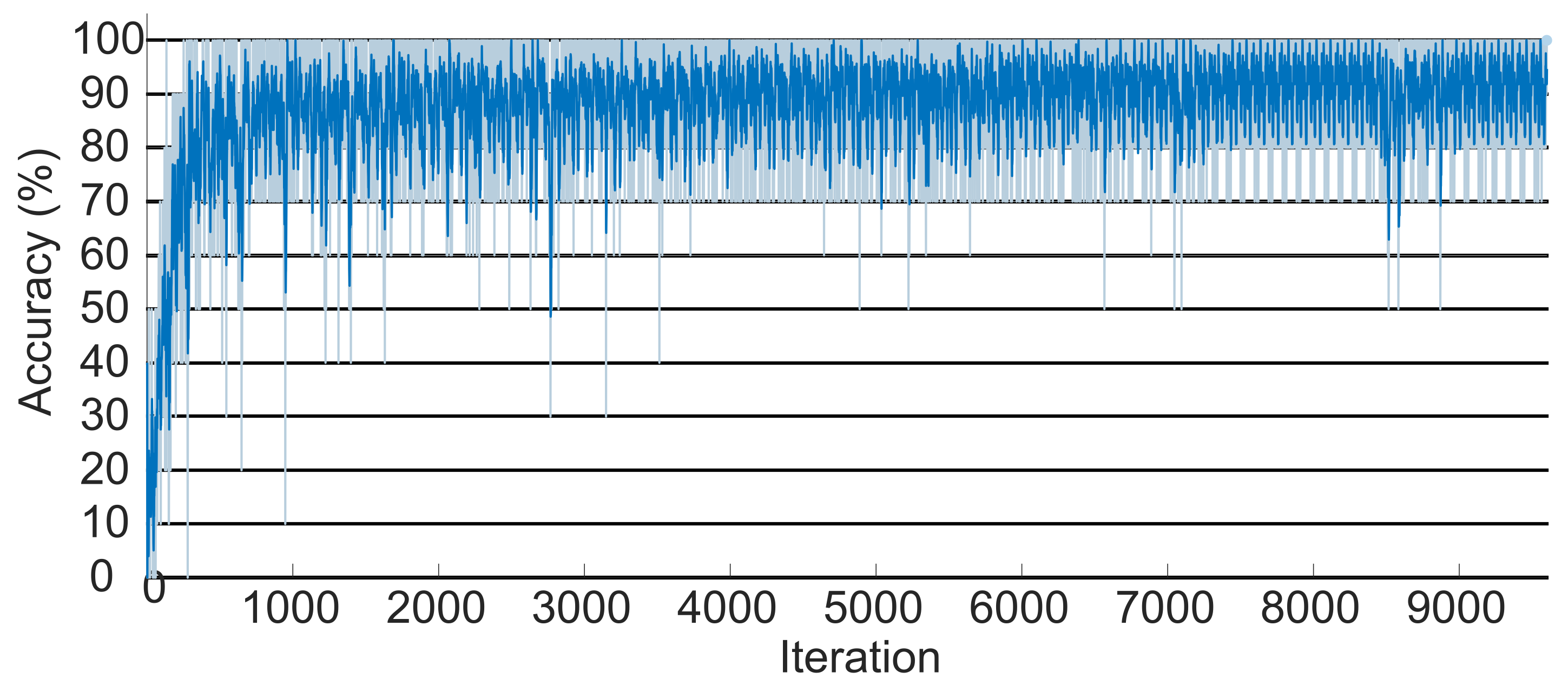
After extracting and selecting the most pertinent characteristics of the EMG signals, a recurrent neural network of the LSTM type, developed in Matlab, was used to classify the signals according to the relative hand motions. The suggested LSTM worked as follows: first, the ten movements were used as references in the neural network classes, where each class contained 120 signals; 80% of them were randomly selected to train the network, and the remaining were used to evaluate the proposed classification algorithm.

The LSTM mastered the dependencies between the periods of the input signals. It used ten fully connected bidirectional recurrent neural network (RNN) layers that learned bidirectional dependencies. The hidden layer had 500 units and 100 epochs per training iteration; these values were found empirically to minimize the loss function by using a mini-batch. Matlab based its LSTM on the work of [25], according to the topology suggested in Figure 2. This LSTM includes weights for the hidden layer, the input weights (W), the recurrent weights (R), and the bias (b). The hidden layer concatenates the matrices as follows:

$$W=\left[\begin{array}{c}{W}_i\\ W_f\\ W_g\\ W_o\end{array}\right],R=\left[\begin{array}{c}{R}_i\\ R_f\\ R_g\\ R_o\end{array}\right],b=\left[\begin{array}{c}{b}_i\\ b_f\\ b_g\\ b_o\end{array}\right]$$

(7)

Here, $i,f,g$, and o determine the input gate, hidden gate, cell candidate, and output gait, respectively. These gates are represented in the following equation:

$$gat{e}_t=\sigma \left(W_{gate}{X}_t+R_{gate}{h}_{t-1}+b_{gate}\right)$$

(8)

Here, t is the time unit, $h_t$ is the hidden state (Equation (9)), X is the time series, and $\sigma$ is the sigmoidal function that determine the activation function:

$$h_t=o_t\odot \sigma \left(c_{{}_t}\right)$$

(9)

where ⊙ is the vector product of the elements (Hadamard product) and cell state ($c_t$).

$$c_t=f_t\odot c_{t-1}+i_t\odot g_t$$

(10)

The Matlab method was employed to classify the signals. Such a method tests the gradient of the loss function and updates the weights. Softmax is used as an activation function, which converts the sum of the weights into probabilities. Based on these probabilities, the LSTM identifies the signal class that is represented with a number between 1 and 10.

2.2.2. Least-Squares Boosting Ensemble

The least-squares boosting ensemble introduces a new learner per ensemble to adapt to the gradient between the first output and the predictions made by previously developed learners. Then, K-fold cross-validation is used to validate the classification results [26]. This validation method randomly subdivides the original sample into K sub-samples. One of these is used for validation, and the remaining for training. The most common K value reported in the literature is 5, which indicates that 80% of the samples are used for training and the remaining for testing [27].

ANOVA (analysis of variance) was the technique applied for feature selection; it examines experimental information when diverse factors are measured across different situations and contrasts the average of different datasets. This information is obtained from k different populations, $Y_{ij}$ is the $i_{th}$ observation from the $i_{th}$ population, ${\mu }_i$ is the mean of the population, and ${\epsilon }_{ij}$ corresponds to the random variation between $Y_{ij}$ and ${\mu }_i$ [28].

$$Y_{ij}={\mu }_i+{\epsilon }_{ij};j=1,..,n_{i}i=1,..,n_k$$

(11)

${\epsilon }_{ij}$ has a normal distribution with a zero mean and variance (${\sigma }^2$). The static test (F) evaluates the hypothesis of equal variance with a $F(n_i-1)$ distribution.

$$F=\frac{S_1^2}{S_2^2}$$

(12)

Here, $S{i}^2$ represents the unbiased estimator of variance for the $i_{th}$ group [29]. The null hypothesis of the ANOVA algorithm is that the compared means have to be equal to each other.

2.3. Human Hand Design in CAD

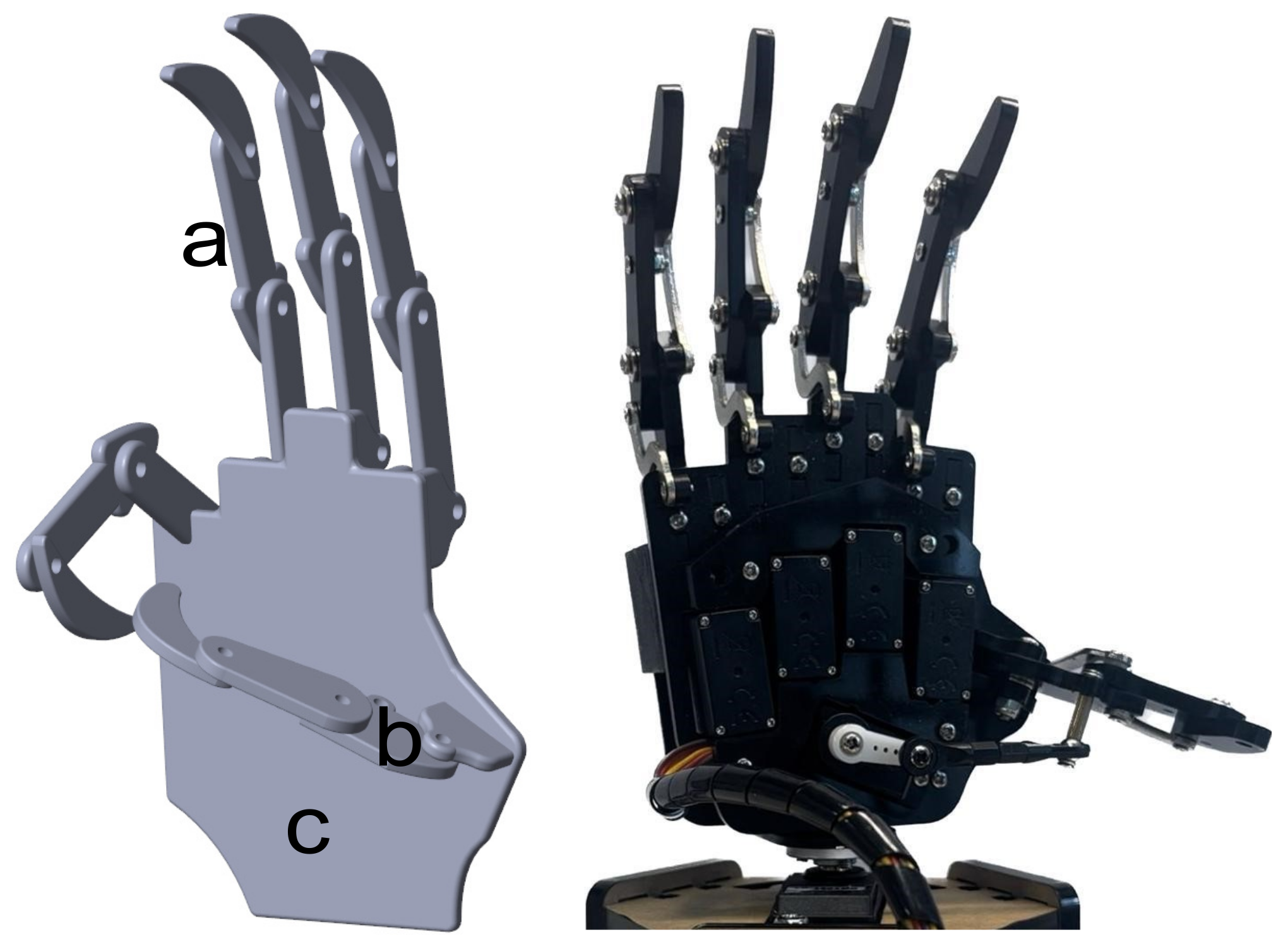
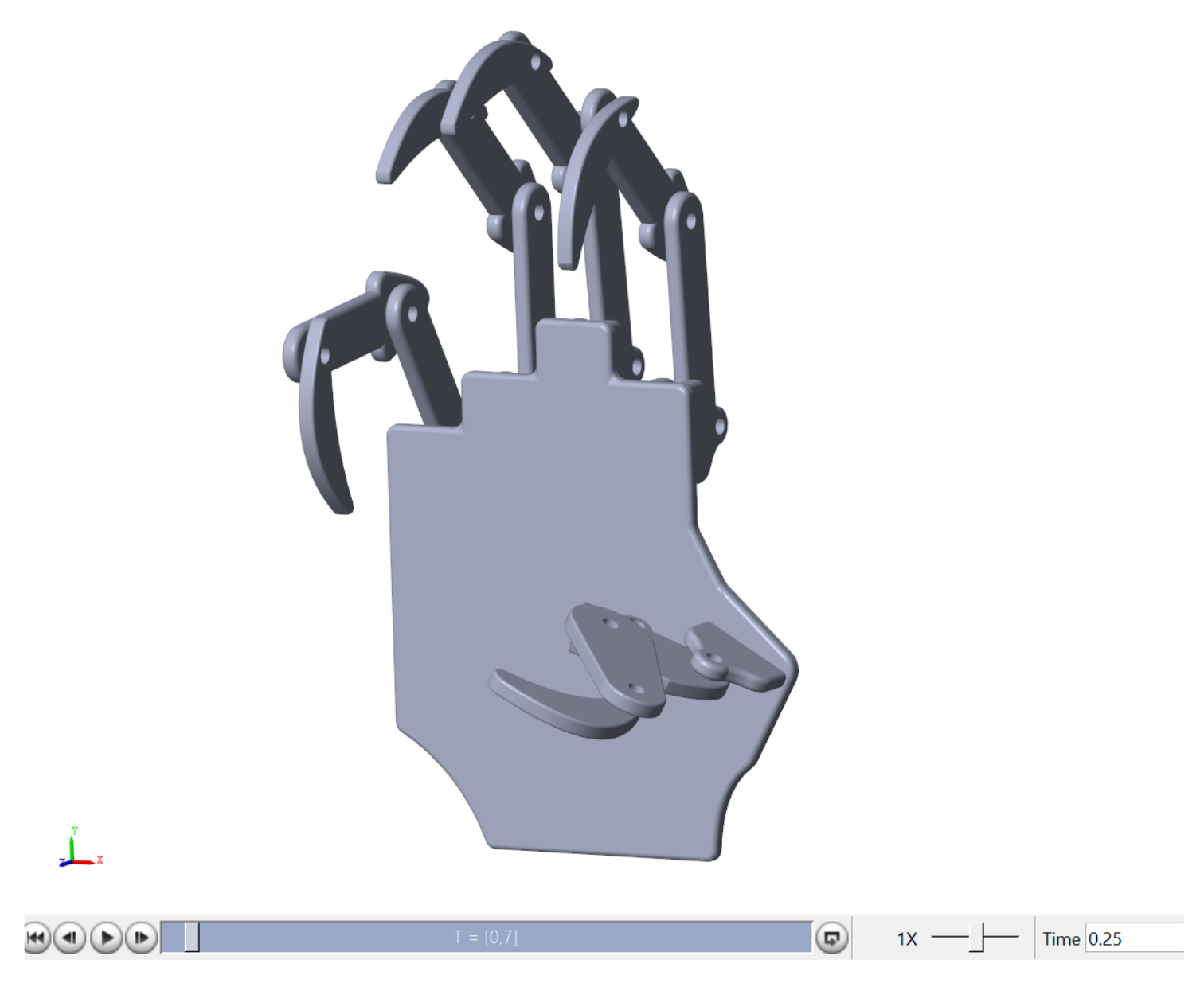
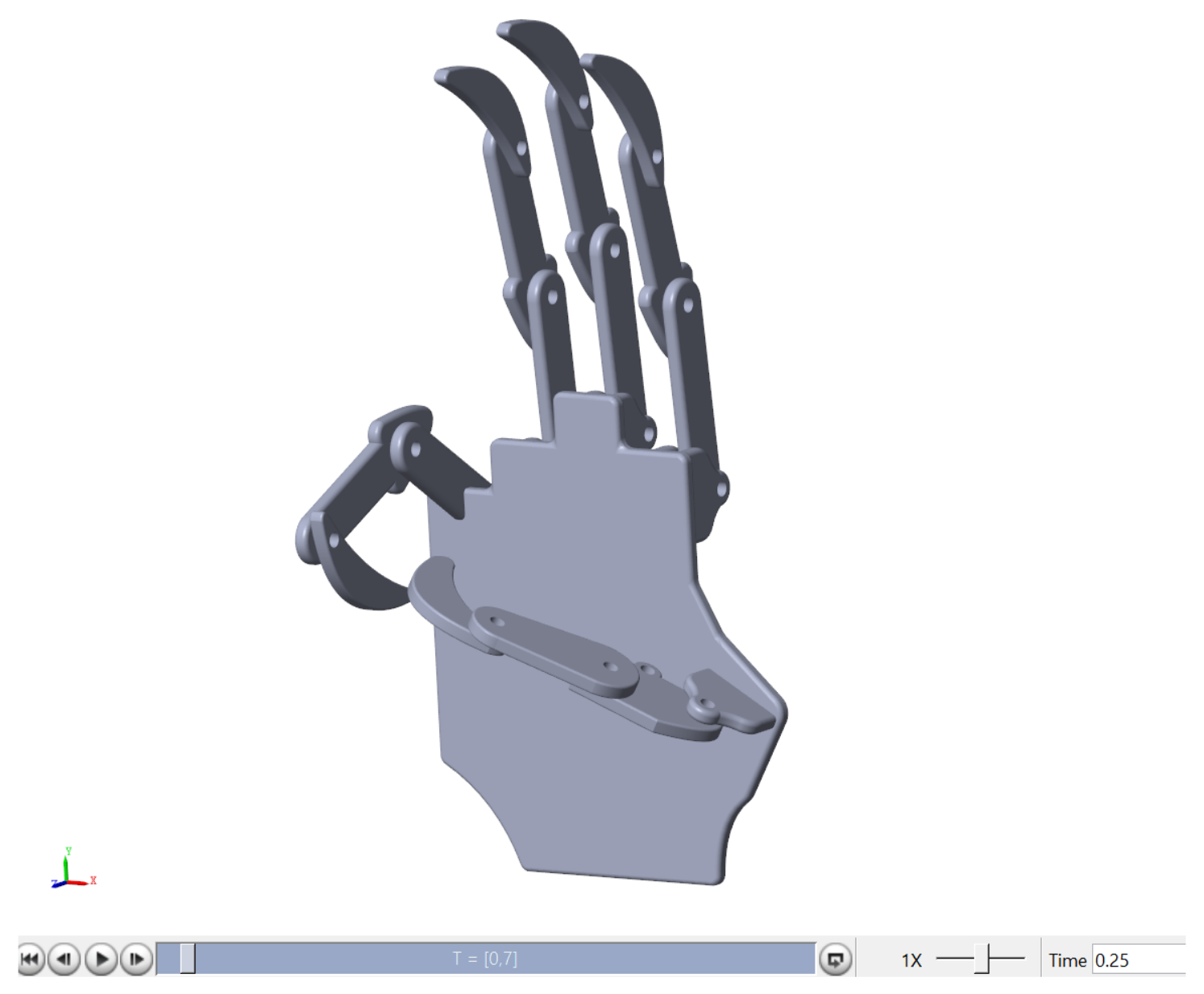
A simulated version of the hand prosthesis prototype was considered to evaluate the relation between the classifier and the controlled motion enforced by the simulated FES. The mechanical design followed the dimensions of the UHand 2.0 prosthesis, an open-source bionic somatosensory robot compatible with diverse digital processing boards. The design is shown on the right side of Figure 3. The dimensions were assessed manually using a vernier caliper. In order to simplify the design and measurement process for the hand, it was broken down into distinct components, including the finger (Figure 3a), thumb (Figure 3b), and palm (Figure 3c). The finger and thumb sections were further divided into three phalanges each.

This design was created in Solidworks^TM (2022) and then exported to Matlab through Simmechanics^TM (2022b), which transferred the model to Simulink/Matlab^TM (2022a) to perform a virtual evaluation of the designed hand prototype.

2.4. Automatic Control for the Prosthetic Hand

Once the design of the prosthetic hand was implemented in Simulink^TM, an automatic controller was proposed to reduce the deviation of the angular position at each articulation with respect to the desired trajectory. Two different controllers were compared: the first was a traditional Proportional–Integral–Derivative (PID) controller, and the second was a Proportional–Derivative (PD) controller complemented with a Super-Twisting sliding-mode algorithm, which estimated the tracking error derivative online to avoid the imprecision and inaccuracy introduced by the usual numerical differentiation methods such as Euler and its derivative methods.

2.4.1. Proportional, Integrative, and Derivative Controller (PID)

The selected PID controller introduced the output signal depending on the tracking error for each of the articulations considered in the prosthetic hand. Simulink has its own PID controller, which is based on Equation (13).

$$u^k\left(s\right)=\left(K_P^k+\frac{K_i^k}{s}+\frac{K_d^{k}s}{T_{f}s+1}\right)U^k\left(s\right)$$

(13)

In Equation (13): $K_P$ represents the proportional gain, $K_i$ is the integrative gain, $K_d$ corresponds to the derivative gain, and $T_f$ is the time of a first-order derivative filter. The input of the controller ($U^k\left(s\right)$) is the k-th input in the respective joint of the proposed hand device. This study considered a class of distributed PID form, which simplified its application but could create a kind of interdependence that introduced transient vibrations in the joint’s motion. Moreover, the calculus of derivatives based on the traditional Euler approximation of derivatives can significantly decrease controller performance related to the tracking quality. Hence, Super-Twisting was introduced, a class of second-order sliding-mode algorithms that can work as robust and exact differentiators or even as non-linear Proportional–Integral controllers.

2.4.2. Proportional and Derivative (PD) and Super-Twisting Controller

The controller, aided by the sliding-mode algorithm, comprised two sections: a PD controller complemented by a Super-Twisting controller. The former is known for its speed control and ability to reduce oscillations. This controller was supplemented with Super-Twisting due to its efficiency in handling disturbances.

In the PD controller, the original trajectory signal was subtracted from the trajectory input of the joint and then amplified by a proportional gain ($K_p$). On the other hand, the trajectory signal was derived, and the velocity of the revolution was subtracted and also amplified by a derivative gain ($K_d$) (8). Both results were added and exported to the original diagram to be the hand torque. The proposed controller u is defined as follows:

$$u\left(t\right)=K_{p}e\left(t\right)+K_d\frac{d}{dt}e\left(t\right)+u_a\left(s\left(t\right)\right)$$

(14)

The Super-Twisting output ($u_a$) is defined by Equation (14), where $e\left(t\right)$ is the tracking error between the reference and the joint signal of the simulated hand prosthesis. The Super-Twisting controller $u_a$ is defined by the following equation:

$$u_a\left(s\right)=-K_1·{\left|s\right|}^2·sign\left(s\right)+v$$

(15)

Here, $K_1$ represents the first gain, which multiplies the sliding surface ($s\in \mathbb{R}$), defined as the combination of the tracking error and its derivative, that is $s=\frac{d}{dt}e\left(t\right)+\Omega e\left(t\right)$, where $\Omega$ is a positive constant. Then, the evolution (v) is described as follows:

$$\dot{v}=-K_{2}sign\left(s\right)$$

(16)

The second gain ($K_2$) was obtained to increase the efficiency of the controller, measured in terms of the tracking error quality.

2.5. FES Design Based on Digital Arbitrary Signal Generator

Although FES has been studied for several years, the signal’s amplitude is still ambiguous, especially depending on the level of the patient’s motion, which could not be complete due to the sickness condition [15,30,31,32]. We considered a fundamental signal proposed as a reference signal satisfying a biphasic shape with a sawtooth shape of 30 Hz and a pulse width of 100 $\mathsf{\mu }$s [15,30,31,32]. At the same time, the trajectories of the simulated hand were obtained and used as the trajectory of reference.

Since FES must work only if the patient cannot complete the required motion, it was necessary to emulate such conditions, leading to what we refer to as sick patient motion or SPM. To obtain the SPM, the gain of the proportional part of either of the chosen controllers for the hand’s prosthesis was reduced ($K_{sick}$) to 10% of the gain ($K_{reference}$) used when the hand could complete the requested motion, or HPM. Then, the FES’ oriented error ${\Delta }_{FES}$ was calculated using the reference and sick movement coordinates for each movement:

$${\Delta }_{FES}=HPM-FES$$

(17)

Here, the amplitude of FES satisfies $SPM\le FES\le HPM$. The proportional electrostimulation signal corresponding to the error obtained previously (17) was proposed to satisfy a linear form (Equation (18)) with respect to the $i-\mathrm{th}$ component of vector ${\Delta }_{FES}$, namely ${\Delta }_{FES,i}$. The slope and ordinate variables $m_i$ and $b_i$ were determined with the following equation, where $S_{Max,i}$ is the maximum value of the error and $S_{Min,i}$ is the minimum error.

$$Y_i=m{\Delta }_{FES,i}+b_i,Y_i\in [V_{Min,i},V_{Max,i}],{\Delta }_{FES,i}\in [S_{Min,i},S_{Max,i}]$$

(18)

Notice that this model could be more complex. Nevertheless, for this study, such an invertible model was sufficient. Notice that this model was used as an artificial data generator for training the LSTM to estimate the signal the FES must apply. Hence, the error ${\Delta }_{FES,i}$ became the input of the designed LSTM. We considered M numerical artificial data generation experiments producing a set of ${\Delta }_{FES}^j$, $j\in [1,M]$ and their corresponding output vectors $Y^j$. A subset of 80%. of the pairs ${\Delta }_{FES}^j,Y^j$ was used for training, and the remaining 20% were used for testing. After that, a regression layer was formed by 15 classes (1 class per finger joint), and 100 hidden units were created. The output of the LSTM, the stimulation signal, was converted into a pulse-width modulation (PWM) with a maximum number of variable steps of 1000 and a voltage amplitude of 2 V. This signal generated by Matlab was exported to a 16-bit digital processing board through an RS-232 protocol-based communication port.

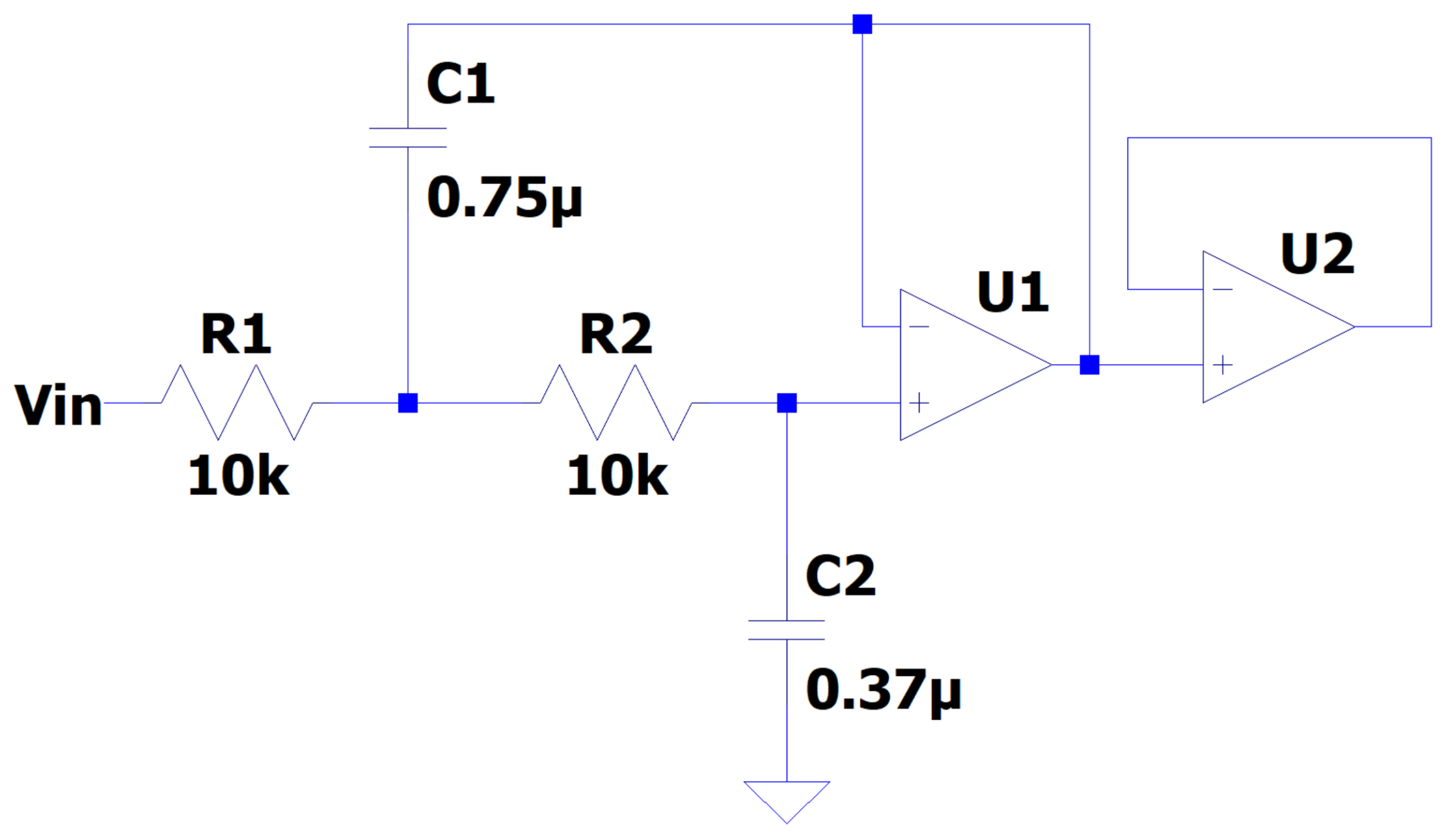
The PWM signal was transformed back to its original shape through a Butterworth low-pass filter of the second order (Figure 4). This signal could be applied directly to the human hand muscles or to the considered prosthesis to perform the complemented motion. The filter was designed with a resistance of 10 k$\Omega$ and using Equation (19), where C is the capacitor, f is the frequency, and R is the resistance.

$$C=\frac{1}{2\pi fR}$$

(19)

The literature average cutoff frequency (30 Hz) was employed. The values of the capacitors were calculated as $C_1=1.414C$ and $C_2=0.7071C$.

2.5.1. Strategy to Assess the FES on the Simulated Hand

Noticing that the simulated hand prosthesis was not a direct model that represented the relationship between the FES electrical signal and the biomechanical motion, this study considered an alternative to express the connection between them.

This strategy used the evolution of error (${\Delta }_{FES}$) between the reference or literature stimulation signal $HP{M}^j$ and the output of the second LSTM $FE{S}^j$ for each of the iterations j. To consider the deviation between the healthy and the LSTM signals, the mean error $H_i$ for each joint of the simulated human hand was obtained using the following set of expressions:

$$H_i=\sum _{j=1}^N{\left({\Delta }_{FES,i}^j\right)}^2$$

(20)

In addition, the difference between the individual gains for the $i-\mathrm{th}$ joint $KHPM,i$ and $K_{SPM,i}$ was obtained, where the symbol $K_{HPM}^i$ refers to the controller gain considered for the simulation of the healthy patient, while $K_{SPM},i$ is the gain used for processing the simulation when the sick patient was evaluated. This differential, $a_i=K_{HPM,i}-K_{SPM,i}$, represents how much gain the sick simulated hand needed to be adjusted according to the following expression:

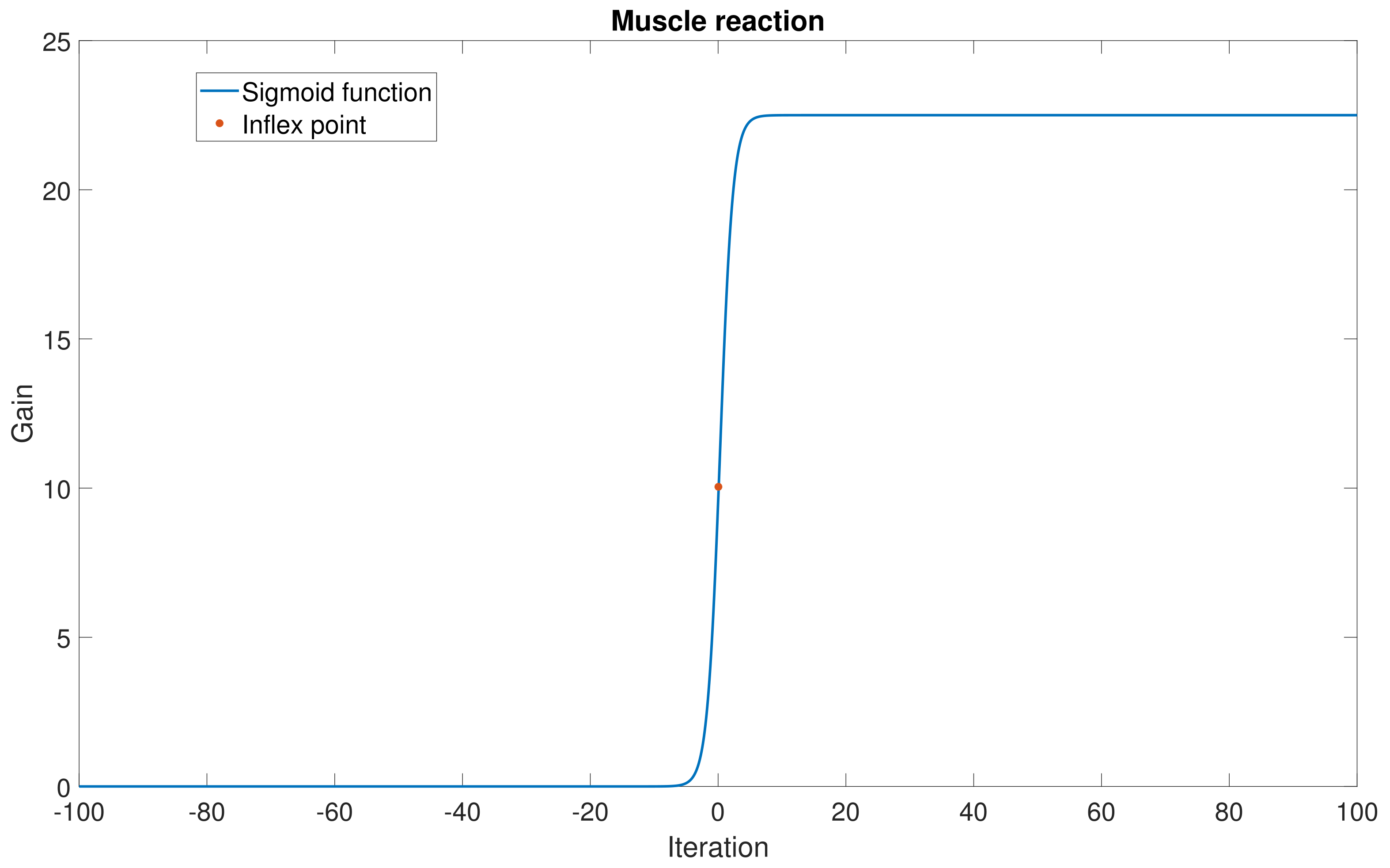
Given the electrophysiological evidence that a sarcomere presents a saturated reaction to the electrical stimulus (justified by the restricted motion performed by the muscle despite the amplitude of the electrical stimulation). One manner in which to represent such a saturated condition is using a sigmoid function evaluated on the estimation of $H_i$, as follows:

$$\begin{array}{c}\Delta K_{p,i}={\displaystyle \frac{a_i}{1+e^{(-c_i(H_i-Nv{s}_i^{inf}))}}}\end{array}$$

(21)

This function has an inflex point proportional to the mean error ($Nv{s}_i^{Inf}=\frac{H_i}{2}$) and the constants $b_i$ and $c_i$ to control its shape. Then, it was demonstrated that Equation (21) obtained the modification to the proportional control gain $\Delta K_{p,i}$, and it was added to correct the proportional gain of the simulated hand. Hence, depending on the estimation error of the LSTM, the gains were adjusted, yielding a closer condition to a healthy or sick patient. This numerical methodology substituted for the necessity of estimating the electro-bio-mechanical model of the simulated hand. Notice that the gain modification strategy could also be applied to the other gains in the controllers considered in this study.

2.5.2. Strategy to Assess the FES on the Prototype of the Prosthesis Hand

In a similar manner to the one considered in the previous subsection, an alternative strategy was used to evaluate the effectiveness of the LSTM classifier for EMG and the associated FES information when the generated signal was applied to the prototype of the prosthetic hand. A series of trajectories was computed to facilitate motion in response to a compromised hand condition. Upon receiving the pre-established FES, the hand had to execute movements in alignment with the reference trajectories, provided that the stimulation signal aligned with the accurately classified EMG signal. However, as the classifier for EMG signals had an accuracy of 91.87%, it could produce imprecise classification. Hence, the strategy considered the assessment of the stimulation error, defined as

$$S_f=S_r-S_c$$

(22)

The vector variable $S_f$ represents the stimulation error corresponding to the generation of the FES signal for all the articulations in the prototype, $S_r$ is the vector of the intended movement stimulation signal, and the vector $S_c$ is the stimulation signal estimated with the application of the LSTM classifier. Notice that this deviation can be calculated considering the validation strategy proposed in this study.

In view of the operative range for the UHand being $[F_{min},F_{max}]$ for all the articulations, there was a need to adjust the value of all components in $S_f$ to match this admissible range. Such an adjustment implies that if the i-th component of $S_{f,i}$ is zero, then an action corresponding to $F_{min}$ must be performed on the prototype, while if this component reaches its maximum value $S_{f,i}^M$, then it should produce the maximum action in the hand, that is $F_{max}$. Given the operative conditions for the hand, including its own internal electronic control, the following relationship can be used:

$${\displaystyle \frac{F_i-F_{min}}{F_{max}-F_{min}}}={\displaystyle \frac{S_{f,i}}{S_{f,i}^M}}$$

(23)

Notice that this expression permits the estimation of the value of $F_i$, which is the command that must be sent to the UHand. Furthermore, $\lambda$ defines the relationship between the hand’s voltage ($V_{UHand}=12$ V for this particular prototype) and the stimulation signal voltage ($V_{Stim}=2$ V), that is, $\lambda =\frac{V_{Stim}}{V_{UHand}}$. After this generation scheme, the new trajectories that must be injected into the physical hand are defined by

$$Uhan{d}_{tr,i}=Healt{y}_{tr,i}-\lambda \ast F_i$$

(24)

Here, $Uhan{d}_{tr,i}$ is the instruction used to stimulate the $i-\mathrm{th}$ articulation of the hand, while $Healt{y}_{tr,i}$ are the trajectories corresponding to the case when a healthy patient is moving the hand. Notice that this strategy induces the requested motion on all articulations in the hand if the classifier based on the LSTM operates effectively. Otherwise, the prototype moves to a different position, confirming this strategy’s applicability.

2.6. Validation

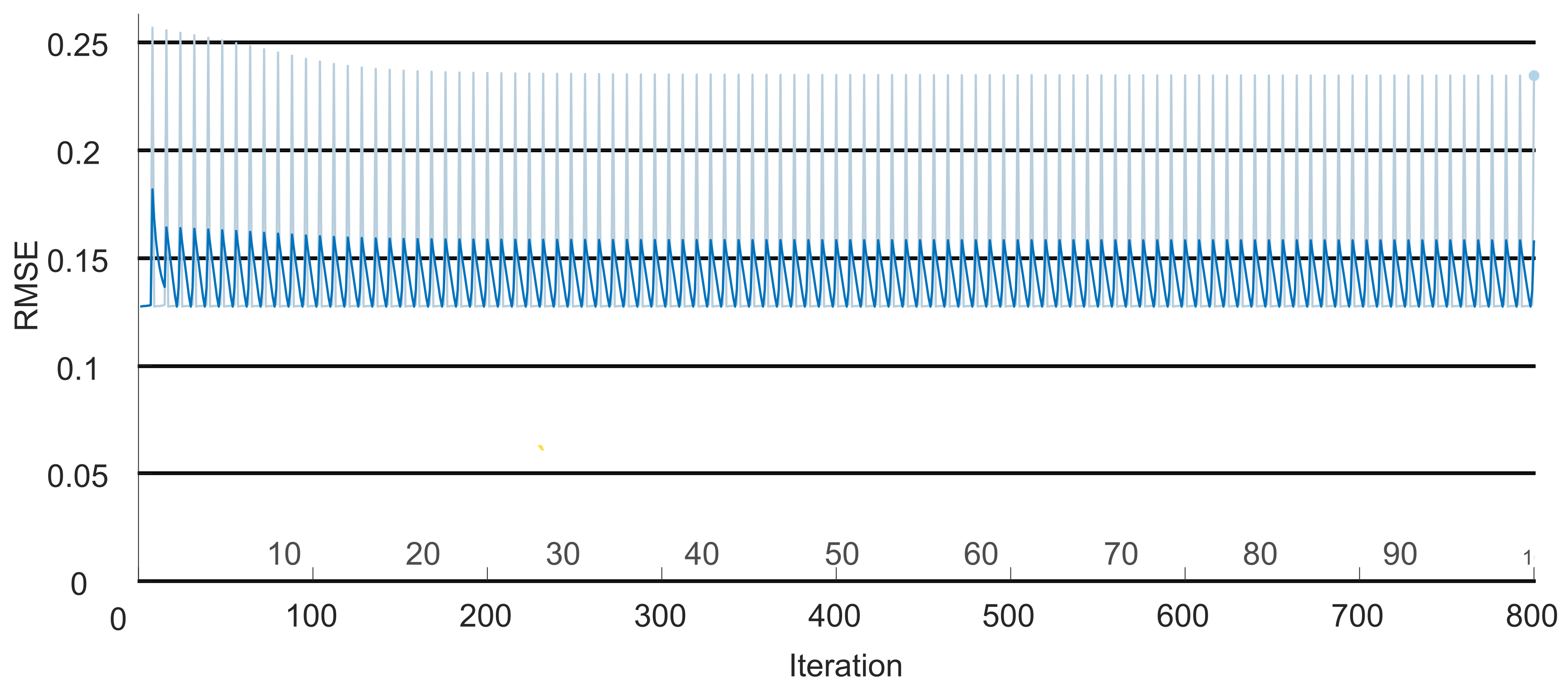
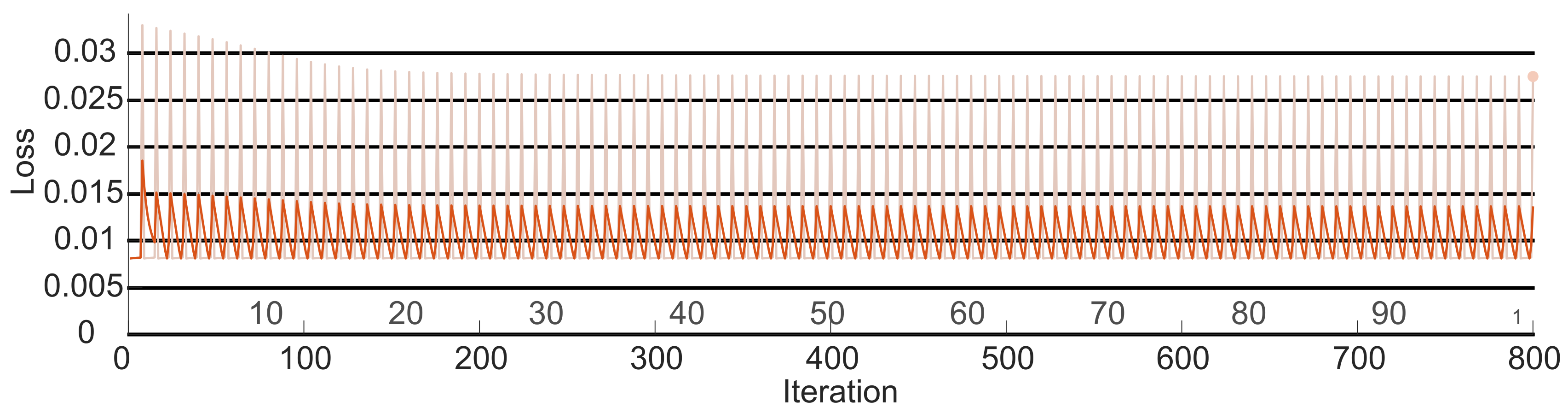
To prove the efficiency of the regression LSTM, a Pareto analysis was carried out. The study proposed by [33] defines a Pareto diagram as a graph where various data classifications are organized in descending order to qualify their behavior. This method states that the error must be below 0.02. To validate that the identification error for the estimated FES signal was below that value, the loss of the signal ($SignalLoss$) at the output of the LSTM ($RMSE$) was obtained as follows:

$$E_1^j={\left(RMS{E}^j-SignalLos{s}^j\right)}^2$$

(25)

Here, j is the iteration corresponding to the signal produced by the FES system. Then, the value for each iteration was determined with the following equation: $E_2=N^{-1}{\sum }_{j=1}^N{E}_1^j$.

3. Results

The results are presented in terms of the classifiers results, the controller’s effectiveness, and the FES operation for both the simulation and experimental evaluation in Simulink^TM and with the prototype of the human hand.

3.1. Classifiers

3.1.1. LSTM

As shown in Figure 5, the first classification task based on LSTM presented, during its first 300 iterations, an exponential accuracy growth from 0 to almost 100 percent. Overall, it achieved a total accuracy of 91.87%, meaning that from the total database of 1200 signals, approximately 1102 were classified correctly. This result is competitive with the studies considered as references herein.

A comparison of the true class and the predicted class was estimated through a confusion matrix (Figure 6). This matrix confirmed that almost all individual motions of the hand’s fingers were classified effectively. It was arduous for the LSTM to differentiate between the individual movement of the annular and index fingers. On the other hand, the neural network did not present any problems classifying combination movements. All these results seem to justify the application of the LSTM with the proposed topology to handle the selection of EMG signals in order to define the expected motion in the hand. From these results, this study evaluated the proposed controllers when regulating the operation of both the simulated and the experimental articulated hand.

3.1.2. Least-Squares Boosting

K-fold cross-validation was employed to test the least-squares boosting performance. Figure 7 compares true and predicted classes. From left to right, the classes are: hand closed (HC), index finger (TI), thumb and little finger (TL), thumb and middle finger (TM), and thumb and ring finger (TR).

This method achieved an overall accuracy of 84.7%. However, it was only effective with the combination of movements. The thumb and ring finger (TR) presented the greatest accuracy of the five measured classes. This result demotivated the application of the boosting algorithm, confirming the applicability of LSTM as an efficient classifier for EMG signals using the evaluated features proposed in this study. Moreover, the confusion matrix analysis confirmed that some particular classes were classified accurately below the permissible values for the class of application considered in this study.

3.2. Evaluation of the Proposed Controllers for the Hand’s Articulations

As mentioned, three different controllers were compared (PID, PD, and POD aided with Super-Twisting). The PID controller implemented in Simulink was used as a benchmark for evaluating the suggested controllers, considering the quality indicators such as motion oscillations and tracking accuracy. Figure 8 shows that during the first 0.5 s, several oscillations on the performed motion for all the articulations (evaluated through the norm of the vector corresponding to the tracking error) appeared with a magnitude beyond the permissible value for the automatic design of FES signals. Even though it achieved hand control after 0.7 s (observed as the convergence of the norm of the tracking error to a region with a maximum magnitude of $1\times {10}^{-4}$), those oscillations could be interpreted as erratic hand movements that could induce the non-controlled stimulation of the hand by the electrical activity. Notice that we selected to present the aggregated evaluation of the controller quality through the norm of the tracking error considering the number of articulations. Nevertheless, the behavior observed here was replicated at each articulation of the hand (simulated or experimental).

The Proportional (red), Derivative (blue), Proportional–Derivative (orange), and control aided with Super-Twisting (green) were compared among themselves and to the benchmark. As shown in Figure 9, neither the Proportional nor the Derivative were competitive because of their convergence time (0.235 s) and the oscillation presented at the beginning of the simulation concerning the evaluation of the norm of the tracking error. However, when both of them worked together, their oscillations were reduced five times, and at the same time, they converged faster (0.076 s). This result coincides with the expected result for a class of state feedback control design, but it was not able to reject the effect of some perturbations or non-modeled sections, as illustrated in the controller comparison. Notice here the oscillations observed in the steady state and the slower convergence, at least when compared to the mixed strategy that used the Super-Twisting algorithm to complement the state feedback form. Such a condition confirms the results proposed by some authors presenting this class of non-linear PID controller.

Although the PD controller displayed oscillations with lower magnitude, the inclusion of the Super-Twisting method exhibited an error amplitude three times smaller at the initial phase of the simulation than the PD outcome (Figure 10). When both controllers worked together, they reduced the initial spike and the oscillation that entails a natural hand movement. The non-linear PID form appears to be a reliable control form for Lagrangian systems such as the prototype (virtual and experimental) considered in this study.

When the results of the PD and Super-Twisting method are compared with the tracking outcomes of the PID controller, the effective tracking of the reference trajectories, the oscillations with smaller amplitudes, and the faster convergence motivate the application of the suggested controller. Although both the PID controller and the PD with Super-Twisting method controlled the hand movement, the latter converged faster and with less error amplitude, manifesting as a natural and fine movement when considering both the observational analysis of the virtual representation of the hand and the motions exhibited by the experimental device.

3.3. FES System Driven by the LSTM Classifier

The output of the second recurrent neural network adjusted the stimulation signal to compensate for the trajectory errors, as expected for a closed-loop FES design. The signals were designed to stimulate the 15 joints of the hand, one movement at a time. Figure 11 shows one of the signals with an amplitude adapted to the patient’s necessities. The amplitude of this signal was regulated according to the detected motion depending on the EMG signal that the proposed LSTM classified.

The signal loss (Figure 12) was subtracted from the output signal to obtain the Pareto value. This estimation permitted the validation of the application of the LSTM over the entire set of EMG signals and the related expected motion. Such analysis achieved a holistic assessment of the LSTM’s performance as a classifier and the related controlled motion for the considered prototypes of hand prostheses under simulation and experimental conditions.

The stimulation signal transformed into a PWM form with a gain of 1000, a maximum charge of 10, 2 V of voltage amplitude, and two charge compensations appears in Figure 13. After that, the signal was exported physically through a digital processing board (Arduino), and it was converted back to its original shape through the low-pass filter that was designed previously. This filter reshaped the signal with a cutoff frequency of 30 Hz, obtaining the required signal to stimulate the hands, considering the action of the LSTM classifier and the effective regulation of the reference trajectories.

Considering the FES Equation (21), the modification of the proportional gain $\Delta K_p$ needed by prototype of the hand prosthesis to enforce the articulation motion according to the reference trajectories is shown in Figure 14. After $\Delta K_{p,i}$ was added to the gain that defined the motion of a sick patient (using the simulation strategy), the simulated hand reproduced the muscle reaction as the reference hand would, illustrating the application of the proposed assessment strategy.

3.4. Muscle Reaction to Stimulation

Figure 15 and Figure 16 show the results of the simulation corresponding to a sick patient who needed the application of the FES and the corrected motion considering the application of the corrected gain evaluated at the same time (0.25 s). In the simulation corresponding to the sick patient, the movements were slow and erratic, while in the second case, with the application of the FES signal, the movements were executed naturally, without delays, and showing oscillation with a small amplitude. These numerical results depict the suggested strategy’s benefits, which allowed us to assess the operation of the entire design considered in this study.

3.5. Movement Results

Once the UHand 2.0 is correctly connected, it receives the electrostimulation coordinates calculated previously. Once it receives the coordinates, the hand can replicate the ten different movements shown in Figure 17 (https://youtube.com/shorts/mjPnZ26WkN4 (accessed on 13 December 2023)) and Figure 18. With the aim of evidencing the controlled motion of the prosthesis prototype, this study produced the following videographic outcome, located at https://youtu.be/M5alalNNf7A (accessed on 13 December 2023), which shows how the prototype was mobilized with the implementation of the proposed controller, the assessment strategy, and the corresponding articulation motions.

4. Discussion

EFS has proven to be a valuable tool in the rehabilitation of patients with motor disabilities. Despite its well-established advantages and a history of use since the 1950s, its effectiveness is still contingent upon patient responses (including movement, pain, or relief) and the expertise of medical specialists.

Numerous studies have delved into the application of this technology for rehabilitation devices. However, there remains a gap in the exploration of critical factors, such as regulating the speed of desired movements and the force applied by muscles during action. To harness this technology for such devices, it is essential to consider key elements of the motor system, including the intended movement, the muscles involved, the type of stimulation signal, and the signal amplitude.

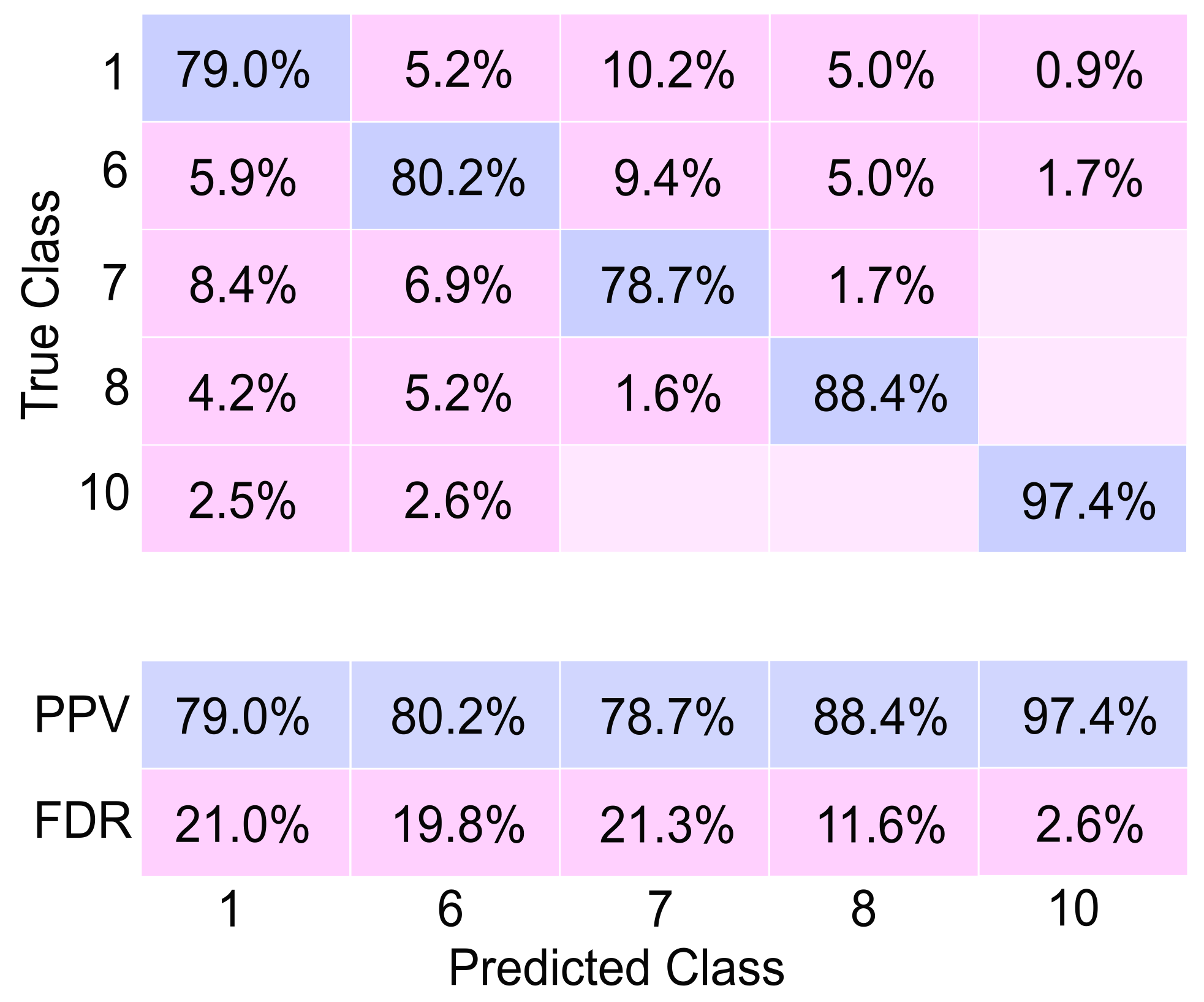
In this study, these parameters were considered to develop a system capable of simulating a human hand with a specific level of motor disability and providing appropriate stimulation for the system to replicate the movements of a healthy hand. A database of hand electromyography (EMG) signals was utilized to classify the user’s intended movements. In this phase, the effectiveness of the EMG signal classifier highlighted in this research represents a significant advancement compared to several previous studies. The achieved efficiency of 91.87% surpasses the performance of the classifiers presented in

Table 1. Comparison of classifiers.

Author	Method	Movement	Accuracy
González Gavilánez [18]	ANNs	Fist, finger stretch, inward move, outward move, and a double tap.	88.3%
Gandolla [20]	ANNs	Pinching, grasping, and fist.	$76\pm 14\%$
Sattar [19]	ANNs	Pronation, supination, and elbow flexion and extension.	94%
Espinoza [21]	Extended Associative Memories (EAMs)	Cylindrical grasp, tip grasp, hook grasp, open hand, palmar grasp, spherical grasp, lateral grasp, and fist.	95.83%
Suppiah [22]	LSTM	Major hand movements.	90.4%

. While the result might seem slightly lower than the classification reported by [19] (94%), a deeper analysis reveals crucial distinctions.

The study by [19] achieved a higher classification accuracy of 94% by focusing on robust movements involving coordinated finger actions. In contrast, the classifier presented in this work showcases a unique capability: the analysis of combined and individual finger movements. Sattar et al. [19] concentrated on assessing strong, combined finger movements, which allowed for a higher accuracy due to the stronger input signals of their analysis. On the other hand, the classifier introduced in this research offers a broader scope, accommodating not only coordinated movements but also individual finger actions. This broader analysis widens the applicability and versatility of the classifier, enabling it to recognize and classify a more comprehensive range of movements.

Therefore, while the accuracy of the classifier might appear marginally lower when compared directly to [19], its ability to analyze and categorize both combined and individual finger movements represents promise for applications in rehabilitation, as it accommodates a broader spectrum of hand movements.

Up to this point, it was possible to emulate the hand movement on the Uhand by applying PD and Super-Twisting controllers in combination with the classifier. This strategy permits the evaluation of the proposed classifier on prototypes of human hands in virtual and physical forms of this device. Moreover, the selected strategies to validate the application of the emulated EFM seem to offer alternative options to evaluate more complex forms of our proposed classifier.

5. Conclusions

Analyzing the proposed methodology’s results, it can be concluded that they are favorable for personalizing FES. Firstly, the initial LSTM-type neural network achieved an efficiency of 91.87%, not only surpassing the average reported in the literature but also outperforming that reported for intricate movements, such as individual finger movements. Similarly, comparing the LSTM classifier and the assembly revealed consistent efficiency across all movements for the former. In contrast, the assembly reported an efficiency of 84.7% only for combined movements.

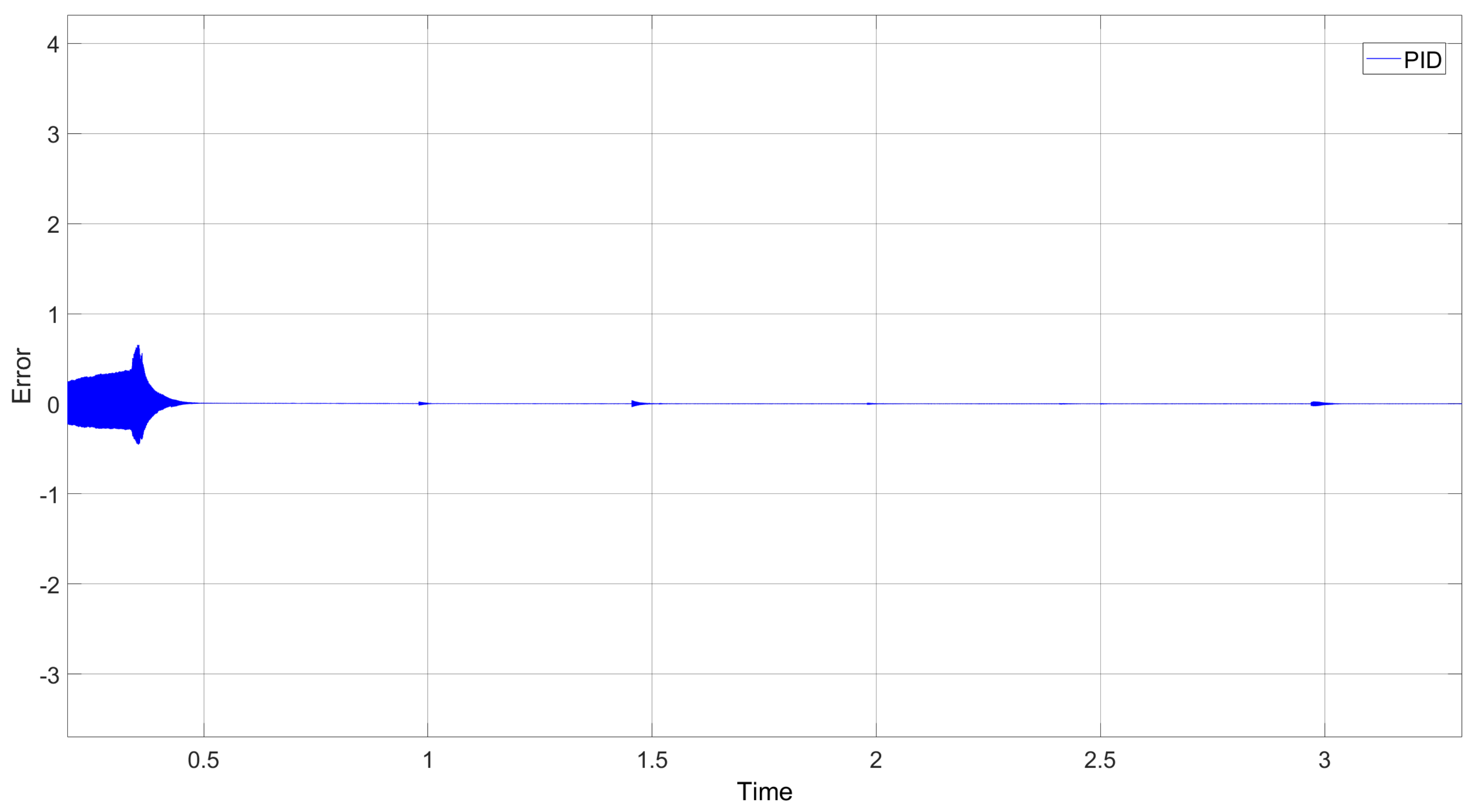
In assessing the proposed controllers, it is evident that the Proportional–Derivative (PD) controller excelled in managing the velocity component. When paired with the Super-Twisting controller, it converged toward zero more rapidly and with reduced amplitude oscillations. Consequently, the simulation of the human hand displayed fine and natural motion. Notably, the use of the PID controller provided by Simulink was dismissed due to its longer convergence period and abrupt oscillations, potentially leading to erratic movements despite ultimately reaching zero. Movements were evaluated after the execution of the movement class, and a precise controller was obtained. This study found that both the simulated and physical hands executed the ten movements in a manner consistent with natural human hand movements.

Based on the outcomes of the initial classification network, the trajectories corresponding to the reference motion were identified. Simultaneously, a model representing a diseased hand was devised by subtracting the previously determined reference coordinates. Using this error vector, the precise stimulation signal required for the individual to replicate the reference model’s movement was obtained. Subsequently, the neural network was assessed under the Pareto model, yielding an error of less than 0.02. This result ensures the efficiency of the signal provided by the second network.

Upon acquiring the stimulation signal, we simulated the responses of both the physical and simulated hands to the provided stimulus. During the simulation, it was observed that the simulated hand approximated the reference hand’s movement. While the movement was not a replica (given that it simulated a hand in rehabilitation), similar behavior was observed in the physical hand.

For future endeavors, a third neural network should be designed to offer feedback. This network would consider the individual’s initial movement, the reference movement, and the resultant movement following stimulation by the system. Its purpose would be to enhance patient safety, monitor real-time system movements, identify potential trajectory changes, and rectify them before they manifest.