Considerations on the Dynamics of Biofidelic Sensors in the Assessment of Human–Robot Impacts
Abstract
:1. Introduction
1.1. State of the Art
1.2. Aim of the Paper
2. Experimental Campaign on a Commercial Biofidelic Sensor
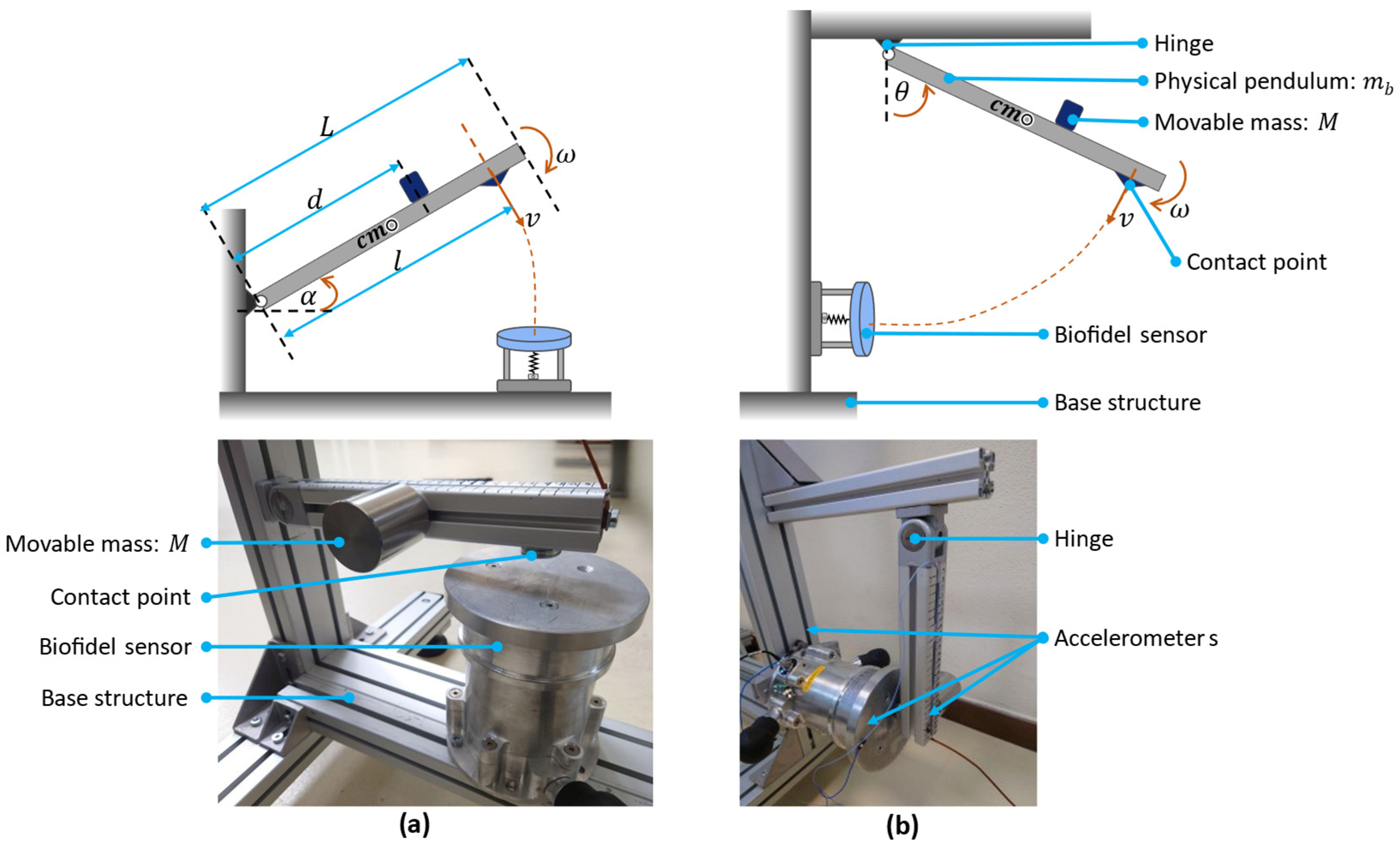
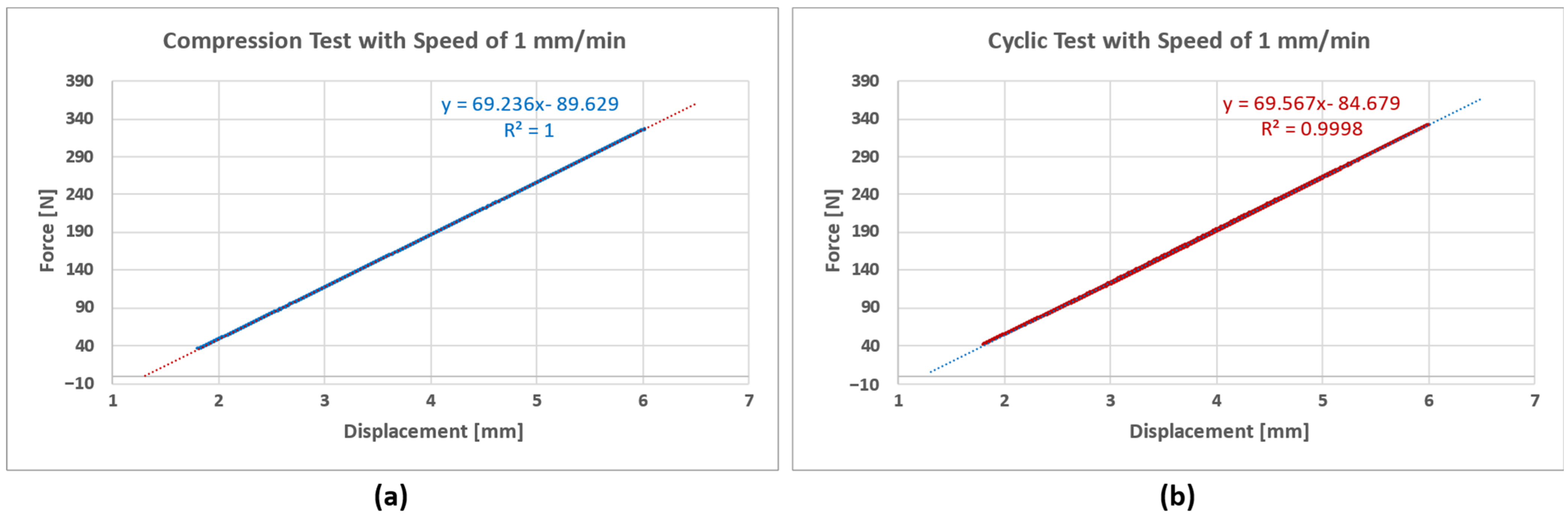
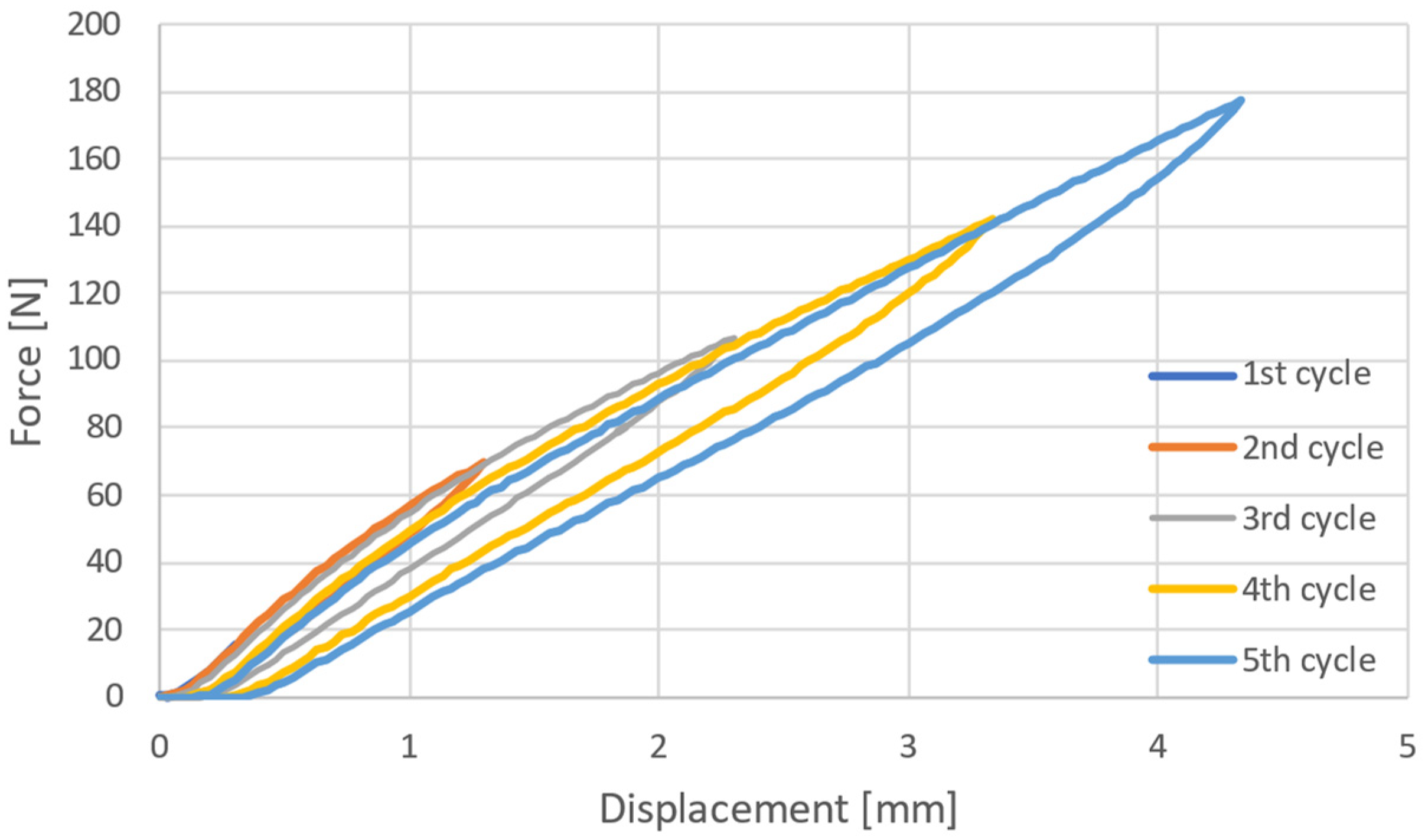
2.1. Setup and Tests
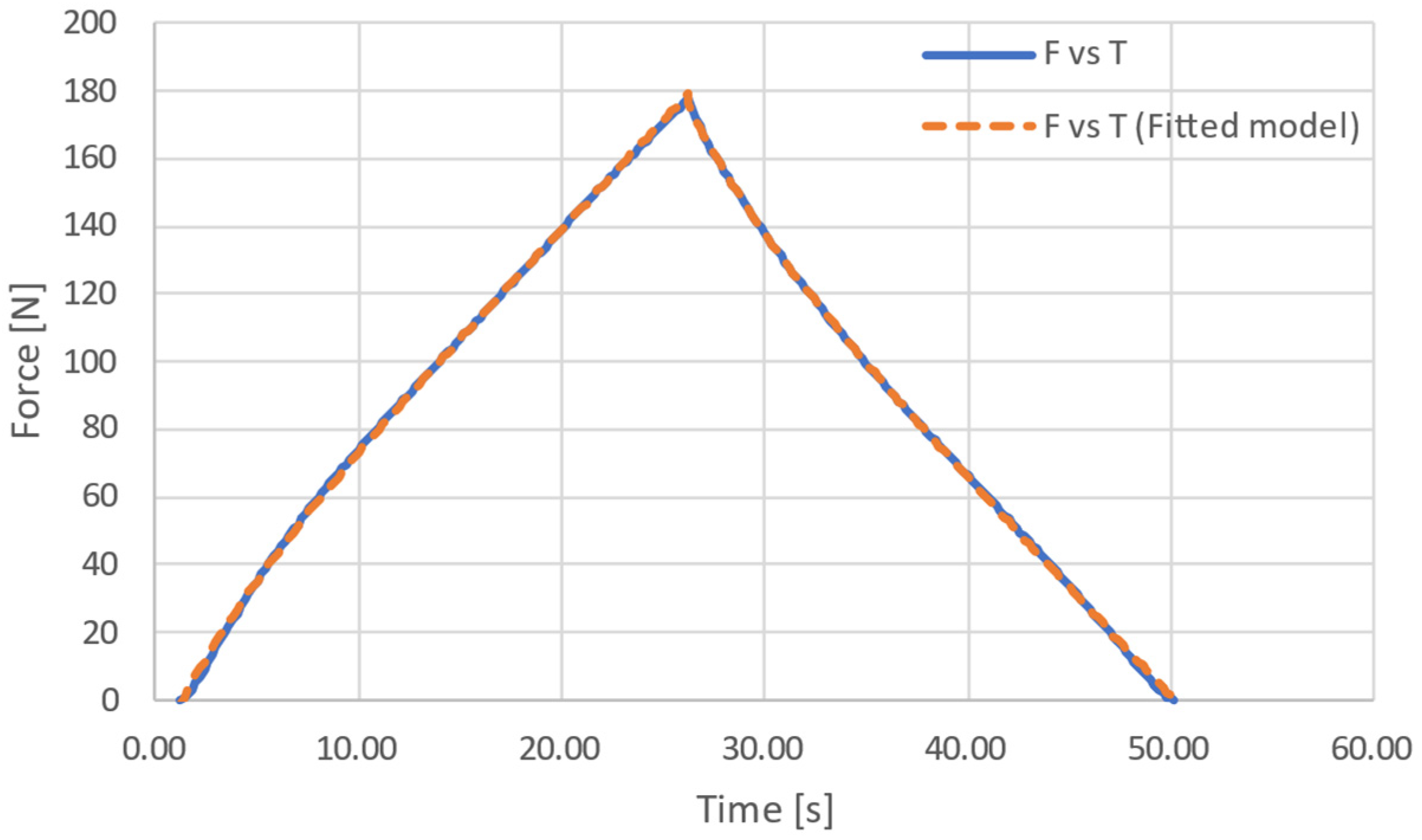
2.2. Mathematical Model
2.2.1. Vertical Configuration of the Force Sensor
2.2.2. Horizontal Configuration of the Force Sensor
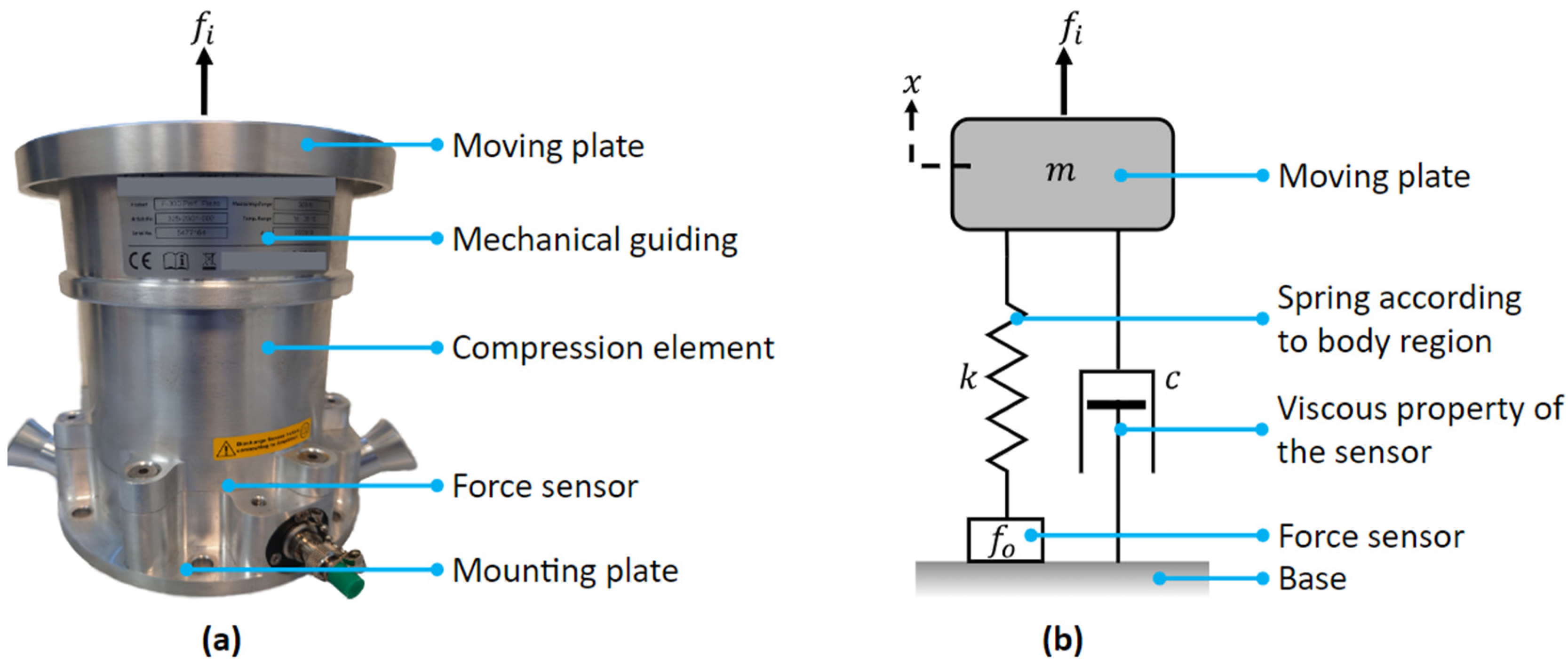
2.3. Dynamic Model of the Biofidelic Measuring Device
2.3.1. Dynamic Model of the Force Sensing Apparatus
- Mass of the moving plate (damping mass), m: includes the mechanical guiding parts of the sensor. It influences the system’s inertia and response to the impact force.
- Spring constant, k: represents the stiffness of the human body region that we aim to replicate with the biofidelic sensor.
- Damping constant, c: represents the sensor’s viscous behaviour generating internal energy dissipation.
- Displacement, x: the displacement of the contact surface typically measured from its rest position.
2.3.2. Dynamic Model of the Damping Material
2.3.3. Complete Model of the Biofidelic Force Measuring Device
3. Test Results and Discussion
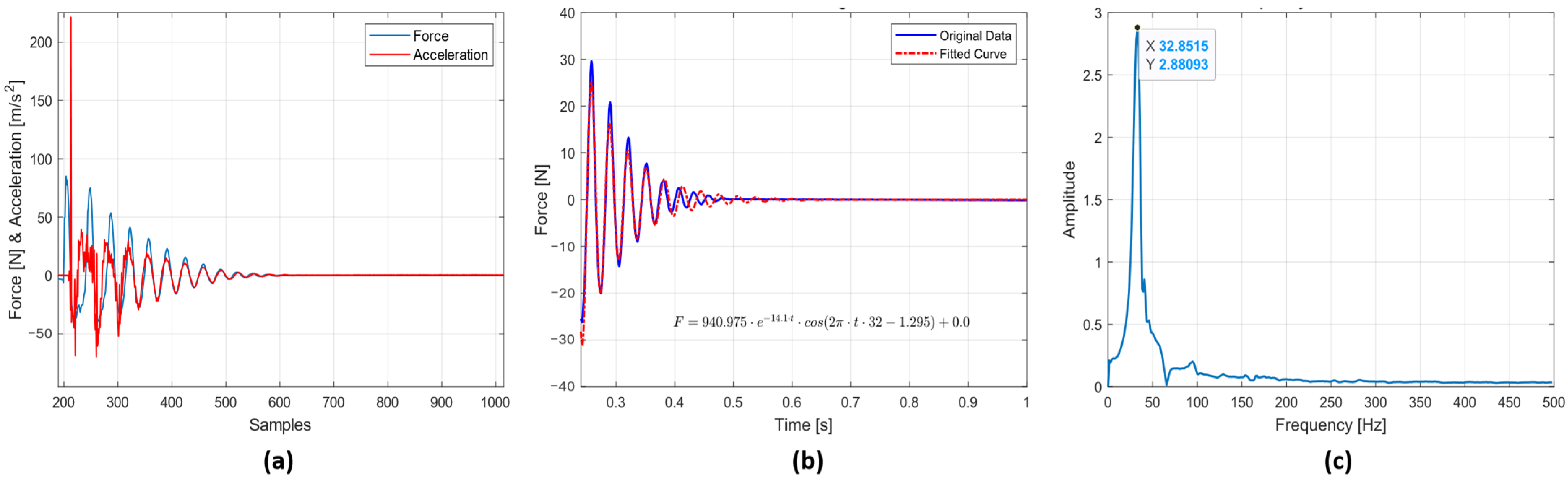
3.1. Parameter Estimation of the Force Sensor
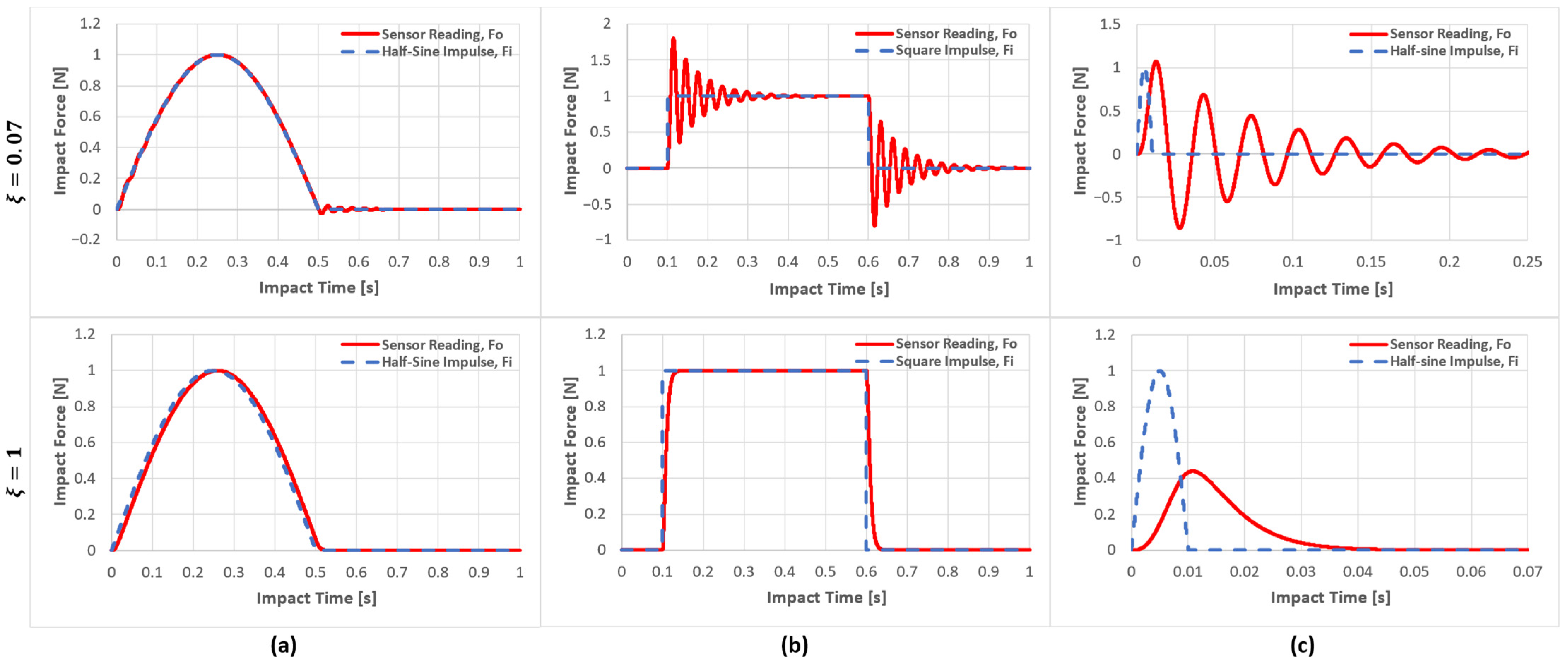
3.1.1. Analysing the Dynamic Behaviour of the Sensor
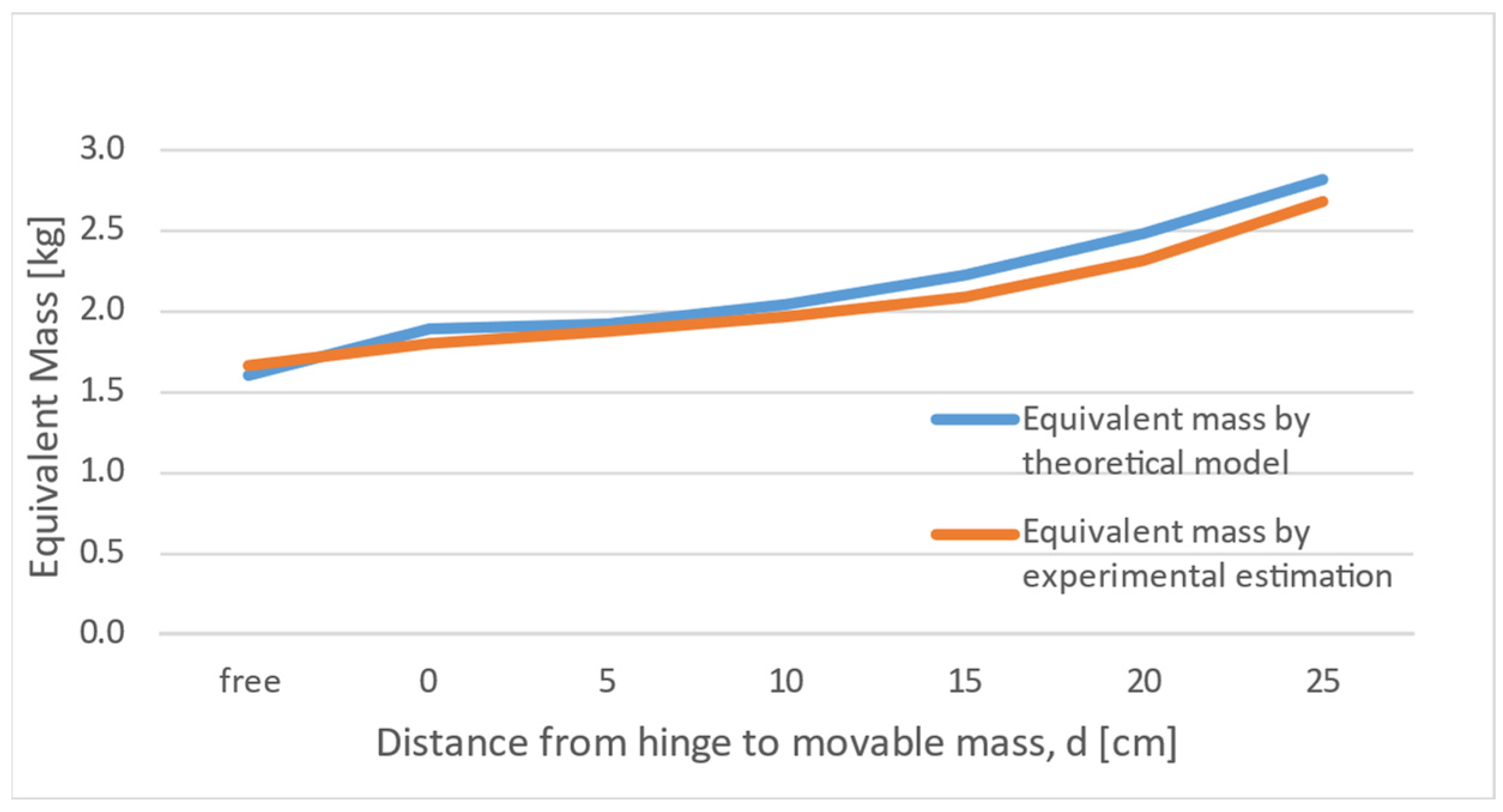
3.2. Physical Pendulum
3.3. Estimating the Parameters of the Damping Material
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
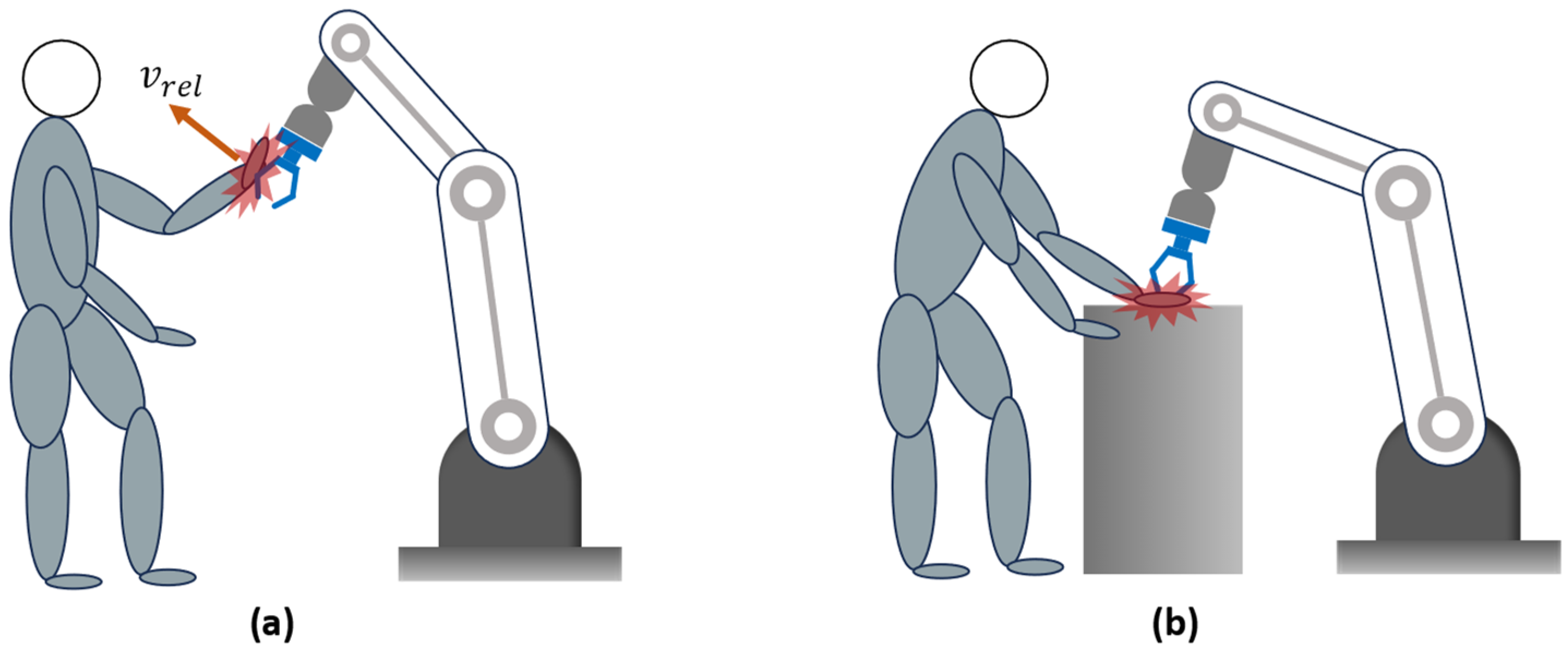
Appendix A. Robot Standards and Human–Robot Impact Modelling


- When a robot impacts a human body part without any constraint, allowing the body part to move freely upon impact, the contact is purely transient, as the human body part can freely move away afterwards.
- Pure quasi-static contact happens when a robot presses a human’s body part against a stationary object, like a wall or a table, at low velocity, and the impacting phase can be neglected. These situations can typically occur while doing tasks, like collaborating on object manipulation or passing objects to each other. The force of interaction depends on the deformability of body segments and the time required for the robot to stop when the impact is detected.
References
- Liang, C.J.; Cheng, M.H. Trends in Robotics Research in Occupational Safety and Health: A Scientometric Analysis and Review. Int. J. Environ. Res. Public Health 2023, 20, 5904. [Google Scholar] [CrossRef] [PubMed]
- Alves, J.; Lima, T.M.; Gaspar, P.D. Is Industry 5.0 a Human-Centred Approach? A Systematic Review. Processes 2023, 11, 193. [Google Scholar] [CrossRef]
- Marvel, J.A.; Zimmerman, M.; Bagchi, S. State-of-the-Art in Human-Robot Interaction; World Scientific: Singapore, 2018; pp. 43–86. [Google Scholar] [CrossRef]
- RIA TR R15.806-2018; Technical Report-Industrial Robots And Robot Systems-Safety Requirements-Testing Methods For Power & Force Limited Collaborative Applications. Robotic Industries Association: Ann Arbor, MI, USA, 2018.
- ISO/FDIS 10218-2; Robotics-Safety Requirements-Part 2: Industrial Robot Systems, Robot Applications and Robot Cells, Under Review. International Organization for Standardization: Geneva, Switzerland, 2021.
- Saenz, J.; Bessler-Etten, J.; Valori, M.; Prange-Lasonder, G.B.; Fassi, I.; Bidard, C.; Lassen, A.B.; Paniti, I.; Toth, A.; Stuke, T.; et al. An Online Toolkit for Applications Featuring Collaborative Robots Across Different Domains. IEEE Trans. Hum.-Mach. Syst. 2023, 53, 657–667. [Google Scholar] [CrossRef]
- ISO/TS 15066:2016; Robots and Robotic Devices-Collaborative Robots. International Organization for Standardization: Geneva, Switzerland, 2016.
- Zimmermann, J.; Huelke, M.; Clermont, M. Experimental Comparison of Biofidel Measuring Devices Used for the Validation of Collaborative Robotics Applications. Int. J. Environ. Res. Public Health 2022, 19, 13657. [Google Scholar] [CrossRef] [PubMed]
- Merkle, A.C.; Carneal, C.M.; Wing, I.D.; Wickwire, A.C.; Paulson, J.M.; Ott, K.A.; Ward, E.E.; Harrigan, T.P.; Roberts, J.C.; Carkhuff, B.G.; et al. Biomechanics and Injury Mitigation Systems Program: An Overview of Human Models for Assessing Injury Risk in Blast, Ballistic, and Transportation Impact Scenarios. Johns Hopkins APL Tech. Dig. 2013, 31, 286–295. [Google Scholar]
- Li, Z.; Ye, J.; Wu, H. A virtual sensor for collision detection and distinction with conventional industrial robots. Sensors 2019, 19, 2368. [Google Scholar] [CrossRef]
- Yamada, Y.; Hirasawa, Y.; Huang, S.; Umetani, Y.; Suita, K. Human-Robot Contact in the Safeguarding Space. IEEE/ASME Trans. Mechatron. 1997, 2, 230–236. [Google Scholar] [CrossRef]
- Ogorodnikova, O. How Safe the Human-Robot Coexistence Is? Theoretical Presentation. Acta Polytech. Hung. 2009, 6, 51–74. [Google Scholar]
- Haddadin, S.; Albu-Schäffer, A.; Hirzinger, G. Safety Evaluation of Physical Human-Robot Interaction via Crash-Testing. Robot. Sci. Syst. III 2007, 3, 217–224. [Google Scholar] [CrossRef]
- Haddadin, S. Towards Safe Robots: Approaching Asimov’s 1st Law. In Springer Tracts in Advanced Robotics; Springer: Berlin/Heidelberg, Germany, 2013; Volume 90, p. 350. Available online: http://www.springer.com/series/5208 (accessed on 12 October 2023).
- Behrens, R.; Pliske, G.; Umbreit, M.; Piatek, S.; Walcher, F.; Elkmann, N. A Statistical Model to Determine Biomechanical Limits for Physically Safe Interactions with Collaborative Robots. Front. Robot. AI 2022, 8, 667818. [Google Scholar] [CrossRef]
- Liu, J.; Yamada, Y.; Akiyama, Y.; Okamoto, S.; Iki, Y. Development of Dummy Based on Impedance Properties of Human Soft Tissue Using a Nonlinear Viscoelastic Model. IEEE Access 2023, 11, 7782–7793. [Google Scholar] [CrossRef]
- Herbster, S.; Behrens, R.; Elkmann, N. Modeling the Contact Force in Constrained Human–Robot Collisions. Machines 2023, 11, 955. [Google Scholar] [CrossRef]
- Herbster, S.; Behrens, R.; Elkmann, N. A New Approach to Estimate the Apparent Mass of Collaborative Robot Manipulators. In Experimental Robotics. ISER 2020. Springer Proceedings in Advanced Robotics; Springer: Cham, Switzerland, 2021; Volume 19. [Google Scholar] [CrossRef]
- Herbster, S.; Behrens, R.; Elkmann, N. A New Conversion Method to Evaluate the Hazard Potential of Collaborative Robots in Free Collisions. In Experimental Robotics, ISER 2020. Springer Proceedings in Advanced Robotics; Springer: Cham, Switzerland, 2020; Volume 19. [Google Scholar] [CrossRef]
- Jeanneau, G.; Bégoc, V.; Briot, S. A Reduced Mass-Spring-Mass-Model of Compliant Robots Dedicated to the Evaluation of Impact Forces. J. Mech. Robot. 2024, 16, 041012. [Google Scholar] [CrossRef]
- Case, J.C.; Rangarajan, N.; Falco, J.; Kimble, K. Towards the Development of Soft Force and Pressure Sensors for Robot Safety Applications. In IEEE Sensors; Institute of Electrical and Electronics Engineers Inc.: New York City, NY, USA, 2021. [Google Scholar] [CrossRef]
- Pungrasmi, T.; Shimaoka, Y.; Okamoto, T.; Watanabe, R. Contact Area Effects on Superficial and Deep Pain Threshold for Service Robot Safety Design using a Pain-sensing System-Development of a Human-inspired Pain-sensing System. Panasonic Tech. J. 2019, 65, 21–26. [Google Scholar]
- Dagalakis, N.G.; Yoo, J.M.; Oeste, T. Human-robot collaboration dynamic impact testing and calibration instrument for disposable robot safety artifacts. Industrial. Robot. 2016, 43, 328–337. [Google Scholar] [CrossRef] [PubMed]
- Scibilia, A.; Valori, M.; Pedrocchi, N.; Fassi, I.; Herbster, S.; Behrens, R.; Saenz, J.; Magisson, A.; Bidard, C.; Kühnrich, M.; et al. Analysis of Interlaboratory Safety Related Tests in Power and Force Limited Collaborative Robots. IEEE Access 2021, 9, 80873–80882. [Google Scholar] [CrossRef]
- Fischer, C.; Neuhold, M.; Steiner, M.; Haspl, T.; Rathmair, M.; Schlund, S. Collision Tests in Human-Robot Collaboration: Experiments on the Influence of Additional Impact Parameters on Safety. IEEE Access 2023, 11, 118395–118413. [Google Scholar] [CrossRef]
- Staab, H.; Byner, C.; Clever, D.; Matthias, B. A Pendulum Apparatus to Evaluate Unconstrained Human-Robot Contact; ABB AG, Corporate Research: Ladenburg, Germany, 2020. [Google Scholar]
- Viscoelastic Models for Linear Viscoelastic Response. Polymerdatabase. Available online: https://polymerdatabase.com/polymer%20physics/Linear%20Viscoelasticity.html (accessed on 17 July 2023).
- Lin, C.Y.; Chen, Y.C.; Lin, C.H.; Chang, K.V. Constitutive Equations for Analyzing Stress Relaxation and Creep of Viscoelastic Materials Based on Standard Linear Solid Model Derived with Finite Loading Rate. Polymers 2022, 14, 2124. [Google Scholar] [CrossRef]
- López-Guerra, E.A.; Solares, S.D. Modeling viscoelasticity through spring-dashpot models in intermittent-contact atomic force microscopy. Beilstein J. Nanotechnol. 2014, 5, 2149–2163. [Google Scholar] [CrossRef]
- Clever, D.; Byner, C.; Staab, H.; Matthias, B. On Peak and Integral Criteria to Assess Physical Contact in Human-Robot-Collaboration (HRC). In Proceedings of the ISR Europe 2022, 54th International Symposium on Robotics, Munich, Germany, 20–21 June 2022; pp. 1–8. [Google Scholar]
- Nise, N.S. Control System Engineering, 8th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Valori, M.; Scibilia, A.; Fassi, I.; Saenz, J.; Behrens, R.; Herbster, S.; Bidard, C.; Lucet, E.; Magisson, A.; Schaake, L.; et al. Validating safety in human–robot collaboration: Standards and new perspectives. Robotics 2021, 10, 65. [Google Scholar] [CrossRef]
- ISO 10218-1:2011; Robots and Robotic Devices-Safety Requirements for Industrial Robots-Part 1: Robots. International Organization for Standardization: Geneva, Switzerland, 2011.
- ISO 10218-2:2011; Robots and Robotic Devices-Safety Requirements for Industrial Robots-Part 2: Robot Systems and Integration. International Organization for Standardization: Geneva, Switzerland, 2011.
- Gualtieri, L.; Rauch, E.; Vidoni, R. Development and validation of guidelines for safety in human-robot collaborative assembly systems. Comput. Ind. Eng. 2022, 163, 107801. [Google Scholar] [CrossRef]
- Kirschner, R.J.; Mansfeld, N.; Peña, G.G.; Abdolshah, S.; Haddadin, S. Notion on the correct use of the robot effective mass in the safety context and comments on ISO/TS 15066. In Proceedings of the 2021 IEEE International Conference on Intelligence and Safety for Robotics (ISR), Tokoname, Japan, 4–6 March 2021; pp. 6–9. [Google Scholar] [CrossRef]





| Company | Sensor | Available Springs (N/mm) | Force Range (N) | Sampling Rate | Bandwidth |
|---|---|---|---|---|---|
| GTE | COBOSAFE CBSF | 10–150 | 10–300 20–500 | kHz | Not provided |
| COBOSAFE CBSF—Basic | 75 | 20–500 | kHz | Not provided | |
| PILZ | PRMS | 10–150 | 0–500 | Not provided | Not provided |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samarathunga, S.M.B.P.B.; Valori, M.; Faglia, R.; Fassi, I.; Legnani, G. Considerations on the Dynamics of Biofidelic Sensors in the Assessment of Human–Robot Impacts. Machines 2024, 12, 26. https://doi.org/10.3390/machines12010026
Samarathunga SMBPB, Valori M, Faglia R, Fassi I, Legnani G. Considerations on the Dynamics of Biofidelic Sensors in the Assessment of Human–Robot Impacts. Machines. 2024; 12(1):26. https://doi.org/10.3390/machines12010026
Chicago/Turabian StyleSamarathunga, S. M. B. P. B., Marcello Valori, Rodolfo Faglia, Irene Fassi, and Giovanni Legnani. 2024. "Considerations on the Dynamics of Biofidelic Sensors in the Assessment of Human–Robot Impacts" Machines 12, no. 1: 26. https://doi.org/10.3390/machines12010026
APA StyleSamarathunga, S. M. B. P. B., Valori, M., Faglia, R., Fassi, I., & Legnani, G. (2024). Considerations on the Dynamics of Biofidelic Sensors in the Assessment of Human–Robot Impacts. Machines, 12(1), 26. https://doi.org/10.3390/machines12010026










