A Predictive Control Model of Bernoulli Production Line with Rework Loop for Real-Time WIP Optimization in Permutation Flowshop
Abstract
:1. Introduction
- (1)
- Most current modeling efforts mainly focus on static production processes, and steady-state analysis is effective in the case of a single large-scale production. In complex and changeable streamlined production processes, compared with transient analysis, the results obtained by steady-state analysis are not accurate enough in some cases. However, the current transient modeling work on production systems is still insufficient.
- (2)
- The rework and reuse of defective products is of great significance to reducing costs, improving manufacturing efficiency, and realizing green manufacturing. Currently, the existing transient modeling work mainly focuses on continuous manufacturing systems, and it is difficult to consider complex re-entrant systems. There is still insufficient research on this link.
- (3)
- In the actual production process, human factors play a large role in the safety, risk management, and quality control of the production system. However, current research on the replacement process usually only considers automatic machines and does not consider manual machines that are affected by the human actions of the machine operator.
- (1)
- This paper presents an analysis of automated and manually operated semi-automated machines and their integration into a displacement flowshop with a rework loop.
- (2)
- This study establishes an instantaneous productivity model suitable for arranging flow operations with rework loops and human factors, and measures basic production performance indicators through a recursive method.
- (3)
- To address the challenges of intelligent control in permutation flowshops and to furnish comprehensive, real-time production insights, a model predictive control system based on discrete event-driven feedback is employed. As a result of these research outcomes, there is a discernible enhancement in the ability to perceive and predict work-in-progress, leading to significant savings in human resources.
2. Problem Description and Model Assumptions
- (1)
- There are M machines and M-1 buffers on the main production line. Among them, there are two rework production lines, on which is an inspection machine which can check whether the products are qualified. Qualified products are recorded as class A products, and unqualified products are recorded as class B products. Qualified products are directly transferred to the buffer, and unqualified products are sent for or wait for reprocessing through the rework production line [31].
- (2)
- At least one machine has sufficient raw materials, and the last machine on the production line of Line 3 will not be blocked [32].
- (3)
- The start time of each production determines the working status of the machine, and the end time of each production determines the status of the buffer [33].
- (4)
- The entire replacement process with re-entry satisfies the assumptions of “time dependent failure” and “pre-processing blocking” [34].
3. Production System Modeling and Predictive Model Control
3.1. Production System Modeling
3.1.1. Machine Reliability Model for Both Manual and Automatic Machines
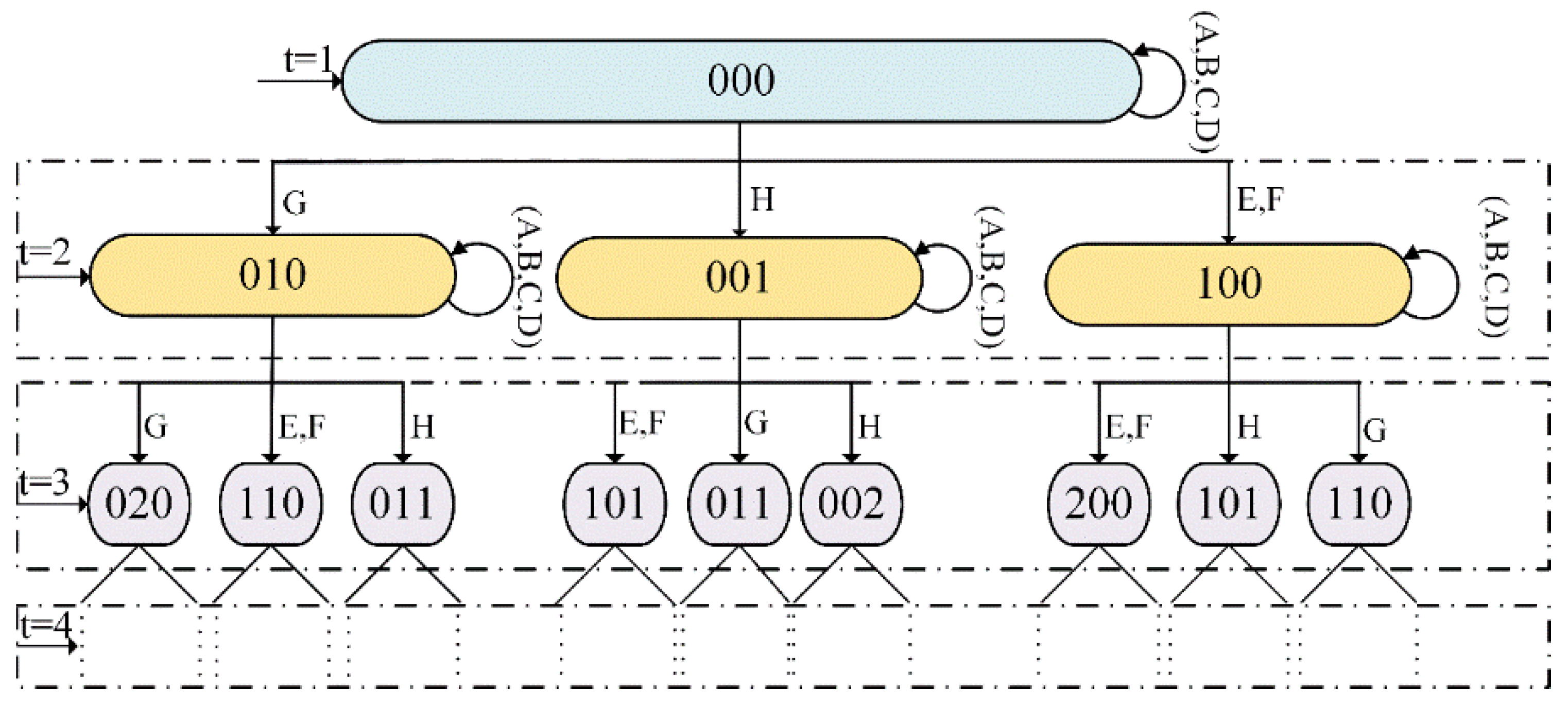
3.1.2. Transient Transition Modeling
- (1)
- Operator P describes the probability of occurrence of event E (i.e., P[E]).
- (2)
- The operator Φ describes the event that the object O is in state S at time t, respectively, Φ (O, S, t).
- (3)
- The operator H describes multiple objects (O1, O2, O3, …) At time t, they are in states (S1, S2, S3, …), respectively, H (O1, O2, O3, …/S1, S2, S3, …, t)
- (4)
- The operator T describes the probability of a particular object O going from state S1 to S2 in time t, respectively, .
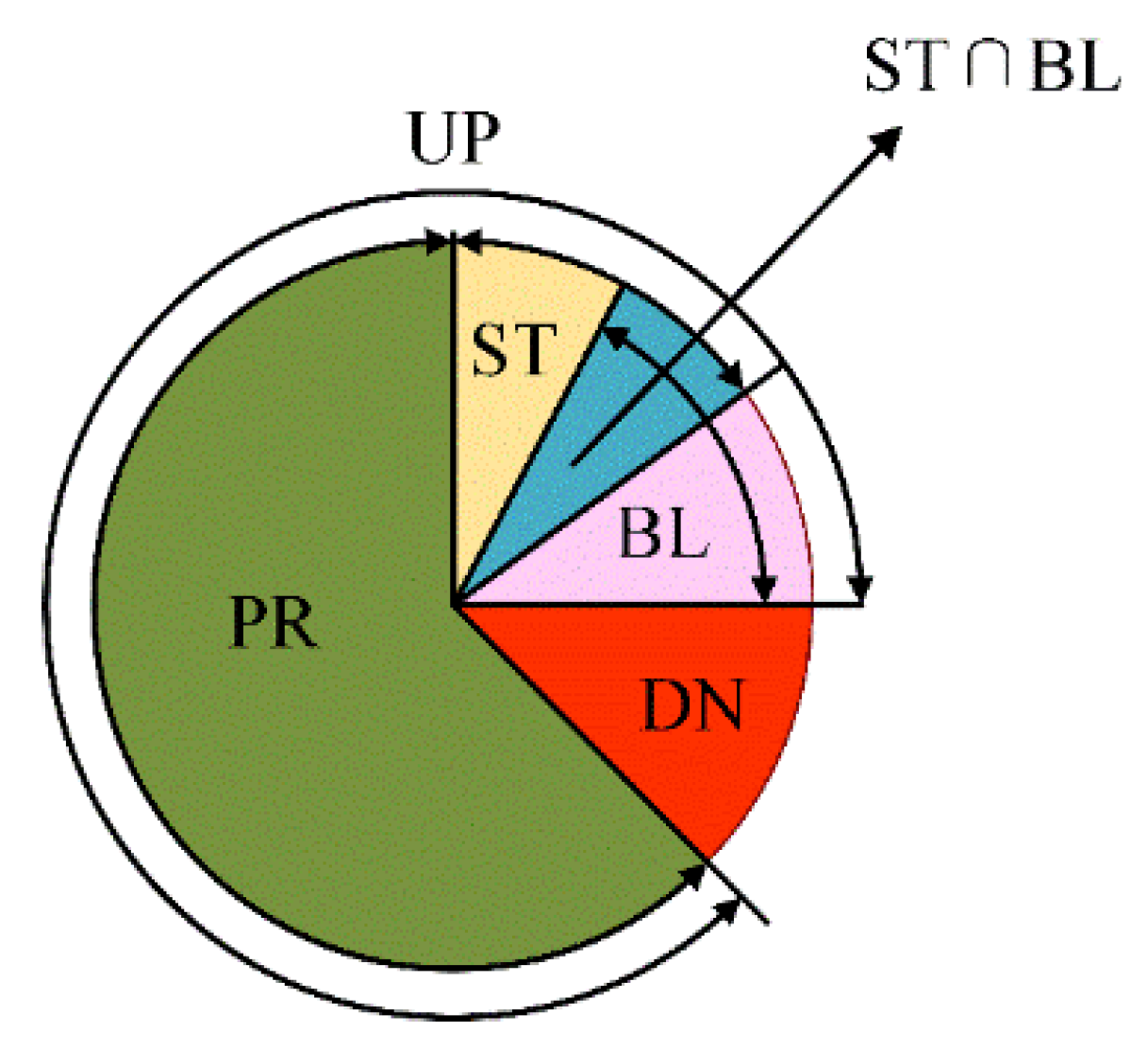
3.1.3. Transient Mapping Analysis
3.1.4. Reverse Modeling of Machine Transient Behavior
3.2. Model Predictive Control
3.2.1. r-WIP Optimization Problem Formulation
- (1)
- To represent the dynamic behavior of a replacement process model with re-entry links, a mathematical model can be established.
- (2)
- To determine when there are non-conforming parts, an event-driven production performance identification method based on the model can be proposed.
- (3)
- To produce the best release time of r-WIP optimization jobs, a discrete event-driven model predictive control is proposed. The following assumptions will be defined so that the dynamic behavior of permutation flow stores with retransmission links can be modeled.
- a.
- SM* defines the last and slowest machine closest to the end of the line, assuming that one or more machines are likely to be hungry or blocked in the re-entry link.
- b.
- When a disturbing event happens, the processing time of the ki-th part at the i, j-th machine is .
- c.
- There is a finite capacity for each buffer .
- d.
- The interference event depends on the operation and can be detected in real time.
- e.
- If the customer’s demand exceeds the production capacity of the replacement process, the replacement process should be run at maximum production capacity.
- f.
- The transportation time between the machine and the buffer can be ignored [35].
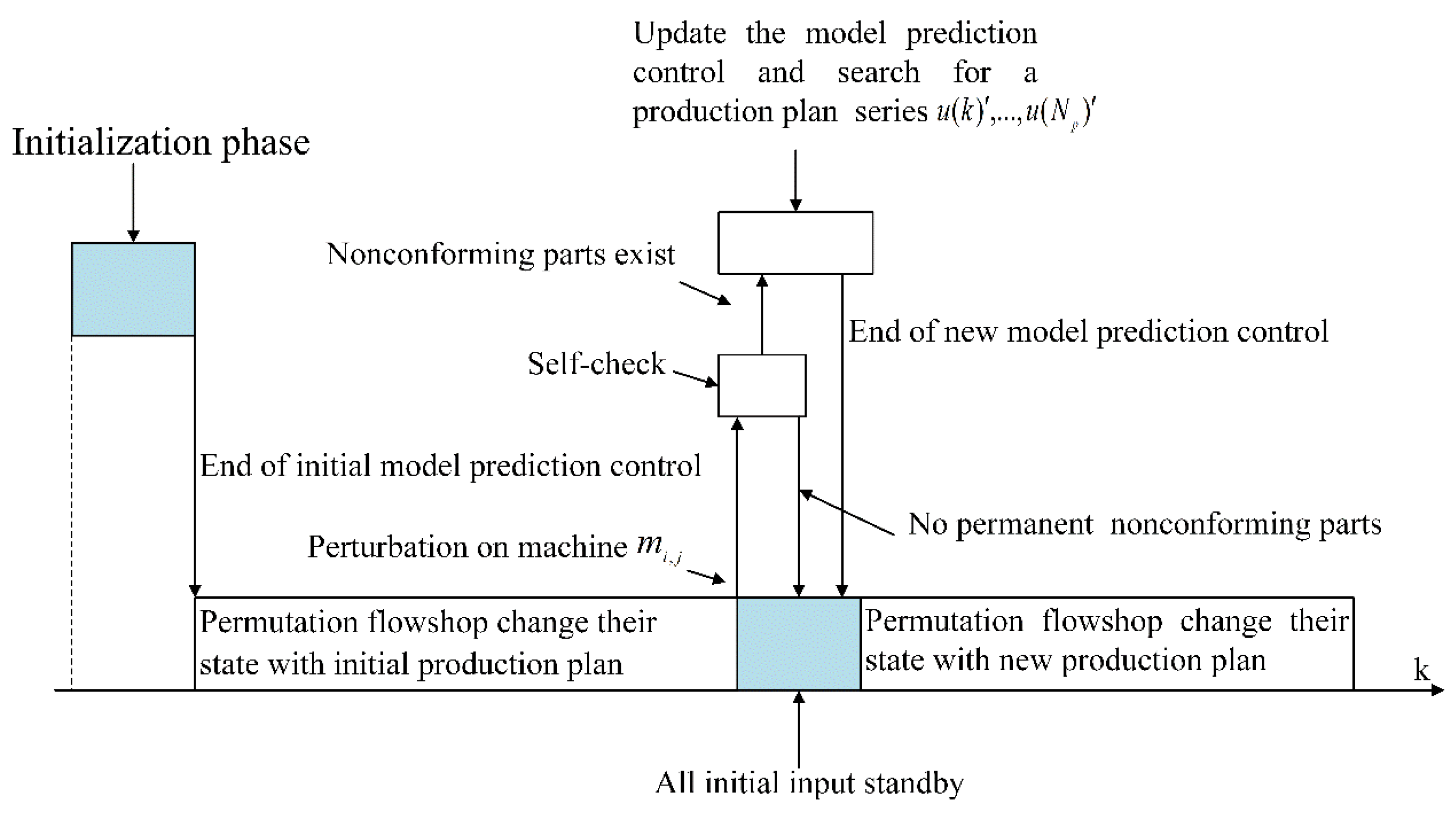
3.2.2. Event-Based Time-Varying Model Predictive Control
4. Solution of the Established Model
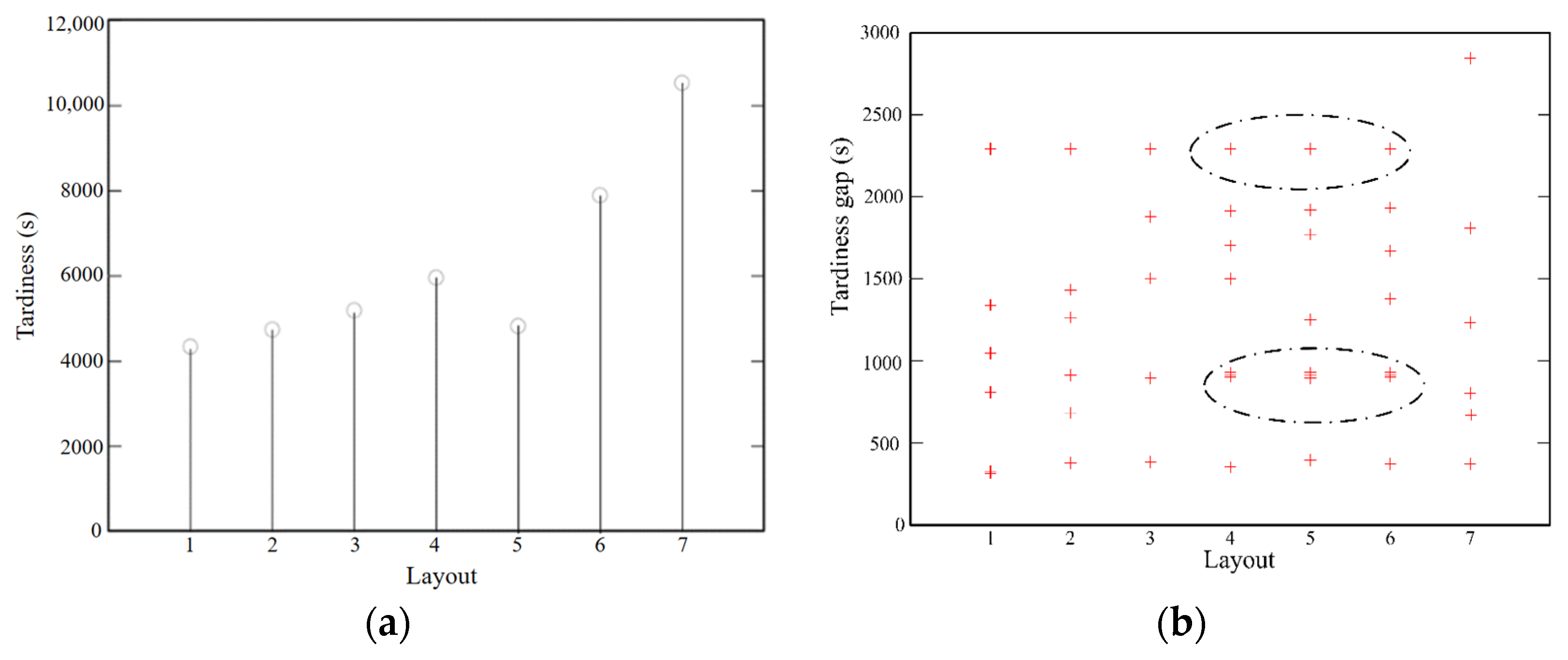
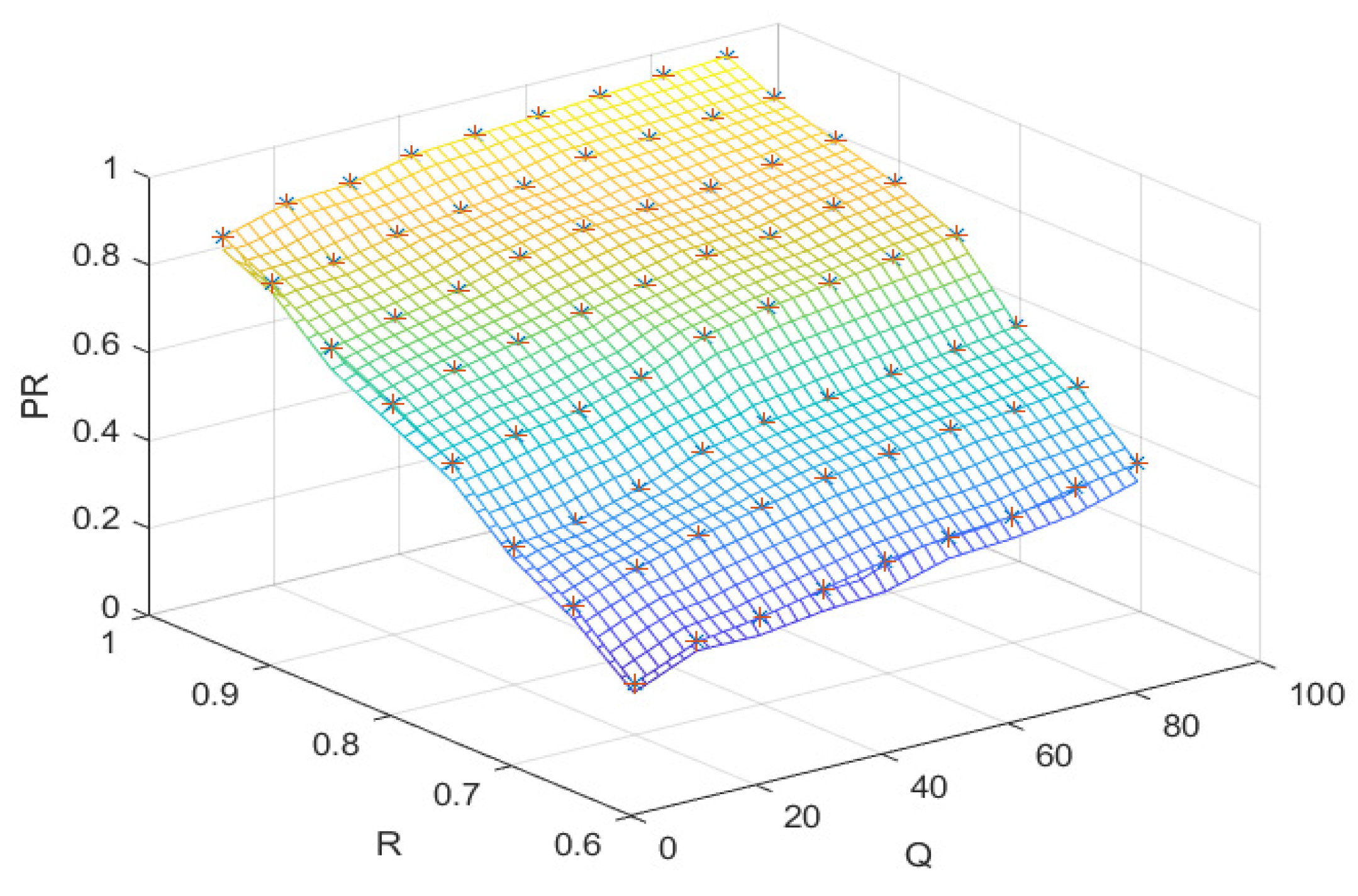
5. Case Study
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gheisariha, E.; Tavana, M.; Jolai, F.; Rabiee, M. A simulation–optimization model for solving flexible flow shop scheduling problems with rework and transportation. Math. Comput. Simul. 2021, 180, 152–177. [Google Scholar] [CrossRef]
- Subramaniyan, M.; Skoogh, A.; Salomonsson, H.; Bangalore, P.; Bokrantz, J. A data-driven algorithm to predict throughput bottlenecks in a production system based on active periods of the machines. Comput. Ind. Eng. 2018, 125, 533–544. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, M.; Cheng, J.; Qi, Q. Digital twin workshop: A new paradigm for future workshop. Comput. Integr. Manuf. Syst. 2017, 23, 1–9. [Google Scholar]
- Chen, J.; Jia, Z.; Huang, L. Multi-type products and dedicated buffers-based flexible production process analysis of serial Bernoulli lines. Comput. Ind. Eng. 2021, 154, 107167. [Google Scholar] [CrossRef]
- Yan, C.B.; Cheng, X.; Gao, F.; Guan, X. Formulation and solution methodology for reducing energy consumption in two-machine Bernoulli serial lines. IEEE Trans. Autom. Sci. Eng. 2020, 19, 522–530. [Google Scholar] [CrossRef]
- Pei, Z.; Yang, P.; Wang, Y.; Yan, C.-B. Energy consumption control in the two-machine Bernoulli serial production line with setup and idleness. Int. J. Prod. Res. 2023, 61, 2917–2936. [Google Scholar] [CrossRef]
- Wang, X.; Dai, Y.; Jia, Z. Energy-efficient on/off control in serial production lines with Bernoulli machines. Flex. Serv. Manuf. J. 2022, 1–26. [Google Scholar] [CrossRef]
- Yan, C.B.; Zheng, Z. Problem formulation and solution methodology for energy consumption optimization in Bernoulli serial lines. IEEE Trans. Autom. Sci. Eng. 2020, 18, 776–790. [Google Scholar] [CrossRef]
- Hadžić, N.; Ložar, V.; Opetuk, T.; Andrić, J. A finite state method in improvement and design of lean Bernoulli serial production lines. Comput. Ind. Eng. 2021, 159, 107449. [Google Scholar] [CrossRef]
- Hadžić, N.; Ložar, V.; Opetuk, T.; Kunkera, Z. The Bernoulli Assembly Line: The Analytical and Semi-Analytical Evaluation of Steady-State Performance. Appl. Sci. 2022, 12, 12447. [Google Scholar] [CrossRef]
- Liu, M.; Xie, J.; Wu, H.; Fu, J.; Ding, G. Research on Workshop Logic Modeling and Simulation Based on Finite State Machine. J. Syst. Simul. 2023, 35, 853–861. [Google Scholar]
- Öztop, H.; Tasgetiren, M.F.; Kandiller, L.; Eliiyi, D.T.; Gao, L. Ensemble of metaheuristics for energy-efficient hybrid flowshops: Makespan versus total energy consumption. Swarm Evol. Comput. 2020, 54, 100660. [Google Scholar] [CrossRef]
- Tang, D.; Wang, J.; Ding, X. Order-Driven Dynamic Resource Configuration Based on a Metamodel for an Unbalanced Assembly Line. Machines 2022, 10, 508. [Google Scholar] [CrossRef]
- Zhao, R.; Zou, G.; Su, Q.; Zou, S.; Deng, W.; Yu, A.; Zhang, H. Digital Twins-Based Production Line Design and Simulation Optimization of Large-Scale Mobile Phone Assembly Workshop. Machines 2022, 10, 367. [Google Scholar] [CrossRef]
- Chen, J.; Shen, Z.J.M. Fast Approximations for Dynamic Behavior in Manufacturing Systems with Regular Orders: An Aggregation Method. IEEE Robot. Autom. Lett. 2023, 8, 7122–7129. [Google Scholar] [CrossRef]
- Pagone, E.; Haddad, Y.; Barsotti, L.; Dini, G.; Salonitis, K. A stochastic evaluation framework to improve the robustness of manufacturing systems. Int. J. Comput. Integr. Manuf. 2023, 36, 966–984. [Google Scholar] [CrossRef]
- Mo, F.; Rehman, H.U.; Monetti, F.M.; Chaplin, J.C.; Sanderson, D.; Popov, A.; Maffei, A.; Ratchev, S. A framework for manufacturing system reconfiguration and optimisation utilising digital twins and modular artificial intelligence. Robot. Comput. Integr. Manuf. 2023, 82, 102524. [Google Scholar] [CrossRef]
- Wang, X.; Gu, W.; Liu, S.; Guo, Z.; Zhan, Y. Modeling of Bernoulli production line with rework loop for real-time work-in-process optimization in permutation flowshop. In Proceedings of the IEEE 6th Advanced Information Technology, Electronic and Automation Control Conference, Beijing, China, 3–5 October 2022; pp. 1266–1270. [Google Scholar]
- Wang, X.; Dai, Y.; Wang, L.; Jia, Z. Transient Analysis and Scheduling of Bernoulli Serial Lines with Multi-Type Products and Finite Buffers. IEEE Trans. Autom. Sci. Eng. 2022, 20, 2367–2382. [Google Scholar] [CrossRef]
- Ma, C.; Jia, Z.; Wang, X.; Ni, Z. Transient Performance Evaluation with Finite Production Run-based Serial Lines: Bernoulli Quality Model. In Proceedings of the 2021 International Conference on Cyber-Physical Social Intelligence (ICCSI), Beijing, China, 18–20 December 2021; pp. 1–6. [Google Scholar]
- Bachar, R.K.; Bhuniya, S.; Ghosh, S.K.; AlArjani, A.; Attia, E.; Uddin, S.; Sarkar, B. Product outsourcing policy for a sustainable flexible manufacturing system with reworking and green investment. Math. Biosci. Eng. 2023, 20, 1376–1401. [Google Scholar] [CrossRef]
- Zhou, B.; Zha, W. Performance evaluation and optimization model for closed-loop production lines considering preventive maintenance and rework process. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2023, 09544089231160514. [Google Scholar] [CrossRef]
- Sun, H.; Xia, T.; Shi, Y.; Leng, B.; Wang, H. Online energy consumption optimization of rework production system based on digital twin. Comput. Integr. Manuf. Syst. 2023, 29, 11. [Google Scholar]
- Jia, Z.; Ni, Z.; Ma, C. Dynamic Process Modeling and Real-Time Performance Evaluation of Rework Production System with Small-Lot Order. IEEE Robot. Autom. Lett. 2023, 8, 2874–2881. [Google Scholar] [CrossRef]
- Khezri, A.; Homri, L.; Etienne, A.; Dantan, J.-Y.; Lanza, G. A Framework for integration of resource allocation and reworking concept into design optimisation problem. IFAC Pap. 2022, 55, 1037–1042. [Google Scholar] [CrossRef]
- Chen, J.; Mohammed, A.; Alexopoulos, T.; Setchi, R. Collaborative human-robot assembly: Methodology, simulation and industrial validation. In International Conference on Sustainable Design and Manufacturing; Springer: Singapore, 2022; pp. 181–190. [Google Scholar]
- Lago Alvarez, A.; Mohammed, W.M.; Vu, T.; Ahmadi, S.; Martinez Lastra, J.L. Enhancing Digital Twins of Semi-Automatic Production Lines by Digitizing Operator Skills. Appl. Sci. 2023, 13, 1637. [Google Scholar] [CrossRef]
- Shi, J.; Chen, M.; Ma, Y.; Qiao, F. A new boredom-aware dual-resource constrained flexible job shop scheduling problem using a two-stage multi-objective particle swarm optimization algorithm. Inf. Sci. 2023, 643, 119141. [Google Scholar] [CrossRef]
- Li, Y.; Chang, Q.; Ni, J.; Brundage, M.P. Event-based supervisory control for energy efficient manufacturing systems. IEEE Trans. Autom. Sci. Eng. 2018, 15, 92–103. [Google Scholar] [CrossRef]
- Zhou, B.; Su, Y. Energy-saving analysis of serial production lines based on the changeable buffers’ storage. J. Harbin Eng. Univ. 2016, 37, 832–836. [Google Scholar]
- Xin, W.; Zequn, Z.; Dunbing, T. Energy-saving Oriented Multi-objective Shop Floor Scheduling for Mixed-line Production of Missile Components. J. Mech. Eng. 2018, 54, 45–54. [Google Scholar]
- Zhang, H.; Tang, D. Output Prediction and Disturbance Analysis of Manufacturing Networks Based on State Space. J. Mech. Eng. 2016, 52, 166–174. [Google Scholar] [CrossRef]
- Pan, Q.K.; Wang, L.; Li, J.Q.; Duan, J.H. A novel discrete artificial bee colony algorithm for the hybrid flowshop scheduling problem with makespan minimization. Omega 4 2014, 5, 42–56. [Google Scholar] [CrossRef]
- Cao, Y.; Subramaniam, V.; Chen, R. Performance evaluation and enhancement of multistage manufacturing systems with rework loops. Comput. Ind. Eng. 2011, 62, 161–176. [Google Scholar] [CrossRef]
- Chen, W.; Liu, H.; Qi, E. Discrete Event-driven Model Predictive Control for Real-time Work-in-process Optimization in Serial Production Systems. J. Manuf. Syst. 2020, 55, 132–142. [Google Scholar] [CrossRef]
- Komenda, J.; Lahaye, S.; Boimond, J.-L.; Boom, T.V.D. Max-plus algebra in the history of discrete event systems. Annu. Rev. Control 2018, 45, 240–249. [Google Scholar] [CrossRef]






| Notation | Interpretation |
|---|---|
| The machine is in a state of non-fault operation in unit time t | |
| A machine or buffer that is out of order within a time unit t | |
| The operation of a machine within a time unit t | |
| The state in which a machine operates non-productively within a time unit t | |
| The machine or buffer operates in a hungry state for a unit time t | |
| The machine or buffer unit is not hungry within unit time t | |
| The operation of a machine or buffer that is blocked for a unit of time t | |
| The state of unblocked operation of a machine or buffer for a unit of time t | |
| The complete set of all possible states of a machine | |
| Time instant at which the machine starts to work on the t-th part | |
| Time instant at which the t-th part leaves the permutation flowshop | |
| Processing time of the t-th part at | |
| The buffer level after the t-th part’s entrance into | |
| The buffer level of just after the t-th part leaves | |
| The control range of discrete event model predictive control | |
| The prediction horizon of the discrete event model predictive control, Nc ≤ Np | |
| The capacity of the buffer | |
| The expiration date of the finished product | |
| The time when the t-th component is fed to the system | |
| A disturbing event that lasts di time when the machine processes the t-th part |
| Type | |||
|---|---|---|---|
| A | × | × | × |
| B | × | × | √ |
| C | × | √ | × |
| D | × | √ | √ |
| E | √ | × | × |
| F | √ | × | √ |
| G | √ | √ | × |
| H | √ | √ | √ |
| Layout Code | Machines on the Main Production Line | Rework Line Machine | Machine Separation | ||
|---|---|---|---|---|---|
| Pi | C | Pi | C | h | |
| 1 | {0.9, 0.8, 0.8, 0.7} | 8 | {0.9, 0.8} | 4 | 1 |
| 2 | {0.9, 0.7, 0.85, 0.8, 0.9} | 10 | {0.9, 0.8} | 4 | 1 |
| 3 | {0.9, 0.7, 0.85, 0.8, 0.9} | 10 | {0.9} | 2 | 1 |
| 4 | {0.9, 0.7, 0.85, 0.8, 0.9} | 10 | {0.9, 0.8} | 4 | 1 |
| 5 | {0.9, 0.7, 0.85, 0.8, 0.9} | 10 | {0.9, 0.8, 0.7} | 6 | 1 |
| 6 | {0.9, 0.7, 0.85, 0.8, 0.9, 0.7} | 12 | {0.9} | 2 | 1 |
| 7 | {0.9, 0.7, 0.8, 0.8, 0.9, 0.7, 0.8, 0.7, 0.9, 0.9} | 20 | {0.9, 0.8, 0.9, 0.7, 0.85} | 10 | 1 |
| Layout Code | Average Inventory Level () | Production Rate (PR) | Rework Rate (RR) | Energy-Consuming Reduction Rate (ECRA) |
|---|---|---|---|---|
| 1 | 0.53 | 0.8959 | 0.31 | 0.11 |
| 2 | 0.47 | 0.7853 | 0.26 | 0.12 |
| 3 | 0.43 | 0.6792 | 0.22 | 0.14 |
| 4 | 0.38 | 0.5878 | 0.18 | 0.18 |
| 5 | 0.34 | 0.6862 | 0.26 | 0.23 |
| 6 | 0.27 | 0.4865 | 0.12 | 0.27 |
| 7 | 0.23 | 0.4842 | 0.09 | 0.31 |
| Processing Times | Average Inventory () | Production Rate (PR) | Rework Rate (RR) | Energy-Consuming Reduction Rate (ECRA) |
|---|---|---|---|---|
| 10 | 5 | 0.8863 | 0.25 | 0.206 |
| 20 | 8 | 0.8886 | 0.20 | 0.235 |
| 50 | 10 | 0.8873 | 0.15 | 0.259 |
| 80 | 10 | 0.8896 | 0.10 | 0.293 |
| 100 | 10 | 0.8912 | 0.10 | 0.326 |
| Processing Times | Average Inventory () | Production Rate (PR) | Rework Rate (RR) | Energy-Consuming Reduction Rate (ECRA) |
|---|---|---|---|---|
| 10 | 20 | 0.8852 | 0.15 | 0.157 |
| 20 | 25 | 0.8867 | 0.17 | 0.209 |
| 50 | 35 | 0.8886 | 0.20 | 0.248 |
| 80 | 40 | 0.8898 | 0.25 | 0.316 |
| 100 | 60 | 0.8926 | 0.25 | 0.324 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, W.; Guo, Z.; Wang, X.; Yang, Y.; Yuan, M. A Predictive Control Model of Bernoulli Production Line with Rework Loop for Real-Time WIP Optimization in Permutation Flowshop. Machines 2024, 12, 20. https://doi.org/10.3390/machines12010020
Gu W, Guo Z, Wang X, Yang Y, Yuan M. A Predictive Control Model of Bernoulli Production Line with Rework Loop for Real-Time WIP Optimization in Permutation Flowshop. Machines. 2024; 12(1):20. https://doi.org/10.3390/machines12010020
Chicago/Turabian StyleGu, Wenbin, Zhenyang Guo, Xianliang Wang, Yiran Yang, and Minghai Yuan. 2024. "A Predictive Control Model of Bernoulli Production Line with Rework Loop for Real-Time WIP Optimization in Permutation Flowshop" Machines 12, no. 1: 20. https://doi.org/10.3390/machines12010020
APA StyleGu, W., Guo, Z., Wang, X., Yang, Y., & Yuan, M. (2024). A Predictive Control Model of Bernoulli Production Line with Rework Loop for Real-Time WIP Optimization in Permutation Flowshop. Machines, 12(1), 20. https://doi.org/10.3390/machines12010020









