A Novel Planning and Tracking Approach for Mobile Robotic Arm in Obstacle Environment
Abstract
:1. Introduction
- (1)
- An improved APF-RRT* algorithm is developed. First, for RRT*, the node selection process is optimized, and the Dubins curve is used to smooth the path. The total turning angle is reduced while decreasing the path length. Second, an APF is used to generate artificial potential fields according to the shape and position of obstacles and keep the random tree away from the obstacles. Therefore, the invalid path branches are reduced, and the speed of planning is accelerated;
- (2)
- A Fuzzy-DDPG-PID controller is established. To promote the adaptiveness of path tracking of the robotic arm in an environment with disturbance, a Fuzzy-DDPG algorithm is integrated with the PID controller. First, to solve the problem of slow disturbance capture in DDPG, the update function and loss function are improved, and the policy-making speed is accelerated. Second, a FNN is proposed to solve the problem of the strong subjectivity of the DDPG online network. The membership function and fuzzy rules of FNN are optimized, and the online network of DDPG can be updated in real-time. Therefore, the response speed and policy-making accuracy are enhanced. By combining the Fuzzy-DDPG with the PID controller, the tracking time, time delay, and error of tracking are reduced. The robustness is enhanced.
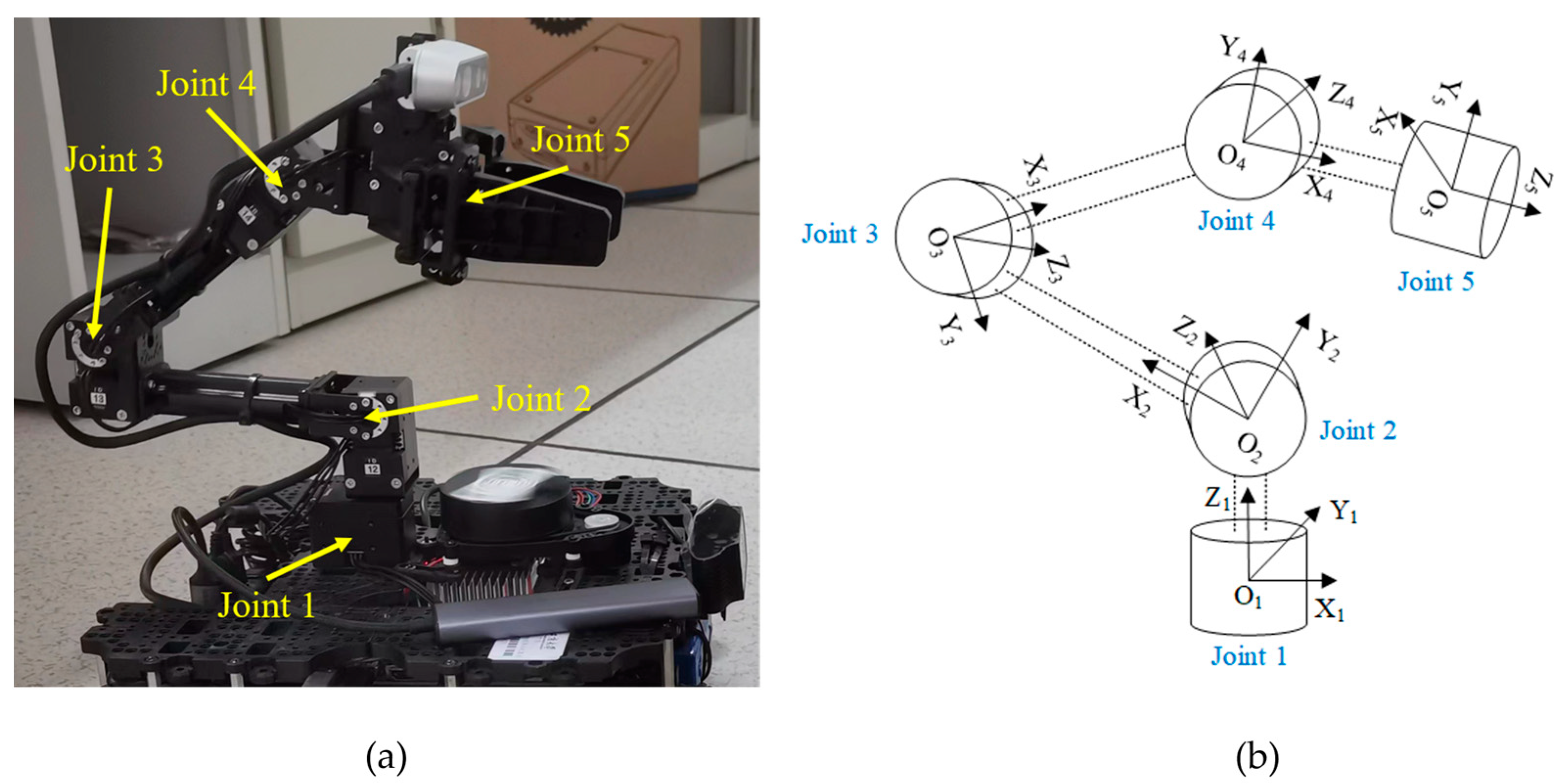
2. The Experimental Platform
3. The Proposed Approach
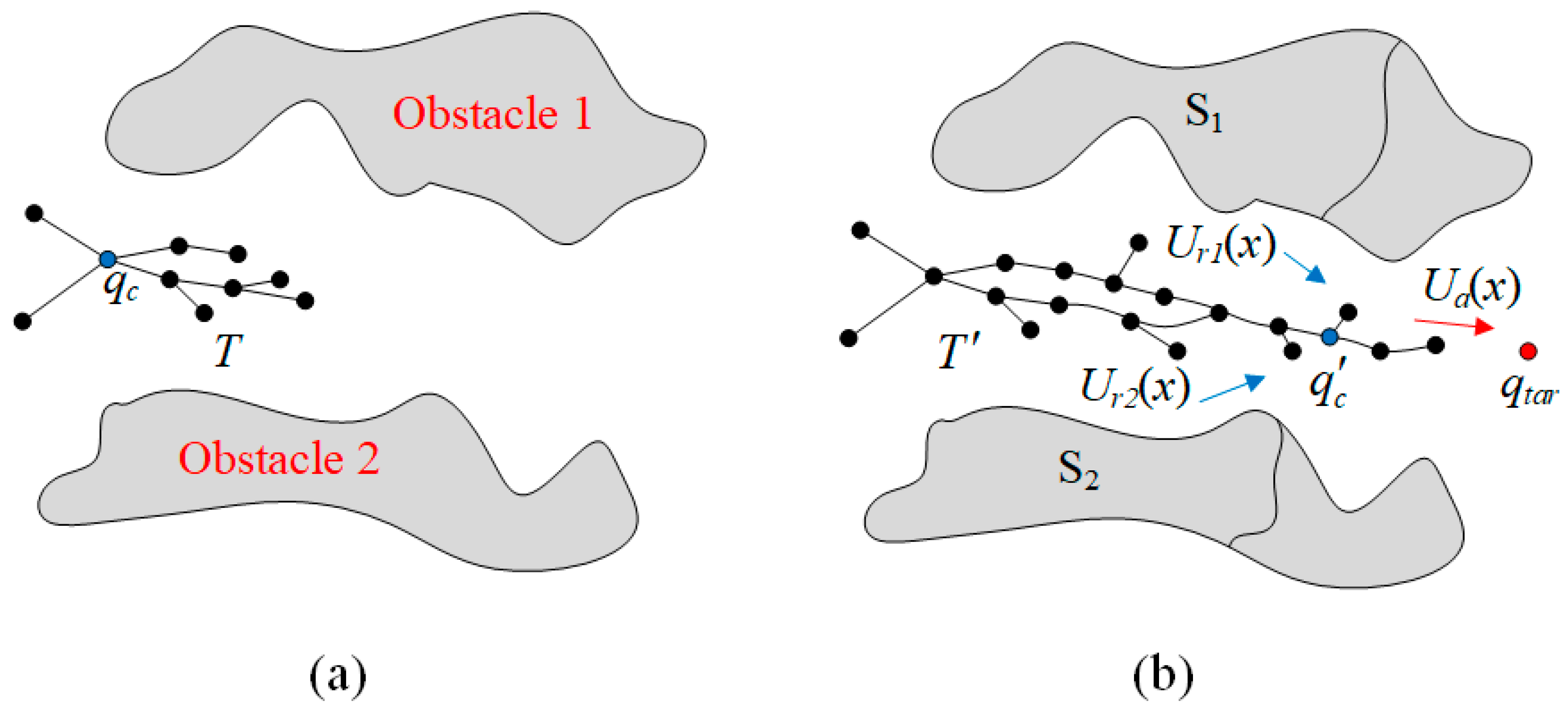
3.1. Planning Based on the Improved APF-RRT*
3.1.1. The Improved RRT*
3.1.2. Addition of APF
| Algorithm: Improved APF-RRT* | |
| Input: Process (stretch, retrieve), obstacle area Si, current state T Output: Path(T, qnew, qmin) | |
| Step 1: | V ← qi; |
| Step 2: | i ← 0; |
| Step 3: | Motion ← Process(stretch, retrieve) |
| Step 4: | For i = 1:N do |
| Step 5: | qrand ← Sample(qinit, T); |
| Step 6: | i ← i +1; |
| Step 7: | qnearest ← Nearest(qrand); |
| Step 8: | qnew ← Steer(qnearest, qtar); |
| Step 9: | if CollisionFree(qnearest, qnew, Si) then |
| Step 10: | qnearest ← Nearest(qnew, D); |
| Step 11: | qparent ← Parent(qnearest, Rk); |
| Step 12: | For j = 1:M do |
| Step 13: | if ExcludeDubinsCircle(qnew) then |
| Step 14: | qnew ← PlanNode(qparent, Ua, Ur); |
| Step 15: | Cost(qmin) = Cost(qnearest) + Cost(qnew, d); |
| Step 16: | T’ ← Path(T, qnew, qmin); |
| Step 17: | Return T’; |
3.2. Tracking Based on the Fuzzy-DDPG-PID
3.2.1. DDPG Algorithm
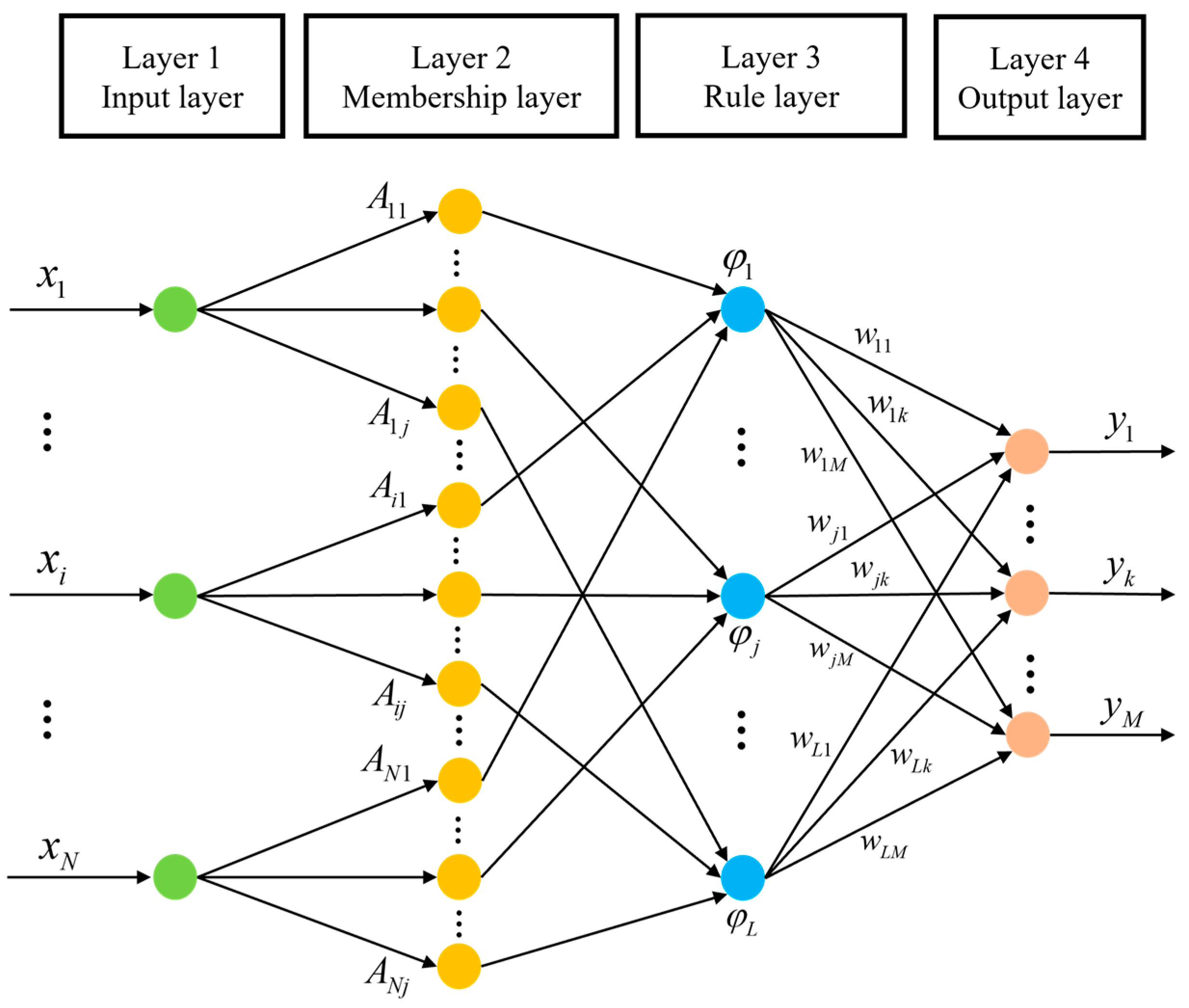
3.2.2. The Addition of FNN
4. Experiments and Analysis
4.1. Experiments and Analysis of Planning
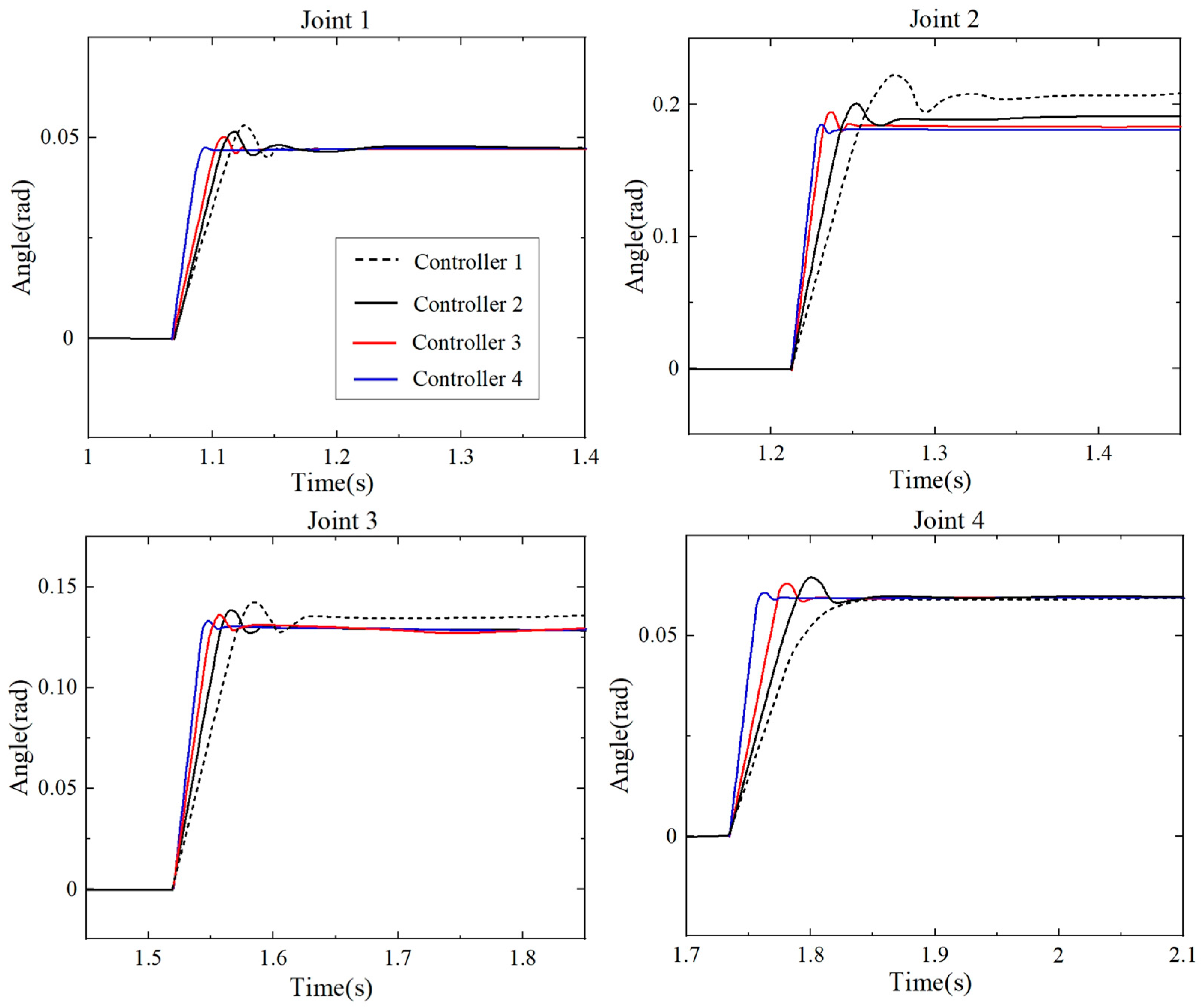
4.2. Experiments and Analysis of Tracking
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Yang, C.G.; Yan, W.S.; Cui, R.X.; Annamalai, A. Admittance-Based Adaptive Cooperative Control for Multiple Manipulators with Output Constraints. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3621–3632. [Google Scholar] [CrossRef] [PubMed]
- Sepehri, A.; Moghaddam, A.M. A Motion Planning Algorithm for Redundant Manipulators using Rapidly Exploring Randomized Trees and Artificial Potential Fields. IEEE Access 2021, 9, 26059–26070. [Google Scholar] [CrossRef]
- Lu, X.H.; Jia, Y.M. Trajectory Planning of Free-Floating Space Manipulators with Spacecraft Attitude Stabilization and Manipulability Optimization. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 7346–7362. [Google Scholar] [CrossRef]
- Wang, L.J.; Lai, X.Z.; Zhang, P.; Wu, M. A Control Strategy Based on Trajectory Planning and Optimization for Two-Link Underactuated Manipulators in Vertical Plane. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 3466–3475. [Google Scholar] [CrossRef]
- Nie, J.M.; Wang, Y.A.; Mo, Y.; Miao, Z.Q.; Jiang, Y.M.; Zhong, H.; Lin, J. An HQP-Based Obstacle Avoidance Control Scheme for Redundant Mobile Manipulators under Multiple Constraints. IEEE Trans. Ind. Electron. 2023, 70, 6004–6016. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. In Proceedings of the 1985 IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985; Volume 2, pp. 500–505. [Google Scholar]
- Lavalle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning. Res. Rep. 1999, 31, 293–308. [Google Scholar]
- Valle, S.M.L.; Kuffner, J.J. Randomized kinodynamic planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar]
- Devaurs, D.; Siméon, T.; Cortés, J. Optimal Path Planning in Complex Cost Spaces with Sampling-Based Algorithms. IEEE Trans. Autom. Sci. Eng. 2016, 13, 415–424. [Google Scholar] [CrossRef]
- Ju, T.; Liu, S.; Yang, J.; Sun, D. Rapidly exploring random tree algorithm-based path planning for robot-aided optical manipulation of biological cells. IEEE Trans. Autom. Sci. Eng. 2014, 11, 649–657. [Google Scholar] [CrossRef]
- Iram, N.; Amna, K.; Zulfiqar, H. A Comparison of RRT, RRT* and RRT*-Smart Path Planning Algorithms. Int. J. Comput. Sci. Netw. Secur. 2016, 16, 20–27. [Google Scholar]
- Gammell, J.D.; Srinivasa, S.S.; Barfoot, T.D. Informed RRT: Optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2997–3004. [Google Scholar]
- Chi, W.Z.; Meng, M.Q.H. Risk-RRT: A robot motion planning algorithm for the human robot coexisting environment. In Proceedings of the 18th International Conference on Advanced Robotics (ICAR), Hong Kong, China, 10–12 July 2017; pp. 583–588. [Google Scholar]
- Yuan, Q.N.; Yi, J.H.; Sun, R.T.; Bai, H. Path Planning of a Mechanical Arm Based on an Improved Artificial Potential Field and a Rapid Expansion Random Tree Hybrid Algorithm. Algorithms 2021, 14, 321. [Google Scholar] [CrossRef]
- Jiang, Q.S.; Cai, K.; Xu, F.Y. Obstacle-avoidance path planning based on the improved artificial potential field for a 5 degrees of freedom bending robot. Mech. Sci. 2023, 14, 87–97. [Google Scholar] [CrossRef]
- Jin, Y. Decentralized adaptive fuzzy control of robot manipulators. IEEE Trans. Syst. Man Cybern. 1998, 28, 47–57. [Google Scholar]
- Mummadi, V. Design of robust digital PID controller for H-bridge soft switching boost converter. IEEE Trans. Ind. Electron. 2011, 58, 2883–2897. [Google Scholar] [CrossRef]
- Wai, R.J.; Lee, J.D.; Chuang, K.L. Real-time PID control strategy for maglev transportation system via particle swarm optimization. IEEE Trans. Ind. Electron. 2011, 58, 629–646. [Google Scholar] [CrossRef]
- Kim, K.; Rao, P.; Burnworth, J. Self-Tuning of the PID Controller for a Digital Excitation Control System. IEEE Trans. Ind. Appl. 2010, 46, 1518–1524. [Google Scholar]
- Muszynski, R.; Deskur, J. Damping of torsional vibrations in high dynamic industrial drives. IEEE Trans. Ind. Electron. 2010, 57, 544–552. [Google Scholar] [CrossRef]
- Khan, M.A.S.K.; Rahman, M.A. Implementation of a wavelet based MRPID controller for benchmark thermal system. IEEE Trans. Ind. Electron. 2010, 57, 4160–4169. [Google Scholar] [CrossRef]
- Wang, J.; Wang, C.H.; Chen, C.L.P. The Bounded Capacity of Fuzzy Neural Networks (FNNs) via a New Fully Connected Neural Fuzzy Inference System (F-CONFIS) with Its Applications. IEEE Trans. Fuzzy Syst. 2014, 22, 1373–1386. [Google Scholar] [CrossRef]
- Cheng, M.B.; Su, W.C.; Tsai, C.C. Robust tracking control of a unicycle-type wheeled mobile manipulator using a hybrid sliding mode fuzzy neural network. Int. J. Syst. Sci. 2010, 43, 408–425. [Google Scholar] [CrossRef]
- Du, G.L.; Liang, Y.H.; Gao, B.Y.; Otaibi, S.A.; Li, D. A Cognitive Joint Angle Compensation System Based on Self-Feedback Fuzzy Neural Network with Incremental Learning. IEEE Trans. Ind. Inform. 2020, 17, 2928–2937. [Google Scholar] [CrossRef]
- Mai, T. Hybrid adaptive tracking control method for mobile manipulator robot based on Proportional–Integral–Derivative technique. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 6463–6480. [Google Scholar] [CrossRef]
- Ander, I.; Elena, L.; Ander, A.; Andoni, R.; Iker, L.; Carlos, T. Learning positioning policies for mobile manipulation operations with deep reinforcement learning. Int. J. Mach. Learn. Cybern. 2023, 14, 3003–3023. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Wang, F.; Ren, B.M.; Liu, Y.; Cui, B. Tracking Moving Target for 6 degree-of-freedom Robot Manipulator with Adaptive Visual Servoing based on Deep Reinforcement Learning PID Controller. Rev. Sci. Instrum. 2022, 93, 045108. [Google Scholar] [CrossRef]
- Geng, H.; Hu, Q.; Wang, Z. Optimization of Robotic Arm Grasping through Fractional-Order Deep Deterministic Policy Gradient Algorithm. J. Phys. Conf. Ser. 2023, 2637, 012006. [Google Scholar] [CrossRef]
- Afzali, S.R.; Shoaran, M.; Karimian, G. A Modified Convergence DDPG Algorithm for Robotic Manipulation. Neural Process. Lett. 2023, 55, 11637–11652. [Google Scholar] [CrossRef]
- Spong, M.W.; Hutchinson, S.; Vidyasagar, M. Robot Modeling and Control. Ind. Robot Int. J. 2006, 17, 709–737. [Google Scholar]
- Yu, J.B.; Yang, M.; Zhao, Z.Y.; Wang, X.Y.; Bai, Y.T.; Wu, J.G.; Xu, J.P. Path planning of unmanned surface vessel in an unknown 593 environment based on improved D*Lite algorithm. Ocean Eng. 2022, 266, 112873. [Google Scholar] [CrossRef]







| Parameters | Definition | Numerical Value |
|---|---|---|
| w (rad/s) | Maximum angular velocity of motor | 0.5 |
| a1 (rad) | Maximum angle of Joint 1 | 2π |
| a2 (rad) | Maximum angle of Joint 2 | π |
| a3 (rad) | Maximum angle of Joint 3 | π |
| a4 (rad) | Maximum angle of Joint 4 | π |
| a5 (rad) | Maximum angle of Joint 5 | 0.5π |
| x (m) | Minimum x-axis length of obstacle | 0.05 |
| y (m) | Minimum y-axis length of obstacle | 0.05 |
| z (m) | Minimum z-axis length of obstacle | 0.05 |
| Rs (m) | Safety range of mobile robotic arm | 0.05 |
| Algorithm Name | Path Length (m) | Total Steering Angle (°) | Branch Account | Planning Time (s) |
|---|---|---|---|---|
| Algorithm 1 | 0.4312 | 95.32 | 34 | 12.64 |
| Algorithm 2 | 0.3264 | 75.21 | 30 | 11.75 |
| Algorithm 3 | 0.2771 | 61.54 | 23 | 10.44 |
| Algorithm 4 | 0.2355 | 54.85 | 15 | 9.31 |
| Coordinates | Algorithm Name | Path Length (m) | Total Steering Angle (°) | Branch Account | Planning Time (s) |
|---|---|---|---|---|---|
| (0.142, 0.137) (−0.145, −0.134) | Algorithm 1 | 0.4134 | 90.43 | 31 | 13.08 |
| Algorithm 2 | 0.3329 | 74.55 | 26 | 12.59 | |
| Algorithm 3 | 0.2726 | 62.13 | 21 | 11.97 | |
| Algorithm 4 | 0.2173 | 50.77 | 13 | 11.05 | |
| (−0.138, 0.143) (0.155, −0.149) | Algorithm 1 | 0.4527 | 97.66 | 40 | 14.62 |
| Algorithm 2 | 0.3591 | 78.73 | 35 | 13.29 | |
| Algorithm 3 | 0.2864 | 64.35 | 27 | 12.47 | |
| Algorithm 4 | 0.2485 | 56.31 | 16 | 10.84 | |
| (0.133, −0.156) (−0.148, 0.143) | Algorithm 1 | 0.4297 | 94.65 | 32 | 12.47 |
| Algorithm 2 | 0.3362 | 76.31 | 24 | 11.77 | |
| Algorithm 3 | 0.2538 | 60.87 | 17 | 10.95 | |
| Algorithm 4 | 0.2253 | 51.94 | 10 | 9.48 |
| Controller | Tracking Time (s) | Time-Delay (s) | Maximum Tracking Error (m) | Minimum Tracking Error (m) |
|---|---|---|---|---|
| Controller 1 | 12.09 | 1.25 | 0.0485 | 0.0309 |
| Controller 2 | 11.46 | 0.97 | 0.0433 | 0.0277 |
| Controller 3 | 9.73 | 0.64 | 0.0359 | 0.0251 |
| Controller 4 | 7.33 | 0.49 | 0.0283 | 0.0195 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Wu, J.; Xu, J.; Wang, X.; Cui, X.; Wang, B.; Zhao, Z. A Novel Planning and Tracking Approach for Mobile Robotic Arm in Obstacle Environment. Machines 2024, 12, 19. https://doi.org/10.3390/machines12010019
Yu J, Wu J, Xu J, Wang X, Cui X, Wang B, Zhao Z. A Novel Planning and Tracking Approach for Mobile Robotic Arm in Obstacle Environment. Machines. 2024; 12(1):19. https://doi.org/10.3390/machines12010019
Chicago/Turabian StyleYu, Jiabin, Jiguang Wu, Jiping Xu, Xiaoyi Wang, Xiaoyu Cui, Bingyi Wang, and Zhiyao Zhao. 2024. "A Novel Planning and Tracking Approach for Mobile Robotic Arm in Obstacle Environment" Machines 12, no. 1: 19. https://doi.org/10.3390/machines12010019
APA StyleYu, J., Wu, J., Xu, J., Wang, X., Cui, X., Wang, B., & Zhao, Z. (2024). A Novel Planning and Tracking Approach for Mobile Robotic Arm in Obstacle Environment. Machines, 12(1), 19. https://doi.org/10.3390/machines12010019









