Experimental Study on the Effect of Microchannel Spacing and Fractal Angle on Bubble Growth Behavior

Abstract

Bubble growth behavior significantly influences boiling heat transfer performance, and different microchannel structures and configurations affect bubble growth behavior. To explore the impact of microchannel structures and configurations on the growth behavior of boiling bubbles, two types of microchannel test plates were fabricated on copper substrates using laser machining technology. It was a parallel configuration plate with five different microchannel spacings and a blade vein configuration plate with four different fractal angles. The bubble growth behavior on these two types of surfaces was studied through visual experiments. The results show that smaller microchannel spacing leads to earlier bubble coalescence and departure times under the same degree of superheat. The 3.00 mm microchannel spacing is the critical interfering distance for the parallel configuration plates, while interference behavior occurs for the bubbles on the simulated vein configuration plates at any fractal angle. Furthermore, in different ranges of superheat, the bubble departure diameter increases with increasing superheat, and the frequency of bubble departure initially increases and then decreases with increasing superheat. This study provides experimental data support and design reference for the design of heat transfer plate structures.

1. Introduction

As the integration density of electronic devices increases, the high heat flux density problem that comes with it will pose a severe challenge to the operational reliability of one of the key components of electronic devices: the chip. Boiling heat transfer, which utilizes the absorption of a large amount of latent heat of vaporization during liquid phase change, became an effective means of addressing chip thermal management issues [1,2].

Over the years, extensive research efforts were devoted to enhancing boiling heat transfer to increase heat transfer efficiency and improve the heat transfer coefficient and peak heat flux density. Passive strengthening techniques that do not require external energy excitation drew widespread attention from scholars. Wenbin Zhou et al. [3] utilized an optimized self-assembled surface of graphene oxide (GO) to significantly enhance the boiling heat transfer performance, resulting in the achievement of a critical heat flux (CHF) of 261 W cm⁻²; Juan C et al. [4] employed a surface treatment method called “Boehmite treatment” to enhance the boiling heat transfer performance of aluminum surfaces. The treated aluminum surface exhibited an 80% higher CHF compared to a similarly roughened copper surface; and Matic Može et al. [5] achieved surface hydrophilicity and hydrophobicity on a substrate through laser processing and hydrophobic treatment. Surprisingly, they found that the hydrophobic surface exhibited comparable (or even higher) CHF values compared to hydrophilic surfaces. Traditionally, hydrophilic surfaces were believed to be more favorable for achieving high CHF values. In the pool boiling experiments conducted by Ji Hoon Kim et al. [6], an astonishing 473% enhancement in CHF was achieved when a mixture of alumina particles (Al₂O₃) and reduced graphene oxide (RGO) colloid particles were combined in a certain proportion, compared to pure water as the working fluid. Other researchers also conducted pool boiling experiments using different nanofluids as the working fluid [7,8,9], and they found that CHF was enhanced compared to water in all cases; Lian Duan et al. [10] discovered a significant improvement in CHF when comparing surfaces with microstructures to smooth surfaces. Other studies also showed that surface microstructures can significantly enhance boiling heat transfer performance [11,12]. Additionally, Matthew Searle et al. [13] demonstrated that this surface treatment can delay the transition from pool boiling to film boiling, thereby improving heat transfer performance.

Among these techniques, the most widely used and convenient method is to modify the surface of the evaporation end, and the microchannel structure attracted more attention due to its high efficiency and low cost for improving heat transfer performance. Dančová, P et al. [14] used CNC technology to process microchannels on copper surfaces with a width of 0.30 mm, a depth of 0.20–0.40 mm, and an interval of 0.10 mm. It was found that when water was used as a working fluid, the heat transfer coefficient of microchannels with a depth of 0.30 mm was twice that of those with depths of 0.20 and 0.30 mm, and similar laws were observed when Novec-649 was used as a working fluid. This is because an increase in the depth of microchannels leads to a decrease in the distance from the heat source and an increase in the bottom temperature, resulting in nucleation at lower heat fluxes and superheats and a higher heat transfer coefficient. An increase in the depth of microchannels also means an increase in the height of micro-fins forming the channel walls. Higher micro-fins have lower temperatures at their tops, reducing the intensity of bubble generation from these surfaces. Wang, L et al. [15] employed electrical discharge wire-cutting technology to prepare T-shaped microchannels with different depths and widths on a copper surface. Experimental results indicate that the width of the microchannel had a greater impact on the boiling heat transfer characteristics than the depth of the microchannel. This is consistent with the conclusion of Ghiu, C.-D et al. [16]. Moreover, Łukasz J. Orman et al. [17] utilized laser processing technology to create microchannel surfaces on copper with varying depths, widths, and micro-fin widths. Through visual experiments, they investigated the heat transfer performance of these different microchannel surfaces. They found that the microchannel depth had the greatest impact on boiling heat transfer performance. Additionally, they proposed that the increase in boiling heat transfer performance was attributed to the increased number of surface pores after laser treatment, leading to a significant increase in nucleation site density, thereby significantly affecting boiling heat transfer performance.

Different cross-sectional shapes of microchannels have a significant impact on boiling heat transfer, and the distribution morphology of microchannels also cannot be ignored in their effect on the heat transfer characteristics [18]. Researchers found that the special vein distribution in heat-resistant plant leaves is one of the guarantees for their efficient heat dissipation capability [19]. Peng Yi [20] established a numerical model based on plant veins to study and analyze indicators such as capillary pressure, permeability, and flow resistance of the liquid–vapor core at the evaporation end. They discovered the influence patterns of fractal angles and dimensions of leaf vein configurations on heat dissipation performance, providing new insights for optimizing heat spreader structures. Zhou et al. [21], inspired by blades, designed a tree-like network with wedge-shaped channels. Boiling heat transfer experiments were conducted under different degrees of superheat at different branch levels. The results show that under capillary force, bubbles dispersed and moved within the wedge-shaped channels, and the mobility of bubbles helped them merge with other bubbles, increasing the heat transfer coefficient.

Although many scholars studied the pool boiling heat transfer characteristics, research on bubble growth behavior during boiling on different microchannel configuration plates is relatively scarce, while the bubble growth behavior on the boiling surface is an important factor that affects surface heat transfer performance [22]. Surface processing with microchannels is a typical method for enhancing surface heat transfer characteristics [23], while biological branching structures are highly efficient mass and heat transfer structures that evolved naturally over millions of years in nature [24]. We summarized the existing research and selected the rectangular microchannel structure along with the commonly used parallel arrangement method for microchannels. Additionally, we focused on the distinctive characteristics of vascular patterns in nature, specifically the fractal angles. Based on this, this study fabricates parallel structure baseplates with the same cross-sectional dimensions but different spacing, as well as microchannel baseplates with different fractal angles. Through visual experiments, the bubble growth behavior on these two types of microchannel baseplates is observed. Different microchannel spacing and fractal angles influencing bubble growth behavior under the same degree of superheat is explained. Additionally, the bubble characteristics on the two types of microchannel baseplates under different degrees of superheat are observed to characterize the effect of superheat on bubble growth behavior. This work provides experimental data support and design reference for the optimization of heat transfer plates.

2. Design of Visualization Experiment

This paper focuses on the visualization experimental design of parallel structure and blade vein-patterned microchannel baseplates. Employing laser processing technology, two types of microchannel configurations are fabricated on copper baseplates. A visualization boiling test platform is designed to investigate the bubble growth behavior on the two types of microchannel surface configurations in nucleate pool boiling experiments using deionized water as the working fluid.

2.1. Baseplate Preparing

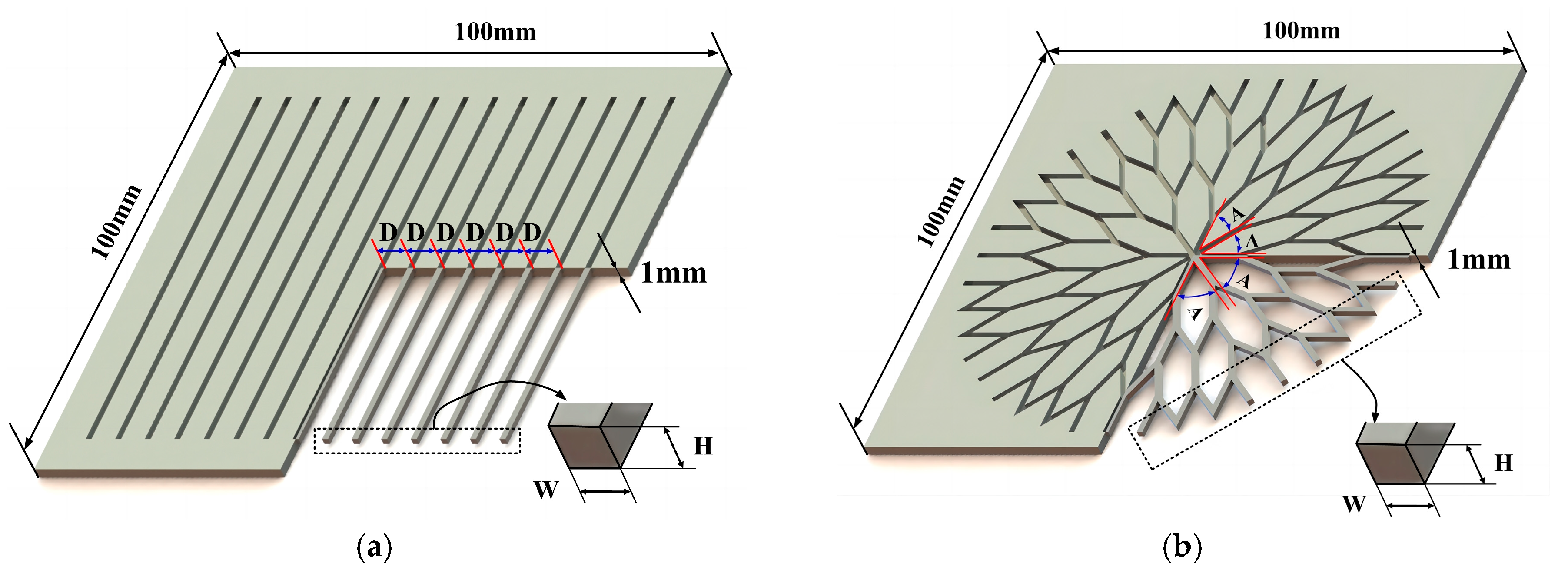
The laser processing technology was used to fabricate two types of microchannel surface configurations on a copper substrate, as shown in Figure 1.

Laser processing parameters exhibit a notable influence on the morphological properties of microchannels. Through conducting numerous experiments, preferable microchannel morphology characteristics on copper surfaces were achieved by obtaining specific laser processing parameters, as presented in

Table 1. Laser processing parameters.

Power (W)	Laser Scanning Speed (mm/s)	Laser Repetition Frequency (KHz)	Laser Scanning Fill Spacing (mm)	Processing Mode
18	300	50	0.01	10 × 10

. It is important to emphasize that, throughout the machining process, the debris remover must remain open continuously to minimize the adverse effects of generated debris on machining quality.

The structural parameters of the microchannel surface on the substrate are shown in

Table 2. Baseplates structural parameters.

Type	Width (W/μm)	Height (H/μm)	Spacing (D/mm)	Fractal Angle (A/°)
Parallel configuration	90	90	0.5	\
Parallel configuration	90	90	1.0	\
Parallel configuration	90	90	2.0	\
Parallel configuration	90	90	3.0	\
Parallel configuration	90	90	4.0	\
Blade vein configuration	90	90	\	18
Blade vein configuration	90	90	\	30
Blade vein configuration	90	90	\	45
Blade vein configuration	90	90	\	60

, and the finished processed substrate is shown in Figure 2.

2.2. Design of Visualized Testing System

A visualized pool boiling experimental system was designed and constructed to investigate the bubble growth behavior of two types of surface configurations during pool boiling. The visual experimental system operates based on the principles shown in Figure 3. The red arrows represent the boiling images captured by the high-speed camera and the regular camera, while the yellow circle points to the magnified image of the area inside the circle.

The boiling chamber in the visual experimental platform is composed of four pieces of quartz glass thermal welding. The open structure allows the cylinder to communicate with the air, ensuring that the pressure of the boiling fluid remains the same as the external atmospheric pressure. The heating device consists of 5 PCs of 100 W heating rods and a temperature controller. The temperature controller controls the power of the five heating rods by collecting the temperature of the heating platform, ensuring that the surface temperature of the heating platform is set to the designated temperature for the experiment. The heating platform is made of pure copper and has reserved installation positions for the heating rods at the bottom. The heating platform is placed in an insulated box made of PTFE material. The data acquisition system consists of multiple Pt100 temperature sensors and a multi-channel temperature acquisition module, which are used to detect the temperature of the heat-conducting copper block, the test baseplates, and the liquid working substance. The high-speed photography system consists of the Japanese Photron Mini-UX100 high-speed camera, a light source, and a computer. It captures high-speed motion bubbles, analyzes the captured video and image information, and studies bubble characteristics. The high-speed camera has a shooting rate of 4000 frames per second and a resolution of 1280 × 1024 pixels. The monitoring data and images obtained from the experiment are stored in the computer.

2.3. Experimental Process and Data Processing

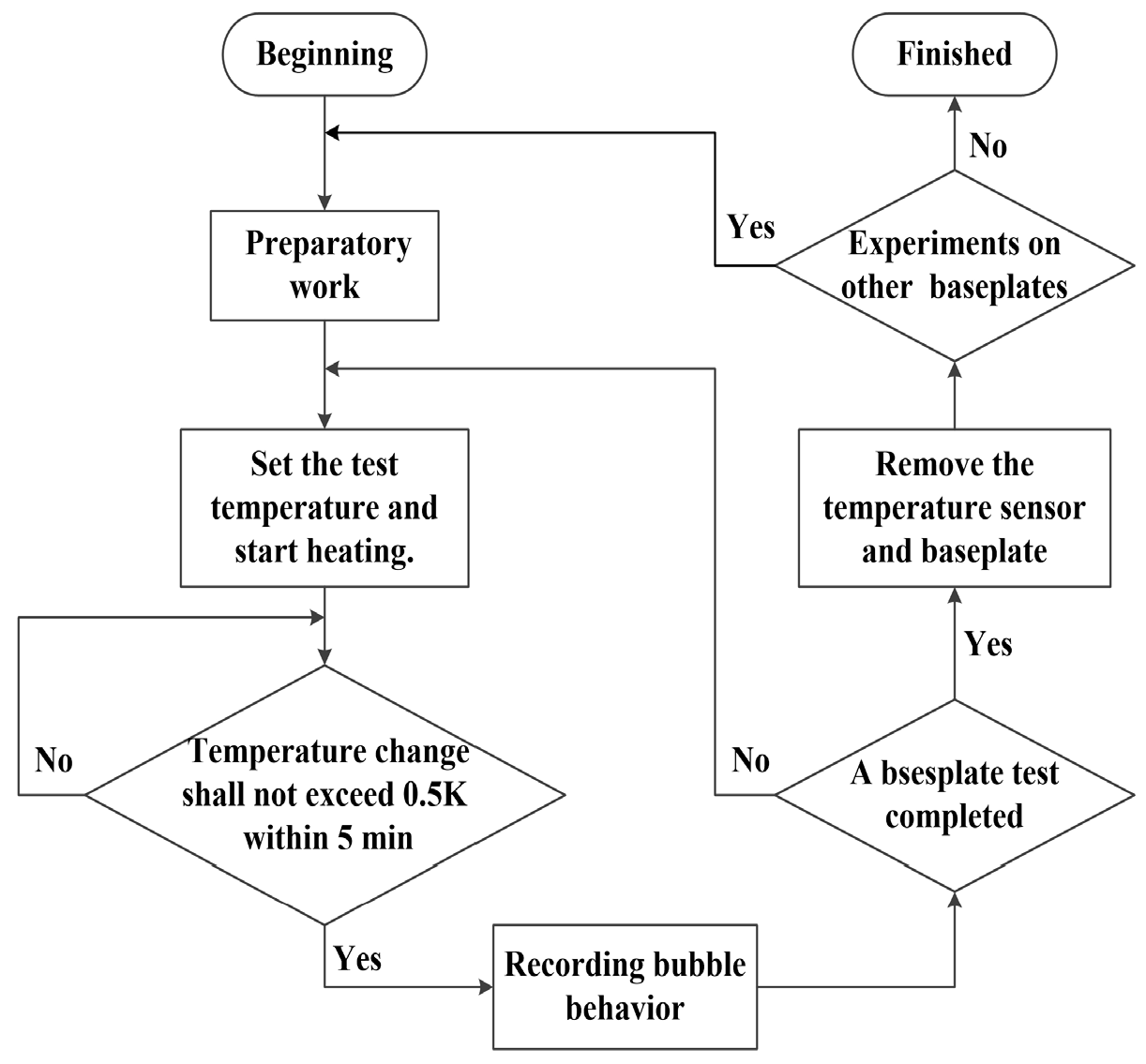
The experiment was conducted under the following conditions: ambient temperature of 20 °C (293.15 K), atmospheric pressure of 95.92 Kpa, and saturated deionized water as the boiling medium. The experimental process is shown in Figure 4:

At the beginning of the experimental preparation, the first step is to conduct the preparatory work, which involves the installation of the experimental test baseplate, sealing any gap between the baseplate and the heating stage, and injecting deionized water to achieve a liquid level of at least 80% of the boiling chamber height. After this, connect all equipment to the test bench, power it on, open the temperature controller, and heat the deionized water in the chamber until it reaches boiling point for at least an hour to remove non-condensable gases. During the boiling process, turn on the LED lights and high-speed camera, adjust the shooting distance and angle, and observe the microstructure and bubbles on the baseplate. Subsequently, adjust the temperature controller settings to lower the temperature of the baseplate below the deionized water’s boiling point, which marks the completion of the preparatory work. Upon completion of the preparatory work, it is necessary to set the desired experimental temperature, open the temperature sensor data acquisition software, and begin to take bubble images when the monitored baseplate temperature fluctuates within a range of less than 0.5 K for five minutes. If planning to conduct further experiments on the same baseplate, it is recommended to maintain the same filming conditions until all tests are completed. After the completion of the baseplate experiment, wait for the heating platform to cool down to room temperature, remove all temperature sensors and the baseplate, and thoroughly clean the heating platform. To conduct experiments on other test baseplates, it is necessary to repeat the experimental process as described above.

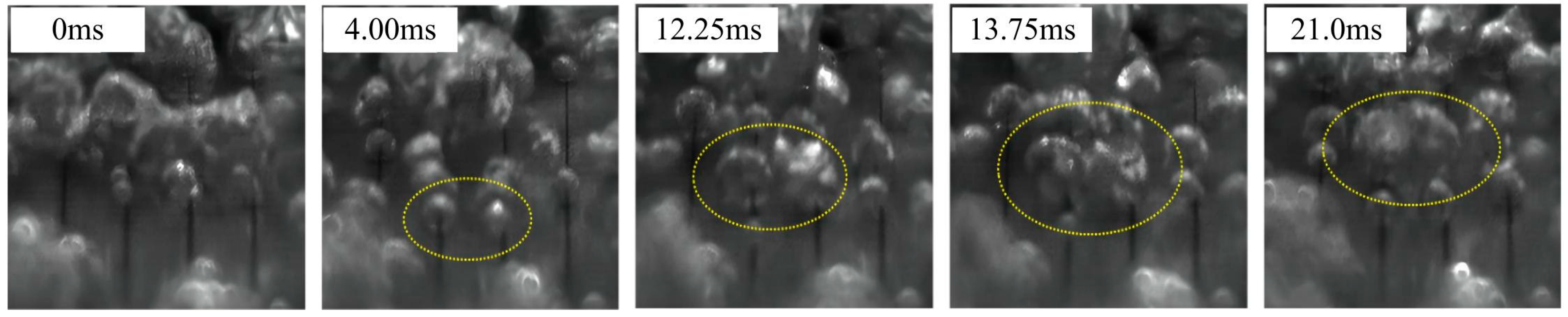
To facilitate the analysis of bubble growth behavior on the baseplates of the two types of microchannels, the moment when the bubbles grow from the nucleation point is defined as the zero moment, 0 ms. The bubbles went through five stages: begin (beginning of growth), growth (the start of interference between bubbles), intervene (continuation of growth after interference), escape (departure from the surface), and return (the production of new bubbles at departure points). The bubble images captured in this study correspond to the aforementioned five stages.

The experimentally obtained image data were processed as follows: the bubble diameter ($D_b$) was referenced to the size of the microchannels on the baseplates ($L_b$), and the corresponding number of pixel points in the bubble image (A) and the number of pixel points in the microchannel image (B) were calculated using image processing software. Therefore, the bubble diameter ($D_b$) was calculated as follows:

$$D_b=\frac{A}{B}{L}_b.$$

(1)

The bubble departure frequency (f/Hz) was defined as the time interval between two frames captured by the high-speed camera, and the frame rate of the high-speed camera used in this experiment was 4000 frames/second. Therefore, 1 Hz = 0.25 ms.

2.4. Error Analysis

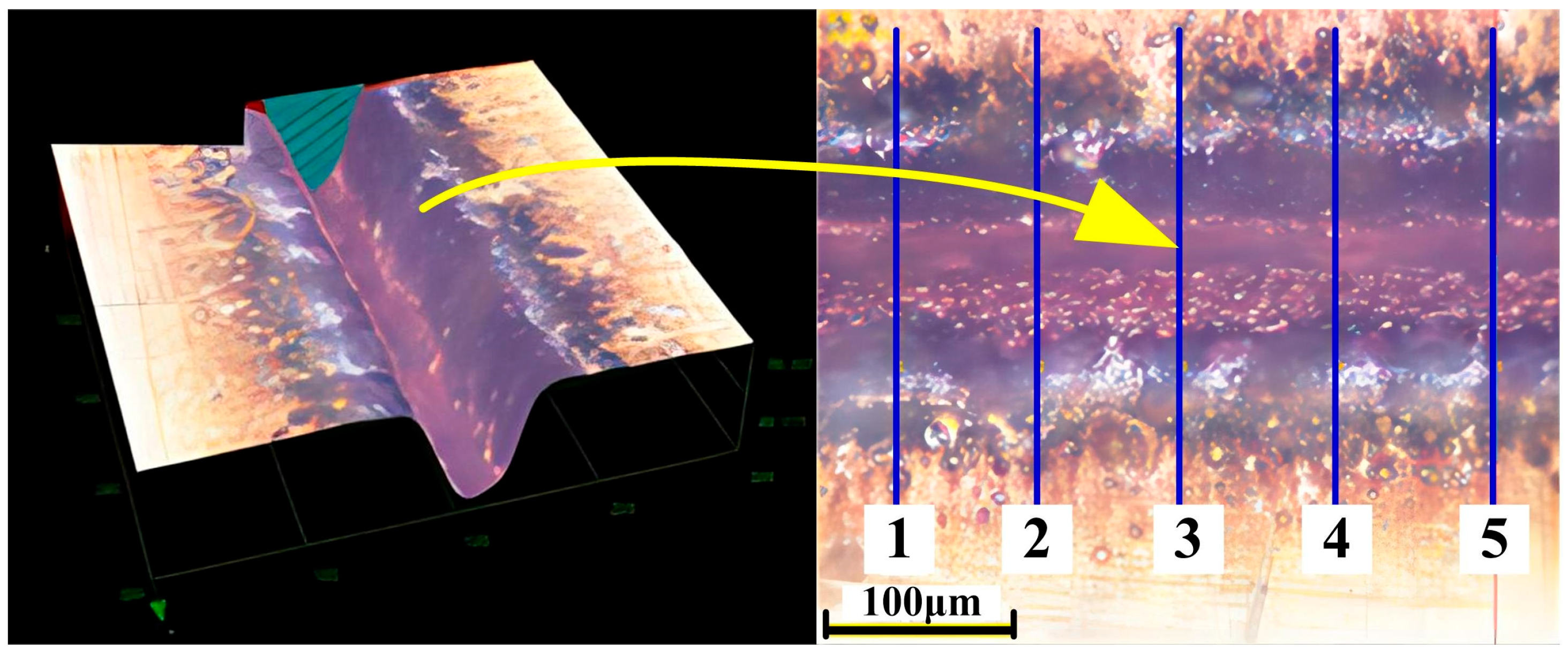
After laser processing, the morphology of the processed pattern was observed under a super depth of field microscope, as shown in Figure 5. Five random measurement lines were delineated on the sample, corresponding to 1–5 on the right side of Figure 5. The measurement instrument is capable of generating the cross-sectional profile of the microchannels in the selected area based on the designated measurement lines. By comparing the measured profile dimensions with the previously determined microchannel dimensions, it was determined that the maximum depth error of the microchannels is 2.01 µm, with an average depth of 90.77 µm. The surface dimension error does not exceed 10%, ensuring the accuracy of the experimental results.

The temperature measurement error required for the Pt100-type sensor used in the experiment is ±0.3 K. The measurement accuracy of the temperature controller is 0.3% FS full scale (FS), where the temperature controller used in the experiment has a full-scale range of 200 °C (413.15 K). According to the error propagation calculation method [25], the measurement error of the bubble diameter caused by microchannel machining error is 0.02 mm, and the temperature measurement error caused by the temperature controller and PT100 temperature sensor is 0.67 K. In the experiment, the degree of superheat is equal to the substrate temperature minus the saturation boiling temperature of deionized water. Due to the constant environmental temperature and atmospheric pressure in the laboratory, the boiling point of deionized water can be considered constant. Therefore, the measurement error of superheat is equal to the aforementioned temperature measurement error of 0.67 K. Additionally, considering the human error in the experiment, the method of acquiring multiple experimental data and taking the average value after excluding the maximum and minimum values is used to minimize the influence of random errors on the experimental results.

In conclusion, the experimental device errors are within the allowable range, and the experimental results are reliable.

To validate the accuracy of the experimental apparatus, three random temperature measurement points were selected on the surface of the heating base. As shown in Figure 6, after setting the temperature controller to 100.00 °C (373.15 K) and waiting for the heating platform to reach the set temperature, a 30 min test revealed that the maximum temperature difference between the three temperature measuring points was 0.95 K and the maximum temperature difference for a single measuring point was 0.52 K. The heating platform maintained an average temperature of 100.25 °C (373.40 K) over the 30 min, with an error that was within an acceptable range. This indicates that the test data generated by the testing platform are accurate.

3. Bubble Growth Behavior on Baseplates

This article performs boiling experiments on structured substrates with different inter-channel spacings for parallel configurations and different fractal angles for blade vein configurations. The boiling surface bubble growth behavior of different microchannel configurations is analyzed, and the impact rules of the inter-channel spacing and fractal angles on bubble growth behavior are identified. Both experiments were captured after stable boiling status for 5 min at a superheat of ΔT = 6 K on the base plate.

3.1. Parallel Configuration Baseplates

This section investigates the growth behavior of boiling bubbles on experimental substrates with five distinct microchannel spacings, employing a high-speed camera. The most distinct bubble growth behavior was selected for observation. The images depicting the progression of bubble growth are arranged in chronological order from left to right, showcasing the following stages: initiation of growth, interference between bubbles, uninterrupted growth post-interference, departure from the surface, and generation of new bubbles at departure points. The specific objects of observation in the images pertaining to bubble growth behavior have been circled using yellow circles.

Figure 7a shows the boiling bubble image on the parallel configuration surface with a microchannel spacing of 0.5 mm. Two nucleation points were randomly selected to observe the interference behavior of bubbles. At time 0 ms, initial bubbles were generated in each adjacent microchannel, and no other bubbles were generated nearby. After 3.50 ms of growth, the two bubbles began to merge, and at 4.75 ms, they fused and detached from the surface. New bubbles were then generated at the original positions after 4.00 ms.

Figure 7b–d shows boiling bubble images with microchannel spacing of 1.0 mm, 2.0 mm, and 3.0 mm, respectively. A large number of bubbles were generated on the microchannels, and the nucleation points were distributed densely and uniformly. Compared with the surface with a microchannel spacing of 0.5 mm, the two bubbles on the surface with a microchannel spacing of 1 mm began to merge at 2.25 ms, 0.25 ms earlier, and completed the fusion and detached from the surface at 6.50 ms. The bubbles on the surface with a microchannel spacing of 2.0 mm began to merge at 5.50 ms later than the previous two spacing cases and completed the fusion and detached from the surface at 3.75 ms, followed by the appearance of new bubbles at 11.00 ms.

The bubbles on the surface with a microchannel spacing of 3.0 mm exhibited similar growth patterns to those in Figure 7a–c. However, the fusion and detachment time was longer, resulting in delayed detachment.

Figure 7e presents the boiling bubble image with a microchannel spacing of 4.0 mm. Unlike the other spacing baseplates, no interference occurred during the entire period from the formation and growth to the detachment of bubbles from the surface. The bubbles experienced 13.75 ms of growth before leaving the surface. This suggests that there is no interference phenomenon in boiling bubbles on the parallel configuration surface with a microchannel spacing of 4.0 mm at ΔT of 6 K.

Based on Figure 8, it was observed that decreasing microchannel spacing led to earlier interference and detachment of bubbles, while larger spacing resulted in longer detachment times. In several experiments, the surface bubbles with a spacing of 3.00 mm exhibited distinctive growth behavior. The growth of bubbles differed under high and low superheating conditions. In the low superheating scenario, bubbles experienced smooth detachment from the wall after the initial growth, fusion, and detachment stages. Conversely, under high superheating, boiling was vigorous, and bubble growth was rapid. Adjacent bubbles did not interfere with each other during the generation, growth, and detachment phases, as depicted in Figure 9. Single bubbles grew for 13.75 ms before detaching from the wall and merging into a larger bubble.

3.2. Blade Vein Configuration Baseplates

Visualization experiments were carried out on four distinct fractal angle configurations of the simulated vein structure substrate to investigate the growth behavior of boiling bubbles. Similar to what was mentioned in Section 3.1, the specific bubble of interest has also been marked with a yellow circle in the image. It was noted that, throughout the boiling process, small bubbles have a tendency to form near the bifurcation points of the microchannels and subsequently converge swiftly to form a larger bubble before detaching from the surface. In contrast to the parallel configuration substrate, the occurrence of bubble interference phenomena was observed on all four tested substrates with varying fractal angles.

Figure 10a shows the boiling image of the blade vein configuration with a fractal angle of 60°. At 0 ms, a very small initial bubble is generated in the channel; at 1.25 ms, the bubble grows, and another bubble forms tightly below it at the branching point. The two bubbles begin to merge at 4.50 ms, and at 12.25 ms, they fuse and detach from the surface. At 16.75 ms, a new bubble is generated at the branching point.

Figure 10b–d shows boiling bubble images on baseplates with fractal angles of 45°, 30°, and 18°, respectively. The bubble morphology is regular, and most of the bubble nucleation sites are located inside the channel. From Figure 10b, it can be seen that the bubble growth behavior during 0–1.25 ms on the surface with a fractal angle of 45° is similar to that in Figure 10a. Notably, at 1.25 ms, a bubble grows from the upper right of the original bubble. At 7.00 ms, the two bubbles begin to merge and completely fuse at 10.75 ms before detaching from the surface. A new bubble is generated at 15.25 ms.

On the surface with a 30° fractal angle in Figure 10c, the early-stage bubble growth behavior is similar to Figure 10a,b. At 1.75 ms, a small bubble is generated above and below the original bubble, and another bubble is generated on the lower right side. By 7.00 ms, the four bubbles initiate the merging process. Subsequently, at 10.75 ms, the bubbles fully merge and detach from the surface. At 13.75 ms, a new bubble is generated at the nucleation site, accompanied by the generation of multiple nearby bubbles. The rate of growth for this new round of bubbles is faster in comparison to the growth observed at the 60° fractal angle.

The growth image of bubbles on the surface of a blade vein configuration with a fractal angle of 18° is shown in Figure 10d. After only 8.00 ms of growth, the bubbles detach from the surface. This detachment time is shorter compared to surfaces with other fractal angles.

By comparing the detachment times in Figure 11 for the four fractal angles, it can be found that as the fractal angle of the microchannels increases, the detachment time also increases. However, there is only a small difference in detachment time between the baseplates with the four fractal angles. The reason for this is that when boiling occurs at the branching points on the blade vein surface, multiple small bubbles are generated, and the growth rate of the bubbles can be accelerated by the merging of multiple bubbles. The surface with a fractal angle of 60° has the longest detachment time for the boiling bubbles among the baseplates with different fractal angles.

4. Characteristics of Bubbles under Different Degrees of Superheat

In the study of the bubble growth behavior on the baseplates with different micro-channel spacing in a parallel structure, it was found that the bubble growth behavior of the test plate with a micro-channel spacing of 3.00 mm differs under high and low degrees of superheat, indicating that the influence of superheat on the bubbles on the baseplates cannot be ignored. In previous studies, the effect of superheat on bubble characteristics was observed to have a significant impact both on hydrophobic and hydrophilic surfaces [26], as well as in non-aqueous working fluids [22].

To investigate the influence of different degrees of superheat on the bubble growth behavior of the two types of micro-channel configurations on the baseplates, two bubble characteristics, namely the bubble departure diameter and the bubble departure frequency during the bubble growth process, were selected to characterize the effect of superheat on the bubble growth behavior [27]. Simultaneously, these two bubble characteristic parameters also affected the boiling heat transfer performance [28]. Therefore, it is necessary to study the bubble characteristics during the bubble growth process in pool boiling.

4.1. Bubble Detachment Diameter

The method in Section 2.3 was employed to conduct a statistical analysis of the bubble departure diameters for nine distinct types of boiling bubbles at varying levels of superheat. Curves were utilized to connect the data points, facilitating the depiction of data trends and minimizing the visual clutter resulting from dense data point distribution. It is crucial to emphasize that the curve connections between adjacent data points serve a visual representation purpose solely and do not accurately represent the actual magnitude of the data.

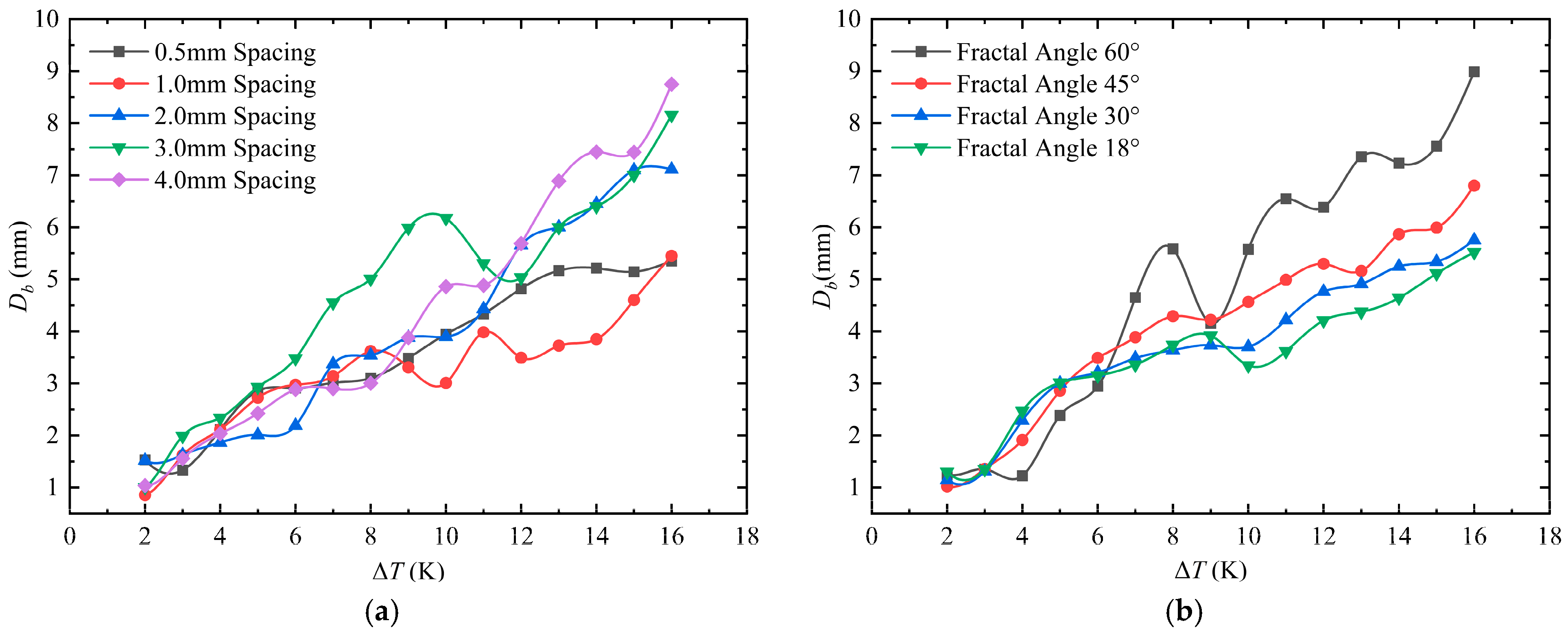
From Figure 12a, it can be observed that the difference in bubble departure diameter on the five baseplates is not significant when ΔT is between 2 K and 5 K. The test plate with a spacing of 0.5 mm has the largest bubble departure diameter at the beginning of boiling. The test plate with a spacing of 3.00 mm has the largest bubble departure diameter when ΔT is between 2 K and 10 K. The surface with a spacing of 4.00 mm has a medium position in the curve of bubble departure diameter when ΔT < 10 K, and the test plate with a spacing of 4 mm has the largest bubble departure diameter throughout the process after ΔT > 12 K.

As shown in Figure 12b, for the blade vein configuration baseplates when ΔT is between 2 K and 6 K, similar to the parallel configuration baseplates, the difference in bubble departure diameter among the groups is small, and the test plate with a fractal angle of 60° has the smallest bubble departure diameter in this range. When ΔT > 6 K, the bubble departure diameter on all four baseplates increases with the increase in superheat, and the test plate with a fractal angle of 60° has a larger bubble departure diameter than other baseplates. This indicates that as the degree of superheat increases, baseplates with larger fractal angles are more conducive to bubble coalescence and growth. In particular, a significant oscillation occurred on the test plate, with a fractal angle of 60°at ΔT = 9 K due to nearby large bubbles attracting small bubbles away from the wall during the bubble growth process.

Combining the bubble departure diameter of the two types of configuration baseplates, it is found that under low superheat conditions, the smaller the microchannel spacing and fractal angle, the larger the bubble departure diameter. A compact surface structure is conducive to positive interference between bubbles, promoting the increase in bubble departure diameter. However, under high superheat conditions, the intensified boiling behavior on a dense structure surface causes more interference between bubbles, which is unfavorable for bubble coalescence and growth, resulting in a decrease in the bubble departure diameter. Overall, the bubble departure diameter increases with the increase in microchannel spacing and fractal angle, and it also increases with the increase in superheat.

4.2. Bubble Detachment Frequency

The measurement method for bubble departure frequency at different degrees of superheat is also derived from Section 2.3. In the test plate with two different microchannel distribution patterns, it was observed that the bubble frequency increased initially and then decreased with increasing degrees of superheat.

From Figure 13a, it can be observed that as the degree of superheat increases, the bubble detachment frequency of the five baseplates shows a trend of first increasing and then decreasing. There is a significant difference in the peak detachment frequency corresponding to different channel spacings at different degrees of superheat. Among them, the 0.5 mm test plate has the highest detachment frequency at ΔT = 5 K, while the peak detachment frequency for the other four spacings occurs at ΔT = 8 K. When 2 K ≤ ΔT ≤ 5 K, the bubble detachment frequency for all five spacings shows an increasing trend. When 5 K < ΔT ≤ 8 K, the bubble detachment frequency on the five baseplates reaches its experimental peak value. The 1.0 mm spacing test plate has the highest detachment frequency at ΔT = 8 K (f = 129.03 Hz), and the highest detachment frequencies for the other structural plates are 2.0 mm (108.11 Hz), 3.0 mm (86.96 Hz), and 4.0 mm (72.73 Hz), respectively. When ΔT > 8 K, the bubble detachment frequency on the five baseplates decreases with the continued increase in ΔT. This is because higher degrees of superheat lead to an increase in nucleation sites, resulting in the accumulation of a large number of bubbles, which promotes bubble coalescence and growth. At the same time, the bubble coalescence time increases, leading to a decrease in the bubble detachment frequency.

As shown in Figure 13b, the bubble detachment frequency of the four baseplates increases initially and then decreases as the degree of superheat rises. The distribution of peak detachment frequencies for the fractal vein configuration is different from that of the parallel structure plates, with the peak concentrations occurring in the range of 7 K ≤ ΔT ≤ 8 K. When ΔT ≤ 4 K, there is minimal difference in the bubble detachment frequencies among the four baseplates due to the absence of bubble interference, resulting in similar bubble frequencies. When 4 K ≤ ΔT ≤ 8 K, the plate with a fractal angle of 15° significantly increases its detachment frequency with increasing wall superheat, reaching a maximum point at ΔT = 7 K (138.15 Hz). The plates with fractal angles of 45° and 60° show a slight increase in detachment frequency as ΔT increases, with their respective maximum values occurring at ΔT = 8 K(81.63 Hz) for the 45° structure and 70.18 Hz for the 60° structure. For ΔT > 8 K, the bubble detachment frequencies of the four baseplates decrease as ΔT continues to rise.

Overall, the bubble detachment frequencies of both types of baseplates increase with increasing degrees of superheat. Under high superheat conditions, a large number of bubbles tend to accumulate, which promotes bubble coalescence and prolongs the bubble coalescence time, leading to a significant decrease in bubble detachment frequency. Therefore, it is advisable to avoid operating both baseplates under high superheat conditions, with the optimal working range for both baseplates being between 6 K and 8 K of superheat.

4.3. Bubble Characteristics on Smooth Surfaces

To gain a more profound insight into the impact of the applied heat transfer surface on the growth behavior of boiling bubbles, bubble characteristic extraction was carried out on a smooth copper surface (Ra = 0.29 μm) under varying degrees of superheat. However, extraction of bubble characteristics was limited to ΔT ≤ 8 K due to the stochastic nature of boiling bubble growth and the significant interference among bubbles at high levels of superheat, as presented in

Table 3. Bubble departure characteristics of smooth copper surfaces at different superheat degrees.

Superheat (K)	Bubble Detachment Diameter (mm)	Bubble Detachment Frequency (Hz)
2	0.39	53.33
4	0.53	81.63
6	0.59	122.57
8	0.65	170.78

.

A notable disparity in bubble characteristics was observed between the smooth surface and the two mentioned surfaces in Table 3. Specifically, the detachment diameter of bubbles on the smooth surface exhibited a significant decrease compared to the other surfaces. However, the detachment frequency of bubbles showed a significant increase when ΔT > 6 K. This phenomenon can potentially be attributed to the intense interference among bubbles growing at the same nucleation site under conditions of high superheat. Further exploration is needed to investigate this intriguing phenomenon.

5. Conclusions

Using laser processing technology, nine surfaces with the same microchannel texture but different microchannel distribution patterns were prepared, including five different spacing parallel configuration surfaces and four different fractal angle imitation blade vein configuration surfaces. Under atmospheric saturated pool boiling conditions, deionized water was used as the working fluid, and the growth behavior of boiling bubbles was observed through visualization research methods. The following conclusions were drawn from the obtained results:

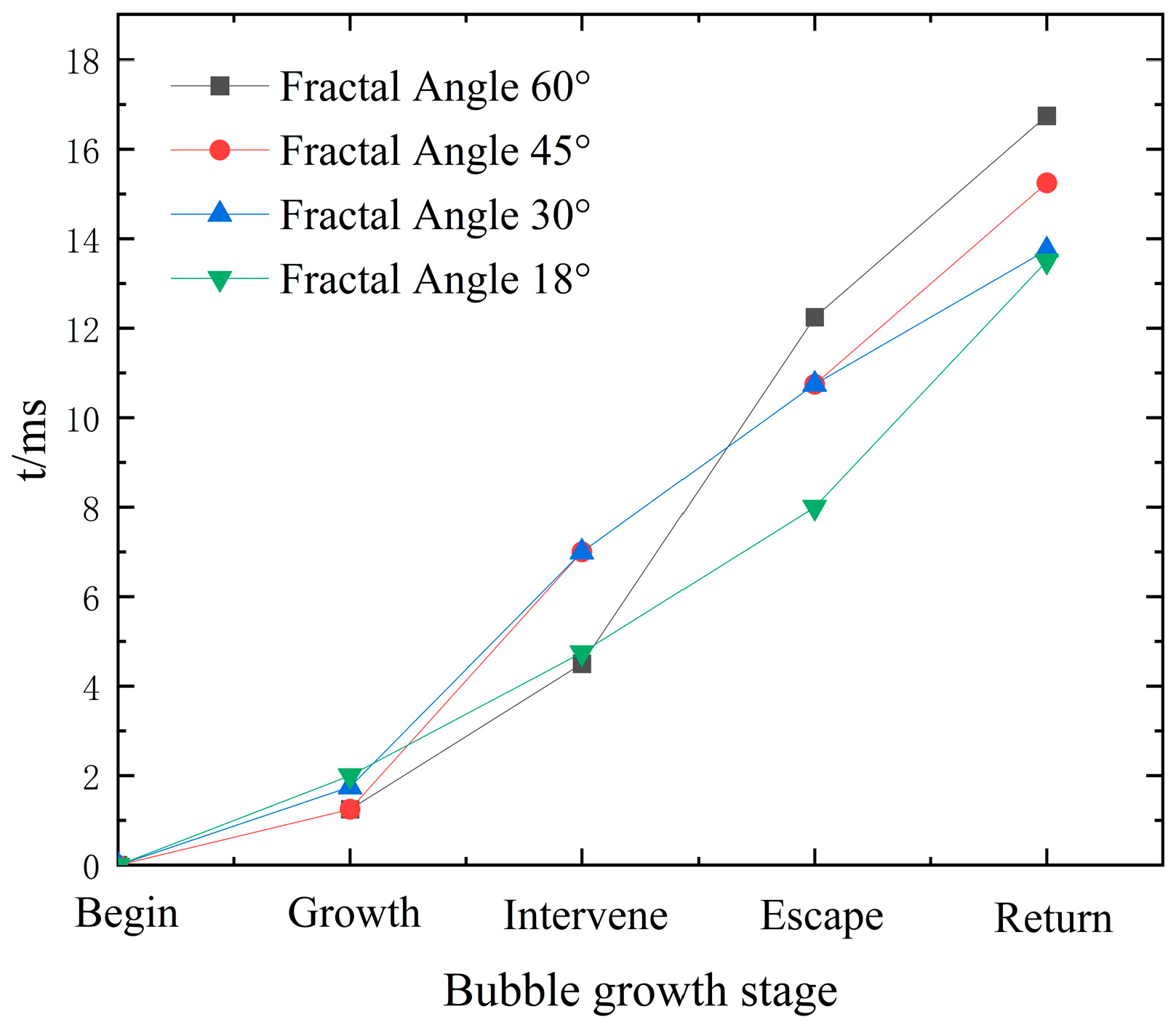
(1) The microchannel spacing has a significant impact on bubble growth behavior. At a degree of superheat of 6 K and microchannel spacing of 0.5 mm to 3.0 mm, adjacent bubbles interfere with each other, while there is no interference between bubbles during the growth process at a microchannel spacing of 4.0 mm. As the microchannel spacing increases, the bubble coalescence time, departure diameter, and departure time all gradually increase. The surface with a microchannel spacing of 4.0 mm has the longest bubble departure time. Particularly, the surface with a microchannel spacing of 3.0 mm has no interference between adjacent bubbles due to the intense boiling of the baseplates at high degrees of superheat, resulting in fast bubble growth.

(2) The larger the microchannel fractal angle, the longer the bubble departure time, but the differences in bubble departure time among the four baseplates with different fractal angles are small. This is because multiple small bubbles are generated during boiling at the branches of the imitation vein surface, and the multiple bubbles can coalesce with each other to accelerate bubble growth.

(3) The degree of superheat significantly affects the bubble growth behavior on the boiling surface. The bubble departure diameter increases with increasing microchannel spacing and fractal angle and increases with an increasing degree of superheat. However, at low degrees of superheat, the smaller the microchannel spacing and fractal angle, the larger the bubble departure diameter. The bubble departure frequency increases first and then decreases with increasing degrees of superheat, indicating that the negative interference between bubbles increases at high degrees of superheat, causing a significant reduction in the bubble departure frequency. For the smooth copper surface, the detachment diameter of bubbles significantly increased on both microchannel surfaces. However, there was a significant disparity in the detachment frequency compared to the previous surfaces, especially when ΔT > 6 K. This interesting phenomenon on the smooth copper surface still requires further exploration.

Our work focuses on the visualization study of boiling bubble behavior on surfaces with different microchannel distribution characteristics. The research findings can provide optimization design references and experimental data support for the boiling heat transfer on the heat sink plate. In future work, we will consider the relationship between bubble behavior and boiling heat transfer performance, and continue to explore the influence of microchannel distribution characteristics on boiling heat transfer performance. This will further contribute to the research value and engineering value in the field of heat transfer.