Abstract
Origami crawling robots, inspired by the principles of origami folding, have emerged as a promising approach for developing lightweight and flexible robots capable of navigating tight spaces. These robots utilize anisotropic friction, where the frictional forces between surfaces vary depending on the direction of motion, enabling controlled movement by changing the robot’s body orientation. While various actuation methods have been explored, such as pneumatic and magnetic systems, they suffer from limitations such as bulkiness or restricted workspace. In this paper, we propose a tendon-driven crawling robot that achieves anisotropic friction by controlling its out-of-plane curvature. By manipulating the robot’s shape and out-of-plane curvature, we can modulate the friction forces and enable efficient crawling motion. To maximize anisotropic friction, we design an asymmetric contact film composed of elastomer and polyester. We analyze the relationship between out-of-plane curvature and frictional force through experiments on flat and sloped surfaces, considering different leg angles and slope angles of the contact film. The results demonstrate the gait loss ratio of 1.96% for the optimized design, highlighting the robot’s ability to crawl efficiently with quick response times and a low-profile system. This research contributes to the advancement of origami-based crawling robots and their potential applications in confined and unstructured environments.
1. Introduction
An origami robot is a type of robot that is designed to move using the principles of origami, the traditional art of paper folding [1]. These robots are typically made from thin, flexible materials that can be folded into complex shapes, allowing them to move in a variety of ways [2,3]. It involves using origami principles to design and create structures and devices that can be folded, unfolded, and reconfigured in a controlled manner [4].
One of the key advantages of origami-based mechanisms is their ability to create complex structures and devices from simple, flat sheets of material [5]. By folding and creasing the material in a precise and controlled manner, engineers can create complex and functional shapes and patterns. Akio et al. performed and validated kinematic modeling of folding paper in a precise and controlled manner using a multi-fingered robotic hand [6]. Also, origami characteristics are available regardless of the size of the structure, even at the nanoscale. Single-stranded DNA particles can be assembled into 2D or 3D dimensional shapes, which can be given functions or perform tasks [7,8,9]. D.-N. Kim et al. presented designs that applied origami mechanisms on a micro-scale or utilized the properties of paper art [10,11]. The flexibility of origami structures can also be applied to continuum robots that require omnidirectionally bending or twisting [12,13]. In addition, they can be designed to be highly compact and portable, and have variable stiffness [14,15], making them ideal for space-constrained applications [16].
Origami crawling robots incorporate the principles of origami folding to create lightweight and flexible structures that can move in different directions and navigate through tight spaces [17]. They typically use anisotropic friction, the frictional forces between two surfaces can be different depending on the direction of motion [18,19,20,21]. This allows the robot to move in a controlled manner by changing the orientation of its body relative to the surface it is crawling on. To achieve anisotropic friction, the origami crawling robot typically has a series of folds or ridges on its body that create a pattern of high and low-friction areas. By adjusting the orientation of its body, the robot can use these different friction areas to grip the surface and move in a particular direction [22].
Researchers have studied various actuation methods for origami crawling robots. For example, Bhovad et al. exploited multi-stability for peristaltic locomotion and achieved anisotropic friction with this structure property [16]. Yu et al. designed the pneumatic-driven crawler using a miura-ori-based body for agile response [23]. Ze et al. presented a crawler powered by magnetic fields, which could easily perform a variety of motions and operate in tight spaces, offering a wide range of application possibilities [24]. Pneumatic and magnetic actuation systems are adopted thanks to the easiness to control and fast response time [20,23,24,25,26,27,28,29]. However, pneumatic-driven robots require bulky systems including pneumatic regulators, compressors, and control boards. Magnetically driven robots have relatively small workspaces because they require a strong magnetic field where their magnitude is exponentially decreased with respect to distance. Researchers also use shape memory alloys [30,31], electrostatic force [32,33], or dielectric materials [17,34,35], using their phase change by heat or electricity. They have the advantage of being lightweight and low profile, but typically have longer response times for cooling. Tendon-driven methods usually use motors as inputs. Tendons are responsible for transferring the motor’s electromotive force to the action points. This method is primarily used to reduce the space from a fixed point on the tendon to the point of force action. It can be one of the best ways to utilize origami’s ability to fold and unfold. The tendon-driven method has the advantage of designing a system that fits the purpose. For example, Yeunhee et al. used the tendons for the origami pump [36]. Instead of building a pneumatic drive system, they succeeded in actuating a pneumatic gripper using an origami chamber and a tendon drive, and also validated the system. In origami crawler research, Hritwick et al. proposed a Yoshimura pattern-based origami crawler with a tendon-driven single-motor mechanism [37]. Ming et al. designed origami continuum modules that include the slave controllers for the snake crawler [38]. The tendon drive in each module increases the overall workspace of the robot. However, since the tendon-driven method is simply pulling and releasing the tendon, it should benefit from additional design for the aforementioned purpose.
In this study, we propose a tendon-driven crawling robot using anisotropic friction by controlling its out-of-plane curvature. The origami robot reconfigures its shape in a controlled manner to change the out-of-plane curvature. The out-of-plane curvature changes the contact angle against the surface, so that it controls the robot’s friction force. We designed the contact film composed of elastomer and polyester to maximize anisotropic friction. The crawling motion is connected within the folded state; it provides low frictional force on the rear side and high friction on the front side. In the deployed state, there is high frictional force on the rear side and low friction on the front side. Thus, the robot can minimize slipping and proceed efficiently during its crawling motion. In addition, the robot has a quick response time by direct motor control of tendons and a low-profile system. We analyzed the relationship between the out-of-plane curvature against friction and validated the model with experiments on flat and sloped surfaces. The parametric study was performed with different leg angles and slope angles of the contact film.
The rest of this article is organized as follows: Section 2 presents the design, mechanism, and fabrication of the robot. Section 3 describes the experimental setup and results for robot crawling with different design parameters. It also demonstrates the robot’s crawling on the sloped surface. Section 4 summarizes this study and its contributions and suggests future work.
2. Design of the Origami Crawling Robot
This section presents the design, mechanism, and fabrication for the origami crawler, methods for the experiment, and the calculation process for the experimental result.
2.1. Characteristics of the Origami Structure
The Kresling structure [39] has four major design parameters (, , , ) as illustrated in Figure 1a. is the number of the base facet sides, is the side length of a base facet, is the half inner angle of the base facet polygon, and is the ratio between the internal angle of the side triangle facet made by the diagonal crease and the angle . The ratio is involved in the deployment state of the Kresling structure and if the does not exceed the specific value, the Kresling structure has mono-stability [16,25]. The parameter values for the Kresling structure used in this study are as follows. = 6, = 30 mm, = 60 and = 0.5. The diameter-to-length ratio is 0.5. This ratio is the value between the circumscribed circle diameter of the base facet and the structure’s body length. The circumscribed circle diameter of the base polygon is 30 mm. The vertical length of the symmetric Kresling structure is 60 mm. The structure stores partial energy of the input power when folded, and the stored energy is emitted during deployment. Utilizing the emitted energy, the overall system can be simplified by reducing the number of actuators controlling the structure.
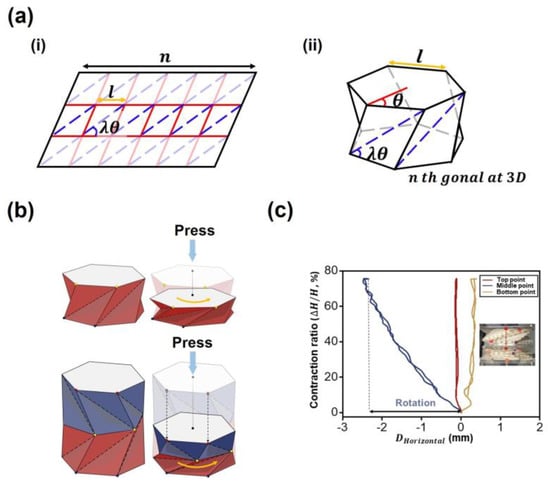
Figure 1.
Kresling structure for the origami crawler: (a) (i) 2D and (ii) 3D diagrams of the Kresling pattern present geometric parameters , , , . (b) Illustration of single and symmetric Kresling structures. (c) Response of the Kresling structure shows the pure translation against the press.
The translational movement of the Kresling structure is coupled with rotational movement. When a Kresling structure moves axially, diagonal creases on the side facets induce folding, resulting in rotational motion on the basal facets shown in Figure 1b. To avoid the coupling of the rotational movement, we adopted the symmetric composition of the Kresling structures whose diagonal creases of Kresling units are reversed to each other to avoid the coupling of rotational motion in Figure 1b. Thus, the proposed structure prevents the relative rotation between the two endpoints of the Kresling structure, so it can simplify the control of the crawling motion.
To validate this structural property, we performed a compression test along the axial direction of the proposed origami structure and checked pure translation shown in Figure 1b. The graph of Figure 1c demonstrates the contraction ratio versus horizontal deviation of selected points of the proposed structure. Thanks to its geometry, both endpoints and the midpoint of the structure have no relative rotational displacement to each other. After the symmetric Kresling structure is folded, it is deployed back by its restoring force and recovers the initial state.
2.2. Origami Crawler Mechanism
The origami crawler consists of an origami structure based on a symmetric Kresling structure with lightweight and high flexibility. That friction property efficiently transfers the forces that occur on the origami structure to the ground for crawling. The robot is driven by motor-driven tendons during folding and by the restoring force of the origami structure during deployment. In the folding and deploying motion, the robot’s out-of-plane curvature is changed. Depending on the values other than the curvature of the robot, the angle between the leg and the ground is adjusted and the frictional force is changed accordingly, as illustrated in Figure 2a. To maximize its anisotropic friction properties, an asymmetric contact film composed of elastomer and polyester is attached to the legs’ surface, as illustrated in Figure 2b. The contact film, which induces anisotropic friction, has wedge patterns as its geometry. As we composed the wedge with the elastomer, which is very flexible, the wedge can be easily bent with an external force. Also, the wedge-shaped surface has a dual-material application, which has different friction levels. With this approach, the friction-induced film switches between friction and slip modes as it bends, as shown in Figure 2b, and the fabrication description is given below in Section 2.4.
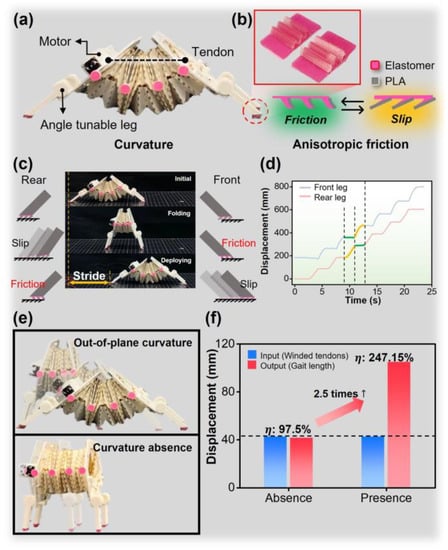
Figure 2.
Concept of the origami crawler: (a) Side view of the crawler including the components and out-of-plane curvature. (b) Schematic of anisotropic friction film based on dual materials. (c) A stride of the origami crawler shows out-of-plane curvature change. (d) Displacement of the origami crawler with anisotropic friction effect. (e) Origami crawler with and without out-of-plane curvature. (f) Comparison with output shows stride-efficient.
2.2.1. The Relationship between the Anisotropic Friction and Out-of-Plane Curvature
By combining the fabricated robot components, we can search for the relationship between out-of-plane curvature and anisotropic friction. One of the ways to mimic crawling motion is to use anisotropic friction. The crawling motion can occur by utilizing two materials that have different frictions from each other. For example, during the tendon-pulled state, the Kresling structure is subject to the same external forces in both directions by the tendons, which are pulled by motors and fixed at the end side of the Kresling body. In that situation, anisotropic friction occurs. The elastomer surfaces of the film adhered to the front feet are in contact with the floor, and, conversely, the polyester surfaces of the wedge of the rear feet are in contact with the floor. The front feet have high friction and act as anchors because of the elastomer, while the rear feet have low friction and slip because of the polyester. Thus, the front of the body, where the front legs are, is fixed, and only the rest of the body folds, while the rear legs move forward. Reversely, during the tendon-released state, the Kresling structure releases stored elastic energy as the structure deploys. The direction of the force applied to each foot is also reversed, causing the wedge of film to bend and anisotropic friction to occur again. The rear feet with the stronger friction act as anchors, and the crawler moves forward as the Kresling structure deploys. Thus, anisotropic friction can be completed systematically as shown in Figure 2c,d. When the robot strides, the relative frictions affect both leg sides. In detail, it is clear that high and low friction switch to each other passively. In Figure 2d, during folding, the rear legs are only active and have displacement, while the front legs are fixed by high friction force and have no displacement. After folding, the crawler deploys, and the front legs have displacement. In each cycle, anisotropic friction works organically, and the crawler can crawl. We add the use of the out-of-plane curvature in the origami crawler. When the origami crawler folds and deploys, there exists a change in curvature because of a bending property of the origami structure. These points of both the anisotropic friction and the curvature change contribute to the origami crawler. Adjusting out-of-plane curvature can make anisotropic friction programmable. Also, out-of-plane curvature can notify the state of the crawler, which is folded or deployed.
2.2.2. The Out-of-Plane Curvature for Stride-Efficient Crawler
In general research about the origami crawler, the crawlers have an absence of curvature change during striding. Thus, the value of the stride efficiency may be just one, theoretically, which is the ratio of the wound tendon length and crawling displacement. On the other hand, the out-of-plane curvature structure has an arc shape, not a straight-line shape. It can be described that the straight line is the chord of the fan shape and the chord and arc are in the same fan in Figure 2e. Thus, the out-of-plane curvature structure, which has an arc, is inevitably good for more stride. In a simple comparison shown in Figure 2f, the out-of-plane curvature crawler is 2.5 times more efficient against the curvature absence structure and the efficiency is 247.15%. The wound tendon length as input is 42.41 mm, and the output as a gait length is 41.34 mm at the curvature absence case and 104.80 mm at the out-of-plane curvature case. Thus, the out-of-plane curvature is effective for more striding and helpful in the view of energy efficiency.
2.3. The Crawling Mechanism of the Robot
To explain curvature changes as a property of this origami crawler, there needs to be a consistent repeat for every cycle. In Figure 3a, out-of-plane curvature changes can be verified during crawling motion expressed as the radius of curvature. Theoretically, the Kresling structure is straight when the origami crawler is folded; thus, the curvature radius at phase 3 should be sharply higher than the other phases. We monitored the phases to analyze the consistency of the crawler’s motion. The data of phase 3 are neglected due to their straight-like formation, forcing the curvature radius to be excessively increased compared to the others. The curvature radiuses at each phase have almost the same values. For example, the mean values of the curvature radius at phases 1, 2, and 4 are 50.83, 38.75, and 39.60 mm, and the standard deviations are 1.70, 1.18, and 0.53 mm, respectively. As the origami body is folded, the arc shape from the side has a low radius, and the center line changes from an arc to a straight line. At the change, phase 3 appears and the curvature of the origami body converges to zero. When the robot is deployed, the center line of the origami body changes reversely from straight to arc. This is shown in Figure 3c. Through comparisons of the curvature change at each phase, the crawler can be verified that it has the same motion behavior at each phase. In addition to a partial check at each phase, it is also important to ensure that the crawler has a consistent range of radius changes as a whole, which can be evidence of constant motion. Although the origami crawler has different curvature radius values at phase 3, the averages of the curvature radiuses are similar against each cycle, and the differences in standard deviation arise from phase 3 in Figure 3b. Accordingly, the out-of-plane curvature can act as an important factor for the crawler.
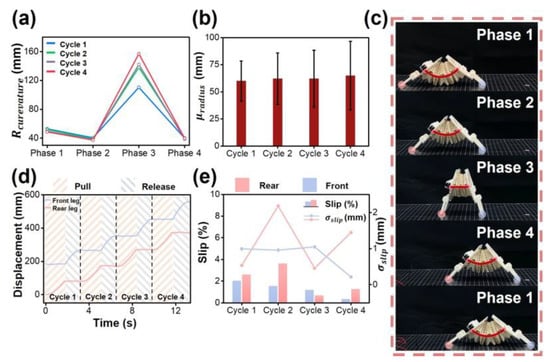
Figure 3.
Mechanism of the origami crawler: (a) Radiuses of curvature at each phase. (b) Average curvature radius values at each cycle. (c) Shot of the origami crawler at each phase. (d) Displacement of Front and rear legs during tendon pull and release. (e) Gait slip at the front and rear legs are presented as percentage and standard deviation.
Also, it is necessary to check that the curvature change is connected to the stride, which uses anisotropic friction, as mentioned in Section 3.3. In Figure 3a,c,d, when the motors pull the tendon fixed on the body plate, the origami structure is folded, and the curvature radius decreases slightly lower at phase 2. The origami structure is fully folded at phase 3, and the radius becomes sharply higher. From phase 1 to phase 3, the front legs have high friction and the rear half of the crawler moves forward. The tendons are released after phase 3, and the radius becomes lower again during the deployment of the origami structure. Through tendon releasing and the front half of the crawler moving forward, the crawler goes by phase 4 and becomes phase 1 when fully deployed again. In every cycle, the legs of the crawler have consistent displacement during the tension changes of the tendons. In Figure 3e, the slip of the left axis is the ratio of the length lost in one stride and stride length, which is presented as a percent, and is a standard deviation of the slip length during motions. The slip rate on each cycle is below 5.00%, especially with the lowest values (0.64% at the front, and 0.31% at the rear), and the standard deviation values are almost under 2 mm. Thus, anisotropic friction works well and the mechanism during the motion is validated, which is the relation between out-of-plane curvature and anisotropic friction.
2.4. Fabrication of the Origami Crawler
We fabricated the Kresling structure with cut the paper (Kent Paper, 220g per 1m2, t = 0.18 mm) using a CO2 laser cutting machine (VLS 2.30 DT, Universal Laser Systems, Scottsdale, AZ, USA) and rolled the patterned sheet into a cylinder shape. The other parts of the robot like the leg and body plate were 3D printed with PLA (Polylactic Acid) using FFF (Fused filament fabrication) 3D printer (Ultimaker S3, Ultimaker). On both end sides of the Kresling structure, we attached a 3D-printed plate with the motor cases on one side and knotted tendons on the other. We also used the 3D-printing method to make a mold. Mold is composed of two materials, PVA (Polyvinyl Alcohol) and PLA. PVA is used as a mold for shaping high-friction material such as silicone, and PLA is for low-friction. After printing the mold, we poured the silicone (Ecoflex 00-50, shore hardness 50A, Smooth-On) and put the mold in the convection oven (DH.WOF05050, Daihan Scientific) to cure the silicone quickly. For placing low friction material on the teeth of silicone perfectly, we melted the PVA mold with water and completed the combined silicone, PLA sheet. We composed a control system including a power source (DP30-05A, TOYOTECH), controller (Arduino MEGA 2560, Arduino), DC gear motors, and motor driver module (SZH-EK001, SZH). The input power to the Arduino was 5 V, 3 A, and the DC motors, which were responsible for winding the tendons that were connected to the motor driver.
3. Result and Discussion
3.1. Experiment Setup
To analyze the origami crawler detail, we placed the origami crawler on a PVC sheet (t = 2.8 mm), as shown in Figure 4a, and actuated the crawler for six cycles. In each cycle, it takes 1800 ms for folding, and about 40 mm of the tendon is wound through a winch attached to the motor shaft. The DC gear motor used in this study runs at 100 rpm; thus, it rotates three times while folding the origami. Since the robot folds as much as the tendons are wound, the contraction ratio is about 69%. After folding, the tendons release for 1500 ms with the origami deploying. The reason why the deploying time is short is that the structure gradually recovers with nonlinear motion. We used open-source software (Kinovea) to calculate curvature and gait length. Video resolution for motion tracking is 3840 × 2160 pixels and 60 fps, so the time step of each shot is 0.167 ms. After collecting motion-tracking data, we extracted the coordinates of each marker and converted them to actual positions in millimeters. This process was automatically performed by Kinovea software by adding the coordinate’s axis and scale information to the video.
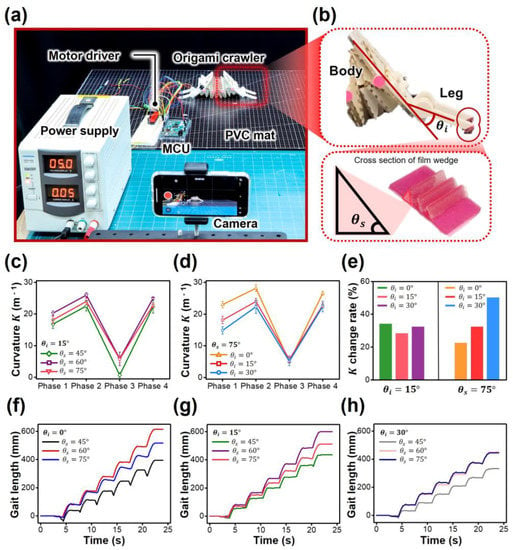
Figure 4.
Measurements of out-of-plane curvature changes and gait length: (a) Testing setup using motion tracking. (b) Illustration of the design parameters, which are the initial angle of leg and the slope angle of friction film . (c) Curvature changes for various and fixed . (d) Curvature changes for various and fixed . (e) Curvature change rate between Phase 1 and 2 of (c,d). (f–h) Gait length for various and fixed . Same procedures as (c–h) were performed at the same experimental setup.
The curvature change can play a crucial role in the locomotion analysis of the origami crawler based on the bending property of the origami structure. Thus, in order to investigate the curvature, the coordinates of four markers are utilized to calculate curvature. As an assumption, four markers are considered to form a parabola and can be calculated as polynomial curve fitting.
3.2. Experiment Results
We aimed to demonstrate the origami crawler, which has programmable friction using the out-of-plane curvature of the Kresling structure. To figure out programmable friction using the curvature, we defined variables as and in Figure 4b. The angle is the initial angle between the leg and body of the crawler. Another angle is a slope angle of the film cross-section adhered below the foot. The initial angle affects the shape of the deployed origami structure. If the initial angle is higher, then the origami structure has more pre-strain caused by the stretches from the feet so that the bending degree of the structure is higher. We selected the values of angle as 0, 15, 30 because the 0 value means that the robot has no pre-strain, and the higher values give the robot intentional stretches. This affects the initial curvature of the robot, so the rate of curvature changes during folding, and deploying varies. The slope angle of friction-induced film affects friction coefficients. This is because the wedge on the film bends well or unbends well depending on the angle . The wedge becomes thinner and sharper at higher so the friction-induced film can easily switch its mode between friction and slip. It is difficult to maintain its own shape under the weight of the robot at too high values, so we selected the values of angle as 45, 60, 75. The cross-section of the wedge is an isosceles right triangle when the is 45, and the higher values make the cross-section sharper and the triangle thinner. In other words, the change in curvature is sensitive to changing the value of and there may be the fitted value of leading to better friction performance for crawling.
In order to figure out the curvature of the origami crawler in detail, we present the average of the curvature values at each phase as shown in Figure 4c,d. Curvature converges to zero theoretically at phase 3; thus, we present differences between phases 1 and 2 for checking the sensitive change. It is identifiable that the change in curvature during folding is more sensitive to increasing for fixed of 75, while the inclination of slopes in Figure 4c is almost the same. In detail, the differences in rates of curvature at fixed between phases 1 and 2 are 22.47% ( = 0), 32.33% ( = 15), and 50.03% ( = 30), as shown in Table 1. In contrast, it is difficult to express a distinction of difference when changing for fixed of 15 as shown in Figure 4c. The differences in rates are 34.03% ( = 45), 28.16% ( = 60), and 32.33% ( = 75). Figure 4e shows the contents of Table 1 schematically. Unlike the case with varied , the case with varied shows that the higher makes the higher curvature change rate. In the case of varied , the standard deviation among the curvature change rates is just 2.46%, unlike the situation of varied , and the small standard deviation means that the curvature change is undetectable. Since the deployed shape of the crawler varies with , the parameter can be selected as the cause of curvature sensitivity. While the angle indicates the sensitivity of curvature change, the angle affects gait length, and especially friction ability. Figure 4f–h include the gait length for all conditions of both parameters during six cycle actuations, which are helpful to detect the friction ability. Despite changing the , the overall stride is always relatively poor when the slope angle of the film cross-section is 45. In Figure 4f, where is 45, the gait loss per cycle is clearly visible, and the mean value of loss is 29.68 mm, as seen in Table 2. The gait loss ratio is 31.41%, and the gait loss ratio means the ratio of gait length to gait loss during one cycle. In addition, when is 30 in Figure 4h, the Kresling structure is so bent that the overall stride is reduced, but it has the lowest stride value when is 45. This is because the wedge is relatively thick and not sensitive to switching modes between friction and slip. It can be also seen that the difficulty of switching modes led to a loss of stride. On the other hand, if is 75, the wedge is so thin that it is difficult to maintain its own shape. This is the reason for reducing the sensitivity of mode switching. However, in Figure 4g, we can see that , which is sensitive to friction, also causes a relatively smooth stride when is 15. In the case of increasing from 60 to 75, gait loss ratios are 1.96%, and 4.91% for fixed of 15, respectively. bends the Kresling structure, putting pre-strain on the robot. This pre-strain affects the surface contact area of friction-induced film, effectively helping to switch between friction and sliding modes and controlling the friction ability. With these two parameters, we can propose an origami crawler with programmable friction.

3.3. Crawling on the Sloped Surface
The proposed crawler can control its out-of-plane curvature to control directional frictional force. We tested the origami crawler on both an uphill and downhill surface, as shown in Figure 5a,b. The slope is composed of a PVC sheet on an aluminum block and its angle can be adjusted with the support jack. Figure 5 illustrates the crawling motion over one cycle on the top of the figure and several cycles on the bottom of the figure. The parameters are = 60, = 0 in Figure 5a,c, and = 15 in Figure 5b. Through Figure 5a, which shows that the crawler moves during four cycles, we can check that the proposed crawler has smooth locomotion on a flat surface. The anisotropic friction is working well in the first cycle, although the center of mass is located on the side of the crawler, which is due to the mass of the motors. While the crawler moves well on a flat surface, its performance declines on an inclined surface, as shown in Figure 5b. Because of the center of mass placed in the back, the origami crawler is front driven by placing the motors in the direction of motion. When the robot crawls on the inclined slope of 15, it takes 13 cycles to move to the end of the slope. We see an effect where the crawler has more cycles than the situation where it is on a flat surface, although we rearranged the center of mass. This is because the restoring force of an origami structure is not enough to push the body perfectly. However, the crawler demonstrates the ability to climb slopes despite its simple structure, proving that anisotropic friction is at work. In addition, there is further evidence that the anisotropic friction film presented above has great performance, as shown in Figure 5c.

Figure 5.
Demonstration of the origami crawler: (a) Locomotion on a flat surface. (b) Climb on the inclined slope of 15. (c) Descent on the declined slope of 15.
When the robot crawls downhill, the anisotropic friction should be effective, and this is because the robot needs to have smooth locomotion. The slope angle of the downhill is 15, and it takes four cycles to move to the end of the slope. During the first cycle, the highlighted yellow mark shows that the front legs have high friction when the crawler folded, and low friction when the crawler deployed. The gravity force increases the amount of contact between the leg and the slope, so the anisotropic friction films may be more effective. These three cases also show the change in out-of-plane curvature, and we can detect the state of the crawler whether it is folded or deployed.
3.4. Motion Implementation on Various Surfaces
In the preceding sections, we compared experiments under parametric study for effective anisotropic friction and demonstrated the friction ability of the crawler in Section 3.3. In this Section, we tested the origami crawler on various surfaces, as shown in Figure 6. There were three cases, each with a floor composed of Kent paper, acrylic plate, and bubble wrap. In Figure 6a, the surface of the Kent paper is relatively dry, and has some roughness. This dry, rough surface was actually compatible with the friction-induced film proposed in this study, and the crawling motion was realized without any problem. On the contrary, the surface of the acrylic plate is not rough, but rather slippery. Unlike the motion on Kent paper, the stride length is slightly reduced, but we can see in Figure 6b that the crawler can be driven without any problem. Lastly, we composed a bumpy surface and actuated the origami crawler. The composed surface is the bubble wrap, which includes the air cap on its own surface. The bubble wrap can be a good example to check for crawling ability because the surface is bumpy, not smooth. In Figure 6c, the crawling motion is better than running on an acrylic plate for the same time period. Mode switching between friction and slip occurs well even on bumpy surfaces, making anisotropic friction effective.

Figure 6.
Crawling on various surfaces: (a) Kent paper. (b) Acrylic plate. (c) Bubble wrap.
4. Conclusions
In this article, we presented a tendon-driven origami crawler robot with anisotropic friction. The proposed design based on a symmetric Kresling structure has mono-stability that is able to store and emit energy. It enables the robot to lower the number of actuators and simplify its system. We control the out-of-curvature by a tendon-driven mechanism. In the folded state with higher curvature, it provides lower frictional force on the rear side and higher friction on the front side, and in the deployed state with lower curvature, vice versa. To maximize anisotropic friction, an asymmetric contact film composed of elastomer and polyester was applied to the contact surface of the robot. The experiment shows increasing the out-of-plane curvature improved the crawling efficiency 2.5 times better, and the parametric study demonstrated that the gait loss ratio has a minimum value of 1.96% when .
We mainly considered the geometric aspects of the contact film only. However, if its electrochemical properties are also considered, then the effect of anisotropic friction might be larger. For example, when microscale structures such as gecko-inspired adhesion [40,41] using an electrostatic force are applied to our structures, they are expected to have decreased gait length loss and improved crawling efficiency. This anisotropic friction allows for an intentional directional drive that prevents friction in unwanted directions and only moves in the desired direction. Also, considering the change in friction capacity according to surface humidity, it is expected that a wide range of motion can be realized. By attaching additional legs to different sides of the robot hexagon, it should be able to operate in closed environments, such as a pipeline inspection, and it is anticipated that there will be a wide range of uses for this robot design.
Author Contributions
Conceptualization, H.K. and J.K; methodology and validation, H.K, S.C., D.K., S.J.L. and S.P.; formal analysis, H.K and S.C.; investigation, H.K. and D.K.; resources, H.K., S.J.L. and S.P.; data curation, H.K. and S.J.L.; writing—original draft preparation, H.K. and J.K.; writing—review and editing, H.K. and J.K; visualization, H.K and S.C; supervision, D.C. and J.K; project administration, J.K; funding acquisition, J.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by an Institute of Information & Communications Technology Planning & Evaluation (IITP) grant funded by the Korean government (MSIT) [No.RS-2022-00155911, Artificial Intelligence Convergence Innovation Human Resources Development (Kyung Hee University)]. Also, this work was supported by the National Research Foundation of Korea(NRF) grant funded by the Korea government(MSIT) [No.2022R1F1A1074359, No.2022K2A9A1A06093664 and No.RS-2023-00210867].
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Rus, D.; Sung, C. Spotlight on Origami Robots. Sci. Robot. 2018, 3, eaat0938. [Google Scholar] [CrossRef]
- Zhao, Z.; Kuang, X.; Wu, J.; Zhang, Q.; Paulino, G.H.; Qi, H.J.; Fang, D. 3D Printing of Complex Origami Assemblages for Reconfigurable Structures. Soft Matter 2018, 14, 8051–8059. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Fan, W.; Chen, G.; Luo, J.; Lu, Q.; Wang, H. A 3D Printable Origami Vacuum Pneumatic Artificial Muscle with Fast and Powerful Motion. In Proceedings of the 2021 IEEE 4th International Conference on Soft Robotics (RoboSoft), New Haven, CT, USA, 12–16 April 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 551–554. [Google Scholar]
- Melancon, D.; Forte, A.E.; Kamp, L.M.; Gorissen, B.; Bertoldi, K. Inflatable Origami: Multimodal Deformation via Multistability. Adv. Funct. Mater. 2022, 32, 2201891. [Google Scholar] [CrossRef]
- Wu, S.; Ze, Q.; Dai, J.; Udipi, N.; Paulino, G.H.; Zhao, R. Stretchable Origami Robotic Arm with Omnidirectional Bending and Twisting. Proc. Natl. Acad. Sci. USA 2021, 118, e2110023118. [Google Scholar] [CrossRef]
- Namiki, A.; Yokosawa, S. Origami Folding by Multifingered Hands with Motion Primitives. Cyborg Bionic Syst. 2021, 2021, 9851834. [Google Scholar] [CrossRef] [PubMed]
- Rothemund, P.W.K. Folding DNA to Create Nanoscale Shapes and Patterns. Nature 2006, 440, 297–302. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Liu, X.; Huang, Q.; Arai, T. Recent Progress of Magnetically Actuated DNA Micro/Nanorobots. Cyborg Bionic Syst. 2022, 2022, 9758460. [Google Scholar] [CrossRef]
- Saccà, B.; Niemeyer, C.M. DNA Origami: The Art of Folding DNA. Angew. Chem. Int. Ed. 2012, 51, 58–66. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.; Lee, C.; Jeon, K.; Lee, J.Y.; Kim, Y.-J.; Lee, J.G.; Kim, H.; Cho, M.; Kim, D.-N. Harnessing a Paper-Folding Mechanism for Reconfigurable DNA Origami. Nature 2023, 619, 78–86. [Google Scholar] [CrossRef]
- Cho, H.; Kim, D.-N. Controlling the Stiffness of Bistable Kirigami Surfaces via Spatially Varying Hinges. Mater. Des. 2023, 231, 112053. [Google Scholar] [CrossRef]
- Zhang, J.; Fang, Q.; Xiang, P.; Sun, D.; Xue, Y.; Jin, R.; Qiu, K.; Xiong, R.; Wang, Y.; Lu, H. A Survey on Design, Actuation, Modeling, and Control of Continuum Robot. Cyborg Bionic Syst. 2022, 2022, 9754697. [Google Scholar] [CrossRef]
- Xu, Y.; Peyron, Q.; Kim, J.; Burgner-Kahrs, J. Design of Lightweight and Extensible Tendon-Driven Continuum Robots Using Origami Patterns. In Proceedings of the 2021 IEEE 4th International Conference on Soft Robotics (RoboSoft), New Haven, CT, USA, 12–14 April 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 308–314. [Google Scholar]
- Kim, J.; Lee, D.-Y.; Kim, S.-R.; Cho, K.-J. A Self-Deployable Origami Structure with Locking Mechanism Induced by Buckling Effect. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; IEEE: Piscataway, NJ, USA, 2015; Volume 2015, pp. 3166–3171. [Google Scholar]
- Kim, S.-J.; Lee, D.-Y.; Jung, G.-P.; Cho, K.-J. An Origami-Inspired, Self-Locking Robotic Arm That Can Be Folded Flat. Sci. Robot. 2018, 3, eaar2915. [Google Scholar] [CrossRef] [PubMed]
- Bhovad, P.; Kaufmann, J.; Li, S. Peristaltic Locomotion without Digital Controllers: Exploiting Multi-Stability in Origami to Coordinate Robotic Motion. Extreme Mech. Lett. 2019, 32, 100552. [Google Scholar] [CrossRef]
- Hu, Q.; Li, J.; Dong, E.; Sun, D. Soft Scalable Crawling Robots Enabled by Programmable Origami and Electrostatic Adhesion. IEEE Robot. Autom. Lett. 2023, 8, 2365–2372. [Google Scholar] [CrossRef]
- Tramsen, H.T.; Gorb, S.N.; Zhang, H.; Manoonpong, P.; Dai, Z.; Heepe, L. Inversion of Friction Anisotropy in a Bio-Inspired Asymmetrically Structured Surface. J. R. Soc. Interface 2018, 15, 20170629. [Google Scholar] [CrossRef]
- Ta, T.D.; Umedachi, T.; Suzuki, M.; Kawahara, Y. A Printable Soft-Bodied Wriggle Robot with Frictional 2D-Anisotropy Surface. J. Inf. Process. 2022, 30, 201–208. [Google Scholar] [CrossRef]
- Sheng, X.; Xu, H.; Zhang, N.; Ding, N.; Zhu, X.; Gu, G. Multi-Material 3D Printing of Caterpillar-Inspired Soft Crawling Robots with the Pneumatically Bellow-Type Body and Anisotropic Friction Feet. Sens. Actuators A Phys. 2020, 316, 112398. [Google Scholar] [CrossRef]
- Ta, T.D.; Umedachi, T.; Kawahara, Y. Design of Frictional 2D-Anisotropy Surface for Wriggle Locomotion of Printable Soft-Bodied Robots. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 6779–6785. [Google Scholar]
- Shepherd, R.F.; Ilievski, F.; Choi, W.; Morin, S.A.; Stokes, A.A.; Mazzeo, A.D.; Chen, X.; Wang, M.; Whitesides, G.M. Multigait Soft Robot. Proc. Natl. Acad. Sci. USA 2011, 108, 20400–20403. [Google Scholar] [CrossRef]
- Yu, M.; Yang, W.; Yu, Y.; Cheng, X.; Jiao, Z. A Crawling Soft Robot Driven by Pneumatic Foldable Actuators Based on Miura-Ori. Actuators 2020, 9, 26. [Google Scholar] [CrossRef]
- Ze, Q.; Wu, S.; Nishikawa, J.; Dai, J.; Sun, Y.; Leanza, S.; Zemelka, C.; Novelino, L.S.; Paulino, G.H.; Zhao, R.R. Soft Robotic Origami Crawler. Sci. Adv. 2022, 8, 7834. [Google Scholar] [CrossRef]
- Pagano, A.; Yan, T.; Chien, B.; Wissa, A.; Tawfick, S. A Crawling Robot Driven by Multi-Stable Origami. Smart Mater. Struct. 2017, 26, 94007. [Google Scholar] [CrossRef]
- Yeow, B.S.; Yang, H.; Sivaperuman Kalairaj, M.; Gao, H.; Cai, C.J.; Xu, S.; Chen, P.; Ren, H. Magnetically Steerable Serial and Parallel Structures by Mold-Free Origami Templating and Domain Setting. Adv. Mater. Technol. 2022, 7, 2101140. [Google Scholar] [CrossRef]
- Jin, T.; Li, L.; Wang, T.; Wang, G.; Cai, J.; Tian, Y.; Zhang, Q. Origami-Inspired Soft Actuators for Stimulus Perception and Crawling Robot Applications. IEEE Trans. Robot. 2022, 38, 748–764. [Google Scholar] [CrossRef]
- Joyee, E.B.; Pan, Y. A Fully Three-Dimensional Printed Inchworm-Inspired Soft Robot with Magnetic Actuation. Soft Robot. 2019, 6, 333–345. [Google Scholar] [CrossRef]
- Liu, M.; Xu, Z.; Ong, J.J.; Zhu, J.; Lu, W.F. An Earthworm-like Soft Robot with Integration of Single Pneumatic Actuator and Cellular Structures for Peristaltic Motion. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 7840–7845. [Google Scholar]
- Wang, W.; Lee, J.-Y.; Rodrigue, H.; Song, S.-H.; Chu, W.-S.; Ahn, S.-H. Locomotion of Inchworm-Inspired Robot Made of Smart Soft Composite (SSC). Bioinspir Biomim. 2014, 9, 46006. [Google Scholar] [CrossRef]
- Onal, C.D.; Wood, R.J.; Rus, D. An Origami-Inspired Approach to Worm Robots. IEEE/ASME Trans. Mechatron. 2013, 18, 430–438. [Google Scholar] [CrossRef]
- Li, J.; Godaba, H.; Zhang, Z.Q.; Foo, C.C.; Zhu, J. A Soft Active Origami Robot. Extreme Mech. Lett. 2018, 24, 30–37. [Google Scholar] [CrossRef]
- Wang, H.; Yamamoto, A.; Higuchi, T. A Crawler Climbing Robot Integrating Electroadhesion and Electrostatic Actuation. Int. J. Adv. Robot. Syst. 2014, 11, 191. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, F.; Jing, Z.; Yu, F.; Chen, Y. A Hybrid Territorial Aquatic Bionic Soft Robot with Controllable Transition Capability. J. Bionic Eng. 2023, 20, 568–583. [Google Scholar] [CrossRef]
- Sriratanasak, N.; Axinte, D.; Dong, X.; Mohammad, A.; Russo, M.; Raimondi, L. Tasering Twin Soft Robot: A Multimodal Soft Robot Capable of Passive Flight and Wall Climbing. Adv. Intell. Syst. 2022, 4, 2200223. [Google Scholar] [CrossRef]
- Kim, Y.; Cha, Y. Soft Pneumatic Gripper With a Tendon-Driven Soft Origami Pump. Front. Bioeng. Biotechnol. 2020, 8, 461. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, H.; Pusalkar, N.; Ren, H. Single-Motor Controlled Tendon-Driven Peristaltic Soft Origami Robot. J. Mech. Robot. 2018, 10, 64501. [Google Scholar] [CrossRef]
- Luo, M.; Yan, R.; Wan, Z.; Qin, Y.; Santoso, J.; Skorina, E.H.; Onal, C.D. OriSnake: Design, Fabrication, and Experimental Analysis of a 3-D Origami Snake Robot. IEEE Robot. Autom. Lett. 2018, 3, 1993–1999. [Google Scholar] [CrossRef]
- Pagano, A.; Leung, B.; Chien, B.; Yan, T.; Wissa, A.; Tawfick, S. Multi-Stable Origami Structure for Crawling Locomotion. In Proceedings of the Volume 2: Modeling, Simulation and Control, Bio-Inspired Smart Materials and Systems; Energy Harvesting, Stowe, VT, USA, 28–30 September 2016; American Society of Mechanical Engineers: New York, NY, USA, 2016. [Google Scholar]
- Hawkes, E.W.; Jiang, H.; Christensen, D.L.; Han, A.K.; Cutkosky, M.R. Grasping Without Squeezing: Design and Modeling of Shear-Activated Grippers. IEEE Trans. Robot. 2018, 34, 303–316. [Google Scholar] [CrossRef]
- Han, A.K.; Hajj-Ahmad, A.; Cutkosky, M.R. Hybrid Electrostatic and Gecko-Inspired Gripping Pads for Manipulating Bulky, Non-Smooth Items. Smart Mater. Struct. 2021, 30, 25010. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).