Torque-Based Control of a Bio-Inspired Modular Climbing Robot
Abstract
1. Introduction
- Wrist actuators become passive whenever the adhesion system is attached to any surface. Thus, the complexity of the kinematic chain is reduced and, consequently, so is the complexity of the static model computation, which is implemented in a robot with a non-defined number of legs.
- A low-weight computational method for computing the static model of a multi-limbed system is presented and, consequently, a gravity compensator is obtained.
- Our static model solver method is compared with the most used one, which is based on the Lagrange equation method and the use of the robot Jacobian. The system is validated in both simulation and hardware experiments.
- The results of the IKCs and the proposed torque-based control are compared using the same robot. The remarkable advantages of torque-based control are highlighted.
2. State of the Art
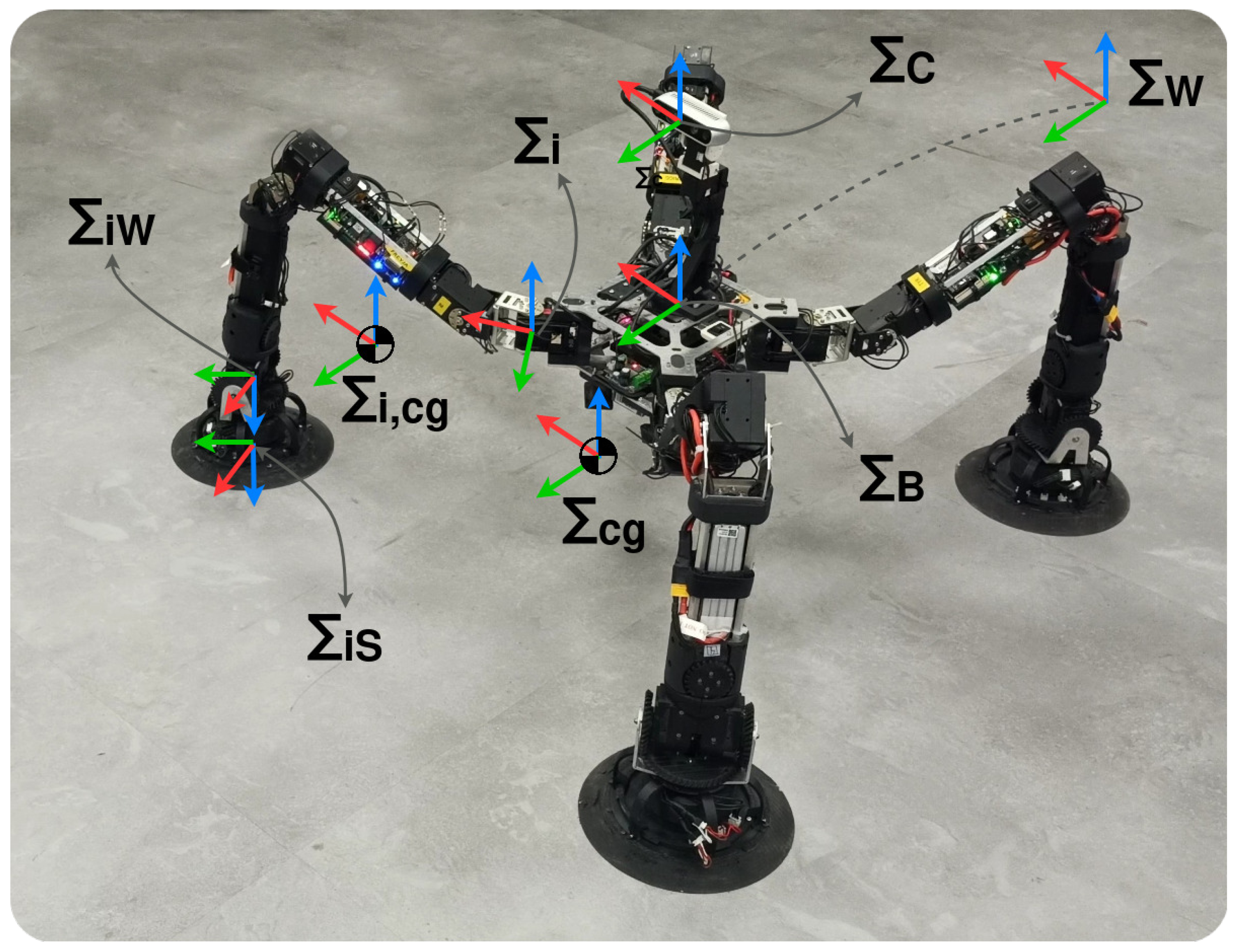
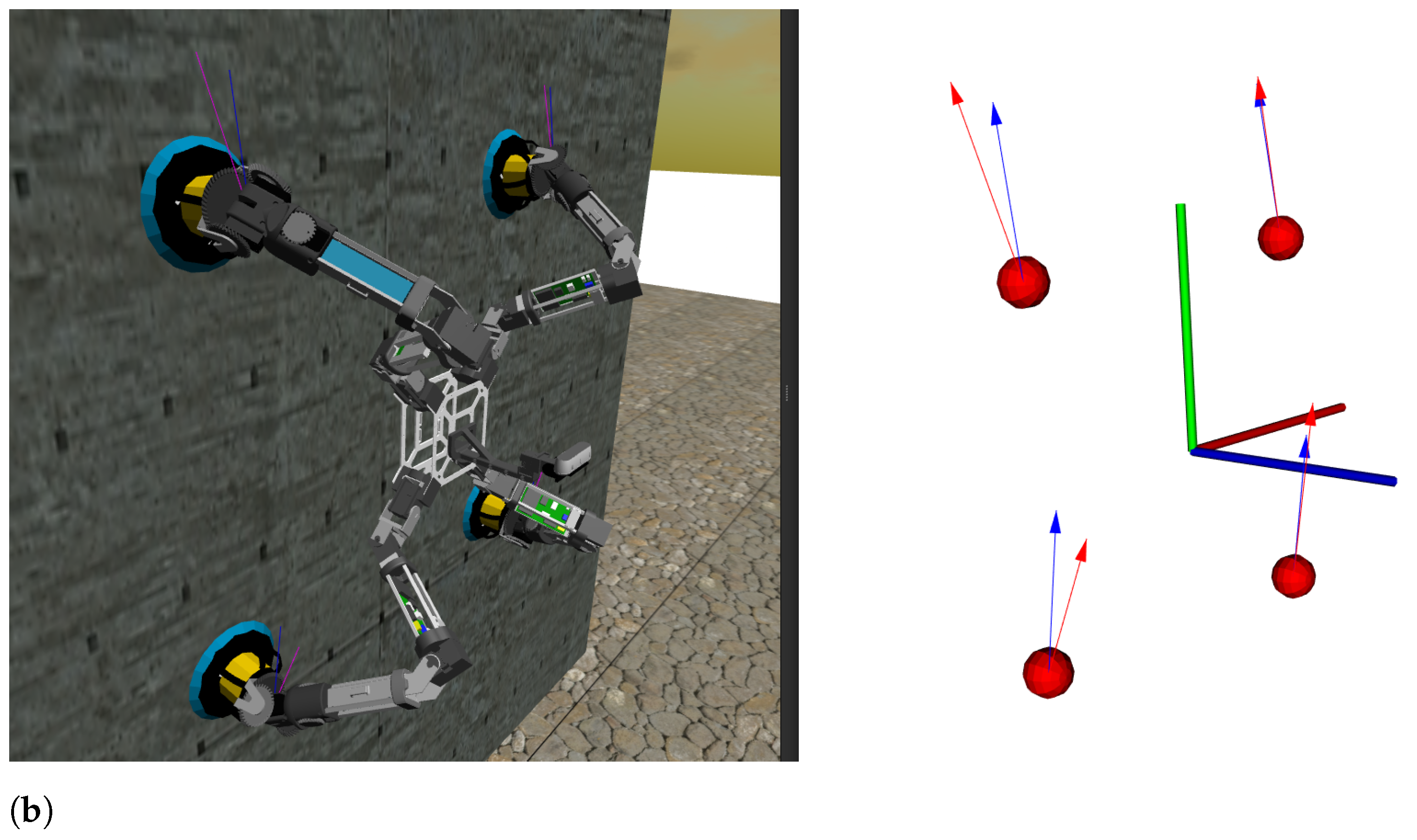
3. ROMERIN Modular Climbing Robot
3.1. Brief Description of the ROMERIN Leg Module
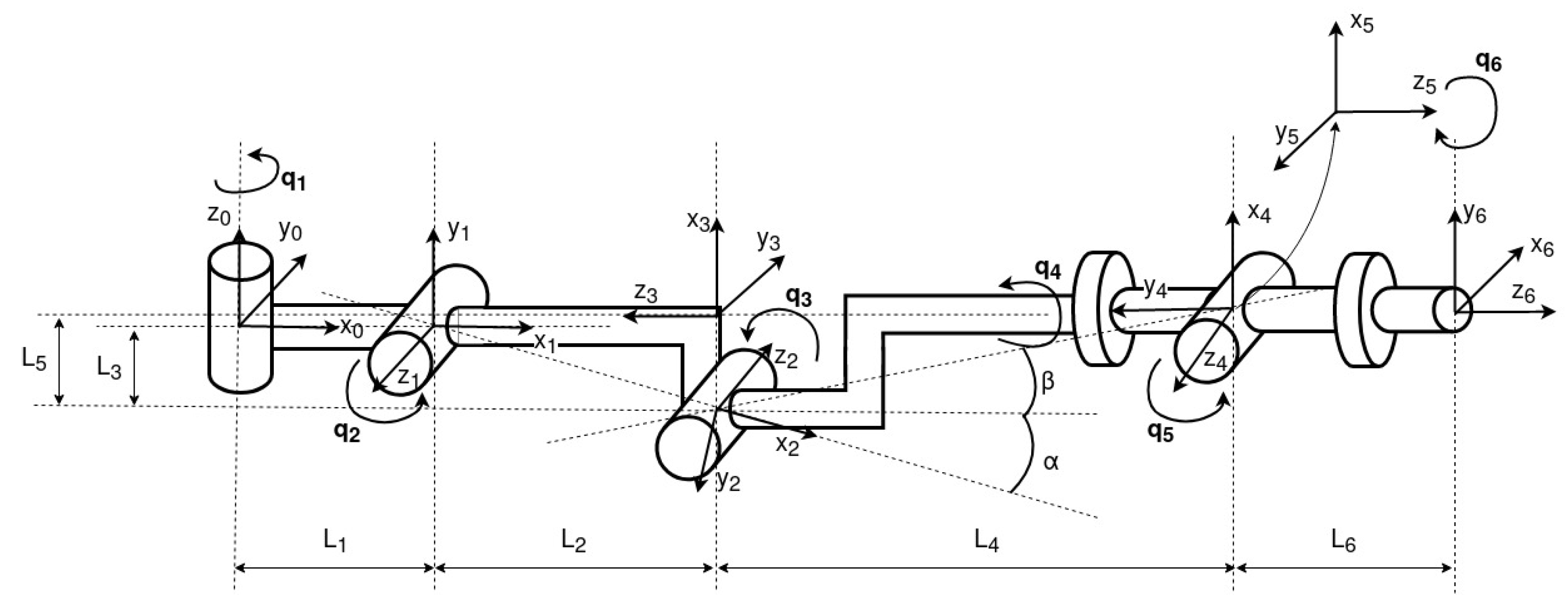
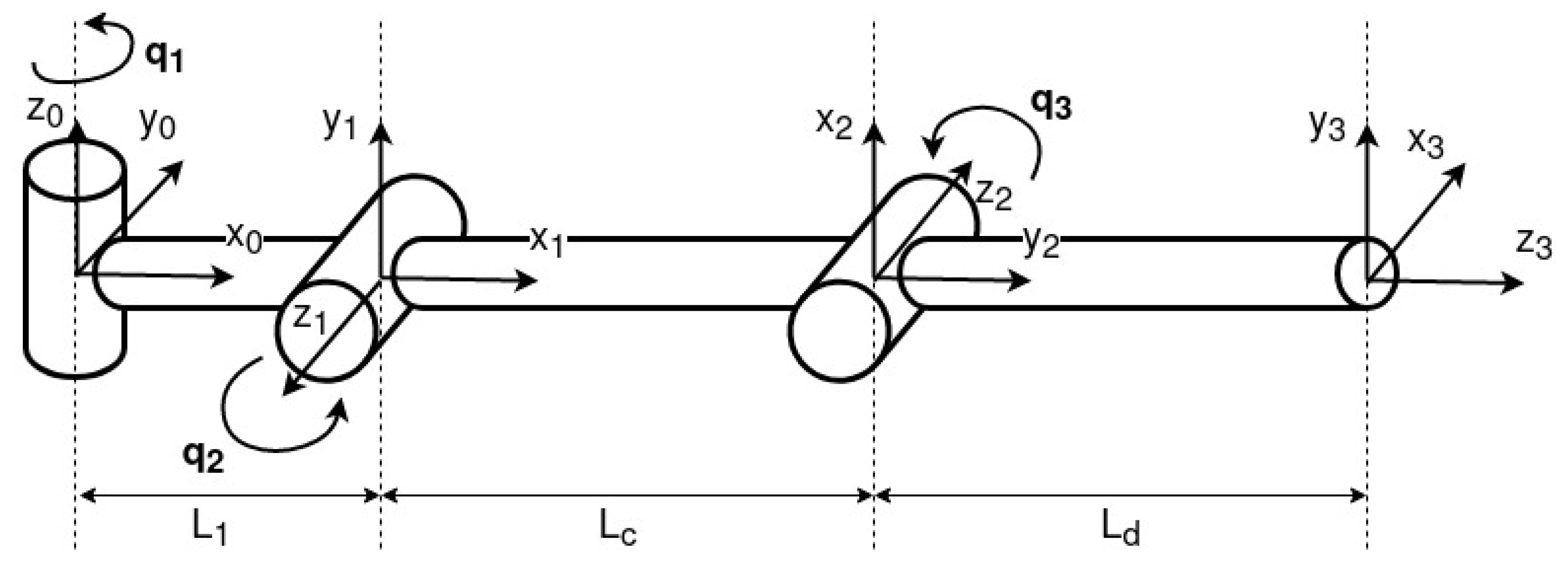
3.2. Kinematic Model of ROMERIN
4. Torque-Based Control of Hyper-Static Multi-Limbed Systems
- When the leg is attached to the environment, the interaction between both is reflected in the appearance of reaction forces. In this case, the module should be controlled by an IDC to avoid an overload of the actuators due to the closing of the kinematic chain.
- When the leg is detached and free, no reaction forces appear in the leg, and therefore it can be controlled with an IKC or by means of an IDC.
4.1. Force Distribution Problem (FDP)
- For a walking legged robot located in the z-plane (opposite to the gravity vector), the normal contact forces of the support feet are positive:This means that if the legged robot is walking on a slope (moving on x-direction), positive tangential forces are strictly required during the stance phase:On the other hand, for climbing legged robots, the normal contact forces of the support can be as negative as desired, as long as it is ensured that the torque of the actuators does not exceed the permissible limits (point 4), and the suction cup is not at risk of detaching from the surface.
- The total normal force of the stance phase is equal to the force produced by the weight of the legged robot. That is, the sum of the reaction forces compensates the gravitation component, and the sum of the momentum is zero:When force/torque sensors are used on the feet, it is possible to observe that the values differ slightly due to motion, assumptions, and inaccuracies. When estimating forces by solving the FDP, the values may differ slightly due to set thresholds for the convergence of numerical methods. Similarly, for climbing robots, there should also be a moment equilibrium.
- For legged robots, the support feet must not slip:where and are the foot forces of leg i of the support phase in the x and y directions, respectively, and is considered the relevant friction coefficient of the ground. For climbing robots, the normal force must be lower than a limit value, which is generally denoted as the grip force :
- Finally, the torques in each actuator have to be lower than their torque limits:where is the maximum articulated torque vector of the leg i; is the Jacobian of the leg i; and is the reaction forces related to .
- Linear-Programming (LP) Method. It is known as the most common programming algorithm for optimizing FDP [47], but many flaws have been detected during its implementation, such as computational cost or discontinuity.
- Compact-Dual Linear-Programming (CDLP) Method. It results in a smaller size problem compared to the LP method by using compact-dual linear programming, but it is unable to completely overcome discontinuity issues [48].
- Analytical Method. This method is implemented mainly for walking robots. It consists of balancing the forces of the support feet in order to prevent legs from slipping.
4.2. Classical Method
4.3. Implemented Method
| Algorithm 1 Gravity torque compensator of module i | ||
| Outputs: | ||
| 1: | for do | |
| 2: | for do | |
| 3: | if then | |
| 4: | Skip | ▹ Only child links |
| 5: | ||
| 6: | ||
| 7: | ▹ Weight torques | |
| 8: | ||
| 9: | ||
| 10: | ||
| 11: | ▹ Torques related to the external forces applied at WP | |
| 12: | ||
| 13: | ||
| 14: | ▹ Project to j joint axis | |
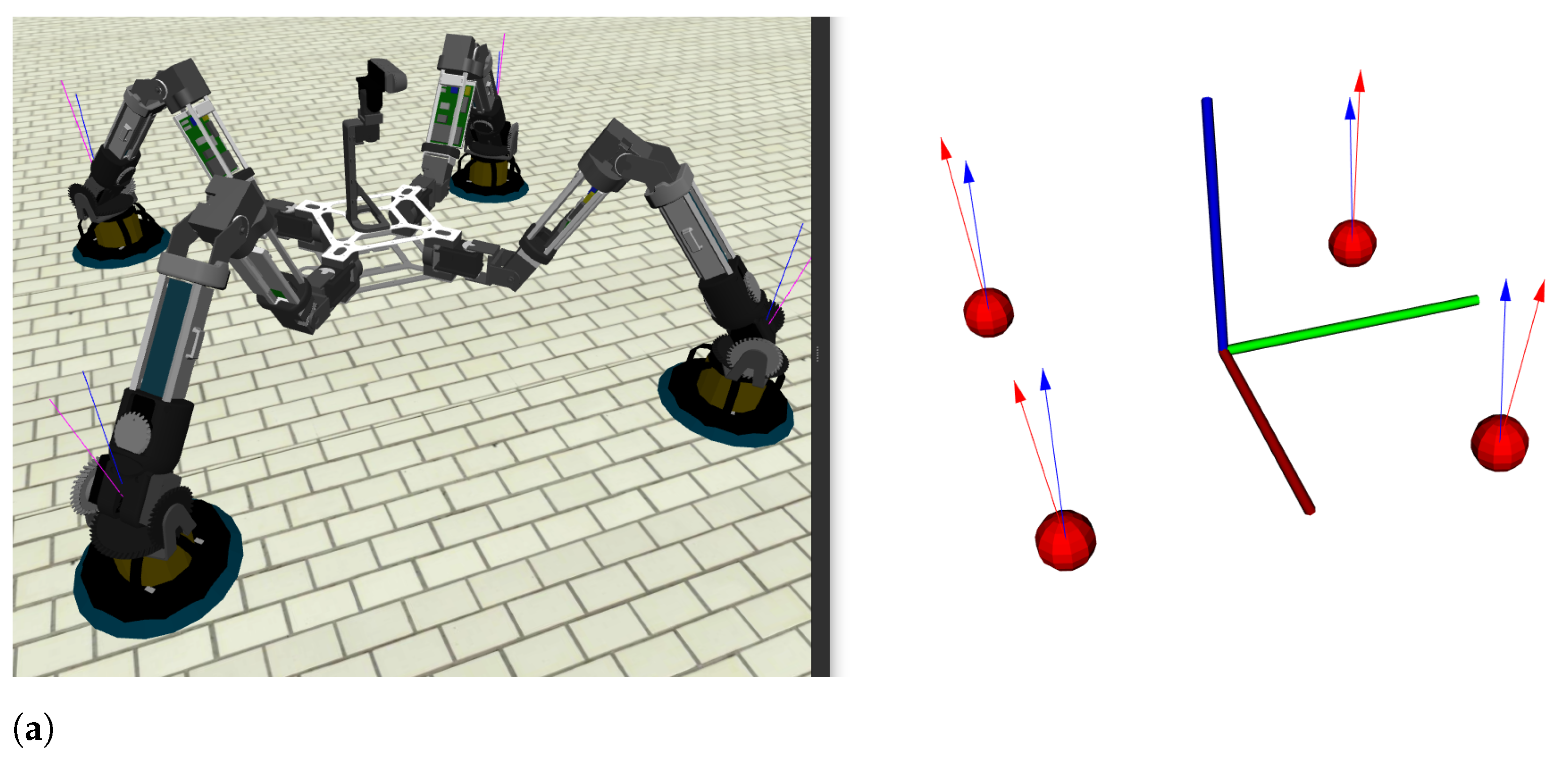
4.4. Comparison of Methods
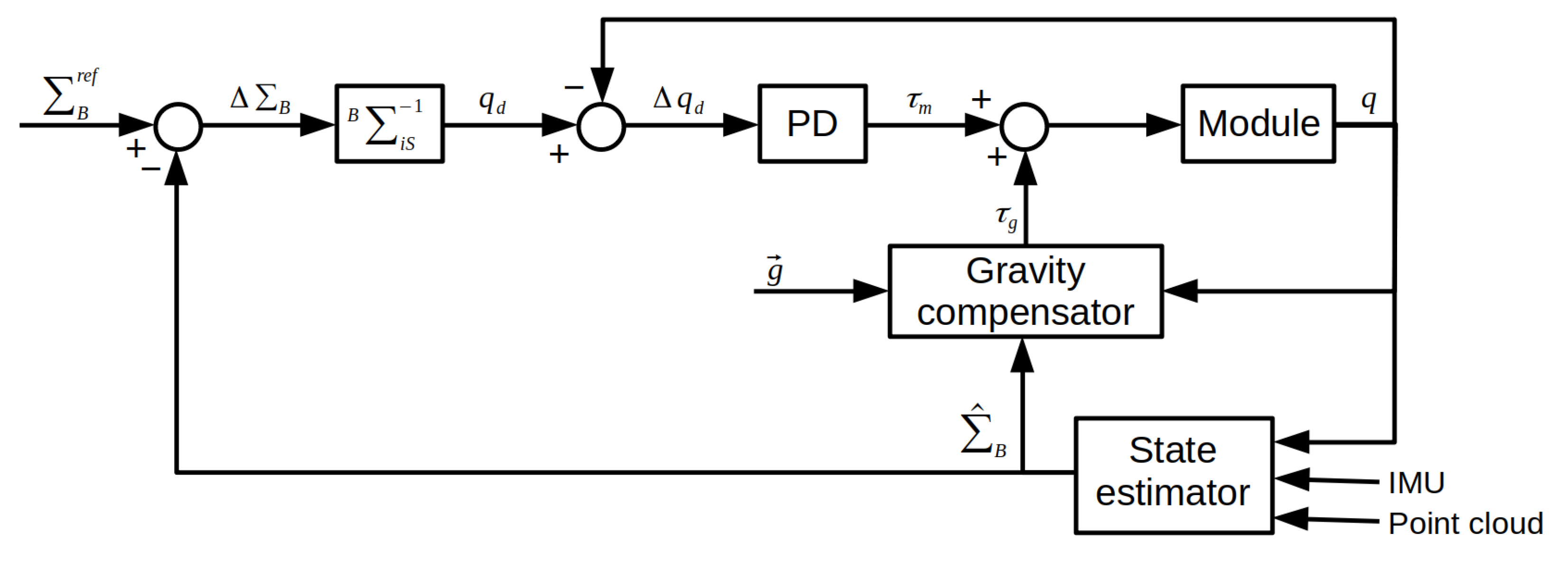
5. Impedance Control of Leg Modules
5.1. State Estimator
5.2. Body Trajectory Tracking Control
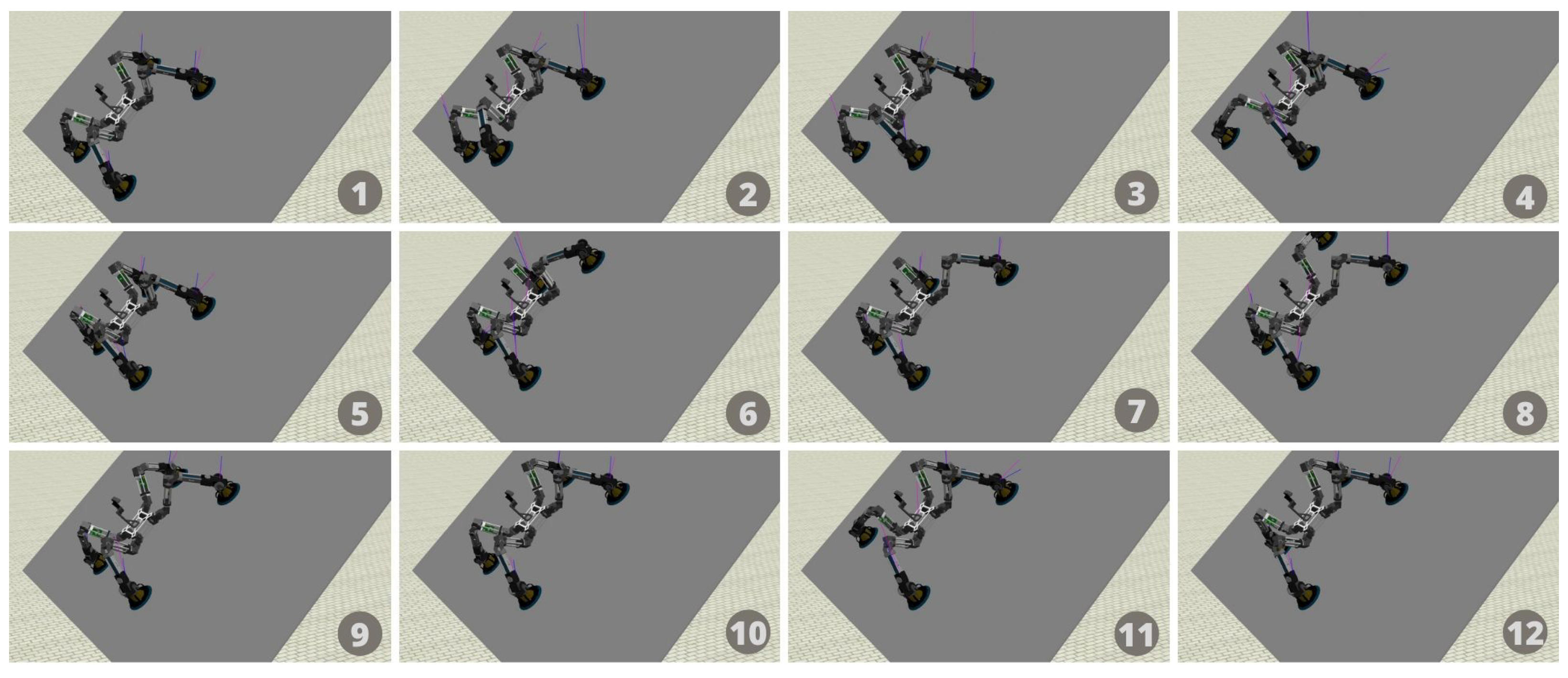
6. Experiments
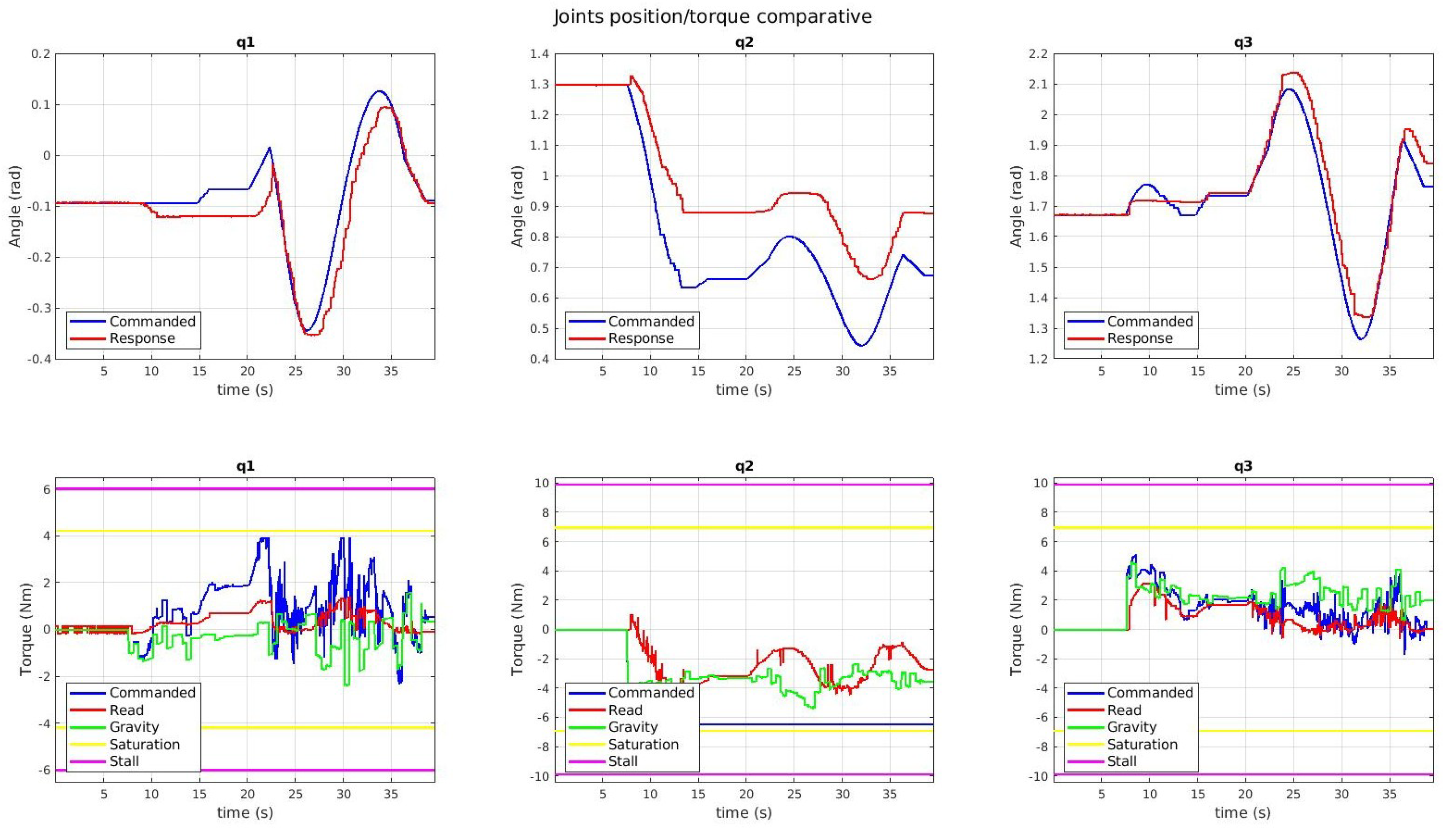
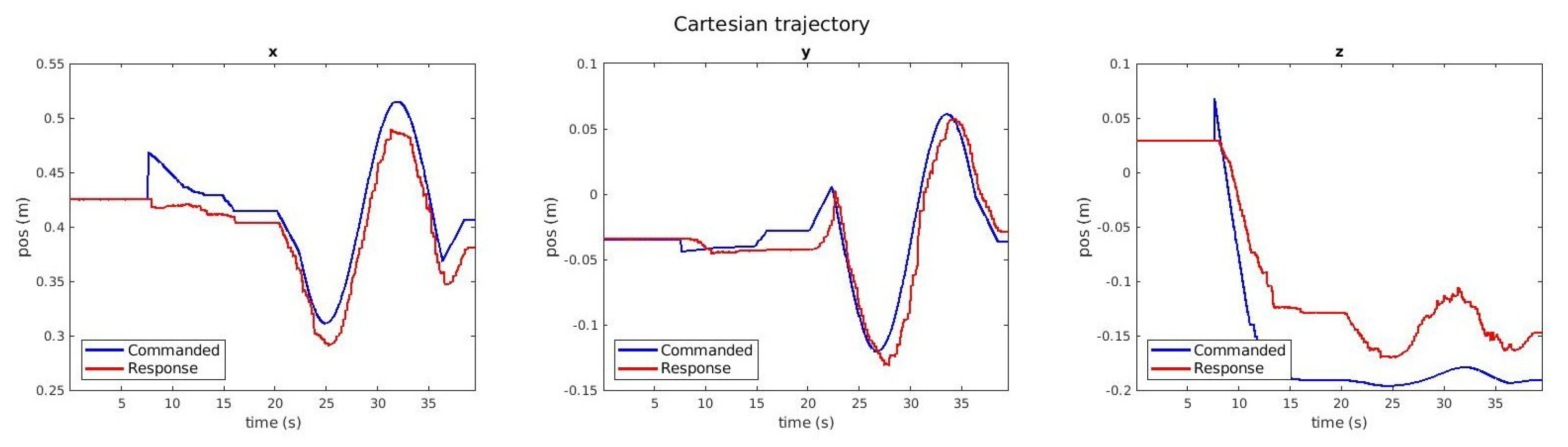
6.1. Torque-Based Control Experiment
6.2. Gravity Compensation
6.3. ROMERIN Gait
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IKC | Inverse kinematic controller |
| IKD | Inverse dynamic controller |
| MoCLORA | Modular Climbing-and-Legged Robotic Organism Architecture |
| WP | Wrist point |
| COM | Center of mass |
| DH | Denavit–Hartenberg |
| DOF | Degrees of freedom |
| FDP | Force distribution problem |
| EKF | Extended Kalman Filter |
References
- Katz, D.; Kenney, J.; Brock, O. How Can Robots Succeed in Uunstructured Environments. In Workshop on Robot Manipulation: Intelligence in Human Environments at Robotics: Science and Systems; Citeseer 2008. Available online: https://citeseerx.ist.psu.edu/doc_view/pid/892f1e4f5b26d0ab44a11de385d95f152d1e6bd0 (accessed on 16 July 2023).
- Prados Sesmero, C.; Buonocore, L.R.; Di Castro, M. Omnidirectional Robotic Platform for Surveillance of Particle Accelerator Environments with Limited Space Areas. Appl. Sci. 2021, 11, 6631. [Google Scholar] [CrossRef]
- Picardi, G.; Astolfi, A.; Chatzievangelou, D.; Aguzzi, J.; Calisti, M. Underwater legged robotics: Review and perspectives. Bioinspir. Biomim. 2023, 18, 031001. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, H.; Gao, H.; Deng, Z.; Ding, L.; Liu, Z. A review of heavy-duty legged robots. Sci. China Technol. Sci. 2013, 57, 298–314. [Google Scholar] [CrossRef]
- Roth, Z. Machines that walk: The adaptive suspension vehicle. Mech. Mach. Theory 1990, 25, 587. [Google Scholar] [CrossRef]
- Li, J.; Gao, H.; Wan, Y.; Humphreys, J.; Peers, C.; Yu, H.; Zhou, C. Whole-Body Control for a Torque-Controlled Legged Mobile Manipulator. Actuators 2022, 11, 304. [Google Scholar] [CrossRef]
- Tanaka, Y.; Shirai, Y.; Lin, X.; Schperberg, A.; Kato, H.; Swerdlow, A.; Kumagai, N.; Hong, D. SCALER: A Tough Versatile Quadruped Free-Climber Robot. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022. [Google Scholar] [CrossRef]
- Qiaoling, D.; Yan, L.; Sinan, L. Design of a micro pole-climbing robot. Int. J. Adv. Robot. Syst. 2019, 16, 172988141985281. [Google Scholar] [CrossRef]
- Kim, D.; Di Carlo, J.; Katz, B.; Bledt, G.; Kim, S. Highly dynamic quadruped locomotion via whole-body impulse control and model predictive control. arXiv 2019, arXiv:1909.06586. [Google Scholar]
- Bellicoso, C.D.; Gehring, C.; Hwangbo, J.; Fankhauser, P.; Hutter, M. Perception-less terrain adaptation through whole body control and hierarchical optimization. In Proceedings of the 2016 IEEE-RAS 16th International Conference on Humanoid Robots (Humanoids), Cancun, Mexico, 15–17 November 2016. [Google Scholar] [CrossRef]
- Herzog, A.; Rotella, N.; Mason, S.; Grimminger, F.; Schaal, S.; Righetti, L. Momentum control with hierarchical inverse dynamics on a torque-controlled humanoid. Auton. Robot. 2015, 40, 473–491. [Google Scholar] [CrossRef]
- Dong, S. Gravity and inertial load adaptive control of wall-climbing robot. J. Eng. 2018, 2019, 442–446. [Google Scholar] [CrossRef]
- Prados, C.; Hernando, M.; Gambao, E.; Brunete, A. ROMERIN: Organismo robótico escalador basado en patas modulares con ventosas activas. Rev. Iberoam. Autom. Inform. Ind. 2022, 20, 175–186. [Google Scholar] [CrossRef]
- Prados, C.; Hernando, M.; Gambao, E.; Brunete, A. MoCLORA—An Architecture for Legged-and-Climbing Modular Bio-Inspired Robotic Organism. Biomimetics 2022, 8, 11. [Google Scholar] [CrossRef]
- Hernando, M.; Gambao, E.; Prados, C.; Brito, D.; Brunete, A. ROMERIN: A new concept of a modular autonomous climbing robot. Int. J. Adv. Robot. Syst. 2022, 19, 17298806221123416. [Google Scholar] [CrossRef]
- Bares, J.E.; Whittaker, W.L. Configuration of Autonomous Walkers for Extreme Terrain. Int. J. Robot. Res. 1993, 12, 535–559. [Google Scholar] [CrossRef]
- Dynamics, B. Spot—The Agile Mobile Robot. 2023. Available online: https://www.bostondynamics.com/products/spot (accessed on 22 May 2023).
- Hutter, M.; Gehring, C.; Jud, D.; Lauber, A.; Bellicoso, C.D.; Tsounis, V.; Hwangbo, J.; Bodie, K.; Fankhauser, P.; Bloesch, M.; et al. ANYmal—A highly mobile and dynamic quadrupedal robot. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Repulic of Korea, 9–14 October 2016. [Google Scholar] [CrossRef]
- Hutter, M.; Gehring, C.; Bloesch, M.; Hoepflinger, M.A.; Remy, C.D.; Siegwart, R. StarlETH: A compliant quadrupedal robot for fast, efficient, and versatile locomotion. In Adaptive Mobile Robotics; World Scientific: Singapore, 2012; pp. 483–490. [Google Scholar] [CrossRef]
- Roennau, A.; Heppner, G.; Nowicki, M.; Dillmann, R. LAURON V: A versatile six-legged walking robot with advanced maneuverability. In Proceedings of the 2014 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Besacon, France, 8–11 July 2014. [Google Scholar] [CrossRef]
- de Santos, P.G.; Cobano, J.; Garcia, E.; Estremera, J.; Armada, M. A six-legged robot-based system for humanitarian demining missions. Mechatronics 2007, 17, 417–430. [Google Scholar] [CrossRef]
- Jakimovski, B.; Meyer, B.; Maehle, E. Self-reconfiguring hexapod robot OSCAR using organically inspired approaches and innovative robot leg amputation mechanism. In Proceedings of the International Conference on Automation, Robotics and Control Systems, ARCS-09, Orlando, FL, USA, 13–16 July 2009. [Google Scholar]
- Kim, H.; Kang, T.; Loc, V.G.; Choi, H.R. Gait Planning of Quadruped Walking and Climbing Robot for Locomotion in 3D Environment. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 2733–2738. [Google Scholar] [CrossRef]
- Parness, A.; Abcouwer, N.; Fuller, C.; Wiltsie, N.; Nash, J.; Kennedy, B. LEMUR 3: A limbed climbing robot for extreme terrain mobility in space. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017. [Google Scholar] [CrossRef]
- Bandyopadhyay, T.; Steindl, R.; Talbot, F.; Kottege, N.; Dungavell, R.; Wood, B.; Barker, J.; Hoehn, K.; Elfes, A. Magneto: A Versatile Multi-Limbed Inspection Robot. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Madrid, Spain, 1–5 October 2018; pp. 2253–2260. [Google Scholar] [CrossRef]
- Peters, G.; Pagano, D.; Liu, D.; Waldron, K. A prototype climbing robot for inspection of complex ferrous structures. In Proceedings of the Emerging Trends in Mobile Robotics; World Scientific: Singapore, 2010. [Google Scholar] [CrossRef]
- Hernando, M.; Alonso, M.; Prados, C.; Gambao, E. Behavior-Based Control Architecture for Legged-and-Climber Robots. Appl. Sci. 2021, 11, 9547. [Google Scholar] [CrossRef]
- Buettner, T.; Heppner, G.; Roennau, A.; Dillmann, R. Nimble Limbs—Intelligent attachable legs to create walking robots from variously shaped objects. In Proceedings of the 2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Hong Kong, China, 8–12 July 2019. [Google Scholar] [CrossRef]
- Montes, H.; Mena, L.; Fernández, R.; Armada, M. Energy-efficiency hexapod walking robot for humanitarian demining. Ind. Robot. Int. J. 2017, 44, 457–466. [Google Scholar] [CrossRef]
- Nabulsi, S.; Sarria, J.; Montes, H.; Armada, M. High-Resolution Indirect Feet–Ground Interaction Measurement for Hydraulic-Legged Robots. IEEE Trans. Instrum. Meas. 2009, 58, 3396–3404. [Google Scholar] [CrossRef]
- Bares, J.; Hebert, M.; Kanade, T.; Krotkov, E.; Mitchell, T.; Simmons, R.; Whittaker, W. Ambler: An autonomous rover for planetary exploration. Computer 1989, 22, 18–26. [Google Scholar] [CrossRef]
- Grieco, J.; Prieto, M.; Armada, M.; de Santos, P.G. A six-legged climbing robot for high payloads. In Proceedings of the 1998 IEEE International Conference on Control Applications (Cat. No.98CH36104), Trieste, Italy, 4 September 1998. [Google Scholar] [CrossRef]
- Spröwitz, A.T.; Tuleu, A.; Ajallooeian, M.; Vespignani, M.; Möckel, R.; Eckert, P.; D’Haene, M.; Degrave, J.; Nordmann, A.; Schrauwen, B.; et al. Oncilla Robot: A Versatile Open-Source Quadruped Research Robot With Compliant Pantograph Legs. Front. Robot. AI 2018, 5, 67. [Google Scholar] [CrossRef]
- Waldron, K.; McGhee, R. The adaptive suspension vehicle. IEEE Control Syst. Mag. 1986, 6, 7–12. [Google Scholar] [CrossRef]
- Hartikainen, K.; Halme, A.; Lehtinen, H.; Koskinen, K. MECANT I: A six legged walking machine for research purposes in outdoor environment. In Proceedings of the 1992 IEEE International Conference on Robotics and Automation, Nice, France, 12–14 May 1992; pp. 157–163. [Google Scholar] [CrossRef]
- Doosti, P.; Mahjoob, M.J.; Dadashzadeh, B. Finite-time control strategy for the running of a telescopic leg biped robot. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 196. [Google Scholar] [CrossRef]
- Kajita, S.; Matsumoto, O.; Saigo, M. Real-time 3D walking pattern generation for a biped robot with telescopic legs. In Proceedings of the 2001 ICRA. IEEE International Conference on Robotics and Automation (Cat. No.01CH37164), Seoul, Republic of Korea, 21–26 May 2001; Volume 3, pp. 2299–2306. [Google Scholar] [CrossRef]
- Miwa, S.; Kinugasa, T.; Oba, K.; Ishihara, T.; Zhang, J.; Hayashi, R.; Yoshida, K. Various gait pattern generation and analysis of semi-passive quadruped walker with telescopic knee based on phase oscillator. Artif. Life Robot. 2023. [Google Scholar] [CrossRef]
- Fishman, A.; Garrad, M.S.; Hinitt, A.; Zanini, P.; Barker, T.; Rossiter, J. A Compliant Telescopic Limb with Anisotropic Stiffness. Front. Robot. AI 2017, 3, 80. [Google Scholar] [CrossRef]
- Mistry, M.; Buchli, J.; Schaal, S. Inverse dynamics control of floating base systems using orthogonal decomposition. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010. [Google Scholar] [CrossRef]
- Righetti, L.; Buchli, J.; Mistry, M.; Schaal, S. Control of legged robots with optimal distribution of contact forces. In Proceedings of the 2011 11th IEEE-RAS International Conference on Humanoid Robots, Bled, Slovenia, 26–28 October 2011; pp. 318–324. [Google Scholar] [CrossRef]
- Hernando, M.; Gómez, V.; Brunete, A.; Gambao, E. CFD Modelling and Optimization Procedure of an Adhesive System for a Modular Climbing Robot. Sensors 2021, 21, 1117. [Google Scholar] [CrossRef]
- Ding, X.; Wang, Z.; Rovetta, A.; Zhu, J. Locomotion Analysis of Hexapod Robot. In Climbing and Walking Robots; InTech: Rijeka, Croatia, 2010. [Google Scholar] [CrossRef]
- Full, R.J.; Koditschek, D.E. Templates and anchors: Neuromechanical hypotheses of legged locomotion on land. J. Exp. Biol. 1999, 202, 3325–3332. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Wu, S.; Zhu, P.; Liu, R. Analysis on the dynamic climbing forces of a gecko inspired climbing robot based on GPL model. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015. [Google Scholar] [CrossRef]
- Provancher, W.R.; Jensen-Segal, S.I.; Fehlberg, M.A. ROCR: An Energy-Efficient Dynamic Wall-Climbing Robot. IEEE/ASME Trans. Mechatron. 2011, 16, 897–906. [Google Scholar] [CrossRef]
- Orin, D.E.; Oh, S.Y. Control of Force Distribution in Robotic Mechanisms Containing Closed Kinematic Chains. J. Dyn. Syst. Meas. Control 1981, 103, 134–141. [Google Scholar] [CrossRef]
- Cheng, F.T.; Orin, D. Efficient algorithm for optimal force distribution in multiple-chain robotic systems-the compact-dual LP method. In Proceedings of the 1989 International Conference on Robotics and Automation, Scottsdale, AZ, USA, 14–19 May 1989. [Google Scholar] [CrossRef]
- Chen, J.S.; Cheng, F.T.; Yang, K.T.; Kung, F.C.; Sun, Y.Y. Solving the optimal force distribution problem in vehicles. In Proceedings of the 1998 IEEE International Conference on Robotics and Automation (Cat. No.98CH36146), Leuven, Belgium, 20 May 1998. [Google Scholar] [CrossRef]
- Nahon, M.A.; Angeles, J. Optimization of Dynamic Forces in Mechanical Hands. J. Mech. Des. 1991, 113, 167–173. [Google Scholar] [CrossRef]
- Hernando, M.; Brunete, A.; Gambao, E. ROMERIN: A Modular Climber Robot for Infrastructure Inspection. IFAC-PapersOnLine 2019, 52, 424–429. [Google Scholar] [CrossRef]
- Paul, R.P. Robot Manipulators, Mathematics, Programming and Control; Inst Tech: Cambridge, MA, USA, 1981. [Google Scholar]
- Hollerbach, J.M. A Recursive Lagrangian Formulation of Maniputator Dynamics and a Comparative Study of Dynamics Formulation Complexity. IEEE Trans. Syst. Man Cybern. 1980, 10, 730–736. [Google Scholar] [CrossRef]
- Luh, J.Y.S.; Walker, M.W.; Paul, R.P.C. On-Line Computational Scheme for Mechanical Manipulators. J. Dyn. Syst. Meas. Control 1980, 102, 69–76. [Google Scholar] [CrossRef]
- Kane, T.R.; Levinson, D.A. The use of Kane’s dynamical equations in robotics. Int. J. Robot. Res. 1983, 2, 3–21. [Google Scholar] [CrossRef]
- Lee, C.; Lee, B.; Nigam, R. Development of the generalized d’Alembert equations of motion for mechanical manipulators. In Proceedings of the The 22nd IEEE Conference on Decision and Control, San Antonio, TX, USA, 15–17 December 1983; pp. 1205–1210. [Google Scholar] [CrossRef]
- Saha, S.K. Dynamics of Serial Multibody Systems Using the Decoupled Natural Orthogonal Complement Matrices. J. Appl. Mech. 1999, 66, 986–996. [Google Scholar] [CrossRef]
- Featherstone, R. A Divide-and-Conquer Articulated-Body Algorithm for Parallel O(log(n)) Calculation of Rigid-Body Dynamics. Part 1: Basic Algorithm. Int. J. Robot. Res. 1999, 18, 867–875. [Google Scholar] [CrossRef]
- Featherstone, R. Rigid Body Dynamics Algorithms; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Vidoni, R.; Gasparetto, A. Efficient force distribution and leg posture for a bio-inspired spider robot. Robot. Auton. Syst. 2011, 59, 142–150. [Google Scholar] [CrossRef]
- Chen, X.; Watanabe, K.; Kiguchi, K.; Izumi, K. Optimal force distribution for the legs of a quadruped robot. Mach. Intell. Robot. Control 1999, 1, 87–93. [Google Scholar]
- Kelly, R.; Davila, V.S.; Perez, J.A.L. Control of Robot Manipulators in Joint Space; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Sesmero, C.P.; Lorente, S.V.; Castro, M.D. Graph SLAM Built over Point Clouds Matching for Robot Localization in Tunnels. Sensors 2021, 21, 5340. [Google Scholar] [CrossRef]




| Name | Value (m) | Name | Value (kg) |
|---|---|---|---|
| 0.068 | 0.212 | ||
| 0.22045 | 0.360 | ||
| 0.01492 | 0.535 | ||
| 0.27991 | 0.205 | ||
| 0.02245 | 0.120 | ||
| 0.087 | 0.292 | ||
| L | 0.65536 | M | 1.724 |
| Joint | d | a | ||
|---|---|---|---|---|
| 1 | 0 | |||
| 2 | 0 | |||
| 3 | 0 | |||
| 4 | 0 | |||
| 5 | 0 | 0 | ||
| 6 | 0 | 0 |
| Method | 4 Legs | 6 Legs | ||
|---|---|---|---|---|
| Classical method | 145 | 165 | 580 | 870 |
| Proposed method | 77 | 95 | 308 | 462 |
| Experiment | Video Start | Environment | Objective |
|---|---|---|---|
| Torque-based control (Section 6.1) | 0:10 | Suction cups over different planes | Verify FDP and impedance control with physical platform |
| Gravity compensation (Section 6.2) | 0:36 | Ground, different planes, wall, and ceiling | Verify gravity compensation and impedance control |
| ROMERIN gait (Section 6.3) | 1:40 | Ground, wall, and ceiling | Verify impedance control with gait |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prados, C.; Hernando, M.; Gambao, E.; Brunete, A. Torque-Based Control of a Bio-Inspired Modular Climbing Robot. Machines 2023, 11, 757. https://doi.org/10.3390/machines11070757
Prados C, Hernando M, Gambao E, Brunete A. Torque-Based Control of a Bio-Inspired Modular Climbing Robot. Machines. 2023; 11(7):757. https://doi.org/10.3390/machines11070757
Chicago/Turabian StylePrados, Carlos, Miguel Hernando, Ernesto Gambao, and Alberto Brunete. 2023. "Torque-Based Control of a Bio-Inspired Modular Climbing Robot" Machines 11, no. 7: 757. https://doi.org/10.3390/machines11070757
APA StylePrados, C., Hernando, M., Gambao, E., & Brunete, A. (2023). Torque-Based Control of a Bio-Inspired Modular Climbing Robot. Machines, 11(7), 757. https://doi.org/10.3390/machines11070757











