A qLPV-MPC Control Strategy for Trajectory Tracking of Quadrotors
Abstract
1. Introduction
2. Quadrotor Dynamics
2.1. E-Frame Dynamics
2.2. B-Frame Dynamics
2.3. C-Frame Dynamics
3. LPV State Space Model of the Quadrotor
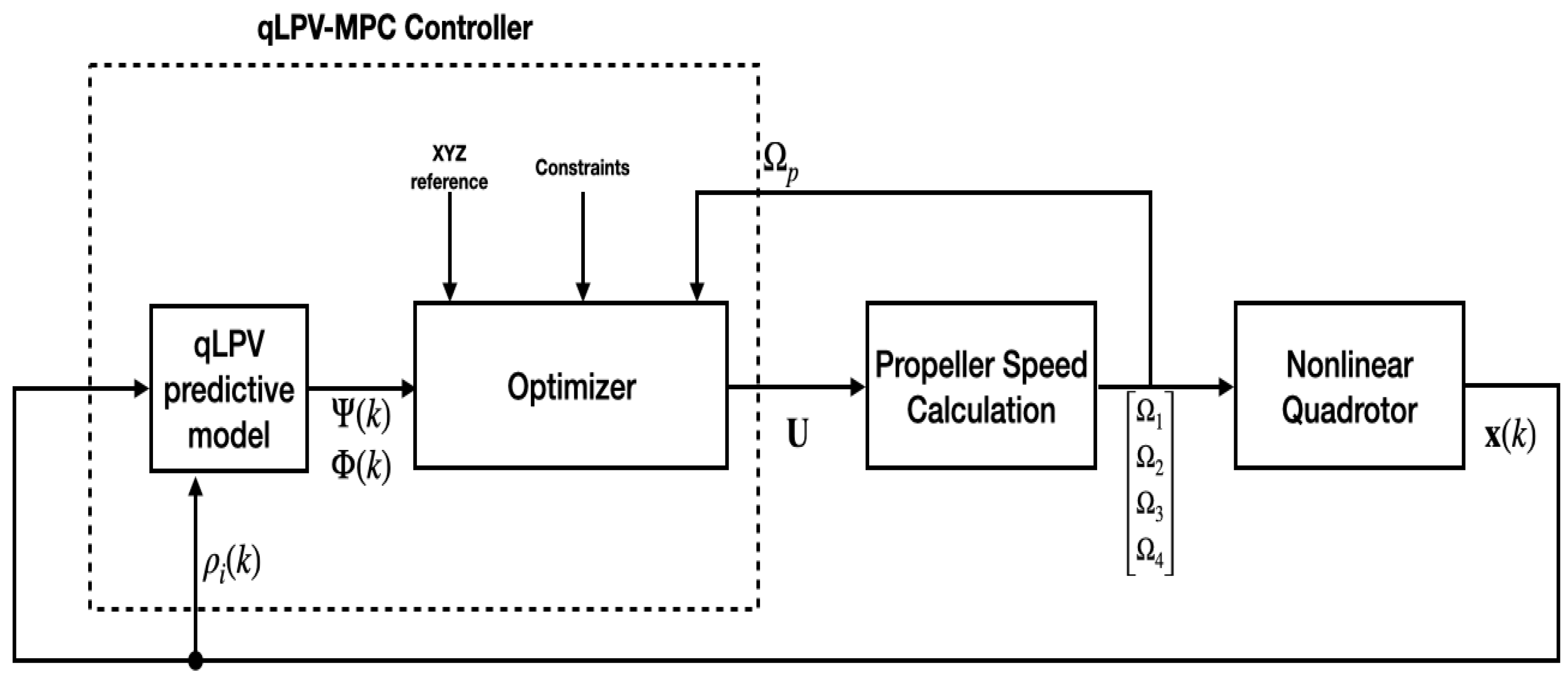
4. Model Predictive Control Based on the LPV Representation of the Quadrotor
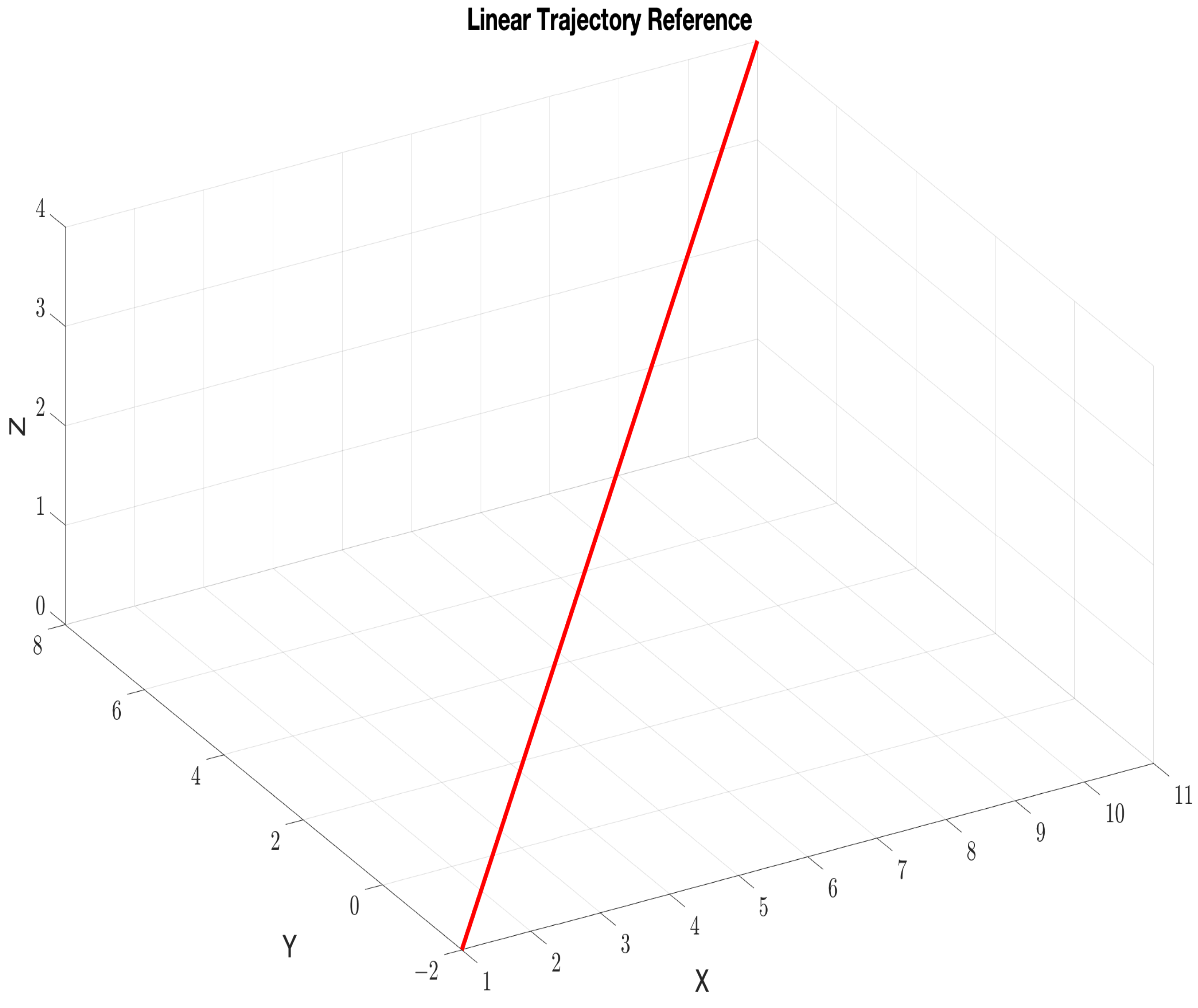
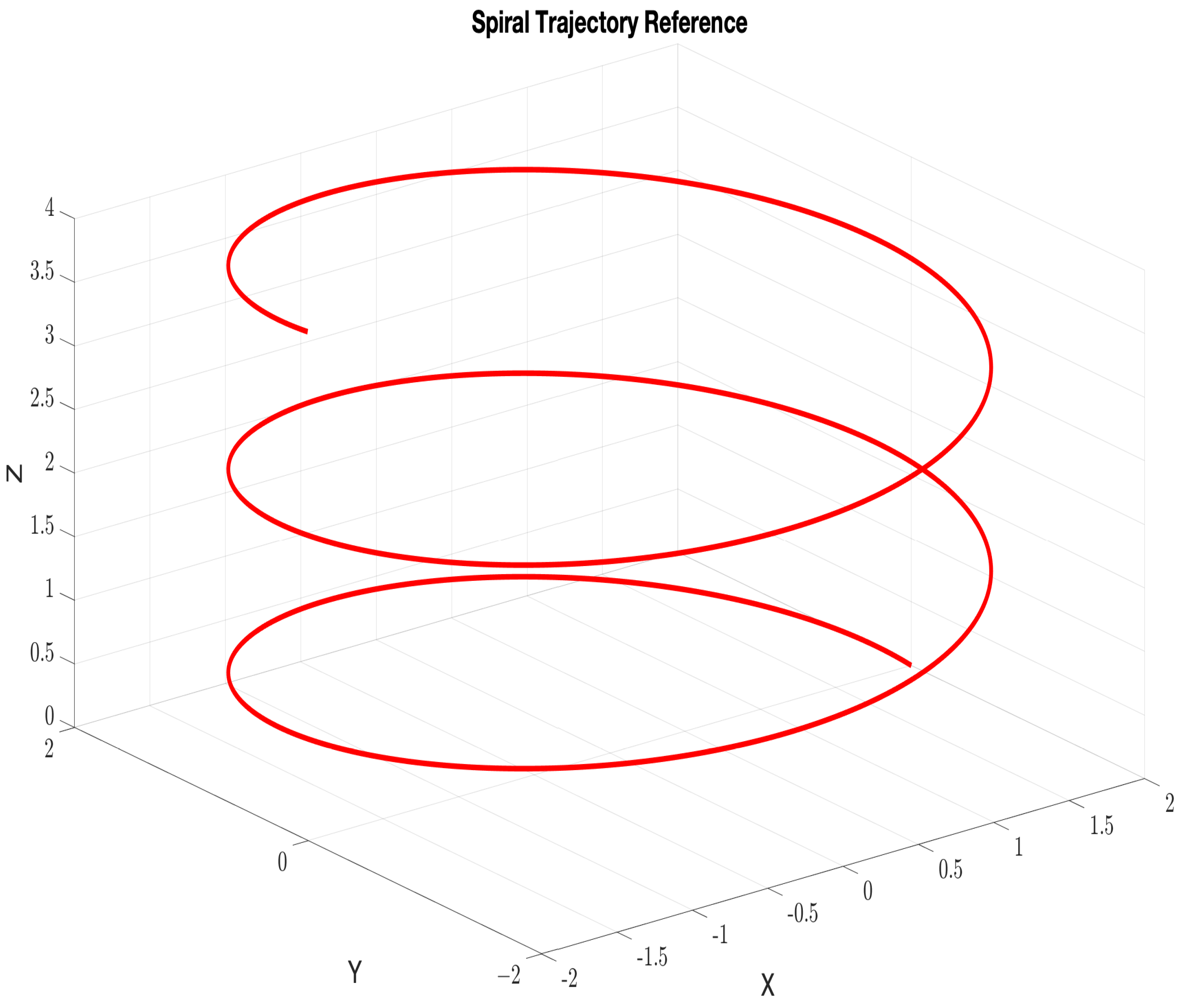
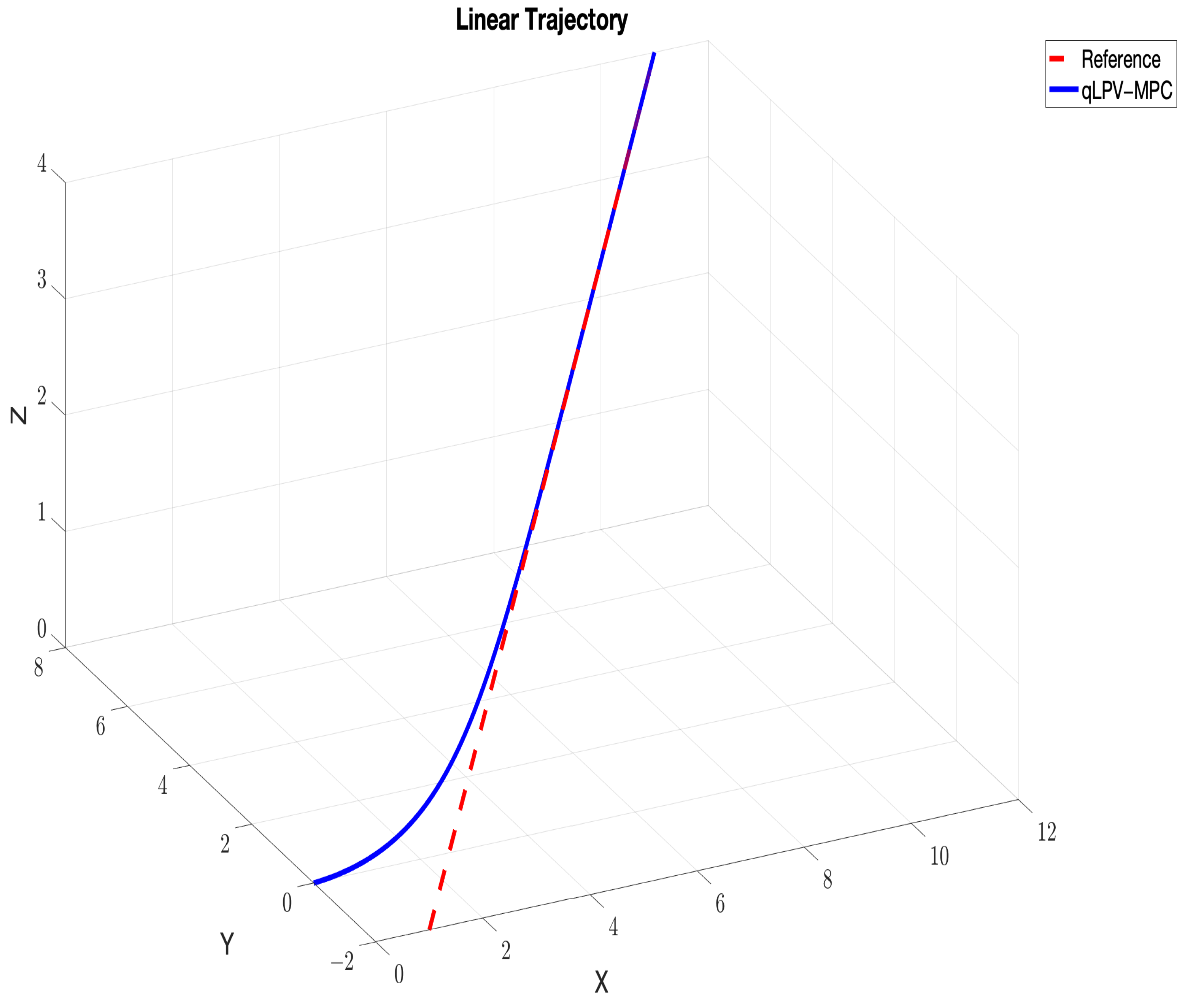
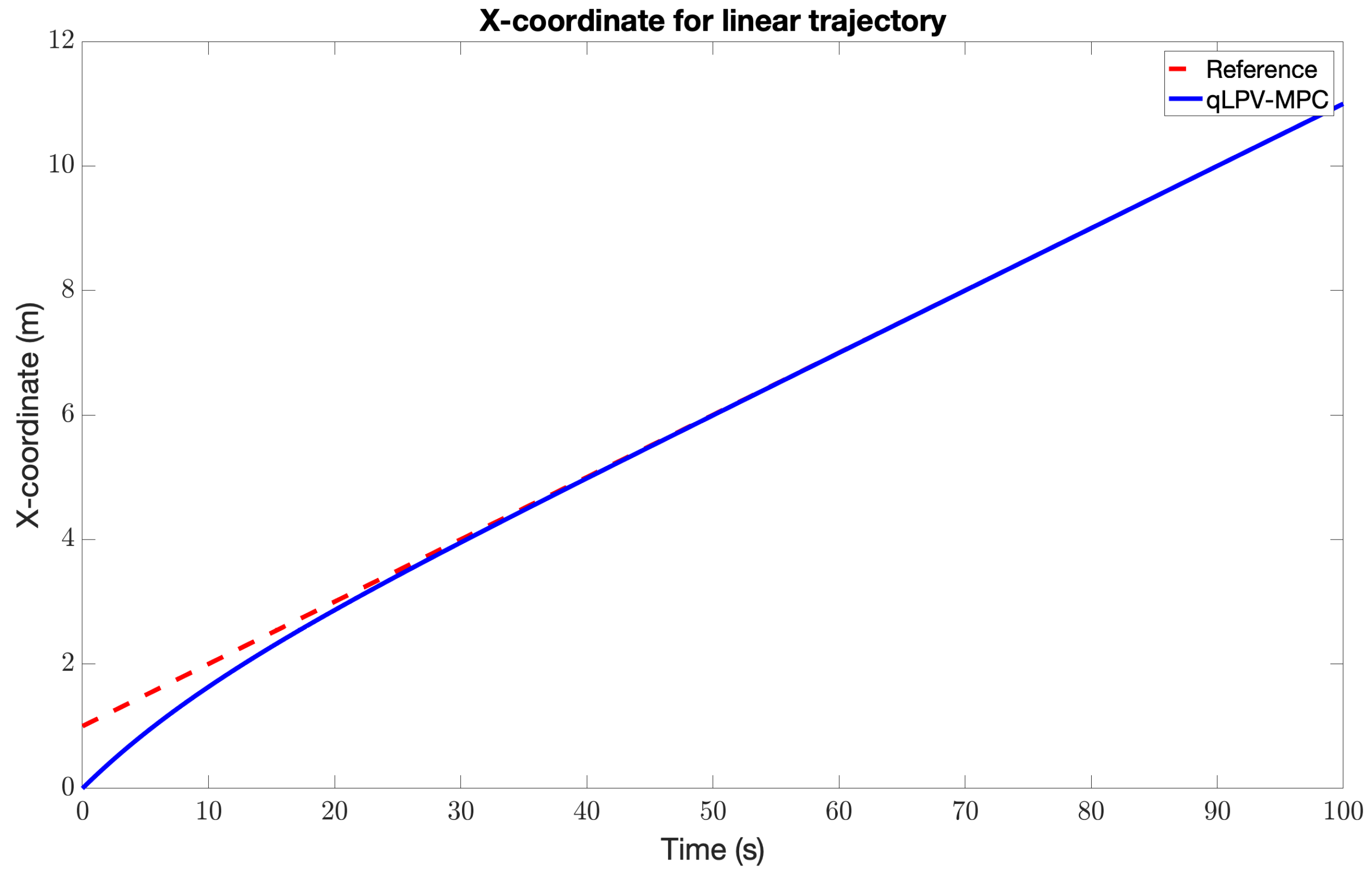
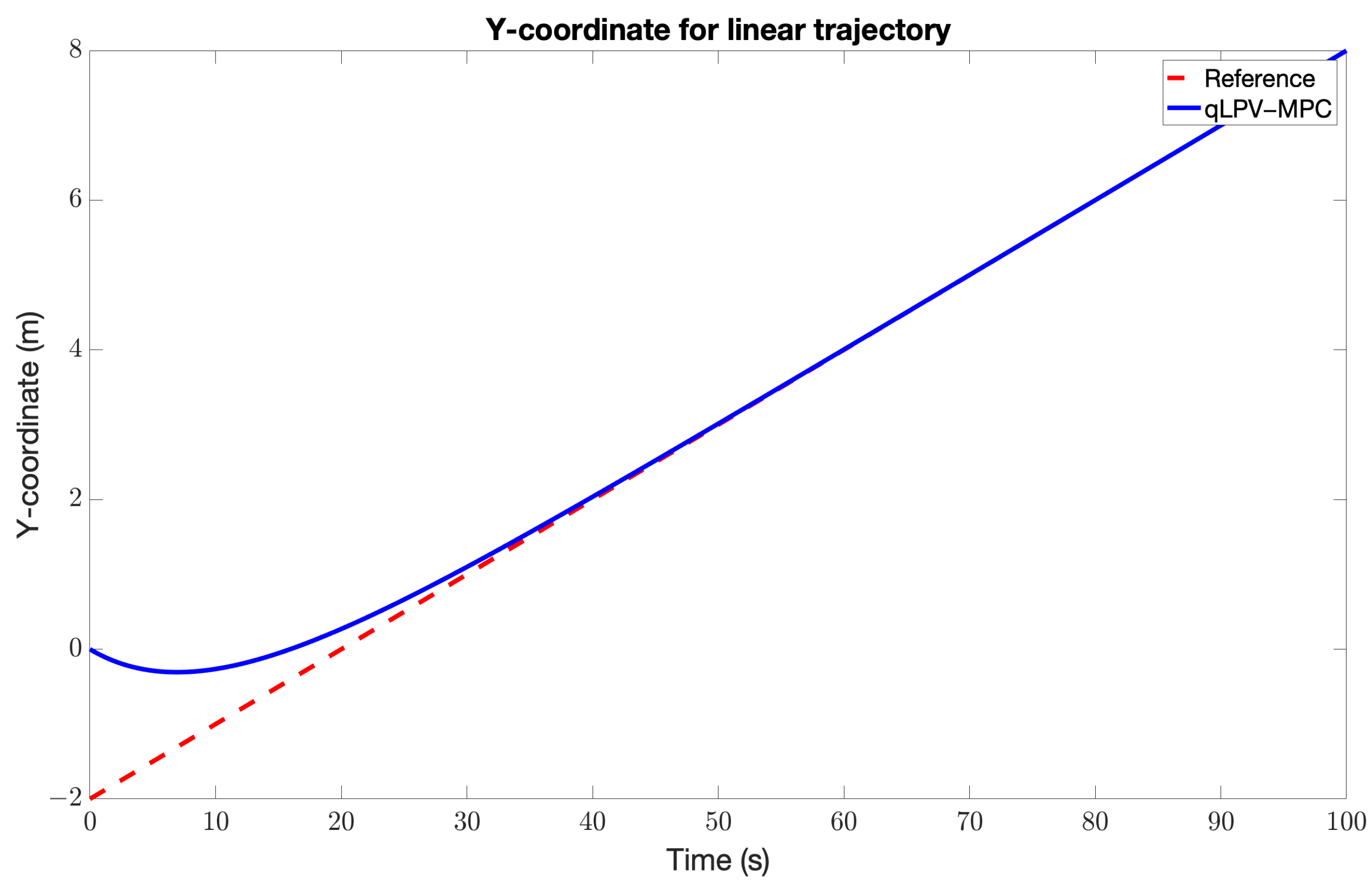
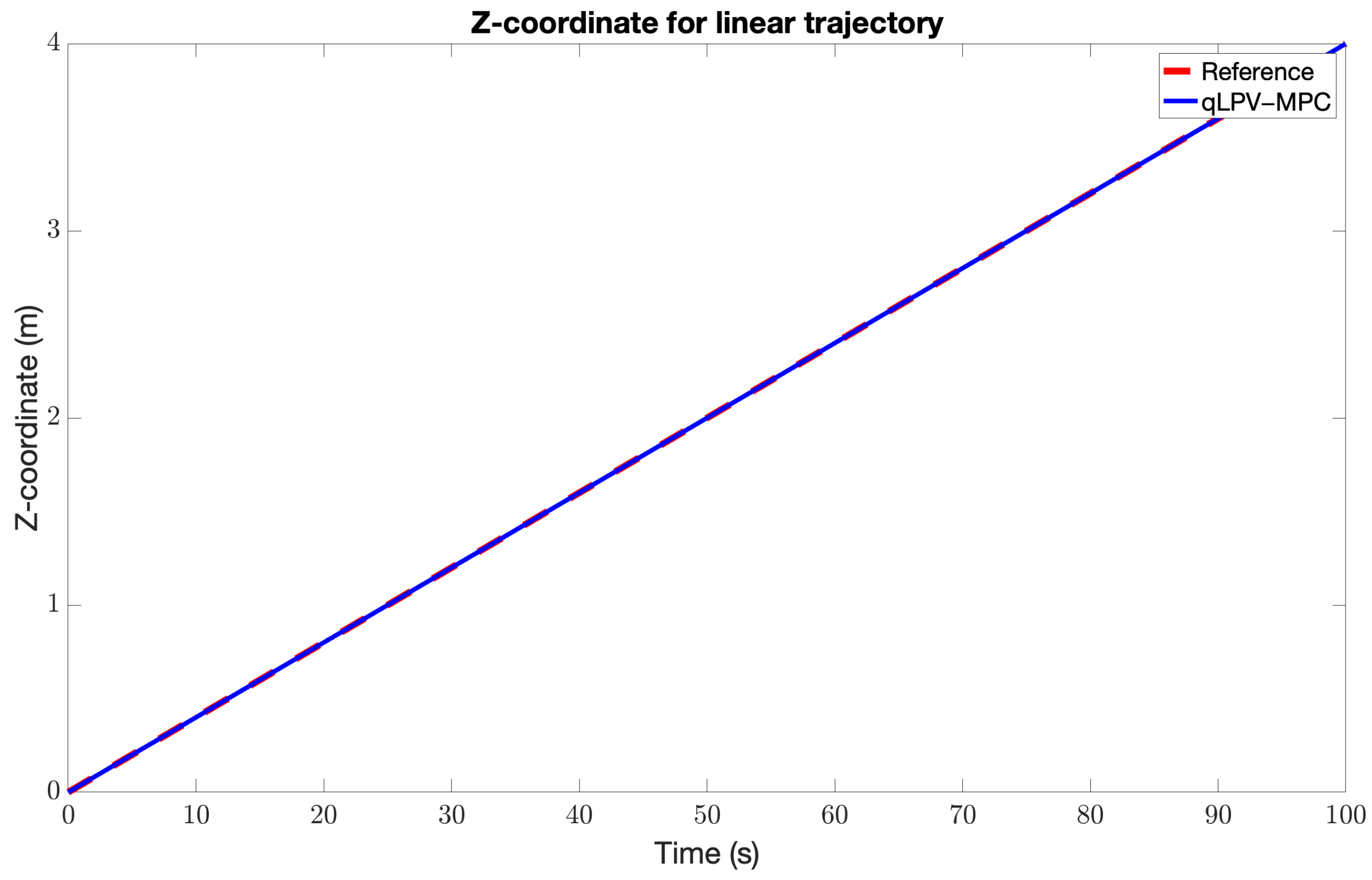
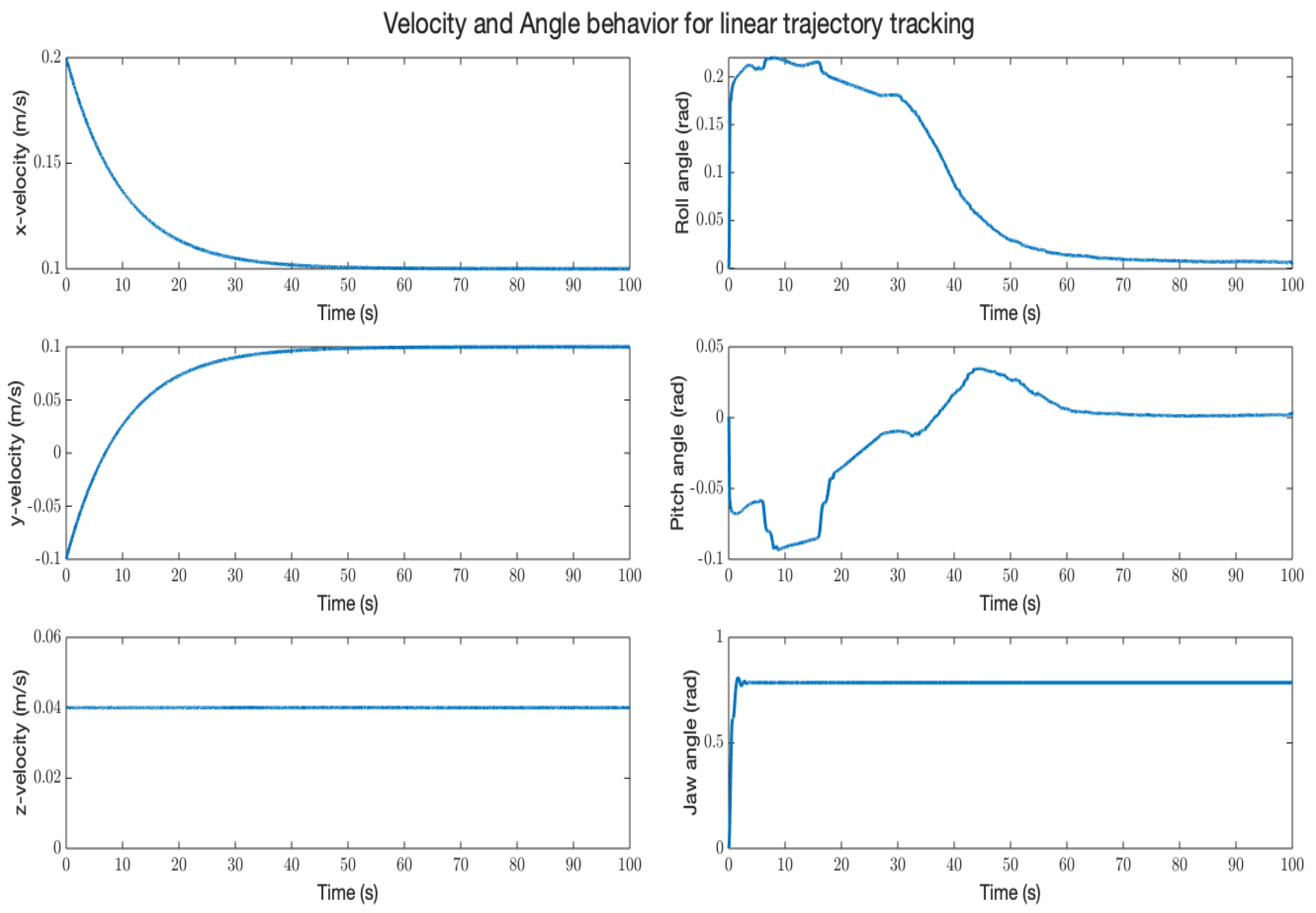
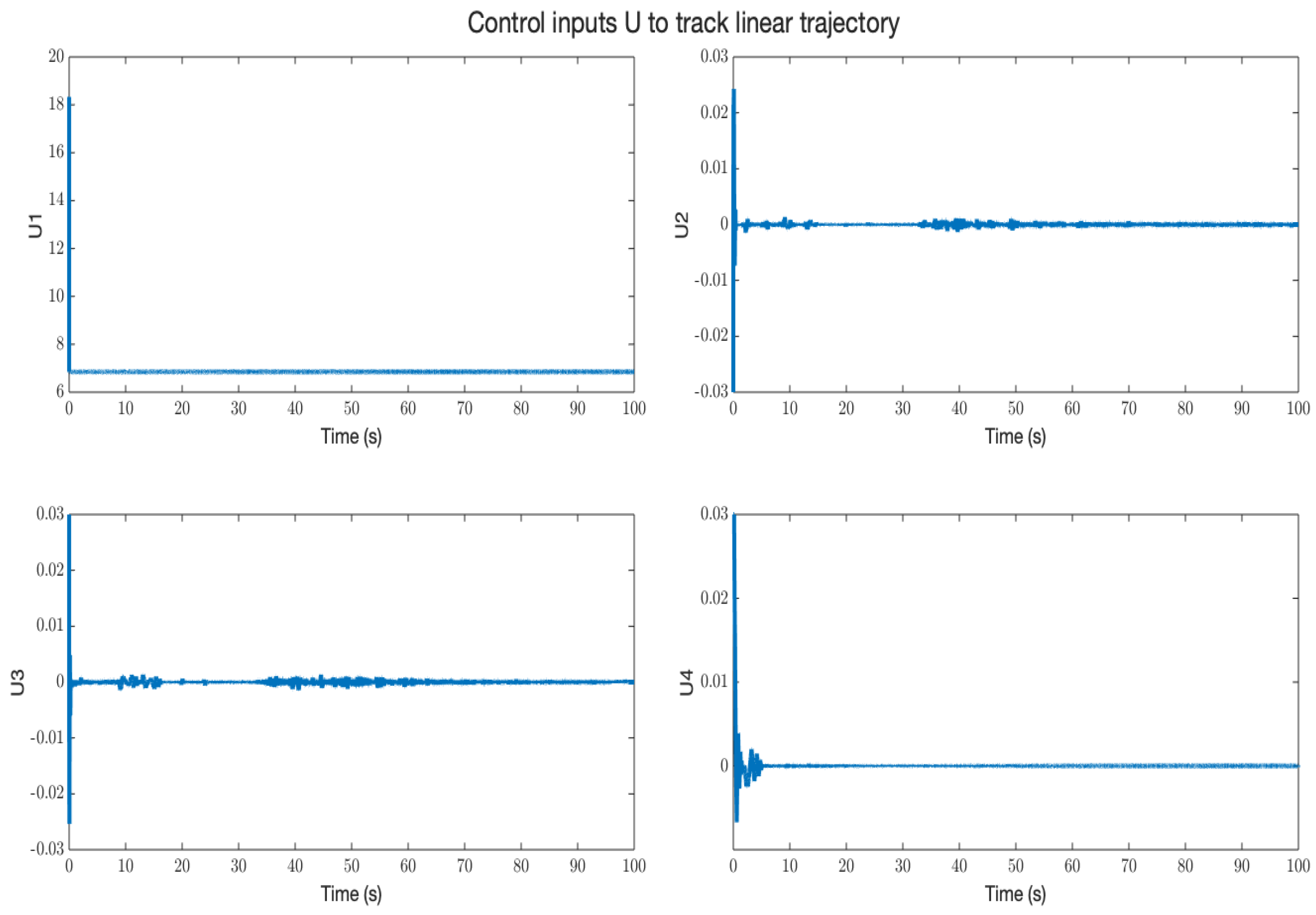
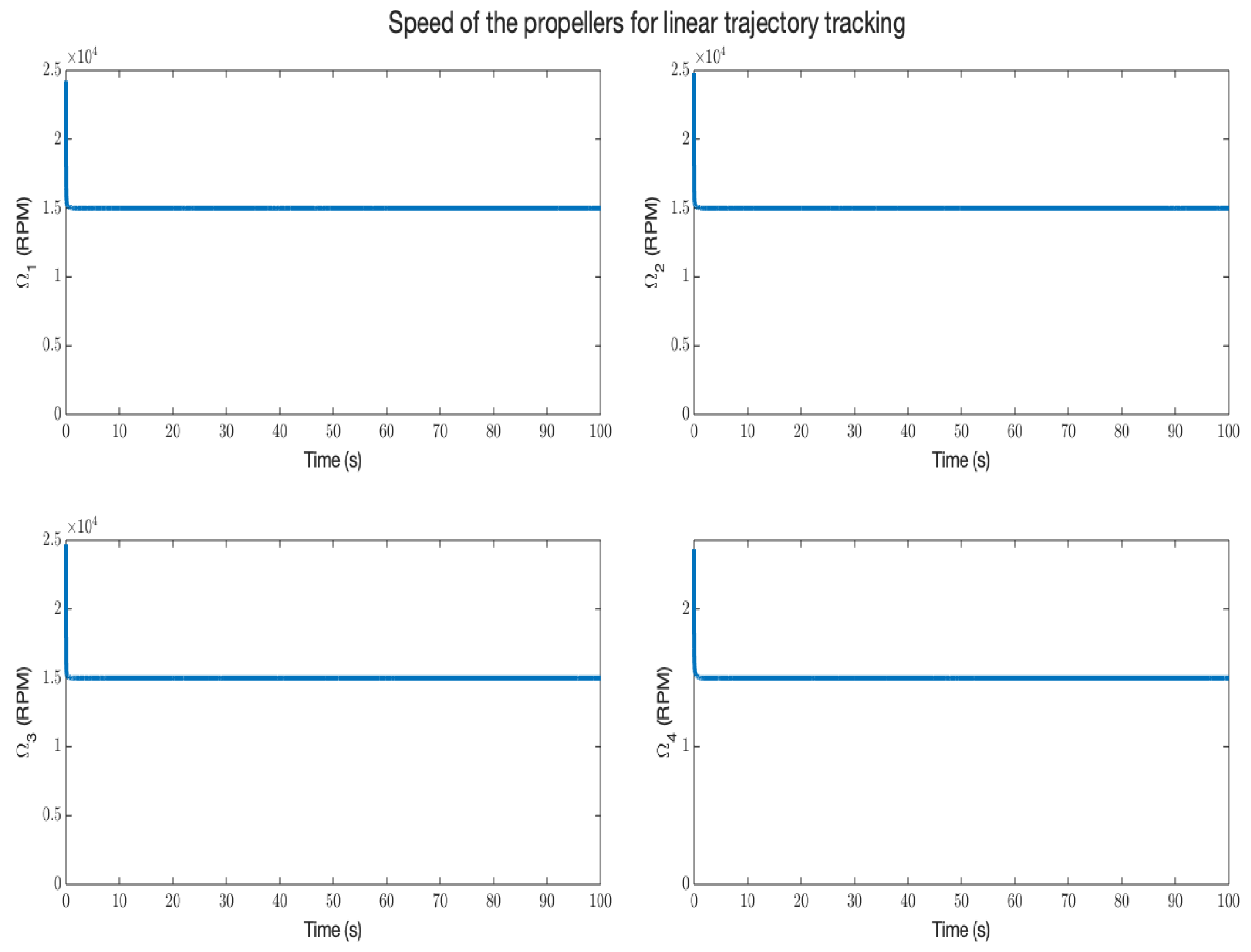
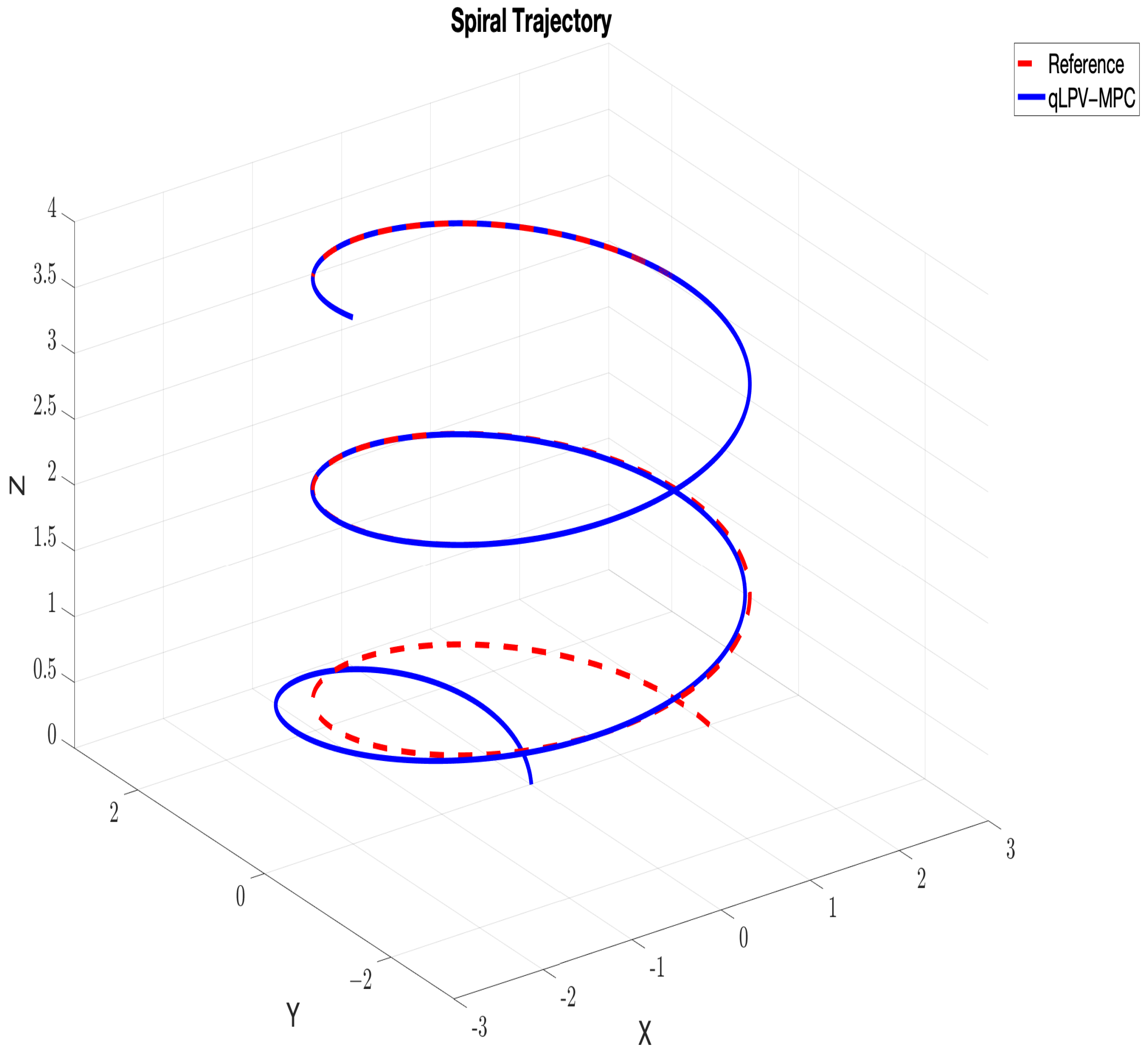
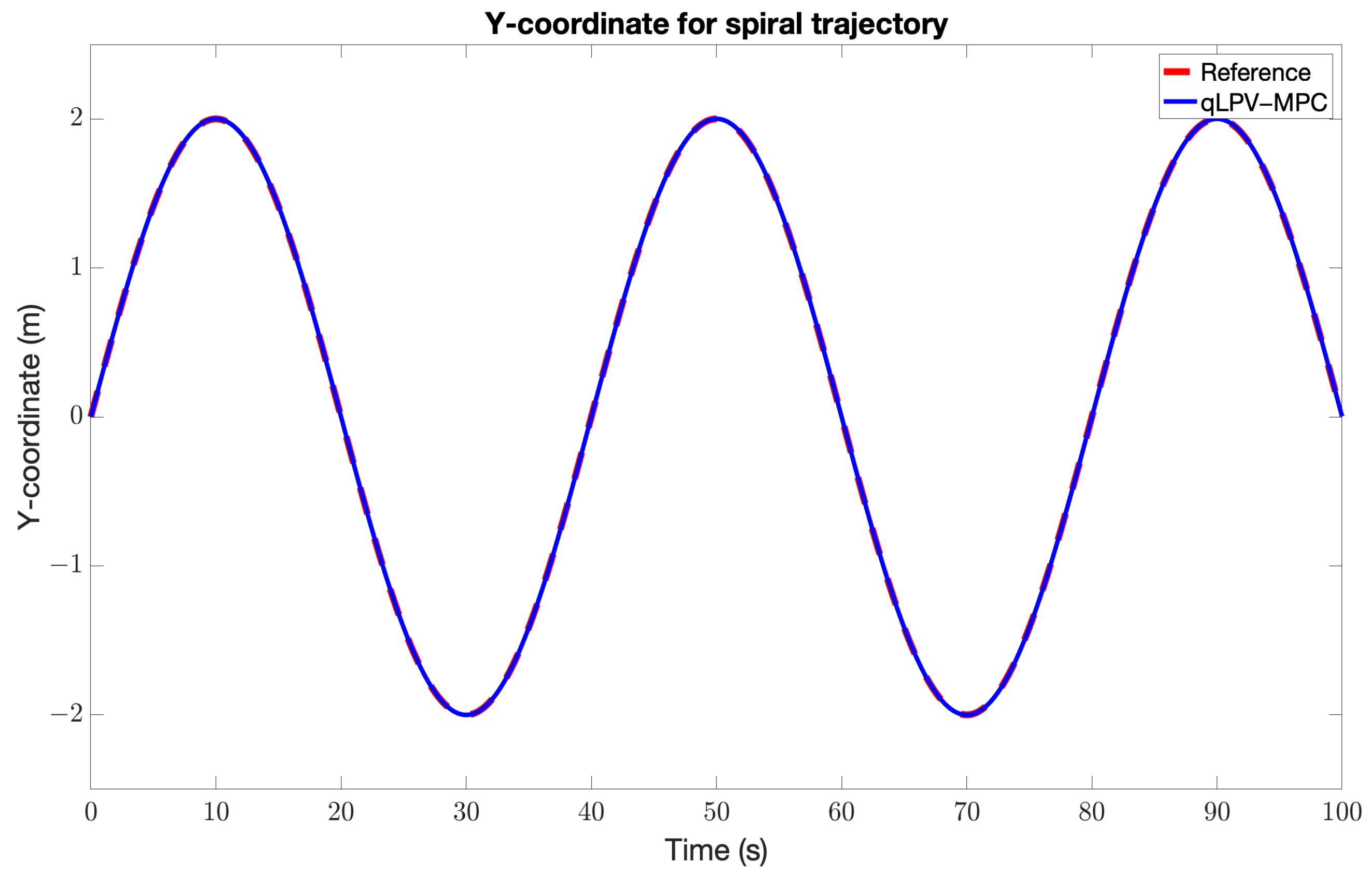
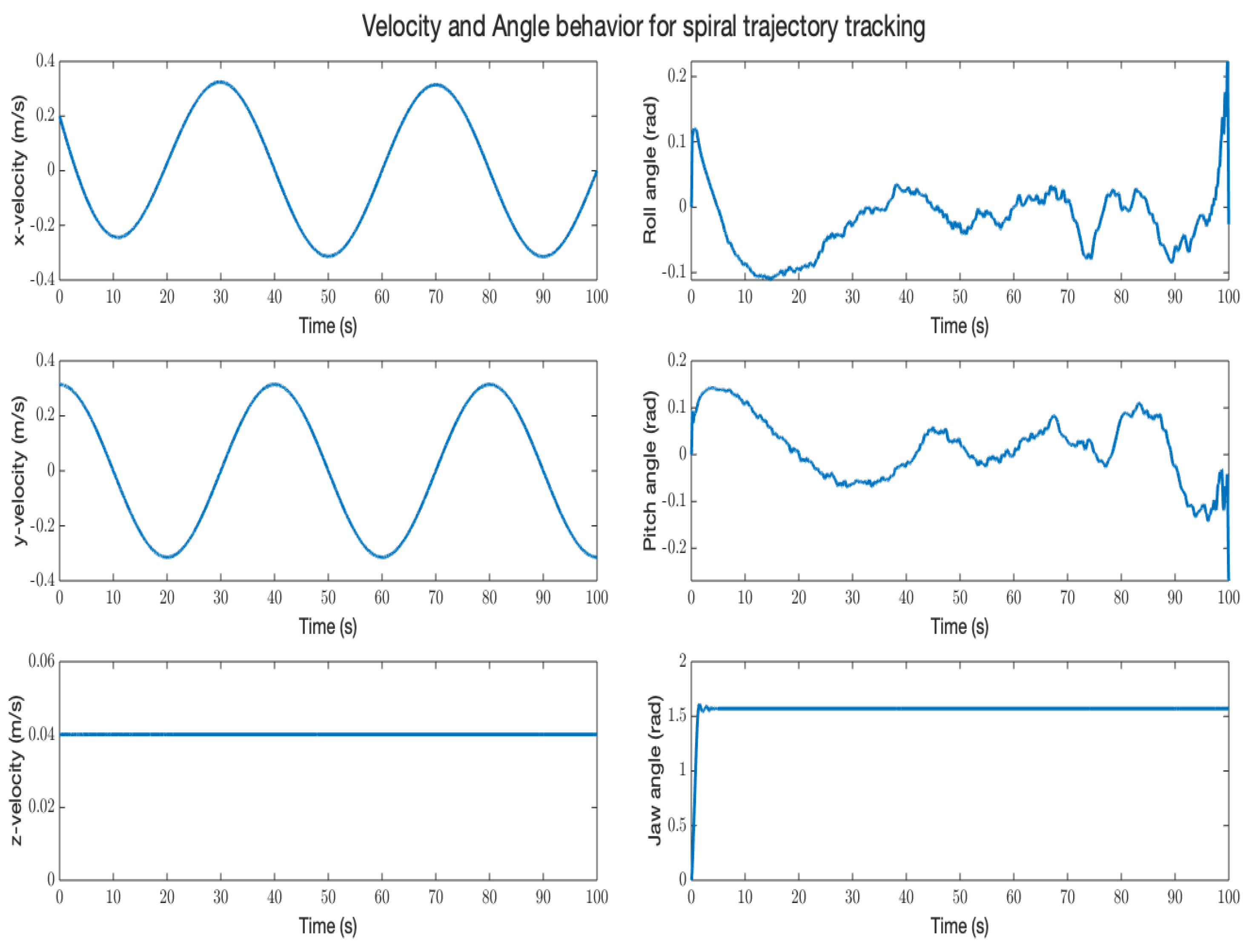
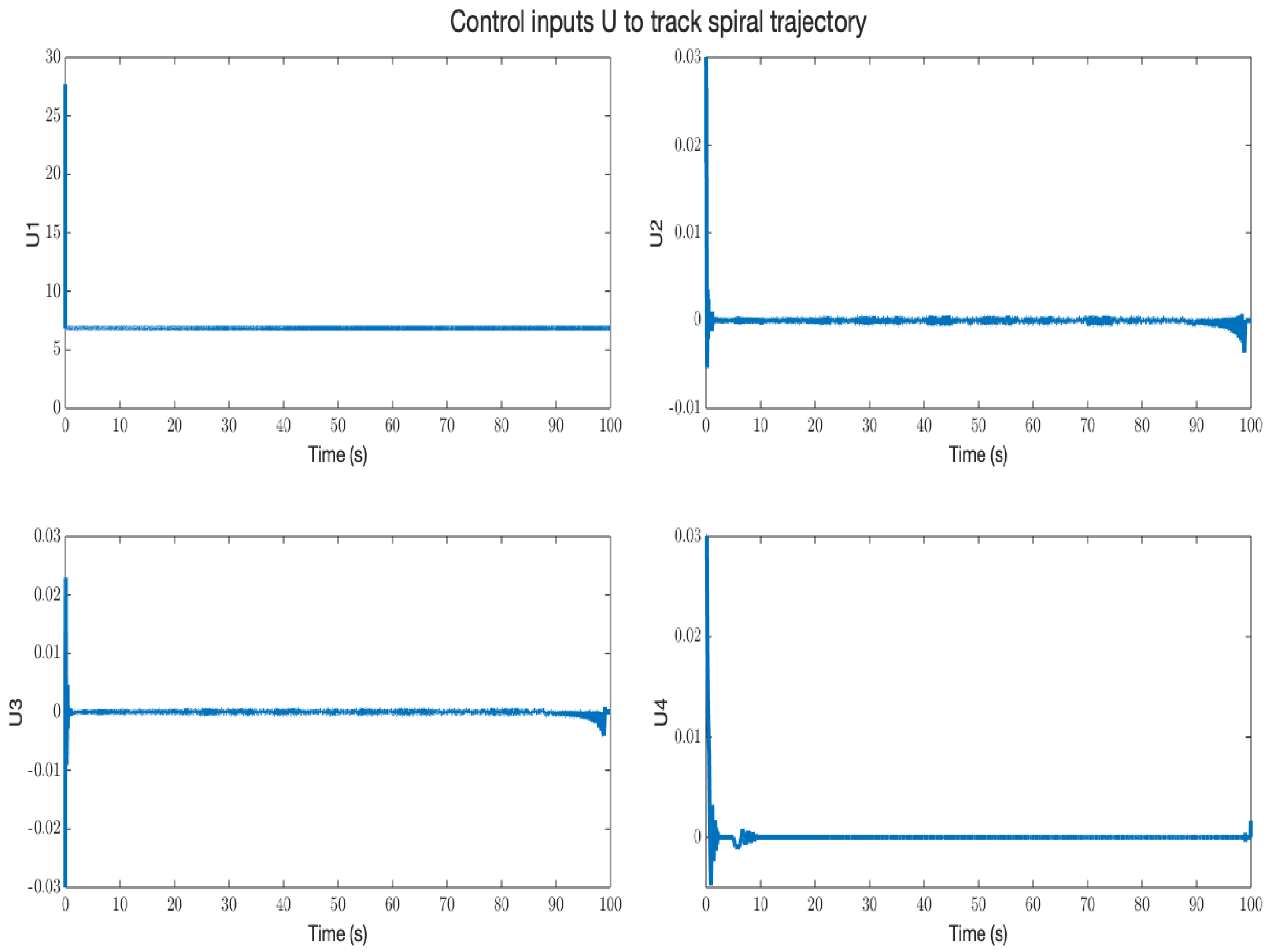
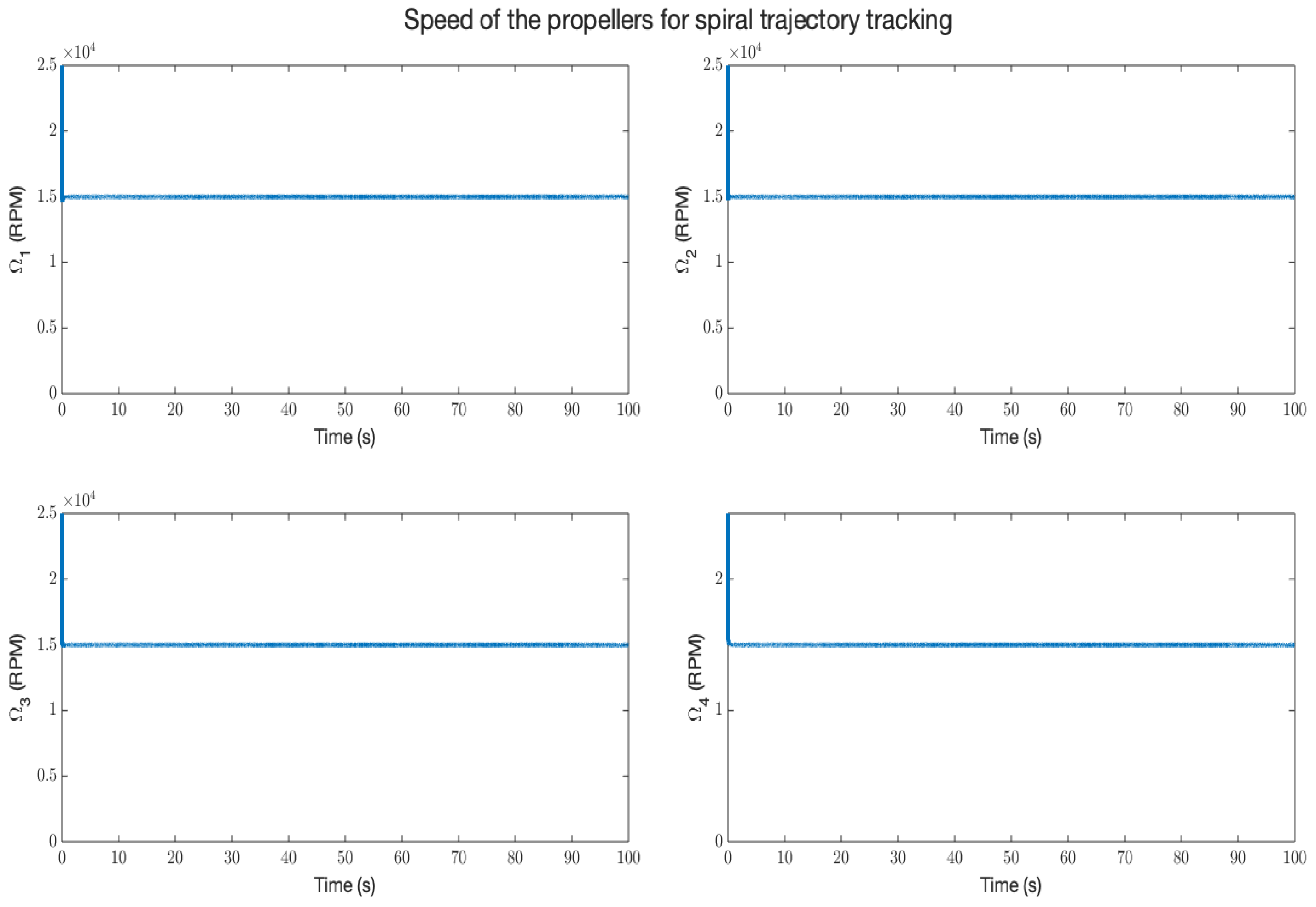
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moreno-Valenzuela, J.; Pérez-Alcocer, R.; Guerrero-Medina, M.; Dzul, A. Nonlinear PID-type controller for quadrotor trajectory tracking. IEEE/ASME Trans. Mechatron. 2018, 23, 2436–2447. [Google Scholar] [CrossRef]
- Abdelhay, S.; Zakriti, A. Modeling of a quadcopter trajectory tracking system using PID controller. Procedia Manuf. 2019, 32, 564–571. [Google Scholar] [CrossRef]
- Idres, M.; Mustapha, O.; Okasha, M. Quadrotor trajectory tracking using PID cascade control. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2017; Volume 270, p. 012010. [Google Scholar]
- El Hamidi, K.; Mjahed, M.; El Kari, A.; Ayad, H. Neural network and fuzzy-logic-based self-tuning PID control for quadcopter path tracking. Stud. Inform. Control 2019, 28, 401–412. [Google Scholar] [CrossRef]
- Minh, L.D.; Ha, C. Modeling and Control of Quadrotor MAV Using Vision-Based Measurement. In Proceedings of the International Forum on Strategic Technology (IFOST), Ulsan, Republic of Korea, 13–15 October 2010; pp. 70–75. [Google Scholar]
- Fessi, R.; Bouallègue, S. LQG controller design for a quadrotor UAV based on particle swarm optimisation. Int. J. Autom. Control 2019, 13, 569–594. [Google Scholar] [CrossRef]
- Bouselima, E.; Ichalal, D.; Mammar, S. Quadrotor Control and Actuator Fault Detection: LQG Versus Robust H-/H∞ observer. In Proceedings of the 2019 4th Conference on Control and Fault Tolerant Systems (SysTol), Casablanca, Morocco, 18–20 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 86–91. [Google Scholar]
- Emam, M.; Fakharian, A. Attitude tracking of quadrotor UAV via mixed H2/H∞ controller: An LMI based approach. In Proceedings of the 2016 24th Mediterranean Conference on Control and Automation (MED), Athens, Greece, 21–24 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 390–395. [Google Scholar]
- Guo, M.; Su, Y.; Gu, D. Mixed H2/H∞ tracking control with constraints for single quadcopter carrying a cable-suspended payload. IFAC-PapersOnLine 2017, 50, 4869–4874. [Google Scholar] [CrossRef]
- Jasim, W.; Gu, D. H∞ path tracking control for quadrotors based on quaternion representation. In Advances in Autonomous Robotics Systems, Proceedings of the 15th Annual Conference, TAROS 2014, Birmingham, UK, 1–3 September 2014; Proceedings 15; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; pp. 72–84. [Google Scholar]
- Kayacan, E.; Maslim, R. Type-2 fuzzy logic trajectory tracking control of quadrotor VTOL aircraft with elliptic membership functions. IEEE/ASME Trans. Mechatron. 2016, 22, 339–348. [Google Scholar] [CrossRef]
- Prayitno, A.; Indrawati, V.; Utomo, G. Trajectory tracking of AR. Drone quadrotor using fuzzy logic controller. TELKOMNIKA (Telecommun. Comput. Electron. Control) 2014, 12, 819–828. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, X.; Zhao, H.; Dai, A.; Zhou, H. Three-dimensional fuzzy control of mini quadrotor UAV trajectory tracking under impact of wind disturbance. In Proceedings of the 2016 International Conference on Advanced Mechatronic Systems (ICAMechS), Melbourne, VIC, Australia, 30 November–3 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 372–377. [Google Scholar]
- Zhou, L.; Zhang, J.; Dou, J.; Wen, B. A fuzzy adaptive backstepping control based on mass observer for trajectory tracking of a quadrotor UAV. Int. J. Adapt. Control Signal Process. 2018, 32, 1675–1693. [Google Scholar] [CrossRef]
- Ganga, G.; Dharmana, M.M. MPC controller for trajectory tracking control of quadcopter. In Proceedings of the 2017 International Conference on Circuit, Power and Computing Technologies (ICCPCT), Kollam, India, 20–21 April 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Eskandarpour, A.; Sharf, I. A constrained error-based MPC for path following of quadrotor with stability analysis. Nonlinear Dyn. 2020, 99, 899–918. [Google Scholar] [CrossRef]
- Benotsmane, R.; Reda, A.; Vásárhelyi, J. Model Predictive Control for Autonomous Quadrotor Trajectory Tracking. In Proceedings of the 2022 23rd International Carpathian Control Conference (ICCC), Sinaia, Romania, 29 May–1 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 215–220. [Google Scholar]
- Abdolhosseini, M.; Zhang, Y.M.; Rabbath, C.A. Trajectory tracking with model predictive control for an unmanned quad-rotor helicopter: Theory and flight test results. In Intelligent Robotics and Applications, Proceedings of the 5th International Conference, ICIRA 2012, Montreal, QC, Canada, 3–5 October 2012; Springer: Berlin/Heidelberg, Germany, 2012; Part I 5; pp. 411–420. [Google Scholar]
- Huang, S.; Teo, R.S.H.; Tan, K.K. Collision avoidance of multi unmanned aerial vehicles: A review. Annu. Rev. Control 2019, 48, 147–164. [Google Scholar] [CrossRef]
- Wang, D.; Pan, Q.; Shi, Y.; Hu, J.; Zhao, C. Efficient nonlinear model predictive control for quadrotor trajectory tracking: Algorithms and experiment. IEEE Trans. Cybern. 2021, 51, 5057–5068. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Lu, H.; Chen, W.H. An explicit MPC for quadrotor trajectory tracking. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 4055–4060. [Google Scholar]
- Kapnopoulos, A.; Alexandridis, A. A cooperative particle swarm optimization approach for tuning an MPC-based quadrotor trajectory tracking scheme. Aerosp. Sci. Technol. 2022, 127, 107725. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, D.; Hu, J.; Pan, Q. Nonlinear model predictive control-based guidance algorithm for quadrotor trajectory tracking with obstacle avoidance. J. Syst. Sci. Complex. 2021, 34, 1379–1400. [Google Scholar] [CrossRef]
- Guevara, B.S.; Recalde, L.F.; Varela-Aldás, J.; Andaluz, V.H.G.; Gandolfo, D.C.; Toibero, J.M. A Comparative Study between NMPC and Baseline Feedback Controllers for UAV Trajectory Tracking. Drones 2023, 7, 144. [Google Scholar] [CrossRef]
- Stastny, T.J.; Dash, A.; Siegwart, R. Nonlinear mpc for fixed-wing uav trajectory tracking: Implementation and flight experiments. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Grapevine, TX, USA, 9–13 January 2017; p. 1512. [Google Scholar]
- Misin, M.; Puig, V. LPV MPC control of an autonomous aerial vehicle. In Proceedings of the 2020 28th Mediterranean Conference on Control and Automation (MED), Saint-Raphael France, 15–18 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 109–114. [Google Scholar]
- Cavanini, L.; Ippoliti, G.; Camacho, E.F. Model predictive control for a linear parameter varying model of an UAV. J. Intell. Robot. Syst. 2021, 101, 57. [Google Scholar] [CrossRef]
- Singh, B.K.; Kumar, A. Model predictive control using LPV approach for trajectory tracking of quadrotor UAV with external disturbances. Aircr. Eng. Aerosp. Technol. 2023, 95, 607–618. [Google Scholar] [CrossRef]
- Qu, S.; Zhu, G.; Su, W.; Swei, S.S.M. LPV Model-based Adaptive MPC of an eVTOL Aircraft During Tilt Transition Subject to Motor Failure. Int. J. Control Autom. Syst. 2023, 21, 339–349. [Google Scholar] [CrossRef]
- Rodríguez Hernández, X. LPV Predictive Control of a Quadrotor. Master’s Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2020. [Google Scholar]



| Variable | Value | Units |
|---|---|---|
| g | 9.8 | m/s |
| m | 0.698 | kg |
| 0.0034 | kg · m | |
| 0.0034 | kg · m | |
| 0.006 | kg · m | |
| 1.302 × 10 | kg · m | |
| b | 7.6184 × 10 | N · s |
| d | 2.6839 × 10 | N · s |
| l | 0.171 | m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodriguez-Guevara, D.; Favela-Contreras, A.; Gonzalez-Villarreal, O.J. A qLPV-MPC Control Strategy for Trajectory Tracking of Quadrotors. Machines 2023, 11, 755. https://doi.org/10.3390/machines11070755
Rodriguez-Guevara D, Favela-Contreras A, Gonzalez-Villarreal OJ. A qLPV-MPC Control Strategy for Trajectory Tracking of Quadrotors. Machines. 2023; 11(7):755. https://doi.org/10.3390/machines11070755
Chicago/Turabian StyleRodriguez-Guevara, Daniel, Antonio Favela-Contreras, and Oscar Julian Gonzalez-Villarreal. 2023. "A qLPV-MPC Control Strategy for Trajectory Tracking of Quadrotors" Machines 11, no. 7: 755. https://doi.org/10.3390/machines11070755
APA StyleRodriguez-Guevara, D., Favela-Contreras, A., & Gonzalez-Villarreal, O. J. (2023). A qLPV-MPC Control Strategy for Trajectory Tracking of Quadrotors. Machines, 11(7), 755. https://doi.org/10.3390/machines11070755






