Performance Optimization of Ultralow-Frequency Electromagnetic Energy Harvester Driven by Eccentric mass
Abstract
1. Introduction
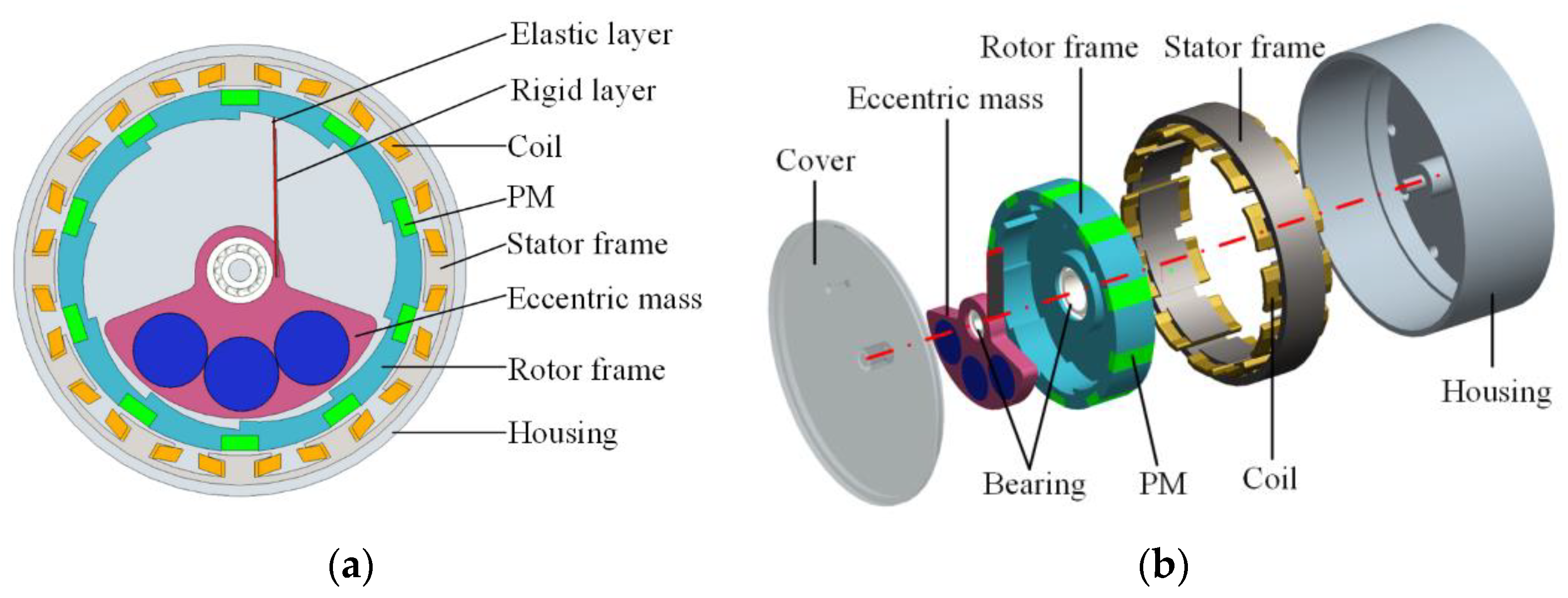
2. Design of EEH
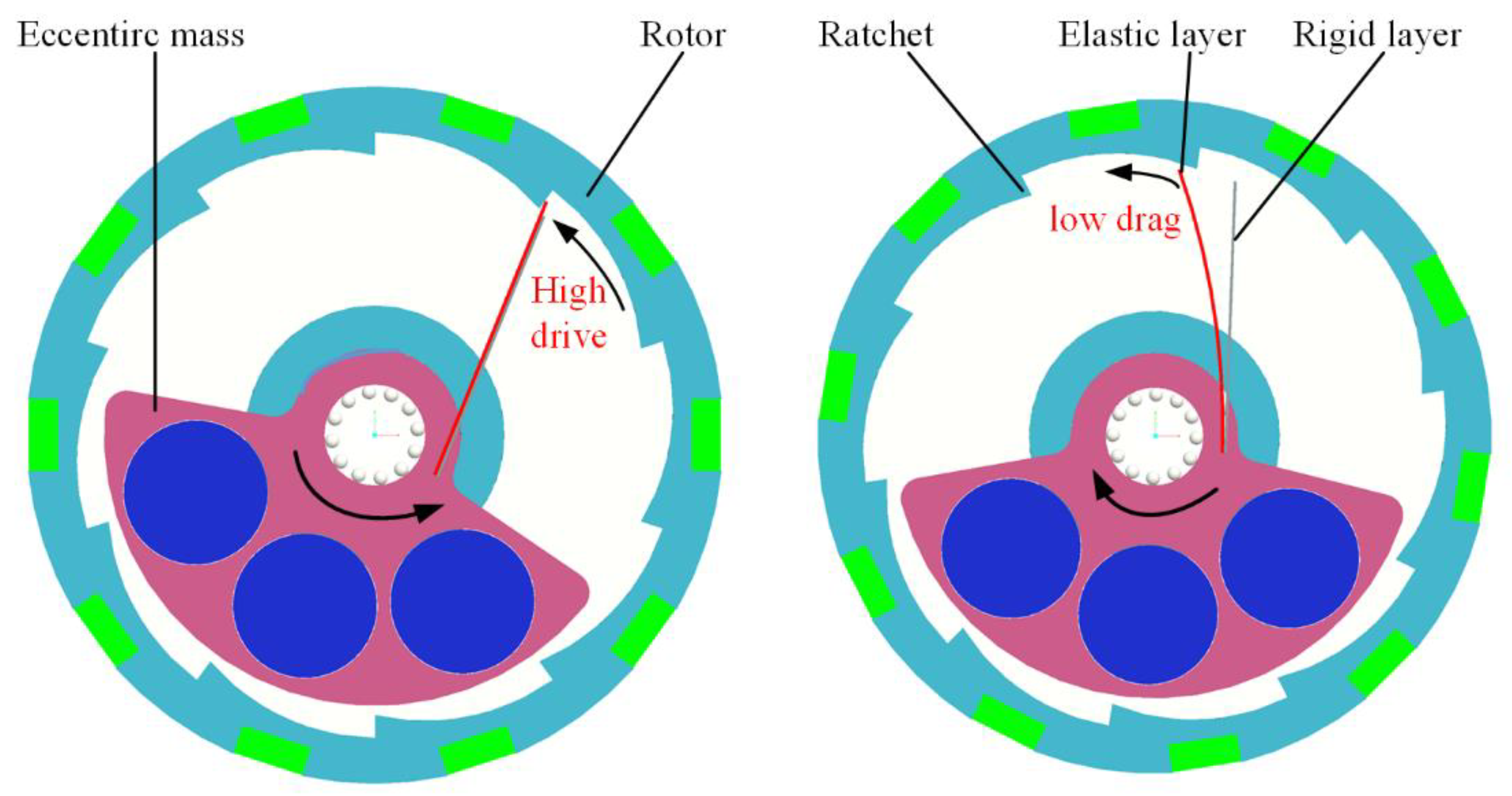
2.1. Vibrational Exciting Principle
2.2. Stator and Rotor Topology
2.3. Dimensions and Materials
3. Electromagnetic Analysis
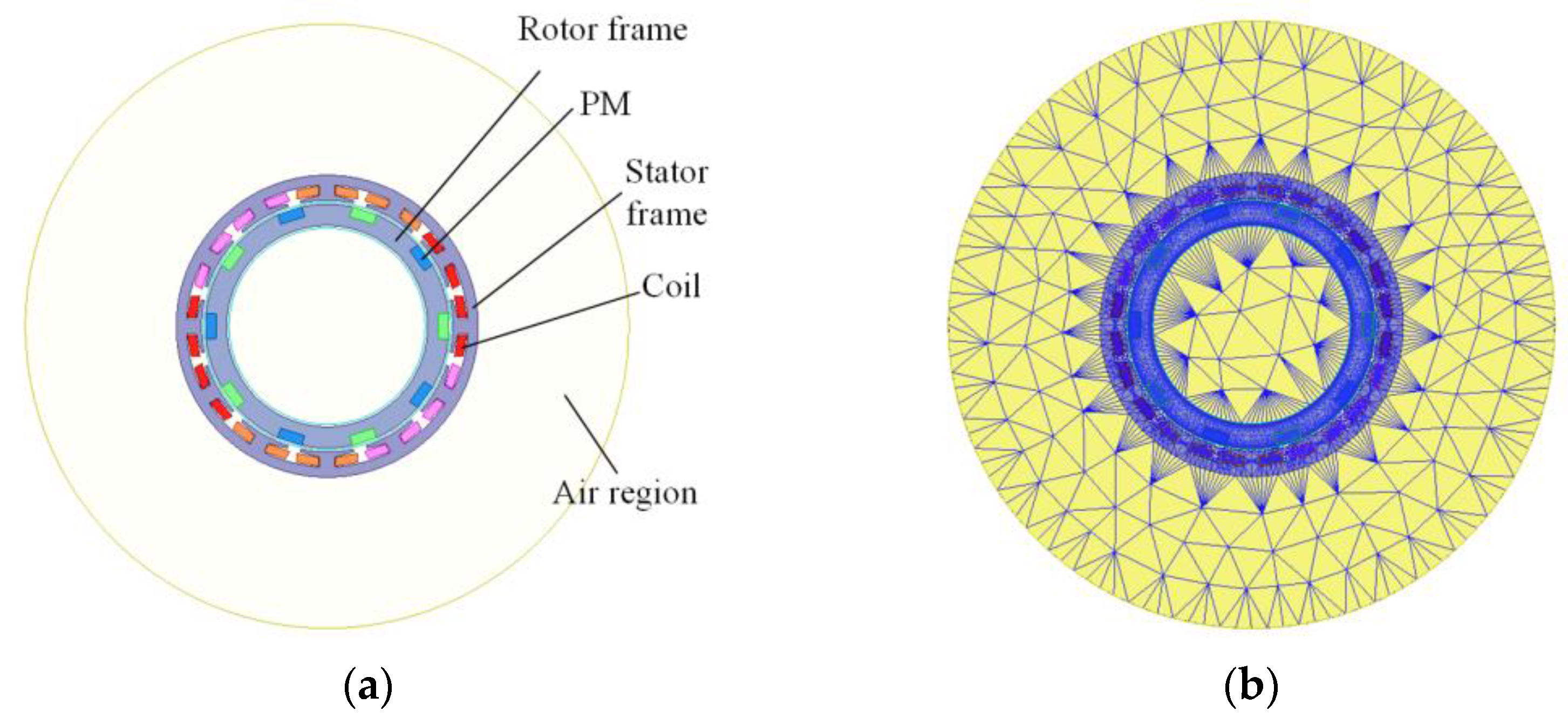
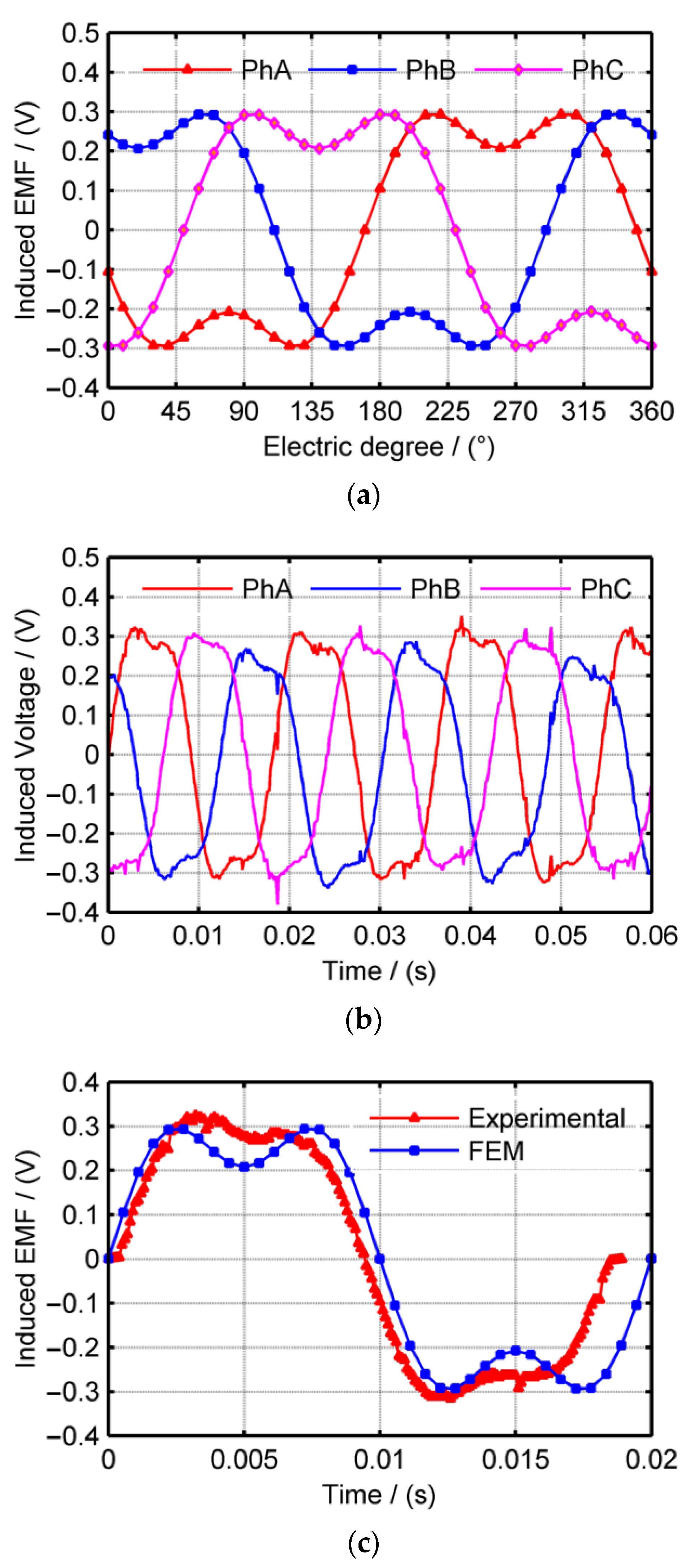
3.1. Comparison of FEM and Experimental Results
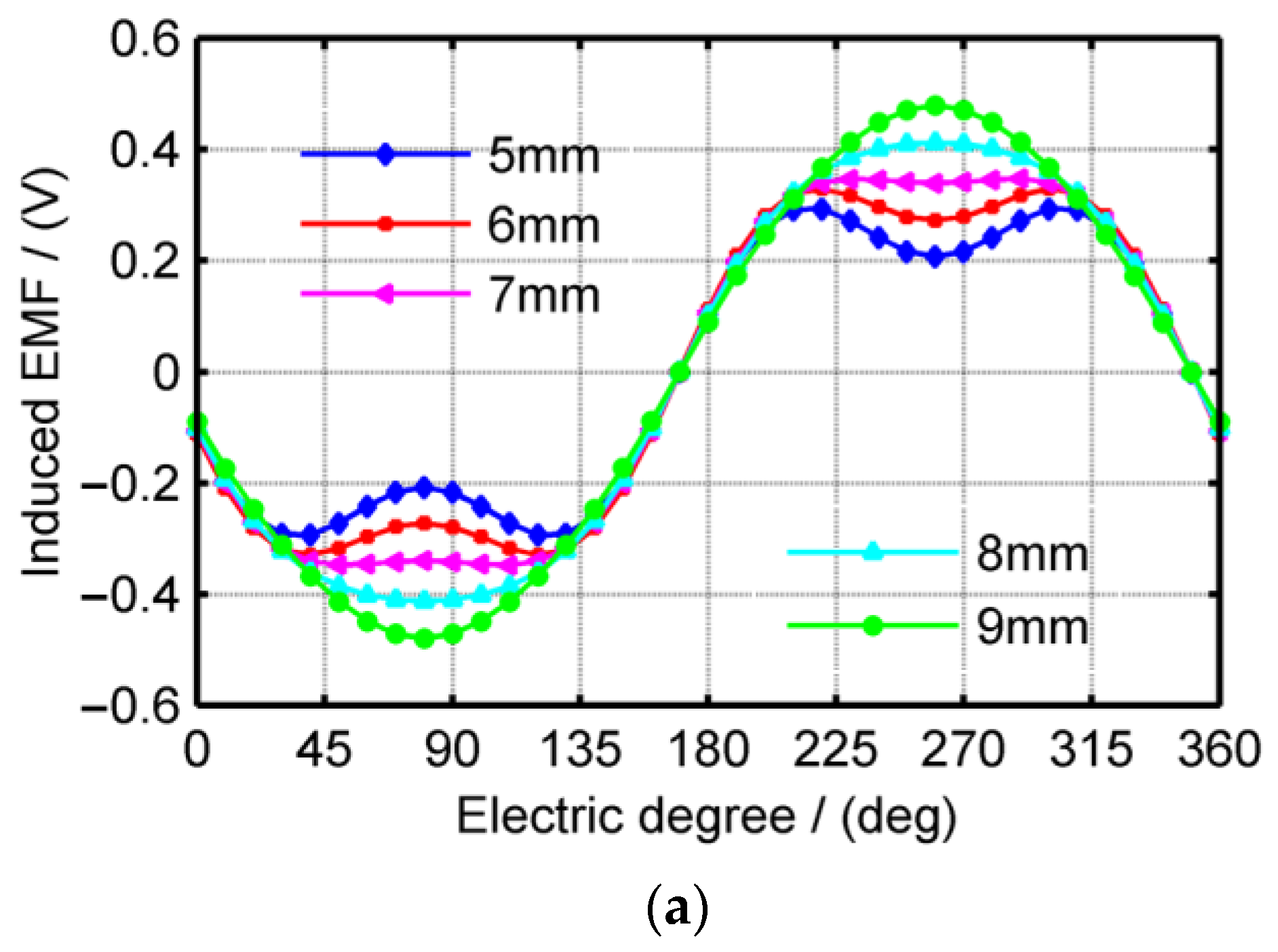
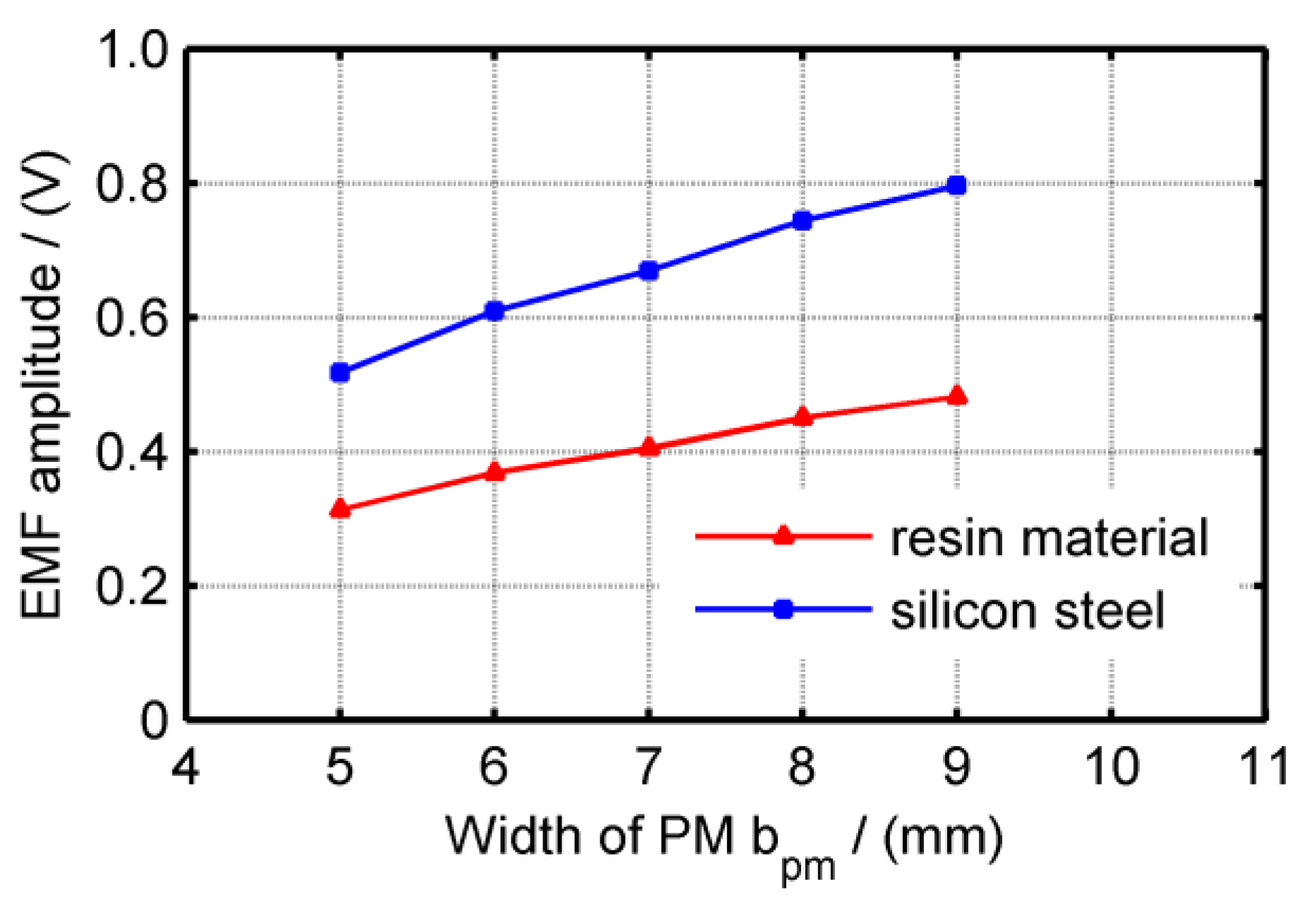
3.2. Magnetic Field Optimization
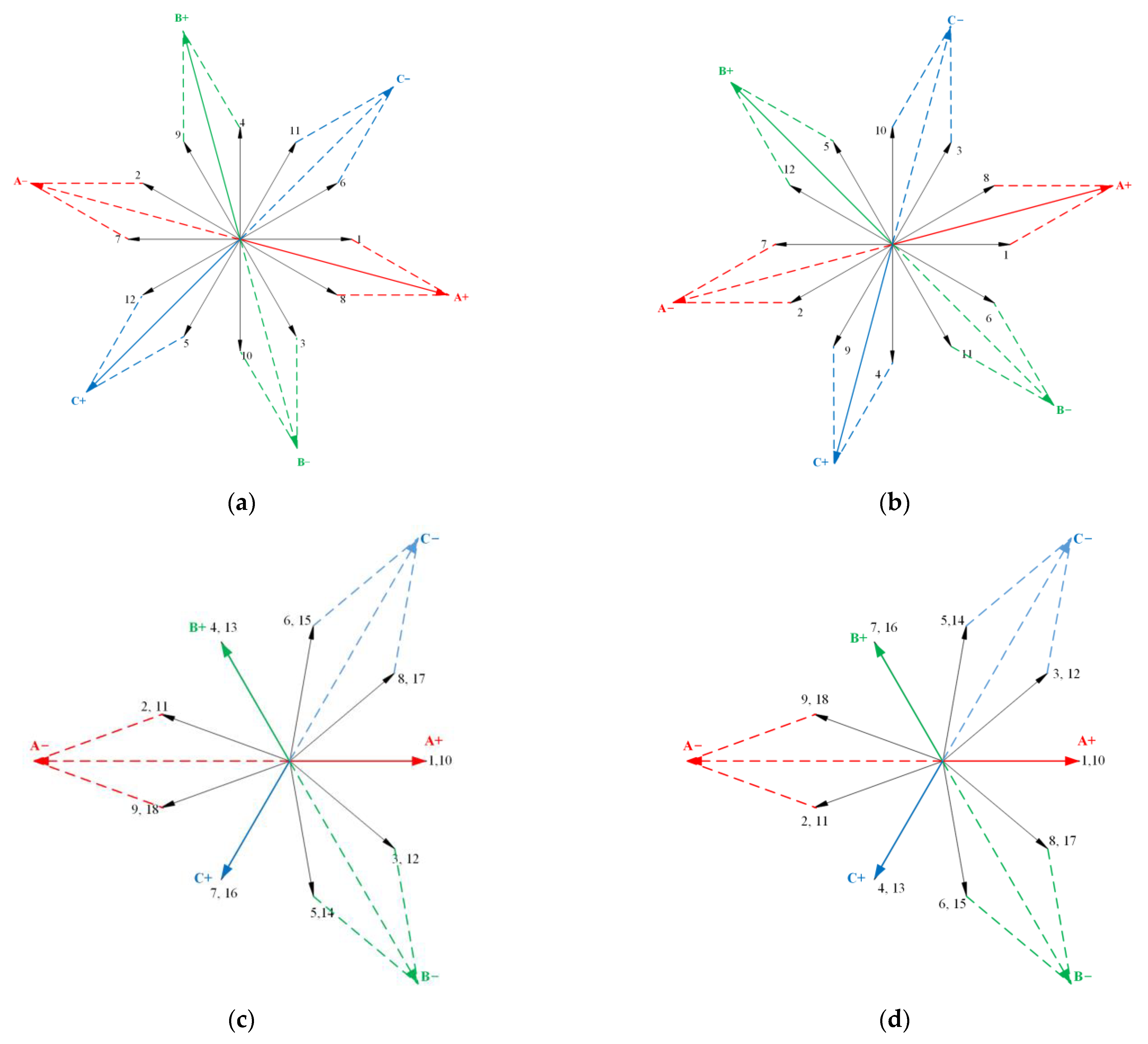
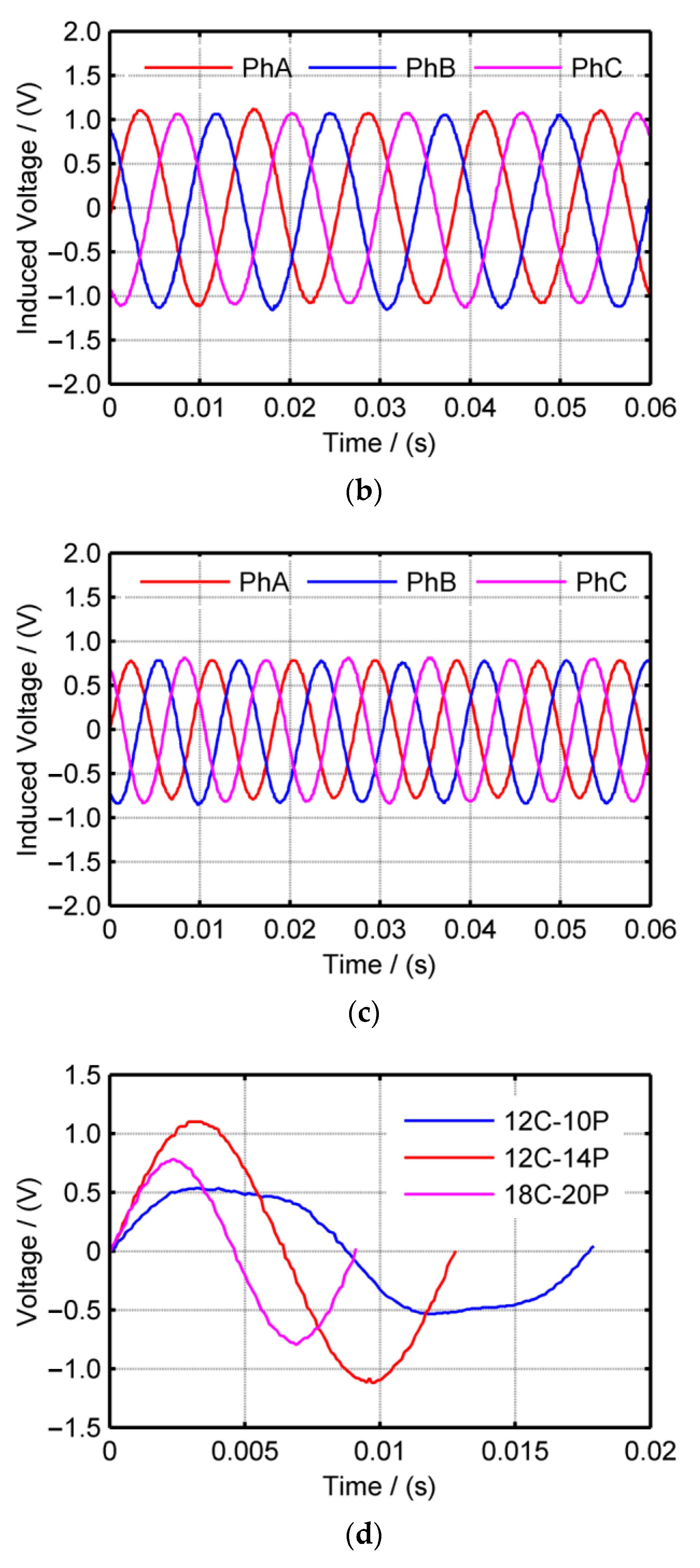
3.3. Configuration of Coil and Pole Number
4. Experiment under Swing Motion
4.1. Test Bench for Swing Motion
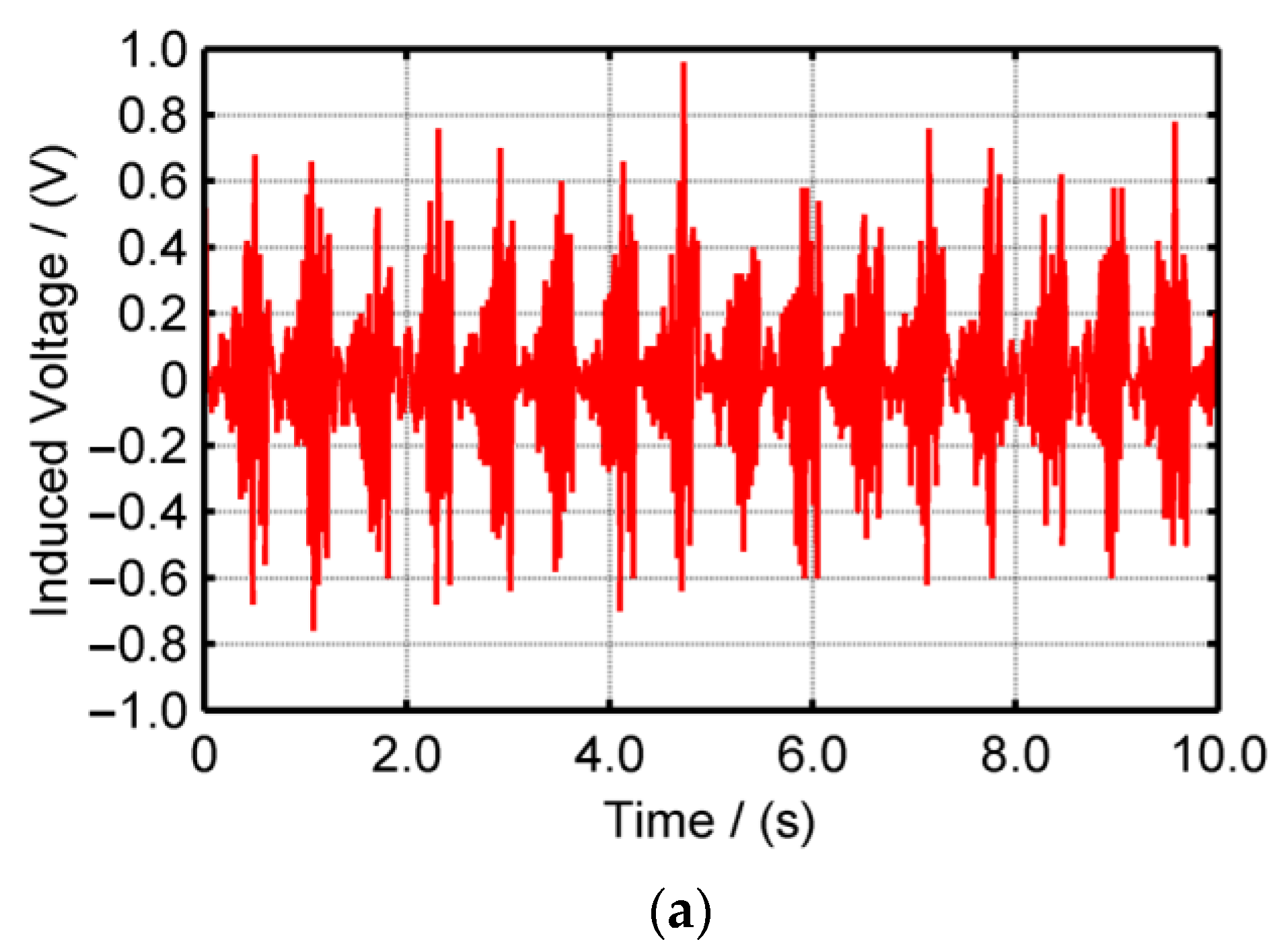
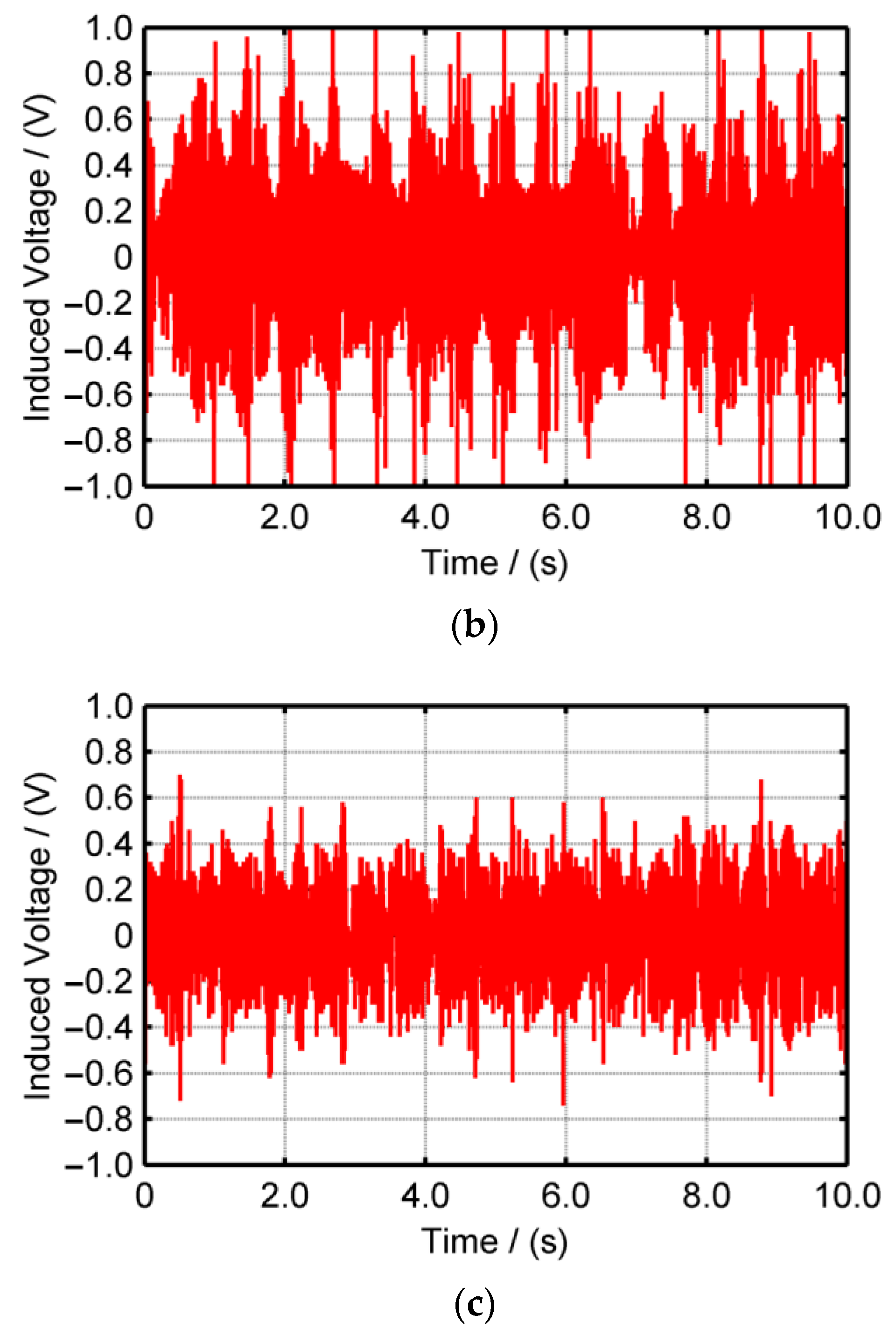
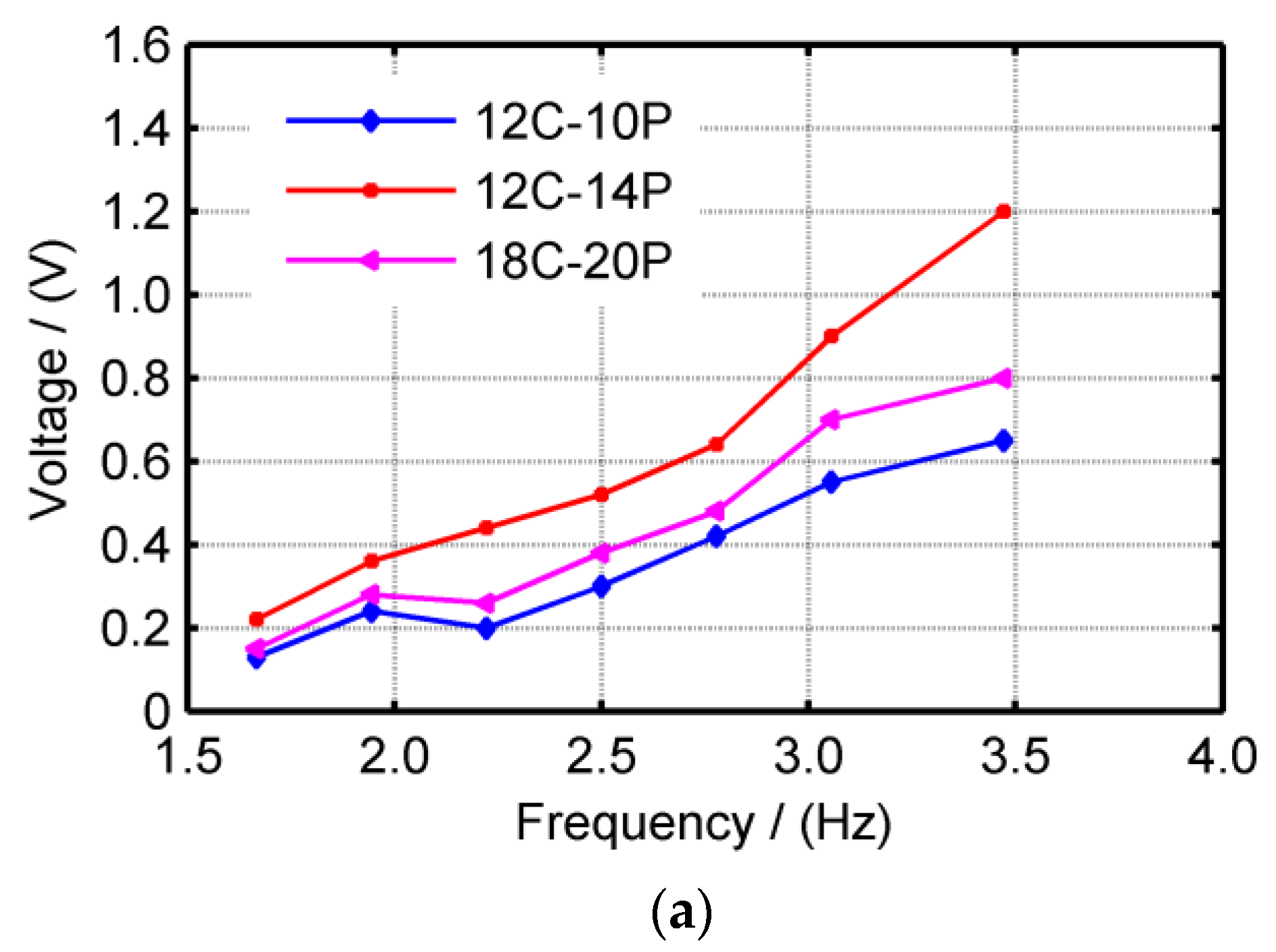
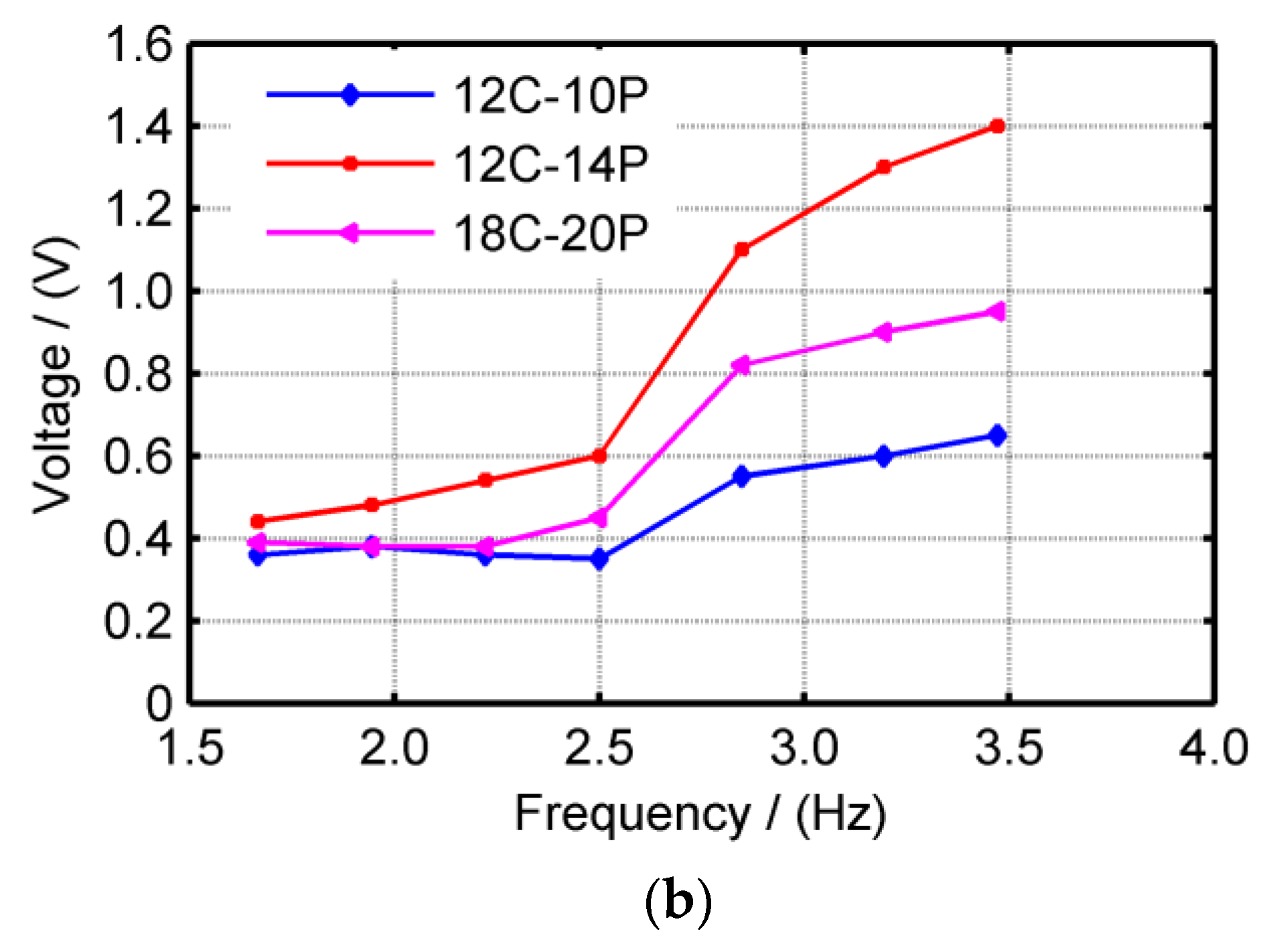
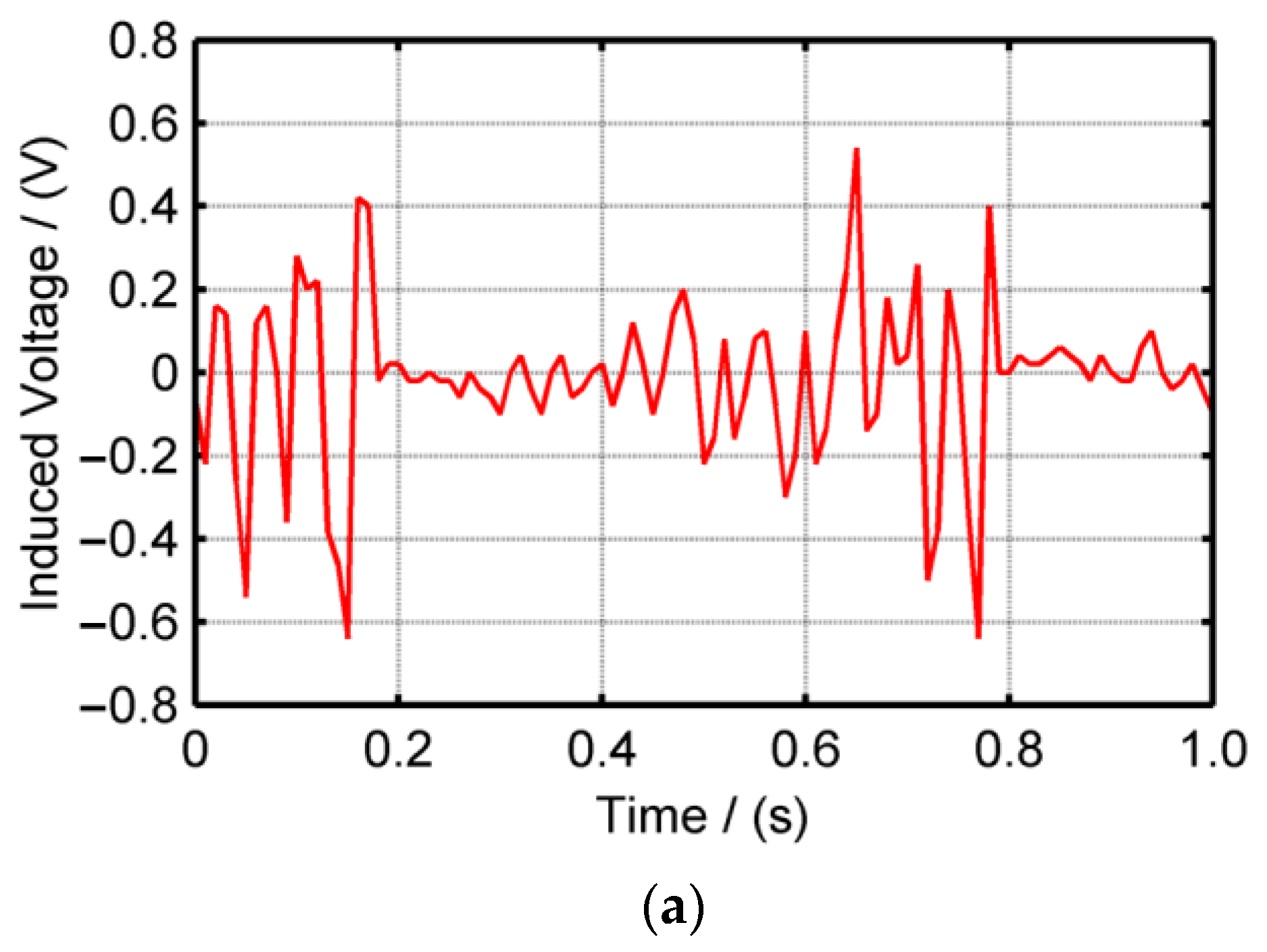
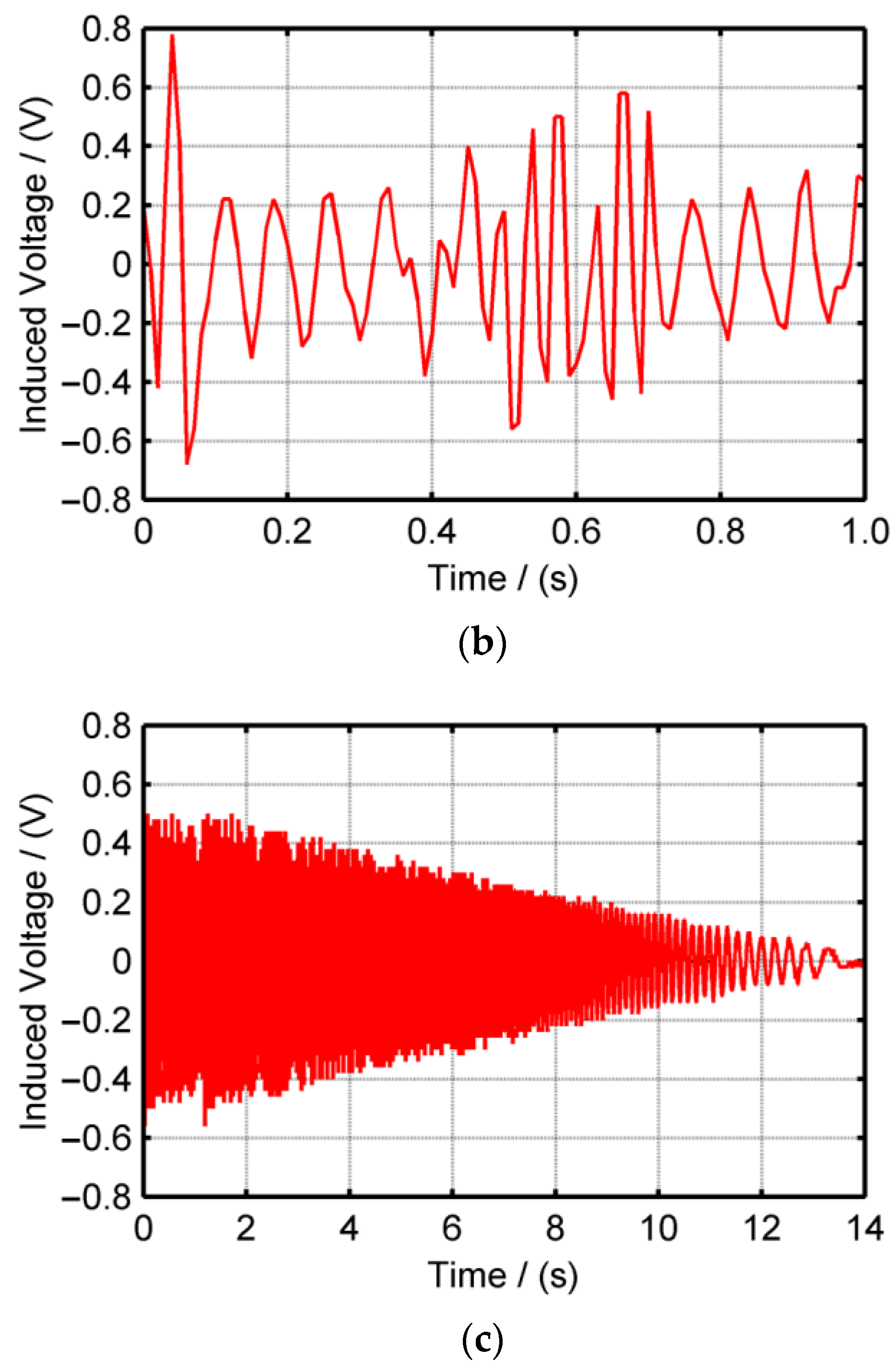
4.2. Performance under Swing Motion
5. Experiment under Linear Reciprocation
5.1. Test Bench for Linear Reciprocation
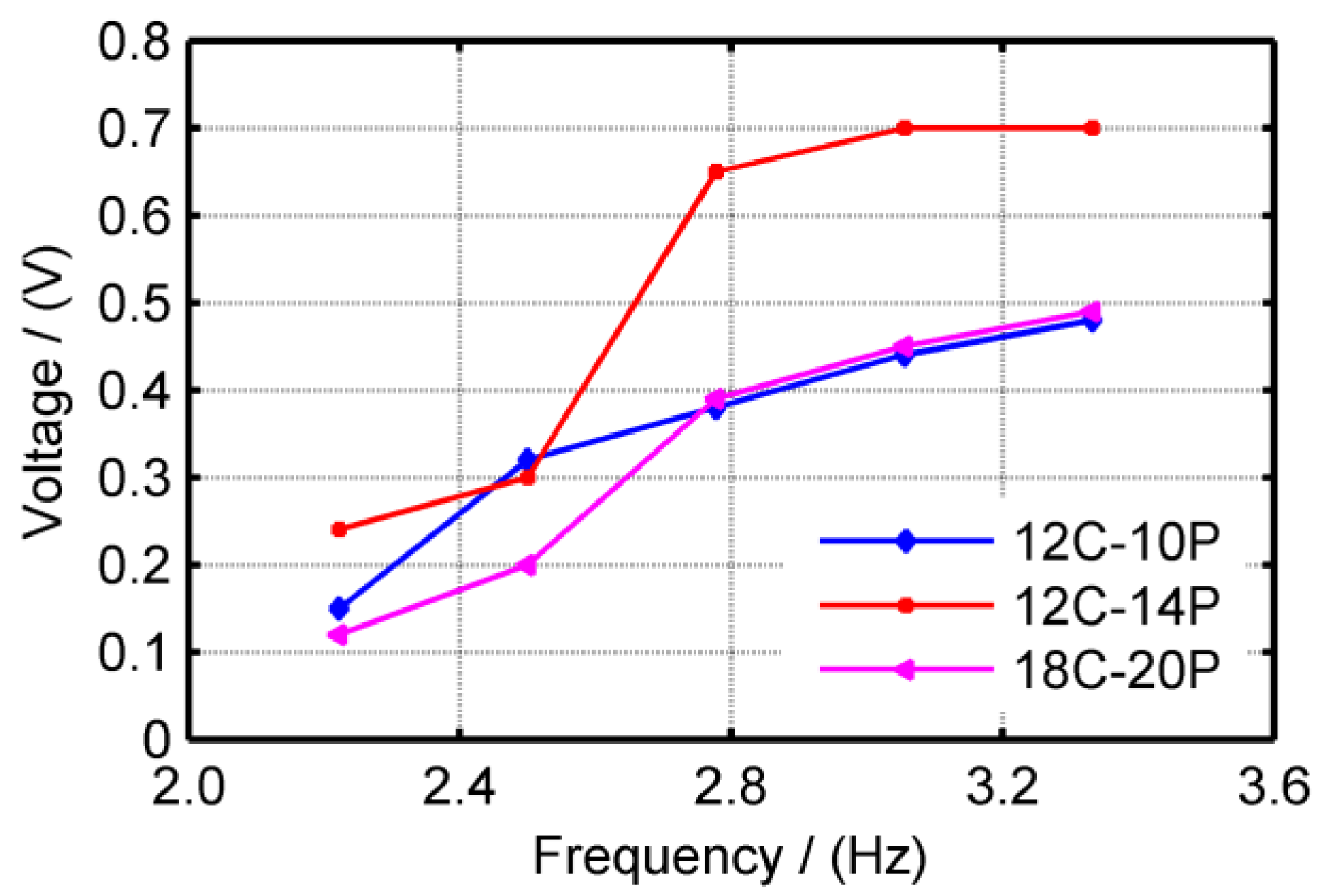
5.2. Performance under Linear Reciprocation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ali, F.; Raza, W.; Li, X.; Gul, H.; Kim, K.H. Piezoelectric energy harvesters for biomedical applications. Nano Energy 2019, 57, 879–902. [Google Scholar] [CrossRef]
- Hasan, M.N.; Sahlan, S.; Osman, K.; Mohamed Ali, M.S. Energy harvesters for wearable electronics and biomedical devices. Adv. Mater. Technol. 2021, 6, 2000771. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, G.; Han, B.; Liu, X. Different kinds of energy harvesters from human activities. Int. J. Energy Res. 2021, 45, 4841–4870. [Google Scholar] [CrossRef]
- Sun, F.; Su, X.; Song, H.-C.; Kang, C.-Y. Energy harvesting performance of a novel nonlinear quad-stable piezoelectric energy harvester with only one external magnet. Machines 2022, 10, 803. [Google Scholar] [CrossRef]
- Jackson, N.; Olszewski, O.Z.; O’Murchu, C.; Mathewson, A. Ultralow-frequency Piezo MEMS energy harvester using thin-film silicon and parylene substrates. J. Micro-Nanolithography MEMS MOEMS 2018, 17, 015005. [Google Scholar]
- Wang, K.; Ouyang, H.; Zhou, J.; Chang, Y.; Xu, D.; Zhao, H. A nonlinear hybrid energy harvester with high ultralow-frequency energy harvesting performance. Meccanica 2021, 56, 461–480. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, Y.; Qiu, Y.; Wu, H.; Qin, W.; Liao, Y.; Yu, Q.; Cheng, H. Stretchable piezoelectric energy harvesters and self-powered sensors for wearable and implantable devices. Biosens. Bioelectron. 2020, 168, 112569. [Google Scholar] [CrossRef]
- Guo, L.; Wang, H.; Braley, J.; Venkiteela, G. Field evaluation of piezoelectric energy harvesters on bridge structure. Machines 2023, 11, 462. [Google Scholar] [CrossRef]
- Muscat, A.; Bhattacharya, S.; Zhu, Y. Electromagnetic vibrational energy harvesters: A review. Sensors 2022, 22, 5555. [Google Scholar] [CrossRef]
- Carneiro, P.M.R.; Ferreira, J.A.F.; Kholkin, A.; Soares dos Santos, M.P. Towards self-adaptability of instrumented electromagnetic energy harvesters. Machines 2022, 10, 414. [Google Scholar] [CrossRef]
- Naito, Y.; Uenishi, K. Electrostatic MEMS vibration energy harvesters inside of tire treads. Sensors 2019, 19, 890. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, T.; Luo, A.; Hu, Y.; Li, X.; Wang, F. Micro electrostatic energy harvester with both broad bandwidth and high normalized power density. Appl. Energy 2018, 212, 362–371. [Google Scholar] [CrossRef]
- Jayasvasti, S.; Thainiramit, P.; Yingyong, P.; Isarakorn, D. Technique for measuring power across high resistive load of triboelectric energy harvester. Micromachines 2021, 12, 766. [Google Scholar] [CrossRef]
- Liu, L.; Shi, Q.; Ho, J.S.; Lee, C. Study of thin film blue energy harvester based on triboelectric nanogenerator and seashore IoT applications. Nano Energy 2020, 66, 104167. [Google Scholar] [CrossRef]
- Halim, M.A.; Park, J.Y. A non-resonant, frequency up-converted electromagnetic energy harvester from human-body-induced vibration for hand-held smart system applications. J. Appl. Phys. 2014, 115, 094901. [Google Scholar] [CrossRef]
- Gutierrez, M.; Shahidi, A.; Berdy, D.; Peroulis, D. Design and characterization of a low frequency 2-dimensional magnetic levitation kinetic energy harvester. Sens. Actuators A Phys. 2015, 236, 1–10. [Google Scholar] [CrossRef]
- Zhao, L.-C.; Zou, H.-X.; Gao, Q.-H.; Yan, G.; Liu, F.-R.; Tan, T.; Wei, K.-X.; Zhang, W.-M. Magnetically modulated orbit for human motion energy harvesting. Appl. Phys. Lett. 2019, 115, 263902. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, A.; Wang, Y.; Dai, X.; Lu, Y.; Wang, F. Rotational electromagnetic energy harvester for human motion application at low frequency. Appl. Phys. Lett. 2020, 116, 053902. [Google Scholar] [CrossRef]
- Chen, J.; Bao, B.; Liu, J.; Wu, Y.; Wang, Q. Pendulum energy harvesters: A review. Energies 2022, 15, 8674. [Google Scholar] [CrossRef]
- Smilek, J.; Hadas, Z.; Vetiska, J.; Beeby, S. Rolling mass energy harvester for very low frequency of input vibrations. Mech. Syst. Signal Process. 2019, 125, 215–228. [Google Scholar] [CrossRef]
- Hou, C.; Chen, T.; Li, Y.; Huang, M.; Shi, Q.; Liu, H.; Sun, L.; Lee, C. A rotational pendulum based electromagnetic/triboelectric hybrid-generator for ultra-low-frequency vibrations aiming at human motion and blue energy applications. Nano Energy 2019, 63, 103871. [Google Scholar] [CrossRef]
- Li, M.; Deng, H.; Zhang, Y.; Li, K.; Huang, S.; Liu, X. Ultra-low frequency eccentric pendulum-based electromagnetic vibrational energy harvester. Micromachines 2020, 11, 1009. [Google Scholar] [CrossRef] [PubMed]
- Halim, M.; Rantz, R.; Zhang, Q.; Gu, L.; Yang, K.; Roundy, S. An electromagnetic rotational energy harvester using sprung eccentric rotor, driven by pseudo-walking motion. Appl. Energy 2018, 217, 66–74. [Google Scholar] [CrossRef]
- Liu, H.; Hou, C.; Lin, J.; Li, Y.; Shi, Q.; Chen, T.; Sun, L.; Lee, C. A non-resonant rotational electromagnetic energy harvester for low-frequency and irregular human motion. Appl. Phys. Lett. 2018, 113, 203901. [Google Scholar] [CrossRef]
- Fan, K.; Hao, J.; Wang, C.; Zhang, C.; Wang, W.; Wang, F. An eccentric mass-based rotational energy harvester for capturing ultralow-frequency mechanical energy. Energy Convers. Manag. 2021, 241, 114301. [Google Scholar] [CrossRef]





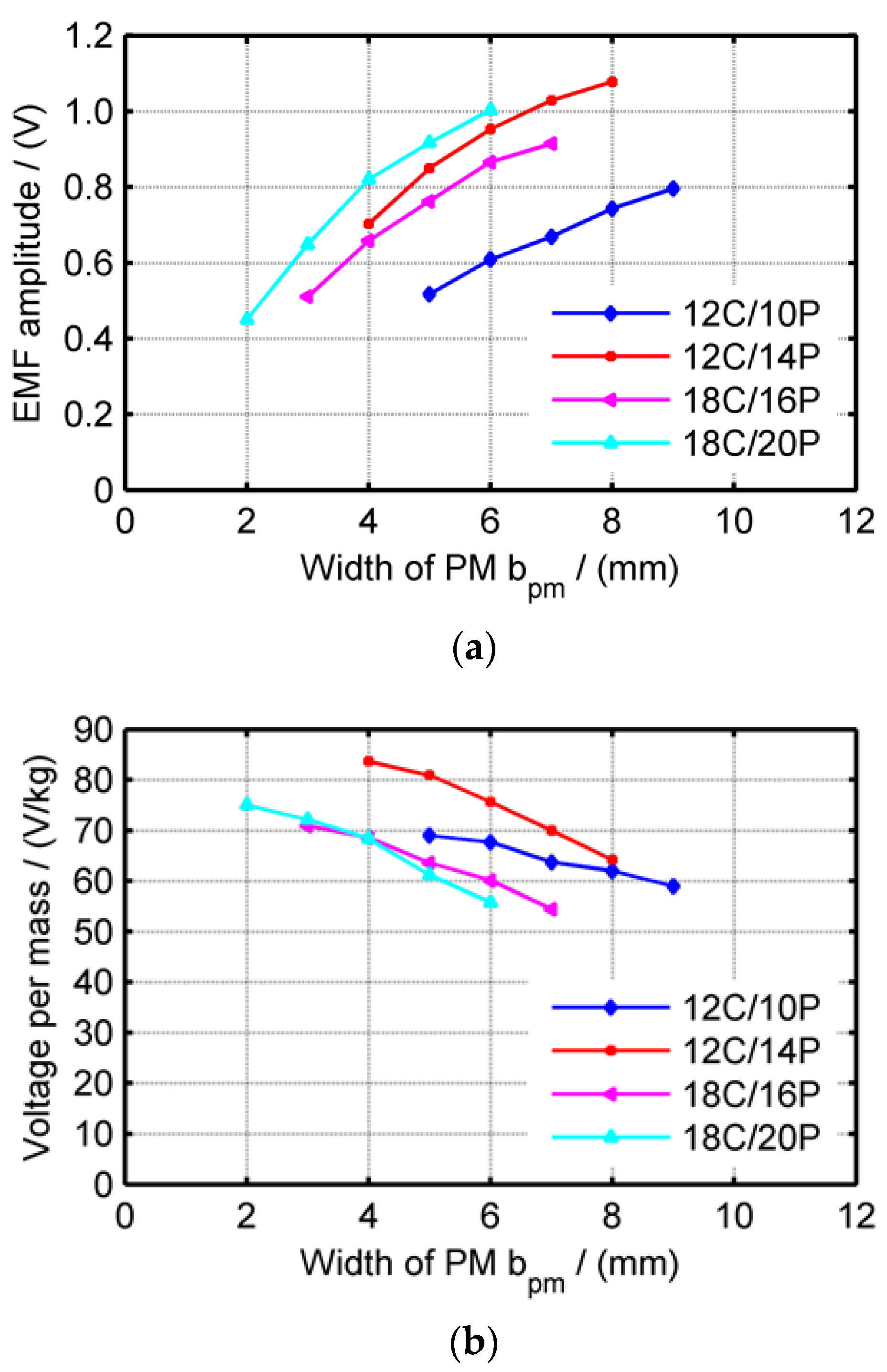




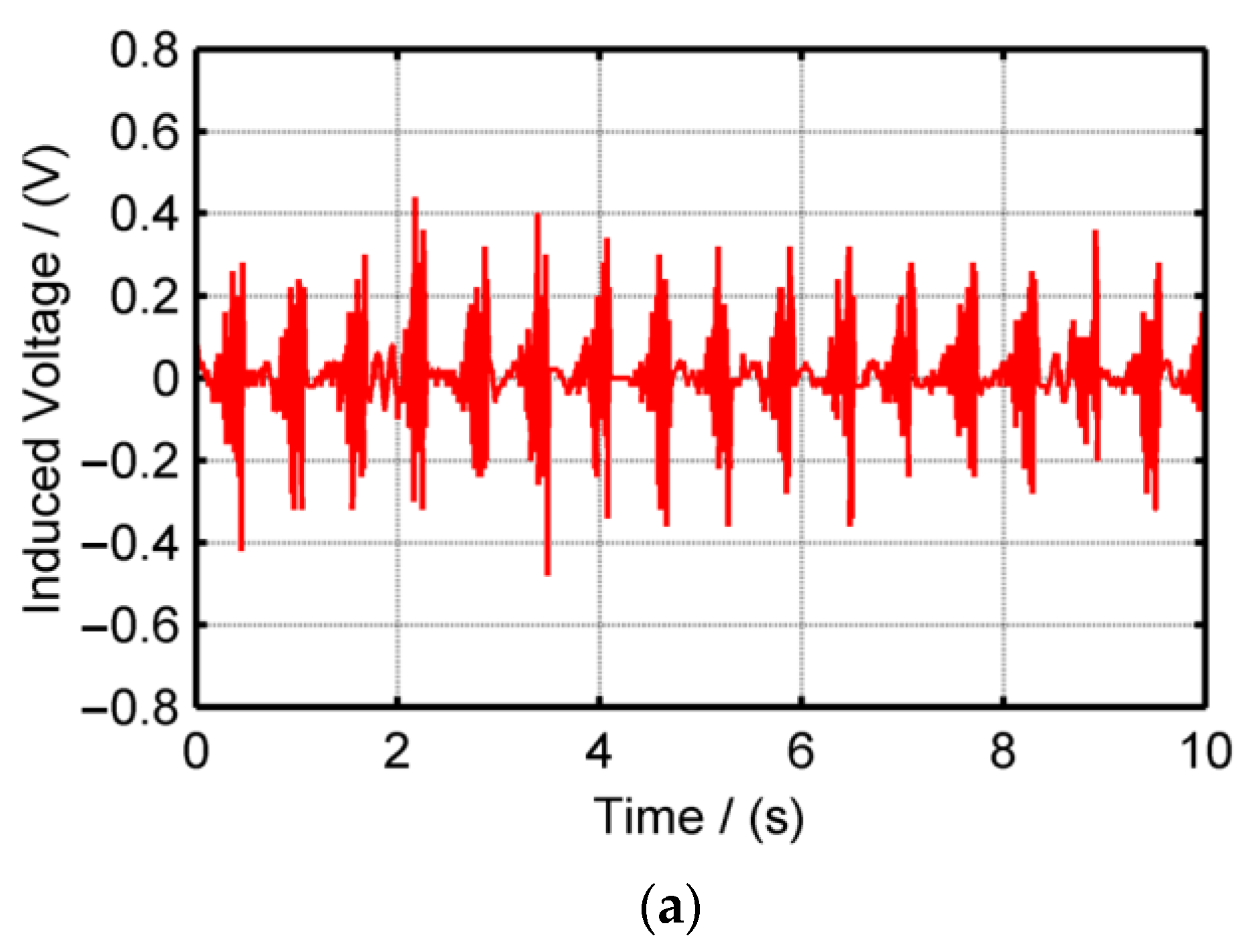
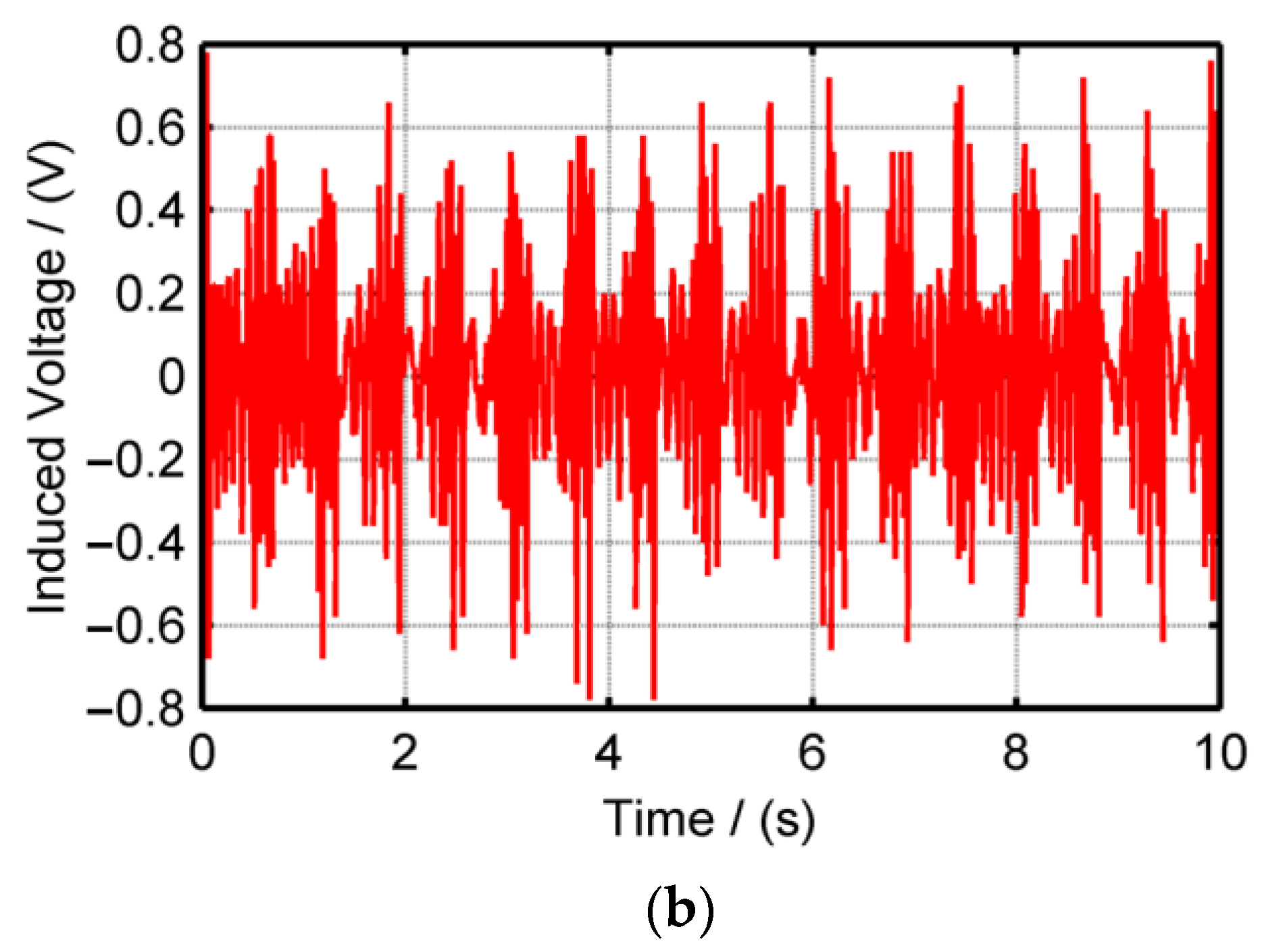
| Configurations | Voltage Amplitude | Harmonic THD (%) | Voltage per Mass (V/Kg) |
|---|---|---|---|
| 12C10P bpm5 mm | 0.517 | 26.86 | 68.997 |
| 12C10P bpm6 mm | 0.609 | 21.09 | 67.684 |
| 12C10P bpm7 mm | 0.669 | 13.74 | 63.739 |
| 12C10P bpm8 mm | 0.744 | 7.81 | 61.983 |
| 12C10P bpm9 mm | 0.796 | 1.44 | 58.971 |
| 12C14P bpm4 mm | 0.703 | 0.74 | 83.682 |
| 12C14P bpm5 mm | 0.850 | 0.56 | 80.923 |
| 12C14P bpm6 mm | 0.953 | 0.29 | 75.611 |
| 12C14P bpm7 mm | 1.029 | 0.21 | 70.002 |
| 12C14P bpm8 mm | 1.078 | 0.36 | 64.164 |
| 18C16P bpm3 mm | 0.511 | 9.72 | 70.926 |
| 18C16P bpm4 mm | 0.658 | 6.46 | 68.554 |
| 18C16P bpm5 mm | 0.763 | 3.04 | 63.569 |
| 18C16P bpm6 mm | 0.866 | 0.66 | 60.149 |
| 18C16P bpm7 mm | 0.915 | 3.12 | 54.457 |
| 18C20P bpm2 mm | 0.450 | 0.17 | 75.034 |
| 18C20P bpm3 mm | 0.649 | 0.11 | 72.138 |
| 18C20P bpm4 mm | 0.820 | 0.12 | 68.368 |
| 18C20P bpm5 mm | 0.917 | 0.06 | 61.153 |
| 18C20P bpm6 mm | 1.004 | 0.08 | 55.767 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, J.; Zhang, C.; Fan, K. Performance Optimization of Ultralow-Frequency Electromagnetic Energy Harvester Driven by Eccentric mass. Machines 2023, 11, 743. https://doi.org/10.3390/machines11070743
Liang J, Zhang C, Fan K. Performance Optimization of Ultralow-Frequency Electromagnetic Energy Harvester Driven by Eccentric mass. Machines. 2023; 11(7):743. https://doi.org/10.3390/machines11070743
Chicago/Turabian StyleLiang, Jintao, Chao Zhang, and Kangqi Fan. 2023. "Performance Optimization of Ultralow-Frequency Electromagnetic Energy Harvester Driven by Eccentric mass" Machines 11, no. 7: 743. https://doi.org/10.3390/machines11070743
APA StyleLiang, J., Zhang, C., & Fan, K. (2023). Performance Optimization of Ultralow-Frequency Electromagnetic Energy Harvester Driven by Eccentric mass. Machines, 11(7), 743. https://doi.org/10.3390/machines11070743







