A Reliable Life Consumption Assessment and Individual Life Monitoring Method for Rolling Bearings

Abstract

Rolling bearings are critical rotating components in aerospace and high-speed trains. The service loads of rolling bearings are generally different from each other, causing significant differences in their damage degrees and reliable life potential. To ensure bearing reliability during service, a reliable life consumption assessment and individual life monitoring method is proposed. Firstly, a small-sample reliable life evaluation method is established based on an accelerated life test conducted at a constant load or load block spectrum before delivery, by which the lower confidence limit of the reliable life of the rolling bearing under any service load can be calculated with the required confidence and reliability. Then, the confidence limits of the reliable life consumption percentage and remaining reliable life percentage for each rolling bearing can be evaluated in real time according to their online monitoring loads and Miner’s law. By this means, individual life monitoring and online life management can be conveniently realized. Compared with traditional bearing life management methods, which do not consider service load differences, this method can more effectively ensure service safety and simultaneously maximize the life potential of bearings.

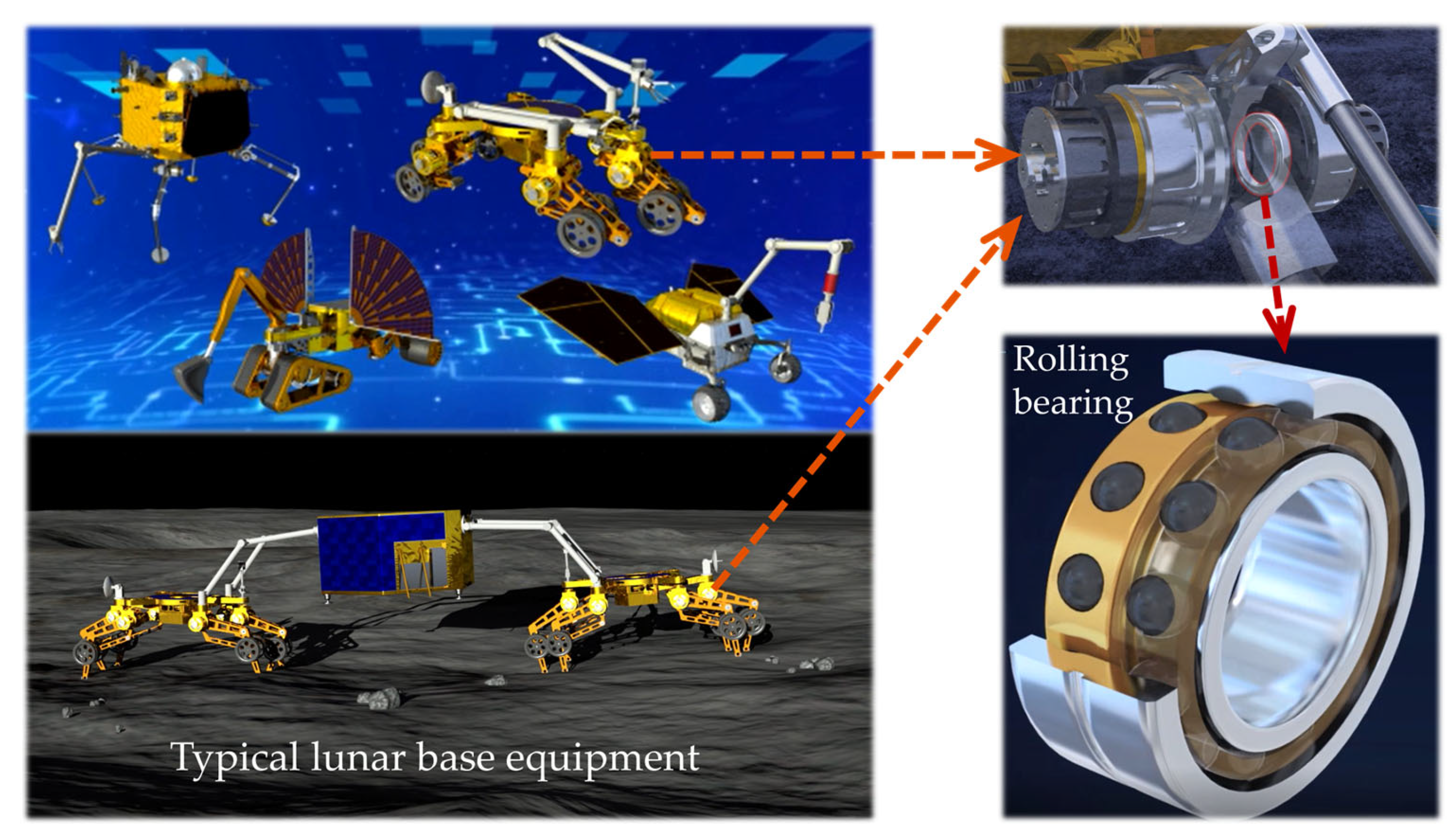
1. Introduction

Rolling bearings are critical rotating components in the aerospace, rail transportation, wind power generation, and other engineering fields, and it is important to ensure their reliability during service [1,2]. Nowadays, many fatigue life assessment models have been developed to predict rolling bearing life [3,4,5,6]. Among them, the L–P theory [7] proposed by Lundberg and Palmgren is the most influential and representative, and it has been simplified and adopted by the ISO. These studies mainly focus on bearing life evaluation or verification during the design phase. With the popularity of the industrial Internet of Things and the requirement of increased bearing reliability, real-time life prediction during service has gradually become another important element in terms of further ensuring bearing safety and reliability [8,9]. In particular, industrial departments require real-time life prediction and active life control for rolling bearings (Figure 1), for example, in the construction of the Chinese lunar base, to meet their long-term service requirements (≥10 years). The research presented in this paper was requested and supported by the relevant research project.

Product life and reliability are not only related to materials, design, and manufacturing, but also depend on the load conditions during service [10,11,12]. Traditional bearing life management methods that involve the same management techniques for all individual bearings based on the reliability estimated in life tests do not consider service load differences between individual bearings. However, the actual service load of a bearing differs from its design or test load, and the service loads of individual bearings also differ. If the service load is severe, the bearing damage and service life will be relatively large and short, and traditional life management will lead to a dangerous assessment. In contrast, if the service load is mild, traditional life management will underestimate the bearing’s potential and result in significant economic waste. Therefore, it is necessary to conduct life monitoring of individual bearings to further ensure service safety and reliability and to fully develop the life potential of bearings.

The current popular approaches for individual bearing life monitoring are generally based on the monitoring of operating parameters (such as vibration signals [8,13,14] and acoustic emission signals [15]) by sensors. In such cases, the remaining useful life can be accurately predicted in real time according to the bearing’s degradation trend. However, these methods might be limited in some aerospace contexts in which the product’s space and weight strictly restrict the placement of the monitoring sensors. Life consumption assessment is another solution with which to achieve individual life monitoring, which has been widely studied and applied in aircraft and engine usage [16,17,18]. It is realized based on the product’s monitored service loads or missions and Miner’s cumulative damage theory. For rolling bearings, online monitoring of their loads (by load transfer analysis or other indirect approaches) or missions is relatively convenient [19], and the calculation formula for dynamic equivalent loads based on axial and radial loads is mature according to the relevant standards. Thus, individual bearing life monitoring can be easily achieved by life consumption assessment, which is lacking in the current research. To ensure that the life consumption assessment is connected with the product’s life determination and extension, which are widely recognized in engineering with high confidence and high reliability, Fu et al. [20] defined reliable damage as the inverse of the product’s reliable life and provided the calculation formulas for damage thresholds and the confidence limits of cumulative damage. On this basis, this paper further proposes a reliable life consumption assessment and individual life monitoring method for rolling bearings.

The main contributions of this paper are as follows:

• A small-sample reliable life evaluation method for rolling bearings is established. It can be used to calculate the lower confidence limit of reliable life under any dynamic equivalent load based on an accelerated life test conducted under a constant load or load block spectrum prior to delivery. This is the foundation for the reliable life consumption assessment of rolling bearings.
• Reliable life consumption and individual life monitoring for each rolling bearing are further achieved based on their service loads or missions. By this means, the confidence limits of reliable life consumption percentages and remaining reliable life percentages can be evaluated in real time with the required reliability and confidence to ensure bearing safety and reliability during service.
• Based on the remaining reliable life and reliable life consumption caused by each mission, online life management for each rolling bearing is realized in order to develop their service life potential.

This paper is organized as follows. In Section 2, a small-sample reliable life evaluation method for rolling bearings is proposed. In Section 3 and Section 4, a reliable life consumption assessment and individual life monitoring method for rolling bearings is proposed. Section 5 provides an example of the method using an illustration. Finally, Section 6 presents a summary of the research presented in this paper.

2. Small-Sample Reliable Life Evaluation for Rolling Bearings

The dynamic equivalent load is denoted as $S$ (linear weighted accumulation of radial and axial loads), and the rolling bearing life under $S$ as $N$ (rotation numbers). Since the bearing life is a random variable, the reliable life $N_R$ with reliability $R$ can be defined, which satisfies

$$P\left(N\ge N_R\right) = R$$

(1)

In engineering practice, a set of accelerated life tests is usually required for the verification of reliability before delivery. By utilizing the test results, the reliable life of the rolling bearings under each dynamic equivalent load can be calculated. In this section, two cases of accelerated life tests with constant loads and load block spectra are discussed, respectively.

When the test sample is large enough, the point estimation of reliable life is usually very close to the true value, and can be directly used. However, in the case of small samples, the point estimate may significantly differ from the true one. In such cases, the confidence degree must be taken into consideration so as to fully ensure reliability, and the lower confidence limit of reliable life should be adopted.

2.1. Acceleration Factor of Reliable Life

The standard dynamic equivalent load of the rolling bears is denoted as $S^{\ast \ast }$ (e.g., rated load, accelerated test load, or others), and the acceleration factor (AF) of $S^{\ast \ast }$ to $S$ is defined as

$$\tau = N_R/N_R^{\ast \ast }$$

(2)

where $N_R^{\ast \ast }$ is the reliable life of the rolling bearings under $S^{\ast \ast }$.

In general, the bearing life follows a two-parameter Weibull distribution, where the shape parameter $\alpha$ can be obtained from engineering experience [21]. For example, the recommended value of $\alpha$ in GB/T 6391 is 1.5 [22]. When the shape parameter is known and independent of the load level, the acceleration factor $\tau$ is independent of the reliability value. Then according to the inverse power law model of the L–P theory [7], the AF can be calculated as

$$\tau = N_R/N_R^{\ast \ast } = N_{0.9}/N_{0.9}^{\ast \ast } = {\left(S^{\ast \ast }/S\right)}^{\epsilon }$$

(3)

where $N_{0.9}$ and $N_{0.9}^{\ast \ast }$ are the reliable life with a reliability of 0.9 and $\epsilon$ is the load–life index, which is 3 for ball bearings and 10/3 for roller bearings [23]. Obtained from tens of thousands of bearing tests, the recommended load–life index values have been adopted by several standards, such as the ISO 281 [24] and the GB/T 6391 [22]. With the improvement of manufacturing technologies, the load–life indices of modern bearings are generally larger than the above value [25,26,27], and the aforementioned load–life index can be replaced by a more accurate value, which would otherwise lead to relatively conservative results for reliable life assessment.

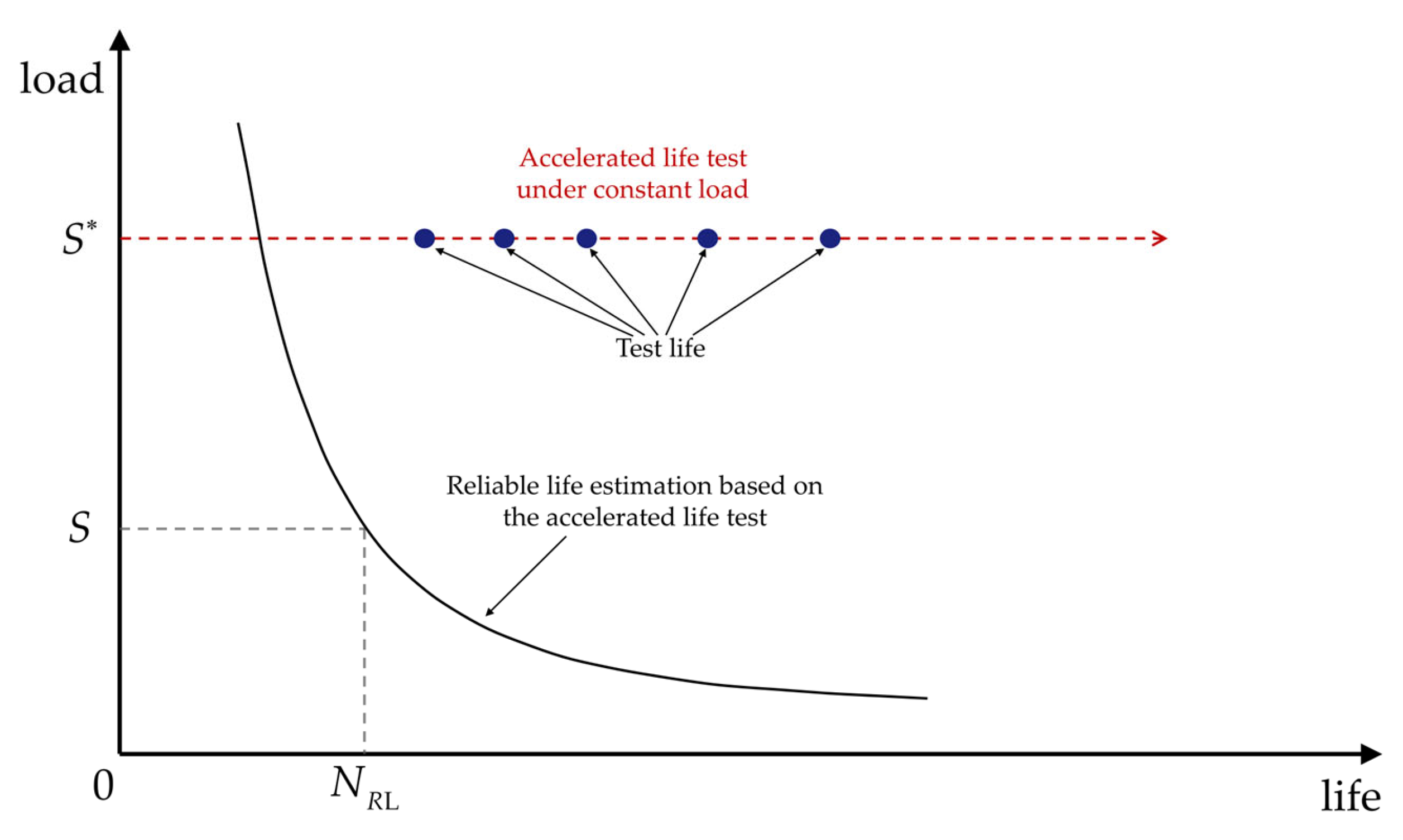
2.2. Reliable Life Evaluation Based on the Accelerated Life Test under Constant Load

As shown in Figure 2, the accelerated life tests of the rolling bears are conducted under the dynamic equivalent load $S^{\ast }$. Based on the test life under $S^{\ast }$, the calculation formula for the lower confidence limit of reliable life under the dynamic equivalent load $S$ is provided below.

Firstly, according to the characteristics of Weibull distribution, the lower confidence limit of the reliable life under the test load $S^{\ast }$ with the confidence of $\gamma$ can be given as

$$N_{R\mathrm{L}}^{\ast } = {\left[-\frac{2\ln R}{{\chi }_{\gamma }^2\left(2n\right)}{\displaystyle \sum _{j = 1}^n{\left(N_j^{\ast }\right)}^{\alpha }}\right]}^{1/\alpha }$$

(4)

which satisfies

$$P\left(N_{R\mathrm{L}}^{\ast }\le N_R^{\ast }\right) = \gamma$$

(5)

where $N_j^{\ast }$ is the test life of the $j_{\mathrm{th}}$ sample, $\alpha$ is the known shape parameter, and ${\chi }_{\gamma }^2\left(2n\right)$ is the $\gamma$-quantile of the chi-square distribution with $2n$ degrees of freedom.

Then, according to Equation (3), the lower confidence limit of the reliable life under $S^{\ast \ast }$ can be calculated as

$$N_{R\mathrm{L}}^{\ast \ast } = N_{R\mathrm{L}}^{\ast }/{\tau }^{\ast }$$

(6)

$${\tau }^{\ast } = {\left(S^{\ast \ast }/S^{\ast }\right)}^{\epsilon }$$

(7)

where ${\tau }^{\ast }$ is the AF of $S^{\ast \ast }$ to $S^{\ast }$. And the lower confidence limit of the reliable life under $S$ can be calculated as

$$N_{R\mathrm{L}} = \tau N_{R\mathrm{L}}^{\ast \ast } = \tau N_{R\mathrm{L}}^{\ast }/{\tau }^{\ast }$$

(8)

They satisfy

$$P\left(N_{R\mathrm{L}}^{\ast \ast }\le N_R^{\ast \ast }\right) = P\left(N_{R\mathrm{L}}\le N_R\right) = \gamma$$

(9)

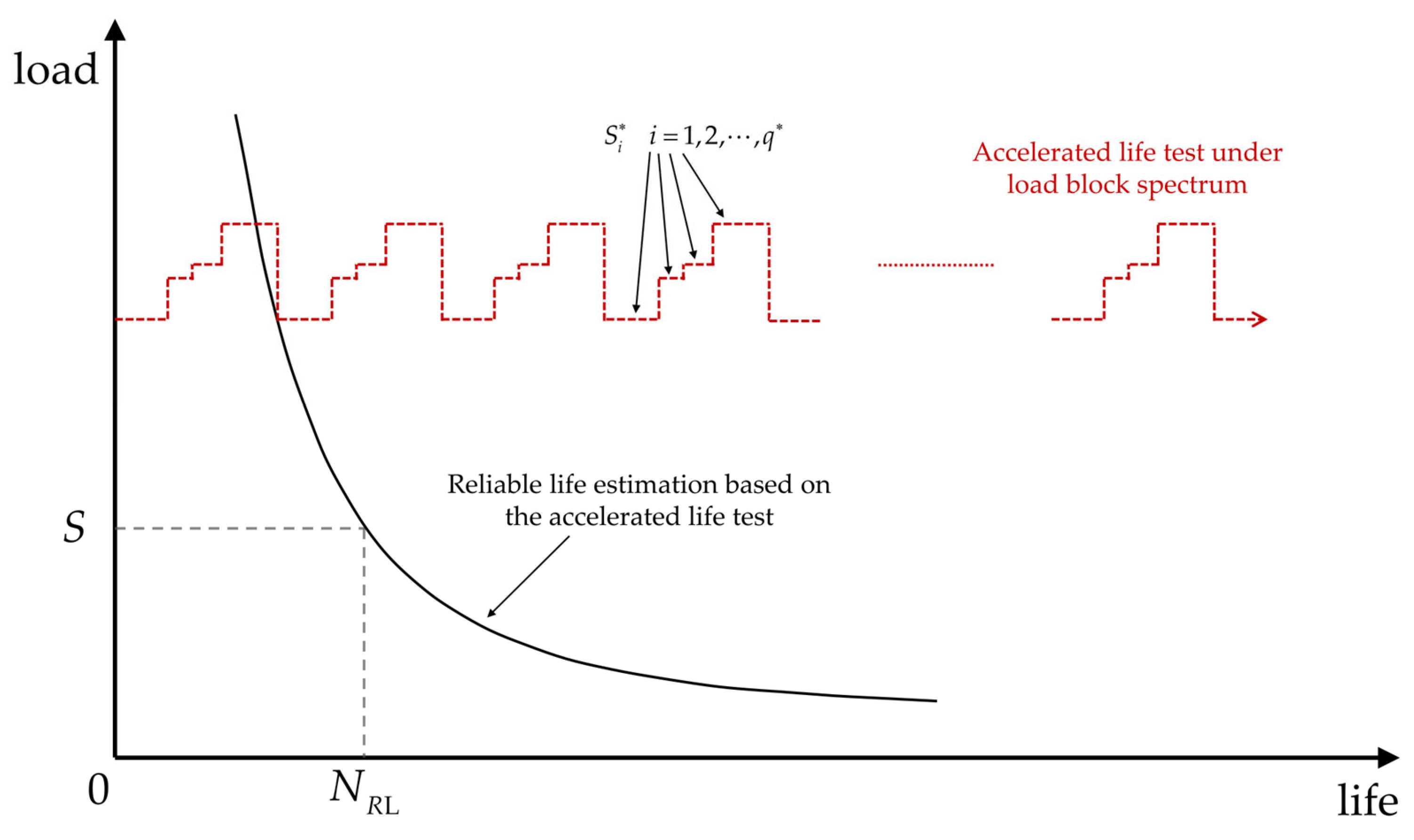
2.3. Reliable Life Evaluation Based on the Accelerated Life Test under a Load Block Spectrum

As shown in Figure 3, the accelerated life tests of the rolling bears are conducted under the load block spectrum composed of a load $S_i^{\ast }$ and a rotation number $n_i^{\ast }$, $i = 1, 2, \cdots , q^{\ast }$. Based on the accelerated life test results, the calculation formula for the lower confidence limit of reliable life under the dynamic equivalent load $S$ is provided below.

Firstly, the lower confidence limit of the reliable life under the test load spectrum with the confidence of $\gamma$ can be given as

$$N_{\mathrm{B},R\mathrm{L}}^{\ast } = {\left[-\frac{2\ln R}{{\chi }_{\gamma }^2\left(2n\right)}{\displaystyle \sum _{j = 1}^n{\left(N_{\mathrm{B},j}^{\ast }\right)}^{\alpha }}\right]}^{1/\alpha }$$

(10)

This satisfies

$$P\left(N_{\mathrm{B},R\mathrm{L}}^{\ast }\le N_{\mathrm{B},R}^{\ast }\right) = \gamma$$

(11)

where $N_{\mathrm{B},j}^{\ast }$ (block spectrum numbers) is the test life of the $j_{\mathrm{th}}$ sample and $N_{\mathrm{B},R}^{\ast }$ is the reliable life of the rolling bearing under the test load spectrum.

Denoting $N_{R\mathrm{L},i}^{\ast }$ as the lower confidence limit of reliable life under $S_i^{\ast }$ with $\gamma$ confidence and $R$ reliability, and ${\tau }_i^{\ast }$ as the AF of $S^{\ast \ast }$ to $S_i^{\ast }$, it can then be derived that

$$N_{R\mathrm{L},i}^{\ast } = {\tau }_i^{\ast }{N}_{R\mathrm{L}}^{\ast \ast },\hspace{1em}i = 1, 2, \cdots , q^{\ast }$$

(12)

$${\tau }_i^{\ast } = {\left(S^{\ast \ast }/S_i^{\ast }\right)}^{\epsilon },\hspace{1em}i = 1, 2, \cdots , q^{\ast }$$

(13)

Then, the reliable damage (defined in Section 3) of the rolling bearing with $\gamma$ confidence and $R$ reliability caused by one test load block spectrum can be calculated as

$$D_{R\mathrm{U}} = {\displaystyle \sum _{i = 1}^{q^{\ast }}\frac{n_i^{\ast }}{N_{R\mathrm{L},i}^{\ast }}} = {\displaystyle \sum _{i = 1}^{q^{\ast }}\frac{n_i^{\ast }}{{\tau }_i^{\ast }{N}_{R\mathrm{L}}^{\ast \ast }}}$$

(14)

Additionally, according to the estimated reliable life $N_{\mathrm{B},R\mathrm{L}}^{\ast }$ under the test load spectrum, the reliable damage of the rolling bearing caused by one test load block spectrum can also be calculated as

$$D_{R\mathrm{U}} = \frac{1}{N_{\mathrm{B},R\mathrm{L}}^{\ast }}$$

(15)

Comparing Equation (14) and Equation (15), it can be determined that

$$\frac{1}{N_{\mathrm{B},R\mathrm{L}}^{\ast }} = {\displaystyle \sum _{i = 1}^{q^{\ast }}\frac{n_i^{\ast }}{{\tau }_i^{\ast }{N}_{R\mathrm{L}}^{\ast \ast }}}$$

(16)

Then, the lower confidence limit of the reliable life under $S^{\ast \ast }$ can be calculated as

$$N_{R\mathrm{L}}^{\ast \ast } = N_{\mathrm{B},R\mathrm{L}}^{\ast }{\displaystyle \sum _{i = 1}^{q^{\ast }}{n}_i^{\ast }/{\tau }_i^{\ast }} = N_{\mathrm{B},R\mathrm{L}}^{\ast }{\displaystyle \sum _{i = 1}^{q^{\ast }}{n}_i^{\ast }{\left(S_i^{\ast }/S^{\ast \ast }\right)}^{\epsilon }}$$

(17)

which satisfies

$$P\left(N_{R\mathrm{L}}^{\ast \ast }\le N_R^{\ast \ast }\right) = \gamma$$

(18)

The lower confidence limit of the reliable life under $S$ can be calculated as

$$N_{R\mathrm{L}} = \tau N_{R\mathrm{L}}^{\ast \ast } = N_{\mathrm{B},R\mathrm{L}}^{\ast }{\displaystyle \sum _{i = 1}^{q^{\ast }}{n}_i^{\ast }{\left(S_i^{\ast }/S\right)}^{\epsilon }}$$

(19)

which satisfies

$$P\left(N_{R\mathrm{L}}\le N_R\right) = \gamma$$

(20)

3. Reliable Life Consumption Assessment for Rolling Bearings

For rolling bearings in the outfield service, the performed missions and corresponding dynamic equivalent loads are generally different from each other, causing differences in bearing damage. Thus, this section focuses on establishing a reliable life consumption assessment method for rolling bearings. Through this method, the upper confidence limit of the reliable life consumption percentage and the lower confidence limit of the remaining reliable life percentage can be evaluated in real time so as to ensure the safety and reliability of rolling bearings during service.

3.1. Reliable Damage and Damage Threshold of the Rolling Bearings

Since the bearing life $N$ is a random variable, the service life must be evaluated with high confidence and reliability in the cases of small samples. Assuming that an individual rolling bearing has worked for $n$ rotations under $S$, then its damage $n/N$ is also a random variable. In this condition, reliability and confidence should also be considered in the evaluation of bearing damage.

In this paper, the reliable damage $n/N_R$ defined by reliable life is adopted for individual rolling bearings [20]. According to Equation (1), the following can be derived:

$$P\left(\frac{n}{N}\le \frac{n}{N_R}\right) = R$$

(21)

which means that the actual damages of 100 R% bearings are smaller than the reliable damage $n/N_R$. This is consistent with the reliability requirement.

When the bearing damage is defined by reliable damage, the damage threshold of the rolling bearing is $N/N_R$ which satisfies

$$P\left(\frac{N}{N_R}\ge 1\right) = R$$

(22)

Thus, it can be ensured that 100R% bearings will not fail before their reliable damage values reach 1. Therefore, it can meet the reliability requirements to take the damage threshold as 1. This is also convenient for engineering applications.

3.2. Reliable Life Consumption, Remaining Reliable Life, and Corresponding Confidence Limits

Damage accumulation under variable loads is a relatively complex process. Current linear and nonlinear damage accumulation theories cannot completely match the product’s actual damage accumulation trajectory, and their error sizes are generally similar [28,29]. Among them, Miner’s linear damage accumulation theory is the simplest and most widely used in engineering. Therefore, this paper adopts Miner’s law for reliable damage accumulation.

Assume that an individual rolling bearing has worked for $n_i$ rotations under $S_i$ at time $t$, $i = 1, 2, \cdots , q$. According to Miner’s law, the reliable life consumption percentage of the rolling bearing with the reliability of R can be defined as

$$L_{\mathrm{C}t} = {\displaystyle \sum _{i = 1}^q\frac{n_i}{N_{R,i}}}$$

(23)

the upper confidence limit of which is

$$L_{\mathrm{CU}t} = {\displaystyle \sum _{i = 1}^q\frac{n_i}{N_{R\mathrm{L},i}}}$$

(24)

Then, the remaining reliable life percentage of the rolling bearing with the reliability of R can be given as

$$L_{Rt} = 1-{\displaystyle \sum _{i = 1}^q\frac{n_i}{N_{R,i}}}$$

(25)

the lower confidence limit of which is

$$L_{R\mathrm{L}t} = 1-{\displaystyle \sum _{i = 1}^q\frac{n_i}{N_{R\mathrm{L},i}}}$$

(26)

where $N_{R,i}$ is the reliable life under $S_i$, and $N_{R\mathrm{L},i}$ is the lower confidence limit of $N_{R,i}$ with the confidence of $\gamma$, which can be estimated according to Section 2 (i.e., Equations (8) or (19)). It can be proven that the confidence levels of $L_{\mathrm{CU}t}$ and $L_{R\mathrm{L}t}$ are still $\gamma$, that is:

$$P\left(L_{\mathrm{CU}t}\ge L_{\mathrm{C}t}\right) = P\left(L_{R\mathrm{L}t}\le L_{Rt}\right) = \gamma$$

(27)

Since the $L_{\mathrm{C}t}$ (or $L_{\mathrm{CU}t}$) and $L_{Rt}$ (or $L_{R\mathrm{L}t}$) are equivalent for all levels of loads and load combinations, they can be easily applied in individual life monitoring and online life management. For example, let $L_{\mathrm{CU}t}$ and $L_{R\mathrm{L}t}$ be the reliable life consumption percentage and remaining reliable life percentage of an individual rolling bearing at time $t$, respectively. Then, the equivalent revolution number of the rolling bearing under $S$ is $L_{\mathrm{CU}t}{N}_{R\mathrm{L}}$, and the lower confidence limit of its remaining reliable life under $S$ with $\gamma$ confidence and $R$ reliability is $L_{R\mathrm{L}t}{N}_{R\mathrm{L}}$.

It is worth noticing that the reliable life consumption assessment can also be directly conducted in units of the working hour instead of revolution number when the rotation speeds of the rolling bearing are the same in accelerated life tests and during service. In addition, the working hour, at different rotation speeds in the tests and the service, can also be uniformly converted into the working hour at the same rotation speed with the equal revolution rule, and then the reliable life consumption assessment can be conducted in units of the working hour. In this case, the units of $N_{R\mathrm{L}}, N_{R\mathrm{L}}^{\ast }, N_{R\mathrm{L}}^{\ast \ast }, N_{R\mathrm{L}, i}, N_{R\mathrm{L}, i}^{\ast }, n, n_i, n_i^{\ast }$ in Section 2 and Section 3 should be changed to working hour.

4. Individual Life Monitoring for Rolling Bearings

In the outfield service of the rolling bearings, the service loads or missions can be tracked for reliable life consumption assessment and individual life monitoring. Referring to the individual life monitoring concept of aircraft and engines [16,17,18], this section mainly discusses the individual life monitoring methods for rolling bearings based on load monitoring and mission monitoring. Moreover, the online life management method for rolling bearings is also provided.

4.1. Load-Based Individual Life Monitoring for Rolling Bearings

The load-based individual life monitoring method requires real-time monitoring for the dynamic equivalent load of each rolling bearing in service. The revolution numbers or working hours under different dynamic equivalent loads should also be recorded. According to the ISO 281 and the GB/T 6391, the dynamic equivalent load can be obtained by weighting the radial load $F_{\mathrm{r}}$ and the axial load $F_{\mathrm{a}}$ of the rolling bearing:

$$S = X{F}_{\mathrm{r}}+Y{F}_{\mathrm{a}}$$

(28)

where $X$ and $Y$ can be found in the ISO 281 and the GB/T 6391. Depending on the product characteristics, there are two load monitoring schemes that can be selected for actual use. One is to install torque or other force sensors on the shafting parts equipped with bearings so the bearing loads can be calculated through the monitored sensor data and the load-transfer relationships among the shafting parts. The other is to establish the relationship between bearing loads and the product’s operating condition parameters so bearing loads can be indirectly monitored through operating condition parameters. For example, bearing loads in aero-engines can be calculated by the relational flight parameters, such as engine throttle position and engine rotation speed.

It can be assumed that the dynamic equivalent load of an individual rolling bearing is monitored during its outfield service, and the rolling bearing has worked for $n_i$ rotations under $S_i$ at time $t$, $i = 1, 2, \cdots , q$. Then, the upper confidence limit of its reliable life consumption percentage at time $t$ with $\gamma$ confidence and $R$ reliability can be evaluated by Equation (24). When $L_{\mathrm{CU}t}<1$, the rolling bearing can still work with the requirements of confidence $\gamma$ and reliability $R$, and the lower confidence limit of its remaining reliable life is $L_{R\mathrm{L}t} = 1-L_{\mathrm{CU}t}$.

4.2. Mission-Based Individual Life Monitoring for Rolling Bearings

Since a rolling bearing experiences different loads when performing different mission types, load monitoring can be replaced by mission monitoring to a certain extent. The mission-based individual life monitoring method is suitable for cases in which the dynamic equivalent load is difficult to monitor online. It requires load calibration for each mission type before bearing service and recording of the performed mission rather than the dynamic equivalent load during bearing service. Due to the convenience of mission records, this method can be easily applied in engineering practice, although its accuracy is slightly lower than that of the load-based method.

It can be assumed that the upper confidence limit of the reliable life consumption percentage of the rolling bearing caused by the $k_{\mathrm{th}}$ mission is $L_{\mathrm{CU},k}$, $k = 1, 2, \cdots , K$. This can be calculated by Equation (24) and the measured dynamic equivalent load history in the mission. Assuming that an individual rolling bearing has conducted the $k_{\mathrm{th}}$ mission $m_k$ times at time $t$, $k = 1, 2, \cdots , K$, then the upper confidence limit of its reliable life consumption percentage at time $t$ with a confidence value of $\gamma$ and a reliability value of $R$ can be evaluated as:

$$L_{\mathrm{CU}t} = {\displaystyle \sum _{k = 1}^K{m}_k{L}_{\mathrm{CU},k}}$$

(29)

When $L_{\mathrm{CU}t}<1$, the rolling bearing can still work with the requirements of confidence $\gamma$ and reliability $R$. The lower confidence limit of its remaining reliable life is $L_{R\mathrm{L}t} = 1-L_{\mathrm{CU}t}$.

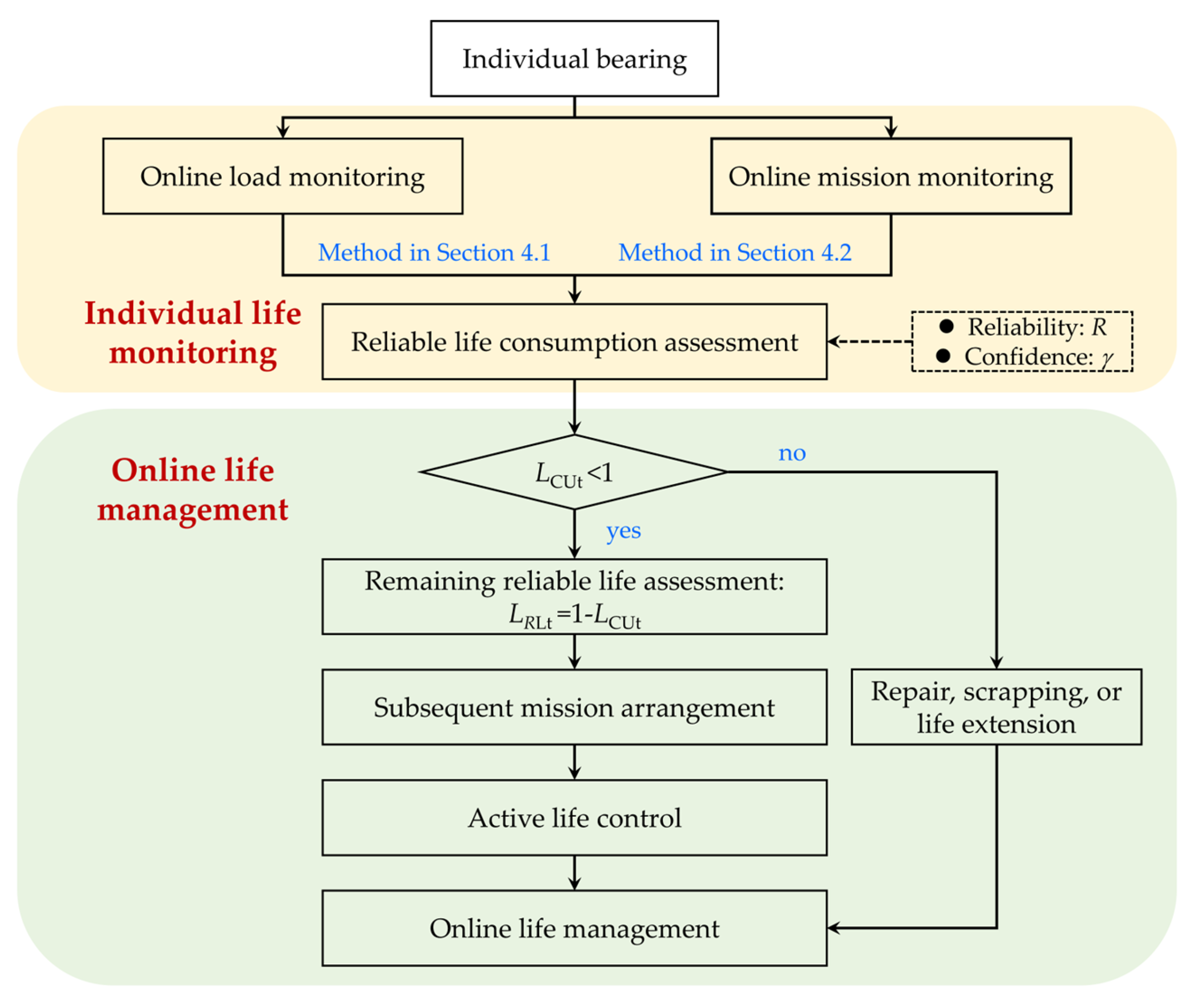
4.3. Online Life Management for Rolling Bearings

Using online data acquisition of loads or missions for an individual bearing, the upper confidence limit of its reliable life consumption percentage and the lower confidence limit of its remaining reliable life percentage can be calculated in real time according to Section 4.1 and Section 4.2. Furthermore, based on this, online life management for the individual bearing can be achieved, as is illustrated in Figure 4.

The $L_{\mathrm{CU}t}$ has the effect of ensuring the bearing’s safety and reliability during service. A rolling bearing with $L_{\mathrm{CU}t}<1$ can still work with the requirements of confidence $\gamma$ and reliability $R$. On the other hand, a rolling bearing with $L_{\mathrm{CU}t}\ge 1$ cannot continue to work according to the reliability requirements. In such a case, repairment, scrapping, and life extension should be arranged in a timely manner.

In addition, different missions relate to different bearing loads and lead to different results in terms of reliable life consumption. Therefore, mission arrangements can be further conducted for individual bearings according to their remaining reliable life percentages and the reliable life consumption percentages caused by each mission. For example, according to the actual needs, a rolling bearing with a higher reliable life consumption percentage can be arranged for relatively mild missions, while a rolling bearing with a lower reliable life consumption percentage can be arranged for relatively severe missions. By these means, active life control for individual bearings can be realized.

Specifically, we can assume that the lower confidence limit of the remaining reliable life percentage of an individual rolling bearing is $L_{R\mathrm{L}t}$ and that the upper confidence limit of the reliable life consumption percentage caused by the $k_{\mathrm{th}}$ mission is $L_{\mathrm{CU},k}$, $k = 1, 2, \cdots , K$. Then, the rolling bearing can still conduct the $k_{\mathrm{th}}$ mission $m_k^{\prime }$ times, where

$$m_k^{\prime } = L_{R\mathrm{L}t}/L_{\mathrm{CU},k}\hspace{1em}k = 1, 2, \cdots , K$$

(30)

In addition, the rolling bearing mission combinations can also be schemed according to

$${\displaystyle \sum _{k = 1}^K{m}_k^{\prime }{L}_{\mathrm{CU},k}}\le L_{R\mathrm{L}t}$$

(31)

where $m_k^{\prime }$ is the number of times the $k_{\mathrm{th}}$ mission is performed in the mission combination.

5. Example

This section adopts a type of spacecraft ball bearing to illustrate the assessment of reliable life consumption and the method of individual life monitoring.

5.1. Reliable Life Evaluation of the Spacecraft Ball Bearing

The bearing’s life follows the two-parameter Weibull distribution with a shape parameter of $\alpha = 1.5$. Accelerated life tests were conducted with five samples under a dynamic equivalent load of $S^{\ast } = 206 \mathrm{N}$. The test results are listed in

Table 1. Accelerated life test results under the dynamic equivalent load of 206 N.

j	1	2	3	4	5
$N_j^{\ast }/\left(\mathrm{h}\right)$	20,319	16,095	13,721	13,396	17,110

[30].

According to Equation (4), the lower confidence limit of the reliable life of the ball bearing under a test load of $S^{\ast } = 206 \mathrm{N}$, with a confidence level of $\gamma = 0.9$ and a reliability level of $R = 0.999$, can be calculated as

$$N_{R\mathrm{L}}^{\ast } = {\left[-\frac{2\ln R}{{\chi }_{\gamma }^2\left(10\right)}{\displaystyle \sum _{j = 1}^5{\left(N_j^{\ast }\right)}^{\alpha }}\right]}^{1/\alpha } = 118.7 \mathrm{h}$$

(32)

Assuming that an individual ball bearing works alternately under three dynamic equivalent loads ($S_1 = 40 \mathrm{N}$, $S_2 = 50 \mathrm{N}$, and $S_3 = 60 \mathrm{N}$), and the rotation speeds of the ball bearing are the same both in accelerated life tests and during service, then the acceleration factor of $S^{\ast } = 206 \mathrm{N}$ (let $S^{\ast \ast } = S^{\ast }$) to $S_i$ ($i = 1, 2, 3$) can be calculated as

$$\left\{\begin{array}{c}{\tau }_1 = {\left(S^{\ast \ast }/S_1\right)}^{\epsilon } = {\left(S^{\ast }/S_1\right)}^{\epsilon } = 136.6\\ {\tau }_2 = {\left(S^{\ast \ast }/S_2\right)}^{\epsilon } = {\left(S^{\ast }/S_2\right)}^{\epsilon } = 69.9\\ {\tau }_3 = {\left(S^{\ast \ast }/S_3\right)}^{\epsilon } = {\left(S^{\ast }/S_3\right)}^{\epsilon } = 40.5\end{array}\right.$$

(33)

where the load–life index is $\epsilon = 3.0$ [30]. Then, the lower confidence limit of the reliable life of the ball bearing under the service load $S_i$ ($i = 1, 2, 3$), with a confidence level of $\gamma = 0.9$ and a reliability level of $R = 0.999$, can be calculated as

$$\left\{\begin{array}{c}{N}_{R\mathrm{L},1} = {\tau }_1{N}_{R\mathrm{L}}^{\ast } = 1.62\times {10}^4 \mathrm{h}\\ N_{R\mathrm{L},2} = {\tau }_2{N}_{R\mathrm{L}}^{\ast } = 8.30\times {10}^3 \mathrm{h}\\ N_{R\mathrm{L},3} = {\tau }_3{N}_{R\mathrm{L}}^{\ast } = 4.80\times {10}^3 \mathrm{h}\end{array}\right.$$

(34)

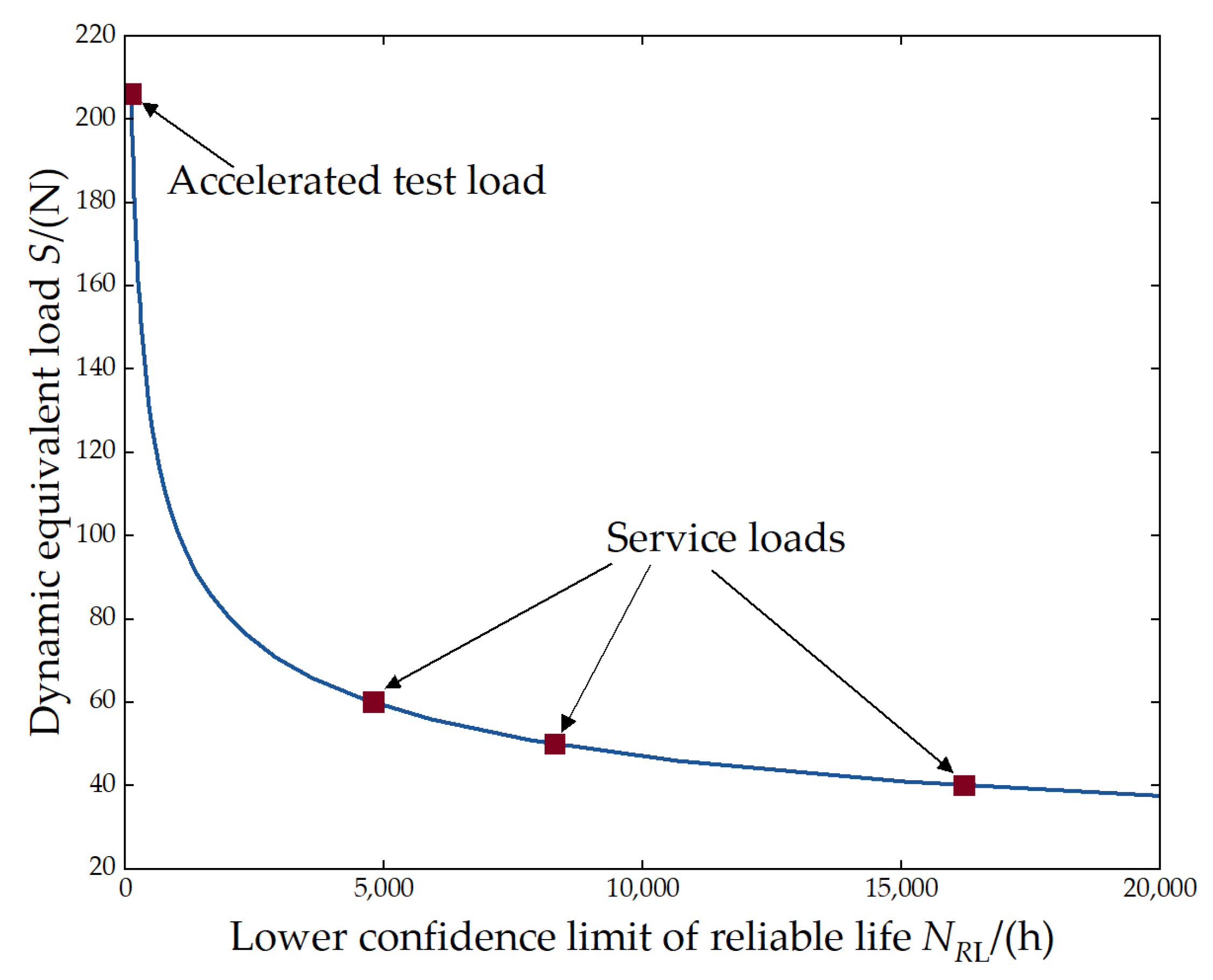
The relationship between the reliable life of the spacecraft ball bearing and the dynamic equivalent load is illustrated in Figure 5.

5.2. Real-Time Assessment for Reliable Life Consumption of Spacecraft Ball Bearings

It can be assumed that the dynamic equivalent load of the individual rolling bearing is monitored during its outfield service, and this bearing has worked for $n_i$ hours under $S_i$ at time $t$: $n_1 = 1006 \mathrm{h}$, $n_2 = 1628 \mathrm{h}$, and $n_3 = 574 \mathrm{h}$. According to Equations (24) and (26), the upper confidence limit of its reliable life consumption percentage and the lower confidence limit of its remaining reliable life percentage can be calculated as

$$L_{\mathrm{CU}t} = {\displaystyle \sum _{i = 1}^3\frac{n_i}{N_{R\mathrm{L},i}}} = 37.76\%$$

(35)

$$L_{R\mathrm{L}t} = 1-L_{\mathrm{CU}t} = 62.24\%$$

(36)

Because $L_{\mathrm{CU}t}<1$, this bearing can still meet the reliability requirements of $\gamma = 0.9$ and $R = 0.999$. The lower confidence limits of its remaining reliable life with $\gamma = 0.9$ and $R = 0.999$ under three dynamic equivalent loads can be calculated as

$$\left\{\begin{array}{c}{L}_{R\mathrm{L}t}{N}_{R\mathrm{L},1} = 1.01\times {10}^4 \mathrm{h}\\ L_{R\mathrm{L}t}{N}_{R\mathrm{L},2} = 5.17\times {10}^3 \mathrm{h}\\ L_{R\mathrm{L}t}{N}_{R\mathrm{L},3} = 2.99\times {10}^3 \mathrm{h}\end{array}\right.$$

(37)

In comparison, the traditional method without individual life monitoring generally evaluates reliable life under the most severe load ($S_3 = 60 \mathrm{N}$) and conducts life management according to the estimated reliable life ($N_{R\mathrm{L},3} = 4.80\times {10}^3 \mathrm{h}$). At time $t$, the individual ball bearing has worked for $n_1+n_2+n_3 = 3208 \mathrm{h}$. According to the traditional method, $3208/\left(4.80\times {10}^3\right) = 66.83\%$ of its reliable life has been consumed and 33.17% of its reliable life remains. The remaining reliable life under each dynamic equivalent load is 1592 h. From

Table 2. Remaining reliable life assessment under different dynamic equivalent loads.

Dynamic Equivalent Load	${\mathit{S}}_1 = 40 \mathbf{N}$	${\mathit{S}}_2 = 50 \mathbf{N}$	${\mathit{S}}_3 = 60 \mathbf{N}$
Remaining reliable life evaluated by the traditional method	1592 h	1592 h	1592 h
Remaining reliable life evaluated by this paper	1.01 × 104 h	5.17 × 103 h	2.99 × 103 h
Remaining reliable life underestimation by the traditional method	8508 h	3578 h	1398 h
Percentage increase of remaining reliable life by this paper	632.0%	324.8%	187.8%

, it can be seen that the traditional life management method significantly underestimated the service life potential of the bearing, resulting in a great waste of service life. In contrast, the individual bearing life monitoring method proposed in this paper can evaluate reliable life consumption according to the specific load history, and can further calculate the remaining reliable life under each load so that the service life potential can be fully developed. Furthermore, although it was attempted to adopt reliable life under the most severe load, it is still possible that the bearing service load may be higher than this severe load. In this case, the traditional life management method will lead to a dangerous result. The individual bearing life monitoring method, on the other hand, can calculate a greater degree of reliable life consumption caused by the higher service load, thus still ensuring the safety and reliability of the bearing.

In addition, the traditional life management method cannot provide scientific guidance on mission arrangements for the ball bearing due to the lack of consideration of service load differences. In contrast, the life monitoring method for individual bearings can scientifically guide its subsequent missions based on its remaining reliable life percentage and the reliable life consumption percentage caused by each mission, thus achieving active life control and management for each individual bearing. This will be illustrated below.

5.3. Online Life Management of the Spacecraft Ball Bearings

We can assume that a ball bearing performs six types of missions during its service; the dynamic equivalent loads in each mission are listed in

Table 3. Dynamic equivalent loads and reliable life consumption percentage of each mission.

k	$\mathbf{Working} \mathbf{Time} \mathbf{under} {\mathit{S}}_1 = 40 \mathbf{N}$	$\mathbf{Working} \mathbf{Time} \mathbf{under} {\mathit{S}}_2 = 50 \mathbf{N}$	$\mathbf{Working} \mathbf{Time} \mathbf{under} {\mathit{S}}_3 = 60 \mathbf{N}$	${\mathit{L}}_{\mathbf{C}\mathbf{U},\mathbf{k}}$
1	4.5 h	9.7 h	12.3 h	0.40%
2	4.8 h	16.5 h	2.5 h	0.28%
3	2.1 h	7.5 h	6.1 h	0.23%
4	17.7 h	3.3 h	1.5 h	0.18%
5	12.7 h	1.8 h	0 h	0.10%
6	2.8 h	4.4 h	0 h	0.07%

. Then, the upper confidence limit of the reliable life consumption percentage of the ball bearing with $\gamma = 0.9$ and $R = 0.999$ caused by each mission is evaluated by Equation (24), and is also listed in Table 3. In this case, the individual ball bearing with $L_{R\mathrm{L}t} = 62.24\%$ can still perform the $k_{\mathrm{th}}$ mission alone $m_k^{\prime }$ times, where

$$\left\{\begin{array}{l}{m}_1^{\prime } = L_{R\mathrm{L}t}/L_{\mathrm{CU},1} = 156\hfill \\ m_2^{\prime } = L_{R\mathrm{L}t}/L_{\mathrm{CU},2} = 222\hfill \\ m_3^{\prime } = L_{R\mathrm{L}t}/L_{\mathrm{CU},3} = 271\hfill \\ m_4^{\prime } = L_{R\mathrm{L}t}/L_{\mathrm{CU},4} = 346\hfill \\ m_5^{\prime } = L_{R\mathrm{L}t}/L_{\mathrm{CU},5} = 622\hfill \\ m_6^{\prime } = L_{R\mathrm{L}t}/L_{\mathrm{CU},6} = 889\hfill \end{array}\right.$$

(38)

In addition, several possible subsequent mission combinations for the ball bearing can also be planned on the premise of

$${\displaystyle \sum _{k = 1}^6{m}_k^{\prime }{L}_{\mathrm{CU},k}}\le L_{R\mathrm{L}t}$$

(39)

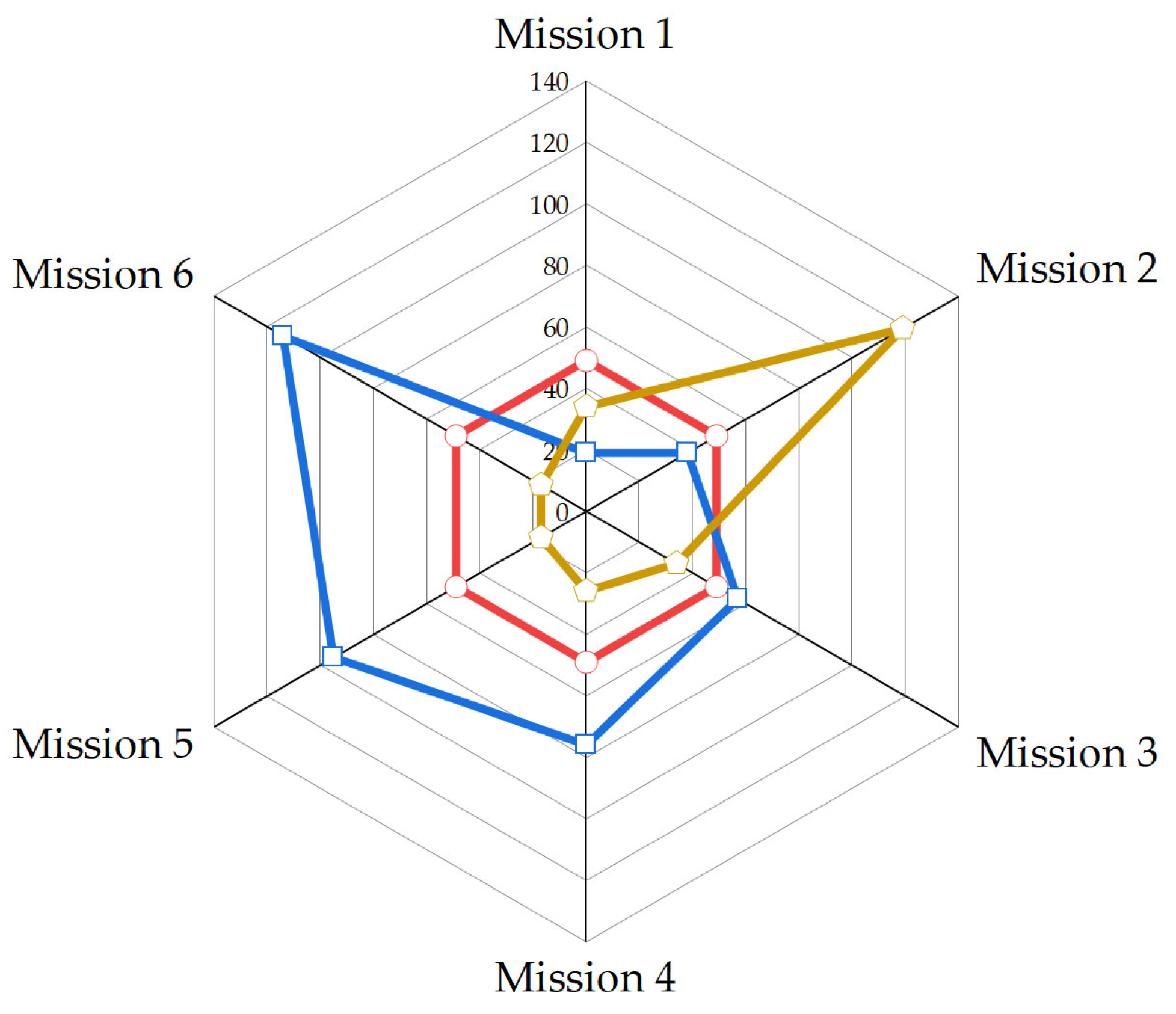
Based on that, three possible subsequent mission combinations (three colors of curves) are provided in Figure 6. In the figure, the scale value on each axis represents the number of times each mission type is conducted within the mission combination, i.e., $m_k^{\prime }$ with k = 1, 2, …, 6. For example, the red curve, which has a scale value of 49 on all axes, means that the bearing can still perform each mission 49 times in the mission combination.

Mission arrangements can be made online for each bearing according to its actual needs in engineering practice. By this means, the remaining reliable life of the ball bearing can be actively controlled in order to exploit its life potential while meeting the reliability demand.

6. Conclusions

A reliable life consumption assessment and an individual life monitoring method for rolling bearings have been developed based on monitored service loads or missions. By this means, the real-time evaluation of the upper confidence limit of the reliable life percentage and the lower confidence limit of the remaining reliable life percentage can be realized. Further, active life control and management can be achieved according to scientific mission arrangements.

The advantages of this method are: (1) Compared with traditional bearing life management methods, which ignore the service load differences, the proposed method can better ensure service safety and simultaneously maximize the life potential; (2) the proposed method is relatively easy to apply in engineering practice because only dynamic equivalent loads or service missions of the bearing need to be monitored online; and (3) accelerated life tests originally used for bearing reliability verification before delivery are adopted, which does not add an additional experimental burden to engineering practice.

The proposed method has a wide range of application scenarios, such as high-speed train rolling bearings, aviation rolling bearings, and spacecraft rolling bearings. In particular, for the future construction of the Chinese lunar base, this method has prospective application value in terms of reliability assurance and life potential development for rolling bearings. In addition, due to the time limitation of bearing life tests, the experimental verification for this method is not discussed in this paper. Experimental validation with service load simulation and application validation for specific products will be considered in our future work.