1. Introduction
Digital twins (DTs) have been perceived in multiple ways. Several descriptions of DTs exist in the scientific literature, many of which have gone beyond the three-dimensional DT proposed by Michael Grieves [
1]. Digital twins are described as virtual substitutes of real-world objects consisting of virtual representations and communication capabilities making up smart objects and acting as intelligent nodes inside the Internet of Things context. Digital twins have reached beyond the field of product lifecycle management, where it was first conceived, into manufacturing processes [
2], communication and networking [
3], construction [
4] and smart grids [
5]. However, the underlying research questions remain; how to best represent a complex multidimensional DT system and how to simplify that representation to reduce twin’s computational complexity and interpretability?
The DT is a multidimensional entity. In [
6], the DT is realized as a five-dimensional living model. It is a collection of simulation models, information models, and IoT data acquisition and processing. Plenty of research is available on the development of these models and data-driven methods [
7]. However, the important area that has been overlooked by the digital twin research community is model reduction. In this study, graph-based methods are proposed for conceptualizing the complex DT representation. To address the computational complexity of the DT, a graph-based model reduction (GBMR) method is proposed. The GBMR method was first conceived as a dimensionality reduction method [
8] but evolved into the virtual entity representation and optimization tool for the DT [
9]. The GBMR method addresses the computational complexity of the DT with a two-step approach: (1) providing a graph-based conceptual model representation of the DT by utilizing a casual graph extraction method known as dimensional analysis and conceptual modeling, and (2) reducing the DT graph model by spectral decomposition and identifying the important parameters in it. The novelty of GBMR lies in representing the physical system as a graph-based model and reducing that graph by finding important parameters dynamically by the DT. The model reduction process helps to optimize the virtual entity performance of the DT as the reduced model uses a subset of important parameters to predict the target parameter of the physical entity.
To that end, the primary contributions of this research work are: (1) provide the development of the GBMR method for fast identification of the important parameters for reducing the computational complexity of the DT, and (2) test the GBMR method with the help of a turbo compressor case study and analyze the results. This paper is structured as follows:
Section 2 provides the state of the art in DT development with a focus on conceptual graph-based methods.
Section 3 introduces the GBMR method. In
Section 4, a case study of the GBMR method is presented for a turbo compressor system including the results and future research directions of the method, and
Section 5 concludes the article.
2. State of the Art
2.1. The Complexity of DT Development
In [
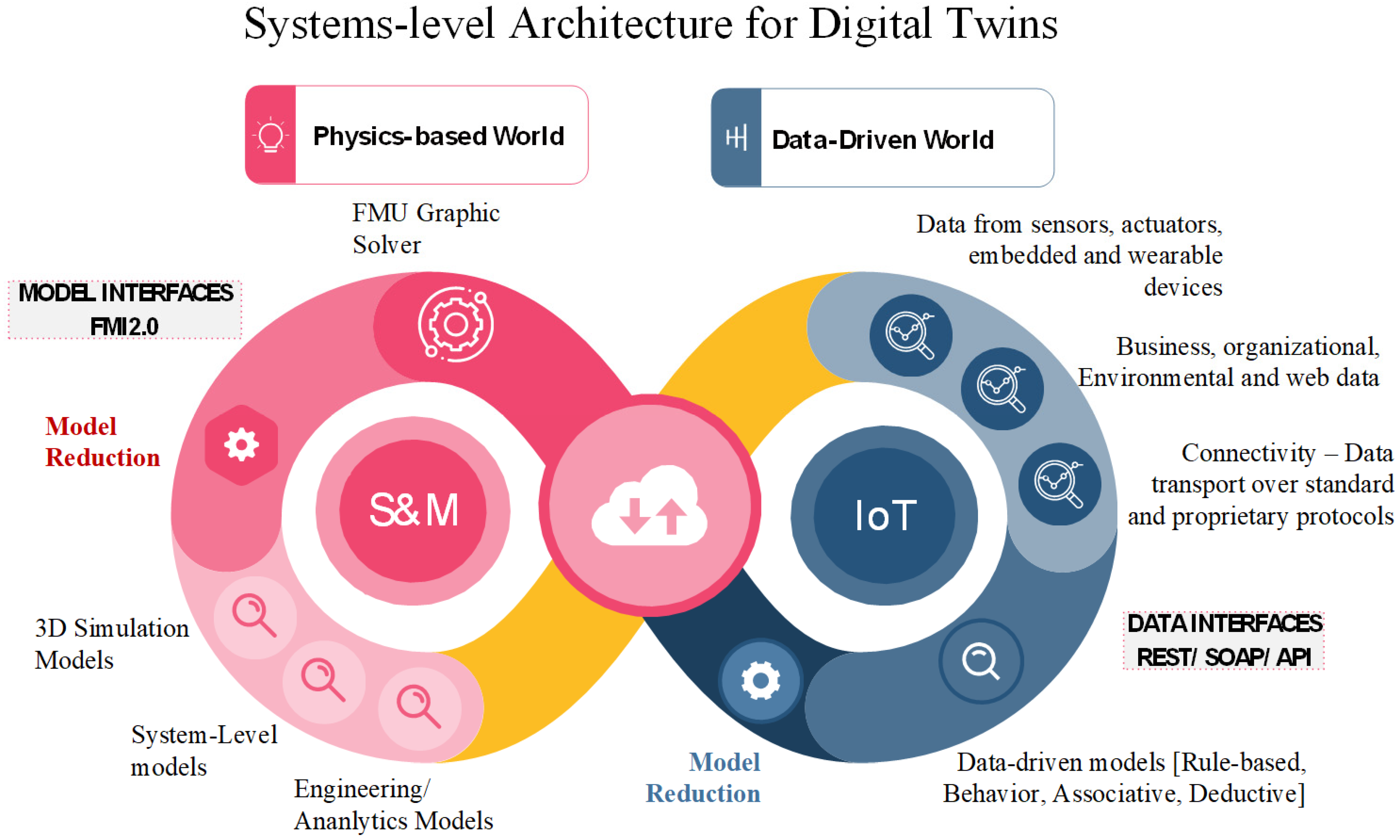
10], the authors propose the technologies enabling DT development, which is the combination of the digital world such as simulation and modeling (S&M) and the physical world such as the IoT. The S&M approach for DTs creates the possibility of modularizing the development of DTs and focusing on the essentials. However, it also introduces large amount of complexity in building and operating such DTs. These models can arise from different domains of the physical object. They are complex, real-time, “living” entities. These models can be organizational information models, engineering models (thermal, fluid, dynamic, electrical or systems-level), rule-based models (associative, deductive or degradation) or purely data-driven models (ANN or deep-learning-based models). The Internet of Things (IoT) or Industrial Internet of Things (IIoT) facilitate building real-time models based on the data.
Figure 1 demonstrates the system-level architecture that combines the IoT/IIoT and S&M to provide the foundation for such DT development. A similar approach was also adopted in [
11] for a DT development.
The right side of
Figure 1 focuses on the IoT part. The IoT provides the following components as building blocks of a digital twin:
Data-driven Models: Data-driven predictive models form the basis of many digital twins. Many such data-driven digital twins can be found in the literature [
12,
13]. These predictive models are built for state estimation, behavior prediction or causal analysis. Machine learning methods such as Bayesian networks and evidential reasoning are used for building these models [
14]. The future state estimation by these methods could serve as the input to many simulation models. Environmental data and other web-based data such as metrological data are also used in building such estimation models, which form an essential part of the virtual entity.
Model Fusion and Model Reduction: The curse of dimensionality is often experienced in building data-driven models. State prediction models or behavior estimation models typically contain several parameters that should be monitored, and data should be collected with sensors and a proper connectivity mechanism. Building high-dimensional and high-fidelity models that replicate the reality with a high degree of accuracy are extremely challenging. These models are computationally extensive. It is also resource consuming to train these models with data from the physical device and develop methods for validating the results. Model fusion provides a mean to generate a hybrid model by combining physics-based and data-driven models and model reduction provides a means to reduce or combine the number of parameters in that hybrid model. In doing so, the hybrid model becomes computationally simplified and takes less time to provide prediction result.
The left side of
Figure 1 focuses on S&M. This part of the figure highlights the advanced simulation models that need to be built to capture the physics of the system. S&M creates the virtual entity of the five-dimensional representation of the digital twin [
15]. The simulation models could be from one or several domains such as analytical models, geometrical models or system-level models. Analytical models such as finite element or computational fluid flow models are necessary to predict the state of the physical entity through software-defined methods such as thermal analysis or stress analysis. Geometrical models purely represent the physical phenomena of the physical entity such as deformation and buckling. The system-level model combines other types of models to provide system-level information such as efficiency and performance. By combining these advanced simulation models, it is possible to represent the complete state of the physical entity. The DT will demand that these advanced simulation models work in unison and possess the capability to provide the updated state of the system based on IoT data. This makes the DT computationally extensive and requires the development of methods, tools and techniques for understanding and reducing the DT’s computational complexity.
Compressing information from these bulky analytical models and making them predict the system state based on real-time data need further advancement of technology. These simulation models are designed to provide a high-fidelity representation of the system without the consideration of a faster prediction of model output. Model reduction is needed for building compressed digital representations from these simulation models [
16]. Model reduction methods are already applied in these advanced simulation environments at an individual component level. This could be traditional methods such as reduced order modeling by proper orthogonal decomposition [
17] or by applying newer deep learning methods [
18,
19]. Metamodeling has been used to reduce the dimensionality of complex systems and is propagated as a class of model reduction as well [
20]. However, there is a lack of a unified method that combines the reduced model from the component to system level.fom curve fitting in the stable region and used
2.2. DT Reference Model
To realize the complexity of the DT development process, a reference model is crucial. The five-dimensional representation of the DT provides such a reference model [
21,
22]. In this section, the five-dimensional representation from the literature is utilized to build a reference model for DTs.
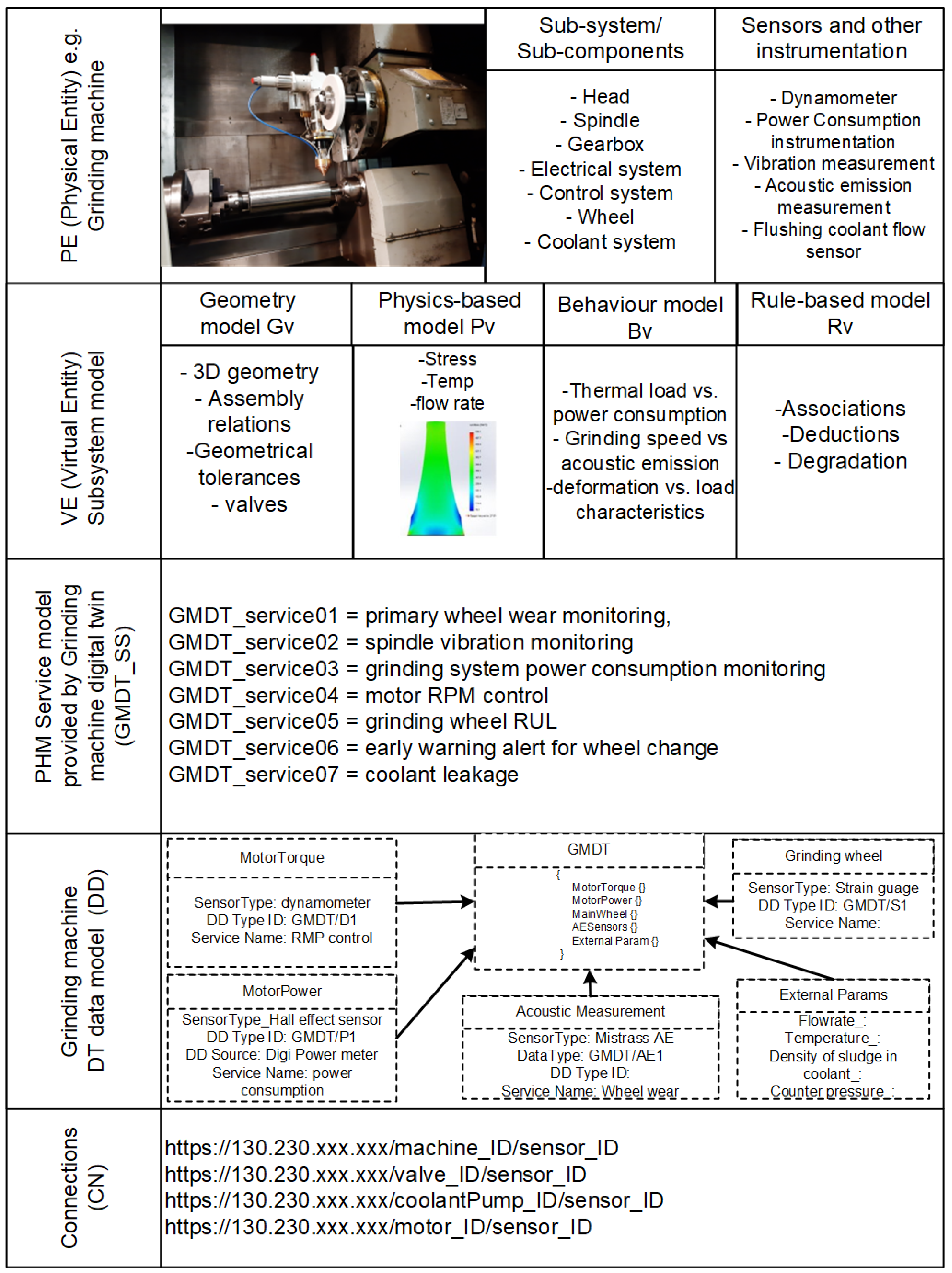
Figure 2 presents the reference model based on a grinding machine case study [
9].
The DT reference model consists of five dimensions:
(1) Physical Entity (PE): This consists of the sub-systems and sensory devices. This could range from sensors, actuators and control systems to the whole sub-system such as the motor drives, spindles or transmission of the machine. PE guides the process of DT development by providing IoT data from these sub-systems. So, the PE also provides communication interfaces, RFID tags or distributed sensor networks.
(2) Virtual Entity (VE): This is the complex virtual representation of the PE. The VE consists of geometric models, analytical- or physics-based models, behavioral models and rule-based models [
23,
24]. The VE may contain detailed geometric models such as 3D CAD models or physics-based models such as finite element models. It may contain various behavior modeling methods such as Markov-chains or ontology-based models. Historical data from the PE are used to create rule-based models. The rule-based models provide the VE with the capacity for judgement, optimization and prediction.
(3) Service: This provides the reason for building a DT that is the digital services. In
Figure 2, it could be services such as grinding wheel wear monitoring or early warning for a wheel change based on the remaining useful life of the wheel. These services fall under the category of prognostics and health management (PHM) services for the grinding machine.
(4) Data model: The data model creates the schema for data exchange between the PE and the VE. In
Figure 2, an example is provided. The grinding machine digital twin requires sensor data to exchange between PE and VE, such as motor torque, motor power, acoustic emission and wheel wear.
(5) Connections: The connections bind the PE to the VE with the help of the data dimension. PE to VE binding defines acquiring data from the sensors on the grinding wheel with API endpoints. Similarly, VE to PE binding provides the output of analytical results to the physical device to perform an action such as grinding wheel speed control.
The VE embeds information from multi-domain models. A model fusion approach is taken to build the VE graph to model the interaction of the parameters with the help of methods such as DACM (
Section 2.3.1) and heuristic search (
Section 2.3.2). The VE graph is denoted as
, where
,
,
and
are the graph representation of parameters in geometric, analytical, behavioral and rule-based domains, respectively. The fused model or
then represents the complete knowledge model of the DT. The
is reduced with graph-based methods such as node importance (
Section 2.4) and evidential reasoning (
Section 2.5).
2.3. Graph-Based Modeling of Complex Systems
2.3.1. Dimensional Analysis and Conceptual Modeling
Dimensional analysis and conceptual modeling (DACM) is a conceptual modeling mechanism used to extract the causal relationship between variables in a physics-based simulation environment [
25]. This method uses the dimensional homogeneity principle to extract the causal relationship between the parameters. DACM is a matured framework and is already applied to use cases in the field of additive manufacturing [
26] and multi-disciplinary design optimization [
27]. The DACM framework starts with functional modeling of the system and the assigning of fundamental variables to the different functions of the model. The functions, associated variables and representative equations are characterized in the causal graph in the form of the cause–effect relationship between the fundamental variables of the functional model. The mathematical machinery to check the propagation of an objective in a causal graph is based on the Vashy–Buckingham pi (π) theorem and the dimensional analysis (DA) theory. DACM encodes the domain knowledge of the system in the form of the directed causal graph. Specific checks are run to identify and remove any loops or contradictions in the graph. This ensures a target-driven directed model. This source of the domain knowledge could be from the literature, empirical relationship or analytical models. DACM is combined with machine learning methods such as the Bayesian network for causal inference. The objective of the causal graph provided by DACM is to arrive at the target variable in the directed acyclical graph or DAG with the help of a set of intermediate dependent and independent variables. Apart from extracting the causal graph, DACM also provides the following checks: (1) it generates sets of behavioral equations associated with the causal graphs, (2) it simulates qualitatively behaviors, (3) it detects contradictions in systems, and (4) it provides a set of analytical concepts for analyzing complex systems.
2.3.2. Greedy Equivalence Search
Chickering, in [
28], provided a method for graph structure learning with a two-phase greedy equivalence search (GES) algorithm from data. Graph structure learning is a sequential process that learns the relations between the random variables (nodes of a graph) that are embedded in the edges simulating a causal influence. The GES algorithm provides a mechanism to obtain such a distribution and represent it in the form of a DAG. The GES approach has an important influence in machine learning methods such as the Bayesian network for graph structure learning. Another experimental GES was proposed by [
29], it was called the greedy interventional equivalence search (GIES) and generalizes the GES algorithm. Interventions distort the value of random variables to throw the graph out of its original causal dependencies and make it find the original DAG. In this article, the GES algorithm is used to discover the accurate causal reasoning of the DT graph.
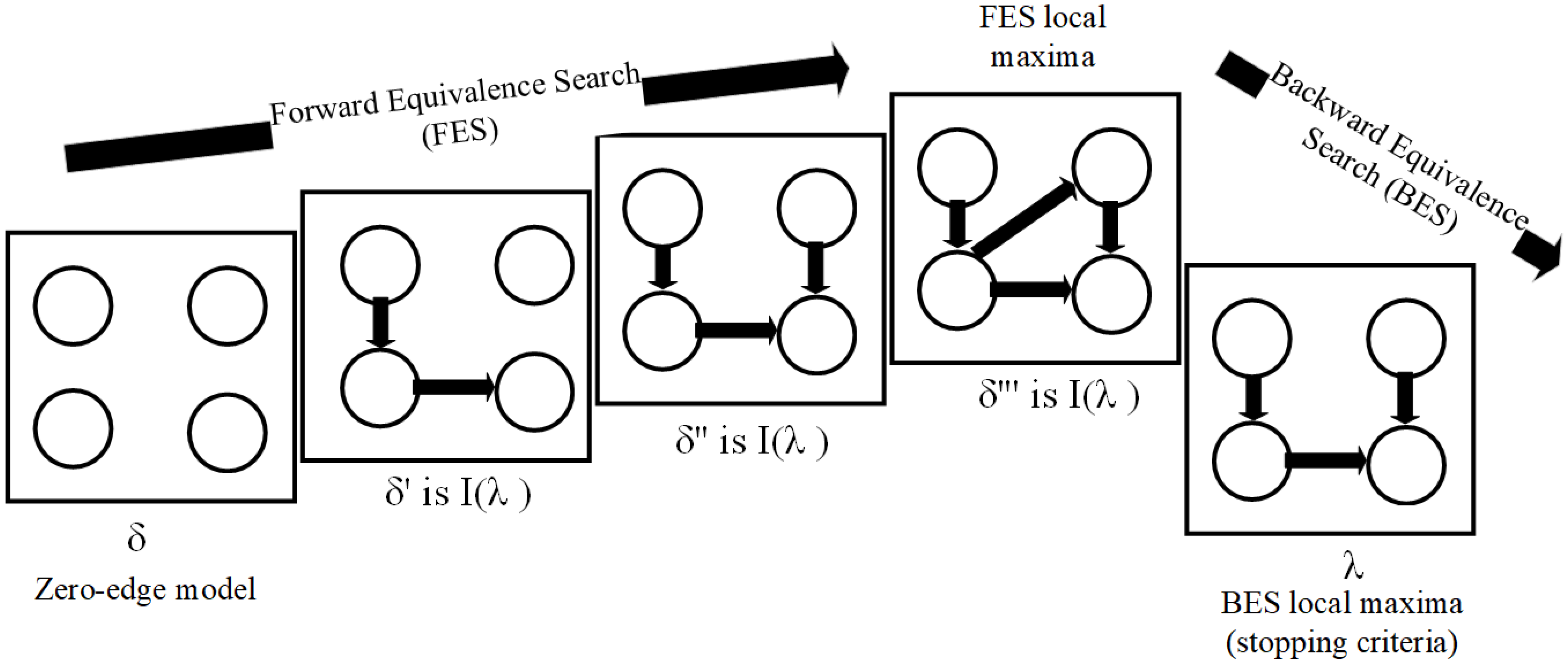
It was proved that, for two DAGs δ and λ, where δ is an I-map of λ, there are a finite sequence of edge additions and reversals in λ, such that: (1) after each edge modification, δ remains I-Map of λ, and (2) after all modification, λ is a perfect map of δ. The two-phase algorithm starts with a graph assuming that there are no dependencies. This is indicated as the zero-edge model. Then, all possible single edges are added till the algorithm reaches a local maximum. The phase of progressively adding single edges in the DAG is known as the forward equivalence search (FES); the corresponding local maxima is known as the FES local maxima. Once the FES algorithm stops at a local maximum, a second-phase greedy algorithm is applied that considers at each step all possible single-edge deletions that can be made to the DAG. This phase is known as the backward equivalence search (BES). The algorithm terminates when the BES local maxima is identified. The concept is demonstrated in
Figure 3.
2.4. Node Importance Measurement
Identifying the node importance in a complex graph is an active field of research in artificial intelligence. Several studies and algorithms have been published to estimate the importance of nodes in a graph [
30,
31]. Graph centrality is a diverse topic in network theory, with several algorithms available to study different network phenomena in complex graphical systems such as finding the shortest path from given node to the target node, predicting the links between the nodes, understanding the relative importance of the nodes in a graph and finding the bridge nodes to detect communities or clusters. Experimental studies have proven the validity of such systems applied to complex networks [
32]. The PageRank algorithm is a popular algorithm in graph centrality measurement in directed graphs. It is a network ranking method developed to compute the ranks of webpages in Google’s search engine results. The PageRank algorithm iteratively converges to a point for the most influential nodes. Hence, it creates a hierarchical node importance ranking system in a DAG. An improved version of this algorithm is used in applications that go beyond search engine ranking, which include impact analysis of graph-based system requirements and graph-based feature selection [
33]. The PageRank
of a node
can be calculated as follows:
The influence of node
in
steps is denoted as
. The higher the value of
, the higher are the chances that it is an important node. The
indicates that the node also depends on the importance of the
node. So, if a high importance node is pointing towards the node, it is considered important. Weighted PageRank (WPR) is a modified form of the PageRank algorithm that is used to rank real system parameters. In WPR, the influence of other nodes can be controlled by selecting appropriate weights [
34].
Eigenvector centrality [
35] is another graph centrality measuring algorithm that is used by social scientists to measure prestige in large connected graphs. EVC identifies nodes by the number of their neighbors and their importance. EVC is calculated with the following formula:
where the largest EVC value is represented by
.
2.5. Evidential Reasoning
The graph centrality and node importance approaches, though mathematically accurate, are often general and yield contradicting results. This results in disparity in the ranking system, introducing uncertainty and incompleteness in the ranking system. The Dempster–Shafer theory (DST) deals with this uncertainty and the incomplete behavior of any ranking system. Having its roots in probability theory, the DST uses data fusion and combinatorial rules to provide a belief function to a set of elements in the domain. The DST is used to combine the information available regarding the nodes in the DT graph and their relative importance obtained from the node importance scores. There are two possible outcomes for each node. The nodes can be high importance (
) or low importance (
). Hence, the frame of discernment (which is a non-empty set containing all mutually exclusive and exhaustive elements) is defined as:
and the power set (which is a set of all possible combinations of the problem in the frame of discernment) is defined as:
. Next, the mass functions are determined by adopting a technique similar to the one described in [
36] for directed networks. The frame of discernment contains all the possible combinations where the combination lies. If there are three hypotheses possible (
), the set of all combinations where the solution lies are:
The maximum and minimum values of the corresponding ranking is used to compute the mass functions with the following formulae:
where
is a tunable parameter that is chosen to avoid the denominator becoming zero. Repeating the steps in Equations (1)–(3) creates a basic probability assignment (BPA) for each node in the form:
There will be the same number of BPAs created as there are nodes in the sets. Now, all the node importance scores obtained from different centrality metrics can be combined with the help of Dempster’s combination rule to generate a new combined ranking for the nodes. Dempster’s combination rule, used in the field of IoT sensor fusion [
37], is modified to obtain the new metric for nodes based on the evidence of whether the node is high importance or low importance:
where
The factor
is a normalization constant known as the conflict coefficient of two BPAs. The higher the value of
, the more conflicting the sources of evidence are and the less information they will combine. Finally, the combined scores of each node based on evidential reasoning is obtained as:
In
Section 2, the complexity involved in building the DT is presented. A reference model from the literature is presented to provide the context to the VE of the DT. To understand the full potential of this VE, a conceptual modeling approach is presented. A correct balance should be struck between the graph–model complexity, speed and accuracy. New methods are needed that quickly capture the underlying structure of the graph–model and generate a reduced representation of that model for faster and less resource intensive computation of the target quantity. This is achieved with the GBMR method.
3. Graph-Based Model Reduction Method
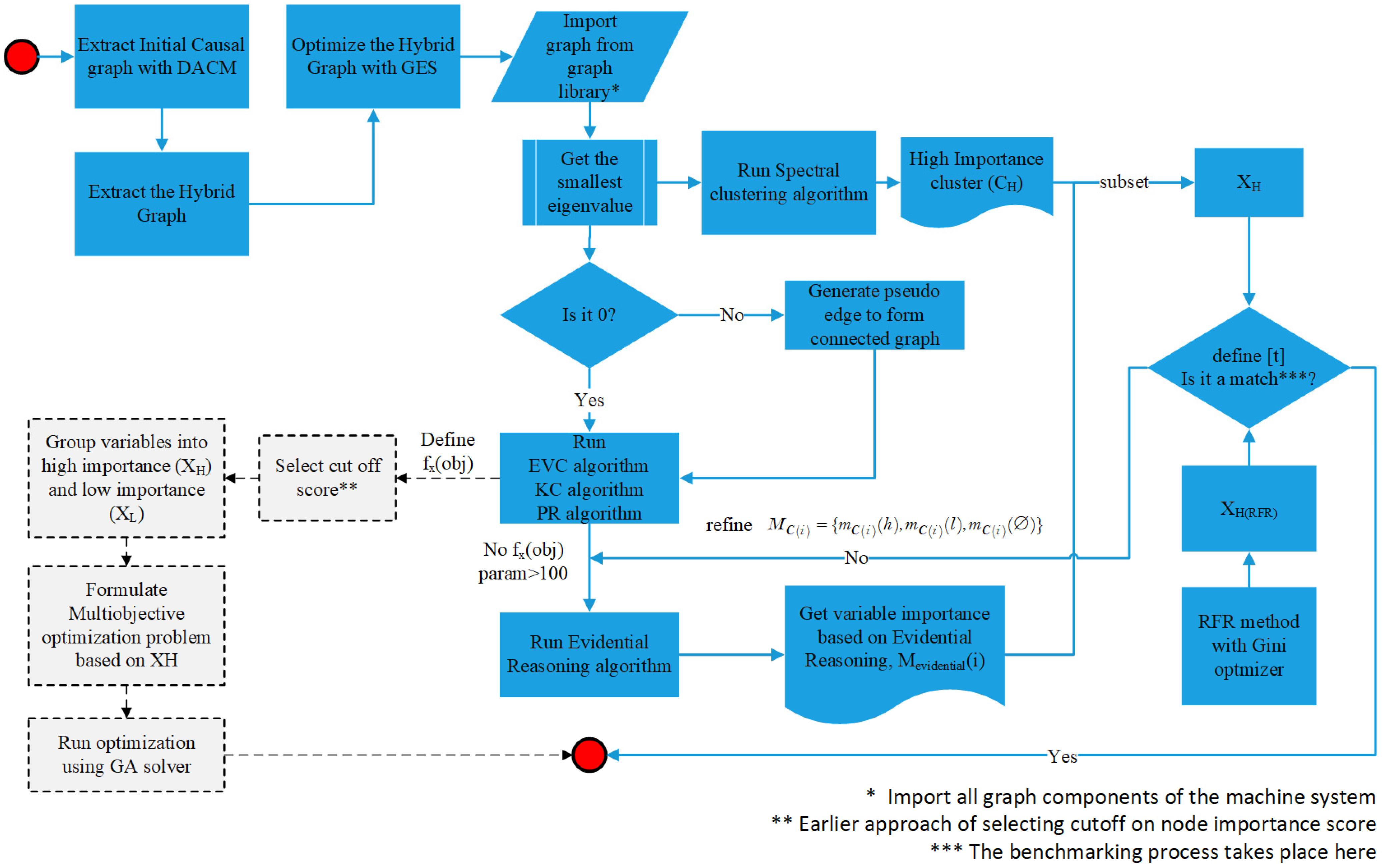
The DT is a living hybrid cross-disciplinary model of a real entity. For this, many cross-platform parameters need to be coupled together. Model fusion facilitates this coupling process by bringing several high-fidelity models from domains described in the DT reference model in
Figure 2 to create a unified model that provides specific digital services. Model fusion is a two-stage process where the first stage is building the multi-disciplinary model by coupling model parameters. The second stage is simplifying that model for faster interpretability and the prediction capacity of target parameters with model reduction. The GBMR method was first presented in [
38]. This section describes the GBMR method as a model fusion strategy for building faster and more accurate DTs. The GBMR method is shown in
Figure 4.
3.1. Initial Graph
The initial graph is the causal graph extracted from the physics defined by the analytical models of the PE. The parameters from FEM models or system-level models are used as inputs to the DACM method. The output of the DACM method is the causal graph containing all nodes and edges from physics-based equations. An alternative to DACM for building the initial network are graph structure learning algorithms from data such as Bayesian networks [
39]. The GBMR was combined with a Bayesian network to obtain the variable importance in the causal graph [
32]. In the Bayesian approach, the conditional probability of each node on the causal graph is calculated based on the available data. Sensitivity analyses were performed to find out the most responsive parameters using a Bayesian inference engine. The initial graph contains information about the relationship between the node and the weighted edges. It also contains information about the target variables that the DT needs to optimize.
3.2. Hybrid Graph
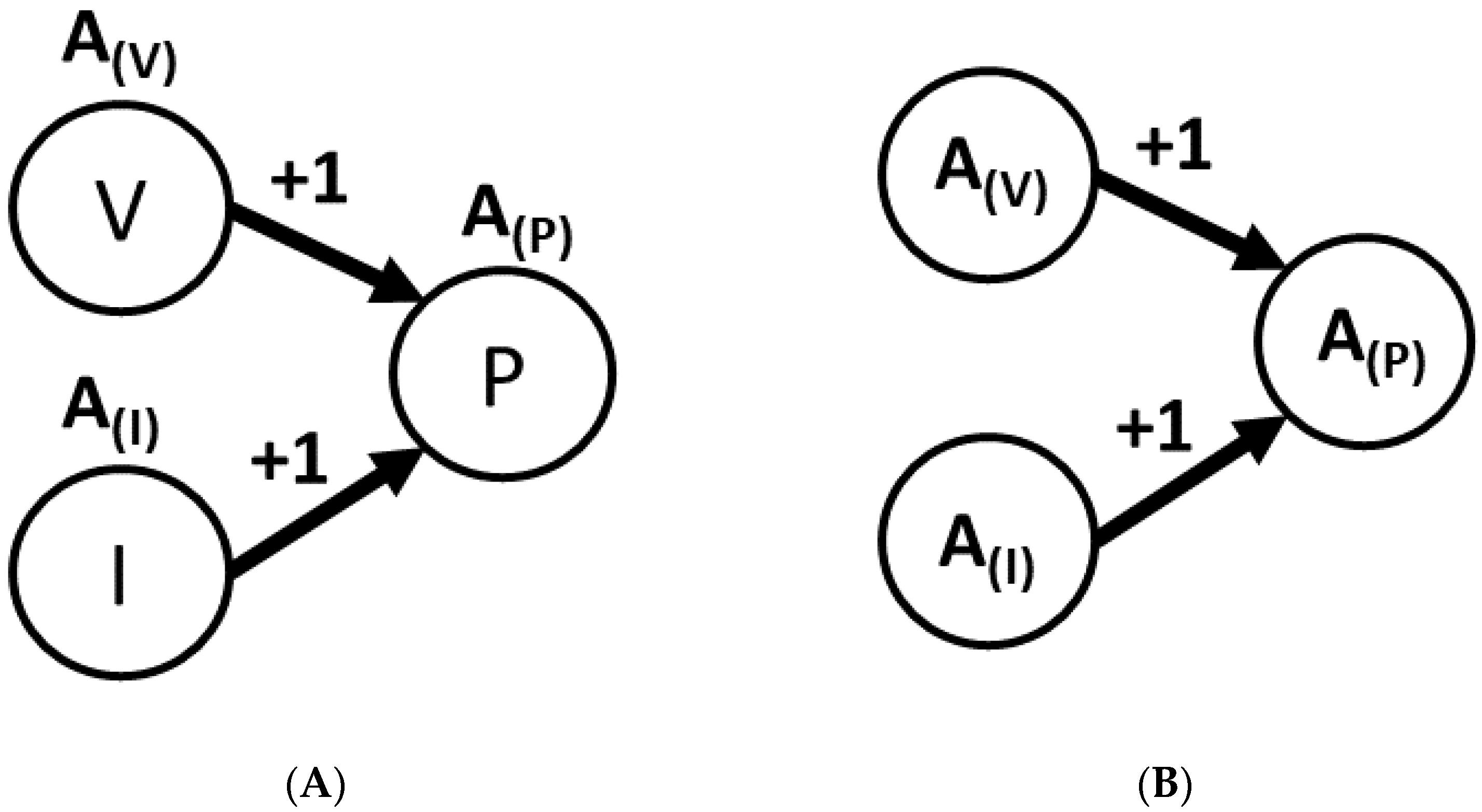
The GBMR process starts with building the initial graph. However, this initial graph is a physics-based representation. The DT is a hybrid representation. There is a need to inject process data into the initial graph generated in the previous step to build such a hybrid graph. Hence, process parameter data is collected with IoT platforms. When the parameter graph and data are available, an analogy modeling technique is followed to generate the relationship between the parameters. For example, the relationship between the power consumption (P), voltage (V) and current (I) of a machine could be established based on the popular relationship
with the initial graph, as shown in
Figure 5A. If the data obtained from the machine contains datasets such as active power (A(P)), active voltage (A(V)) and active current (A(I)), the datapoints could be appended to the initial graph and a hybrid graph could be established, as shown in 5b.
3.3. Heuristic Method for Hybrid Graph
The hybrid graph consists of several parameters. Though the relationship is defined by the underlying physics, it is not necessary that a relationship exists between the two entities. Hence, a heuristic approach is taken in this article. A greedy search algorithm, such as the GES, is applied to construct the final graph. As mentioned in the
Section 2.3.2, the GES progressively generates and removes edges in the graph with FES. It finally stops at the point where the BES hits the local maxima. This process is computationally extensive. For graphs with a high number of nodes, this process is performed in stages. The GES algorithm is suited for high-dimensional datasets. GES was applied in for causal model discovery in directed graphs such as the hybrid network in [
40]. The GES provides the final graph, which serves as an input to the model reduction method.
3.4. Graph Spectral Cluster
The evolution of the GBMR method continued when more fundamental questions were raised about the causal graph structure. The hybrid graph input to the GBMR method assumes that the causal graph structure is complete when the node-importance measuring algorithms are run on it. This is indicated by a * sign in
Figure 4 when importing the graph from the graph library. That means that the graph structure does not change at runtime (no nodes or edges are added or removed). Hence, it becomes possible to segment the bigger graph into structurally similar chunks. A spectral clustering-based graph-cut method for DAGs was used for this purpose [
41]. The spectral clustering method learns the graph structure and provides the hierarchical clusters based on the graph Laplacian [
42]. The spectral clustering algorithm classifies the parameters into cluster membership based on the adjacency matrix. The spectral clustering algorithm computes the normalized graph Laplacian such that:
where
is the un-normalized graph Laplacian and
is the degree matrix. The algorithm defines three parameters: the number of clusters in which the graph should be split, the affinity or adjacency matrix of the graph and the random state used to initialize the graph decomposition method. Because of this graph decomposition, the nodes that belong to similar clusters can be identified that might have similar behavior in the graph.
3.5. Importance Measurement
In GBMR, graph centrality methods such as WPR and EVC are used for the hybrid graph to identify the important nodes. If the smallest eigenvalue is 0, the node importance can be measured. When these nodes are identified according to the WPR score, they are compared with the spectral clustering algorithm result. When both the node centrality algorithms and spectral clustering rank the node as high, the node is declared as an important node. If the eigenvalues are not zero, the hierarchical node rankings could be applied. This check is made in the GBMR method soon after the hybrid graph is obtained. If the hybrid graph provides zero or negative eigenvalues, that means the graph is not complete. There are some edges that are connected in the wrong locations or some nodes that are not connected at all. In either case, the input graph is invalid. If there are nodes that cannot be connected in a legitimate graph with all other nodes and edges in place, a pseudo-node is generated to the nearest neighbor to make the graph valid.
The WPR algorithm uses three important parameters to reach the final score. The maximum iterations allow users to define how many iterations of the PageRank should be performed. In most cases, the WPR score stabilizes after 100 iterations. The damping factor is defined as 0.85, which indicates a gradual convergence towards the final score. Finally, the weights on the directed graph are added as per the power law defined by DACM. A threshold is selected by combining the domain-specific expert knowledge and piecewise linear regression of the centrality score. The development of a generic method of threshold measurement is currently being researched and should be treated as a future direction of this article. Hence, the variables can be moved into a high importance matrix [XH] and a low importance matrix [XL].
3.6. Consolidation of Importance
The GBMR method further evolved when the eigenvector centrality algorithms such as EVC and Katz were compared with the output obtained from the modified PageRank algorithm; the match of important parameters was less than 60%. It was discovered that the accuracy of the node importance depends on the ranking method selected. To address this issue, evidential reasoning techniques such as the Dempster–Shaffer theory were used for consolidating the node importance scores. The DST complements the GBMR method by providing a belief structure to decide when a node is considered of high importance. The mass functions are calculated and
was computed. Even though the node is differentially ranked by the node ranking algorithm, the DST helps to take a decision by fusing the available information of the nodes that are contradictory in their ranking. An aggregated node ranking is achieved with the application of the DST, which is used to select the parameters for DT the optimization problem [
38].
3.7. Validation
The GBMR method is validated by benchmarking it against a machine learning method known as the random forest regressor (RFR) with its associated Gini importance. RFR with Gini importance is a fast and accurate way of analyzing the feature importance in high dimensional data. The benchmarking process provides an estimate of the relevance of the important parameters. Gini provides a superior method of feature importance measurement than other methods such as PCA. The RFR and Gini optimizer provide a parameter ranking stored in XH(RFR). XH(RFR) is compared with XH to check the number of parameters declared important by both methods. It may not be a one hundred percent match. A threshold [t] is defined at this stage. If the match percentage is below [t], the mass functions and BPA from Equation (6) is reevaluated and the process is run again.
An alternative approach to the RFR method was to analyze the GBMR method by the formulation of an optimization problem. This is shown in
Figure 4 by the dotted boxes. The problem was formulated as a multi-objective optimization case. The objective function is setup with the target variables of the DAG and the parameters from X
H used to attain the target variables. An empirical approach was taken to determine a Pareto efficient solution. However, formulating such a multi-objective optimization problem is challenging in situations containing a high number of parameters. Multi-objective problem formulation cannot be meaningfully developed when the number of parameters is high.
At this stage, the major component of the GBMR method is explained. Now, the validity of this method is demonstrated with the help of a turbo compressor case study in the next section.
4. GBMR Case Study with a Turbo Compressor System
This case study demonstrates the GBMR method for building the DT of a turbo compressor system. The purpose of this case study is to showcase the following:
1. DT as a graphical representation of a system, built to provide specific outcomes;
2. Utilize the GBMR framework to demonstrate how this conceptual DT is useable in a real scenario providing a digital service;
3. Validation by benchmarking the GBMR method against machine-learning-based methods.
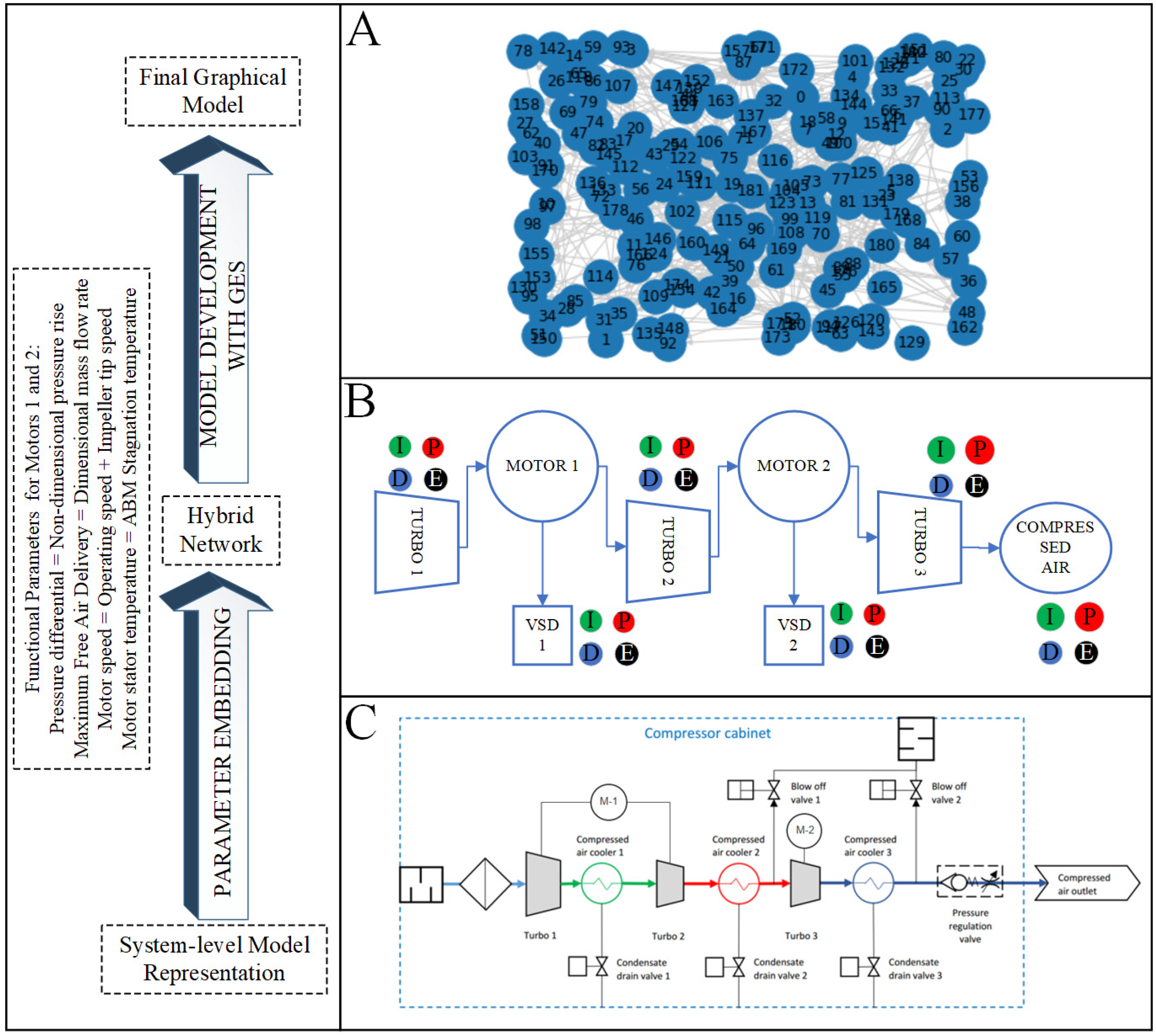
4.1. The Graph-Based Model of the Turbo Compressor System
The GBMR method is applied on the graph-based representation of the system. The initial graph is constructed with DACM, as described in
Figure 4. Conditional restrictions are applied on the hybrid graph by the turbo compressor system such as (1) the graph has to be completed. All nodes should have at least 1 edge connecting it to the whole graph, and (2) the target parameters are identified by propagation of strategic objectives in the causal graph. The causal graph is at least checked for loops and contradictions and they are removed. The parameters from the initial graph are appended to the system level model and the hybrid graph is established. The hybrid graph is treated as the input to a GES algorithm. GES algorithms use a sequence of forward and backward searches to create the final hybrid graph. The final graph is the knowledge model that consists of the details from both physics-based and data domains. The final graph is used as an input to the model reduction process. The need of a DT is to understand and mitigate the effects of dynamic instabilities in the turbo compressor system.
There are two types of dynamic instabilities known as stall and surge [
43]. Stalling is a complex flow instability originating from regions of flow stagnation that are created near the impeller blade confinements of the centrifugal compressor known as stall cells. Turbo compressors are at risk of developing stall cells that result in eventual impeller failure. Stalling can be progressive or abrupt in nature. A progressive stall is the more common and riskier form of stall. Stalling is a precursor to surge, which is the principal destabilizing phenomenon in turbo compressors. Due to stalling, the compressor cannot generate enough pressure at the outlet to match the pressure built up inside it. This forces the compressed air to flow back towards the inlet, resulting in a rapid asymmetrical oscillation known as surge oscillation. Hence, surge mitigation requires precise and accurate modeling and control methods. For that, the Greitzer compression system model is adopted as a foundation for building the graph-based VE [
44].
4.1.1. The Initial Graph Development
Surge is a gradual build-up phenomenon whose occurrence can be understood by monitoring the pressure rise in the compressor (
), the plenum pressure rise (
), mass flow rate of compressed air (
) and mass flow rate at the throttle (
). These variables and their interrelationship are defined by the Greitzer compression system model, which provides a lumped parameter model of the compression system. The mathematical equation needed to build the Greitzer compression system model is described in equations A.1 through A.9 in
Appendix A. This model provides the basic physics-based causal formulation of turbo compressor system.
The causal model is used to extract and represent the causal relationship between the variables in the Greitzer compression system model. The result graph obtained is shown in
Figure 6. This network is built to optimize the stability of the compression system. The stability is quantified with
,
and
from the Greitzer compression system model. This is indicated with red color variables. These are called performance variables in the conceptual modeling nomenclature. The variables in red color are the target variables defined by the system. The blue variables are the dependent variables that are dependent on the green variables known as independent variables. The black variables are exogenous variables that are not affected by external or internal change. The weights on the edge of the network are assigned as per the power law and utilized in the GBMR approach.
4.1.2. The Hybrid Graph Development
The initial graph captures the physics-based representation of the system; however, it is bound to the steady state of the system and its implication is theoretical. In earlier studies, efforts were made to define the practical usage of this causal graph entity using theories from artificial intelligence. In this article, the utility of the physics-based initial graph is set to guide the development of a graph-based representation of the system-level model. System-level models, such as those in the
Figure 7C, represent the dynamic state of the system that is related to the physical phenomena guiding it. In the VSD unit of turbo fans and motor systems shown in
Figure 5B, the variables from the dynamic system model could be organized and the causality between these variables can be extracted guided by the initial graph (i.e., the Greitzer compression system model). Therefore, embedding the parameters or the network from
Figure 4 into the relevant sections of
Figure 7C, a hybrid of the physics-based and the systems-level models is created. This combination of the physics-based and systems-level models is known as the hybrid graph. The resulting hybrid graph is the dynamic system-level model in DAG form.
The methodology described in
Section 3.2 is used to build the hybrid graph. The factors affecting the pressure differential parameters in the three turbo motors and compressor system in the systems-level model: pressure differential, maximum free air delivery, motor speed and motor stator temperature, could be associated with a non-dimensional pressure rise, dimensional mass flow rate, impeller tip speed and stagnation temperature, respectively, from the initial graph. Similarly, the surge limit could be connected to the set pressure and the motor rpm could be connected to the active power based on the physics of the system. The same methodology is repeated to create the causal model of the whole system. Additional parameters where this methodology cannot be applied such as state variables or ON/OFF signals are considered independent if they could be connected to a dependent variable. If the variable has no association with the physics of the system, the assumption is made to consider it as exogenous.
4.1.3. GES Algorithm
The hybrid graph serves as the input to the GES algorithm as described in
Section 2.3.2. The graph is transformed into an adjacency matrix embedding the relationship on the edges with
weight signifying the presence of a relationship. Here, n is the weight on the edges of the initial graph. FES and BES maxima are computed with Gaussian likelihood score with the python library known as sempler [
45]. The result of the GES algorithm is the hybrid graph that serves as an input to the GBMR method.
5. Results and Discussion
5.1. Node Importance
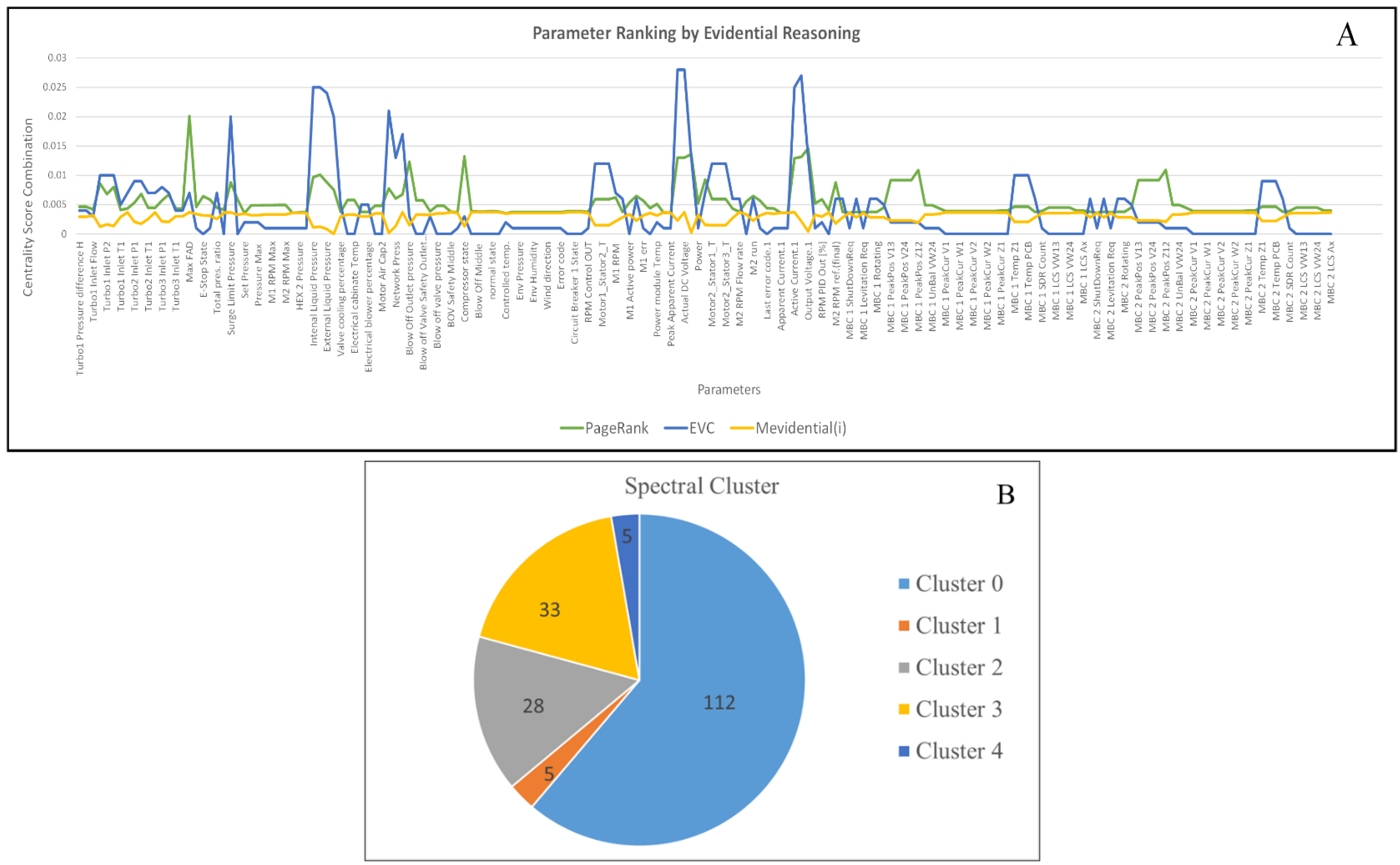
The hybrid network is a complete knowledge model in line with the VE representation of the DT, embedding the relationship obtained from the underlying physical phenomena, the system-level information model and the data collected from the turbo compressor system. The final network contains 183 nodes. This provides a good use case for demonstrating the GBMR method. The result of the ranking algorithms is presented in
Figure 8A, and a spectral decomposition of the hybrid graph is shown in
Figure 8B.
The spectral method and the node ranking methods are conducted parallelly. The spectral clustering algorithm is applied to obtain the structure preserving graph cuts. The spectral clustering algorithm is developed with python API that uses the clustering of normalized Laplacian. The eigenvector plot clearly indicates that there are five peaks with zero eigenvalues, indicating the presence of five ways that the graph could be partitioned. The cluster membership result of the parameters is indicated in
Figure 8B. Cluster0 contains 112 parameters; the second biggest cluster, cluster3, contains 33 parameters; the third biggest cluster, cluster2, contains 28 parameters. The two remaining small clusters contain five parameters each. If the clusters are reconstructed with the number of clusters as six, no change was observed in cluster0, cluster2 or cluster3. The smaller clusters start fragmenting as number of clusters increases. It is interesting to note that the small clusters contain nodes that are farther from the center of the graph, where the target variables are located. The target variables such as FAD, motor voltage and active power consumption all belong to the cluster0.
The WPR and EVC scores are shown in
Figure 8A. The WPR scores of nodes in cluster0 are consistent. The intersection of the high WPR scores with cluster0 are agreeable, except the environmental parameters that were added to the dataset externally. The highest WPR score was given to maximum FAD. This is consistent with the hybrid graph, as FAD was considered as a target variable. The WPR also nominated motor speed as important, which was associated with FAD in the hybrid graph. EVC agrees with the WPR in many cases; however, EVC differs in the ranking scheme given by WPR. State variables such as the motor state and turbo state differ considerably between EVC and WPR. Hence, the consolidated ranking results are obtained from the node importance algorithms with DST. This is indicated by the difference between the blue and green lines in
Figure 8A. DST was applied to this hierarchical ranking system to find a combined ranking. This is indicated by the yellow line and marked as the final evidential mass or
. DST is able to consider all the available pieces of evidence in deciding whether a node is important or not and can give a trusted final decision. After application of DST, the nodes were rearranged, and the nodes lying in the intersection of cluster0, cluster2 and cluster3 with
were considered as important nodes. These nodes were stored in a high importance parameter matrix [X
H] and the other variables were kept in a low importance parameter matrix [X
L]. The GBMR process is documented in [
46].
Because so many variables were declared as important (173 params), a cutoff was set to the
score. When a threshold of lower limit of 25% of the
score was selected, the number of important parameters obtained was 145. So, a 22.4% reduction in parameters was obtained. That is, with 22.4% fewer parameters, the hybrid graph will be able to compute the target variables. The values of the target variables were measured from the reduced model and computed and compared with the values from the literature presented in [
43]. These values are free air delivery and pressure differential for all turbo compressors ([Turbox_OUT_P]-Turbox_IN_P), where x is 1, …,3. The error in the free air delivery is (
) and is less than 4%. The error in pressure differential is e = (Turbox_OUT_P-Turbox_IN_P)-
and is less than 6%. The maximum value from the DST scores is 0.0037. Considering a lower threshold than 25% results in the selection of 178 parameters (or a 2.73% reduction). This makes the GBMR very inefficient. On the other hand, a higher threshold eliminates important parameters ranked highly by both EVC and WPR. This result is valid for the selected threshold, which is obtained by a numerical analysis. For a different threshold, the percentage reduction will vary. It should be mentioned here that an accurate method for obtaining the threshold is under consideration and should be realized as a future direction of this research. These parameters are used to construct a benchmarking procedure for the turbo compressor case study.
5.2. Validation of GBMR Method through Benchmarking
A validation by benchmarking approach was designed for the GBMR method when applied to the VE representation of the DT. The benchmarking method compares the GBMR method with machine-learning-based approaches applied to the hybrid model of turbo compressors. The validity of the method can be proven in case more complex models are used. This is because GBMR uses graph-based methods and algorithms to build and reduce the complex model. A complex model will generate a complex graph. The spectral decomposition and node importance algorithms used in GBMR can be applied to any type of complex graph. Classical methods such as the RFR [
47] or a mixture of the RFR and a deep learning method such as CRNN [
48] are used to find the statistically significant parameters that contribute most to explaining the target outcomes when a large number of feature sets are present in the data. Such approaches become necessary because, unlike other domains, large training datasets are not readily available for identifying important variables for compressor surge prediction.
The RFR is a type of ensemble method machine learning algorithm. It consists of several decision trees, each constructed based on a randomly selected subset of the training data set. CART, a popular training algorithm, is used for this. The training indicated that the individual trees learn some features in the training data and the ensemble of all trees learn the features present in the turbo compressor dataset. The estimation happens by voting or sampling some statistical value for the estimations of the individual trees [
49]. A by-product of the training of the RFR is combined feature importance. Feature importance is a method of ranking features based on how much each feature reduces the impurity of the estimation through the nodes of the decision trees. The importance of each feature is calculated by normalizing the total reduction in impurity that the feature causes. The feature importance identification can be performed by two methods: Gini importance [
50] and permutation importance [
51]. It was experimentally observed that the importance distribution in Gini could be skewed by ranking some features much higher than others. Hence, the permutation importance was used to estimate the importance of the features. The permutation importance is calculated by using a trained estimator and dataset, such as the RFR. The algorithm first uses the estimator to calculate a baseline output using some metric on the dataset, then permutes a feature of the dataset and re-calculates the output metric. This is repeated with the other features. The difference of these metrics then indicates the importance of each feature in the dataset with respect to the estimator output.
The dataset used to build GBMR is used for validation with the RFR method. The dataset consists of all parameters from the turbo compressor system shown in
Figure 7C. The data is split into three zones for three turbo compressor fans. It contains physical parameters such as the inlet and outlet pressure, inlet and outlet temperature of rotor and stator, pressure ratios, maximum free air delivery (MAX. FAD), RPM of fans, active power consumption of motors, peak currents, voltages and positions of the motors, internal liquid flow temperature and levels and cooling valve temperatures. It also contains state parameters such as rotor stop state, fluid rise state, speed control state, error states and compressor states. Finally, it consists of operational data such as surge limit and environmental data such as atmospheric temperature, pressure, humidity, and dew points.
Experiment Design for Validation
The RFR method is chosen in this study to benchmark the results obtained from the GBMR method. The RFR algorithm was built with a python-based machine learning library scikit-learn. An experiment was designed to achieved that. These data were obtained from an industrial turbo compressor system. The RFR was trained with 517,902 samples using the dataset described above with 183 variables as inputs. The target of the training was the power variable calculated as a sum of power variables from the two-motor assembly in the VSD compressor line. A hold-out test data set of 129,475 was left out of the training data. The hyperparameters of the regressor training were as follows:
Number of trees = 200;
Maximum depth of a tree = 10;
The minimum samples required for a split = 2;
The accuracy of the trained model on the training data = 0.9998;
Holdout test dataset accuracy = 0.9997.
The top 20 important variables from permutation importance and GBMR are listed in
Table 1. The parameters are presented in order from high to low.
Figure 9 presents the top 20 parameters obtained from the two methods. The common parameters selected by the two methods are more important than the order of the parameters. The parameters with higher importance score are the most important parameters obtained from both of the methods. In the benchmarking process, the parameter set obtained from the permutation importance serves as a control.
5.3. Discussion
A sample of the top twenty parameters is taken to demonstrate the accuracy of the GBMR method compared with the RFR method. Both methods capture the significant parameters from the three motors and main compression parameters. Both methods return active current and active power as important parameters. This is in line with the hybrid graph, where the current and voltage were considered as inputs to several parameters including the turbo motor pressure and temperature. Both methods indicate the motor RPM as an important parameter; however, the RFR indicates it is the most significant variable by a large margin, with a mix of power and current variables also indicated. This is because of the permutation importance; the peak is distinctly noticeable in
Figure 9. The significance of Motor2 RPM is likely because it explains the operational condition of the motor that runs the last compressor stage and therefore works with the highest pressures. This is clearly linked to the highest energy consumption rate, making the apparent current, active current, output voltage and active power crucial parameters in surge control. The compressor state is correlated with the maximum free air delivery, which in turn is related to the active power of the system. The air pressure value at the intake and compressor-control-related variables are also seen as important parameters. A calculated parameter, surge limit, is marked as an important parameter by both RFR and MR. The surge limit is computed from the pressure rise in the compressor and the maximum free air delivery. This is because of using node importance methods to rank order the parameters. The parameter pointing to important parameters is also considered important.
In the sample of the top 20 parameters, 15 parameters match from both methods. This amounts to a 75% match between the two methods. The RFR is a data-driven method and does not contain any knowledge of the physics of the parameters involved. The GBMR, on the other hand, works on the hybrid representation. The 75% match indicates that both methods attempt to identify the common important features in the parameters. The percentage match between the parameters obtained from the two methods increases up to 78% when top 100 parameters are considered. The motor currents and voltages are identified as important parameters in the [X
H] set, as they point to the high importance parameter active power. The parameters in [X
L] are ignored for benchmarking purposes. When the values of [X
L] are considered, the benchmark percentage will vary. GBMR still provides a fast method to quickly capture the influential system parameters. The model for the RFR is retrained, but the basic result of M2 RPM importance remains the same with the existing data from the turbo compressor. The GBMR results seem similar because of the application of evidence theory. Evidence theory tends to remove any disagreement between different ranking score and provides the relative importance for the parameter. This is indicated by the yellow curve in
Figure 8A.
To understand the simplification of the computational complexity obtained by GBMR, it is possible to compare the training time of the RFR method with the total execution time of the GBMR method. The training time of the RFR method is 81.3471 min. The total execution time of the GBMR method, which is a summation of graph structure learning, spectral decomposition and importance measurement, is 72.2318 min. Hence, GBMR is 9.1153 min faster in identifying the reduced model.
6. Conclusions
This work presents the research activities on the VE optimization of the DT with the help of a model fusion technology. The VE is a computationally complex entity, comprising of models from different domains, that tries to faithfully replicate the state of the PE. The VE combines advanced simulation models such as system-level models with data-driven prediction models to predict the state of the PE. This article describes the GBMR method for optimizing the performance of the VE with a two-step approach: (1) providing a graph-based conceptual model representation of the VE, and (2) reducing the VE graph model by identifying the important parameters in it. The GBMR embeds all the parameters and their relationships in a graph model and facilitates application of graph algorithms for measuring node importance. Therefore, GBMR facilitates modeling of physical systems in the form of graphs and the reduction of such models based on graph algorithms. The GBMR makes the VE more efficient, as the reduced model uses a subset of parameters to predict the target parameters in the PE.
The GBMR method is tested with the help of a turbo compressor case study. The GBMR method is benchmarked against a machine-learning-based approach known as the random forest regressor, which also estimates the important parameters in a given dataset with the help of permutation importance. Both the GBMR and RFR methods were applied on the turbo compressor dataset, and it was found that both methods find 75% common parameters in no fixed order. These important parameters bear maximum contribution towards the performance of the VE.
Methods such as GBMR become important in the context of DTs because they help to simplify the VE development but still capture both the physics-based and data-driven aspects of the twin. With the help of the GBMR, the DT becomes more context aware by knowing the important parameter that it needs to monitor and optimize to obtain the fastest result. The GBMR method aids in the fast computation of the target parameters that the DT is trying to replicate by capturing the intricacies of a multi-domain system. It will also become imperative to integrate methods such GBMR with the DT frameworks and perform computational tests on entire complex DT systems such as the turbo compressor system described in this article. It is possible to convince PE owners about what is essential in their system with GBMR and how resource allocation and optimization can be performed effectively with DTs. The GBMR method is a python-based software package that can be used as a virtual sensor or a prototyping tool where quick estimation regarding the system and the effort needed to build a VE representation can be analyzed effectively.
Author Contributions
Conceptualization, A.C. and H.V.; methodology, A.C.; software, A.C.; validation, A.C., H.V. and K.T.K.; formal analysis, A.C.; investigation, A.C.; resources, J.L.; writing—review and editing, A.C., H.V. and K.K; visualization, A.C.; supervision, K.T.K.; project administration, K.T.K.; funding acquisition, K.T.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Business Finland under the project named SNOBI, and the project number 545/31/2020.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to acknowledge the SNOBI project funded by Business Finland for making this research possible. The authors would also like to acknowledge the contribution of Tamturbo Oy for their support towards this research work.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in the manuscript:
| AMB | Active Magnetic Bearing |
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| CERN | European Organization for Nuclear Research |
| CRNN | Convolutional Recurrent Neural Network |
| DAG | Directed Acyclical Graph |
| DST | Dempster–Shafer Theory |
| DT | Digital Twin |
| EVC | Eigenvector Centrality |
| DACM | Dimension Analysis Conceptual Modeling |
| FEM | Finite Element Model |
| FMI | Functional Mockup Interface |
| FMU | Functional Mockup Unit |
| GES | Greedy Equivalent Search |
| GBMR | Graph-based Model Reduction |
| IP | Internet Protocol |
| IPv6 | Internet Protocol version 6 |
| IoT | Internet of Things |
| ML | Machine Learning |
| M2M | Machine-to-Machine |
| M2S | Machine-to-System |
| PCA | Principal Component Analysis |
| PE | Physical Entity |
| RFR | Random Forest Regressor |
| S&M | Simulation and Modeling |
| VE | Virtual Entity |
| VSD | Variable Speed Drive |
| WPR | Weighted PageRank |
Appendix A
List of equations for surge modeling
Appendix A.1. Greitzer Compression System Model
Appendix A.2. Helmholtz Frequency ()
Appendix A.3. Original Greitzer Compression System Model with Non-Dimensional Variables
Appendix A.4. Greitzer Stability Parameter (B) Governs the Intensity of Surge Instability in the Greitzer Model
Appendix A.5. For Subsonic Flows
Appendix A.6. Curve Fitting to Determine the Steady-State Pressure and Flow Rate Measurements
H, W: constant computed from pressure rise and flow rate corresponding to surge point (predicted params from curve fitting in the stable region and used to correct ).
Appendix A.7. Variation of Impeller Tip Clearance with AMB. Isentropic Efficiency of Compressor
Appendix A.8. (Non-Dimensional Compressor Pressure Rise) as a Function of and
Appendix A.9. Level I Stability Analysis (Initial Screening to Identify Safe Compressor Operations)
References
- Grieves, M.; Vickers, J. Digital Twin: Mitigating Unpredictable, Undesirable Emergent Behavior in Complex Systems. In Transdisciplinary Perspectives on Complex Systems: New Findings and Approaches; Kahlen, F.-J., Flumerfelt, S., Alves, A., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 85–113. [Google Scholar] [CrossRef]
- Kannan, K.; Arunachalam, N. A Digital Twin for Grinding Wheel: An Information Sharing Platform for Sustainable Grinding Process. J. Manuf. Sci. Eng. 2019, 141, 021015. [Google Scholar] [CrossRef]
- Khan, L.U.; Saad, W.; Niyato, D.; Han, Z.; Hong, C.S. Digital-Twin-Enabled 6G: Vision, Architectural Trends, and Future Directions. IEEE Commun. Mag. 2022, 60, 74–80. [Google Scholar] [CrossRef]
- Gürdür Broo, D.; Bravo-Haro, M.; Schooling, J. Design and implementation of a smart infrastructure digital twin. Autom. Constr. 2022, 136, 104171. [Google Scholar] [CrossRef]
- Jiang, Z.; Lv, H.; Li, Y.; Guo, Y. A novel application architecture of digital twin in smart grid. J. Ambient Intell. Hum. Comput. 2022, 13, 3819–3835. [Google Scholar] [CrossRef]
- Tao, F.; Cheng, J.; Qi, Q.; Zhang, M.; Zhang, H.; Sui, F. Digital twin-driven product design, manufacturing and service with big data. Int. J. Adv. Manuf. Technol. 2018, 94, 3563–3576. [Google Scholar] [CrossRef]
- Yang, X.; Ran, Y.; Zhang, G.; Wang, H.; Mu, Z.; Zhi, S. A digital twin-driven hybrid approach for the prediction of performance degradation in transmission unit of CNC machine tool. Robot. Comput.-Integr. Manuf. 2022, 73, 102230. [Google Scholar] [CrossRef]
- Chakraborti, A.; Nagarajan, H.P.N.; Panicker, S.; Mokhtarian, H.; Coatanéa, E.; Koskinen, K.T. A Dimension Reduction Method for Efficient Optimization of Manufacturing Performance. Procedia Manuf. 2019, 38, 556–563. [Google Scholar] [CrossRef]
- Chakraborti, A.; Heininen, A.; Koskinen, K.T.; Lämsä, V. Digital Twin: Multi-dimensional Model Reduction Method for Performance Optimization of the Virtual Entity. Procedia CIRP 2020, 93, 240–245. [Google Scholar] [CrossRef]
- Qi, Q.; Tao, F.; Hu, T.; Anwer, N.; Liu, A.; Wei, Y.; Wang, L.; Nee, A.Y.C. Enabling technologies and tools for digital twin. J. Manuf. Syst. 2021, 58, 3–21. [Google Scholar] [CrossRef]
- Liu, Z.; Meyendorf, N.; Mrad, N. The role of data fusion in predictive maintenance using digital twin. AIP Conf. Proc. 2018, 1949, 020023. [Google Scholar] [CrossRef]
- Darvishi, H.; Ciuonzo, D.; Eide, E.R.; Rossi, P.S. Sensor-Fault Detection, Isolation and Accommodation for Digital Twins via Modular Data-Driven Architecture. IEEE Sens. J. 2021, 21, 4827–4838. [Google Scholar] [CrossRef]
- Selvaraj, P.; Radhakrishnan, P.; Adithan, M. An integrated approach to design for manufacturing and assembly based on reduction of product development time and cost. Int. J. Adv. Manuf. Technol. 2009, 42, 13–29. [Google Scholar] [CrossRef]
- Verbert, K.; Babuška, R.; De Schutter, B. Bayesian and Dempster–Shafer reasoning for knowledge-based fault diagnosis–A comparative study. Eng. Appl. Artif. Intell. 2017, 60, 136–150. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, M.; Nee, A.Y.C. Chapter 6—Cyber–Physical Fusion in Digital Twin Shop-Floor. In Digital Twin Driven Smart Manufacturing; Tao, F., Zhang, M., Nee, A.Y.C., Eds.; Academic Press: Cambridge, MA, USA, 2019; pp. 125–139. [Google Scholar] [CrossRef]
- Kapteyn, M.G.; Knezevic, D.J.; Huynh, D.B.P.; Tran, M.; Willcox, K.E. Data-driven physics-based digital twins via a library of component-based reduced-order models. Int. J. Numer. Methods Eng. 2022, 123, 2986–3003. [Google Scholar] [CrossRef]
- Fresca, S.; Manzoni, A. POD-DL-ROM: Enhancing deep learning-based reduced order models for nonlinear parametrized PDEs by proper orthogonal decomposition. Comput. Methods Appl. Mech. Eng. 2022, 388, 114181. [Google Scholar] [CrossRef]
- Wang, M.; Li, H.-X.; Chen, X.; Chen, Y. Deep Learning-Based Model Reduction for Distributed Parameter Systems. IEEE Trans. Syst. Man Cybern.: Syst. 2016, 46, 1664–1674. [Google Scholar] [CrossRef]
- Morimoto, M.; Fukami, K.; Zhang, K.; Nair, A.G.; Fukagata, K. Convolutional neural networks for fluid flow analysis: Toward effective metamodeling and low dimensionalization. Theor. Comput. Fluid Dyn. 2021, 35, 633–658. [Google Scholar] [CrossRef]
- Cui, C.; Hu, M.; Weir, J.D.; Wu, T. A recommendation system for meta-modeling: A meta-learning based approach. Expert Syst. Appl. 2016, 46, 33–44. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, H.; Liu, A.; Nee, A.Y.C. Digital Twin in Industry: State-of-the-Art. IEEE Trans. Ind. Inform. 2019, 15, 2405–2415. [Google Scholar] [CrossRef]
- Tao, F.; Xiao, B.; Qi, Q.; Cheng, J.; Ji, P. Digital twin modeling. J. Manuf. Syst. 2022, 64, 372–389. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, M.; Liu, Y.; Nee, A.Y.C. Digital twin driven prognostics and health management for complex equipment. CIRP Ann. 2018, 67, 169–172. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, M. Digital Twin Shop-Floor: A New Shop-Floor Paradigm Towards Smart Manufacturing. IEEE Access 2017, 5, 20418–20427. [Google Scholar] [CrossRef]
- Coatanea, E.; Roca, R.; Mokhtarian, H.; Mokammel, F.; Ikkala, K. A Conceptual Modeling and Simulation Framework for System Design. Comput. Sci. Eng. 2016, 18, 42–52. [Google Scholar] [CrossRef]
- Mokhtarian, H.; Coatanéa, E.; Paris, H.; Mbow, M.M.; Pourroy, F.; Marin, P.R.; Vihinen, J.; Ellman, A. A Conceptual Design and Modeling Framework for Integrated Additive Manufacturing. J. Mech. Des. 2018, 140, 081101. [Google Scholar] [CrossRef]
- Wu, D.; Coatanéa, E.; Wang, G. Employing knowledge on causal relationship to assist multidisciplinary design optimization. J. Mech. Des. 2019, 141, 041402. [Google Scholar] [CrossRef]
- Chickering, D.M. Optimal Structure Identification With Greedy Search. J. Mach. Learn. Res. 2002, 3, 507–554. [Google Scholar]
- Hauser, A. Characterization and Greedy Learning of Interventional Markov Equivalence Classes of Directed Acyclic Graphs. J. Mach. Learn. Res. 2012, 13, 2409–2464. [Google Scholar]
- Zhang, W.Y.; Zhang, S.; Guo, S.S. A PageRank-based reputation model for personalised manufacturing service recommendation. Enterp. Inf. Syst. 2017, 11, 672–693. [Google Scholar] [CrossRef]
- Chen, D.; Lü, L.; Shang, M.-S.; Zhang, Y.-C.; Zhou, T. Identifying influential nodes in complex networks. Phys. A: Stat. Mech. Its Appl. 2012, 391, 1777–1787. [Google Scholar] [CrossRef]
- Hu, P.; Fan, W.; Mei, S. Identifying node importance in complex networks. Phys. A: Stat. Mech. Its Appl. 2015, 429, 169–176. [Google Scholar] [CrossRef]
- Henni, K.; Mezghani, N.; Gouin-Vallerand, C. Unsupervised graph-based feature selection via subspace and pagerank centrality. Expert Syst. Appl. 2018, 114, 46–53. [Google Scholar] [CrossRef]
- Shang, Q.; Deng, Y.; Cheong, K.H. Identifying influential nodes in complex networks: Effective distance gravity model. Inf. Sci. 2021, 577, 162–179. [Google Scholar] [CrossRef]
- Bonacich, P.; Lloyd, P. Eigenvector-like measures of centrality for asymmetric relations. Soc. Netw. 2001, 23, 191–201. [Google Scholar] [CrossRef]
- Mo, H.; Deng, Y. Identifying node importance based on evidence theory in complex networks. Phys. A: Stat. Mech. Its Appl. 2019, 529, 121538. [Google Scholar] [CrossRef]
- Ghosh, N.; Paul, R.; Maity, S.; Maity, K.; Saha, S. Fault Matters: Sensor data fusion for detection of faults using Dempster–Shafer theory of evidence in IoT-based applications. Expert Syst. Appl. 2020, 162, 113887. [Google Scholar] [CrossRef]
- Chakraborti, A.; Heininen, A.; Väänänen, S.; Koskinen, K.T.; Vainio, H. Evidential Reasoning based Digital Twins for Performance Optimization of Complex Systems. Procedia CIRP 2021, 104, 618–623. [Google Scholar] [CrossRef]
- Scanagatta, M.; Salmerón, A.; Stella, F. A survey on Bayesian network structure learning from data. Prog. Artif. Intell. 2019, 8, 425–439. [Google Scholar] [CrossRef]
- Ramsey, J.; Glymour, M.; Sanchez-Romero, R.; Glymour, C. A million variables and more: The Fast Greedy Equivalence Search algorithm for learning high-dimensional graphical causal models, with an application to functional magnetic resonance images. Int. J. Data Sci. Anal. 2017, 3, 121–129. [Google Scholar] [CrossRef]
- von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Kang, Z.; Shi, G.; Huang, S.; Chen, W.; Pu, X.; Zhou, J.T.; Xu, Z. Multi-graph fusion for multi-view spectral clustering. Knowl.-Based Syst. 2020, 189, 105102. [Google Scholar] [CrossRef]
- Yoon, S.Y.; Lin, Z.; Allaire, P.E. Control of Surge in Centrifugal Compressors by Active Magnetic Bearings; Springer: London, UK, 2013. [Google Scholar] [CrossRef]
- Giarré, L.; Bauso, D.; Falugi, P.; Bamieh, B. LPV model identification for gain scheduling control: An application to rotating stall and surge control problem. Control Eng. Pract. 2006, 14, 351–361. [Google Scholar] [CrossRef]
- Sempler Library. Available online: https://sempler.readthedocs.io/en/latest/ (accessed on 5 September 2022).
- GBMR. 2022. Available online: https://github.com/anandashankar/gbmr (accessed on 15 April 2023).
- Grömping, U. Variable Importance Assessment in Regression: Linear Regression versus Random Forest. Am. Stat. 2009, 63, 308–319. [Google Scholar] [CrossRef]
- Choi, K.; Fazekas, G.; Sandler, M.; Cho, K. Convolutional recurrent neural networks for music classification. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Menze, B.H.; Kelm, B.M.; Masuch, R.; Himmelreich, U.; Bachert, P.; Petrich, W.; Hamprecht, F.A. A comparison of random forest and its Gini importance with standard chemometric methods for the feature selection and classification of spectral data. BMC Bioinform. 2009, 10, 213. [Google Scholar] [CrossRef] [PubMed]
- Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation importance: A corrected feature importance measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).