Reactive Power Optimization Based on the Application of an Improved Particle Swarm Optimization Algorithm

Abstract

Climate change, improved energy efficiency, and access to contemporary energy services are among the key topics investigated globally. The effect of these transitions has been amplified by increased digitization and digitalization, as well as the establishment of reliable information and communication infrastructures, resulting in the creation of smart grids (SGs). A crucial aspect in optimizing energy production and distribution is reactive power optimization, which involves the utilization of algorithms such as particle swarm optimization (PSO). However, PSO algorithms can suffer from premature convergence and being trapped in local optima. Therefore, in this research the design and development of an improved PSO algorithm for minimization of power loss in the context of SGs is the key contribution. For digital experimentation and benchmarking of the proposed framework, the IEEE 30-bus standardized model is utilized, which has indicated that an improvement of approximately 11% compared to conventional PSO algorithms can be achieved.

1. Introduction

1.1. Problem Statement

Key elements for addressing climate change, enhancing energy efficiency, and gaining access to contemporary energy services are included among others in the United Nations 2030 Agenda for Sustainable Development [1]. More specifically, Sustainable Development Goal (SDG) 9 refers to resilient infrastructure, inclusive and sustainable industrialization, and innovation. In the same context, SDG 7 aims to ensure public access to affordable, reliable, sustainable, and modern energy [2]. Governments have assured unprecedented commitment to upgrade energy grids, which calls for significant financial investments and creative upgrades from energy utilities [3]. Energy utilities are required to manage the technological characteristics of the power grid, which are becoming increasingly complex in the current volatile business environment [4]. Over the past few decades, the production and distribution of electricity have undergone significant change, shifting from traditional centralized production to a distributed, small-scale producer-consumer (prosumer) model that is connected to the distribution network [5]. This evolution has been facilitated by the establishment of suitable infrastructure for information exchange and communications. However, despite the innovations followed by the concept of the smart grid (SG), certain challenges have arisen providing fertile ground for further research [6,7]. The SG can be defined and realized as an electrical energy distribution grid which supports bidirectional energy and information flow supported by advanced information/communication, sensing, measurement, and integrated control functionalities [8]. The added value of these characteristics is that they render the SG more flexible, reliable, resilient, stable, and sustainable [9]. The SG business model was motivated by the need to: (a) improve reliability, (b) improve the efficiency of electricity production and distribution, (c) provide energy-as-a-service to prosumers, and (d) reduce the environmental impact of the electrical power industry [10]. Grid-edge distributed energy resources (DERs), which encapsulate distributed generation, are becoming more popular due to the increasing demand for zero-carbon generation in the electricity sector. The rising adoption of these smaller-scale resources is causing significant changes to the conventional methods of electricity dispatch, device control, and market compensation mechanisms in the industry. Thus, it becomes apparent that updated and extended electricity market structures are required. Such new electricity market models need to support flexibility in terms of energy production and consumption, as well as to provide a sustainable framework for their integration. It is of utmost importance to maintain high-quality power, and grid stability [11].

1.2. Research Contribution

Therefore, in this research the prerequisites for the SG market structure focusing on the control of reactive power are investigated. Furthermore, the key contribution of the presented research, and taking into consideration the research trends and literature gaps identified so far, is focused on the development and digital experimentation of an improved particle swarm optimization (PSO) algorithm for minimization of power loss in the context of the SG. Specifically, reactive power should be further investigated since SGs are characterized by the need for reactive power management to maintain power quality and stability. The proposed improved PSO algorithm aims to optimize the reactive power control in SGs by minimizing power losses and maintaining grid stability. The algorithm’s performance is evaluated using a case study of a practical distribution system, demonstrating its effectiveness in reducing power losses and improving power quality in SGs. The proposed approach addresses an ongoing challenge regarding reactive power optimization in SGs, offering a valuable contribution to the development of efficient and sustainable power systems.

1.3. Manuscript Organization

The remainder of the manuscript is structured as follows. In Section 2, the most pertinent literature is investigated regarding the topics of metaheuristic algorithms and SGs. Then, in Section 3, the modelling of the SG, is presented and discussed. In Section 4, the development strategy for the particle swarm optimization algorithm is discussed. In Section 5, the experimental setup based on IEEE 30-bus standardized model is presented. Then, in Section 6, the software tool implementation is presented. The manuscript is then concluded in Section 7, and future research directions are discussed taking into consideration the limitations and implications of the current work.

2. Literature Review

2.1. Common Optimization Objectives in Smart Grids

In terms of the literature, the above-mentioned challenges are examined through the scope of optimization techniques. The main requirement is that such techniques must support the handling of a larger set of diverse design variables (DVs), as well as taking into consideration a plethora of measurements related to the operation of the SG. Additionally, the optimization methods must offer accurate solutions while maintaining low computational complexity, especially when dealing with multiple optimization objectives. The most common optimization objectives in SG problems are listed as follows [12]:

(a)

Generation cost (GC);

(b)

Real power losses (RPL);

(c)

Transient stability (TST);

(d)

Voltage profile improvement (VPI);

(e)

Emissions (EM);

(f)

Grid resiliency (GR).

Swarm intelligence (SI) methods resemble decentralized, self-organized groups of biological organisms. Therefore, in order to address the challenges discussed in the previous paragraphs, a plethora of metaheuristic algorithms along with emerging variations are employed in the literature. For instance, Luo et al. in 2013 [13] and Moon et al. in 2013 [14] implemented ant colony optimization (ACO) and hybrid genetic algorithms in order to minimize flow and job shop makespan and reduce electricity costs. Due to the complexity of engineering problems, heuristic and metaheuristic algorithms may not always yield global optima. As a result, further elaboration is required with the implementation of additional algorithms, such as mixed integer programming (MIP), which was used by the authors in [15,16] in order to determine the optimal manufacturing schedule that minimizes electricity costs in a flow shop, considering predetermined pricing conditions. Among the most studied and implemented SI algorithms in the literature is particle swarm optimization (PSO). For example, Nappu et al. [17] proposed a method based on PSO in order to monitor and manage energy transmission in congested electrical grids, taking into account energy pricing schemes along with other energy transmission constraints. Similarly, Morandi et al. [18] implemented PSO in order to tackle the issue of optimal power flow problem.

2.2. Optimization Algorithms for Smart Grid Optimization

As discussed previously, metaheuristics encompasses a broad range of optimization techniques that draw inspiration from mechanisms of nature and animal behavioral patterns. While a few of these methods emerged in the mid-20th century, it is in recent decades, fueled by the advancements in artificial intelligence (AI) and the exponential growth of computational power, that they have gained significant prominence [19]. Among other applications, SGs have also provided fertile ground for research in this area. Consequently, in this section an overview of the most commonly implemented metaheuristic search algorithms is presented. Furthermore, as part of this section the strengths and weaknesses are also discussed.

One of the first attempts to implement PSO algorithm in optimal power flow (OPF) is described by Abido [20]. This is interesting research, since the authors have proved that algorithm indicates low sensitivity in variations of the particle multitude. Suboptimal calibration of hyperparameters of PSO methods is a key issue. Therefore, Sehiemy et al. [21] employed a hybrid method in order to ensure high robustness of the proposed PSO method. Similarly, Zhao et al. in [22] developed an improved PSO algorithm, which incorporates a multi-stage penalty function. Among the research reported, there are several instances that focus on the acceleration/improvement of the convergence rate. For example, Vlachogiannis et al. in [23] tested three PSO algorithms in order to validate that the concept of coordinate aggregation can facilitate the improvement of the algorithm’s convergence rate. In the same concept, Allaoua and Laoufi [24] have managed to reduce computational time by classifying model constraints into two categories, (i) active, and (ii) passive. An alternative hybridization model has been proposed by the authors in [25], where poorly performing parameters of the ACO algorithm are eliminated with the utilization of a genetic algorithm and the best performing parameters are accordingly re-evaluated. Mo et al. in [26,27] investigated the benefits of implementing PSO along with transient stability constraints. This approach is based on the formation of differential and algebraic equations for the description of the constraints. Furthermore, an inertia-based weighting method is implemented in order to enable the dynamic transition of the algorithm between exploration and exploitation. The same approach was also used by Luo et al. in [28] for a stability-oriented PSO. The basic innovation of this research is the update of the weights according to a user-defined stability condition.

Chaotic behavior has been incorporated in a number of research projects related to optimal power flow, such as in [29], in which the authors developed a whale optimization algorithm and the algorithm’s weights were updated using chaotic maps. In the context of reactive power minimization, Yang and Liao [30] developed an adaptive PSO algorithm which is based on the use of dynamically changed weight factors. The authors in [31] proposed a hybrid method based on the combination of modified dragonfly algorithm (MDA) and bat search algorithm (BSA) for improving power flow in smart grids by inducing reactive power injections in the system. To handle time-varying loads and wind power uncertainties, uncertainty-oriented methods were developed for the bacteria foraging algorithm (BFA) [32]. Furthermore, the dragonfly algorithm (DFA) is employed for multi-objective OPF in RES (renewable energy sources)-heavy grids [31]. In [17], a PSO-based method is applied to congested transmission grids, taking into consideration energy pricing schemes while respecting transmission system constraints. Finally, [18] utilizes a PSO-based algorithm to solve the optimal power flow problem while incorporating a more realistic modeling of slack bus characteristics in microgrids.

In the context of swarm algorithms, Tripathy and Mishra [33] developed a bacteria foraging algorithm, focusing on improving the stability of the network and minimizing power loss by adjusting reactive power. Similarly, Medani et al. in [34] proposed the utilization of a whale optimization algorithm (WOA) for the minimization of reactive power dispatch.

As has already been discussed and taking into consideration the form of modern electrical power grids, there is a plethora of variables and aspects that can and should be modelled. In

Table 1. Most common optimization algorithms for Smart Grids.

Algorithm Name	Advantages	Disadvantages
Artificial Bee Colony	Easy to implement, good at exploring a wide search space	Slow convergence rate, may converge to suboptimal solutions
Bat Algorithm	Good for continuous optimization problems, adaptable to different functions	Inefficient for discrete optimization problems, requires detailed calibration of parameters
Cuckoo Search	Simple implementation, good for large-scale optimization	Slow rate of convergence, may converge to suboptimal solutions
Differential Evolution	Fast convergence, good for high-dimensional optimization	Can get stuck in local optima, may require fine-tuning of parameters
Firefly Algorithm	Good for multimodal optimization, scalable to large problems	Slow rate of convergence, requires detailed calibration of parameters
Genetic Algorithm	Versatile, good for a wide range of problems, can handle noisy data	Slow rate of convergence rate, may converge to suboptimal solutions
Particle Swarm Optimization (PSO)	Fast convergence, easy to implement, good for multimodal optimization	May converge to suboptimal solutions, requires detailed calibration of parameters
Simulated Annealing	Good for complex optimization problems, can handle noise in the objective function	Slow rate of convergence, requires detailed calibration of parameters
Whale Optimization Algorithm	Good for multimodal optimization, can handle noisy data	Slow rate of convergence, requires fine-tuning of parameters

, the most common metaheuristic optimization algorithms have been compiled with regard to their implementation in the optimization of SGs.

2.3. Smart Grid Trends

The close correlation between smart grids (SGs) and the evolution of smart cities, aimed at fostering a highly intelligent and advanced society (referred to as Society 5.0), is emphasized. Furthermore, the benefits that SGs bring to the modern industry (referred to as Industry 5.0) are underscored. To fully harness the potential of the ongoing technological shift, it is crucial for the SG to embrace tailored solutions that provide advanced measurement capabilities and deliver a personalized customer experience, known as mass personalization [2].

The utilization of the concurrent technological advances, in conjunction with the corresponding software and hardware tools within the SG is crucial since electrical power producing and distribution companies are capable of quickly identifying and rectifying any imbalances between energy supply and demand. By extension, (i) electrical energy reliability, (ii) enhanced service quality, and iii) reduced expenses, can be achieved [35]. In an attempt to efficiently organize and plan the interconnections within an SG, the National Institute for Standards and Technology (NIST) and the Smart Grid Interoperability Panel (SGIP) have developed a new framework, covering seven important aspects of the SG, among others, energy transmission and generation, service providers, distribution network, customers, market domain, and network operators [36,37].

The advancement of SGs heavily depends on communication technologies, as they play a vital role in efficiently managing and processing substantial volumes of data generated by diverse applications. These data need to be constantly monitored and analyzed to enable real-time responses [38]. Energy companies face the key challenge of determining the specific communication requirements and selecting the most appropriate technology to ensure secure, cost-effective, and reliable data management across the entire system [39,40].

In the present era, it is of utmost importance to supply cities with energy in a manner that minimizes their ecological footprint and optimizes energy utilization. SGs strive to accomplish this objective by advocating for increased demand of electrification, acknowledging that electricity serves as the most efficient and environmentally friendly energy carrier due to its emission-free nature at the point of use. These intelligent algorithms enhance the current systems and facilitate the advancement of services, harnessing the full potential of renewable energies.

The deployment of an SG encompasses several vital components, including public and private institutions, electric companies, and, most importantly, the network users. Numerous factors warrant attention, such as the continuous integration of new technologies into electrical distribution grids, advancements in energy efficiency, and the regulatory framework supporting the transition in the energy model. Another significant aspect is the shift in consumer behavior and the increased integration of renewable distributed generation and storage. Additionally, it is crucial to incorporate the social dimension by involving citizens in the decision-making process regarding their city’s energy demand. The implementation of SG paradigms, as outlined in this study, often necessitates collaborative efforts among government entities, electric companies, and representatives of civil society at all levels [41].

Smart cities and SGs are expected to offer significant benefits to society, primarily focused on energy conservation, leading to a substantial reduction in CO₂ emissions, which have also been subject to the SDG discussed by the United Nations, following the notion of net-zero emissions. As a result, the services related to energy can be categorized into two main groups, namely: (i) the availability of data on electrical energy consumption, and (ii) the management of energy data. The objective is to improve environmental conditions and enhance the sustainability of future cities. With the support of the infrastructure resulting from the deployment and advancement of SG, smart cities are now within reach for everyone, allowing consumers to access detailed information about their home’s electricity usage, compare their consumption with similar users, and receive personalized recommendations to reduce energy consumption in a smart way. These services enable consumers to act, plan and manage their energy consumption, interact with controllable loads, and make autonomous and intelligent decisions. Furthermore, energy service providers are expected to offer their customers a wider range of services and systems to actively manage their energy demand [42].

In addition, small businesses and residential complexes are important beneficiaries of the consumption and energy management information services provided by SGs. They will be able to enhance their energy efficiency and consumption, resulting in cost savings, which by extension will facilitate the enhancement of the quality of life within smart and intelligent cities of the future (Society 5.0) [43].

The implementation of these technologies and systems in such initiatives will also simplify the process of energy acquisition from renewable energy generation systems into the distribution network, resulting in more environment-friendly SGs. Additionally, the concepts of micro-generation, micro-storage, and the utilization of related control algorithms will allow for the possibility of self-supply or even exporting excess energy to the distribution network via a domestic microgrid. Finally, the seamless integration of self-consumption practices will be enabled by the infusion of intelligence into the grid.

Therefore, SG optimization algorithms need also to focus on the adoption of a plethora of cutting-edge digital technologies for the mitigation of inherent network capacity issues, the reduction of energy losses, and the improvement of service delivery efficiency (i.e., better user experience and quality of service) [44]. As a result, in the bulleted list below, the most pertinent benefits have been compiled:

• More efficient network activity monitoring;
• More efficient mitigation of distribution service interruptions and reduction of the total number of affected customers;
• Faster and more reliable malfunction management;
• Reconfiguration of network structure in near real-time;
• Provision of new services toward better quality of service and user experience,

Based on the information provided, it can be concluded that the various SG models discussed in this study have the potential to revolutionize the traditional energy supply system. In addition to improving distribution system management, SG technology can also bring added value to end-users. This can be achieved by adopting four emerging trends related to SGs, which are currently being implemented in distribution systems. In the following list, four fundamental trends which are often found in SGs are discussed:

• Demand response initiatives: Engaging users in the energy supply system has become a necessity for ensuring service availability and quality during high-demand periods. Smart grids leverage the widespread adoption of intelligent appliances to exert greater control over demand, which in turn facilitates the provision of more economic services to customers [45].
• Smart metering: Deploying advanced metering infrastructure empowers these algorithms to swiftly detect service disruptions and exert better control over energy demand. Additionally, users gain access to more appealing energy rates, encouraging them to adjust their consumption patterns accordingly, and thus to lower energy bills [46].
• Residential energy management: The proliferation of the Internet of Things has extended to household electrical appliances, enabling their administration through applications that offer users pertinent information about their energy consumption, rates, and connected devices [47].
• Renewable energies: The algorithms outlined in this section incorporate local power generation sources into the primary grid, leveraging service users who have the capability to inject renewable energy. By employing various compensation mechanisms, both smart grids and customers reap the advantages of this collaboration [48].

The use of SG technologies presents several challenges in aspects such as (i) energy demand, (ii) consumption, and (iii) energy production. Transmission capacity needs to be improved to accommodate more renewable resources, and small systems such as houses, and buildings need to be integrated into the larger system efficiently. To achieve this, a communication infrastructure must be in place to enable the sharing of information in both directions, allowing for the operational generation, storage, and trade of energy. In order to achieve real-time information analysis, it is imperative that all stakeholders are actively participating within the system. Further to that, it is also important to implement policies that govern their conduct, educate consumers, safeguard data against cyber threats, establish pricing mechanisms, define terms for buying and selling, optimize asset utilization, prevent energy theft, and mitigate the risk of blackouts.

While existing research papers do not explicitly focus on developing models to facilitate infrastructure investment and the continuous improvement of grid architectures, advanced components, monitoring systems, and prediction models, some do highlight the importance of conducting thorough system analysis to minimize power procurement and production expenses. Ensuring energy sustainability and environmental preservation necessitates a comprehensive examination of operating costs for electric utilities, IT and data management systems, energy-efficient devices, and the reduction of power plant emissions. However, current systems face ten main problems such as insufficient transmission capacity to accommodate renewable resources, inefficient integration of small systems into the larger grid, lack of a communication infrastructure for information sharing, absence of policies to regulate behavior and prevent energy theft and blackouts, and high-power purchase and production costs, among others. Moreover, there are ten major challenges facing SGs, including sub-optimal power distribution networks, vulnerabilities in cyberattacks, and environmental risks when collecting large-scale and fine-grained SG data, and serious security flaws [49,50,51]. Nonetheless, there are also ten opportunities that SGs provide, among others, environment-friendly communication, more efficient energy consumption, outlier mining, exploiting the broadcast nature of wireless communications, and integration of sensing systems along with the necessary infrastructure for cloud, fog, and edge computing. Hence, SGs offer the following benefits among others [52]:

• They provide models to detect malicious nodes in the SG and utilize outlier denial and outlier mining scenarios;
• They perform extensive big data analytics, with power electronics providing added value for both renewable energy sources and SGs;
• They provide additional functionalities for monitoring active devices and network traffic in home area networks (HAN), neighborhood area networks (NAN) and wide area networks (WAN);

However, despite the advantages discussed in the previous paragraphs there are certain limitations, which can be described as follows:

• Increased technology implementation costs: lack of low-cost controllers suitable for:

  o 

  smart metering;

  o 

  prediction of energy utilization patterns;

  o 

  monitoring of energy demand;

  o 

  energy conservation.

• Lack of legislation and pricing schemes for energy storage and energy sharing in SGs.
• Lack of suitable and empirical models for sensor networks in order to conduct more detailed/accurate simulations of the physical network systems.
• The need for high communication network requirements to transmit, sense, and control data while ensuring the QoS (Quality of Service) requirements of SGs.

In continuation to the above-mentioned infrastructure optimization regarding topologies for HAN, NAN, and WAN, taking into consideration factors such as network size, communication protocols, and sensors to be integrated is still an open challenge for SG engineers. Moreover, monitoring components should enable the rapid diagnosis, and with the utilization of the emerging prescriptive analytics to provide specific recommendations for medicating the effects of any grid malfunctions, thus aiming to minimize any power quality disturbances.

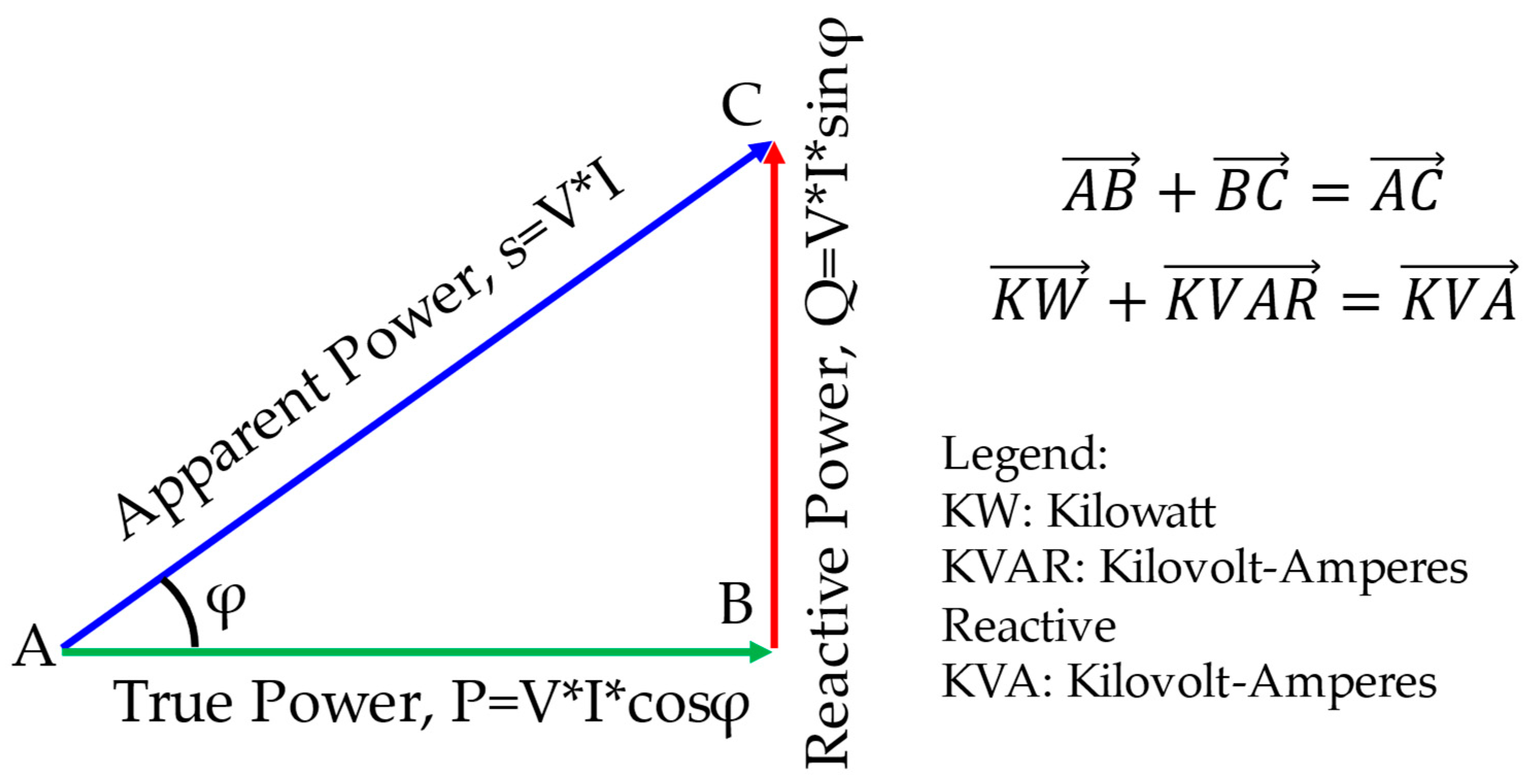
2.4. Reactive Power Injection

In addition to the reactive power optimization strategies discussed before, in the literature there are also strategies for reactive power injection. Such strategies are based on the intentional injection of reactive power into an electrical system. They are used to regulate voltage levels and stabilize the grid. Reactive power injection strategies, such as constant average active power control, constant active current control, constant peak current control, and thermal optimized control, aim to optimize the injection of reactive power in order to ensure efficient and reliable utilization of power systems, particularly in scenarios like low-voltage ride-through (LVRT) operation [53]. Low-voltage ride-through (LVRT) is an important requirement for RES, in order to remain connected to the grid and provide continuous power supply during grid faults or voltage dips. LVRT capability is essential for PV systems to ensure grid resilience and prevent disruptions. Reactive power injection during LVRT helps stabilize grid voltage and support the recovery of the grid after the disturbance.

Constant average active power control is a strategy used in power systems, including renewable energy sources such as photovoltaic (PV) systems, to regulate the active power output at a specific average value. The objective of constant average active power control is to maintain a steady power injection into the grid, regardless of variations in environmental conditions or grid voltage [54].

Constant active current control is a control strategy commonly used in power electronic systems, including RES for the regulations of the output current at a specific level. The objective of this strategy is to maintain a consistent and controlled current injection into the grid, irrespective of variations in environmental conditions or grid voltage [55].

Constant peak current control is a control strategy employed in power electronic systems to regulate the peak current value at a predetermined level. The objective of constant peak current control is to maintain a consistent and controlled peak current output [56].

Thermal optimized control is a control strategy utilized in various systems, including power electronic systems like photovoltaic (PV) systems, to optimize thermal performance and ensure efficient operation. The objective of thermal optimized control is to actively manage and regulate system temperatures, preventing overheating and maximizing energy conversion efficiency [57].

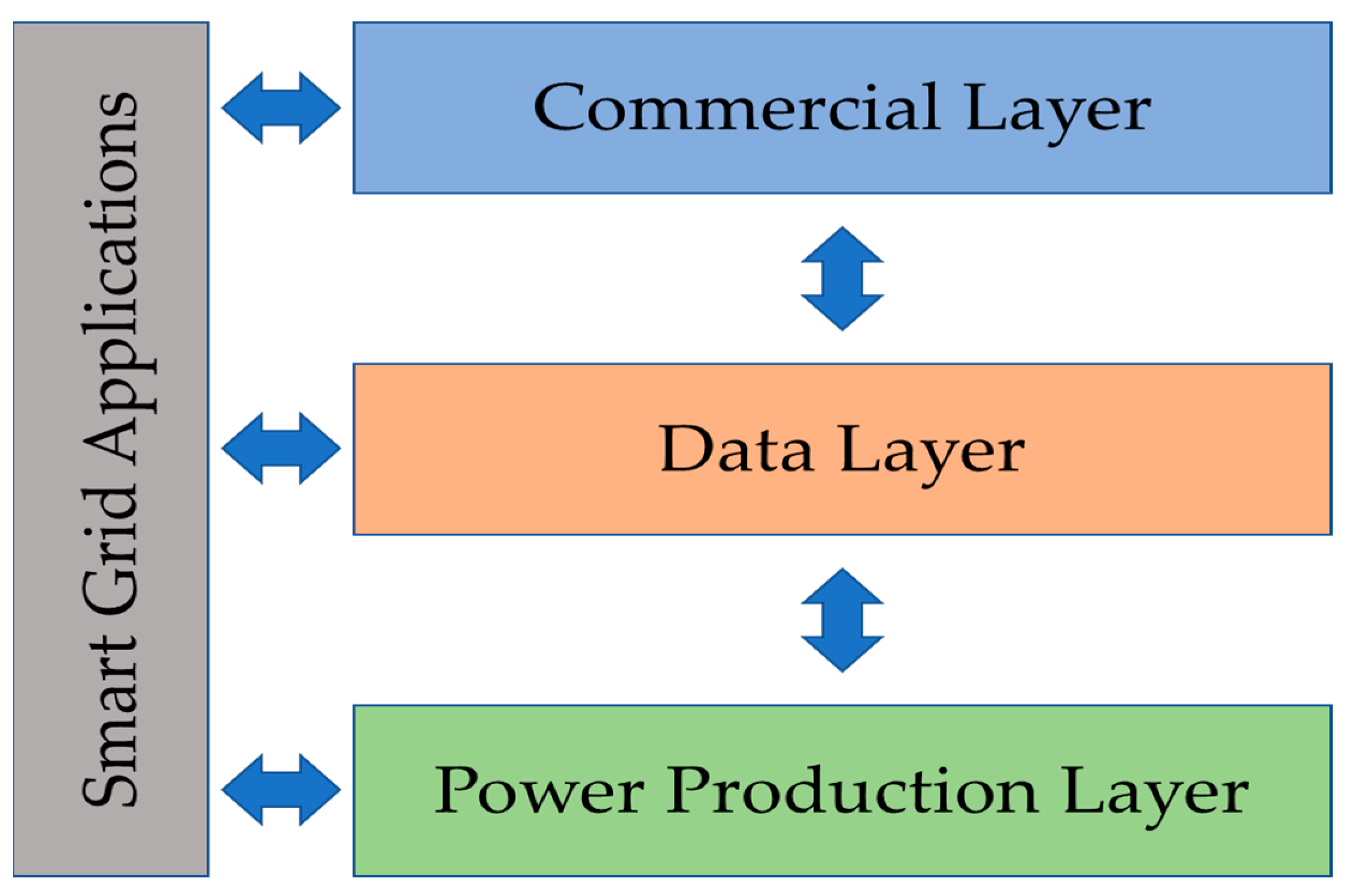
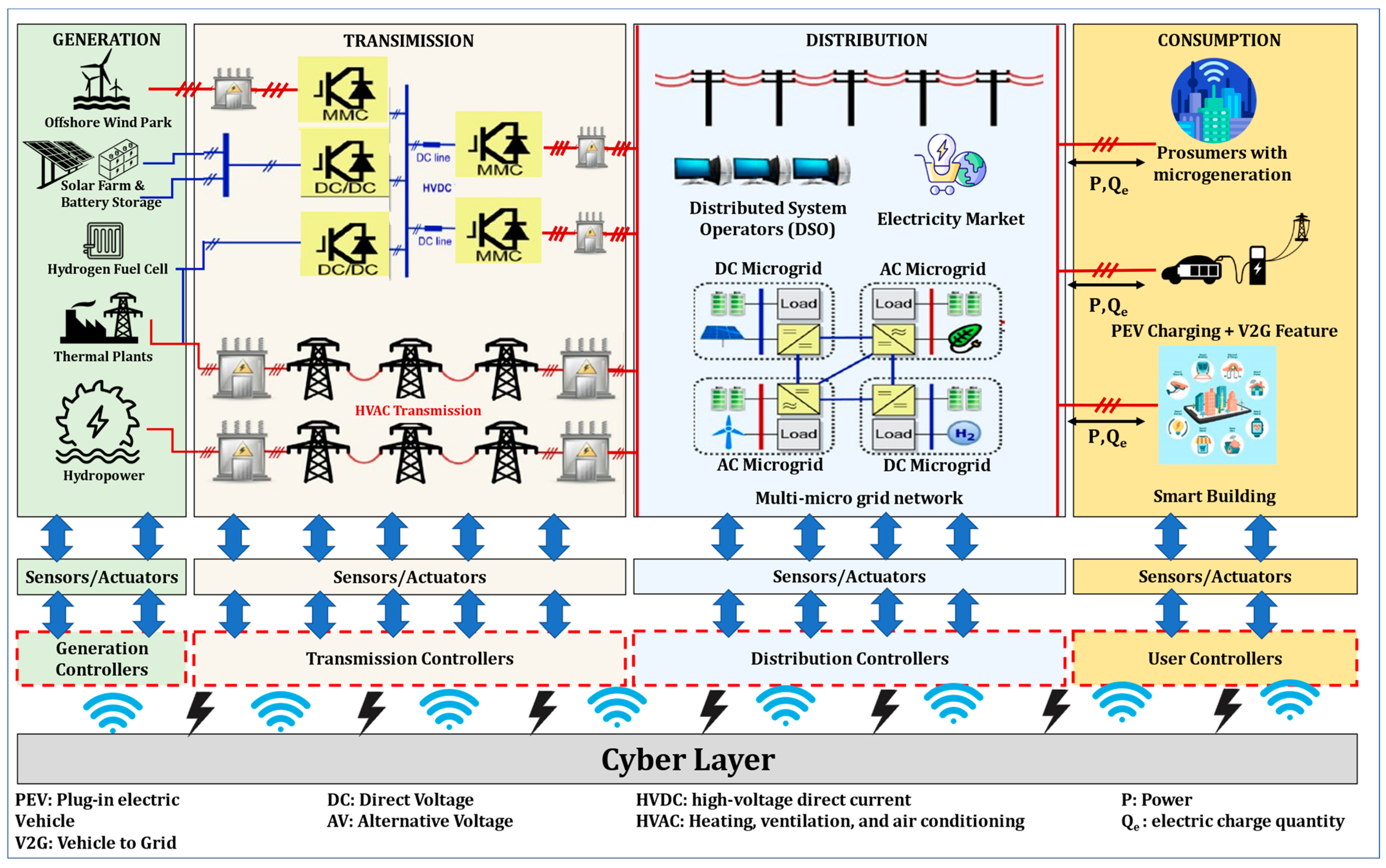
3. Smart Grid Modelling

The SG is a complex system that has developed in a digital information environment with various energy sources. From a high-level point of view, the SG is composed of three layers and accommodates three flows, as presented in Figure 1. The power layer, which involves electricity production, transmission, and distribution, relies on electric and electronic equipment and supports an electrical flow. The data layer connects all the components and supports bidirectional flows of information and interactions between different parties. Finally, the commercial layer involves pricing, wholesaling, and power services and generates a flow of financial transactions. SG applications operate across the three layers and include functions related to reliability, operational efficiency, load prediction, demand response, and pricing. The objects that interact with each other in the SG include loads, sources, storage systems, transmitters, regulators, and smart meters.

In an electrical grid there are several parameters which can be optimized. However, regarding SGs, which rely on the utilization of electrical power generated by renewable energy resources, it is important to minimize reactive power. In Figure 2, the architecture of the SG is presented as a cyberphysical system (CPS). The architecture presented in Figure 1 is divided into four main horizontal layers, in particular (i) the generation layer, (ii) the transmission layer, (iii) the distribution layer, and (iv) the consumption layer. Further to that, the architecture also consists of three vertical layers which facilitate understanding of the cyberphysical nature of the SG. The first horizontal layer is essentially the grouping of the above-mentioned vertical layers and consists of all the physical installations on the grid. The second horizontal layer comprises the sensing systems, and includes the sensors, the actuators, and the controllers installed on the physical equipment in order to enable the collection of data and automated control of the physical equipment. Lastly, the third horizontal layer is comprised of the cloud computing infrastructure, which is mandatory for the acquisition of data, data processing, and implementation of suitable intelligent algorithms for control of the physical systems.

Circulation of reactive power within the SG plays a key role in the performance of various components in power systems, particularly in industrial equipment [58]. Electronic devices play a crucial role in generating reactive power, and it is essential to install reactive power compensation devices properly to minimize their consumption. The selection of appropriate capacitor banks or other similar network components is a common method for managing reactive power [59]. However, if power capacitors are not properly chosen, the risk of harmonic waves appearing in the local network rises, which poses a significant risk for the correct operation of capacitance elements, which are required for power factor correction. Consequently, in order to improve the system’s performance and efficiency, suitable reactive power compensation devices must be chosen based on the total load and improved power factor.

The goal of the mathematical model is to calculate the optimal power flow for given structural parameters while taking into consideration the load of the grid. In addition, the optimal power flow is subject to certain constraints, which are discussed below. Consequently, for each iteration, the conductance of $G_{i,j}$ between two nodes, i and j, is considered. Furthermore, the voltage of each node is also required, and indicated as $V_i$ and $V_j$ respectively.

In Figure 3, the power triangle is illustrated. Following the standardized convention, φ angle is used in order to represent the “voltage phase angle difference” between nodes i and j.

4. Particle Swarm Optimization—PSO

In the context of this section, the development of the improved PSO algorithm aiming toward minimization of the reactive power in the grid is discussed.

4.1. Objective Function

Considering the discussion of the previous paragraphs, the objective of the optimization algorithm is to minimize the amount of apparent power loss, as presented in Equation (1):

$${minP}_{loss}=\sum _{i=1}^n\sum _{j=1}^n{G}_{i,j}(V_i^2+V_j^2-2V_i{V}_j\cos {\phi }_{ij})$$

(1)

where, P_loss corresponds to the reactive power, i.e., the power loss between the nodes i and j. The final objective function for the PSO algorithm is presented in Equation (2):

$$f={minP}_{loss}+{\lambda }_v{\sum }_{i=1}^n{\left(\frac{V_i-V_i^{lim}}{V_i^{max}-V_i^{min}}\right)}^2+{\lambda }_q{\sum }_{j=1}^n{\left(\frac{Q_i-Q_i^{lim}}{Q_j^{max}-Q_j^{min}}\right)}^2$$

(2)

where, ${\lambda }_v$ is the penalty for voltage, ${\lambda }_q$ is the penalty for reactive power in the power generators of the grid. The objective function is bound to the following constraints. Initially, the true power $P_i$ is the balanced based on the conductance $G_{i,j}$ and the susceptance $B_{i,j}$ of the nodes i and j, as expressed in Equation (3):

$$P_i-V_i{\sum }_{j=1}^n{V}_j\left(G_{i,j}\cos {\phi }_{i,j}+B_{i,j}\sin {\phi }_{ij}\right)=0$$

(3)

Similarly, the reactive power is subject to the following constraint:

$$Q_i-V_i{\sum }_{j=1}^n{V}_j\left(G_{i,j}\sin {\phi }_{i,j}-B_{i,j}\cos {\phi }_{ij}\right)=0$$

(4)

The generator voltage (V_Gen,i) is bound by the minimum and maximum allowed values:

$$V_{Gen,i}^{min}\le V_{Gen,i}\le V_{Gen,i}^{max}$$

(5)

4.2. Inertia Weight Strategy

Briefly, it is stressed that the inertia weight in PSO is used in order to adjust each particle’s velocity in accordance with the previous iteration velocity of the particles. The selection of an adaptive inertia weight strategy on PSO is important since it affects the balance between the global and the local search. Specifically, the selection of an appropriate strategy can minimize the possibility of the PSO algorithm becoming stuck on local optima [60,61].

Consequently, in order to achieve a greater accuracy for the proposed PSO algorithm the chaotic inertia weight strategy is implemented. The equations used for the calculations are provided below.

$$w=\left(w_1-w_2\right)\ast \frac{{MAX}_{iteration}-iteration}{{MAX}_{iteration}}+w_2\ast z$$

(6)

where, $w_1$ is the initial value of the weight factor and $w_2$ corresponds to the final value of the inertia weight. ${MAX}_{iteration}$ is the maximum iterative time and “iteration” referring to the current iterative time. For the calculation of the chaotic inertia weight, the logistic mapping formula is used, which is as follows:

$$z=r\ast z(1-z)$$

(7)

where, z, and $z\in (0,1)$, represent the inertia weight, and the growth rate, respectively. Parameter r is the growth rate or bifurcation parameter. It is used for determining the behavior and stability of the system. Based on the literature, when r > 3.56995, chaotic behavior occurs. Consequently, in the proposed model r = 4 in order to achieve chaotic behavior. The pseudocode for initialization and update of the inertia weight is provided below, in Algorithm 1.

Algorithm 1. Pseudocode for PSO inertia weight calculation

Pseudocode for inertia weight calculation

For i = 1 to 1000

Rand(z), $\forall z\in (0,1)$, select a random value for z

$z=r\ast z(1-z)$, calculate

$w=\left(w_1-w_2\right)\ast \frac{{MAX}_{iteration}-iteration}{{MAX}_{iteration}}+w_2\ast z$

EndFor

Chaotic movement is a complex phenomenon that exhibits several distinctive characteristics such as randomicity, ergodicity, and regularity. Randomicity refers to the unpredictable nature of chaotic motion, while ergodicity implies that the system can explore all possible states. Regularity, on the other hand, means that there is a certain degree of order within the system. Because of these unique properties, chaos theory can be leveraged in various applications, including the design of optimization algorithms. In particular, the chaos principle has been utilized to develop the inertia weight strategy for particle swarm optimization (PSO) algorithms. This approach aims to prevent the algorithm from becoming trapped in local optima, which can hinder the search for the global optimum. By introducing chaotic behavior into the inertia weight strategy, the PSO algorithm can explore the search space more thoroughly and efficiently, thereby improving its performance. Overall, the use of chaos theory in optimization algorithms has shown promising results and has the potential to enhance various applications in different fields.

4.3. PSO Acceleration Coefficients

Since the PSO algorithm is inspired by the motion of birds as they form a flock, two hyperparameters, also known as acceleration coefficients or learning factors, c₁ and c₂ are utilized in an attempt to simulate the socialization and the instincts of the birds. Specifically, c₁ in PSO is used in order to define the ability of the swarm to be influenced by the best solution identified by a single particle. Equation (8) expresses the value of c₁:

$$c_1=c_{1,s}+\left(c_{1,e}-c_{1,s}\right)\ast \sin \left(\frac{\pi }{2}{\left(1-\frac{T}{T_{max}}\right)}^m\right)$$

(8)

where, $c_{1,s}$ is the starting value of c₁ and $c_{1,e}$ is the ending value. Similarly, c₂ is used in order to define the ability of the swarm to be influenced by the global best solution of the problem, and is expressed in Equation (9):

$$c_2=c_{2,s}-\left(c_{2,e}-c_{2,s}\right)\ast \sin \left(\frac{\pi }{2}{\left(1-\frac{T}{T_{max}}\right)}^m\right)$$

(9)

where, $c_{2,s}$ is the starting value of c₂ and $c_{2,e}$ is the ending value, and m is the control factor in both Equations (5) and (6).

Following the discussion of the previous paragraphs, in Algorithm 2 a pseudocode describing the functioning of the proposed PSO algorithm, and its parameters is presented. The complete implementation of the improved PSO is provided in Appendix A (Algorithm A1).

Algorithm 2. Main particle swarm optimization pseudocode

Improved PSO inertia pseudocode

Initialize PSO

Set particles to 20

Set max number of iterations MAXiteration = 1000

Set acceleration coefficients

While i < MAXiteration do

For each particle n in particles N

$w=\left(w_1-w_2\right)\ast \frac{{MAX}_{iteration}-iteration}{{MAX}_{iteration}}+w_2\ast z$

Update particle position

Check and/or update bests

EndFor

Check for convergence

Update iteration i = i+1

EndWhile

Return best solution

End

5. Experimental Setup

In order to test the applicability of the proposed framework for the optimization of reactive power within SGs, the IEEE 30-bus system has been setup [62]. The IEEE 30-bus test case represents a simple approximation of the American Electric Power system, and consists of 15 buses, two generators, and three synchronous condensers (Figure 4). This grid has been selected for the experimental validation since it has been used by similar research, and therefore, serves as a good reference point. In the developed model, generators were installed on nodes 1, 3, 4, 6, 7, and 10. Voltage regulators were installed at branches 6–9, 6–10, 4–12, and 27–28. Reactive power compensation equipment is installed at nodes 11, 12, 13, 18, 20, 22, 25, 28, and 29. Finally, the power of the grid for the experiments is set at 100 MW.

In order to validate the initial speculations, three experiments were executed. In the first experiment the reactive power for the grid was calculated without implementing any optimization. In the second experiment the grid was measured following the minimization of the reactive power by implementing the standard form of the PSO algorithm. Finally, in the third experiment, the standard PSO was replaced by the improved version proposed in this research. In

Table 2. Experimental results.

Optimization Stage	Network Loss (MW)	Loss Reduction (MW)	Loss Reduction Percentage
Not optimized	9.259	-	-
Standard PSO	7.683	0.369	−7.66%
Improved PSO	7.432	0.693	−10.67%

, the results extracted from the experimental run are compiled. The first column indicates the optimization strategy adopted; in the second column, the total network loss in Mega Watts (MW) is presented; in the third column, the reduction of total power loss is presented with reference to the initial value; and in the fourth row, the percentage of total power loss is calculated.

The results indicate that implementation of the improved PSO algorithm has the potential to provide a significant improvement of approximately 11% compared to the conventional PSO algorithm. Consequently, with the integration of the proposed algorithm, reduction of power loss in SG systems while satisfying operational constraints is feasible.

6. Software Tool Implementation

In this paragraph, the software and hardware used for development of the optimization algorithm is discussed. Concretely, the PSO has been scripted using Python v3.10.11 programming language in conjunction with Microsoft Visual Studio Code™ v1.79.2 IDE (Integrated Development Environment). The design and implementation of the experimental power grid, as presented in Section 5, Matlab R2020b was used along with Simulink 10.2, which is a graphical programming environment for modeling, simulating, and analyzing multidomain dynamical systems. The execution of the experiments was performed using a PC with an Intel CORE i7 CPU, 16GB RAM Memory, and an NVIDIA 1060 GPU with 8 GB dedicated memory.

7. Conclusions and Outlook

In this research, the development of a PSO algorithm was presented in order to minimize power loss as well as to minimize power outages in SGs, by focusing on the optimization of reactive power. The results presented in the previous sections indicate that although the reactive power has been minimized, there is still room for further improvement. Concretely, with implementation of the improved PSO algorithm, a reduction to the total power loss of approximately 11% was achieved. However, besides optimization of the power flow, it is important to consider the power demands of the customers, especially of industrial/manufacturing clients, in order to optimize the power flow, based on their production schedule, as well as to regulate the peak hours.

By monitoring the reactive power levels of equipment, maintenance engineers are capable of detecting possible malfunctions in the equipment’s operating conditions, and by extension, to identify potential faults before they cause significant damage to the industrial equipment. Therefore, reactive power measurements can be used in combination with other parameters, including temperature, vibration, and sound for the identification of possible causes of the fault and schedule maintenance accordingly [63].

Despite the fact that the presented research indicates a promising potential for minimization of total power loss in the SG, there are several limitations that should be addressed in the future. Among the key players of the SG are electric vehicles (EVs), which have not been taken into consideration in the current research. However, integration of EVs in the SG model can be beneficial in terms of load management and optimization of resource utilization. Concretely, EVs can not only be considered as consumers for the SG, instead they can also be treated as mobile energy storage devices, which are capable of storing electrical energy during off-peak hours and discharging it during peak hours, in an attempt to facilitate balancing the demand and supply of electricity. In this context, batteries play a crucial role in the SG system, preventing voltage collapse and offering the required energy for EV charging. With the integration of EVs into the SG, the model can be further expanded to include additional objects such as charging stations, smart meters, and regulators, which enable the management of EV charging based on the energy availability and the preferences of the EV owners. Overall, the integration of EVs in the SG model can lead to a more efficient, reliable and sustainable energy system [64].

One of the limitations of the current research is the lack of data and models from different countries and grids with different scales and configurations. Consequently, in order to test the applicability, as well as the efficiency of the proposed improved PSO algorithm, it is necessary to perform additional tests in different setups/case studies. Further to that, it is imperative to consider the decentralized and distributed nature of the modern SG, which requires adaptation of the current method.

Consequently, future research will be focused on integrating the proposed algorithm on an industrial product-service system (IPSS) that has been developed in order to help companies regulate their demand in off-peak hours for regulating the electrical power tariffs and reduce the power outages in the grid. The distribution management system plays a vital role in the continuous operation of the SG. It is closely linked to the upper part of the power system, such as energy management systems, and other active systems in the distribution grid. Over the years, various major versions of distribution management systems have emerged. The conventional type was mostly controlled manually to manage the distribution network, whereas the current version comprises several main departments, with operations and planning tasks being the primary components. The other two sections deal with power market interactions and ancillary works. The advanced distribution management system is the newest version, responsible for managing all major transformations across the distribution grid. Although it is not yet widely employed in a normal grid-wide range, experts and researchers are working hard to adapt its essential actions to the significant changes happening throughout the power distribution systems [65].

In addition to that, further elaborating the presented algorithm by integrating an artificial immune system will also be investigated in the future. Concretely, so far, the PSO has proven to be a valuable tool for solving multi-variable, non-linear mathematical models, which constitutes it a valid selection for solving issues within the SG. However, in the future in order to avoid premature optimization, avoid falling into local optima (either minima or maxima), and improve the convergence speed, the artificial immune algorithm will be integrated into the presented framework.

Another promising aspect for future investigation would be the addition of “self-healing” capabilities for the network. Concretely, an electrical power distribution network, regardless of the smart capabilities and the implementation of Industry 4.0 cutting edge technologies, will suffer from inevitable power outages and power distribution issues. Consequently, with the utilization of intelligent optimization algorithms, such as PSO, it becomes feasible to investigate alternative network reconfigurations similar to the context of the presented research [66].