Abstract
This paper presents a cascade predictive control structure based on field-oriented control (FOC) in the dq rotor reference frame for the synchronous reluctance machine (SynRM). The constant d-axis current control strategy was used, and thus, the electromagnetic torque was directly controlled by the q-axis current. Because the model of the two axes of currents from the inner loop is a coupled non-linear multivariable one, to control in a non-interaction and linear way the two currents, their decoupling was achieved through feedforward components. Following the decoupling, two independent monovariable linear systems resulted for the two current dynamics that were controlled using model predictive control (MPC) algorithms, considering their ability to automatically handle the state bounds. The most important bounds for SynRM are the limits imposed on currents and voltages, which in the dq plane correspond to a circular limit. To avoid computational effort, linear limitations were adopted through polygonal approximations, resulting in rectangular regions in the dq plane. For the outer loop that controls the angular speed with a constrained MPC algorithm, the q-axis current closed-loop dynamics and the torque linear equation were considered. To evaluate the performance of the proposed cascade predictive control structure, a simulation study using MPC controllers versus PI ones was conducted.
1. Introduction
High-performance electric drive systems are now designed to fulfill the main requirements, such as fast transients, high power density, high efficiency, and low rotor inertia. On a large scale, the most popular electric machine is the induction one, but it has low efficiency and a low power range, which makes it inappropriate for this kind of application. A secondary option is represented by the permanent magnet synchronous machine, with various benefits such as high efficiency and low rotor inertia, but with the main drawback of the demagnetization phenomenon when operating at high temperatures. At last, the synchronous reluctance machine (SynRM) becomes an attractive solution for a large range of power and speed, being a low-cost machine with eco-friendly environmental impact and multiple benefits, such as compact sizes, low mass and rotor inertia, and the rotor having no electric windings, cage, or permanent magnets. For the modern applications of SynRM drives, advanced control algorithms are used to obtain high performances such as fast transient regimes, good tracking results, and efficient disturbance rejection [1,2].
For the efficient control of alternating current machines, their modeling is based on the dq0 transformation [3,4], which generates dq axes models. The main control strategies of SynRM based on the dq axes model are divided into the following categories [5,6,7]: constant d-axis current control (when the torque is varied by the q-axis current), current angle control (with the groups: fast torque response, maximum power factor control, maximum torque per ampere control), and active flux control. These control strategies are usually implemented using the field-oriented control (FOC) concept, which involves a cascade control structure with an outer loop for angular speed control and an inner loop for d-axis and q-axis current control. To control the d-axis and q-axis currents independently, decoupling feedforward components are frequently used in both current control loops.
For the FOC approach, simple control solutions, such as proportional–integral (PI) controllers, are dominant in many applications, but their main drawback is the inability to deal with constraints in a nonconservative way. For example, a cascade structure based on FOC that uses the constant d-axis current strategy and whose two loop controllers are PI is given in [8]. In [6], the performances obtained with PI controllers are comparatively analyzed for the main control strategies of SynRM implemented in a cascade control structure based on FOC. An FOC strategy with PI controllers whose gains are designed using quantitative feedback theory for robust speed and current control of SynRMs under model uncertainty is presented in [9]. The current control problem of the SynRM is a quadratically constrained problem, and for this reason, a solution was the use of model predictive control (MPC) algorithms that can automatically handle the constraints. However, at the beginning, the main problem with using MPC algorithms for SynRM control was the computational complexity. Compared to the conventional FOC structure with PI controllers, for which the computation time of the control law is around 10 microseconds, in the case of MPC controllers, the computation time increases approximately five times. However, at the same time, in conventional FOC schemes, other calculations are necessary to ensure safe operation regarding the physical limitation, which increases the execution time [10]. In recent years, with advances in hardware and solver development, the MPC strategy has been successfully implemented in SynRM control systems [6,7,8] without involving high costs. For predictive current control, based on the way in which the switching action of the power inverter is produced, the finite set or continuous set approach is used. Thus, in [11], a current predictive control algorithm for a finite set of switching actions of the power inverter was introduced based on a one-step-ahead prediction model obtained by the discretization of the continuous time-coupled non-linear multivariable dq current model with the forward Euler method. Using a cost function with soft constraints, the optimal switching vector for the inverter was selected. A similar current predictive control algorithm is presented in [12], considering a coupled linear multivariable dq current model by using a constant rotor electrical angular speed. The overcurrent protection is obtained by adding a variable to the cost function that considers the safety current limits. Recently, model-free MPC current controllers have been developed. Thus, this approach is presented in [13] using a model-free MPC current controller based on a finite-set unconstrained approach. For current prediction, current measurements are continually updated and stored in a look-up table. A similar approach, where an improved unconstrained model-free MPC current control based on a flux-current map of SynRM is considered for considering the nonlinear magnetic features of SynRM, can be found in [14]. A finite-state direct predictive control for SynRM drives is presented in [15] based on the hierarchical selection strategy of the optimal voltage vector and the dynamic scaling of the voltage amplitude, which keeps the current ripple limited. Starting from the multivariable model of dq currents and the monovariable one obtained by decoupling, in [16], MPC current controllers with constraints based on the continuous set approach are designed and their performances are compared.
For the outer loop, meant to control the angular speed of SynRM, the PI controller is the most frequently used [5,6,8]. Due to the difficulty of this controller regarding constraint handling, MPC algorithms are also used for speed control [17].
Although the MPC with finite set control is widely used in SynRM control due to certain benefits, the high switching frequency required by this strategy [18,19] reduces the performance of practical applications, becoming an impediment for real-time implementation. At the same time, for MPC with a finite set control strategy, the handling of constraints is difficult. The overcurrent protection is usually obtained by adding a soft constraint set in the cost function that considers the safety current limits, while the voltage limitations are directly imposed by the searching algorithm, which generates a voltage magnitude in the admissible domain.
Regarding the continuous set approach used for field-oriented predictive control of SynRM, according to the authors’ knowledge, few results have been reported. Thus, in [20], the design and implementation of a current controller for a SynRM based on the continuous set nonlinear model predictive control is described. For a permanent magnet assisted synchronous reluctance motor (PMA-SynRM), starting from the nonlinear dynamical model in [21], the design of a continuous set MPC based on an augmented linearized model is presented.
For the design of the control algorithms from the above references, the ideal model of SynRM (i.e., no saturation and losses) was generally used, with few exceptions such as from [6], where a non-ideal model mainly due to the saturation of the d-axis was considered, or [9], from which the model uncertainty was taken into account.
In this paper, a cascade predictive control structure based on FOC in the dq rotor reference frame for an ideal SynRM was proposed. Among the FOC-based SynRM control strategies, constant d-axis current control was chosen, which provides direct control of the electromagnetic torque through the q-axis current. Because the model of the two axes of currents from the inner loop is a coupled non-linear multivariable one, to control in a non-interaction and linear way the two currents, their decoupling was achieved through feedforward components. In this way, the dynamics of the d-axis current, which must be constant, are not influenced by the q-axis current variations. After decoupling, two independent monovariable linear systems resulted for the two current dynamics that were controlled using MPC algorithms due to their ability to automatically handle the bounds imposed on the states.
The most important bounds for SynRM are the limits imposed on currents and voltages, which in the dq plane correspond to circular regions. To avoid computational effort, linear limitations were adopted through polygonal approximations, resulting in rectangular regions in the dq plane. For the d-axis current, the upper limit was imposed as its reference, and thus, the parameter of the circular region transformation related to the currents into a rectangular one was defined by the ratio between the d-axis current reference and the maximum stator current. The transformation of the circular region related to the voltages into a rectangular one in the dq plane was carried out by a parameter chosen by the user. To obtain the constraints imposed on the outputs of the MPC current controllers, the voltage limitations in the dq plane were considered, to which the maximum values of the feedforward components were appropriately added. For the outer loop that controls the angular speed with a constrained MPC algorithm, the q-axis current closed-loop dynamics and the linear equation of the torque depending on the q-axis current were considered. To eliminate the steady-state speed error due to unmeasured disturbance generated by the load torque and modeling errors, the user speed reference of the MPC speed controller is replaced by adding an integral action and a feedforward component.
The MPC algorithms were designed in such a way to obtain reference tracking by adding an additional state to the plant model to obtain an input increment, which becomes an optimization variable. The cost functions and related constraints used for MPC algorithm design were transformed into a quadratic programming (QP) problem. To avoid the infeasibility of the QP problem, some constraints are treated as soft constraints by using a slack variable. The implementation is performed in Matlab-Simulink using the facilities offered by the MPC Designer from the Model Predictive Control Toolbox. To evaluate the performance of the proposed cascade predictive control structure based on FOC in the dq rotor reference frame for SynRM, a simulation study using MPC controllers versus PI ones was conducted. PI controllers, often used for the cascade control of SynRM in industrial applications, were designed using the pole-placement method, and to limit some variables imposed by the constraints, saturation-type blocks were introduced at the output of the controllers together with the related anti-windup mechanisms. Since the design method introduces a zero in the closed-loop system, a zero-cancelation ZC block was used in order not to alter the performances. Through a comparative analysis of the performances obtained with the MPC and ZC-PI controllers, respectively, the better-performing behavior of the predictive control cascade structure was revealed. In the end, it is analyzed if the performances are preserved when considering a non-ideal model of SynRM, mainly due to the saturation of the d-axis.
This paper proposes the following new contributions with respect to the state of the art:
- (i)
- a new cascade FOC-based speed control of SynRM using MPC algorithms for both the inner current loop and the outer one, which allow to include the existing safety and hardware constraints directly in the optimization problem.
- (ii)
- the current control with linear monovariable MPC algorithms, after the nonlinear multivariable model of the electrical system decoupling.
- (iii)
- considering the dynamics of the inner current control loop in the design of the outer-loop controller.
- (iv)
- transforming the upper limits on the current and voltage magnitude, which correspond to a circular limit in the dq plane, into linear limits through polygonal approximations with the computational effort decreasing.
- (v)
- analysis of the cascade predictive control structure’s robustness to model uncertainty.
The rest of the paper is organized as follows: In Section 2, the dq SynRM model with physical limits and the cascade predictive control structure in the dq rotor reference frame are presented. Section 3 is dedicated to the design of the inner and outer loops of the proposed cascade predictive control structure. A comparative analysis of the performances obtained with the MPC and ZC-PI controllers is given in Section 4. The conclusions of the paper are presented in Section 5.
2. SynRM Cascade Predictive Control Structure in the Rotor Reference Frame
In this paper, a cascade predictive control structure is proposed for SynRM currents and angular speed control in the rotor reference frame.
2.1. Plant Model and Physical Limits
The dq SynRM model is composed of the electrical circuit, torque generator, and mechanical system models [5,6]. The electrical circuit is described by the current equations:
where (ud,uq), (id,iq), and (Ld,Lq) are voltages, currents, and inductances on the d-axis and q-axis, and Rs is the stator resistance. The torque generator is described by the following equation:
and the equation of the mechanical system is given by:
where (ωe,ωm) denote the electrical and mechanical speeds, with , p being the number of pole pairs, and (Te,Tl) denote the electromagnetic and load torques.
The electrical circuit model (1) of the SynRM is multivariable and non-linear as it includes the product of the electrical angular velocity and the dq currents. At the same time, critical constraints are imposed on the electrical variables, the most important of which refers to the limitation of currents and voltages whose upper limits on the magnitude correspond to a circular limit in the dq plane. Using the generic notation for current and voltage signals, the main constraint becomes:
where M is the maximum phase amplitude of the stator current , respectively, of the stator voltage . Typically, is determined from the motor specifications, and if space vector pulse-width modulation is used for the inverter control with DC-link voltage , . Due to the high computational effort imposed by the circular limit (4), its approximation through linear polygonal limitations was chosen. Thus, the circular region is approximated by a rectangular one defined by the maximum values [22]:
where is a parameter that determines the configuration of the rectangular region. Using limits (5), the linear constraints become:
The circular and rectangular regions are represented in Figure 1, from which it can be seen that the rectangular area is smaller than the circular one.
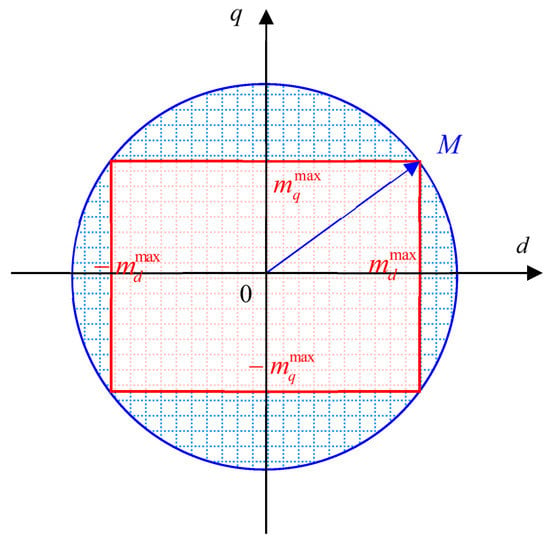
Figure 1.
The rectangular approximation of the circular region.
The torque generator model (2) is also non-linear due to the product of the two currents. Usually, for the mechanical system, a constraint is imposed on the angular speed limits of the motor:
In the following, to simplify the notations, the time variable t will be omitted.
2.2. Cascade Predictive Control Structure
Using the electrical circuit, the torque generator, and the mechanical system models (1), (2), and (3), the cascade predictive control structure of a SynRM in the rotor reference frame from Figure 2 was developed for the currents and the motor angular speed control. Since the dynamics of the mechanical system are slower compared to the electrical ones, the outer loop is intended for mechanical speed regulation and the inner one for dq current control. For both loops, MPC was chosen as the control law due to the superior performance obtained and the possibility of considering in the design phase the constraints originating from physical limits.
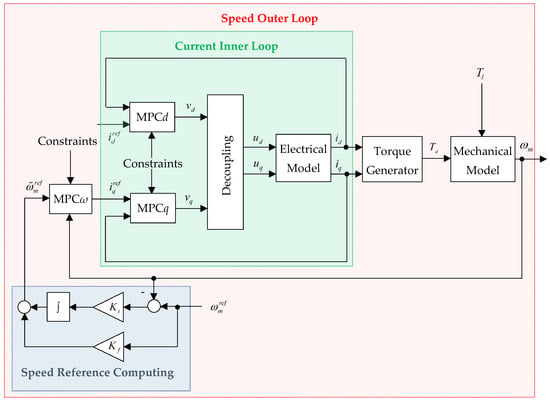
Figure 2.
The cascade predictive control structure.
Among the cascade control strategies of SynRM, the one based on keeping the current on the d-axis constant was chosen [23]. In this way, the current on the q-axis will be the one that controls the electromagnetic torque, and relation (2) becomes a linear one.
The inner loop has a multivariable and non-linear model of the electrical circuit (1). The plant model is decoupled using the feedforward control components from the decoupling block, resulting in two linear monovariable systems that are controlled with MPCd and MPCq controllers whose output variables are and . The first monovariable system will control the current for which the constant reference is imposed, and the second one, the current for which the reference is generated by the outer-loop controller. Considering the possibility of treating the state bounds by the MPC controllers intended for the inner current loop, the linear constraints (6) adapted to the currents − and the voltages − will be used.
For the outer loop, the plant is composed of the inner loop for the current control because the current is considered constant, the torque generator, and the mechanical system. By adopting the control strategy based on keeping the d-axis current constant, the outer plant is a linear one that will be controlled by the MPCω controller. To eliminate the steady-state error due to unmeasured disturbance generated by the load torque and modeling errors, an integral action and a feedforward component with the gains and are added for the offset-free tracking. Thus, the reference of the MPCω controller will be replaced by [24]:
where the gains and are chosen in such a way as to influence the dynamics of the control system as little as possible. The outer-loop controller will limit the angular speed by using the linear constraint (7).
3. Design of the Cascade Predictive Control Structure
The design of the proposed cascade predictive control structure in Figure 2 consists of solving the control problems of the two loops. Firstly, the feedforward control components and the MPCd and MPCq controllers related to the inner loop are designed for controlling the and currents considering the constraints imposed by the physical limits. Secondly, the MPCω controller related to the outer loop is designed to control the angular speed of the motor in the presence of load torque and constraints.
3.1. Inner Current Loop Design
Considering the control problems imposed on the internal loop, the control structure from Figure 3 was chosen.

Figure 3.
The inner current-loop control structure of SynRM.
The plant is described by Equation (1), which highlights a non-linear multivariable system whose main channels are described by the transfer functions of the R-L circuits:
where are the time constants of R-L circuits. Considering that both the feedforward components and the MPCd/q predictive controllers are discrete-time types, for their design, model (1) is discretized with the forward Euler method, resulting in:
for which the following notations were used:
The first two terms of the right side of Equation (10) represent the discrete-time model of the R-L circuit, and the last term is the interaction between the channels of the multivariable system. To eliminate interactions containing nonlinearities, feedforward components are used, as described by:
resulting for the voltages uj the expressions:
where vj represents the input variables of the two decoupled monovariable R-L circuits.
Replacing uj given by (13) in (10), the decoupled monovariable discrete-time models are obtained:
that will become plants for MPCd/q controllers.
For the currents to track their references , the increment is:
is considered an input signal, the reason for which the model (10) is extended with the new state , resulting in the augmented model:
Using the compact form of the model (16):
the linear prediction model can be easily determined:
and finally, the output prediction:
Considering the linear constraints (6) imposed on the electrical variables, in the following they will be specified for the currents ij and the voltages vj. Thus, for the currents, the maximum values result in:
where ci is a parameter that fixes the maximum value of the stator current according to the nominal value . Knowing that the id current is positive and upper limited by , the parameter will be and the current linear constraints related to (6) and (5) become:
The constraints imposed on the vj voltages depend on the uj voltage constraints generated by the physical limitations and the relationships (13) between vj and uj. First, the maximum values of the uj voltages are determined based on Equation (5):
and then, the maximum values of the feedforward components ufj are determined using the maximum values of the currents ij and the nominal electrical angular velocity :
Introducing the maximum values of the voltages uj and ufj in (13), the maximum values of the voltages vj are obtained:
and thus, the linear constraints related to the control signals of the two MPC current controllers are found:
Considering the tracking of the references by the currents , the constrained quadratic cost function is chosen in the form:
where is the future control sequence, hpj and hcj are the prediction and control horizons, δjn and λjp are the real positive weight factors of the output and the control signals. The slack variable is introduced to allow constraints violations together with the nonnegative weights and , while the term is added to penalize in the cost function with .
The constrained quadratic cost function (26), by substituting the output prediction (19), can be reformulated as a QP problem, which leads to the optimal solution [25]:
where the involved matrices Hj, Fj, Gj, Wj and Sj of adequate sizes are determined as in [26].
According to the receding horizon principle, only the first element of is used to determine the control signal applied to the decoupling controller:
Since the strategy of keeping the id current constant was considered, the reference for the current control loop was chosen based on the active flux concept [27]:
and thus, the electromagnetic torque of the SynRM motor is now given by the linear relationship:
which replaces the non-linear expression (2) of the torque.
3.2. Outer Speed Loop Design
For the outer loop, the plant consists of the designed inner closed-loop system of the iq current, to which the mechanical system model (3) is added, considering the electromagnetic torque (30). Usually, the dynamics of the inner closed-loop system of the iq current are approximated with a first-order element whose time constant is correlated with the closed-loop dynamics:
Based on the two models (31) and (3) with the electromagnetic torque (30), the outer-loop plant model, having as input um the reference and as output the mechanical speed is described by:
where the following notations were used:
To obtain output free tracking, a new state is added to the system states (32), resulting in the augmented model:
For the augmented model (34), the input is the increment and thus will track the reference . Considering a zero-load disturbance , the model (34) can be put into its compact form:
based on which the linear prediction model is simply determined:
Using (36), the output prediction is directly found:
Having in view the necessity to track the reference by the controlled output and the limitations regarding the controlled output and the input signal , a quadratic constrained cost function of the form was chosen:
where is the future control sequence, hpm and hcm are the prediction and control horizons, is the slack variable used to relax the constraints together with the nonnegative weights , δjm, and λjm are the real positive weights factors of the output and the control signals, is the slack variable weight, are the limits of the speed. Since , are chosen according to the second inequality from (21).
The quadratic cost function (38) subject to the linear constraints can be reformulated as a QP problem by substituting the output prediction (37), which leads to the optimal solution [25]:
where the involved matrices Hm, Fm, Gm, Wm and Sm of adequate sizes are determined as in [26].
Based on the receding horizon principle, only the first element of is used to determine the control signal applied to the inner control loop of the current as a reference:
4. Illustrative Case Study
To evaluate the performance of the proposed cascade predictive control structure for SynRM, a simulation study was carried out using a Simulink model of the motor in dq coordinates and predictive controllers from the MPC Simulink Library.
The simulation results were compared with those obtained with a cascade regulation structure with ZC-PI controllers instead of MPC ones, often used in industrial applications. For the design of the PI controllers, the pole placement method was used [28], considering the R-L plant transfer function for the current controllers:
and the mechanical plant transfer function for the speed controller, neglecting the inner-loop dynamics:
Following the design of the PI controllers, the tuning parameters of the current and speed controllers resulted in:
where is the natural frequency and is the loop attenuation of the inner/outer-loop systems. Furthermore, a zero appears in the closed-loop transfer function, which can be canceled by introducing a zero-cancellation block ZC in the feedforward path [25].
The saturation used for ZC-PI controllers output constraints requires an anti-windup mechanism [29].

Table 1.
SynRM specifications.
The sampling period for the controller design was chosen at Ts = 100 microseconds according to the requirements of the current loops’ dynamics.
With the SynRM parameters from Table 1, the inner plant model used for MPC current controller design turns into:
and the outer plant model, including inner-loop dynamics for MPC speed controller design, becomes:
The simulation study is performed in a Matlab-Simulink environment, by using the MPC Designer block from the Model Predictive Control Toolbox. Since the control strategy based on keeping the current constant on the d-axis was chosen for the cascade predictive control structure of SynRM, the reference for id is calculated with [30].
The limit values of the constraints were determined based on the method from Section 2, using the rectangular regions from Figure 1. The circle radius M for currents is given by and for voltages by . Since for the constant current on the d-axis, the limitation is imposed, the value was adopted. For the voltages, uj constraints, was assumed, and for the vj voltages, Equations (24) and (25) were used to obtain the imposed limitations.
For the speed reference computation, the following gain values are selected: and .
Thus, Table 2 summarizes the tuning parameters and constraints for both MPC and PI controllers.

Table 2.
Tuning parameters and constraints for controllers of the two cascade structures.
The outer speed-loop tracking results for both MPC and ZC-PI controllers of the SynRM cascade structure are depicted in Figure 4. The speed reference is set at a constant value that corresponds to the nominal one . A no-load start of SynRM is considered, and then, after 4 s, a load torque of value is applied, which represents the main disturbance that acts on SynRM. As it can be seen in Figure 4, for the MPC control the settling time , which is much smaller than the settling time achieved with the ZC-PI control. Additionally, ZC-PI speed control response has a very small overshoot, while MPC speed control has no overshoot.
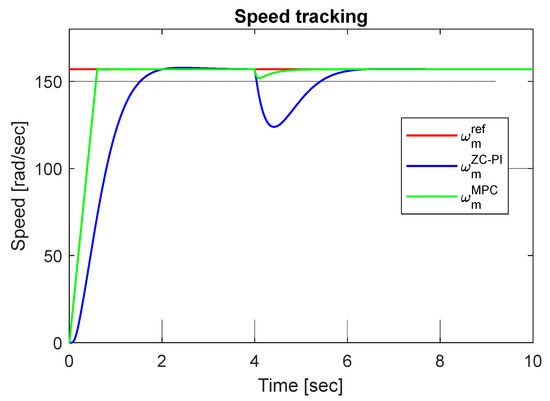
Figure 4.
The speed tracking results.
Moreover, when the load torque is applied, the speed variations are much higher with ZC-PI control compared to MPC. It can be mentioned that in the no-load start conditions of SynRM, the fast outer speed closed-loop dynamics with MPCω generates a high value of the controller output, which will be limited by the imposed constraints. The same limitation is also applied to the q-axis current reference. Therefore, the current references and their tracking, which are presented in Figure 5, have a major influence on SynRM operation.
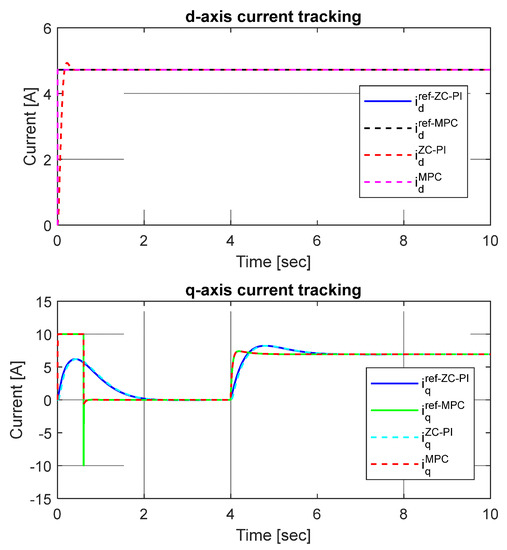
Figure 5.
The inner current-loop tracking results.
The current constraints are established according to Table 2. For the d-axis, the MPC current response is faster than the corresponding ZC-PI one . Moreover, compared with the ZC-PI current response , the MPC current response presents no overshoot. On the q-axis, both current responses, and , must track their current references which are provided by the speed controller. At the start of the SynRM drive, the q-axis MPC current response has a larger value than the ZC-PI one and is limited by the constraints. When the load torque is applied (Figure 6), the response is faster than the ZC-PI one , and both responses present small overshoots.

Figure 6.
The electromagnetic and load torques.
The electromagnetic and load torques are illustrated in Figure 6. As a constant d-axis current control was chosen, the electromagnetic torque depends linearly on the q-axis current. Thus, for the no-load start conditions, when the q-axis current of the MPC structure has its maximum value imposed by the constraints, the electromagnetic torque presents a higher value in comparison with the one obtained by the ZC-PI controller , which will lead to a smaller settling time. When the load torque is applied, a faster response of the electromagnetic torque related to the MPC structure is obtained, with a faster load rejection.
The output current controllers and the input voltages of the SynRM dq model are illustrated in Figure 7.

Figure 7.
The output of the current controllers and the input voltages of SynRM dq model.
The MPCd/q controller outputs are limited by the adopted constraints from Table 2. However, in comparison with the ZC-PI controller outputs , the MPC controller outputs present high-variation components that are limited by the imposed constraints. Taking into account (23–24), the input voltages of the SynRM dq model and depend on the controller outputs and , and on current limitations via the feedforward decoupling voltages. Therefore, due to current controller output constraints, the input voltages of the SynRM dq model are limited.
Based on the above simulation results, it can be concluded that the MPC algorithms with related constraints used in the proposed FOC cascade control structure improve the dynamic performance in comparison with the classical PI control.
Since the design of the MPC controllers is based on the use of a SynRM ideal model, it is further analyzed to see if the performances are preserved for a non-ideal model, which includes saturation and iron losses. The effects of saturation and iron losses depend quite a lot on the type of machine, but studies carried out on machines have shown that iron loss effects can be ignored and only the saturation of the d-axis can be taken into consideration. If the synRM rotor is axially laminated, the q-axis has minimum saturation, and thus, the Lq inductance can be considered to be the unsaturated value, and the d-axis has a pronounced saturation that reduces the Ld inductance when the machine operates near or at rated conditions [6]. In what follows, the robustness of the proposed cascade predictive control structure for SynRM is analyzed when the value of the inductance Ld changes due to saturation, as in [6]. The robustness test consisted of considering the decreasing of the inductance Ld from its nominal value Ldn = 0.186 H to the two small values Ldsat1 = 0.167 H and Ldsat2 = 0.158 H due to saturation, while the model used for MPC and decoupling controllers’ synthesis uses the nominal parameters from Table 1.
For the robustness testing, a speed reference containing three steps , each with a duration of N sampling periods, was used, and, for the performance evaluation, the following index was considered:
To appreciate how much the indices vary in the two cases generated by saturation in relation to the nominal index , the robustness overshoot is defined:
The speed tracking responses obtained with the nominal inductance Ldn and those resulting from the two saturated inductances Ldsat1 and Ldsat2 are comparatively presented in Figure 8, considering a speed reference with the step values , and , each having the duration of sampling periods.

Figure 8.
Speed tracking for nominal and saturation values of the inductance Ld.
For the responses related to the nominal and the two saturated inductances, the following performance indices: , and resulted. Based on these, the robustness overshoots were calculated: and . It is observed that the performance indices exceed their target as the inductance Lsati decreases, resulting in an increase in the robustness overshoots. The performance alteration due to saturation is mainly generated by the decoupling controllers. However, for small decreases in the inductance Ld, the proposed cascade predictive control structure for SynRM proves to be robust when considering the effect of saturation.
5. Conclusions
The cascaded MPC control structure based on FOC in the rotor reference frame allows us to obtain a high-performance SynRM drive. By using the feedforward decoupling technique, the multivariable inner current loop of the cascade structure is transformed into two monovariable non-interaction linear systems, and thus, the two currents are independently controlled. Since the control strategy based on keeping the current on the d-axis constant was chosen for the cascade predictive control structure, the electromagnetic torque depends only on the q-axis current component, and hence, a linear MPC outer-loop controller is used.
The critical constraints imposed on the electrical variables whose upper limits on magnitude correspond to a circular limit in the dq plane were transformed into linear constraints through polygonal approximations to reduce the computational effort.
The steady-state angular speed error due to the unmeasured disturbance introduced by the load torque and modeling errors is eliminated by adding an integral action and a feedforward component to the angular speed reference computation.
The performance of the proposed cascade predictive control structure based on FOC in the dq rotor reference frame for SynRM was evaluated in a simulation study using MPC controllers versus PI ones, resulting in better behaviors for the MPC algorithms. At the same time, the structure proved to be robust at saturation on the d-axis.
Author Contributions
Conceptualization, M.C. and C.L.; methodology, C.L.; software, M.C.; validation, M.C. and C.L.; formal analysis, C.L.; investigation, C.L.; resources, M.C.; writing—original draft preparation, M.C.; writing—review and editing, C.L.; visualization, M.C.; supervision, C.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data availability is not applicable to this article as the study did not report any data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Heidari, H.; Rassõlkin, A.; Kallaste, A.; Vaimann, T.; Andriushchenko, E.; Belahcen, A.; Lukichev, D.V. A review of synchronous reluctance motor-drive advancements. Sustainability 2021, 13, 729. [Google Scholar] [CrossRef]
- Pellegrino, G.; Jahns, T.; Bianchi, N.; Soong, W.; Cupertino, F. The Rediscovery of Synchronous Reluctance and Ferrite Permanent Magnet Motors; Springer International Publishing: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Baimel, D.; Belikov, J.; Guerrero, J.M.; Levron, Y. Dynamic modeling of networks, microgrids, and renewable sources in the dq0 reference frame: A Survey. IEEE Access 2017, 5, 21323. [Google Scholar] [CrossRef]
- Levron, Y.; Belikov, J.; Baimel, D. A tutorial on dynamics and control of power systems with distributed and renewable energy sources based on the dq0 transformation. Appl. Sci. 2018, 8, 1661. [Google Scholar] [CrossRef]
- Sul, S.K. Control of Electric Machine Drive Systems; John Wiley and Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Betz, R.E.; Lagerquist, R.; Jovanovic, M.; Miller, T.J.E.; Middleton, R.H. Control of synchronous reluctance machines. IEEE Trans. Ind. Appl. 1993, 29, 1110–1122. [Google Scholar] [CrossRef]
- Hadla, H. Predictive Load Angle and Stator Flux Control of SynRM Drives for the Full Speed Range. Ph.D. Dissertation, Coimbra University, Coimbra, Portugal, August 2018. [Google Scholar]
- Toliyat, H.A.; Shi, R.; Xu, H. A DSP-Based Vector Control of Five-Phase Synchronous Reluctance Motor. In Proceedings of the Conference Record of the 2000 IEEE Industry Applications Conference. Thirty-Fifth IAS Annual Meeting and World Conference on Industrial Applications of Electrical Energy, Rome, Italy, 8–12 October 2000; pp. 1759–1765. [Google Scholar]
- Poola, R.; Hanamoto, T. Atomated QFT-based pi tuning for speed control of SYNRM drive with analytical selection of qft control specifications. Energies 2022, 15, 642. [Google Scholar] [CrossRef]
- Carpiuc, S.C.; Lazar, C. Fast real-time constrained predictive current control in permanent magnet synchronous machine based automotive traction drives. IEEE Trans. Transp. Electrif. 2015, 1, 326–335. [Google Scholar] [CrossRef]
- Farhan, A.; Abdelrahem, M.; Saleh, A.; Shaltout, A.; Kennel, R. Simplified sensorless current predictive control of synchronous reluctance motor using online parameter estimation. Energies 2020, 13, 492. [Google Scholar] [CrossRef]
- Hadla, H.; Santos, F. Performance comparison of field-oriented control, direct torque control, and model-predictive control for SynRMs. Chin. J. Electr. Eng. 2022, 8, 24–37. [Google Scholar] [CrossRef]
- Carlet, P.G.; Tinazzi, F.; Bolognani, S.; Zigliotto, M. An effective model-free predictive current control for synchronous reluctance motor drives. IEEE Trans. Ind. Appl. 2019, 55, 3781–3790. [Google Scholar] [CrossRef]
- Carlet, P.G.; Tinazzi, F.; Ortombina, L.; Bianchi, N. Sensorless Motor Parameter-Free Predictive Current Control of Synchronous Reluctance Motor Drives. In Proceedings of the International Conference on Electrical Machines (ICEM), Valencia, Spain, 5–8 September 2022; pp. 1464–1470. [Google Scholar]
- Antonello, R.; Carraro, M.; Peretti, L.; Zigliotto, M. Hierarchical scaled-states direct predictive control of synchronous reluctance motor drives. IEEE Trans. Ind. Electron. 2016, 63, 5176–5185. [Google Scholar] [CrossRef]
- Costin, M.; Lazar, C. Comparative Study of Predictive Current Control Structures for a Synchronous Reluctance Machine. In Proceedings of the 26th International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 19–21 October 2022; pp. 530–535. [Google Scholar]
- Liu, T.-H.; Ahmad, S.; Mubarok, M.S.; Chen, J.-Y. Simulation and implementation of predictive Speed controller and position observer for sensorless synchronous reluctance motors. Energies 2020, 13, 2712. [Google Scholar] [CrossRef]
- Geyer, T.; Papafotiou, G.; Morari, M. Model predictive direct torque control—Part I: Concept, algorithm, and analysis. IEEE Trans. Ind. Elect. 2009, 56, 1894–1905. [Google Scholar] [CrossRef]
- Cimini, G.; Bernardini, D.; Bemporad, A.; Levijoki, S. Online Model Predictive Torque Control for Permanent Magnet Synchronous Motors. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015. [Google Scholar]
- Zanelli, A.; Kullick, J.; Eldeeb, H.M.; Frison, G.; Hackl, C.M.; Diehl, M. Continuous control set nonlinear model predictive control of reluctance synchronous machines. IEEE Trans. Control Syst. Technol. 2022, 30, 130–141. [Google Scholar] [CrossRef]
- Moghaddam, H.A.; Rezaei, O.; Vahedi, A.; Saeidi, M.; Ehsani, M.M. A continuous control set of the model predictive controller of PMA-SynRM machine for high-performance flywheel energy storage system. Int. J. Dyn. Control 2022, 10, 1553–1566. [Google Scholar] [CrossRef]
- Wang, L.; Chai, S.; Yoo, D.; Gan, L.; Ng, K. PID and Predictive Control of Electrical Drives and Power Converters; Wiley: New York, NY, USA, 2015. [Google Scholar]
- Hilairet, M.; Lubint, T.; Tounzi, A. Variable reluctance machines: Modeling and control. In Control of Non-Conventional Synchronous Motors, Louis, J.P., Ed.; Wiley: London, UK; Hoboken, NJ, USA, 2012; pp. 287–328. [Google Scholar]
- Bolognani, S.; Bolognani, S.; Peretti, L.; Zigliotto, M. Design and implementation of model predictive control for electrical motor drives. IEEE Trans. Ind. Electron. 2009, 56, 1925–1936. [Google Scholar] [CrossRef]
- Bemporad, A. Model Predictive Control Design: New Trends and Tools. In Proceedings of the 45th IEEE Conference on Decision & Control, San Diego, CA, USA, 13–15 December 2006; pp. 6678–6683. [Google Scholar]
- Bemporad, A.; Morari, M.; Ricker, N.L. Model Predictive Control Toolbox for Matlab—User’s Guide; The Mathworks, Inc.: Natick, MA, USA, 2023; Available online: https://www.mathworks.com/help/pdf_doc/mpc/mpc_ug.pdf (accessed on 14 March 2023).
- Boldea, I.; Paicu, M.C.; Andreescu, G.-D. Active flux concept for motion sensorless unified AC drives. IEEE Trans. Power Electron. 2008, 23, 2612–2618. [Google Scholar] [CrossRef]
- Stulrajter, M.; Sustek, P. Motor Control Application Tuning (MCAT) Tool for 3-Phase PMSM, Application Note; Freescale Semiconductor: Austin, TX, USA, 2013. [Google Scholar]
- Åström, K.J.; Hägglund, T. PID Controllers: Theory, Design, and Tuning; ISA—The Instrumentation, Systems and Automation Society: Triangle, NC, USA, 1995. [Google Scholar]
- Hadla, H.; Cruz, S. Active Flux Based Finite Control Set Model Predictive Control of Synchronous Reluctance Motor Drives. In Proceedings of the 18th European Conference on Power Electronics and Applications (EPE’16 ECCE Europe), Karlsruhe, Germany, 5–9 September 2016. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).