Integration of sEMG-Based Learning and Adaptive Fuzzy Sliding Mode Control for an Exoskeleton Assist-as-Needed Support System
Abstract
1. Introduction
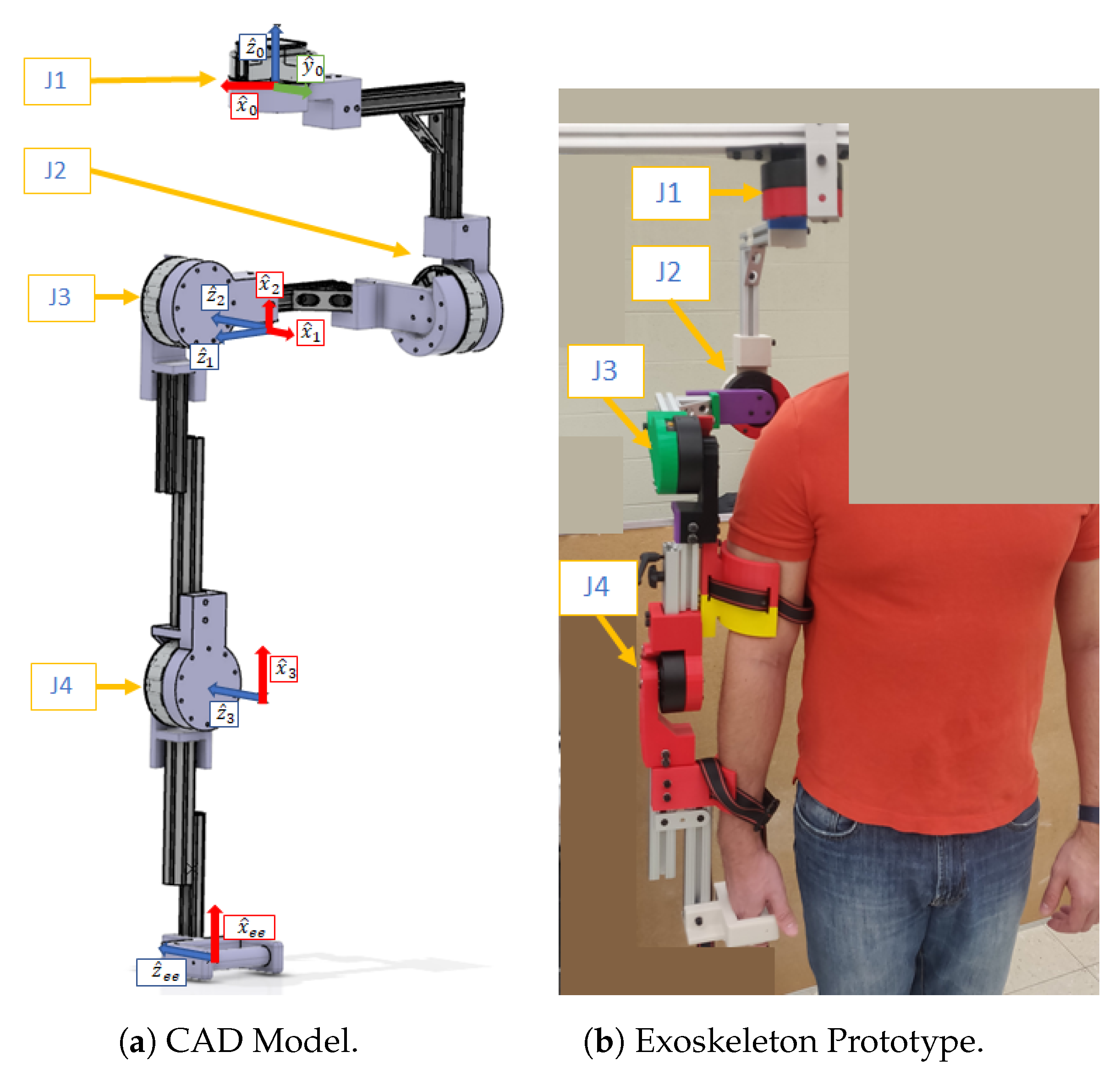
2. Description of the Exoskeleton
| Algorithm 1: RNEA as in [31] |
Forward Iteration
Backward Iteration
|
Inertia Parameters of the Exoskeleton
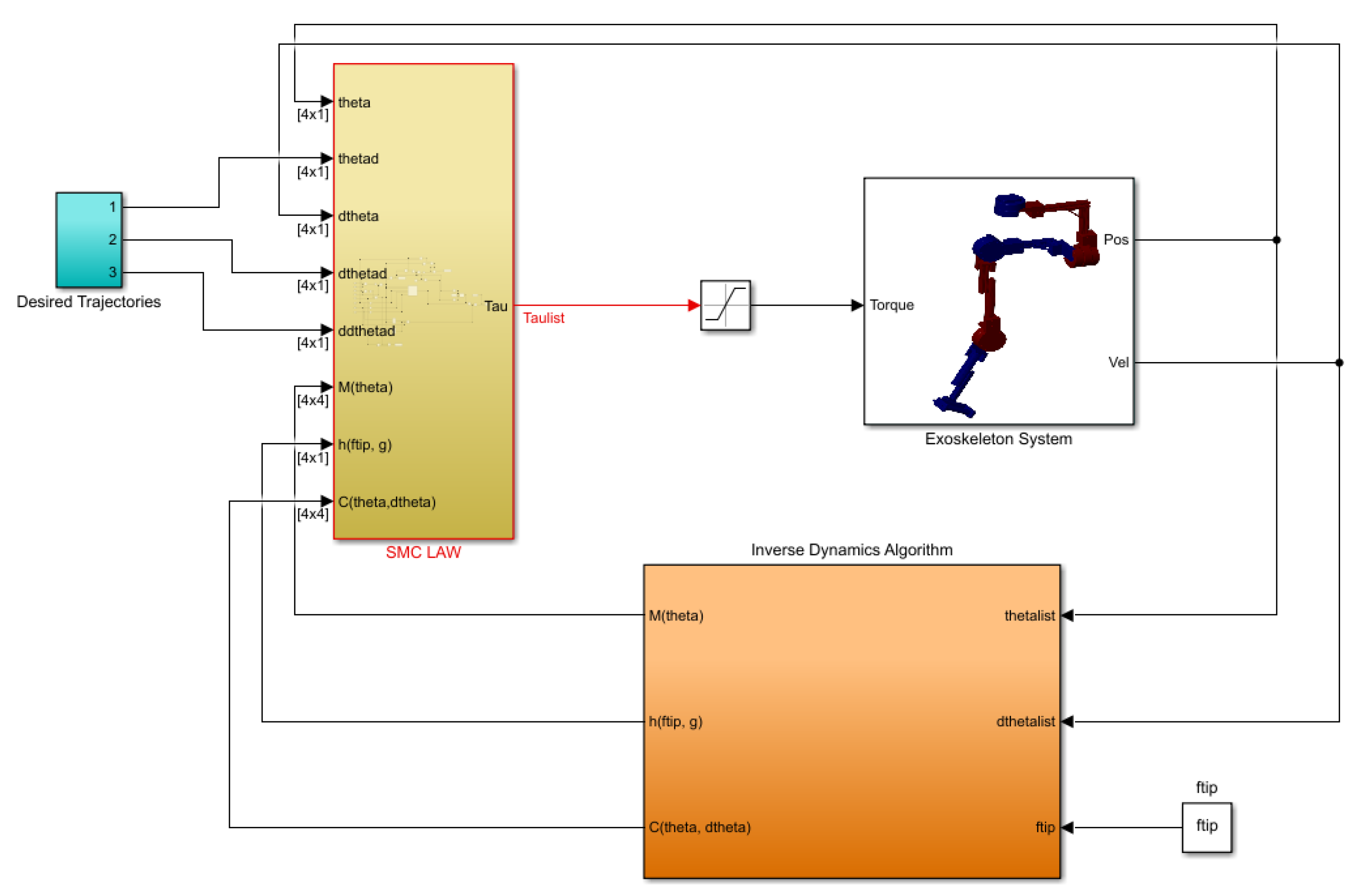
3. Sliding Mode Control Law
Control Law Derivation:
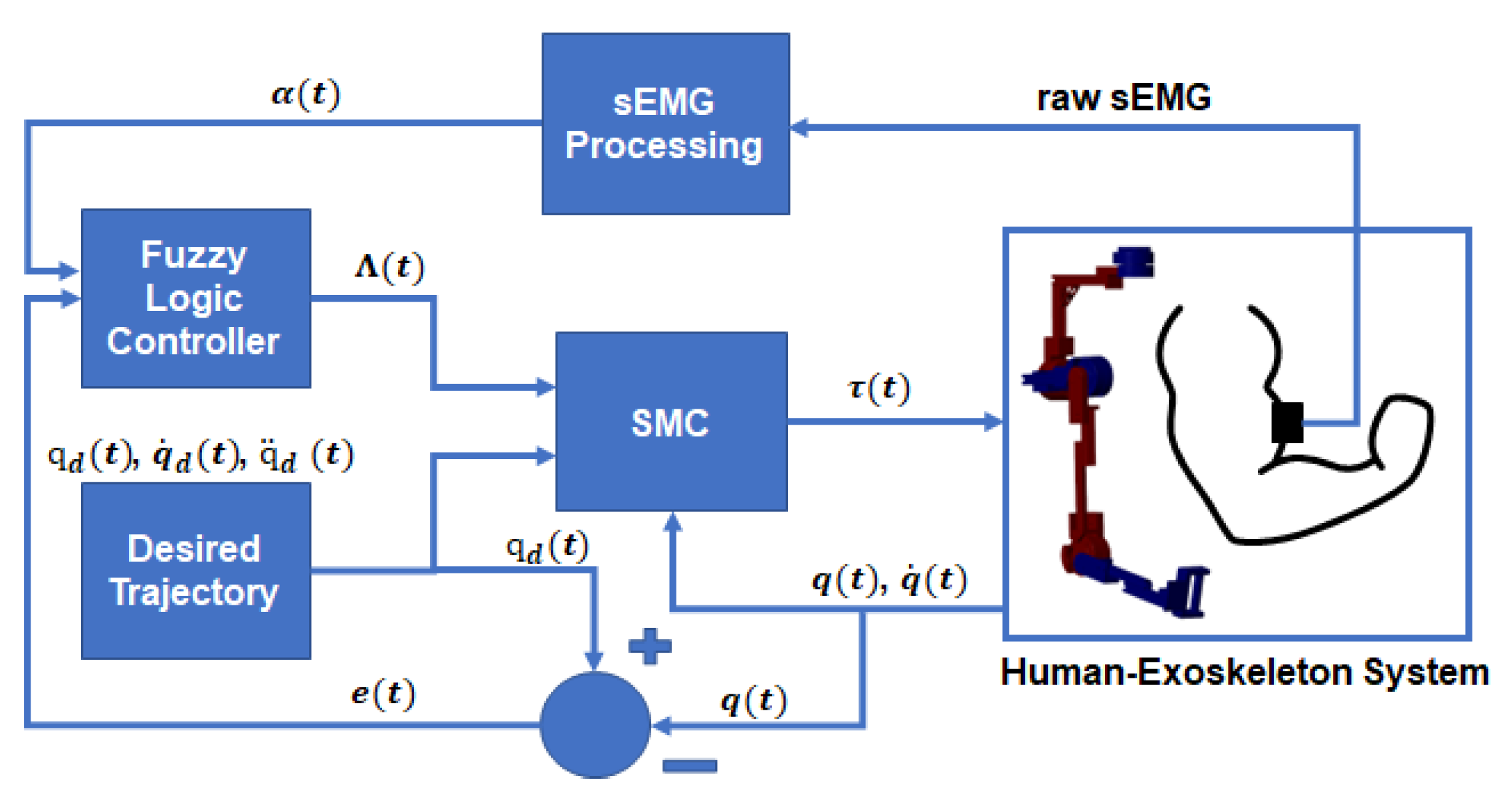
4. A Proposed AAN Control Strategy
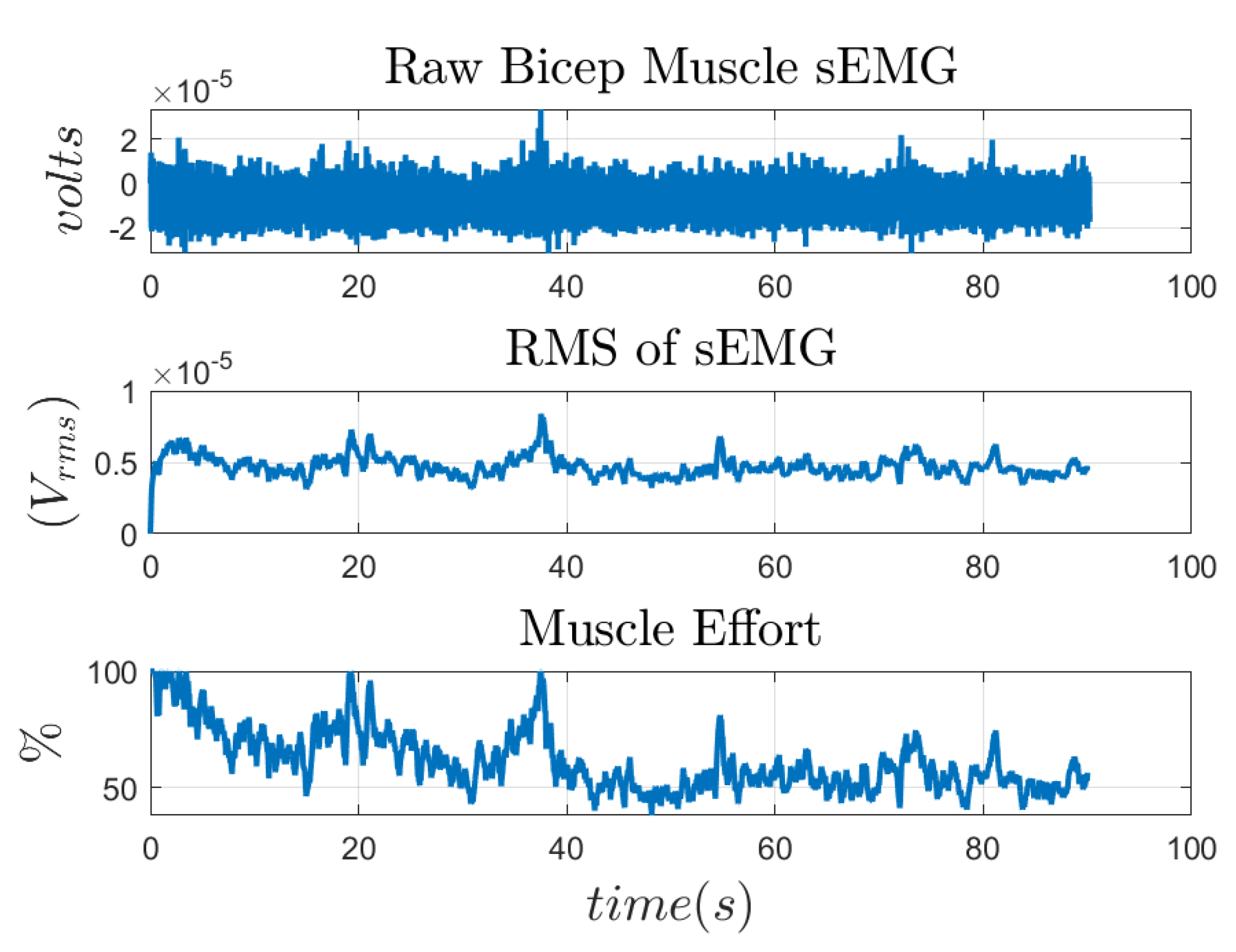
4.1. Adaptive Muscle Effort Level Algorithm
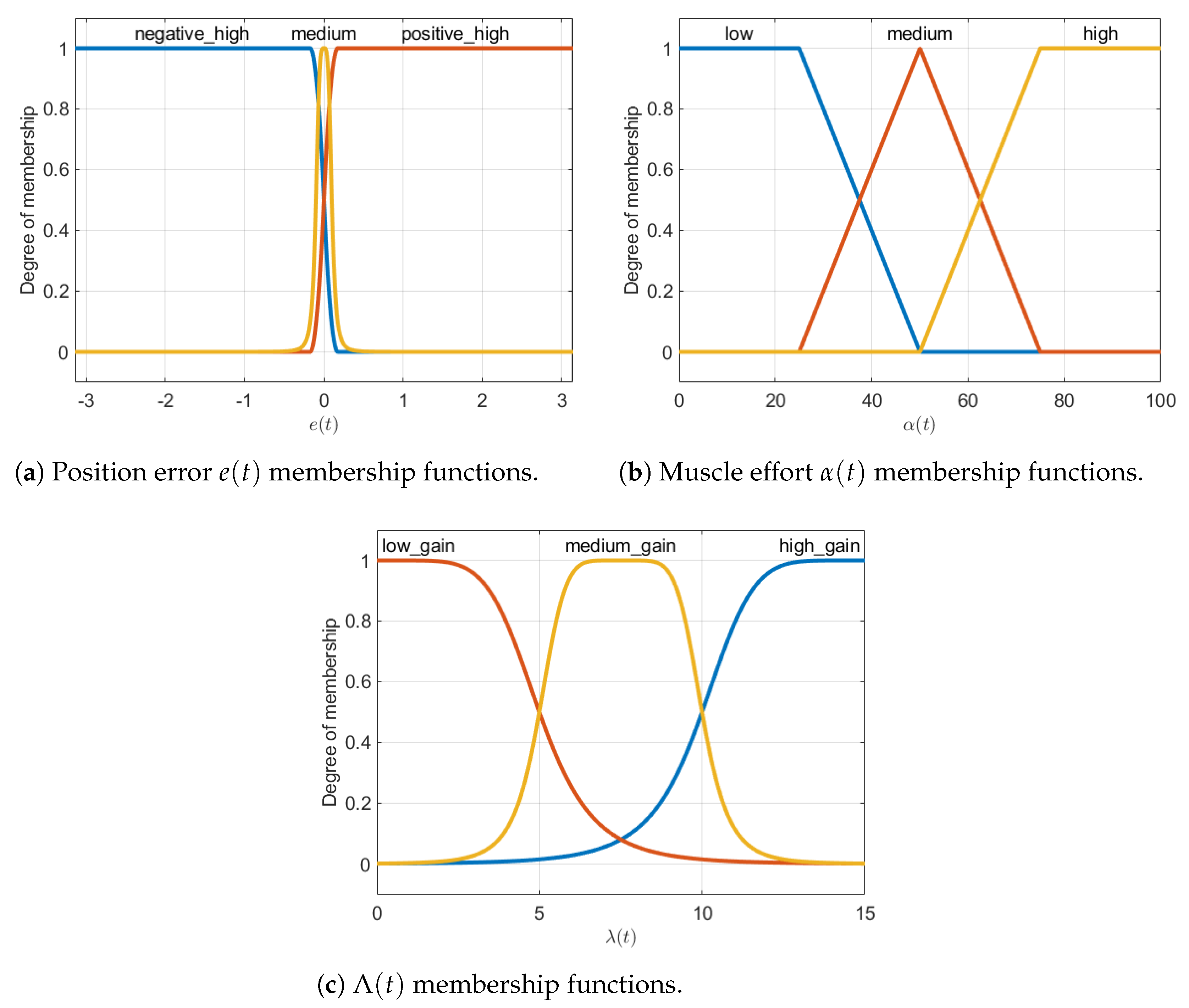
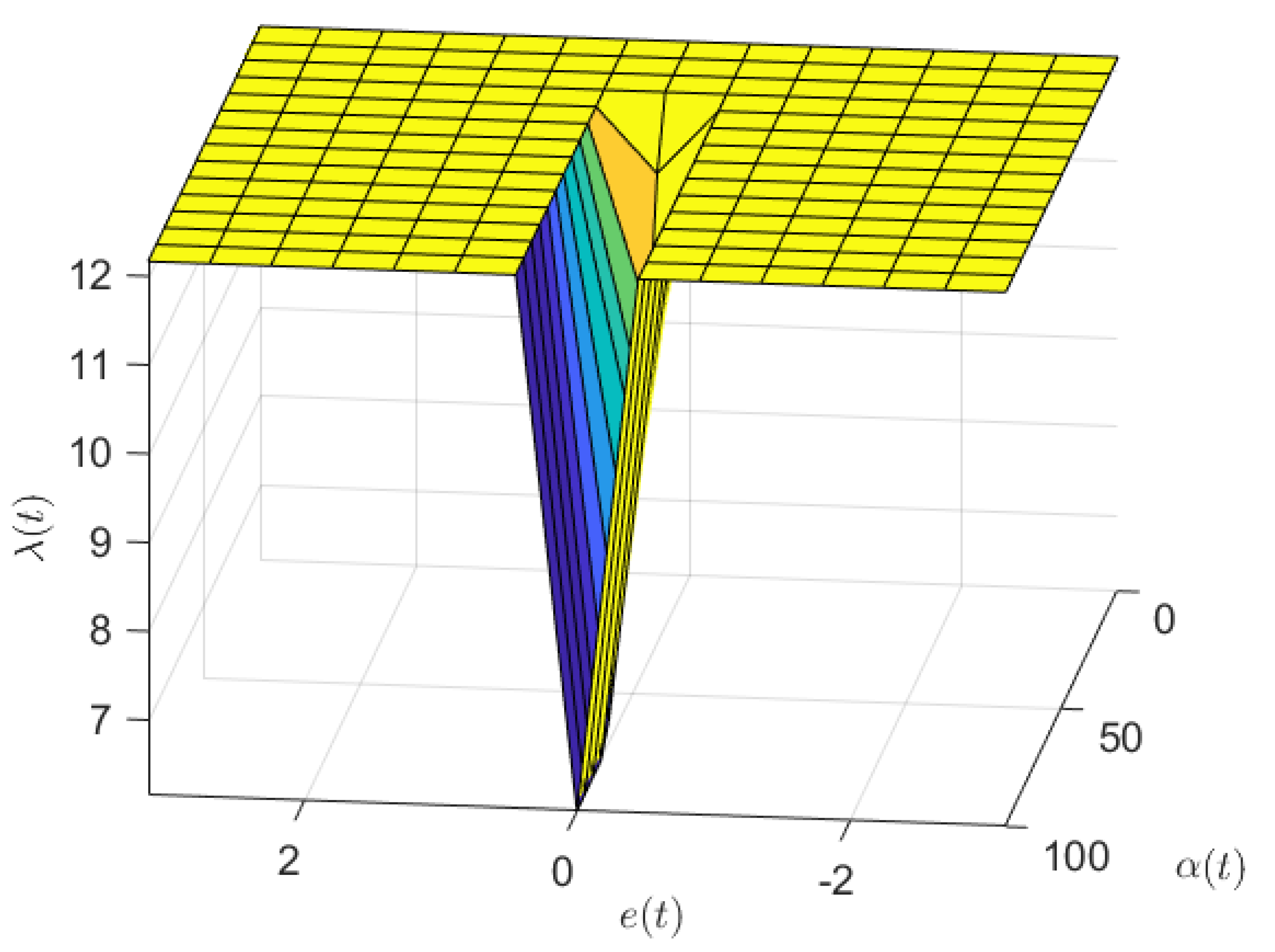
4.2. Fuzzy SMC Law
- If is positive high, then is high.
- If is negative high, then is high.
- If is medium and is high, then is low.
- If is medium and is medium, then is medium.
- If is medium and is low, then is high.
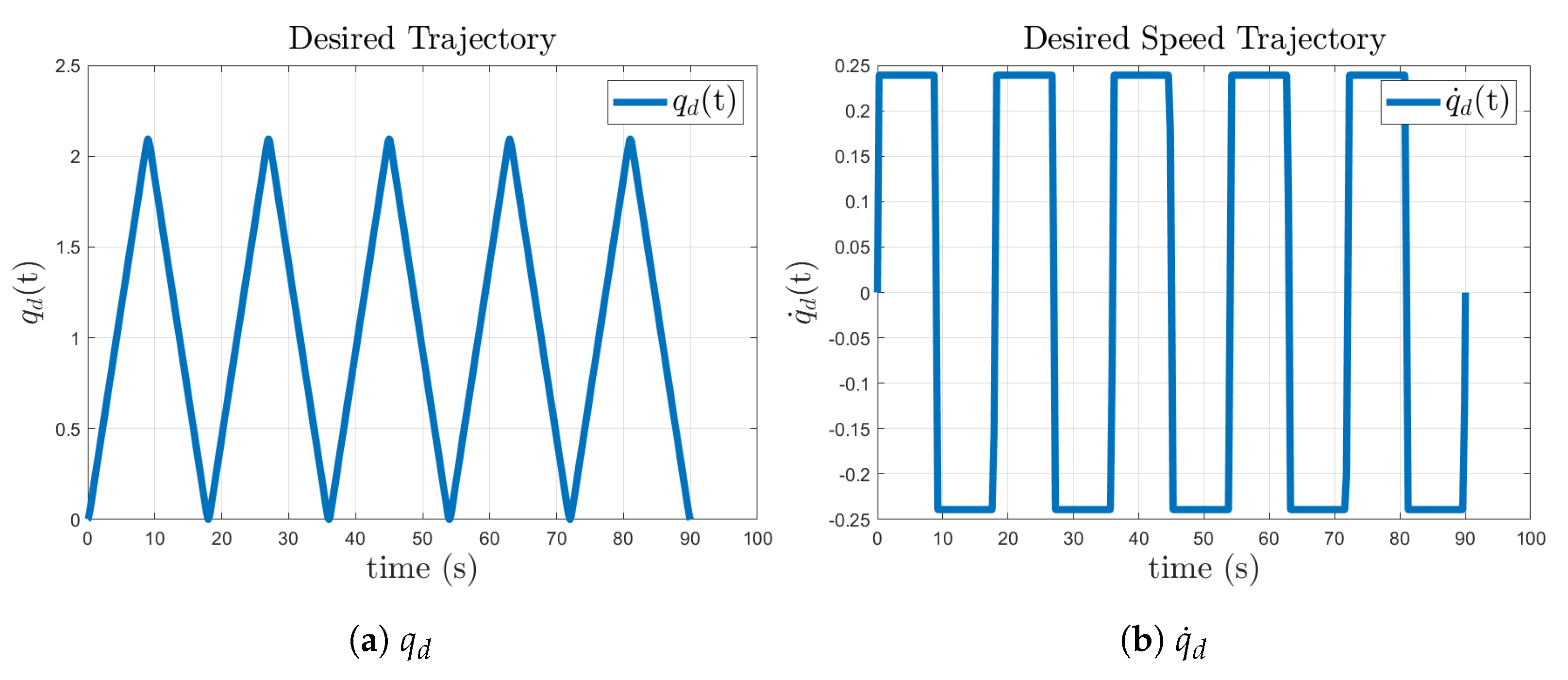
5. Results and Discussion
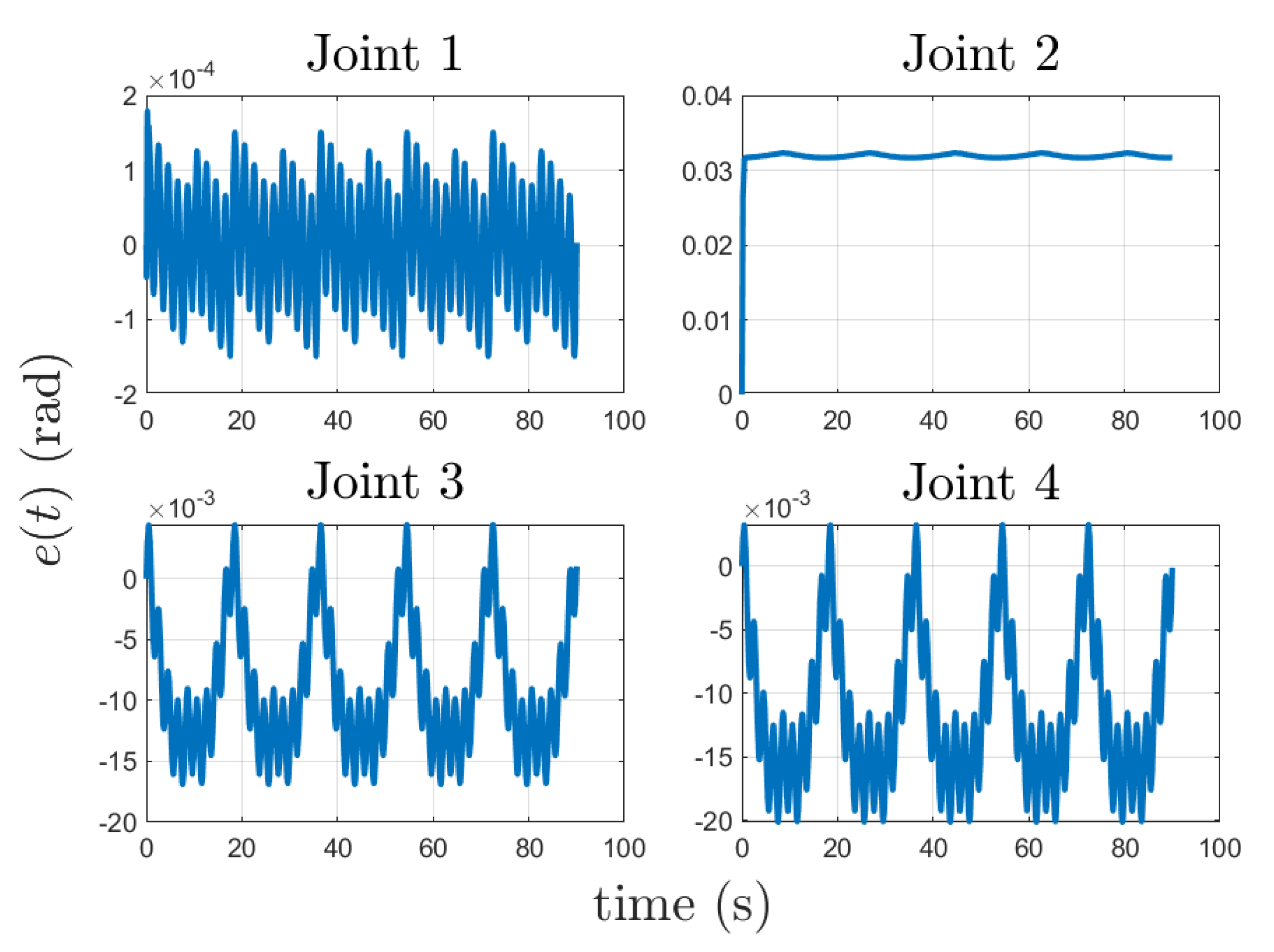
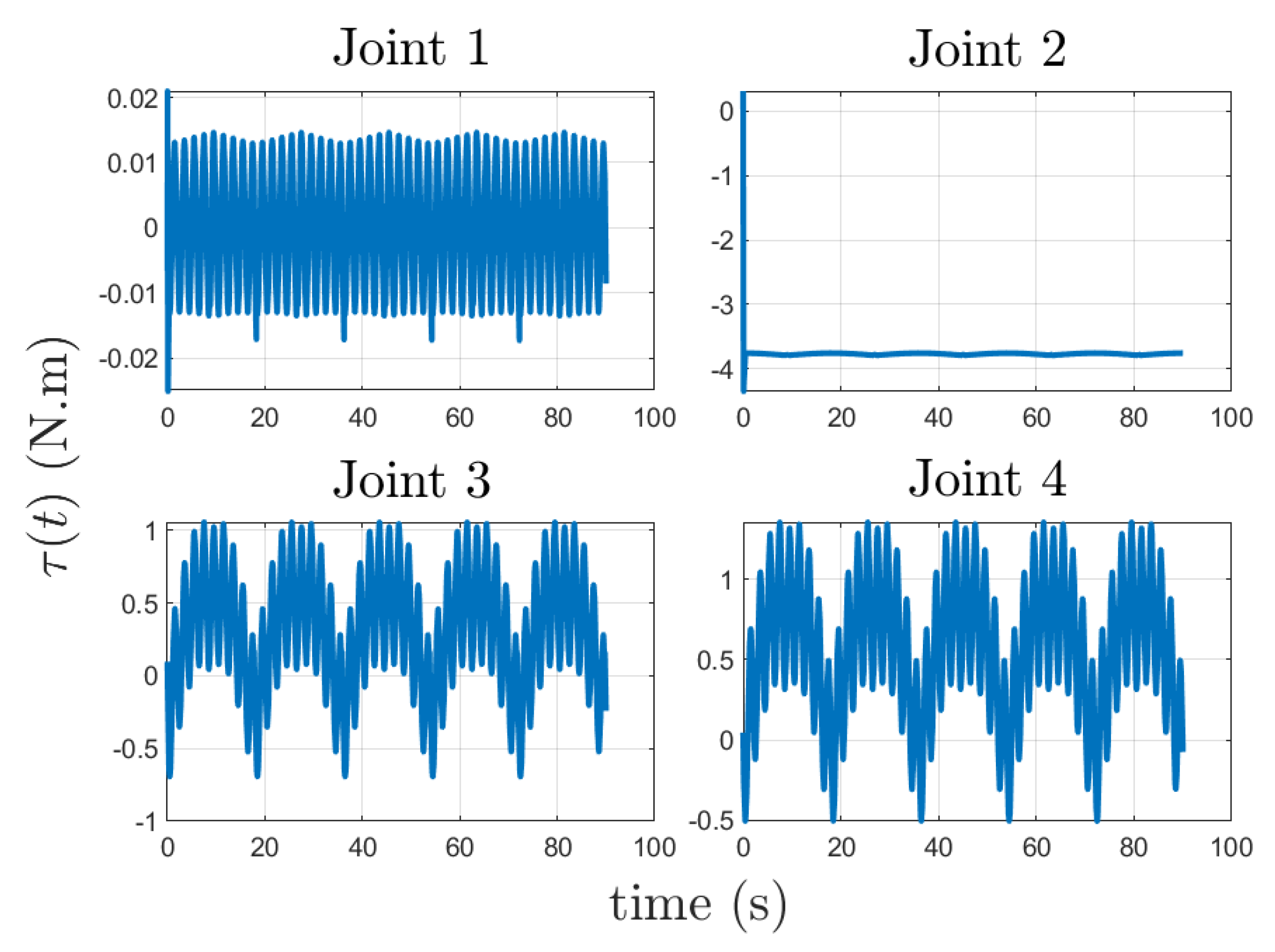
5.1. Implementation without Assistance
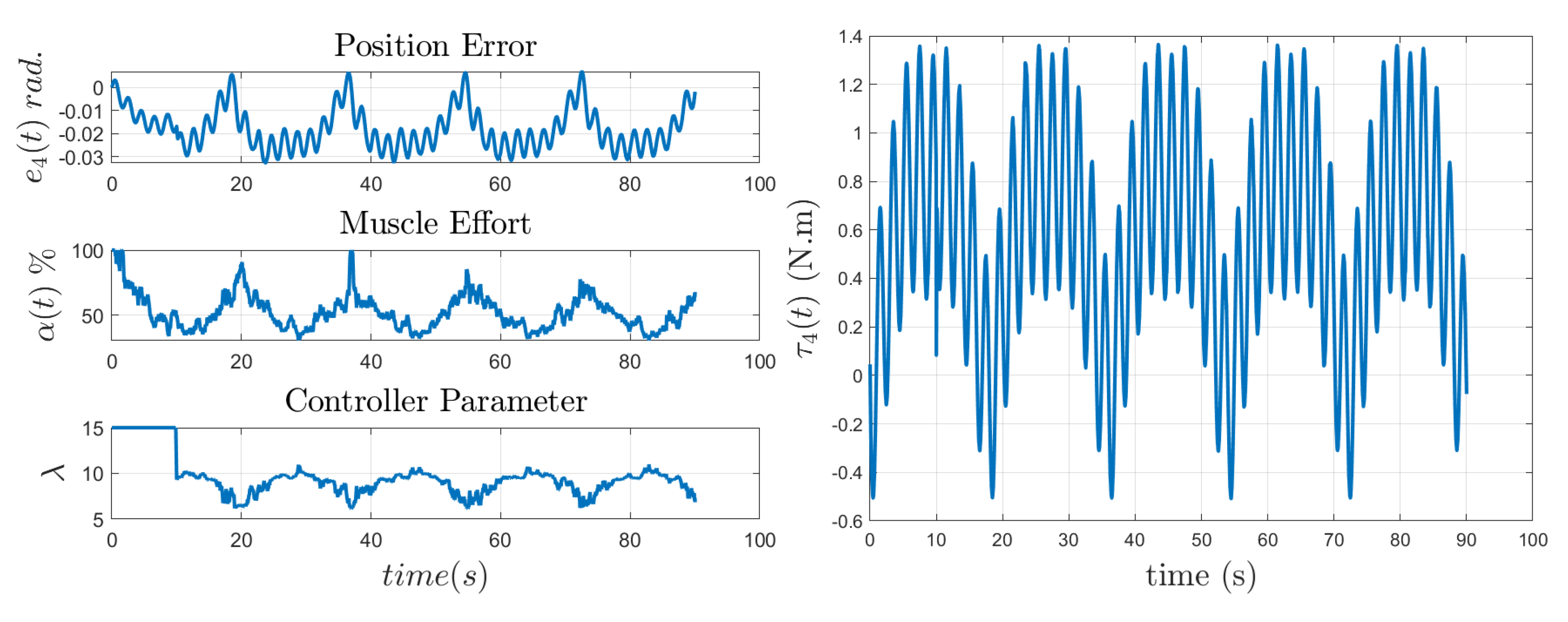
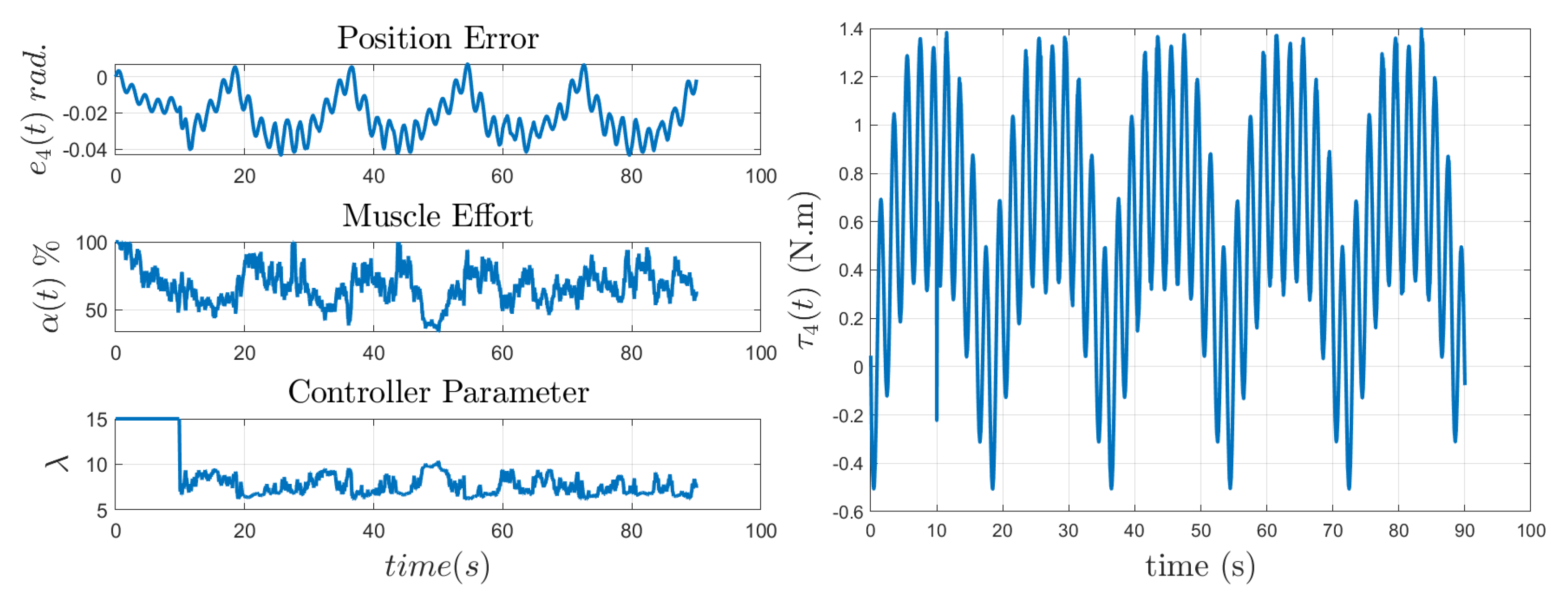
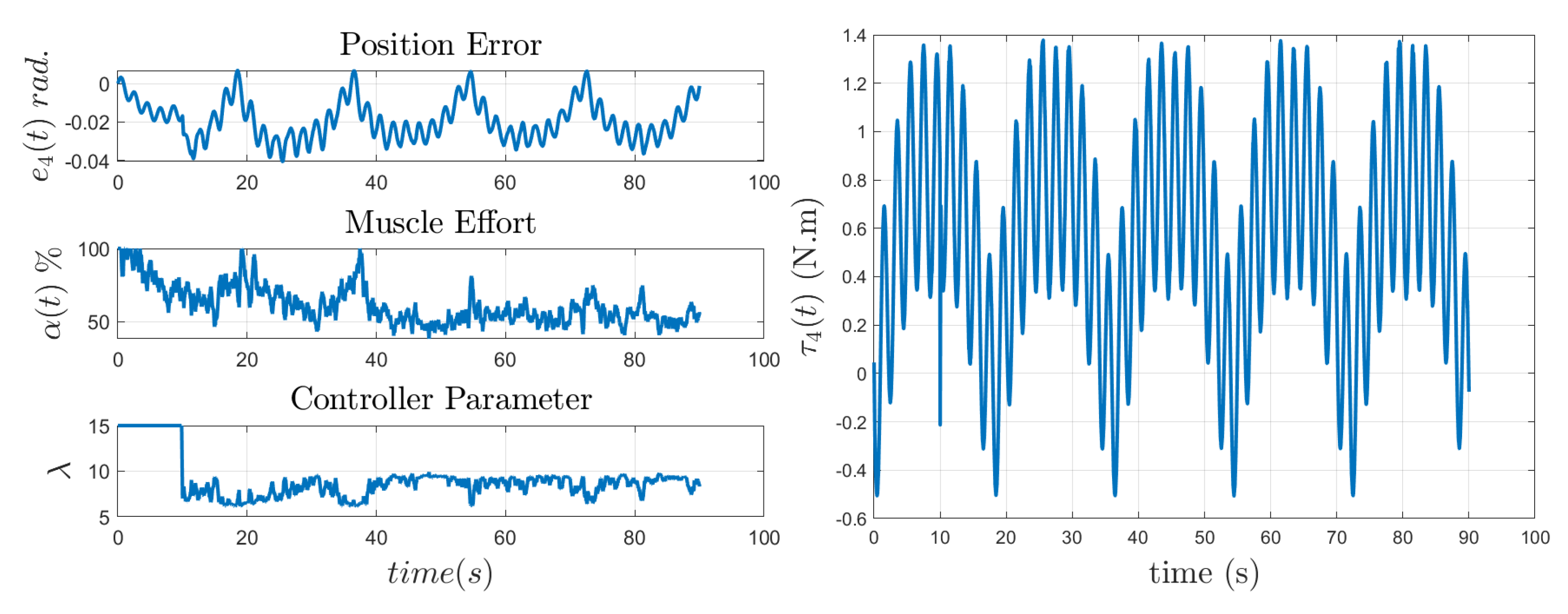
5.2. Implementation with Assistance
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Special Symbols
| Vector of torque and forces exerted by joints | |
| Sliding surfaces vector | |
| Positive-definite matrix of decaying exponential rate of the state trajectory errors | |
| Decaying exponential rate of the state trajectory error | |
| Signum operation | |
| Saturation operation | |
| Boundary layer value to smooth out the switching operation in the SMC | |
| Current surface EMG values | |
| Current maximum surface EMG values | |
| Calculated muscle effort |
References
- Krebs, H.; Volpe, B.; Aisen, M.; Hogan, N. Increasing productivity and quality of care: Robot-aided neuro-rehabilitation. J. Rehabil. Res. Dev. 2000, 37, 639–652. [Google Scholar] [PubMed]
- Benjamin, E.J.; Blaha, M.J.; Chiuve, S.E.; Cushman, M.; Das, S.R.; Deo, R.; Floyd, J.; Fornage, M.; Gillespie, C.; Isasi, C.; et al. Heart disease and stroke statistics-2017 update: A report from the American Heart Association. Circulation 2017, 135, e146–e603. [Google Scholar]
- Klamroth-Marganska, V.; Blanco, J.; Campen, K.; Curt, A.; Dietz, V.; Ettlin, T.; Felder, M.; Fellinghauer, B.; Guidali, M.; Kollmar, A.; et al. Three-dimensional, task-specific robot therapy of the arm after stroke: A multicentre, parallel-group randomised trial. Lancet Neurol. 2014, 13, 159–166. [Google Scholar] [CrossRef] [PubMed]
- Cai, L.L.; Fong, A.J.; Liang, Y.; Burdick, J.; Edgerton, V.R. Assist-as-needed training paradigms for robotic rehabilitation of spinal cord injuries. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation (ICRA 2006), Orlando, FL, USA, 15–19 May 2006; pp. 3504–3511. [Google Scholar]
- Hogan, N. Impedance control: An approach to manipulation: Part I—Theory. J. Dyn. Syst. Meas. Control 1985, 107, 1–7. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, L.; Tong, J.; Zhang, L. Arm rehabilitation robot impedance control and experimentation. In Proceedings of the 2006 IEEE International Conference on Robotics and Biomimetics, Kunming, China, 17–20 December 2006; pp. 914–918. [Google Scholar]
- Agarwal, P.; Deshpande, A.D. Subject-specific assist-as-needed controllers for a hand exoskeleton for rehabilitation. IEEE Robot. Autom. Lett. 2017, 3, 508–515. [Google Scholar] [CrossRef]
- Teramae, T.; Noda, T.; Morimoto, J. EMG-based model predictive control for physical human–robot interaction: Application for assist-as-needed control. IEEE Robot. Autom. Lett. 2017, 3, 210–217. [Google Scholar] [CrossRef]
- Mehdi, H.; Boubaker, O. Stiffness and impedance control using Lyapunov theory for robot-aided rehabilitation. Int. J. Soc. Robot. 2012, 4, 107–119. [Google Scholar] [CrossRef]
- George, J.A.; Gunnell, A.J.; Archangeli, D.; Hunt, G.; Ishmael, M.; Foreman, K.B.; Lenzi, T. Robust torque predictions from electromyography across multiple levels of active exoskeleton assistance despite non-linear reorganization of locomotor output. Front. Neurorobot. 2021, 15, 700823. [Google Scholar] [CrossRef]
- Vélez-Guerrero, M.A.; Callejas-Cuervo, M.; Mazzoleni, S. Artificial intelligence-based wearable robotic exoskeletons for upper limb rehabilitation: A review. Sensors 2021, 21, 2146. [Google Scholar] [CrossRef]
- Fleischer, C.; Wege, A.; Kondak, K.; Hommel, G. Application of EMG Signals for Controlling Exoskeleton Robots; Walter de Gruyter: New York, NY, USA, 2006. [Google Scholar]
- Hameed, H.K.; Hassan, W.Z.W.; Shafie, S.; Ahmad, S.A.; Jaafar, H. A review on surface electromyography-controlled hand robotic devices used for rehabilitation and assistance in activities of daily living. JPO J. Prosthetics Orthot. 2020, 32, 3–13. [Google Scholar] [CrossRef]
- Lambelet, C.; Lyu, M.; Woolley, D.; Gassert, R.; Wenderoth, N. The eWrist—A wearable wrist exoskeleton with sEMG-based force control for stroke rehabilitation. In Proceedings of the 2017 International Conference on Rehabilitation Robotics (ICORR), London, UK, 17–20 July 2017; pp. 726–733. [Google Scholar]
- Zhong, B.; Cao, J.; Guo, K.; McDaid, A.; Peng, Y.; Miao, Q.; Xie, S.; Zhang, M. Fuzzy logic compliance adaptation for an assist-as-needed controller on the Gait Rehabilitation Exoskeleton (GAREX). Robot. Auton. Syst. 2020, 133, 103642. [Google Scholar]
- Fuzzy logic systems for engineering: A tutorial. Proc. IEEE 1995, 83, 345–377. [CrossRef]
- Al Rezage, G.; Tokhi, M. Fuzzy PID control of lower limb exoskeleton for elderly mobility. In Proceedings of the 2016 IEEE International Conference on Automation, Quality and Testing, Robotics (AQTR), Cluj-Napoca, Romania, 19–21 May 2016; pp. 1–6. [Google Scholar]
- Louie, D.R.; Mortenson, W.B.; Durocher, M.; Schneeberg, A.; Teasell, R.; Yao, J.; Eng, J.J. Efficacy of an exoskeleton-based physical therapy program for non-ambulatory patients during subacute stroke rehabilitation: A randomized controlled trial. J. Neuroeng. Rehabil. 2021, 18, 1–12. [Google Scholar]
- Vaughan-Graham, J.; Brooks, D.; Rose, L.; Nejat, G.; Pons, J.; Patterson, K. Exoskeleton use in post-stroke gait rehabilitation: A qualitative study of the perspectives of persons post-stroke and physiotherapists. J. Neuroeng. Rehabil. 2020, 17, 1–15. [Google Scholar]
- Chen, H.; Ou, H.; Chen, H. A Method for Rehabilitation of Hand Dysfunction by Cyber Glove. In Proceedings of the 2015 International Conference on Advanced Engineering Materials and Technology, Guangzhou, China, 22–23 August 2015; Atlantis Press: Paris, France, 2015; pp. 393–396. [Google Scholar]
- Mocan, M.; Vlaicu, S.I.; Farcaș, A.D.; Feier, H.; Dragan, S.; Mocan, B. Cardiac rehabilitation early after sternotomy using new assistive VR-enhanced robotic exoskeleton—study protocol for a randomised controlled trial. Int. J. Environ. Res. Public Health 2021, 18, 11922. [Google Scholar] [PubMed]
- Qian, Z.; Bi, Z. Recent development of rehabilitation robots. Adv. Mech. Eng. 2015, 7, 563062. [Google Scholar]
- Pan, Y.T.; Kang, I.; Joh, J.; Kim, P.; Herrin, K.R.; Kesar, T.M.; Sawicki, G.S.; Young, A.J. Effects of bilateral assistance for hemiparetic gait post-stroke using a powered hip exoskeleton. Ann. Biomed. Eng. 2023, 51, 410–421. [Google Scholar]
- Graf, E.; Wirz, M.; Pauli, C.; Bauer, C. Ankle kinematics during walking with a soft exoskeleton in people with dropfoot–a case series. In Proceedings of the XXVIII Congress of the International Society of Biomechanics, Online, 25–29 July 2021. [Google Scholar]
- Chiș, L.C.; Copotoiu, M.; Moldovan, L. Different types of exoskeletons can improve the life of spinal cord injury’s patients—A meta-analysis. Procedia Manuf. 2020, 46, 844–849. [Google Scholar]
- Du Plessis, T.; Djouani, K.; Oosthuizen, C. A review of active hand exoskeletons for rehabilitation and assistance. Robotics 2021, 10, 40. [Google Scholar]
- Sarkisian, S.V.; Ishmael, M.K.; Lenzi, T. Self-aligning mechanism improves comfort and performance with a powered knee exoskeleton. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 629–640. [Google Scholar] [CrossRef]
- Denavit, J.; Hartenberg, R.S. A kinematic notation for lower-pair mechanisms based on matrices. J. Appl. Mech. 1955, 22, 215–221. [Google Scholar]
- Zefran, M.; Bullo, F. Lagrangian dynamics. In Robotics and Automation Handbook; Citeseer: Gaithersburg, MD, USA, 2005; pp. 5–1. [Google Scholar]
- Khalil, W. Dynamic modeling of robots using newton-euler formulation. In Informatics in Control, Automation and Robotics; Springer: Berlin/Heidelberg, Germany, 2011; pp. 3–20. [Google Scholar]
- Lynch, K.M.; Park, F.C. Modern Robotics; Cambridge University Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Featherstone, R. Plucker basis vectors. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation (ICRA 2006), Orlando, FL, USA, 15–19 May 2006; pp. 1892–1897. [Google Scholar]
- Kelly, R.; Davila, V.S.; Loría, A. Computed-Torque Control and Computed-Torque+ Control. In Control of Robot Manipulators in Joint Space; Springer: London, UK, 2005; pp. 227–241. [Google Scholar]
- Ullah, M.I.; Ajwad, S.A.; Islam, R.U.; Iqbal, U.; Iqbal, J. Modeling and computed torque control of a 6 degree of freedom robotic arm. In Proceedings of the 2014 International Conference on Robotics and Emerging Allied Technologies in Engineering (iCREATE), Islamabad, Pakistan, 22–24 April 2014; pp. 133–138. [Google Scholar]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice Hall Englewood Cliffs: Hoboken, NJ, USA, 1991; Volume 199. [Google Scholar]
- Edwards, C.; Spurgeon, S. Sliding Mode Control: Theory and Applications; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Slotine, J.J.E.; Li, W. On the adaptive control of robot manipulators. Int. J. Robot. Res. 1987, 6, 49–59. [Google Scholar]
- Young, K.D.; Utkin, V.I.; Ozguner, U. A control engineer’s guide to sliding mode control. IEEE Trans. Control Syst. Technol. 1999, 7, 328–342. [Google Scholar]
- Rahman, M.H.; Saad, M.; Kenné, J.P.; Archambault, P.S. Control of an exoskeleton robot arm with sliding mode exponential reaching law. Int. J. Control Autom. Syst. 2013, 11, 92–104. [Google Scholar]
- Echeandia, S.; Wensing, P.M. Numerical methods to compute the coriolis matrix and christoffel symbols for rigid-body systems. J. Comput. Nonlinear Dyn. 2021, 16, 091004. [Google Scholar]
- Sabut, S.K.; Sikdar, C.; Kumar, R.; Mahadevappa, M. Improvement of gait & muscle strength with functional electrical stimulation in sub-acute & chronic stroke patients. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 2085–2088. [Google Scholar]
- Fukuda, T.Y.; Echeimberg, J.O.; Pompeu, J.E.; Lucareli, P.R.G.; Garbelotti, S.; Gimenes, R.O.; Apolinário, A. Root mean square value of the electromyographic signal in the isometric torque of the quadriceps, hamstrings and brachial biceps muscles in female subjects. J. Appl. Res. 2010, 10, 32–39. [Google Scholar]
- Konrad, P. The abc of emg. In A Practical Introduction to Kinesiological Electromyography; Noraxon Inc.: Scottsdale, AZ, USA, 2005; Volume 1, pp. 30–35. [Google Scholar]
- Mamdani, E.H.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J.-Man-Mach. Stud. 1975, 7, 1–13. [Google Scholar]
- Heo, H.J.; Son, Y.; Kim, J.M. A trapezoidal velocity profile generator for position control using a feedback strategy. Energies 2019, 12, 1222. [Google Scholar]

| Link | ||||
|---|---|---|---|---|
| 1 | 0 | −0.275 | ||
| 2 | 0 | 0 | ||
| 3 | −0.413 | 0 | 0 | |
| 4 | −0.297 | 0 | 0 |
| Link | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Mass | 1.398 | 1.264 | 1.306 | 0.425 |
| Ixx | 0.076 | 0.013 | 0.028 | 0.008 |
| Iyy | 0.165 | 0.035 | 0.198 | 0.029 |
| Izz | 0.089 | 0.023 | 0.172 | 0.022 |
| Ixy | 0.0002 | 0.002 | 0.008 | 0.002 |
| Ixz | −0.078 | −0.006 | 0.063 | −0.011 |
| Iyz | 0.0000882 | 0.00026 | −0.003 | −0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delgado, P.; Gonzalez, N.; Yihun, Y. Integration of sEMG-Based Learning and Adaptive Fuzzy Sliding Mode Control for an Exoskeleton Assist-as-Needed Support System. Machines 2023, 11, 671. https://doi.org/10.3390/machines11070671
Delgado P, Gonzalez N, Yihun Y. Integration of sEMG-Based Learning and Adaptive Fuzzy Sliding Mode Control for an Exoskeleton Assist-as-Needed Support System. Machines. 2023; 11(7):671. https://doi.org/10.3390/machines11070671
Chicago/Turabian StyleDelgado, Pablo, Nathan Gonzalez, and Yimesker Yihun. 2023. "Integration of sEMG-Based Learning and Adaptive Fuzzy Sliding Mode Control for an Exoskeleton Assist-as-Needed Support System" Machines 11, no. 7: 671. https://doi.org/10.3390/machines11070671
APA StyleDelgado, P., Gonzalez, N., & Yihun, Y. (2023). Integration of sEMG-Based Learning and Adaptive Fuzzy Sliding Mode Control for an Exoskeleton Assist-as-Needed Support System. Machines, 11(7), 671. https://doi.org/10.3390/machines11070671






