Abstract
This paper introduces a new method for kinematic modeling of the robot arm by deriving a new elegant mathematical formula based on the axis vector with the tangent of the rotation angle. For this purpose, an innovative analytical quaternion is introduced through integration between Axis-Invariants and unit quaternion features named Ju-Gibbs quaternion, which expresses the body rotation with non-redundant parameters compared with the quaternions in literature. Two theorems based on the new form of the quaternion are developed and proved for the kinematic modeling of the robot arm. The first is attitude alignment, which is essential in multiaxial rotation systems. The second theorem for the wrist inverse kinematic (IK) solution is utilized to obtain the joint variables for the last joints of the end effector. In order to verify the effectiveness and accuracy of the proposed method, a numerical example and simulation of different structural configurations of robot and human arms are intensively studied. The novel quaternion provides a new tool for kinematic analysis and reduces the computational complexity of the kinematic solutions of the Robot-Arms wrist. Furthermore, the method laid a new foundation for the IKs of multi-axis systems based on Axis-Invariant and tangent quaternion.
1. Introduction
The development of mathematical theories for kinematics analysis of the rigid bodies and study of the robotics kinematics analysis has received much attention in the last decades [1]. The aim is to derive more appropriate forms representing the theoretical kinematics and describe the connection between the links that form the rigid bodies’ kinematics. Indeed, not only in terms of kinematic transformations description but also for presenting elegant and simplified formula to obtain the best solutions for the problems related to kinematics and dynamics of the bodies, computer graphics, and robotics kinematics analysis [2].
The kinematics body in three-dimensional space (3D) can be described by different kinematics theories such as analytical mechanics, vector analysis, algebra, and geometric algebra theorems [1,3]. The development of kinematics theories is due to Unit’s equations describing the kinematics of geometric structures in the form of a rotation matrix [4]. Then through vectors as in Rodrigues parameters, which express rotation by integrating the rotation angle with the coordinate components of the axis, which is sometimes called the Rodrigues vector-parameter [5]. The quaternion is also widely applied to represent the orientation configuration of the kinematic mechanism and the Robot-Arm. The quaternion is used to describe the orientation of a rigid body only by four elements. The theory was established algebraically by Hamilton [6]. It is more elegant in the representation of rotation, but it lacks the display pose of the body in a compact form. That is accomplished by using two independent variables and combining them separately. That led Clifford to provide a broad generalization of these numbers called biquaternions [7], and then have been developed into dual vectors and dual quaternions formulas for use in the studies of geometry and mechanics by [8]. It integrates translation and rotation in a single state, making the solution more explicit and robust. Therefore, the dual quaternions mathematical formula has achieved more attention than the unit quaternion formula [9]. Besides the algebraic transformation, the analytical representations of kinematics are also obtained through the matrices such as the rotation matrix 3 × 3 for representing the orientation [10]. It was then developed into a 4 × 4 homogeneous matrix to express the rotation and translation in 3D space. This representation concept was first applied through Denavit & Hartenberg (D-H); it is a most popular tool requiring fewer parameters to describe the relation between joint motions and link status in kinematic systems [11]. Furthermore, several theories with different approaches are used in mathematical and physical applications to represent the modeling of kinematics bodies. Such as screw and Lie group theories, wherein the screw theory provides the geometric setting and the Lie group theory gives the analytic framework for intuitive and efficient modeling of rigid body mechanisms [12]. While the product of exponentials (POE) is used for mathematical concepts to determine the infinite relative motion of joints of the kinematic chains [13]. In addition to rotation tensors [14], Gibbs parameterization [15,16], and computer algebra approach. Which are expressed in different parameters for describing the rotation and displacement in kinematic theories and formulas for analyzing the forward and inverse kinematic problems for Robot-Arms [17].
The mathematical theories developed by mathematicians have been widely applied to the physical application of those theories to kinematics mechanisms and robotics. In the recent period, different studies have been made on these theories for developing them from time to time to find closed and simplified solutions to the kinematic systems’ problems. In [18], proposed a decoupling method to calculate the joints of the spherical wrist. The IK solutions method is not optimal for different configurations of robot arms. Li et al. [19] introduced the IK solution for 6-DOF based on the rotation matrix. The robot arm model is divided into position and the inverse attitude solution for the last joints with Euler’s wrist. The method was optimal, but some solution results cannot be possible due to robot wrist singularity. Zhao et al. [20], decoupled the 6R into three-part 2R,4R and 6R chains to solve the particular Robot-Arm’s IK problem, which has three successive axes parallel to each other. The method cannot fully describe the Robot-Arm’s geometric information. Besides its still, the derivation process is complicated. F.Xiao et al. [21] proposed general methods for decoupling by selecting a different cut point and the orientation setting at the end of sub-chains, then new equations after deformation are given in 3-DOF of 6-DOF. The method is optimal and accurate, but it is not easy to apply for redundant robot arms.
The IK’s analytical solutions for redundant Robot-Arms were introduced in [22]. The Newton–Raphson method was utilized for secondary adjustment. The algorithm avoided jumping between interconnected configurations of the robot Kinematic Chain (KC), singularities, joint limitations, and the Jacobite matrix’s defects. In addition to that, the methods are not universal for applying to multi-chain. Kucuk et al. [23] used the decomposition method described in [24]; to solve the IK problem of non-spherical wrist Robot-Arms. The solutions are achieved by one-dimensional investigation analysis, and other joint angles variables are obtained by inverse substitution [25]. Their approach does not work intuitively for complex geometric relations. An et al. [26] presented a solution for IK by integrating the Paden-Kahan subproblems method with the exponential theory based on vector parameters. The [27] used the dual quaternion based on screw theory to obtain the analytical solution of IK. The solution processes effectiveness and efficiency were verified in a numerical example. Their methods lack general principles of the closure solution for different robotics arm wrists [28].
The methods for obtaining the solutions and kinematic parameters mainly affect the bodies’ kinematic and dynamic modeling efficiency, particularly for describing robotics’ kinematics and the Multi Axis Systems (MASs). Yet, an exhaustive engineering and mathematical analysis of kinematic modeling theories still need more development. That can be achieved only by combining and complementing them into new approaches and methods, giving a significant chance to improve the previous kinematics solutions and lay new approaches and foundations for tackling current challenges. Based on those criteria, the quaternion can be the most appropriate and powerful tool for describing kinematic body rotation and obtaining the attitude directions of the end effector (EF) of robots. To the best of our knowledge, recent studies have yet to be conducted to improve and use the unit quaternion to represent rotation in rigid bodies and concurrently obtain the IK solutions of the kinematic systems.
In this regard, this paper presents a new approach to kinematic modeling of the robot arm based on the axis vector and the tangent half angle. The aim is to propose a new optimal mathematical formulation to represent the body’s rotation and desired orientation by integrating the axis invariant vector with features of the quaternion. The novel quaternion vector is expressed only by three variable quantities, while the scalar part remains constant and does not change with the rotation of the axis. The method also demonstrates how to obtain the direction alignment for the MASs and get the IK solution of the robot arm wrist using mathematical derivations and proofs. In addition, a comparison of the proposed method to the literature is carried out; to show the proposed method’s uniform expression, simplicity, and generality. The tangent quaternion introduces a different tool for kinematic analysis and reduces the computing cost of Robot-Arms wrist kinematic solutions by reducing the parameters. Based on the Axis-Invariant and quaternions features, the approach offered a new basis for MAS’s kinematics modeling and IK solutions.
The following Section 2 shows the basic concept of the configuration of KC topology based on axis vectors and discusses the 3D rotation geometrical interpretations based on the properties of the Axis-Invariant theory. Section 3 illustrates the arithmetic operations and 3D rotation based on quaternions and a new analytical quaternion. The kinematics analysis and comparison between the literature with the new quaternion are presented in this section too. Based on the new quaternion, the orientation alignment theorem and the orientation IK solutions theorem is illustrated in Section 4; hence all the arithmetic operations and proofs are presented in the Appendix A. In Section 5, several numerical examples of the robot arms with different structural configurations are illustrated and discussed. In Section 6, the conclusion is presented.
2. The Kinematic and Mathematical Framework
The rotation of the rigid body can be displayed with different parameters and forms depending on theories and methods used to represent the kinematics of mechanisms. In this paper, kinematic theories are explained and applied through the robotic kinematic mechanism. Most of the technical and topological symbols of the KC used in this paper are illustrated in the Nomenclature. These symbols are not only for conciseness but also for describing the partial structure ordering and topological relation feature of the MASs. The choice for the notation comes in this works from the fact that we are interested in the geometric properties of the kinematic modeling tools in the 3D Cartesian space and Natural coordinate systems and axis vectors of kinematics systems [29]. The left superscript and the right subscript indicate the coordinate system and KC (k-th joints) order to which a particular vector is referred.
2.1. The Kinematics Modeling of Robot Arm
The serial robot arm is composed of a number of joints (revolute or prismatic) and linkages that connect between the base and EF of the robot arm. The joint variables are scalar, and the algebraic product between the joint variables is called compound variables. The joint and link are the smallest part of the kinematic system, and the minimum KC contains two joints. The robotics’ joints and links are expressed as basic components of the mechanism systems. The joint numbers determine the DOF of robotics. We describe each joint with the unit axis vector () and links parameters () which describe the link length and offset in single-column vector form; that formulate the kinematic parameters, as shown in Figure 1.
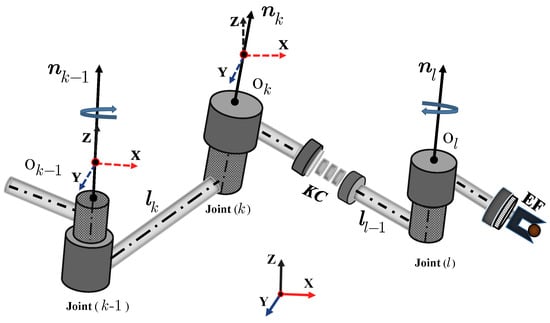
Figure 1.
Kinematic axis chains.
The axis-vector represents the unit direction of the kinematic axis and is the natural reference axis, of which its members = determine unit direction; and the angular position determines the magnitude of fixed-axis rotation [19]. Therefore, the axis vector is also termed the Axis-Invariant in [29]. The axis invariant is a free vector, and it is always directed to the outside of the origin of the frame. It has a fixed origin and is constrained by the structure links vector is measured from the origin of the link (predecessor link) to leaf link (l) (successor) at time . At the initial time, all the natural frames share a common attitude, and any joint pair has zero position. After any rotation by from the joint () to the projection on the successor joint (), the translation can be described by position vector (), which describes the successive translation from the base to the EF of the robot arm. For further clarification, when a robot system is in its initial state (Home position), all joint variables are defined to be zero; at this condition, the position vector is equal to the link vector (), between each independent joint axis. That is because all links’ coordinate systems coincide with the body coordinate system.
The fixed axis theory isomorphism with Euler Rodriguez’s formula in its mathematical form, but its physical explanation is more analytically straightforward and precise in representing kinematic mechanisms connectivity [5]. It can also be applied effectively to solve many theoretical and practical engineering problems [16,30].
2.2. Wrist Types and Structures
The 6-DOF robot arm is commonly used in several fields. The 6R robot arm has different structure configurations between joints and linkages between them. The first three joints are responsible for getting a position of robot arm, while the last three joints control the wrist joint orientation of the EF.
Although the class of robot arms mentioned above with this feature is quite broad, we will focus on the most common types of robot wrist: (a) Euler’s wrist: axis No. 4, No. 5 and No. 6 intersect at one point (wrist center); (b) axis No. 4 and axis No. 5 intersect at one point, and axis No. 5 and axis No. 6 intersect at another point this type is named Offset wrist or Non-Spherical wrist; (c) general wrist in which the axis No. 4 does not intersect with axis No. 5 and axis No. 6 in robot frame, or axis No. 5 does not cross axis No. 6 that is the three-axis do not have any common intersect. This kind of general robot arm is controlled by axis’s No. 4 and No. 5 for the desired attitude, defined as a redundant robot arm wrist, which is often infinitely rotating its end-effector to align with the desired position and attitude; some types of robot arm wrists are shown in Figure 2.
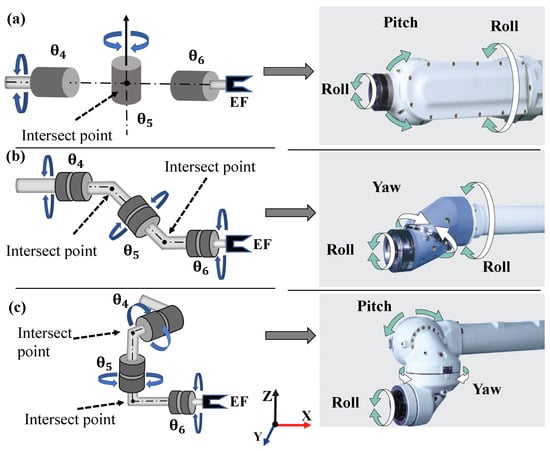
Figure 2.
The structures of (a) General wrist (b) Offset wrist (c) Euler’s wrist.
The last three joint variables can be calculated in different methods to achieve the alignment between the wrist center position and desired positions in most decoupling robot arms.
In this work will focus only on the forward and IK solutions of the wrists of the robots. Therefore, the positioning problem solution methods go out of the scope of this paper, so they will not be covered here.
2.3. The Transformations of the Kinematics Body
There are several tools to describe the transformation of the robot arm and kinematic systems. They have some advantages for describing some systems and disadvantages for modeling other kinematic systems. We will briefly focus on some common tools used for kinematic problem solutions and consider how to improve them. In order to obtain the optimal kinematic equations that are used to model the forward and IKs of the Multi axes kinematic systems.
2.3.1. Rotation Matrix
The Robot-Arm is frequently designed with special architecture to reduce the structures’ common constraints and allow decoupling of the positioning from the orientation problems. The architecture of the robot arm design determines how difficult or simplicity to describe the kinematic modeling of robot arms into optimal mathematical formulas [16]. The rotational matrix is commonly used for the general robot arm to describe the forward and IKs based on the axis vector the Rodrigues’ rotation matrix can be expressed as:
the is the identity matrix, and ). Equation (1) is shown that the rotation matrix is a multilinear equation containing sin and cos of rotation angle. Where the desired orientation of KC with several joints can be obtained by the successive multiplying of as:
for the position vector the coordinate transformation of the general robot arm can be represented as:
2.3.2. Euler Angles
The most common method to represent the orientation of a rigid body. It is a set of 3- angles named roll , pitch , and yaw [1,17]. The three coordinate rotations in sequence can describe any rotation of the kinematic system. they are easy to understand and easy to use. The rotation Sequences are essential in Euler angles. In fact, of the 27 possible sequences of three (X, Y, Z) axes. There are only 12 that meet the constraint that no two consecutive numbers in a valid sequence may be equal. In the kinematic transformation, it is easy obtaining an inverse mapping between the Euler angles and the rotation matrix [3]. The triple rotations in a 3D coordinate system can be presented as:
The main drawbacks of Euler angles are that (1) they are less accurate than unit quaternions when used to integrate small-scale changes in orientation over time, and (2) some essential functions of Euler angles have singularities. (3) It cannot add or subtract Euler angles to express the transformation between the kinematic base frame to the wrist EF frame because they are not vectors [17]. It needs to convert the Euler angles to a representation that can be composed, such as a rotation matrix or unit quaternion.
2.3.3. Unit Quaternion
Fixed axis rotation is uniquely represented in quaternion form to represent the rotation in 3D space; it is determined by the and rotation of the half-angle. The quaternion has four parameters in one column. It can represent 4 × 1 an array, where it is defined in the vectors part in three-element by integrating the direction sine of the rotation axis, and further a scalar with the cosine of the half-angle. In this paper, the quaternion notation does not correspond to the [6]. Here the real part of quaternions is ordered at the quaternion element’s last [31].
where is a vector part, is a scalar part, and The characteristics of quaternion algebra are summarized in Table 1. In quaternion construction, the addition and subtraction are commutative and associative, where the quaternion product is not commutative in the general case. The conjugate is the same as the inverse in mathematical expression; it requires only changing the sign of the vector part, for KC that means the order chain connectivity change so and are equivalent. In this paper, the axis vector is considered invariant, because its direction is specified in advance before modeling, so the cannot be redefined.

Table 1.
The properties and mathematical operation of unit quaternion.
The quaternion multiplication can also be represented in the forward rotation operation of the axis chain as:
The orientation equations are expressed by matrices, Euler angles and quaternions for desired orientation, where the linkages offset is not effective for obtaining the attitude alignment. From the aforementioned, it is clearly shown that the polarity and connectivity between joints and links of the robot’s arms based on the axis invariant theory are more flexible for expressing the kinematics modeling of the MAS.
Table 2 summarize some features and computation cost operation beside the parameters number related to memory storage of parameters needs for more details [2,32].

Table 2.
The main algebraic approaches for kinematic modeling.
Compared to the Cartesian axis chain’s attitude analysis, the rotation matrices and quaternion are the primary tools used for describing the rotation and orientation of rigid bodies (because the orientation part in Homogenous Matrix and dual quaternion is a rotation matrix and unit quaternion, respectively). Whereas the quaternion has more features over the matrices for the representation of the orientation and rotation of the robot arm [1,2]. The quaternion is faster computation, less noise representing pure rotation [32], and simple rotation interpolation [31]. It is more compact, with only 4 elements, more numerically stable for kinematic modeling, and compared to the Euler angles, composing and avoiding the gimbal lock problem or singularity in robotics is simpler [17,33].
Therefore, the quaternion is suitable for the kinematic modeling of bodies. Besides these advantages and superior, the quaternion has several shortcomings that warrant further investigation and resolution, such as:
- Unit quaternions require more arithmetic and are less intuitive than Euler angles and Exponential matrices.
- Compared to homogeneous transformation matrices and dual quaternion, the unit quaternions have a rotation and no translation.
- Unit quaternions have four parameters, but compact rotation representation can only use three.
- Obtaining IK solutions with optimal equations using pure quaternion is difficult.
Those drawbacks are one of the main motivations for proposing a new analytical theory that uses minimum parameters to describe robotic kinematic transformations, which must be equal to the natural constraints in 3D space.
From the aforementioned, in order to obtain an optimal expression for describing the rotation of the robotic arm and multi kinematic axis chains, the next part demonstrates and analyzes with more depth the new analytical quaternion formula based on an integration between axis invariant parameters and quaternion features; where this research is developed based on patent [34].
3. Quaternion and Kinematic Analysis
In this section, a new analytical quaternion was proposed to describe the rotation of multi-axis chains and achieve optimal kinematics modeling formulas, including eliminating variables, dimensionality reduction, and symbol analysis. In addition to performing an analytical comparison of the quaternions in the forward kinematic of the EF of the robot’s wrist.
3.1. New Analytical Quaternion
The natural space has 6D; from this perspective, it is clear that the position and orientation equations based on rotation vectors, rotation matrices and unit quaternion do not meet the minimum requirements for describing kinematic equations robots formula [9,31]. Therefore, the kinematic equations must be constructed not to be redundant, for describing the kinematic transformations of MASs. To enhance quaternion features and eliminate some existing cons of a unit quaternion. The tangent quaternion named Ju-Gibbs attitude quaternion; is proposed as an analytical quaternion to describe the orientation of bodies in a unified form, which is the isomorphism to unit quaternion established by Hamilton and JPL for analytical description and kinematic solutions, but not fully homomorphism for numerical calculation [6,34]; it is defined as:
where is the vector part and is a scalar part.
The multiplication algorithm of such Ju-Gibbs quaternion and the operation product still results in the rotational formula [6,12,16]. It is similar to the complex multiplication law [3]; rotations of quaternions and in 3D space is shown in Figure 3. The quaternion can write in universal form as
where · denotes the quaternion multiplication.
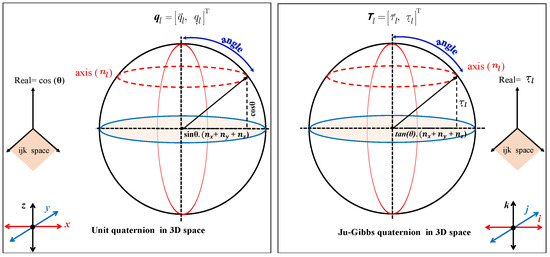
Figure 3.
The quaternions rotation in 3D space.
From Equations (7) and (8) the quaternion multiplication can represent the forward rotation operation of the kinematic axis chain as
where is matrix. Equation (9) showed that the quaternion multiplication could be replaced by its matrix calculation called a quaternion concatenation calculation; it is written as
3.2. Canonical Formula of Ju-Gibbs Quaternion
The other motivation for proposing a new analytical quaternion besides the cos in fourth elements looks redundant in kinematic modeling. The new quaternion has represented the rotation of bodies in a simple, compact form and further reduces the number of kinematic equations. Therefore, It is presented in tangent half angles rather than sin/cos angles, and the reference part does not change in the rotation of a single join.
Lemma 1.
The scalar for KC in Ju-Gibbs quaternion form; that is true only for all single joints of KC and for kinematic joints pair if the axes , are orthogonal, and as well as is termed as canonical Ju-Gibbs quaternion of .
Proof.
The calculation of scalar product means the projection of vectors, which form a reference axis for rotation, or termed the fourth axis of rotation in 4D quaternion space. For two axes rotation, the reference axis is for the inner product; the term for all orthogonal axis vector (), thus the .
In contrast, the scalar part of quaternion for parallel axes depends on the value of the joint’s angle (). The attitude of the single joint of KC can be expressed by canonical Ju-Gibbs quaternion as:
from Equations (7) and (13), the modulus square of can be for non-orthogonal axis and for orthogonal multi-axis and single-axis in canonical form. In addition, for the unit quaternion in Equation (5), the sin and cos of half angle’s square modulus equal 1, making a strong constrain in kinematic modeling analysis, which is another drawback that needs to be considered and solved in the new quaternion. □
Lemma 2.
For parallel or adjacent orthogonal axes with , and as well as , the property of module of analytical quaternion is shown as:
the is used to reduce the degrees of kinematic equations and is utilized for the general decoupling requirements of robot arm wrists. The additional algorithmic operations and proof details are clarified in Appendix A.
3.3. Attitude Alignment for 6-DOF Robot Arm Based on Ju-Gibbs Quaternion
The orientation equations of the 6R robot based on the Ju-Gibbs quaternion are expressed as:
the kinematic Equations (1) and (15) are concerning structural vectors and joint variables. The Equation (15) in terms of are for attitude alignment.
To deal with the Ju-Gibbs quaternion calculation for inverse orientation solutions, we need to separate the wrist structures parameter from the position joint variables to simplify the computational complexities called decoupling between the position and orientation of the robot’s arm. For decoupled robots, the equation The Equation (15) is expressed as:
consider Equation (13), (15) and (16), the desired alignment of the 6-DOF robot arm based on the Ju-Gibbs quaternion is
and the attitude equation is also equal
where is desired quaternion and for attitude in vector form; where that indicates both joints are in the zero states or no rotation, and the robot is in the initial attitude or home position.
Remark 1.
For the general 6R robot arm the direction of the wrist is mainly determined by the 4-th and 5-th axes, which control the orientation of the last joint attached to the robot’s EF.
According to Remark the Equations (1), (2) and (15), have described the kinematic system of the general 6R robot arm; in terms of translational and rotational motion. The last axis of the Robo-Arm must be aligned with the desired direction to perform the required operation. If the robot does not have tools fixed at the EF (i.e., tool center point (TCP) = 0); thus, the last joint is just infinitely rotating the EF of the robot arm to align with the desired position and attitude. The first 5-axes, control the position of axis No. 6 to align with the desired position and the direction, then control axis 4 to satisfy the radial alignment (in most robots, arm joints 4 and 6 rotate in the same direction). Therefore, the General 6R Robo-Arm only needs to establish the position and attitude equation with the first five Joint Variables. Thus, the orientation equations of the 6R robotic arm can be represented in the vector form as:
where desired quaternion; actually, only three elements are enough to present the orientations so that the scalar part can be equal to the unit for desired attitude alignment. For the sake of clarity, consider the desired unit quaternion in (5) and (7) respectively. Where the equivalent numerical factor between the unit and Ju-Gibbs quaternions for the 6R decoupling Robo-Arm can be denoted by
from (14), (A3) and (A4) the modular is ; Thus the equivalent factor between quaternions can be expressed by
where .
The factor can be used to convert between both quaternions in numerical experiments, and they are totally independent of the analytical orientation description. Where the feature of the simplified and unified variable of our proposed method for high-DOF kinematic and n-DOF IK orientation solution of robot arm wrist. More details and the relationship between the two quaternions approaches are provided in Appendix A.4.
From mentioned above clearly show that Ju-Gibbs quaternion is isomorphic with unit quaternion in kinematic modeling. Compared with the Euler angles, rotation matrices, and quaternion, the attitude alignment represented by the Ju-Gibbs quaternion needs less computational and operational costs to obtain the robot wrist’s orientation alignment. Additionally, the Ju-Gibbs quaternion carries all the advantages of the unit quaternion over matrices for the kinematic modeling and also has another feature that is non-redundant in orientation representation.
Some properties of an analytical quaternion are shown above for arithmetic and general kinematic concept. The following section discusses more properties of Ju-Gibbs quaternion related to the kinematic system. It also shows how they can be used to derive a compact formula for representing the forward and IK.
4. Kinematic Analysis Based on Ju-Gibbs Quaternion
This section shows the analytical quaternion for representing the kinematic of the robot’s arm. The two theorems are derived based on analytical Ju-Gibbs quaternion for finding the desired attitude of the EF in forward and IK based on axis vector invariant.
4.1. Orientation Alignment of the Robot Arm Wrist
Based on the study of rotation vectors in kinematic theories [1,3,16]. A new theorem for attitude alignment based on Ju-Gibbs quaternion is shown and proved as follows:
Theorem 1.
Case 1.For orthogonal axes:
Considering the KC definition in Section 2.1, if axis-vector aligns to the desired axis-vector , and if the robot arm greater than 2-DOF and ; then there exists at least one of Ju-Gibbs quaternion for multiaxial rotation, the desired attitude of the robot wrist can be obtained as:
thus
and
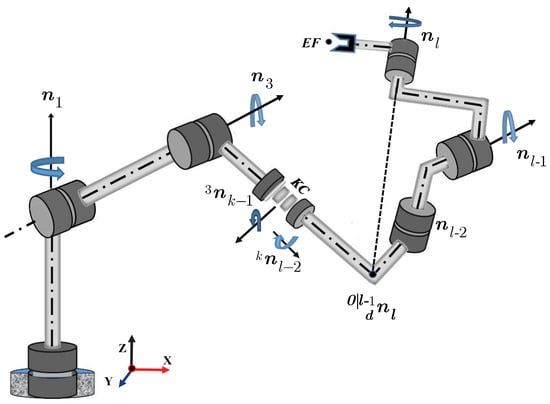
where is the desired vector of the last two joints and the is tangent half angles of combining of two last joints from EF of robot wrist. Figure 4 is shown an arbitrary configuration of a robot arm with a common orthogonal architecture. The Theorem 1 is proved in Appendix A.3.

Figure 4.
Decoupled robot arm.
Case 2. For non-orthogonal axes: To deal with the constraint of the non-orthogonal axes or there is no projection between the last axis with position axes in Equations (A17) and (A18); Assume that the KC has k-th joints for decouple robot arm. The first axes are used to determine the position; while the last two axes from EF, which are attached to the last joint radially or axially, are used to control the desired orientation of the robotic arm. In this case, the alignment and desired orientation will be obtained as 2-DOF for the wrist.
Since the orientation of the EF is given in unit quaternion or matrix , that mean the elements of desired quaternion are known. However, it is still needed to find the combined quaternion rotation of frames No. () and No. () for desired quaternion . From Equation (8) the ; and from Equations (8) and (A6) we take feature of the modulus invariance of Ju-Gibbs quaternion in Equation (14); then result in:
and
where from Equation (19) the will be achieved from:
Note the orientation solutions in this case mainly depend on axis invariant parameters of robot arm-wrist and first joint variables of axes To avoid singularity, the this is valid for joint angles range ; and the scaler part of quaternion in canonical form.
Theorem 1 described the attitude alignment based on the integration between the Caley transformation and Ju-Gibbs quaternion [15]. The theorem can also be obtained the desired quaternion of axis No. () and No. () of the n-DOF robot arm in optimal expression as in equations Equations (10), (18) and (19). The following part shows how to obtain the wrist angles in the joint space by deriving a new formula to find the IK solution of the robot wrist in closed form.
4.2. Direction IKs Solution Based on Ju-Gibbs Quaternion
Based on the kinematic structural vector and properties of analytical quaternion shown in Equations (10), (15) and (16). The orientation problem solution can be represented analytically. The desired orientation alignment will be obtained from Theorem 1; if the projection of the first axes on the last axis rotation of EF of the robot arm is known. Hence the direct IK for the last two joints () and () of the robot wrist can be obtained by using the analytical quaternion for n-DOF of the robot arm, as follow:
Theorem 2.
For the sake of clarity, we assume that k-th is the number of KC. Combined with the previous methods mentioned above, consider k = 6, so the robot arm has 6-DOF. For the robot arm and the desired Ju-Gibbs quaternion of axis No. 5 is denoted as , consider Equations (8) and (22), and Theorem 1. The first three joints in term are intended to determine the 3D coordinates of the EF, while the last joints to define the orientation. Where the robotic arm orientation equation can be defined as:
the first three joints are not taken here because the and are related to position alignment projection for the last two joints. The desired attitude alignment based on analytical quaternion can be expressed as:
thus the scaler part for is equal to unit 1 if the Ju-Gibbs quaternion is in canonical form. Then from Equations (12) and (28), obtain:
where the is desired vector part and is half companied angle from the projection of axis No. 3 to axis No. 5 of the wrist in . Rearrange the Equation (29) for more simplification by separate the structure parameters form joints variables result in
where is the matrix of adjacent axes vectors denote as:
the inverse square matrix of , and results in
where and ; the and are independent and they are determined the structural parameters of . From Equations (31) and (32) if the axis of rotation No. 4 perpendicular with No. 5 () that the still exists and the determinant of the matrix is ; and , if that the , the is not valid, if the is nonsingular Equation (29) results in:
consider Equations (30) substituting (31) and (29) into Equation (28), obtain
From the last row of Equation (29) and the first of Equation (34) the scalar part of Ju-Gibbs quaternion is equivalent to:
hence the scalar part of attitude quaternion is unit if and are perpendicular (), and when they are non-orthogonal, the scalar part depends on the value of the joint angle between them. From Equation (34), the attitude alignment based on Ju-Gibbs quaternion can be obtained in tangent form and the orientation direct inverse solution is obtained as
that for all . and if the IK solutions obtain by
Equation (34) shows that the robot wrist’s attitude alignment depends mainly on the axes of rotation No. 4 and No. 5. The first row of Equation (34) is the unity that indicates both joints are in the zero states or no rotation, and the robot is in the initial attitude or home position. From Equations (36) and (37) we proof that the desired orientation can be aligned by joint (4) or joint (5) independently or aligned to the desired attitude by a value of both last joints’ rotations, as shown in the last row. Therefore, it is concluded that for the general 6R robot arm only needs to establish the position and attitude equation with the first five joint variables.
Theorem 2 can be utilized for kinematic modeling of robot arm and MAS in forward and IKs. This method sets the foundation for proposing the general direction IK theorem for the orientation problem, which can obtain the orientation IK solution in joint space for any robot above 2-DOF. The Theorem 2 has more arithmetical operation details in Appendix A.5.
In this section, the analytical quaternion for representing the kinematic modeling of the robot’s wrist was demonstrated. Two analytical theorems based on axis vector invariant and Ju-Gibbs quaternion were proposed and proofed for the orientation alignment and the direction IK solution for decoupled robot arm wrists. The following section will show the numerical examples and the experimental simulation for the robot and the Human wrists to verify the method and theorems.
5. Applications of Ju-Gibbs Quaternion and Experiments
This section first uses Theorem 1 for the attitude alignment in forward kinematic. Secondly, from Theorem 2, the orientation IK solution is obtained analytically for different robot arms configurations finally, the discussion appears at the end to illustrate the features of the theorems in kinematic solutions and compare them with the literature.
5.1. Orientation Solution
The 6R decoupling robot arm consists of one of the robot arm configurations as in Figure 4; they have a 2R decoupling robot wrist and 1R robot palm. The attitude inverse solution of the 3R decoupling robot wrist is that: When the structural parameter, the desired attitude of 6R, and the attitude of the first three joints are given; the attitude inverse solution can be acquired by calculating the axis No. 4 and axis No. 5 joint variables to align the orientation to the desired direction, and then align the radial axis of axis No. 6 to the desired radial direction. The solution process is divided into two steps. First, obtain the attitude alignment from Theorem 1 and then the IK solution from Theorem 2. The main steps for the proposed IK solution algorithm are as followed:
- i
- Converting the given orientation (i.e., Homogenous matrix, rotation matrix, sin/cos unit quaternions) to a new tangent quaternion (Ju-Gibbs) and unifying the variables from sin/cos to tan half angles.
- ii
- Separate between the position and orientation quaternions variables.
- iii
- Calculate the inverse position quaternion and position modulus from given position joint variables Equation (25).
- iv
- Obtain the desired wrist attitudes from orientation quaternion obtained from
- (a)
- Theorem 1.
- (b)
- Steps (ii and iii) above.
- v
The algorithms for obtain the desired attitude alignment and for obtain the wrist IK are illustrated in details as follows:
5.1.1. Solution for General Robot Arm with n-DOF
For orientation alignment, we need to find the projection of the first joints related to the position state on the last joint of the robot arm EF. Then, the orientation alignment can be obtained from Equations (22) and (23) by considering the conditional constrain in Equations (A17) and (A18) for the axes that are parallel and orthogonal in projection as shown in the Algorithm 1.
| Algorithm 1: Orientation alignment for n-DOF robot arm wrist |
 |
Based on the Theorem 1 and considering the KC in Section 2.1 and Figure 4; the Table 3 is illustrated the desired attitude alignment quaternion for different configurations of the robot’s arms.

Table 3.
Desired attitude alignment of different configurations of the 6-DOF robot arm.
5.1.2. Fast IK Solution of Based on Ju-Gibbs Quaternion
The attitude inverse solution can be obtained from Theorem 2 based on the analytical quaternion. Where the Equations (36) and (37) are used with both conditions to obtain the joint variables and of the robot wrist in the closed-form. Where the wrist joint variables angle No. 4 and No. 5 can be obtained from Equations (36) or (37) as shown in the Algorithm 2.
| Algorithm 2: Direction Inverse kinematic solution for n-DOF robot arm Wrist |
 |
5.2. Numerical Experiments and Simulation
In order to verify the accuracy and efficiency of the proposed method, the simulation is initially applied to the 6-DOF robot and 7-DOF Human arms. The proposed method is compared with the unit quaternion and rotation matrix methods in terms of time cost and the number of parameters.
The validation and accuracy of the proposed algorithm are verified by taking 1000 groups of poses of the Human arm, and the method is performed to find the orientation IKs. The experiments and programming are developed and implemented on a computer with Intel Core (TM) i5-7400 3.20 GHz processor with 8 GB RAM.
5.2.1. Direction IK
For 6-DOF IK attitude solution Considering the KC in and the desired orientation obtained based on Theorem 1. Then from Theorem 2 If , , we can obtain . The Direct IK can be found for different robot arms configurations, as shown in Table 4.

Table 4.
Direction IK of different configurations of the 6-DOF robot arm.
The solution based on the proposed method in this paper can be applied to any robot arm up to n-DOF. If the projection of axis () on the last axis (n) is known, the desired orientation alignment will be found from Theorem 1. The projection of axis must not be parallel with the last joint’s rotation axis to avoid singularity. Then the direct IK for joint () and () is obtained by Theorem 2. In contrast, the structure parameters are given or measured directly by the natural axis fixed frame theorem, which were proposed in references [29].
5.2.2. Orientation IK for 6-DOF Robot-Wrist
For verification, our method; given the structure parameter of the 6-DOF Robot -arm in Figure 5 and Table 5. The joints angle response for EF positioning are Known; and the desired orientation is obtain from Algorithm 1 or given as desired poses. Then the solution of the wrist joint variables can be obtained from Equations (36) or (37) and then take them into Equation (17) to find if the robot EF attached with tools as introduced in Remark in Section 3.3. The wrist IK solution and time cost are shown in the last 4th columns of Table 5.
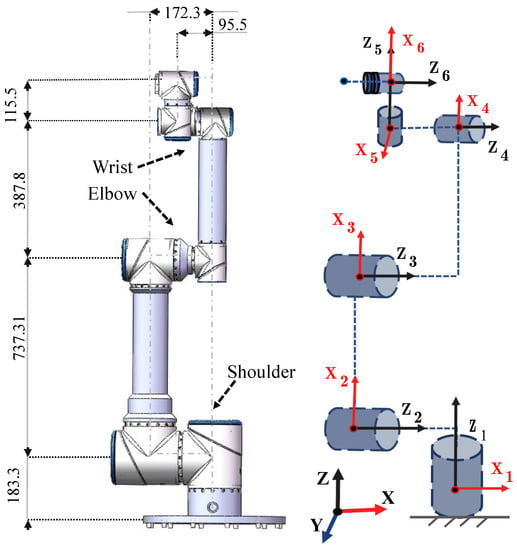
Figure 5.
Schematic diagram and coordinate frames of the 6R robot arm model (Home position).

Table 5.
Orientation IK for 6-DOF robot arm-offset wrist.
5.2.3. Orientation IK for Redundant Robot Arm (Human Wrist)
The robot arm has similarities with the Human arm and wrist in structures. The shoulder and elbow joints are responsible for position, same as the three first joints in the robot arm. The wrist is responsible for orientation direction control the axis No. 6 and No. 7 is the same as the Carpal bone; where the Radial/Ulnar devotion axis and Flexion/Extension axis with offset are response for the orientation motion of the wrist, as shown in Figure 6. Theorem 1 is workable and most appropriate for obtaining the desired orientation alignment of the Phalanges (fingers) and Metacarpal [35]. That if the projection of arm is not parallel or equal with the axis of rotation Phalanx’s axis with some limitation and restriction mentioned in Equation (A16), (A17) and (A18) respectively.
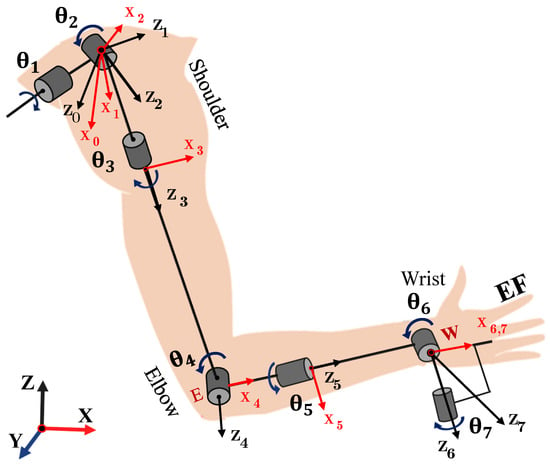
Figure 6.
Exoskeleton and coordinate frames of the 7-DOF Human arm model.
In any event, the coordinate transformation of frame No. 1 to frame No. 5 for all five joints angle components of position quaternions is assumed to be known here for Shoulder and Elbow joints . Then the desired quaternion of (Radial/Ulnar) devotion axis No. 6 and (Flexion/Extension) axis No. 7 can be achieved from Equations (25) and (28).
For numerical experiments and simulation consider structure parameter of 7-DOF Arm. The process solutions are illustrated in Algorithm 2. The structure parameter and the Human arm actual data, movement and limitation deviations and workspace are shown in Table 6. The 5 group of joint variables calculated via the proposed IK algorithm are shown in Table 7. The Elbow joints’ is set = 0; this means no rotation, which proves that the method is also valid for prismatic joints and can give orientation IK solutions.

Table 6.
The kinematic parameter of 7-DOF Human arm.

Table 7.
The IK solution for 7-DOF Human- wrist.
A comparison study is conducted to evaluate the effectiveness of tangent quaternion in improving the speed and efficiency of orientation IK solutions. The proposed method has shown less complexity and computational cost in IK solutions compared with the unit quaternion and rotation matrix methods in literature [23,26,36], as shown in Table 8. Where the time cost of the unit quaternion is increasing for high-DOF and the rotation matrix is more difficult to obtain the IK solution for redundant robot arms. In contrast, our method is stable in time cost for MASs with different configurations of the offset wrists.

Table 8.
Comparison of the proposed method with rotation matrix and unit quaternion.
5.2.4. IK Simulation Experiment of 7-DOF
For more verification to check the accuracy and the validation of the propose method for solve the orientation IK for any DOF. The algorithm’s simulation implementation in the human wrist’s whole attitude workspace is then discussed. The 1000 joint angle sets are selected randomly, corroding to the ranges of human arm joint angles listed in Table 6.
Figure 7 is illustrated the (Flexion/Extension) joint No. 6 error; the average error is 0.052 × 10 except for the errors in tests 285, 300, and 650. The Figure 8 is shown the (Radial/Ulnar) joint No. 7 error for all the tests. The average error is 0.17 × 10 except for the errors in test 450.
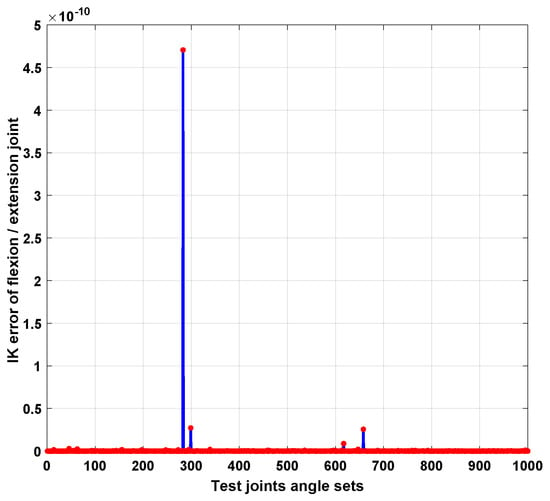
Figure 7.
Performance of an algorithm for 1000 joint angle tests (Wrist IK error for Flexion/Extension movement).
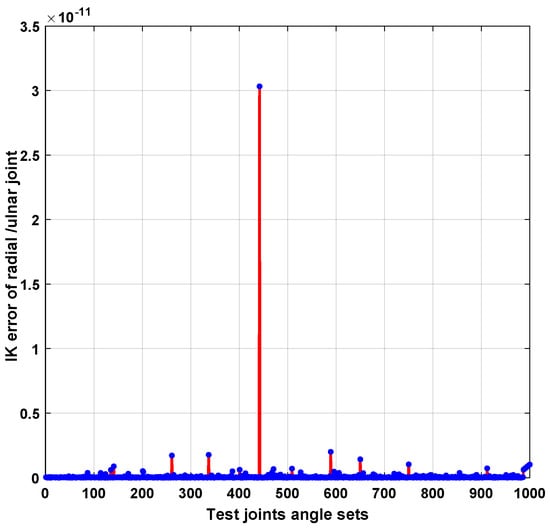
Figure 8.
Performance of an algorithm for 1000 joint angle tests (Wrist IK error for Radial/Ulnar movement).
Figure 9 is shown the orientation errors for all the tests, the average error is (6.3 × 10); where only 3.6% of the tests are greater than 4.83 × 10; while the rest of the simulation results in the range between (0 and 5.0 × 10). In addition, the computational time of the algorithm did not exceed 0.017 s to obtain the IK solution. The minimum error, maximum error, mean, and standard deviation of the wrist joints and orientations of the IK solutions for the 7-R Arm are demonstrated Table 9.
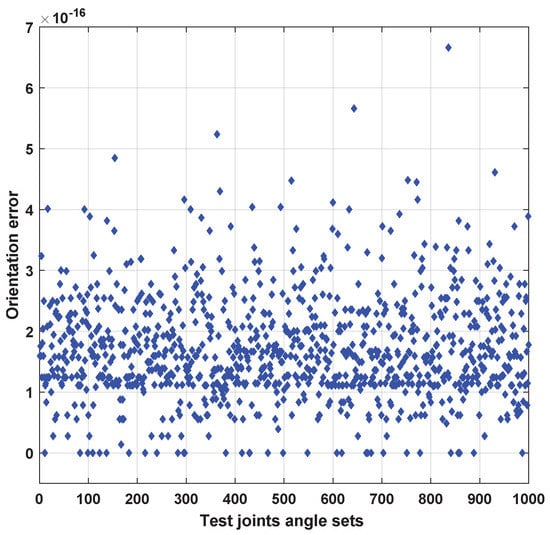
Figure 9.
Performance of an algorithm for 1000 joint angle tests (Arm orientation errors).

Table 9.
Statistical analysis of error of invers kinematic solutions of orientation and wrist joints.
5.3. Discussion
A new analytic quaternion for kinematic modeling has been proved. The proved theorems showed that the analytical Ju-Gibbs quaternion and numerical unit quaternion were isomorphic in Equations (5) and (28)–(37). The transformation modeling of the Forward kinematic attitude was determined intuitively using Ju-Gibbs analytic quaternion and compared with unit quaternion in literature. The results showed that the new quaternion is more optimal and unique for kinematic modeling. The scalar part remains constant for a single or intersecting axis and does not change with the rotation, as shown in Equation (13), which requires less memory space and reduces the computational cost operation. Compared with matrices and unit quaternion, the rotation matrix requires 18 adds and 27 multiplications, while the quaternion needs only 12 additions and 16 multiplications [29]. In addition, the vector elements of the quaternion are present only in the tangent half form to represent the rotation rather than sin/cos in literature [6]. Also, the square modulus of sin and cos of a unit quaternion strongly constrain the kinematic [3,6] modeling analysis. In contrast, in the Ju-Gibbs quaternion, the product operation of square modulus still results in kinematic equations, as shown in Equation (14) and Proof 2. Therefore, the expression forms are more concise in kinematic transformations based on the Ju-Gibbs quaternion.
Additionally, the results noted that the lengths of the linkages and offset between the wrist joints do not impact attitude alignment and the IK solution of the robot’s wrist. Only the direction of the axis of rotation has a significant effect on the orientation solutions, as shown in Table 3. On the other hand, the proposed method has some significant limitations in addition to the operating range boundaries for the tangent half-angle ; first, not all the robot wrist configurations can obtain the desired alignment from Theorem 1. Nevertheless, at least one of the Ju-Gibbs quaternion exists for multiaxial rotation. Secondly, if the projection of axis is parallel with the last joint’s rotation axis, the desired attitude alignment cannot be obtained from Theorem 1, as shown in Equations (A17) and (A18); In this case, the attitude or quaternion takes norm-multiplication between adjacent axes as in Equation (12). If all these limitations are considered, and solutions in Equations (36) and (37) are still equal to an infinite (not valid) of such kinematic parameters, which means there are no IK solutions to the EE pose; also, there is no such geometric meaning.
The simulation and numerical examples applied for different robot arm configurations indicated that the method could work from 2-DOF to n-DOF KC. Furthermore, the proposed method differs from Raghavan an Roth [37], who used tangent half angles to obtain the IK solution using a numeric polynomial vector equation. Most notably, this is the first study to investigate a method that takes a unique approach that uses a novel quaternion to obtain forward and IK solutions analytically.
6. Conclusions
This work introduced new methods in kinematics bodies analysis. The principle of transformation and rotation between chains and robot kinematic modeling were explained briefly based on axis invariant theory. A new analytic quaternion has been proposed in this paper based on the axis vector and the tangent half-angle integrated with the rotation axis components. The basic expressions and arithmetic operations for the innovative of Ju-Gibbs quaternion were illustrated. Besides sharing many similarities with Hamilton and JPL quaternions forms, the Ju- Gibbs quaternion is non-redundant and has more features than the quaternion in literature.
In addition, two theorems were derived and proofed based on the new quaternion for obtaining the orientation alignment of the EF and obtaining the direct IK solution for the robot’s arm wrist. The methods were applied for different configurations of robots’ arms wrists. Additionally, a comparative analysis is performed based on the proposed method with the literature. The results showed that the Kinematic modeling based on Ju-Gibbs quaternion is featured by the uniform expression and the concise, structured hierarchical model to ensure the generality of the analytical solution in forward and IK. The proposed method demonstrated an elegant use in studying kinematics bodies and robot arms based on new quaternion. These novel methods also provide evidence that their use in robotics kinematics will lead to new solutions or the simplification of existing ones and, in most cases, improve performance in robotic engineering and MASs.
Future research directions include combining the new theory developed in this paper to work with all types of parallel and hybrid robots, thoroughly obtaining the position and orientation IK solution together based on proposed concepts to obtain a simple and unified formula that can describe the poses of the bodies in an optimal and compact form. Such as dual-quaternion, developed from unit quaternion, and Homogenous matrix, which developed from a rotation matrix.
Author Contributions
Conceptualization and methodology, H.J. and A.A.; software, A.A., Y.Y. and H.X.; validation, A.A.; formal analysis, H.J.; writing—original draft preparation, A.A.; writing—review, H.J.; visualization, A.A. and Y.Y.; supervision, and did the formal analysis and reviewed and edited the manuscript, H.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China for the project “Dynamic modeling and force control of multi-axis systems based on axis invariants” [Grant No. NSFC 61673010], and funded by the Graduate Research and Innovation Project of Jiangsu Province for the project “Research on inverse kinematics of 6R robots” [Grant No. KYCX20-0221].
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Symbols | Definition | Symbols | Definition |
| Axis-Vector represents the connection from link to link l respectively | Ju-Gibbs quaternion | ||
| Skew- symmetric matrix of axis vector () | Skew-symmetric matrix of quaternion vector part | ||
| Sine half-angle | Ju-Gibbs quaternion modulus square | ||
| Cosine half-angle | Scalar part of unit quaternion | ||
| Tangent half-angle | Scalar part of Ju-Gibbs quaternion | ||
| Angular position around Axis-vector | Axis-vector on the projection of link from the right to the left coordinate system | ||
| The kinematic joint pair | Aligns to the desired Axis-vector | ||
| Rotation matrix from frame 0 to frame l | 3D zero matrix | ||
| Unit Quaternion | 1 | 3D unit matrix |
Abbreviations
The following abbreviations are used in this manuscript:
| MAS | Multi Axis System |
| KC | Kinematic Chain |
| IK | Inverse Kinematic |
| EF | End Effector |
Appendix A
Appendix A.1
Appendix A.2. Ju-Gibbs Quaternion in Canonical Formula
From Equation (13), the attitude of the single joint of KC can be expressed by canonical Ju-Gibbs quaternion as:
The ; and , Only if . Equations (8) and (12). results in:
from Equations (13), (14) and (A3) that
and when in canonical form; then according to Equations (7), (14) and (A4) the quaternion modulus square is expressed as:
thus from Equations (8), (13) and (14) result in:
From Equation (13), note that the unit quaternion and direction quaternion define as and respectively.
Appendix A.3. Proof of the Theorem 1
Considering Equations (1) and (7). Based on the Cayley transformation in [15,31], which introduced a kinematics transformation without KC indexes. The can represent in Cayley parameter by Multiply then Equation (1) result in
where substitute into Equation (A7), then
after privation, the then
so the is an orthogonal rotation matrix. From Equation (A9), obtain
where is the projection of from a frame into the frame 0. Equation (A10) results in
and
due the and are unit vectors, assume and , we can obtain
Equation (A13) shows and are commonly orthogonal. if Equations (A12) and Equation (A13) result in the optimal Axis-vector as follows:
and
Appendix A.4. Comparative of the Numerical Experiments between Quaternions
To demonstrate the Gu-Gibbs quaternion is isomorphism with unit quaternion, we take the attitude alignment for proof kinematic modeling of the last two joints for the 6-DOF robot arm: Considering the attitude of unit quaternion in Equation (5) yields
or simplify the Equation (A19) results in:
From Equation (30) the inverse square matrix of, and Equation (31) the invertible square matrix of adjacent axes vectors shows as
from Equation (30), (31) and (A21) if is not valid, there exists Equation (A20) results in:
where in . According to Equations (A21) and (A22) obtain
Equation (A23) results in:
the ; the Equations (A23) and (A24) yields
finally Equations (34) and (A25) show that Ju-Gibbs quaternion is the isomorphism of unit quaternion in kinematic modeling. From the equations above the unit quaternion is shown it has more process and computational cost compared with the proposed approaches.
Appendix A.5. The Continuous of the Theorem 2 Proof
For proof (37) in Section 4.2 Considering Equations (28)–(37); There are four equations and two independent variables. the direct IK of the orientation robot wrist can be obtained as (a) First, If from Equation (34) by using the second and third-row then
(b) Second, if From Equations (5) and (A26) and Table 1, if , we obtain:
substitute Equation (A27) result in:
if . Equation (A28) shows that the tri-axes, , and , are orthogonal to each other. if , obtain:
the constraint formulation can be obtained from the 4th row of Equation (34).
now put Equation (A29) into Equation (A26) to obtain Equation (37). That If results in:
according to Equations (A26), (A30) and (A31), the Equation (37) is verified.
References
- Haslwanter, T. 3D Kinematics; Springer: Cham, Switzerland, 2018; 191p. [Google Scholar] [CrossRef]
- Funda, J.; Paul, R. A computational analysis of screw transformations in robotics. IEEE Trans. Robot. 1990, 6, 348–356. [Google Scholar] [CrossRef]
- Murray, R.; Li, Z.; Sastry, S. A Mathematical Introduction to Robotic Manipulation; CRC Press: Boca Raton, FL, USA, 1994; p. 519. [Google Scholar] [CrossRef]
- Crowe, M.J. A History of Vector Analysis: The Evolution of the Idea of a Vectorial System; Courier Corporation: North Chelmsford, MA, USA, 1994. [Google Scholar]
- Bisshopp, K.E. Rodrigues’ Formula and the Screw Matrix. ASME J. Eng. Ind. 1969, 91, 179–184. [Google Scholar] [CrossRef]
- Hamilton, W. Lectures on Quaternions: Containing a Systematic Statement of a New Mathematical Method. Available online: https://l1nq.com/ClrIR (accessed on 30 March 2023).
- Clifford, M.A. Preliminary sketch of biquaternions. Proc. Lond. Math. Soc. 1871, 4, 381–395. [Google Scholar] [CrossRef]
- Kotelnikov, A. Screw calculus and some applications to geometry and mechanics. Ann. Imp. Univ. Kazan 1895, 24. [Google Scholar]
- Cohen, A.; Shoham, M. Hyper Dual Quaternions representation of rigid bodies kinematics. Mech. Mach. Theory 2020, 150, 103861. [Google Scholar] [CrossRef]
- Kahveci, D.; Gok, I.; Yayl, Y. Some variations of dual Euler–Rodrigues formula with an application to point–line geometry. J. Math. Anal. Appl. 2018, 459, 1029–1039. [Google Scholar] [CrossRef]
- Lee, C.C.; Stammers, C.; Mullineux, G. On the historical overview of geometric algebra for kinematics of mechanisms. In International Symposium on History of Machines and Mechanisms; Springer: Cham, Switzerland, 2009; pp. 21–34. [Google Scholar] [CrossRef]
- Muller, A. Screw and Lie group theory in multibody kinematics. Multibody Syst. Dyn. 2018, 43, 37–70. [Google Scholar] [CrossRef]
- Brockett, R. Robotic manipulators and the product of exponentials formula. In Mathematical Theory of Networks and Systems; Springer: Berlin/Heidelberg, Germany, 1984; pp. 120–129. [Google Scholar] [CrossRef]
- Norris, A. Euler-Rodrigues and Cayley formulae for rotation of elasticity tensors. Math. Mech. Solids 2008, 13, 465–498. [Google Scholar] [CrossRef]
- Kruglov, S.I.; Barzda, V. Modified Gibbs’s representation of rotation matrix. arXiv 2017, arXiv:1703.00300. [Google Scholar]
- Dai, J. Euler–Rodrigues formula variations, quaternion conjugation and intrinsic connections. Mech. Mach. Theory 2015, 92, 144–152. [Google Scholar] [CrossRef]
- Angeles, J. Fundamentals of Robotic Mechanical Systems: Theory, Methods, and Algorithms; Springer: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Brandstotter, M.; Angerer, A.; Hofbaur, M. An analytical solution of the inverse kinematics problem of industrial serial manipulators with an ortho-parallel basis and a spherical wrist. In Proceedings of the Austrian Robotics Workshop, Linz, Austria, 22–23 May 2014; p. 7. [Google Scholar]
- Li, Q.; Ju, H.; Xiao, P. Kinematics analysis and optimization of 6R manipulator. IOP Conf. Ser. Mater. Sci. Eng. 2020, 816, 012016. [Google Scholar] [CrossRef]
- Zhao, R.; Shi, Z.; Guan, Y.; Shao, Z.; Zhang, Q.; Wang, G. Inverse kinematic solution of 6R robot manipulators based on screw theory and the Paden–Kahan subproblem. Int. J. Adv. Robot. Syst. 2018, 15, 17–29. [Google Scholar] [CrossRef]
- Xiao, F.; Li, G.; Jiang, D.; Xie, Y.; Yun, J.; Liu, Y.; Huang, L.; Fang, Z. An effective and unified method to derive the inverse kinematics formulas of general six-DOF manipulator with simple geometry. Mech. Mach. Theory 2021, 159, 104265. [Google Scholar] [CrossRef]
- Faria, C.; Ferreira, F.; Erlhagen, W.; Monteiro, S.; Bicho, E. Position-based kinematics for 7-DoF serial manipulators with global configuration control, joint limit and singularity avoidance. Mech. Mach. Theory 2018, 121, 317–334. [Google Scholar] [CrossRef]
- Kucuk, S.; Bingul, Z. Inverse kinematics solutions for industrial robot manipulators with offset wrists. Appl. Math. Model. 2014, 38, 1983–1999. [Google Scholar] [CrossRef]
- Fu, Z.; Yang, W.; Yang, Z. Solution of inverse kinematics for 6R robot manipulators with offset wrist based on geometric algebra. J. Mech. Robot. 2013, 5, 031010. [Google Scholar] [CrossRef] [PubMed]
- Trinh, C.; Zlatanov, D.; Zoppi, M.; Molfino, R. A geometrical approach to the inverse kinematics of 6R serial robots with offset wrists. In Proceedings of the ASME 2015 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Boston, MA, USA, 2–5 August 2015. [Google Scholar] [CrossRef]
- An, H.; Seo, T.; Lee, J. Generalized solution for a sub-problem of inverse kinematics based on product of exponential formula. J. Mech. Sci. Technol. 2018, 32, 2299–2307. [Google Scholar] [CrossRef]
- Lin, P.F.; Huang, M.B.; Huang, H.P. Analytical solution for inverse kinematics using dual quaternions. IEEE Access 2019, 7, 166190–166202. [Google Scholar] [CrossRef]
- Shirafuji, S.; Ota, J. Kinematic synthesis of a serial robotic manipulator by using generalized differential inverse kinematics. IEEE Trans. Robot. 2019, 35, 1047–1054. [Google Scholar] [CrossRef]
- Ahmed, A.; Yu, M.; Chen, F. Inverse Kinematic Solution of 6-DOF Robot-Arm Based on Dual Quaternions and Axis Invariant Methods. Arab. J. Sci. Eng. 2022, 47, 15915–15930. [Google Scholar] [CrossRef]
- Wahballa, H.; Duan, J.; Wang, W.; Dai, Z. Experimental Study of Robotic Polishing Process for Complex Violin Surface. Machines 2023, 11, 147. [Google Scholar] [CrossRef]
- Trawny, N.; Roumeliotis, S. Indirect Kalman filter for 3D attitude estimation. Univ. Minn. Dept. Comp. Sci. Eng. Tech. Rep. 2005, 2, 2005. [Google Scholar]
- Aspragathos, N.; Dimitros, J. A comparative study of three methods for robot kinematics. IEEE Syst. J. Man Cybern. Part B 1998, 28, 135–145. [Google Scholar] [CrossRef]
- Craig, J. Introduction to robotics: Mechanics and control. Pearson Educ. 2005, 388. [Google Scholar]
- Ju, H. An Axis-Invariant Based Inverse Kinematics Modeling and Solution Method for General 7R Manipulators. China Patent CN109033688B, 31 March 2020. [Google Scholar]
- Bajaj, N.; Spiers, A.; Dollar, A. State of the art in artificial wrists: A review of prosthetic and robotic wrist design. IEEE Trans. Robot. 2019, 35, 261–277. [Google Scholar] [CrossRef]
- Ayiz, C.; Kucuk, S. The kinematics of industrial robot manipulators based on the exponential rotational matrices. In Proceedings of the 2009 IEEE International Symposium on Industrial Electronics, Seoul, Republic of Korea, 5–8 July 2009; pp. 977–982. [Google Scholar] [CrossRef]
- Raghavan, M.; Roth, B. Inverse Kinematics of the General 6R Manipulator and Related Linkages. J. Mech. Des. 1993, 115, 502–508. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).