Experimental Investigation and Modeling of Force-Induced Surface Errors for the Robot-Assisted Milling Process
Abstract
1. Introduction
2. Experimental Setup
3. Model Construction Based on the Response Surface Methodology
4. Experimental Results and Analysis
4.1. Experimental Results
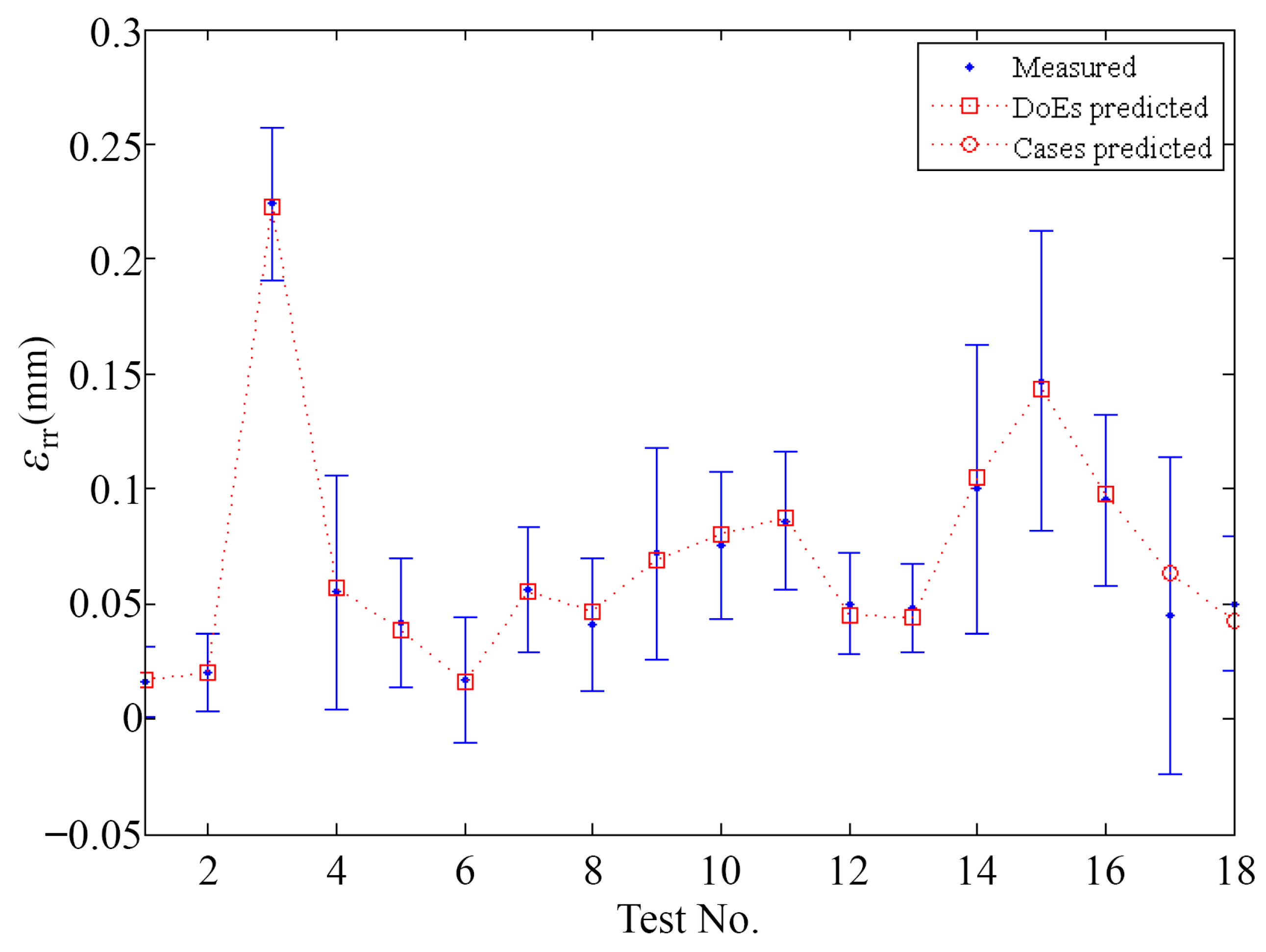
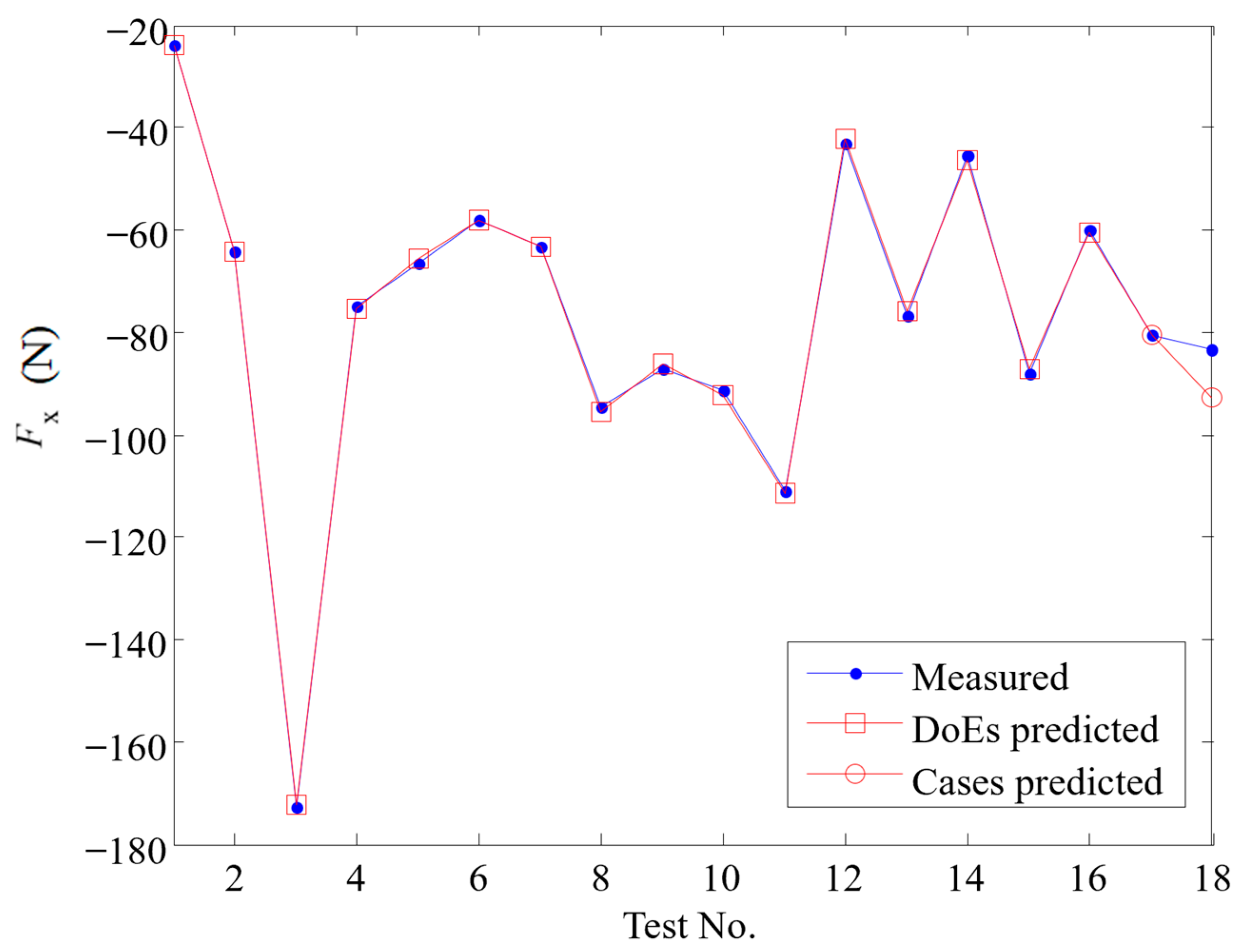
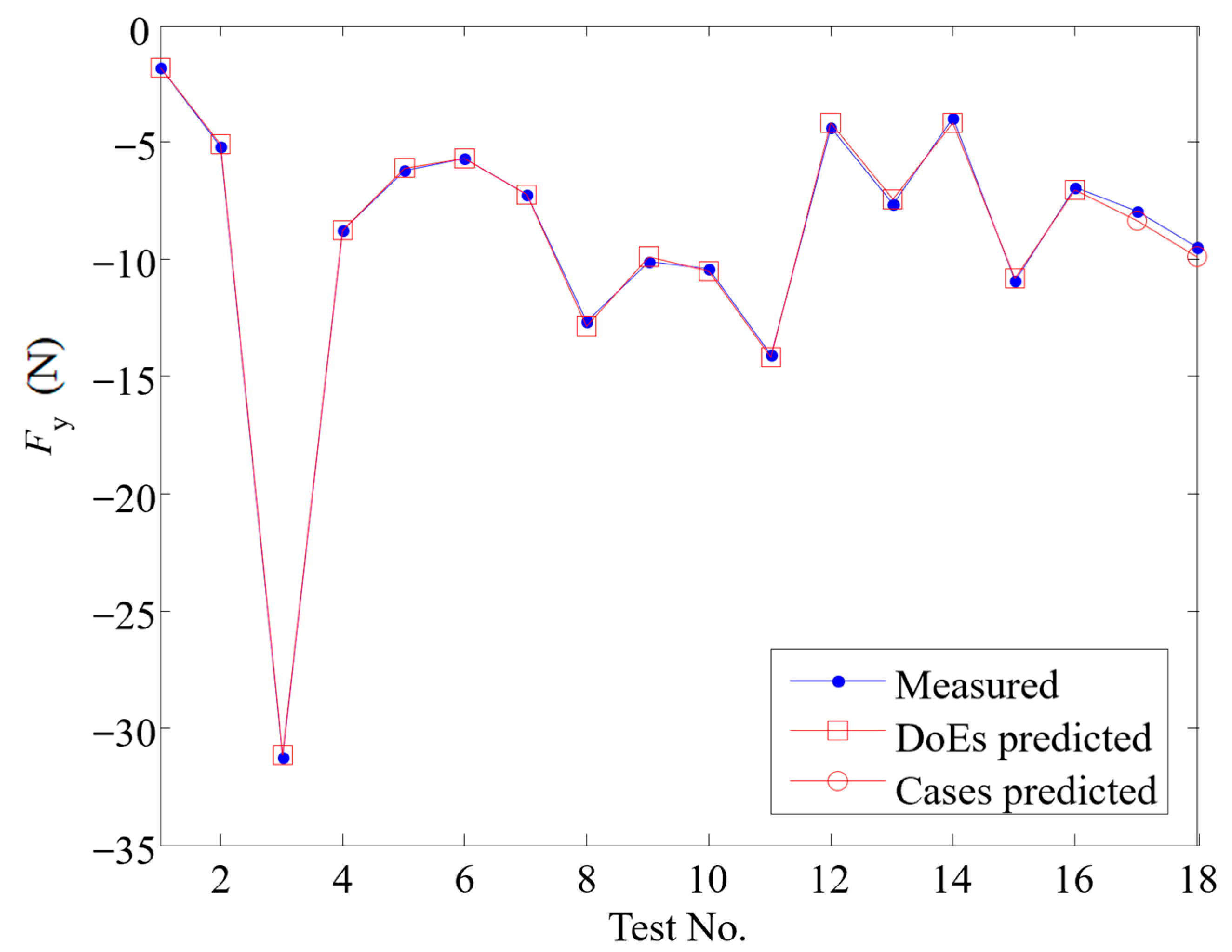
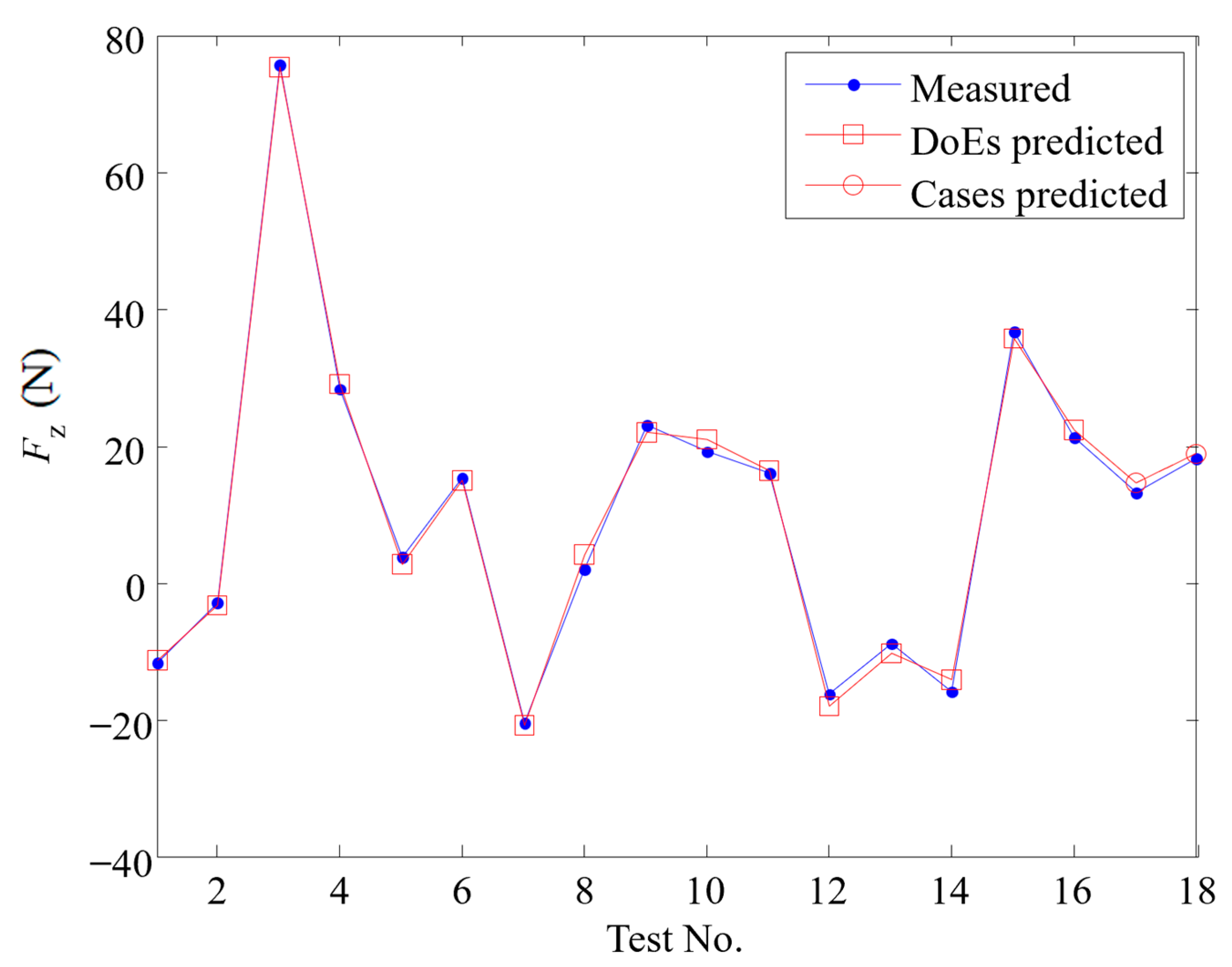
4.2. Response Surface Model Accuracy Analysis
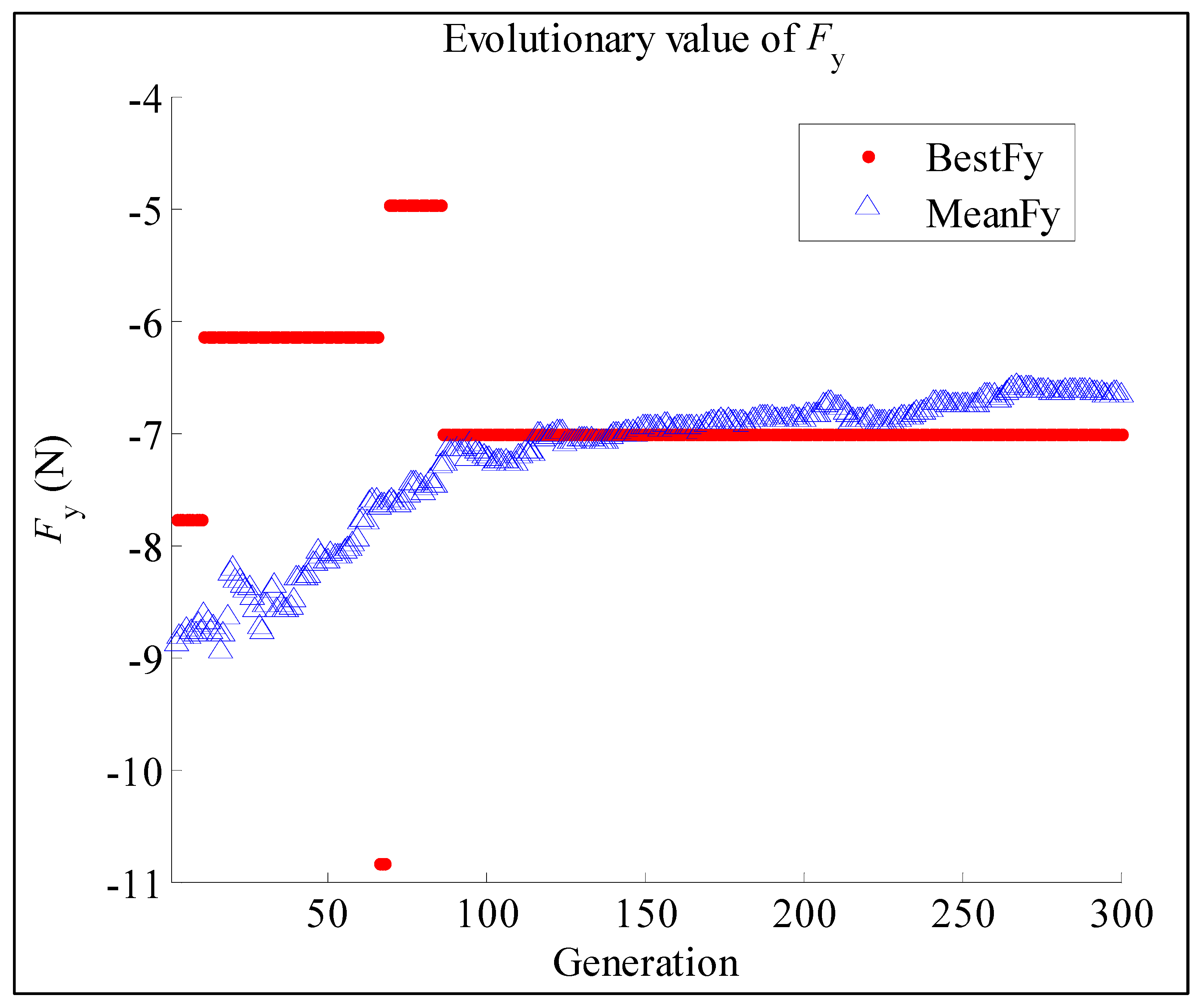
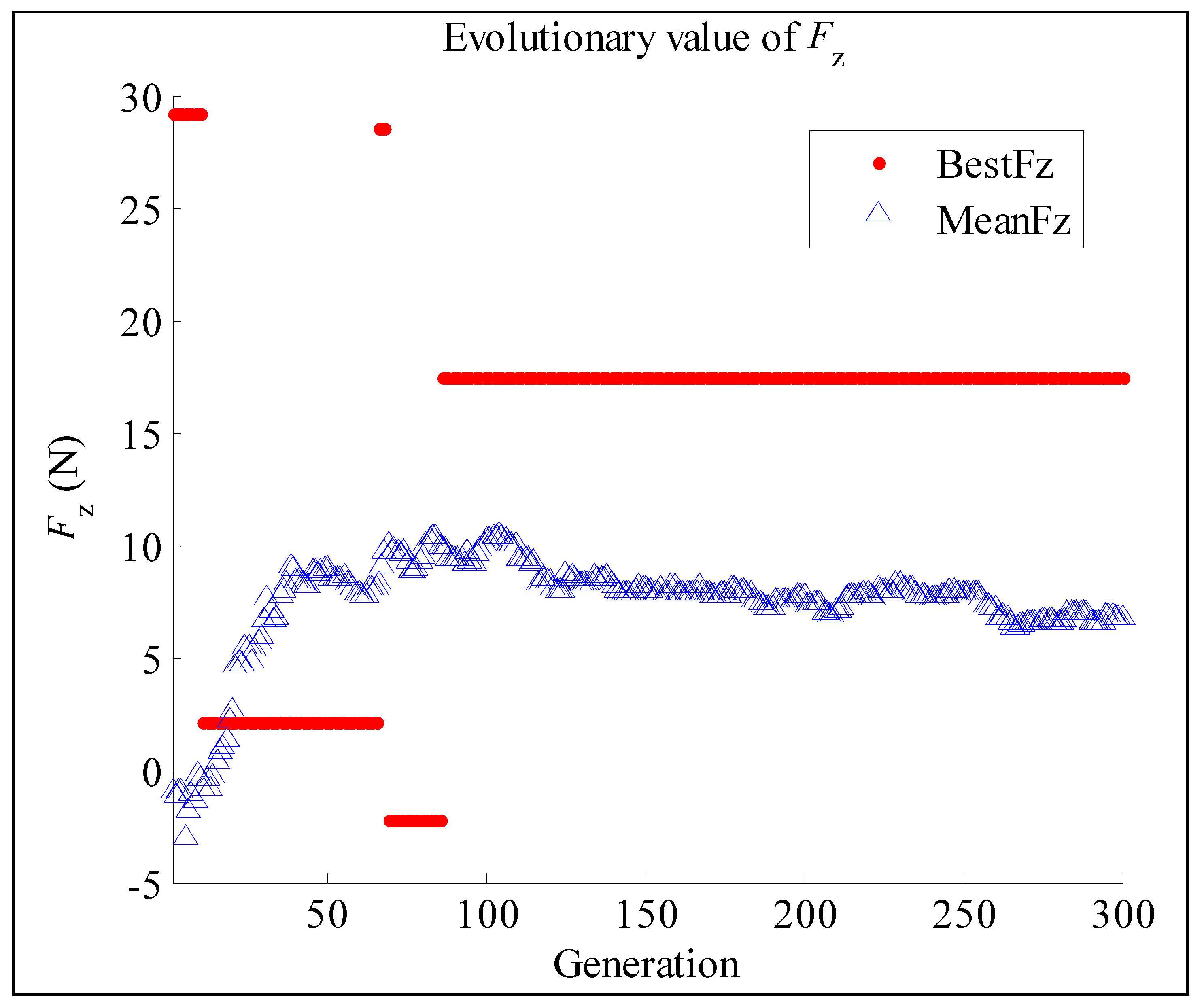
5. Process Optimization Based on Evolutionary Algorithm
6. Conclusions
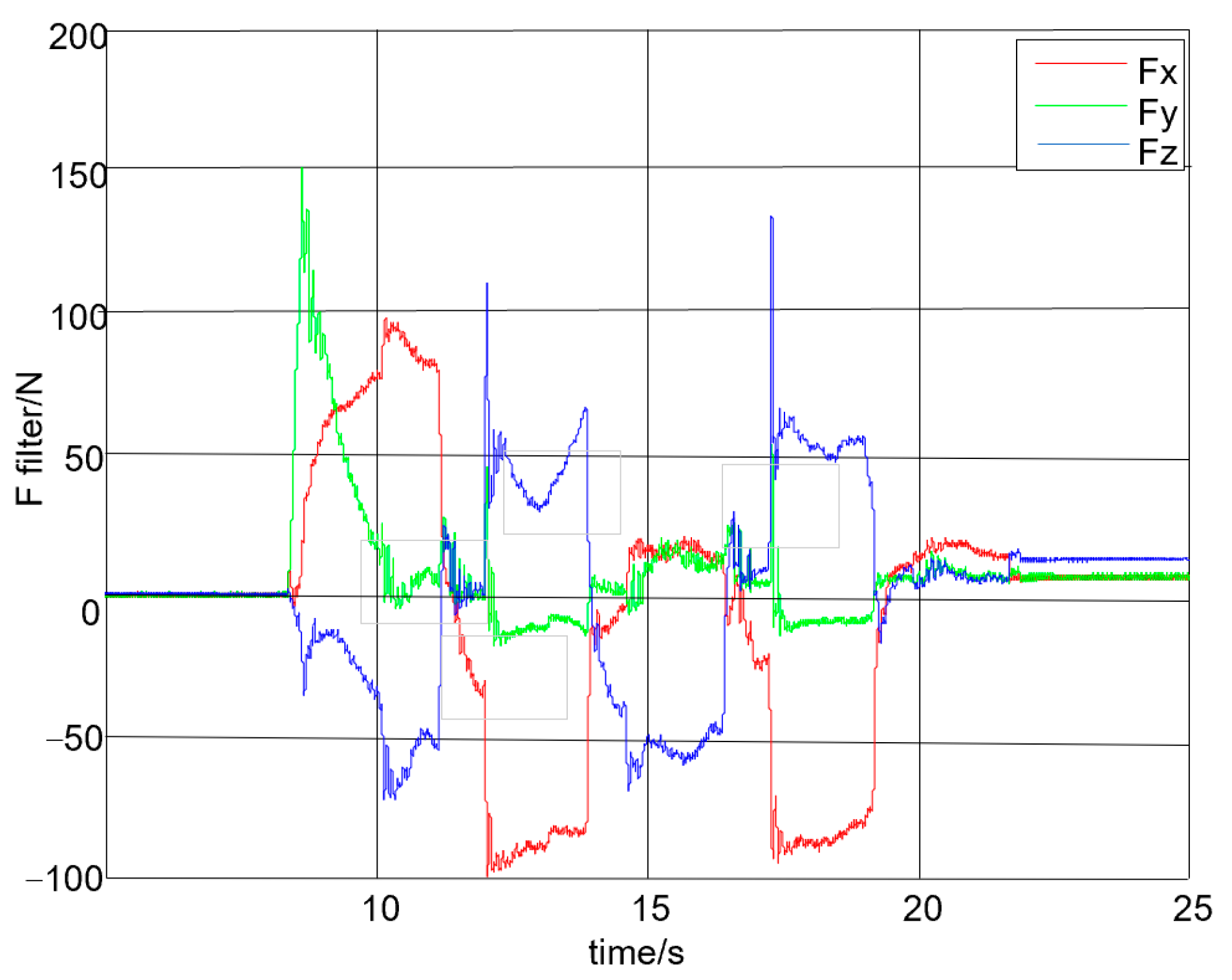
- The relationship between the ZL114A aluminum alloy robot-assisted milling process parameters and the milling force, as well as the surface error after machining, was investigated through milling machining experiments, machining surface measurement experiments, and milling-force measurement experiments. The process of milling robots demonstrates the phenomenon of “pulling the tool inwards in the up milling process while pushing the tool outwards in the down milling process”, excessive upward radial milling force should therefore be avoided as much as possible in practical application, in order to reduce the risk of cutting into the complex inner wall of cylindrical castings.
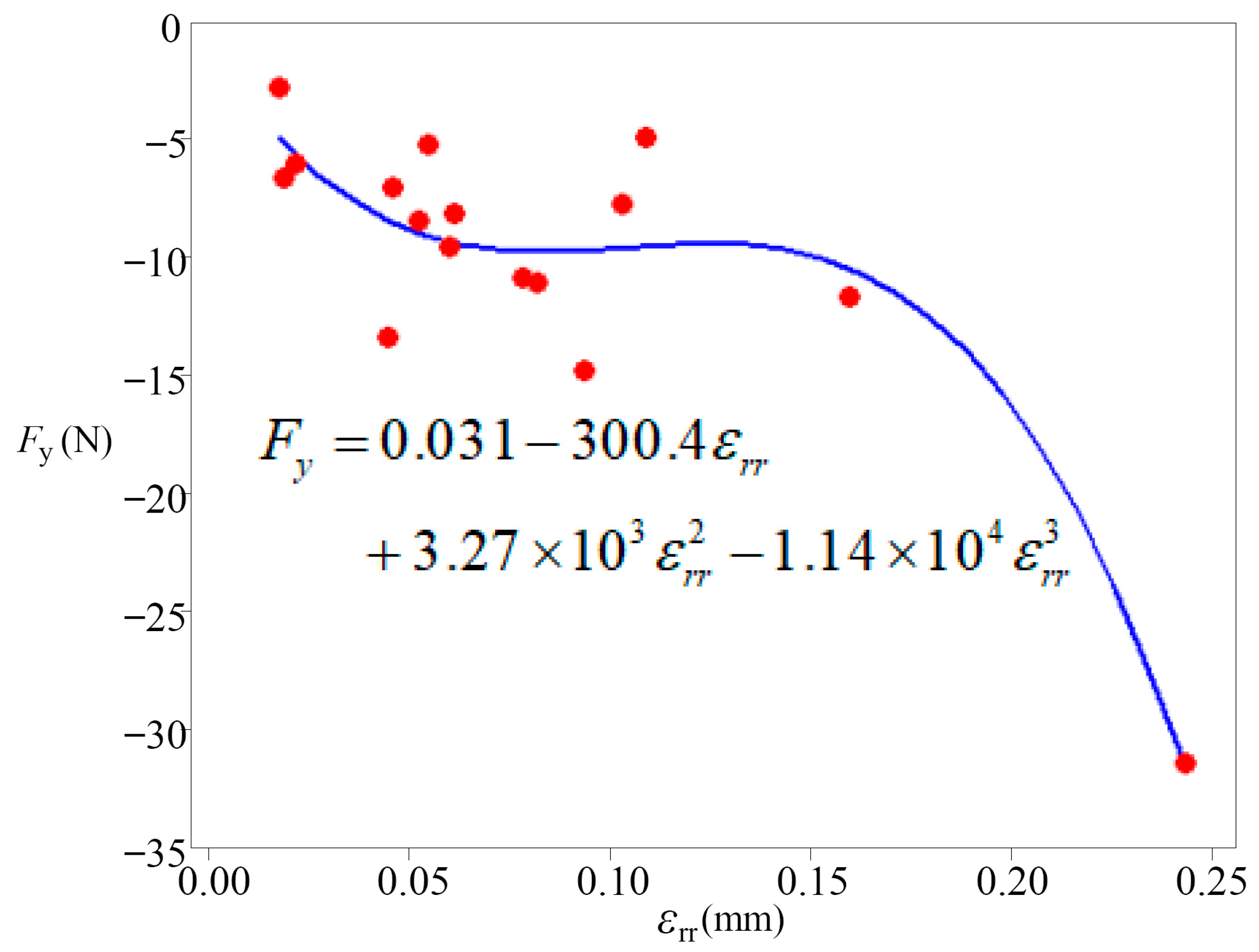
- Experimental results have shown that machined surfaces with different milling parameters have different surface qualities and mechanical properties. The optimization of the machining parameters of the milling process can improve the milling performance and the surface quality of the robot, and the machined area error can be kept within an appropriate range, which provides a theoretical foundation for practical application in later plants.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, Y.; Zhou, Y.; Ke, Z.; Tian, K.; Wang, B. Stiffener layout optimization framework by isogeometric analysis-based stiffness spreading method. Comput. Methods Appl. Mech. Eng. 2022, 390, 114348. [Google Scholar] [CrossRef]
- Chen, F.; Zhu, J.; Du, X.; Zhang, R.; Zhang, W. Shape preserving topology optimization for structural radar cross section control. Chin. J. Aeronaut. 2022, 35, 198–210. [Google Scholar] [CrossRef]
- Putra, G.L.; Kitamura, M.; Takezawa, A. Structural optimization of stiffener layout for stiffened plate using hybrid GA. Int. J. Nav. Archit. Ocean Eng. 2019, 11, 809–818. [Google Scholar] [CrossRef]
- Liu, Z.; Cho, S.; Takezawa, A.; Zhang, X.; Kitamura, M. Two-stage layout–size optimization method for prow stiffeners. Int. J. Nav. Archit. Ocean Eng. 2019, 11, 44–51. [Google Scholar] [CrossRef]
- Zhou, L.; Sigmund, O.; Zhang, W. Self-supporting structure design with feature-driven optimization approach for additive manufacturing. Comput. Methods Appl. Mech. Eng. 2021, 386, 114110. [Google Scholar] [CrossRef]
- Ji, W.; Wang, L. Industrial robotic machining: A review. Int. J. Adv. Manuf. Technol. 2019, 103, 1239–1255. [Google Scholar] [CrossRef]
- Krüger, J.; Zhao, H.; Reis De Ascencao, G.; Jacobi, P.; Surdilovic, D.; Schöll, S.; Polley, W. Concept of an offline correction method based on historical data for milling operations using industrial robots. Prod. Eng. 2016, 10, 409–420. [Google Scholar] [CrossRef]
- Cen, L.; Melkote, S.N.; Castle, J.; Appelman, H. A Wireless Force-Sensing and Model-Based Approach for Enhancement of Machining Accuracy in Robotic Milling. IEEE/ASME Trans. Mechatron. 2016, 21, 2227–2235. [Google Scholar] [CrossRef]
- Chen, P.Y.; Liu, S.; Jin, S.; Gu, Q. Geometric Modeling and Characterization of Wall Thickness for Complex Cylindrical Thin-Walled Parts with Uncertain Manufacturing Deviations. In Proceedings of the ASME 2021 International Mechanical Engineering Congress & Exposition (IMECE), Online, 1–5 November 2021. [Google Scholar]
- Rivière-Lorphèvre, E.; Huynh, H.N.; Ducobu, F.; Verlinden, O. Cutting Force Prediction in Robotic Machining. Procedia CIRP 2019, 82, 509–514. [Google Scholar] [CrossRef]
- Liu, S.; Jin, S.; Zhang, X.P.; Chen, K.; Tian, A.; Xi, L.F. A coupled model for the prediction of surface variation in face milling large-scale workpiece with complex geometry. J. Manuf. Sci. Eng. -Trans. ASME 2019, 1410, 31009–31014. [Google Scholar] [CrossRef]
- Liu, S.; Jin, S. Predicting milling force variation in time and space domain for multi-toothed face milling. Int. J. Adv. Manuf. Technol. 2020, 108, 2269–2283. [Google Scholar] [CrossRef]
- Abou-El-Hossein, K.A.; Kadirgama, K.; Hamdi, M.; Benyounis, K.Y. Prediction of cutting force in end-milling operation of modified AISI P20 tool steel. J. Mater. Process. Technol. 2007, 182, 241–247. [Google Scholar] [CrossRef]
- Ratnam, C.; Arun Vikram, K.; Ben, B.S.; Murthy, B.S.N. Process monitoring and effects of process parameters on responses in turn-milling operations based on SN ratio and ANOVA. Measurement 2016, 94, 221–232. [Google Scholar] [CrossRef]
- Ni, J.; Dai, R.; Yue, X.; Zheng, J.; Feng, K. Contribution Ratio Assessment of Process Parameters on Robotic Milling Performance. Materials 2022, 15, 3566. [Google Scholar] [CrossRef] [PubMed]
- Vakondios, D.; Kyratsis, P.; Yaldiz, S.; Antoniadis, A. Influence of milling strategy on the surface roughness in ball end milling of the aluminum alloy Al7075-T6. Measurement 2012, 45, 1480–1488. [Google Scholar] [CrossRef]
- Hassanpour, H.; Sadeghi, M.; Shajari, S. Empirical Modeling and Analysis of Surface Roughness in Milling Process of Nickel-Based Super Alloy Nimonic 115 through Response Surface Methodology. Adv. Mater. Res. 2011, 325, 430–435. [Google Scholar] [CrossRef]
- Persoons, W.; Vanherck, P. A Process Model for Robotic Cup Grinding. CIRP Ann. -Manuf. Technol. 1996, 45, 319–325. [Google Scholar] [CrossRef]
- Vakondios, D.; Kyratsis, P.; Yaldiz, S.; Antoniadis, A. Robotic grinding and polishing for turbine-vane overhaul. J. Mater. Process. Technol. 2002, 127, 140–145. [Google Scholar]
- Sun, Y.; Giblin, D.J.; Kazerounian, K. Accurate robotic belt grinding of workpieces with complex geometries using relative calibration techniques. Robot. Comput. -Integr. Manuf. 2009, 25, 204–210. [Google Scholar] [CrossRef]
- Ren, X.; Cabaravdic, M.; Zhang, X.; Kuhlenkötter, B. A local process model for simulation of robotic belt grinding. Int. J. Mach. Tools Manuf. 2007, 47, 962–970. [Google Scholar] [CrossRef]
- Song, Y.; Yang, H.; Lv, H. Intelligent Control for a Robot Belt Grinding System. IEEE Trans. Control Syst. Technol. 2013, 21, 716–724. [Google Scholar]
- Yang, F.; Xing, Y.; Li, X. A comprehensive error compensation strategy for machining process with general fixture layouts. Int. J. Adv. Manuf. Technol. 2020, 107, 2707–2717. [Google Scholar] [CrossRef]
- Jin, S.; Liu, S.; Zhang, X.P.; Chen, K. A unified prediction model of 3D surface topography in face milling considering multi-error sources. Int. J. Adv. Manuf. Technol. 2019, 102, 705–717. [Google Scholar] [CrossRef]
- Xu, P.; Gao, Y.; Yao, X.; Ng, Y.H.; Liu, K.; Bi, G. Influence of process parameters and robot postures on surface quality in robotic machining. Int. J. Adv. Manuf. Technol. 2023, 124, 2545–2561. [Google Scholar] [CrossRef]
- Li, W.; Li, B.; He, S.; Mao, X.; Qiu, C.; Qiu, Y.; Tan, X. A novel milling parameter optimization method based on improved deep reinforcement learning considering machining cost. J. Manuf. Process. 2022, 84, 1362–1375. [Google Scholar] [CrossRef]
- Qin, H.; Li, Y.; Xiong, X. Workpiece Pose Optimization for Milling with Flexible-Joint Robots to Improve Quasi-Static Performance. Appl. Sci. 2019, 9, 1044. [Google Scholar] [CrossRef]
- Vijay, S.; Krishnataj, V. Machining Parameters Optimization in End Milling of Ti6A14V. Procedia Eng. 2013, 64, 1079–1088. [Google Scholar] [CrossRef]
- Hou, T.; Su, C.; Liu, W. Parameters optimization of a nano-particle wet milling process using the Taguchi method, response surface method and genetic algorithm. Powder Technol. 2007, 173, 153–162. [Google Scholar] [CrossRef]
- Budak, E. Analytical Models for High Performance Milling: Part II: Process Dynamicsand Stability. Int. J. Mach. Tools Manuf. 2006, 46, 1489–1499. [Google Scholar] [CrossRef]
- Merdol, D.; Altintas, Y. Virtual Simulation and Optimization of Milling Applications: Part II: Optimization and Feedrate Scheduling. J. Manuf. Sci. Eng. 2008, 130, 051005. [Google Scholar] [CrossRef]
- Kumar, D.; Chandna, P.; Pal, M. Efficient optimization of process parameters in 2.5 D end milling using neural network and genetic algorithm. Int. J. Syst. Assur. Eng. Manag. 2018, 9, 1198–1205. [Google Scholar] [CrossRef]
- Campatelli, G.; Lorenzini, L.; Scippa, A. Optimization of process parameters using a Response Surface Method for minimizing power consumption in the milling of carbon steel. J. Clean. Prod. 2014, 66, 309–316. [Google Scholar] [CrossRef]
- Li, C.; Li, L.; Tang, Y.; Zhu, Y.; Li, L. A comprehensive approach to parameters optimization of energy-aware CNC milling. J. Intell. Manuf. 2019, 30, 123–138. [Google Scholar] [CrossRef]
- Velchev, S.; Kolev, I.; Ivanov, K.; Gechevski, S. Empirical models for specific energy consumption and optimization of cutting parameters for minimizing energy consumption during turning. J. Clean. Prod. 2014, 80, 139–149. [Google Scholar] [CrossRef]
- Kuram, E.; Ozcelik, B.; Bayramoglu, M.; Demirbas, E.; Simsek, B.T. Optimization of cutting fluids and cutting parameters during end milling by using D-optimal design of experiments. J. Clean. Prod. 2013, 42, 159–166. [Google Scholar] [CrossRef]
- Goswami, S.; Ghosh, S.; Chakraborty, S. Reliability analysis of structures by iterative improved response surface method. Struct. Saf. 2016, 60, 56–66. [Google Scholar] [CrossRef]
- Neşeli, S.; Yaldız, S.; Türkeş, E. Optimization of tool geometry parameters for turning operations based on the response surface methodology. Measurement 2011, 44, 580–587. [Google Scholar] [CrossRef]
- Karafotias, G.; Hoogendoorn, M.; Eiben, A.E. Parameter Control in Evolutionary Algorithms: Trends and Challenges. IEEE Trans. Evol. Comput. 2015, 19, 167–187. [Google Scholar] [CrossRef]







| Parameter Level | Spindle Speed [r/min] | Feed per Tooth [mm/tooth] | Cutting Depth [mm] | Radial Cutting Depth [mm] |
|---|---|---|---|---|
| 1 | 6000 | 0.03 | 1.0 | 3.2 |
| 2 | 9000 | 0.04 | 1.5 | 6.4 |
| 3 | 12,000 | 0.05 | 2.0 | 9.6 |
| 4 | 15,000 | 0.06 | 2.5 | 12.8 |
| Number | Parameter Level | Up Milling | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Spindle Speed | Feed per Tooth | Cutting Depth | Radial Cutting Depth | Fx | Fy | Fz | εrr | Standard Deviation | |
| [r/min] | [mm/tooth] | [mm] | [mm] | [N] | [N] | [N] | [mm] | ||
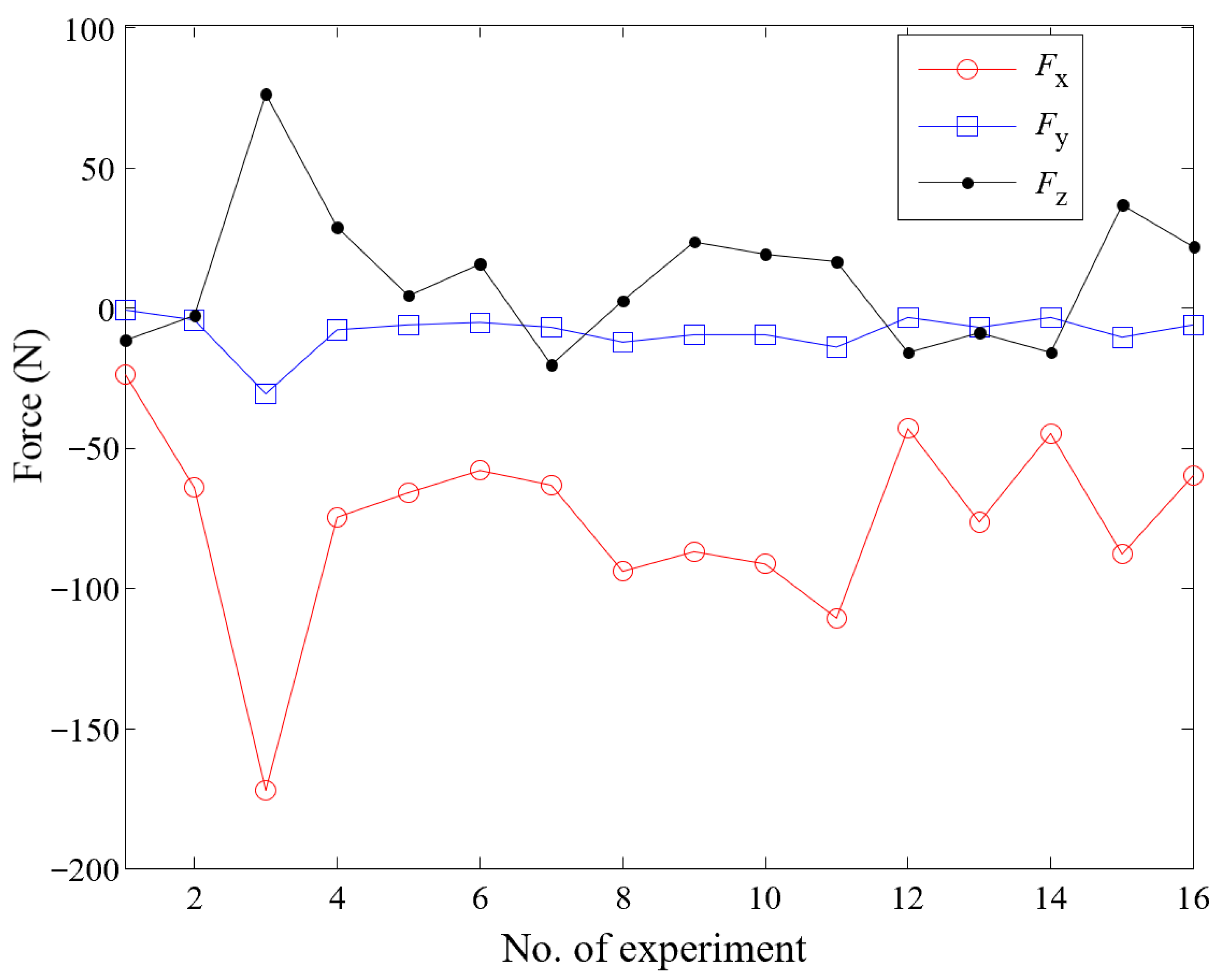
| 1 | 6000 | 0.03 | 1 | 3.2 | −23.89 | −1.75 | −11.81 | 0.016 | 0.015 |
| 2 | 6000 | 0.04 | 1.5 | 6.4 | −64.10 | −5.12 | −3.06 | 0.02 | 0.017 |
| 3 | 6000 | 0.06 | 2.5 | 12.8 | −172.68 | −31.25 | 75.73 | 0.224 | 0.033 |
| 4 | 8000 | 0.05 | 1.2 | 11.2 | −74.84 | −8.71 | 28.18 | 0.055 | 0.051 |
| 5 | 9000 | 0.03 | 1.5 | 9.6 | −66.55 | −6.18 | 3.83 | 0.042 | 0.028 |
| 6 | 9000 | 0.04 | 1 | 12.8 | −58.12 | −5.69 | 15.21 | 0.017 | 0.027 |
| 7 | 9000 | 0.05 | 2.5 | 3.2 | −63.24 | −7.24 | −20.50 | 0.056 | 0.027 |
| 8 | 9000 | 0.06 | 2 | 6.4 | −94.53 | −12.66 | 2.06 | 0.041 | 0.029 |
| 9 | 10,000 | 0.05 | 1.6 | 8 | −87.04 | −10.04 | 22.99 | 0.072 | 0.046 |
| 10 | 12,000 | 0.03 | 2 | 12.8 | −91.55 | −10.34 | 19.21 | 0.075 | 0.032 |
| 11 | 12,000 | 0.04 | 2.5 | 9.6 | −111.11 | −14.08 | 15.86 | 0.086 | 0.030 |
| 12 | 12,000 | 0.06 | 1.5 | 3.2 | −43.19 | −4.33 | −16.24 | 0.050 | 0.022 |
| 13 | 15,000 | 0.03 | 2.5 | 6.4 | −76.81 | −7.62 | −8.83 | 0.048 | 0.019 |
| 14 | 15,000 | 0.04 | 2 | 3.2 | −45.47 | −3.92 | −15.97 | 0.10 | 0.063 |
| 15 | 15,000 | 0.05 | 1.5 | 12.8 | −87.95 | −10.93 | 36.76 | 0.147 | 0.065 |
| 16 | 15,000 | 0.06 | 1 | 9.6 | −59.82 | −6.92 | 21.40 | 0.095 | 0.037 |
| T1 | 8000 | 0.04 | 1.6 | 9.6 | −80.45 | −7.97 | 13.27 | 0.045 | 0.069 |
| T2 | 13,000 | 0.03 | 1.8 | 11.2 | −83.17 | −9.47 | 18.17 | 0.050 | 0.029 |
| Correlation Coefficient | Fx | Fy | Fz | εrr |
|---|---|---|---|---|
| 0.9954 | 0.9996 | 0.9996 | 0.9979 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, Y.; Gu, Q.; Liu, S.; Yang, C. Experimental Investigation and Modeling of Force-Induced Surface Errors for the Robot-Assisted Milling Process. Machines 2023, 11, 655. https://doi.org/10.3390/machines11060655
Jin Y, Gu Q, Liu S, Yang C. Experimental Investigation and Modeling of Force-Induced Surface Errors for the Robot-Assisted Milling Process. Machines. 2023; 11(6):655. https://doi.org/10.3390/machines11060655
Chicago/Turabian StyleJin, Yongqiao, Qunfei Gu, Shun Liu, and Changqi Yang. 2023. "Experimental Investigation and Modeling of Force-Induced Surface Errors for the Robot-Assisted Milling Process" Machines 11, no. 6: 655. https://doi.org/10.3390/machines11060655
APA StyleJin, Y., Gu, Q., Liu, S., & Yang, C. (2023). Experimental Investigation and Modeling of Force-Induced Surface Errors for the Robot-Assisted Milling Process. Machines, 11(6), 655. https://doi.org/10.3390/machines11060655





