Abstract
The traffic management system holds immense importance due to its significant impact on human living standards. With the advent of advanced technologies such as natural language processing and autonomous vehicles, this study proposes a novel cooperative traffic management system based on collection auctions at an isolated unsignalized intersection, taking into account the users’ preferences for passing the intersection while being subject to their social credits. Once vehicles enter the vehicle-to-infrastructure communication zone, drivers provide the intersection control center with their bidding information, which reflects their urgency for right-of-way. According to the traffic and biding information, the vehicles’ passing sequence is optimized by the control center, in order to maximize the drivers’ average satisfaction. To demonstrate the effectiveness of the proposed system, a series of simulation experiments were conducted under varying traffic volumes. The simulation results were then compared with several other traffic control systems from the literature. It was shown that the proposed algorithm demonstrates superior performance in terms of computational time, traffic delay, and drivers’ personal satisfaction.
1. Introduction
Traffic congestion remains one of the most pressing issues in cities, as it not only contributes to air pollution but also results in economic losses [1]. For instance, according to a study conducted by Schrank and Lomax [2], the average American commuter loses approximately 42 h each year due to city traffic congestion. Among the various factors that contribute to traffic congestion, intersections are particularly problematic as they involve the crossing of several incompatible traffic streams. Moreover, with the rapid growth in urbanization and economic development, traffic demand has increased significantly, thereby exacerbating traffic congestion problems. However, expanding the existing infrastructure is not always a viable solution, as it is not only costly but also time-consuming [3]. Consequently, researchers have been exploring advanced traffic control strategies to enhance traffic efficiency without resorting to the expansion of the transportation infrastructure. A range of emerging technologies, such as language intelligence, information and communication technology, and connected and automated vehicles, leverage the development of intelligent transportation systems (ITS), which have shown considerable promise in addressing congestion problems [4,5]. For example, immediate path planning, speed control, and navigation by language communication with drivers support traffic efficiency and safety. The technology of autonomous vehicles (AVs), in particular, has been deemed as a significant innovation that has the potential to enhance traffic assignment efficiency and road capacity, thus mitigating congestion on existing roadways and intersections [6,7]. Furthermore, some AVs are equipped with language intelligence technology that enables drivers to use natural language to communicate with the vehicles [8]. In this regard, an ITS framework can be developed with decision-making through language communication, where drivers can command vehicles with language intelligence without a manual transmission. For example, the AVs exchange information with intersection control centers using vehicle-to-infrastructure (V2I) technology, and the traffic management system makes control decisions based on the information. The decision results are sent back to the vehicles through V2I in a way of informing the drivers through language intelligence [9]. As such, coordination among various traffic management-related elements, such as drivers, AVs, and infrastructure, can be optimized in a more automatic and intelligent manner in the near future. Therefore, it is imperative to develop efficient traffic management systems that leverage the emerging technologies to enhance traffic management system efficiency at isolated intersections without additional infrastructure investments.
Based on the relevant literature, the traffic management system using advanced technologies, such as AVs, language intelligence, and V2I, has two main areas of research focus. The first pertains to cooperative autonomous traffic control mechanisms in signal-free intersections [6,10,11,12]. The cooperative traffic management procedure involves the following steps: when an AV enters the V2I communication zone, it is marked as a new vehicle and sends its estimated arrival time at the intersection border to the control center. Subsequently, upon receiving the estimated arrival time of all new approaching AVs inside the communication zone via V2I connection, the control center globally optimizes the passing sequence of all new AVs, with the aim of minimizing their total travel time delay. Finally, each AV is allocated a personal right-of-way determined by the control center through the V2I connection, based on the optimal passing sequence. However, a latent limitation of the above traffic management system is that it treats all AVs equally in the global optimization process, based on their personal arrival status at the intersection, without considering each vehicle’s priority to pass through the intersection. The value-of-time of each driver differs considerably in reality, due to the various urgencies of traffic resources, travel purposes, and travel time budgets [13]. Hence, the above cooperative traffic control management model does not specially and separately consider each vehicle’s priority in passing through the intersection.
The second area of interest in the literature pertains to the auction-based autonomous intersection management system [14,15,16,17,18]. These studies aim to allocate the right-of-way to AVs through auction operations within traditional intersections that contain traffic signals and stop lines. The cooperative control procedure for this system involves several steps. Initially, the traffic management center located in the intersection receives and groups the bidding information from all vehicles within the V2I communication range. Subsequently, the control center optimizes the signal phase, prioritizing the collection of payments from the vehicles while adhering to related safety constraints. Essentially, the vehicles with higher bids are granted a greater opportunity to pass through the intersection earlier. Finally, all vehicles cross through the intersection during the distributed green phase. However, the aforementioned cooperative traffic control model has several limitations in the new traffic environment with AVs. Specifically, the intersection is controlled based on traffic signal timings, which restricts the ability to take right-of-ways to pass through the intersection with the signal phase order or during the available phase. Additionally, during the constraint of the minimum phase duration, some green time may be assigned to lanes with fewer vehicles, leading to the inefficient utilization of traffic resources.
This study proposes a novel autonomous intersection control model based on collection auctions, leveraging language intelligence, AVs, and V2I technologies to overcome the limitations of the existing cooperative traffic control models. The contributions of this paper are twofold:
- A cooperative traffic control model is proposed for complex and unsignalized intersections, which takes into account drivers’ personal preferences for using traffic resources. The model integrates a process of collection auctions where drivers bid to pass based on their distributed social credit, which ensures social equality. Each driver is assigned an initial social credit at the beginning of time periods, and the drivers’ personal preferences for traffic resources are mathematically transformed into their personal adjusted travel time delay, based on the bidding degree and real travel time delay;
- A metaheuristic algorithm is applied to optimize the passing sequence of AVs through the intersection. The metaheuristic algorithm is chosen over exact methods to meet the real-time control demands from the traffic environment. This is because, with the increase in traffic volume, the control problem becomes an NP-hard problem. Moreover, each vehicle’s right-of-way at the intersection is obtained from the optimized passing sequence.
The remainder of the paper is structured as follows. In Section 2, the framework for the cooperative traffic control model based on collection auctions is presented, along with the associated safety constraints and objective of the control problem. Section 3 introduces the genetic algorithm for optimizing the passing sequence of AVs at the intersection, with the aim of maximizing drivers’ average satisfaction while ensuring compliance with safety constraints. Section 4 outlines the simulation experiments carried out and evaluates the efficiency of the proposed algorithm, with comparisons among other typical traffic control algorithms and the recent ITS-based traffic control methods reported in the literature. The final section presents the main findings of this work, along with some suggestions for future research.
2. Problem Description
This section presents a detailed description of the cooperative traffic management problem to be addressed. First, an overview of the traffic management system is provided, which includes the intersection structure under investigation, and the collection auctions process involving various traffic-related elements, such as drivers, vehicles, and the intersection control center. Subsequently, various headway measures are elaborated upon to ensure safety for incompatible streams and continuous vehicles in the same streams within the intersection. Finally, an analysis of the optimization complexity is presented for the proposed traffic control problem.
In this study, the proposed cooperative traffic management model is predicated on a number of assumptions, including: (1) all vehicles are equipped with autonomous technology and language intelligence, allowing for the recognition of driver auction information; (2) message transmission delay in V2I communication is disregarded; (3) lane-changing behavior within the V2I communication zone is prohibited due to safety concerns; (4) the overtaking operation is forbidden for all autonomous vehicles in each lane within the V2I communication zone, with adherence to the first-in-first-out (FIFO) rule governing the passing sequence through the intersection; and (5) the proposed cooperative traffic management system does not include pedestrians or nonmotorized traffic objects for the sake of clarity.
The definitions of all the principal variables or notations applied in the work are summarized in Table 1.

Table 1.
Definitions of principal variables applied or notations.
2.1. System Overview
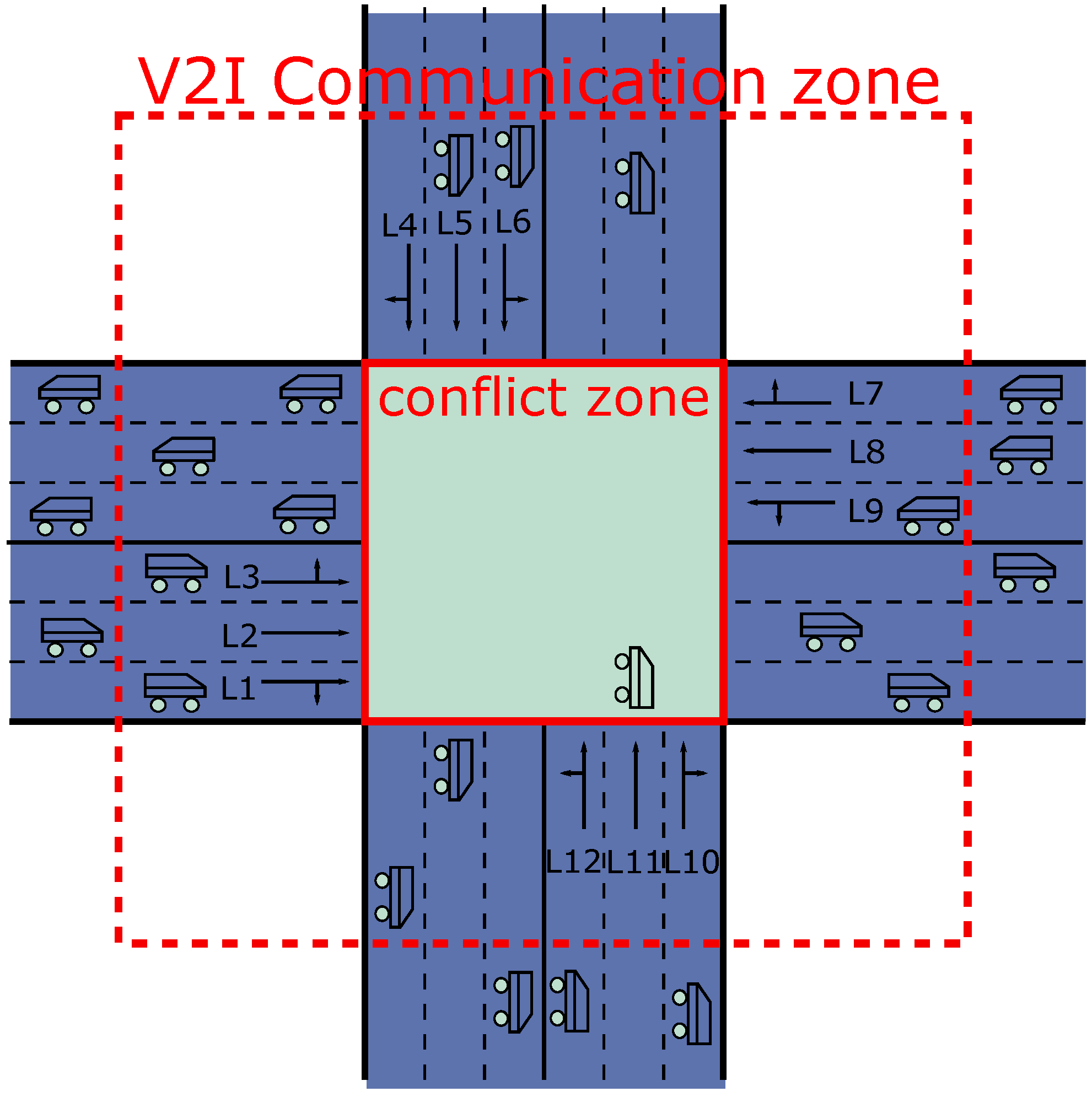
Figure 1 presents the intersection investigated in this study, comprising four approaches, each with three entrance lanes designated for specific vehicle maneuvers, such as left-turn, through, or straight. The intersection includes a V2I communication zone (indicated by the red box) where arriving autonomous vehicles can communicate bid information with the control center. The communication zone has a maximum communication length of 300 m from the intersection border. A small red box highlights the potential conflict zone, which arises due to the overlap of the trip for vehicles arriving from incompatible streams and continuous vehicles in the same streams. The intersection contains a large number of potential conflict points, as shown in Table 2, which summarizes the relationships between any two lanes, indicating the possibility of conflict between them. In Table 2, the “O” mark signifies the conflict possibility between two lanes. For example, the presence of an “O” between lanes 1 and 4 implies that autonomous vehicles from these lanes are prohibited from passing through the intersection zone simultaneously to avoid accidents.
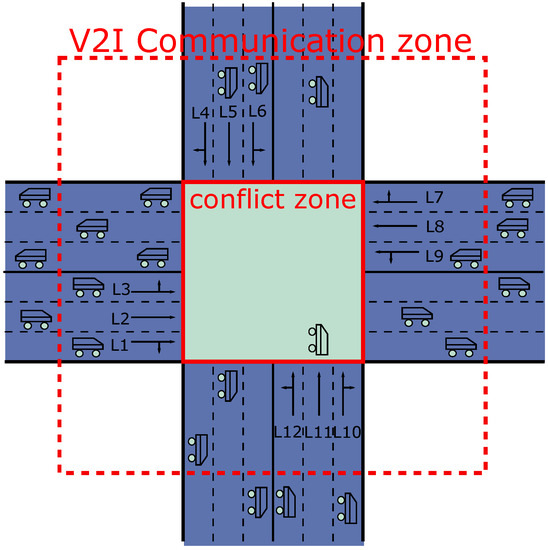
Figure 1.
Structure of the intersection to be researched without traffic lights.

Table 2.
Conflict relationship among vehicles from different lanes.
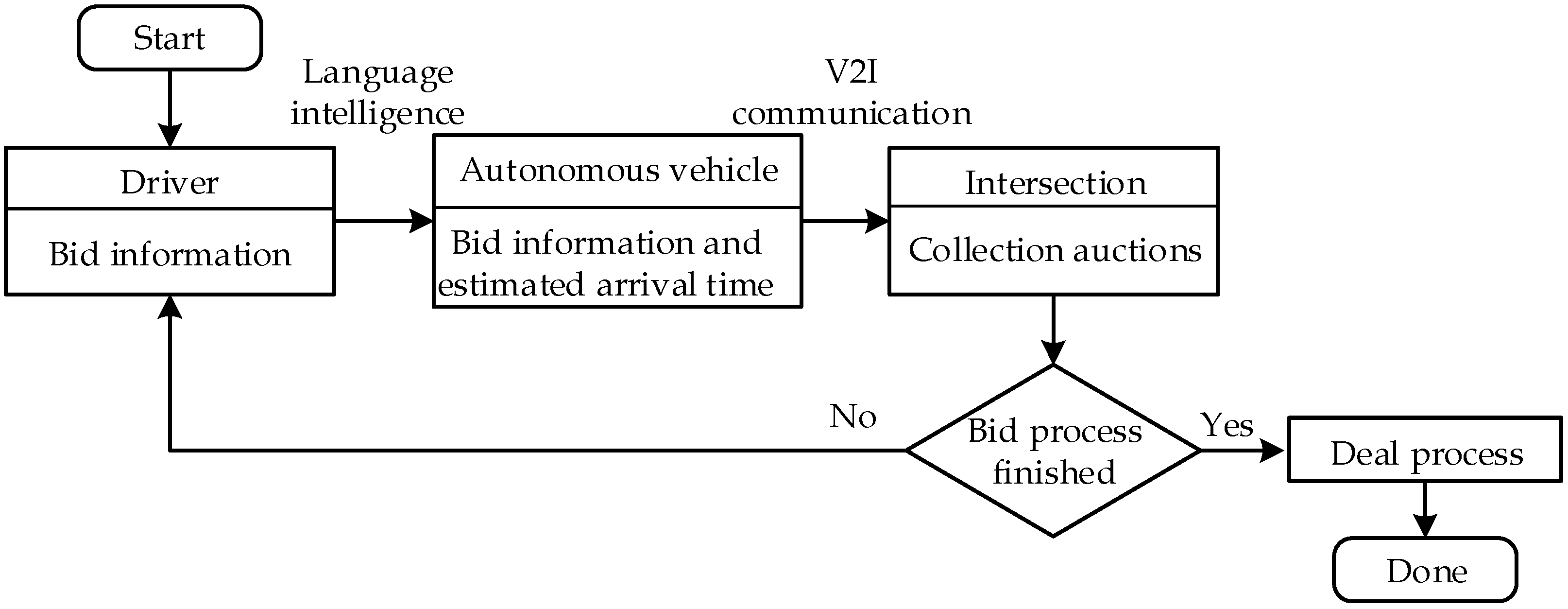
Figure 2 provides a flowchart of the bidding process among drivers, vehicles, and the intersection control center. Upon arrival at the communication zone, a new autonomous vehicle applies language intelligence (speech recognition technology) to recognize the driver’s bid information. Bid information means the social credit points (bid coefficient K in Table 1) that driver intends to bid for the right-of-way. The bid coefficient is chosen within the range . Subsequently, the vehicle conveys a message containing both the movement and bid information to the intersection control center via V2I communication. Once all the movement and bid information from the new vehicles is collected, the intersection control center calculates the optimal passing sequence of all vehicles (including bid and nonbid ones) within the zone and sends this sequence back to each vehicle. The sequence information is immediately known by each driver through language intelligence, allowing them to modify their bid information within the constraint range or accept the controller’s decision on the current passing sequence, which is optimized based on the current bid information. If the driver wants to modify the bid information and the bid process is not yet finished, a new bid process is launched to globally consider the modified bid information. The bid process is automatically closed once a new vehicle arrives at the intersection border (i.e., the red box in Figure 1), and the deal process is executed based on the final optimal passing sequence. New vehicles inside the optimal passing sequence are marked as old vehicles to differentiate themselves from other new arrivals. In the event that new vehicles enter the communication zone before the end of the previous passing sequence, the intersection control center launches a new optimization process solely for the new arriving vehicles, excluding the executed (old) vehicles that must comply with the current optimal passing sequence. This process avoids the inconvenience of emergency brakes for some drivers in the event of updating their passing sequences with new arrivals. Note that the vehicles’ bidding availability and amounts are subject to the balance of social credits that were assigned at the beginning of the periodic, e.g., one week. Overall, the bid-based traffic control structure accounts for drivers’ personal preferences while optimizing feasible passing sequences.
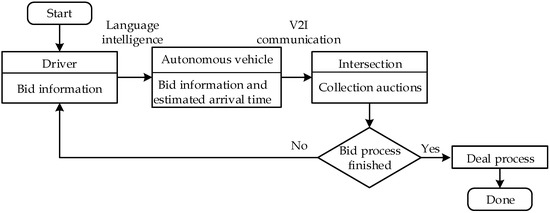
Figure 2.
Bid and collection auction-based traffic management system control flow chart.
2.2. Headway
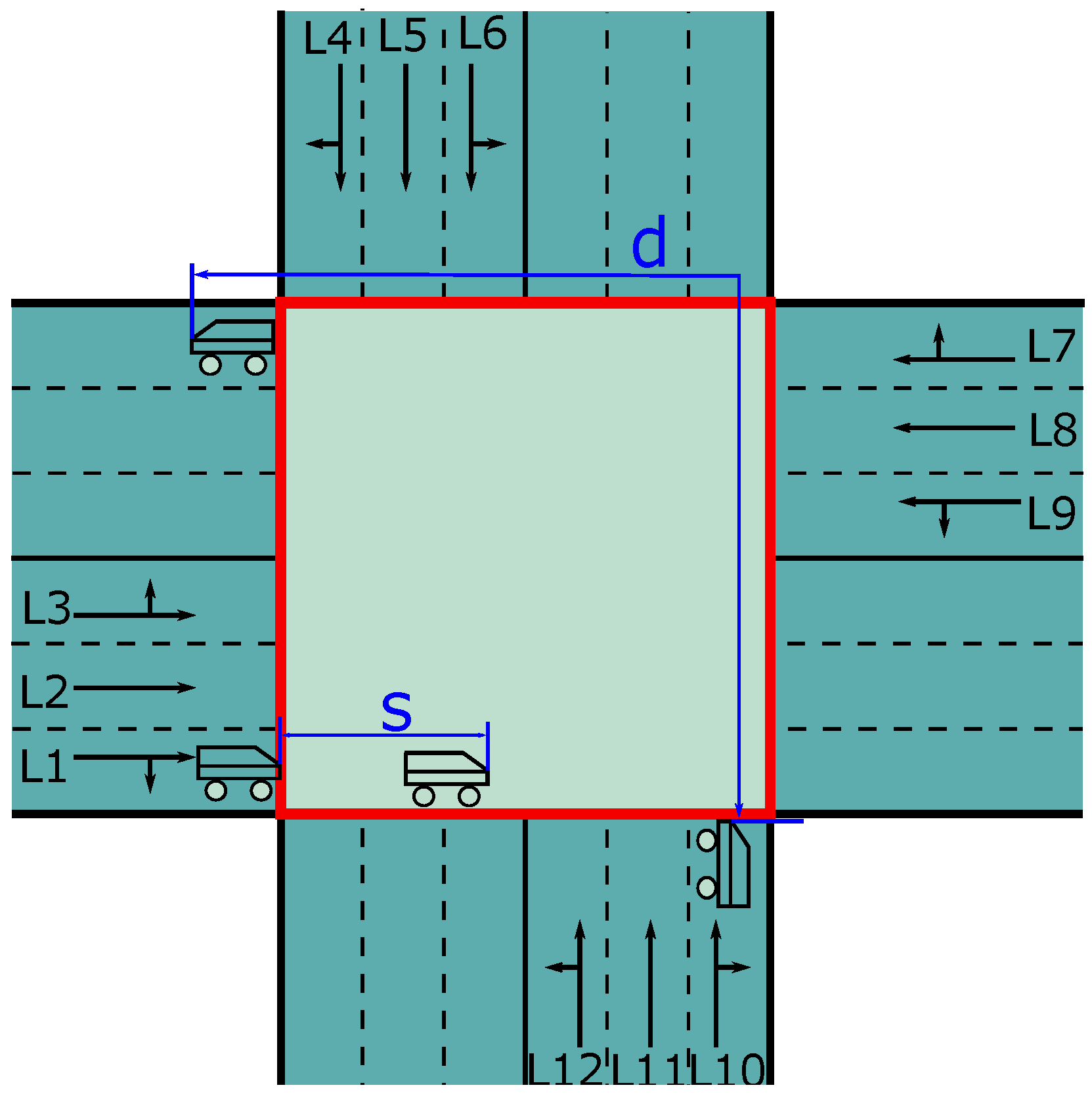
To guarantee safety between vehicles traveling in different streams, a distance interval, commonly referred to as headway, must be established between two vehicles in the same lane or incompatible lanes. Figure 3 illustrates the two parameters that determine the headway. It should be noted that the headway is not required for vehicles traveling in compatible lanes, such as lanes 1 and 3.
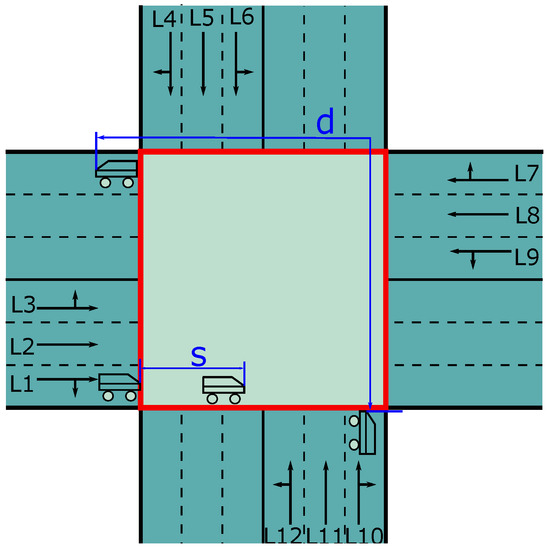
Figure 3.
Various headway requirements.
- s: The minimum time interval that should be maintained between two successive vehicles from the same lane;
- d: The minimum time interval that must elapse between the entry of two vehicles into the intersection from incompatible streams, irrespective of their specific movements within the intersection, is subject to the same headway requirement.
As depicted in Figure 3, two successive vehicles in lanes and require a headway d, which comprises the start-up lost time of the car [19] and the passage time through the intersection. The determination of the values of the parameters d and s is generally influenced by multiple factors, such as weather conditions, intersection dimensions, pavement surface conditions, and drivers’ preferences. According to the literature, empirical observation is one of the most accurate methods to estimate these parameters [20,21]. However, as the estimation of these parameter values is beyond the scope of this study, the widely accepted standards in [22] are employed in this work.
2.3. Optimal Problem Complexity Analysis
The primary challenge in optimizing the passing sequence in real time is associated with the computational complexity problem, given that each vehicle is treated individually during the optimization process. It was necessary to analyze the number of feasible solutions before exploring a suitable algorithm.
Proposition 1.
Consider an intersection with a total of L entrance lanes, and let denote the number of planning vehicles in each lane. If no overtaking behavior is allowed, then the total number of feasible passing sequences of all vehicles can be expressed as shown in Equation (1).
At the intersection depicted in Figure 1, the number of lanes is , with representing the number of new arrival vehicles in each lane l. The total number of new vehicles to be optimized at the intersection is given by the sum of for all lanes, i.e., . The number of possible ordered sequences of all new vehicles can be computed as . However, since all new vehicles must follow the “First-In-First-Out” (FIFO) rule in the same lane, which prohibits lane-change behavior before entering the intersection, the total possibilities are further divided by the product of factorials of for all lanes, i.e., . Consequently, the final number of feasible sequences can be calculated using Equation (1). The computational complexity of finding an appropriate algorithm to optimize the passing sequence in real time for each vehicle is exacerbated by the fact that each vehicle must be considered individually during the optimal process.
In accordance with Equation (1), a slight increase in the number of new vehicles leads to a significant increase in the problem complexity. Consequently, exhaustive search algorithms may not be capable of finding the global optimal solution within an acceptable computation time. For instance, the branch and bound algorithm was successfully employed in the work of [23] to determine the optimal passing sequence at a simple intersection with a single lane. Although the method proposed in [23] can be readily extended to optimize any intersection layout, the computation time was expected to escalate considerably as the complexity of intersection geometries increases. As a result, exact algorithm-based traffic control methods may not always fulfill real-time requirements in a more intricate traffic network. The need for a computationally efficient method to resolve the sequential optimization problem is even more apparent in the context of bid-based traffic control at intersections due to the additional time required for drivers to decide on the bid negotiation in practice. This provides the motivation for seeking metaheuristic algorithms to solve complicated problems (e.g., the traveling salesman problem [24]) within an acceptable computation time. Therefore, this study employs the genetic algorithm (GA) [25] to address the NP-hard optimal traffic control problem for the intersection illustrated in Figure 1.
3. Algorithm Proposed
The genetic algorithm (GA) is an optimization technique inspired by biological evolution that aims to find the optimal solution to a given problem through the processes of selection, reproduction, and mutation. The GA mimics the natural selection process by reproducing one generation after another while eliminating the unfit solutions, allowing the fittest solution to survive and eventually dominate the population. Solutions are represented as chromosomes or genes within a population, which is the set of all feasible solutions within a defined boundary. The fitness function is used to determine the quality of each chromosome, and the ranking process is used to produce a list of chromosomes according to their fitness. The selection process selects the fitter chromosomes and discards the unfit ones to maintain the same population size. In the reproduction stage, the selected chromosomes become the parents of the next generation, and the new chromosomes produced form the population of the new generation. The GA stops when one of the stopping criteria is reached, such as the number of generations or solutions that reach the limit of the fitness function. The GA has been shown to be effective in solving complex problems such as the traveling salesman problem and can provide computationally efficient solutions for problems that are otherwise difficult to solve [26,27].
3.1. Population of Chromosomes
In this study on cooperative traffic management based on auctions, the population refers to the set of chromosomes or solutions, which need to be defined. Specifically, the chromosomes represent the passing sequence of vehicles through the intersection. To encode the passing sequence, the entrance lane index of each vehicle is utilized instead of the vehicle identity. This is due to the adherence of new vehicles in the same lane to the “FIFO” rule, which prohibits overtaking. Hence, the sequence of new vehicles can be converted into lane indexes. The coding approach for the passing sequence reduces the computational complexity by excluding invalid solutions during the evolution process. Consequently, all generated random passing sequences are deemed legal. The code of each chromosome is mathematically represented in Equation (2).
The determination of the number of chromosomes in the population is crucial as it affects both the speed and accuracy of the optimization process. The selection of an excessively large population size may result in a longer computation time required to find the fittest solution, while a small population may hinder the genetic algorithm’s ability to locate optimal solutions. Thus, the number of chromosomes must be selected with great care to ensure a balance between speed and accuracy in the traffic management system. In this study, the population size is set to be 10% of the traffic volume, implying that the genetic algorithm generates a population of such magnitude to obtain the fittest solution. The population size should be tailored to the traffic volume, as a larger population is necessary to avoid local optimal solutions as the traffic volume increases.
3.2. Generations and Reproductions
The determination of the number of generations in which the genetic algorithm needs to be run is a critical aspect that requires careful consideration. The number of generations serves as a stopping criterion for the genetic algorithm, and it terminates when the algorithm has reached a predetermined number of generations. In the context of traffic flow control, the number of genetic algorithm generations is set to equal the traffic volume. This decision is based on a thorough analysis of the impact of the number of generations on the algorithm’s performance. A long computation time will be incurred if too many generations are allowed, whereas an insufficient number of generations may reduce the algorithm’s efficiency, as it fails to identify the optimal chromosome within the population. The number of generations should also be adapted to the traffic volume rather than being a fixed value, as a larger traffic volume demands a correspondingly higher number of generations to prevent the occurrence of a local optimum solution.
The crossover fraction is a parameter that specifies the amount of information inherited by offspring from their parents during the reproduction process. In this process, chromosomes are paired and selected to become the parents of the next generation. The crossover fraction determines the proportion of parental information transmitted to the offspring, thereby generating new chromosomes. In this study, a crossover fraction of 0.8 was employed, indicating that each pair of parents, denoted A and B, will produce two offspring. The offspring will inherit 80% of the values from parent A and 20% from parent B, while the other offspring will inherit 20% from parent A and 80% from parent B, as expressed in Equations (3) and (4).
where X and Y are the new generations of inheritance.
3.3. Fitness Function
The fitness function is a crucial component of the genetic algorithm, as it guides the selection of fit chromosomes from the population. The fitness function assigns a fitness value to each chromosome in the population, based on a predetermined rule or equation. In this study, the fitness function is formulated in Equation (5). The objective is to minimize the sum of adjusted time delays (i.e., the fitness function) for all new vehicles. The adjusted time delay is computed by adding a parameter K to the actual time delay to account for the driver’s preferences, as shown in Equation (6). The parameter K is set to be one for all vehicles by default (the K can be any integral number within CR), but during the bidding process, drivers who wish to pass the intersection earlier (e.g., in this study, PR = 10%) may increase their bid by increasing the value of K, which is subject to the balance of the social credits that they own. The actual time delay experienced by a vehicle is calculated as the difference between the departure time from the intersection stop line and the virtual arrival time in a free-flow scenario, as illustrated in Equation (7). The fitness function is applied to calculate the total adjusted time delay for all new vehicles within the communication zone, subject to safety constraints related to headway as previously mentioned.
where
The fitness limit constitutes an additional stopping criterion for the genetic algorithm, which is established as the target value that the fitness function must achieve. The attainment of the fitness limit, as the output of the fitness function, signifies the discovery of the most suitable chromosome and will result in the termination of the genetic algorithm. In the context of traffic flow control, the fitness limit is specified to be zero. Subsequently, any chromosome that generates a fitness value of zero or less, after undergoing evaluation in the fitness function, will be recognized as the optimal solution by the genetic algorithm.
4. Experimental Analysis
This section presents a series of simulation experiments to evaluate the performance of the proposed algorithm under different traffic volumes. The intersection structure used in the simulations is depicted in Figure 1, while the simulation parameters are provided in Table 3. A random allocation process assigns drivers who can bid for early intersection passage at a predefined penetration rate PR = 10%. Personal preferences are expressed by the coefficient K, as defined in Equation (6). In the simulation experiments, the values of K are randomly generated within the constraint range , and are used as final bid decisions. Traffic volumes vary from 100 (veh/h/l) to 400 (veh/h/l), leading to a large variation in the total number of new vehicles for the optimization process. The parameters of the genetic algorithm are set according to the traffic volume, to improve performance compared to fixed parameter settings. Fixed settings based on for a traffic volume of 400 (veh/h/l) will result in computational waste for a case with a much lower number of new vehicles, such as a traffic volume of 100 (veh/h/l). The present work utilized a microscopic traffic simulation model implemented in C++ in a personal framework. The simulation system was executed on a desktop computer with six 3.5 (GHz) Intel processors. The Gipps model was used to simulate vehicle behavior [28], as it has been shown to achieve higher accuracy in traffic simulations than other similar models [29]. The Poisson distribution was applied to generate traffic volumes in each lane, as it accurately represents the actual characteristics of the arrival flow of vehicles [30,31].

Table 3.
Simulation parameters.
This section presents three series of simulations to evaluate the performance of the proposed genetic algorithm. Firstly, the simulation results are compared with those obtained by an exact algorithm to demonstrate the accuracy of the genetic algorithm. Secondly, the proposed traffic control algorithm is compared with traditional traffic control methods to assess its effectiveness. Lastly, a comparison is made between the proposed method and other relevant methods applied to intelligent traffic control systems in the literature.
4.1. Comparisons with the Exact Algorithm
In this subsection, the accuracy and efficiency of the proposed GA method are demonstrated by comparing it with the exact branch and bound algorithm (B&B) presented in [23]. Fifty tests were conducted for both the B&B and GA, with the traffic volume ranging from 100 to 400 (veh/h/l). The performance of the two algorithms was evaluated using three criteria, which are given as follows:
- The relative percentage deviation (PRD) is a performance index used to evaluate the accuracy of the proposed GA algorithm. It is calculated as the percentage difference between the optimal solution obtained by the exact B&B algorithm and the solution obtained by the GA algorithm;
- The optimal solution found percentage (OSFP) is a performance index that was used to measure the accuracy of the proposed GA algorithm in finding the global optimal solution. Like PRD, OSFP is also an accuracy performance index and is defined as the percentage of times that the GA algorithm is able to find the global optimal solution in comparison to the exact B&B algorithm;
- The calculation time (CT) is an efficiency performance index that quantifies the amount of computing time required to determine the optimal solution.
In this section, Table 4 presents a performance comparison between the exact B&B algorithm and the proposed GA algorithm. As the problem scale increased, the average OSFP diminished, with a minimum of 10% observed in the case of high traffic volume 400 (veh/h/l). This trend can be attributed to the significant increase in the solution space with increasing traffic volumes. However, it is worth noting that the heuristic-based GA algorithm aims to provide a near-optimal solution within a reasonable computing time, without guaranteeing the global optimal solution, which is ensured by the B&B algorithm.

Table 4.
Simulation results comparison between the B&B and GA algorithms.
Moreover, the average PRD index remained low even with the increase in traffic volume. This index serves as a measure of accuracy, indicating the percentage difference between the optimal solutions obtained by the GA and B&B algorithms. The average PRD value remained at a mere 2.89% even in high traffic volume, indicating that the GA algorithm can obtain near-optimal solutions compared to the exact B&B algorithm. The low PRD index demonstrates the high accuracy of the GA algorithm in finding optimal or near-optimal solutions.
Next, we examine the efficiency index, CT. It is noteworthy that even for the high traffic volume tests, the proposed GA algorithm preserved a low CT value, which was significantly less than the one executed in the B&B algorithm. Based on the comparison of the aforementioned three indexes, it is evident that the proposed GA algorithm delivered a consistent performance under diverse traffic volumes while consuming significantly fewer calculation resources in contrast to the exact B&B algorithm.
Comparison with the Traditional Traffic Control Strategies
In this subsection, we compare the proposed GA algorithm with two conventional traffic control methods: fixed time control (FT) [32] and adaptive traffic control strategy (ATCS) [33]. In the FT control, the number of phases is four. Each phase contains all the movements (left turn, right turn, and go straight) from the same approach. The cycle length is 100 s. Each phase has 25 s, with 20 s of green time, 2 s of yellow time, and 3 s of red time. Table 5 summarizes the simulation results obtained from 50 tests, and the average values are presented. The findings reveal that the proposed GA algorithm outperformed both traditional adaptive and fixed time traffic control methods in terms of reducing the average adjusted time delay for all vehicles. Furthermore, it is worth noting that the bid coefficient K was uniformly set to one for all vehicles, and when K was greater than one, it implies that the vehicle bid for its right-of-way at the intersection. The GA-based bid-based traffic control strategy can prioritize the bidding vehicles with , leading to substantially lower average adjusted time delays (less than 1s) compared to those of all the vehicles. In contrast, traditional traffic control methods cannot give priority to the bidding vehicles. In terms of computation time (CT), traditional methods consume negligible time, and the GA algorithm requires slightly more, but is still within 0.1 s.

Table 5.
Performance comparison with the traditional traffic control strategies.
Thus, the proposed GA algorithm demonstrates superior control over the traditional traffic control methods, as evidenced by its ability to significantly reduce the average adjusted time delay for all vehicles, particularly the bidding vehicles.
4.2. Comparison with Other Intelligent Transportation Systems
This section assesses the efficiency of intersection control using the proposed GA algorithm in comparison with other intelligent transportation systems reported in the literature. To this end, we conducted 50 tests on all the compared systems, with varying traffic volumes ranging from 100 to 400 (veh/h/l) at an interval of 50 (veh/h/l).
- The ACS system, as described in Wu et al. (2012), employs a model in which all AVs have equal priority (), and there are no traffic lights at the intersection. The right-of-way of each vehicle is communicated via V2I communication based on the optimal passing sequence obtained;
- The BBPSC system, proposed by Kentaro et al. in [14], is a model in which all AVs compete for right-of-way at intersections controlled by traffic lights. The AVs transmit their bid information to the infrastructure through V2I communication, and the allocation of traffic resources is regulated by signal phases;
- The FCFS system [34] refers to a basic control method for autonomous intersection control that operates without traffic lights. Specifically, this method allows vehicles to pass through the intersection according to their arrival order at the intersection border.
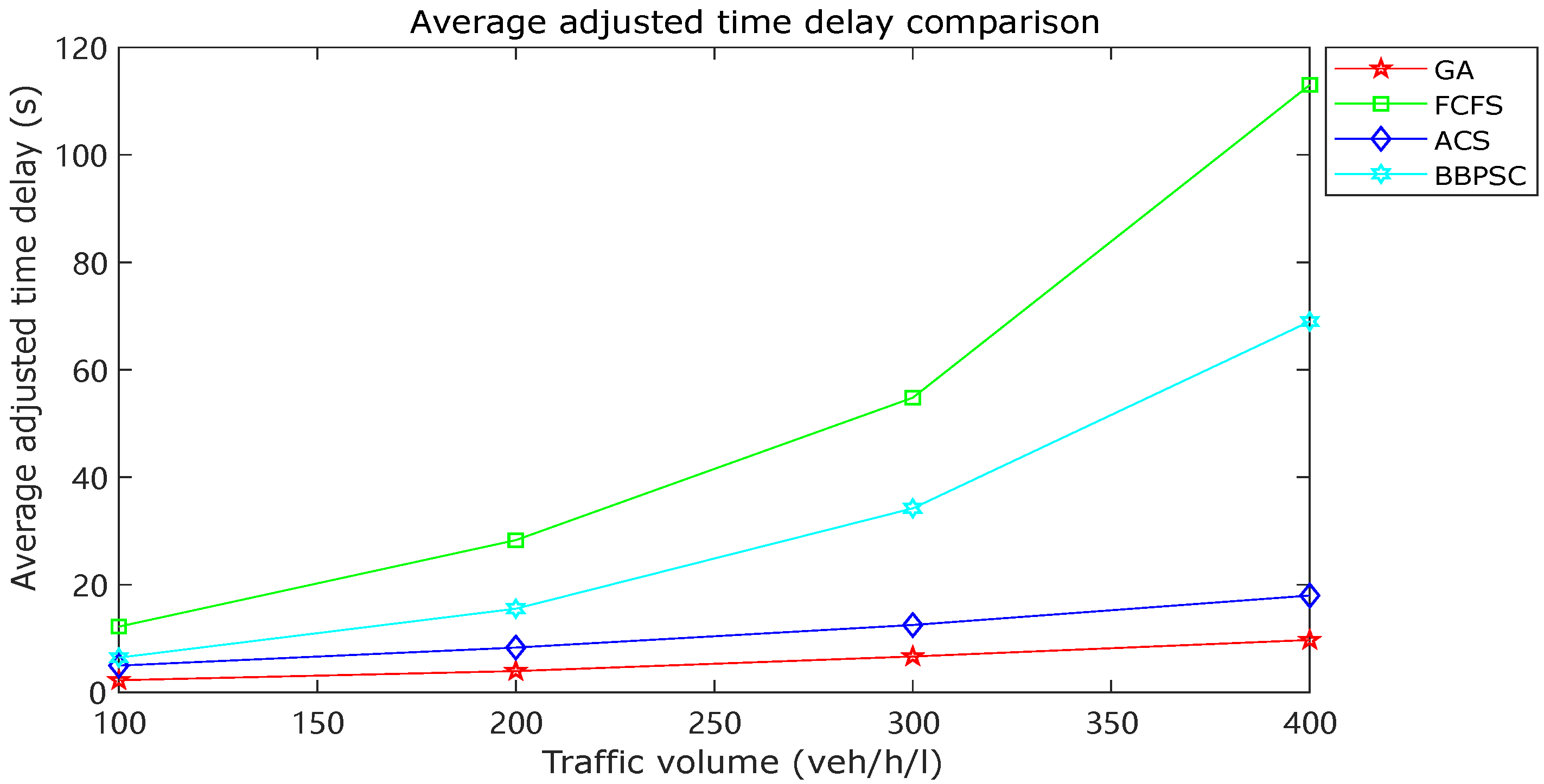
4.2.1. Comparison of Adjusted Time Delay
In Figure 4, the adjusted time delay is compared among the aforementioned traffic control models. It was observed that the GA algorithm outperformed the other models with significantly lower values. This demonstrates that the GA algorithm has the most superior performance in conducting a global search for the optimal solution based on the arrival information of each vehicle. Conversely, the FCFS system exhibited the poorest performance since the passing sequence of vehicles was not globally optimized.
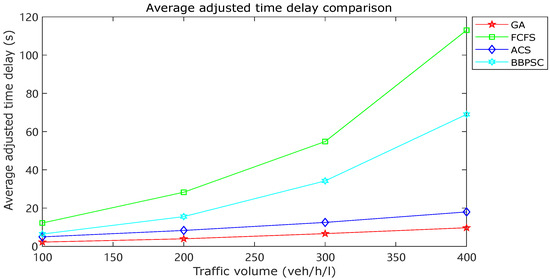
Figure 4.
Average adjusted time delay comparison.
4.2.2. Comparison of Actual Time Delay
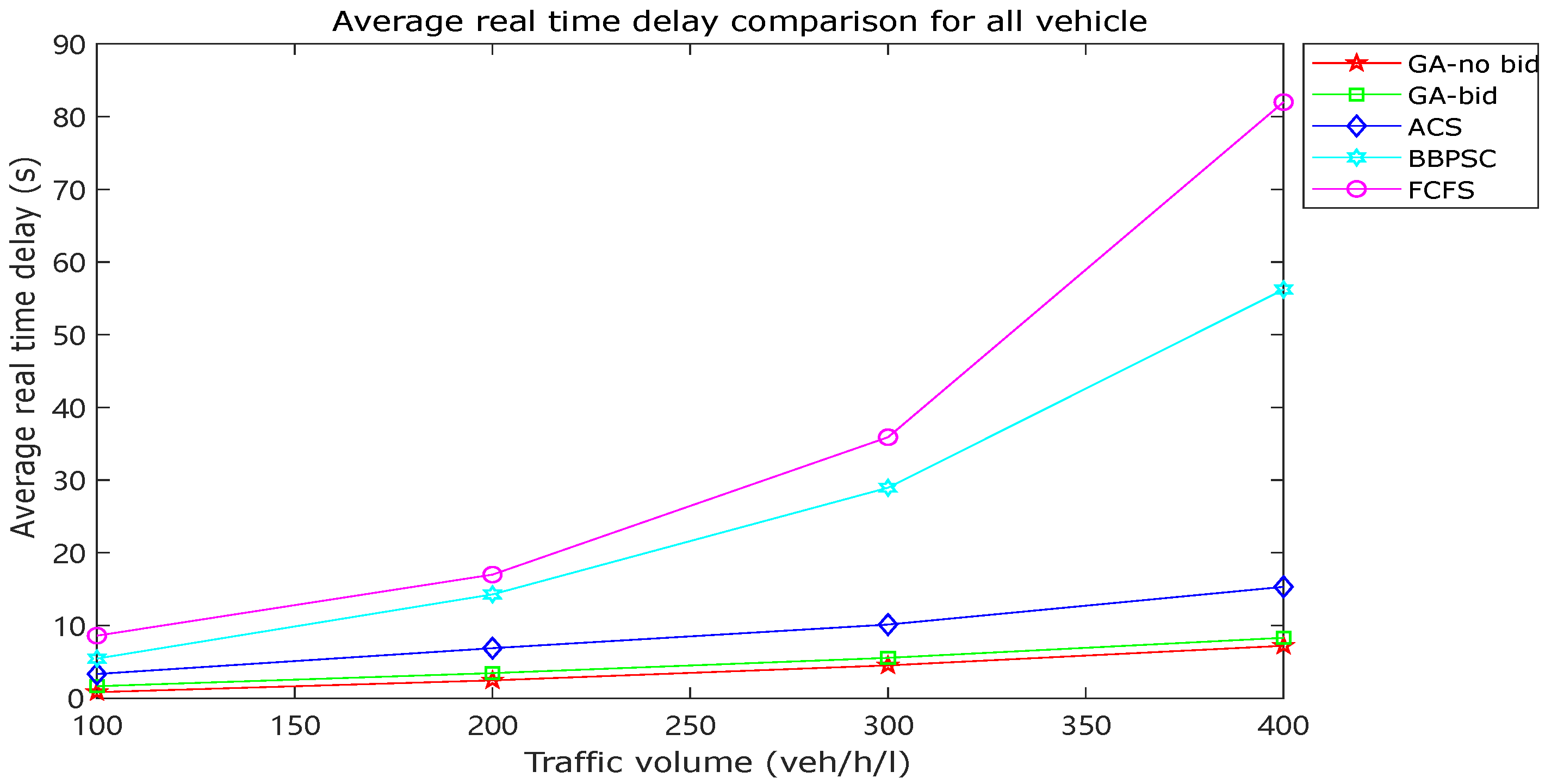
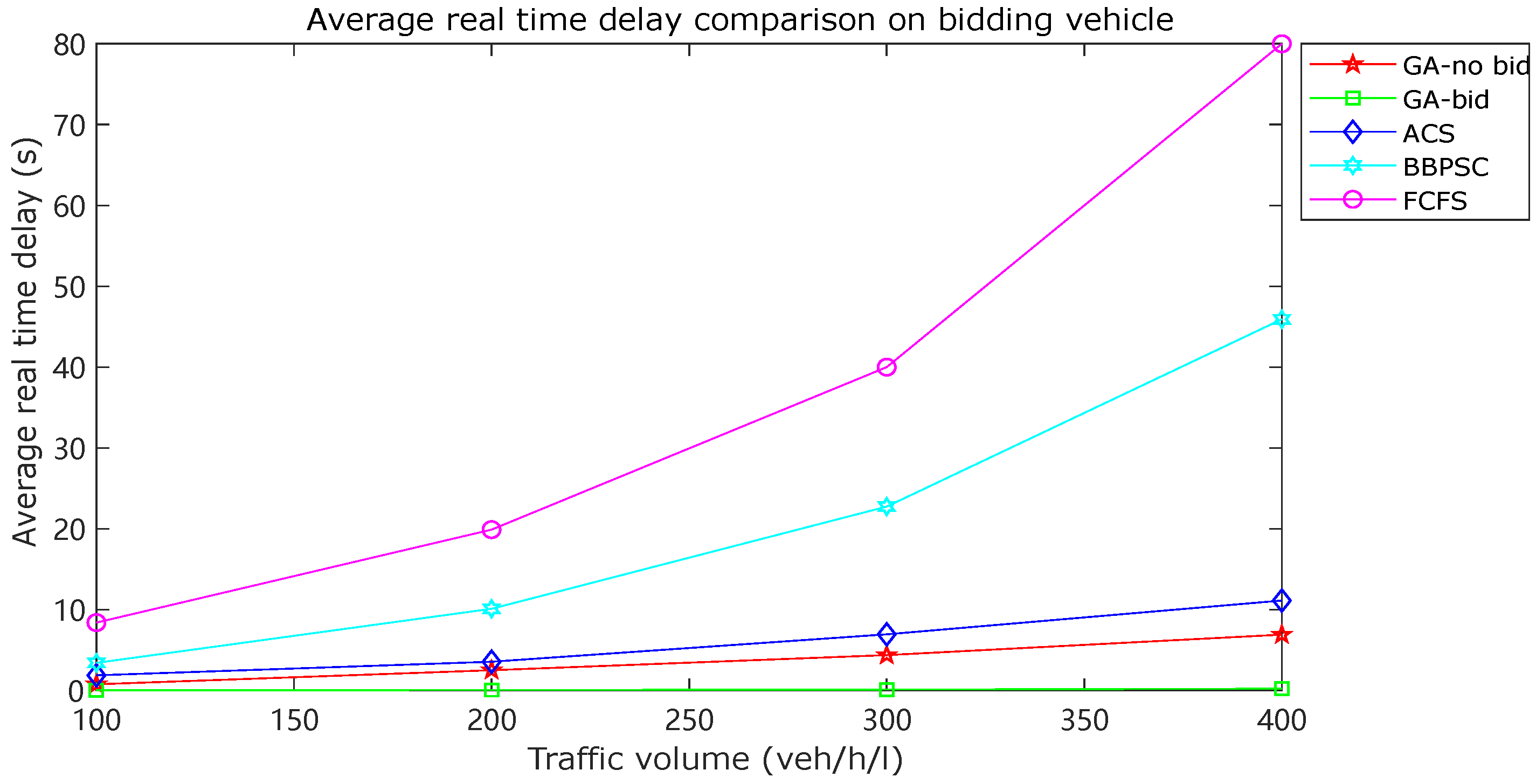
Figure 5 presents a comparison of the average actual time delay among various traffic control strategies. The “GA-no bid” profile corresponds to the case where no vehicle bids for priority and the default value of is used. The “GA-bid” profile represents a scenario where 10% of vehicles use the bid-based traffic control strategy with different coefficients K (). The comparison between these two profiles indicates that the proposed GA algorithm had a negligible impact on the average actual time delay. Figure 6 focuses on the average actual time delay of bidding vehicles only and compares various methods. The comparison between the “GA-no bid” and “GA-bid” profiles demonstrates that the bid-based traffic control strategy can effectively reduce traffic delay for bidding vehicles, which are expected to have priority to pass the intersection as soon as possible. When compared with other intelligent transportation systems, the proposed GA algorithm consistently outperformed them in reducing the delay for bidding vehicles.
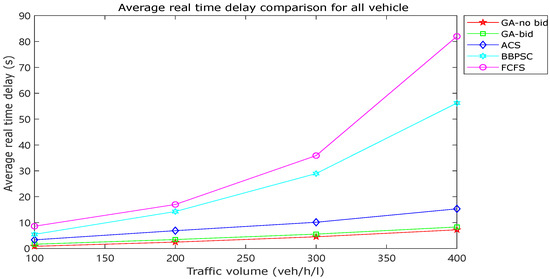
Figure 5.
Comparison of average actual time delay for all vehicles.
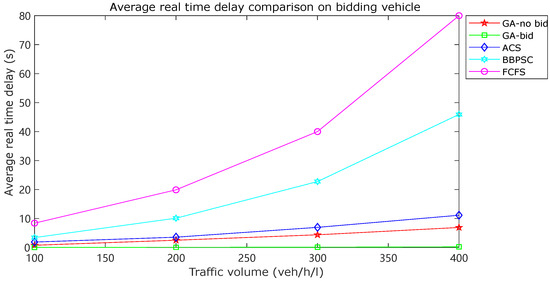
Figure 6.
Comparison of average actual time delay for bidding vehicles.
4.2.3. Comparison of Calculation Time
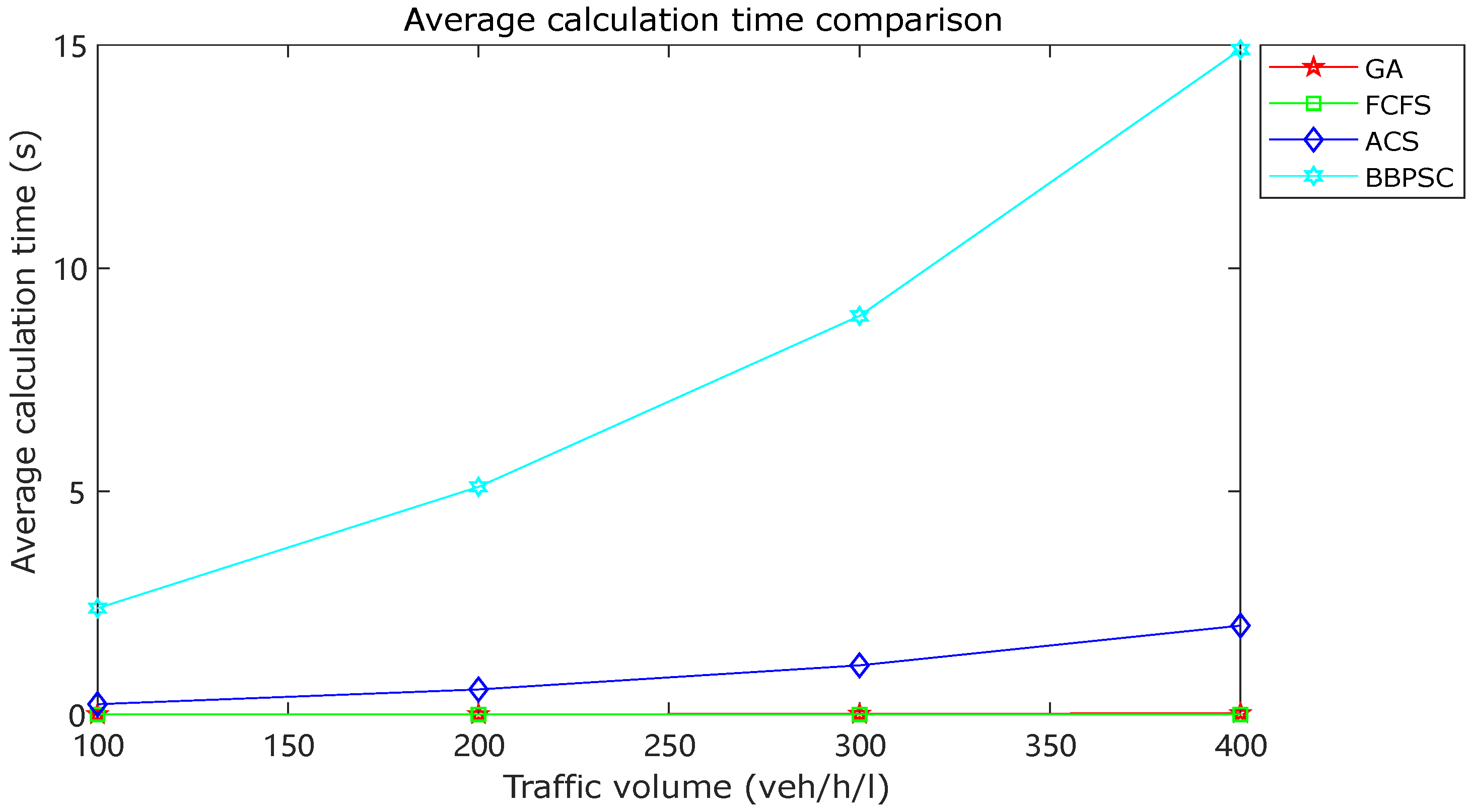
The comparison of computational time is depicted in Figure 7. As the FCFS strategy does not involve any optimization process, its computation time was nearly negligible. In contrast, the proposed GA algorithm exhibited a significantly lower computation time than the other strategies, thereby highlighting the efficacy of the GA algorithm in meeting real-time constraints.
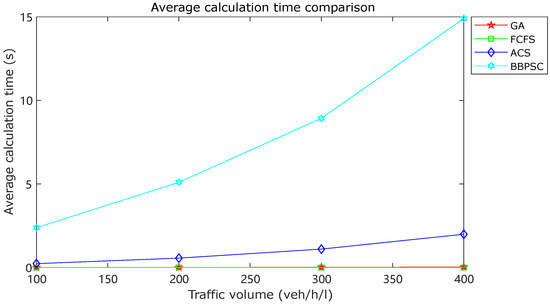
Figure 7.
Average calculation time comparison.
5. Conclusions
This paper introduces a novel bid-based traffic control method for a complex intersection with autonomous vehicles, where traditional traffic signals are absent. The proposed method utilizes language intelligence technology to identify the driver’s bid information, which is then transmitted to the intersection control center along with the arrival information of the vehicles. In this study, we employed the GA algorithm to globally optimize the vehicle passing sequence by minimizing the adjusted time delay, which was associated with the bid information. The proposed method provides priority to the vehicles with bids, which can significantly reduce the time delay compared to other control methods. The simulation results demonstrate the efficacy of the proposed GA algorithm in reducing the time delay for all simulated vehicles, particularly for those with bids.
However, there are several limitations in our study that require attention in future work. Firstly, the auction-based control mechanism is a simplified version regarding the configuration of drivers’ social credits, measured with the bidding coefficient associated with each vehicle’s time delay. Our model is a static one with the actual balance of drivers’ social credits (i.e., the assumption of a bidding penetration ratio of PR = 10% with random ). Therefore, the constraint of the driver’s bid resources, i.e., the dynamic balance of social credits, has not yet been added to the control model. This especially relevant in the case where one driver passes by multiple intersections and executes the bid process several times. Secondly, the current study assumed that all vehicles at the unsignalized intersection were autonomous. However, in the future, it would be necessary to extend the bid-based control approach to account for the priorities of other road users, such as pedestrians, buses, and other vehicles that require special services. In addition, the social credit assigned to drivers can be linked to punishment (e.g., for traffic violations) and reward (e.g., for ride-sharing) mechanisms to produce benefits for both users and society.
Author Contributions
Conceptualization, J.L. and Y.F.; methodology, B.Y.; software, Y.F.; validation, J.L. and B.Y.; formal analysis, B.Y.; investigation, Y.F.; resources, J.L.; data curation, J.L.; writing—original draft preparation, J.L. and B.Y.; writing—review and editing, J.L. and B.Y.; visualization, J.L.; supervision, B.Y.; project administration, B.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available on reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- The European Court of Auditors. Urban Mobility in the EU; Technical Report; European Union: Luxembourg, 2019. [Google Scholar]
- Schrank, D.; Eisele, B.; Lomax, T.; Bak, J. 2015 Urban Mobility Scorecard; Texas Transportation Institute: College Station, TX, USA, 2015. [Google Scholar]
- Litman, T. Generated Traffic and Induced Travel: Implications for Transport Planning; Technical Report; Victoria Transport Policy Institute: Victoria, BC, Canada, 2017. [Google Scholar]
- Shladover, S. Connected and automated vehicle systems: Introduction and overview. J. Intell. Transp. Syst. 2018, 3, 190–200. [Google Scholar] [CrossRef]
- Yang, K.; Guler, S.I.; Menendez, M. Isolated intersection control for various levels of vehicle technology: Conventional, connected, and automated vehicles. Transp. Res. Part C Emerg. Technol. 2016, 72, 109–129. [Google Scholar] [CrossRef]
- Wu, J.; Abbas-Turki, A.; El Moudni, A. Cooperative driving: An ant colony system for autonomous intersection management. Appl. Intell. 2012, 37, 207–222. [Google Scholar] [CrossRef]
- Guler, S.; Menendez, M.; Meier, L. Using connected vehicle technology to improve the efficiency of intersections. Transp. Res. Part C Emerg. Technol. 2014, 46, 121–131. [Google Scholar] [CrossRef]
- Sestino, A.; Peluso, A.; Amatulli, C.; Guido, G. Let me drive you! The effect of change seeking and behavioral control in the Artificial Intelligence-based self-driving cars. Technol. Soc. 2022, 70, 102017. [Google Scholar] [CrossRef]
- Lioris, J.; Pedarsani, R.; Tascikaraoglu, F.; Varaiya, P. Platoons of connected vehicles can double throughput in urban roads. Transp. Res. Part C Emerg. Technol. 2017, 77, 292–305. [Google Scholar] [CrossRef]
- Wu, J.; Abbas-Turki, A.; Correia, A.; El Moudni, A. Discrete Intersection Signal Control. In Proceedings of the IEEE International Conference on Service Operations and Logistics, and Informatics, Philadelphia, PA, USA, 27–29 August 2007; pp. 1–6. [Google Scholar]
- Liang, X.J.; Guler, S.I.; Gayah, V.V. An equitable traffic signal control scheme at isolated signalized intersections using Connected Vehicle technology. Transp. Res. Part C Emerg. Technol. 2020, 110, 81–97. [Google Scholar] [CrossRef]
- Liang, X.; Guler, S.I.; Gayah, V.V. Traffic signal control optimization in a connected vehicle environment considering pedestrians. Transp. Res. Rec. 2020, 2674, 499–511. [Google Scholar] [CrossRef]
- Small, K. Valuation of travel time. Econ. Transp. 2012, 1, 2–14. [Google Scholar] [CrossRef]
- Iio, K.; Zhang, Y.; Quadrifoglio, L. Bid-Based Priority Signal Control in a Connected Environment: Concept. Transp. Res. Rec. 2019, 2673, 737–747. [Google Scholar] [CrossRef]
- Iliopoulou, C.; Kampitakis, E.; Kepaptsoglou, K.; Vlahogianni, E.I. Dynamic traffic-aware auction-based signal control under vehicle to infrastructure communication. Phys. A Stat. Mech. Its Appl. 2022, 608, 128258. [Google Scholar] [CrossRef]
- Iliopoulou, C.; Kepaptsoglou, K.; Vlahogianni, E. A Survey on Market-Inspired Intersection Control Methods for Connected Vehicles. IEEE Intell. Transp. Syst. Mag. 2022, 15, 2–16. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, S.; Teng, L. Method of Controlling Vehicles at Intersections Based on the Auction Algorithm. In Proceedings of the Journal of Physics: Conference Series, Xi’an, China, 25–27 October 2019; IOP Publishing: Bristol, UK, 2020; Volume 1453, p. 012050. [Google Scholar]
- Carlino, D.; Boyles, S.D.; Stone, P. Auction-based autonomous intersection management. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013), The Hague, The Netherlands, 6–9 October 2013; pp. 529–534. [Google Scholar]
- Kutz, M. Handbook of Transportation Engineering; McGrawHill: New York, NY, USA, 2004. [Google Scholar]
- Chen, X.; Li, L.; Zhang, Y. A Markov Model for Headway/Spacing Distribution of Road Traffic. IEEE Trans. Intell. Transp. Syst. 2010, 11, 773–785. [Google Scholar] [CrossRef]
- Bertolazzi, E.; Biral, F.; Da Lio, M.; Saroldi, A.; Tango, F. Supporting Drivers in Keeping Safe Speed and Safe Distance: The SASPENCE Subproject Within the European Framework Programme 6 Integrating Project PReVENT. IEEE Trans. Intell. Transp. Syst. 2010, 11, 525–538. [Google Scholar] [CrossRef]
- Cohen, S. Ingénierie du Trafic Routier: Éléments de Théorie du Trafic et Applications; Cours de l’École Nationale des Ponts et Chaussées; Presses de l’École Nationale des Ponts et Chaussées: Paris, France, 1990. [Google Scholar]
- Yan, F.; Dridi, M.; El Moudni, A. Control of traffic lights in intersection: A new branch and bound approach. In Proceedings of the International Conference on Service Systems and Service Management, Melbourne, VIC, Australia, 30 June–2 July 2008; pp. 1–6. [Google Scholar]
- Halim, A.; Ismail, I. Combinatorial optimization: Comparison of heuristic algorithms in travelling salesman problem. Arch. Comput. Methods Eng. 2019, 26, 367–380. [Google Scholar] [CrossRef]
- Mirjalili, S. Genetic Algorithm. In Evolutionary Algorithms and Neural Networks: Theory and Applications; Springer International Publishing: Cham, Switzerland, 2019; pp. 43–55. [Google Scholar] [CrossRef]
- Reeves, C.; Rowe, J.E. Genetic Algorithms: Principles and Perspectives: A Guide to GA Theory; Springer Science & Business Media: Berlin, Germany, 2002; Volume 20. [Google Scholar]
- Teo, K.; Kow, W.; Chin, Y. Optimization of Traffic Flow within an Urban Traffic Light Intersection with Genetic Algorithm. In Proceedings of the 2010 Second International Conference on Computational Intelligence, Modelling and Simulation, Bali, Indonesia, 28–30 September 2010; pp. 172–177. [Google Scholar] [CrossRef]
- Gipps, P. A behavioural car-following model for computer simulation. Transp. Res. Part B Methodol. 1981, 15, 105–111. [Google Scholar] [CrossRef]
- Panwai, S.; Dia, H. Comparative evaluation of microscopic car-following behavior. IEEE Trans. Intell. Transp. Syst. 2005, 6, 314–325. [Google Scholar] [CrossRef]
- May, A.D. Traffic Flow Fundamentals; Prentice Hall: Englewood Cliffs, NJ, USA, 1990. [Google Scholar]
- Mannering, F.L.; Washburn, S.S. Principles of Highway Engineering and Traffic Analysis, 7th ed.; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar]
- Gao, Y.; Xu, L.; Hu, H.; Han, H.; Yang, X. Multi-objective optimization method for fixed-time signal control at intersection. China J. Highw. Transp. 2011, 24, 82. [Google Scholar]
- Fang, F.C.; Elefteriadou, L. Development of an Optimization Methodology for Adaptive Traffic Signal Control at Diamond Interchanges. J. Transp. Eng.-ASCE 2006, 132, 629–637. [Google Scholar] [CrossRef]
- Dresner, K.; Stone, P. A multiagent approach to autonomous intersection management. J. Artif. Intell. Res. 2008, 31, 591–656. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).