A Hybrid Damper with Tunable Particle Impact Damping and Coulomb Friction
Abstract
1. Introduction
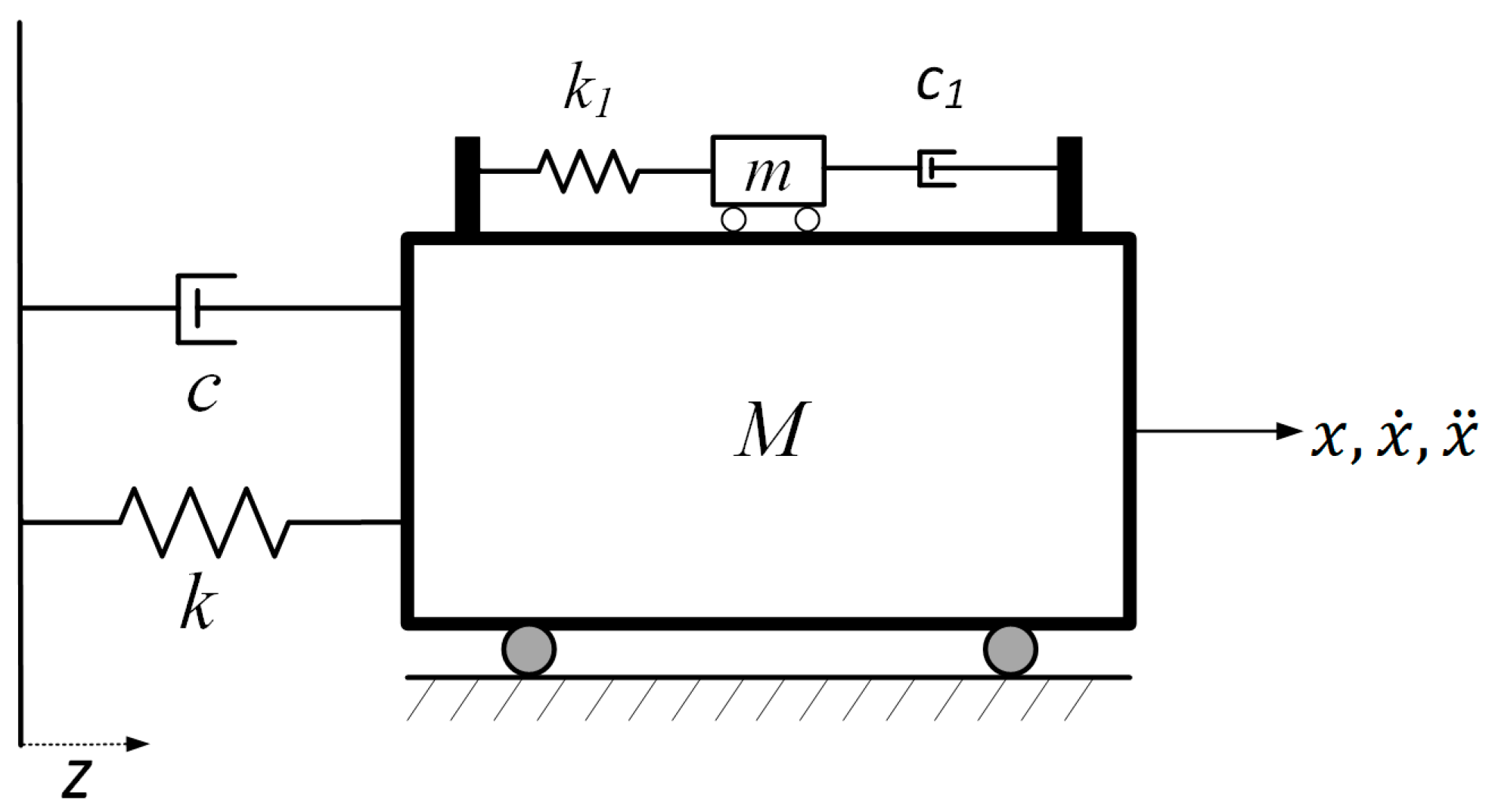
2. Numerical Modelling and Experimental Validation
Experimental Identification of Model Parameters
3. Experimental Setup and Structural Parameters Identification
4. Results for SDOF Structure
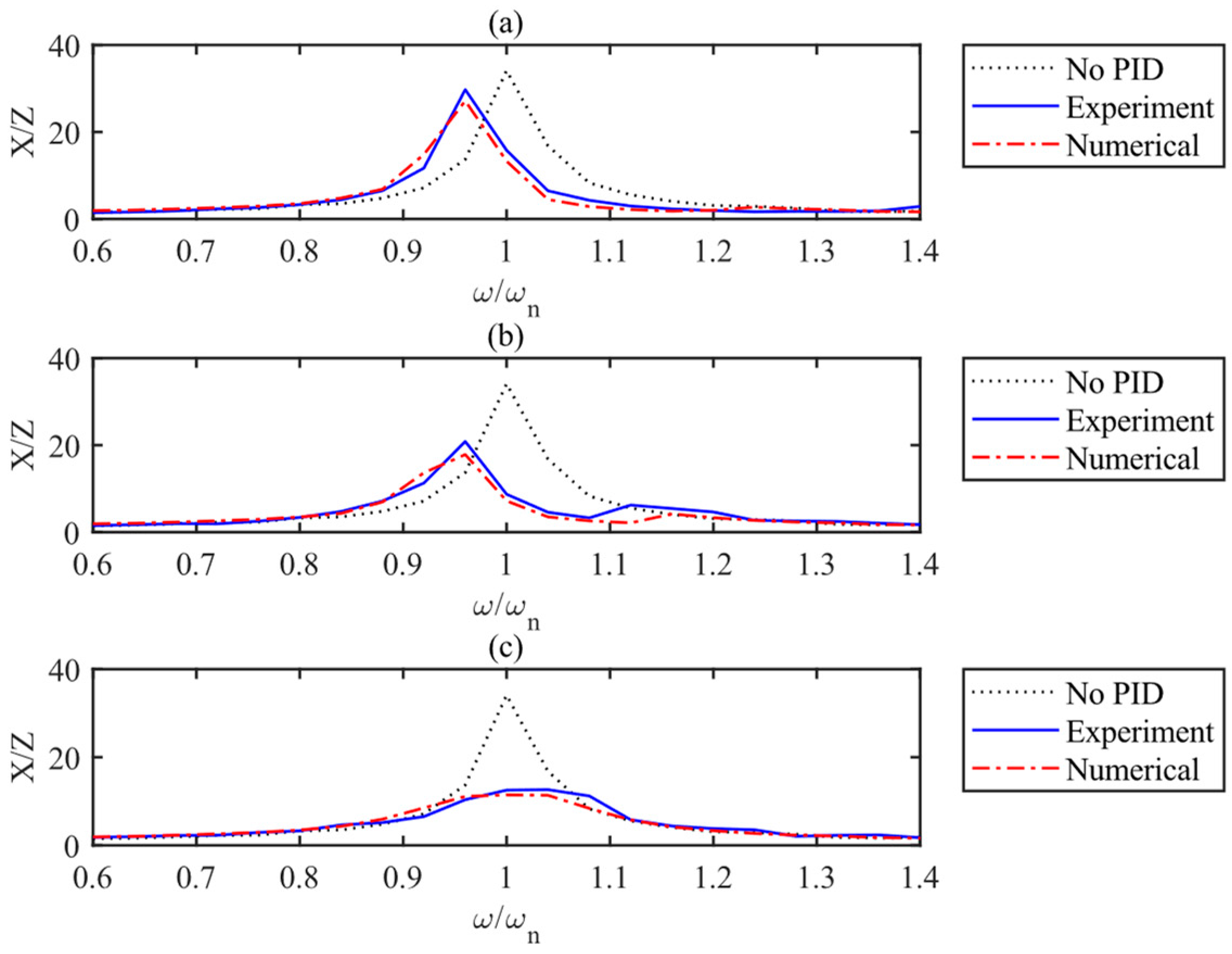
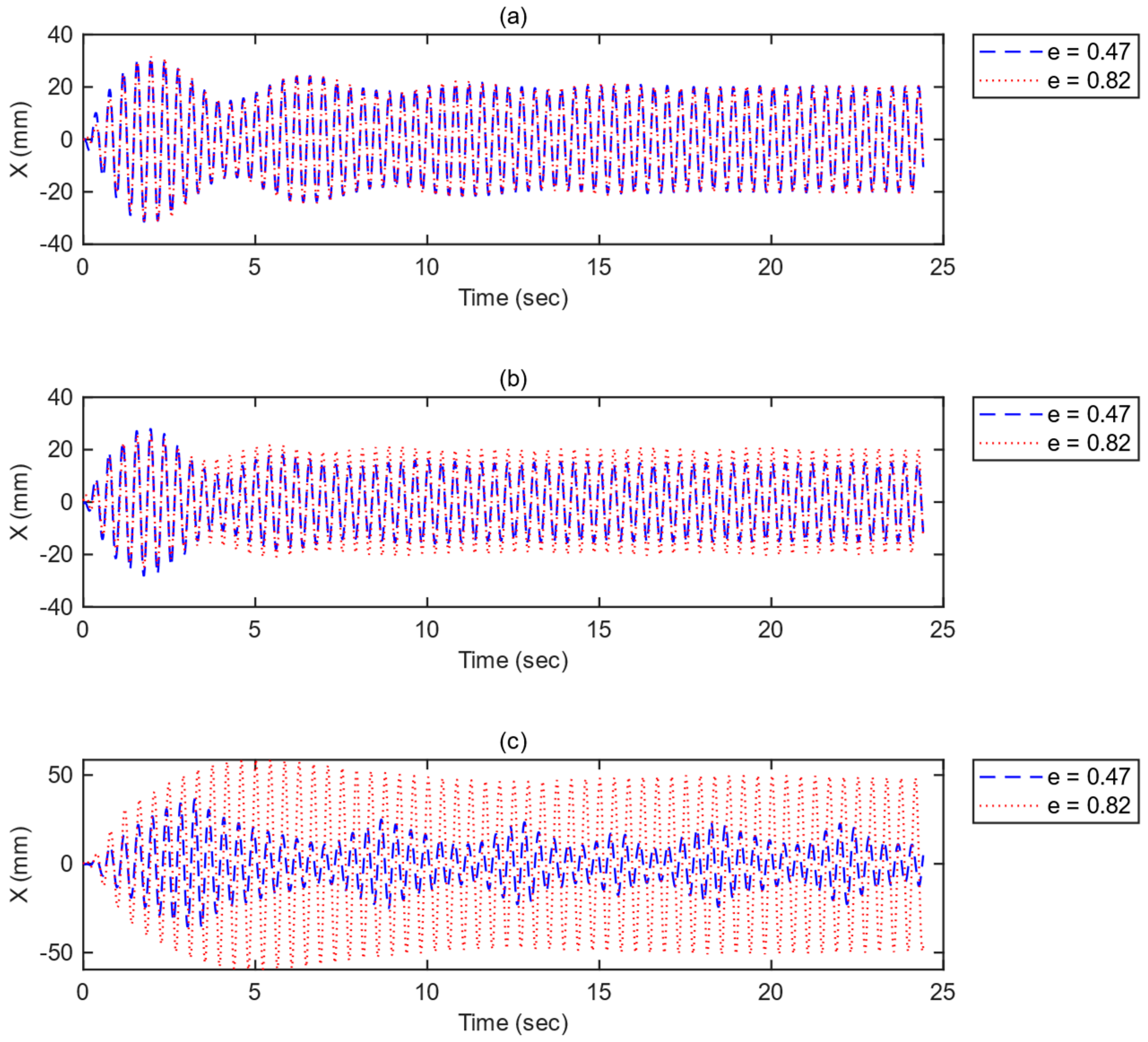
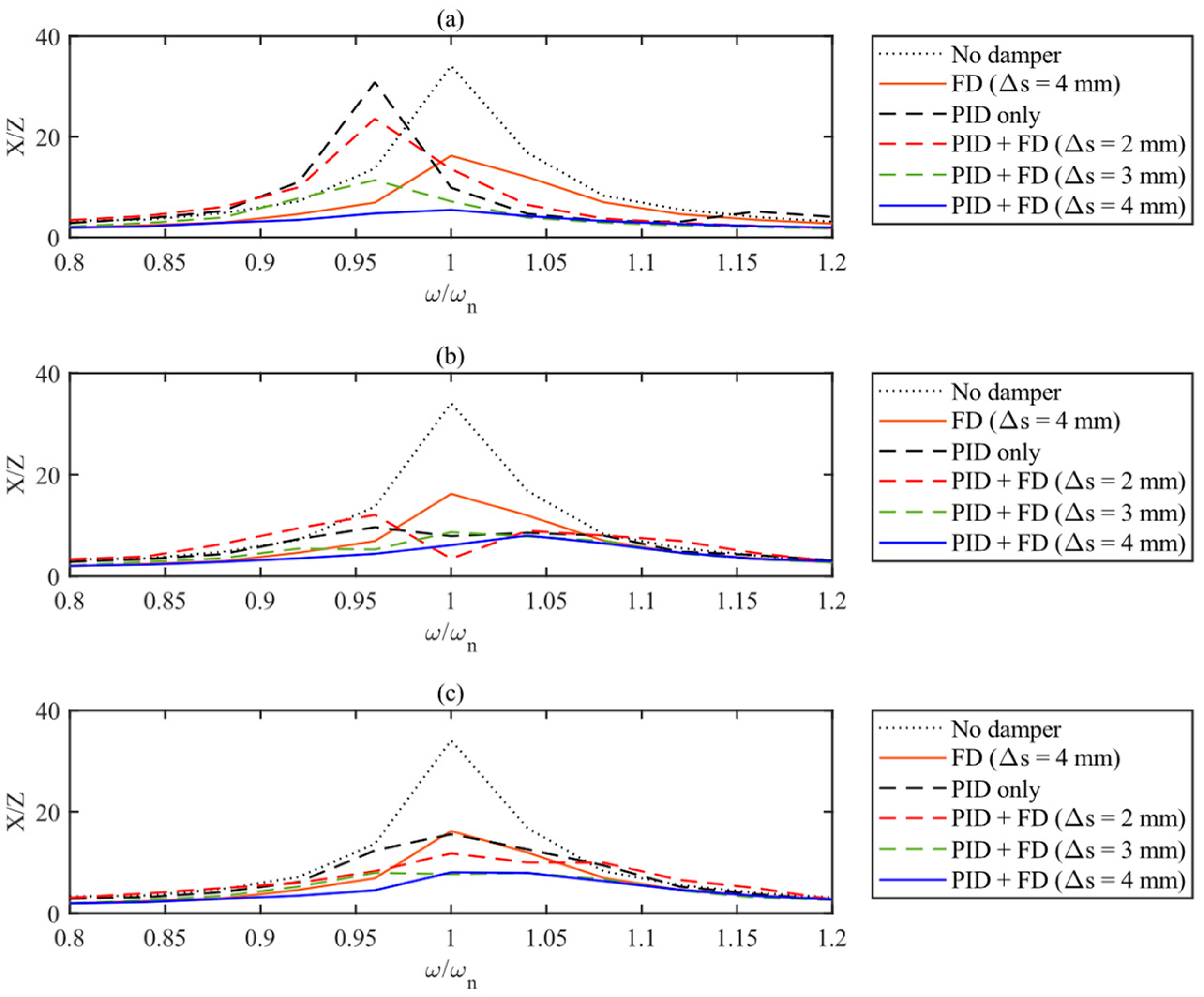
4.1. Particle Impact Damper (PID)
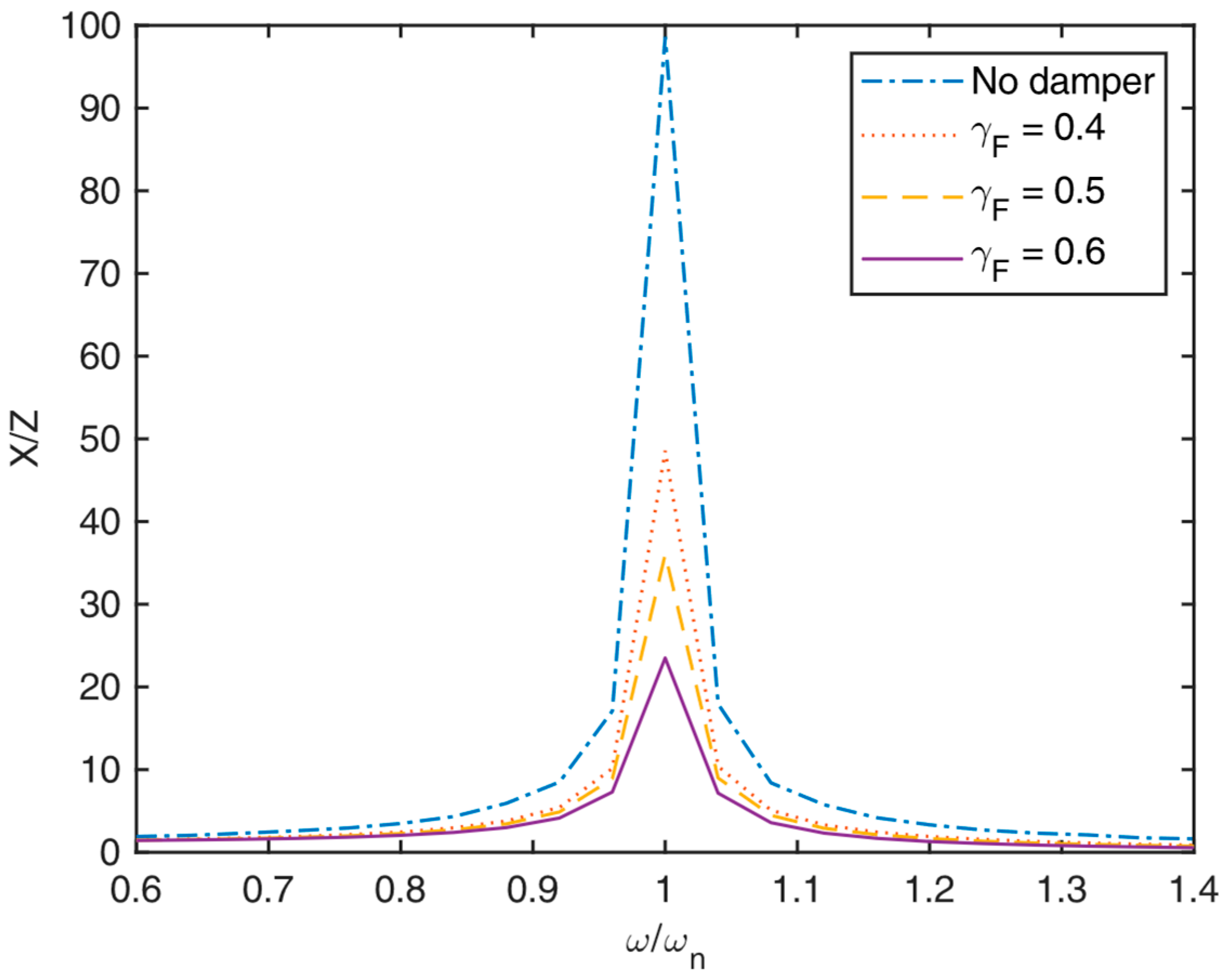
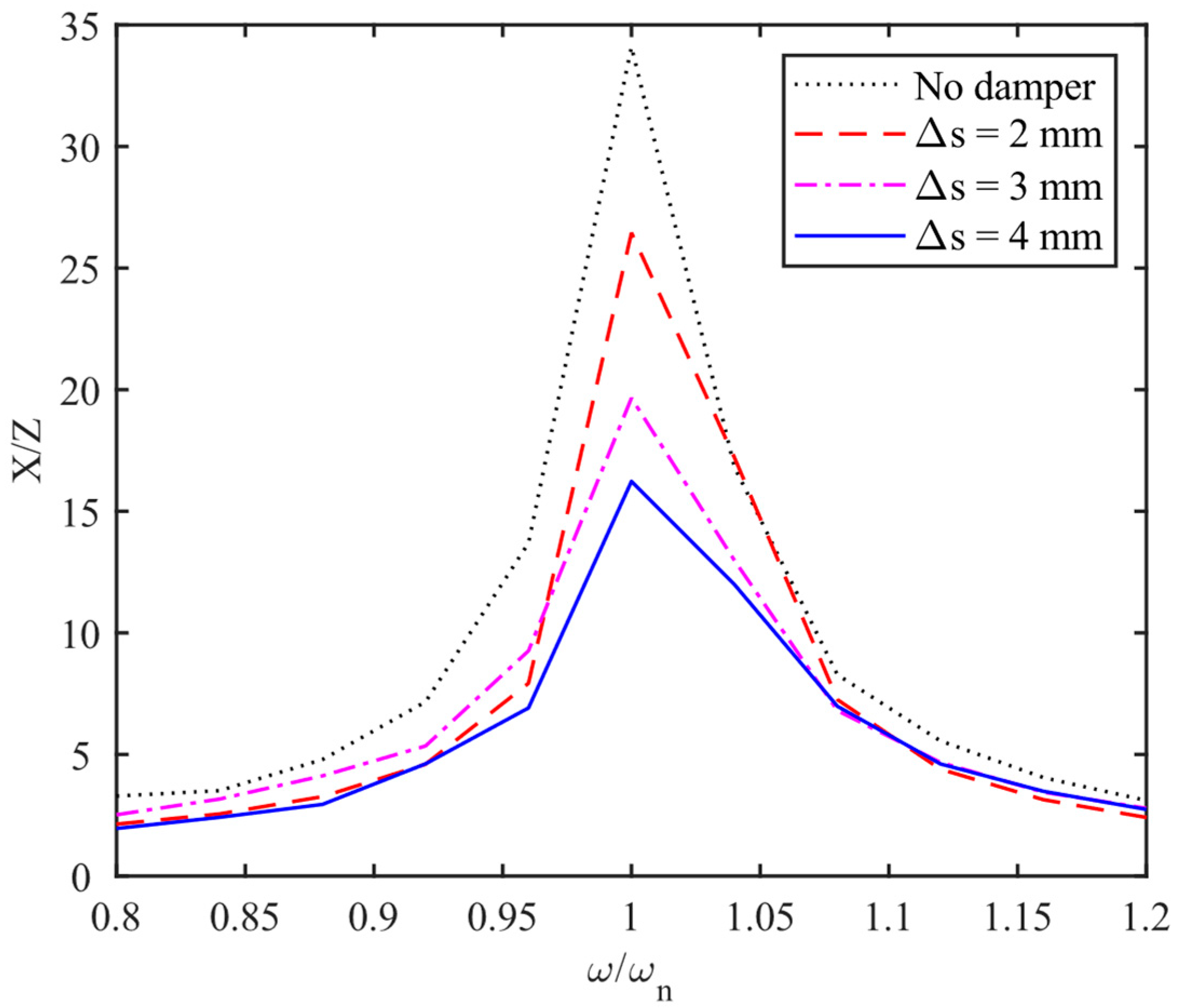
4.2. Friction Damper (FD)
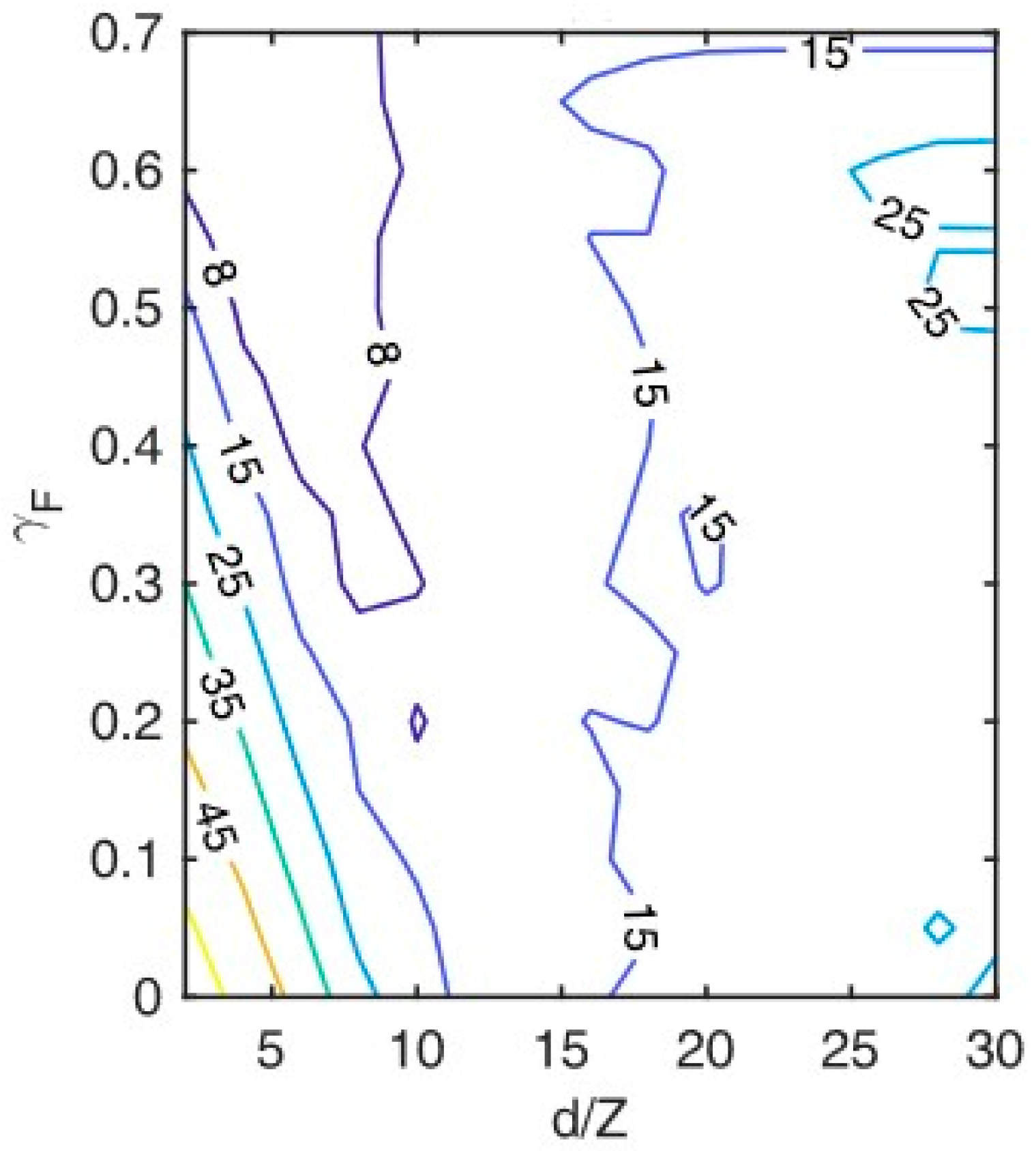
4.3. Hybrid Damper (PID + FD)
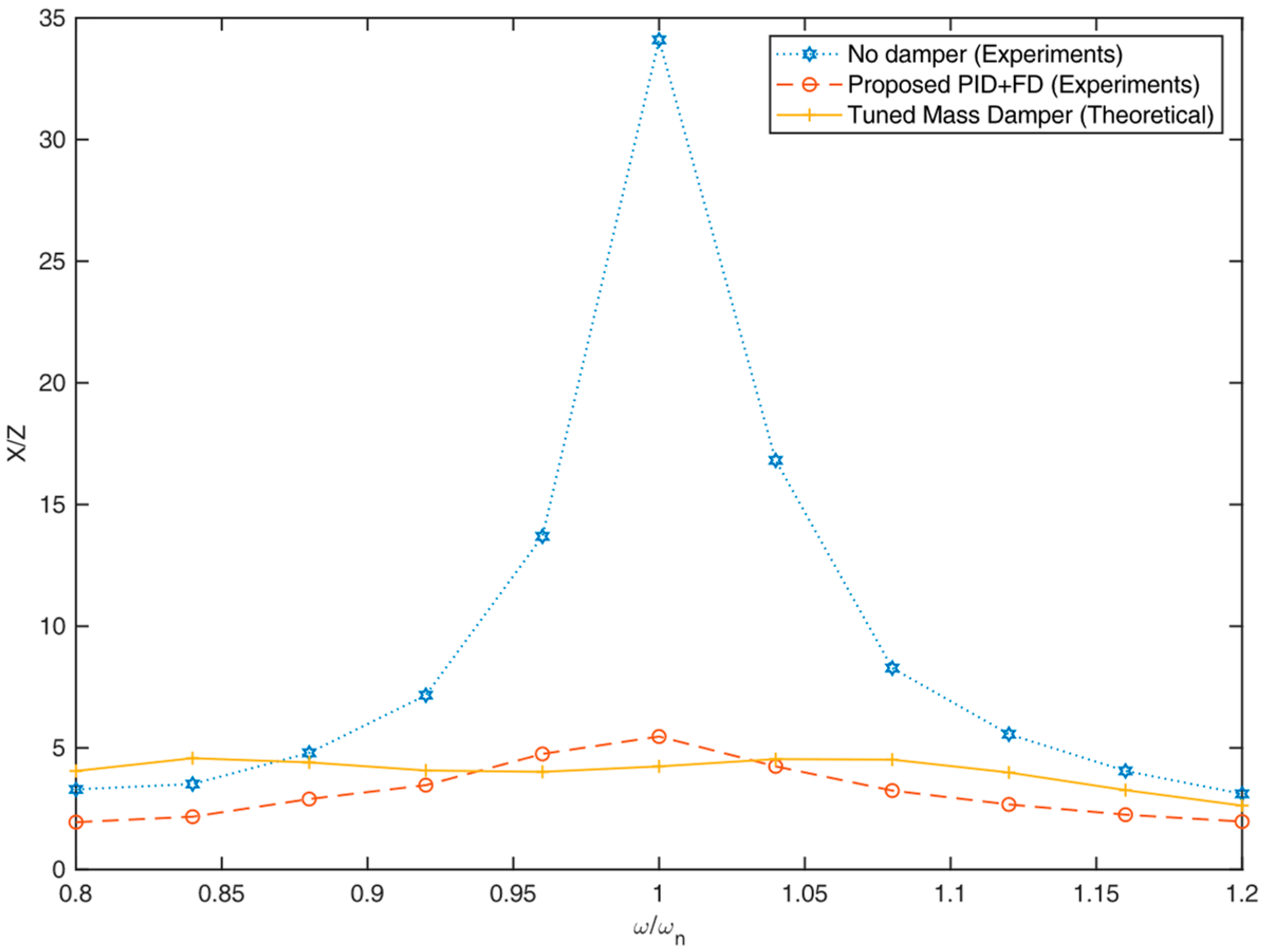
4.4. Comparison with an Optimally Tuned Mass Damper
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | |
| Acceleration of primary structure; | |
| Acceleration of particle; | |
| Amplitude of support motion; m | |
| Clearance; | |
| Coefficient of restitution | |
| Damping coefficient; | |
| Displacement of support; m | |
| Displacement of particle; | |
| Displacement of primary structure; | |
| Excitation force; N | |
| Initial position of primary structure; | |
| Initial position of particle; | |
| Initial velocity of primary structure; | |
| Initial velocity of particle; | |
| Mass of primary structure; | |
| Mass of primary structure; | |
| Spring constant; | |
| Velocity of support; | |
| Velocity of particle; | |
| Velocity of primary structure; | |
| Velocity of particle after nth impact; | |
| Velocity of particle before nth impact; | |
| Velocity of primary structure after nth impact; | |
| Velocity of primary structure before nth impact; | |
| Greek Symbols | |
| Coefficient of friction (external) | |
| Coefficient of friction (internal) | |
| Frequency of excitation force; rad/s | |
| Friction to excitation force amplitude ratio | |
| Natural frequency of primary structure; rad/s | |
| Mass ratio | |
| Abbreviations | |
| PID | Particle impact damper |
| RMS | Root mean square |
| FD | Friction damper |
| SDOF | Single degree of freedom |
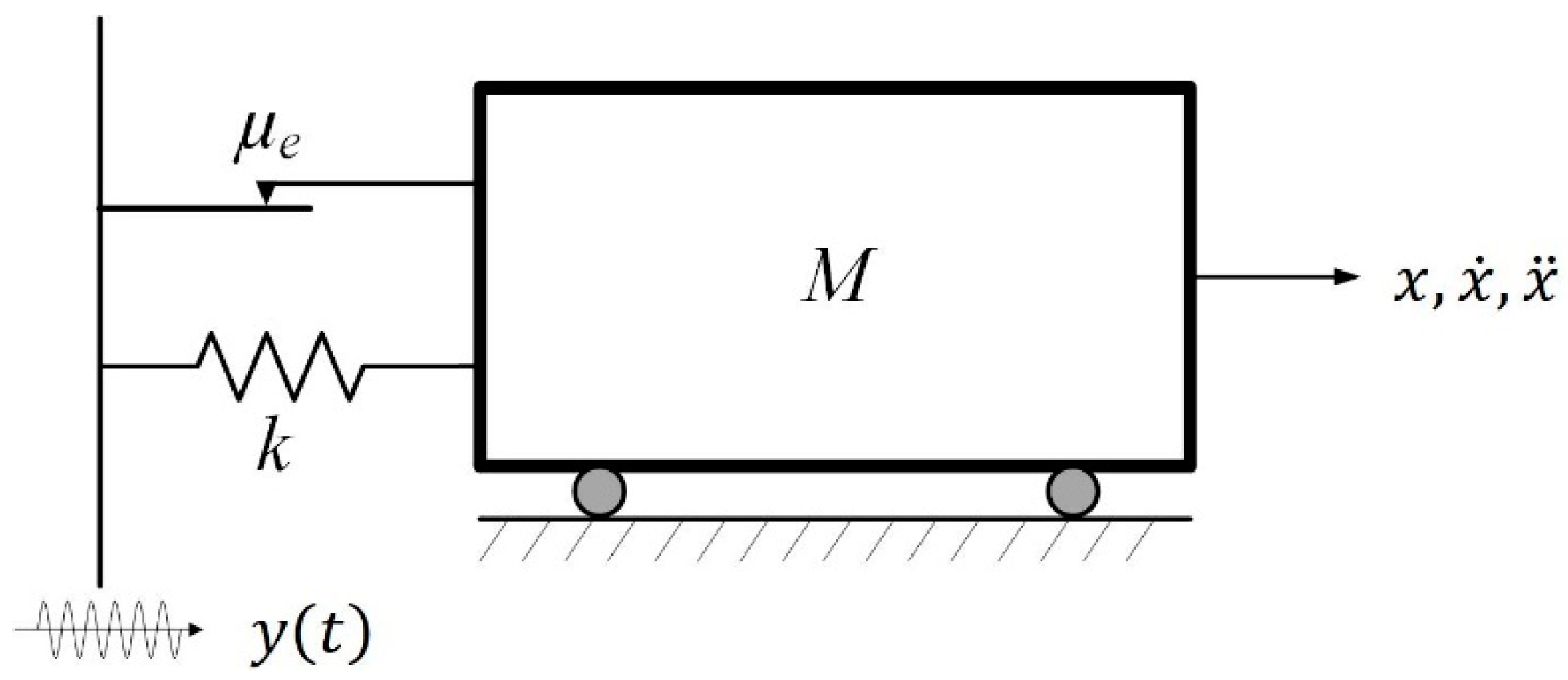
Appendix A. Steady-State Response of an SDOF Structure with Friction Damper under Harmonic Base Excitations
Appendix B. Random Excitation Case

| No Damper | TMD | PID | FD | PID + FD | |
|---|---|---|---|---|---|
| Maximum amplitude (m) | 0.1671 | 0.1473 | 0.0851 | 0.1400 | 0.0790 |
| RMS amplitude (m) | 0.0335 | 0.0238 | 0.0168 | 0.0200 | 0.0106 |
References
- Mrad, C.; Titirla, M.D.; Larbi, W. Comparison of Strengthening Solutions with Optimized Passive Energy Dissipation Systems in Symmetric Buildings. Appl. Sci. 2021, 11, 10103. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Y.; Tu, J.; Li, Z.; Wang, Q. Development and Vibration Control of Frequency Adjustable Tuned Mass Damper Based on Magnetorheological Elastomer. Materials 2022, 15, 1829. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Sedaghati, R.; Esmailzadeh, E. Vibration suppression of structures using tuned mass damper technology: A state-of-the-art review. J. Vib. Control 2022, 28, 812–836. [Google Scholar] [CrossRef]
- Lin, G.L.; Lin, C.C.; Chen, B.C.; Soong, T.T. Vibration control performance of tuned mass dampers with resettable variable stiffness. Eng. Struct. 2015, 83, 187–197. [Google Scholar] [CrossRef]
- Werkle, H.; Butz, C.; Tatar, R. Effectiveness of “Detuned” TMD’s for Beam-Like Footbridges. Adv. Struct. Eng. 2013, 16, 21–31. [Google Scholar] [CrossRef]
- Taflanidis, A.A.; Angefides, D.C.; Scruggs, J.T. Simulation-based robust design of mass dampers for response mitigation of tension leg platforms. Eng. Struct. 2009, 31, 847–857. [Google Scholar] [CrossRef]
- Marano, G.C.; Greco, R. Robust Optimum Design of Tuned Mass Dampers for High-Rise Buildings under Moderate Earthquakes. Struct. Des. Tall Spec. Build. 2009, 18, 823–838. [Google Scholar] [CrossRef]
- Ueng, J.M.; Lin, C.C.; Wang, J.F. Practical design issues of tuned mass dampers for torsionally coupled buildings under earthquake loadings. Struct. Des. Tall Spec. Build. 2008, 17, 133–165. [Google Scholar] [CrossRef]
- Wang, J.F.; Lin, C.C.; Chen, B.L. Vibration suppression for high-speed railway bridges using tuned mass dampers. Int. J. Solids Struct. 2003, 40, 465–491. [Google Scholar] [CrossRef]
- Rana, R.; Soong, T.T. Parametric study and simplified design of tuned mass dampers. Eng. Struct. 1998, 20, 193–204. [Google Scholar] [CrossRef]
- Wang, Q.; Dan, D. A simplified modeling method for multi-particle damper: Validation and application in energy dissipation analysis. J. Sound Vib. 2022, 517, 116528. [Google Scholar] [CrossRef]
- Friend, R.D.; Kinra, V.K. Particle impact damping. J. Sound Vib. 2000, 233, 93–118. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, Z.X.; Masri, S.F.; Lu, X.L. Particle impact dampers: Past, present, and future. Struct. Control Health Monit. 2018, 25, e2058. [Google Scholar] [CrossRef]
- Lu, Z.; Huang, B.; Wang, Z.X.; Zhou, Y. Experimental Comparison of Dynamic Behavior of Structures with a Particle Damper and a Tuned Mass Damper. J. Struct. Eng. 2018, 144, 04018211. [Google Scholar] [CrossRef]
- Tomlinson, G.R.; Pritchard, D.; Wareing, R. Damping characteristics of particle dampers—Some preliminary results. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2001, 215, 253–257. [Google Scholar] [CrossRef]
- Lu, Z.; Li, K.; Zhou, Y. Comparative Studies on Structures with a Tuned Mass Damper and a Particle Damper. J. Aerosp. Eng. 2018, 31, 04018090. [Google Scholar] [CrossRef]
- Saeki, M. Impact damping with granular materials in a horizontally vibrating system. J. Sound Vib. 2002, 251, 153–161. [Google Scholar] [CrossRef]
- Gagnon, L.; Morandini, M.; Ghiringhelli, G.L. A review of particle damping modeling and testing. J. Sound Vib. 2019, 459, 114865. [Google Scholar] [CrossRef]
- Xu, Z.W.; Wang, M.Y.; Chen, T.N. Particle damping for passive vibration suppression: Numerical modelling and experimental investigation. J. Sound Vib. 2005, 279, 1097–1120. [Google Scholar] [CrossRef]
- Ibrahim, R.A. Vibro-Impact Dynamics: Modeling, Mapping and Applications; Springer: Berlin/Heidelberg, Germany, 2009; Volume 43. [Google Scholar]
- Lu, Z.; Lu, X.L.; Jiang, H.J.; Masri, S.F. Discrete element method simulation and experimental validation of particle damper system. Eng. Comput. 2014, 31, 810–823. [Google Scholar] [CrossRef]
- Michon, G.; Almajid, A.; Aridon, G. Soft hollow particle damping identification in honeycomb structures. J. Sound Vib. 2013, 332, 536–544. [Google Scholar] [CrossRef]
- Olson, S.E. An analytical particle damping model. J. Sound Vib. 2003, 264, 1155–1166. [Google Scholar] [CrossRef]
- Bapat, C.N.; Sankar, S. Single Unit Impact Damper in Free and Forced Vibration. J. Sound Vib. 1985, 99, 85–94. [Google Scholar] [CrossRef]
- Marhadi, K.S.; Kinra, V.K. Particle impact damping: Effect of mass ratio, material, and shape. J. Sound Vib. 2005, 283, 433–448. [Google Scholar] [CrossRef]
- Papalou, A.; Masri, S.F. An experimental investigation of particle dampers under harmonic excitation. J. Vib. Control 1997, 4, 361–379. [Google Scholar] [CrossRef]
- Cheng, C.C.; Wang, J.Y. Free vibration analysis of a resilient impact damper. Int. J. Mech. Sci. 2003, 45, 589–604. [Google Scholar] [CrossRef]
- Li, X.W.; Yang, Y.; Shi, W.X. Study on the Damping Effect of Particle Dampers considering Different Surface Properties. Shock Vib. 2019, 2019, 8293654. [Google Scholar] [CrossRef]
- Veeramuthuvel, P.; Sairajan, K.K.; Shankar, K. Vibration suppression of printed circuit boards using an external particle damper. J. Sound Vib. 2016, 366, 98–116. [Google Scholar] [CrossRef]
- Chen, J.L.; Georgakis, C.T. Tuned rolling-ball dampers for vibration control in wind turbines. J. Sound Vib. 2013, 332, 5271–5282. [Google Scholar] [CrossRef]
- Shah, B.M.; Pillet, D.; Bai, X.M.; Keer, L.M.; Wang, Q.J.; Snurr, R.Q. Construction and characterization of a particle-based thrust damping system. J. Sound Vib. 2009, 326, 489–502. [Google Scholar] [CrossRef]
- Du, Y.C.; Wang, S.L. Modeling the fine particle impact damper. Int. J. Mech. Sci. 2010, 52, 1015–1022. [Google Scholar] [CrossRef]
- Zhang, R.L.; Wu, C.J.; Zhang, Y.T. A novel technique to predict harmonic response of Particle-damping structure based on ANSYS (R) secondary development technology. Int. J. Mech. Sci. 2018, 144, 877–886. [Google Scholar] [CrossRef]
- Jin, J.; Yang, W.; Koh, H.I.; Park, J. Development of tuned particle impact damper for reduction of transient railway vibrations. Appl. Acoust. 2020, 169, 107487. [Google Scholar] [CrossRef]
- Badri, Y.; Sassi, S.; Hussein, M.; Renno, J. Experimental and numerical investigation of damping in a hybrid automotive damper combining viscous and multiple-impact mechanisms. J. Vib. Control 2021, 28, 3676–3687. [Google Scholar] [CrossRef]
- Titirla, M.D. A State-of-the-Art Review of Passive Energy Dissipation Systems in Steel Braces. Buildings 2023, 13, 851. [Google Scholar] [CrossRef]
- Gagnon, L.; Morandini, M.; Ghiringhelli, G.L. A review of friction damping modeling and testing. Arch. Appl. Mech. 2020, 90, 107–126. [Google Scholar] [CrossRef]
- Hartog, J.P.D. Forced vibrations with combined viscous and coulomb damping. Lond. Edinb. Dublin Philos. Mag. J. Sci. 2009, 9, 801–817. [Google Scholar] [CrossRef]
- Mansour, W.M.; Filho, D.R.T. Impact Dampers with Coulomb Friction. J. Sound Vib. 1974, 33, 247–265. [Google Scholar] [CrossRef]
- Hundal, M.S. Response of a Base Excited System with Coulomb and Viscous Friction. J. Sound Vib. 1979, 64, 371–378. [Google Scholar] [CrossRef]
- Ziaee, M.; Hejazi, F. Development of Non-sticking Steady-State solution for structures with hybrid damping mechanism. Structures 2023, 47, 233–245. [Google Scholar] [CrossRef]
- Sun, R.Q.; Wong, W.O.; Cheng, L. A tunable hybrid damper with Coulomb friction and electromagnetic shunt damping. J. Sound Vib. 2022, 524, 116778. [Google Scholar] [CrossRef]
- Sun, R.Q.; Wong, W.O.; Cheng, L. Hybrid electromagnetic shunt damper with Coulomb friction and negative impedance converter. Int. J. Mech. Sci. 2022, 230, 107552. [Google Scholar] [CrossRef]
- Xia, X.J.; Zheng, M.Y.; Liu, P.F.; Zhang, N.; Ning, D.H.; Du, H.P. Friction observer-based hybrid controller for a seat suspension with semi-active electromagnetic damper. Mechatronics 2021, 76, 102568. [Google Scholar] [CrossRef]
- Atam, E. Friction Damper-Based Passive Vibration Control Assessment for Seismically-Excited Buildings Through Comparison With Active Control: A Case Study. IEEE Access 2019, 7, 4664–4675. [Google Scholar] [CrossRef]
- Popescu, F.D.; Radu, S.M.; Kotwica, K.; Andraș, A.; Kertesz, I. Simulation of the Time Response of the ERc 1400-30/7 Bucket Wheel Excavator’s Boom during the Excavation Process. Sustainability 2019, 11, 4357. [Google Scholar] [CrossRef]
- Lu, Z.; Lu, X.L.; Masri, S.F. Studies of the performance of particle dampers under dynamic loads. J. Sound Vib. 2010, 329, 5415–5433. [Google Scholar] [CrossRef]
- Marino, L.; Cicirello, A.; Hills, D.A. Displacement transmissibility of a Coulomb friction oscillator subject to joined base-wall motion. Nonlinear Dyn. 2019, 98, 2595–2612. [Google Scholar] [CrossRef]
- Levitan, E.S. Forced Oscillation of a Spring-Mass System having Combined Coulomb and Viscous Damping. J. Acoust. Soc. Am. 1960, 32, 1265–1269. [Google Scholar] [CrossRef]
- Min, K.W.; Seong, J.Y.; Kim, J. Simple design procedure of a friction damper for reducing seismic responses of a single-story structure. Eng. Struct. 2010, 32, 3539–3547. [Google Scholar] [CrossRef]
- López, I.; Busturia, J.M.; Nijmeijer, H. Energy dissipation of a friction damper. J. Sound Vib. 2004, 278, 539–561. [Google Scholar] [CrossRef]
- Spencer, B.F.; Nagarajaiah, S. State of the Art of Structural Control. J. Struct. Eng. 2003, 129, 845–856. [Google Scholar] [CrossRef]
- Ding, Q.; Chen, Y. Analyzing resonant response of a system with dry friction damper using an analytical method. J. Vib. Control 2008, 14, 1111–1123. [Google Scholar] [CrossRef]
- Jaisee, S.; Yue, F.; Ooi, Y.H. A state-of-the-art review on passive friction dampers and their applications. Eng. Struct. 2021, 235, 112022. [Google Scholar] [CrossRef]
- Wong, W.O. Optimal design of a hysteretic vibration absorber using fixed-points theory. J. Acoust. Soc. Am. 2016, 139, 3110. [Google Scholar] [CrossRef] [PubMed]
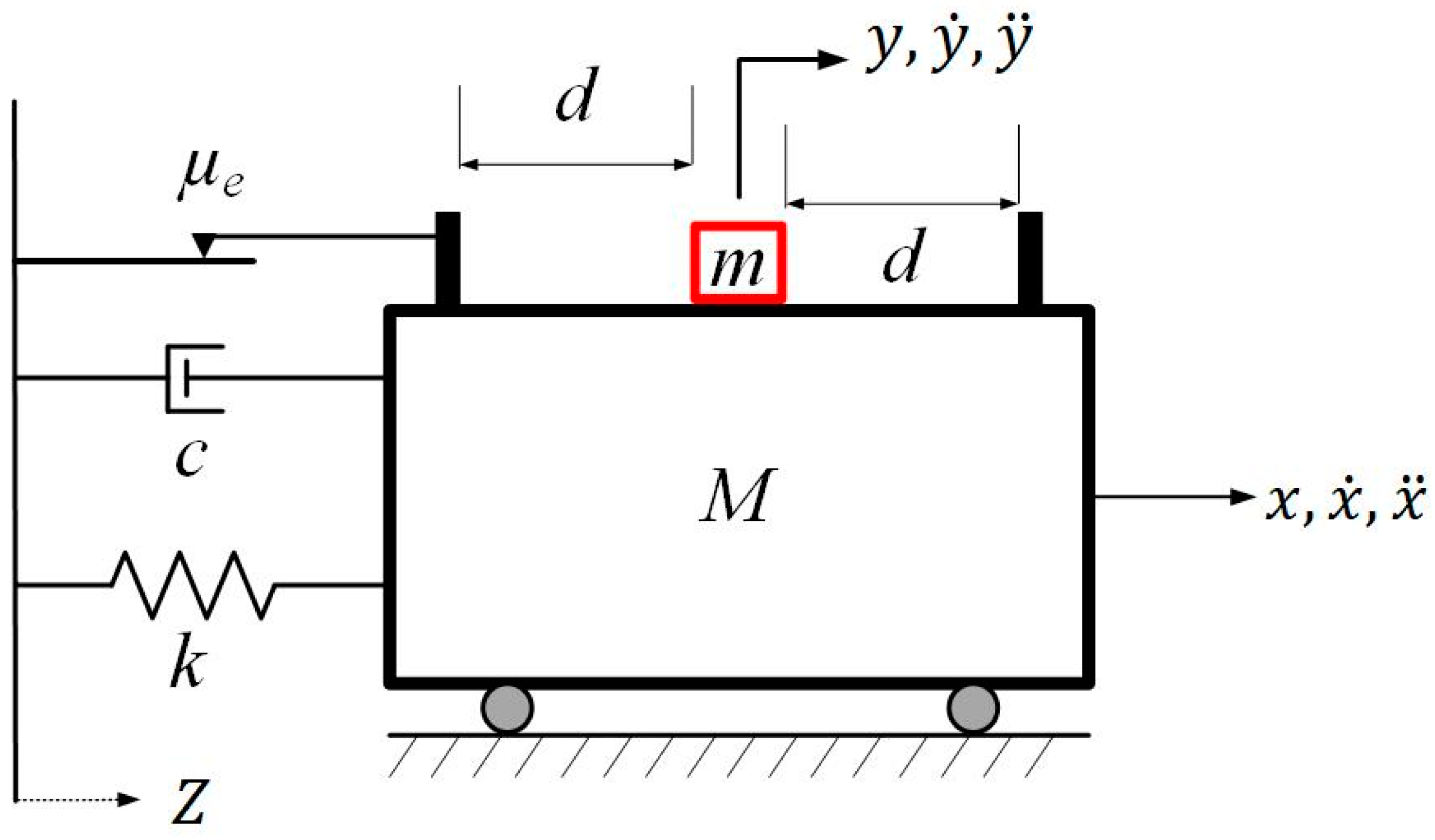
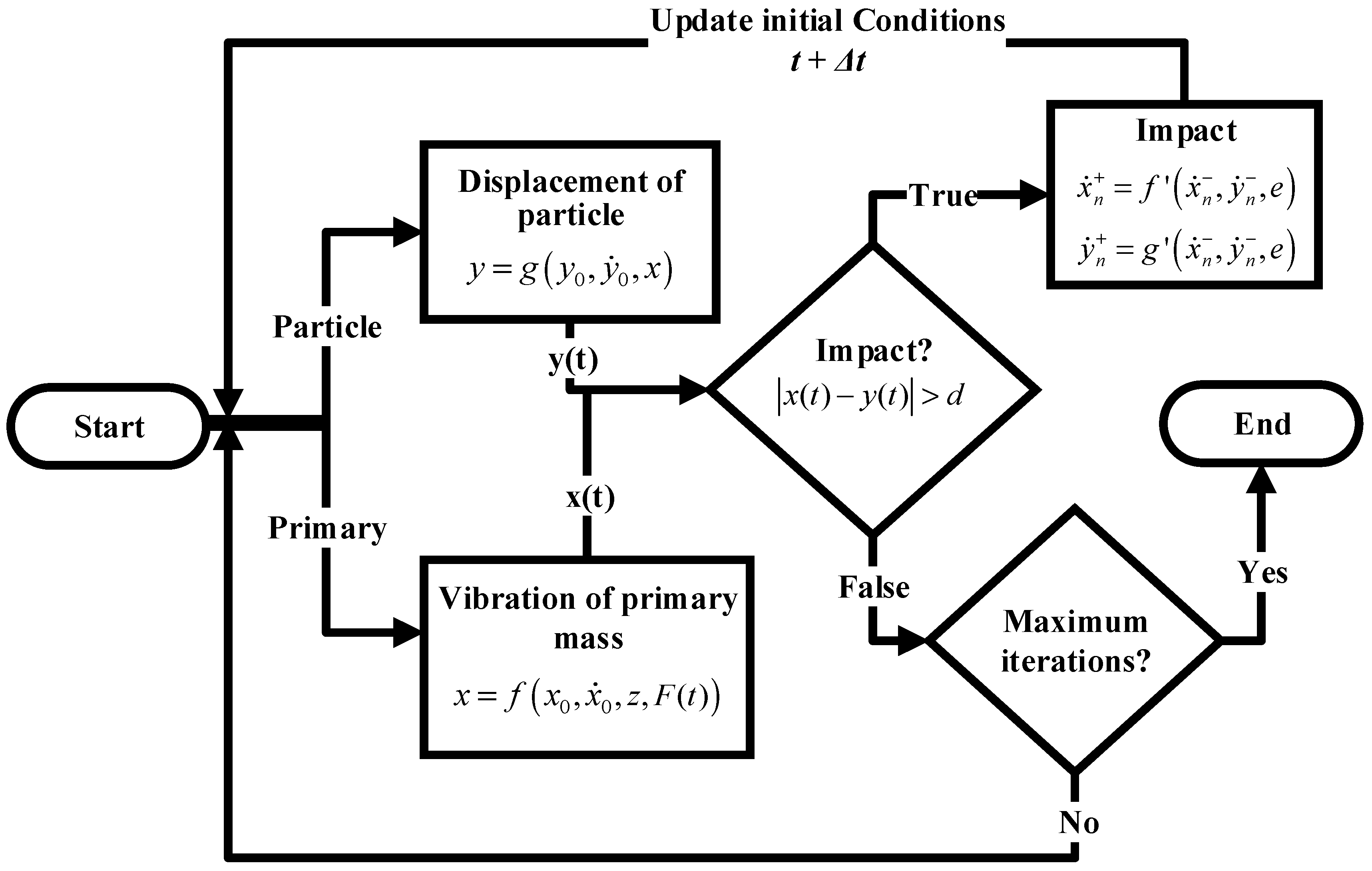

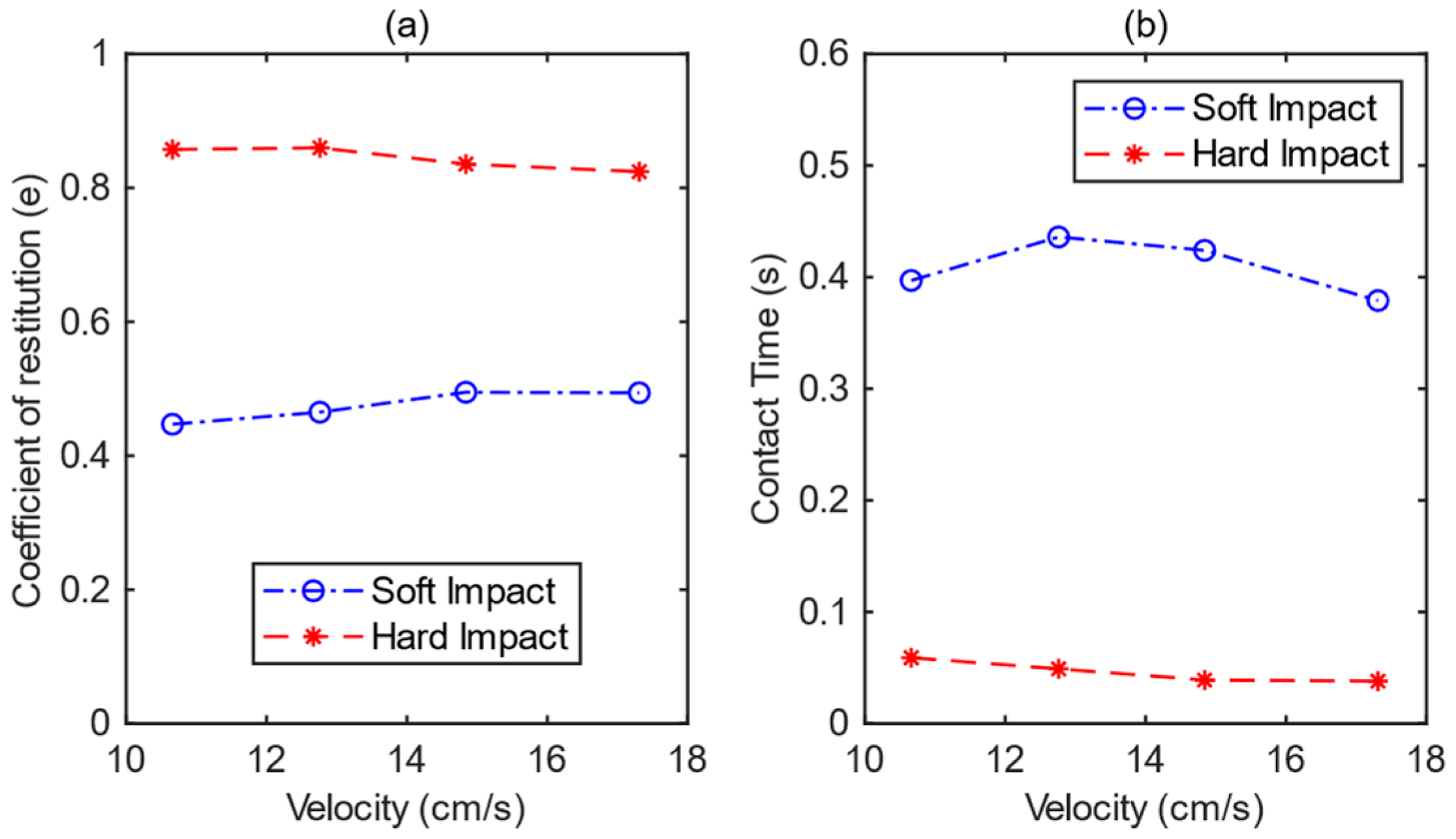


| Hard/Soft Impact | Contact Time (s) | Coefficient of Restitution |
|---|---|---|
| Hard Impact (Steel–Aluminum) | 0.046 | 0.82 |
| Soft Impact (Steel–Foam) | 0.411 | 0.47 |
| System Parameters | Magnitude |
|---|---|
| Damping ratio () | 0.0038 |
| Natural frequency () | 2.5 Hz |
| Mass of primary structure () | 1605 g |
| Coefficient of restitution (Steel to PU Foam) | 0.47 |
| Coefficient of restitution (Steel to Aluminum) | 0.82 |
| Mass of particle | 160 g |
| d = 7.5 mm | d = 22.5 mm | d = 37.5 mm | |
|---|---|---|---|
| PID only | 29.73 | 9.64 | 15.06 |
| FD only (Δs = 4 mm) | 16.22 | 16.22 | 16.22 |
| Hybrid (PID + FD) | 5.46 | 7.99 | 8.06 |
| TMD | |||
| Mass ratio | Optimal frequency ratio | Optimal damping ratio | |
| 0.1 | 0.9091 | 0.1679 | |
| Hybrid Damper (PID + FD) | |||
| Mass ratio () | Relative clearance () | Coefficient of restitution () | Spring compression () |
| 0.1 | 5 | 0.47 | 4 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akbar, M.A.; Wong, W.-O.; Rustighi, E. A Hybrid Damper with Tunable Particle Impact Damping and Coulomb Friction. Machines 2023, 11, 545. https://doi.org/10.3390/machines11050545
Akbar MA, Wong W-O, Rustighi E. A Hybrid Damper with Tunable Particle Impact Damping and Coulomb Friction. Machines. 2023; 11(5):545. https://doi.org/10.3390/machines11050545
Chicago/Turabian StyleAkbar, Muhammad Ayaz, Wai-On Wong, and Emiliano Rustighi. 2023. "A Hybrid Damper with Tunable Particle Impact Damping and Coulomb Friction" Machines 11, no. 5: 545. https://doi.org/10.3390/machines11050545
APA StyleAkbar, M. A., Wong, W.-O., & Rustighi, E. (2023). A Hybrid Damper with Tunable Particle Impact Damping and Coulomb Friction. Machines, 11(5), 545. https://doi.org/10.3390/machines11050545







