Optimization Research for the Adjusting Device of the Mechanical Vertical Drilling Tool Based on the Adjusting Torque

Abstract

The utilization of the adjusting device has been shown to significantly enhance the precision and stability of the mechanical vertical drilling tool. However, the inappropriate size of the structural parameters of the adjusting device will greatly affect its performance. Therefore, further improvements are necessary in order to optimize its performance. In order to achieve this, a thorough examination of the working principle and the various factors that influence the adjusting device is crucial. Through simulation and experimental methods, the function of the adjusting device was evaluated and potential solutions for the negative adjusting torque were proposed. By selecting appropriate values for the influencing factors, a more desirable adjusting torque with a reduced range of negative values can be obtained. Through a comparative analysis, the difference before and after optimization was evaluated. Furthermore, it was determined that the negative adjusting torque was caused by a reflux, primarily due to the diameter of the inlet and the flux area of the lower orifices. After optimization, the range of the adjusting torque that was beneficial to the adjusting device was extended to 15°~0°, providing a practical application in the drilling industry and serving as guidance for further optimization of the mechanical vertical drilling tool.

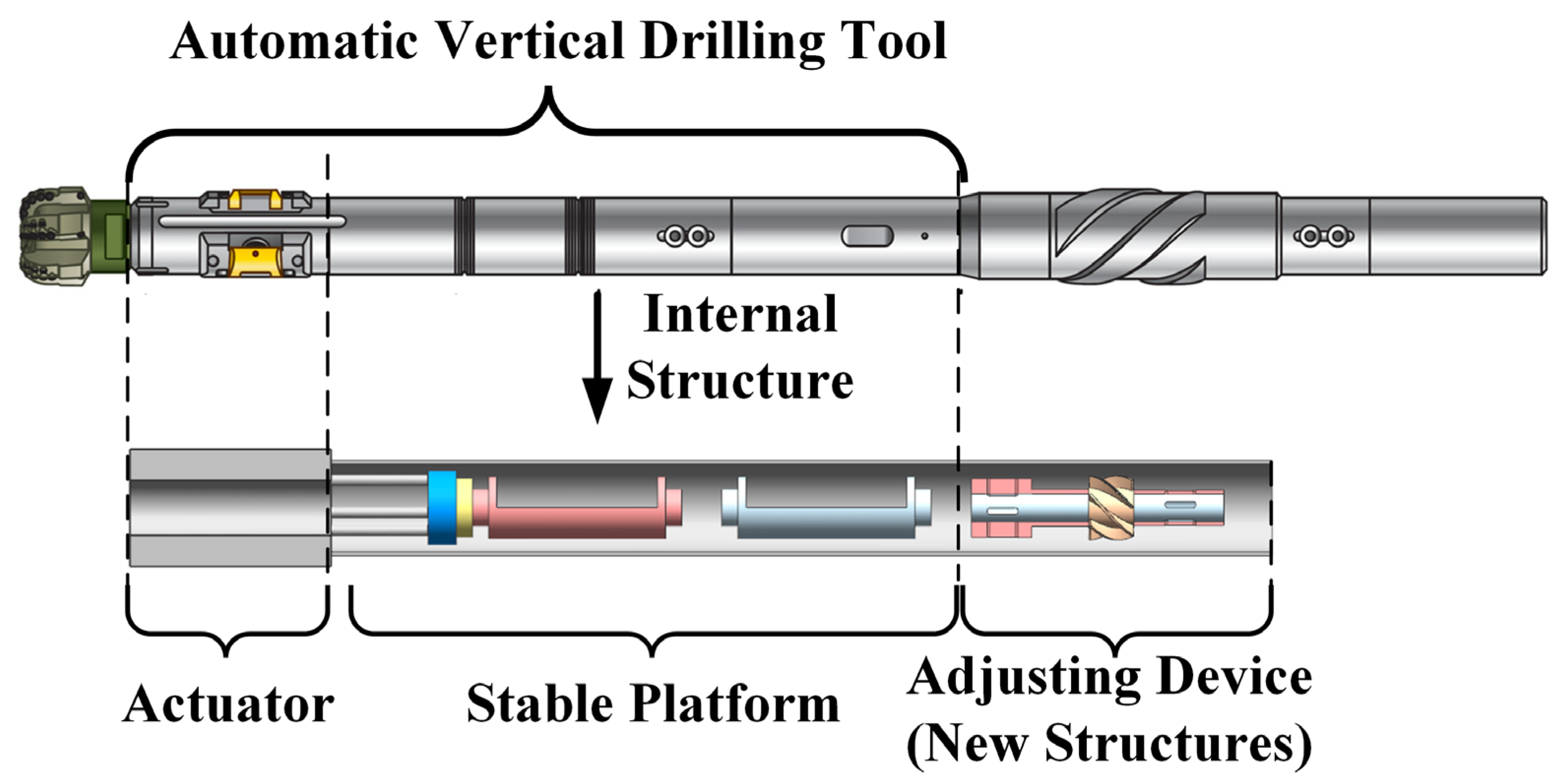
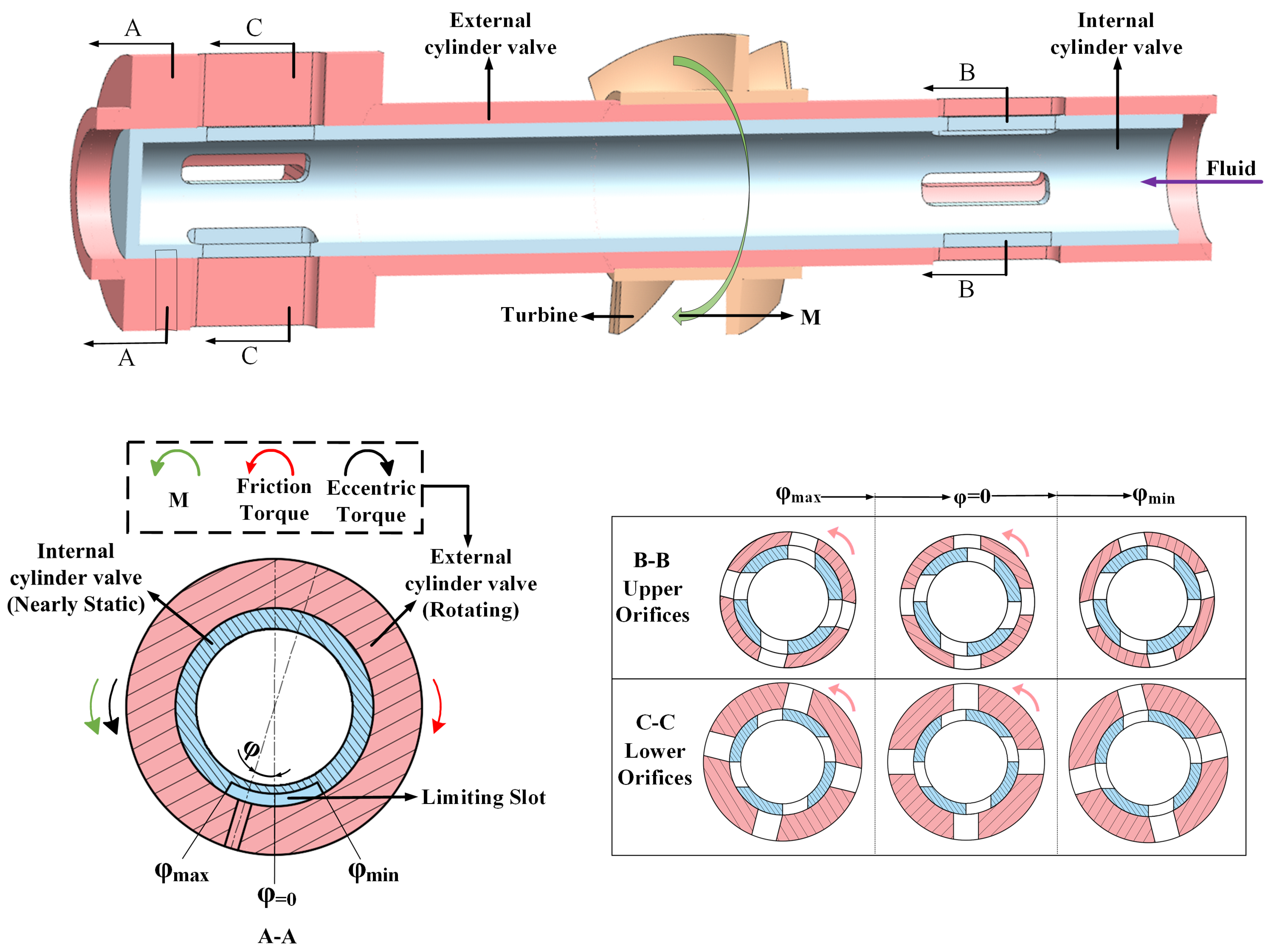
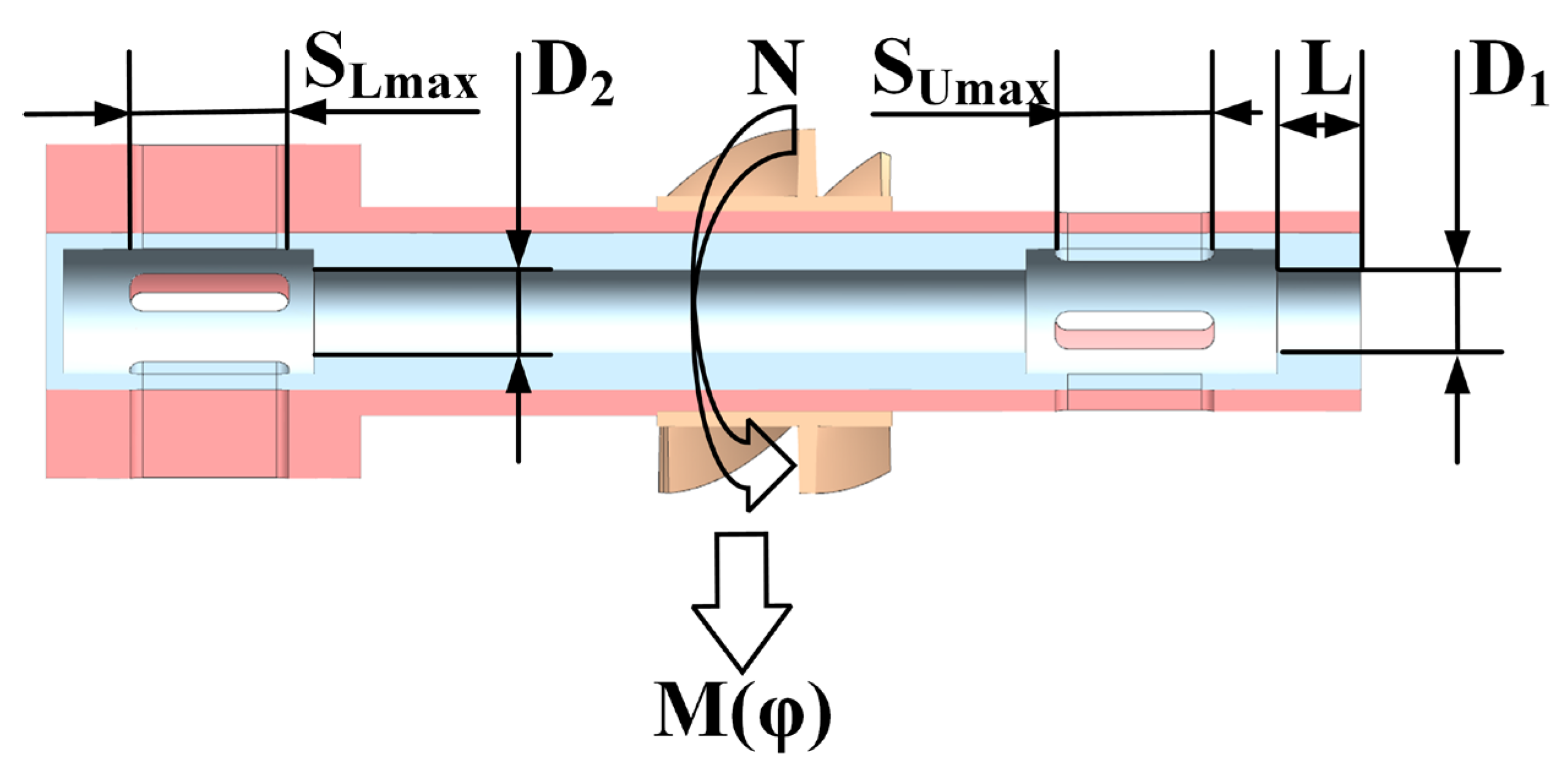
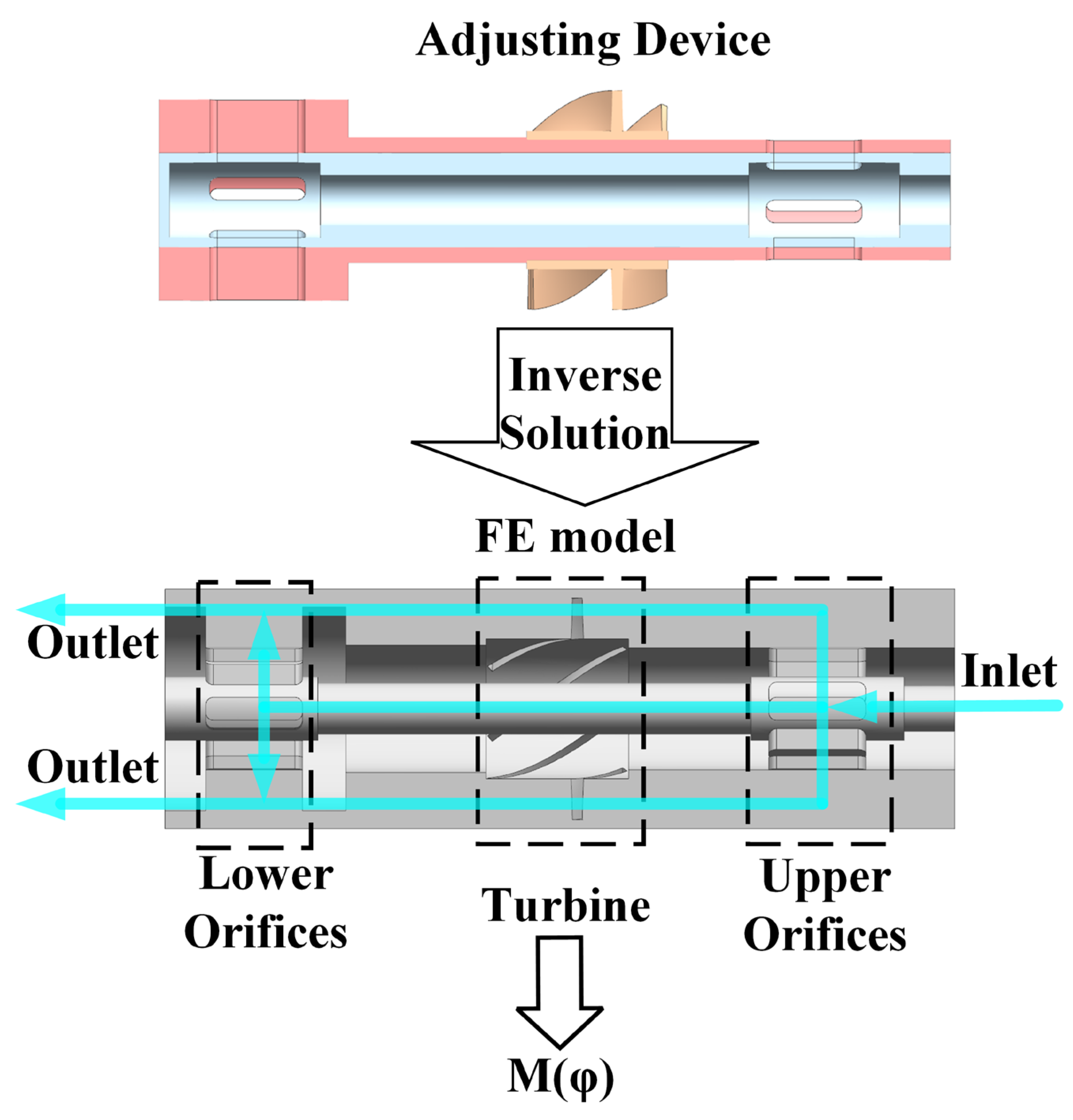
1. Introduction

In recent years, in response to the increasing depth of boreholes in drilling and the corresponding requirements for supporting technologies, such as ultra-high-speed drilling in deep wells, the mechanical automatic vertical drilling tool (MVDT) has undergone rapid development [1,2,3,4], as shown in Figure 1. The MVDT utilizes the eccentric torque of the eccentric block in the stable platform to automatically prevent and correct the deviation of the wellbore downhole [5,6,7]. However, the internal frictional resistance can impede the effectiveness of the eccentric torque and negatively impact the deviation control accuracy of the MVDT [8,9]. which can produce the control error. This error can be expressed as an angle [10], referred to as the deflection angle (φ). While φ is affected by frictional resistance and cannot be completely eliminated, it can be mitigated through the implementation of an adjusting device.

The adjusting device, which is mounted on top of the MVDT and connected to the eccentric block, comprises two cylinder valves and a turbine [11]. φ is converted into the difference in the rotation angle between the valves. Additionally, the turbine provides torque, which reduces φ in a closed-loop manner by balancing the frictional resistance. As a result, the stability and accuracy of the MVDT are enhanced.

In previous experiments, we have manufactured two sets of MVDT prototypes, one with a regulating device and one without, by collecting the pushing force of the actuator in both prototypes and then comparing the deviation correction effect of the two prototypes [12]. The research has demonstrated that the adjusting device has a positive impact on the MVDT. However, it was also found that although the stability of the MVDT improved with the addition of the adjusting device, the improvement is still limited.

As the adjusting device is a newly developed device composed of multiple structures, there is currently limited research on the device as a whole. However, many scholars have conducted preliminary research on the development of the device. Mokaramian et al. simulated the mechanical power of turbines and proposed optimized parameters for turbines [13]. Li et al. developed a dynamic model of the stable platform’s eccentric block, investigated the impact of torsional vibration on the eccentric block, and proposed an optimized design for a stable platform with a turbine [14,15]. Jinasena et al. proposed a mathematical model that can serve as an online return flow rate measurement and loss detection tool in conventional drilling [16]. Wang et al. presented a theoretical model for measuring friction and designed a set of measurement rigs to investigate the frictional characteristics of PDC bearings, and pointed out that the friction force at the upper plate valve is the main factor affecting the accuracy of the eccentric system [17,18]. Chai et al. studied the influence of φ on the MVDT trajectory by establishing a trajectory model for MVDT, and pointed out the relationship between the friction torque of the plate valve and the gravity torque of the eccentric block [10]. Although many scholars have studied specific issues within the adjusting device, there is limited research on how to improve the overall effectiveness of the device, and further research on the device as a whole is still needed.

Based on the above issues, this paper conducts a comprehensive study on the adjusting device in order to improve its performance. The working characteristics of the adjusting device are described, and its performance issues are identified through simulation. The structure of the adjusting device is optimized, and optimal parameters are proposed. By comparing the performance of the adjusting device before and after optimization, the reasons for its poor performance are discussed. Finally, the performance of the adjusting device can be improved, and suggestions and references are provided for further research on the MVDT.

2. Design Solution

In this section, the working principle of the adjusting device is first described and the influencing factors are revealed.

2.1. Working Principle of the Adjusting Device

Prior to explaining the principle of the adjusting device, it is necessary to understand the working principle of the entire drilling tool, as the adjusting device is located inside the tool. The schematic diagram of the MVDT equipped with the adjusting device is shown in Figure 1. When the drilling tool tilts, the two eccentric blocks in the stable platform will deflect under the influence of gravity. However, due to the frictional resistance, the eccentric block closer to the actuator will deviate from the correct inclination position and ultimately come to rest at φ from the lower side of the borehole. Since this eccentric block is connected to the plate valve and serves to transmit the inclination signal to the actuator, the accuracy of the drilling tool’s tilt correction will decrease when φ appears. On the other hand, since the eccentric block located further away from the actuator is installed in an oil chamber with lower resistance, its deviation position is very close to the ideal lower side of the borehole. This eccentric block does not transmit inclination signal but only serves to indicate the ideal position of the eccentric block used for signal transmission, with φ representing the difference between the ideal and actual positions of the eccentric block used for signal transmission [9,10].

When the two eccentric blocks have different deflection positions, the adjusting device can balance the friction torque by providing a closed-loop torque acting on the eccentric blocks affected by the friction torque, thereby reducing φ and ultimately improving the borehole deflection correction accuracy. To achieve this goal, the two eccentric blocks are, respectively, fixedly connected to the internal and external cylinder valves in the adjusting device. Among them, the external cylinder valve is fixedly connected to the eccentric block that is affected by the frictional resistance, so the deflection position of the external cylinder valve will also be influenced by the frictional resistance and thus deflect φ. At the same time, since the internal cylinder valve is fixedly connected to the eccentric block in the low-resistance oil chamber, the internal cylinder valve will hardly be affected by the frictional resistance and thus deflect. Therefore, the relative deflection error of the two eccentric blocks is transformed into the relative deflection error of the internal and external cylinder valves [11], which is φ.

Furthermore, both the internal cylinder valve and the external cylinder valve are designed with multiple upper orifices and lower orifices, which enables the change in the flow direction of the fluid [19]. As φ changes, the flux area of the upper orifices (S_U) and the flux area of the lower orifices (S_L) follow an inverse relationship; as S_U increases, S_L decreases, and vice versa.

In addition, the turbine is attached to the external cylinder valve and is subject to the fluid from the upper orifices, resulting in an adjusting torque denoted by M. M that can be used to balance the frictional torque. It should be noted that once the rotating direction of the MVDT and the turbine have been established, the friction torque and direction of M are also determined [20]. The friction torque is constant due to rotational friction, and the direction of M is designed to be counter to the direction of the friction torque. To simplify the research, the direction of the friction torque is set clockwise, the direction of φ is considered positive when the external cylinder valve (or the eccentric block) is deflected solely by the friction torque, and the direction of M is considered positive when it is in opposition to the direction of the friction torque. It should be noted that the constant direction of the friction torque hardly allows φ to become negative, and in order to avoid a dead point, a limiting slot is designed in the internal cylinder valve to limit the maximum range of φ, assuming that the absolute values of φ_max and φ_min are equal. This is shown in view A-A of Figure 2. As φ increases in the positive direction, S_U will increase while S_L will decrease, as shown in views B-B and C-C in Figure 2.

Given the above conditions, the complete operational process of the regulating device is as follows: when the drilling tool is inclined, both eccentric blocks will deflect under the influence of gravity, but one of them will experience an increase in the positive direction of φ due to the effect of frictional resistance. This will gradually increase S_U and decrease S_L. At this point, the fluid flows more readily through the upper orifices [21,22]. After flowing through the upper orifices, the fluid impacts on the turbine and causes M to increase in a positive direction [23]. M is then applied through the external cylinder valve to the eccentric block that is affected by friction torque. It overcomes the friction torque on the eccentric block, corrects its deflection position, and gradually brings φ closer to zero.

As φ decreases, the external cylinder valve will also deflect to the correct position under the influence of the fixed connection. This causes S_U to decrease and S_L to increase, allowing the drilling fluid to flow more easily through the lower orifices. This will gradually reduce M until it is almost equal to the friction torque, at which point φ and M will hardly change. The deflection position of the external cylinder valve and the eccentric block will approach a stable state that is closer to the ideal position. Subsequently, the actuator will receive a more accurate inclination signal and will gradually steer the drilling direction to become perpendicular. Thereafter, the adjusting device will not function until the next time the drilling tool tilts. This process occurs in a continuous cycle. The adjusting device provides a closed-loop M to balance the friction torque, thereby enhancing the precision and stability of the MVDT.

2.2. Influencing Factors of the Structure

M is effective when it exceeds the friction torque, and its magnitude is primarily influenced by variations in φ. Consequently, M can be employed as a metric for assessing the performance of the adjusting device, with φ being the primary factor influencing M. Furthermore, other factors that are associated with the adjusting device also have an impact on M and should be studied, as demonstrated in Figure 3.

The turbine plays a direct role in determining M, but the impact of turbines has been well established in prior research [24,25,26,27]. The effect of the turbine on M can be determined once its structure is established. However, since the turbine and the external cylinder valve rotate at the same speed (N), N also affects the fluid velocity as it passes through the turbine [28].

Additionally, it should be noted that due to the presence of the limiting slot, the turbine will only rotate within the range of φ_min < φ < φ_max. Since M changes continuously with φ, the resultant force acting on the external cylinder valve (or the eccentric block affected by frictional resistance) will also vary continuously, indicating that N is not a constant. Therefore, before investigating the influence of other structural parameters of the adjusting device on M, the effect of N on M should be eliminated first.

Moreover, the structural parameters of the adjusting device need to be taken into consideration. The flow rate at the turbine is a factor [29] in the M, which relates to the adjusting torque as follows:

$$M\propto Q_U$$

(1)

where Q_U is the flow rate at the turbine (Q_U is also the flow rate at the upper orifices. Q_L is the flow rate at the lower orifices, which will be mentioned later). An increase in Q_U results in an increase in M. In the adjusting device, as φ changes, the primary factor influencing Q_U is the relationship between S_U and S_L [30].

To simplify the description, the opening areas of the upper and lower orifices in the internal cylinder valve are denoted as S_U1 and S_L1, respectively. Similarly, the opening areas of the upper and lower orifices in the external cylinder valve are denoted as S_U2 and S_L2, respectively. When φ varies, S_U equals the area of the overlap between S_U1 and S_U2. In particular, when φ reaches φ_max, S_U reaches its maximum value, which is equal to the maximum value of S_U1 and S_U2 (abbreviated as S_Umax). At the same time, if it is assumed that the maximum value of S_L1 and S_L2 is S_Lmax, then the relationship between S_L, S_L1, S_L2, and S_Lmax is also similar to the above rule, as flowing Equations (4) and (5). The S_Umax and S_Lmax were shown in Figure 3. At this point, under the condition that $\left|{\phi }_{max}\right|$ is equal to $\left|{\phi }_{min}\right|$, the above parameters can be expressed by the following equation:

$$S_U=(\frac{1}{2}+\frac{\phi }{2{\phi }_{max}})S_{Umax}$$

(2)

$$S_L=(\frac{1}{2}-\frac{\phi }{2{\phi }_{max}})S_{Lmax}$$

(3)

$$S_{Umax}=max\left\{S_{U1},S_{U2}\right\}$$

(4)

$$S_{Lmax}=max\left\{S_{L1},S_{L2}\right\}$$

(5)

Therefore, the effect of S_Umax and S_Lmax on M needs to be investigated due to their effect on Q_U.

Furthermore, it is well known that the head loss will affect the flow rate in the flowline [31]; therefore, Q_U will also be affected by the head loss caused by the structure of the adjusting device, and it needs to be considered in the effect on M. In hydromechanics, the head loss can be expressed as follows:

$$h_w=\lambda \frac{l}{d}\times \frac{u^2}{2g}$$

(6)

where $h_w$ is the head loss, it can indicate the extent of flow loss. $\lambda$ and $u$ are viscosity and velocity, respectively.

Although both parameters can affect $h_w$, they are not structural parameters of the adjusting device, and the research on the effect of head loss on flow rate is already mature [32]. Therefore, we will not further study these parameters in this paper. However, $l$ and $d$ refer to the length and diameter of the flow pipe, respectively. This means that the length or width of some structures in the adjusting device will also affect Q_U, and their impact on M cannot be ignored. Considering the limitation of the overall size of the MVDT, as well as the linear loss of fluid pressure and the local loss in the adjusting device [33], we selected the length of the inlet (L), the diameter of the inlet (D₁), and the diameter of the center flow channel inside the internal cylinder valve (D₂) as important parameters affecting the effectiveness of the device, which need to be carefully selected when optimizing the structure of the adjusting device.

In summary, M is influenced by φ as well as other structural parameters of the adjusting device such as N, D₁, L, D₂, S_Umax, and S_Lmax. However, the exact influence of these parameters on M remains unclear and requires further investigation, and the relationship between them will be studied through simulation. In addition, due to the interdependent relationship between various components of the adjusting device, it has become difficult to directly measure the precise values of M and φ through experiments. Therefore, we conducted experiments on the MVDT prototypes and indirectly obtained the variation of φ under the influence of M.

3. Validation and Methodology

In this section, a three-dimensional finite element model (FE model) is presented, which is solved using computational fluid dynamics simulation (CFD simulation). The variation of M with φ (M(φ) for short) is examined. The impact of various influencing factors is analyzed, and the optimal values are determined. To confirm the efficacy of the adjusting device after optimization, prototype experiments were conducted.

3.1. Validation of FE Model Simulation

In order to investigate the effect of the adjusting device in the fluid environment of the downhole, the FE model is established. The FE model is a fluid domain obtained through the inverse solution of the adjusting device, as depicted in Figure 4.

After the fluid enters the inlet of the FE model, M(φ) can be obtained by monitoring the torque at the wall where the turbine is present [34]. In addition, the maximum range of φ is chosen to be −15° to 15°. The boundary conditions [35] for the simulation are shown in

Table 1. The boundary conditions for the CFD simulation.

Boundary Condition	Value
External temperature (°C)	20
Atmospheric pressure (Mpa)	0
Mass flow inlet (kg/s)	8
Pressure outlet (Mpa)	0
Density (kg/m3)	998.2
Dynamic viscosity (N·s/m2)	0.001003

.

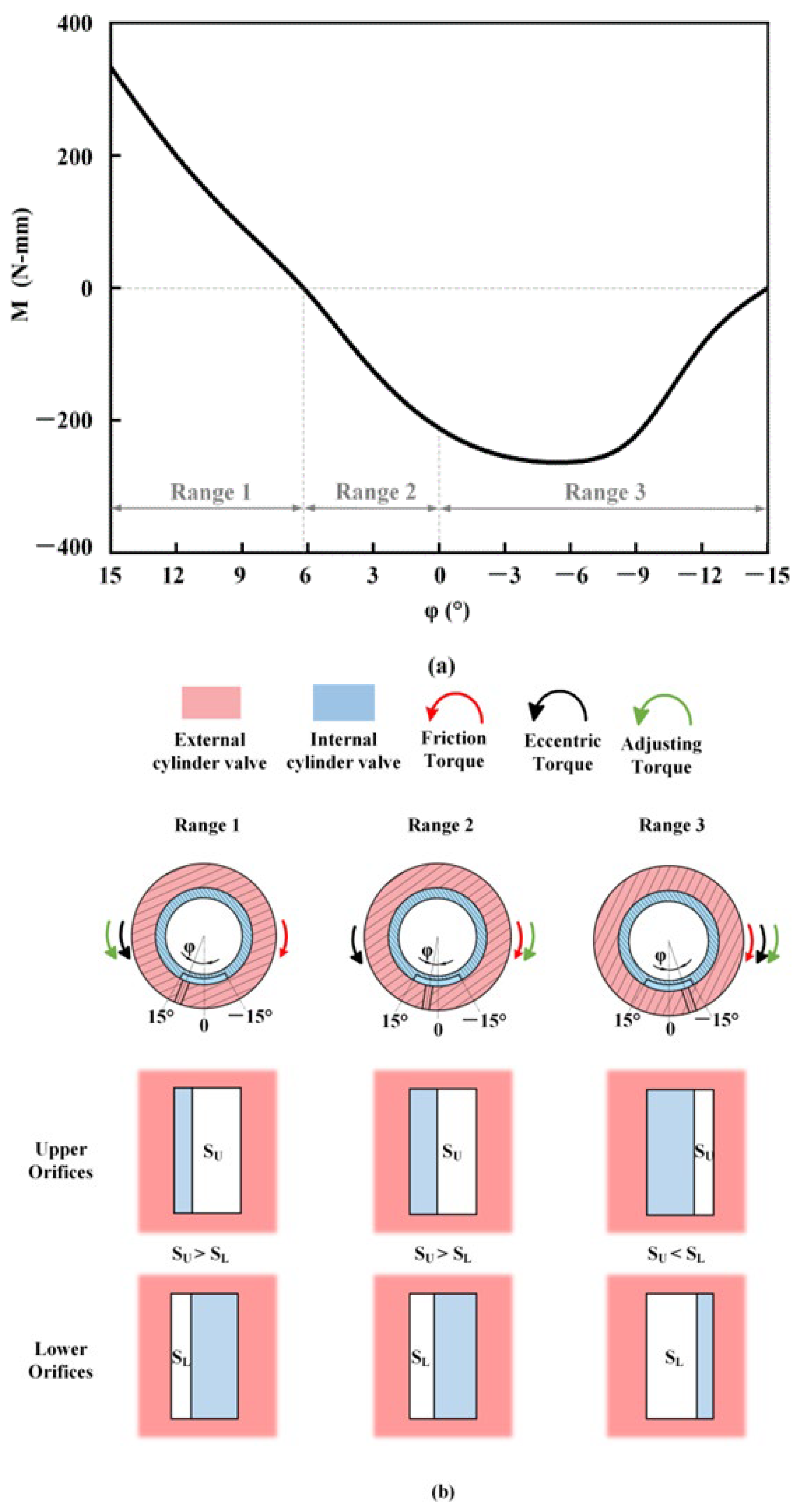
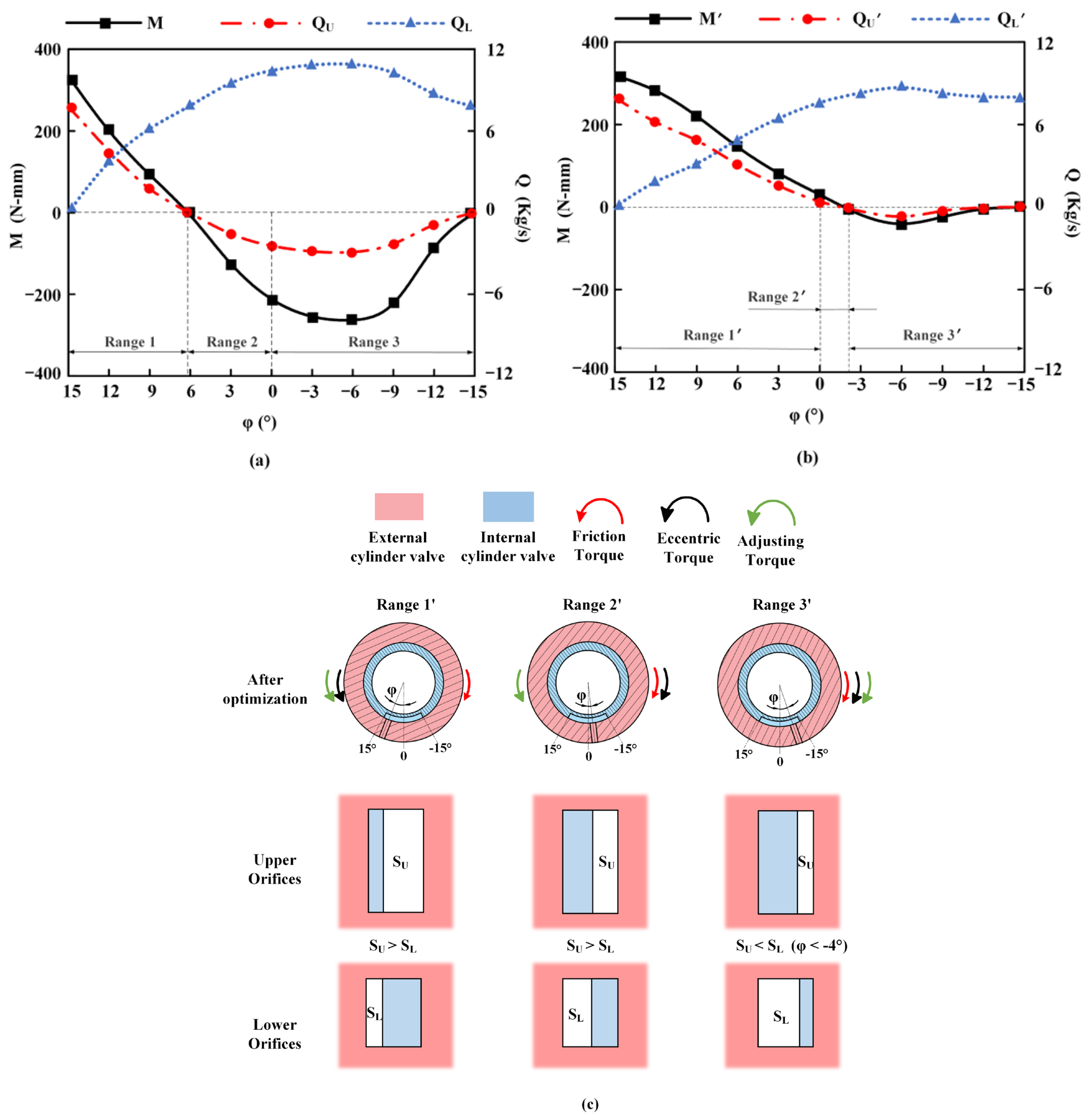
The results of the simulation are presented in Figure 5a. As φ varies from 15° to −15°, the variation of M(φ) is observed to be monotonic, with a minimum value followed by an increase to zero. Furthermore, the values of M(φ) can be divided into three ranges. In ranges 1 and 2, S_U is found to be greater than S_L. Conversely, when M(φ) is within range 3, the magnitudes of S_U and S_L are observed to be inversely proportional to those observed in ranges 1 and 2. Figure 5b illustrates the variations of S_U and S_L, corresponding to Figure 2, and their values can be calculated using Equations (2) and (3).

M(φ) is positive when it falls within range 1, which allows it to balance the friction torque as designed. At this point, φ will tend toward zero under the combined influence of M and the eccentric torque, thereby improving the stability and accuracy of the MVDT.

In addition, although S_U is similarly greater than S_L in range 2, M(φ) is negative and its direction is the same as the friction torque. This indicates that φ has a tendency to move away from zero under the combined effect of the friction torque and M(φ). However, as mentioned in Section 2, the occurrence of negative values for M(φ) is extremely rare in range 2. Even if the negative value of M(φ) may exist due to the turbine being too close to the lower orifices or the kinetic energy of the fluid flowing out of the lower orifices being too large, this negative value should be small rather than large, as shown in Figure 5. The occurrence of large negative values of M(φ) will affect the effectiveness of the regulating device, so the causes of this phenomenon need to be further studied.

Additionally, M(φ) has large negative values in range 3. Although the direction of M(φ) is the same as the friction torque, φ will still approach zero under the combined effect of the three torques. However, this does not align with the design principle of the adjusting device, as the hands of the turbine are not in the optimal position.

In summary, based on the working principle of the adjusting device, M(φ) is in line with expectations in range 1 and φ can be reduced by the effect of M. However, the presence of unexpected negative M values is not only unreasonable, but it also impacts the effectiveness of the adjusting device. Therefore, it is important to minimize negative M values and further investigate the factors that influence the adjusting device to resolve this issue.

3.2. Solutions for Negative Adjusting Torque

To obtain the desired M(φ) and solve the problem of negative M, the impact of influencing factors as described in Section 2.2 was researched. To simplify the study, a suitable range of values was chosen for each influence factor, as shown in

Table 2. Range of values for the influencing factors.

Influencing Factors	Range of Value
φ (°)	−15~15
N (r/min)	−120~120
D1 (mm)	15~35
L (mm)	15~35
D2 (mm)	15~35
SUmax (mm2)	180~360
SLmax (mm2)	180~360

.

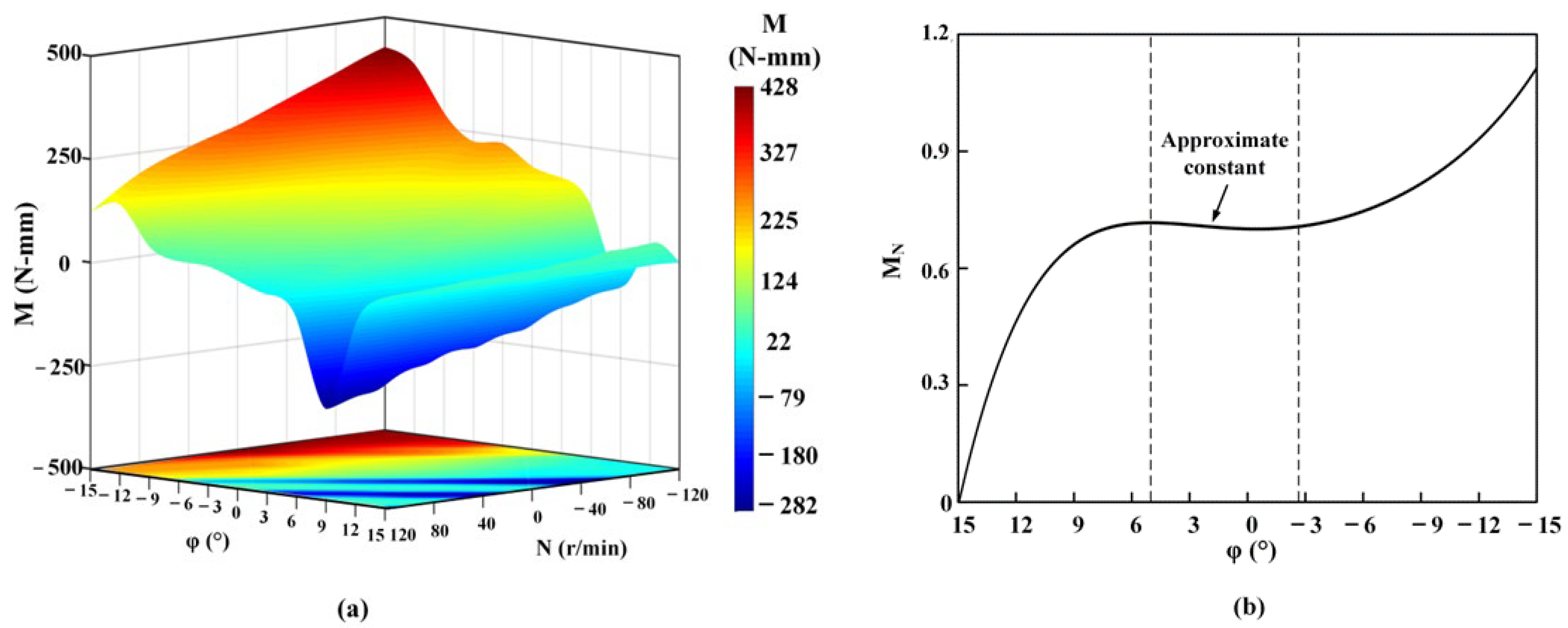
The influence of N on M(φ) (denoted as M(φ,N)) should be excluded first. The result of M(φ,N) is shown in Figure 6a, and the partial derivative of N with respect to M(φ,N) (M_N for short) is shown in Figure 6b.

The results of the simulation indicate that when the variable N is held constant, the variation of M(φ,N) with respect to φ exhibits a similar trend to that described in Section 3.1. Furthermore, when φ is held constant, M(φ,N) gradually decreases as N transitions from negative to positive values. This can be attributed to the fact that when the direction of N is opposite to that of M, there is a greater resistance that must be overcome in order to rotate the turbine, resulting in a larger value of M(φ,N).

In addition, the rate of change in M(φ,N) with respect to N, denoted as M_N, increases as φ transitions from a positive value to a negative value. As φ approaches zero, M_N tends to approach a constant value. This observation suggests that at this point, there is a linear relationship between N and M(φ,N), indicating that N has a consistent effect on M(φ,N). However, as φ gradually approaches zero, the impact of N on the performance of the adjusting device is limited.

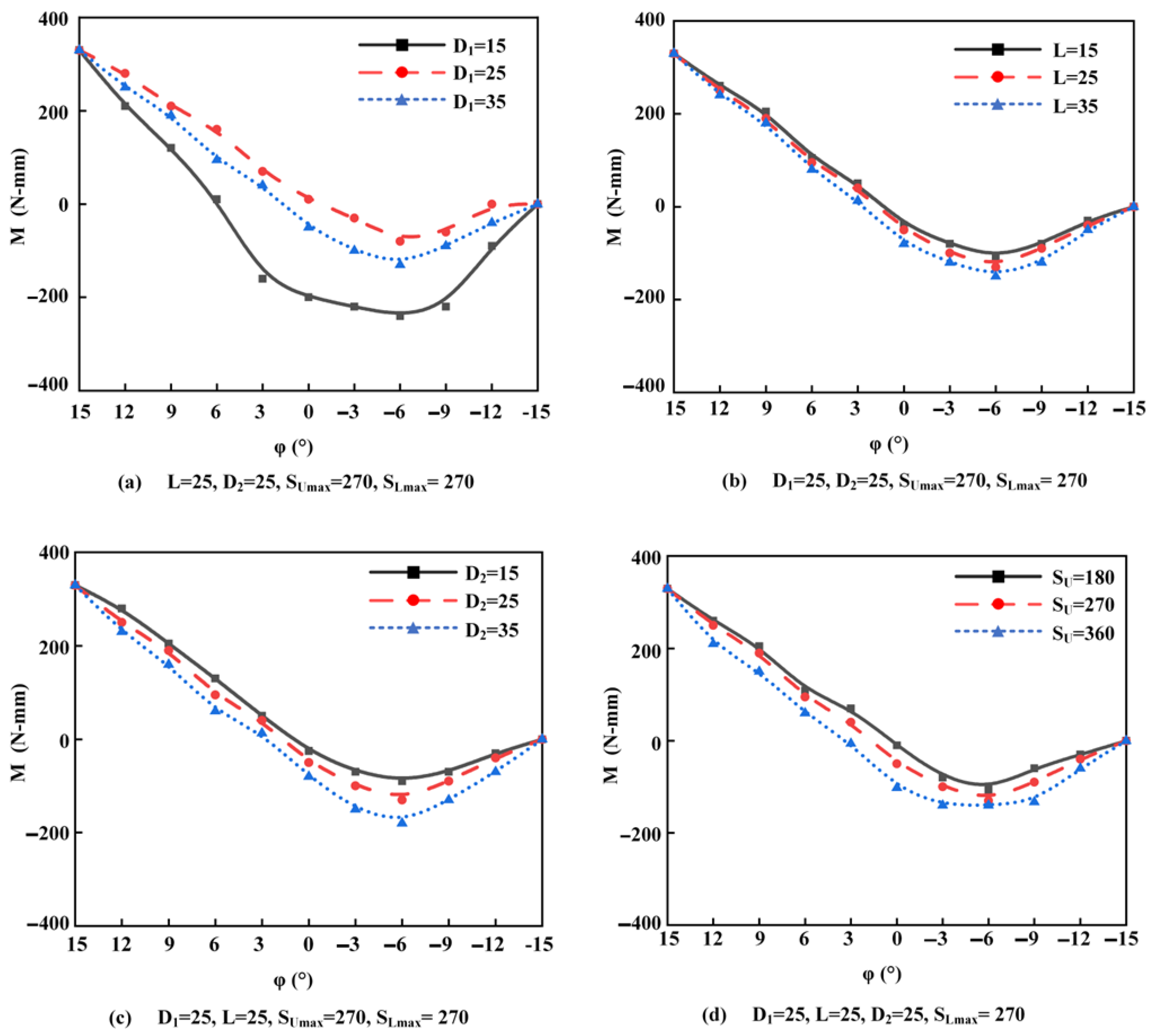
Subsequently, to investigate the effect of others factors on M(φ), the result under a single variable was obtained by simulation, as shown in Figure 7.

M(φ) demonstrates a consistent variation in response to different single variables. As φ ranges from 15° to −15°, M(φ) decreases from a consistent value to its respective minimum and subsequently increases to zero. The variation of M(φ) is monotonically increasing. However, it should be noted that different single variables have distinct impacts on the values of M(φ) and the negative regions thereof. In order to simplify the research, the effect of each factor will be examined, specifically when φ is equal to zero.

The orthogonal experiment’s method was used to investigate the effects of D₂, L, and D₂ on M(φ), as these factors do not change with φ. The method allows for the determination of the weights of these factors and their preferred values through the use of range analysis. The factors were denoted as x and different values for each factor were denoted as y (y = 1, 2, 3). The results of M(x,y) were obtained at different x and y values and are shown in

Table 3. Factor serial numbers under φ = 0.

y	x
	D1 (mm)	L (mm)	D2 (mm)
1	15	15	15
2	25	25	25
3	35	35	35

and

Table 4. Scheme of orthogonal experiment under φ = 0.

Number of Experiments	y			Result
	x = D1	x = L	x = D2	M(x,y) (N-mm)
1	1	1	1	9.5
2	1	2	3	−58.9
3	1	3	2	−71.1
4	2	1	3	6.7
5	2	2	2	13.3
6	2	3	1	52.9
7	3	1	2	19.1
8	3	2	1	29
9	3	3	3	5.4

.

The results of the range method analysis are presented in

Table 5. Range method results of orthogonal experiment under φ = 0.

x	D1			L			D2
y	1	2	3	1	2	3	1	2	3
K(x,y)	−120.5	72.9	53.5	35.3	−16.6	−12.8	91.4	−38.7	−46.6
k(x,y)	−40.2	24.3	17.8	11.8	−5.5	−4.3	30.5	−12.9	−15.6
R(x)	64.5			17.3			46.1
Preferred value	25			15			15
Influence weight	D1 > D2 > L

. The summation of M(x,y) is denoted as K(x,y). The average of K(x,y) is represented as k(x,y), which can be used to determine the optimal values of each factor. R(x) represents the range of k(x,y) and reflects the weight of the influence of x on M. The equation relations can be represented as follows:

$$K\left(x,y\right)={\displaystyle \sum }_{i=1}^{n=3}M\left(x,i\right)$$

(7)

$$k\left(x,y\right)=\frac{K\left(x,y\right)}{3}$$

(8)

$$R\left(x\right)=k{\left(x,y\right)}_{max}-k{\left(x,y\right)}_{min}$$

(9)

The results of the orthogonal experiments indicate that when φ = 0, the preferred values of x can be obtained by selecting k(x,y) values that are positive and close to zero. Additionally, the influence weight of x is greater when R(x) is larger. The data in Table 5 show that the most significant influencing factor is D₁, and M can be significantly affected by making adjustments to it. These preferred values will be used in further research.

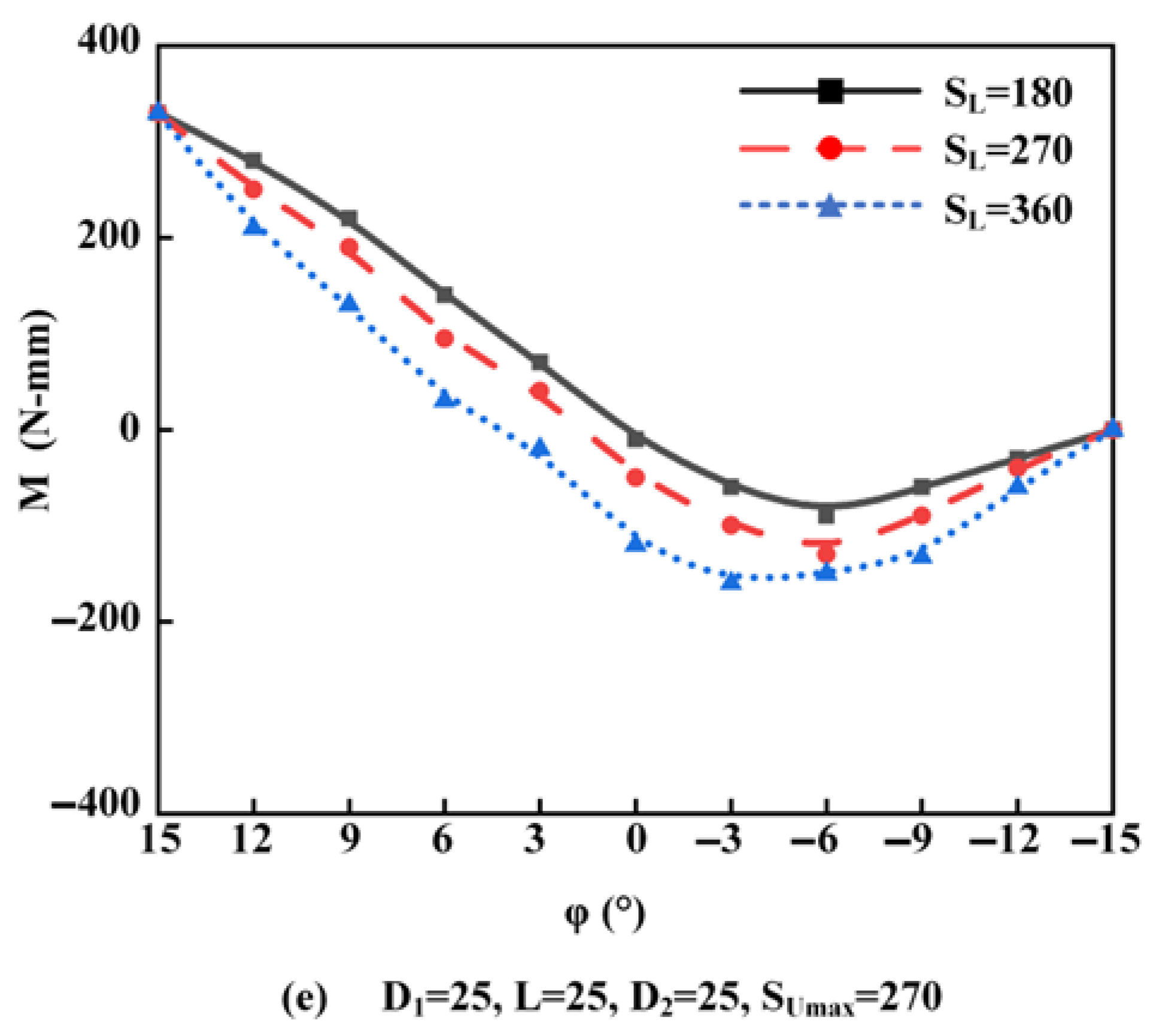
Furthermore, M is directly affected by S_Umax and S_Lmax. When φ is constant, the influence of S_Umax and S_Lmax on M is shown in Figure 8.

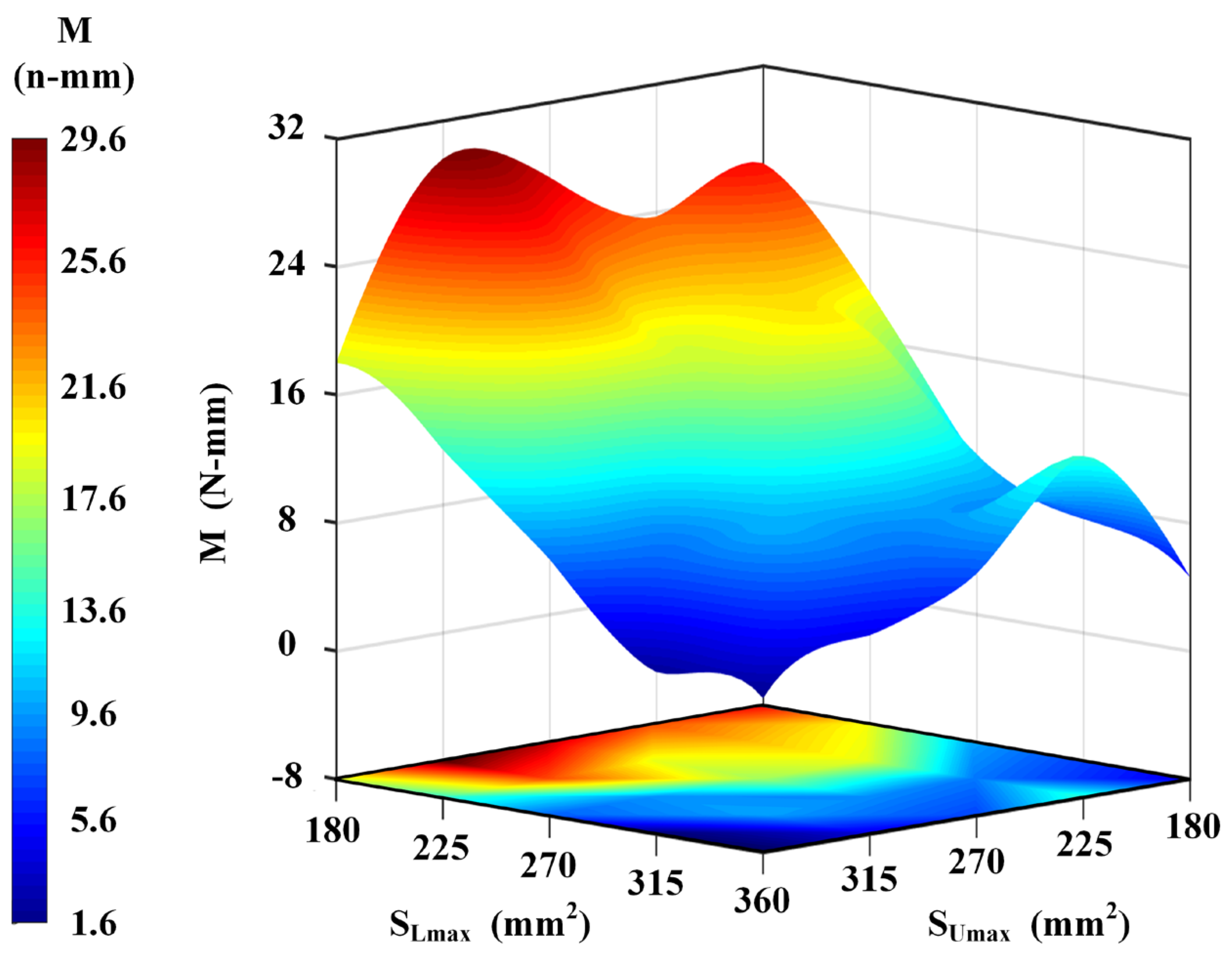
The simulation results indicate that both S_Umax and S_Lmax exert significant effects on M. When S_Umax remains constant, M decreases as S_Lmax increases, and the change in M is obvious at any value of S_Umax. According to Equation (3), when φ is constant, S_L decreases with decreasing S_Lmax. Consequently, the resistance of fluid flowing out from the lower orifice will increase, and it will be more likely to flow out from the upper orifice, thereby affecting the turbine and increasing M. On the other hand, when S_Lmax remains constant, M undergoes irregular changes with the change in S_Umax, although this change is not as pronounced as the degree of M changing with S_Lmax. This is particularly evident at S_Lmax = 180 and S_Lmax = 360. Since the upper orifice is close to the entrance of the adjusting device, when S_Umax changes and S_U changes, not only will the resistance of the fluid flowing out of the upper orifice change, but also the magnitude and direction of the fluid velocity will be affected. Under the combined action of multiple factors, M will change with the change in S_Umax, and the pattern of the change is not as obvious as that of M changing with S_Lmax.

Based on simulation results, when φ is equal to zero, M has the maximum value at S_Lmax of 180 mm. Therefore, 180 mm is selected as the optimal parameter for S_Lmax. At the same time, since the influence of S_Umax on M is not as obvious as that of S_Lmax, and if S_Umax is too large or too small, it will affect the positioning relationship between the turbine and the outer sleeve valve. Therefore, considering the need for the overall size of the regulating device and simplifying the subsequent experimental processing steps, the optimal parameters for S_Umax and S_Lmax are selected, as shown in

Table 6. Preferred values of S_Umax and S_Lmax.

Parameters	Preferred Values (mm2)
SUmax	310
SLmax	180

.

It should be noted that S_Umax and S_Lmax are not equal after optimization, which means that when S_U equals S_L, φ will be less than zero. According to Equations (2) and (3), at this point, φ is approximately −4°, while before optimization, S_U is equal to S_L when φ = 0. Therefore, by increasing S_Umax and decreasing S_Lmax, the fluid can flow more easily out of the upper orifice, thereby reducing the negative value of M(φ).

In summary, the influencing factors above were optimized by simulation and their preferred values are used in the next analysis.

3.3. Validation by Experiment Test

In order to verify the efficacy of the adjusting device, two prototypes of the MVDT were tested, as depicted in Figure 9. The structures of the prototypes were largely identical, with the exception of the adjusting device. The experimental setup for the MVDT was designed to simulate subterranean operating conditions and it also allowed for the measurement of the inclination angle of the well, providing insight into the deviation control accuracy of the MVDT [15].

By performing experiments using the two prototypes of the MVDT, three types of experimental results can be obtained: the first one is the well inclination correction effect of the prototype without the adjusting device; the second one is the well inclination correction effect of the prototype with the adjusting device prior to optimization; and the last one is the well inclination correction effect of the prototype with the optimized adjusting device installed. By comparing these three sets of experimental results, we can ascertain whether the adjusting device can enhance the well inclination correction effect of the MVDT and whether the optimized design of the adjusting device can improve the performance of the MVDT.

Due to the complexity of disassembling the prototypes and the interdependent nature of the components, it is challenging to directly measure M. However, by utilizing statistical and computational methods, it is possible to obtain φ from experimental data. Therefore, we utilized two characteristics of the MVDT and combined them with the measured thrust data of the actuator in the experiment to calculate φ.

MVDT exhibits two characteristics. As described in the introduction, when the MVDT is tilted, the actuator generates pushing forces in different directions, but the magnitude of the pushing force at the higher side of the wellbore is larger than that at the lower side. In addition, due to the periodic rotation of MVDT, the pushing forces in each direction will produce peaks and valleys with different phases over time. The pushing force in a direction will increase when the corresponding flow path of the actuator is connected by the plate valve [9,17,36].

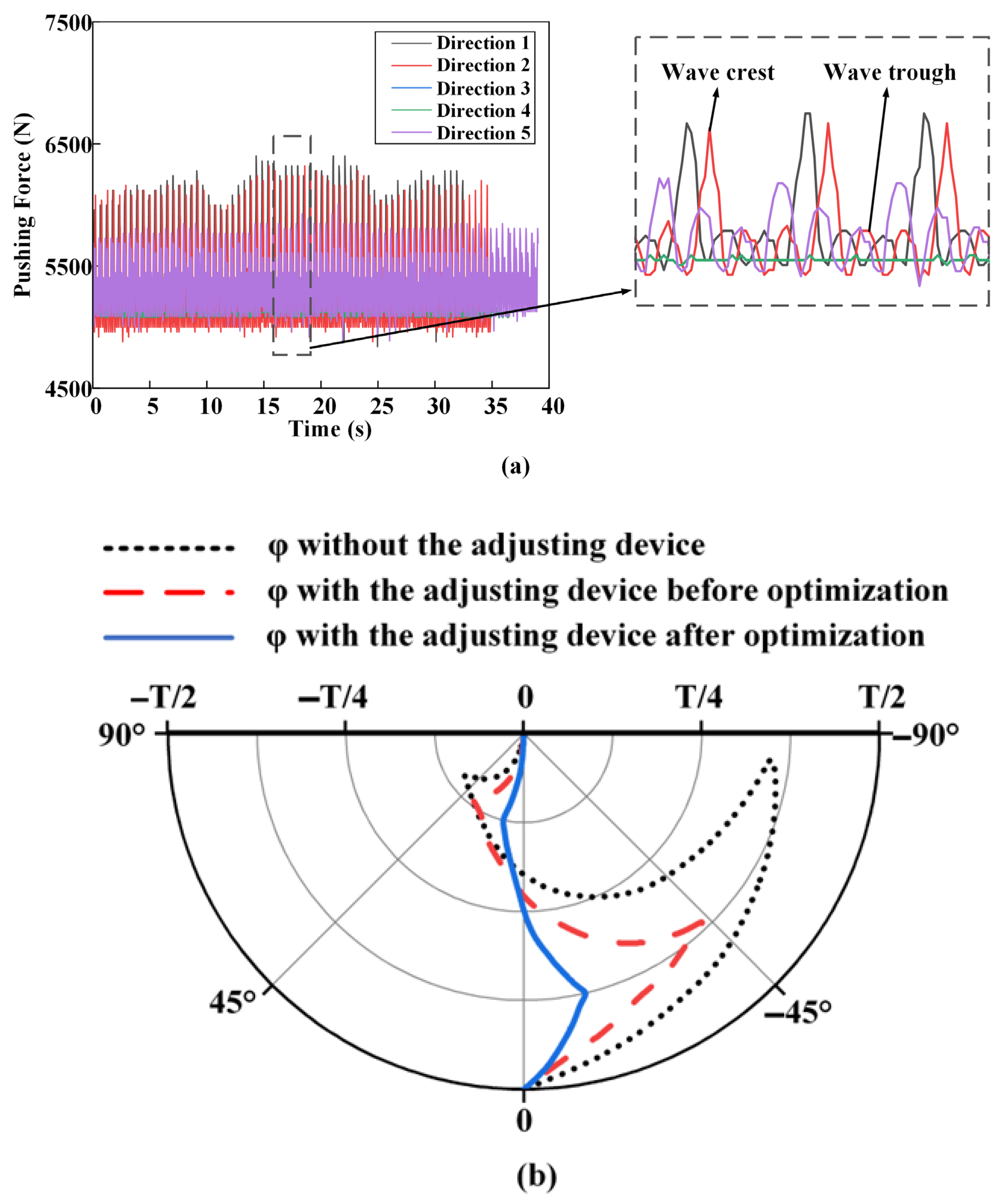
Due to the abundance of experimental data, we present only a set of pushing force data from one particular experiment, as shown in Figure 10a. The data demonstrates the different wave crests and troughs of pushing force in various directions over time. It can be observed that there is a distinct difference in the magnitude of the pushing force between the higher side and lower side of the wellbore. Moreover, for the directions 1, 2, and 5 of pushing forces located on the higher side of the wellbore (direction 3 and 4 located on the lower side of the wellbore), their time phase, peak magnitude, and duration of peak are all different as time progresses.

Using the aforementioned characteristics, we have calculated the relationship between φ and time in previous research [12], as shown in Figure 10b. This variation is periodic due to the uniform rotating speed of the MVDT. Under the three different experimental conditions in Figure 10b, φ shows a similar pattern of variation. It first reaches a positive maximum, then a negative maximum, before ultimately returning to zero.

From Section 2.1, it can be inferred that the smaller the range of variation of φ and the closer its maximum value is to zero, the better the performance of the MVDT. As shown in Figure 11b, when there is no adjusting device, the range of φ is the largest, particularly when φ is negative. This suggests that although the MVDT without an adjusting device can correct wellbore deviation, its performance still needs improvement.

The red dashed line in Figure 10b indicates that the range of φ is significantly reduced when the pre-optimized adjusting device is added. The maximum value of φ, when positive, decreased from approximately 60° to approximately 40°, and from approximately 90° to approximately 50° when negative. This observation serves as evidence of the regulating torque’s impact on φ and its ability to enhance the precision of the MVDT. However, it should be noted that the range of φ remains substantial and the improvement in the adjusting device on the MVDT is constrained prior to optimization.

The black curve in Figure 10b indicates that the range of φ is significantly reduced with the optimized adjusting device, especially when φ is negative. By implementing a solution for values of the negative M, φ is limited to a range of approximately ±15° under the influence of M′. This reduction in the range of φ serves as evidence of the effectiveness of the optimization on the adjusting device, and it ultimately enhances the accuracy and stability of the MVDT system.

4. Results and Discussions

In this section, the effect of solutions for negative M is discussed. The reasons for negative M are investigated by comparing the results before and after optimization.

The present study sought to further investigate the underlying mechanisms responsible for the observed effects of the proposed solutions. To this end, the simulation results obtained in Section 3.1 were compared against the results obtained with the preferred values of each influencing factor. Additionally, the parameters of Q_U and Q_L were examined in order to gain further insights into the reason for the negative M. For the purposes of clarity and concision, the parameters of M, Q_U, and Q_L were denoted prior to optimization, and M′, Q_U′, and Q_L′ were used to denote the parameters following optimization.

Same as M, M′ can also be divided into three ranges, as shown in Figure 11. The difference is that when φ is in range 1′, S_U is larger than S_L. When φ is in range 2′, S_U is still greater than S_L, and in range 3′, S_U is only smaller than S_L when −4° < φ < −15°, as described in Section 3.2. Due to fluid inertia, it is unavoidable for M of M′ to be non-zero when S_U equals S_L, irrespective of whether the adjusting device is optimized or not.

However, From Figure 11a, it can be observed that prior to optimization, when M equals zero, the value of φ is approximately 6°, while φ is zero when S_U equals S_L according to the calculation of Equations (2) and (3), resulting in a difference of 6° between the two values. However, after optimization, Figure 11b shows that when M equals zero, the value of φ is approximately −2.5°, while φ is approximately −4° when S_U equals S_L, resulting in a difference of 1.5° between the two values. This indicates that, regardless of whether the adjusting device is optimized or not, the difference between the value of φ when the adjusting torque is zero and when S_U equals S_L is not equal. However, after optimization, this difference is smaller. This also allows for a larger effective range for M′. Figure 11c illustrates the variations of S_U and S_L at different stages for a convenient comparison of their magnitudes. As described in Section 3.2, S_U is greater than S_L in both range 1′ and range 2′, while in range 3, S_U is smaller than S_L when φ is approximately less than −4°.

An analysis of the results of the optimized solution revealed that when M′ is within the range 1′, it is positive and exhibits a similar effect to that of M within range 1, whereby it enables φ to approach zero. However, compared to M, the decrease in M′ is more gradual. This is because, at the same φ, the degree to which the optimized S_U is greater than S_L is greater than that before optimization, and combined with the adjustment of the structure parameters such as D₁ to their optimal values, this leads to a slower rate of change in M′. Since M(φ) is continuous, when M and M′ approach zero, a gentler range of φ change is needed for M′ to reach zero, which is also reflected in the fact that range 1′ (15°~0°) in the figure is larger than range 1 (approximately 15°~6°). Additionally, it was noted that M′ maintains a relatively high value when φ is smaller (approximately 6°~0), indicating that M′ is capable of balancing the friction torque and adjusting φ when M is not.

Moreover, when M′ is within range 2′, despite the direction of M′ being opposite to that of the friction torque, φ will still move away from zero as a result of the combined effects of the friction torque and the eccentric torque. However, range 2′ is significantly smaller than range 2, indicating that the effect of the adjusting device is reduced in both ranges. Furthermore, the absolute value of M′ is less than that of M. Given that the interior of the adjusting device constitutes a closed flow field environment, it is not possible to completely eliminate the negative M, but it can be mitigated through optimization. Therefore, the aforementioned results demonstrate that the negative effect of M′ is less pronounced.

In range 3′, the optimization of the adjusting device resulted in a decrease in the absolute value of M′ in comparison to that of M. Despite the combined effect of the three torques leading to φ approaching zero, a negative value of M′ is still present. In order to further investigate the reasons for the emergence of negative M and M′, the flow rate of the orifices was observed.

The conservation of mass principle dictates that the sum of Q_U and Q_L (or Q_U′ and Q_L′) must equal the total mass flow. This serves as a validation of the simulation results. Q_U and Q_U′ are considered to be positive when the fluid flows out of the external cylinder valve, from the inlet, through the upper orifices. Similarly, Q_L and Q_L′ are considered to be positive when the fluid flows out of the external cylinder valve and through the lower orifices. Conversely, their values will be negative when the fluid is flowing in the opposite direction.

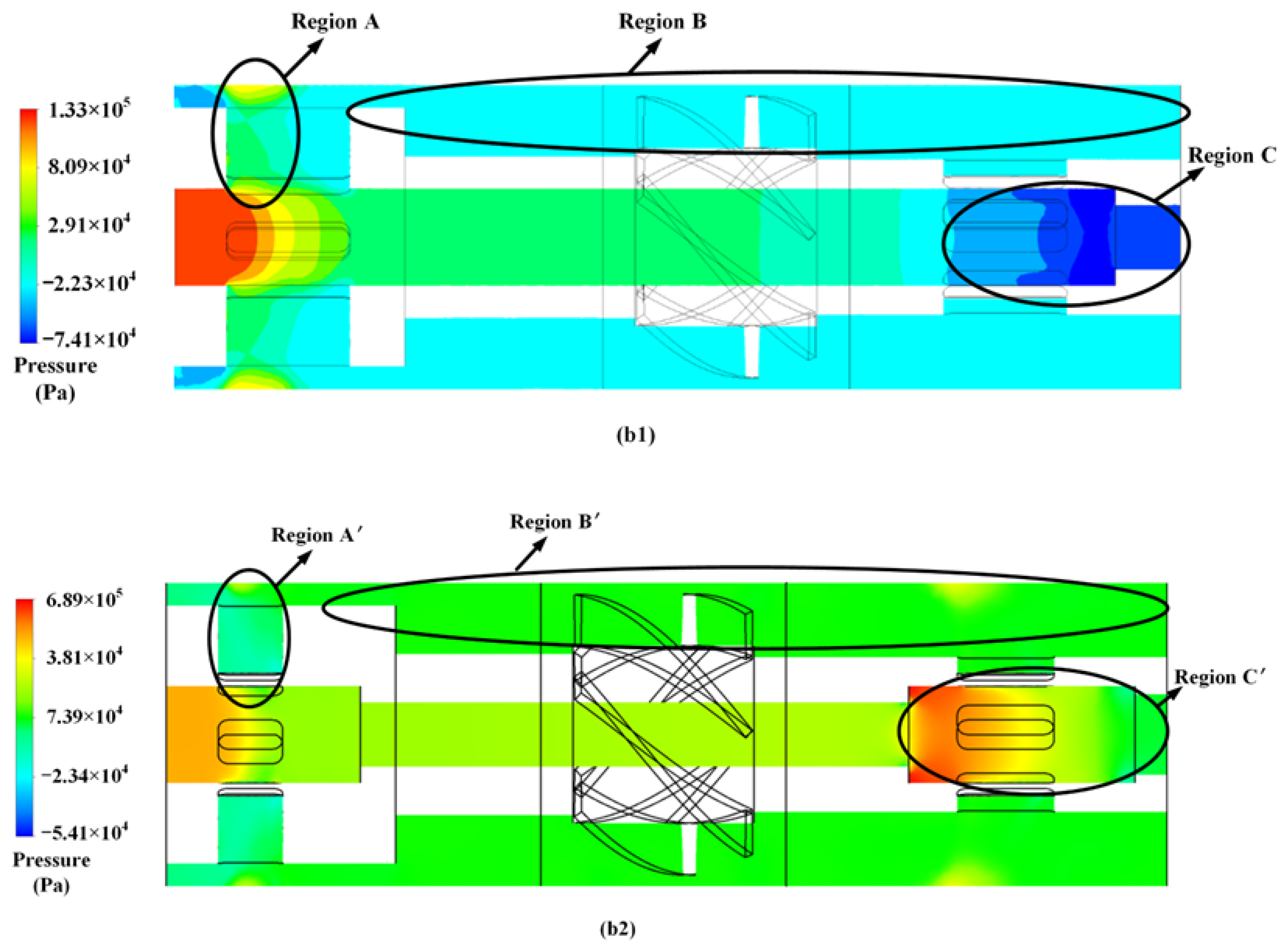
The trend of Q_U and Q_U′ is similar to that of M and M′, and they both exhibit negative values within the same range. This suggests the presence of a fluid phenomenon within the adjusting device, specifically reflux [37]. The reflux is responsible for the negative value of M, and it occurs in range 2, range 3, and range 3′. The reflux expands the range 2 and diminishes the effectiveness of the adjusting device. Therefore, further investigation into the causes of reflux is necessary. The chart of the flow field conditions in the adjusting device when φ = 0 has been observed, as depicted in Figure 12.

Prior to optimization, it was observed, as depicted in Figure 12(a1), that the majority of fluid flows directly from the inlet to the lower orifices and subsequently out of the adjusting device. However, a portion of the fluid, known as the reflux, flows in the opposite direction, back through the turbine, and out of the upper orifices from the lower orifices. This results in a change in the direction of M. Subsequently, the reflux circulates out of the adjusting device. Following optimization, it was noted, as illustrated in Figure 12(a2), that the reflux was significantly mitigated. As a result, the turbine was not impacted by the reflux, highlighting the effectiveness of the implemented solutions.

The results indicate that the proposed solutions have a significant impact on the performance of the adjusting device. It was observed that, under a constant total flow rate, the fluid velocity at the inlet is highly influenced by the value of D₁. When D₁ is smaller, the fluid velocity increases, resulting in a higher inertia [38]. This can lead to the phenomenon of reflux, where the fluid does not flow out of the upper orifices from the internal cylinder valve, even if S_U is greater than S_L. This explains the limited effect of changes in S_U and L on the parameter M. Additionally, it was found that a reduction in D₂ and S_L increases the fluid resistance and reduces the occurrence of reflux.

Additionally, to gain a deeper understanding of the underlying causes of reflux, an analysis of the pressure patterns within the adjusting device was conducted, as depicted in Figure 12(b1,b2). For the sake of brevity, the pressure region in proximity to the lower orifices prior to optimization has been designated as region A (with region A′ denoting the corresponding region after optimization). Similarly, the region in which the turbine is located has been referred to as region B (or region B′), and the pressure region in the vicinity of the upper orifices has been labeled region C (or region C′). A comparison of the average pressures across these regions reveals a hierarchy of values, with region C′ > region B′ > region A′ > region A > region B > region C.

It is well established that fluid flow is directed from regions of higher pressure to regions of lower pressure, and that the pressure of a fluid decreases as the flow rate increases [39]. Prior to optimization, the reflux fluid flows from region A to region B as it exits the lower orifices due to the pressure differential between the two regions. Additionally, the increased fluid velocity at the inlet results in a decrease in the pressure in region C, potentially even reaching negative values [40]. The negative pressure in region C also impacts the fluid in regions A and B, contributing to the phenomenon of reflux. As a result, M assumes negative values within ranges 2 and 3 as a consequence of the reflux.

After optimization, there is no negative pressure in region C′, and the pressure in region A′ and region B′ has a more uniform distribution. Moreover, the higher pressure in region C′ makes the fluid flow more easily from region C′ to region B′. Although negative M still exists in range 3′, the impact of the reflux on the adjusting device has been significantly reduced after optimization, and the performance of the adjusting device has improved.

In summary, by optimizing the adjusting device, the reflux phenomenon has been significantly weakened. A more desirable M can be obtained to balance the friction torque. The performance of the adjusting device has been significantly improved. The solutions of the negative M contribute to the effectiveness of the adjusting device and can improve the stability and accuracy of MVDT, which can provide recommendations for the following research.

5. Conclusions and Suggestions

In this study, the working principle of the adjusting device is examined, and the factors that influence its function are analyzed. The performance of the device is evaluated through simulations and experiments, and solutions for the negative adjusting torque are proposed. Additionally, a comparison of the device’s performance before and after optimization is provided.

The adjusting device can influence the accuracy of the mechanical vertical drilling tools (MVDT) by generating the adjusting torque. The flow areas of the upper and lower orifices will change with the variation of the deflection angle, thus producing adjusting torque in a closed loop. However, improper structural parameters of the adjusting device can lead to negative fluid pressure in the adjusting device and can cause fluid reflux. The reflux can cause a negative adjusting torque and impact the performance of the adjusting device.

The optimization of factors affecting the adjusting device can reduce the negative adjusting torque and achieve a more desirable adjusting torque. The diameter of the inlet and the flux area of the lower orifices have a large effect on the adjusting torque, and their preferred values were selected as 25 mm and 180 mm², respectively. After optimization, the effective range of the adjusting torque will increase to about [−15°, 0]. In addition, experiment tests have shown that the pre-optimized adjusting device can improve the performance of the MVDT, but with limited effect. With the addition of the optimized adjusting device, the negative values of the deflection angle are significantly reduced, and its overall range can be controlled within [−15°, 15°], verifying the accuracy of the simulation. This indicates that optimizing the adjusting device can improve the performance of MVDT and provide a reference for further research on MVDT.