Field Evaluation of Piezoelectric Energy Harvesters on Bridge Structure
Abstract
1. Introduction
2. Piezoelectric-Based Cantilevers for Bridge Vibration Conditions
2.1. Vibration Features of a Bridge
2.2. Cantilever Design Options
3. Experimental Program
3.1. Laboratory Tests
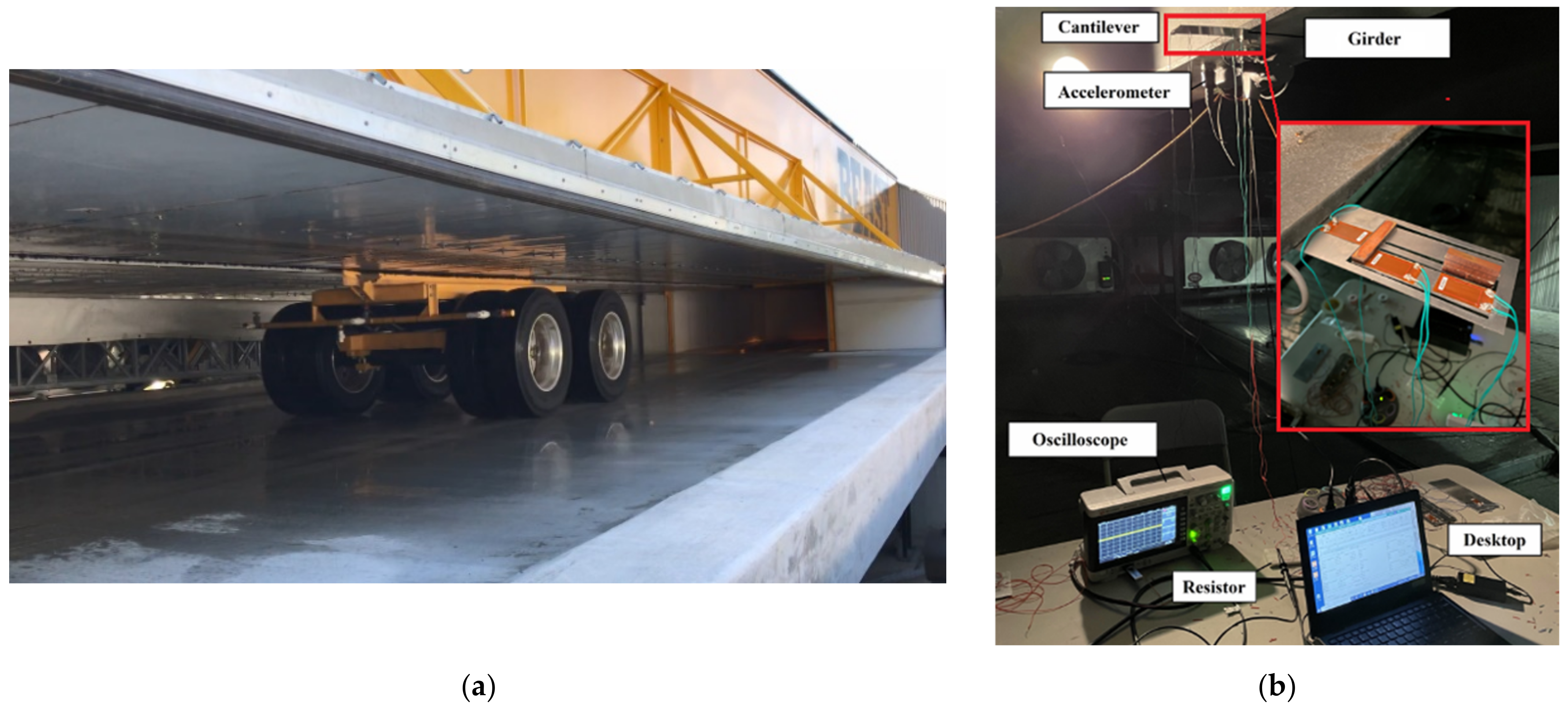
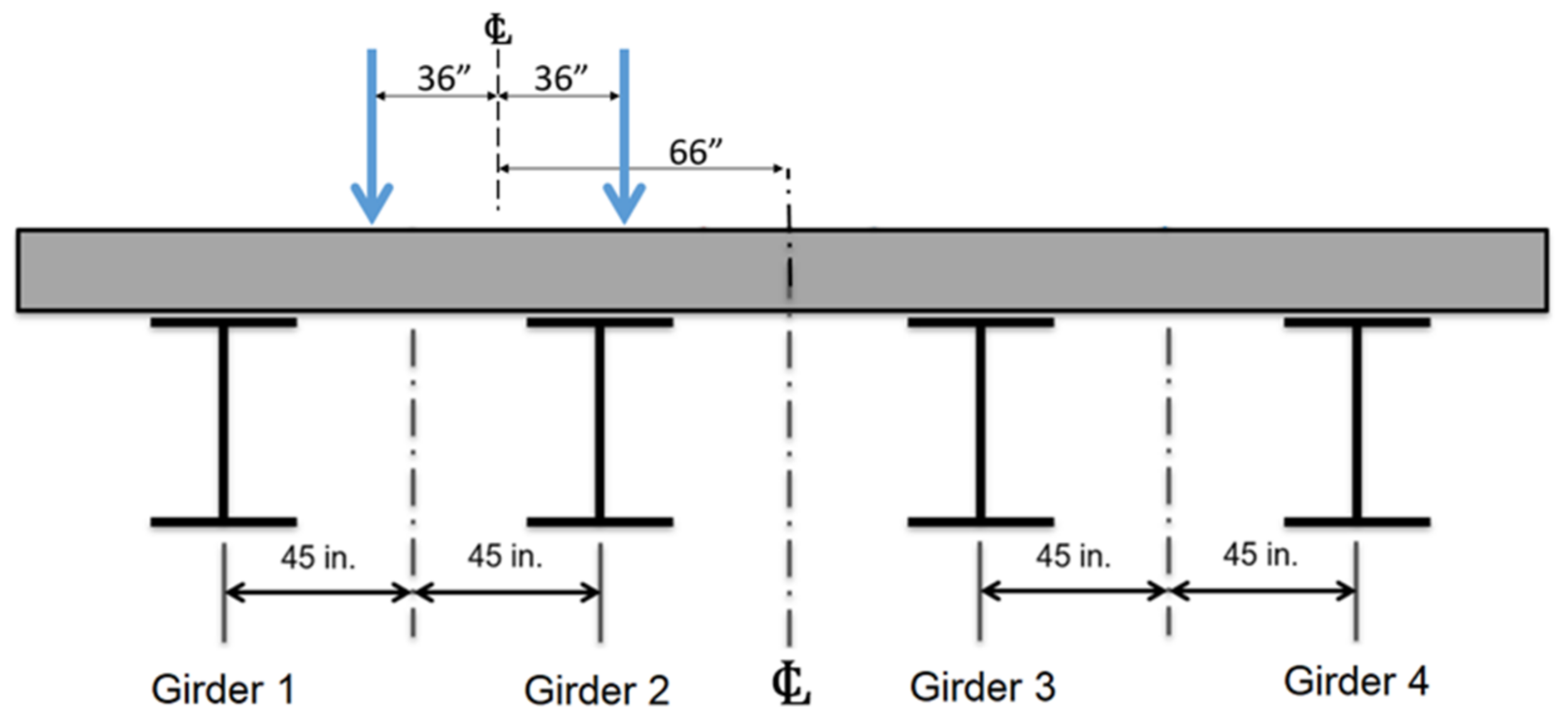
3.2. Full-Scale Bridge Tests
3.3. Energy Calculation
4. Laboratory Test Results of Piezoelectric Cantilevers
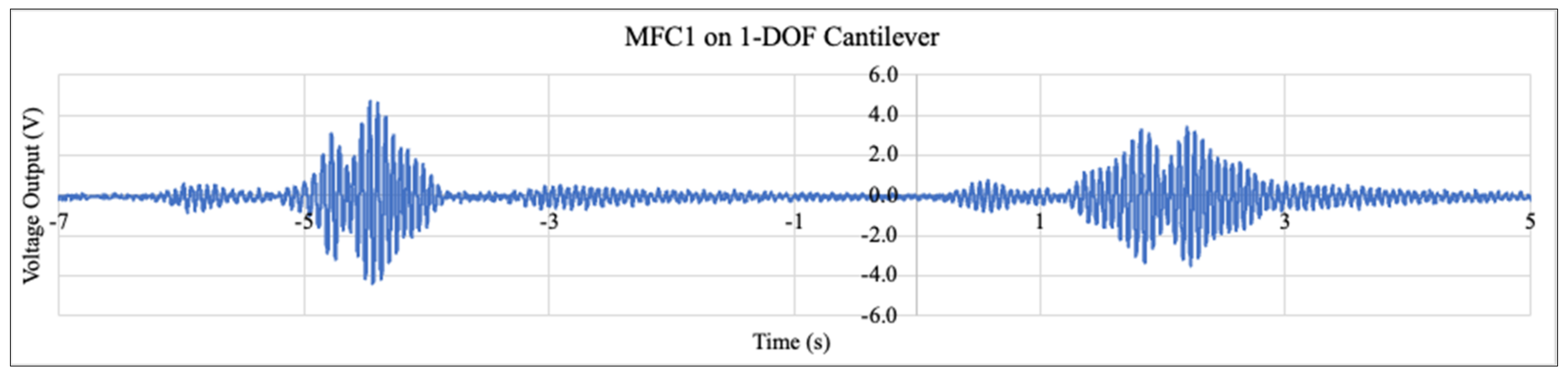
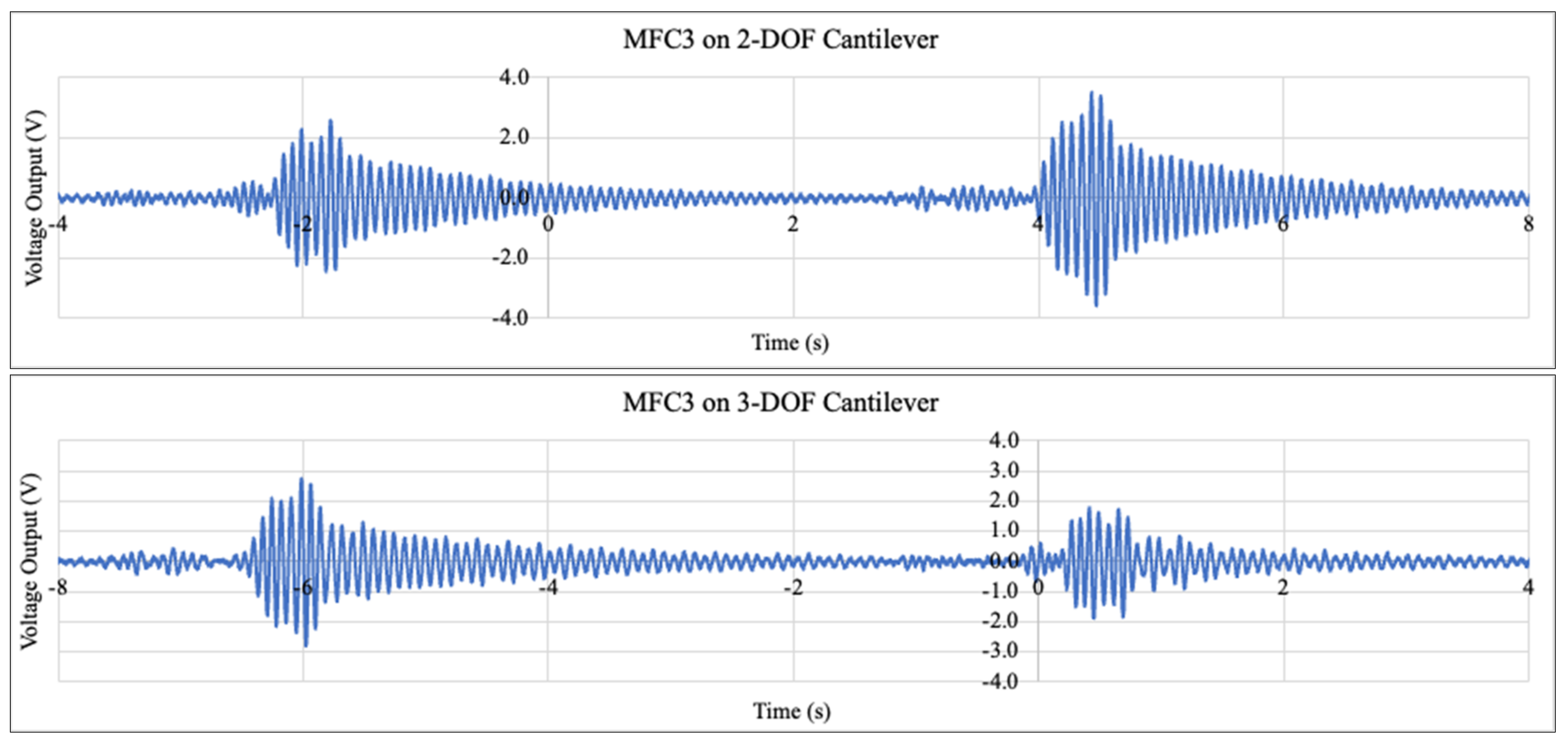
4.1. Voltage Outputs and Resonant Frequencies of Different Cantilevers
4.2. Optimal Resistive Loads
5. Accelerations and Voltage Outputs on a Full-Scale Bridge
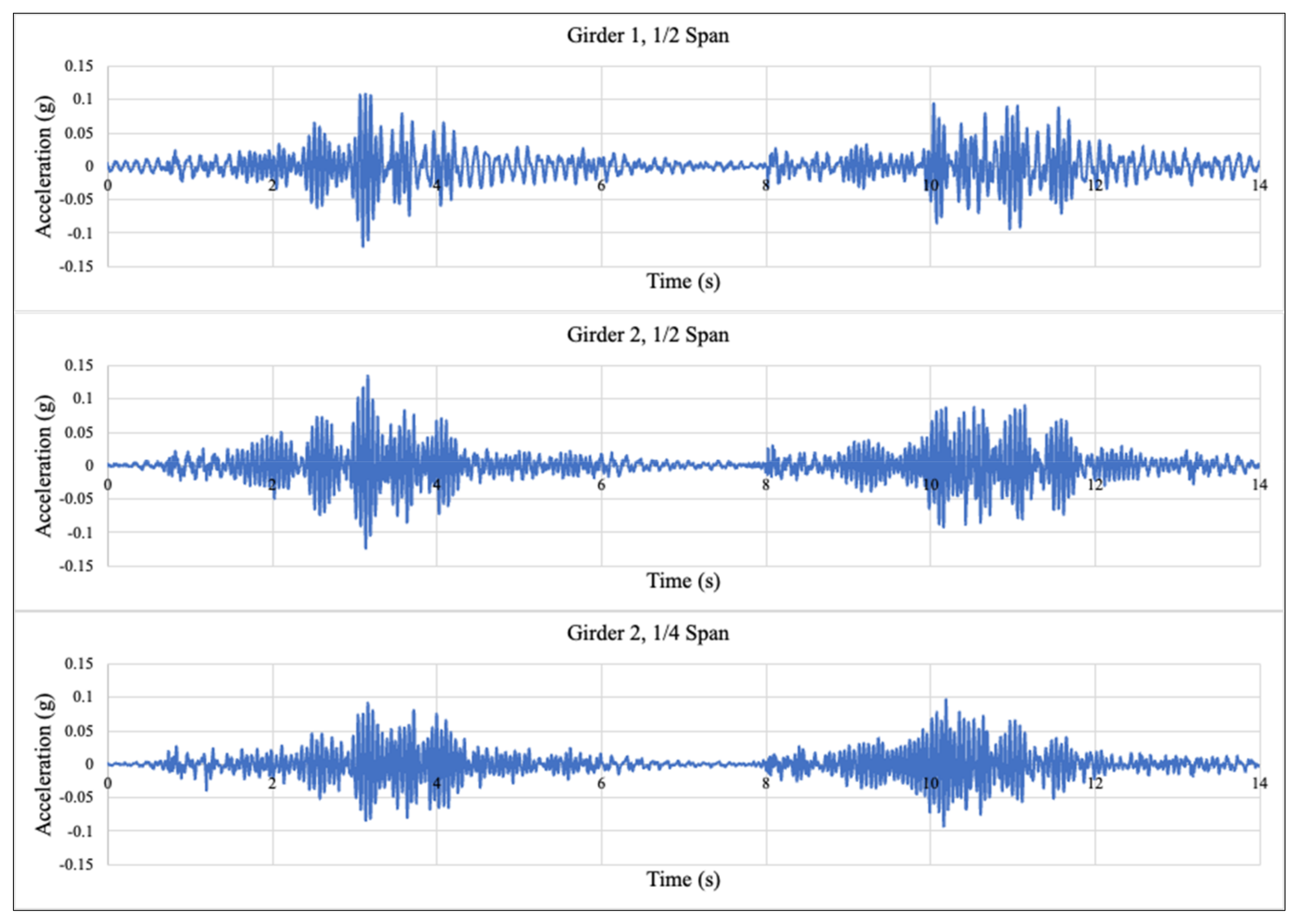
5.1. Accelerations Measured at Test Locations of a Bridge
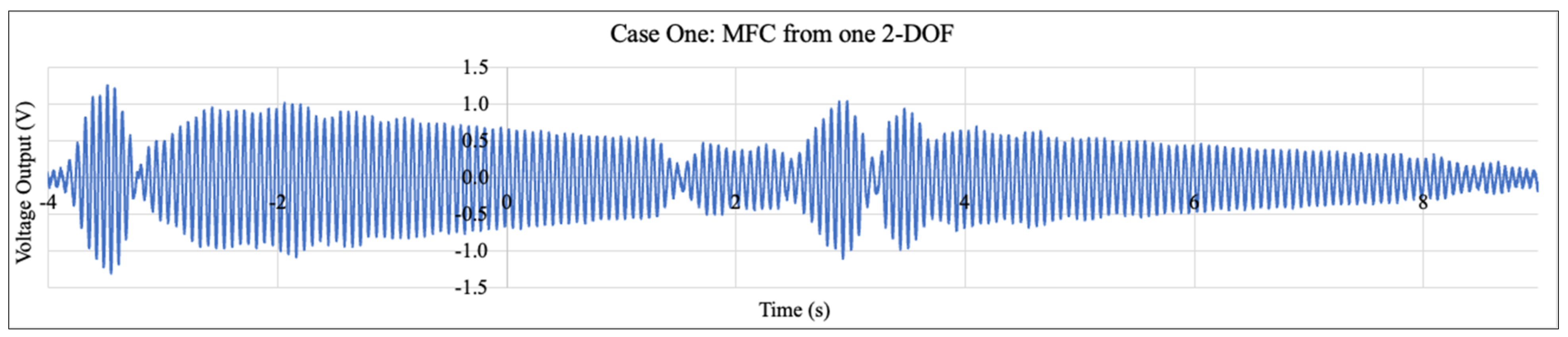
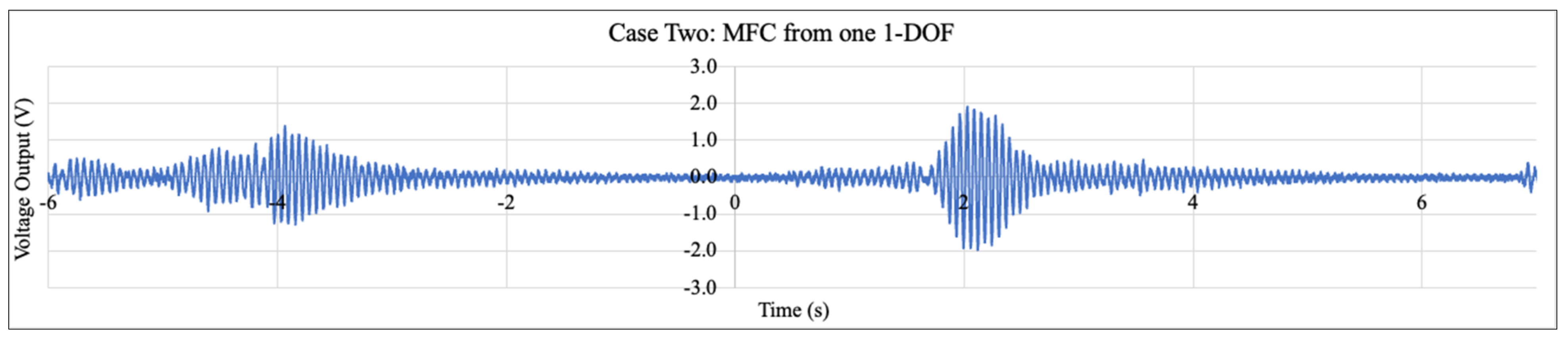
5.2. Voltage Outputs from Different Cantilevers
6. Energy Harvesting Performance under Bridge Vibrations
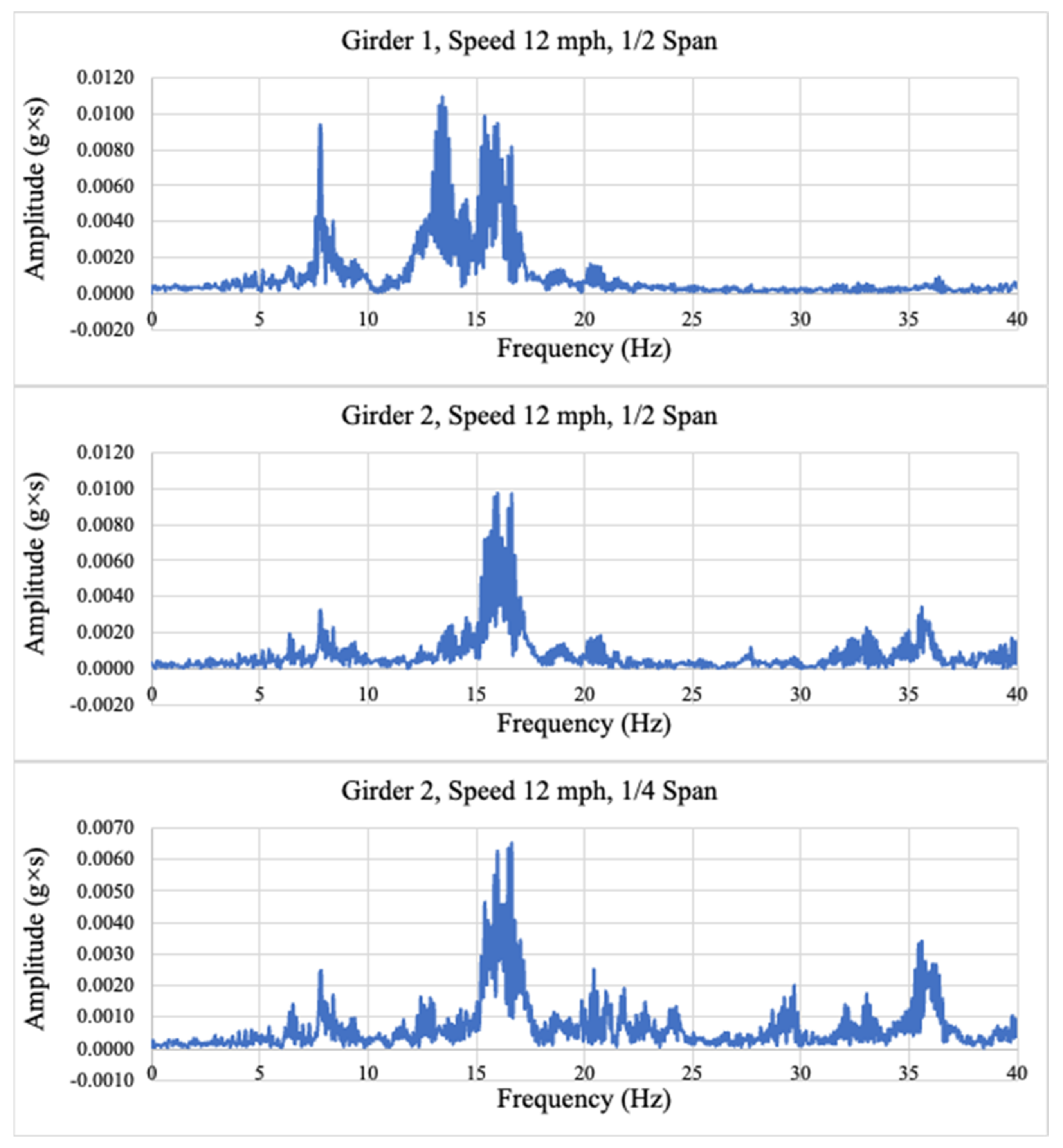
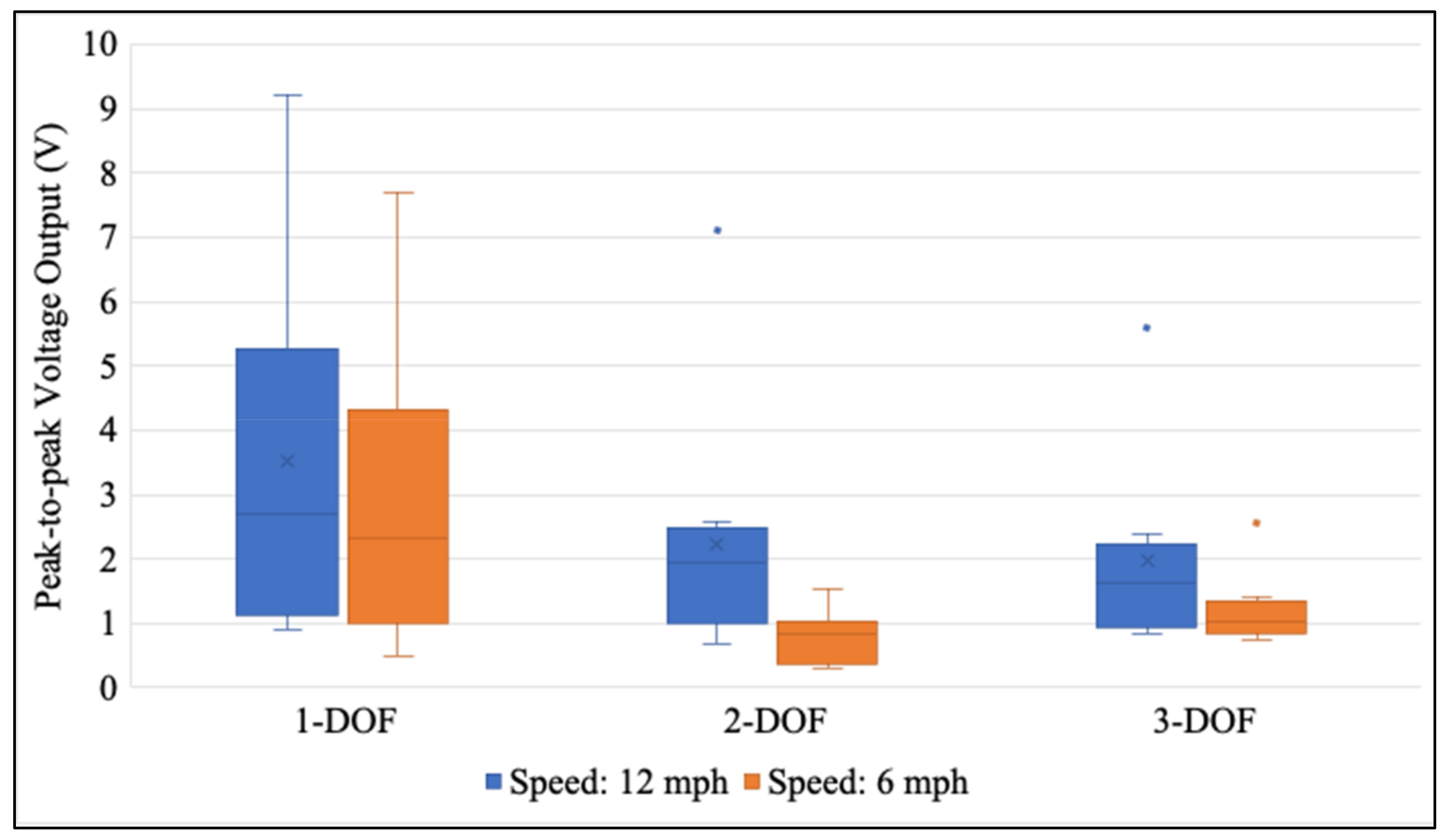
6.1. Effect of Loading Speeds
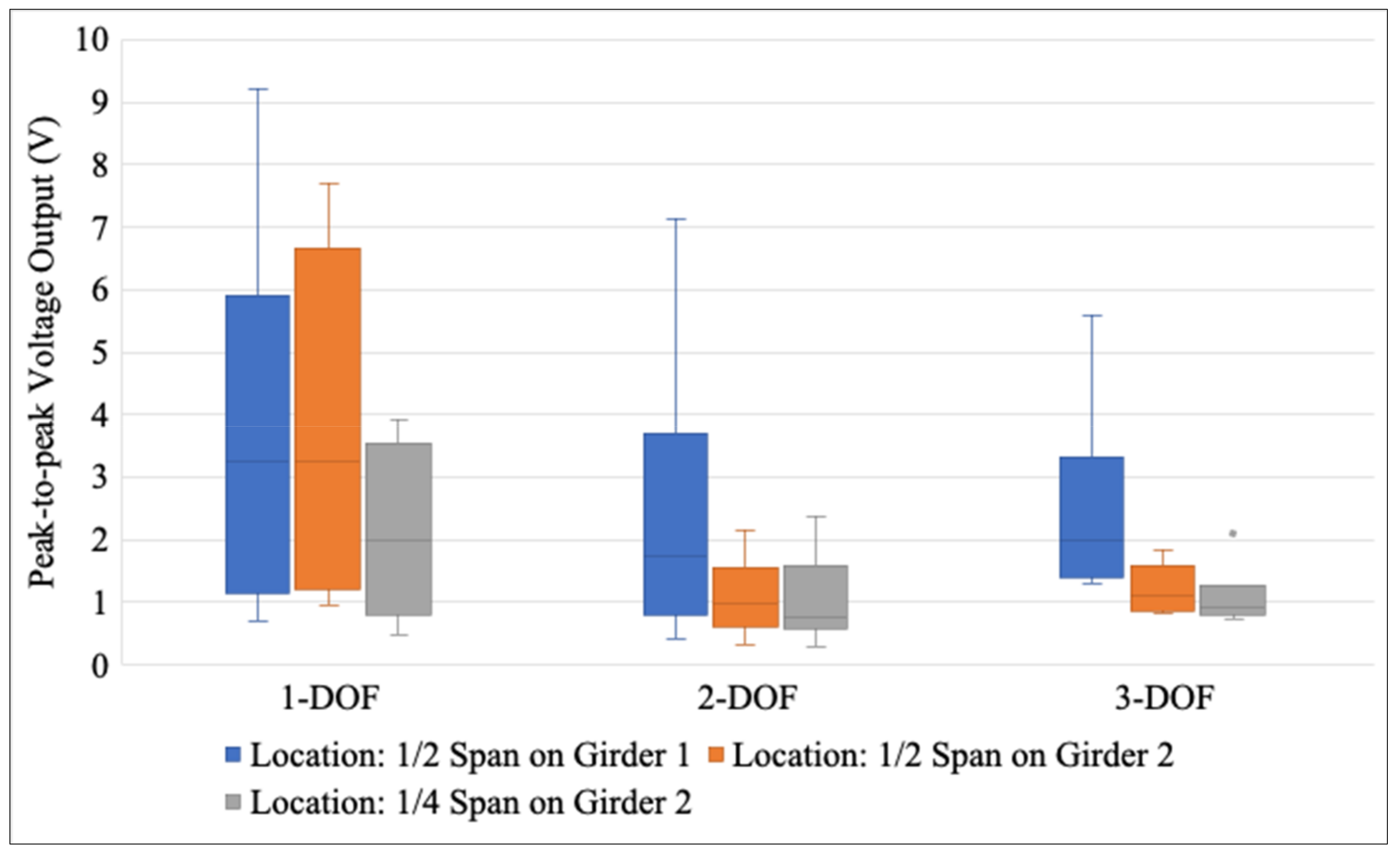
6.2. Effect of Installation Locations
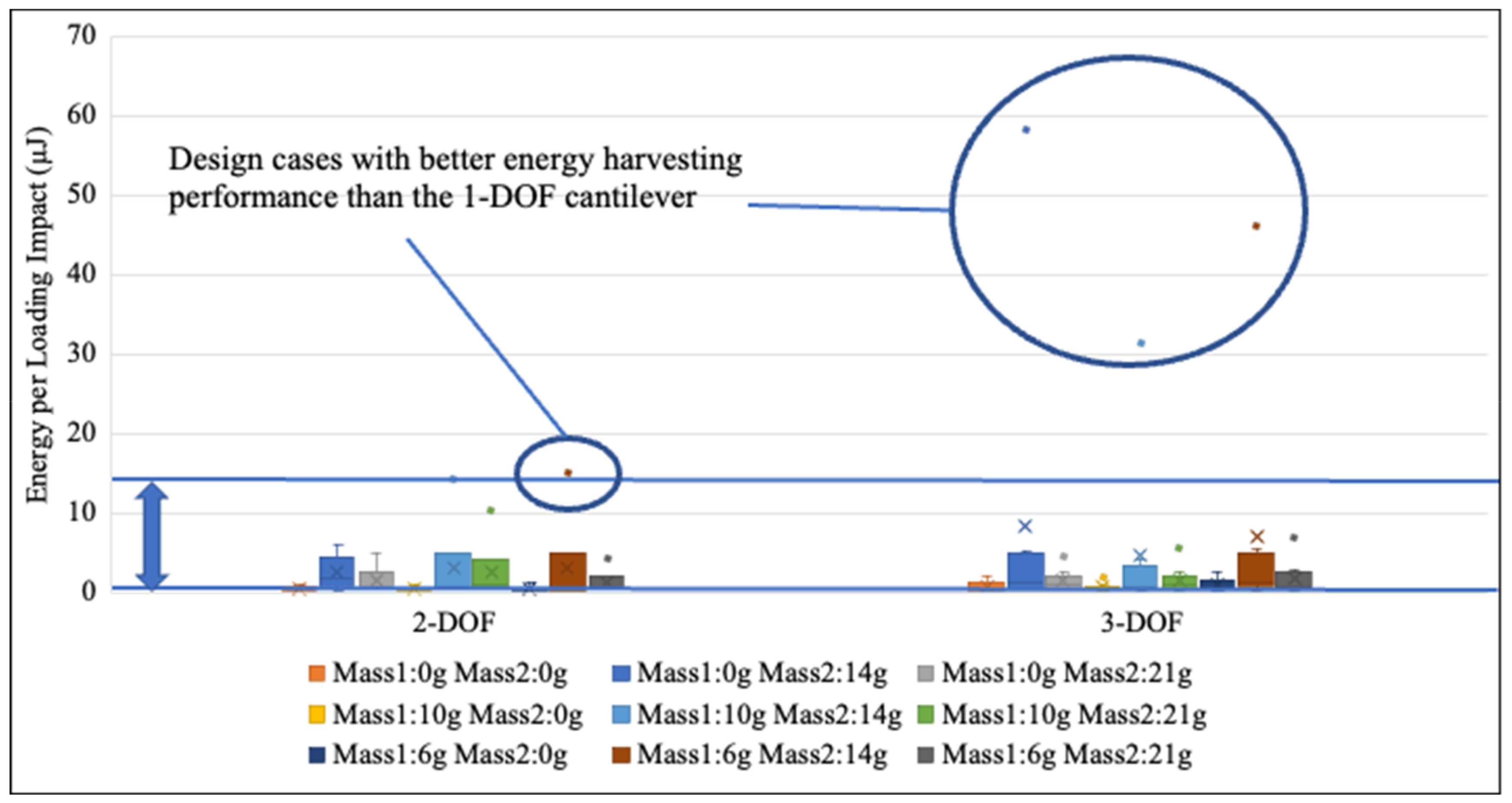
6.3. Effect of Mass Combinations on Cantilevers
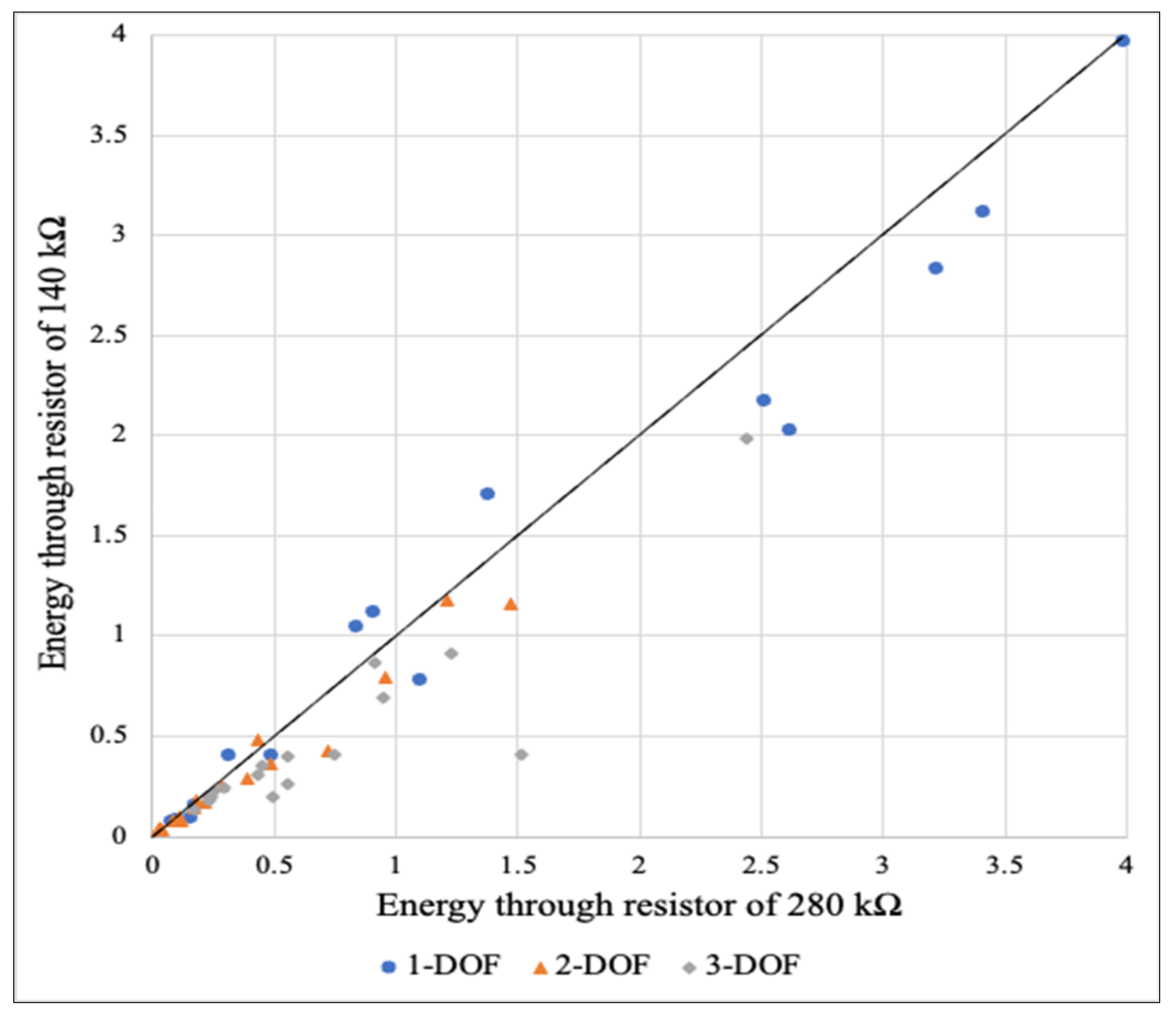
6.4. Effect of Resistive Load
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, L.; Wang, H. Non-intrusive movable energy harvesting devices: Materials, designs, and their prospective uses on transportation infrastructures. Renew. Sustain. Energy Rev. 2022, 160, 112340. [Google Scholar] [CrossRef]
- Shin, Y.-H.; Jung, I.; Noh, M.-S.; Kim, J.H.; Choi, J.-Y.; Kim, S.; Kang, C.-Y. Piezoelectric polymer-based roadway energy harvesting via displacement amplification module. Appl. Energy 2018, 216, 741–750. [Google Scholar] [CrossRef]
- Jasim, A.; Yesner, G.; Wang, H.; Safari, A.; Maher, A.; Basily, B. Laboratory testing and numerical simulation of piezoelectric energy harvester for roadway applications. Appl. Energy 2018, 224, 438–447. [Google Scholar] [CrossRef]
- Chen, C.; Sharafi, A.; Sun, J.-Q. A high density piezoelectric energy harvesting device from highway traffic—Design analysis and laboratory validation. Appl. Energy 2020, 269, 115073. [Google Scholar] [CrossRef]
- Jung, I.; Shin, Y.-H.; Kim, S.; Choi, J.-Y.; Kang, C.-Y. Flexible piezoelectric polymer-based energy harvesting system for roadway applications. Appl. Energy 2017, 197, 222–229. [Google Scholar] [CrossRef]
- Hwang, W.; Kim, K.-B.; Cho, J.Y.; Yang, C.H.; Kim, J.H.; Song, G.J.; Song, Y.; Jeon, D.H.; Ahn, J.H.; Hong, S.D.; et al. Watts-level road-compatible piezoelectric energy harvester for a self-powered temperature monitoring system on an actual roadway. Appl. Energy 2019, 243, 313–320. [Google Scholar] [CrossRef]
- Wang, C.H.; Wang, S.; Li, Q.J.; Wang, X.; Gao, Z.; Zhang, L. Fabrication and performance of a power generation device based on stacked piezoelectric en-ergy-harvesting units for pavements. Energy Convers. Manag. 2018, 163, 196–207. [Google Scholar] [CrossRef]
- Cao, Y.S.; Zhang, F.; Sha, A.; Liu, Z.; Hao, Y.; Hao, Y. Energy conversion models and characteristics under various inner connections of a novel packaged piezoelectric transducer for pavements. Energy Convers. Manag. 2021, 245, 114563. [Google Scholar] [CrossRef]
- Zhang, H.; Qin, W.; Zhou, Z.; Zhu, P.; Du, W. Piezomagnetoelastic energy harvesting from bridge vibrations using bi-stable characteristics. Energy 2023, 263, 125859. [Google Scholar] [CrossRef]
- Guo, L.; Wang, H.; Soares, L.; Lu, Q.; Brito, L. Multi-physics modelling of piezoelectric pavement system for energy harvesting under traffic loading. Int. J. Pavement Eng. 2021, 23, 3647–3661. [Google Scholar] [CrossRef]
- Jasim, A.; Wang, H.; Yesner, G.; Safari, A.; Szary, P. Performance Analysis of Piezoelectric Energy Harvesting in Pavement: Laboratory Testing and Field Simulation. Transp. Res. Rec. J. Transp. Res. Board 2019, 2673, 115–124. [Google Scholar] [CrossRef]
- Wang, L.; Tong, X.; Yang, H.; Wei, Y.; Miao, Y. Design and analysis of a hollow triangular piezoelectric cantilever beam harvester for vibration energy collection. Int. J. Pavement Res. Technol. 2019, 12, 259–268. [Google Scholar] [CrossRef]
- Trafford, R.; Russo, D.; Clark, C.; Shin, S.; Schmalzel, J.L. Characterization of Piezoelectric Cantilever Beams for use in Roadside Vibration Energy Harvesting. In Proceedings of the 2019 IEEE Sensors Applications Symposium, Sophia Antipolis, France, 11–13 March 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Camara, A.; Ruiz-Teran, A. Multi-mode traffic-induced vibrations in composite ladder-deck bridges under heavy moving vehicles. J. Sound Vib. 2015, 355, 264–283. [Google Scholar] [CrossRef]
- Peigney, M.; Siegert, D. Piezoelectric energy harvesting from traffic-induced bridge vibrations. Smart Mater. Struct. 2013, 22, 095019. [Google Scholar] [CrossRef]
- Karimi, M.; Karimi, A.; Tikani, R.; Ziaei-Rad, S. Experimental and theoretical investigations on piezoelectric-based energy harvesting from bridge vibrations under travelling vehicles. Int. J. Mech. Sci. 2016, 119, 1–11. [Google Scholar] [CrossRef]
- Cahill, P.; Jaksic, V.; Keane, J.; O’Sullivan, A.; Mathewson, A.; Ali, S.F.; Pakrashi, V. Effect of road surface, vehicle, and device characteristics on energy harvesting from bridge–vehicle interactions. Comput.-Aided Civ. Infrastruct. Eng. 2016, 31, 921–935. [Google Scholar] [CrossRef]
- Li, M.; Jing, X. Novel tunable broadband piezoelectric harvesters for ultralow-frequency bridge vibration energy harvesting. Appl. Energy 2019, 255, 113829. [Google Scholar] [CrossRef]
- Khan, F.; Ahmad, I. Review of Energy Harvesters Utilizing Bridge Vibrations. Shock. Vib. 2015, 2016, 1–21. [Google Scholar] [CrossRef]
- Ali, S.F.; Friswell, M.I.; Adhikari, S. Analysis of energy harvesters for highway bridges. J. Intell. Mater. Syst. Struct. 2011, 22, 1929–1938. [Google Scholar] [CrossRef]
- Gaglione, A.; Rodenas-Herraiz, D.; Jia, Y.; Nawaz, S.; Arroyo, E.; Mascolo, C.; Soga, K.; Seshia, A.A. Energy neutral operation of vibration energy-harvesting sensor networks for bridge applications. In Proceedings of the International Conference on Embedded Wireless Systems and Networks, Madrid, Spain, 14–16 February 2018; pp. 1–12. [Google Scholar]
- Sazonov, E.; Li, H.; Curry, D.; Pillay, P. Self-Powered Sensors for Monitoring of Highway Bridges. IEEE Sens. J. 2009, 9, 1422–1429. [Google Scholar] [CrossRef]
- Tong, X.; Song, S.; Wang, L.; Yang, H. A preliminary research on wireless cantilever beam vibration sensor in bridge health monitoring. Front. Struct. Civ. Eng. 2017, 12, 207–214. [Google Scholar] [CrossRef]
- Xue, H.; Hu, Y.; Wang, Q.-M. Broadband piezoelectric energy harvesting devices using multiple bimorphs with different operating frequencies. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 2104–2108. [Google Scholar] [CrossRef] [PubMed]
- Qi, S.; Shuttleworth, R.; Oyadiji, S.O.; Wright, J. Design of a multiresonant beam for broadband piezoelectric energy harvesting. Smart Mater. Struct. 2010, 19, 094009. [Google Scholar] [CrossRef]
- Chen, S.; Ma, L.; Chen, T.; Liu, H.; Sun, L.; Wang, J. Modeling and verification of a piezoelectric frequency-up-conversion energy harvesting system. Microsyst. Technol. 2017, 23, 2459–2466. [Google Scholar] [CrossRef]
- Tang, X.; Zuo, L. Enhanced vibration energy harvesting using dual-mass systems. J. Sound Vib. 2011, 330, 5199–5209. [Google Scholar] [CrossRef]
- Ye, Z.; Lu, Y.; Wang, L.B. Investigating the pavement vibration response for roadway service condition evaluation. Adv. Civ. Eng. 2018, 2018, 2714657. [Google Scholar] [CrossRef]
- Museros, P.; Moliner, E.; Martínez-Rodrigo, M. Free vibrations of simply-supported beam bridges under moving loads: Maximum resonance, cancellation and resonant vertical acceleration. J. Sound Vib. 2013, 332, 326–345. [Google Scholar] [CrossRef]






| 1-DOF | 2-DOF | 3-DOF | |
|---|---|---|---|
| Baseline outline dimension (mm3) | 170 70 1 | ||
| Baseline mass group (g) | Mass 1: 10 | Mass 1: 10 Mass 2: 21 | Mass 1: 10 Mass 2: 21 Mass 3: 32 |
| Outline dimension by scale 1.1 and 1.2 (mm3) | 187 77 1 | ||
| 204 84 1 | |||
| Mass combinations (g) | Mass 1: 0, 6, 10 Mass 2: 0, 14, 21 | Mass 1: 0, 6, 10 Mass 2: 0, 14, 21 Mass 3: 32 | |
| 1-DOF | RF1 (Hz) | Peak 1 (V) | 2-DOF | RF1 (Hz) | Peak 1 (V) | RF2 (Hz) | Peak 2 (V) | ||||||
| Size, scale | MFC1 | MFC2 | MFC3 | Size, Scale | MFC1 | MFC2 | MFC3 | MFC1 | MFC2 | MFC3 | |||
| 1 | 16.5 | 38.2 | 19.1 | 6.3 | 1 | 11.0 | 16.5 | 2.0 | 6.6 | 12.0 | 6.2 | 9.4 | 36.0 |
| 2 | 13.0 | 51.0 | N/A | N/A | 2 | 9.8 | 22.7 | N/A | 5.8 | 11.0 | 8.8 | N/A | 10.5 |
| 3 | 11.4 | 56.7 | N/A | N/A | 3 | 9.0 | 26.9 | N/A | 8.0 | 9.8 | 17.1 | N/A | 47.0 |
| 3-DOF | RF1 (Hz) | Peak 1 (V) | RF2 (Hz) | Peak 2 (V) | RF3 (Hz) | Peak 3 (V) | |||||||
| Size, scale | MFC1 | MFC2 | MFC3 | MFC1 | MFC2 | MFC3 | MFC1 | MFC2 | MFC3 | ||||
| 1 | 7.1 | 17.3 | 11.7 | 1.3 | 11.4 | 8.8 | 15.5 | 42.2 | 21.3 | 8.2 | 15.1 | 5.7 | |
| 2 | 6.0 | 16.3 | 14.7 | 2.2 | 10.5 | 4.7 | 13.7 | 43.0 | 18.0 | 5.6 | 18.5 | 4.8 | |
| 3 | 5.6 | 16.1 | 7.3 | 1.2 | 9.5 | 7.2 | 3.1 | 34.6 | 16.3 | 6.4 | 10.3 | 4.0 | |
| 2-DOF | Peak 1 (V) | Peak 2 (V) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Mass 1 (g) | Mass 2 (g) | RF1 (Hz) | MFC1 | MFC2 | MFC3 | RF2 (Hz) | MFC1 | MFC2 | MFC3 |
| 0 | 0 | 16.7 | 12.5 | 1.1 | 5.2 | 29.5 | 2.9 | 4.1 | 25.0 |
| 6 | 0 | 12.5 | 10.7 | 1.0 | 2.4 | 27.5 | 6.0 | 4.0 | 23.9 |
| 10 | 0 | 11.0 | 13.7 | 0.5 | 1.9 | 13.7 | 2.4 | 0.4 | 1.4 |
| 0 | 14 | 13.3 | 15.7 | 8.0 | 29.5 | 17.7 | 5.6 | 2.2 | 5.6 |
| 6 | 14 | 12.0 | 12.5 | 2.2 | 6.8 | 14.0 | 5.0 | 8.4 | 28.5 |
| 10 | 14 | 11.3 | 11.7 | 0.8 | 2.3 | 13.8 | 6.4 | 10.0 | 37.0 |
| 0 | 21 | 11.7 | 14.5 | 10.1 | 37.8 | 17.5 | 7.4 | 1.6 | 4.2 |
| 6 | 21 | 11.7 | 15.9 | 6.6 | 25.5 | 12.0 | 9.0 | 4.6 | 17.1 |
| 10 | 21 | 11.0 | 16.5 | 2.0 | 6.6 | 12.0 | 6.2 | 9.4 | 36.0 |
| 3-DOF (Mass 3:32 g) | Peak 1 (V) | Peak 2 (V) | Peak 3 (V) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mass 1 (g) | Mass 2 (g) | RF1 (Hz) | MFC1 | MFC2 | MFC3 | RF2 (Hz) | MFC1 | MFC2 | MFC3 | RF3 (Hz) | MFC1 | MFC2 | MFC3 |
| 0 | 0 | 7.8 | 20.9 | 14.5 | 6.0 | 24.5 | 12.1 | 16.5 | 30.2 | 25.0 | 10.5 | 12.9 | 31.0 |
| 6 | 0 | 7.3 | 20.0 | 12.5 | 2.0 | 22.7 | 12.1 | 20.9 | 12.9 | 25.0 | 8.0 | 6.0 | 32.0 |
| 10 | 0 | 7.1 | 19.3 | 14.9 | 2.0 | 20.7 | 4.8 | 16.1 | 6.0 | 25.0 | 8.8 | 8.8 | 32.0 |
| 0 | 14 | 7.8 | 20.1 | 15.3 | 3.2 | 13.5 | 9.2 | 23.3 | 47.5 | 31.0 | 6.4 | 10.1 | 4.4 |
| 6 | 14 | 7.3 | 19.3 | 11.7 | 3.2 | 13.4 | 8.4 | 12.9 | 40.2 | 23.0 | 8.8 | 20.9 | 6.4 |
| 10 | 14 | 7.2 | 14.5 | 10.1 | 2.8 | 13.3 | 8.4 | 13.3 | 42.6 | 21.0 | 10.9 | 25.3 | 8.8 |
| 0 | 21 | 7.8 | 20.9 | 14.5 | 2.8 | 11.7 | 8.4 | 22.5 | 54.3 | 31.0 | 8.0 | 11.6 | 4.0 |
| 6 | 21 | 7.3 | 17.7 | 12.9 | 2.8 | 11.5 | 9.6 | 20.5 | 51.5 | 23.0 | 8.4 | 19.3 | 7.2 |
| 10 | 21 | 7.1 | 17.3 | 11.7 | 1.3 | 11.4 | 8.8 | 15.5 | 42.2 | 21.3 | 8.2 | 15.1 | 5.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, L.; Wang, H.; Braley, J.; Venkiteela, G. Field Evaluation of Piezoelectric Energy Harvesters on Bridge Structure. Machines 2023, 11, 462. https://doi.org/10.3390/machines11040462
Guo L, Wang H, Braley J, Venkiteela G. Field Evaluation of Piezoelectric Energy Harvesters on Bridge Structure. Machines. 2023; 11(4):462. https://doi.org/10.3390/machines11040462
Chicago/Turabian StyleGuo, Lukai, Hao Wang, John Braley, and Giri Venkiteela. 2023. "Field Evaluation of Piezoelectric Energy Harvesters on Bridge Structure" Machines 11, no. 4: 462. https://doi.org/10.3390/machines11040462
APA StyleGuo, L., Wang, H., Braley, J., & Venkiteela, G. (2023). Field Evaluation of Piezoelectric Energy Harvesters on Bridge Structure. Machines, 11(4), 462. https://doi.org/10.3390/machines11040462








