Induction Motor Noise Source Separation and Identification Based on Adaptive Scale-Space Mode Extraction
Abstract
1. Introduction
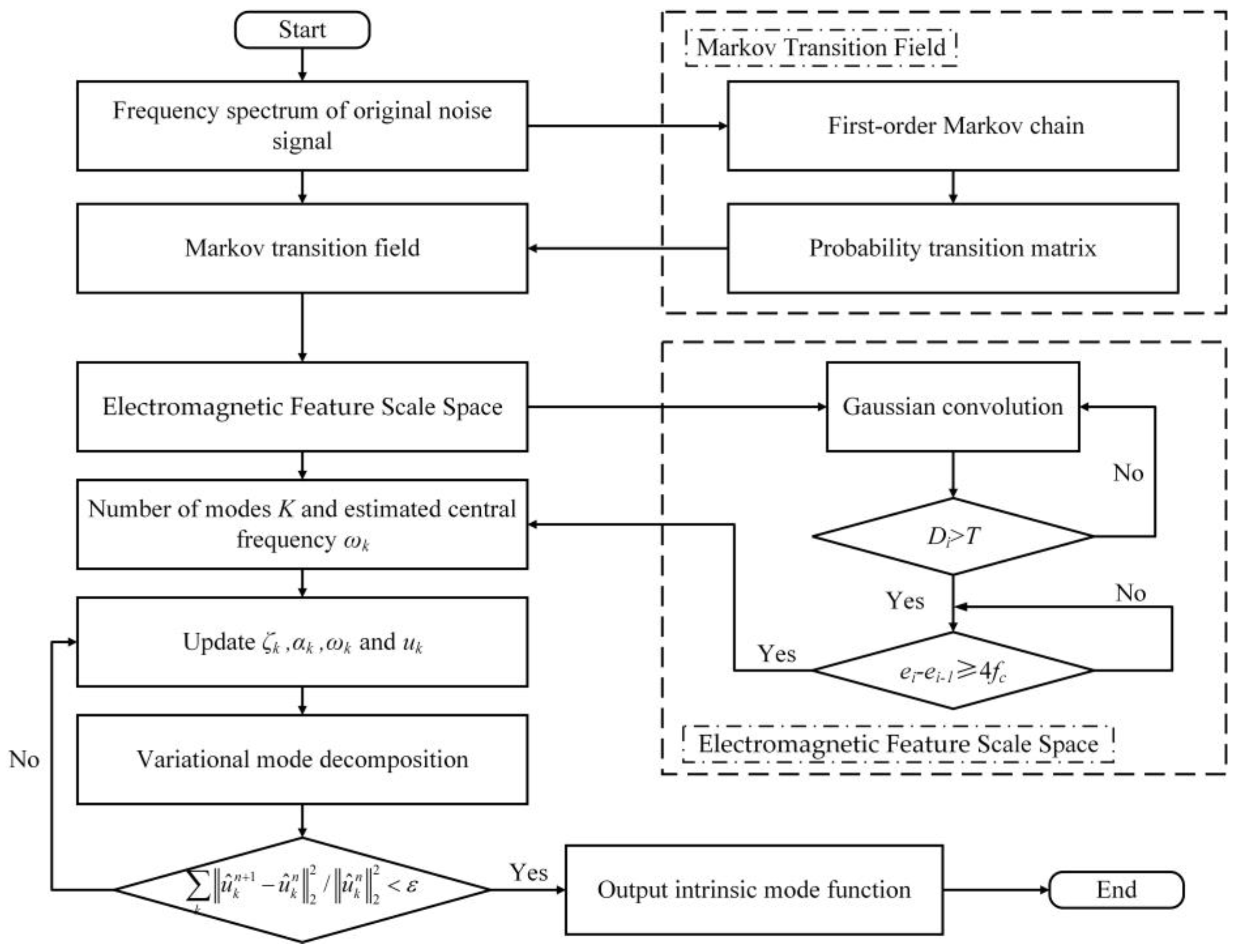
2. Methodologies
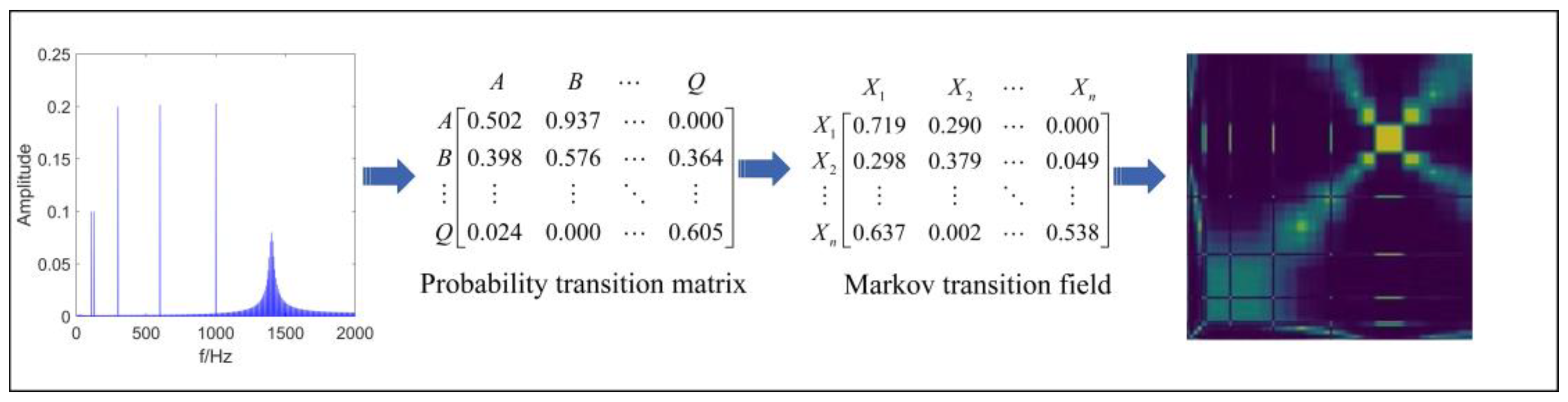
2.1. Markov Transition Field
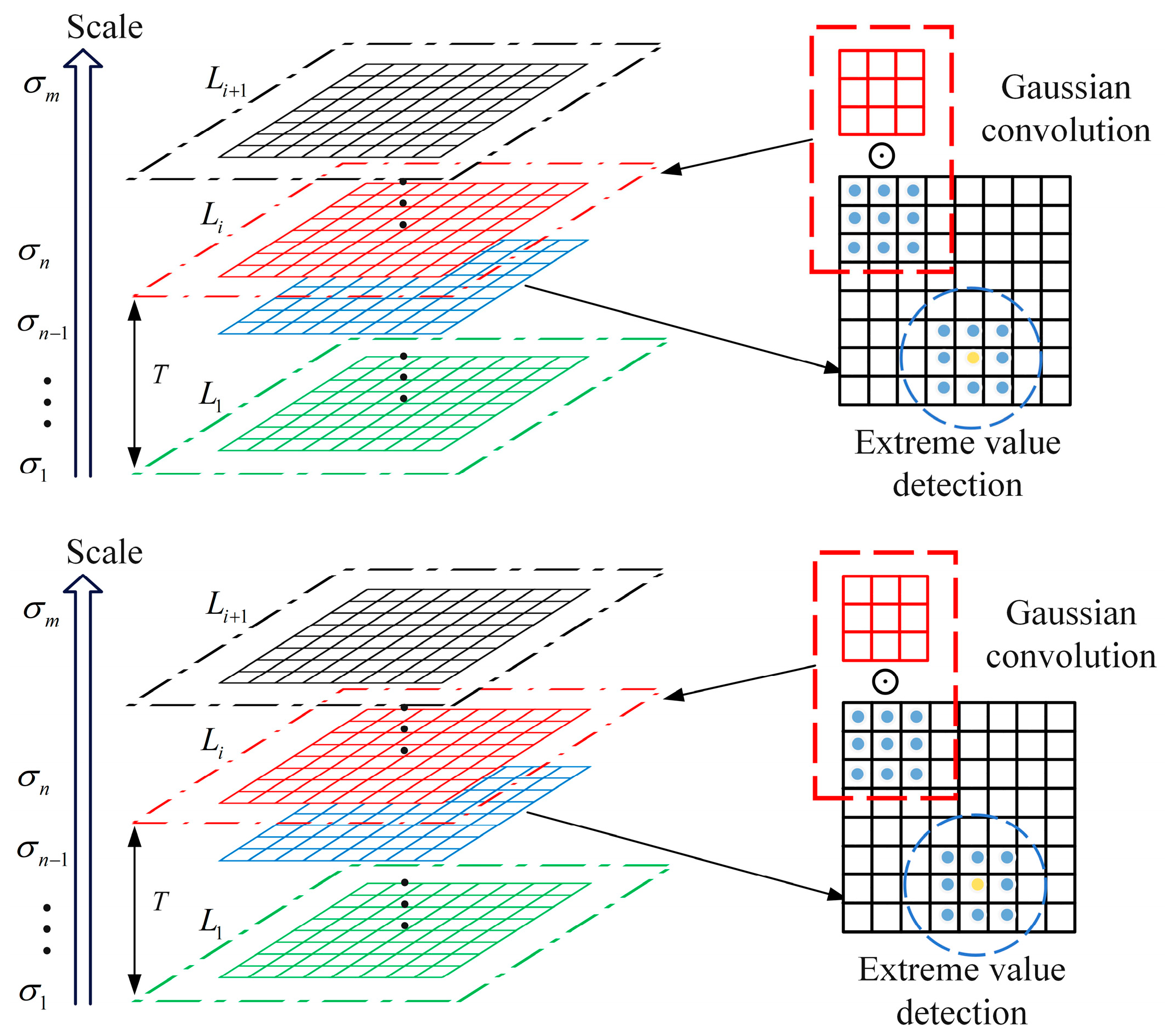
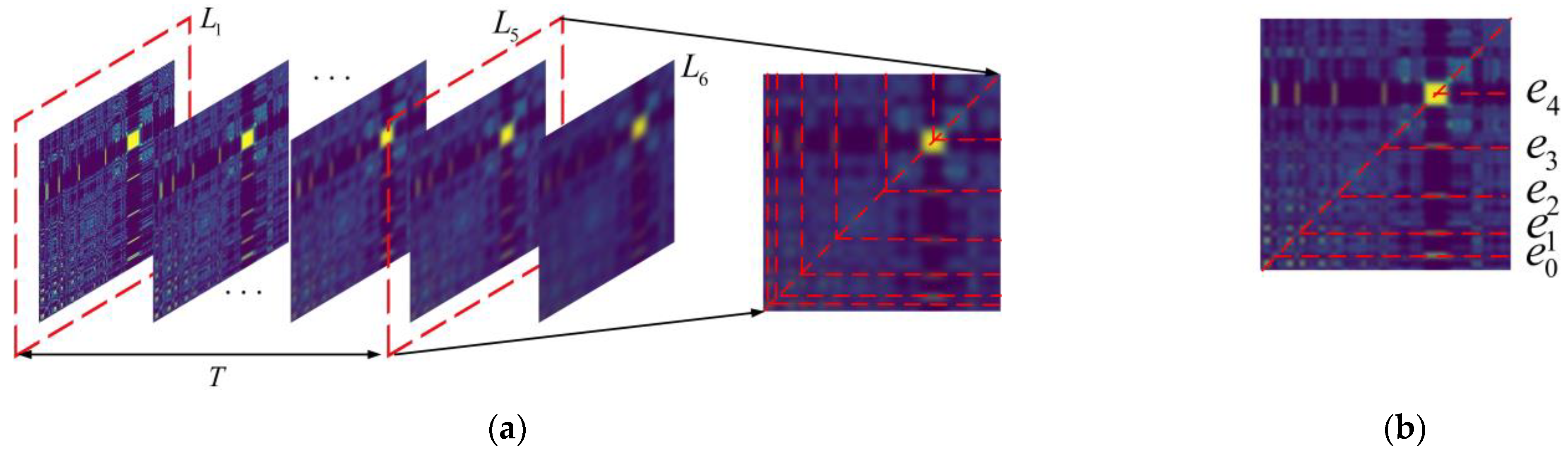
2.2. Electromagnetic Feature Scale Space
2.3. Adaptive Penalty Factor
3. Adaptive Scale-Space Mode Extraction
3.1. Parameters Selection
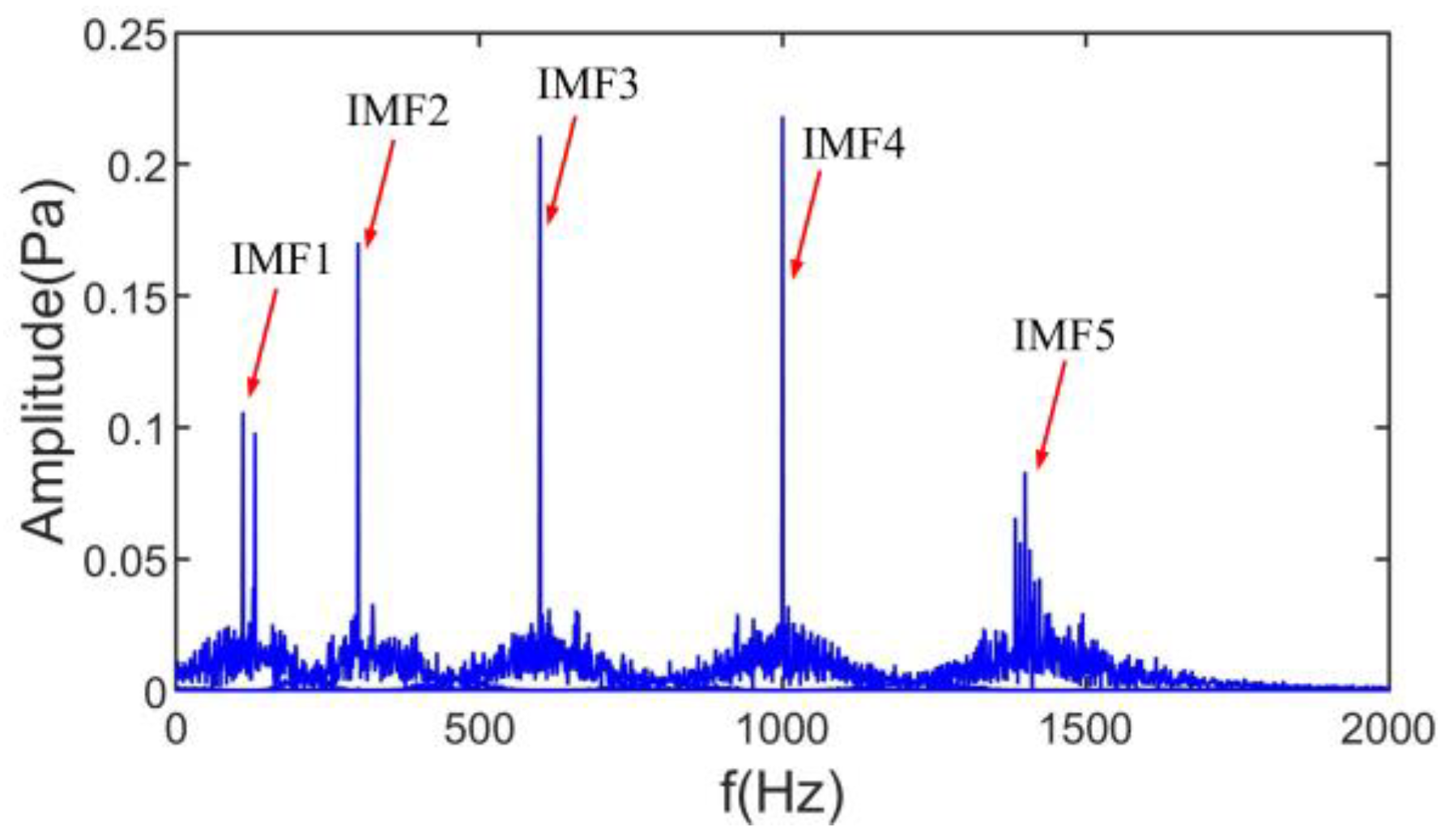
3.2. Simulation
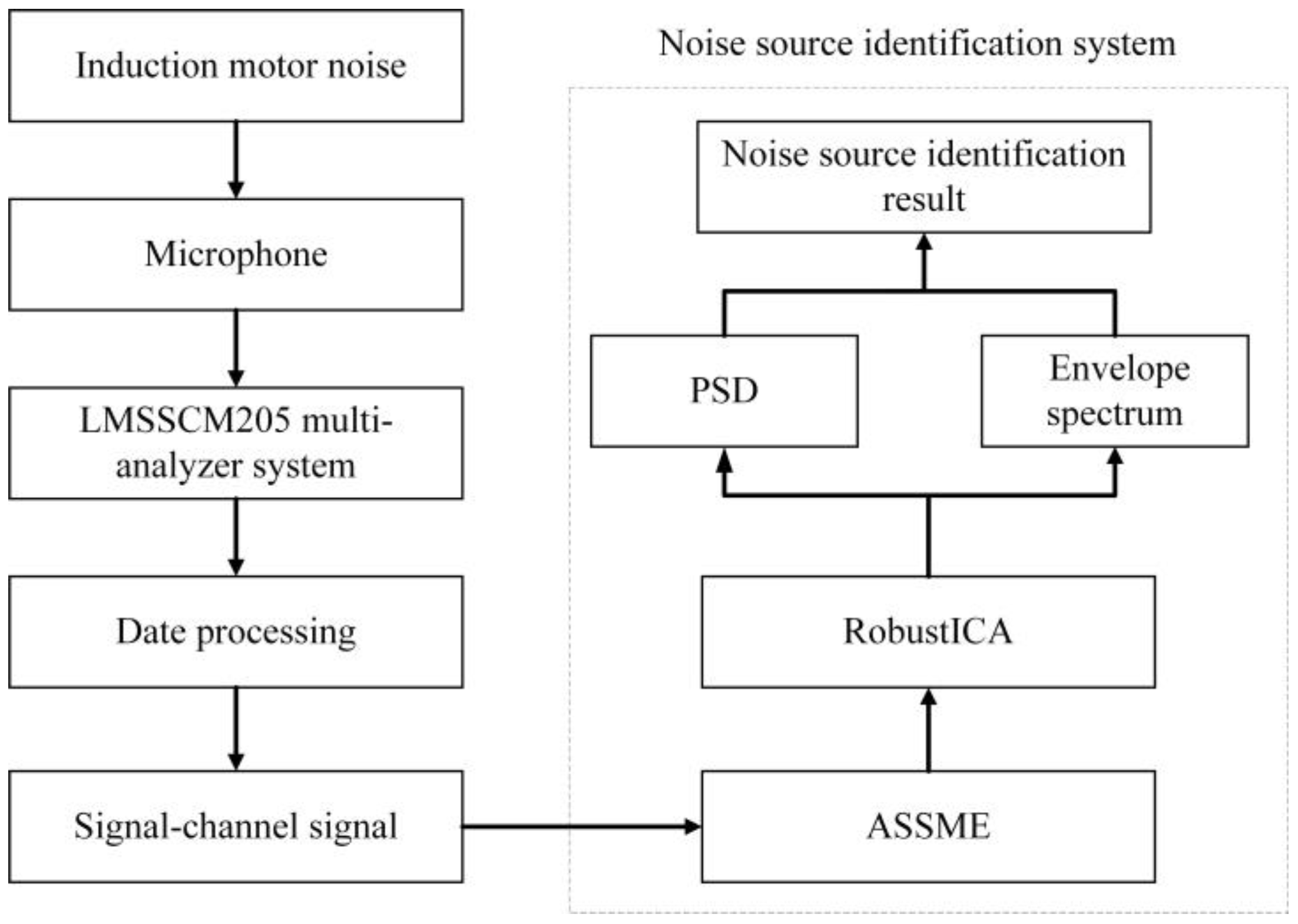
4. Separation and Identification of Induction Motor Noise Source
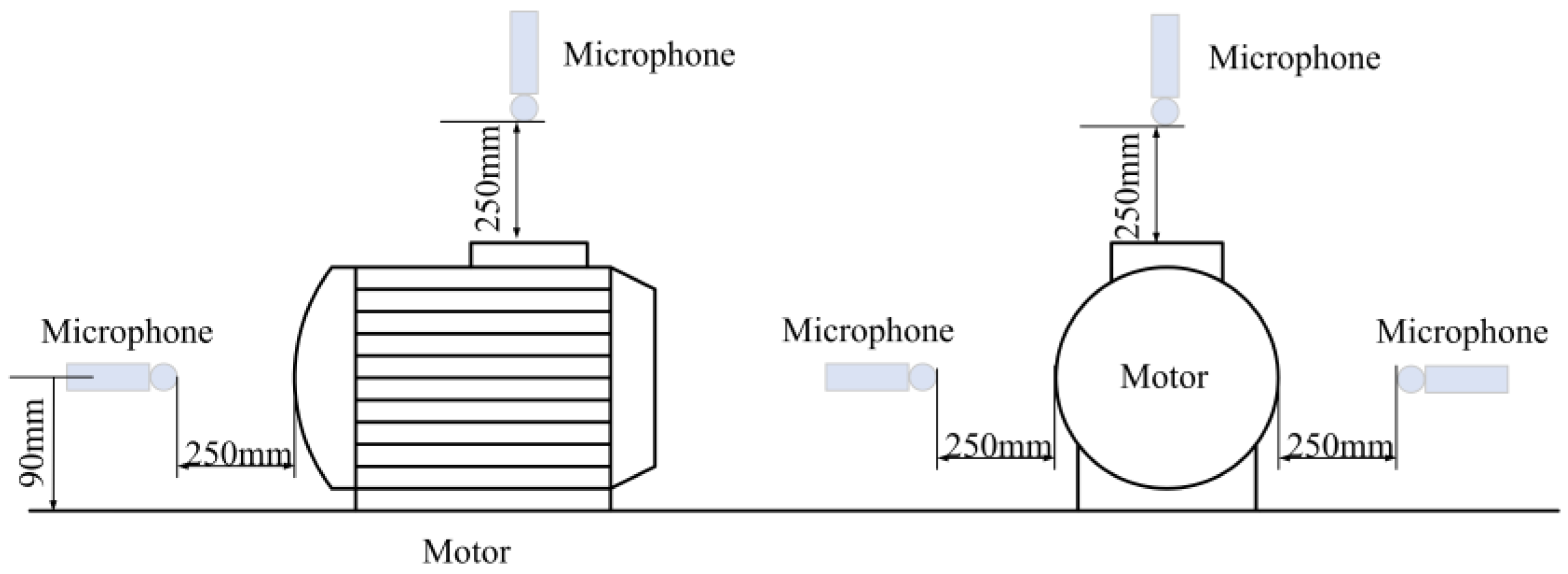
4.1. Tests and Datasets
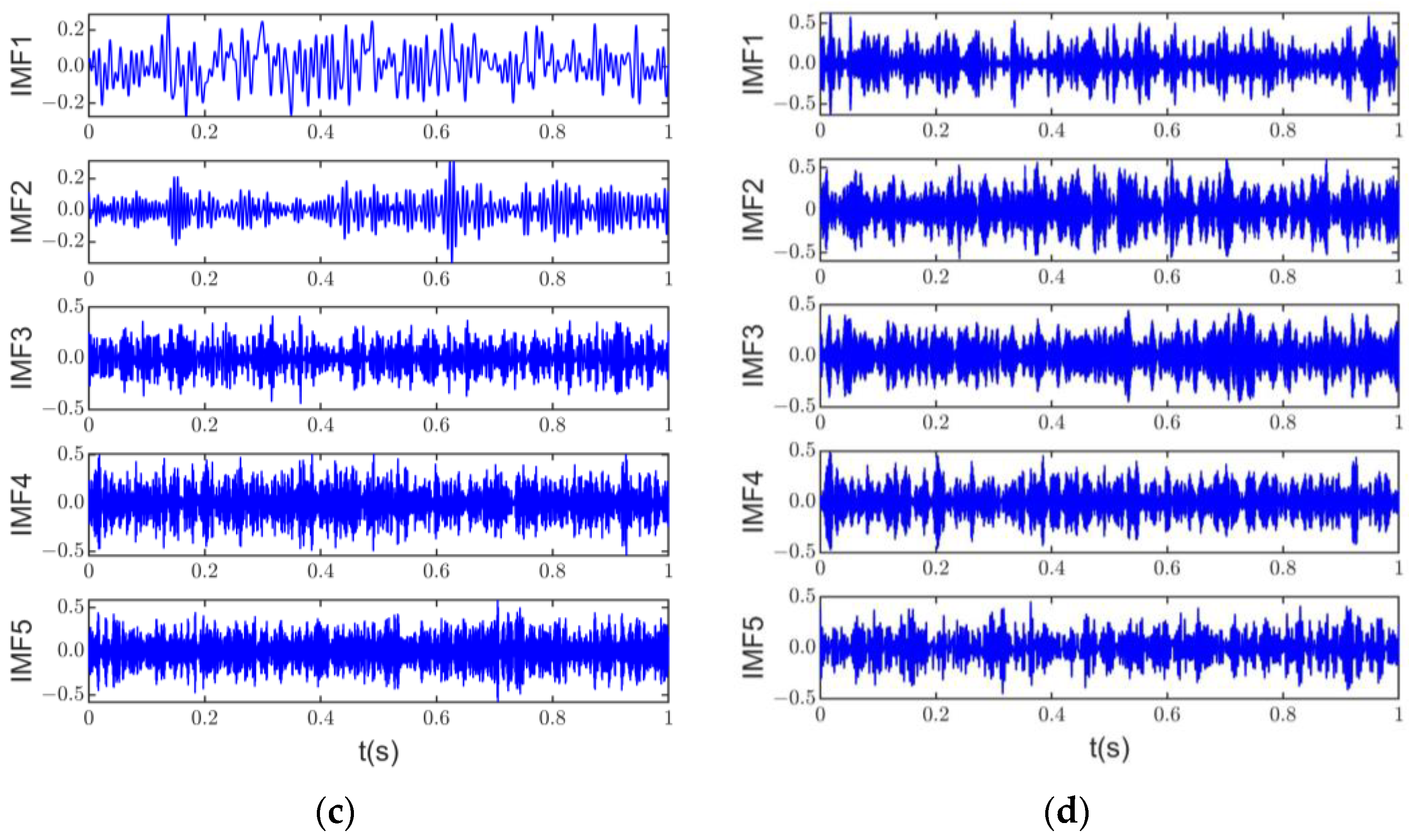
4.2. Date Processing
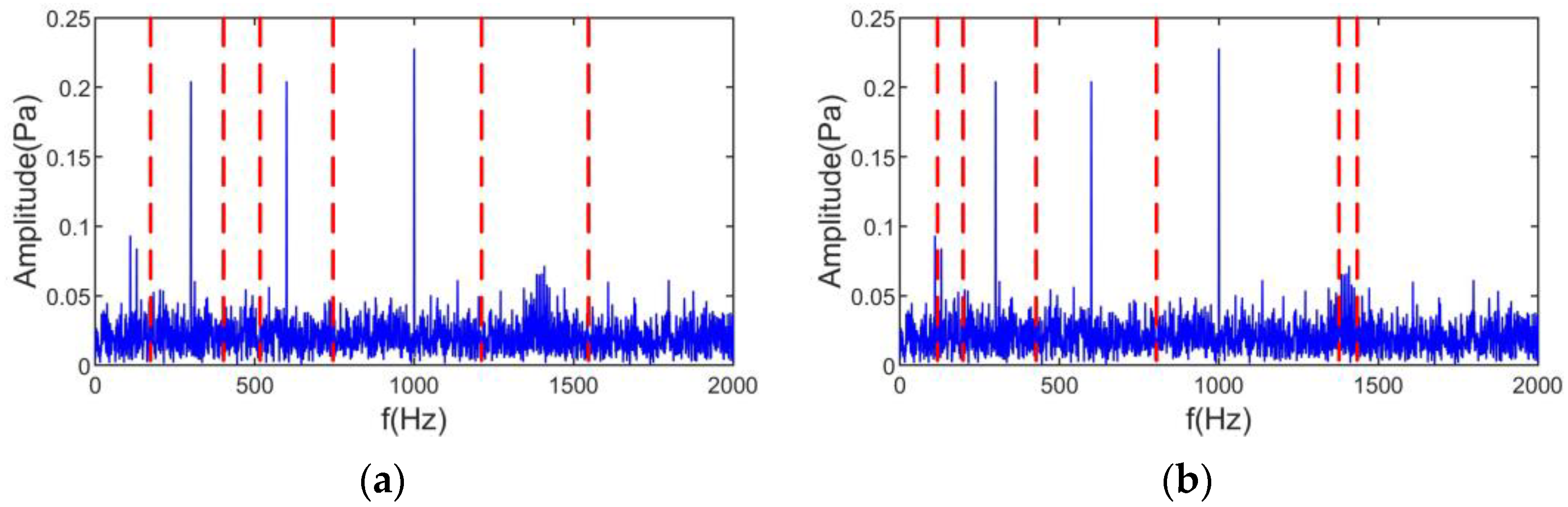
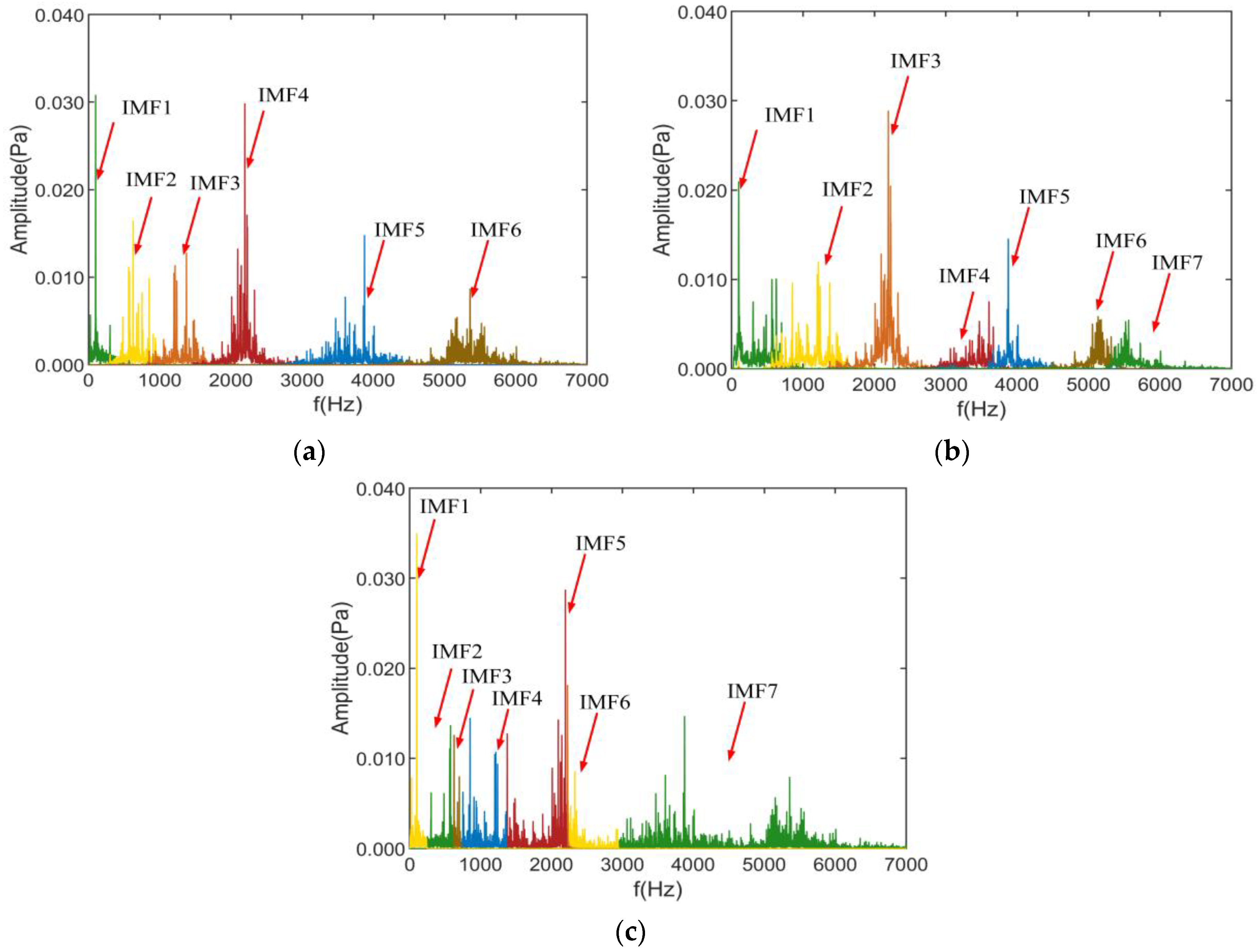
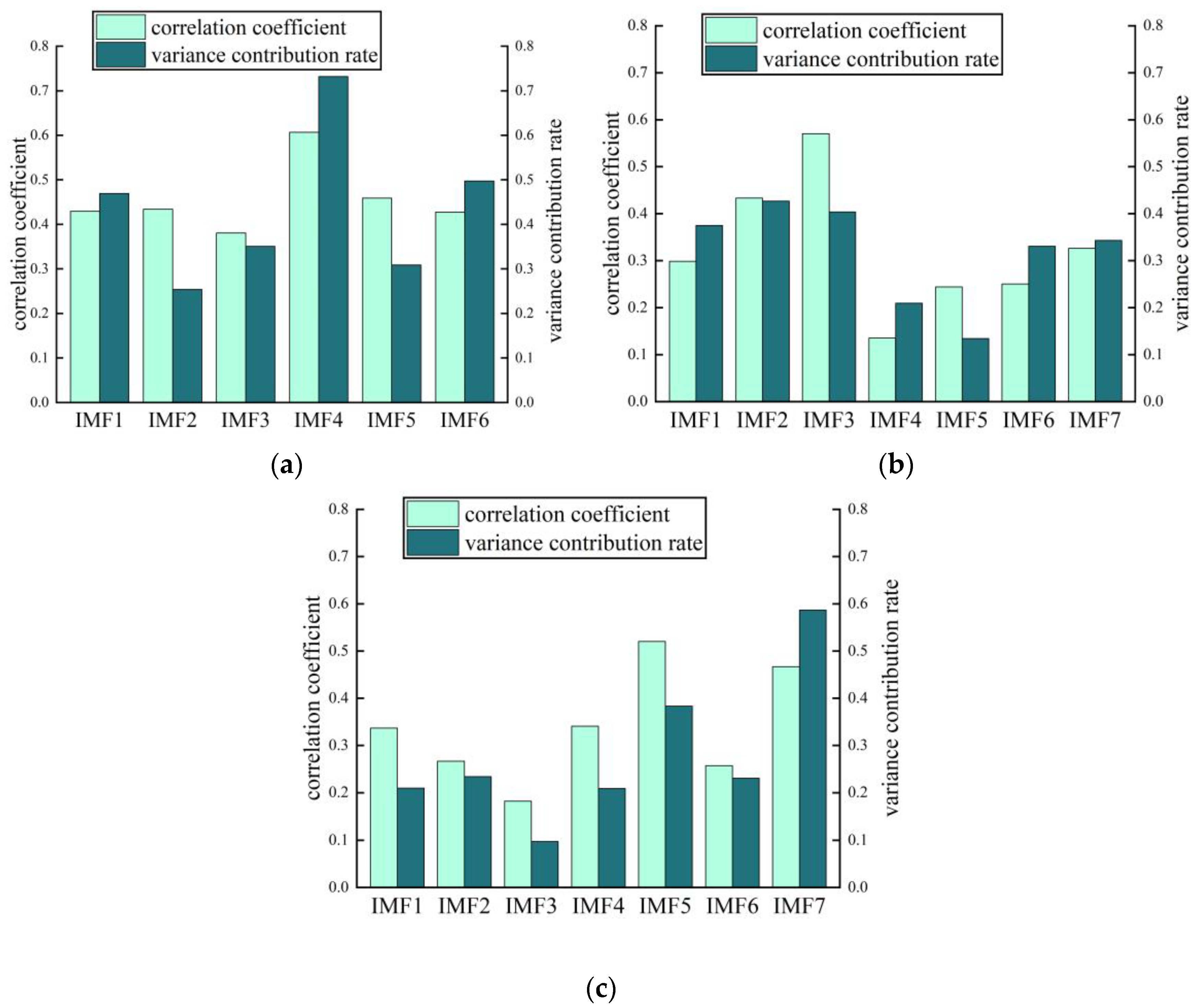
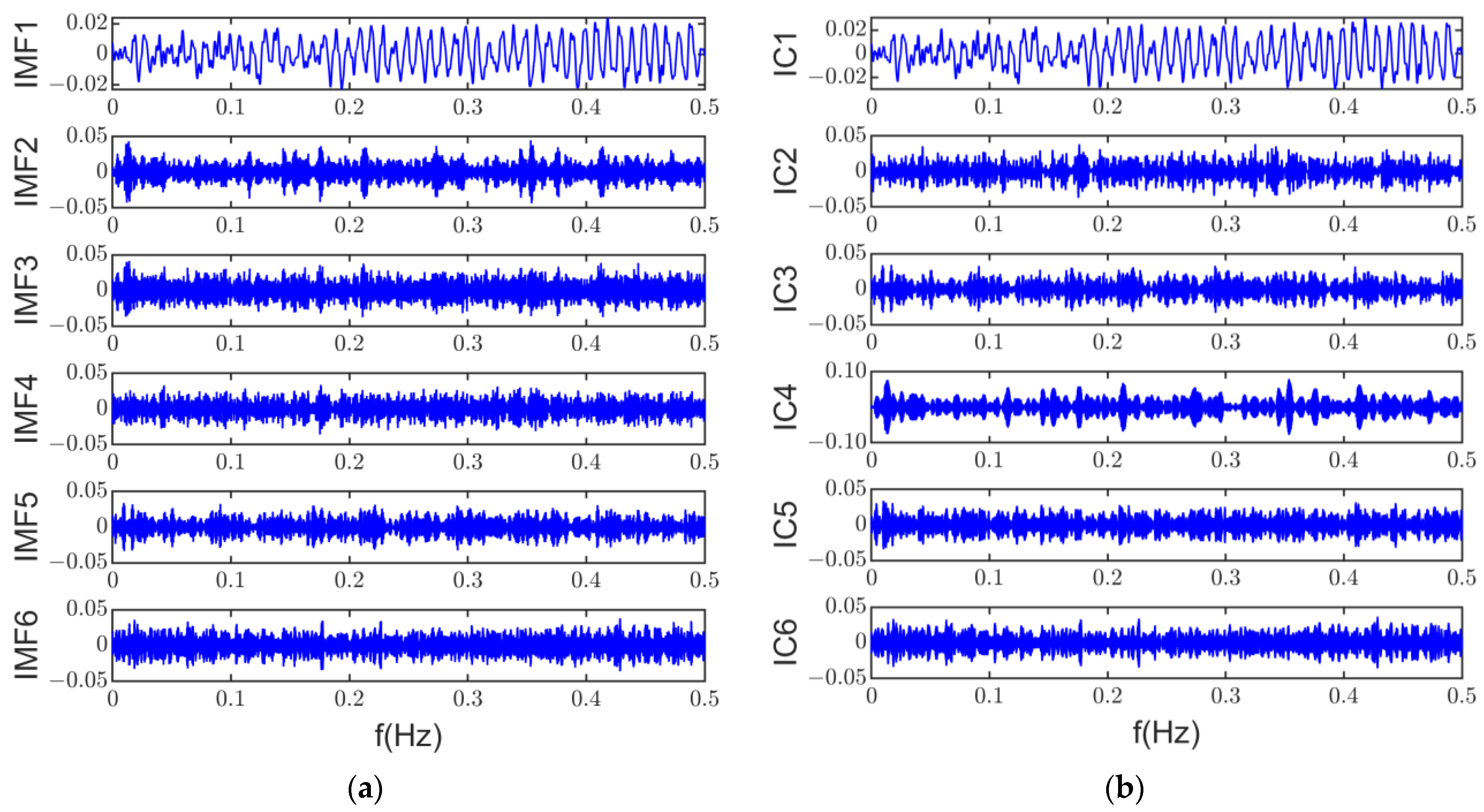
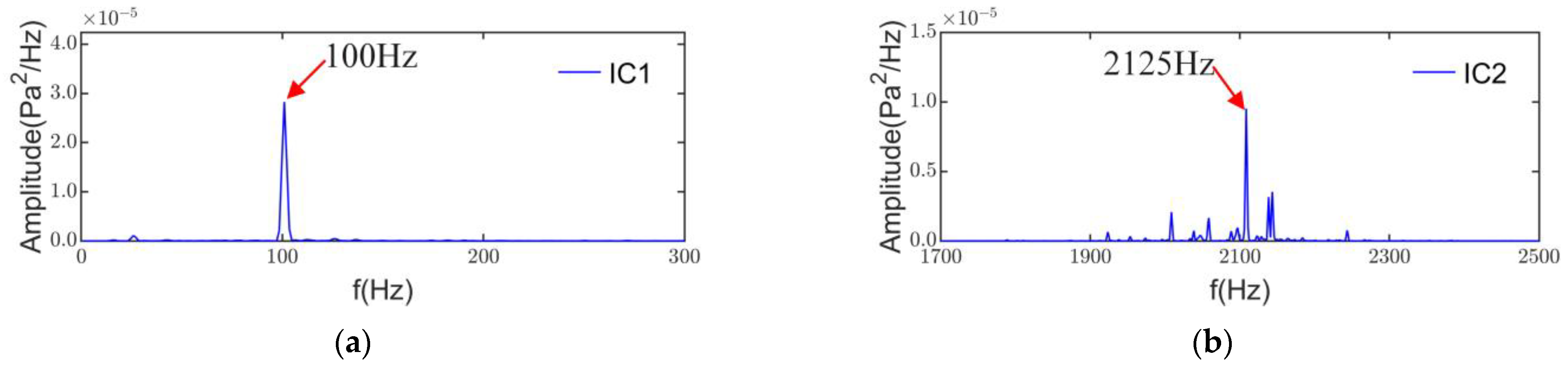
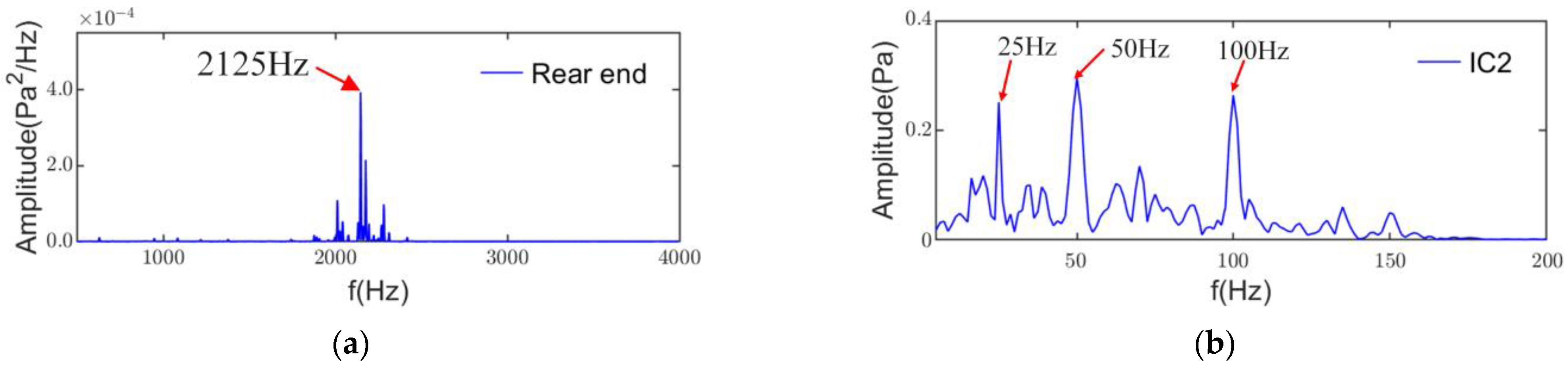
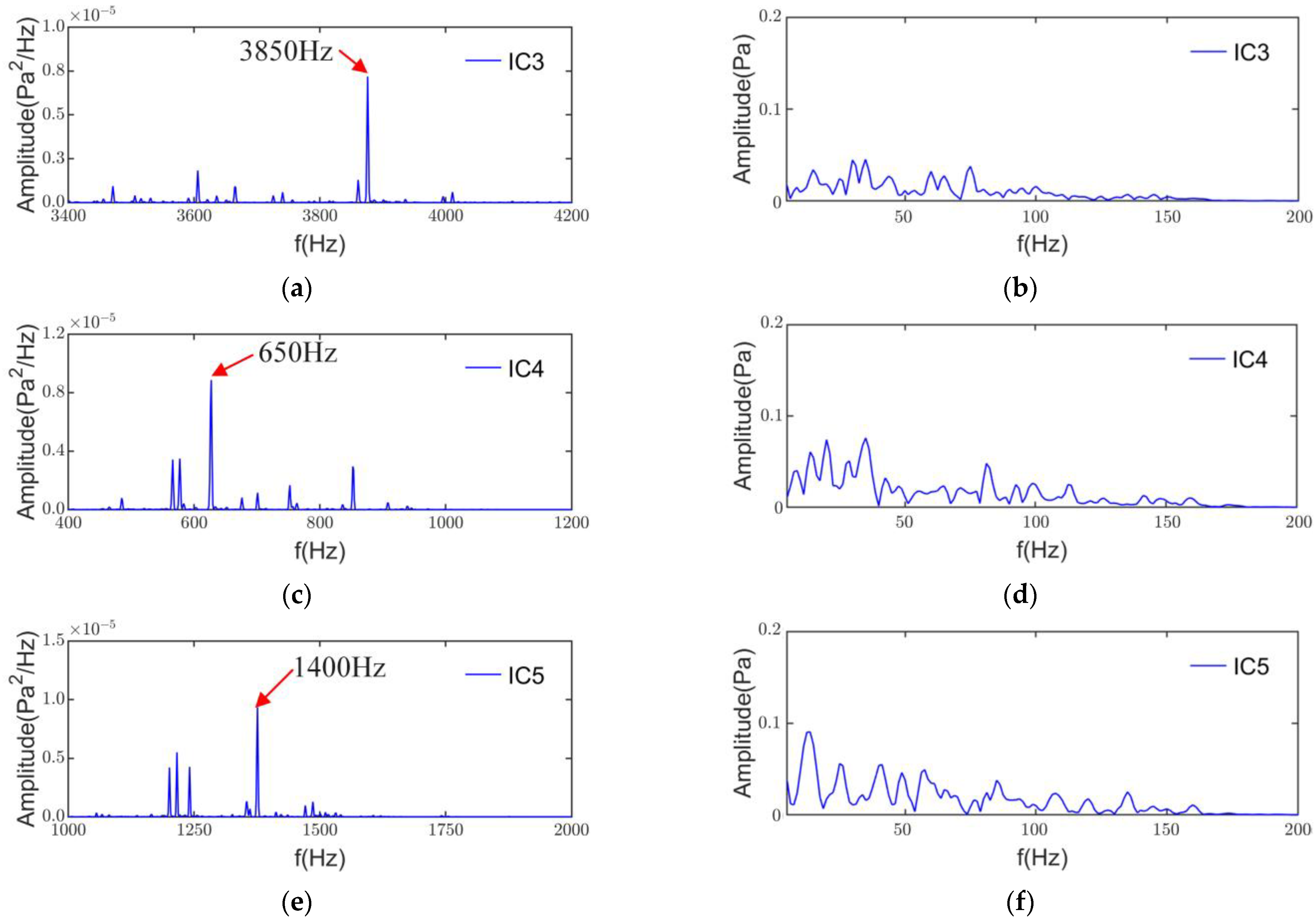
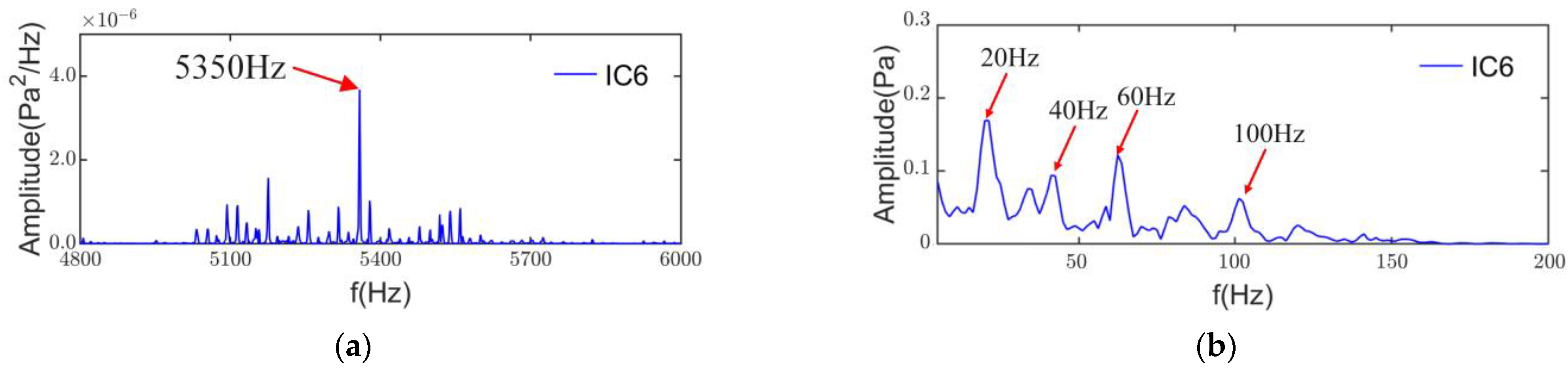
4.3. Noise Source Separation and Identification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gan, C.; Wu, J.H.; Sun, Q.G.; Kong, W.B.; Li, H.Y.; Hu, Y.H. A Review on Machine Topologies and Control Techniques for Low-Noise Switched Reluctance Motors in Electric Vehicle Applications. IEEE Access 2018, 6, 31430–31443. [Google Scholar] [CrossRef]
- Seshadri, A.; Lenin, N.C. Review based on losses, torque ripple, vibration and noise in switched reluctance motor. IET Electr. Power Appl. 2020, 14, 1311–1326. [Google Scholar] [CrossRef]
- Deng, W.; Zuo, S. Electromagnetic vibration and noise of the permanent-magnet synchronous motors for electric vehicles: An overview. IEEE Trans. Transp. Electrif. 2019, 5, 59–70. [Google Scholar] [CrossRef]
- Chu, N.; Liu, Q.; Yu, L.; Huang, Q.; Ning, Y.; Wu, D.Z.; Mohammad-Djafari, A.L. High-resolution localization of rotating acoustic sources: An experimental investigation and axial fan application. Measurement 2022, 196, 111149. [Google Scholar] [CrossRef]
- Wang, R.; Liu, T.; Zhang, C.Y.; Yu, L.; Li, J.Q. Noise source localization in permanent magnet synchronous motors under time-varying speed working conditions. Appl. Acoust. 2022, 192, 108724. [Google Scholar] [CrossRef]
- Verma, S.P.; Balan, A. Determination of radial-forces in relation to noise and vibration problems of squirrel-cage induction motors. IEEE Trans. Energy Convers. 1994, 9, 404–412. [Google Scholar] [CrossRef]
- Mao, Y.N.; Zhao, W.X.; Zhu, S.D.; Chen, Q.; Ji, J.H. Vibration Investigation of Spoke-Type PM Machine With Asymmetric Rotor Considering Modulation Effect of Stator Teeth. IEEE Trans. Ind. Electron. 2021, 68, 9092–9103. [Google Scholar] [CrossRef]
- Zhu, S.D.; Zhao, W.X.; Liu, G.H.; Mao, Y.X.; Sun, Y.H. Effect of Phase Shift Angle on Radial Force and Vibration Behavior in Dual Three-Phase PMSM. IEEE Trans. Ind. Electron. 2021, 68, 2988–2998. [Google Scholar] [CrossRef]
- Fang, H.Y.; Li, D.W.; Guo, J.X.; Xu, Y.S.; Qu, R.H. Hybrid Model for Electromagnetic Vibration Synthesis of Electrical Machines Considering Tooth Modulation and Tangential Effects. IEEE Trans. Ind. Electron. 2021, 68, 7284–7293. [Google Scholar] [CrossRef]
- Fang, H.Y.; Li, D.W.; Qu, R.H.; Yan, P. Modulation Effect of Slotted Structure on Vibration Response in Electrical Machines. IEEE Trans. Ind. Electron. 2019, 66, 2998–3007. [Google Scholar] [CrossRef]
- Wang, L.; Bao, X.H.; Di, C.; Zhou, Y. Influence on Vibration and Noise of Squirrel-Cage Induction Machine with Double Skewed Rotor for Different Slot Combinations. IEEE Trans. Magn. 2016, 52, 7000804. [Google Scholar] [CrossRef]
- Chai, F.; Li, Y.; Pei, Y.L.; Yu, Y.J. Analysis of Radial Vibration Caused by Magnetic Force and Torque Pulsation in Interior Permanent Magnet Synchronous Motors Considering Ai-Gap Deformations. IEEE Trans. Ind. Electron. 2019, 66, 6703–6714. [Google Scholar] [CrossRef]
- Huang, N.; Long, S.; Wu, M.; Shih, H.H.; Zheng, Q.; Yen, N.; Tung, C.; Liu, H.; Shen, Z. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Society. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Mourad, N. Automatic correction of eye blink artifact in single channel EEG recording using EMD and OMP. In Proceedings of the Signal Processing Conference, Lisbon, Portugal, 1–5 September 2014. [Google Scholar]
- Deng, X.; Pang, L.; Jiang, K.; Wang, X. Single-channel blind signal separation method for time-frequency overlapped signal based on CEEMD-FastICA. In Proceedings of the 2016 IEEE 13th International Conference on Signal Processing (ICSP), Chengdu, China, 6–10 November 2016. [Google Scholar]
- Du, X.F.; Li, Z.J.; Bi, F.R.; Zhang, J.H.; Wang, X.; Shao, K. Source Separation of Diesel Engine Vibration Based on the Empirical Mode Decomposition and Independent Component Analysis. Chin. J. Mech. Eng. 2012, 25, 557–563. [Google Scholar] [CrossRef]
- Jiang, H.K.; Li, C.L.; Li, H.X. An improved EEMD with multiwavelet packet for rotating machinery multi-fault diagnosis. Mech. Syst. Signal Process. 2013, 36, 225–239. [Google Scholar] [CrossRef]
- Smith, J.S. The local mean decomposition and its application to EEG perception data. J. R. Soc. Interface 2005, 2, 443–454. [Google Scholar] [CrossRef]
- Bi, F.R.; Li, L.; Zhang, J.; Ma, T. Source identification of gasoline engine noise based on continuous wavelet transform and EEMD-RobustICA. Appl. Acoust. 2015, 100, 34–42. [Google Scholar] [CrossRef]
- Yao, J.C.; Xiang, Y.; Qian, S.C.; Wang, S.; Wu, S.W. Noise source identification of diesel engine based on variational mode decomposition and robust independent component analysis. Appl. Acoust. 2017, 116, 184–194. [Google Scholar] [CrossRef]
- Zhou, Q.D.; Zhang, J.H.; Zhou, T.Y.; Qiu, Y.B.; Jia, H.J.; Lin, J.W. A parameter-adaptive variational mode decomposition approach based on weighted fuzzy-distribution entropy for noise source separation. Meas. Sci. Technol. 2020, 31, 125004. [Google Scholar] [CrossRef]
- Yang, Z.X.; Rong, H.J.; Wong, P.K.; Angelov, P.; Vong, C.M.; Chiu, C.W.; Yang, Z.X. A Novel Multiple Feature-Based Engine Knock Detection System using Sparse Bayesian Extreme Learning Machine. Cogn. Comput. 2022, 14, 828–851. [Google Scholar] [CrossRef]
- Xin, Y.; Li, S.M.; Zhang, Z.Z. Adaptive Reinforced Empirical Morlet Wavelet Transform and Its Application in Fault Diagnosis of Rotating Machinery. IEEE Access 2019, 7, 65150–65162. [Google Scholar] [CrossRef]
- Liu, Z.C.; Ding, J.M.; Lin, J.H.; Huang, Y. A Rolling Bearing Fault Diagnosis-Optimized Scale-Space Representation for the Empirical Wavelet Transform. Shock. Vib. 2018, 2018, 2749689. [Google Scholar] [CrossRef]
- Ma, J.; Wu, J.D.; Wang, X.D. Incipient fault feature extraction of rolling bearings based on the MVMD and Teager energy operator. ISA Trans. 2018, 80, 297–311. [Google Scholar] [CrossRef]
- Huang, Y.; Lin, J.H.; Liu, Z.C.; Wu, W.Y. A modified scale-space guiding variational mode decomposition for high-speed railway bearing fault diagnosis. J. Sound Vib. 2019, 444, 216–234. [Google Scholar] [CrossRef]
- Wang, Z.J.; Yang, N.N.; Li, N.P.; Du, W.H.; Wang, J.Y. A new fault diagnosis method based on adaptive spectrum mode extraction. Struct. Health Monit. Int. J. 2021, 20, 3354–3370. [Google Scholar] [CrossRef]
- Wang, M.J.; Wang, W.J.; Zhang, X.N.; Iu, H.H.C. A New Fault Diagnosis of Rolling Bearing Based on Markov Transition Field and CNN. Entropy 2022, 24, 751. [Google Scholar] [CrossRef] [PubMed]
- Lempel, A.; Ziv, J. A universal algorithm for sequential data compression. IEEE Trans. Inf. Theory 1977, 23, 337–343. [Google Scholar]
- Cormack, G.V.; Horspool, R. Data Compression Using Dynamic Markov Modelling. Comput. J. 1987, 30, 541–550. [Google Scholar] [CrossRef]
- Gilles, J.; Heal, K. A parameterless scale-space approach to find meaningful modes in histograms—Application to image and spectrum segmentation. Int. J. Wavelets Multiresolution Inf. Process. 2014, 12, 1450044. [Google Scholar] [CrossRef]
- Al-khafaji, S.L.; Zhou, J.; Zia, A.; Liew, A.W.C. Spectral-Spatial Scale Invariant Feature Transform for Hyperspectral Images. IEEE Trans. Image Process. 2018, 27, 837–850. [Google Scholar] [CrossRef]
- Zhang, W.N. Combination of SIFT and Canny Edge Detection for Registration Between SAR and Optical Images. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4007205. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]



| Characteristics | Parameter |
|---|---|
| pole pair (p) | 2 |
| Number of stator/rotor slots (z1/z2) | 24/30 |
| Power supply frequency (fc) | 50 [Hz] |
| Power supply method | PWM |
| Carrier frequency (fs) | 5.2 [KHz] |
| No-load speed | 1500 [rpm] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Gu, Y.; Chen, C.; Wang, L.; Sun, X. Induction Motor Noise Source Separation and Identification Based on Adaptive Scale-Space Mode Extraction. Machines 2023, 11, 449. https://doi.org/10.3390/machines11040449
Wang Z, Gu Y, Chen C, Wang L, Sun X. Induction Motor Noise Source Separation and Identification Based on Adaptive Scale-Space Mode Extraction. Machines. 2023; 11(4):449. https://doi.org/10.3390/machines11040449
Chicago/Turabian StyleWang, Zhengqi, Yanling Gu, Changzheng Chen, Lipeng Wang, and Xianming Sun. 2023. "Induction Motor Noise Source Separation and Identification Based on Adaptive Scale-Space Mode Extraction" Machines 11, no. 4: 449. https://doi.org/10.3390/machines11040449
APA StyleWang, Z., Gu, Y., Chen, C., Wang, L., & Sun, X. (2023). Induction Motor Noise Source Separation and Identification Based on Adaptive Scale-Space Mode Extraction. Machines, 11(4), 449. https://doi.org/10.3390/machines11040449





