Design and Control of an Energy-Efficient Speed Regulating Method for Pump-Controlled Motor System under Negative Loads
Abstract
1. Introduction
2. System Formulation
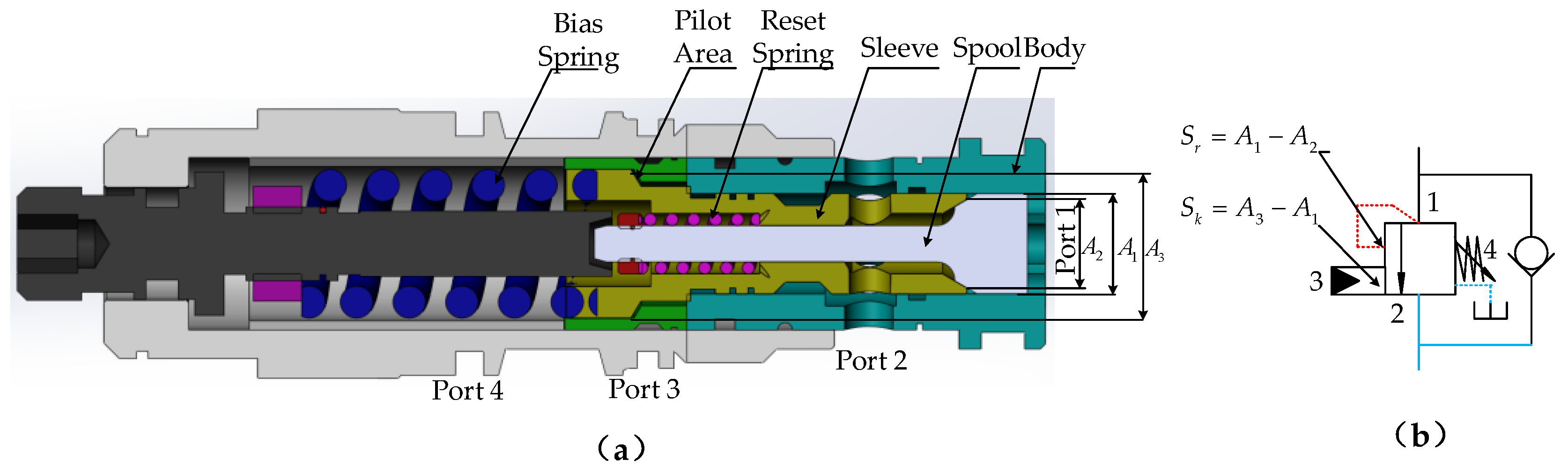
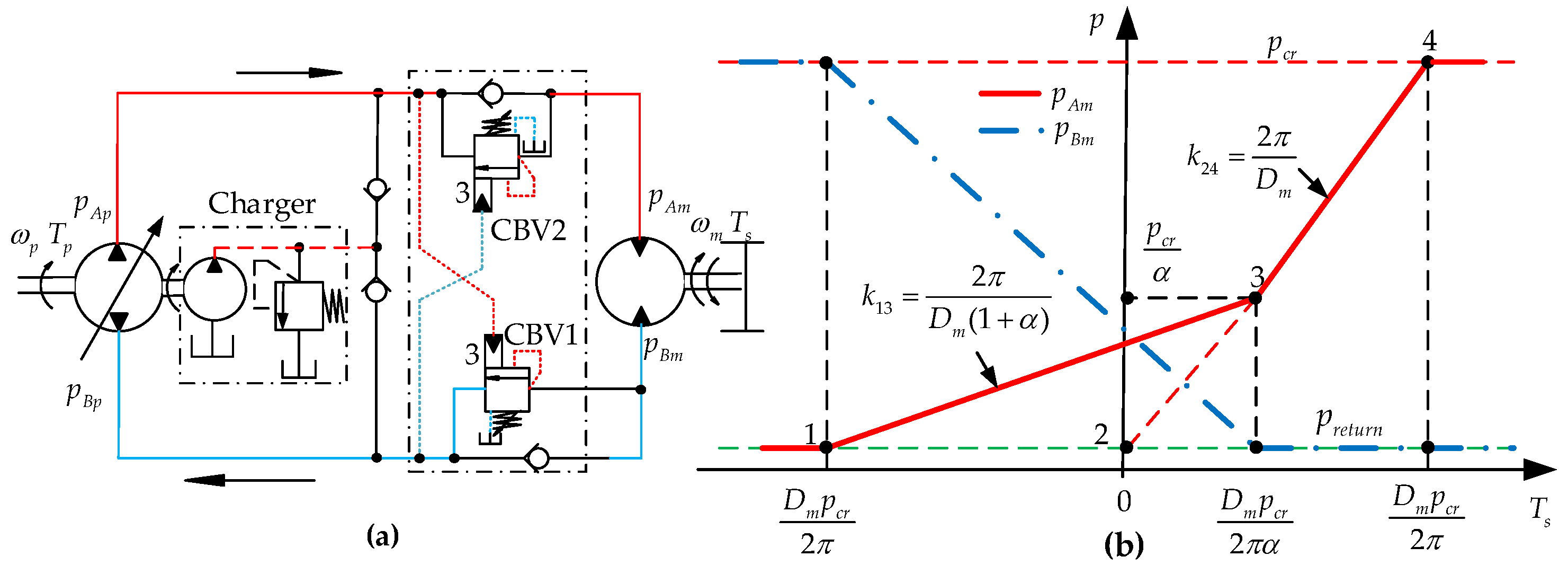
2.1. Typical Configuration with CBV
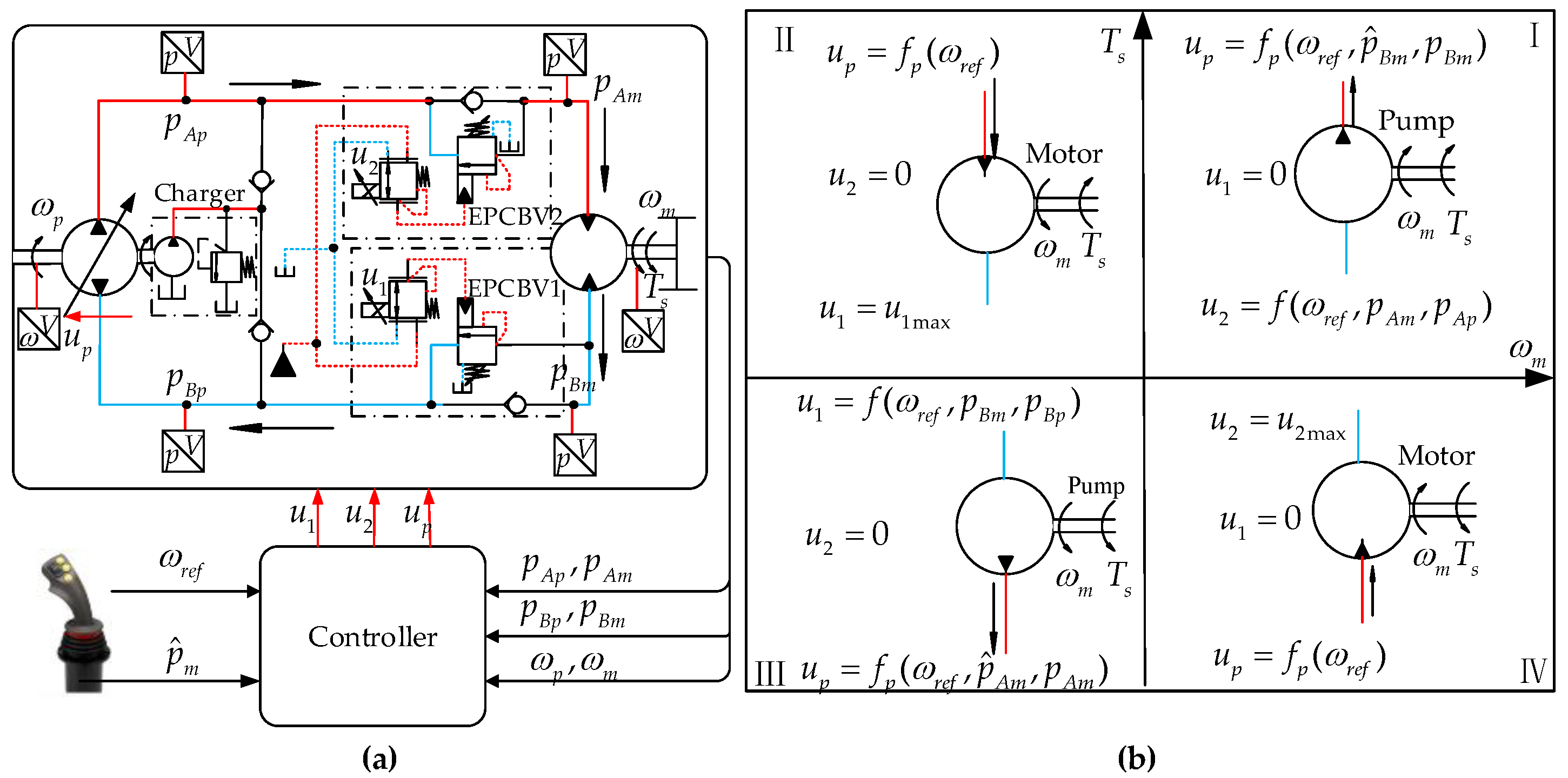
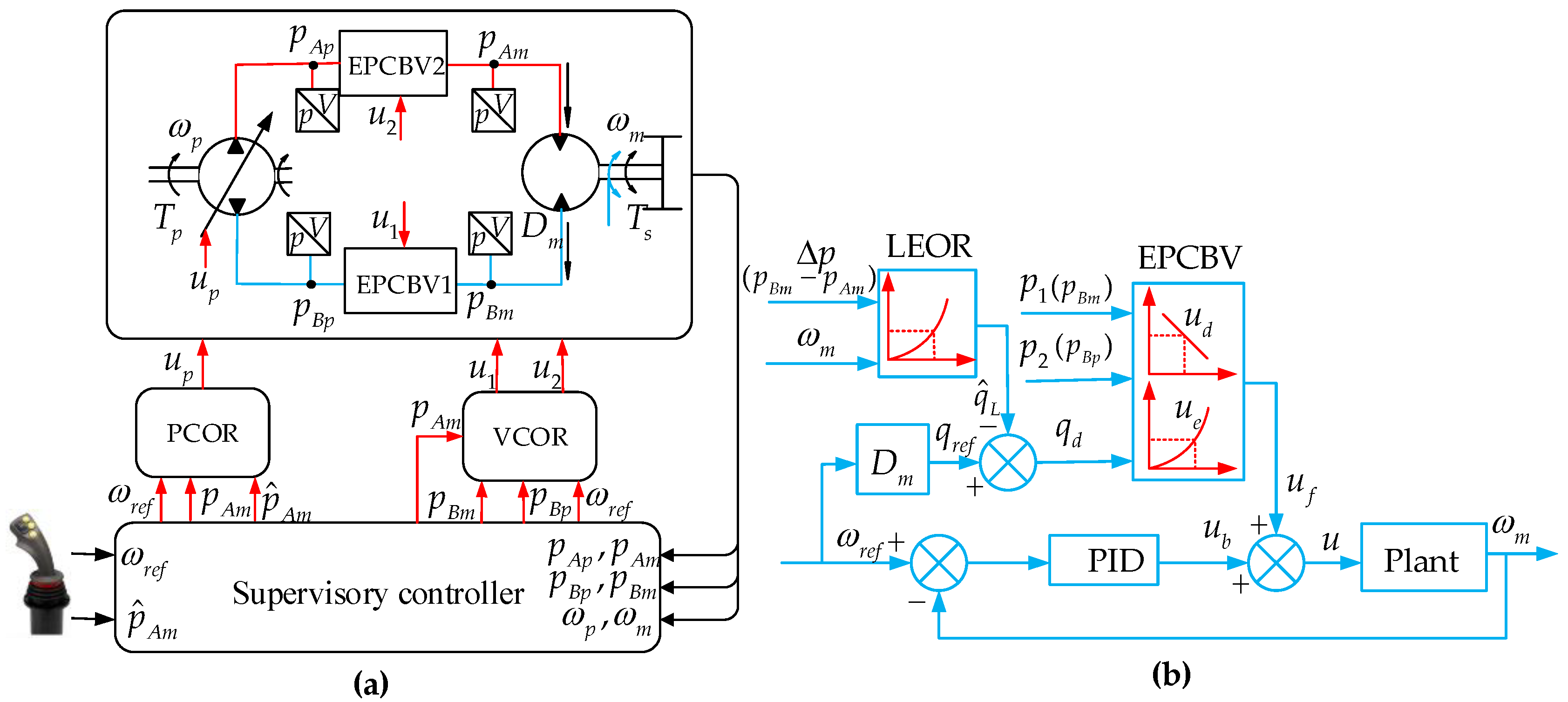
2.2. Principle of the Proposed Scheme Based on EPCBV
3. System Modelling
3.1. Model of PCMH System
3.2. Flow Model of EPCBV
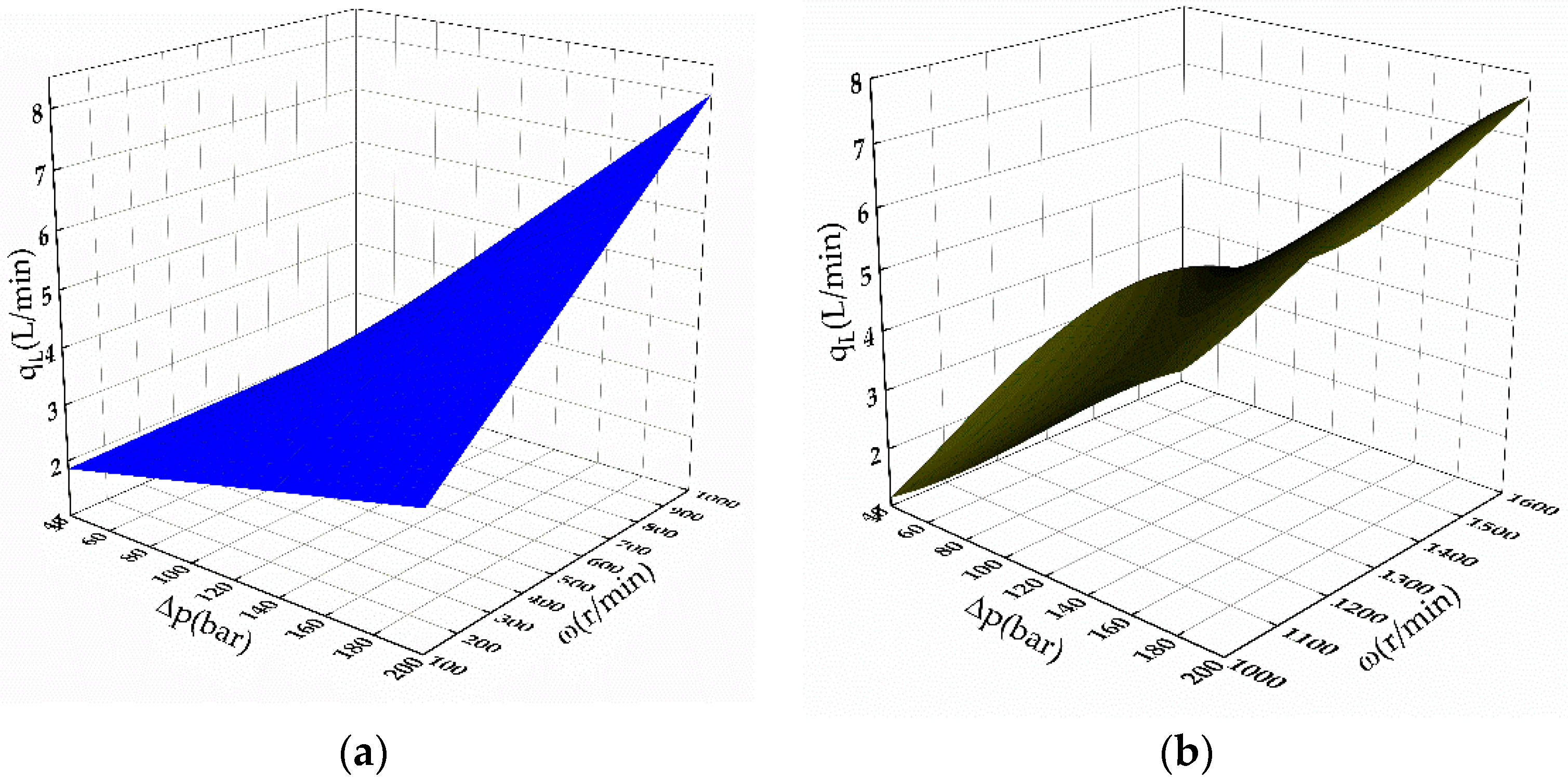
3.3. Motor Leakage Estimator (LEOR)
4. Controller Design
4.1. Supervisory Controller
4.2. Velocity Controller (VCOR)
4.2.1. Feedforward Control
4.2.2. Feedback Control
4.3. Pressure Control (PCOR)
5. Experimental Investigation
5.1. Test Bench Setup
5.2. Experimental Programs
5.2.1. T-CBV System
5.2.2. EPCBV System
5.3. Experimental Results Analysis
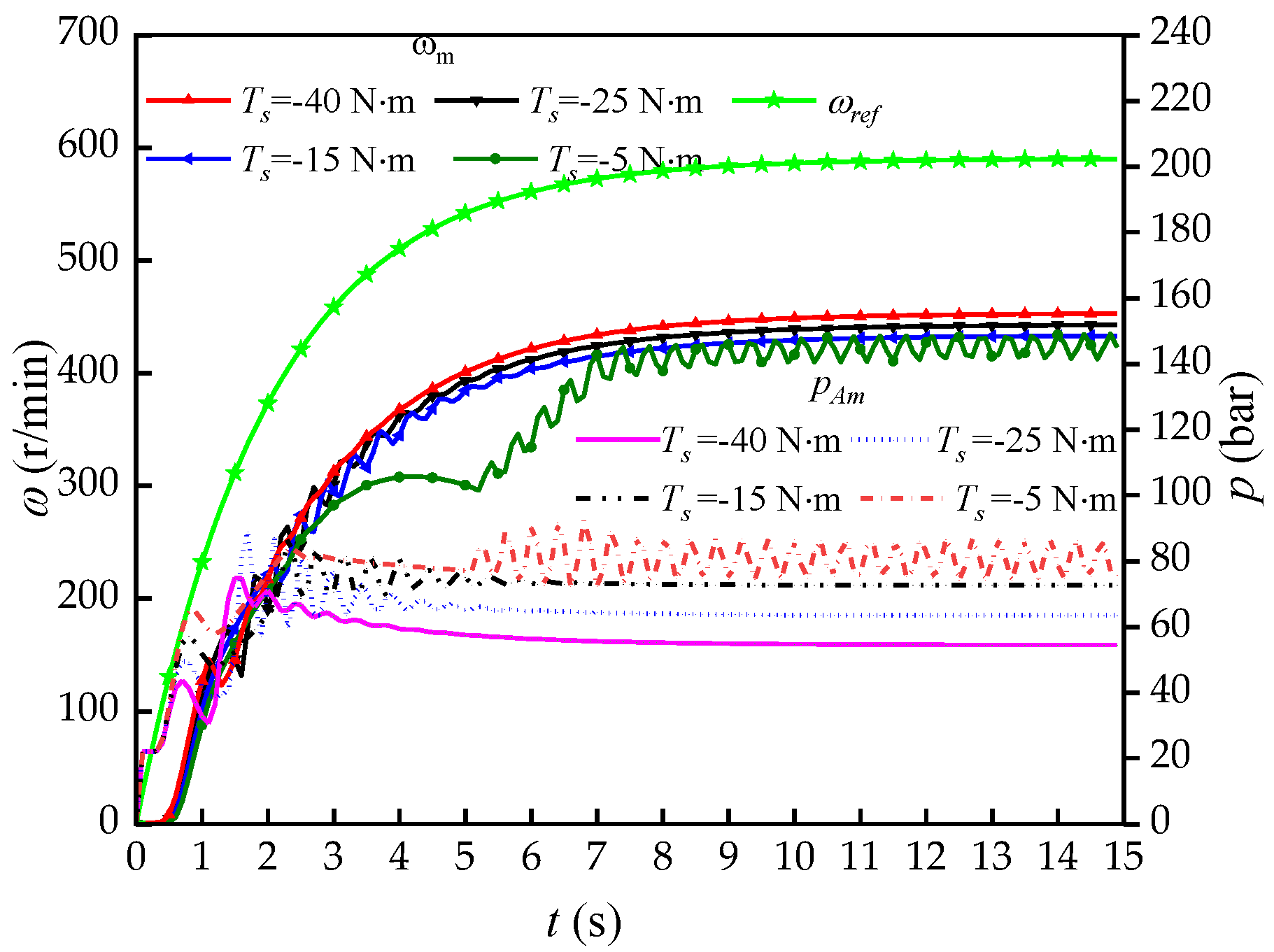
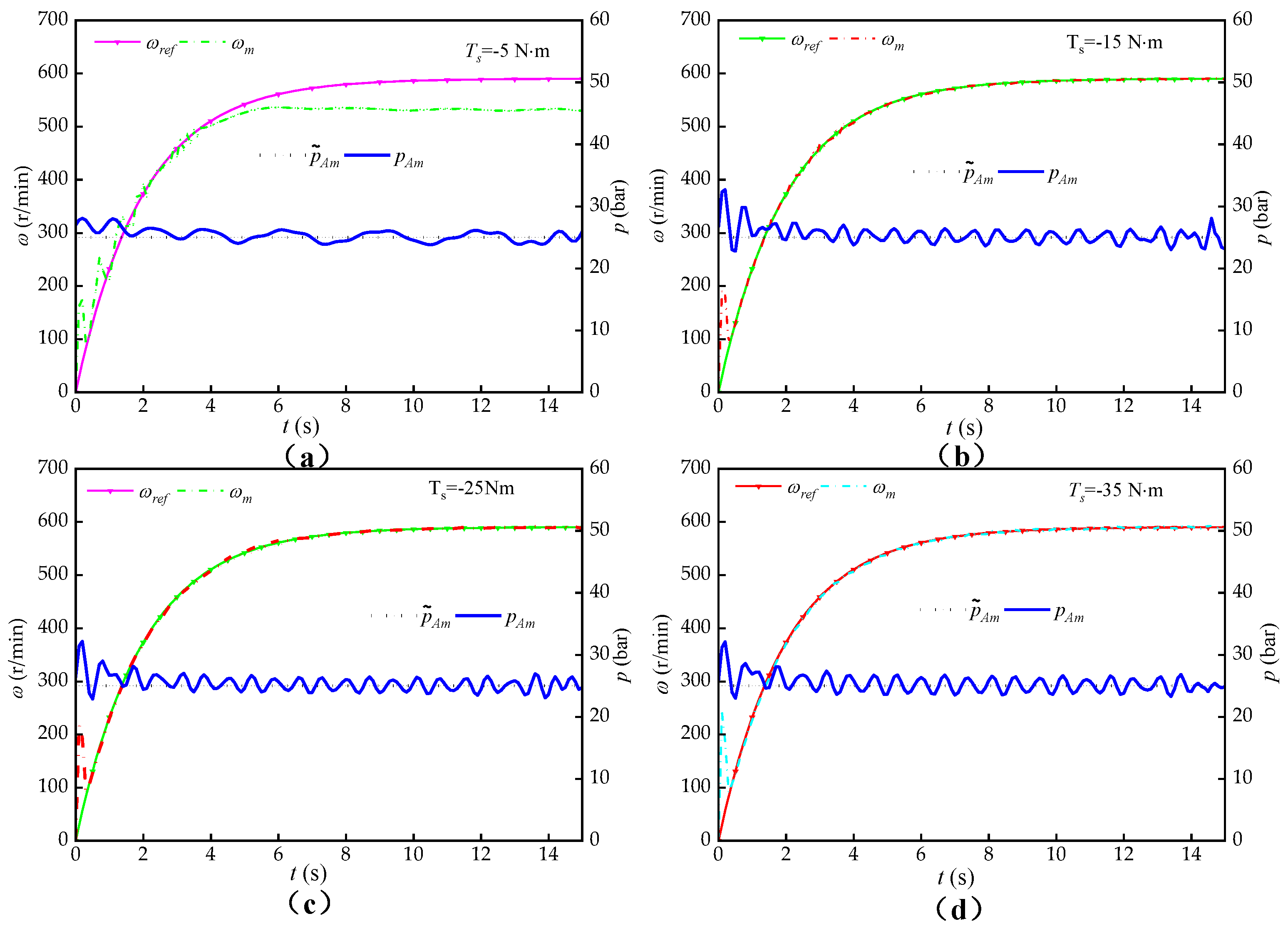
5.3.1. Stability Analysis
5.3.2. Accuracy Analysis
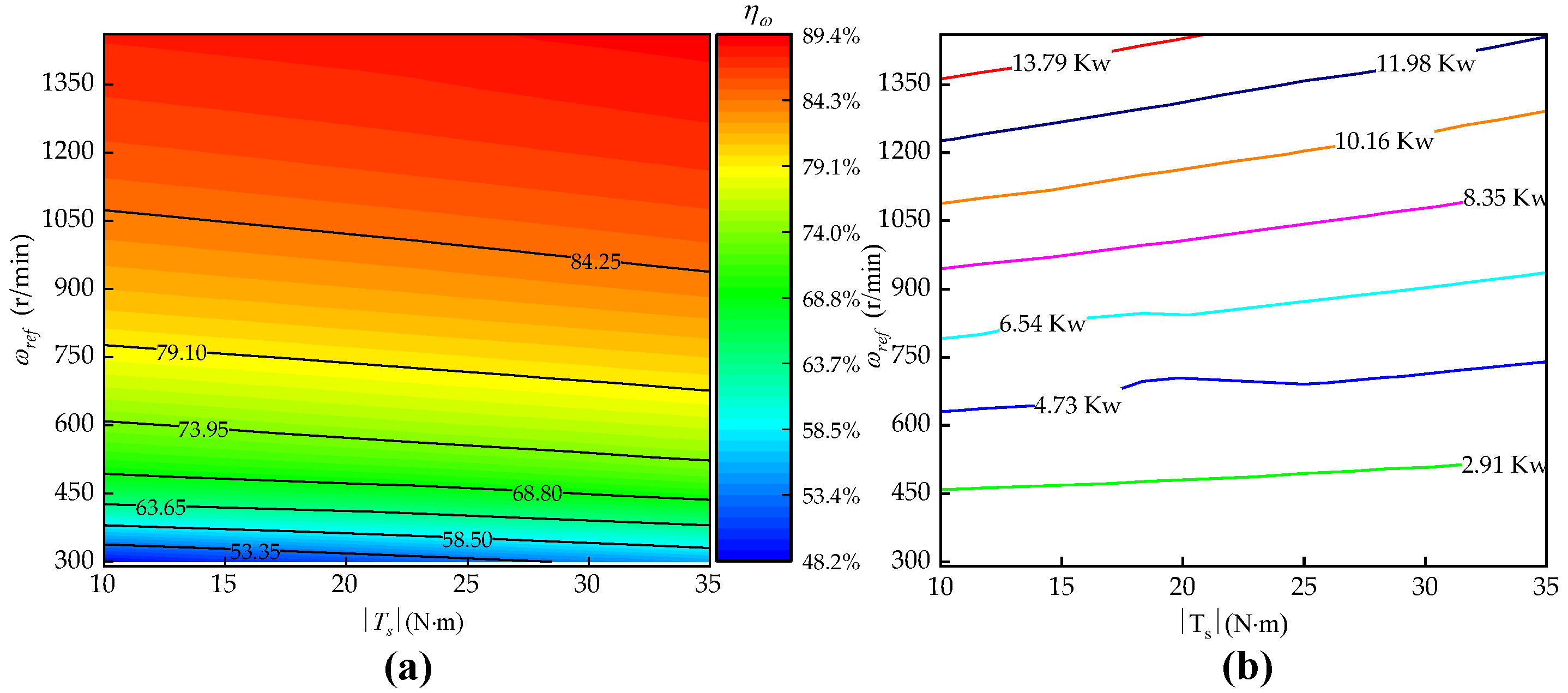
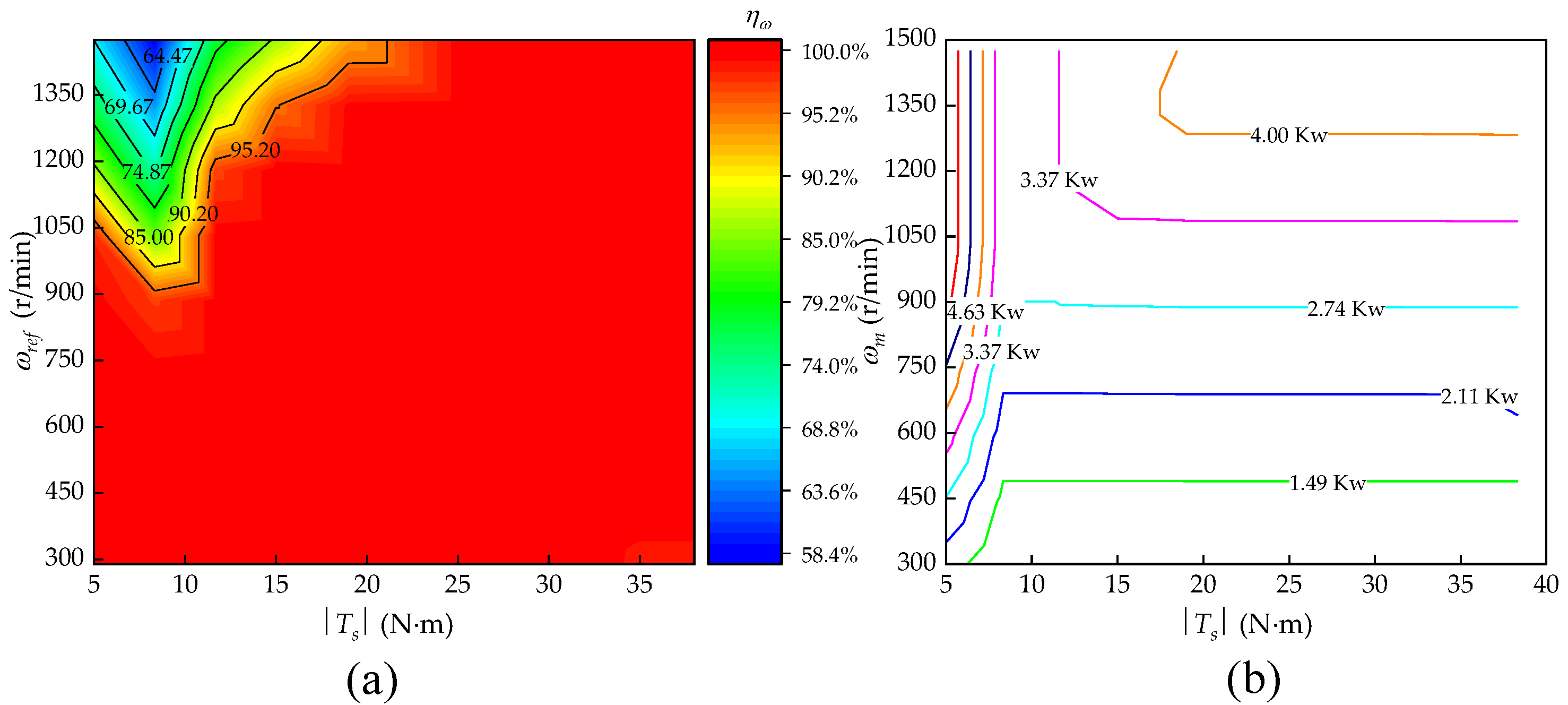
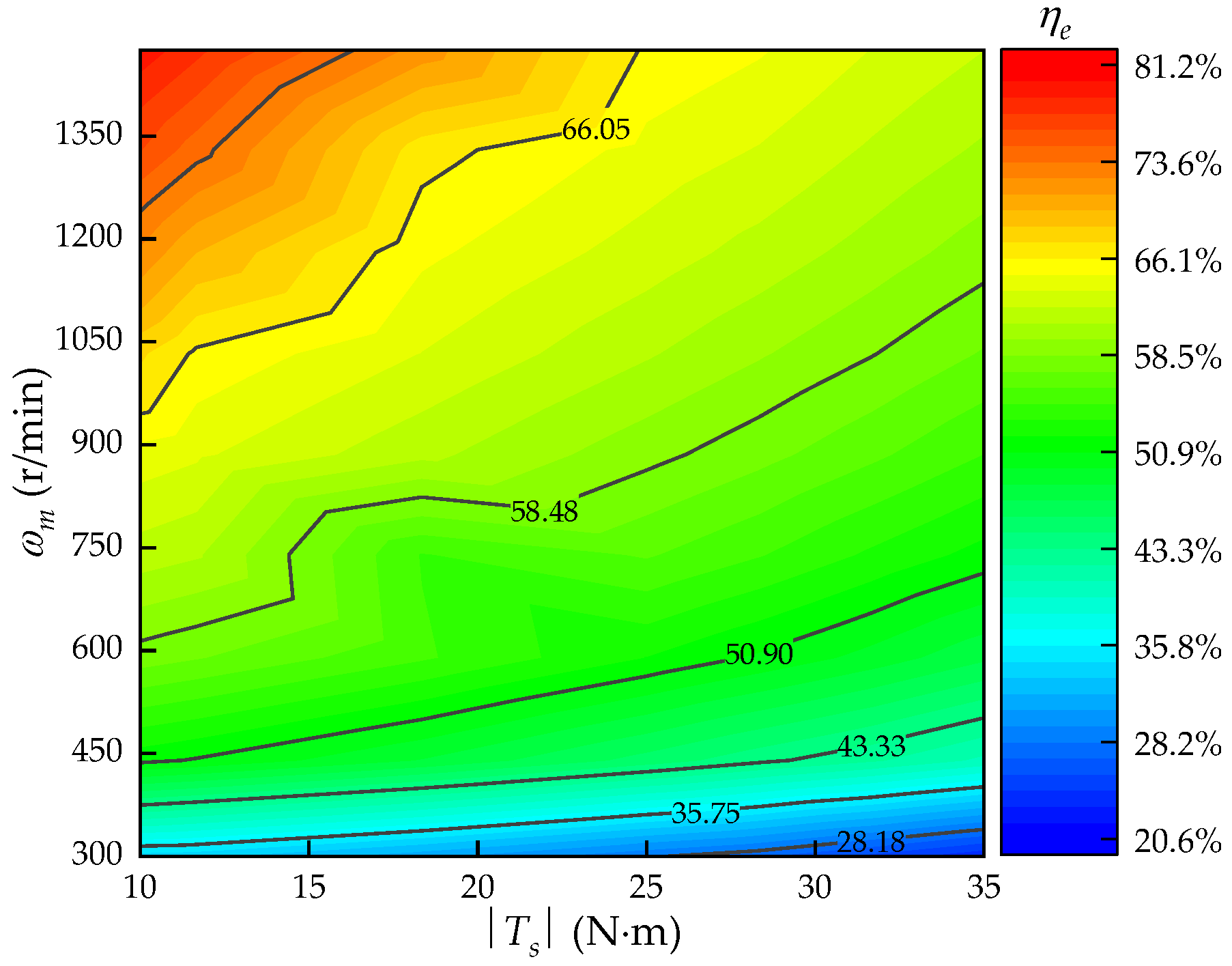
5.3.3. Energy Consumption Analysis
6. Discussions
7. Conclusions
- Both the EPCBV system and T-CBV system can effectively prohibit the motor from self-accelerating. However, the EPCBV system shows better adaption than T-CBV system to varying negative loads and maintains higher stability than T-CBV in all the working conditions.
- The speed control accuracy of the EPCBV system can be maintained above 95% in most of the operating conditions, while the speed accuracy of the T-CBV system is varying from 48% to 90%, depending very much on working conditions.
- Under most operating conditions, the maximum power consumption is about 4 Kw and is far less than that of the T-CBV system, which is about 13.79 Kw under the same operating condition. The power-saving ratio between the EPCBV and T-CBV varies from 20% to 82%, depending on the working conditions of the PCMH system; however, it goes beyond 50% in most of the operating range of the system.
- The EPCBV system shows accuracy decrease and power consumption increase in the regions where the flow saturation of the EPCBV occurs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sakaino, S.; Sakuma, T.; Tsuji, T. A control strategy for electro-hydrostatic actuator considering static friction, resonance, and oil Leakage. IEEJ J. Ind. Appl. 2019, 8, 279–286. [Google Scholar] [CrossRef]
- Ai, C.; Kong, X.; Wang, J. Study on the applicable wind speed model of wind farm and high-frequency wind simulation. Adv. Mater. Res. 2012, 562–564, 1074–1078. [Google Scholar] [CrossRef]
- Ye, H.; Ni, X.; Chen, H.; Li, D.; Pan, W. Constant speed control of hydraulic travel system based on neural network algorithm. Processes 2022, 10, 944. [Google Scholar] [CrossRef]
- Ansari, B.; Aligholami, M.; Khosroshahi, A.R. An experimental and numerical investigation into using hydropower plant on oil transmission lines. Energy Sci. Eng. 2022, 10, 4397–4410. [Google Scholar] [CrossRef]
- Yang, X.; Gong, G.; Yang, H.; Jia, L.; Zhou, J. An Investigation in Performance of a Variable-Speed-Displacement Pump-Controlled Motor System. IEEE/ASME Trans. Mechatron. 2017, 22, 647–656. [Google Scholar] [CrossRef]
- Vardhan, A. Energy saving analysis of the hydrostatic drives used in the rotary head system of the blast hole drill rig. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2019, 233, 1086–1097. [Google Scholar] [CrossRef]
- Karpenko, M.; Prentkovskis, O.; Šukevičius, Š. Research on high-pressure hose with repairing fitting and influence on energy parameter of the hydraulic drive. Eksploat. I Niezawodn. Maint. Reliab. 2022, 24, 25–32. [Google Scholar] [CrossRef]
- Łopatka, M.J.; Krogul, P.; Rubiec, A.; Przybysz, M. Preliminary Experimental Research on the Influence of Counterbalance Valves on the Operation of a Heavy Hydraulic Manipulator during Long-Range Straight-Line Movement. Energies 2022, 15, 5596. [Google Scholar] [CrossRef]
- Li, Y.; He, L. Counterbalancing speed control for hydrostatic drive heavy vehicle under long down-slope. IEEE/ASME Trans. Mechatron. 2015, 20, 1533–1542. [Google Scholar] [CrossRef]
- Ho, T.H.; Ahn, K.K. Design and control of a closed-loop hydraulic energy-regenerative system. Autom. Constr. 2012, 22, 444–458. [Google Scholar] [CrossRef]
- Bury, P.; Stosiak, M.; Urbanowicz, K.; Kodura, A.; Kubrak, M.; Malesińska, A. A case study of open and closed-loop control of hydrostatic transmission with proportional valve start-up process. Energies 2022, 15, 1860. [Google Scholar] [CrossRef]
- Sørensen, J.K.; Hansen, M.R.; Ebbesen, M.K. Novel concept for stablishing a hydraulic circuit containing counterbalance valve and pressure compensated flow supply. Int. J. Fluid Power 2016, 17, 153–162. [Google Scholar] [CrossRef]
- Imam, A.; Rafiq, M.; Jalayeri, E.; Sepehri, N. A pump-controlled circuit for single-rod cylinders that incorporates limited throttling compensating Valves. Actuators 2018, 7, 13. [Google Scholar] [CrossRef]
- Nordhammer, P.A.; Bak, M.K.; Hansen, M.R. A method for reliable motion control of pressure compensated hydraulic actuation with counterbalance valves. In Proceedings of the 12th International Conference on Control, Automation and Systems, Jeju Island, Republic of Korea, 17–21 October 2012. [Google Scholar]
- Sciancalepore, A.; Vacca, A.; Weber, S. An energy efficient method for controlling hydraulic actuators using counterbalance valves with adjustable pilot. J. Dyn. Sys. Meas. Control 2021, 143, 111007. [Google Scholar] [CrossRef]
- Ritelli, G.F.; Vacca, A. Energetic and dynamic impact of counterbalance valves in fluid power machines. Energy Convers. Manag. 2013, 76, 701–711. [Google Scholar] [CrossRef]
- Berne, L.J.; Raush, G.; Roquet, P.; Gamez-Montero, P.-J.; Codina, E. Graphic method to evaluate power requirements of a hydraulic system using load-holding valves. Energies 2022, 15, 4558. [Google Scholar] [CrossRef]
- Jin, M.; Wang, Q. Energy-saving control for electro-hydraulic systems under time-varying negative loads. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2018, 232, 608–621. [Google Scholar] [CrossRef]
- Zagar, P.; Scheidl, R. Sliding mode analysis of a counterbalance valve induced instability in an electrohydraulic drive. J. Dyn. Sys. Meas. Control 2022, 144, 041004. [Google Scholar] [CrossRef]
- Vardhan, A.; Dasgupta, K. Mapping the efficiency of the hydrostatic drive for the rotary head of drill machine using high-speed low-torque hydraulic motors. Arab. J. Sci. Eng. 2018, 43, 4703–4712. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Q. Adaptive robust tracking control of a proportional pressure-reducing valve with dead zone and hysteresis. Trans. Inst. Meas. Control 2017, 40, 2151–2166. [Google Scholar] [CrossRef]
- Xu, B.; Ding, R.; Zhang, J.; Cheng, M.; Sun, T. Pump/valves coordinate control of the independent metering system for mobile machinery. Autom. Constr. 2015, 57, 98–111. [Google Scholar] [CrossRef]
- Lyu, L.; Chen, Z.; Yao, B. Development of pump and valves combined hydraulic system for both high tracking precision and high energy efficiency. IEEE Trans. Ind. Electron. 2019, 66, 7189–7198. [Google Scholar] [CrossRef]
- Xu, B.; Hu, M.; Su, Z. Characteristics of volumetric losses and efficiency of axial piston pump with respect to displacement conditions. J. Zhejiang Univ. Sci. A 2016, 17, 186–201. [Google Scholar] [CrossRef]
- Gao, B.; Li, X.; Zeng, X.; Chen, H. Nonlinear control of direct-drive pump-controlled clutch actuator in consideration of pump efficiency map. Control Eng. Pract. 2019, 91, 104110. [Google Scholar] [CrossRef]
- Cheng, M.; Xu, B.; Zhang, J.; Ding, R. Pump-based compensation for dynamic improvement of the electrohydraulic flow matching system. IEEE Trans. Ind. Electron. 2017, 64, 2903–2913. [Google Scholar] [CrossRef]
- Helian, B.; Chen, Z.; Yao, B.; Lyu, L.; Li, C. Accurate motion control of a direct drive hydraulic system with an adaptive nonlinear pump flow compensation. IEEE/ASME Trans. Mechatron. 2021, 26, 2593–2603. [Google Scholar] [CrossRef]
- Tan, Y.; Yu, X.; Wang, X.; Lv, Q.; Shi, M. Interaction analysis and multi-response optimization of transformer winding design parameters. Int. Commun. Heat Mass Transf. 2022, 137, 106233. [Google Scholar] [CrossRef]
- Xu, B.; Cheng, M.; Yang, H.; Zhang, J.; Sun, C. A hybrid displacement/pressure control scheme for an electrohydraulic flow matching system. IEEE/ASME Trans. Mechatron. 2015, 20, 2771–2782. [Google Scholar] [CrossRef]
- Lyu, L.; Chen, Z.; Yao, B. Advanced valves and pump coordinated hydraulic control design to simultaneously achieve high accuracy and high Efficiency. IEEE Trans. Control Syst. Technol. 2021, 29, 236–248. [Google Scholar] [CrossRef]
- Ding, R.; Zhang, J.; Xu, B.; Cheng, M. Programmable hydraulic control technique in construction machinery: Status, challenges and countermeasures. Autom. Constr. 2018, 95, 172–192. [Google Scholar] [CrossRef]
- Jin, M.; Wang, Q. Efficient pump and meter-out control for electrohydraulic system with time-varying negative load. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2018, 232, 1170–1181. [Google Scholar]
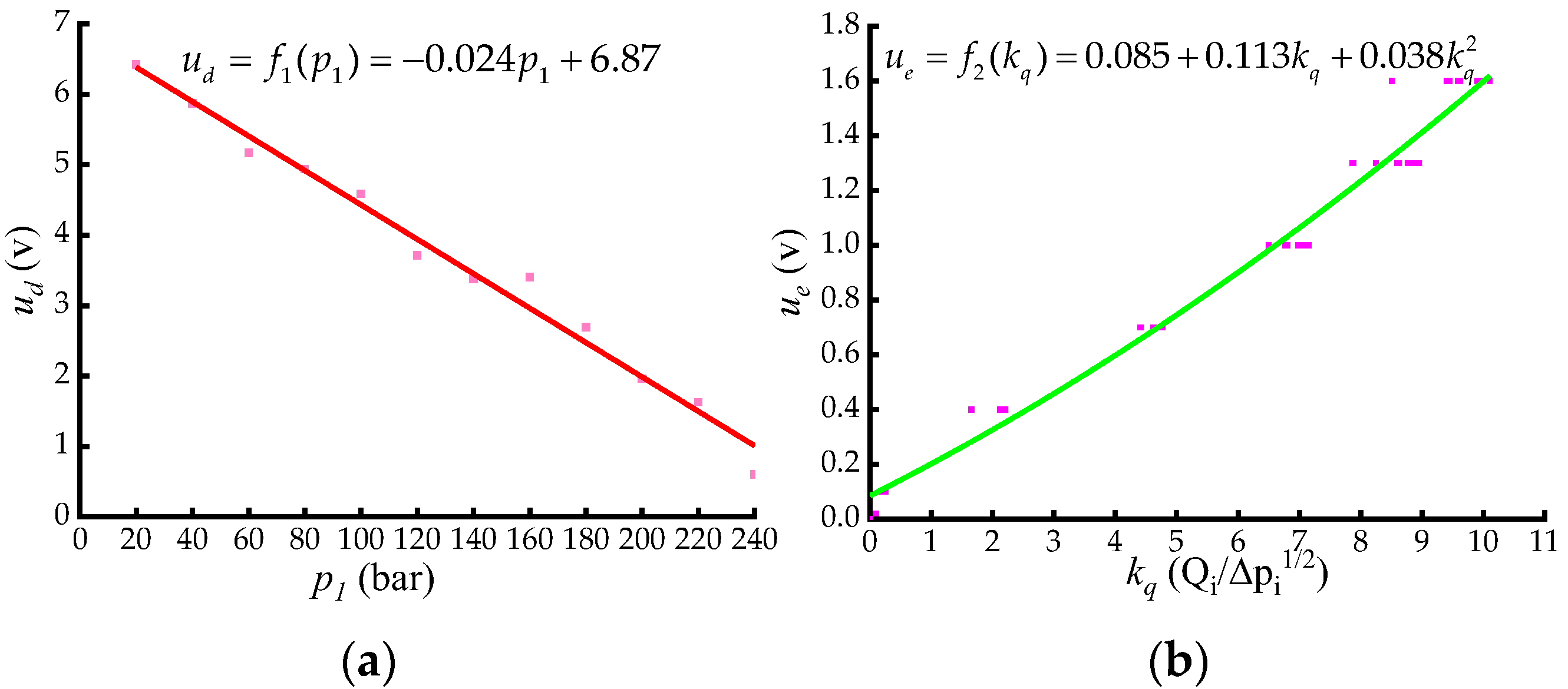

| Components | Type | Parameters | Components | Type | Parameters |
|---|---|---|---|---|---|
| IPM1 | Hilectro HP12529-G402F-R1 | Rated Power: 109 Kw | Torque and Speed Sensor 2 | Interface T4-300 NM | Torque range: 0–150 Nm |
| Rated Torque: 260 Nm | Torque accuracy: ±0.2% | ||||
| Speed range: 500–4000 r/min | Speed accuracy: ±0.03% | ||||
| IPM2 | Hilectro HP11812-G502F-R1 | Rated Power: 57 Kw | Pressure Sensor 1–3 | HYDAC HDA4745-A-600-Y00 | Pressure range: 0–400 bar |
| Rated Torque: 110 Nm | Accuracy: ±0.25% | ||||
| Speed range: 0–5000 r/min | Output: 4–20 mA | ||||
| Pump | Rexroth A4VG40EP4 | Displacement: 0–40 cc/r | Flow Sensor 1–2 | Hydrotechnik QT 110 | Flow range: 0–75 L/min |
| Control signal: 200–600 mA | Accuracy: 1% | ||||
| Rated Pressure: 400 bar | Output: 4–20 mA | ||||
| Hydraulic motor | Rexroth A6VE28EP2 | Displacement: 28 cc/r | Torque and Speed Sensor 1 | Interface T4-300 NM | Torque range: 0–300 Nm |
| Rated pressure: 400 bar | Torque accuracy: ±0.2% | ||||
| EPCBV | SUN CWCG-T21A | Pilot ratio: α = 5 | Speed accuracy: ±0.03% | ||
| Rated Flow: 60 L/min | Torque and Speed Sensor 2 | Interface T4-150 NM | Torque range: 0–150 Nm | ||
| Output pressure: 0–100 bar | Torque accuracy: ±0.2% | ||||
| VTOZ MA-RZGO-a-010-100 | Output pressure: 0–100 bar | Speed accuracy: ±0.03% | |||
| Control signal: 200–600 mA | T-CBV | SUN CACALHN | Pilot ratio: α =3 | ||
| Controller | Rexroth-RC28/14 | Periods: 5 ms | Rated flow: 60 L/min |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| KP | 1 | kγ | 0.05 bar/s |
| KI | 0.3 | nDpmax | 1 L/min |
| KD | 0.04 | kt | −0.05 bar−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhang, Y.; Li, G.; Liu, R.; Zhou, X. Design and Control of an Energy-Efficient Speed Regulating Method for Pump-Controlled Motor System under Negative Loads. Machines 2023, 11, 437. https://doi.org/10.3390/machines11040437
Wang H, Zhang Y, Li G, Liu R, Zhou X. Design and Control of an Energy-Efficient Speed Regulating Method for Pump-Controlled Motor System under Negative Loads. Machines. 2023; 11(4):437. https://doi.org/10.3390/machines11040437
Chicago/Turabian StyleWang, Huashuai, Yanbin Zhang, Geqiang Li, Rongsheng Liu, and Xin Zhou. 2023. "Design and Control of an Energy-Efficient Speed Regulating Method for Pump-Controlled Motor System under Negative Loads" Machines 11, no. 4: 437. https://doi.org/10.3390/machines11040437
APA StyleWang, H., Zhang, Y., Li, G., Liu, R., & Zhou, X. (2023). Design and Control of an Energy-Efficient Speed Regulating Method for Pump-Controlled Motor System under Negative Loads. Machines, 11(4), 437. https://doi.org/10.3390/machines11040437





