A Genetic Algorithm-Controlled Solar Tracker Robot with Increased Precision Due to Evolution
Abstract
1. Introduction
2. Problem Solving
2.1. Theoretical Background
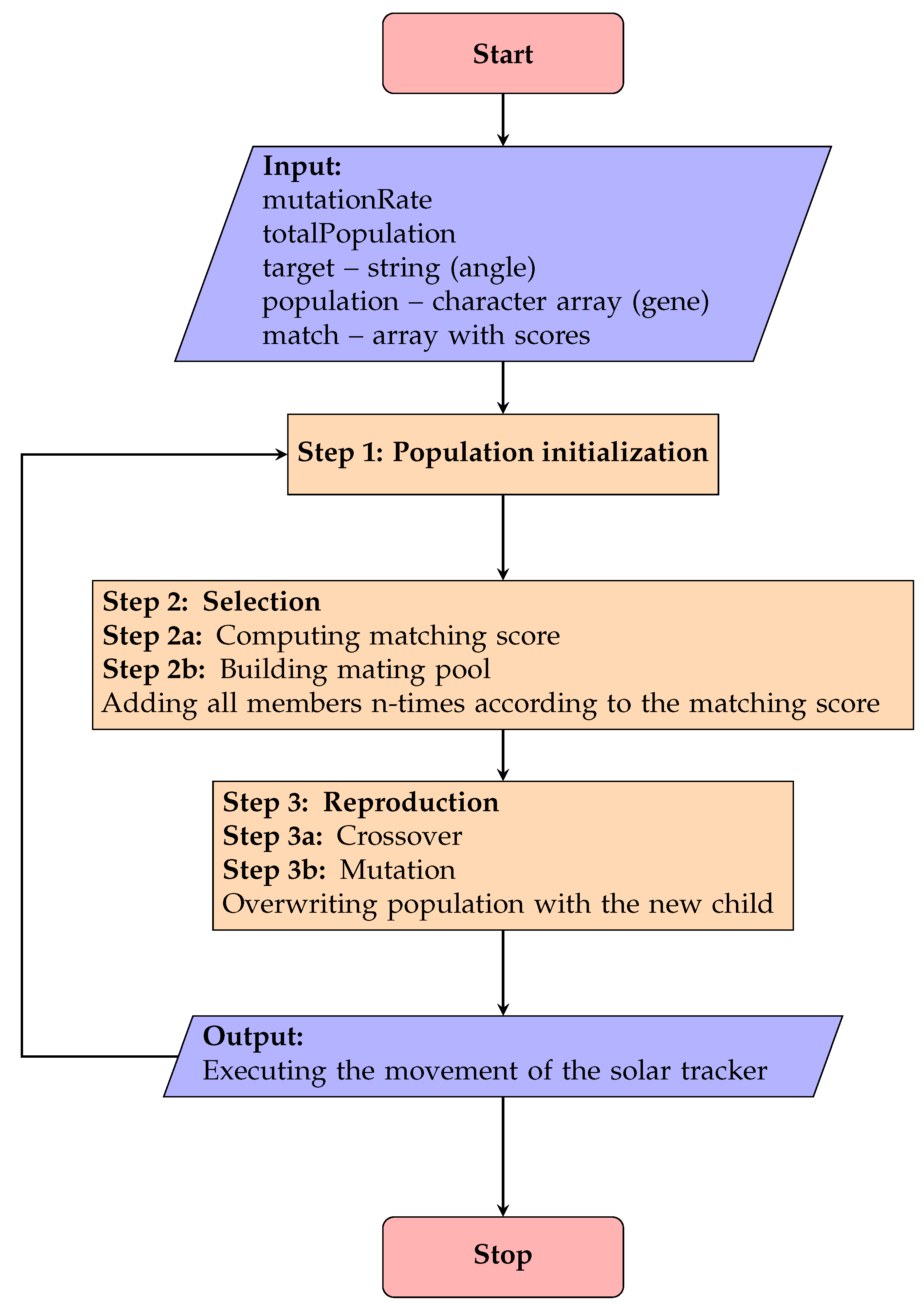
2.2. The Proposed Genetic Algorithm
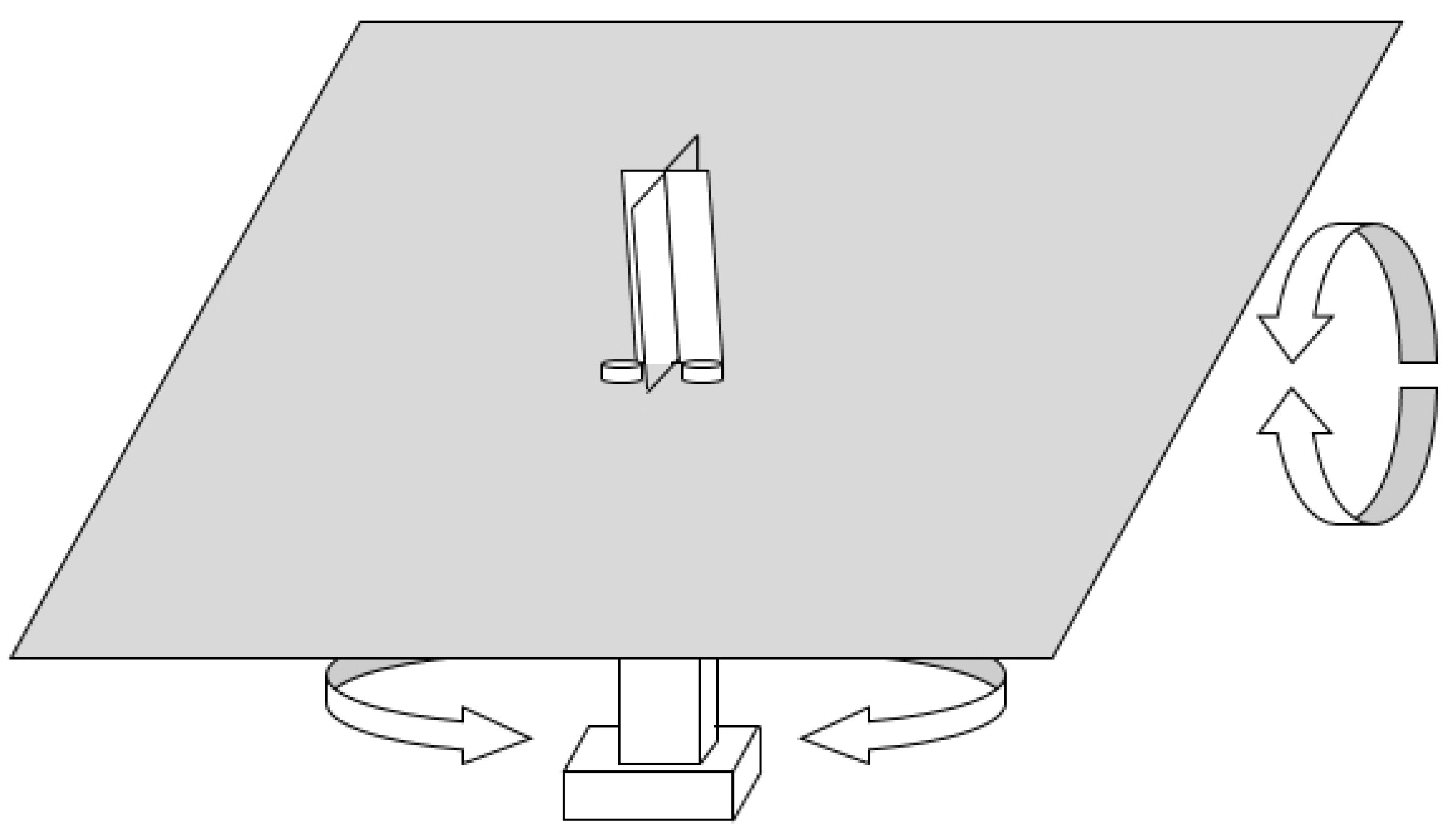
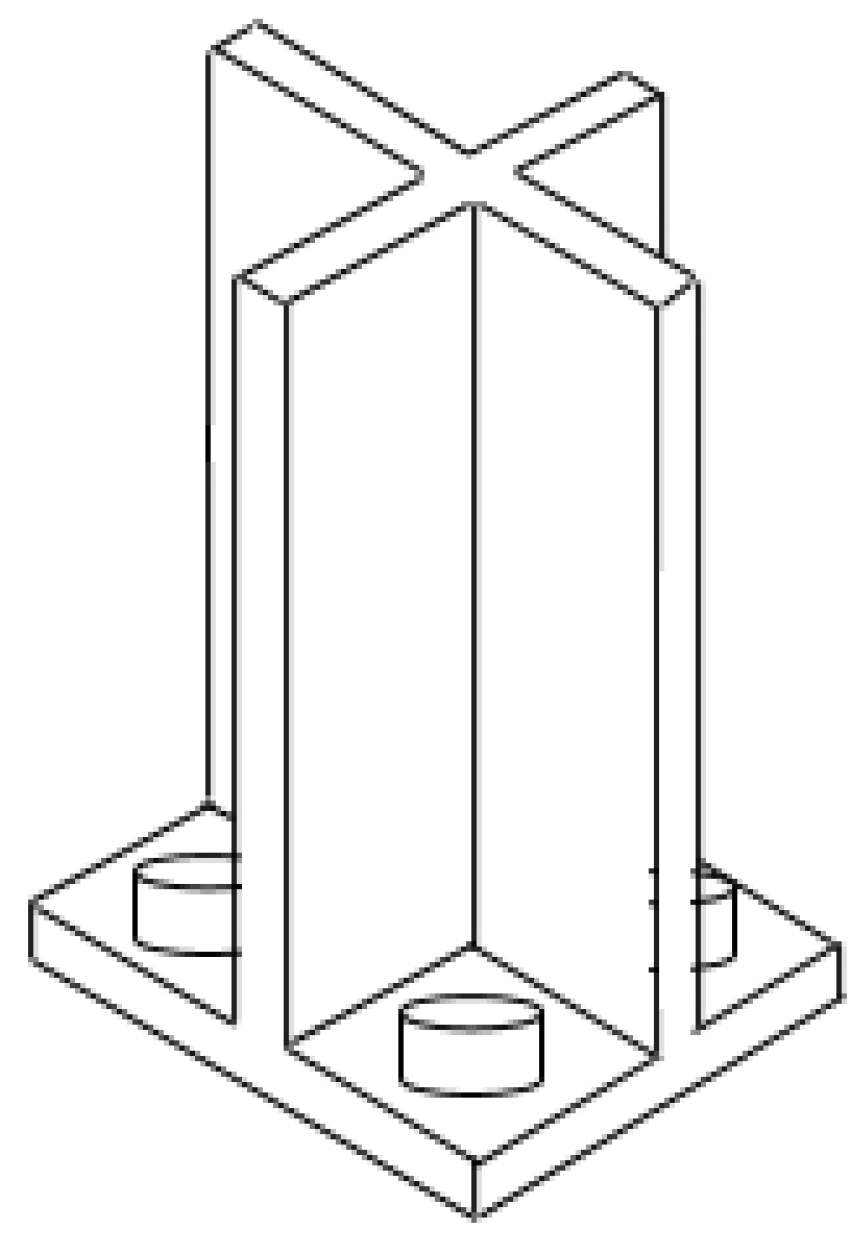
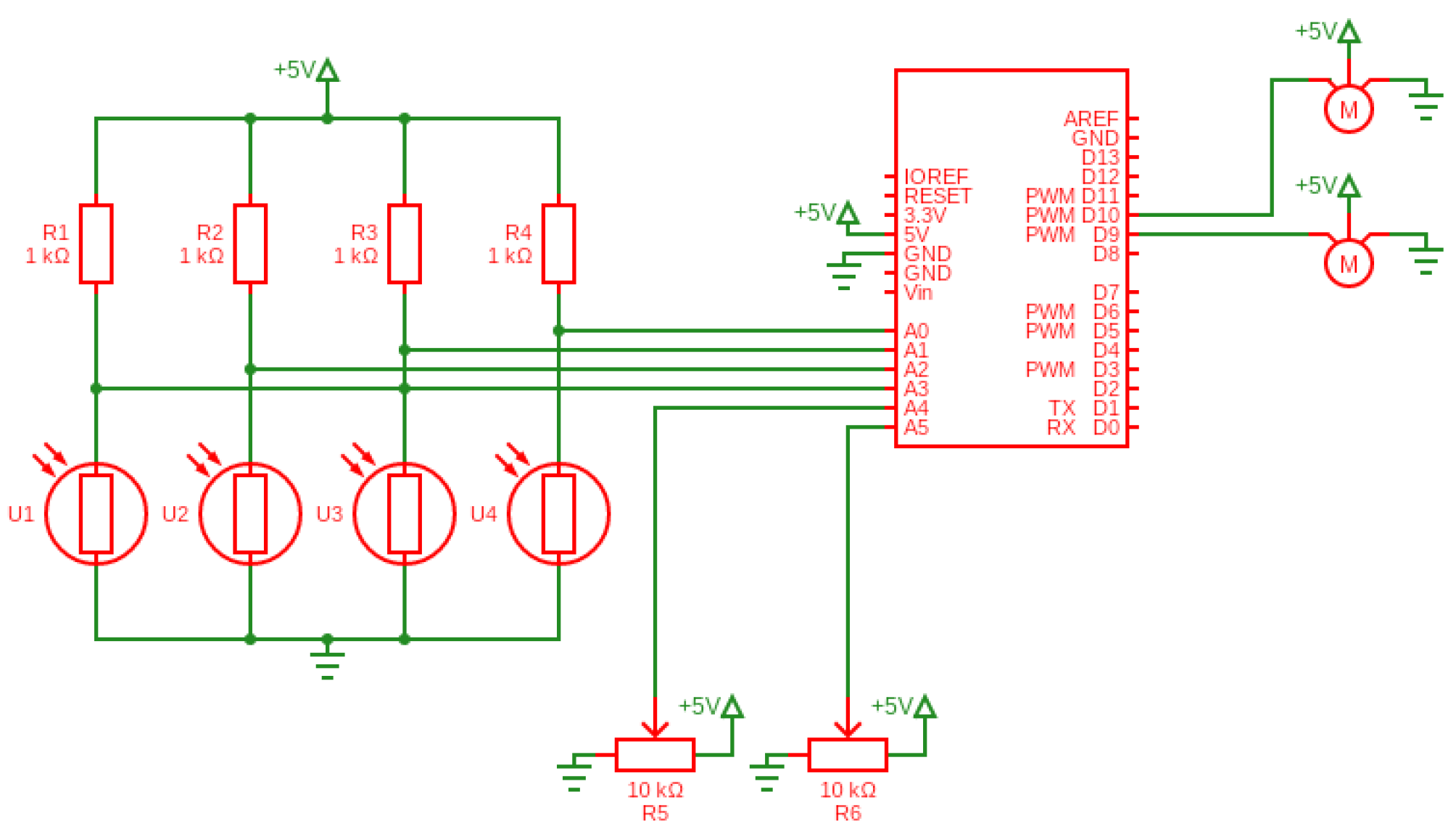
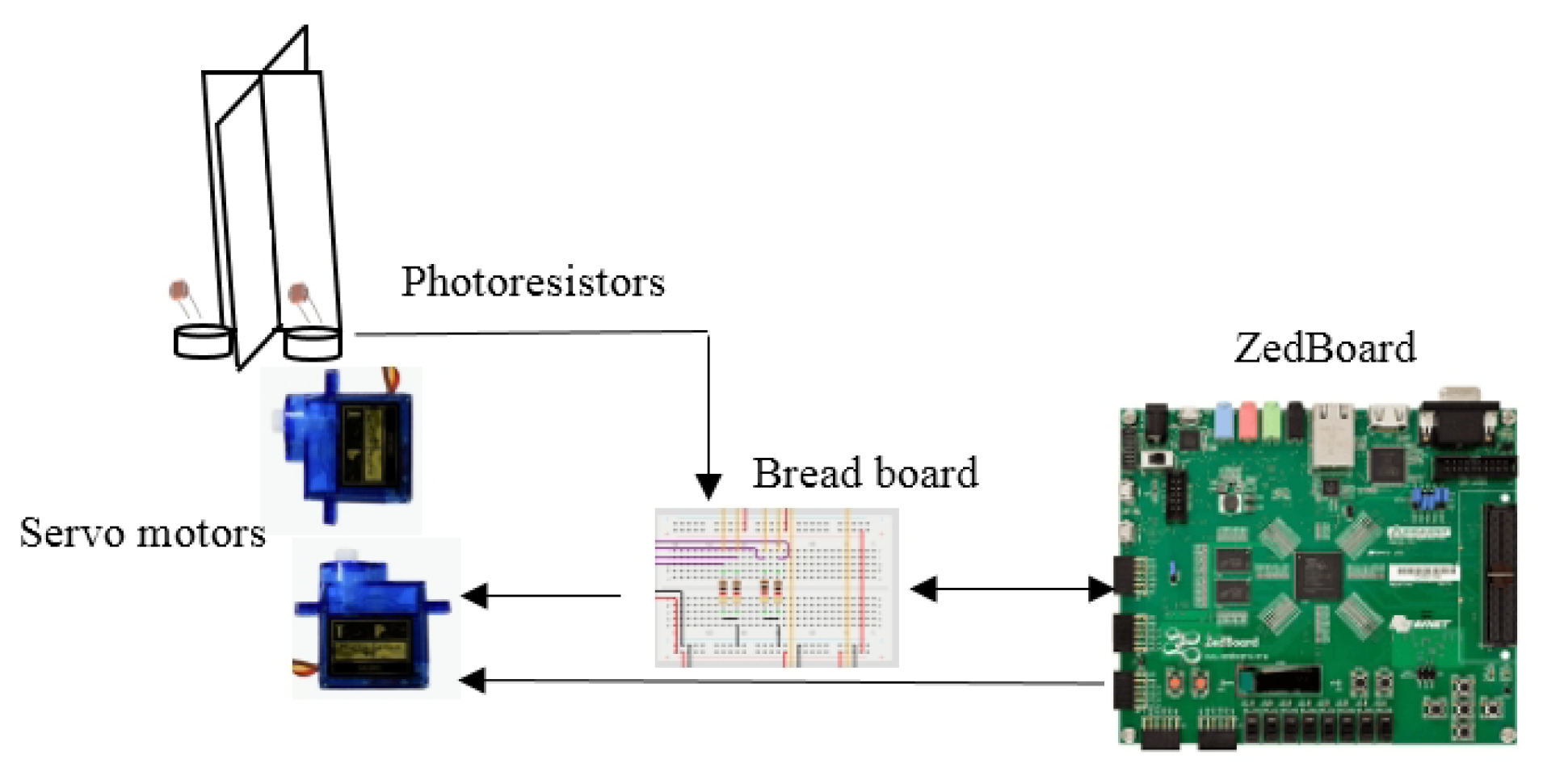
2.3. Hardware Implementation
3. Results
3.1. Experimental Results
3.2. Discussions
4. Conclusions
- The algorithm was used by the solar tracker robot to track the Sun with more precision.
- The algorithm was put in an implementable form for the computer source code.
- The idea of how to glue the two motors in order for the solar tracker to be able to make horizontal and vertical movements is original.
- The genesis of all formulas was demonstrated and validated through controlled robotic movement.
- The robot was built, the circuit was made, and the software was written by the authors.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CdTe | Cadmium tellurium |
| CIGS | Copper indium gallium selenide |
| PDW | Passive dynamic walking |
| DoF | Degrees of freedom |
| 3D | Three-dimensional |
| AC | Alternating current |
| DSP | Digital signal processing |
| Coordinates | |
| MEMS | Microelectromechanical systems |
| ASCII | American Standard Code for Information Interchange |
| f | Fitness function |
| Gene (character) | |
| Target gene (character) | |
| Crossover parameter | |
| Generation number | |
| Total generation number | |
| , | Minimum, maximum |
| Random middle point | |
| Mutation rate or parameter | |
| N | Number of joints () |
| K | Total kinetic energy |
| P | Potential energy |
| Joint variable for the joint | |
| First time derivative for | |
| Generalized force (torque) at the joint | |
| Generalized joint coordinates | |
| Mass matrix or kinetic energy matrix | |
| Centrifugal and Coriolis forces | |
| Gravity force | |
| Generalized forces | |
| Inertia at joint k when joint k accelerates () | |
| Inertia observed at joint k when joint j accelerates | |
| Coefficient of the centrifugal force at joint k when joint i is moving () | |
| Coriolis force at joint k when both joints i and j are moving | |
| , | Masses |
| M | Mass matrix, all the mass |
| Linear acceleration terms | |
| Quadratic velocity terms | |
| Nonlinear configuration terms | |
| g | Gravity acceleration vector |
| Location of the center of mass for link i | |
| Place of the center point of the mass | |
| r | Place of reference |
| Differential component of the mass at point r | |
| Mass of particle i | |
| Distance to particle i | |
| DNAs | Deoxyribonucleic acids |
| Cartesian coordinate system | |
| FPGA | Field-programmable gate arrays |
| SoC | System on a chip |
| GA | Genetic algorithm |
References
- Lim, T.; Kwak, P.; Song, K.; Kim, N.; Lee, J. Automated dual-axis planar solar tracker with controllable vertical displacement for concentrating solar microcell arrays. Prog. Photovoltaics 2017, 25, 123–131. [Google Scholar] [CrossRef]
- Fathabadi, H. Comparative study between two novel sensorless and sensor based dual-axis solar trackers. Sol. Energy 2016, 138, 67–76. [Google Scholar] [CrossRef]
- Rustu, E.; Ali, S. Performance comparison of a double-axis sun tracking versus fixed PV system. Sol. Energy 2012, 86, 2665–2672. [Google Scholar]
- Lee, C.Y.; Chou, P.C.; Chiang, C.M.; Lin, C.F. Sun Tracking Systems: A Review. Sensors 2009, 9, 3875–3890. [Google Scholar] [CrossRef] [PubMed]
- Mousazadeh, H.; Keyhani, A.; Javadi, A.; Mobli, H.; Abrinia, K.; Sharifi, A. A review of principle and sun-tracking methods for maximizing solar systems output. Renew. Sustain. Energy Rev. 2009, 13, 1800–1818. [Google Scholar] [CrossRef]
- De Macedo, M.M.; Saldias, C.E.P.; Ando Junior, O.H. Mathematical Modeling of a Solar Tracker System Two Axes for Generation Photovoltaics. IEEE Lat. Am. Trans. 2016, 14, 4054–4062. [Google Scholar] [CrossRef]
- Kaur, T.; Mahajan, S.; Verma, S.; Gambhir, J. Arduino based low cost active dual axis solar tracker. In Proceedings of the ICPEICES 2016—1st International Conference on Power Electronics, Intelligent Control and Energy Systems, Delhi, India, 4–6 July 2016; pp. 1–5. [Google Scholar]
- Saumya, G.; Ankit, M.; Paurush, B. Prototype of household inverter using dual-axis solar tracker to overcome shortage of energy. In Proceedings of the InCITe 2016—International Conference on Information Technology, Noida, India, 6–7 October 2016; pp. 160–165. [Google Scholar]
- Fathabadi, H. Novel high efficient offline sensorless dual-axis solar tracker for using in photovoltaic systems and solar concentrators. Renew. Energy 2016, 95, 485–494. [Google Scholar] [CrossRef]
- Adapa, B.; Mamidi, R.P.; Alapati, S. Spacing Optimization Study of Single-axis Polar Mounted Solar-thermal Passive Tracker based Solar Photovoltaic Plan. Int. J. Renew. Energy Res. 2016, 6, 1491–1495. [Google Scholar]
- Jovanovic, V.M.; Ayala, O.; Seek, M.; Marsillac, S. Single Axis Solar Tracker Actuator Location Analysis. In Proceedings of the SoutheastCon 2016, Norfolk, VA, USA, 30 March–3 April 2016. [Google Scholar]
- Agee, J.T.; Davidson, I.E.; Kombani, L.T. Intelligent Proportional Integral Control of a Polar Axis Solar Tracker. In Proceedings of the PSC 2016—Clemson-University Power Systems Conference, Clemson, SC, USA, 8–11 March 2016. [Google Scholar]
- Geijtenbeek, T.; van de Panne, M.; van der Stappen, A.F. Flexible Muscle-Based Locomotion for Bipedal Creatures. ACM Trans. Graph. 2013, 32, 1–11. [Google Scholar] [CrossRef]
- Renan, V.; Eduardo, A.; Teo, R. Trajectory Planning For Car-like Robots Through Curve Parametrization And Genetic Algorithm Optimization With Applications To Autonomous Parking. IEEE Lat. Am. Trans. 2022, 20, 309–316. [Google Scholar]
- Loredo-Flores, A.; Gonzalez-Galvan, E.J.; Cervantes-SÁnchez, J.J.; Martinez-Soto, A. Optimization of Industrial, Vision-Based, Intuitively Generated Robot Point-Allocating Tasks Using Genetic Algorithms. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2008, 38, 600–608. [Google Scholar] [CrossRef]
- Gary, P.; Richard, Z. Learning Area Coverage for a Self-Sufficient Hexapod Robot Using a Cyclic Genetic Algorithm. IEEE Syst. J. 2014, 8, 778–790. [Google Scholar]
- Estrada, F.A.C.; Lozada, J.C.H.; Gutiérrez, J.S.; Valencia, M.I.C. Performance between Algorithm and micro Genetic Algorithm to solve the robot locomotion. IEEE Lat. Am. Trans. 2019, 17, 1244–1251. [Google Scholar] [CrossRef]
- Jamwal, P.K.; Hussain, S.; Xie, S.Q. Three-Stage Design Analysis and Multicriteria Optimization of a Parallel Ankle Rehabilitation Robot Using Genetic Algorithm. IEEE Trans. Autom. Sci. Eng. 2015, 12, 1433–1446. [Google Scholar] [CrossRef]
- Tsai, C.C.; Huang, H.C.; Chan, C.K. Parallel Elite Genetic Algorithm and Its Application to Global Path Planning for Autonomous Robot Navigation. IEEE Trans. Ind. Electron. 2011, 58, 4813–4821. [Google Scholar] [CrossRef]
- Kamio, S.; Iba, H. Adaptation technique for integrating genetic programming and reinforcement learning for real robots. IEEE Trans. Evol. Comput. 2005, 9, 318–333. [Google Scholar] [CrossRef]
- Tewolde, G.S.; Sheng, W. Robot Path Integration in Manufacturing Processes: Genetic Algorithm Versus Ant Colony Optimization. IEEE Trans. Syst. Man Cybern.-Part A Syst. Humans 2008, 38, 278–287. [Google Scholar] [CrossRef]
- Hornby, G.S.; Takamura, S.; Yamamoto, T.; Fujita, M. Autonomous evolution of dynamic gaits with two quadruped robots. IEEE Trans. Robot. 2005, 21, 402–410. [Google Scholar] [CrossRef]
- Tsai, C.C.; Huang, H.C.; Lin, S.C. FPGA-Based Parallel DNA Algorithm for Optimal Configurations of an Omnidirectional Mobile Service Robot Performing Fire Extinguishment. IEEE Trans. Ind. Electron. 2011, 58, 1016–1026. [Google Scholar] [CrossRef]
- Walker, J.H.; Garrett, S.M.; Wilson, M.S. The balance between initial training and lifelong adaptation in evolving robot controllers. IEEE Trans. Syst. Man Cybern. Part B (Cybernetics) 2006, 36, 423–432. [Google Scholar] [CrossRef]
- Huang, H.C. SoPC-Based Parallel ACO Algorithm and its Application to Optimal Motion Controller Design for Intelligent Omnidirectional Mobile Robots. IEEE Trans. Ind. Informatics 2013, 9, 1828–1835. [Google Scholar] [CrossRef]
- Kamel, M.A.; Yu, X.; Zhang, Y. Real-Time Fault-Tolerant Formation Control of Multiple WMRs Based on Hybrid GA–PSO Algorithm. IEEE Trans. Autom. Sci. Eng. 2021, 18, 1263–1276. [Google Scholar] [CrossRef]
- Gao, G.; Mei, Y.; Xin, B.; Jia, Y.H.; Browne, W.N. Automated Coordination Strategy Design Using Genetic Programming for Dynamic Multipoint Dynamic Aggregation. IEEE Trans. Cybern. 2022, 52, 13521–13535. [Google Scholar] [CrossRef]
- Ju, Z.; Ji, X.; Li, J.; Liu, H. An Integrative Framework of Human Hand Gesture Segmentation for Human–Robot Interaction. IEEE Syst. J. 2017, 11, 1326–1336. [Google Scholar] [CrossRef]
- Datta, R.; Pradhan, S.; Bhattacharya, B. Analysis and Design Optimization of a Robotic Gripper Using Multiobjective Genetic Algorithm. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 16–26. [Google Scholar] [CrossRef]
- Jamwal, P.K.; Hussain, S. Multicriteria Design Optimization of a Parallel Ankle Rehabilitation Robot: Fuzzy Dominated Sorting Evolutionary Algorithm Approach. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 589–597. [Google Scholar] [CrossRef]
- Yamasaki, F.; Endo, K.; Kitano, H.; Asada, M. Acquisition of humanoid walking motion using genetic algorithm-Considering characteristics of servo modules. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (Cat. No.02CH37292), Washington, DC, USA, 11–15 May 2002; Volume 3, pp. 3123–3128. [Google Scholar]
- Kong, J.S.; Lee, B.H.; Kim, J.G. A study on the gait generation of a humanoid robot using genetic algorithm. In Proceedings of the SICE 2004 Annual Conference, Sapporo, Japan, 4–6 August 2004; Volume 1, pp. 187–191. [Google Scholar]
- Endo, K.; Maeno, T.; Kitano, H. Co-evolution of morphology and walking pattern of biped humanoid robot using evolutionary computation: Designing the real robot. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation (Cat. No.03CH37422), Taipei, Taiwan, 14–19 September 2003; Volume 1, pp. 1362–1367. [Google Scholar]
- Choi, S.H.; Choi, Y.H.; Kim, J.G. Optimal walking trajectory generation for a biped robot using genetic algorithm. In Proceedings of the 1999 IEEE/RSJ International Conference on Intelligent Robots and Systems. Human and Environment Friendly Robots with High Intelligence and Emotional Quotients (Cat. No.99CH36289), Kyongju, Republic of Korea, 17–21 October 1999; Volume 3, pp. 1456–1461. [Google Scholar]


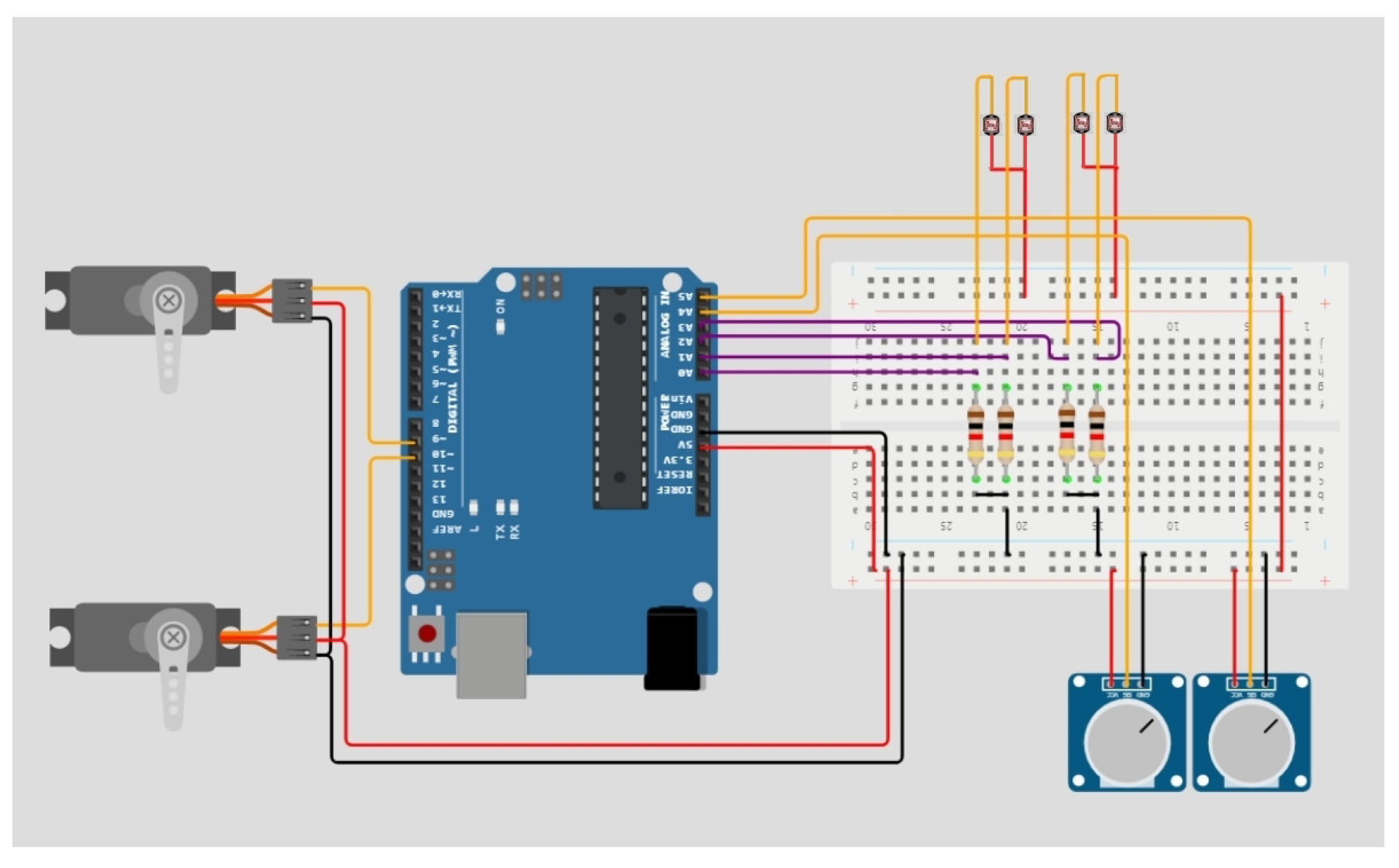

| Total population | 150 | Generation number | 50 |
| Crossover rate | 0.75 | Mutation rate | 0.01 |
| String length | 8bits | ||
| Fitness function | |||
| GA Parameter | Proposed Approach | F. Yamasaki et al. [31] | Jung-Shik Kong et al. [32] | K. Endo et al. [33] | Sang-Ho Choi et al. [34] |
|---|---|---|---|---|---|
| Total population | 150 | 50 | 100 | 200 | 60 |
| Generation number | 50 | 50 | 300 | 300 | 50 |
| Crossover rate | 0.75 | 0.9 | 0.08 | 0.8 | 0.92 |
| Mutation rate | 0.01 | 0.02 | 0.05 | 0.05 | 0.03 |
| String length (bits) | 8 | - | - | - | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szabo, R.; Ricman, R.-S. A Genetic Algorithm-Controlled Solar Tracker Robot with Increased Precision Due to Evolution. Machines 2023, 11, 430. https://doi.org/10.3390/machines11040430
Szabo R, Ricman R-S. A Genetic Algorithm-Controlled Solar Tracker Robot with Increased Precision Due to Evolution. Machines. 2023; 11(4):430. https://doi.org/10.3390/machines11040430
Chicago/Turabian StyleSzabo, Roland, and Radu-Stefan Ricman. 2023. "A Genetic Algorithm-Controlled Solar Tracker Robot with Increased Precision Due to Evolution" Machines 11, no. 4: 430. https://doi.org/10.3390/machines11040430
APA StyleSzabo, R., & Ricman, R.-S. (2023). A Genetic Algorithm-Controlled Solar Tracker Robot with Increased Precision Due to Evolution. Machines, 11(4), 430. https://doi.org/10.3390/machines11040430






