Grasping of Solid Industrial Objects Using 3D Registration

Abstract

Robots allow industrial manufacturers to speed up production and to increase the product’s quality. This paper deals with the grasping of partially known industrial objects in an unstructured environment. The proposed approach consists of two main steps: (1) the generation of an object model, using multiple point clouds acquired by a depth camera from different points of view; (2) the alignment of the generated model with the current view of the object in order to detect the grasping pose. More specifically, the model is obtained by merging different point clouds with a registration procedure based on the iterative closest point (ICP) algorithm. Then, a grasping pose is placed on the model. Such a procedure only needs to be executed once, and it works even in the presence of objects only partially known or when a CAD model is not available. Finally, the current object view is aligned to the model and the final grasping pose is estimated. Quantitative experiments using a robot manipulator and three different real-world industrial objects were conducted to demonstrate the effectiveness of the proposed approach.

1. Introduction

The term Industry 4.0 was used for the first time in 2011 in order to denote the fourth industrial revolution, which includes the actions needed to create smart factories [1]. In these smart factories, a novel type of robots, called collaborative robots (or cobots) [2] are used in order to overcome the classical division of labor, which requires robots to be confined in safety cages far away from human workers. In the context of Industry 4.0, collaborative robots are designed to work in unstructured environments by leveraging learning capabilities. A challenging issue in collaborative robotics is the grasping of partially known objects. This problem can be divided into other small tasks, equally important, that include object localization, grasp pose detection and estimation and force monitoring during the grasp phase. Moreover, the choice of the contact point between the robot end-effector and the object and the type and amount of forces to be applied are a nontrivial tasks. The object localization and grasp pose detection task can be resolved by using vision sensors that allow the robot to get information about the environment without entering in contact with it.

It is important to notice that the visual techniques have some drawbacks. In particular, they are affected by the lighting conditions of the environment and the object texture or reflection. Moreover, calibration errors and partial occlusions can occur, especially in the presence of an eye-in-hand configuration, i.e., when the camera is rigidly mounted on the robot end-effector (see Figure 1). This configuration differs from the so-called eye-to-hand setup, where the camera observes the robot within its work space. A camera in an eye-in-hand configuration has a limited but more precise view of the scene, whilst a camera in an eye-to-hand configuration has a global but less detailed sight of the scene [3].

Figure 1. Robot and camera setup for the data acquisition.

In this work, we focused on the problem of grasping partially known objects for which a model is not available, with an industrial robot equipped with an eye-in-hand depth sensor in an unstructured environment.

The proposed method consists of two steps:

• The generation of a model of the object based on a set of point clouds acquired from different points of view. The point clouds are merged by means of a 3D registration procedure based on the ICP algorithm. Once the model is obtained, the grasping pose is selected. It is worth noticing that such a procedure is needed only once.
• The alignment of the obtained model with the current view of the object in order to detect the grasping pose.

The contributions of the paper are threefold.

• As a difference with respect to expensive 3D scanning systems usually adopted for large production batches, the proposed strategy only requires an off-the-shelf low-cost depth sensor to generate the model and to acquire the current view of the object. Moreover, the proposed system is highly flexible with respect to the position of the object, and it allows one to acquire different views of the object, since the camera is mounted on the wrist of a robot manipulator.
• According to the Industry 4.0 road map, our system is robust to possible failures. In fact, it can detect a potential misalignment between the acquired point cloud and the model. In such a case, the point of view is modified and the whole procedure is restarted.
• While deep-learning-based approaches to object grasping pose detection usually require a huge quantity of data and a high computational burden to train the network, the proposed approach exploits a fast model reconstruction procedure.

The rest of the paper is organized as follows. Related work is discussed in Section 2. Our strategy for grasping the objects and the adopted methods are described in Section 3. The hardware setup and the software details are presented in Section 4. Section 5 shows the experimental tests conducted by considering three different automotive components. Finally, conclusions are drawn in Section 6.

2. Related Work

In this section, the related approaches to object grasping pose detection and some recent registration methods are analyzed.

2.1. Object Grasping

Approaches to the problem of object grasping can be roughly classified into analytic and data-driven [4].

• Analytic methods require a knowledge (at least partial) of the object features (e.g., shape, mass, material) and a model of the contact [5].
• Data-driven approaches aim at detecting the grasp pose candidates for the object via empirical investigations [6].

Among data-driven methods, deep-learning-based approaches are becoming very popular thanks to the availability of powerful Graphics Processing Units (GPUs). More specifically, in order to make deep learning techniques very effective, a database with geometric object models and a number of good grasp poses is needed. In [7], convolutional neural networks (CNNs) were adopted with a mobile manipulator, in order to perform a 2D object detection, which, combined with the depth information, allowed the manipulator to grasp the object. They proposed an improvement of the structure of the Faster R-CNN neural network to achieve a better performance and a significant reduction in computational time.

In [8,9], a generative grasping convolutional neural network (GG-CNN) was proposed. It directly generated a grasp pose and quality measure for every pixel in an input depth image, and it was fast enough to perform grasping in dynamic environments. Given a depth image $\mathit{I}\in \mathrm{I}{\mathrm{R}}^{h\times w}$, where h and w are the height and width of the image, respectively, a grasp is described by $\tilde{\mathit{g}}=(\mathit{s},\tilde{\varphi },\tilde{w},q)$, where $\mathit{s}=(u,v)$ is the center in pixel of the box representing the grasp pose, $\tilde{\varphi }$ is the grasp rotation in the camera reference frame, $\tilde{w}$ is the grasp width in image coordinates, i.e., the gripper’s width required for a successful object grasp, and q is a scalar quality measure, representing the chances of grasp success.

The set of grasp poses in the image space is referred as the grasp map of I, denoted by G, from which it is possible to compute the best visible grasp in the image reference frame. Then, through the calibration matrices, this pose is expressed in the inertial reference frame to command the robot and grasp the object.

In CNN-based grasping approaches, when the camera is in an eye-in-hand configuration, once the grasp pose is determined, often, the robot executes the motion without visual feedback since occlusion appears under a certain distance. For this reason, a precise calibration between the camera and the robot and a completely structured environment are often required. Recently, in [10], grasping of partially known objects in unstructured environments was proposed based on an extension to an industrial context of the well-known technique of background subtraction [11]. In [12], the authors proposed a CNN-based architecture, named GraspNet, in charge of distinguishing on the object surface the candidate grasping region.

In the case of unknown objects, where it is assumed neither object knowledge nor grasp pose candidates are available, some approaches approximate the object with shape primitives, e.g., by determining the quadratic function that best approximates the shape of the object using multiview measurements [13]. Other approaches require to identify some features in sensory data for generating grasp pose candidates [14]. The concept of familiar objects, i.e., known objects similar to those to be grasped in terms of shape, color, texture or grasp poses was exploited in [6]: to transfer the grasp experience, the objects were classified on the basis of a similarity metric. Similarly, in [15], the grasp pose candidates were determined by identifying parts on which a grasp pose had already been successfully tested, and in [16] the objects were classified in categories characterized by the same grasp pose candidates. In [17], a data-driven object grasp approach using only depth-image perception was proposed. In this case, a deep convolutional neural network was trained in a simulated environment. The grasps were generated by analytical grasp planners and the algorithm learned grasping-relevant features. At execution time, a single-grasp solution was generated for each object. In [18], some strategies that exploited shape adaptation were presented. Two types of adaptation were used to implement these strategies: the hand/object and the hand/environment adaptation. The first allowed one to simplify the scene perception. Indeed, the algorithm could make errors in determining the object shape, because they were canceled by the shape adaptation. Moreover, shape adaptation also occurred between the hand and the environment, i.e., the algorithm optimized the grasping strategy based on the constraints induced by the environment.

The work proposed in [19] focused on grasping unknown objects in cluttered scenes. A shape-based method, called symmetry height accumulated features (SHAF), was introduced. This method reduced the scene description complexity, and the use of machine learning techniques became feasible. SHAF derived from height accumulated features (HAF) [20]. The HAF approach is based on the idea that to grasp an object from the top, parts of the end-effector need to envelop the object and, for this reason, need to go further down than the top of the object. Considering small regions, the differences between the average heights give an abstraction of the objects shape. The HAF approach does not check if there is symmetry between features, hence, in [19], this approach was extended by an additional feature type. These symmetry features were used to train a Support Vector Machine (SVM) classifier.

An approach that required as input only the raw depth data from a single frame, did not use explicit object model and was free from online training was proposed in [21]. The inputs of the algorithm were a depth map and a registered image acquired from a stereo sensor. The first step consisted of finding a candidate grasp pose in a 2D slice of the depth map. After that, based on the idea that a solid grasp required that the shape of the grasped part should be similar to the shape of the gripper’s interior, the regions of the depth map which better approximated the 3D shape of the gripper’s interior were computed. To choose between all the found regions, an objective function that assigned a score to each region was defined and needed to be maximized. The method was reliable and robust, but since only a single view was exploited, uncertainties on the grasp pose selection could be experienced due to the presence of occluded regions. To overcome this problem, different views can be added.

2.2. Three-Dimensional Registration

Thanks to the diffusion of powerful graphical processors and low-cost depth sensors, many 3D registration algorithms have been proposed to solve the object localization and reconstruction problem [22]. For example, in [23], the reconstruction of a nonflat steel 3D surface was performed by means of the 3D digital image correlation (3D-DIC) method [24]. Such a method leads to very accurate results but requires a time-consuming elaboration and the presence of a known pattern on the surface. Another technique that overcomes this drawback is the iterative closest point (ICP) [25], based on an iterative minimization of a suitable cost function. The ICP algorithm has been adopted to reconstruct an entire object starting from point clouds acquired from different views [26,27]. In [28], the ICP, combined with a genetic algorithm in order to improve its robustness to local minima, was adopted in an automotive factory environment in order to estimate the pose of car parts. The problem of local minima was addressed also by [29], where a global optimal ICP, based on a branch-and-bound theory, was presented. A recent algorithm for the registration of point clouds in the presence of outlier can be found in [30], where the registration problem was reformulated using a truncated least-squares cost function. It allowed the decoupling of the scale, rotation, and translation estimation in three subproblems solved in cascade thanks to an adaptive voting scheme.

3. Proposed Approach

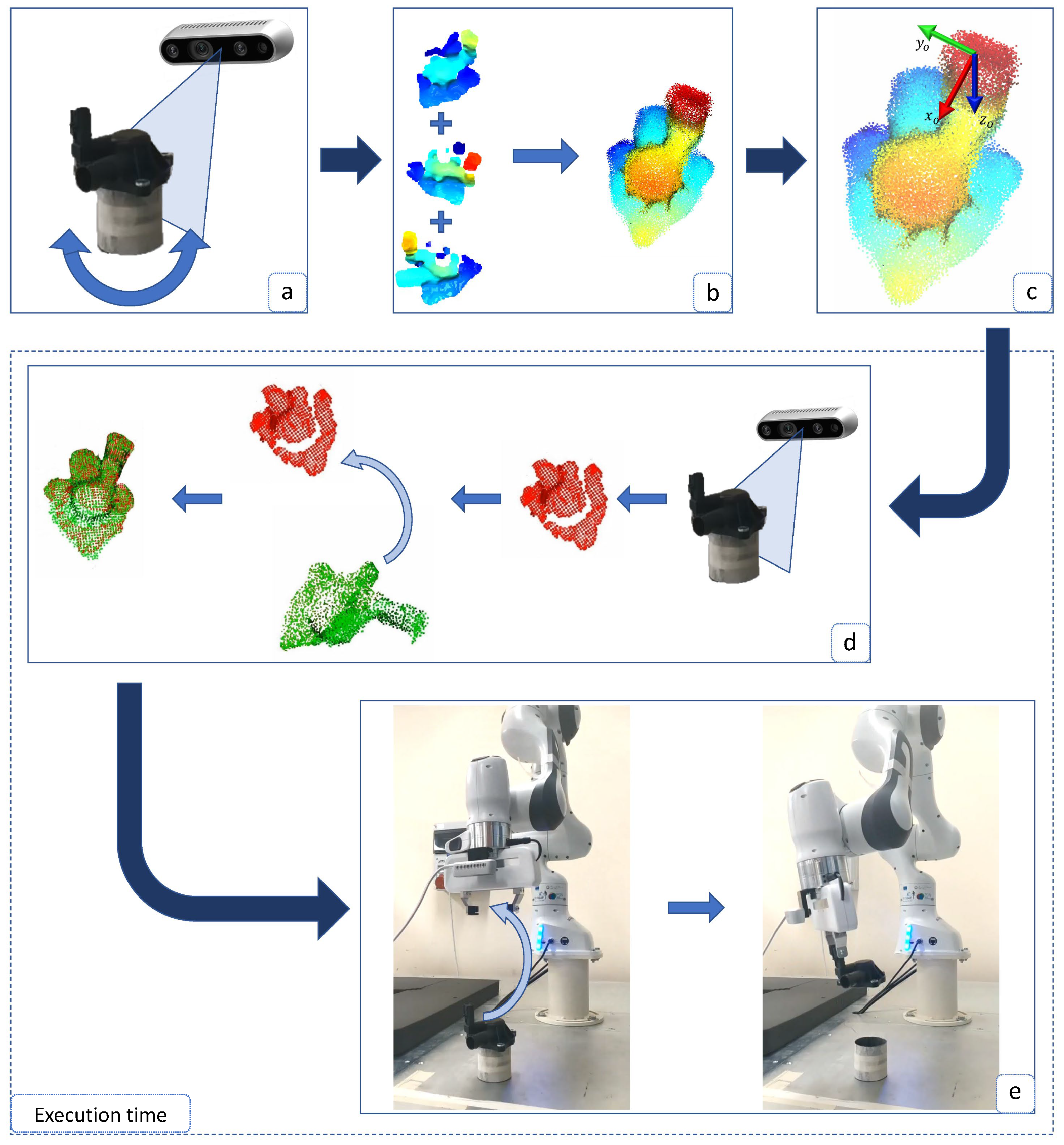
The proposed strategy is shown in Figure 2 and includes the following steps:

(a)

The 3D data of the object are acquired from different points of view, e.g., by using an RGB-D camera, in order to obtain n different point clouds of various portions of the object.

(b)

The point clouds are merged to obtain the model of the object surface, through a registration algorithm.

(c)

A frame that represents the best grasping pose for the object is attached to a point of the model built in the previous step. The grasping point is selected on the basis of the object geometry and the available gripper. Since more than a grasping point can be defined for each object, the one closest to the end-effector frame is selected.

(d)

The model is aligned to the current point cloud, in order to be able to transport the grasp pose on the current object. As a measure of the alignment, a fitness metric is computed. Thus, in the case of a bad alignment, the robot can move the camera in a new position, acquire the object point cloud from a different point of view and repeat the alignment.

(e)

The current grasp pose is transformed into the robot coordinates frame through the camera–end-effector calibration matrix and the robot is commanded to perform the grasp.

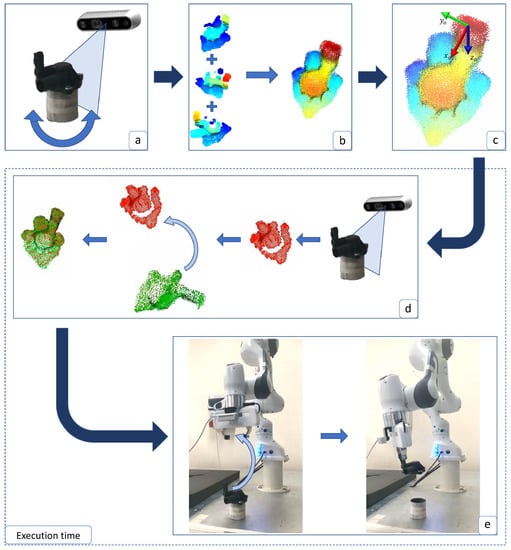
Figure 2. Proposed strategy. (a) Object data acquisition; (b) Model generation; (c) Grasp pose fixing. At execution time: (d) object data acquisition and overlapping with the model; (e) coordinate frame transformation and object grasping.

The registration algorithm used to merge the initial point clouds to obtain the object model was the iterative closest point algorithm (ICP) [25]. In particular, the point-to-plane version described in [31,32] was used. The calibration matrix was computed by acquiring a series of images of a calibration target, in arbitrary positions. A calibration target is a panel, with a predefined pattern, and the calibration software tool knows exactly its size, the color tone and the surface roughness.

3.1. Object Model Reconstruction

Consider two point clouds obtained by the same surface from two different points of view, $\mathcal{S}$ and $\mathcal{Q}$. They are registered if, for any pair of corresponding points $s_i\in \mathcal{S}$ and $q_j\in \mathcal{Q}$, representing the same point on the surface, there exists a unique homogeneous transformation matrix $\mathit{T}\in \mathrm{I}{\mathrm{R}}^{4\times 4}$ such that

$$\forall s_i\in \mathcal{S},\exists q_j\in \mathcal{Q}|\parallel \mathit{T}{\tilde{s}}_i-{\tilde{q}}_j\parallel =0.$$

(1)

The symbol $\tilde{}$ in (1) is the homogeneous representation of the coordinate vectors [33], i.e., $\widetilde{s_i}={\left[s_i^{\mathrm{T}}1\right]}^{\mathrm{T}}$.

Consider n point clouds acquired by means of an RGB-D camera from different views, ${\mathcal{P}}_i$ ($i=1,\cdots ,n$), the registration requires to find the homogeneous transformation matrices, ${\mathit{T}}_i$, that align the point clouds in a common reference frame.

To this aim, the same approach followed in [32], based on the point-to-plane iterative closest point (ICP) algorithm, was adopted. More specifically, the transformation matrix ${\mathit{T}}_j^i$ ($j=i+1,\cdots ,n$) that aligned ${\mathcal{P}}_j$ to ${\mathcal{P}}_i$ was derived by minimizing the following cost function with respect to ${\mathit{T}}_j^i$

$$\mathcal{C}({\mathit{T}}_j^i)=\sum _{{\mathsf{\pi }}_{j,l}\in {\mathcal{P}}_j,{\mathsf{\pi }}_{i,l}\in {\mathcal{P}}_i}{\left({({\mathit{T}}_j^i{\tilde{\mathsf{\pi }}}_{j,l}-{\tilde{\mathsf{\pi }}}_{i,l})}^{\mathrm{T}}{\tilde{\mathit{n}}}_{j,l}^i\right)}^2,$$

(2)

where ${\tilde{\mathit{n}}}_{j,l}^i={\mathit{T}}_j^i{\tilde{\mathit{n}}}_{j,l}$ is the homogeneous representation of the unit vector normal to the surface represented by the point cloud ${\mathcal{P}}_j$ in the point ${\mathsf{\pi }}_{j,l}$. Each ${\mathit{T}}_j^i$ was characterized by 12 unknown components: by resorting to a a least-squares estimation, finding the matrix ${\mathit{T}}_j^i$ that minimized the cost function (2) required at least 4 pairs of corresponding points.

This method was exploited in the multiway registration algorithm, implemented in the Open3D library [34], which was run to register the acquired point clouds, ${\mathcal{P}}_i$.

The registered point clouds were finally merged in a single point cloud to have the reconstructed object model, i.e.,

$${\mathcal{P}}_r=\bigcup _{i=1}^n\bigcup _{j=1}^{N_i}{\mathit{T}}_i{\tilde{\mathsf{\pi }}}_{i,j}.$$

(3)

3.2. Grasp Point Estimation

Once the model of the object was built, one grasp point candidate, O, was selected, and the relative coordinate frame ${\mathcal{F}}_o=O,x_o{y}_o{z}_o$ was defined. The RGB-D camera acquired a point cloud, ${\mathcal{P}}_a$, of the object to be grasped, and such a point cloud was aligned to the known one (3) representing the model. Again, a procedure based on the ICP algorithm was applied:

• A set of local features, called fast point feature histograms (FPFH), were extracted from each point of ${\mathcal{P}}_a$ [35];
• The corresponding points of the two point clouds were computed by using a RANSAC (random sample consensus) algorithm [36]: at each iteration, given $\mu$ points randomly extracted from ${\mathcal{P}}_r$, the corresponding points of ${\mathcal{P}}_a$ were the nearest with respect to the extracted features.
• The transformation matrix computed at the previous step was used as an initial guess for the ICP algorithm aimed at refining the alignment.

If the acquired point cloud was not very detailed, the previous algorithm led to accurate results only in the presence of a small orientation error between the two point clouds, otherwise poor surface alignments could be obtained. To avoid this issue and to have an accurate estimation of the grasping pose, the acquired point cloud was compared with $n_R$ different point clouds, obtained by rotating the reconstructed model by an angle $2\pi /n_R$. The point cloud with the best match was then selected to compute the grasping pose. The best match was measured through a fitness metric, which measured the overlapping area between the two point clouds. In particular, the fitness was computed as the ratio between the number of correspondence points, i.e., points for which the corresponding point in the target point cloud had been found and the number of the points in the target point cloud.

Once the point cloud model ${\mathcal{P}}_r$ was aligned with the acquired one ${\mathcal{P}}_a$, it was possible to localize the position of the grasping point O and the orientation of the corresponding reference frame in the camera coordinate frame. Finally, trough a camera calibration process [37], it was possible to compute the camera–end-effector transformation and transform the grasping pose in the robot’s base coordinate frame.

3.3. Grasping

Define the coordinate frame ${\mathcal{F}}_e$ attached to the robot’s end-effector as shown in Figure 3. The grasp requires the alignment of ${\mathcal{F}}_e$ to the object’s frame ${\mathcal{F}}_o$. To this aim, a trajectory planner for the end-effector was implemented by assigning three way-points, namely, the current pose, a point along the z axis of the object reference frame at a distance of 10 cm to the origin O, and the origin of the object frame O.

Figure 3. Reference frames for the end-effector, the camera and the object.

Regarding the orientation of ${\mathcal{F}}_e$, the planner aligned the axis $z_e$ to $-z_o$ and $y_e$ to $y_o$ before reaching the second way-point, and then it was kept constant for the last part of the path.

By denoting with $x_d$ and $x_e$ the desired and the actual end-effector pose, respectively, the velocity reference for the robot joints, ${\dot{\mathit{q}}}_r$, were computed via a closed-loop inverse kinematics algorithm [33]

$${\dot{\mathit{q}}}_r={\mathit{J}}^{†}\left(\mathit{q}\right)({\dot{\mathit{x}}}_d+\mathit{K}({\mathit{x}}_d-{\mathit{x}}_e)),$$

(4)

where ${\mathit{J}}^{†}\left(\mathit{q}\right)$ is the right pseudoinverse of the Jacobian matrix, and $\mathit{K}\in \mathrm{I}{\mathrm{R}}^{6\times 6}$ is a matrix of positive gains.

4. Implementation

The experimental setup consisted of a collaborative robot Franka Emika Panda [38] equipped with an Intel RealSense D435 camera [39] in an eye-in-hand configuration as shown in Figure 1. The libfranka C++ open-source library was used to control the robot by means of an external workstation through an Ethernet connection. The workstation, equipped with an Intel Xeon 3.7 GHz CPU with 32 GB RAM, ran the Ubuntu 18.04 LTS operating system with a real-time kernel. The camera was calibrated with a set of 30 images of a 2D checkerboard flat pattern through the method developed in [37]. Vision software ran on the same workstation of the robot control, while the camera data acquisition required the librealsense2 library.

5. Experimental Results

The proposed approach was evaluated by considering three different objects used in a real-world automotive factory. Each object was located above the table surface to allow a faster background elimination from the point cloud.

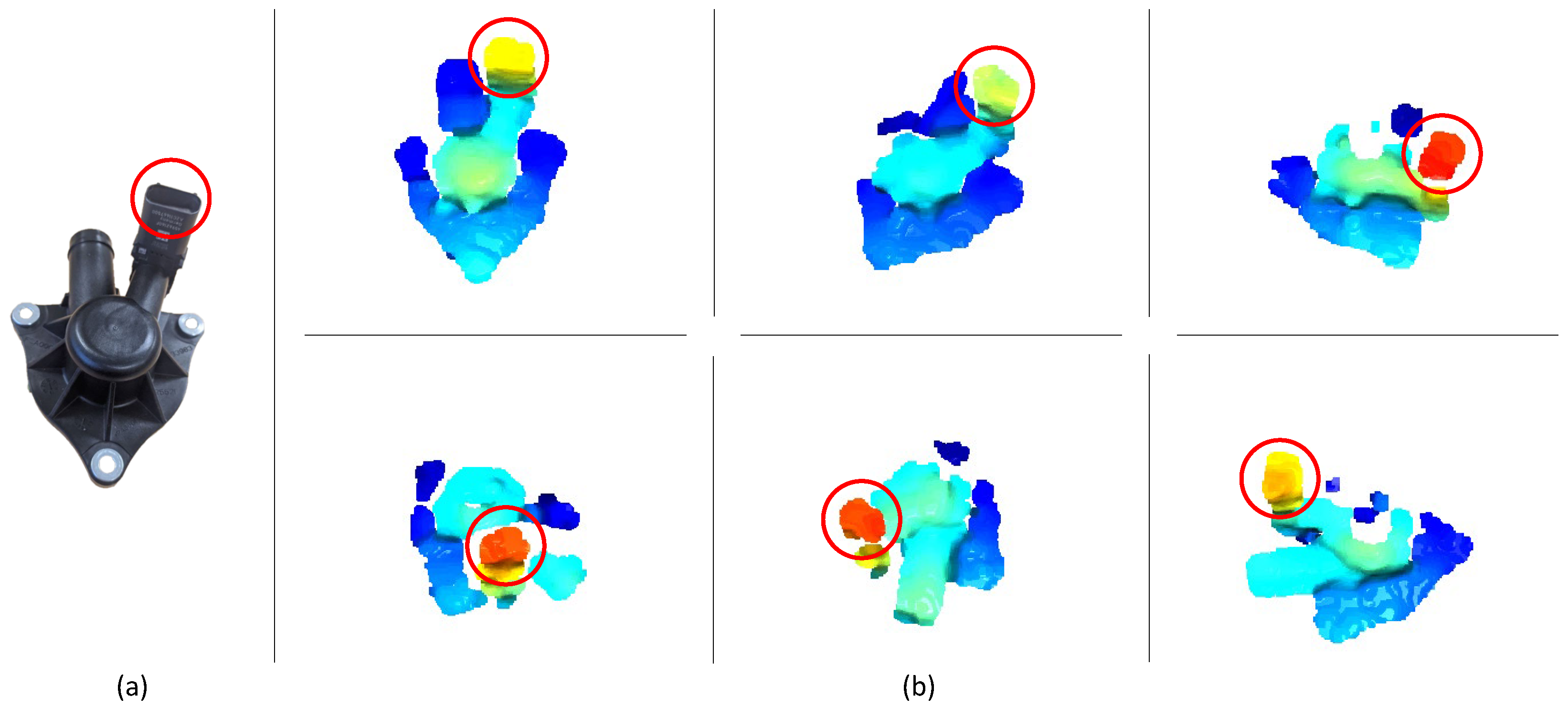
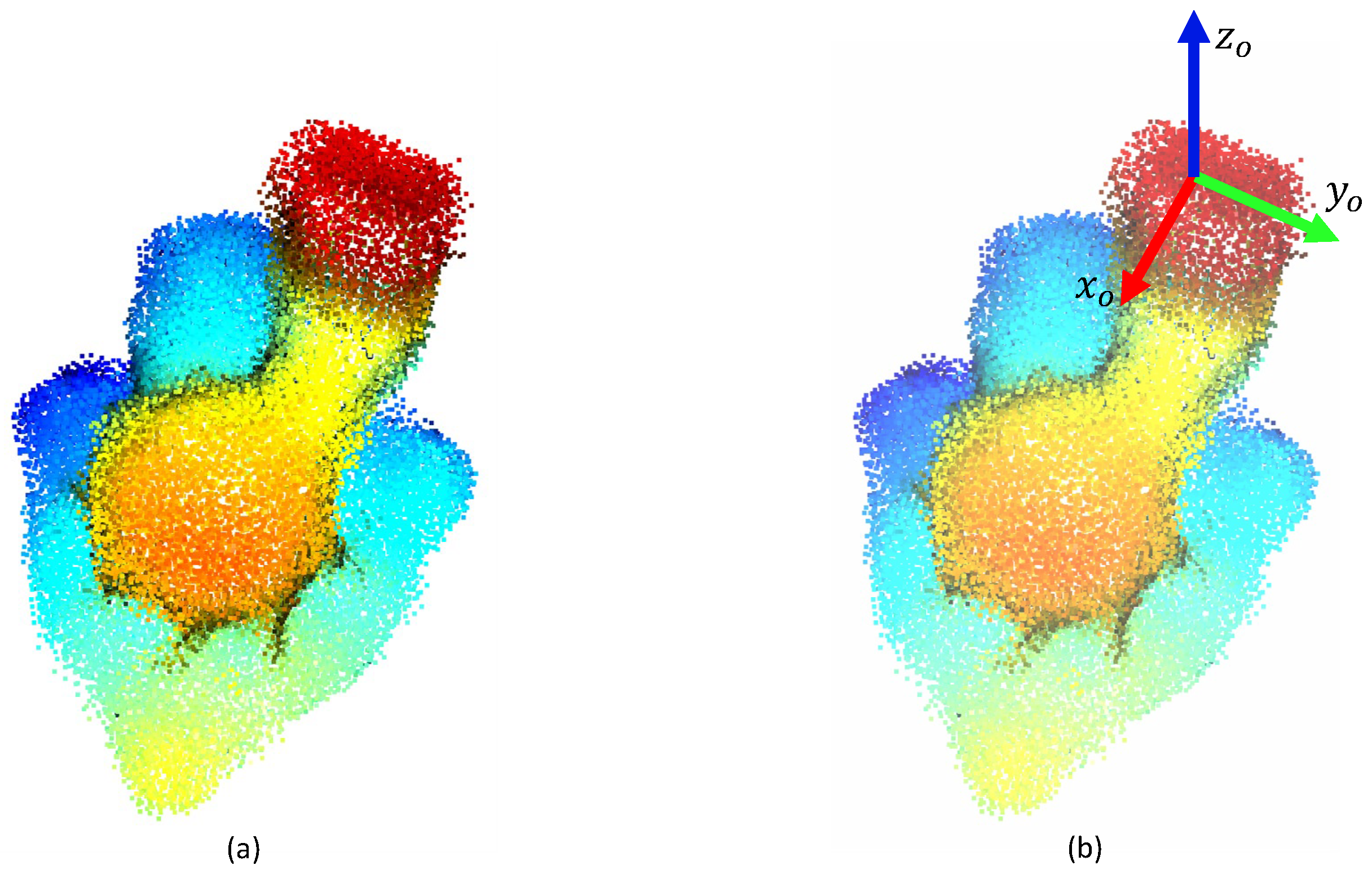
To generate the model, having the camera in a fixed position, the object was rotated to allow the data acquisition in 30 different configurations. Examples of acquired point clouds are shown in Figure 4. Then, according to the method described in Section 3.1, these point clouds were merged by using the ICP algorithm and a point cloud of the whole object was obtained (see Figure 5a). This point cloud represented the object model in which the grasp pose was selected, by using any modeling software. An example of a grasping pose is shown in Figure 5b.

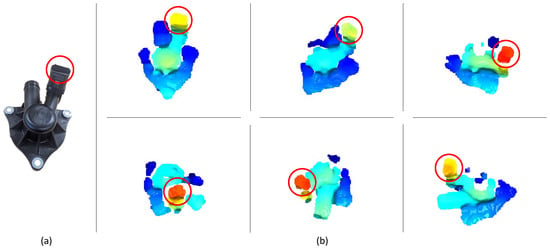
Figure 4. Plastic oil separator crankcase (a) and some examples of acquired point clouds (b). The red circle indicates the same part in the various views.

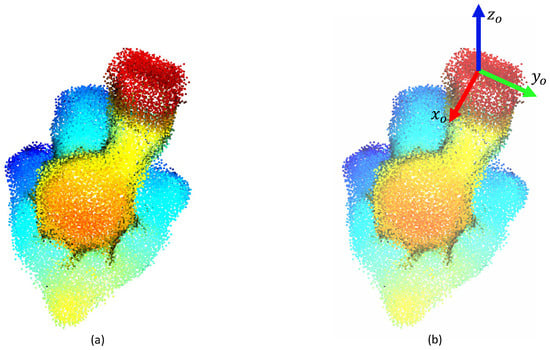
Figure 5. (a) Generated model for the plastic oil separator crankcase; (b) Grasp pose selection.

The mechanical workpieces used in the experiments and their corresponding generated model are shown in Figure 6.

Figure 6. Mechanical workpieces and respective generated models: (a) plastic oil separator crankcase, (b) metal oil separator crankcase, (c) air pipe.

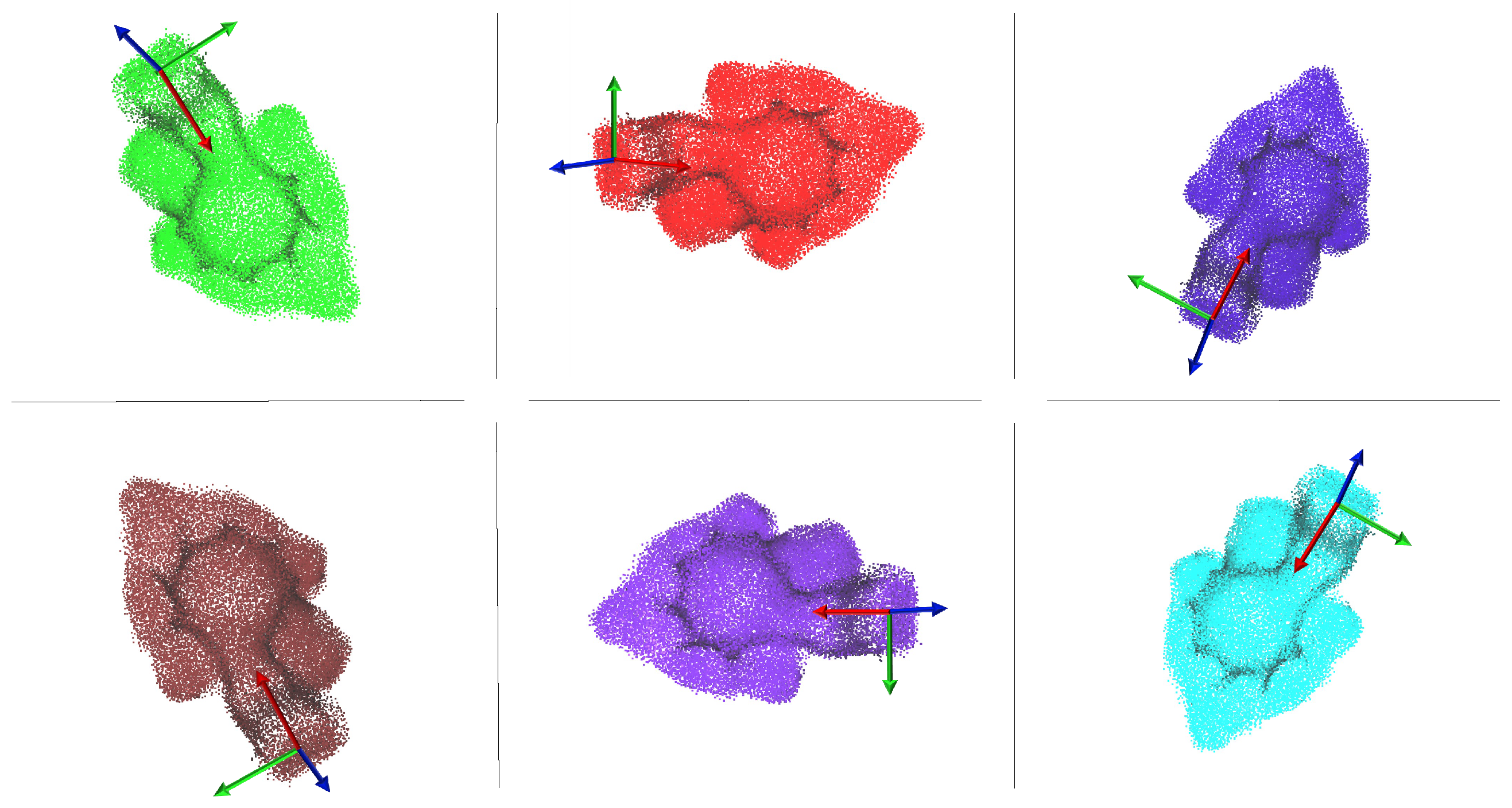
When an object needed to be grasped, its point cloud was acquired and overlapped with the one that represented the model. As detailed in Section 3.2, the current point cloud was compared with the model point cloud with eight different orientations, in order to find the best matching one. Figure 7 shows the models with different orientations.

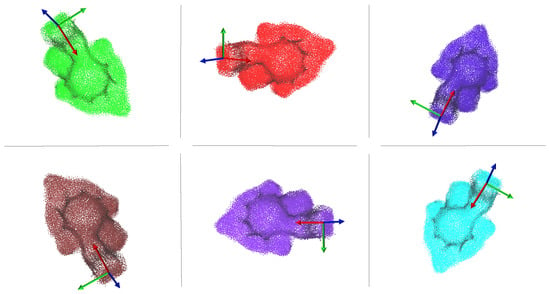
Figure 7. Example of the various models with different orientations for the plastic oil separator crankcase. The red, green and blue arrows represent the x, y and z axes, respectively.

In order to evaluate our approach the following procedure was implemented:

• For each model orientation, a maximum number of 100 iterations was established;
• Two thresholds for the fitness were defined: threshold $f_l$ below which the overlap was considered failed and threshold $f_h$ above which the overlap was considered good enough;
• During the overlapping, if threshold $f_h$ was exceeded, the algorithm stopped and no further comparisons were made;
• If no overlap exceeded threshold $f_h$, the one with the highest fitness was considered;
• If no overlap exceeded threshold $f_l$, the algorithm reported a failure.

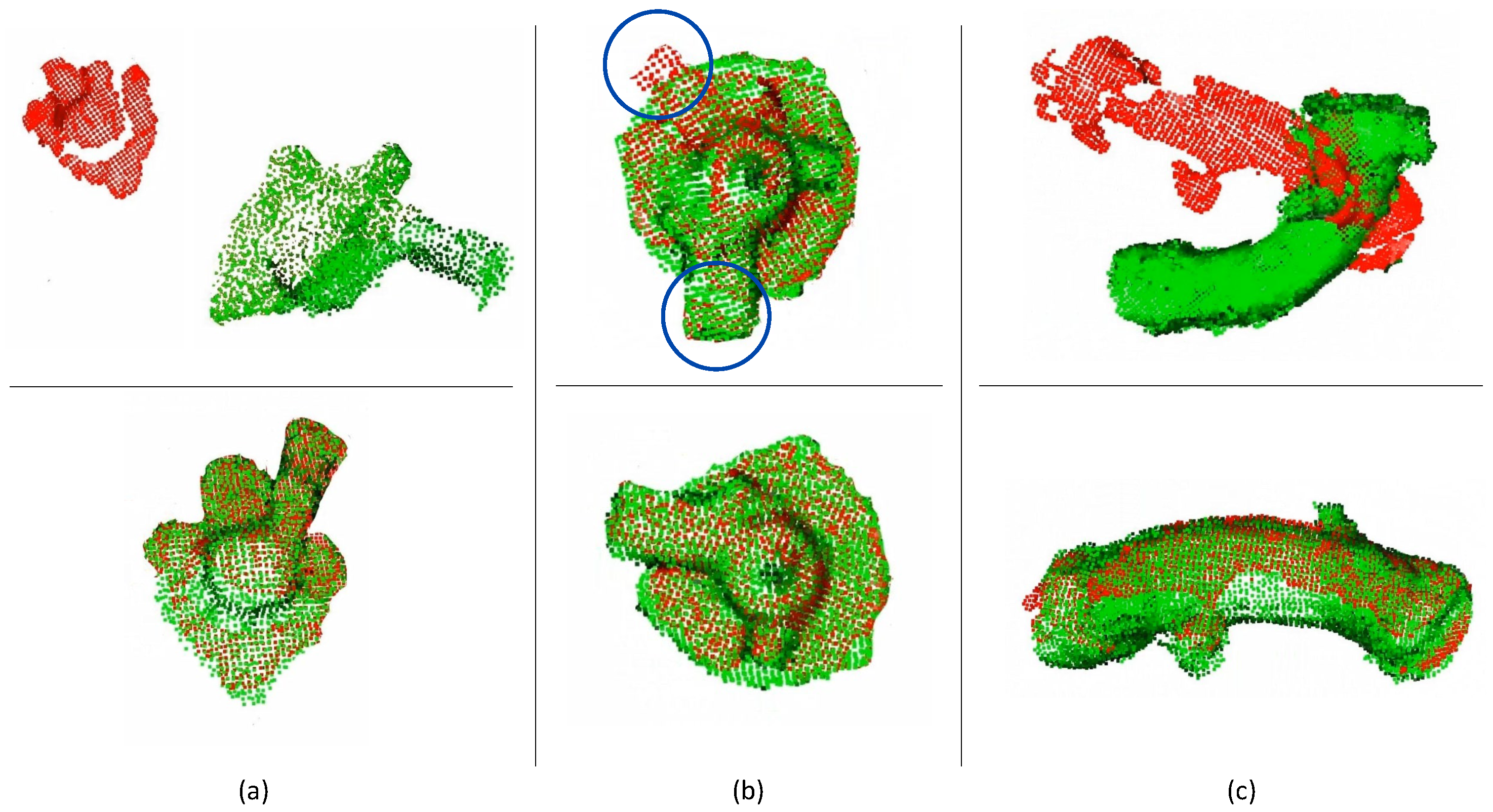
Examples of correct and incorrect overlaps for the three considered workpieces are reported in Figure 8.

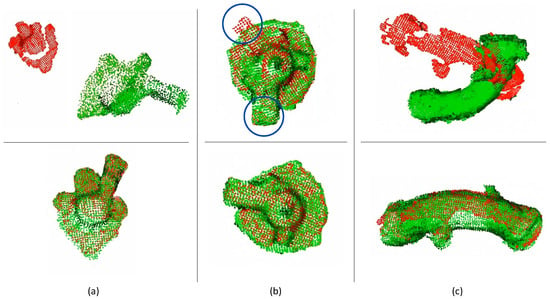
Figure 8. Examples of overlap failure (top row) and success (bottom row) for three objects: (a) plastic oil separator crankcase, (b) metal oil separator crankcase, (c) air pipe. The current point clouds acquired by the depth sensor are in red, while the model point clouds are in green. The blue circles highlight the nonoverlap for the metal oil separator crankcase by indicating the same object part not aligned.

In the case of a failure, the robot manipulator moved the camera around the object in order to acquire a new image from a different point of view. Then, the whole procedure was restarted.

After the above procedure, the labeled grasp pose could be projected on the current object, which was referred with respect to the robot base frame. After a further transformation, by using the camera–end-effector calibration matrix, the robot could be commanded to perform the object grasp.

Regarding the plastic and metal oil separator crankcases (see Figure 6a,b), the algorithm was able to find the match and the robot was able to grasp the object.

Define the estimation grasping position and orientation errors as

$$\begin{array}{ccc}\hfill {\mathit{e}}_p^o& =& {\mathit{p}}^o-{\widehat{\mathit{p}}}^o,\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill {\mathit{e}}_{\varphi }^o& =& {\mathsf{\varphi }}^o-{\widehat{\mathsf{\varphi }}}^o,\hfill \end{array}$$

(6)

where p ($\mathsf{\varphi }$) is the actual grasping point position (orientation, expressed as a triple of Euler angles [33]) while $\widehat{\mathit{p}}$ ($\widehat{\mathsf{\varphi }}$) are the estimates provided by the visual algorithm. The superscript ^o means that all the variables are expressed in the object frame ${\mathcal{F}}_o$.

Table 1 and Table 2 report the errors for the plastic oil separator crankcase and the metal one, respectively. A set of snapshots of the grasping procedure for the two objects is detailed in Figure 9.

Table 1. Test results for the plastic oil separator crankcase. The position errors are in mm while the orientation errors are in rad.

Test	${\mathit{e}}_{{\mathit{p}}_{\mathit{x}}}$	${\mathit{e}}_{{\mathit{p}}_{\mathit{y}}}$	${\mathit{e}}_{{\mathit{p}}_{\mathit{z}}}$	${\mathit{e}}_{{\mathit{\varphi }}_{\mathit{x}}}$	${\mathit{e}}_{{\mathit{\varphi }}_{\mathit{y}}}$	${\mathit{e}}_{{\mathit{\varphi }}_{\mathit{z}}}$
1	1.964	5.316	5.858	0.293	0.084	0.273
2	4.759	1.076	4.006	0.176	0.123	0.233
3	8.460	1.400	1.040	0.048	0.116	0.237
4	0.600	0.380	0.000	0.304	0.072	0.142
5	2.260	2.300	8.200	0.392	0.263	0.130
6	0.310	3.320	6.433	0.169	0.489	0.083
7	5.011	1.637	5.641	0.133	0.171	0.164
8	4.989	1.151	4.758	0.219	0.146	0.230
9	1.240	1.331	5.402	0.202	0.065	0.155
10	4.373	0.095	10.515	0.016	0.170	0.107
11	5.966	1.398	3.785	0.101	0.019	0.179
12	1.442	4.579	5.702	0.104	0.052	0.189
13	4.529	1.033	10.044	0.048	0.115	0.099
14	2.042	1.057	3.729	0.092	0.033	0.113
15	3.533	1.509	2.023	0.110	0.088	0.166
16	2.202	5.128	3.623	0.084	0.154	0.043
17	4.798	3.496	7.289	0.066	0.019	0.216
18	7.122	2.755	13.521	0.012	0.254	0.146
Mean error	3.644	2.164	5.643	0.143	0.135	0.161
Standard deviation	2.219	1.542	3.299	0.103	0.110	0.059

Table 2. Test results for the metal oil separator crankcase. The position errors are in mm while the orientation errors are in rad.

Test	${\mathit{e}}_{{\mathit{p}}_{\mathit{x}}}$	${\mathit{e}}_{{\mathit{p}}_{\mathit{y}}}$	${\mathit{e}}_{{\mathit{p}}_{\mathit{z}}}$	${\mathit{e}}_{{\mathit{\varphi }}_{\mathit{x}}}$	${\mathit{e}}_{{\mathit{\varphi }}_{\mathit{y}}}$	${\mathit{e}}_{{\mathit{\varphi }}_{\mathit{z}}}$
1	1.143	3.243	13.409	0.039	0.015	0.133
2	3.157	2.066	10.148	0.005	0.051	0.146
3	0.852	6.250	4.402	0.013	0.042	0.291
4	8.063	7.524	0.843	0.024	0.017	0.018
5	6.522	4.445	7.708	0.012	0.019	0.053
6	2.922	0.093	5.704	0.024	0.005	0.068
7	1.727	2.234	6.592	0.013	0.002	0.096
8	0.379	1.559	11.784	0.013	0.026	0.009
9	7.802	1.887	7.063	0.060	0.091	0.054
10	8.114	0.677	8.383	0.023	0.054	0.028
11	2.548	1.079	8.268	0.002	0.040	0.079
12	2.814	2.884	6.487	0.169	0.003	0.183
13	0.816	0.460	13.407	0.017	0.024	0.157
14	5.874	0.002	7.367	0.070	0.189	0.073
15	9.727	0.415	2.165	0.001	0.105	0.000
16	5.761	0.153	9.530	0.038	0.101	0.012
17	4.702	3.785	0.587	0.091	0.082	0.027
18	5.360	2.653	7.143	0.002	0.029	0.051
Mean error	4.349	2.301	7.277	0.034	0.050	0.082
Standard deviation	2.845	2.077	3.616	0.041	0.047	0.073

Figure 9. Snapshots of the grasping procedure for two different objects: (a–e) a point cloud is acquired; (b–f) the robot approaches the object close to the estimated grasping point; (c–g) the end-effector grasps the object; (d–h) the object is raised by the robot.

As can be observed, on 18 successfully tests conducted in different light conditions due to the presence of natural light in the environment, the mean error was about $3.82$ mm ($0.15$ radians) for the plastic oil separator crankcase and $4.64$ mm ($0.06$ radians) for the metal one. However, a wide deviation was experienced in the different tests, as witnessed by the values of the standard deviations in the Tables. This was mainly due to the adoption of low-detailed point clouds. More generally, regarding the whole experimental campaign, a success rate of $88.3\%$ was experienced for the plastic oil separator crankcase and $84.8\%$ for the metal one.

Although the model was well-built, for the air pipe (see Figure 6c), the experiments showed that the search for the best match was not successful. This was probably due to the symmetry of the object and the model not being very accurate. The algorithm was not able to find a match because many portions of the object were quite similar. Correct overlaps were found only when the object orientations were close to those considered for the model. In this case, a success rate of only $32.7\%$ was experienced.

The obtained results show that the proposed method can be promising for the grasping of partially known objects in the absence of a CAD model, but it requires a further investigation in order to better analyze the features required for a correct execution of the registration and make it work on symmetric components as well.

A video of the execution can be found at https://web.unibas.it/automatica/machines.html (accessed on 14 March 2023) while the code is available in the GitHub repository at https://github.com/sileom/graspingObjectWithModelGenerated.git (accessed on 14 March 2023).

6. Conclusions

A method to handle the problem of grasping partially known objects in an unstructured environment was proposed. The approach could be used in the absence of accurate object models and consisted of a comparison between a point cloud of the object and a model built from a set of point clouds previously acquired. The experiments, conducted on a set of mechanical workpieces used in real-world automotive factories, showed that the method was applicable in the case of objects with particular shapes, but not in the case of objects with symmetric shape. Camera features influenced the overall performance: a more accurate sensor could allow us to build a more detailed model to improve the performance and robustness of the approach. Future work will be devoted to extending the method to any kinds of components.