An Investigation of Factors Influencing Tool Life in the Metal Cutting Turning Process by Dimensional Analysis †
Abstract
1. Introduction
2. Methodology
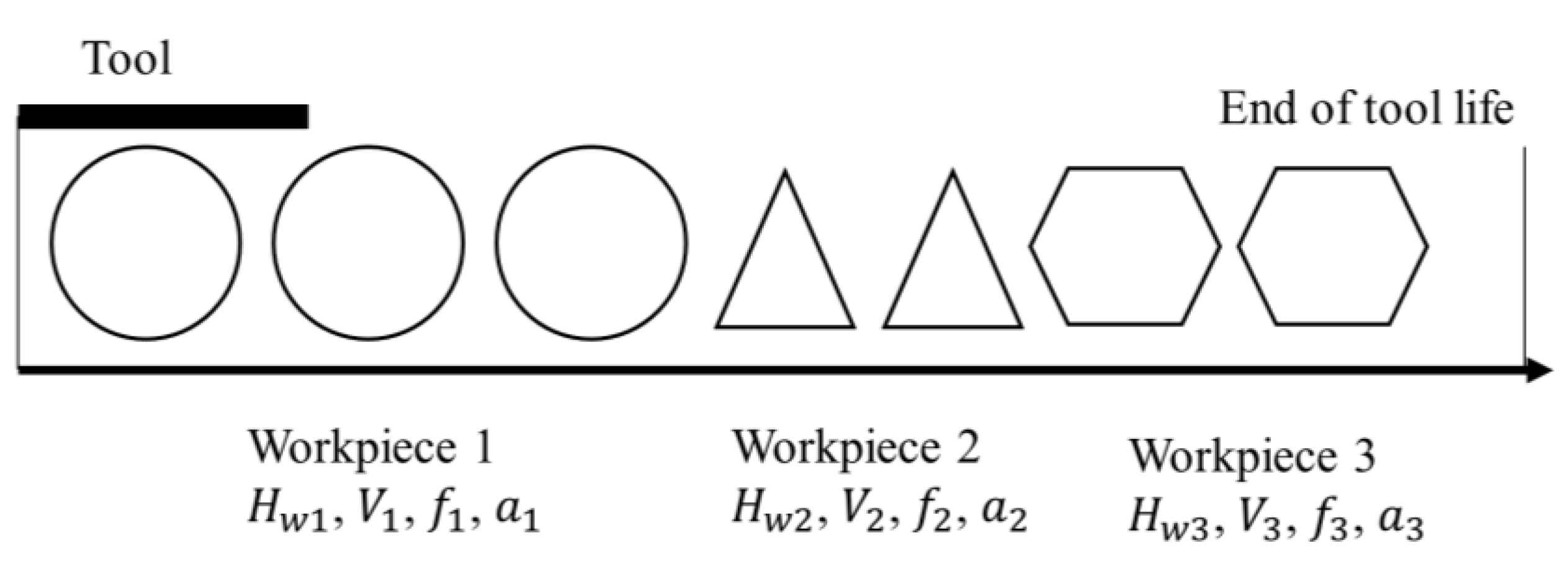
2.1. The Scope of the Analysis and Review Methodology
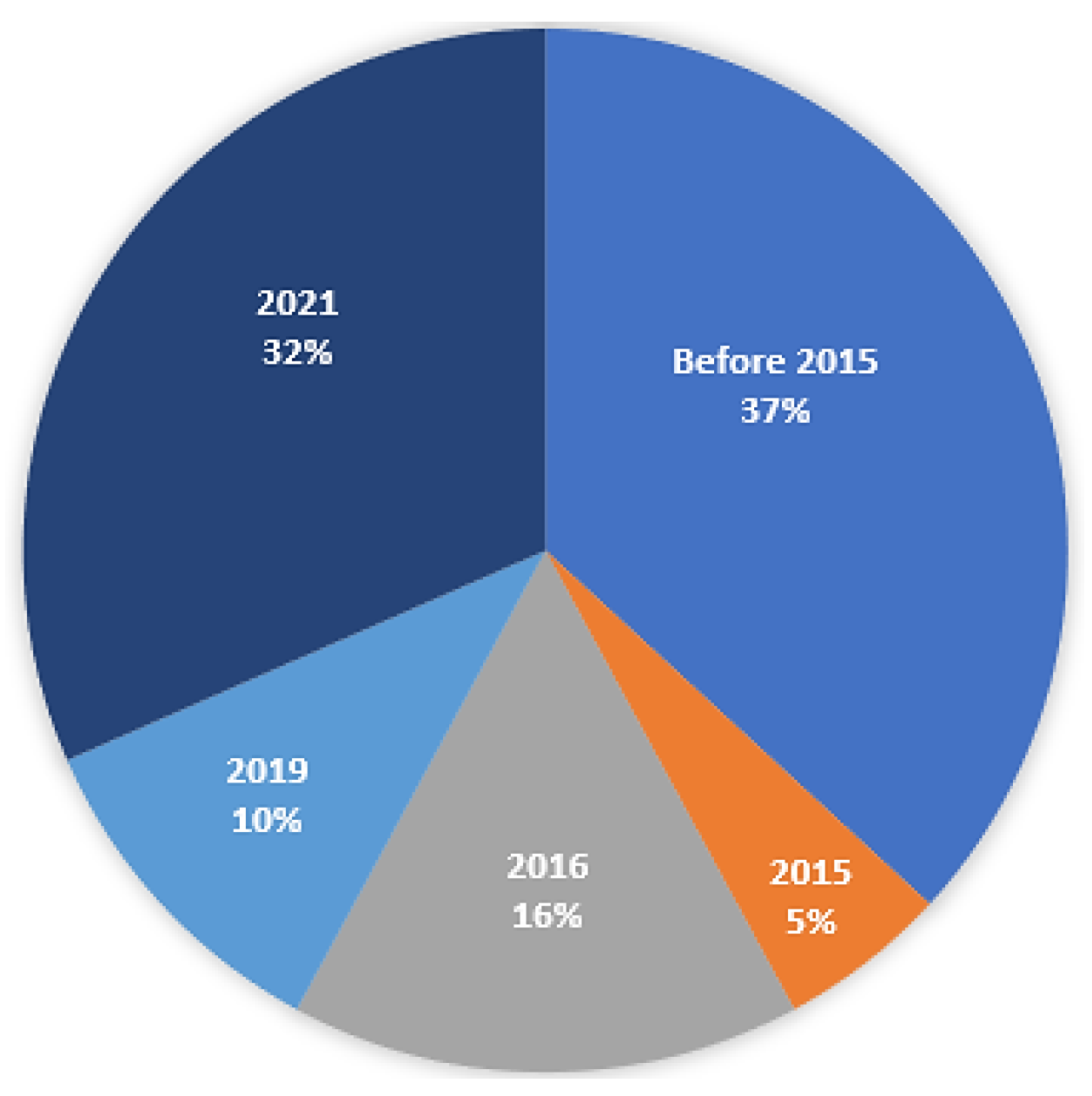
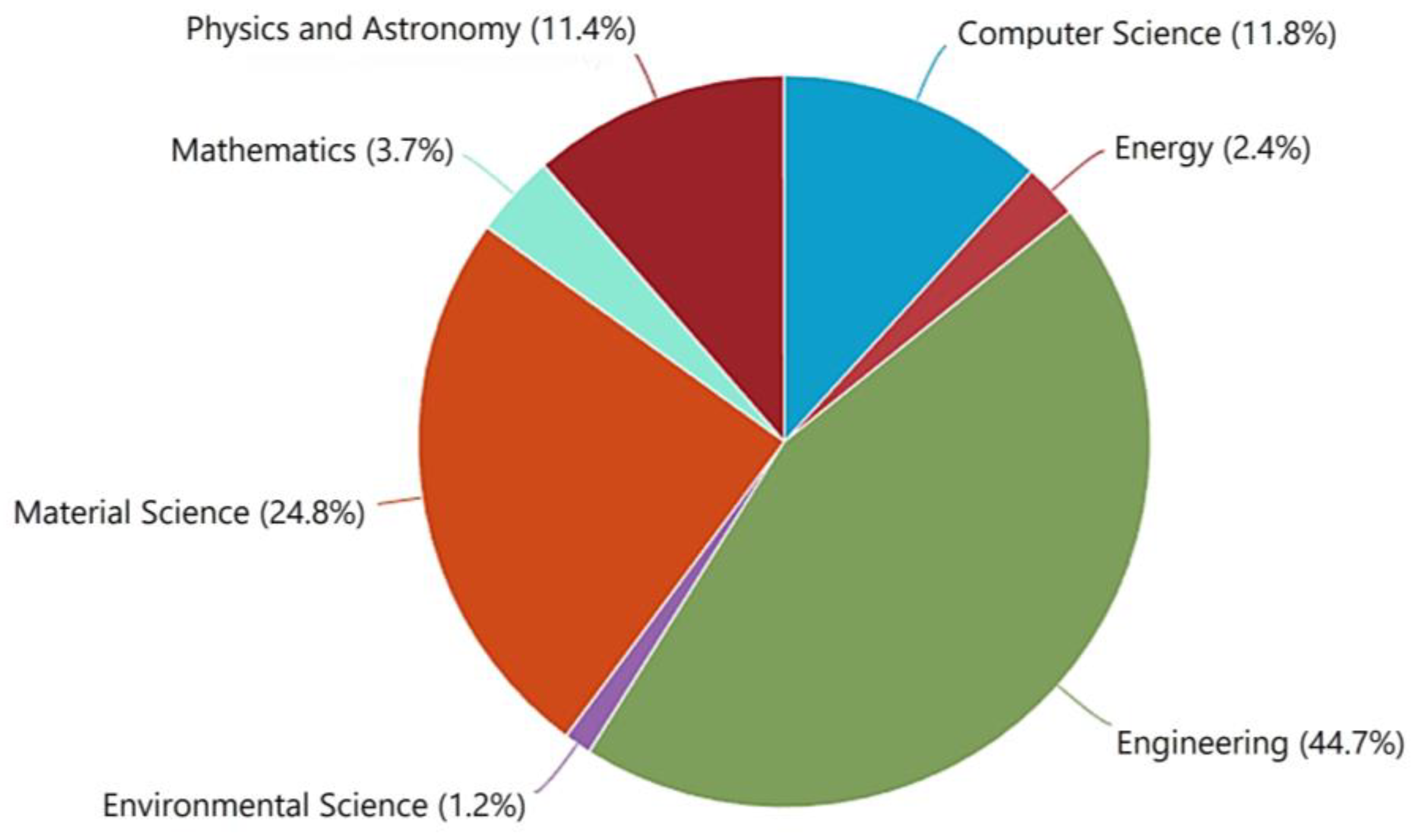
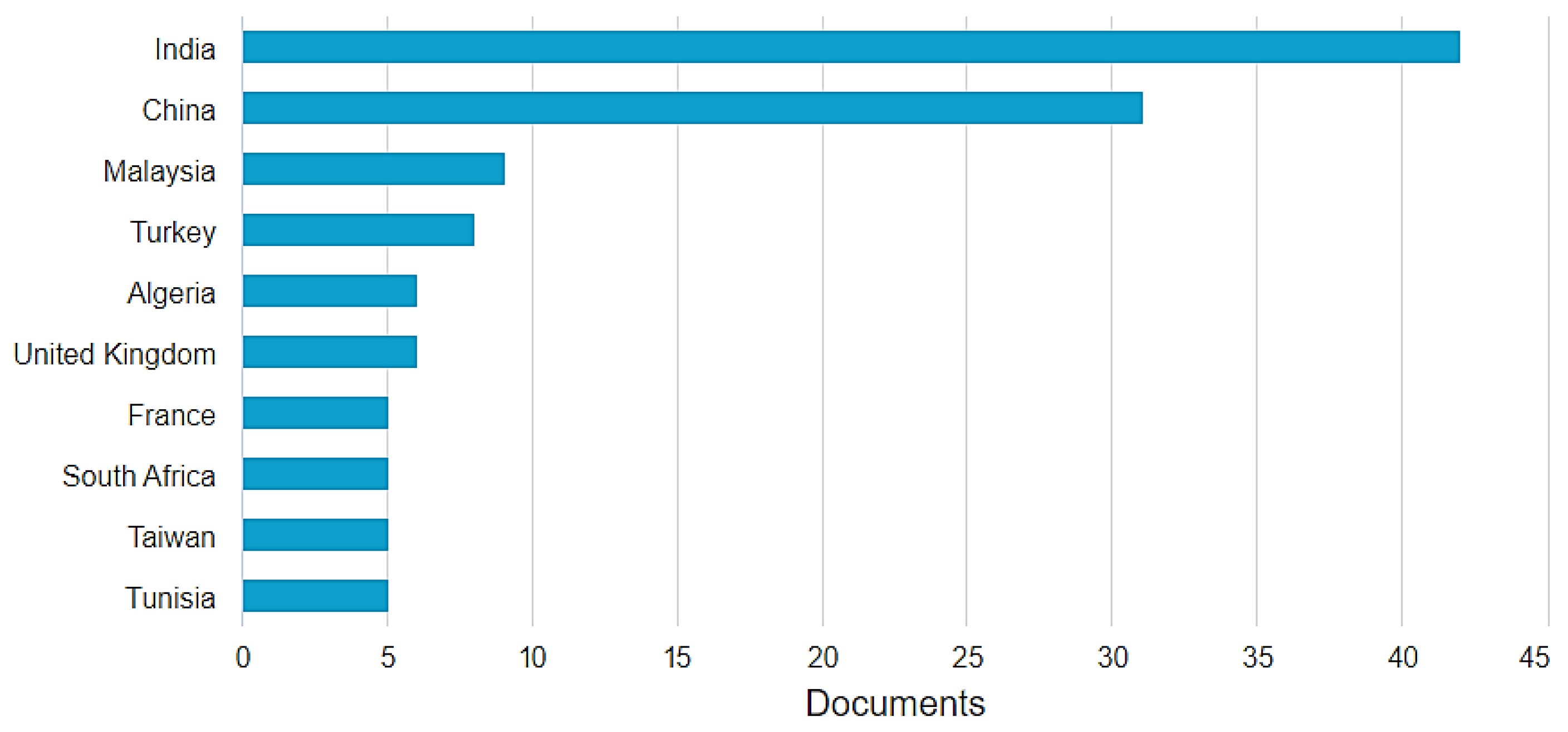
2.2. Bibliometrics Analysis
2.3. Dimensional Analysis
- Determine the given quantity for the problem.
- Determine the answer to the problem (desired quantity).
- Using equivalents as conversion factors, establish the unit path from the given quantity to the desired quantity.
- Configure the conversion factors so that the cancelled units can be returned.
- To determine the numerical value of the desired quantity, multiply the numerators, the denominators, and the product of the numerators by the product of the denominators.
3. Result
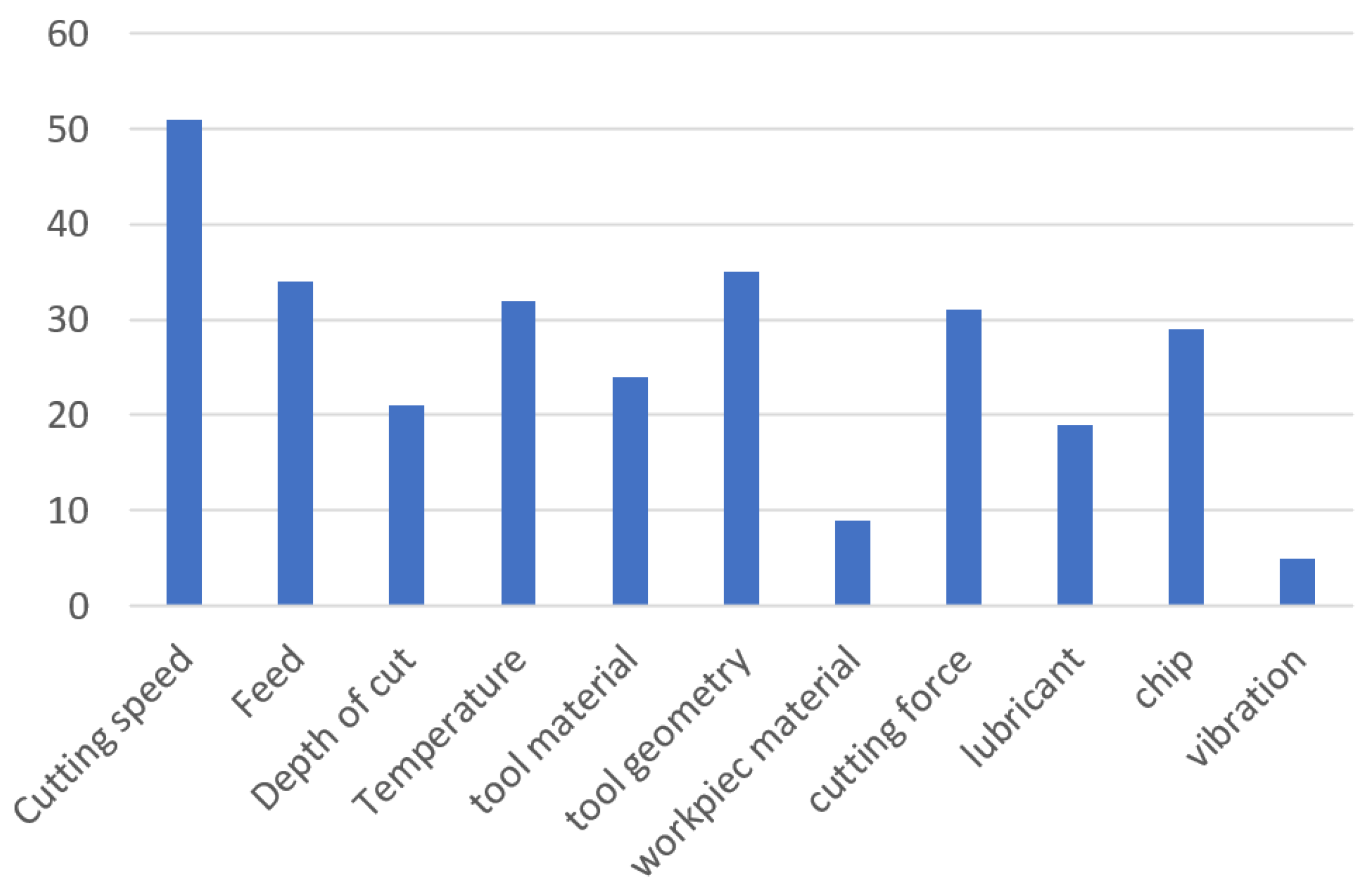
3.1. Research-Literature Review
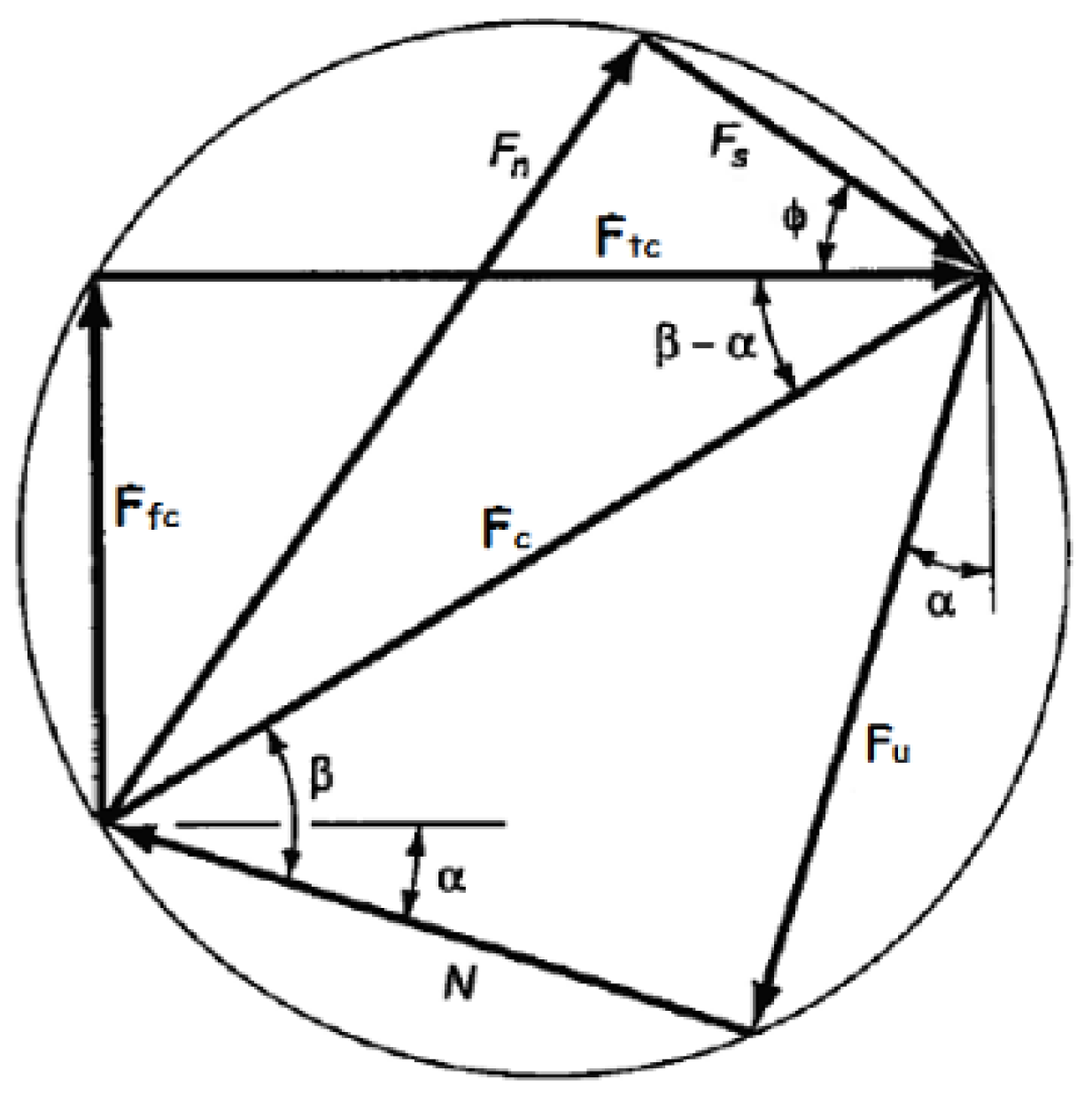
3.2. Dimensional Analysis
- M (mass)
- L (length)
- T (time)
- Tool life (Z): T
- Tool hardness (:
- Workpiece hardness (:
- Cutting speed ():
- Feed rate (f):
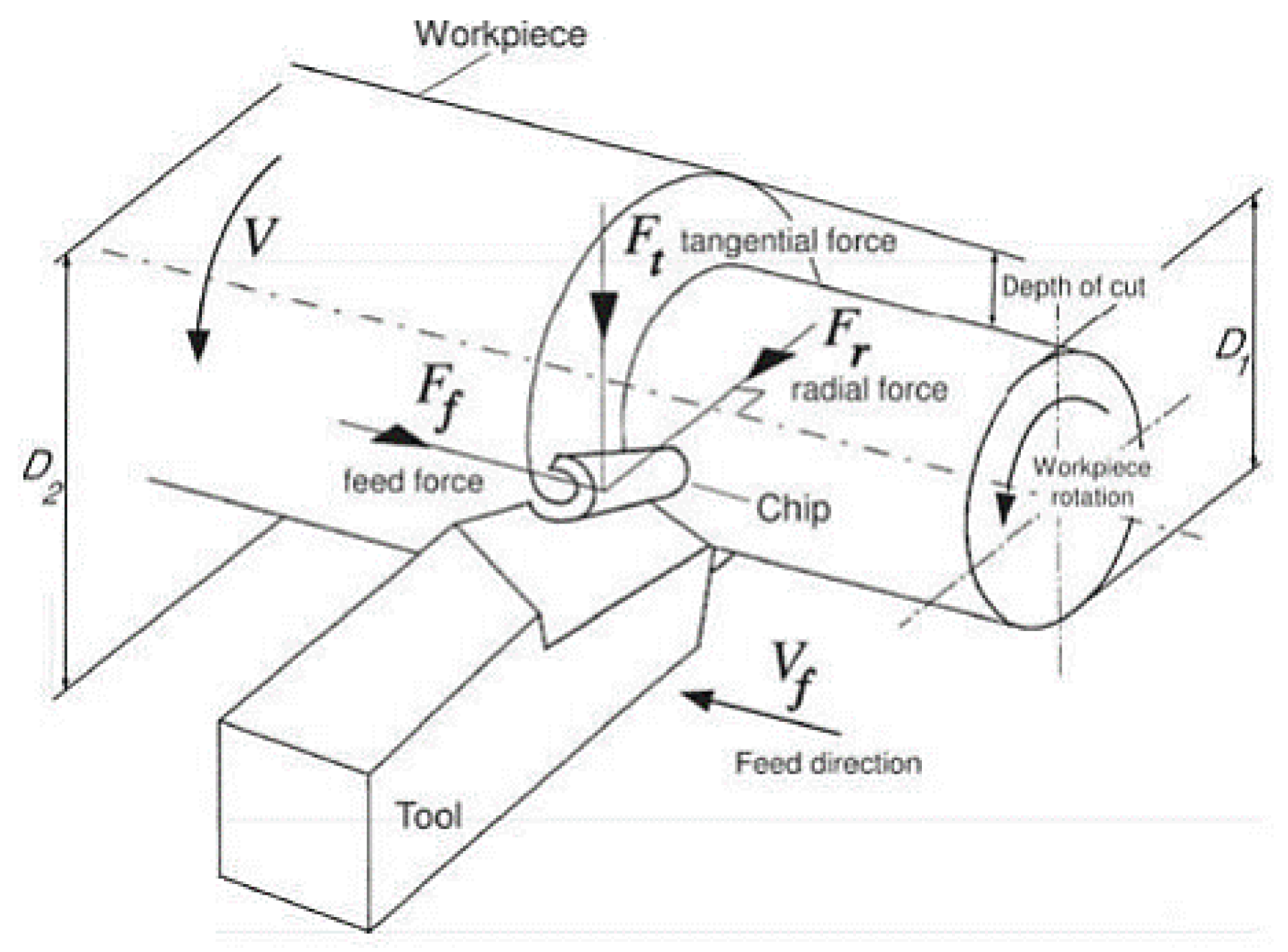
- Depth of cut (a):
- Cutting Force (F):
- Cutting temperature (
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Groover, M.P. Fundamentals of Modern Manufacturing: Materials, Processes, and Systems; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Grigoriev, S.N.; Gurin, V.D.; Volosova, M.A.; Cherkasova, N.Y. Development of residual cutting tool life prediction algorithm by processing on CNC machine tool. Mater. Werkst. 2013, 44, 790–796. [Google Scholar] [CrossRef]
- Urbikain, G.; Alvarez, A.; López de Lacalle, L.N.; Arsuaga, M.; Alonso, M.A.; Veiga, F. A reliable turning process by the early use of a deep simulation model at several manufacturing stages. Machines 2017, 5, 15. [Google Scholar] [CrossRef]
- Upadhyaya, G.S. “Trent EM, Wright PK: Metal cutting,” Butterworth-Heinemann”, Boston”, 2000. Sci. Sinter. 2004, 36, 54. [Google Scholar]
- Seemuang, N.; McLeay, T.; Slatter, T. Using spindle noise to monitor tool wear in a turning process. Int. J. Adv. Manuf. Technol. 2016, 86, 2781–2790. [Google Scholar] [CrossRef]
- Xu, W.; Cao, L. Optimal tool replacement with product quality deterioration and random tool failure. Int. J. Prod. Res. 2015, 53, 1736–1745. [Google Scholar] [CrossRef]
- Aslantas, K.; Ucun, I.; Cicek, A. Tool life and wear mechanism of coated and uncoated Al2O3/TiCN mixed ceramic tools in turning hardened alloy steel. Wear 2012, 274, 442–451. [Google Scholar] [CrossRef]
- Kuntoğlu, M.; Aslan, A.; Pimenov, D.Y.; Usca, Ü.A.; Salur, E.; Gupta, M.K.; Mikolajczyk, T.; Giasin, K.; Kapłonek, W.; Sharma, S. A Review of Indirect Tool Condition Monitoring Systems and Decision-Making Methods in Turning: Critical Analysis and Trends. Sensors 2020, 21, 108. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.; Yan, T.; Li, N.; Guo, L. Recurrent convolutional neural network: A new framework for remaining useful life prediction of machinery. Neurocomputing 2020, 379, 117–129. [Google Scholar] [CrossRef]
- Dhananjay Patange, A.; Jegadeeshwaran, R. A machine learning approach for vibration-based multipoint tool insert health prediction on vertical machining centre (VMC). Measurement 2021, 173, 108649. [Google Scholar] [CrossRef]
- Bazaz, S.M.; Ratava, J.; Lohtander, M.; Varis, J. Graph-based analysis of tool life parameters of the turning process in small-lot production. In Flexible Automation and Intelligent Manufacturing: The Human-Data-Technology Nexus; Kim, K.-Y., Monplaisir, L., Rickli, J., Eds.; Lecture Notes in Mechanical Engineering; Springer International Publishing: Cham, Switzerland, 2023; pp. 141–148. [Google Scholar] [CrossRef]
- Ham, I.; Hitomi, K.; Yoshida, T. Group Technology: Applications to Production Management; Springer Science & Business Media: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Ronen, B.; Karp, R. An information entropy approach to the small-lot concept. IEEE Trans. Eng. Manag. 1994, 41, 89–92. [Google Scholar] [CrossRef]
- Davé, V.R.; Hartman, D.A.; King, W.H.; Cola, M.J.; Vaidya, R.U. Strategy for small-lot manufacturing. Los Alamos Sci. 2003, 28, 63–67. [Google Scholar]
- Hildenbrand, J.; Dahlström, J.; Shahbazi, S.; Kurdve, M. Identifying and Evaluating Recirculation Strategies for Industry in the Nordic Countries. Recycling 2021, 6, 74. [Google Scholar] [CrossRef]
- He, Y.; Li, Y.; Wu, T.; Sutherland, J.W. An energy-responsive optimization method for machine tool selection and operation sequence in flexible machining job shops. J. Clean. Prod. 2015, 87, 245–254. [Google Scholar] [CrossRef]
- Lööf, H.; Heshmati, A.; Asplund, R.; Nåås, S.-O. Innovation and Performance in Manufacturing Industries: A Comparison of the Nordic Countries; SSE/EFI Working Paper Series in Economics and Finance; Stockholm School of Economics, The Economic Research Institute (EFI): Stockholm, Sweden, 2001. [Google Scholar]
- Lamminen, L.; Wadman, B.; Küttner, R.; Svinning, T. Prototyping and Low Volume Production of Sheet Metal Components; Nordic Council of Ministers: Copenhagen, Denmark, 2004. [Google Scholar]
- Li, C.; Xiao, Q.; Tang, Y.; Li, L. A method integrating Taguchi, RSM and MOPSO to CNC machining parameters optimization for energy saving. J. Clean. Prod. 2016, 135, 263–275. [Google Scholar] [CrossRef]
- Kurada, S.; Bradley, C. A review of machine vision sensors for tool condition monitoring. Comput. Ind. 1997, 34, 55–72. [Google Scholar] [CrossRef]
- Liu, C.; Li, Y.; Hua, J.; Lu, N.; Mou, W. Real-time cutting tool state recognition approach based on machining features in NC machining process of complex structural parts. Int. J. Adv. Manuf. Technol. 2018, 97, 229–241. [Google Scholar] [CrossRef]
- Modlen, G. Manufacturing Engineering and Technology. By Serope Kalpakjian (Addison-Wesley, 1989.)[Pp. xix + 2022.] Price: £1995. Int. J. Prod. Res. 1990, 28, 431. [Google Scholar] [CrossRef]
- Tamizharasan, T.; Selvaraj, T.; Noorul Haq, A. Analysis of tool wear and surface finish in hard turning. Int. J. Adv. Manuf. Technol. 2006, 28, 671–679. [Google Scholar] [CrossRef]
- Kwon, Y.; Fischer, G.W. A novel approach to quantifying tool wear and tool life measurements for optimal tool management. Int. J. Mach. Tools Manuf. 2003, 43, 359–368. [Google Scholar] [CrossRef]
- Bazaz, S.M.; Lohtander, M.; Varis, J. The prediction method of tool life on small lot turning process—Development of Digital Twin for production. Procedia Manuf. 2020, 51, 288–295. [Google Scholar] [CrossRef]
- Bhuiyan, M.S.H.; Choudhury, I.A.; Nukman, Y. An innovative approach to monitor the chip formation effect on tool state using acoustic emission in turning. Int. J. Mach. Tools Manuf. 2012, 58, 19–28. [Google Scholar]
- Gephi. Available online: https://gephi.org (accessed on 10 February 2023).
- Kitchenham, B. Procedures for performing systematic reviews. Keele UK Keele Univ. 2004, 33, 1–26. [Google Scholar]
- Childs, T.H.; Maekawa, K.; Obikawa, T.; Yamane, Y. Metal Machining: Theory and Applications; Butterworth-Heinemann: Oxford, UK, 2000. [Google Scholar]
- Davim, J.P. Machining: Fundamentals and Recent Advances; Springer: London, UK, 2008. [Google Scholar]
- Choudhury, I.A.; El-Baradie, M.A. Tool-life prediction model by design of experiments for turning high strength steel (290 BHN). J. Mater. Process. Technol. 1998, 77, 319–326. [Google Scholar] [CrossRef]
- Chinchanikar, S.; Choudhury, S.K. Investigations on machinability aspects of hardened AISI 4340 steel at different levels of hardness using coated carbide tools. Int. J. Refract. Met. Hard Mater. 2013, 38, 124–133. [Google Scholar] [CrossRef]
- Davim, J.P.; Maranhão, C.; Faria, P.; Abrão, A.; Rubio, J.C.; Silva, L.R. Precision radial turning of AISI D2 steel. Int. J. Adv. Manuf. Technol. 2009, 42, 842–849. [Google Scholar] [CrossRef]
- Velan, M.V.G.; Shree, M.S.; Muthuswamy, P. Effect of cutting parameters and high-pressure coolant on forces, surface roughness and tool life in turning AISI 1045 steel. Mater. Today Proc. 2021, 43, 482–489. [Google Scholar] [CrossRef]
- Özel, T. Computational modelling of 3D turning: Influence of edge micro-geometry on forces, stresses, friction and tool wear in PcBN tooling. J. Mater. Process. Technol. 2009, 209, 5167–5177. [Google Scholar] [CrossRef]
- Saini, S.; Ahuja, I.S.; Sharma, V.S. Residual stresses, surface roughness, and tool wear in hard turning: A comprehensive review. Mater. Manuf. Process. 2012, 27, 583–598. [Google Scholar] [CrossRef]
- Kataoka, R.; Shamoto, E. Influence of vibration in cutting on tool flank wear: Fundamental study by conducting a cutting experiment with forced vibration in the depth-of-cut direction. Precis. Eng. 2019, 55, 322–329. [Google Scholar] [CrossRef]
- Oraby, S.; Hayhurst, D. Cutting tool condition monitoring using surface texture via neural network. Int. J. Math. Comput. Tools Manuf. 2004, 44, 1261–1269. [Google Scholar] [CrossRef]
- Scherge, M.; Shakhvorostov, D.; Pöhlmann, K. Fundamental wear mechanism of metals. Wear 2003, 255, 395–400. [Google Scholar] [CrossRef]
- Peng, Y.; Miao, H.; Peng, Z. Development of TiCN-based cermets: Mechanical properties and wear mechanism. Int. J. Refract. Met. Hard Mater. 2013, 39, 78–89. [Google Scholar] [CrossRef]
- Binder, M.; Klocke, F.; Doebbeler, B. Abrasive wear behavior under metal cutting conditions. Wear 2017, 376, 165–171. [Google Scholar] [CrossRef]
- Marinov, V. Experimental study on the abrasive wear in metal cutting. Wear 1996, 197, 242–247. [Google Scholar] [CrossRef]
- Svenningsson, I.; Tatar, K. On the mechanism of three-body adhesive wear in turning. Int. J. Adv. Manuf. Technol. 2021, 113, 3457–3472. [Google Scholar] [CrossRef]
- Luo, X.; Cheng, K.; Holt, R.; Liu, X. Modeling flank wear of carbide tool insert in metal cutting. Wear 2005, 259, 1235–1240. [Google Scholar] [CrossRef]
- Viswanathan, K.; Mahato, A.; Yeung, H.; Chandrasekar, S. Surface phenomena revealed by in situ imaging: Studies from adhesion, wear and cutting. Surf. Topogr. Metrol. Prop. 2017, 5, 014002. [Google Scholar] [CrossRef]
- Kato, K. Classification of wear mechanisms/models. In Wear–Materials, Mechanisms and Practice; Wiley: Hoboken, NJ, USA, 2005; pp. 9–20. [Google Scholar]
- Molinari, A.; Nouari, M. Modeling of tool wear by diffusion in metal cutting. Wear 2002, 252, 135–149. [Google Scholar] [CrossRef]
- Bushlya, V.; Lenrick, F.; Ståhl, J.-E.; M’Saoubi, R. Influence of oxygen on the tool wear in machining. CIRP Ann. 2018, 67, 79–82. [Google Scholar] [CrossRef]
- Pálmai, Z. Proposal for a new theoretical model of the cutting tool’s flank wear. Wear 2013, 303, 437–445. [Google Scholar] [CrossRef]
- Stephenson, D.A.; Agapiou, J.S. Metal Cutting Theory and Practice; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Qehaja, N.; Kyçyku, A. Tool life modeling based on cutting parameters and work material hardness in turning process. Mach. Technol. Mater. 2017, 11, 356–359. [Google Scholar]
- Gåård, A.; Hallbäck, N.; Krakhmalev, P.; Bergström, J. Temperature effects on adhesive wear in dry sliding contacts. Wear 2010, 268, 968–975. [Google Scholar] [CrossRef]
- Talib, N.A. Studying the effect of cutting speed and feed rate on tool life in the turning processes. Diyala J. Eng. Sci. 2010, 181–194. [Google Scholar]
- Nalavade, N.D.; Waghmare, C.A. Experimental Investigation of Rake Angle and Cutting Speed on Cutting Force, Tool Life and Tool Vibration of AISI 1020 Steel on CNC Turning by Using Single Point Cutting Tool. Available online: https://www.academia.edu/download/53676406/IOSR_JP.pdf (accessed on 13 September 2022).
- Gorczyca, F.E. Application of Metal Cutting Theory; Industrial Press Inc.: Norwalk, CT, USA, 1987. [Google Scholar]
- Królczyk, G.; Gajek, M.; Legutko, S. Effect of the cutting parameters impact on tool life in duplex stainless steel turning process. Teh. Vjesn.-Tech. Gaz. 2013, 20, 587–592. [Google Scholar]
- Ojolo, S.J.; Ogunkomaiya, O. A study of effects of machining parameters on tool life. Int. J. Mater. Sci. Appl. 2014, 3, 183–199. [Google Scholar] [CrossRef]
- Sandvik Coromant. Modern Metal Cutting: A Practical Handbook; Sandvik Coromant: Sandviken, Sweden, 1994. [Google Scholar]
- Astakhov, V.P. Tribology of Metal Cutting; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Lee, W.B.; To, S.; Sze, Y.K.; Cheung, C.F. Effect of material anisotropy on shear angle prediction in metal cutting—A mesoplasticity approach. Int. J. Mech. Sci. 2003, 45, 1739–1749. [Google Scholar] [CrossRef]
- Laakso, S.V.; Agmell, M.; Ståhl, J.-E. The mystery of missing feed force—The effect of friction models, flank wear and ploughing on feed force in metal cutting simulations. J. Manuf. Processes 2018, 33, 268–277. [Google Scholar] [CrossRef]
- Mo, S.P.; Axinte, D.A.; Hyde, T.H.; Gindy, N.N.Z. An example of selection of the cutting conditions in broaching of heat-resistant alloys based on cutting forces, surface roughness and tool wear. J. Mater. Process. Technol. 2005, 160, 382–389. [Google Scholar] [CrossRef]
- Li, K.; Gao, X.-L.; Sutherland, J.W. Finite element simulation of the orthogonal metal cutting process for qualitative understanding of the effects of crater wear on the chip formation process. J. Mater. Process. Technol. 2002, 127, 309–324. [Google Scholar] [CrossRef]
- Huang, Y.; Dawson, T.G. Tool crater wear depth modeling in CBN hard turning. Wear 2005, 258, 1455–1461. [Google Scholar] [CrossRef]
- Hua, J.; Shivpuri, R. A cobalt diffusion based model for predicting crater wear of carbide tools in machining titanium alloys. J. Eng. Mater. Technol. 2005, 127, 136–144. [Google Scholar] [CrossRef]
- Graves, A.; Norgren, S.; Wan, W.; Singh, S.; Kritikos, M.; Xiao, C.; Crawforth, P.; Jackson, M. On the mechanism of crater wear in a high strength metastable β titanium alloy. Wear 2021, 484, 203998. [Google Scholar] [CrossRef]
- Mia, M.; Al Bashir, M.; Dhar, N.R. Modeling of principal flank wear: An empirical approach combining the effect of tool, environment and workpiece hardness. J. Inst. Eng. India Ser. C 2016, 97, 517–526. [Google Scholar] [CrossRef]
- Zhao, T.; Zhou, J.M.; Bushlya, V.; Ståhl, J.E. Effect of cutting edge radius on surface roughness and tool wear in hard turning of AISI 52100 steel. Int. J. Adv. Manuf. Technol. 2017, 91, 3611–3618. [Google Scholar] [CrossRef]
- Sredanović, B.; Globocki-Lakić, G.; Kramar, D.; Pušavec, F. Influence of workpiece hardness on tool wear in profile micro-milling of hardened tool steel. Tribol. Ind. 2018, 40, 100. [Google Scholar] [CrossRef]
- Lokireddi, V.G.R.; Vajrapu, S.S.; Vijay, S. Performance analysis of uncoated tools for machining of hard to cut materials. Mater. Today Proc. 2022, 60, 902–906. [Google Scholar] [CrossRef]
- Abidi, Y. Analysis of the compromise between cutting tool life, productivity and roughness during turning of C45 hardened steel. Prod. Eng. Arch. 2021, 27, 30–35. [Google Scholar] [CrossRef]
- Singh, A.; Singh, E.R. In metal turning, effect of tool rake angles and lubricants on cutting tool life and surface finish: A review. Int. Res. J. Eng. Technol. IRJET 2016, 3, 696–700. [Google Scholar]
- Hu, C.; Zhuang, K.; Weng, J.; Zhang, X.; Ding, H. Cutting temperature prediction in negative-rake-angle machining with chamfered insert based on a modified slip-line field model. Int. J. Mech. Sci. 2020, 167, 105273. [Google Scholar] [CrossRef]
- Azaath, L.M.; Mohan, E.; Natarajan, U. Effect of rake angle and tool geometry during machining process of AISI 4340 steel in finite element approach. Mater. Today Proc. 2021, 37, 3731–3736. [Google Scholar] [CrossRef]
- Kishore, D.S.C.; Rao, K.P.; Mahamani, A. Investigation of cutting force, surface roughness and flank wear in turning of In-situ Al6061-TiC metal matrix composite. Procedia Mater. Sci. 2014, 6, 1040–1050. [Google Scholar] [CrossRef]
- Das, S.R.; Dhupal, D.; Kumar, A. Study of surface roughness and flank wear in hard turning of AISI 4140 steel with coated ceramic inserts. J. Mech. Sci. Technol. 2015, 29, 4329–4340. [Google Scholar] [CrossRef]
- Childs, T.H.C.; Maekawa, K.; Maulik, P. Effects of coolant on temperature distribution in metal machining. Mater. Sci. Technol. 1988, 4, 1006–1019. [Google Scholar] [CrossRef]
- Astakhov, V.P. The assessment of cutting tool wear. Int. J. Mach. Tools Manuf. 2004, 44, 637–647. [Google Scholar] [CrossRef]
- Rahman, M.A.; Amrun, M.R.; Rahman, M.; Kumar, A.S. Investigation of the critical cutting edge radius based on material hardness. Int. J. Adv. Manuf. Technol. 2017, 88, 3295–3306. [Google Scholar] [CrossRef]
- Dogra, M.; Sharma, V.S.; Sachdeva, A.; Suri, N.M.; Dureja, J.S. Tool wear, chip formation and workpiece surface issues in CBN hard turning: A review. Int. J. Precis. Eng. Manuf. 2010, 11, 341–358. [Google Scholar] [CrossRef]
- Shokrani, A.; Dhokia, V.; Newman, S.T. Environmentally conscious machining of difficult-to-machine materials with regard to cutting fluids. Int. J. Mach. Tools Manuf. 2012, 57, 83–101. [Google Scholar] [CrossRef]
- Tangjitsitcharoen, S.; Moriwaki, T. Intelligent monitoring and identification of cutting states of chips and chatter on CNC turning machine. J. Manuf. Processes 2008, 10, 40–46. [Google Scholar] [CrossRef]
- Sekhar, R.; Singh, T.P. Mechanisms in turning of metal matrix composites: A review. J. Mater. Res. Technol. 2015, 4, 197–207. [Google Scholar] [CrossRef]
- Abukhshim, N.A.; Mativenga, P.T.; Sheikh, M.A. An investigation of the tool-chip contact length and wear in high-speed turning of EN19 steel. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2004, 218, 889–903. [Google Scholar] [CrossRef]
- El Hakim, M.A.; Shalaby, M.A.; Veldhuis, S.C.; Dosbaeva, G.K. Effect of secondary hardening on cutting forces, cutting temperature, and tool wear in hard turning of high alloy tool steels. Measurement 2015, 65, 233–238. [Google Scholar] [CrossRef]
- Copenhaver, R.; Rubeo, M.A.; Guzorek, S.; Landge, S.; Smith, K.S.; Ziegert, J.; Schmitz, T.L. A fundamental investigation of modulated tool path turning mechanics. Procedia Manuf. 2017, 10, 159–170. [Google Scholar] [CrossRef]
- Hagberg, W. Temperature Effect on Insert Tool Life in Dry Machining. Master’s Thesis, Luleå University of Technology, Luleå, Sweden, 2021. [Google Scholar]
- Kalpakjian, S.; Schmid, S.R.; Musa, H. Manufacturing Engineering and Technology: Machining; China Machine Press: Beijing, China, 2011. [Google Scholar]
- Kartha, A.; Subramanian, S. Turning of Tool Steel: Study on the Effect of Insert Grade and Entering Angle on Tool Life. Master’s Thesis, KTH Industrial Engineering and Management, Stockholm, Sweden, 2020. [Google Scholar]
- Bermingham, M.J.; Kirsch, J.; Sun, S.; Palanisamy, S.; Dargusch, M.S. New observations on tool life, cutting forces and chip morphology in cryogenic machining Ti-6Al-4V. Int. J. Mach. Tools Manuf. 2011, 51, 500–511. [Google Scholar] [CrossRef]
- Sadílek, M.; Dubský, J.; Sadílková, Z.; Poruba, Z. Cutting forces during turning with variable depth of cut. Perspect. Sci. 2016, 7, 357–363. [Google Scholar] [CrossRef]
- Benardos, P.G.; Mosialos, S.; Vosniakos, G.-C. Prediction of workpiece elastic deflections under cutting forces in turning. Robot. Comput.-Integr. Manuf. 2006, 22, 505–514. [Google Scholar] [CrossRef]
- Kosaraju, S.; Anne, V.; Ghanta, V. Effect of rake angle and feed rate on cutting forces in an orthogonal turning process. In Proceedings of the International Conference on Trends in Mechanical and Industrial Engineering, Odisha, India, 11–13 December 2020. [Google Scholar]
- Altintas, Y.; Ber, A. Manufacturing Automation: Metal Cutting Mechanics, Machine Tool Vibrations, and CNC Design. Appl. Mech. Rev. 2001, 54, B84. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, A.; Ranganath, M.S.; Singh, R.C. Review of effect of tool geometry variation on finish turning and improving cutting tool life. In Proceedings of the International Conference of Advance Research and Innovation (ICARI-2014), New Delhi, India, 10 January 2014. [Google Scholar]
- Sharma, K.; Mahto, D.G.; Sen, S.S. In metal turning, effect of various parameters on cutting tool: A Review. Int. J. Appl. Innov. Eng. Manag. IJAIEM 2013, 2, 32–38. [Google Scholar]
- Kountanya, R.K.; Endres, W.J. A high-magnification experimental study of orthogonal cutting with edge-honed tools. In Proceedings of the Manufacturing Engineering, New York, NY, USA, 11–16 November 2001; American Society of Mechanical Engineers: New York, NY, USA, 2001; pp. 157–164. [Google Scholar] [CrossRef]
- Sutter, G.; Molinari, A. Analysis of the cutting force components and friction in high speed machining. J. Manuf. Sci. Eng. 2005, 127, 245–250. [Google Scholar] [CrossRef]
- Rao, C.J.; Rao, D.N.; Srihari, P. Influence of cutting parameters on cutting force and surface finish in turning operation. Procedia Eng. 2013, 64, 1405–1415. [Google Scholar] [CrossRef]
- Rao, C.J.; Sreeamulu, D.; Mathew, A.T. Analysis of tool life during turning operation by determining optimal process parameters. Procedia Eng. 2014, 97, 241–250. [Google Scholar] [CrossRef]
- Magadum, S.; Kumar, S.A.; Yoganath, V.G.; Srinivasa, C.K.; GuruMurthy, T. Evaluation of tool life and cutting forces in cryogenic machining of hardened steel. Procedia Mater. Sci. 2014, 5, 2542–2549. [Google Scholar] [CrossRef]
- Palanikumar, K. Application of Taguchi and response surface methodologies for surface roughness in machining glass fiber reinforced plastics by PCD tooling. Int. J. Adv. Manuf. Technol. 2008, 36, 19–27. [Google Scholar] [CrossRef]
- Ogedengbe, T.S.; Okediji, A.P.; Yussouf, A.A.; Aderoba, O.A.; Abiola, O.A.; Alabi, I.O.; Alonge, O.I. The effects of heat gener-ation on cutting tool and machined workpiece. J. Phys. Conf. Ser. 2019, 1378, 022012. [Google Scholar] [CrossRef]
- Hussain, G.; Alkahtani, M.; Alsultan, M.; Buhl, J.; Gupta, M.K. Chip formation, cutting temperature and forces measurements in hard turning of Gcr15 under the influence of PcBN chamfering parameters. Measurement 2022, 204, 112130. [Google Scholar] [CrossRef]
- Günay, M.; Korkut, I.; Aslan, E.; Şeker, U. Experimental investigation of the effect of cutting tool rake angle on main cutting force. J. Mater. Process. Technol. 2005, 166, 44–49. [Google Scholar] [CrossRef]
- Saglam, H.; Unsacar, F.; Yaldiz, S. Investigation of the effect of rake angle and approaching angle on main cutting force and tool tip temperature. Int. J. Mach. Tools Manuf. 2006, 46, 132–141. [Google Scholar] [CrossRef]
- Pawade, R.S.; Joshi, S.S.; Brahmankar, P.K.; Rahman, M. An investigation of cutting forces and surface damage in high-speed turning of Inconel 718. J. Mater. Process. Technol. 2007, 192, 139–146. [Google Scholar] [CrossRef]
- Zhou, J.M.; Walter, H.; Andersson, M.; Stahl, J.E. Effect of chamfer angle on wear of PCBN cutting tool. Int. J. Mach. Tools Manuf. 2003, 43, 301–305. [Google Scholar] [CrossRef]
- Nategh, M.J.; Amini, S.; Soleimanimehr, H. Modeling the force, surface roughness and cutting temperature in ultrasonic vibration-assisted turning of Al7075. Adv. Mater. Res. 2010, 83, 315–325. [Google Scholar] [CrossRef]
- Ay, H.; Yang, W.-J. Heat transfer and life of metal cutting tools in turning. Int. J. Heat Mass Transf. 1998, 41, 613–623. [Google Scholar] [CrossRef]
- Williams, J.A. Mechanics of Machining: An Analytical Approach to Assessing Machinability: By P.L.B. Oxley; Ellis Horwood: Chichester, UK, 1989; p. 242. ISBN 0-7458-0007-6. [Google Scholar]
- Yanda, H.; Ghani, J.A.; Che Haron, C.H. Effect of rake angle on stress, strain and temperature on the edge of carbide cutting tool in orthogonal cutting using FEM simulation. J. Eng. Technol. Sci. 2010, 42, 179–194. [Google Scholar] [CrossRef]
- Sulaiman, S.; Roshan, A.; Borazjani, S. Effect of cutting parameters on cutting temperature of TiAL6V4 alloy. Appl. Mech. Mater. 2013, 392, 68–72. [Google Scholar] [CrossRef]
- Ji, J.; Yang, Q.; Chen, P.; Lu, K.; Wu, Y. An improved mathematical model of cutting temperature in end milling Al7050 based on the influence of tool geometry parameters and milling parameters. Math. Probl. Eng. 2021, 2021, 5705091. [Google Scholar] [CrossRef]
- Dhar, N.R.; Kamruzzaman, M. Cutting temperature, tool wear, surface roughness and dimensional deviation in turning AISI-4037 steel under cryogenic condition. Int. J. Mach. Tools Manuf. 2007, 47, 754–759. [Google Scholar] [CrossRef]
- Anagonye, A.U.; Stephenson, D.A. Modeling cutting temperatures for turning inserts with various tool geometries and materials. J. Manuf. Sci. Eng. 2002, 124, 544–552. [Google Scholar] [CrossRef]
- Agrawal, C.; Wadhwa, J.; Pitroda, A.; Pruncu, C.I.; Sarikaya, M.; Khanna, N. Comprehensive analysis of tool wear, tool life, surface roughness, costing and carbon emissions in turning Ti–6Al–4V titanium alloy: Cryogenic versus wet machining. Tribol. Int. 2021, 153, 106597. [Google Scholar] [CrossRef]
- Xie, J.; Luo, M.J.; Wu, K.K.; Yang, L.F.; Li, D.H. Experimental study on cutting temperature and cutting force in dry turning of titanium alloy using a non-coated micro-grooved tool. Int. J. Mach. Tools Manuf. 2013, 73, 25–36. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; Dhar, N.R. The effect of applying high-pressure coolant (HPC) jet in machining of 42CrMo4 steel by uncoated carbide inserts. J. Mech. Eng. 2008, 39, 71–77. [Google Scholar] [CrossRef]
- Aramcharoen, A. Influence of cryogenic cooling on tool wear and chip formation in turning of titanium alloy. Procedia CIRP 2016, 46, 83–86. [Google Scholar] [CrossRef]
- Ghuge, N.C.; Mahalle, A.M. Influence of cutting fluid on tool wear and tool life during turning. Int. J. Mod. Trends Eng. Res. IJMTER 2016, 3, 23–27. [Google Scholar]
- Liu, M.; Takagi, J.; Tsukuda, A. Effect of tool nose radius and tool wear on residual stress distribution in hard turning of bearing steel. J. Mater. Process. Technol. 2004, 150, 234–241. [Google Scholar] [CrossRef]
- Akhavan Niaki, F.; Mears, L. A comprehensive study on the effects of tool wear on surface roughness, dimensional integrity and residual stress in turning IN718 hard-to-machine alloy. J. Manuf. Processes 2017, 30, 268–280. [Google Scholar] [CrossRef]
- Jacobus, K.; DeVor, R.E.; Kapoor, S.G. Machining-Induced Residual Stress: Experimentation and Modeling. J. Manuf. Sci. Eng. 2000, 122, 20–31. [Google Scholar] [CrossRef]
- Liang, X.; Liu, Z.; Wang, B.; Song, Q.; Cai, Y.; Wan, Y. Prediction of residual stress with multi-physics model for orthogonal cutting Ti-6Al-4V under various tool wear morphologies. J. Mater. Process. Technol. 2021, 288, 116908. [Google Scholar] [CrossRef]
- Diniz, A.E.; Micaroni, R. Influence of the direction and flow rate of the cutting fluid on tool life in turning process of AISI 1045 steel. Int. J. Mach. Tools Manuf. 2007, 47, 247–254. [Google Scholar] [CrossRef]
- Palanisamy, S.; McDonald, S.D.; Dargusch, M.S. Effects of coolant pressure on chip formation while turning Ti6Al4V alloy. Int. J. Mach. Tools Manuf. 2009, 49, 739–743. [Google Scholar] [CrossRef]
- Hughes, J.I.; Sharman, A.R.C.; Ridgway, K. The effect of cutting tool material and edge geometry on tool life and workpiece surface integrity. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2006, 220, 93–107. [Google Scholar] [CrossRef]
- Dhar, N.R.; Islam, M.W.; Islam, S.; Mithu, M.A.H. The influence of minimum quantity of lubrication (MQL) on cutting temperature, chip and dimensional accuracy in turning AISI-1040 steel. J. Mater. Process. Technol. 2006, 171, 93–99. [Google Scholar] [CrossRef]
- Kim, D.M.; Kim, H.I.; Park, H.W. Tool wear, economic costs, and CO2 emissions analysis in cryogenic assisted hard-turning process of AISI 52100 steel. Sustain. Mater. Technol. 2021, 30, e00349. [Google Scholar] [CrossRef]
- Varadarajan, A.S.; Philip, P.K.; Ramamoorthy, B. Investigations on hard turning with minimal cutting fluid application (HTMF) and its comparison with dry and wet turning. Int. J. Mach. Tools Manuf. 2002, 42, 193–200. [Google Scholar] [CrossRef]
- Özbek, O.; Saruhan, H. The effect of vibration and cutting zone temperature on surface roughness and tool wear in eco-friendly MQL turning of AISI D2. J. Mater. Res. Technol. 2020, 9, 2762–2772. [Google Scholar] [CrossRef]
- Bowers, B.; Schatzman, L. Dimensional analysis. In Developing Grounded Theory; Routledge: Abington, UK, 2016; pp. 86–126. [Google Scholar]



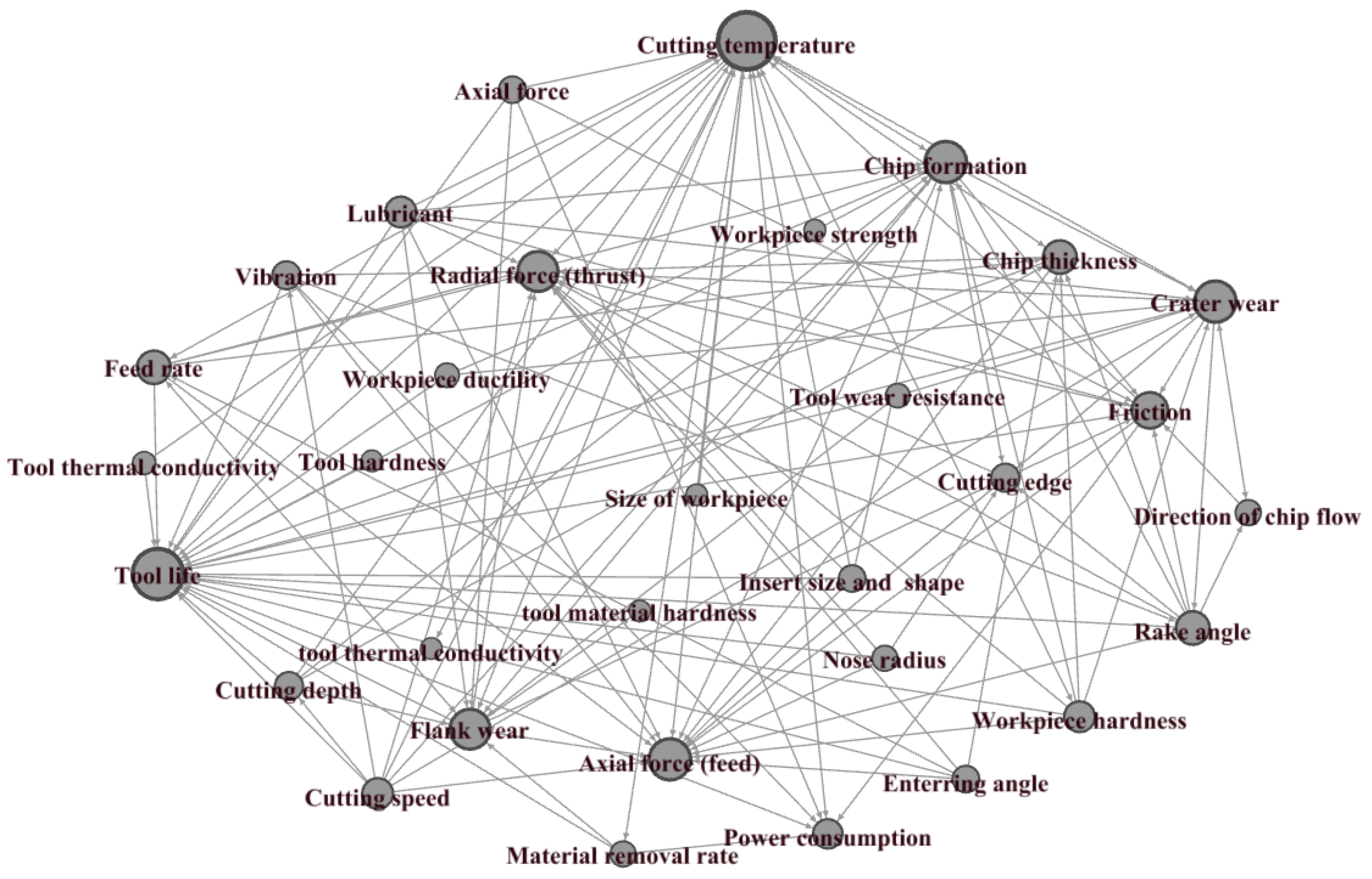
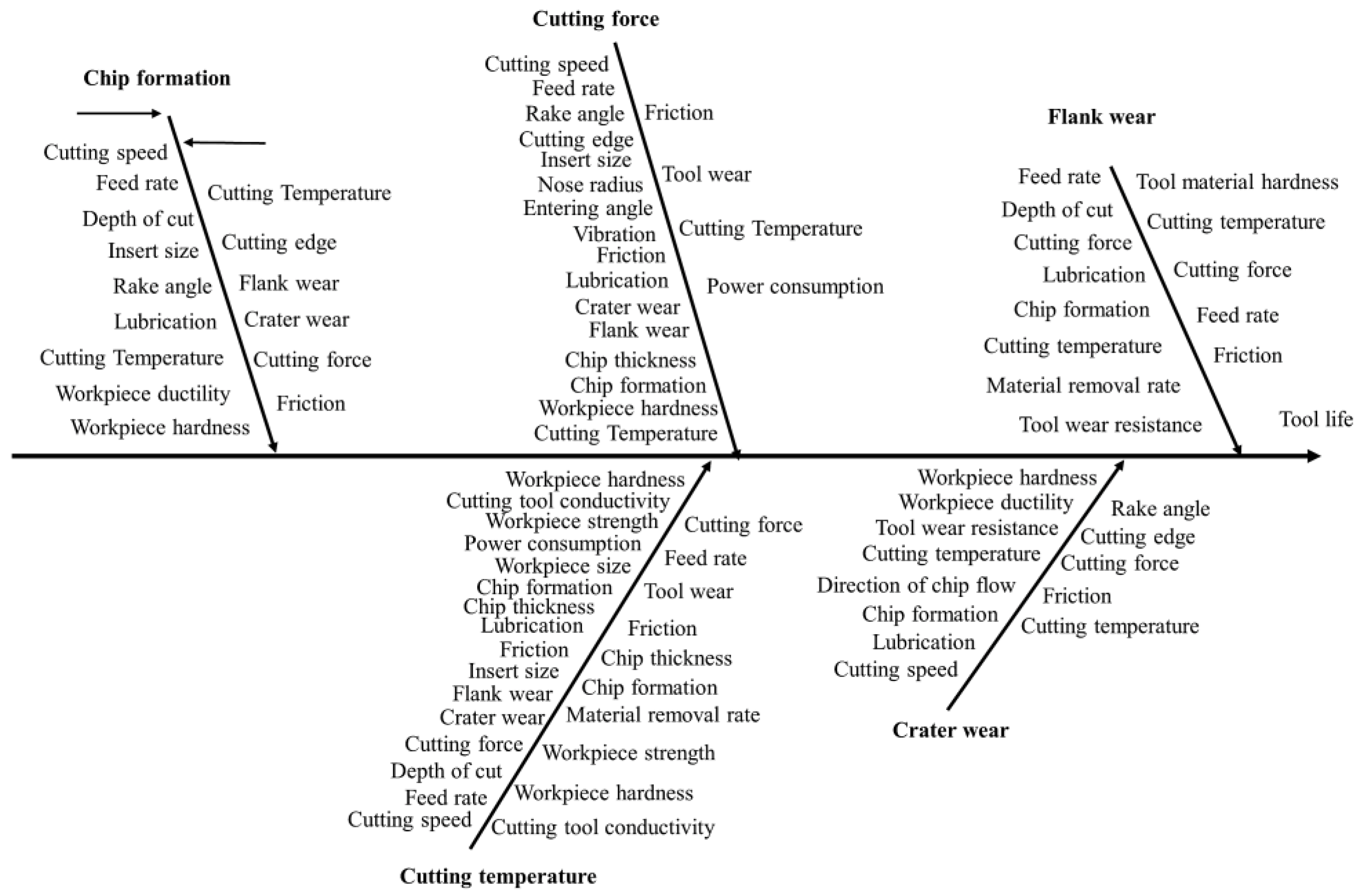
| Workpiece Hardness | Tool Thermal Conductivity | Tool Wear resistance | Tool Material Hardness | Nose Radial | Rake Angle | Cutting Edge | Flank Wear | Crater Wear | Feed Rate | Cutting Depth | Material Removal Rate | Axial Force (Feed) | Radial Force (Thrust) | Cutting Temperature | Chip Formation | Chip Thickness | Direction of Chip Flow | Lubrication | Power Consumption | Vibration | Friction | Tool Life | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Workpiece hardness | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| Workpiece strength | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Workpiece ductility | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Tool thermal conductivity | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Tool wear resistance | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Size of workpiece | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Insert size & shape | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Tool hardness | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
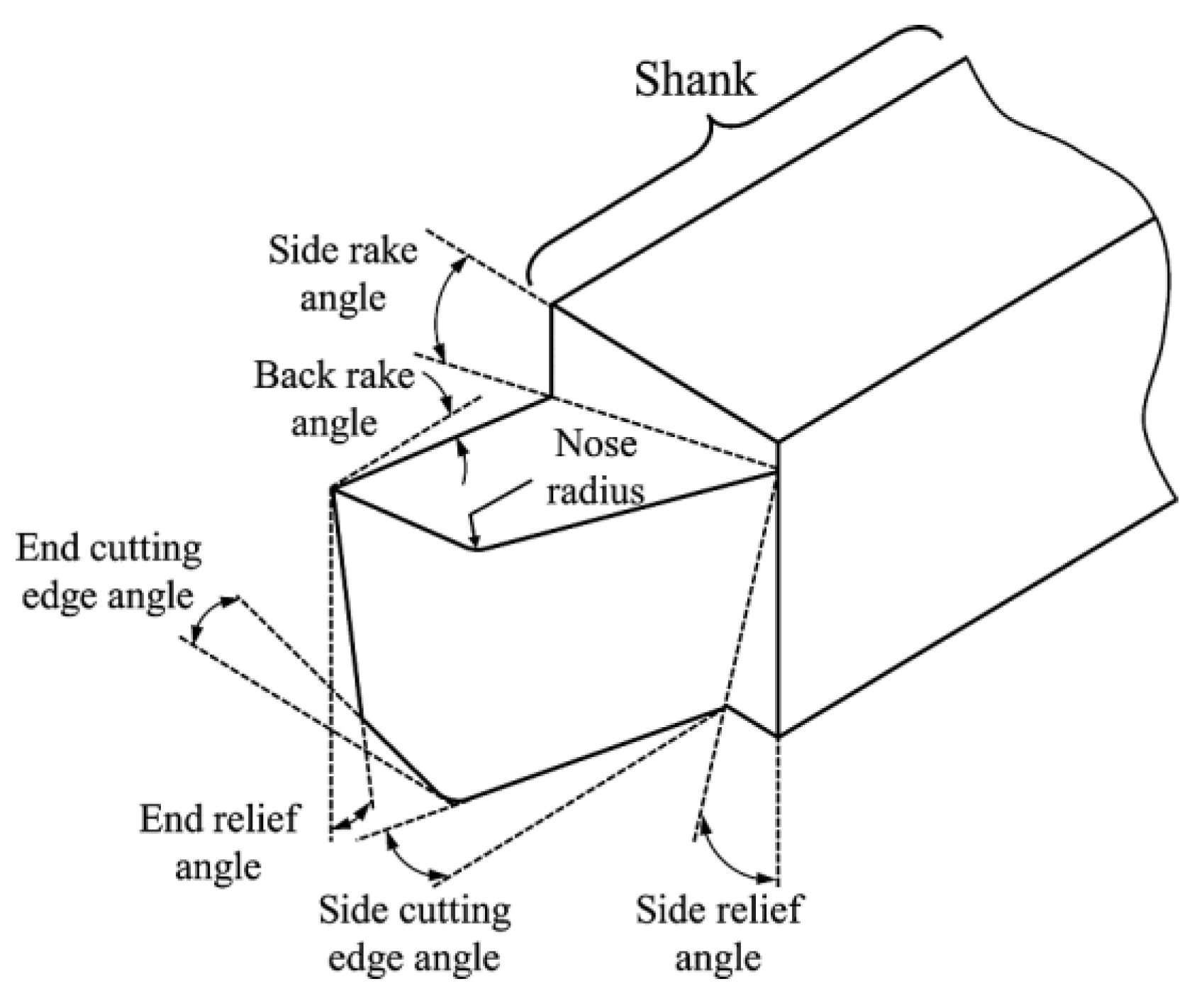
| Nose radius | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Rake angle | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| Entering angle | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| Cutting angle | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Flank wear | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| Crater wear | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| Cutting speed | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| Feed rate | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| Cutting depth | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| Material removal rate | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| Axial force | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| Radial force | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| Cutting temperature | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| Chip formation | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| Chip thickness | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Direction of chip flow | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| Lubrication | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| Power consumption | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Vibration | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| Friction | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| Tool life | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bazaz, S.M.; Ratava, J.; Lohtander, M.; Varis, J. An Investigation of Factors Influencing Tool Life in the Metal Cutting Turning Process by Dimensional Analysis. Machines 2023, 11, 393. https://doi.org/10.3390/machines11030393
Bazaz SM, Ratava J, Lohtander M, Varis J. An Investigation of Factors Influencing Tool Life in the Metal Cutting Turning Process by Dimensional Analysis. Machines. 2023; 11(3):393. https://doi.org/10.3390/machines11030393
Chicago/Turabian StyleBazaz, Sara M., Juho Ratava, Mika Lohtander, and Juha Varis. 2023. "An Investigation of Factors Influencing Tool Life in the Metal Cutting Turning Process by Dimensional Analysis" Machines 11, no. 3: 393. https://doi.org/10.3390/machines11030393
APA StyleBazaz, S. M., Ratava, J., Lohtander, M., & Varis, J. (2023). An Investigation of Factors Influencing Tool Life in the Metal Cutting Turning Process by Dimensional Analysis. Machines, 11(3), 393. https://doi.org/10.3390/machines11030393







