Higher-Order Hexahedral Finite Elements for Structural Dynamics: A Comparative Review
Abstract
1. Introduction
2. FE Formulation for Structural Dynamics Problems
2.1. Variational Integral Form of the Virtual Work Principle
2.2. Spatial Discretization
2.3. Numerial Integration Using Gauss–Legendre Quadrature
2.4. Equations of Motion and Eigenvalue Problem
2.5. Estimating the FE Accuracy for Dynamic Applications
3. Key Factors for a Good FE Formulation
4. Different Formulations of the Hexahedral (Brick) Element
4.1. Serendipity Brick Elements
4.2. Under-Integration vs. Full-Integration Schemes
5. Results and Discussion
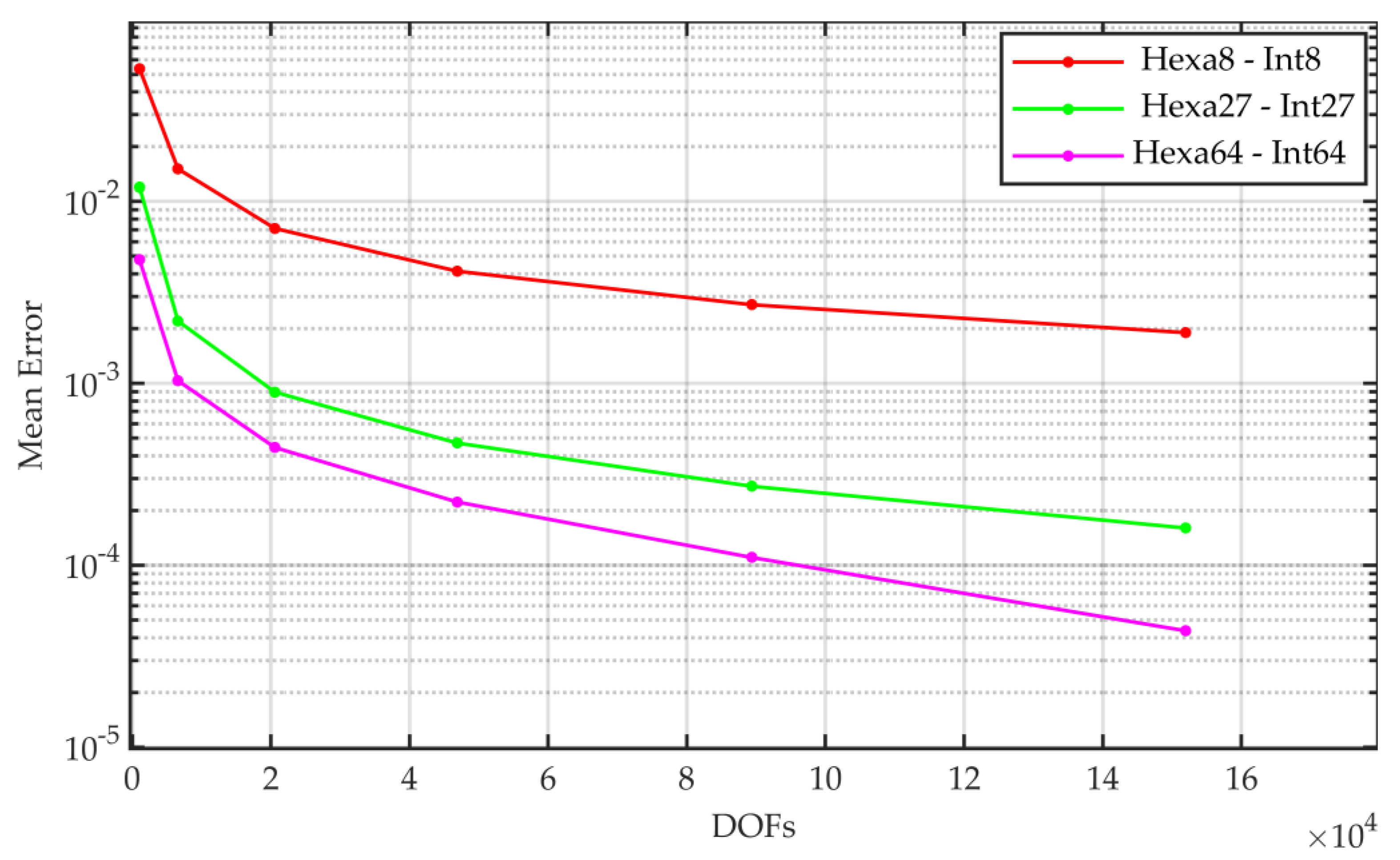
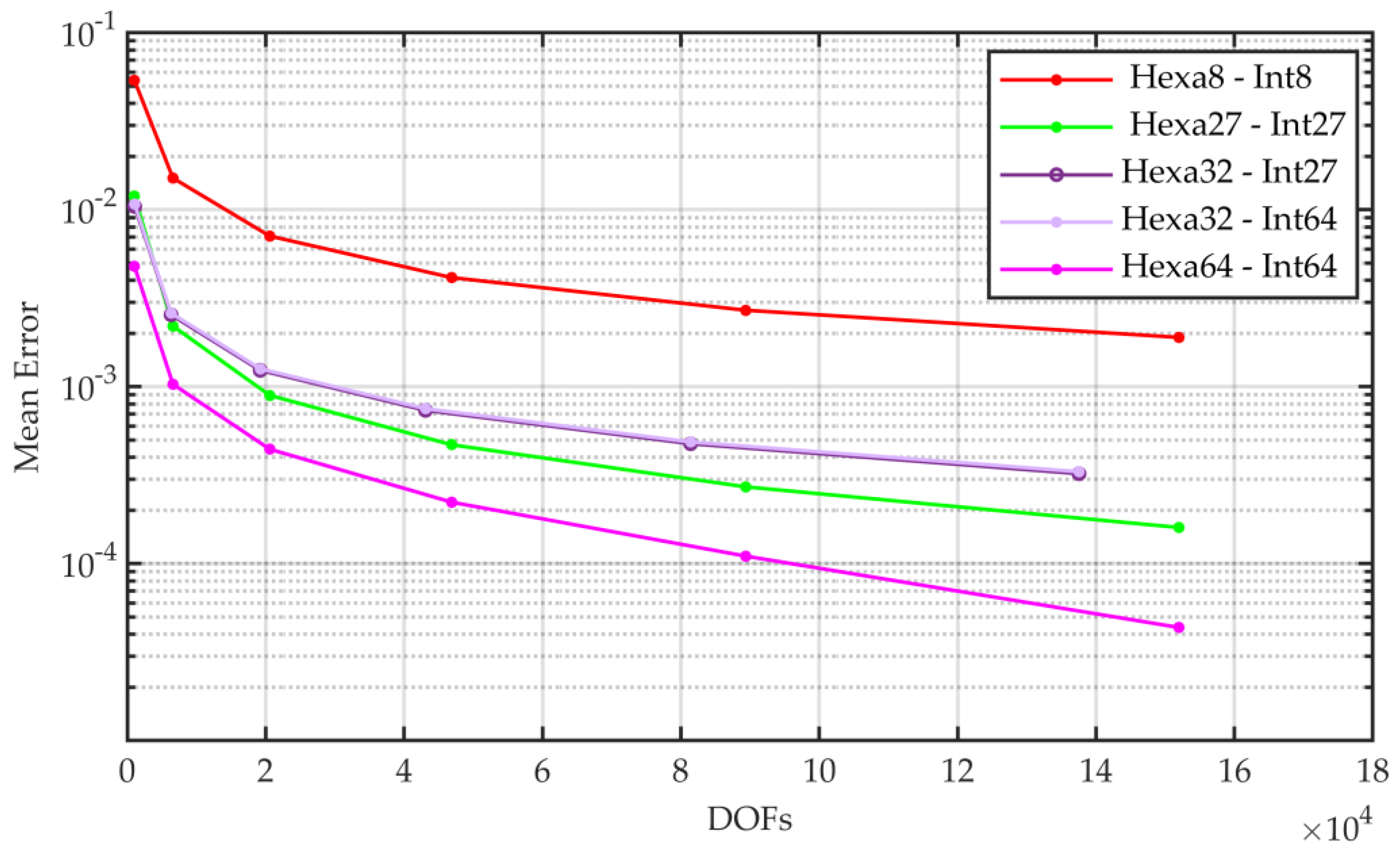
5.1. Accuracy Convergence
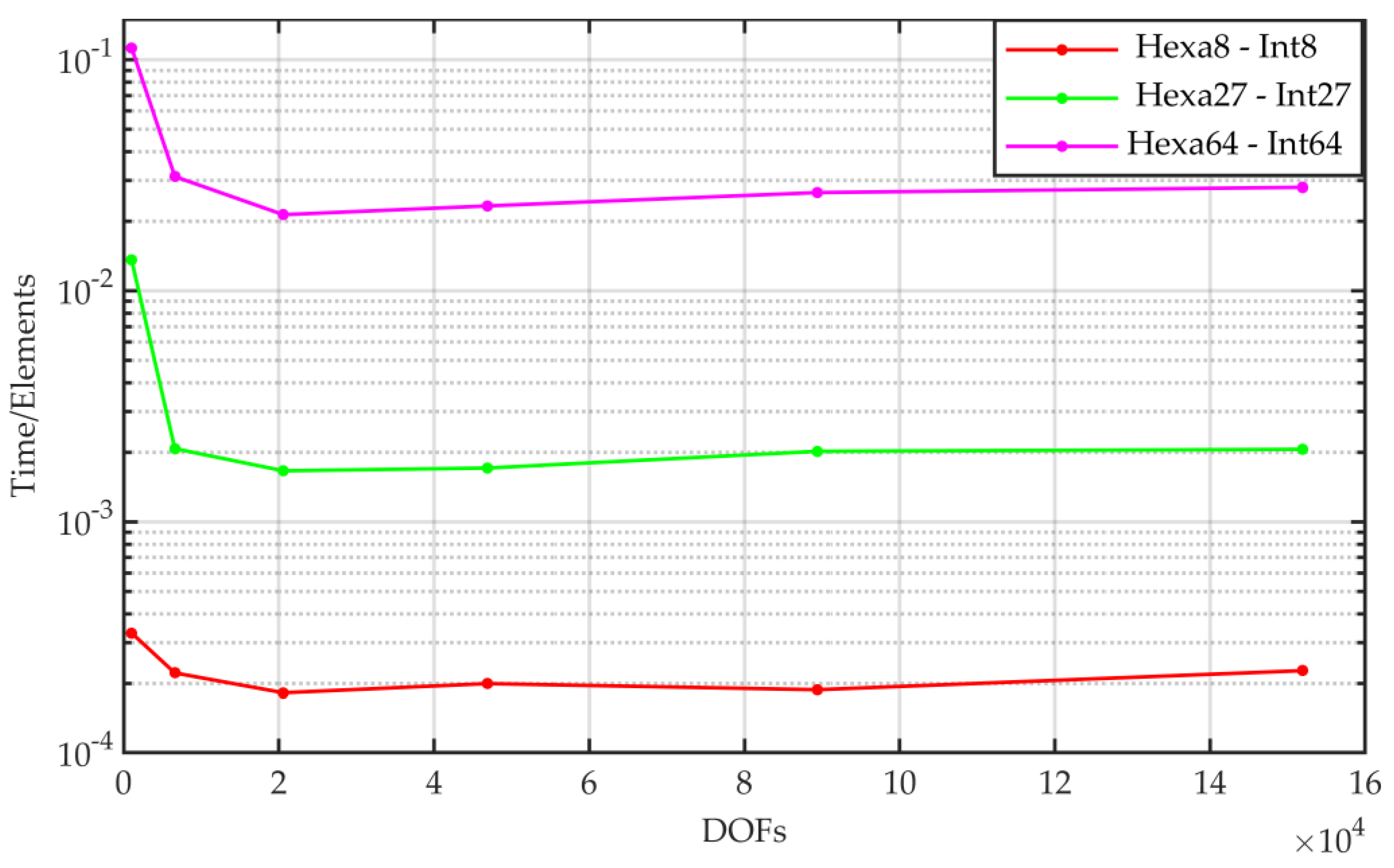
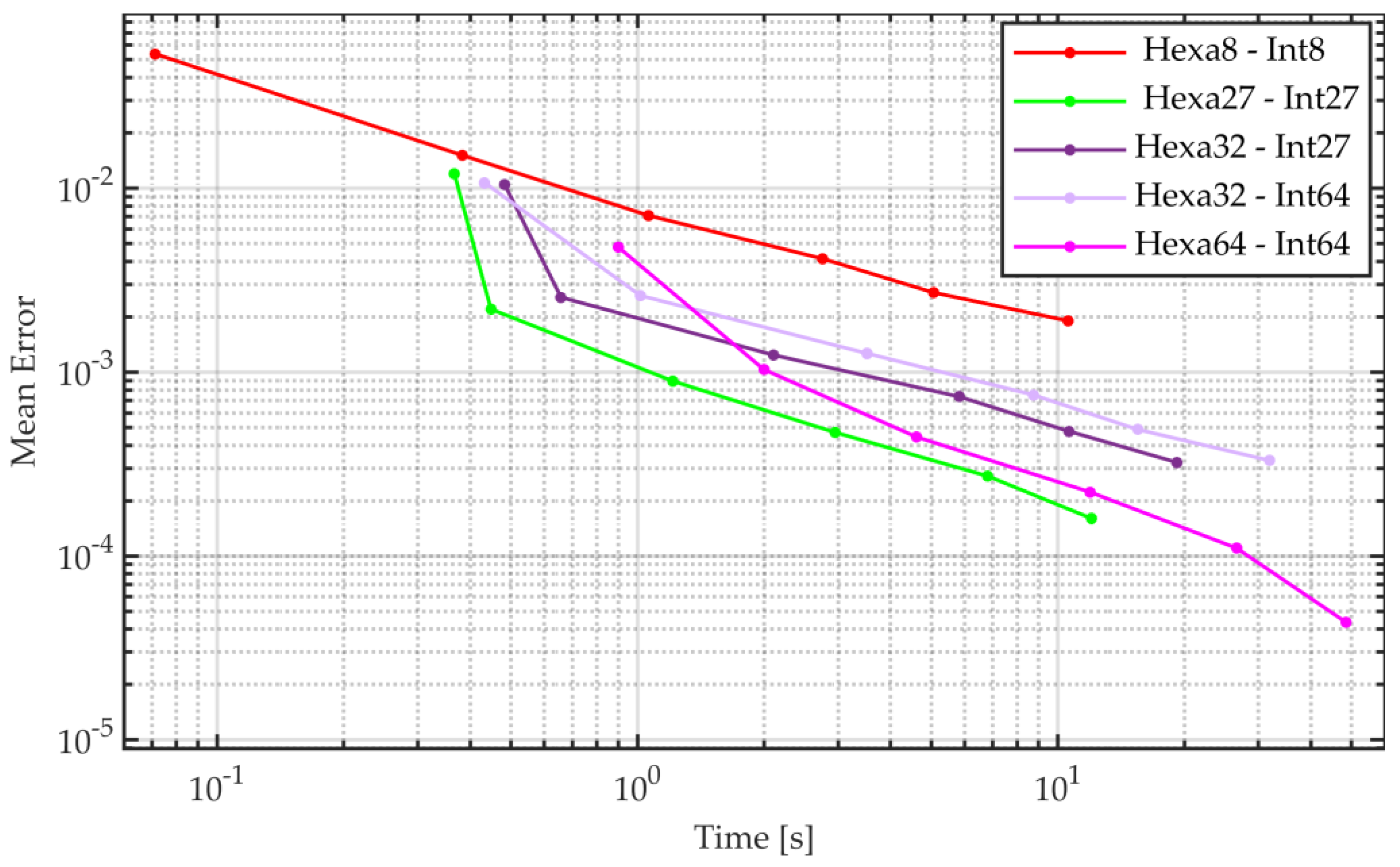
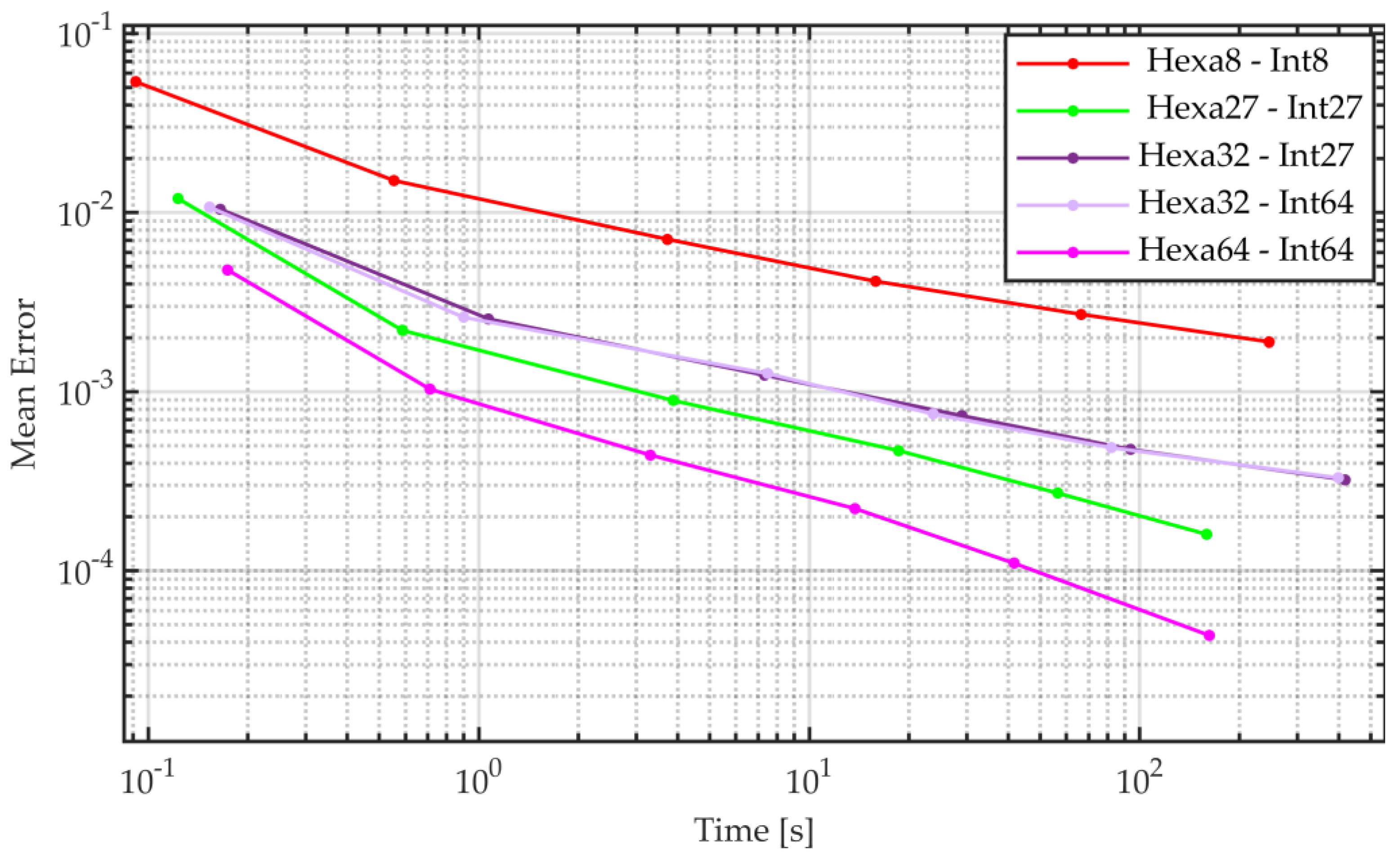
5.2. Accuracy vs. Assembly Time
5.3. Accuracy vs. Eigenvalue Computational Time
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Linear Brick Element
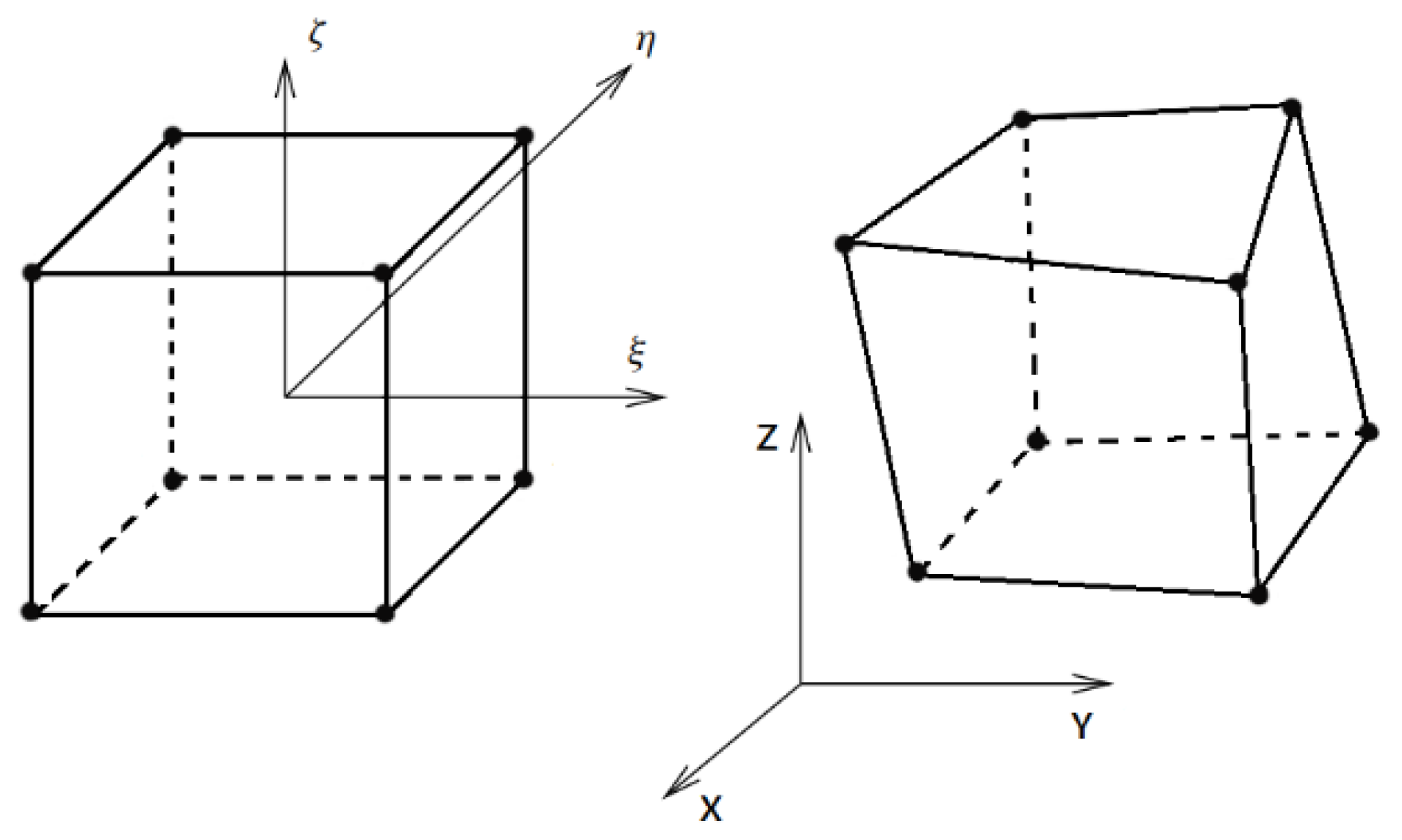
| Corner Nodes (8×) | |
|---|---|
| for | |
Appendix A.2. Quadratic Brick Element
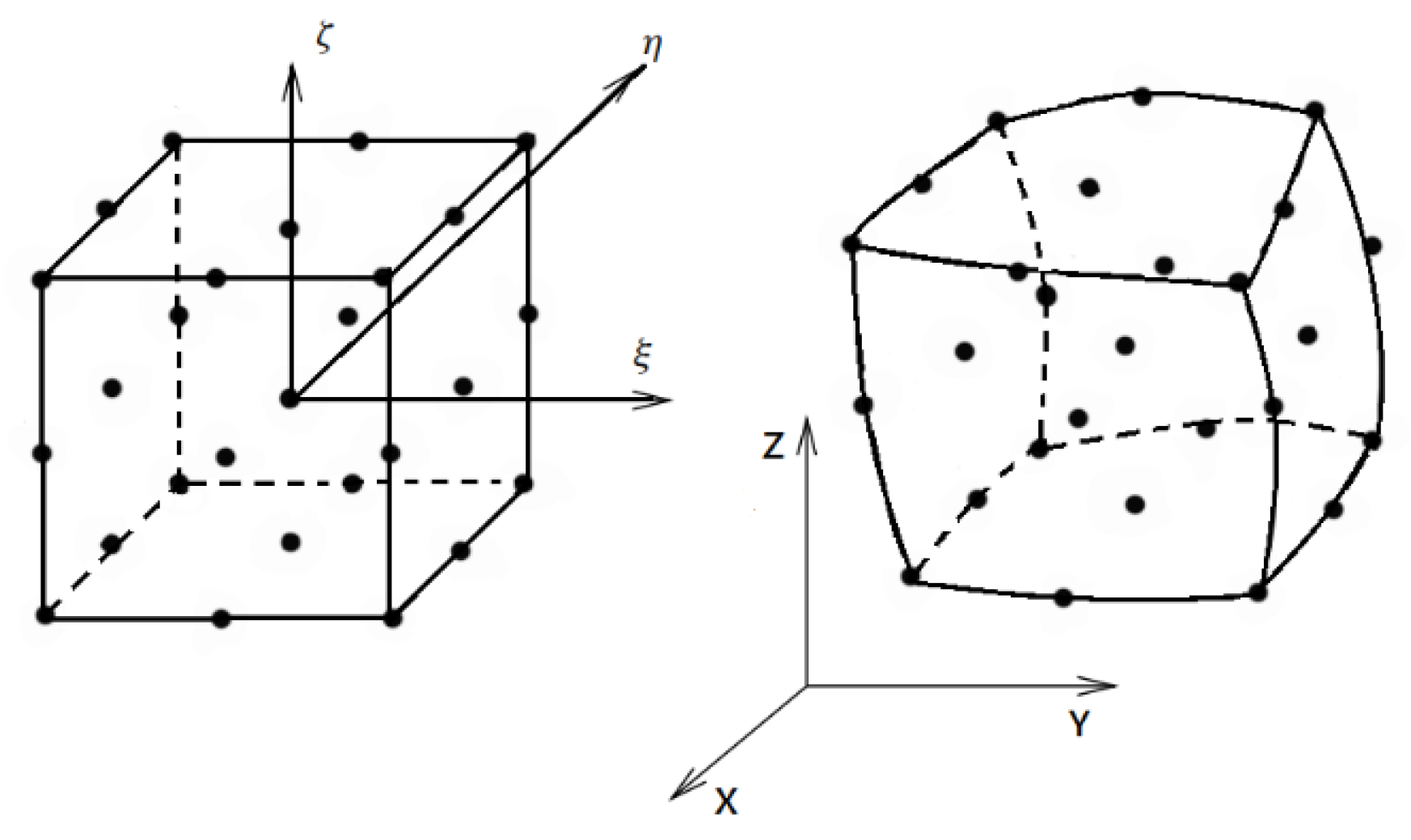
| Corner Nodes (8×) | |
| for | |
| Mid-Edge Nodes (12×) | |
| for | |
| for | |
| for | |
| Mid-Face Nodes (6×) | |
| for | |
| for | |
| for | |
| Mid-Volume Node (1×) | |
| for | |
Appendix A.3. Cubic Brick Element

| Corner Nodes (8×) | |
| for | |
| Mid-Edge Nodes (24×) | |
| for | |
| for | |
| for | |
| Mid-Face Nodes (24×) | |
| for | |
| for | |
| for | |
| Mid-Volume Node (8×) | |
| for | |
Appendix A.4. Second-Order Serendipity Element
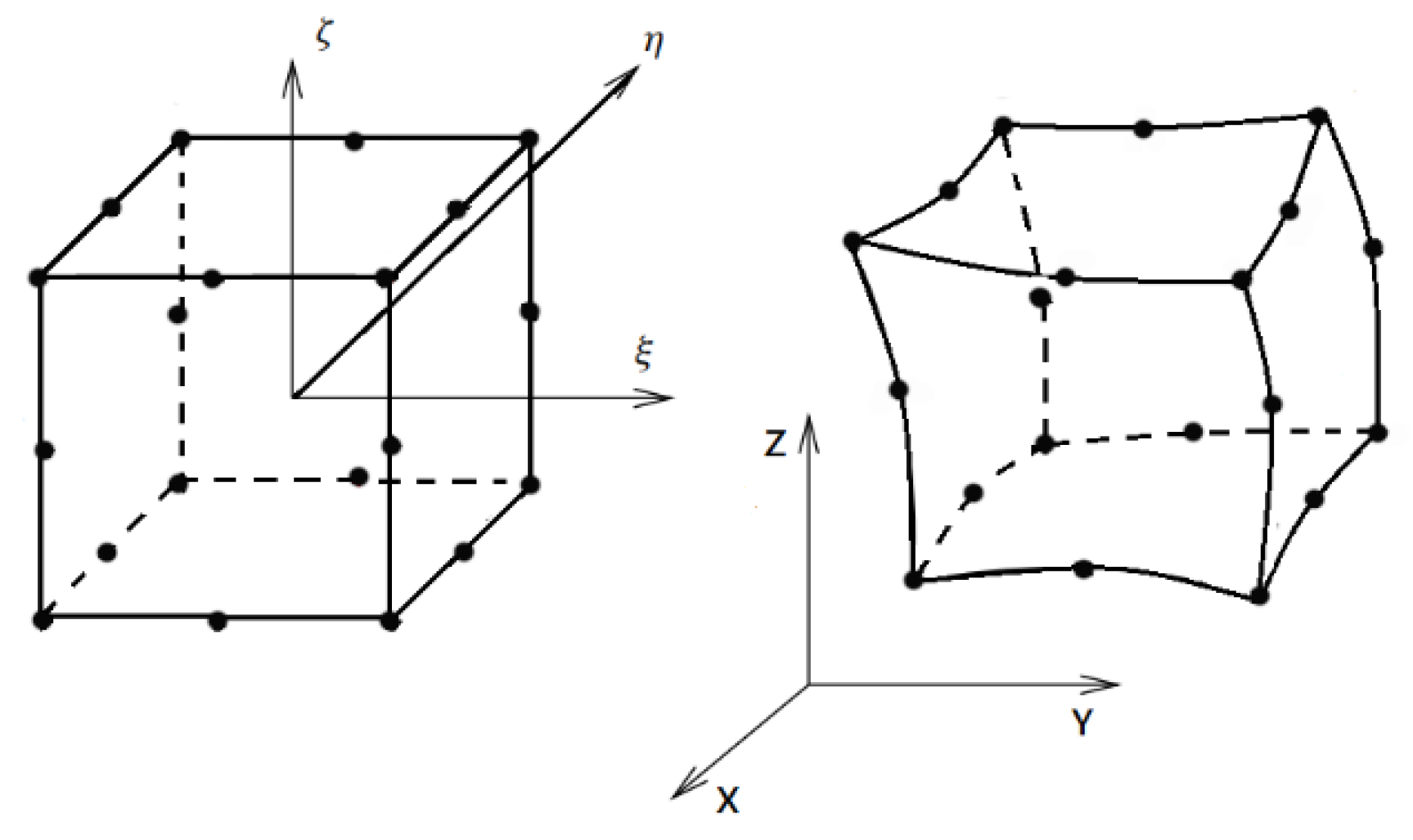
| Corner Nodes (8×) | |
| Mid-Edge Nodes (12×) | |
Appendix A.5. Third-Order Serendipity Element
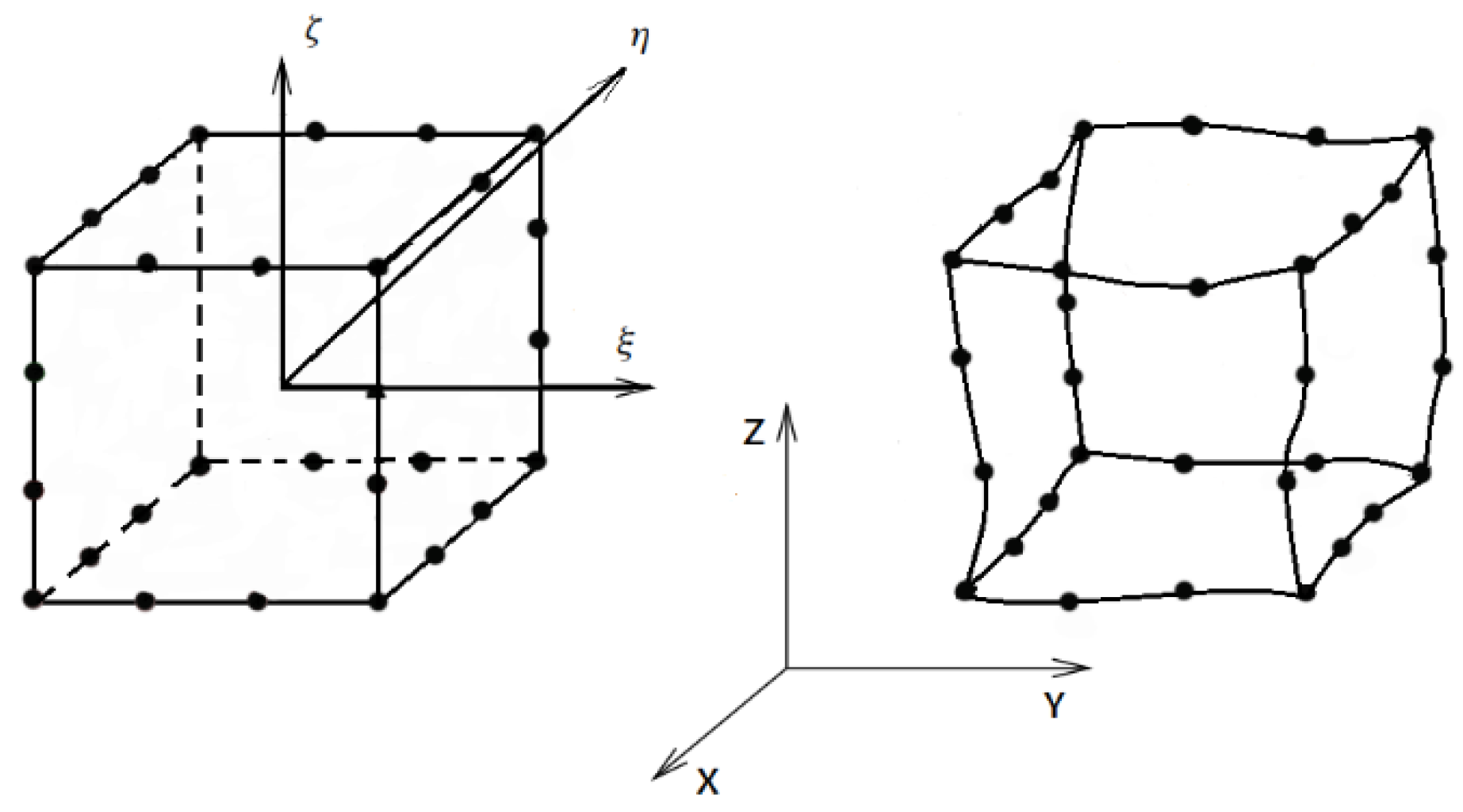
| Corner Nodes (8×) | |
| Mid-Edge Nodes (24×) | |
References
- Greco, F.; Arroyo, M. High-order maximum-entropy collocation methods. Comput. Methods Appl. Mech. Eng. 2020, 367, 113115. [Google Scholar] [CrossRef]
- Badia, S.; Codina, R.; Espinoza, H. Stability, Convergence, and Accuracy of Stabilized Finite Element Methods for the Wave Equation in Mixed Form. J. Numer. Anal. 2014, 52, 1729–1752. [Google Scholar] [CrossRef]
- Trefethen, L.N. Accuracy, Stability and Convergence. In Finite Difference and Spectral Methods for Ordinary and Partial Differential Equations, 1st ed.; Cornell University: Ithaca, NY, USA, 1996; Chapter 4; pp. 146–188. [Google Scholar]
- Gabard, G.; Astley, R.J.; Tahar, M.B. Stability and accuracy of finite element methods for flow acoustics: General theory and application to one-dimensional propagation. Int. J. Numer. Methods Eng. 2005, 63, 947–973. [Google Scholar] [CrossRef]
- Willberg, C.; Duczek, S.; Vivar Perez, J.M.; Schmicker, D.; Gabbert, U. Comparison of different higher order finite element schemes for the simulation of Lamb waves. Comput. Methods Appl. Mech. Eng. 2012, 241, 246–261. [Google Scholar] [CrossRef]
- Niiranen, J. A-Priori and a-Posteriori Error Analysis of Finite Element Methods for Plate Models. Ph.D. Thesis, Helsinki University of Technology, Espoo, Finland, 2007. [Google Scholar]
- Kröner, A.; Kröner, H. A priori error estimates for finite element approximations of regularized level set flows in higher norms. Appl. Numer. Math. 2022, 171, 307–328. [Google Scholar] [CrossRef]
- Irimie, S.; Bouillard, P. A residual a posteriori error estimator for the finite element solution of the Helmholtz equation. Comput. Methods Appl. Mech. Eng. 2001, 190, 4027–4042. [Google Scholar] [CrossRef]
- Guddati, M.N.; Yue, B. Modified integration rules for reducing dispersion error in finite element methods. Comput. Methods Appl. Mech. Eng. 2004, 193, 275–287. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.C.D. An hp-version adaptive finite element algorithm for eigensolutions of moderately thick circular cylindrical shells via error homogenisation and higher-order interpolation. Eng. Comput. 2022, 39, 1874–1901. [Google Scholar] [CrossRef]
- Jonckheere, S.; Bériot, H.; Dazel, O.; Desmet, W. An adaptive order finite element method for poroelastic materials described through the Biot equations. Int. J. Numer. Methods Eng. 2022, 123, 1329–1359. [Google Scholar] [CrossRef]
- Demkowiczt, L.; Babuska, I. P interpolation error estimates for edge finite elements of variable order in two dimensions. SIAM J. Numer. Anal. 2004, 41, 1195–1208. [Google Scholar] [CrossRef]
- Apel, T. Interpolation in h-Version Finite Element Spaces. In Encyclopedia of Computational Mechanics, Online ed.; Wiley: Chichester, MA, USA, 2004; Volume 1, pp. 67–101. [Google Scholar]
- Jodlbauer, D.; Langer, U.; Wick, T. Parallel Matrix-Free Higher-Order Finite Element Solvers for Phase-Field Fracture Problems. Math. Comput. Appl. 2020, 25, 40. [Google Scholar] [CrossRef]
- Drouet, G.; Hild, P. An accurate Local Average Contact (LAC) method for nonmatching meshes in 2D and 3D. Numer. Mathods 2017, 136, 467–502. [Google Scholar] [CrossRef]
- Lin, T.; Lin, Y.; Sun, W. Error estimation of a class of quadratic immersed finite element methods for elliptic interface problems. Disc. Cont. Dyn. Syst. 2007, 7, 807–823. [Google Scholar] [CrossRef]
- Benzley, S.; Perry, E.; Merkley, K.; Clark, B. A Comparison of All Hexagonal and All Tetrahedral Finite Element Meshes for Elastic and Elasto-plastic Analysis. In Proceedings of the 4th International Meshing Roundtable, Sandia National Laboratories, Albuquerque, NM, USA, 6 October 1995. [Google Scholar]
- Rand, A.; Gillette, A.; Bajaj, C. Quadratic serendipity finite elements on polygons using generalized barycentric coordinates. Math. Comput. 2014, 83, 2691–2716. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.R.; Quek, S.S. The Finite Element Method. A Practical Course, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2013; p. 456. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.R. The Finite Element Method: Its Basis and Fundamentals, 7th ed.; Butterworth-Heinemann: Oxford, UK, 2013; p. 756. [Google Scholar]
- Belytschko, T.; Fish, J. A First Course in Finite Elements, 1st ed.; Wiley: Hoboken, NJ, USA, 2007; p. 320. [Google Scholar]
- Arnold, D.N.; Awanou, G. Finite element differential forms on cubical meshes. Math. Comput. 2014, 83, 1551–1570. [Google Scholar] [CrossRef]
- Wang, Y. An h-version adaptive FEM for eigenproblems in system of second order ODEs: Vector Sturm-Liouville problems and free vibration of curved beams. Eng. Comput. 2020, 38, 1807–1830. [Google Scholar] [CrossRef]
- Wang, L.; Zhong, H. A time finite element method for structural dynamics. Appl. Math. Model. 2017, 41, 445–461. [Google Scholar] [CrossRef]
- Bathe, K.J.; Wilson, E.L. Numerical Methods in Finite Element Analysis, 1st ed.; Prentice Hall: Hoboken, NJ, USA, 1976; p. 528. [Google Scholar]
- Bathe, K.J. Finite Element Procedures, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 2014; p. 1065. [Google Scholar]
- Pashkevich, A.; Klimchik, A.; Chablat, D.; Wenger, P. Accuracy Improvement for Stiffness Modeling of Parallel Manipulators. In Proceedings of the CIRP Conference on Manufacturing Systems, Grenoble, France, 3–5 June 2009. [Google Scholar]
- Tsukerman, I. A General Accuracy Criterion for Finite Element Approximation. IEEE Trans. Magn. 1998, 34, 2425–2428. [Google Scholar] [CrossRef]
- González-Estrada, O.A.; Natarajan, S.; Ródenas, J.J.; Bordasad, S.P. Error estimation for the polygonal finite element method for smooth and singular linear elasticity. Comput. Math. Appl. 2021, 92, 109–119. [Google Scholar] [CrossRef]
- Banz, L.; Hernández, O.; Stephan, E.P. A priori and a posteriori error estimates for ℎ𝑝-FEM for a Bingham type variational inequality of the second kind. Comput. Math. Appl. 2022, 126, 14–30. [Google Scholar] [CrossRef]
- Cook, R.D.; Malkus, D.S.; Plhesha, M.E.; Witt, R.J. Concepts and Applications of Finite Element Analysis; John Wiley & Sons: New York, NY, USA, 2002; p. 719. [Google Scholar]
- Hughes, T.J.R.; Evans, J.A.; Reali, A. Finite element and NURBS approximations of eigenvalue, boundary-value, and initial-value problems. Comput. Methods Appl. Mech. Eng. 2014, 272, 290–320. [Google Scholar] [CrossRef]
- Gratsch, T.; Bathe, K.J. A posteriori error estimation techniques in practical finite element analysis. Comput. Struct. 2005, 83, 235–265. [Google Scholar] [CrossRef]
- Babuska, I.; Rheinboldt, W.C. Error estimates for adaptive finite element computations. SIAM J. Numer. Anal. 1978, 15, 736–754. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Zhu, J.Z. A Simple Error Estimator and Adaptive Procedure for practical Engineering Analysis. Int. J. Numer. Methods. Eng. 1987, 24, 337–357. [Google Scholar] [CrossRef]
- Demkowicz, L.; Kurtz, J.; Pardo, D.; Paszynski, M.A. Computing with hp-Adaptive Finite Elements, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2007; p. 440. [Google Scholar]
- Demkowicz, L.; Kurtz, J.; Qiu, F. hp-adaptive finite elements for coupled multiphysics wave propagation problems. Comput. Methods. Mech. 2010, 1, 19–42. [Google Scholar]
- Nguyen-Hoang, S.; Sohn, D.; Kim, H.-G. A new polyhedral element for the analysis of hexahedral-dominant finite element models and its application to nonlinear solid mechanics problems. Comput. Methods Appl. Mech. Eng. 2017, 324, 248–277. [Google Scholar] [CrossRef]
- Talebi, H.; Zi, G.; Silani, M.; Samaniego, E.; Rabczuk, T. A Simple Circular Cell Method for Multilevel Finite Element Analysis. J. Appl. Math. 2012, 2012, 526846. [Google Scholar] [CrossRef]
- Fan, Q.; Zhang, Q.; Liu, G. A Stress Analysis of a Conical Pick by Establishing a 3D ES-FEM Model and Using Experimental Measured Forces. Appl. Sci 2019, 9, 5410. [Google Scholar] [CrossRef]
- Neto, M.A.; Amaro, A.; Roseiro, L.; Cirne, J.; Leal, R. Engineering Computation of Structures: The Finite Element Method, 1st ed.; Springer: Cham, Switzerland, 2015; p. 327. [Google Scholar]
- Kuhn, C.; Muller, R. Exponential finite element shape functions for a phase field model of brittle fracture. In Proceedings of the XI International Conference on Computational Plasticity Fundamentals and Applications, Barcelona, Spain, 7–9 September 2011. [Google Scholar]
- Christ, D.; Cervera, M.; Chiumenti, M. A mixed Finite Element formulation for incompressibility using linear displacement and pressure interpolations. In Monograph CIMNE, 1st ed.; CIMNE: Barcelona, Spain, 2003; pp. 1–79. [Google Scholar]
- Felippa, C. Shear Locking in Turner Triangle. In Introduction to Finite Element Methods, 1st ed.; Aerospace Engineering Sciences Department, University of Colorado: Boulder, CO, USA, 2004; Volume 1, p. 791. [Google Scholar]
- Visintainer, M.R.; Bittencourt, E.; Braun, A.L. A numerical investigation on contact mechanics applications using eight-node hexahedral elements with underintegration techniques. Lat. Am. J. Solids Struct. 2021, 18, 1–31. [Google Scholar] [CrossRef]
- Li, K.P.; Cescotto, S. An 8-node brick element with mixed formulation for large deformation analyses. Comput. Methods Appl. Mech. Eng. 1997, 141, 157–204. [Google Scholar] [CrossRef]
- Zhu, Y.Y.; Cescotto, S. Unified and mixed formulation of the 8-node hexahedral elements by assumed strain method. Comput. Methods Appl. Mech. Eng. 1997, 129, 177–209. [Google Scholar] [CrossRef]
- Ntioudis, S. Hourglass Control in Non-Linear Finite Element Analysis, Using Hexahedral Elements. Ph.D. Thesis, University of Thessaly, Volos, Greece, 12 October 2018. [Google Scholar]
- Liu, G.R.; Nguyen-Xuan, H.; Nguyen-Thoi, T. A variationally consistent αFEM (VCαFEM) for solution bounds and nearly exact solution to solid mechanics problems using quadrilateral elements. Int. J. Numer. Methods Eng. 2011, 85, 461–497. [Google Scholar] [CrossRef]
- Flanagan, D.P.; Belytschko, T. A uniform strain hexadron and quadrilateral with orthogonal hourglass control. Internat. J. Numer. Methods Eng. 1981, 17, 679–706. [Google Scholar] [CrossRef]
- Hughes, T.G.R. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis, 1st ed.; Dover Publications: Mineola, NY, USA, 2000; p. 704. [Google Scholar]
- Reese, S.; Wriggers, P. A stabilization technique to avoid hourglassing in finite elasticity. Int. J. Numer. Methods Eng. 2000, 48, 79–109. [Google Scholar] [CrossRef]
- Araujo-Cabarcas, J.C.; Engström, C. On spurious solutions in finite element approximations of resonances in open systems. Comput. Math. Appl. 2017, 74, 2385–2402. [Google Scholar] [CrossRef]
- Mirbagheri, Y.; Nahvi, H.; Parvizian, J.; Düster, A. Reducing spurious oscillations in discontinuous wave propagation simulation using high-order finite elements. Comput. Math. Appl. 2015, 70, 1640–1658. [Google Scholar] [CrossRef]
- Ko, Y.; Bathe, K.-J. A new 8-node element for analysis of three-dimensional solids. Comput. Struct. 2018, 202, 85–104. [Google Scholar]
- Karpik, A.; Cosco, F.; Mundo, D. On the Profitability of Higher Order FE Formulations for Structural Dynamics. In Proceedings of the IFToMM, Naples, Italy, 7–9 September 2022. [Google Scholar]
- Danielson, K.T.; Adley, M.D.; Williams, T.N. Second-order finite elements for Hex-Dominant explicit methods in nonlinear solid dynamics. Finite Elements Anal. Des. 2016, 119, 63–77. [Google Scholar] [CrossRef]
- Liu, Y. Effects of Mesh Density on Finite Element Analysis. SAE Tech. Pap. 2013, 1375, 1–8. [Google Scholar]
- Rachowicz, W.; Pardob, D.; Demkowicz, L. Fully automatic hp-adaptivity in three dimensions. Comput. Methods Appl. Mech. Eng. 2006, 195, 4816–4842. [Google Scholar] [CrossRef]
- Song, S.; Braun, M.; Wiegard, B.; Herrnring, H.; Ehlers, S. Combining H-Adaptivity with the Element Splitting Method for Crack Simulation in Large Structures. Materials 2022, 15, 240. [Google Scholar] [CrossRef] [PubMed]
- Babuska, I.; Szabo, B.A.; Katz, I.N. The p-version of the finite element method. SIAM J. Numer. Anal. 1981, 18, 515–545. [Google Scholar] [CrossRef]
- Eisenträger, S.; Atroshchenko, E.; Makvandi, R. On the condition number of high order finite element methods: Influence of p-refinement and mesh distortion. Comput. Math. Appl. 2020, 80, 2289–2339. [Google Scholar] [CrossRef]
- López Machado, N.A.; Vielma Pérez, J.C.; López Machado, L.J. An 8-Nodes 3D Hexahedral Finite Element and an 1D 2-Nodes Structural Element for Timoshenko Beams, Both Based on Hermitian Intepolation, in Linear Range. Mathematics 2022, 10, 836. [Google Scholar] [CrossRef]
- Babuska, I.; Szabo, B. On the Rates of Convergence of the Finite Element Method. Int. J. Numer. Meth. Eng. 1982, 18, 323–341. [Google Scholar] [CrossRef]
- Babuska, I. The p- and hp-Versions of the Finite Element Method: The State of the Art, Finite Elements. In Book Finite Elements: Theory and Applications, 1st ed.; Springer: New York, NY, USA, 2011; Volume 1, p. 312. [Google Scholar]
- Lo, S.H. Finite Element Mesh Generation, 1st ed.; CRC Press: Boca Raton, FL, USA, 2015; p. 672. [Google Scholar]
- Zhoul, P.L.; Cen, S.; Huang, J.B.; Li, C.F.; Zhang, Q. An unsymmetric 8-node hexahedral element with high distortion tolerance. Int. J. Numer. Meth. Eng. 2016, 109, 1130–1158. [Google Scholar]
- Shang, Y.; Li, C.F.; Jia, K.Y. Jia 8-node hexahedral unsymmetric element with rotation degrees of freedom for modified couple stress elasticity. Int. J. Numer. Methods Eng. 2020, 121, 2683–2700. [Google Scholar] [CrossRef]
- Parrish, M.; Borden, M.; Staten, M.; Benzley, S. A Selective Approach to Conformal Refinement of Unstructured Hexahedral Finite Element Meshes. In Book Proceedings of the 16th International Meshing Roundtable, 1st ed.; Springer: Washington, DC, USA, 2014; Volume 1, pp. 251–268. [Google Scholar]
- Schneider, T.; Hu, Y.; Gao, X.; Dumas, J.; Zorin, D.; Panozzo, D. A large-scale comparison of tetrahedral and hexahedral elements for solving elliptic PDEs with the finite element method. ACM Trans. Graph. 2022, 41, 1–14. [Google Scholar] [CrossRef]
- Mohsen, A.; Moslemi, H.; Seddighian, M.R. An Improved Nodal Ordering for Reducing the Bandwidth in FEM. J. Serbian Soc. Comput. Mech. 2018, 12, 126–143. [Google Scholar] [CrossRef]
- Zeng, K. Automatic Generation of Compact Models for the Efficient Calculation of MEMS Structures, 1st ed.; Cuvillier Verlag: Göttingen, Germany, 2005; p. 150. [Google Scholar]
- Zhang, J.; Kikuchi, F. Interpolation error estimates of a modified 8- node serendipity finite element. Numer. Math. 2000, 85, 503–524. [Google Scholar] [CrossRef]
- Arnold, D.N.; Awanou, G. The serendipity family of finite elements. Found. Comput. Math. 2011, 11, 337–344. [Google Scholar] [CrossRef]
- Browning, R.S. A Second-Order 19-Node Pyramid Finite Element Suitable for Lumped Mass Explicit Dynamic Methods in Nonlinear Solid Mechanics. Ph.D. Thesis, University of Alabama at Birmingham, Birmingham, AL, USA, September 2020. [Google Scholar]
- Lee, N.; Bathe, K.-J. Effects of element distortions on the performance of isoparametric elements. Int. J. Numer. Methods Eng. 1993, 36, 3553–3576. [Google Scholar] [CrossRef]
- Liu, G.R.; Nguyen-Xuan, H.; Nguyen-Thoi, T. A theoretical study on the smoothed FEM (S-FEM) models: Properties, accuracy and convergence rates. Int. J. Numer. Methods Eng. 2010, 84, 1222–1256. [Google Scholar] [CrossRef]
- Kressner, D. The Krylov-Schur Algorithm. In Numerical Methods for General and Structured Eigenvalue Problem, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 1, pp. 113–130. [Google Scholar]
- Cosco, F.; Greco, F.; Desmet, W.; Mundo, D. GPU accelerated initialization of local maximum-entropy meshfree methods for vibrational and acoustic problems. Comput. Methods Appl. Mech. Eng. 2020, 36, 113089. [Google Scholar] [CrossRef]





| Integration Schemes | ||||
|---|---|---|---|---|
| Order | Nodes | 2 × 2 × 2 | 3 × 3 × 3 | 4 × 4 × 4 |
| Linear | 8 | Hexa8-Int8 | ||
| Quadratic Serendipity | 20 | Hexa20-Int8 1 | Hexa20-Int27 | |
| Quadratic | 27 | Hexa27-Int27 | ||
| Cubic Serendipity | 32 | Hexa32-Int27 1 | Hexa32-Int64 | |
| Cubic | 64 | Hexa64-Int64 | ||
| Young’s Modulus E, GPa | Density ρ, kg/m3 | Poisson’s Ratio ν |
|---|---|---|
| 206.94 | 7829 | 0.288 |
| Test Name | Shape Type | Integration Scheme | N. of Elements in All Directions | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Hexa8-Int8 | Linear | 2 × 2 × 2 | 6 | 12 | 18 | 24 | 30 | 36 | |
| Hexa20-Int8 2 | Quadratic | 2 × 2 × 2 | 4 | 7 | 11 | 15 | 19 | 23 | |
| Hexa20-Int27 | Quadratic | 3 × 3 × 3 | 4 | 7 | 11 | 15 | 19 | 23 | |
| Hexa27-Int27 | Quadratic | 3 × 3 × 3 | 3 | 6 | 9 | 12 | 15 | 18 | |
| Hexa32-Int27 2 | Cubic | 3 × 3 × 3 | 3 | 6 | 9 | 12 | 15 | 18 | |
| Hexa32-Int64 | Cubic | 4 × 4 × 4 | 3 | 6 | 9 | 12 | 15 | 18 | |
| Hexa64-Int64 | Cubic | 4 × 4 × 4 | 2 | 4 | 6 | 8 | 10 | 12 | 14 1 |
 |  |  |  | 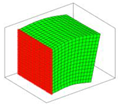 |
| Mode 1 2732.90, Hz | Mode 2 2732.90, Hz | Mode 3 3730.90, Hz | Mode 4 6520.08, Hz | Mode 5 7244.23, Hz |
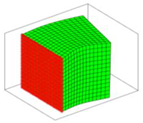 | 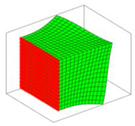 | 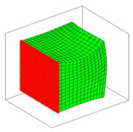 |  | 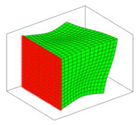 |
| Mode 6 7244.23, Hz | Mode 7 8944.78, Hz | Mode 8 10,599.78, Hz | Mode 9 11,034.94, Hz | Mode 10 11,267.65, Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karpik, A.; Cosco, F.; Mundo, D. Higher-Order Hexahedral Finite Elements for Structural Dynamics: A Comparative Review. Machines 2023, 11, 326. https://doi.org/10.3390/machines11030326
Karpik A, Cosco F, Mundo D. Higher-Order Hexahedral Finite Elements for Structural Dynamics: A Comparative Review. Machines. 2023; 11(3):326. https://doi.org/10.3390/machines11030326
Chicago/Turabian StyleKarpik, Anna, Francesco Cosco, and Domenico Mundo. 2023. "Higher-Order Hexahedral Finite Elements for Structural Dynamics: A Comparative Review" Machines 11, no. 3: 326. https://doi.org/10.3390/machines11030326
APA StyleKarpik, A., Cosco, F., & Mundo, D. (2023). Higher-Order Hexahedral Finite Elements for Structural Dynamics: A Comparative Review. Machines, 11(3), 326. https://doi.org/10.3390/machines11030326







