Design, Kinematics and Workspace Analysis of a Novel 4-DOF Kinematically Redundant Planar Parallel Grasping Manipulator

Abstract

This article presents a model of a novel 4-DOF kinematically redundant planar parallel grasping manipulator. As distinct from the traditional 4-DOF manipulator, the proposed design includes an extensible platform, which provides kinematic redundancy. This constructive feature is used for grasping. The article discusses the inverse and forward kinematics of the proposed manipulator. The inverse kinematics algorithm provides the analytical relations between the platform coordinates and the driven (controlled) coordinates. The forward kinematics algorithm allows defining different assembly modes of the manipulator. Both algorithms are demonstrated using numerical examples. The article discusses different designs of the manipulator in which its links are placed in one, two, or three layers. Based on these designs, we performed their workspace analyses.

1. Introduction

One of the most common designs of parallel mechanisms, manipulators and robots in engineering is the planar design. Mechanisms of this type are widely used in many industrial and technological applications, for example, in pick-and-place operations [1,2], medical devices [3,4,5], machining technologies [6,7], high-speed operations [8], packaging technologies [9], depaneling procedures [10], gripping operations [11], high-precision manipulations [12,13], walking architectures [14,15], etc.

Among planar parallel mechanical systems, considerable attention is paid to the study of 4-RRR manipulators. Structurally, these are 3-RRR manipulators with an additional RRR chain. In the technical literature, there are a number of publications that address individual issues of the analysis of 4-RRR manipulators. For instance, the inverse position problem, the problems of velocities and accelerations, as well as the dynamic analysis of the manipulator have been considered in [16]. In this study, the authors conduct a comparative analysis of 3-DOF (abbr. expansion: degree of freedom) 4-RRR, 3-RRR and 2-RRR manipulators, on the basis of which it is concluded that the dynamic performance of the 4-RRR manipulator is better than the dynamic performance of 3-RRR and 2-RRR manipulators. In [17], the authors propose an approach for dynamic balancing the 4-RRR manipulator. Based on this approach the authors propose the DUAL-V prototype, which provides high-speed motion with low base vibration. The authors of [18] summarize general approaches for dynamic balancing of 4-RRR-type manipulators and their synthesis by using reactionless mechanisms.

The authors of [19] provide a workspace analysis of the 4-RRR manipulator. Reachable, orientation and nonsingular workspaces have been constructed. Another study on workspace construction is presented in [20]. Here the authors propose a numerical approach that is based on the Genetic algorithm, which allows identifying the singularity-free space of the manipulator and defining the effects of joint positions on the singularity-free space. A singularity analysis of the manipulator is presented in [21]. The paper has proposed a method that is based on a geometric approach. The authors of [22], using the example of the 4-RRR manipulator, demonstrate an approach to determine closeness to singularities using screw theory.

Wrench capabilities (the maximal forces and torques that might be applied or sustained by a manipulator) of planar parallel manipulators, including the 4-RRR manipulator, are studied in [23]. Wrench capabilities are used in path planning and manipulator design (they allow the exploration of such parameters as the actuator torque capabilities and the element dimensions). The authors of [24], using the example of the 4-RRR manipulator, demonstrate a novel method of the optimum design. The method takes into consideration both the kinematic and dynamic characteristics. The authors of [25] propose an approach for the minimization of revolute joint clearances applied for the 4-RRR manipulator. The authors established a dynamic model of the manipulator with joint clearances and applied two-step Bathe integration to solve the highly nonlinear equations.

In the works discussed above, the 4-RRR manipulator has actuation redundancy (when extra actuators are added in passive joints or extra actuated kinematic chains are introduced [26]). Another type of redundancy is kinematic redundancy (when extra actuated links are added in one or several kinematic chains of a parallel manipulator changing its structure to get extra DOFs [26]). Examples of planar kinematically redundant manipulators, their design and analysis methods are considered in [27,28,29,30].

The presence of redundancy in the 4-RRR manipulators compared to 3-RRR manipulators allows reducing the number of singularities and increasing the rigidity of their structures, as well as having better positioning accuracy [31] and better dynamic performance in some regions within the workspace [16], which is sufficiently important for the efficient operation of parallel manipulators.

It should be noted that the works with 4-RRR manipulators discussed above actually study only one manipulator scheme having actuation redundancy. In this article, we propose a novel 4-RRR manipulator with kinematic redundancy. In addition, in this manipulator, the fourth DOF is proposed for grasping procedures.

The article has the following organization. Section 2 describes the structure of the proposed 4-DOF kinematically redundant planar parallel grasping manipulator. This section also discusses various designs with consideration of different rotation angles in joints. Section 3 discusses analytical algorithms of the inverse and forward kinematics. Section 4 continues this analysis and provides numerical examples of solving both problems (inverse and forward). Section 5 analyzes the workspace of the manipulator based on the different designs shown in Section 2. Section 5 also analyzes gripping force distribution along the workspace for the three-layer design. Section 6 discusses the obtained results. Section 7 summarizes the results and presents directions for future research.

2. Manipulator Design

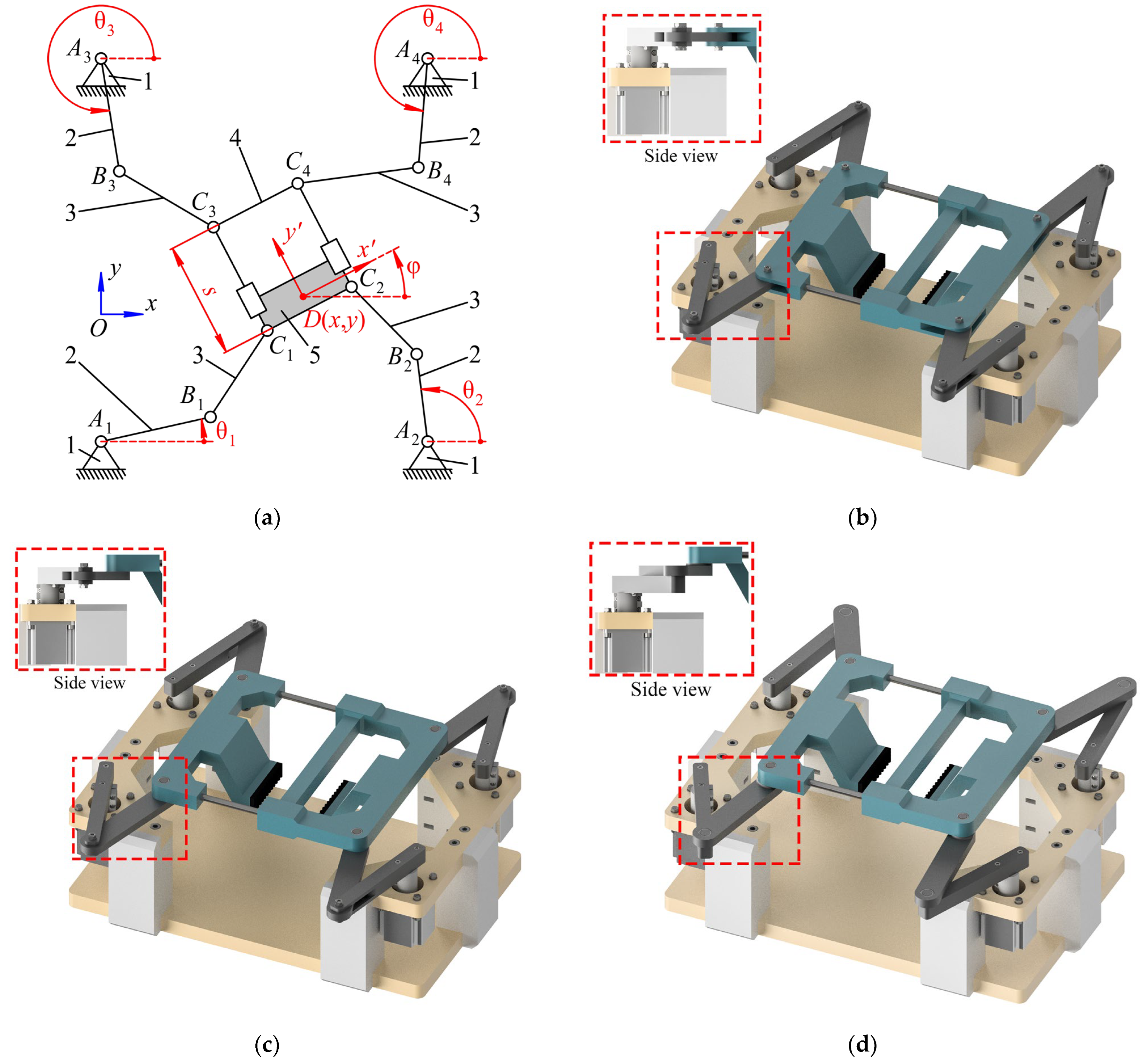
Here we consider a new design of the 4-DOF kinematically redundant planar parallel grasping manipulator. Figure 1a shows its structural scheme with kinematic notations. Here, link 1 is the fixed one, links 2 are the cranks (driving links), links 3 are the couplers and links 4 and 5 are the parts of the extensible moving platform.

The manipulator consists of four identical planar RRR kinematic chains. Here “R” denotes a revolute joint, and the underscore means that the joint is actuated. Axes of all twelve revolute joints (A_i, B_i, and C_i, i = 1…4) are parallel to each other. The moving platform of the manipulator has two parts that are connected via passive prismatic joints, which allow the platform to change its length. It should be noted that, theoretically, one prismatic joint would be enough to describe the kinematics of the manipulator. In this particular example, however, we will use two prismatic joints with parallel axes as it will be closer to the possible design of the actual manipulator. As long as these joints work synchronously, their number is irrelevant in the kinematic analysis.

One can see that the discussed manipulator is planar as its moving platform has three DOFs: two translations and one rotation in a plane. The additional DOF is a translation between the platform parts. The position of the moving platform is described by the coordinates x and y of point D, while its orientation is described by rotation angle φ. The design of the manipulator also allows controlling the length s of the moving platform by changing input angles ${\mathsf{\theta }}_i$. Therefore, the discussed manipulator is kinematically redundant (the kinematic redundancy is produced by an extensible platform, which includes two movable parts by contrast with the redundantly actuated 4-RRR manipulator discussed above). Four drives allow controlling three movements in a plane and one movement between platform parts. For the sake of simplicity, from this point, we also assume that the moving platform of the manipulator has a rectangular shape.

The proposed manipulator could be applied as a grasping device due to the extension of the moving platform. So the grasping object might be fixed between platform parts and then replaced. Figure 1b–d demonstrates such CAD models of the grasping manipulator in which all links are in a single layer (b), in two layers (c), and in three layers (c). Furthermore, in this article, we will perform the workspace analysis to calculate the dimensions of the workspaces to compare based on these designs.

3. Kinematic Analysis

3.1. Inverse Kinematics

For the inverse kinematics, the x and y coordinates are known, along with the rotation angle φ and the length of the moving platform s. The task is, therefore, to find corresponding values of the input angles ${\mathsf{\theta }}_i$.

The solution to the inverse kinematics is rather straightforward and similar to other planar manipulators with RRR kinematic chains. First, we find the coordinates of point C_i in the fixed reference frame Oxy:

$$\left[\begin{array}{c}{x}_{Ci}\\ y_{Ci}\end{array}\right]=R\left[\begin{array}{c}{x}_{Ci}^{\prime }\\ y_{Ci}^{\prime }\end{array}\right]+\left[\begin{array}{c}x\\ y\end{array}\right],$$

(1)

where $x_{Ci}^{\prime }$ and $y_{Ci}^{\prime }$ are the coordinates of C_i in the moving reference frame Dx’y’ and R is a rotation matrix that defines the orientation of the moving platform:

$$R=\left[\begin{array}{cc}\cos \mathsf{\phi }& -\sin \mathsf{\phi }\\ \sin \mathsf{\phi }& \cos \mathsf{\phi }\end{array}\right].$$

(2)

It should be noted that $x^{\prime }$ coordinates for all C_i and $y^{\prime }$ coordinates for C₁ and C₂ are constant and defined by the manipulator design, while $y^{\prime }$ coordinates of C₃ and C₄ depend on the value of s. Since we assumed that the moving platform has a rectangular shape, we can designate the following constant geometrical parameters: $x_{C1}^{\prime }$ = $x_{C3}^{\prime }$ = $x_{C13}^{\prime }$, $x_{C2}^{\prime }$=$x_{C4}^{\prime }$=$x_{C24}^{\prime }$, $y_{C1}^{\prime }$=$y_{C2}^{\prime }$= $y_{C12}^{\prime }$, therefore:

$$y_{C3}^{\prime }=y_{C4}^{\prime }=y_{C12}^{\prime }+s.$$

(3)

Now the coordinates of C_i in Oxy are known, for each chain we write the following equation:

$${\left(x_{Ci}-x_{Bi}\right)}^2+{\left(y_{Ci}-y_{Bi}\right)}^2-l_{BiCi}^2=0,$$

(4)

where the coordinates of point B_i can be expressed using ${\mathsf{\theta }}_i$ as follows:

$$x_{Bi}=x_{Ai}+l_{AiBi}{\cos \mathsf{\theta }}_i, y_{Bi}=y_{Ai}+l_{AiBi}{\sin \mathsf{\theta }}_i.$$

(5)

Here $x_{Ai}$ is the coordinate of point A_i in Oxy and $l_{AiBi}$ is the length of A_iB_i. Then, since $l_{BiCi}$, which is the length of B_iC_i, is known, each ${\mathsf{\theta }}_i$ can be found by solving the following equation obtained by substituting (5) into (4):

$${\left(x_{Ci}-x_{Ai}-l_{AiBi}{\cos \mathsf{\theta }}_i\right)}^2+{\left(y_{Ci}-y_{Ai}-l_{AiBi}{\sin \mathsf{\theta }}_i\right)}^2-l_{BiCi}^2=0.$$

(6)

It is well-known that for planar RRR chains the inverse kinematics can be solved analytically (the task is equivalent to finding the points of intersection for two circles). Therefore, in general, for any i, Equation (6) will yield two solutions, and the total number of solutions for the inverse kinematics of the manipulator in any non-singular point is equal to sixteen.

3.2. Forward Kinematics

For the forward kinematics, the task is to find coordinates of the moving platform x, y, angle φ and length s for a given set of input angles ${\mathsf{\theta }}_i$. First, since ${\mathsf{\theta }}_i$ are known, $x_{Bi}$ and $y_{Bi}$ will also be known, according to (5). This means, that (4) is a quadratic polynomial equation with two unknown variables, namely $x_{Ci}$ and $y_{Ci}$. Thus, for the whole manipulator, we have four such equations with eight unknowns.

Now, let us examine the moving platform. Since it has a rectangular shape, C₁C₂ is always parallel to C₃C₄ and C₁C₃ is always parallel to C₂C₄. This fact allows us to write two more equations using the unknowns mentioned above:

$$x_{C2}-x_{C1}=x_{C4}-x_{C3}, y_{C2}-y_{C1}=y_{C4}-y_{C3}.$$

(7)

By rearranging (7) and substituting in (4) for i = 4 we can exclude $x_{C4}$ and $y_{C4}$ from the latter. Then, the system of four quadratic polynomial equations (4) can be written as follows:

$$\begin{gathered} {\left(x_{C1}-x_{B1}\right)}^2+{\left(y_{C1}-y_{B1}\right)}^2-l_{B1C1}^2=0, \\ {\left(x_{C2}-x_{B2}\right)}^2+{\left(y_{C2}-y_{B2}\right)}^2-l_{B2C2}^2=0, \\ {\left(x_{C3}-x_{B3}\right)}^2+{\left(y_{C3}-y_{B3}\right)}^2-l_{B3C3}^2=0, \\ {\left(x_{C2}-x_{C1}+x_{C3}-x_{B4}\right)}^2+{\left(y_{C2}-y_{C1}+y_{C3}-y_{B4}\right)}^2-l_{B4C4}^2=0. \end{gathered}$$

(8)

Now we are left with four equations and six unknowns. Further inspection of the moving platform’s geometry allows us to write two more independent equations.

The first, again, is related to the fact that the moving platform has a rectangular shape, which means that C₁C₂ and C₁C₃ are orthogonal, and the dot product of the corresponding vectors should be equal to zero:

$$(x_{C2}-x_{C1})·(x_{C3}-x_{C1})+\left(y_{C2}-y_{C1}\right)·\left(y_{C3}-y_{C1}\right)=0.$$

(9)

The second comes from the fact that the length of C₁C₂ (denoted as $l_{C1C2}$), unlike C₁C₃, is always constant:

$${(x_{C2}-x_{C1})}^2+{\left(y_{C2}-y_{C1}\right)}^2-l_{C1C2}^2=0.$$

(10)

Thus, (8), (9) and (10) form a system of six quadratic polynomial equations with six unknowns. After solving the system using any suitable numerical method, the values of $x_{C1}$, $y_{C1}$, $x_{C2}$, $y_{C2}$, $x_{C3}$, $y_{C3}$ will be obtained, and Equation (7) can be used to find $x_{C4}$ and $y_{C4}$, if needed. After that, coordinates of the moving platform along with its length can be easily found, starting with s and φ:

$$s=\sqrt{{\left(x_{C3}-x_{C1}\right)}^2+{\left(y_{C3}-y_{C1}\right)}^2}, \mathsf{\phi }=\mathrm{atan}2\left(y_{C2}-y_{C1},x_{C2}-x_{C1}\right).$$

(11)

It should be noted that, technically, s in (11) can be a negative number, but since it most likely can be only positive in real-life design, we neglect the possibility of the negative solution for the sake of simplicity.

After φ is known, $x$ and $y$ can be obtained from (1), for instance:

$$\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}{x}_{C1}\\ y_{C1}\end{array}\right]-R\left[\begin{array}{c}{x}_{C1}^{\prime }\\ y_{C1}^{\prime }\end{array}\right].$$

(12)

4. Numerical Example

To demonstrate the solution to the inverse and forward kinematics we will use the manipulator with the following geometry (in meters): $x_{A1}$ = −0.115, $y_{A1}$ = −0.200, $x_{A2}$ = 0.115, $y_{A2}$ = −0.200, $x_{A3}$ = −0.115, $y_{A3}$ = 0.200, $x_{A4}$ = 0.115, $y_{A4}$ = 0.200, $l_{AiBi}$ = 0.130, $l_{BiCi}$ = 0.130, $x_{C13}^{\prime }$ = −0.115, $x_{C24}^{\prime }$ = 0.115, $y_{C12}^{\prime }$ = −0.070. We also set the limits for the value of s to be equal to 0.140 m and 0.220 m.

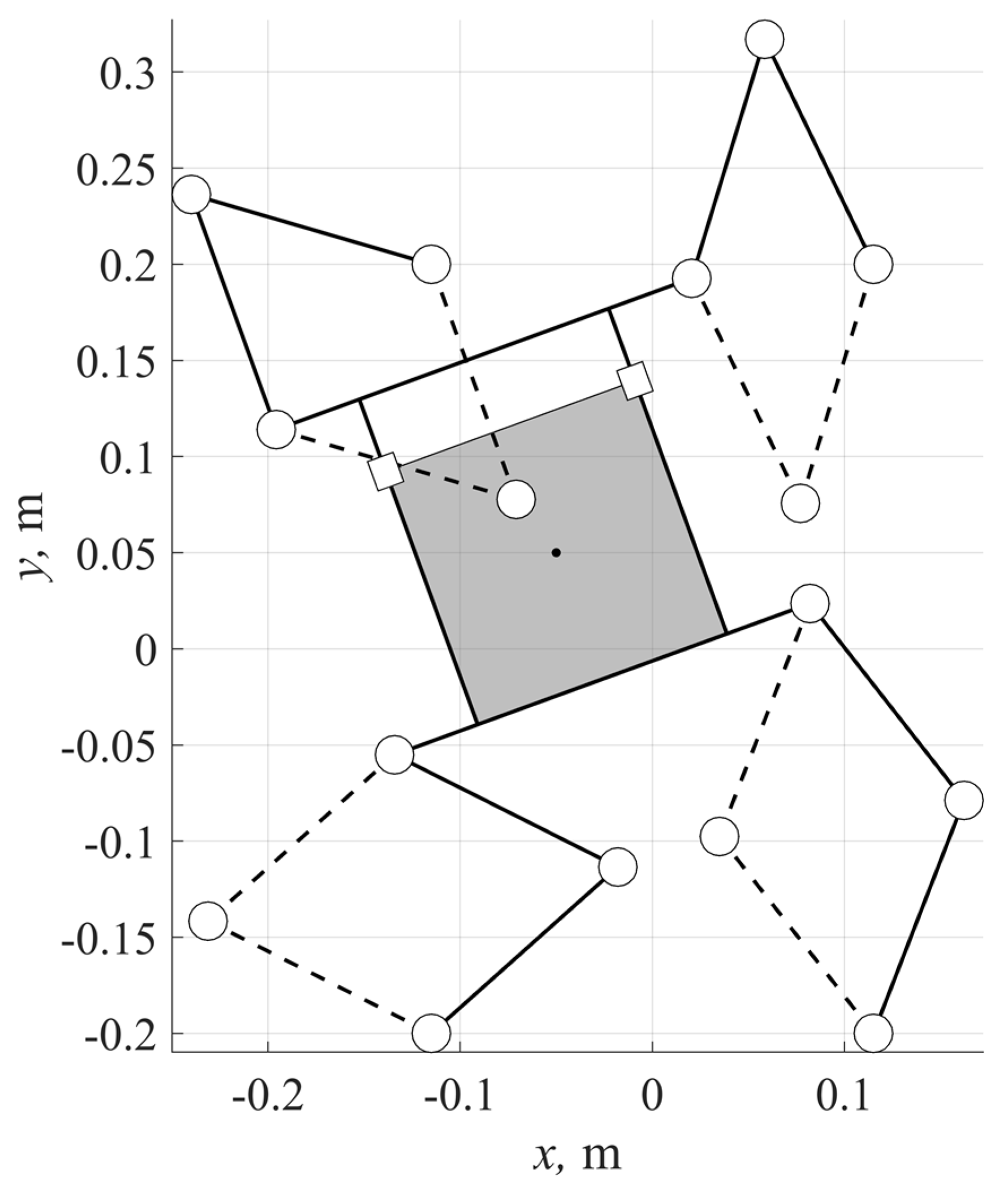
Figure 2 shows an example of the inverse kinematics solution for $x$ = −0.050 m, $y$ = 0.050 m, φ = 20 deg, s = 0.18 m.

As we mentioned above, there are sixteen possible solutions to the inverse kinematics (two for each chain) in any non-singular point. The solid lines in Figure 2 correspond to the first set of input angles (in degrees): ${\mathsf{\theta }}_1$ = 41.720, ${\mathsf{\theta }}_2$ = 68.754, ${\mathsf{\theta }}_3$ = 163.781, ${\mathsf{\theta }}_4$ = 115.809, while the dashed lines correspond to the second set of the input angles (in degrees): ${\mathsf{\theta }}_1$ = 153.318, ${\mathsf{\theta }}_2$ = 128.037, ${\mathsf{\theta }}_3$ = −70.152, ${\mathsf{\theta }}_4$ = −106.978. Theoretically, any combination of these angles is a valid solution to the inverse kinematics.

There are several methods to approach the forward kinematics numerically, namely, dialytic elimination, Groebner basis, and homotopy (polynomial) continuation [32], which are commonly used in similar research. In this work, we will utilize the latter by using Bertini package [33] through the MATLAB environment in order to solve the system of Equations (8)–(10). We also use the first set of input angles ${\mathsf{\theta }}_i$ mentioned above as an example. The result of the calculation of the forward kinematics is presented in

Table 1. Solutions to the forward kinematics.

Solution #	x, m	y, m	φ, deg	s, m
1	0.00153	−0.13144	0.35013	0.40051
2	0.12390	−0.02729	49.86840	0.41721
3	−0.05000	0.05000	20.00000	0.18000
4	−0.02240	0.07427	16.21927	0.40693
5	0.15676	−0.08402	25.10639	0.60040
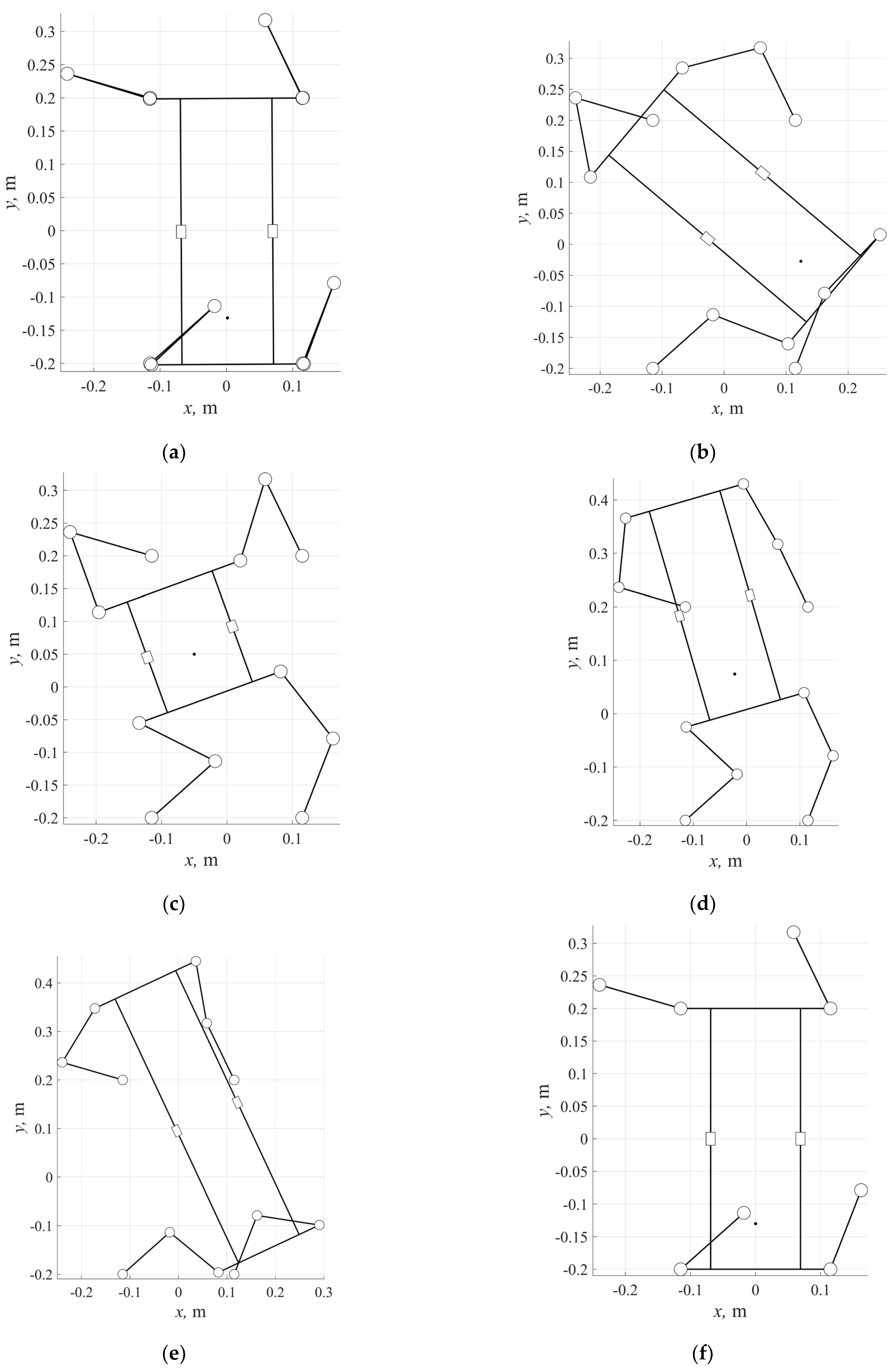
6	0.0000	−0.13000	0.00000	0.40000

and visualized in Figure 3. Note that the value of s is not limited in any way in this example.

First, we can see that in this example there are only six real-number solutions to the forward kinematics. We can also clearly see that solution 3 corresponds precisely to the solution of the inverse kinematics, which was used as an input to solve the forward kinematics. It is worth mentioning that five other possible solutions will not be probably feasible in practice as there is a linkage interference present in one way or another. Solutions 1 and 6 are also worth some attention. These solutions are very close to each other, and while solution 1 is close to a serial singularity, solution 6 is precisely a serial singularity. Due to the manipulator parameters used in this example, more precisely, $l_{AiBi}$ = $l_{BiCi}$ and $l_{A1A2}$ = $l_{A3A4}$ = $l_{C1C2}$ = $l_{C3C4}$, there will always be a valid real-number solution for any set of input angles ${\mathsf{\theta }}_i$ with coinciding points A_i and C_i in each leg.

5. Workspace Analysis

5.1. Workspace Size and Singularity

The next step is to analyze the workspace of the manipulator (size and shape). We will use the same dimensions as those we used previously for the numerical examples of kinematics analysis. During the analysis we can use an iterative approach: each coordinate is changed within a certain range with a specified step, then for each point (set of coordinates) we try to solve the inverse kinematics problem. If there is a real-number solution to this problem, then the point belongs to the workspace. It is also clear that both the size and the shape of the workspace can be greatly dependent on the design choices. For instance, let us consider the case when the moving platform and all the links of each kinematic chain are in the same layer (Figure 1b). In this case, the angle between links A_iB_i and B_iC_i cannot be less than a certain value which is defined by the design features of the links. The same is also true for the angle between B_iC_i and the moving platform. Therefore, the actual workspace of the manipulator will be smaller than the theoretical one. To address this issue, we can displace the moving platform and/or the coupler (B_iC_i) in each chain to a parallel layer (Figure 1c,d).

In addition to the shape and size of the workspace, manipulator singularities can also be studied during the iteration analysis. By taking partial derivatives of the constraint equations, we can obtain two following matrices:

$$A=\left[\begin{array}{cccc}\frac{\partial F_1}{\partial x}& \frac{\partial F_1}{\partial y}& \frac{\partial F_1}{\partial \mathsf{\phi }}& \frac{\partial F_1}{\partial s}\\ \frac{\partial F_2}{\partial x}& \frac{\partial F_2}{\partial y}& \frac{\partial F_2}{\partial \mathsf{\phi }}& \frac{\partial F_2}{\partial s}\\ \frac{\partial F_3}{\partial x}& \frac{\partial F_3}{\partial y}& \frac{\partial F_3}{\partial \mathsf{\phi }}& \frac{\partial F_3}{\partial s}\\ \frac{\partial F_4}{\partial x}& \frac{\partial F_4}{\partial y}& \frac{\partial F_4}{\partial \mathsf{\phi }}& \frac{\partial F_4}{\partial s}\end{array}\right], B=\left[\begin{array}{cccc}\frac{\partial F_1}{\partial {\mathsf{\theta }}_1}& 0& 0& 0\\ 0& \frac{\partial F_2}{\partial {\mathsf{\theta }}_2}& 0& 0\\ 0& 0& \frac{\partial F_3}{\partial {\mathsf{\theta }}_3}& 0\\ 0& 0& 0& \frac{\partial F_4}{\partial {\mathsf{\theta }}_4}\end{array}\right],$$

(13)

where F_i is the i-th constraint Equation (6).

According to Gosselin and Angeles [34], Type I (serial) singularity occurs when det(B) = 0, and Type II (parallel) singularity occurs when det(A) = 0. Here we are mainly interested in parallel singularities as their impact on the manipulator’s performance can be significant. Therefore, during the iteration analysis of the workspace, we can calculate matrix A using (13) in each point and analyze the sign of its determinant. If in two neighboring points, this sign is different, then there must be a singular point between these two points. Figure 4 shows positive values of det(A) in red and negative values in blue.

Let us now consider numerical examples. To visualize the workspace, we will use an iterative approach analyzing points within the range of [−0.3, 0.3] for both $x$ and $y$ coordinates with a step of 0.003 m. The rotation angle of the moving platform in these examples is zero and s is set to its extreme values of 0.140 m or 0.220 m. The results are demonstrated in Figure 4.

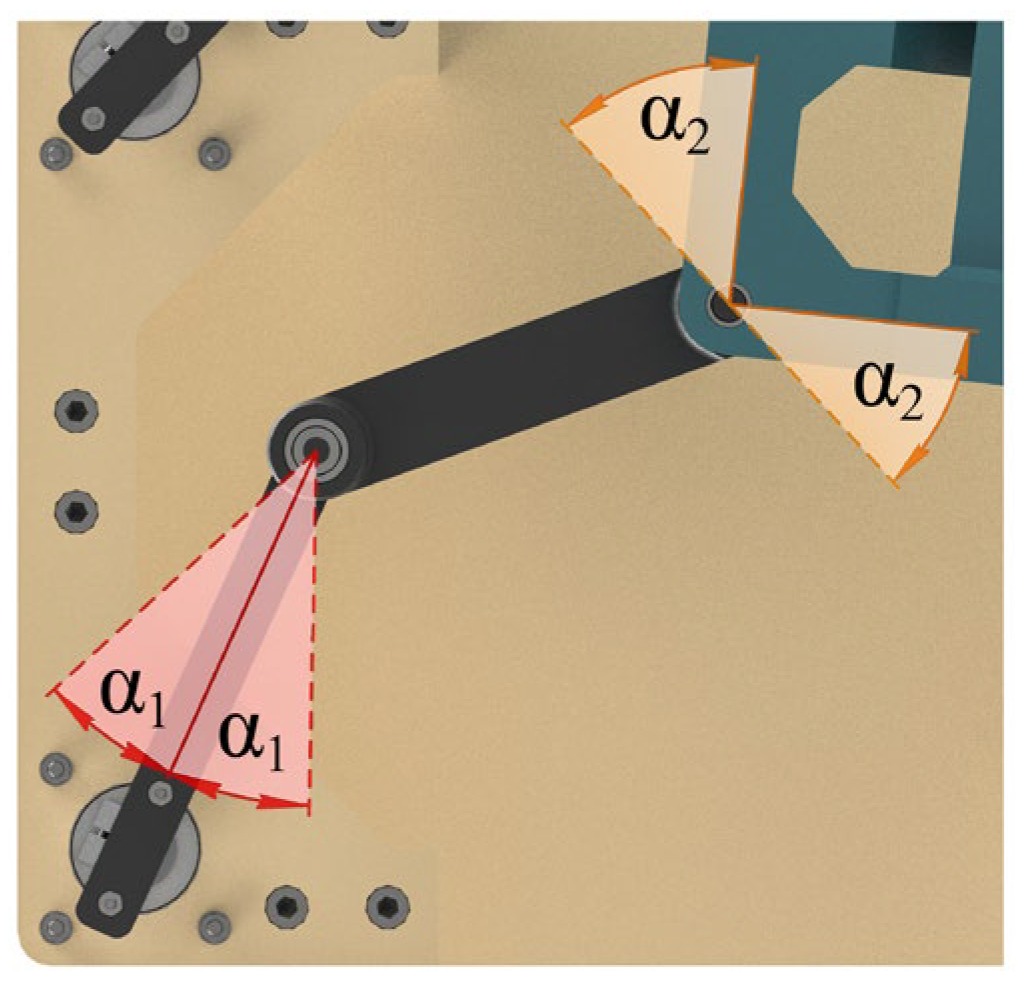
For the first example (Figure 4a,b), all links and the moving platform are placed in the same layer. The minimal allowed value of the angle between A_iB_i and B_iC_i was found (using the CAD model) to be equal to ${\mathsf{\alpha }}_1$ = 23.26 deg, and for B_iC_i and the moving platform, the threshold is ${\mathsf{\alpha }}_2$ = 48.88 deg. Both angles are demonstrated in Figure 5. For the second example (Figure 4c,d) the moving platform is located above all intermediate links, thus only angle ${\mathsf{\alpha }}_1$ between A_iB_i and B_iC_i is limited. Finally, in the third example (Figure 4e,f), no limitations are present for both mentioned angles.

One can clearly see the difference between the presented examples. For the third design variant, the workspace is roughly two times bigger than for the first variant. It can also be seen that singular points for the analyzed orientation of the moving platform are, in general, located near the edge of the workspace.

5.2. Gripping Force Analysis

Since the manipulator design allows it to act as a gripping device, it is crucial to analyze the gripping force and how it changes over the workspace. To do that we first obtain the transposed Jacobian matrix of the manipulator:

$$J^T={\left(J^{-1}\right)}^T={\left(-B^{-1}A\right)}^T.$$

(14)

Then we can calculate torque T_ai in each active joint by taking the dot product of the i-th row of J^T with the vector of external load F, i.e.:

$$\left[\begin{array}{c}{T}_{a1}\\ T_{a2}\\ T_{a3}\\ T_{a4}\end{array}\right]=-J^{T}L=-J^T\left[\begin{array}{c}{F}_x\\ F_y\\ T_z\\ F_s\end{array}\right],$$

(15)

where $F_x$ and $F_y$ are the external forces that act parallel to Ox and Oy, respectively; T_z is the external torque; and F_S is the force acting on/from the gripper.

Since the system of Equation (15) is linear, it is possible to separate actuation torques produced by external forces and torque $T_{ai}^{ex}$ and the torques that correspond to the gripping force $T_{ai}^s$:

$$\left[\begin{array}{c}{T}_{a1}\\ T_{a2}\\ T_{a3}\\ T_{a4}\end{array}\right]=\left[\begin{array}{c}{T}_{a1}^{ex}\\ T_{a2}^{ex}\\ T_{a3}^{ex}\\ T_{a4}^{ex}\end{array}\right]+\left[\begin{array}{c}{T}_{a1}^s\\ T_{a2}^s\\ T_{a3}^s\\ T_{a4}^s\end{array}\right]=-J^T\left[\begin{array}{c}{F}_x\\ F_y\\ T_z\\ 0\end{array}\right]-J^T\left[\begin{array}{c}0\\ 0\\ 0\\ F_s\end{array}\right].$$

(16)

Now let us assume that the gripping force is equal to 1 N. Then:

$$\widehat{T_{ai}^s}=-j_{Ti,4},$$

(17)

where $j_{Ti,4}$ is the element of the i-th row and 4-th column of $J^T$ and $\widehat{T_{ai}^s}$ is the torque in the i-th drive that corresponds to a unit gripping force.

Let T_motor be the torque of the actual driving motor torque used in the manipulator. Assuming that all four actuated joints utilize the same type of motor, we can now calculate the maximum allowed value of the gripping force for each active joint as follows:

$$F_{si}^{max}=\frac{T_{motor}-T_{ai}^{ex}}{\widehat{T_{ai}^s}}·1\mathrm{N}.$$

(18)

Finally, for the whole manipulator in a certain configuration, we can write:

$$F_s^{max}=min\left(F_{s1}^{max},F_{s2}^{max},F_{s3}^{max},F_{s4}^{max}\right),$$

(19)

where $F_s^{max}$ includes the maximum possible gripping force for a given configuration of the manipulator and external load.

Let us now consider a numerical example. We will use a widely available NEMA23-type stepper motor with 1.8 N·m holding torque. For the sake of simplicity, we conduct a static analysis with no external load, i.e., F_x = 0, F_y = 0, T_z = 0, using the same iterative approach as before. The results of the analysis for the three-layer manipulator with s = 0.18 m and several values of φ are shown in Figure 6.

One can clearly see that the areas of lower gripping force values are located near Type II singularities, since, as expected, when the manipulator is close to this type of singularities, the load on the actuated joints rapidly increases.

6. Discussion

When analyzing the gripping force (and indeed when performing any force analysis) of a manipulator with stepper motors, the torques in its drives are highly dependent on the rotation speed. In this article, we perform an analysis in statics, but when moving, the torque of the NEMA23-type stepper motor may be less than 1.8 N·m (holding torque value for this motor). Accordingly, when designing a manipulator prototype for a specific purpose, it is necessary to know not only the external loads and the required gripping force, but also the rotation speed. It is possible, and logical, that servomotors would be the best option for a manipulator prototype. However, it should be noted that the cost of servomotors significantly exceeds the cost of stepper motors.

As for the advantages and disadvantages of the suggested design, we would like to note the following. The three-layer design obviously has unlimited rotation angles of the neighboring links, which is definitely an advantageous feature. However, this solution also has a certain disadvantage, which is in a less reliable hinge design. If one detail is covered by another (i.e., when the links are in the same layer), then the bearings can be placed in the female part and then the hinge axis will be a beam on two supports; and if one detail is above the other one (i.e., when the links are in different layers), then each detail will have its own bearing and the axle load will be cantilevered.

The developed manipulator is proposed as a general-purpose grasping device. Accordingly, the provided number and type of DOFs are selected for allowing a wide range of different applications providing manipulations without requiring design modifications.

7. Conclusions

The article has presented the novel variation of a planar 4-DOF manipulator, which is suggested for grasping operations. Due to having four drives and realizing planar motion, the manipulator has kinematic redundancy. It should be noted that, compared to the redundantly actuated 4-RRR manipulator, the additional DOF (platform extension) of the proposed manipulator also allows reducing the loads in drives. The manipulator has been analyzed in terms of the inverse and forward kinematics and workspace. For the inverse kinematics, an analytical solution is presented, while the forward kinematics is solved numerically using the Bertini and MATLAB packages. Next, the workspace and parallel singularity iterative analysis is presented for three variants of the manipulator design with different values of feasible rotation angles between the links. The material presented in this article forms a basis for subsequent kinematic (velocity and acceleration) and dynamic analyses of the manipulator and its optimal design. Additionally, the developed CAD models serve as a basis for prototyping the manipulator.