Abstract
Parameter identification of the dynamic model of collaborative robots is the basis of the development of collaborative robot motion state control, path tracking, state monitoring, fault diagnosis, and fault tolerance systems, and is one of the core contents of collaborative robot research. Aiming at the identification of dynamic parameters of the collaborative robot, this paper proposes an identification algorithm based on weighted least squares and random weighted particle swarm optimization (WLS-RWPSO). Firstly, the dynamics mathematical model of the robot is established using the Lagrangian method, the dynamic parameters of the robot to be identified are determined, and the linear form of the dynamics model of the robot is derived taking into account the joint friction characteristics. Secondly, the weighted least squares method is used to obtain the initial solution of the parameters to be identified. Based on the traditional particle swarm optimization algorithm, a random weight particle swarm optimization algorithm is proposed for the local optimal problem to identify the dynamic parameters of the robot. Thirdly, the fifth-order Fourier series is designed as the excitation trajectory, and the original data collected by the sensor are denoised and smoothed by the Kalman filter algorithm. Finally, the experimental verification on a six-degree-of-freedom collaborative robot proves that the predicted torque obtained by the identification algorithm in this paper has a high degree of matching with the measured torque, and the established model can reflect the dynamic characteristics of the robot, effectively improving the identification accuracy.
1. Introduction
At present, robot technology is developing towards intelligence, and the manufacturing mode is also changing. In recent years, collaborative robots have received extensive attention and research around the world. According to the definition in ISO10218-2, a robot that can interact directly with humans in a designated collaborative area is called a collaborative robot. Compared with traditional industrial robots, collaborative robots have the benefits of high security, good versatility, sensitivity, precision, ease of use, and human–machine collaboration. The above advantages make collaborative robots not only applicable in the manufacturing field, but also gives them potential application value in the fields of home service and rehabilitation medicine—for example, compliant robotic arms in the industrial field, surgical robots in the medical field, wearable rehabilitation assistance robots, and anti-terrorist and explosion-proof robots in special applications [1,2]. Utilizing the technology of human–machine fusion, the establishment of a fusion robot technology with intrinsic safety, human–machine collaborative cognition, and behavioral mutual assistance can provide support for emerging new application scenarios such as industry, service, and medical care. To break through the challenges of existing robots in the four aspects of environmental adaptability, task adaptability, safety, and interactive capabilities, it is urgent to study a new generation of human–machine fusion robots [3,4].
As collaborative robot technology is developing towards high speed and high intelligence, people also put forward higher requirements on its control accuracy. In the course of human–robot collaboration—affected by uncertain factors such as robot joint friction, the moment of inertia and nonlinearity, end load, and external disturbance—people cannot directly measure robot parameters and it is challenging to model [5]. In addition, the precision requirements of the machining process are gradually increasing. If the method of obtaining inertia parameters from CAD software is used to model each part of the robot, the dynamic model of the robot cannot be accurately established. Currently, the only effective way to obtain the precise dynamic parameters of the robot is the robot parameter identification method based on experiments [6,7]. The identification of robot dynamic parameters includes six steps: dynamic modeling, model linearization, excitation trajectory optimization, experimental data sampling and preprocessing, parameter calculation, and experimental authentication [8]. The parameter estimation determines the accuracy of the entire identification. The joint model of the robot is an important part of dynamic modeling. In many previous research results, the method of joint modeling was neglected, and the Coulomb viscous friction model or Stribec friction model were often used to represent the overall friction of the joint [9,10]. The current difficulties in dynamic parameter identification mainly lie in the following: (1) Insufficient prediction accuracy. Due to the limitation of the identification algorithm on the model, the precision of the robot model used in the identification method is insufficient and the accuracy of the predicted torque based on this model is also limited. (2) Predict torque fluctuations, which are caused by discontinuous jumps in a large range of predicted values at certain nodes in the dynamic model. (3) The error peak, which is due to the inaccurate description of the dynamic characteristics of the special motion state by the traditional friction model, resulting in a large deviation compared with the actual required torque value near these motion states. Therefore, obtaining accurate robot dynamic parameters becomes particularly important [11,12].
For tandem robots represented by collaborative robots, it is necessary to establish their joint models to improve the overall model accuracy. Kircanski et al. [13] carried out identification work on joint friction and joint stiffness. However, the friction torque is not estimated approximately, which leads to inaccurate parameters and does not improve the accuracy of the model. Atkeson et al. [14] used the WLS-based serials identification method to obtain the robot’s dynamic parameters, which can accurately predict the force and torque generated by load movement; however, this method has many identification times and ignores the coupling between joints. This leads to increased recognition time and the inability to obtain the dynamic parameters of complex robot joints accurately and in a timely manner. Liu et al. [15] improved the genetic algorithm by using the inter-cell generation method and the large mutation strategy, which effectively improved the identification accuracy of the dynamic parameters of the space robot; however, the algorithm is complex in the calculation, slow in convergence, and needs to adjust many parameters. Sun et al. [16] used genetic algorithms to identify the parameters of the dynamics model of industrial robots. This algorithm can effectively avoid local optimal solutions but its efficiency will be affected because of the need to design a tedious coding and decoding process. Chen et al. [17] discussed the application of the artificial neural network algorithm in robot dynamic parameter identification such that the structure and weight of the neural network have clear physical meaning, but only the identification of inertial parameters on both sides of the end of the robot was analyzed, and there was no research on parameter identification of other joints of the robot. Wang et al. [18] proposed an identification algorithm based on an adaptive particle swarm optimization genetic algorithm for the dynamic parameter identification of flexible joint robots. In order to improve the convergence speed of the particle swarm optimization algorithm, the algorithm uses a dynamic adaptive adjustment strategy and introduces a new genetic algorithm hybrid cross-mutation mechanism to avoid particle swarms getting stuck in local optima. Due to joint flexibility and complex friction sources, this method cannot accurately reflect the internal friction of joints. Zhang et al. [19] proposed a model parameter identification method based on combination, proposed a hybrid genetic algorithm and cosine trajectory, took the multi-joint series robot as the research object, and carried out friction parameter identification experiments, which further improved the accuracy of the robot dynamics model. However, this article did not study other nonlinear disturbance factors in the joint. Guo et al. [20] designed an identification method based on particle swarm optimization (PSO) for robot dynamics parameter identification. In order to obtain the dynamic parameters of the robot, the PSO algorithm was used to calibrate the dynamic model of the robot according to the motion state and torque of each joint. Experiments show that the parameters obtained by this method are correct and feasible. However, the algorithm is not conducive to global search and is prone to local optimum problems. Lin et al. [21] proposed a hybrid estimation strategy for the parameter identification of underwater vehicles; for the rough estimation of the dynamic parameters of underwater vehicles, the least squares (LS) algorithm is used, and the improved particle swarm optimization (IPSO) algorithm is used for the accurate estimation. The advantage of the least squares method is that it can improve the identification accuracy; however, its calculation is complex. When the amount of computation is large, the real-time performance will be greatly reduced [22] and there is a problem of limited search space. Cao et al. [23] designed a dual quantum behavior PSO algorithm for parameter identification of parallel robots. For the covariance matrix of measurement noise and process noise, the QPSO-1 algorithm is suitable. For the optimization of motion parameter error estimated by the EKF algorithm, the QPSO-2 algorithm is adopted. Experimental results show that this method significantly improves localization accuracy. Liu et al. [24] proposed a connection combination method based on improved artificial fish swarm algorithm for dynamic parameter identification, which can identify the independent value of the required parameters and avoid the impact of load changes. However, the convergence speed of this algorithm is slow and it is difficult to ensure real-time performance.
Inspired by the above point of view, to ensure the cooperation between humans and collaborative robots and realize the precise and stable control of the collaborative robots system, this paper designs an improved algorithm based on weighted least squares and random weight particle swarm optimization to identify the parameters of robot dynamics. Firstly, the Lagrange method is used to establish the dynamic model of the collaborative robot and determine the joint dynamic parameters to be identified. Because measurement noise will be generated when collecting raw data, the weighted least squares method is adopted. The identification algorithm is designed by adding the measurement torque noise to form the weight coefficient matrix. The weighted least squares method is used to generate the initial solution, and the search range is set to about 10% according to the absolute value of the initial solution. Secondly, based on traditional particle swarm optimization (TPSO), a random weight particle swarm algorithm is proposed, and the random weight particle swarm algorithm is used to make the dynamic parameters to be identified quickly jump out of a small local search range under the influence of random weights, speed up the identification in a large search range, and obtain accurate optimal parameters. Finally, due to the noise and burr in the original data collected, the Kalman filtering algorithm is used to filter the data, and good denoising and smoothing effects are achieved. The validity of the WLS-RWPSO algorithm is verified on a 6-DOF collaborative robot. The results show that the identification algorithm used in this paper can accurately identify the dynamic parameters and effectively improve the identification accuracy of the dynamic parameters compared with the identification results of LS-PSO and WLS-PSO identification algorithms.
The rest of the paper is organized as follows: Section 2 establishes the dynamic equations of the collaborative robot system subject to frictional disturbances. Section 3 introduces the weighted least squares algorithm and the random weight particle swarm algorithm, and analyzes the stability and convergence of the random weight particle swarm algorithm. Section 4 introduces the design of the excitation trajectory for parameter identification and the preprocessing of the experimental raw data. Section 5 introduces the experimental collaborative robot system and its dynamics parameter identification process using the WLS-RWPSO algorithm, and verifies the performance and efficiency of the WLS-RWPSO method by comparing it with the WLS-PSO algorithm. Section 6 presents the conclusions.
2. Robot Dynamics Modeling
The robotic arm is assumed to be a tandem robotic arm in the study. Without loss of generality, the dynamic equation of the n-DOF tandem robot is obtained by using the Lagrangian method [25]:
In order to improve the real-time performance, reduce the identification cost, and improve the identification accuracy, the dynamic equation of the collaborative robot is linearized. Without changing the robot model, according to the method proposed by Swevers et al. [26], this paper includes the influence of other factors on the inertial parameters of the robotic arm through the identification process to obtain a set of comprehensive parameters that meet the accuracy of calculation. The dynamic equation is expressed in the linear form of dynamic parameters through parameter transformation:
where is the observation matrix and is the inertial parameter matrix to be identified. For a given robot whose inertial parameters are constant, the linearization of robot joint moments greatly simplifies the entire parameter identification process.
In addition to the joint torque required to drive the link movement, the dynamic equation of the robot actually includes additional torque caused by factors such as friction and the moment of inertia of the motor rotor [27]. The joint friction includes Coulomb friction, viscous friction and static friction. This paper does not model static friction. The joint friction moment consists of Coulomb viscous friction:
where is the friction torque, is the coefficient of viscous friction, and c is the Coulomb coefficient of friction.
By approximating this function to a tangent hyperbolic function, the non-smooth function in the robot model can be avoided, which is expressed as follows:
where is a constant that makes the slope of the tangent hyperbolic function very steep near zero. Simultaneous Equations (2) and (3) can obtain the complete robot dynamics linearization equation:
where is the motor torque vector, is the observation matrix, and is the robot dynamics parameter vector.
The parameters of the dynamic equation are determined by the unknown parameter , which is expressed as
where is the actual parameter of connecting rod i; j is the number of robot joints; and , , , and , respectively, represent the actual mass, moment of inertia, viscous friction coefficient, and Coulomb friction coefficient of the connecting rod.
In addition, because not every dynamic parameter has an impact on torque, is not a full rank matrix. For removing redundant parameters, the linear recombination method is used to obtain a minimum set of parameters [8]:
where is the observation matrix, is the total dynamic parameter vector containing the minimum dynamic parameters and friction parameters of the connecting rod, p is the minimum number of kinetic parameters, and is the number of friction parameters.
3. WLS-RWPSO Identification Algorithm
3.1. Weighted Least Squares Algorithm
During the identification process, the robot is moved along a certain trajectory, the joint torque and joint angle of the robot at N different times are sampled, and the joint angular velocity and angular acceleration of the collaborative robots are calculated and filtered by difference. The processed data are substituted into Equation (7) as follows:
where represents moment observations and represents the observation matrix.
In fact, due to measurement errors and other reasons, non-homogeneous linear Equation (8) will generally result in incompatible equations. Although the incompatible equations cannot find the solution that fully satisfies the conditions, it can find the least squares solution
The least squares solution of Equation (8) is
Since the motor torque data of each joint of the robot have different levels of noise, for the parameter estimation problem of heteroscedasticity, the weighted least squares estimation has a better effect and the weighted least squares method is used:
where is the number of dynamic parameter combinations of joint j, and the weighting matrix is
The robot dynamic parameter identification adopts the least squares method to solve, and the dynamic parameter of the robot can be obtained:
where is the diagonal matrix [28] formed by measuring the variance of moment , which is called weight matrix.
3.2. Basic Particle Swarm Algorithm
The particle swarm algorithm is an optimization method for parameter calculation, in which the solution of each optimization problem is a bird in the search space, called a particle, and the fitness value of each particle is determined by the optimization function. There is always a speed to determine the orientation and removal of each particle, and to follow the current optimal particle to search in the solution space. The benefits of the PSO algorithm are as follows: Compared with other intelligent algorithms, PSO relies on particle speed to complete the search. There is no crossover and mutation operation, and the search speed is fast. Only the best particles will transfer information to other particles in iterative evolution. Since the particle swarm algorithm has the characteristic of memory, the best historical position of the particle swarm can be remembered and transferred to other particles. The particle swarm optimization algorithm adopts real number coding, which is directly determined by the solution of the problem, and the number of variables of the solution of the problem is directly used as the dimension of the particle. It has few adjustment parameters, simplicity in formation, and is easy to apply in engineering.
The particle velocity and update position equation are
where ; G is the search space dimension; is the population size; is the local learning factor; is the global learning factor; W is the inertia weight; and are the random numbers that obey the distribution; and and are the local optimum and the global optimum, respectively.
3.3. Particle Swarm Algorithm Based on Random Weight
In the particle swarm optimization algorithm, parameter particles will gather to their own best historical position and the best historical position of the population; so, it is easy to form a rapid convergence effect of the particle population, and it is prone to local extreme, premature astringency, or stagnation phenomena, resulting in imprecise parameter identification [29]. In particular, the local and global optimal search ability of parameter particles will be affected by inertia weight. Larger weights are conducive to jumping out of local optima, while smaller weights will enhance local search capabilities and facilitate algorithm convergence [30]. Aiming at the problems, POS tends to be limited in the search space, easily falls into local optima, and has unsatisfactory convergence rates. In this paper, we have designed a method of randomly selecting weight values so that the influence of the historical speed of parameter particles on the current speed is random, which can effectively increase the large search range and prevent parameters from falling into local optimal solutions, speed up parameter identification, and improve parameter identification accuracy. In the random weight method, the dynamic parameters to be identified can quickly jump out of the local small search range under the influence of the random weight, accelerate the identification speed in the large search range, and obtain accurate optimal parameters. The random weight W can be calculated by the following formula:
where is the parameter adjustment factor, represents random numbers from a standard normal distribution, and represents a random number between 0 and 1. The random weight particle swarm algorithm can avoid falling into the local optimum to a certain extent, increase the range of parameter particle search, and help improve the accuracy of the parameter identification of the robot. The dynamic parameter identification process of the collaborative robot is shown in Figure 1.

Figure 1.
RWPSO identification flow chart.
3.4. Stability and Convergence Analysis of Random Weight Particle Swarm Algorithm
Assuming that the number of population particles is , the global optimal position of population particles can be obtained:
Let , by sorting out Equations (13) and (14):
where , ; w, , and change adaptively during the iterative process; and varies randomly in the interval with iteration. At this time, belongs to the time-varying matrix. According to the system theory, it can be known that
where is the system state transition matrix, expressed as
where .
Assume ; define scalar function as vector norm ; then, the following hold:
(1) .
(2) . However, the values of w, , and make , so is negatively determined.
(3) When , .
According to the Lyapunov stability theorem, the system is asymptotically stable—that is, the algorithm is stable.
According to Equation (18), when the modulus of eigenvalues of is less than 1, it can be obtained that
When and are fixed, and . is a point on the line connecting and . According to Equation (13) and the root mean square error, it can be seen that eventually tends to , which shows that the algorithm converges.
4. Identify Experimental Design
4.1. Design of Excitation Trajectory
A reasonable design of excitation trajectory for parameter identification can hasten the convergence speed of parameter estimation and improve the precision of parameter estimation. The robot excitation trajectory design can be performed in two steps: The first step is to parameterize the joint trajectory. The second step uses the optimization algorithm to determine the undetermined coefficients in the joint trajectory function according to the designed objective function and motion constraint conditions.
In view of the fact that the finite Fourier series has the advantages of convenient data processing, insensitivity to measurement noise, and easy implementation in the parametric representation of the robot joint trajectory [31,32], this paper uses the finite Fourier series to realize the joint trajectory of the collaborative robot parameterization [33]. The joint angle of the i-th joint of the collaborative robot is denoted as
where is the fundamental frequency of the Fourier series and is the joint angle offset.
Each joint of the robot uses the same fundamental frequency to ensure the periodicity of the excitation trajectory. The parameterized motion trajectory of each joint of the space robot contains undetermined coefficients. By reasonably selecting , , and , the motion of the manipulator can meet the PE conditions of parameter identification.
In order to obtain the angular velocity and angular acceleration of joint i, the first and second derivatives of Equation (21) with respect to time can be calculated:
Since the excitation trajectory is constrained by conditions such as motor torque, joint position, joint velocity, joint acceleration, and workspace, the designed trajectory needs to meet the following conditions:
where is the condition number of the observation matrix. To reduce the theoretical error of identification, it is necessary to optimize the parameters in the above trajectory, and reduce the influence of noise on the identification accuracy by reducing the condition number of the observation matrix [34]. and are the minimum and maximum joint positions, respectively; is the maximum joint velocity; is the maximum joint acceleration; is the trajectory parameter; and is the maximum joint torque. The essence of the parameter optimization of the excitation trajectory is a multi-variable constrained nonlinear function optimization problem [35,36]. The parameters are optimized using the fmincon function in the Matlab optimization toolbox.
4.2. Data Preprocessing
When the collaborative robot tracks the excitation trajectory, the joint position and motor current are collected, and the motor current is converted into the motor torque through the torque constant. Due to the measurement noise interference of the original data, it is necessary to denoise and smooth the collected data before the identification experiment.
Combining with the problems studied in this paper, the torque displayed by the theoretical model of the collaborative robot at a certain moment is used as the predicted torque in the Kalman filter algorithm, and the torque of the collaborative robot measured by the sensor is used as the measured torque in the Kalman filter algorithm; then, the established state equation and the measurement equation are expressed as
where is the system state variable at time k, and are the system parameters, is the control variable of the system, is the system input relationship matrix, H is the state output transition matrix, is the noise deviation of the robot control system, and is the sensor measurement noise deviation.
The essence of the Kalman filter algorithm is to use recursive thinking to reduce the impact of noise. Each operation cycle contains two stages: time update and measurement update. The former uses the system model and the estimates for the previous cycle to obtain the prior estimate; the latter uses the actual measured output together with the prior estimate to obtain a posterior estimate of the state.
Time update stage: transition from time to time k.
where is to use the optimal estimate at time to predict the estimated state variable, which is called the prior estimate value, at time k. Q is the noise covariance of the control system; is the estimated value of the covariance of the system at time k.
Measurement update phase: Use the output at time k to correct the prior estimate .
where is the Kalman gain at time k and R is the measurement noise covariance.
The Kalman filter only uses the first two-order information (mean and covariance) of the state in the update rule; so, the Kalman filter has the following advantages: (1) The acquisition of the mean and covariance of the unknown distribution only needs to save less. (2) The mean and covariance have linear transitivity. (3) The set of mean and covariance estimates can be used to characterize additional characteristics of the distribution.
Therefore, for the torque signal collected by the sensor, the Kalman filter algorithm [37] is used to preprocess the original data and compare them with the five-point thrice smoothing method [38]. The comparison between the torque signal before and after processing is shown in Figure 2.
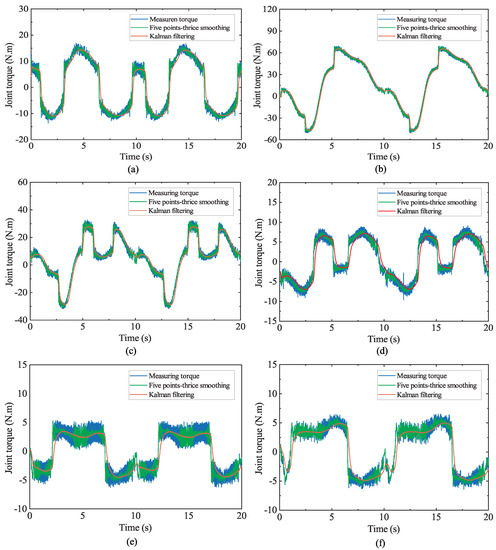
Figure 2.
Data preprocessing.
The experiment usually cannot directly measure the joint velocity and acceleration. If the joint position is differentiated, the measurement noise will be amplified. In order to reduce the impact of measurement noise when collecting the original torque signal, through the Butterworth filter function in Matlab, the joint angle q is first differentially calculated and then low-passed. The actual angular velocity and angular acceleration of the connecting rod are obtained by filtering and noise reduction to reduce the noise influence caused by differential processing.
In Figure 2a–f, the collected original torque data are represented by a blue line; the green line and the red line are the torque data processed by the five-point thrice smoothing method and the Kalman filtering method, respectively. It can be obtained from Figure 2 that before signal processing, the acceleration signal is noisy, has many burrs, and has certain data mutation points. If it is used for parameter identification calculation, it will lead to a large deviation. However, the torque signal after Kalman filter processing is smooth and has low data distortion; it also has a better processing effect than the five-point thrice smoothing method, which can be used for parameter identification calculation.
5. Experimental Results and Analysis
5.1. Simulation Verification of Structure Simplification Results
The experiment was carried out on the six-degree-of-freedom collaborative robot ROCR6, as shown in Figure 3, and the modified DH parameters are also shown in Table 1. The excitation trajectory of the joint is a 5-order Fourier series with a fundamental frequency of 0.05 Hz and a bandwidth of 0.25 Hz. The joint angle and joint torque in motion are sampled at a frequency of 1000 Hz, with a total 20,000 sets of original data. An excess of data will reduce the efficiency of identification and cause the fluctuation of bad data. To improve the efficiency, 2000 groups of joint positions and motor current signals required for identification are obtained in the 20 s motion process as the original data required for identification.
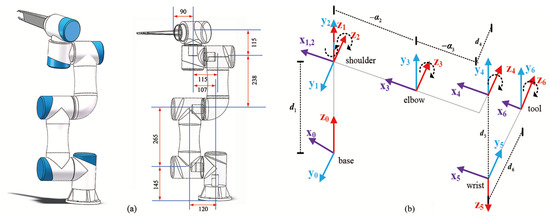
Figure 3.
The experimental platform ROCR6 and its improved DH model. (a) Experimental platform ROCR6. (b) Modified DH model.

Table 1.
Improved DH parameters of ROCR6.
The experiments send the excitation trajectories to the control platform, which ensures that all joints reach the commanded positions and receive real-time measurements of the actual values (joint position q, joint torque ).
The system is identified by basic PSO and RWPSO, respectively. The number of population is selected as 200, the learning factor is 1.5, is 3, the inertia weight is 1.3, and the maximum number of iterations is 200.
The fitness change curve during the identification process is shown in Figure 4. It can be seen from the figure that the initial particle search range (0–370) obtained by applying the RWPSO is obviously larger than the search range (0–201) of the basic PSO. When updating the position and velocity information, the basic PSO takes about 83 generations to converge, while the RWPSO takes about 20 generations to reach convergence, which shows that the improved algorithm has significantly improved the convergence speed and parameter particle search range.
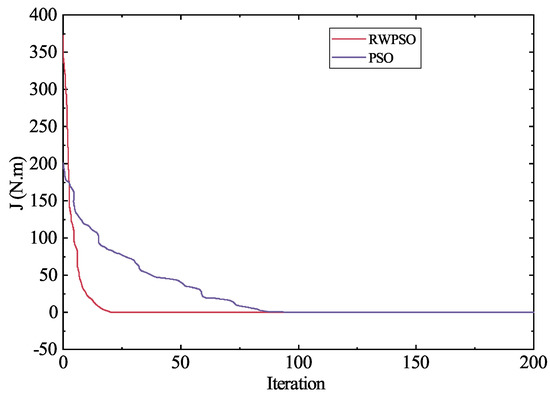
Figure 4.
Iteration curves of two algorithms.
To identify the inertial parameters of the collaborative robot, given the excitation track of the joint, as shown in Figure 5, drive the joint axis to track the excitation track and identify the inertial parameters of the link.
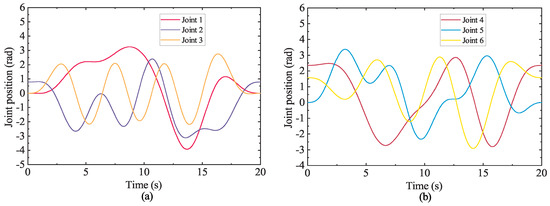
Figure 5.
Robot excitation trajectory. (a) Excitation trajectories of joints 1, 2, and 3. (b) Excitation trajectories of joints 4, 5, and 6.
Taking the first three joints of the collaborative robot as an example, the identification values of the robot dynamics parameters are obtained through the WLS-RWPSO algorithm identification, and the results are shown in Table 2. Among the 21 identification parameters in Table 2, the first 15 are inertia parameters and the last 6 are friction parameters.

Table 2.
Results of the identification of robot dynamics parameters.
According to the dynamic parameters identified by the WLS-PSO, LS-PSO, and WLS-RWPSO algorithms, the predicted torque under the excitation track is calculated and compared with the actual torque. The results are shown in Figure 6. Figure 6a–f show the predicted torque of each joint under three different algorithms. It can be seen from Figure 6 that under the identification trajectory, the predicted torque of the three algorithms is close to the actual torque; however, on the whole, the predicted torque of the WLS-PSO algorithm is better than that of the other two algorithms, which shows that the WLS-RWPSO algorithm has a better effect on the prediction of torque. The identification effect of the algorithm will be further analyzed in combination with the verification trajectory.
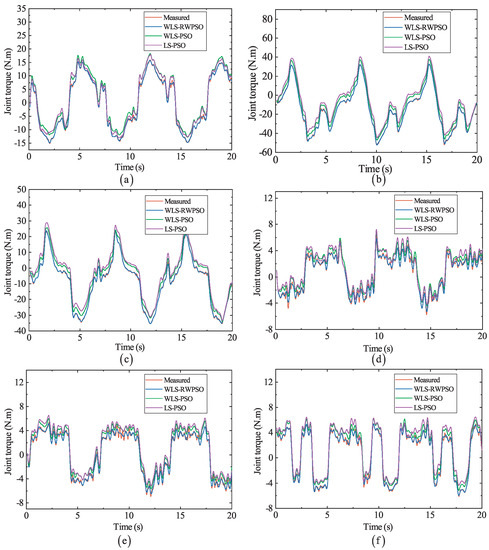
Figure 6.
Joint moments of collaborative robots predicted by different algorithms. (a) Predicted torque of joint 1 by identification. (b) Predicted torque of joint 2 by identification. (c) Predicted torque of joint 3 by identification. (d) Predicted torque of joint 4 by identification. (e) Predicted torque of joint 5 by identification. (f) Predicted torque of joint 6 by identification.
To further compare the identification accuracy of the two algorithms, this paper introduces the root mean square error (RMS) to verify the validity of the identified model:
where is the average torque value after identification. If the value of is closer to 0, the identification accuracy is higher. In addition, in order to show the advantages of our method compared with traditional recognition methods, we list the root mean square (RMS) of the validation residuals of different recognition methods in Table 3, where LS-PSO is the standard least-squares particle swarm optimization algorithm, and WLS-PSO is the weighted least-squares particle swarm optimization algorithm.

Table 3.
The root mean square error of different algorithm identifications.
The above results show that our proposed WLS-RWPSO algorithm is compared with these two methods. Taking joint 2 and joint 3 as examples, the predicted torque obtained by the three recognition methods is compared with the measured joint torque. The recognition accuracy of this algorithm for joint 2 is 16.1% and 10.5% higher than that of the LS-PSO algorithm and WLS-PSO algorithm, respectively, and the recognition accuracy of joint 3 is 12.2% and 11.5% higher than that of the LS-PSO algorithm and WLS-PSO algorithm, respectively. The corresponding predicted torque is closer to the measured joint torque. It can be seen that WLS-RWPSO algorithm has stronger optimization ability and higher recognition accuracy.
5.2. Model Validation
After the completion of parameter identification, it is necessary to evaluate and verify the accuracy of parameters. It is worth noting that the significance of parameter identification itself is that under any given trajectory, the predictive value of motor output torque can be obtained based on the identified parameters; then, the control current of the joint motor can be obtained. In order to verify the validity of the dynamic parameters identified by WLS-RWPSO, the verification trajectory is selected as a Fourier series different from the previous excitation trajectory, and the robot joint is driven by the controller to track according to the verification trajectory. The identified dynamic parameters are used to predict the torque of the verification track. The experimental verification process is shown in Figure 7. After sorting out the torque vector obtained, the joint torque of each joint under the verification track can be obtained, as shown in Figure 8, Figure 8a–f show the comparison between the predicted torque and the actual torque of each joint of the robot. ( is the measured torque of the identification track, is the measured torque of the verification track, and is the predicted torque of the verification track).
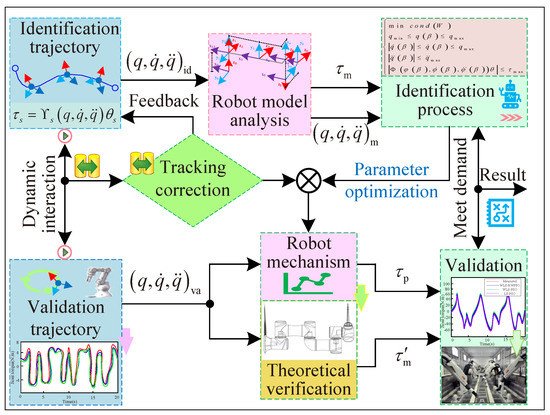
Figure 7.
Flow chart of experimental validation.
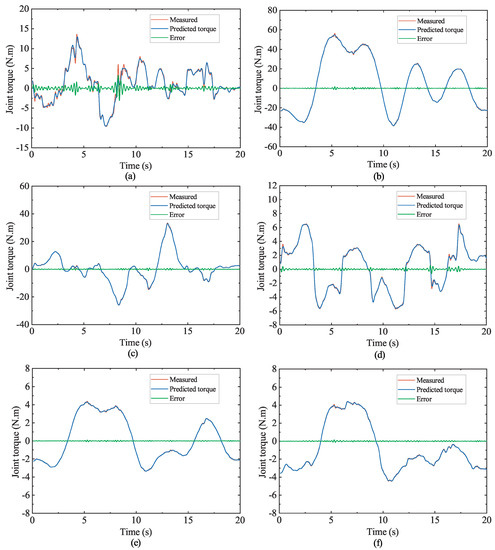
Figure 8.
Comparison of predicted torque and measured torque of collaborative robot. (a) Predicted torque of joint 1 by identification. (b) Predicted torque of joint 2 by identification. (c) Predicted torque of joint 3 by identification. (d) Predicted torque of joint 4 by identification. (e) Predicted torque of joint 5 by identification. (f) Predicted torque of joint 6 by identification.
It can be seen from Figure 8 that the deviation between the joint torque calculated by this identification method and the actual torque is small, and the torque curve is closer to the actual torque on the whole, which further proves that the WLS-RWPSO algorithm has higher accuracy in identifying the robot dynamic model and can accurately predict the dynamics characteristics of the robot system.
6. Conclusions
This paper summarizes the basic knowledge of dynamics model identification of collaborative robots and proposes identification strategies based on WLS-RWPSO. The optimal value of the fitness function obtained by the WLS-RWPSO algorithm is the smallest, which is not prone to local optima, is convenient for global search, and can better improve the accuracy of parameter identification. In the data preprocessing, the raw data collected by the sensor are preprocessed with the Kalman filter algorithm, which achieved good denoising and smoothing effects. In order to ensure the accuracy of parameter identification under disturbance, the excitation trajectory is designed based on finite Fourier series.
The identification algorithm proposed by the collaborative robot is tested to evaluate its performance and compared with WLS-PSO. The experimental results show that the WLS-RWPSO parameter identification algorithm proposed in this paper can accurately identify the dynamic parameters of the cooperative robot and has fast convergence speed, strong optimization ability, and certain engineering significance.
The identification algorithm proposed in this paper is helpful to improve the accuracy and stability of the trajectory control of the collaborative robot; however, there are still some shortcomings:
(1) This paper does not consider its inherent complex nonlinear behavior.
(2) When the collaborative robot moves along the specified excitation track, the sudden change of friction torque is not considered at the joint commutation, which makes us unable to obtain more accurate friction prediction.
Therefore, in future work, we will be committed to integrating these factors into the proposed parameter identification process. In addition, the control system of the collaborative robot can be designed by using the improved identification algorithm to further expand its application scope.
Author Contributions
Conceptualization, M.T.; data curation, Y.Y.; formal analysis, Y.Y., W.W. and Y.Z.; funding acquisition, M.T.; investigation, Y.Y., W.W., B.A. and Y.Z.; methodology, M.T., Y.Y. and B.A.; project administration, M.T.; resources, M.T. and W.W.; software, Y.Y.; supervision, M.T. and B.A.; validation, B.A., W.W. and Y.Z.; visualization, Y.Y. and B.A.; writing—original draft preparation, M.T. and Y.Y.; writing—review and editing, M.T. and B.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Foundation of China (grant numbers 61663021, 71763025, and 61861025) and the Project of Basic Research Innovation Group of Gansu Province, China (grant number 18JR3RA133).
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work was financially supported by the National Science Foundation of China (grant numbers 61663021, 71763025, and 61861025) and the Project of Basic Research Innovation Group of Gansu Province, China (grant number 18JR3RA133).
Conflicts of Interest
This manuscript has not been published or presented elsewhere in part or in its entirety and is not under consideration by any other journal. We have read and understood your journal’s policies, and we believe that neither the manuscript nor the study violate any of these. The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PSO | Particle Swarm Optimization |
| WLS | Weighted Least Squares |
| LS | Least Squares |
| RWPSO | Random Weighted Particle Swarm Optimization |
| TPSO | Traditional Particle Swarm Optimization |
| RMS | Root Mean Square |
References
- Ding, H. Basic theory and key technology of fusion robot. Robot Ind. 2016, 6, 12–17. [Google Scholar]
- Bisen, A.; Payal, H. Collaborative robots for industrial tasks: A review. Mater. Today Proc. 2022, 52, 500–504. [Google Scholar] [CrossRef]
- Xu, W.; Cui, J.; Liu, B. Human-robot collaborative disassembly line balancing considering the safe strategy in remanufacturing. J. Clean. Prod. 2021, 324, 129158. [Google Scholar] [CrossRef]
- Olivares-Alarcos, A.; Foix, S.; Borgo, S. OCRA–An ontology for collaborative robotics and adaptation. Comput. Ind. 2022, 138, 103627. [Google Scholar] [CrossRef]
- Leboutet, Q.; Roux, J.; Janot, A. Inertial parameter identification in robotics: A survey. Appl. Sci. 2021, 11, 4303. [Google Scholar] [CrossRef]
- Ren, T.; Dong, Y.; Wu, D. Collision detection and identification for robot manipulators based on extended state observer. Control Eng. Pract. 2018, 79, 144–153. [Google Scholar] [CrossRef]
- Nguyen, V.; Melkote, S. Hybrid statistical modelling of the frequency response function of industrial robots. Robot.-Comput.-Integr. Manuf. 2021, 70, 102134. [Google Scholar] [CrossRef]
- Qin, Z.; Baron, L.; Birglen, L. A new approach to the dynamic parameter identification of robotic manipulators. Robotica 2010, 28, 539–547. [Google Scholar] [CrossRef]
- Tao, J. Research on Human/Position Compliance Control of Industrial Machines Based on Dynamic Parameter Identification; Huazhong University of Science and Technology: Wuhan, China, 2019. [Google Scholar]
- Sun, Y. Research and Implementation of Dynamic Modeling and Feedforward Control Method for Heavy-Duty Robot; Southeast University: Nanjing, China, 2017. [Google Scholar]
- Urrea, C.; Pascal, J. Design, simulation, comparison and evaluation of parameter identification methods for an industrial robot. Comput. Electr. Eng. 2018, 67, 791–806. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, X. Identification method for load dynamics parameters of industrial robots. Robot 2020, 42, 325–335. [Google Scholar] [CrossRef]
- Kircanski, N.; Goldenberg, A. An experimental study of nonlinear stiffness, hysteresis, and friction effects in robot joints with harmonic drives and torque sensors. Int. J. Robot. Res. 1997, 16, 214–239. [Google Scholar] [CrossRef]
- Atkeson, C.; An, C.; Hollerbach, J. Estimation of inertial parameters of manipulator loads and links. Int. J. Robot. Res. 1986, 5, 101–119. [Google Scholar] [CrossRef]
- Liu, Y.; Li, G.; Xia, D. Identification of dynamic parameters of space robot based on improved genetic algorithm. J. Harbin Inst. Technol. 2010, 11, 1734–1739. [Google Scholar]
- Sun, Y.; Zhou, B. Dynamic parameter identification of industrial robot based on genetic algorithm. Ind. Control Comput. 2017, 30, 1–3. [Google Scholar]
- Chen, E.; Liu, Z. Artificial neural network method for identification of inertial parameters of robot end arm. China Mech. Eng. 2006, 17, 268–271. [Google Scholar]
- Wang, Y.; Wang, Y. Dynamic parameter identification of flexible joint robot based on adaptive particle swarm optimization genetic algorithm. J. Metrol. 2019, 41, 60–66. [Google Scholar]
- Zhang, T.; Hu, L.; Zou, Y. Identification of improved friction model for robot based on hybrid genetic algorithm. J. Zhejiang Univ. (Eng. Sci.) 2021, 55, 801–809. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, L.; Han, K. Dynamic parameter identification of robot manipulators based on the optimal excitation trajectory. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018; pp. 2145–2150. [Google Scholar] [CrossRef]
- Lin, M.; Yang, C.; Li, D. Hybrid strategy based model parameter estimation of irregular-shaped underwater vehicles for predicting velocity. Robot. Auton. Syst. 2020, 127, 103480. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, B. Parameter identification of supercapacitor equivalent circuit model using nonlinear least square method. J. Xi’an Jiaotong Univ. 2020, 54, 10–18. [Google Scholar]
- Cao, H.; Nguyen, H.; Nguyen, T. Robot Calibration Method Based on Extended Kalman Filter–Dual Quantum Behaved Particle Swarm Optimization and Adaptive Neuro-Fuzzy Inference System. IEEE Access 2021, 9, 132568. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, Z.; Wang, H. Parameter identification of collaborative robot based on improved artificial fish swarm algorithm. In Proceedings of the 2020 International Conference on High Performance Big Data and Intelligent Systems, Shenzhen, China, 23 May 2020; Volume 1, p. 7. [Google Scholar] [CrossRef]
- Spong, M.; Hutchinson, S.; Vidyasagar, M. Robot Modeling and Control; John Wiley and Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Swevers, J.; Verdonck, W.; De Schutter, J. Dynamic model identification for industrial robots. IEEE Control Syst. Mag. 2007, 27, 58–71. [Google Scholar] [CrossRef]
- Ding, L.; Wu, H.; Yao, Y. Dynamic model identification for 6-DOF industrial robots. J. Robot. 2015, 2015, 9. [Google Scholar] [CrossRef]
- Tu, X. Research on key Technology of Industrial Robot Motion Control Based on Dynamic Feedforward; Huazhong University of Science and Technology: Wuhan, China, 2018. [Google Scholar]
- Chen, Q.; Zheng, Y.; Jiang, H. Dynamic model identification for 6-DOF industrial robots. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2021, 49, 51. [Google Scholar] [CrossRef]
- Slotine, J.; Li, W. On the adaptive control of robot manipulators. Int. J. Robot. Res. 1987, 6, 49–59. [Google Scholar] [CrossRef]
- Wu, W.; Zhu, S.; Jin, X. Identification of robot dynamic parameters based on improved fourier series. J. Zhejiang Univ. 2013, 47, 231–323. [Google Scholar] [CrossRef]
- Neubauer, M.; Gattringer, H.; Bremer, H. A persistent method for parameter identification of a seven-axes manipulator. Robotica 2015, 33, 1099–1112. [Google Scholar] [CrossRef]
- Gautier, M.; Poignet, P. Extended Kalman filtering and weighted least squares dynamic identification of robot. Control Eng. Pract. 2001, 9, 1361–1372. [Google Scholar] [CrossRef]
- Wu, W. Joint Friction Analysis and Low Speed High Precision Motion Control of Multi Degree of Freedom Serial Robot; Zhejiang University: Hangzhou, China, 2013. [Google Scholar]
- Khalil, W.; Gautier, M.; Lemoine, P. Identification of the payload inertial parameters of industrial manipulators. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 4943–4948. [Google Scholar] [CrossRef]
- Kubus, D.; Kroger, T.; Wahl, F. On-line estimation of inertial parameters using a recursive total least-squares approach. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3845–3852. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, H. Improved kalman filtering for discrete linear systems with correlated noises. J. Northeast. Univ. 2010, 31. [Google Scholar]
- Ding, L.; Wu, H.; Yao, Y. Chaotic artificial bee colony algorithm for system identification of a small-scale unmanned helicopter. Int. J. Aerosp. Eng. 2015, 2015, 801874. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).