Abstract
This paper focuses on the steering motion control of an in-wheel motor-drive robot. The influence of the pulse-width modulation (PWM) duty cycle on steering motion and the steering control method have not yet been proved. Thus, this study aimed to design a steering controller for the off-center steer-by-wire system of a robot. The influence of the PWM duty cycle on the steering motion under different conditions is firstly tested on a test bench. Based on the optimal duty cycles of different cases found in the test, a two-stage fuzzy controller of the duty cycle is designed for the steering system. The first stage of the controller is used to dynamically adjust the PWM duty cycle of the electromagnetic friction lock (EFL). The second stage is designed to realize the self-tuning of the fuzzy controller’s quantization factor and the scale factor. Through two-stage control, the motion of the in-wheel motor and the EFL can be coordinated to realize stable and rapid steering. Considering the robots’ primary application in field roads at present, road tests were ultimately conducted to verify the proposed method. The test results show that the angle response rate of the steering arm is elevated with the increase in the steering angle signal. The proposed controller can sensitively track the target angles with smaller overshoot, yaw rate and lateral acceleration, and better steering accuracy than the PID (proportional–integral–differential) controller under different working conditions.
1. Introduction
The technological advancement of wheeled mobile robots opens the door to many new applications in digital farming [1]. Wheeled robots are widely used for repetitive, strenuous, or dull tasks [2,3,4]. Different wheeled robots have different steering systems, such as the in-wheel-motor steering system, Mecanum wheel steering system, and wheel–leg steering system [5,6]. In-wheel motor driving is of interest for its advantages of energy saving and flexibility [7]. Motion control of the steering system is a core issue for in-wheel motor-driven mobile robots. However, working conditions change continuously, presenting difficulties and challenges to steering controllers. Therefore, a steering motion controller that can quickly adapt to various steering demands is essential for an agricultural wheeled robot.
Increasing effort has been devoted to developing a steering controller for a wheeled robot. Some researchers designed a wheel force distribution controller to achieve the resultant active control moment by controlling the drive motor, steer motor, and suspension actuator [8]. In the literature, the authors of [9] proposed a steering-motor–turning-angle-based model to estimate the steering angles according to the motor turning angle and the wheel steering angles. A dual-steering mode based on direct yaw moment control was developed for multiwheel-hub-motor-driven vehicles [10]. An improved sliding mode controller was designed to adapt to the uncertainty of parameters with stable posture control performance [11]. A nonlinear decoupling control method was proposed to improve the stability and robustness of an in-wheel motor-drive electric vehicle [12]. Zhang et al. [13] proposed a disturbance observer by which the motor torque could be implemented according to wheel torque allocation. On the whole, the abovementioned research indicated that the motion control of the steering system is important for wheeled robot performance, and it is necessary to further study the steering motion controller of a wheeled robot in changing conditions.
However, the dynamics of these wheeled robots are highly coupled, nonlinear, and time-varying, presenting great challenges to motion control [14]. Additionally, the structure composed of numerous motors and electronic control units also makes the driving and steering control of mobile robots extremely complex [15]. Wheeled mobile robots face severe uncertainties in diversified working environments, making it challenging to build accurate system models for control. In these cases, traditional model-based control methods may cause divergence with their long running time or large oscillation [16]. For electrical mobile robots, intelligent steering control is very important in the control of navigation, wheel slip, stability, and braking [17,18,19,20,21,22]. An artificial neural network, genetic algorithm, and fuzzy logic can solve nonlinear problems when developing algorithms for robot controls. These methods can directly establish the controllers by avoiding the least important parameters, creating a fast response, and having easy troubleshooting and uncomplicated coding [23]. It is imperative to develop an intelligent controller to improve the steering performance of wheeled robots.
The objective of this study is to design a steering controller for the off-center steer-by-wire system of an in-wheel motor-drive robot. During the steering process, to ensure stable and effective operation, the motion of the off-center arm (OCA) needs to change dynamically according to the steering intention. Because the robot is a pure wire control structure, it is essential to study its control method to adapt to working conditions quickly. Therefore, it is necessary to study the parameter dynamic control method for the off-center steering system of the wheeled robot. We propose a two-stage fuzzy controller to match the motion of the steering mechanism to the steering intention. First, based on the character influence test of the pulse-width modulation (PWM) parameters of the electromagnetic friction lock (EFL), the influence law of the PWM parameters on an off-center steering system under different working conditions is proved. Secondly, the control method of an off-center steering system based on two-stage fuzzy logic is designed, enabling the wheeled robot to adapt to different steering intentions. Finally, the control method verification test is carried out on the road. This research can provide support for the steering motion control of this kind of wheeled robot.
The rest of the paper is organized as follows. Section 2 describes the materials and methods, including the system structure, test design, and a description of the control method. Section 3 is dedicated to the analysis of the results. Finally, the discussion and conclusion are provided in Section 4.
2. Materials and Methods
2.1. System Structure Design
The overall structure and work scenario of the robot chassis is shown in Figure 1. The chassis mainly includes four off-center steering mechanisms, an electronic control unit, and an actuator. The field information collected by the robot is transmitted to the terminal platform through the mobile network, and the background manager can remotely control the robot and terminal actuator. Each off-center steering mechanism consists of an EFL, an off-center axis, an OCA, and an in-wheel motor (Figure 2a). By employing an off-center steering mechanism, the driving and steering systems of the robot can be combined because both the driving force and steering force come from the in-wheel motor [24]. Compared with the conventional steering system, the structure is greatly simplified. It can achieve multiple motion modes for flexible working in a narrow or closed environment [25] (Figure 2a). A tracking system based on a Wheatstone bridge circuit is used to transfer the target steering signals to the steering system [26]. Then, PWM technology is employed to control the releasing and locking of the EFL [27]. If the PWM signal is at a low level, the EFL is released. Driven by the in-wheel motor, the OCA can rotate around the steering axis in this case. If the PWM signal is at a high level, the EFL is locked, and the OCA can transfer the driving force of the wheel to the chassis.
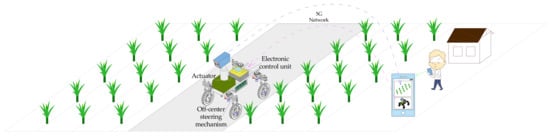
Figure 1.
Working diagram of the wheeled-robot chassis.
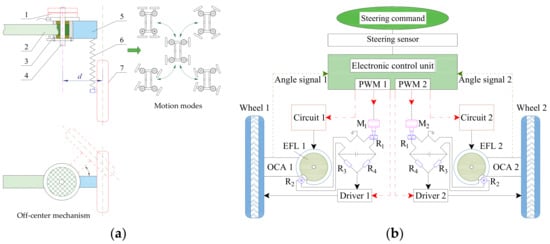
Figure 2.
Schematic of system structure: (a) off-center steering mechanism and motion modes of the robot; (b) steering composition of the steering system. Note: 1. EFL; 2. the chassis frame; 3. precision multiturn potentiometer (R2 in Figure 2b); 4. off-center axis; 5. OCA; 6. suspension; 7. in-wheel motor. d represents off-center distance. R1, R2, R3, and R4 represent the four arms of the Wheatstone bridge circuit. M1 and M2 represent the driving motors of the bridge circuit arm.
Figure 2b shows three control signals cooperating to complete the steering. The first is the steering signal, which controls the in-wheel motor, causing it to accelerate or decelerate through the bridge circuit and motor driver, allowing the electric wheel to turn around the off-center axis. The second is the PWM signal, which controls the opening and closing of the EFL and further adjusts the angular velocity of the OCA to match the motion of the electric wheel. The third is the feedback signal of the electric wheel state, which enables the steering angle of the OCA to be constantly fed back to the electronic control unit and the steering process to achieve a closed-loop control. To maintain smooth steering, the steering command issued must enable the steering arm to rotate rapidly around the steering axis. To achieve this function, the duty cycle of the PWM control signal of the EFL must be adjusted in real time to match this movement. The PWM parameters should be dynamically adjusted according to the steering command size and driving speed to adapt to the current steering target of the robot.
2.2. Test of Steering Control Parameters
2.2.1. Test Factors and Indexes
To obtain the PWM duty cycles suitable for steering under different working conditions, this study uses a self-made steering arm test bench for duty cycle selection tests. This section discusses the influence of the PWM duty cycle on the steering performance of the OCA under different driving speeds, steering angle signal sizes, and the change rate of the steering angle. According to previous research [28], the available range of the PWM duty cycle is 20~80% and the duty cycle is set at 13 levels: 20%, 25%, 30%, 35%, 40%, 45%, 50%, 55%, 60%, 65%, 70%, 75%, and 80%. Each treatment was repeated three times and averaged.
The performance of the steering system is determined by the speed of the steering response, the accuracy of the steering angle, and the suction force between the locking plates of the EFL. The suction force only depends on the electric current of the EFL. Therefore, this test uses three indicators to evaluate the steering performance: the angular velocity of the steering arm, the angle error, and the electric current of the EFL.
2.2.2. Steering Condition Setting
Four test conditions impact the steering process, including the change value of the angle signal, angle signal change rate, traveling speed of the wheeled robot, and steering form of the off-center steering mechanism. Selecting typical working conditions for the tests is necessary to explore the steering characteristics effectively. The details are as follows:
Angle signal δt (target angle): During the wheeled robot’s steering process, the steering arm’s rotation angle range is 0~40°. Thus, three typical target angles are set in this test, 10°, 20°, and 30°, represented by δt1, δt2, and δt3 for the sake of brevity, respectively.
Angular velocity signal ωt (target angular velocity): According to the steering requirements of the wheeled robot, three typical target angular velocities are set, 1.05 rad·s−1, 3.14 rad·s−1, and 5.23 rad·s−1, which are represented by ωt1, ωt2, and ωt3, respectively.
Rotation speed of in-wheel motor nt: The rotation speed of the in-wheel motor can be divided into three typical speeds: slow, medium, and fast, namely, 30, 60, and 90 r·min−1. These speeds are represented by nt1, nt2, and nt3, respectively.
Steering form of the off-center steering mechanism: When the robot turns its two front wheels, the motion of the in-wheel motor of the left front wheel is different from that of the right front wheel (Figure 3). When the robot turns to the left direction, wheel 1 on the inner side (the wheel near the turning center O) reaches the target angle through deceleration, and wheel 2 on the outer side (the wheel away from the turning center O) reaches the target angle through acceleration. When the robot turns to the right, the principle is just the opposite. The motion state of the outer steering arm is denoted as mt1, and the motion state of the inner steering arm is denoted as mt2. The parameter codes are presented in Table 1. In total, there are 54 combinations of the abovementioned working conditions.
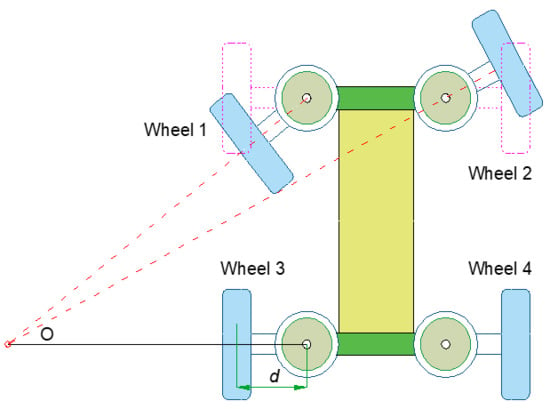
Figure 3.
Steering schematic of the wheeled-robot chassis. Wheels 1, 2, 3, and 4 express the left front, right front, left rear, and right rear wheels, respectively.

Table 1.
List of test cases.
2.2.3. Test Method
Figure 4 shows the structural diagram of the steering arm test bench [29]. The steering arm can rotate around the steering axis on the test bench. The wheel is placed vertically on the horizontal turntable. During the test, the horizontal turntable and the in-wheel motor run at the same initial rotation speed through the controller. The steering arm’s movement under different initial in-wheel motor rotation speeds can be simulated in the test bench. After the test, the data acquisition and data storage are stopped. The equipment returns to zero and waits for the next test. Section 2.2.2 describes the initial rotation speed, divided into 30, 60, and 90 r·min−1. Then, the tests are carried out according to different combinations of steering form, angle signal, and angular velocity signal.
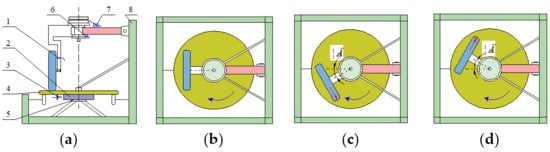
Figure 4.
Motion diagram of the off-center steering mechanism on the steering test bench: (a) composition of the test bench (front view); (b) initial position (vertical view); (c) steering of acceleration form; (d) steering of deceleration form. 1. Rotation speed sensor; 2. support tray; 3. rotation speed sensor; 4. horizontal turntable; 5. driving motor of horizontal turntable; 6. angular transducer; 7. current sensor of the EFL; 8. bench frame. Note: The red arrow is the initial forward direction of the wheel, and the blue arrow is the rotation direction of the horizontal turntable. δsf and δsr are the steering angle of the left front wheel and right front wheel, respectively.
Figure 4a shows the composition of the test bench. The angular transducer (22hp-10, 0–5 KΩ, Sakae Company, Japan) is used to detect the steering angle of the OCA, and the electric current sensor is used to obtain the electric current of the EFL. The accurate process time is obtained from the clock of the data acquisition system. Figure 4b shows the initial position before the test. Figure 4c simulates the rotation process of the left front wheel when the robot moves forward, and Figure 4d simulates the rotation process of the right front wheel. The object of the steering test bench is shown in Figure 5.

Figure 5.
Object of the test bench: (a) switch power supply; (b) control panel; (c) computer; (d) EFL; (e) electric current sensor; (f) data acquisition card; (g) angular transducer.
The steering duration t is obtained through the data acquisition system (Figure 5b,f), and the angular velocity of the steering arm is computed as follows:
where t is the steering duration (s) and δs is the actual angle of steering (°).
Since the angle signal collected by the angular transducer (Figure 5g) is a voltage signal, it is necessary to calibrate the numerical relationship between the angle δs and the voltage Uδ. After calibration, there is a linear relationship between them, shown as Equation (2).
where Uδ is the voltage difference caused by the change in the angular transducer (V).
The rotation angle error δer is the difference between the actual angle and the target angle, presented as Equation (3).
where δt is the target angle (°).
The electric current measured by the Hall current sensor (Figure 5e) is presented as voltage in the data acquisition system. Through calibration, the relationship between the electric current and voltage is shown, as follows:
where UI is the voltage difference caused by the electric current change in the EFL (V).
2.2.4. Analysis of Optimal Duty Cycle
As this test has three indexes, it is necessary to consider all indexes for a comprehensive evaluation. Methods for the weight allocation of each index in comprehensive evaluation can be classified into the objective method and the subjective method. Subjective weight is determined only by the experience of the decision-maker. Objective weight is decided by solving mathematical models without the decision-maker’s preferences, for example, the entropy method, principal element analysis, multiple objective programming, etc. Compared with subjective methods, the entropy method can avoid the error caused by the human factor [30]. The index weight is determined by the observation value of each index [31]. The entropy method has simple operation and is suitable for the comprehensive evaluation of this study. Thus, the angular velocity of the OCA ωs, rotation angle error δer and electric current of EFL Ic are unified as a comprehensive evaluation index through the entropy method. It is assumed that there are a (a = 13) test groups and b (b = 3) indexes, while λij is introduced to denote the j indexes of the i test group (i represents 1, 2, …, and a, j denotes 1, 2, …, and b). The process of the entropy method is summarized as follows.
(1) Standardization of the index.
Because larger values of ωs lead to a better index, a positive index equation is used:
Smaller values of δer and Ic lead to a better index, so a negative index equation is used:
(2) The weight of each index is computed as:
(3) The entropy value of the j index is given by:
(4) The information entropy redundancy of the j index is expressed as:
(5) The weight of the j index is computed as:
(6) The comprehensive evaluation index is expressed as:
Based on the above evaluation procedure, the comprehensive evaluation index value can be obtained (cf. Equation (11)). The closer the index comprehensive evaluation index is to 1, the better the performance of the steering.
Deduced by the entropy method, the average angular velocity of the steering arm, angle error, and electric current of the EFL are 0.3, 0.3, and 0.4, respectively. Finally, the comprehensive indexes under various working conditions are drawn into a scatter curve, as presented in Figure 6.
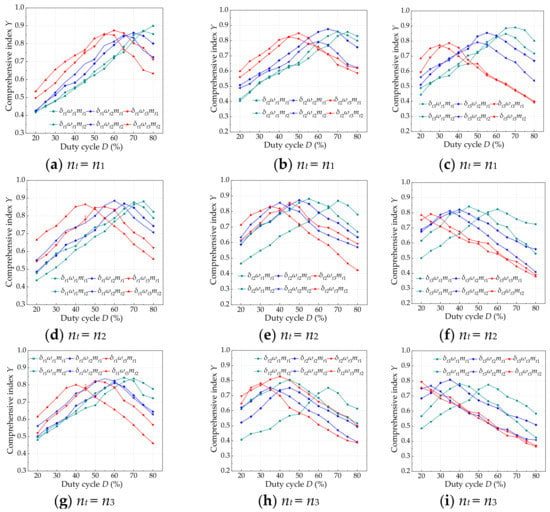
Figure 6.
Effect of duty cycle on comprehensive index under different conditions.
From Figure 6, under the test condition of nt1-δt1-ωt1, the comprehensive index shows an increasing linear trend with the growth of the duty cycle. Except for under the nt1-δt1-ωt1 condition, the comprehensive indexes increase until reaching the maximum point and decrease afterwards under all other test conditions. The comprehensive index has a maximum value for each working condition and the corresponding duty cycle of the maximum index value is the optimal duty cycle (denoted as Dopt) under each condition.
In order to obtain the optimal duty cycle under all test conditions, the 1stOpt software (15 Pro; 7D High Technology Inc., China) was used to conduct nonlinear regression on the relationship between the index value and the duty cycle. For example, in the nt2-δt2-ωt2-mt2 case, the fitting curve is shown in Figure 7 and the regression equation is presented as Equation (12). The duty cycle corresponding to the peak value of the fitting curve is the optimal duty cycle. With this method, the optimal duty cycle under all test conditions can be obtained, and the results are shown in Table 2. From Table 2, it can be seen that the optimal duty cycle varies under different test conditions. To maintain the good steering performance of the robot, the duty cycle of the PWM signal should be adjusted in real time to adapt to dynamic driving conditions according to the optimal duty cycles obtained.
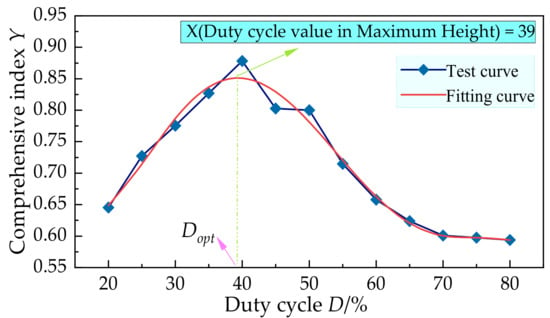
Figure 7.
Fitting curve of test results under the condition nt2-δt2-ωt2-mt2.

Table 2.
Optimal duty cycles under different test conditions.
Y(D) = 1.85 − 0.194D + 0.0108D2 − 2.54 × 10−4D3 + 2.67 × 10−6D4 − 1.04 × 10−8D5 (R2 = 0.9801)
2.3. Control Method Design for Steering
2.3.1. Structure of the Control System
As the working condition of the wheeled robot is nonlinear and random, it is difficult to conduct steering control only based on the mathematical model. To adjust the PWM signal according to the obtained optimal duty cycles, it is necessary to find a method to quickly identify the steering signal, including the change value of the angle signal and angular velocity signal. There are two methods for signal identification: fuzzy logic and artificial neural networks. Artificial neural networks need a considerable amount of basic data for network training. The fuzzy control method does not need a precise mathematical model of the system and too much data for rule-making. Thus, this paper introduces a fuzzy control method to identify the change value of the angle signal and angular velocity signal.
The structure of the PWM duty cycle fuzzy control method of the steering system is presented in Figure 8. The system’s input is the target angle signal (δt) and the output is the actual steering angle (δs). The input signal is then decomposed into the change value of the angle signal and angular velocity signal (denoted as ∆δt and ∆δ′t, respectively), and both are input into the fuzzy controller. The fuzzy control rules are designed to judge the input working conditions composed of these two signals. The quantization factor (kz) and scale factor (ku) are adjusted by a sub-fuzzy controller. The duty cycle is then adjusted according to the optimal PWM duty cycle obtained previously. In this way, the angular velocity of the OCA, steering angle error, and electric current of the EFL can be dynamically adjusted, and the steering effect can be improved. Therefore, the proper design of a fuzzy controller is the key to the dynamic control of the PWM signal.
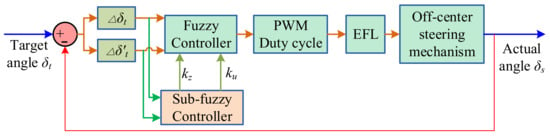
Figure 8.
Schematic diagram of the fuzzy control method.
2.3.2. Design of Fuzzy Controller
As the fuzzy controller has two input signals, a two-dimensional controller is adopted in this study. The inputs of the fuzzy control are the change value of the angle signal and angular velocity signal. The output is the duty cycle of the PWM signal (Dc). To increase the controller’s sensitivity, the input/output language variable values are divided into seven fuzzy subsets from small to large: NB, NM, NS, ZE, PS, PM, and PB. As shown in Figure 9, the maximum steering angle of the wheel is 40°. The angle is denoted as +40° when the OCA turns clockwise around the off-center axis, and −40° when it turns counterclockwise. Thus, the basic domain of the fuzzy controller is set as [−40°, +40°].
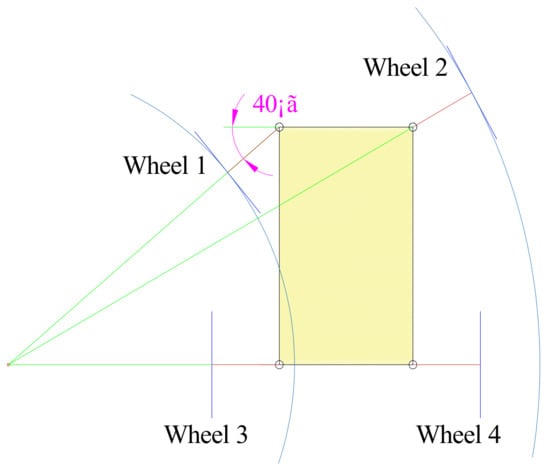
Figure 9.
Schematic diagram for the maximum value of the steering wheel angle.
It can be found from the pretest that the maximum angular velocity of the OCA is 0.52 rad·s−1. Therefore, considering the direction of rotation, the basic domain of the angle transformation rate is [−0.52 rad·s−1, +0.52 rad·s−1]. The range of the duty cycle is [20%, 80%]. To facilitate the implementation of fuzzy control, the basic domain is set as [0.2, 0.8].
In fuzzy control, it is necessary to convert the basic domain into a fuzzy domain for easy implementation, which is converted by Equation (13). Here, [α, β] is the basic domain of the variable. By this method, the fuzzy domain of ∆δt, ∆δ′t, and Dc is set as [−6, 6], [−6, 6], and [−6, 6], respectively.
where x denotes the actual value of the variable and y denotes the value of the variable in the fuzzy domain.
When ∆δt and ∆δ′t are zero, they are used as a ZE subset. The trigonometric function with high sensitivity is selected as the membership function for input and output. The membership function curve is shown in Figure 10. According to the steering control demands, the fuzzy rules are formulated, as shown in Table 3. The center of gravity method is used to solve the fuzzy rules, as shown in Equation (14).
where η denotes the output value of the fuzzy controller, μi denotes the membership, and f(μi) denotes the trigonometric membership function.

Figure 10.
Membership function curve of fuzzy controller: (a) change in angle signal ∆δt; (b) change in angular velocity ∆δ′t; (c) PWM duty cycle Dc.

Table 3.
Fuzzy control rules of PWM duty cycle.
2.3.3. Parameter Self-Tuning of Fuzzy Controller
- (1)
- Definition of quantization factor and scale factor
The quantization factor and scale factor are key parameters that affect the impact of fuzzy control. If the basic domain of the input of the fuzzy controller is [−x1, x2] and the corresponding fuzzy domain is [−r, -r + 1, …, 0, r − 1, r], the quantization factor of the fuzzy controller can be expressed as kz = r/x. The basic domain of the quantization factor is [−r/x1, r/x2]. If the basic domain of the output of the fuzzy controller is [−y1, y2] and the corresponding fuzzy domain is [−l, −l + 1, …, 0, l − 1, l], the scale factor of the fuzzy controller can be expressed as ku = y/l. The basic domain of the scale factor is [−y1/l, y2/l].
However, achieving a good control effect by only using fixed quantization and scale factors is difficult. Thus, this study uses the self-tuning method of the quantization factor and scale factor to continuously adjust the fuzzy controller parameters based on the changing conditions. The adaptive performance of the system can be enhanced in this way.
The quantization factor of the change value of the angle signal and angular velocity, and the scale factor of the PWM signal duty cycle, is denoted as kz1, kz2, and kuo, respectively. According to the steering demands of the robot, when both ∆δt and ∆δ′t have high values, it is necessary to properly reduce kz1 and kz2 to cut the resolution of the working conditions and increase kuo to improve the response rate. When both ∆δt and ∆δ′t have low values, it is necessary to increase kz1 and kz2 to improve the resolution of the working conditions and the response rate and reduce kuo to diminish overshoot.
- (2)
- Self-correction of quantization factor and scale factor
A secondary fuzzy controller is designed to realize the self-tuning of fuzzy controller’s quantization and scale factors. The initial quantization factors of ∆δt and ∆δ′t are 2 and 20, respectively, and the initial scale factor of Dc is 1. The basic domain of kz1, kz2, and kuo is [−2, 2], [−20, 20], and [0.2, 0.8], respectively. After transformation by Equation (13), the fuzzy domain of kz1, kz2, and kuo, is [−6, 6], [−6, 6], and [−6, 6], respectively. Since the high sensitivity in the self-tuning process is not conducive to steering control, the convex function membership curve is selected in the secondary controller, as shown in Figure 11. The input/output language variable values are divided into five fuzzy subsets from small to large: NB, NS, ZE, PS, and PB. Based on this, the fuzzy rules of kz1 and kz2 are shown in Table 4. The center of gravity method is also used to solve the fuzzy rules.

Figure 11.
Membership function curve of fuzzy self-tuning control: (a) quantization factor kz1; (b) quantization factor kz2; (c) scale factor kuo.

Table 4.
Fuzzy control rules of quantization factor/scale factor.
2.4. Verification Test for the Steering Control Method
2.4.1. Test Instrument
The controller’s hardware is developed for the robot prototype to verify the effectiveness of the proposed control method. The controller mainly consists of single-chip modules (STM32F103ZET6, STMicroelectronics Company, Switzerland), bridge circuit modules, accessory circuits, and stepper motors (YH42BYGH47-401A, MICROSTEP, Wenzhou, China) and their drivers. The C language control program edited by Keil uVision 5 software (v5.35; Keil Software Company, the United States) is loaded into the MicroAutoBox real-time system. The embedded electronic control units are implemented on STM32 units to perform tests on the road. The control panel is presented in Figure 12a.
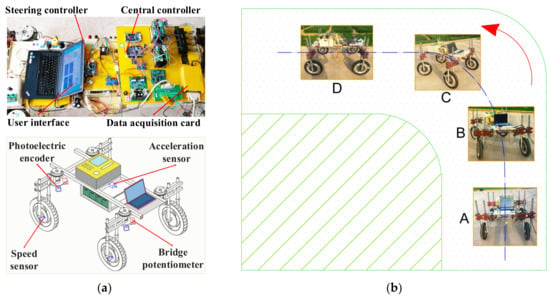
Figure 12.
Test scenes of the road tests: (a) composition of the prototype system; (b) motion scene of steering test.
The steering angles are detected using an angular transducer (22HP-10, SAKAE Company, Tokyo, Japan; 0–5 kΩ). The speed sensors (D046, Guangzhou Logo Electronics Company, Guangzhou, China; 0–1000 r/min) are used to measure the speeds of the in-wheel motors. The duration of steering is calculated by a clock integrated into the data-acquisition system. The acquisition system includes an industrial personal computer (610H, Advantech Technology Corporation, Beijing, China) and a data-acquisition card (USB7648B, Beijing Zhongtai Research Ltd., Beijing, China). An inertial sensor (WT61C232, Shenzhen Wiite Intelligent Technology Company, Shenzhen, China) is used to measure the acceleration.
2.4.2. Test Method and Process
Hardened roads are the main working scenario of the robot chassis, so we carried out the verification test under these conditions. According to the working conditions set in Section 2.2.2, this study adopts three typical combined working conditions for the verification test: nt1-δt1-ωt1, nt2-δt2-ωt2, and nt3-δt3-ωt3. From condition nt1-δt1-ωt1 to nt3-δt3-ωt3, the change value of the angle signal, steering angle change rate, and traveling speed show an increasing trend. The steering test scenario is presented in Figure 12b. The specific test process is as follows.
First, the stability of various mechanical connections of the wheeled-robot chassis and the correct connection of various control and power supply lines are checked before the tests. Second, the data acquisition system starts collecting data. The wheeled robot travels in a straight line at an in-wheel-motor-rotation speed of 30 r·min−1 (nt1), and then sends out an angle signal with a size of 10° (δt1) and angular velocity of 1.05 rad·s−1 (ωt1) to perform the steering operation. Then, a steering signal of the same size but opposite direction is used to realize the righting of robot steering. After the test is completed, the tests under working conditions nt2-δt2-ωt2 and nt3-δt3-ωt3 are carried out successively. Finally, the steering motion and the data acquisition are complete, and the data are stored in the controller.
In order to observe the superiority of the controller, the control performance of this method is compared with that of the PID control method. The system structure design of the PID control method is presented in Figure 13. The system’s input is the target angle signal and the output is the actual angle of the steering arm. The difference between the actual steering angle and the target steering angle is constantly input to the PID controller. After the calculation of proportion, integral, and derivative, an adjustment value is generated to change the electric current of EFL and further control the steering motion of the OCAs. In this way, the angular velocity of the OCAs and the angle error can be adjusted and the OCAs can quickly track the target steering angle.
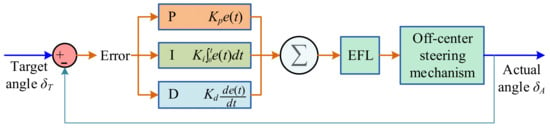
Figure 13.
Schematic diagram of the PID control method for the robot steering system.
3. Results
3.1. Analysis of Steering Angle Changes
Figure 14 shows the angle changes of the left and right front steering arms, and the motion trajectories under the three working conditions. From Figure 14a–c, it can be seen that the steering responses are rapid under PID control. However, there are large overshoots of steering angle which occur in all three tests. In these three cases, the maximum overshoots relative to the target angles are 2.03°, 2.31°, and 2.65°, respectively. The maximum time delays between the actual angle and angle signal in the working conditions nt1-δt1-ωt1, nt2-δt2-ωt2, and nt3-δt3-ωt3 are 0.9 s, 1.4 s, and 1.3 s, respectively.
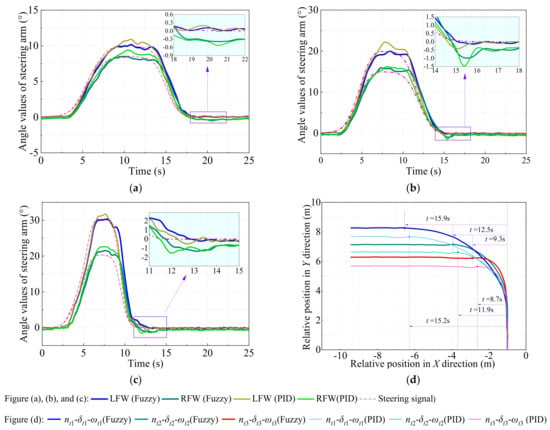
Figure 14.
Angle changes and trajectories under different conditions: (a) condition nt1-δt1-ωt1; (b) condition nt2-δt2-ωt2; (c) condition nt3-δt3-ωt3; (d) centroid trajectories of the robot. Note: LFW denotes the left front wheel; RFW denotes the right front wheel.
Under the proposed method, the actual angle curve is in good agreement with the input angle signal (Figure 14a–c). The maximum time delay between the actual angle and angle signal in the working conditions nt1-δt1-ωt1, nt2-δt2-ωt2 and nt3-δt3-ωt3 is 0.8 s, 1.3 s, and 1.2 s, respectively. Although there are certain delays in the angle response of the steering arm, these delays are all within the acceptable range (0 to 2 s) and the angle response is rapid in terms of the low-speed application of the wheeled-robot chassis. In these three cases, the maximum overshoots relative to the target angles of 10°, 20°, and 30° are 0.92°, 1.43°, and 1.91°, respectively, for the left wheel. From condition nt1-δt1-ωt1 (Figure 14a) to condition nt3-δt3-ωt3 (Figure 14b), the curve slope of the rising and falling sections of the steering arm increases, indicating that the angle response rate of the steering arm is elevated with the increase in the angular velocity. The proposed method can dynamically adjust the movement of the steering arm with the change in steering signal. Due to the influence of random factors on the road surface, there is a certain fluctuation in the angle change in the steering arm, especially during the process of switching the rotation direction of OCA. When the steering arm returns to the initial position again, there is a deviation between the target angle and the actual steering angle. However, these deviations are within the acceptable range in robot applications. Therefore, according to the above analysis, the proposed controller can sensitively track the target angles with only a slight overshoot under different working conditions. Compared with the traditional PID control, the proposed method improves the control effect.
Figure 14d shows the centroid trajectories of the robot under different conditions. The turning radius under PID control is less than that of fuzzy control in three cases. However, due to the large overshoot of the steering angle, the trajectories of turning have poor smoothness under PID control. The steering time for conditions nt1-δt1-ωt1, nt2-δt2-ωt2, and nt3-δt3-ωt3 is 14.8 s, 11.3 s, and 10.1 s, respectively. Under fuzzy control, in conditions nt3-δt3-ωt3, the rotation speed of the in-wheel motor, change in the angle signal, and angular velocity are larger than those of the other two conditions. The OCAs rotate fast in this case, and the time required for the robot to turn to the target direction is the shortest among these three conditions, at approximately 9.3 s. The turning radius is also the minimum among these three conditions. The steering time of condition nt1-δt1-ωt1 and condition nt2-δt2-ωt2 is 15.9 s and 12.5 s, respectively. There is an excellent correlation between the actual steering angle and the steering signal for the left front wheel in all conditions. It is thus clear that the angle of the OCAs can track the target angle, and the steering motion of the off-center steering mechanisms can adapt to the changes in the steering signal.
3.2. Analysis of Motion Posture Stability
The lateral acceleration and yaw rate are two key indexes used to evaluate the motion stability of the robot chassis. The changes in yaw rate during steering are shown in Figure 15a. Under fuzzy control, the yaw rate peaks for the conditions nt1-δt1-ωt1, nt2-δt2-ωt2, and nt3-δt3-ωt3 are 8.12, 12.35, and 23.91 deg·s−1, respectively. In condition nt3-δt3-ωt3, the yaw rate quickly rises to a peak and then falls in 2 s, with minor fluctuations. Thus, the initial speed has a significant influence on the yaw rate. Specifically, the amplitude of the yaw rate rises with the increase in driving speed. Under PID control, the yaw rate is higher than that of fuzzy control, and the difference becomes obvious at high speeds. The maximum difference in yaw rate between the PID control and fuzzy control is 5 deg·s−1, which occurs in condition nt3-δt3-ωt3.
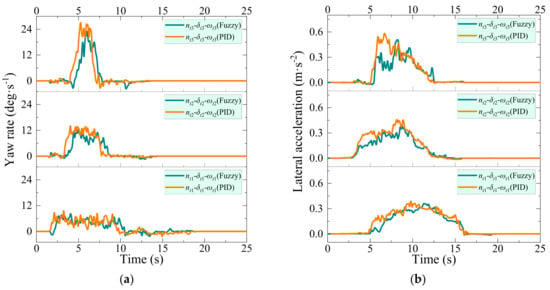
Figure 15.
Kinematic parameter variation curve: (a) changes in yaw rate; (b) changes in lateral acceleration.
The changes in lateral acceleration during steering are shown in Figure 15b. The lateral acceleration peaks are 0.37, 0.39, and 0.53 m·s−2 in conditions nt1-δt1-ωt1, nt2-δt2-ωt2, and nt3-δt3-ωt3, respectively. The higher the driving speed, the greater the peak value of lateral acceleration. With the increase in driving speed, the fluctuation in lateral acceleration increases. Under condition nt3-δt3-ωt3, the rising and falling sections of the lateral acceleration are steep, but relatively gentle under conditions nt1-δt1-ωt1 and nt2-δt2-ωt2. To achieve the steering target, the steering arm must rotate quickly under the high travelling speed of condition nt3-δt3-ωt3. Thus, the turning process of the robot is extremely short, resulting in sizeable lateral acceleration. The lateral acceleration under PID control is higher than that of fuzzy control, and the difference also becomes obvious in the case of high speed. The maximum difference in lateral acceleration between the PID control and fuzzy control is 0.15 m·s−2, which occurs in condition nt3-δt3-ωt3. Generally, the yaw rate and lateral acceleration under fuzzy control are within the normal range. Fuzzy control is superior to PID control for the off-center steer-by-wire system. The previous road test shows that the robot chassis will roll over or drift when the yaw rate is greater than 34 deg·s−1 and the lateral acceleration is greater than 0.95 m·s−2. In this test, the yaw rate and lateral acceleration in the extreme case nt3-δt3-ωt3 did not reach the extreme value [26,29]. The steering system has acceptable stability and good agility, indicating that the controller is feasible.
4. Discussion and Conclusions
This paper proposes a steering motion controller for the off-center steering mechanism for an agricultural wheeled robot. The main advantage of our method is that no complicated mathematical models are needed. The control algorithm is easy to implement in hardware, making it more practical.
There are several existing structures similar to the proposed robot; for example, a tomato-harvesting robot designed for greenhouses [32], a platform for autonomous navigation in kiwifruit orchards [33], and a robot for the in-row weed control of vegetables [34]. However, most of these studies use additional auxiliary mechanisms for steering. For this reason, the control principles of the steering system are essentially different from this study. The coordination between steering motors during travelling needs to be controlled separately. In this paper, the off-center steering mechanism with the combined driving and steering system is expected to simplify the steering system of the wheeled robot and reduce control difficulty.
The motion control of the steering mechanism is crucial to the regular and stable travelling of a wheeled robot. Various studies have adopted a cooperative control method for wheeled robots. For example, the coordinated motion control system proposed by Liu et al. [35] achieved a significant performance in the coordinated motion control of four-wheel-leg robotic systems. The double closed-loop joint control strategy designed by Li et al. [36] optimized a four-in-wheel motor-driven electric vehicle torque distribution of hub motors. Ding et al. [37] presented an optimum velocity model using a predictive control method for a redundantly actuated mobile robot under steering strategy constraints. Sorour et al. [38] proposed a complementary route with an instantaneous center of rotation controller for steerable wheeled mobile robots using a novel evaluation metric of the command fulfillment index. It should be noted that there are pronounced differences from our study. Most of these studies use conventional mathematical control models and focus on theoretical and simulation analyses. Few studies have been conducted on a special test bench to acquire the control parameters. To allow the dynamic adaptation of the motion of the off-center steering mechanism with real-time demand, this study first finds the optimal control parameters through experimentation. Then, a two-stage fuzzy control method is implemented on the prototype of the robot chassis. The control feature extraction based on the test data brings more practicability to the control strategy, making it especially suitable for controlling the discrete PWM signal duty cycle.
The results show that the overall effect of fuzzy control is better than that of PID control. In PID control, the tracking of the angle to the target angle is achieved according to the feedback of steering angle error. However, the off-center steering mechanism of the robot is a steer-by-wire structure, and the steering angle is controlled by electromagnetic attraction. In the process of robot steering, it is necessary to identify the steering intention in advance, which cannot be achieved by PID control. The adopted fuzzy controller can prejudge the steering trend according to the change in angle signal and angular velocity signal. Thus, timely handling can be achieved. Additionally, the secondary fuzzy controller also improves the adjustment accuracy. Therefore, under fuzzy control, the overshoot of the angle and the peak values of yaw rate and lateral acceleration are smaller than those of PID control. In this paper, due to the nonlinear effect of EFL of the steer-by-wire system and the demand for steering signal identification, the fuzzy control method is adopted. In a similar steer-by-wire system of wheeled robots or an electric vehicle chassis with independent driving and steering structures, such as greenhouse transportation wheeled robots, logistics wheeled robots, and explosion-proof wheeled robots, this method can be used to overcome the difficulties of steering control based on accurate models. This method can also be used to identify the steering command and improve the target angle following the performance of the steering system.
Occasionally, individual tests demonstrated extreme results. The steering angle of the left front wheel presented a large overshoot when returning to the initial position. This is mainly caused by small changes in the electric current of the EFL. Additionally, large fluctuations occasionally occurred with lateral acceleration in condition nt3-δt3-ωt3 of the road test. In this case, the chassis’ speed is relatively fast and the influence of random factors on the pavement is enhanced. However, these changes have little impact on the overall test effect and are within an acceptable range.
There are several limitations of this study. The fuzzy method has an empirical dependence and the coordination of the steering motion may deteriorate under some conditions. Given this, the fuzzy rules may need to be adjusted according to the actual operating conditions of the robot chassis. An experimental test on hardened pavement verified the control method. There are differences from a real environment, and further farmland tests are needed in future research.
In conclusion, the present study proposed a fuzzy controller to solve the dynamic control for the off-center steer-by-wire system of an agricultural monitoring robot. Through analyses of the influence of the PWM duty cycle on the steering performance, a fuzzy dynamic control method for the PWM signal duty cycle is designed. Specifically, a two-stage fuzzy control regulation is presented to realize the self-calibration of controller parameters, which can be used to obtain excellent steering angle tracking performances. A hardened pavement test ultimately verifies the feasibility and effectiveness of the steering control method. The proposed control strategy has the advantages of high responsiveness and accuracy with no complicated mathematical model and can be easily implemented in hardware. Compared with the traditional PID control method, the proposed control methodology can effectively enable the motion of the OCAs to adapt to changes in the steering signal and reduce the angle error, yaw rate, and lateral acceleration. Improving the interwheel coupling control algorithm through machine learning could be an area of interest for future work.
Author Contributions
Conceptualization, J.Q.; methodology, J.Q. and Z.Z.; software, Z.Z. and H.L.; validation, Z.Z. and H.L.; formal analysis, J.Q.; investigation, Z.Z. and M.L.; resources, Z.Z. and H.L.; data curation, Z.Z. and H.L.; writing—original draft preparation, J.Q.; writing—review and editing, X.X.; visualization, Z.Z. and M.L.; supervision, X.X.; project administration, J.Q. and X.X.; funding acquisition, J.Q. and R.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Jiangsu Provincial Natural Science Foundation (grant number BK20210823); the Jiangsu Agricultural Science and Technology Innovation Fund (grant number CX (21) 3153); the Yangzhou University Interdisciplinary Research Foundation for Crop Science Discipline of Targeted Support (yzuxk202007); the Jiangsu Modern Agricultural Machinery Equipment and Technology Demonstration and Promotion Project (NJ2021-28); the High-end Talent Support Program of Yangzhou University.
Institutional Review Board Statement
Informed consent was obtained from all subjects involved in the study.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge the anonymous reviewers for their valuable input.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mondal, S.; Ray, R.; Reddy-N, S.; Nandy, S. Intelligent controller for nonholonomic wheeled mobile robot: A fuzzy path following combination. Math. Comput. Simulat. 2022, 193, 533–555. [Google Scholar] [CrossRef]
- Cheng, C.; Fu, J.; Su, H.; Ren, L. Recent advancements in agriculture robots: Benefits and challenges. Machines 2023, 11, 48. [Google Scholar] [CrossRef]
- Spykman, O.; Gabriel, A.; Ptacek, M.; Gandorfer, M. Farmers’ perspectives on field crop robots—Evidence from Bavaria, Germany. Comput. Electron. Agric. 2021, 186, 106176. [Google Scholar] [CrossRef]
- Ouyang, C.; Hatsugai, E.; Shimizu, I. Tomato disease monitoring system using modular extendable mobile robot for greenhouses: Automatically reporting locations of diseased tomatoes. Agronomy 2022, 12, 3160. [Google Scholar] [CrossRef]
- Xiao, H.; Yu, D.; Philip-Chen, C.L. Self-triggered-organized Mecanum-wheeled robots consensus system using model predictive based protocol. Inf. Sci. 2022, 590, 45–59. [Google Scholar] [CrossRef]
- Wang, L.; Lei, T.; Si, J.; Xu, K.; Wang, X.; Wang, J.; Wang, S. Speed consensus control for a parallel six-wheel-legged robot on uneven terrain. ISA Trans. 2022, 129, 628–641. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.; Zheng, J.; Chai, R.; Nguyen-Hung, T. Robust tracking control of a differential drive wheeled mobile robot using fast nonsingular terminal sliding mode. Comput. Electron. Agric. 2021, 96, 107488. [Google Scholar] [CrossRef]
- Zhang, Y.; Ni, J.; Tian, H.; Wu, W.; Hu, J. Integrated robust dynamics control of all-wheel-independently-actuated unmanned ground vehicle in diagonal steering. Mech. Syst Signal. Pr. 2022, 164, 108263. [Google Scholar] [CrossRef]
- Qiu, Q.; Fan, Z.; Meng, Z.; Zhang, Q.; Cong, Y.; Li, B.; Wang, N.; Zhao, C. Extended Ackerman steering principle for the coordinated movement control of a four-wheel drive agricultural mobile robot. Comput. Electron. Agric. 2018, 152, 40–50. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, X.; Liu, C.; Wei, S. Dual-steering mode based on direct yaw moment control for multi-wheel hub motor driven vehicles: Theoretical design and experimental assessment. Def. Technol. 2022, 18, 49–61. [Google Scholar] [CrossRef]
- Ni, L.; Wu, L.; Zhang, H. Parameters uncertainty analysis of posture control of a four-wheel-legged robot with series slow active suspension system. Mech. Mach. Theory 2022, 175, 104966. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, W. Decoupling control of steering and driving system for in-wheel-motor-drive electric vehicle. Mech. Syst Signal. Pract. 2018, 101, 389–404. [Google Scholar] [CrossRef]
- Zhang, J.; Li, S.; Meng, H.; Li, Z.; Sun, Z. Variable gain based composite trajectory tracking control for 4-wheel skid-steering mobile robots with unknown disturbances. Control. Eng. Pract. 2023, 132, 105428. [Google Scholar] [CrossRef]
- Tu, X.; Gai, J.; Tang, L. Robust navigation control of a 4WD/4WS agricultural robotic vehicle. Comput. Electron. Agric. 2019, 164, 104892. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, D.; Zhu, S.; Feng, J. Distributed active disturbance rejection control for Ackermann steering of a four-in-wheel motor drive vehicle with deception attacks on controller area networks. Inf. Sci. 2020, 540, 370–389. [Google Scholar] [CrossRef]
- Liu, D.; Tang, M.; Fu, J. Robust adaptive trajectory tracking for wheeled mobile robots based on Gaussian process regression. Syst. Control. Lett. 2022, 163, 105210. [Google Scholar] [CrossRef]
- Mishra, D.K.; Thomas, A.; Kuruvilla, J.; Kalyanasundaram, P.; Prasad, K.R.; Haldorai, A. Design of mobile robot navigation controller using neuro-fuzzy logic system. Comput. Electr. Eng. 2022, 101, 108044. [Google Scholar] [CrossRef]
- Khalaji, A.K.; Jalalnezhad, M. Robust forward\\backward control of wheeled mobile robots. ISA Trans. 2021, 115, 32–45. [Google Scholar] [CrossRef]
- Jiang, L.; Wang, S.; Xie, Y.; Xie, S.; Zheng, S.; Meng, J. Fractional robust finite time control of four-wheel-steering mobile robots subject to serious time-varying perturbations. Mech. Mach. Theory 2022, 169, 104634. [Google Scholar] [CrossRef]
- Li, L.; Cao, W.; Yang, H.; Geng, Q. Trajectory tracking control for a wheel mobile robot on rough and uneven ground. Mechatronics 2022, 83, 102741. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Z.; Zhang, L.; Dorrell, D.G. Braking/steering coordination control for in-wheel motor drive electric vehicles based on nonlinear model predictive control. Mech. Mach. Theory 2019, 142, 103586. [Google Scholar] [CrossRef]
- Mérida-Calvo, L.; Rodríguez, A.S.-M.; Ramos, F.; Feliu-Batlle, V. Advanced motor control for improving the trajectory tracking accuracy of a low-cost mobile robot. Machines 2023, 11, 14. [Google Scholar] [CrossRef]
- Roshanianfard, A.; Noguchi, N.; Okamoto, H.; Ishii, K. A review of autonomous agricultural vehicles (The experience of Hokkaido University). J. Terramech. 2020, 91, 155–183. [Google Scholar] [CrossRef]
- Song, S.; Qu, J.; Li, Y.; Zhou, W.; Guo, K. Fuzzy control method for a steering system consisting of a four-wheel individual steering and four-wheel individual drive electric chassis. J. Int. Fuzzy Syst. 2016, 31, 2941–2948. [Google Scholar] [CrossRef]
- Qu, J.; Guo, K.; Zhang, Z.; Song, S.; Li, Y. Coupling control strategy and experiments for motion mode switching of a novel electric chassis. Appl. Sci. 2020, 10, 701. [Google Scholar] [CrossRef]
- Song, S.; Guo, K. Automatic tracking steering system for off-centered flexible chassis steering axis based on fuzzy-PI composite control. J. Int. Fuzzy Syst. 2018, 35, 187–195. [Google Scholar] [CrossRef]
- Qu, J.; Guo, K.; Gao, H.; Song, S.; Li, Y.; Zhou, W. Experiments on collaborative characteristics of driving and steering for agricultural flexible chassis based on PWM signal. Trans. CSAE 2018, 34, 75–81. [Google Scholar] [CrossRef]
- Qu, J.; Guo, K.; Li, Y.; Song, S.; Gao, H.; Zhou, W. Experiment and optimization of mode switching controlling parameters for agricultural flexible chassis. Trans. CSAM 2018, 49, 346–352. [Google Scholar] [CrossRef]
- Song, S.; Li, Y.; Qu, J.; Zhou, W.; Guo, K. Design and test of flexible chassis automatic tracking steering system. Int. J. Agr. Biol. Eng. 2017, 10, 45–54. [Google Scholar]
- Huang, W.; Zhang, Y.; Yu, Y.; Xu, Y.; Xu, M.; Zhang, R.; Dieu, G.J.D.; Yin, D.; Liu, Z. Historical data-driven risk assessment of railway dangerous goods transportation system: Comparisons between entropy weight method and scatter degree method. Reliab. Eng. Syst. Safe 2021, 205, 107236. [Google Scholar] [CrossRef]
- Li, Q.; Hu, H.; Ma, L.; Wang, Z.; Arıcı, M.; Li, D.; Luo, D.; Jia, J.; Jiang, W.; Qi, H. Evaluation of energy-saving retrofits for sunspace of rural residential buildings based on orthogonal experiment and entropy weight method. Energy. Sustain. Dev. 2022, 70, 569–580. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, B.; Fan, J.; Hu, X.; Wei, S.; Li, Y.; Zhou, Q.; Wei, C. Development of a tomato harvesting robot used in greenhouse. Int. J. Agr. Biol. Eng. 2017, 10, 140–149. [Google Scholar] [CrossRef]
- Jones, M.H.; Bell, J.; Dredge, D.; Seabright, M.; Scarfe, A.; Duke, M.; MacDonald, B. Design and testing of a heavy-duty platform for autonomous navigation in kiwifruit orchards. Biosyst. Eng. 2019, 187, 129–146. [Google Scholar] [CrossRef]
- Utstumo, T.; Urdal, F.; Brevik, A.; Dørum, J.; Netland, J.; Overskeid, Ø.; Berge, T.W.; Gravdahl, J.T. Robotic in-row weed control in vegetables. Comput. Electron. Agric. 2018, 154, 36–45. [Google Scholar] [CrossRef]
- Liu, D.; Wang, J.; Wang, S. Coordinated motion control and event-based obstacle-crossing for four wheel-leg independent motor-driven robotic system. Mechatronics 2022, 81, 102697. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; Yang, S. The study on differential steering control of in-wheel motor vehicle based on double closed loop system. Energy Procedia 2018, 152, 586–592. [Google Scholar] [CrossRef]
- Ding, T.; Zhang, Y.; Ma, G.; Cao, Z.; Zhao, X.; Tao, B. Trajectory tracking of redundantly actuated mobile robot by MPC velocity control under steering strategy constraint. Mechatronics 2022, 84, 102779. [Google Scholar] [CrossRef]
- Sorour, M.; Cherubini, A.; Khelloufi, A.; Passama, R.; Fraisse, P. Complementary-route based icr control for steerable wheeled mobile robots. Robot. Auton. Syst. 2019, 118, 131–143. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).