A Two-Step Approach to Scheduling a Class of Two-Stage Flow Shops in Automotive Glass Manufacturing

Abstract

Driven from real-life applications, this work aims to cope with the scheduling problem of automotive glass manufacturing systems, that is characterized as a two-stage flow-shop with small batches, inevitable setup time for different product changeover at the first stage, and un-interruption requirement at the second stage. To the best knowledge of the authors, there is no report on this topic from other research groups. Our previous study presents a method to assign all batches to each machine at the first stage only without sequencing the assigned batches, resulting in an incomplete schedule. To cope with this problem, if a mathematical programming method is directly applied to minimize the makespan of the production process, binary variables should be introduced to describe the processing sequence of all the products, not only the batches, resulting in huge number of binary variables for the model. Thus, it is necessary and challenging to search for a method to solve the problem efficiently. Due to the mandatory requirement that the second stage should keep working continuously without interruption, solution feasibility is essential. Therefore, the key to solve the addressed problem is how to guarantee the solution feasibility. To do so, we present a method to determine the minimal size of each batch such that the second stage can continuously work without interruption if the sizes of all batches are same. Then, the conditions under which a feasible schedule exists are derived. Based on the conditions, we are able to develop a two-step solution method. At the first step, an integer linear program (ILP) is formulated for handling the batch allocation problem at the first stage. By the ILP, we need then to distinguish the batches only, greatly reducing the number of variables and constraints. Then, the batches assigned to each machine at the first stage are optimally sequenced at the second step by an algorithm with polynomial complexity. In this way, by the proposed method, the computational complexity is greatly reduced in comparison with the problem formulation without the established feasibility conditions. To validate the proposed approach, we carry out extensive experiments on a real case from an automotive glass manufacturer. We run ILP on CPLEX for testing. For large-size problems, we set 3600 s as the longest time for getting a solution and a gap of 1% for the lower bound of solutions. The results show that CPLEX can solve 96.83% cases. Moreover, we can obtain good solutions with the maximum gap of 4.9416% for the unsolved cases.

1. Introduction

Due to globalization, products are diversified and should be produced in a customized way with small batches and low cost. To do so, a manufacturing system should be flexible. One important flexibility type of a production system is characterized by the capability to produce multiple product types. To produce different products in a single system, changeovers are performed frequently due to the small batch size and setups often required [1]. In many cases, the setup activities take significant time, which cannot be ignored in operating a system. Flow-shop systems are widely adopted production systems. In a classical flow-shop system, a set of jobs are sequentially processed at multiple stages, where each stage has one machine only. If there is at least one stage consisting of more than one machine, the system is addressed as a flexible flow-shop [2]. A flexible flow-shop is also called a hybrid flow shop. Scheduling a flexible flow-shop production system that processes a variety of product types with small batches is an important issue in industrial applications.

In this paper, we investigate the scheduling problem of automotive glass manufacturing systems (AGMSs) that is described as follows. In an automotive context, there are many glass products and all of them should be produced in a single AGMS. For a glass product to be produced in an AGMS, there are five processing steps: pre-processing, bending, Polyvinyl Butyral (PVB) stretching and lamination, vacuuming, and final inspection. The shapes of different products produced in an AGMS are different, changeovers for producing different products are inevitable. For the addressed AGMS, setups with significant time for a changeover are required at Step 1. At Step 2, dies are used to form different shapes for different products. By proper process planning, dies can be changed when a machine is operating, leading to no setup time. Furthermore, in an AGMS, no setup is required for Steps 3–5 either and Steps 2–5 are designed to be paced to maximize the productivity. Therefore, an AGMS is a typical two-stage flow-shop (TSFS), where Step 1 forms the first stage, while the other steps form the second stage. Further, there are multiple machines at both Stages 1 and 2. Thus, an AGMS is also a two-stage flexible flow-shop (TSFFS).

For the addressed AGMS, the second stage is naturally recognized and designed as the bottleneck in practice since a machine at the second stage cannot be interrupted so as to keep the processing environment (i.e., temperature) due to quality assurance requirements. Thus, this work aims to minimize the makespan of TSFFSs with small batches, sequence-independent setup time at the first stage and no-interruption requirement at the second stage. For this addressed problem, a set of ζ batches (each batch can be treated as a job) are processed. To meet the no-interruption requirement for Stage 2, when a product in a batch is completed by a machine at Stage 1, this product should be scheduled to be processed at Stage 2 immediately without waiting for the completion of the entire batch. Furthermore, after processing a product in a batch that is previously completed by machine i, the next product processed by Stage 2 may be a product from a different batch completed by machine j with i ≠ j. Thus, if a mathematical programming method is directly applied to minimize the makespan of the presented TSFFS in this work, we need binary variables to identify the processing sequence of all the products but not only the batches. In this way, a huge number of binary variables should be introduced, leading to a model size that is extremely large. Thus, it is an important issue to search for a method such that the problem can be efficiently solved, which it is very challenging. This motivates us to conduct this work.

Due to the mandatory requirement that the second stage should keep working continuously without interruption, solution feasibility is essential. Therefore, the key to solve the addressed problem is how to guarantee solution feasibility. To do so, this work makes the following contributions:

(1)

We present a method to determine the minimal size of each batch such that the second stage can continuously keep working without interruption if the sizes of all batches are same;

(2)

The conditions under which a feasible schedule exists are derived;

(3)

Based on the conditions, we are able to develop a two-step solution method;

(3.1)

At the first step, an integer linear program (ILP) is formulated for handling the batch allocation problem at the first stage.

(3.2)

At the second step, the batches assigned to each machine at the first stage are optimally sequenced by an algorithm with polynomial complexity.

For the proposed two-step method, at the first step, we need to distinguish the batches only, greatly reducing the number of variables and constraints in the ILP. In this way, by the proposed method, we greatly reduce the computational complexity in comparison with the problem formulation without the established feasibility conditions.

The rest of the paper is constructed as follows. Section 2 briefly reviews the related work. Section 3 analyzes properties of the system. Then, a two-step solution method is proposed in Section 4. Experimental results are given to test the performance of the proposed method in Section 5. Finally, the last section concludes this work.

2. Literature Review

Many studies have been conducted on flow-shop scheduling problems. For flow-shop scheduling problems, there are various variants, considering different constraints, scheduling scenarios, and optimization objectives [3]. The main constraints include setup time [4], limited buffers [5], uncertain processing time [6], due dates [7], etc. Many researchers attempt to solve such scheduling problems by using mathematical models [4,8], meta-heuristics algorithms [5,9], artificial intelligence [4], and methods based on scheduling policy [10,11]. Interested readers can refer to the surveys in [3,12,13] for more details about the scheduling analysis of flow-shop systems. Since the addressed scheduling problem comes from a real AGMS that is treated as a TSFS, this work mainly reviews the works related to the scheduling problems of TSFS.

Some studies have been carried out for TSFS system scheduling problems. With one machine at Stage 1, by considering the machine breakdown, [14] propose efficient approaches to minimize the makespan. With one machine at Stage 2, based on a branch and bound technique, [15] developed an algorithm to find an optimal schedule. With arbitrary arrival time of jobs, [16] present an ant colony algorithm to schedule a TSFS system. A multi-objective hybrid ant colony algorithm is constructed by [17] to trade off the makespan and total energy costs for a two-stage blocking permutation flow-shop. For a no-waiting TSFS, [18] design a linear-time combinatorial algorithm.

By considering independent setup time, [19] construct several heuristic algorithms for scheduling a TSFS. With the fuzzy makespan and total agreement index as objective, [20] adopt a diversified teaching–learning-based algorithm for a TSFS with sequence-dependent setup time. By applying reinforcement learning, [21] propose a novel approach for the TSFS system scheduling problem. In addition, efficient algorithms are presented for two-stage assembly flow-shops [22,23,24,25]. In such a system, normally, the first stage is used to fabricate multiple types of components, while the second stage assembles the components to form the final product.

For a TSFS system, if each stage has one machine only, the system becomes a two-machine flow shop (TMFS) and great efforts have been made for scheduling such systems. With sequence-independent setup time, the branch and bound techniques are employed to optimize the makespan in [26]. In [27,28], methods are proposed to minimize makespan by considering the release dates, while in [29], several metaheuristics are examined by considering both release dates and blocking constraint. To minimize the total tardiness, lower bounds and dominance conditions are established in [30]. In addition, there are studies [31,32] that focus on TMFSs with deteriorating jobs. Note that there are extensive studies on scheduling TMFSs. Due to the fact that the addressed AGMS in this work is much more complex, we do not make an extensive review on this issue, in order to save space.

To the best knowledge of the authors, there is no report on the scheduling problem of TSFFSs with small batches, sequence-independent setup time at the first stage and no-interruption requirement at the second stage from other research groups. For the addressed problem in this work, our previous study presents a method to assign all batches to each machine at Stage 1 for being processed [33]. However, it gives no way to sequence the assigned batches, resulting in an incomplete schedule. Moreover, it does not present how to find the minimal size of each batch such that Stage 2 can continuously work without interruption if the sizes of all batches are same. Notice that the key to present the existence conditions of a feasible schedule is to determine the minimal sizes of all batches. This motivates us to perform this work such that the addressed problem can be completely solved.

3. Scheduling Analysis

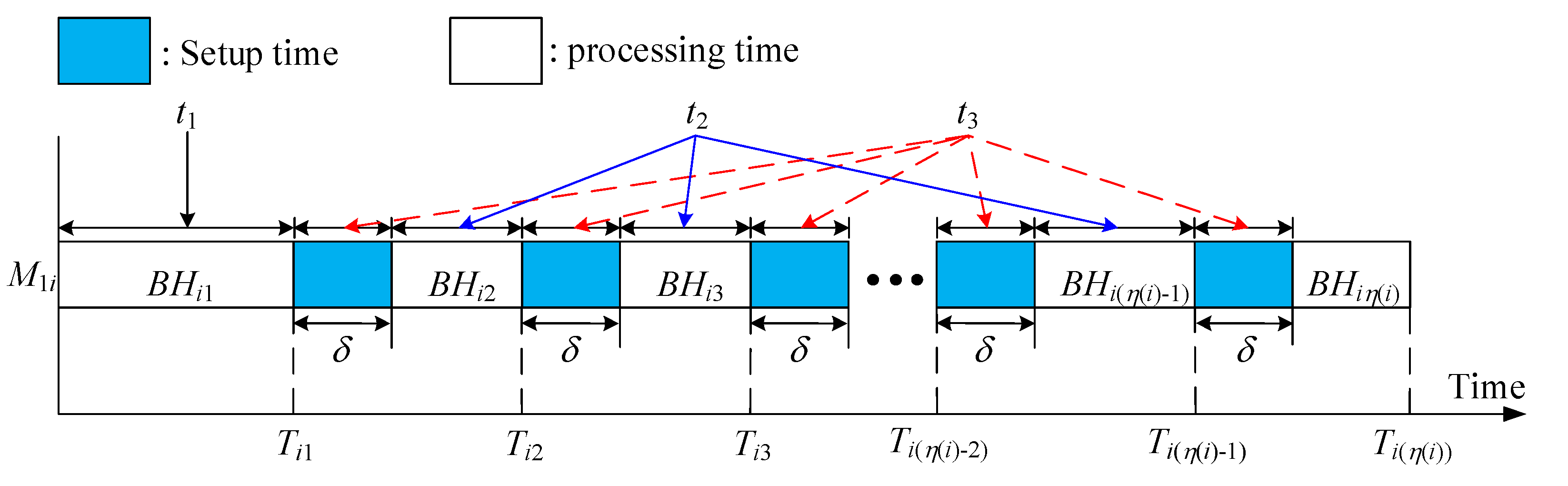
3.1. System Description

Before presenting the proposed method, we first introduce the addressed AGMS as follows.

(1)

There are parallel multiple machines with same processing functions at each stage;

(2)

Only one product can be processed by a machine at a time;

(3)

At Stage 1, a batch should be processed by a single machine without splitting;

(4)

Stage 2 is the bottleneck;

(5)

Stage 1 has the setup time;

(6)

Each batch contains identical products;

(7)

For any two batches, their product types are different, with the result that if one batch is just processed at Stage 1, setup time is required before another one is processed next; and

(8)

After its completion at Stage 1, a product is ready to be processed immediately by a machine at Stage 2.

Since each stage has multiple machines, g ≥ 1 and h ≥ 1 are used to denote the number of machines at Stages 1 and 2, respectively. Further, let ℕ_k = {1, 2, …, k}. Then, M_1i, i∈ℕ_g, and M_2j, j∈ℕ_h, represent the i-th and j-th machines at the two stages, respectively. Figure 1 describes an AGMS with small batches to be processed and multiple machines at each stage. The time for processing a product of any type by M_1i and M_2j is known and denoted as α and μ, respectively. Further, the setup time for a machine at Stage 1 is known and it is represented by δ. Without setup time at Stage 2, we treat the h machines there as just one machine, leading to that the processing time of a product at Stage 2 is β = $\frac{\mu }{h}$ time units.

We ensure that $\frac{\alpha }{g}$ < β should hold, otherwise some machines at the second stage have to be interrupted from time to time due to the setups for M_1i, i∈ℕ_g. In that case, the problem is similar to schedule a single machine. For such a scheduling problem, there are extensive studies [34,35,36,37,38,39,40]. Thus, to ensure the non-interruption requirement of machines at the second stage, it should satisfy $\frac{\alpha }{g}$ < β when the system is designed. By the experience of the authors with some companies in China, this is true for AGMSs. With $\frac{\alpha }{g}$ < β and the non-interruption constraint, it is a great challenge to maximize the productivity by finding a feasible schedule for processing multiple products, which is the aim of this work.

3.2. Properties of the System

Due to there being many glass products for automotives, in an AGMS, the number of machines at the first stage is much less than the number of product types to be produced. Moreover, the total number of products to be produced for a scheduling horizon is much greater than the number of products in a batch. To maximize the throughput of an AGMS, the key is that one should properly allocate the batches to the machines at the first stage and sequence them for each M_1i, i∈ℕ_g. Suppose that η(i) batches are allocated to M_1i, i∈ℕ_g. Let BH_ij, i∈ℕ_g and j∈ℕ_η(i), denote the j-th one in the η(i) batches with its batch size being b_ij. Without loss of generality, it is assumed that, at time zero, the system starts to process batch BH_i1, i∈ℕ_g. We use T_ij to denote the completion time of batch BH_ij, i∈ℕ_g and j∈ℕ_η(i). Then, we have

$$T_{ij}=\mathit{\alpha } \times {{\displaystyle \sum }}_{d=1}^j{b}_{id}+(j-1)\times \mathit{\delta }, i\in {\mathbb{N}}_{\mathbf{g}} \mathrm{and} j\in {\mathbb{N}}_{\mathit{\eta }\mathbf{\left(}\mathbf{i}\mathbf{\right)}}$$

(1)

Note that T_iη(i) gives the time when M_1i, i∈ℕ_g, completes its allocated batches. Let ϑ_it be the average production rate of M_1i, i∈ℕ_g, in [0, t], i.e., the average number of products completed by M_1i per unit time in [0, t]; and T_min = min(T_iη(i)| i∈ℕ_g). The following lemma can be obtained.

Lemma 1.

If${{\displaystyle \sum }}_{i=1}^g{\vartheta }_{it}$≥  $\frac{1}{{\beta }^{\prime }}$ ,∀t∈(0, T_min], then Stage 2 can operate uninterruptedly during (0, T_min].

Proof. 

With ϑ_it being the average production rate of M_1i, i∈ℕ_g, in [0, t], the average production rate of Stage 1 in [0, t] is ${{\displaystyle \sum }}_{i=1}^g{\vartheta }_{it}$. Notice that the maximal production rate of Stage 2 is $\frac{1}{\beta }$. Thus, if ${{\displaystyle \sum }}_{i=1}^g{\vartheta }_{it}$ ≥ $\frac{1}{{\beta }^{\prime }}$ ∀t ∈ (0, T_min], then, at any time point in (0, T_min], the production rate of Stage 1 is greater than or equal to that of Stage 2. That is to say that there are always products for Stage 2 to process and no machine needs to stop in (0, T_min], i.e., the lemma holds. □

With Lemma 1, we obtain the uninterrupted operation condition of Stage 2. In practice, due to significant setup time at Stage 1, if some machines at Stage 1 are switching from processing one batch to another, it may result in Stage 1 being unable to feed enough products to the machines at Stage 2 (the bottleneck), leading to some machines at Stage 2 being unable to keep continuously working. To solve this problem, similar to the basic idea of the drum-buffer-rope [41,42], buffers (the inventory) can be used to protect the bottleneck such that the uninterrupted operation condition of Stage 2 shown in Lemma 1 is satisfied. Therefore, it is important to schedule the batches to be processed at Stage 1. Moreover, it is necessary to determine the minimal size of each batch such that Stage 2 can continuously work without interruption if the sizes of all batches are the same. Thus, for more general cases, it is possible to find a method to schedule the batches to be processed at Stage 1 so as to protect the bottleneck by the inventory.

Suppose that all the machines at Stage 1 process batches with the same size in a paced way. In other words, the size of all batches to be processed are same and all the machines at Stage 1 start to process a batch at the same time. In this way, all the machines switch from producing a type of product to another type at the same time as well. Then, we can determine the minimal size of each batch denoted by Θ such that Stage 2 can operate continuously with no interruption.

Lemma 2.

Suppose that all the g machines at Stage 1 perform the product processing and switching operations in a paced way and the size of the batches to be processed are same. Then, if the size of each batch is no less than Θ =$\frac{\delta }{g\times \beta -\alpha }$Stage 2 can operate uninterruptedly.

Proof. 

When the g machines at the first stage start to process a batch at the same time, then the inventory between Stages 1 and 2 should increase over time due to $\frac{\alpha }{g}$ < β. Assume that after t₀ time units elapse, a batch at each machine at Stage 1 is just completed. At this time, every one of the g machines switches from processing one batch to another exactly at the same time. Then, the inventory between the two stages decreases over time since Stage 2 continuously consumes the inventory. After δ time units elapse, the inventory reaches zero. In this way, there are always products for Stage 2 to produce such that it cannot be interrupted since the g machines at Stage 1 start to process a batch at the same time, leading to the inventory between Stages 1 and 2 increasing over time. This means that in this situation, the size of the batches is minimal. The inventory between Stages 1 and 2 changes periodically over time, as shown in Figure 2. Thus, we have that during time t₀, each machine at Stage 1 can produce Θ = $\frac{t_0}{\alpha }$ products, i.e., a batch. In total, Stage 1 produces $g\times \frac{t_0}{\alpha }$ products. During time t₀ + δ, Stage 2 just consumes $\frac{t_0+\delta }{\beta }$ products. Note that $g\times \frac{t_0}{\alpha }=\frac{t_0+\delta }{\beta }$ and t₀ = αΘ, leading to Θ = $\frac{\delta }{g\times \beta -\alpha }$ Therefore, the lemma holds. □

Notice that Θ > 0 since $\frac{\alpha }{g}$ < β results in α < gβ. With Lemmas 1 and 2, to develop a method such that Stage 2 can operate uninterruptedly, we have the following result for one of the cases.

Theorem 1.

Given that BH_ij, i∈ℕ_g and j∈ℕ_η(i), is the j-th batch in the processing sequence for M_1i, for ∀t ∈ (0, T_min], ${{\displaystyle \sum }}_{i=1}^g{\vartheta }_{it}$ ≥ $\frac{1}{\beta }$ holds if b_ij ≥ Θ, ∀j∈ℕ_η(i) and ∀i∈ℕ_g.

Proof. 

With $\frac{\alpha }{g}$< β, as illustrated in Figure 3, before the completion of the first batch, the production rate of M_1i is $\frac{1}{\alpha }$ > $\frac{1}{g\beta }$, at time t₁ ∈ [0, T_i1], i∈ℕ_g.

As illustrated in Figure 3, it follows from (1) that, at time T_iu + δ, 1 ≤ u ≤ η(i) − 1, η(i) ≥ 2, and i∈ℕ_g, the average production rate of M_1i can be calculated as

$$\frac{{{\displaystyle \sum }}_{j=1}^u{b}_{ij}}{T_{iu}+\delta }=\frac{{{\displaystyle \sum }}_{j=1}^u{b}_{ij}}{\alpha \times {{\displaystyle \sum }}_{j=1}^u{b}_{ij}+u\times \delta }$$

With b_ij ≥ Θ, i∈ℕ_g and j∈ℕ_η(i), ${{\displaystyle \sum }}_{j=1}^u{b}_{ij}$ ≥ u × Θ holds. Notice that a > 0, b > 0, and c > 0 are constants, so, we can obtain a monotonically increasing function f₁(x) = $\frac{ax}{bx+c}$. Then, with constants α, u, and δ, another monotonically increasing function f₂(x) = $\frac{x}{\alpha x+u\delta }$ can be obtained. Replace x by u × Θ in f₂(x), resulting in f₂(u × Θ) = $\frac{1}{g\beta }$. Since x = ${{\displaystyle \sum }}_{j=1}^u{b}_{ij}$ ≥ u × Θ, f₂(${{\displaystyle \sum }}_{j=1}^u{b}_{ij}$) ≥ $\frac{1}{g\beta }$ holds, resulting in $\frac{{{\displaystyle \sum }}_{j=1}^u{b}_{ij}}{T_{iu}+\delta }$ ≥ $\frac{1}{g\beta }$, implying that, at time T_iu + δ, i∈ℕ_g, η(i) ≥ 2, and 1 ≤ u ≤ η(i) − 1, the production rate of M_1i is no less than $\frac{1}{g\beta }$.

As illustrated in Figure 3, it follows from (1) that, at any time t₂ ∈ (T_iu + δ, T_i(u+1)], i∈ℕ_g, η(i) ≥ 2, and 1 ≤ u ≤ η(i) − 1, the average production rate of M_1i can be calculated as

$$\frac{{{\displaystyle \sum }}_{j=1}^u{b}_{ij}+\left(\frac{t_2-T_{iu}-\delta }{\alpha }\right)}{t_2}=\frac{{{\displaystyle \sum }}_{j=1}^u{b}_{ij}+\left(\frac{t_2-T_{iu}-\delta }{\alpha }\right)}{\alpha \times \left[{{\displaystyle \sum }}_{j=1}^u{b}_{ij}+\left(\frac{t_2-T_{iu}-\delta }{\alpha }\right)\right]+u\times \delta }$$

Since ${{\displaystyle \sum }}_{j=1}^u{b}_{ij}+\left(\frac{t_2-T_{iu}-\delta }{\alpha }\right)$ > ${{\displaystyle \sum }}_{j=1}^u{b}_{ij}$ ≥ u × Θ holds, we have f₂(${{\displaystyle \sum }}_{j=1}^u{b}_{ij}+\left(\frac{t_2-T_{iu}-\delta }{\alpha }\right)$) > $\frac{1}{g\beta }$, i.e., $\frac{{{\displaystyle \sum }}_{j=1}^u{b}_{ij}+\left(\frac{t_2-T_{iu}-\delta }{\alpha }\right)}{t_2}$ > $\frac{1}{g\beta }$. Hence, at time t₂, T_iu + δ < t₂ ≤ T_i(u+1), i∈ℕ_g, η(i) ≥ 2, and 1 ≤ u ≤ η(i) − 1, the production rate of M_1i is greater than $\frac{1}{g\beta }$.

As illustrated in Figure 3, it follows from (1) that, at any time t₃ ∈ (T_iu, T_iu + δ), i∈ℕ_g, η(i) ≥ 2, and 1 ≤ u ≤ η(i) − 1, the average production rate of M_1i can be calculated as

$$\frac{{{\displaystyle \sum }}_{j=1}^u{b}_{ij}}{t_3}=\frac{{{\displaystyle \sum }}_{j=1}^u{b}_{ij}}{\alpha \times {{\displaystyle \sum }}_{j=1}^u{b}_{ij}+\left(u-1\right)\times \delta +t_3-T_{iu}}$$

Due to 0 < t₃ − T_iu < δ, we have

$$\frac{{{\displaystyle \sum }}_{j=1}^u{b}_{ij}}{t_3}=\frac{{{\displaystyle \sum }}_{j=1}^u{b}_{ij}}{\alpha \times {{\displaystyle \sum }}_{j=1}^u{b}_{ij}+\left(u-1\right)\times \delta +t_3-T_{iu}} > \frac{{{\displaystyle \sum }}_{j=1}^u{b}_{ij}}{\alpha \times {{\displaystyle \sum }}_{j=1}^u{b}_{ij}+u\times \delta }=f_2\left({{\displaystyle \sum }}_{j=1}^u{b}_{ij}\right) \ge \frac{1}{g\beta }$$

Hence, at time t₃, T_iu < t₃ < T_iu + δ, i∈ℕ_g, η(i) ≥ 2, and 1 ≤ u ≤ η(i) − 1, the production rate of M_1i is greater than $\frac{1}{g\beta }$.

Therefore, by summarizing the production rates of the g machines, we conclude that, at any time during (0, T_min], ${{\displaystyle \sum }}_{i=1}^g{\vartheta }_{it}$ ≥ $\frac{1}{\beta }$, or the total production rate of Stage 1 is greater than or equal to $\frac{1}{\beta }$ for any t ∈ (0, T_min]. □

In this case, to ensure that the machines at Stage 2 can operate uninterruptedly, it requires that the number of products in any batch should be greater or equal to Θ. By the conditions given in Theorem 1, it implies that before any changeover for product switching, there is enough inventory in the buffer between the two stages such that Stage 2 cannot be starved during the setup time δ. Furthermore, by Theorem 1, it can be concluded that, if the conditions given in Theorem 1 are satisfied, different batch sequences do not affect the production rate of Stage 2, since it is always in operation no matter how the batches are sequenced. However, there may be batches with size less than Θ. It raises a question if Stage 2 can operate uninterruptedly if batches with size less than Θ exist. The following theorem presents an answer to it.

Theorem 2.

Given that BH_ij, i∈ℕ_g and j∈ℕ_η(i), is the j-th batch in the processing sequence for M_1i, then for any t ∈ (0, T_min], ${{\displaystyle \sum }}_{i=1}^g{\vartheta }_{it}$ ≥ $\frac{1}{\beta }$ holds if ${{\displaystyle \sum }}_{j=1}^s{b}_{ij}$ ≥ s × Θ, ∀i∈ℕ and ∀s∈ℕ_η(i)−1.

Proof. 

Similar to Theorem 1, at time t₄ ≤ T_i1, i∈ℕ_g, the production rate of M_1i is $\frac{1}{\alpha }$ > $\frac{1}{g\beta }$. It follows from (1) that, at any time t₅ ∈ [T_iu + δ, T_i(u+1)], i∈ℕ_g, η(i) ≥ 2, and 1 ≤ u ≤ η(i) − 1, the average production rate of M_1i can be calculated as

$$\frac{{{\displaystyle \sum }}_{j=1}^u{b}_{ij}+\left(\frac{t_5-T_{iu}-\delta }{\alpha }\right)}{t_5}=\frac{{{\displaystyle \sum }}_{j=1}^u{b}_{ij}+\left(\frac{t_5-T_{iu}-\delta }{\alpha }\right)}{\alpha \times \left[{{\displaystyle \sum }}_{j=1}^u{b}_{ij}+\left(\frac{t_5-T_{iu}-\delta }{\alpha }\right)\right]+u\times \delta }$$

Due to ${{\displaystyle \sum }}_{j=1}^u{b}_{ij}+\left(\frac{t_5-T_{iu}-\delta }{\alpha }\right)$ ≥ ${{\displaystyle \sum }}_{j=1}^u{b}_{ij}$ ≥ u × Θ, by Theorem 1, f₂(${{\displaystyle \sum }}_{j=1}^u{b}_{ij}+\left(\frac{t_5-T_{iu}-\delta }{\alpha }\right)$) ≥ $\frac{1}{g\beta }$, i.e., $\frac{{{\displaystyle \sum }}_{j=1}^u{b}_{ij}+\left(\frac{t_5-T_{iu}-\delta }{\alpha }\right)}{t_5}$ ≥ $\frac{1}{g\beta }$ holds. Hence, at time t₅, T_iu + δ ≤ t₅ ≤ T_i(u+1), i∈ℕ_g, η(i) ≥ 2, and 1 ≤ u ≤ η(i) − 1, the production rate of M_1i is no less than $\frac{1}{g\beta }$.

It follows from (1) that, at any time t₆ ∈ (T_iu, T_iu + δ), i∈ℕ_g, η(i) ≥ 2, and 1 ≤ u ≤ η(i) − 1, the average production rate of M_1i can be calculated as

$$\frac{{{\displaystyle \sum }}_{j=1}^u{b}_{ij}}{t_6}=\frac{{{\displaystyle \sum }}_{j=1}^u{b}_{ij}}{\alpha \times {{\displaystyle \sum }}_{j=1}^u{b}_{ij}+\left(u-1\right)\times \delta +t_6-T_{iu}}.$$

Just as Theorem 1, with 0 < t₆ − T_iu < δ, we can obtain

$$\frac{{{\displaystyle \sum }}_{j=1}^u{b}_{ij}}{t_6} > \frac{{{\displaystyle \sum }}_{j=1}^u{b}_{ij}}{\alpha \times {{\displaystyle \sum }}_{j=1}^u{b}_{ij}+u\times \delta }=f_2({{\displaystyle \sum }}_{j=1}^u{b}_{ij}) \ge \frac{1}{g\beta }$$

Hence, at time t₆ with T_iu < t₆ < T_iu + δ, i∈ℕ_g, η(i) ≥ 2, and 1 ≤ u ≤ η(i) − 1, the production rate of M_1i is greater than $\frac{1}{g\beta }$, resulting in that, during (0, T_min], ${{\displaystyle \sum }}_{i=1}^g{\vartheta }_{it}$ ≥ $\frac{1}{\beta }$, or the total production rate of Stage 1 is no less than $\frac{1}{\beta }$ for any t ∈ (0, T_min]. □

In this case, there exist schedules such that when some machines at Stage 1 execute setup activities, there are enough products that have been processed at Stage 1 in the buffer between the stages such that Stage 2 cannot be starved. Then, we examine the case that the batch size of every batch is less than Θ. In this case, we have the following result.

Theorem 3.

Given that BH_ij, ∀i∈ℕ_g and∀j∈ℕ_η(i) with η(i) ≥ 2, is the j-th batch in the processing sequence for M_1i, then interruptions of Stage 2 cannot be avoided in time interval (0, T_min] if b_ij < Θ, ∀i∈ℕ_g, ∀j∈ℕ_η(i)with η(i) ≥ 2.

Proof. 

It follows from (1) that, at time T_iu + δ, i∈ℕ_g, η(i) ≥ 2, and 1 ≤ u ≤ η(i) − 1, the production rate of M_1i can be calculated as

$$\frac{{{\displaystyle \sum }}_{j=1}^u{b}_{ij}}{T_{iu}+\delta }=\frac{{{\displaystyle \sum }}_{j=1}^u{b}_{ij}}{\alpha \times {{\displaystyle \sum }}_{j=1}^u{b}_{ij}+u\times \delta }.$$

With b_ij < Θ, ∀i∈ℕ_g, ∀j∈ℕ_η(i), and η(i) ≥ 2, ${{\displaystyle \sum }}_{j=1}^u{b}_{ij}$ < u × Θ holds. It follows from Theorem 1 that f₂(${{\displaystyle \sum }}_{j=1}^u{b}_{ij}$) < f₂(u × Θ) = $\frac{1}{g\beta }$ holds, resulting in that, at time T_iu + δ, i∈ℕ_g, η(i) ≥ 2, and 1 ≤ u ≤ η(i) − 1, the production rate of M_1i is less than $\frac{1}{g\beta }$, leading to ${{\displaystyle \sum }}_{i=1}^g{\vartheta }_{it}$ < $\frac{1}{\beta }$, t = T_iu + δ. This means that Stage 2 should be starved for some time in (0, T_min], or the theorem holds. □

In this case, during the time when some machine is performing setups, there are not enough products in the buffer between the two stages for Stage 2 to process such that Stage 2 has to stop. Up until now, we have examined the existence of a feasible schedule and established the corresponding conditions. It should be pointed out that, to satisfy the condition given in Theorem 2, one needs to properly schedule the batches to be produced. Thus, to solve the scheduling problem of AGMSs, based on Theorems 1 and 2, we present a two-step method to find an optimal schedule by developing a mathematical programming model.

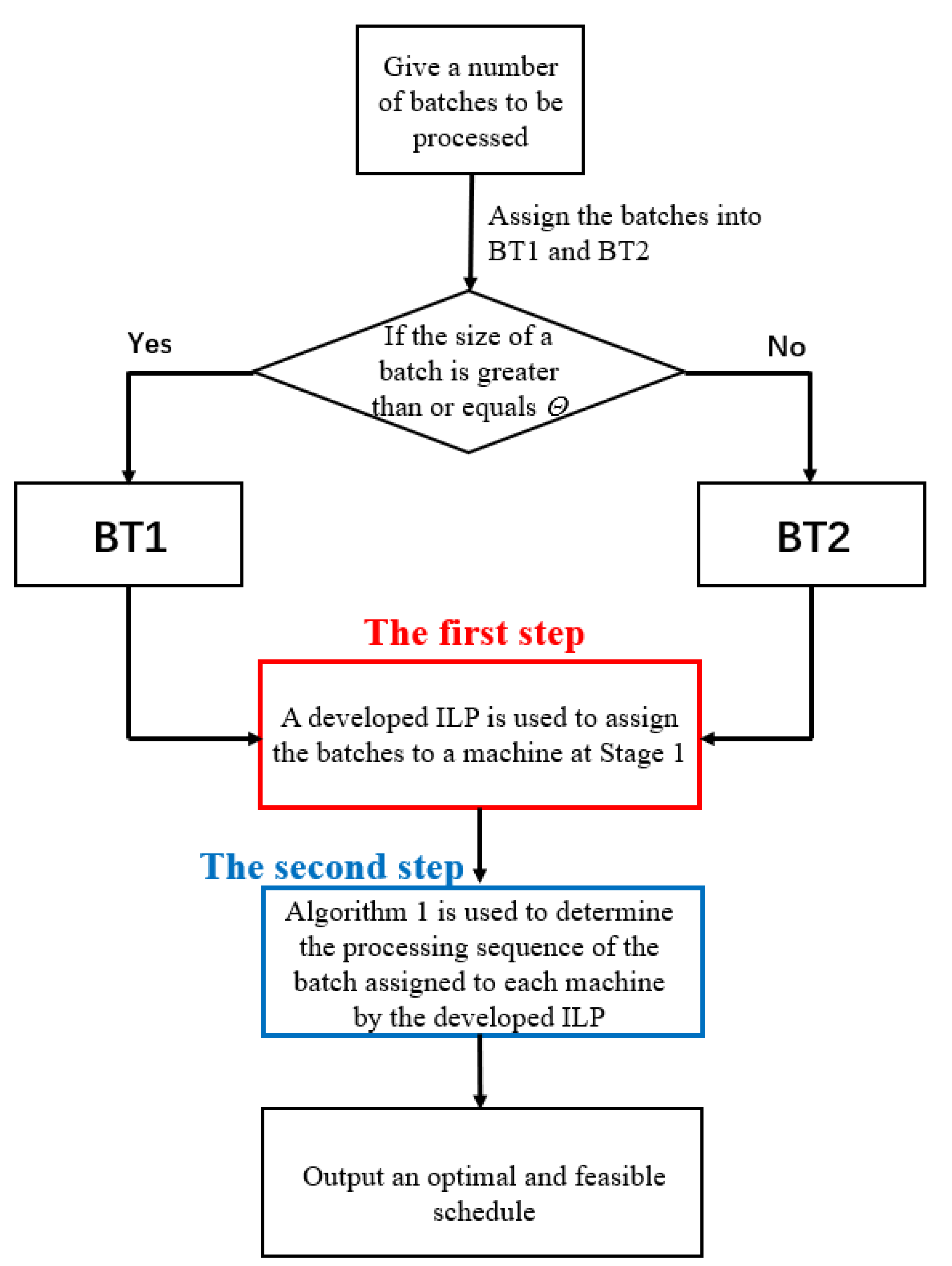
4. Two-Step Solution Method

With the above schedule existence conditions, this section presents a two-step solution method. First, at Step 1, we propose an ILP model to allocate the batches to different machines at Stage 1. Then, the batches to be produced by each machine at Stage 1 are sequenced at Step 2 to obtain the optimal solution.

4.1. Formulating the ILP

To effectively schedule the addressed AGMS, we need to allocate the batches to different machines at Stage 1 to balance the workloads and make a schedule feasible. As discussed above, batch size is crucial to find a feasible schedule. Thus, we partition the batches into two parts. Let Θ = $\frac{\delta }{g\times \beta -\alpha }$. Then, the set of batches with their sizes being greater or equal to Θ forms the first part called Batch Type 1 and denoted by BT1, and the other batches form the other part called Batch Type 2 and denoted by BT2. Assume that |BT1| = n and |BT2| = m such that we have in total n + m batches to be produced. We number the batches in BT1 and BT2 by consecutive integer numbers such that their index sets are denote as ℕ_n and ℕ_m, respectively. Further, let O_i ≥ Θ, i∈ℕ_n, be the batch size of the i-th batch in BT1 and Φ_j < Θ, j∈ℕ_m, the batch size of the j-th batch in BT2.

By Theorem 2, ${{\displaystyle \sum }}_{i=1}^g{\vartheta }_{it}$ ≥ $\frac{1}{\beta }$ holds for any t ∈ (0, T_min], if ${{\displaystyle \sum }}_{j=1}^s{b}_{ij}$ ≥ s × Θ, ∀i∈ℕ_g and ∀s∈ℕ_η(i)−1. In this case, by Lemma 1, we are sure that a feasible schedule can be found. However, in some cases, ${{\displaystyle \sum }}_{j=1}^s{b}_{ij}$ ≥ s × Θ may not hold for any i∈ℕ_g and s∈ℕ_η(i)−1. In this case, to ensure that a feasible schedule can be found, we need to add some extra products into the assigned batches so as to make the conditions given in Theorem 2 satisfied. Without loss of generality, we assume that extra products are added into BH_i1 for any machine i∈ℕ_g at Stage 1 and the number of products added to M_1i is ξ_i. Then, based on Theorem 2, we present the ILP as follows. The symbols for this model are given in the Nomenclature.

ILP: minimize Γ

(2)

$$\mathrm{S}. \mathrm{t}. {{\displaystyle \sum }}_{i=1}^g{x}_{ij}=1, j\in {\mathbb{N}}_{\mathbf{n}},$$

(3)

$${{\displaystyle \sum }}_{i=1}^g{y}_{ij}=1, j\in {\mathbb{N}}_{\mathbf{m}},$$

(4)

$$1 \ge {{\displaystyle \sum }}_{w=1}^m{z}_{iw}, i\in {\mathbb{N}}_{\mathbf{g}},$$

(5)

$${{\displaystyle \sum }}_{w=1}^m{z}_{iw} \ge y_{\mathrm{ij}}, j\in {\mathbb{N}}_{\mathbf{m}} \mathrm{and} i\in {\mathbb{N}}_{\mathbf{g}},$$

(6)

y_ij ≥ z_ij, j∈ℕ_m and i∈ℕ_g,

(7)

$${{\displaystyle \sum }}_{j=1}^m\left[y_{ij}\times \left({\mathit{\Phi }}_j\times \alpha +\mathit{\delta }\right)\right]+{\mathit{\xi }}_i \times \mathit{\alpha }-\mathit{\delta }+{{\displaystyle \sum }}_{j=1}^n\left[x_{ij}\times \left(O_j\times \alpha +\mathit{\delta }\right)\right] \le \mathsf{\Gamma }, i\in {\mathbb{N}}_{\mathbf{g}},$$

(8)

$${{\displaystyle \sum }}_{j=1}^m\left[\left(y_{ij}-z_{ij}\right)\times {\Phi }_j\right]+{\zeta }_i+{{\displaystyle \sum }}_{j=1}^n\left(x_{ij}\times O_j\right)\ge {{\displaystyle \sum }}_{j=1}^m\left[\left(y_{ij}-z_{ij}\right)\times \Theta \right]+{{\displaystyle \sum }}_{j=1}^n\left(x_{ij}\times \Theta \right)$$

(9)

In the above ILP, Γ presents the completion time of all batches at Stage 1. Thus, Objective (2) optimizes the total completion time. Constraints (3) and (4) ensure that a batch in both BT1 and BT2 is allocated to a single machine. Constraints (5) and (6) state that one of batches in BT2 allocated to M_1i, i∈ℕ_g, should be put at the last position for producing. Constraint (7) says that if no batch in BT2 is allocated to M_1i, i∈ℕ_g, i.e., y_ij = 0, i∈ℕ_g and j∈ℕ_m, then we have z_ij = 0, i∈ℕ_g and j∈ℕ_m. Constraint (8) enforces that the total completion time of batches that are allocated to M_1i should not be longer than Γ. For Constraint (9), two cases exist and they are Case 1: ${{\displaystyle \sum }}_{w=1}^m{z}_{iw}$ = 0; and Case 2: ${{\displaystyle \sum }}_{w=1}^m{z}_{iw}$ = 1. For the former, it follows from Constraint (6) that y_ij = 0, j∈ℕ_m, holds, implying that M_1i produces no batches in BT2. Hence, according to Theorem 1, the production rate of M_1i is always greater or equal to $\frac{1}{g\beta }$. For the latter, if ${{\displaystyle \sum }}_{j=1}^m\left[\left(y_{ij}-z_{ij}\right)\times {\Phi }_j\right]$ + ξ_i + ${{\displaystyle \sum }}_{j=1}^n\left(x_{ij}\times O_j\right)$ ≥ ${{\displaystyle \sum }}_{j=1}^n\left(x_{ij}\times \Theta \right)$ + ${{\displaystyle \sum }}_{j=1}^m\left[\left(y_{ij}-z_{ij}\right)\times \Theta \right]$, i∈ℕ_g, by Theorem 2, the satisfaction of Constraint (9) implies that the production rate of M_1i is no less than $\frac{1}{g\beta }$ all the time. Therefore, Constraint (9) ensure that the obtained solution is feasible even batches in BT2 are produced by M_1i, i∈ℕ_g.

4.2. Batch Sequencing for Machines at Stage 1

With the above developed ILP, batches are allocated to each machine at Stage 1 without determining their sequence for feasibility. Thus, based on the solution obtained by solving the ILP, we need to sequence the batches allocated to each machine such that the conditions given in Theorem 2 are met to ensure the feasibility of a solution. Assume that, by solving the ILP, the set of batches allocated to M_1i, i∈ℕ_g, is Λ_i. We have |Λ_i| = η(i) if z_ij = 0, otherwise |Λ_i| = η(i)−1 if z_ij = 1. Then, Algorithm 1 is used to sequence the batches for M_1i, i∈ℕ_g, such that the conditions given in Theorem 2 are ensured.

Algorithm 1:	Batch sequencing for M1i, i∈ℕg, based on the solution of ILP.
Input:	η(i), Θ, and Λi, i∈ℕg
Output:	BHij, i∈ℕg and j∈ℕη(i)−1
1:	Λi′ = ∅ /*initialize the sequenced batches*/;
2:	Choose a batch in Λi and set it to be BHi1 such that ξi + bi1 ≥ Θ;
3:	Λi′ ←Λi′ ∪{BHi1};
4:	Λi ←Λi\{BHi1};
5:	s = 2;
6:	While s ≤ η(i) − 1
7:	Choose a batch in Λi and set it to be BHis such that ξi + ${{\displaystyle \sum }}_{j=1}^s{b}_{ij}$ ≥ s × Θ;
8:	Λi′ ←Λi′ ∪{BHis};
9:	Λi ←Λi\{BHis};
10:	s = s +1;
11:	End;

In Algorithm 1, Statement 2 ensures that when the first batch BH_i1 is determined, we have ξ_i + b_i1 ≥ Θ, i.e., the conditions given in Theorem 2 are met. Then, by Statements 6–11 in Algorithm 1, it ensures that, with every batch being added, the conditions given in Theorem 2 are met. After performing Statement 11, it results in Λ_i = ∅ or |Λ_i| = 1. If Λ_i = ∅, we can conclude that z_ij = 1. In this case, all the batches have been sequenced. If |Λ_i| = 1, we simply put the remaining batch in Λ_i at the last position. In this way, we obtain a feasible schedule.

Let us analyze the worst-case running time of the algorithm. There are two situations as follows.

Situation 1.

If no batch in BT2 is allocated to M_1i (i.e., z_ij = 0), initially, there are η(i) batches in Λ_i. At this time, the running time of Statements 2 and 7 can be treated as a constant since ξ_i + ${{\displaystyle \sum }}_{j=1}^s{b}_{ij}$ ≥ s × Θ should be held no matter which batches in Λ_i is selected based on Theorem 1. Thus, the running time of performing Statements 6–11 is O(η(i)), leading to the worst-case running time of the algorithm is O(η(i)).

Situation 2.

If z_ij = 1 holds, initially, there are η(i) − 1 batches in Λ_i. Thus, the worst-case running time of Statement 2) is O(η(i) − 1) = O(η(i)). By performing Statement 6–11, it needs to make a selection for η(i) − 2 times. From the first time to the last time, the worst-case running time of the selections by performing Statement 7) is O(η(i) − 2), O(η(i) − 3), …, O(1), respectively. Thus, the worst-case running time of performing Statements 6–11 is O($\frac{\left(\eta \left(i\right)-2+1\right)\left(\eta \left(i\right)-2\right)}{2}$) = O((η(i))²).

From the above analysis, the computational complexity of this algorithm is O((η(i))²) for the worst-case. Note that, to obtain a feasible solution, Statement 2 requires to choose a batch such that ξ_i + b_i1 ≥ Θ holds, while Statement 7 needs to choose a batch such that ξ_i + ${{\displaystyle \sum }}_{j=1}^s{b}_{ij}$ ≥ s × Θ holds. It raises a question whether we can find such batches in performing these two statements. The following result answers this question.

Theorem 4.

Given a solution Λ_i from the ILP, Algorithm 1 can find a feasible schedule.

Proof. 

Given Λ_i obtained by solving the ILP, it follows from Constraint (9) that no matter how the batches in Λ_i are sequenced, we have ξ_i +  ${{\displaystyle \sum }}_{j=1}^{\eta \left(i\right)-1}{b}_{ij}$ ≥ (η(i) − 1) × Θ, i∈ ℕ_g. Hence, executing Statement 2 can find a batch in Λ_i as BH_i1 to make inequality ξ_i + b_i1 ≥ Θ hold. Then, after Statements 3–5 are executed, we repeatedly execute Statements 6–10. Assume that when we execute Statement 7 with s = k, 2 ≤ k ≤ η(i) − 1, there is no batch in Λ_i to make ξ_i + ${{\displaystyle \sum }}_{j=1}^k{b}_{ij}$ ≥ k × Θ satisfied. This implies that the size of every batch in the current Λ_i is less than Θ due to that ξ_i + ${{\displaystyle \sum }}_{j=1}^{k-1}{b}_{ij}$ ≥ (k − 1) × Θ holds. Moreover, no matter how we sequence the remaining batches in the current Λ_i, we ξ_i + ${{\displaystyle \sum }}_{j=1}^d{b}_{ij}$ < d × Θ, k ≤ d ≤ η(i) − 1 must hold, which contradicts the inequality ξ_i + ${{\displaystyle \sum }}_{j=1}^{\eta \left(i\right)-1}{b}_{ij}$ ≥ (η(i) − 1) × Θ, i∈ℕ_g. Thus, there is no problem for executing Statement 7) in Algorithm 1 and the theorem holds. □

It follows from Theorem 2 and the above discussion that, by the ILP and Algorithm 1 together, we can obtain a schedule such that the production rate of M_1i is no less than $\frac{1}{g\beta }$ at any time and the total production rate of Stage 1 is no less than $\frac{1}{\beta }$ at any time in (0, T_min]. Hence, according to Lemma 1, Stage 2 can operate uninterruptedly in (0, T_min].

Note that the ILP together with Algorithm 1 forms a two-step solution method. Figure 4 demonstrates how the two-step solution method is applied to solve a real problem. Specifically, given the batches to be produced, they are partitioned into two parts (i.e., BT1 and BT2) at first. Then, the developed ILP is used to assign the batches to the machines at Stage 1. At last, Algorithm 1 is responsible for sequencing the batches for each machine at Stage 1. In this way, an optimal and feasible schedule is obtained such that Stage 2 can operate uninterruptedly.

Remark 1.

In this work, for the addressed AGMS, we first analyze the properties of the system and establish the existence condition of feasible solutions by presenting Theorems 1–3. Then, based on the conditions, we develop a two-step solution approach that is implemented by the ILP and Algorithm 1 together. Notice that the problem may be solved in an integrated way by using mathematical programming without establishing the solution existence conditions. However, by doing so, many more binary variables are introduced into the model, resulting in greater difficulty in finding a solution. Thus, by the proposed two-step approach, we greatly reduce the computational burden such that we can find a solution even for large-size application problems, which is demonstrated by the experimental results given in the next section.

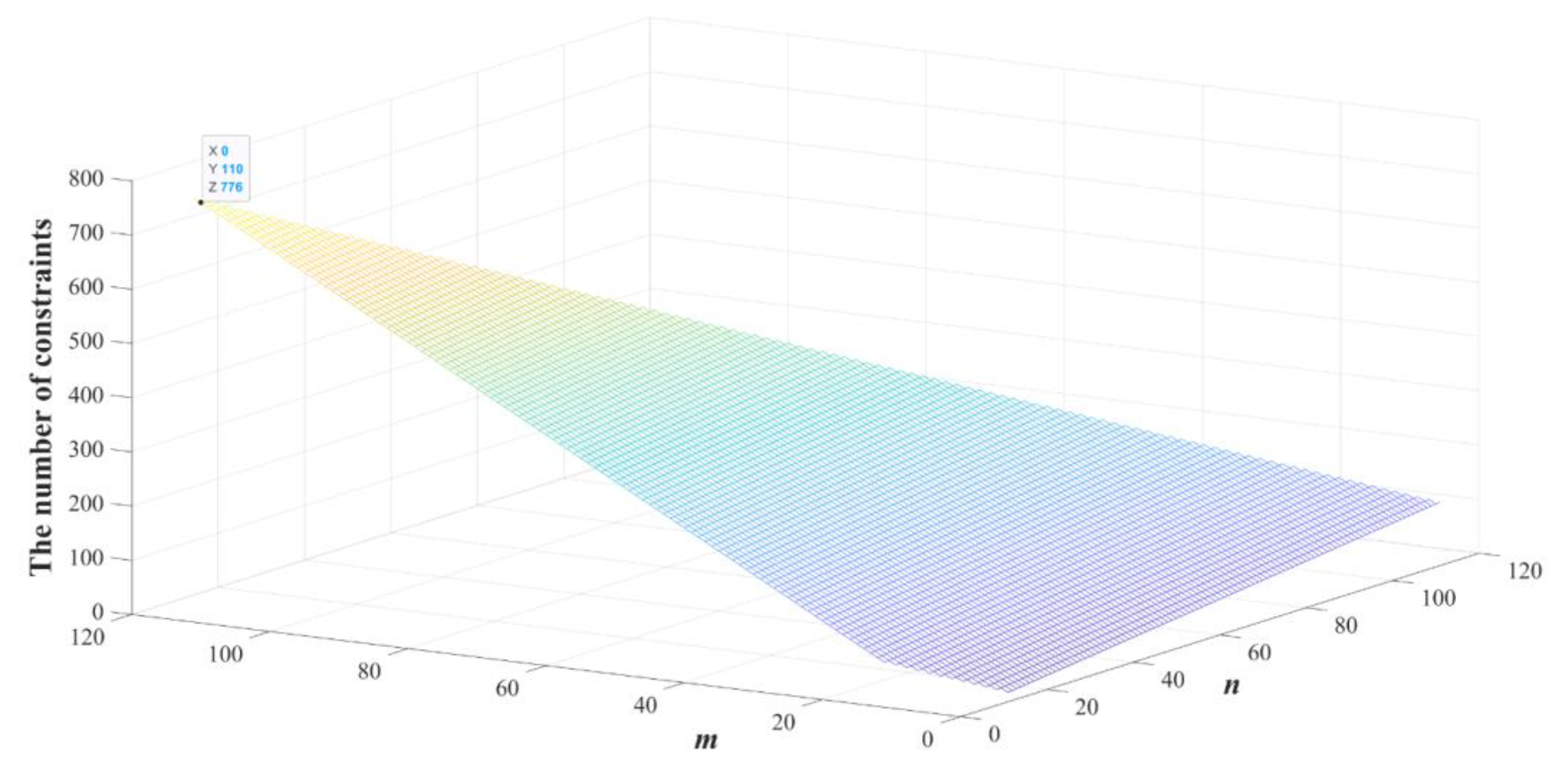
5. Experimental Results

This section uses a real-life AGMS from a company in China as a case problem for validation. As previously described, this AGMS contains five processing steps with the first step and Steps 2–5 forming Stages 1 and 2, respectively; and Stage 2 is the bottleneck and cannot be interrupted. In the experiments, without loss of generality, we just treat Step 2 as the second stage.

For this AGMS, three and five machines are configured for Steps 1 and 2 (g = 3 and h = 5), respectively. It takes 30 s (α = 30 s) for machine M_1i, i ∈ ℕ₃, to complete a product at Step 1, while it takes 55 s (μ = 55 s) for machine M_2i, i ∈ ℕ₅, to complete a product at Step 2. It takes 1800 s (δ = 1800 s) to complete setup for M_1i, i ∈ ℕ₃, while it does not need setup for Step 2. Hence, we obtain $\frac{\alpha }{g}$ = 10 s < β = 11 s and Θ = $\frac{\delta }{g\times \beta -\alpha }$ = 600. Usually, during a scheduling horizon, we have no more than 100 batches for producing and the batch size falls in the interval [50, 1150]. For this case problem, we also have the following property. Let Ω denote the batch size for an arbitrary batch. Then, we have Ω mod 5 = 0 or Ω mod 10 = 0. With batch size in [50, 1150], batches whose size is less than 600 exist for producing. Then, according to the above parameters, numerical experiments are performed and results are presented to validate the proposed approach.

In the experiments, we use CPLEX to solve the ILP presented in this paper on a laptop with twelve Intel(R) Core(TM) i7-10750H CPU @ 2.60 GHz. The time taken for finding a solution depends on how many batches to be scheduled. When we need to schedule a small number of batches, we can obtain an optimal solution by an exact solution way. However, if there are a large number of batches to schedule, an exact solution method is not efficient and often impossible to find an optimal solution in a given limited time. Let ζ be the number of batches for the AGMS to produce. Given a ζ in [11, 30], we use CPLEX to solve 30 cases and we randomly generate the batch size in [50, 1150] for each case. In total, we generate 600 cases to test the developed ILP.

By experiments, for the cases with ζ ∈ [11, 24], optimal solutions can be obtained by the developed ILP for all the cases within 3600 s, while for the cases with ζ ∈ [25, 30], within 3600 s, only parts of these cases can be solved such that optimal solutions are obtained. Experimental results for problems with ζ ∈ [11, 24] and ζ ∈ [25, 30] are summarized in

Table 1. Experimental results for cases with ζ ∈ [11, 24].

ζ	ILP
	Ave. Running Time (s)	Numsolved
11	0.15	30
12	0.19	30
13	0.35	30
14	0.17	30
15	0.20	30
16	1.15	30
17	0.58	30
18	0.90	30
19	22.73	30
20	4.64	30
21	7.02	30
22	122.98	30
23	224.28	30
24	118.15	30

and

Table 2. Experimental results for problems with ζ ∈ [25, 30].

ζ	ILP
	Numsolved	Ave. Running Time (s)	Numunsolved	Running Time (s)
25	27	366.66	3	3600
26	19	298.31	11	3600
27	23	356.15	7	3600
28	15	124.76	15	3600
29	18	257.70	12	3600
30	18	98.07	12	3600

, respectively. Note that Num_solved and Num_unsolved represent the number of cases that the ILP can and cannot solve within 3600 s, respectively. For the unsolved cases with ζ ∈ [25, 30] as shown in Table 2, CPLEX can obtain a solution with a gap between the obtained solution and the lower bound of an optimal one. Such results are summarized in

Table 3. Gaps between current solutions and lower bounds of optimal solutions.

ζ	ILP
	Numunsolved	Average Gap	Maximum Gap
25	3	1.17%	1.7789%
26	11	1.019%	2.2558%
27	7	0.0094%	0.1115%
28	15	0.8524%	5.2856%
29	12	0.3864%	2.6207%
30	12	0.0083%	0.0106%

. From Table 3, we can observe that the gaps are less than 1.5%, implying that CPLEX can obtain very good solutions if optimal solutions cannot be obtained within 3600 s.

For much larger size cases (i.e., ζ > 30), to save time in the experiments, we set a condition to terminate the running of CPLEX as follows by observing the gap between the current solution and a lower bound of an optimal solution. The running of CPLEX terminates if such a gap is less than 1% or this gap cannot be achieved within 3600 s. In this way, we test the proposed approach as follows. Given a ζ > 30, 30 experiments (i.e., 30 cases) are carried out for the ILP. In the experiments, we limit the batches to be produced being no more than 110 that it is less than 100 in practice. Thus, a total of 2400 cases are generated to test the proposed method.

In the experiments, when a case cannot be solved within 3600 s even for achieving a gap of 1%, a gap between the current solution and the lower bound of an optimal one can be obtained when CPLEX terminates according to the termination condition. Thus, given a ζ, 30 gaps for 30 randomly generated cases can be obtained so as to obtain a boxplot for each ζ ∈ [31, 110]. In this way, in total, we have 80 boxplots for different situations with different ζ ∈ [31, 110] and they are shown in Figure 5. From the boxplots, we can intuitively know the central location and dispersion range of the gaps for each situation, and if the gaps obtained by the ILP for different situations are stable, i.e., check if the ILP can obtain good solutions for different situations stably.

It follows from the boxplots that for 91.25% of (or 73) situations (boxplots), the median number is no more than 0.5%. For the rest of the seven situations, the median number is just a little larger than 0.5%. This means that for each situation, the median number of gaps is relatively small. Further, from Figure 5, we can intuitively know that most of the gaps for each situation are no more than 1%. Meanwhile, by observing the shapes of boxplots, the gaps obtained by the ILP are quite small and stable for different situations. Further, we observe that it can solve 96.83% of the cases by the ILP for a gap of 1% within 3600 s, while only 3.17% of the cases (i.e., 76 cases) cannot be solved. For these unsolved cases, we have that the average gap of these cases is 2.1827% and the maximum gap is 4.9416%. Therefore, based on the data analysis for the much larger size problems, good solutions for different situations can be obtained by CPLEX within a reasonable time, i.e., the established approach is efficient and effective in terms of practical applications.

To understand the reason behind the data analysis results, we also try to analyze the ILP. For real application problems from an AGMS in China, the size of the ILP is directly affected by the number of batches to be produced since the number of machines at Step 1 is determined. Then, by adjusting the number of batches in BT1 and BT2, the changes of the number of variables and constraints of the ILP are shown in Figure 6 and Figure 7, respectively. From Figure 6 and Figure 7, we can observe that the number of variables and constraints are linear with the number of batches for producing. This means that for real application problems, as the number of batches increases, the number of variables or constraints increases linearly rather than exponentially. This leads to the fact that even if the size of the problems increases, the ILP is still applicable for obtaining good solutions.

As we have emphasized in the Introduction, if the problem is formulated by a mathematical programming model without the established feasibility conditions, we need to identify all the products for sequencing instead of just identifying the batches, leading to a huge number of binary variables being necessary to form the model. However, by the proposed two-step solution method, to formulate the ILP, we need to identify and allocate the batches only so that there are much fewer binary variables and constraints. Hence, the computational complexity for solving the problem is greatly reduced. Moreover, by Algorithm 1, we can efficiently sequence the batches for producing by a machine. This is why the proposed method can find good solutions within a reasonable time.

In practice, often a mid-term schedule is generated for an AGMS and this is hierarchically carried out in a two-step way, as follows:

(1)

At the first step, according to the customer orders, a relatively rough schedule is developed for a relatively long-time horizon that typically lasts for a month. This scheduling horizon is divided into several uniform slots with each slot lasting for 5–7 days. Then, with the capacity of the AGMS considered, this schedule determines the batches to be produced in each time slot by using simple heuristic algorithms, such that the batches can be produced by the due date.

(2)

At the second step, detailed schedules are generated to realize the rough schedule for each time slot. Such detailed schedules are also called short-term schedules. For each detailed schedule, it needs to schedule all the activities in an AGMS just as performed in this paper such that the process constraints are satisfied and the productivity of the system is maximized to optimize the profit.

In this way, a mid-term schedule is formed by the rough schedule and the detailed schedules together. Such a mid-term schedule is repeatedly updated to govern the operation of an AGMS and this is the routine work for an AGMS. It can be seen from the development of the scheduling method presented in this paper, it is not an easy job to generate a detailed schedule for an AGMS. However, in practice, currently this job is done manually by the production engineers. This is a great burden for such an engineer. Moreover, it is very hard to manually generate a detailed schedule to satisfy process constraints and optimize productivity. The proposed approach in this paper provides an effective way to solve this problem.

6. Conclusions

It is well known that auto models are greatly diversified, leading to a great number of glass products for autos such that automotive glass manufacturing becomes an important part of the automotive industry. An AGMS can be treated as a two-stage flow-shop. In an AGMS, there are strict process constraints: (1) setup with significant time is necessary for the machines at Stage 1; and (2) the machines at the second stage cannot be interrupted. Furthermore, an AGMS operates in customization mode such that there are frequent changeovers for producing different product types. These properties make the scheduling problem of AGMS very challenging. This work investigates this challenging problem by establishing feasible schedule existence conditions. With the conditions, a two-step approach is developed to solve the problem. At the first step, an ILP model is built to allocate the batches to machines at Stage 1. Then, a simple algorithm is given to sequence the batches for each machine. Thanks to the conditions, the size of the ILP is significantly reduced such that good solutions can be obtained in a reasonable time even for large application problems. Extensive experiments are also used to demonstrate the efficiency and effectiveness of the developed approach. For small-size problems, with the number of batches being no more than 24, by CPLEX, ILP can find optimal solutions within 3600 s. For problems with larger sizes, it fails to obtain optimal solutions for all cases within 3600 s. Nevertheless, we set 3600 s as the longest time for obtaining a solution and a gap of 1% for the lower bound of solutions. Then, results show that CPLEX can solve 96.83% cases. Moreover, we can obtain good solutions with the maximum gap 4.9416% for the unsolved cases.

Work in process has important effects on the cost for an AGMS. Hence, it is meaningful to minimize the temporary inventory between the stages. However, we do not take this factor into consideration. In the future, we aim to extend the proposed approach by considering this factor.