Structural Design and Theoretical Analysis of Jetting Spin Type Lotus Root Digging Machine Based on CFD

Abstract

In order to solve the problem that digging lotus roots manually was high in labor intensity, low in efficiency and easy to damage lotus roots, and, in view of the defects of the high cost of existing digging lotus roots equipment and the cumbersome operating process needing a certain experience in technology, a jetting spin type digging lotus root machine is designed. Combined with the mechanism of hydraulic digging lotus root, a rotation pipeline is designed, so as to simplify the whole machine structure and increase the digging width. It takes only manpower or vehicles to push forward to perform digging lotus root work, with simple operation and low manufacturing cost. Pro/Engineer 3D design software and CAD 2D drawing software are used to design key working parts such as rotation pipeline, spray-head, nozzle, etc. In addition, key parameters of nozzle structure are designed. Through validation, the intensity of jet flow impact force produced by the diameter 17 mm nozzle to lotus root surface is 97.22 N, and the pressure is 0.20 MPa, which produces no damage to lotus root. By means of a mechanical analysis method, combined with CFD flow field analysis and fluid dynamics analysis, the rotational speed mathematical model of rotation pipeline in water is established through MATLAB software solving and calculating. In addition, the influence of nozzle structural parameters on rotational speed of rotation pipeline is made clear. By using the kinematic analysis method, the rotational speed mathematical model of rotation pipeline associated with the jetting impact frequency of single point and the time of each impact is established, and from which the restricting factors of the working speed of jetting spin type digging lotus root machine is obtained, so as to improve the efficiency of digging lotus roots machine under the premise of ensuring the digging depth and the quality of lotus roots. Through the CFD flow field analysis and dynamic analysis, the mathematical model of loss power of rotating pipeline is established. Through comprehensive analysis, the mathematical model of working speed associated with digging time and speed of rotary pipe and effective range radius of jet impact for digging lotus root machine is obtained, which provides a theoretical basis for adjustment of working parameters of digging lotus root machine.

1. Introduction

The lotus root of the modern variety grows in the soil at a depth of 0.3–0.4 m, lying flat on the bottom of the mud. There is no obvious distribution pattern in the field. Lotus root farmers prefer to use hand-held water guns to dig lotus roots, which has low cost, low fuel consumption, low failure rate, stable and reliable work, but low efficiency and high labor intensity. Digging lotus roots in winter will cause great damage to the health of lotus root farmers. To sum up, the mechanization of lotus root harvesting in China is still at an advanced stage. In recent years, the main method used by lotus root farmers to dig lotus roots has been improved to manual water gun excavation, that is, hand-held water guns scour the soil above the lotus roots, and then extract the lotus roots from the soil, which is labor-intensive, low in efficiency, and low in mechanization. Because the lotus root grows in deep silt, its growth and location are irregular, the research and development of mining machinery is difficult, the mechanism of mining is not clear, and the basic theory needs in-depth research to realize the mechanized harvesting of lotus roots. To sum up, the mechanization of lotus root harvesting in China is still at an advanced stage. In the initial stage, lotus root digging and harvesting technology and equipment are still in the process of exploration. In 2004, Xia Junfang, Huang Haidong, Zhang Guozhong, and others from the Engineering College of Huazhong Agricultural University developed the 4CWO-3.2 boat-type automatic lotus root digging machine. In 2007, the Engineering College of Nanjing Agricultural University designed the 4SWJ-1 boat-type hydraulic root digging machine, which has a compact structure, reliable operation, stable operation, automatic walking, and stable and accurate lotus root digging operations. In 2010, Meng Fanliang and others in Weishan County, Shandong Province designed a boat-type hydraulic lotus root digging machine. The engine drives the stern shaft screw propeller through the gearbox to form a propulsion device. The hydraulic oil pump and the hydraulic valve control the hydraulic oil cylinder to drive the movement of the lotus digging mechanism. In response to the demand for mechanised lotus root harvesting, and with the aim of effectively improving the efficiency of root digging, reducing the intensity of manual root digging operations and reducing the rate of injury, a jet self-rotating root digger has been designed, drawing on the traditional water gun flushing method of digging roots, with the aim of achieving a larger working width with the digger being propelled only by human power or a vehicles, without the need for a human or institutional swing nozzle. Attaching the machine to a walking vehicles in the root field will also solve the problem of root farmers digging into the water in winter causing physical injury. This paper introduces the structural parameters and working principles of jetting spin type lotus root digging machine, focusing on the operating mechanism of key components, with a view to providing a theoretical basis for subsequent performance testing and promotion of the machine [1,2,3,4,5,6,7,8].

2. Materials and Methods

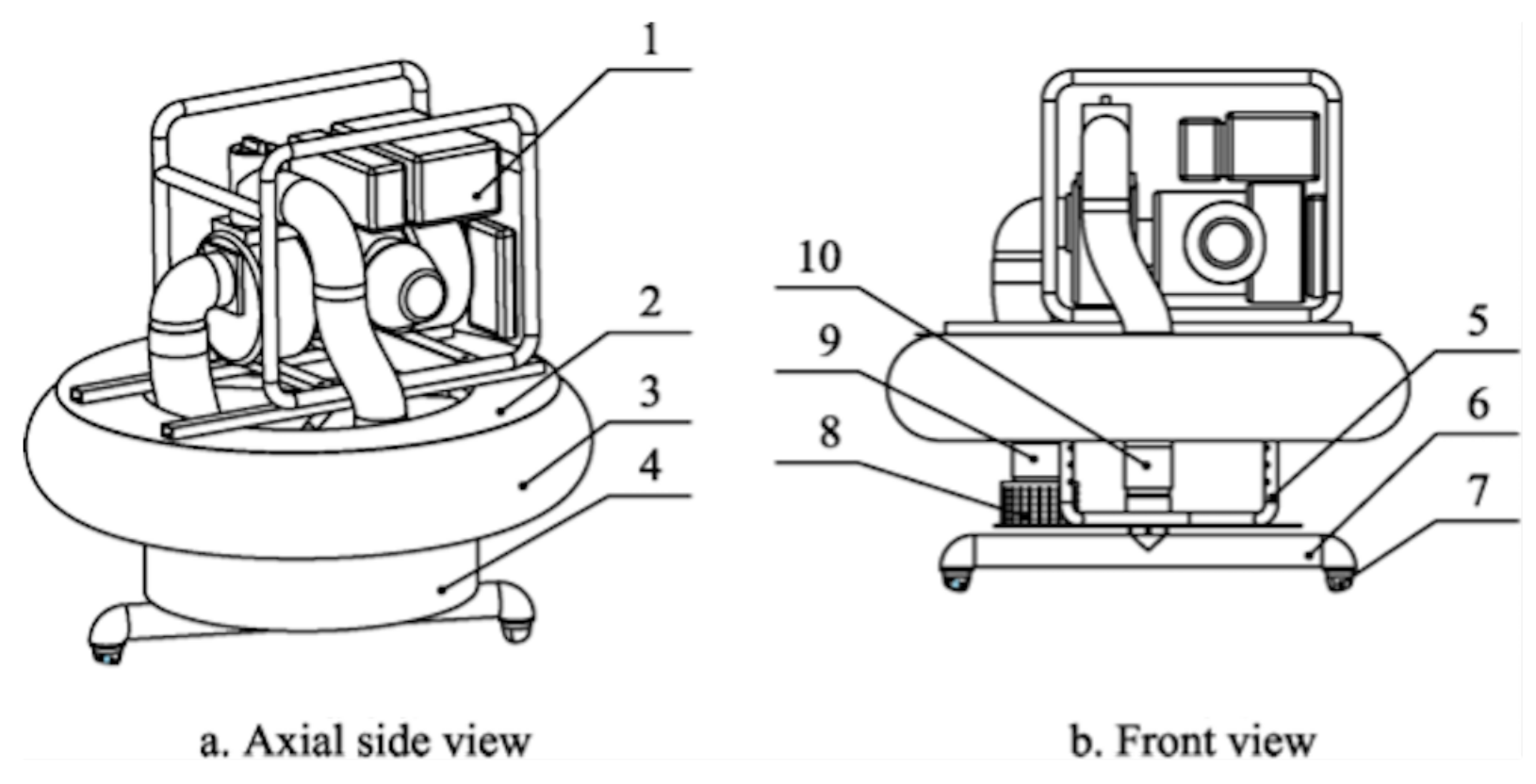
2.1. Machine Structure Design

The jetting spin type lotus root digging machine consists of a water pump, frame, floating ring and rotating pipe. The aim of this design is to reduce the overall weight of the lotus root digging machine and to be able to provide sufficient power for the water jets, so a larger flow rate and lighter weight petrol engine water pump needs to be selected. According to the research, the size of the water pump used for hand-held water gun digging is mostly a 2 inch water pump or a 3 inch water pump. A 3 inch water pump can be used for two people to dig roots at the same time with a water gun, and the power is sufficient to dig out the lotus roots. The 3 inch petrol pump (HONDA WB30XH) was chosen as the power source for the machine with a flow rate of 35 m³/h and a head of 17.3 m. In addition, the inlet diameter of the water pump is 80 mm, and the suction lift is 8 m. The machine was driven by a 4 KW petrol engine with a transistor magnet ignition system. An inflatable rubber ring with an outer diameter 0.9 m, and and inner diameter of 0.53 m was used as the floating ring to change the height of the machine in the water by controlling the amount of inflation. A telescopic bracket is designed inside the frame to adjust the distance between the rotating pipe and the floating ring to change the distance of the nozzle from the mud surface, and the maximum value is 0.43 m. The bottom of the machine is provided with a rotating pipe, which has a sealed rotatable tee connection and can rotate around the center of the outlet pipe orifice. The nozzles at both ends of the pipe eject water, and the reaction force of the water can make the rotating pipe rotate, and the nozzles make a circular movement around the central axis of the outlet pipe orifice. As shown in Figure 1, the machine uses the water jet generated by the pump to impact the soil, and the reaction force of the impacted soil prompts the pipe to rotate, increasing the width of the lotus root harvesting operation without an additional power mechanism, reducing energy consumption, simplifying the structure, and reducing the weight of the machine [9,10,11,12,13,14,15,16,17]. The machine can be slowly pushed forward with the aid of a carrier or human power, making it easy to operate and effectively reducing the operator’s labour intensity [18].

2.2. Rotating Pipe Structure

At the bottom of the machine are nozzles with a rotating circumference diameter of 1000 mm, which is greater than the length of the whole lotus root. A swivel joint is connected in the middle of the rotating pipe to achieve rotational movement relative to the frame, as shown in Figure 2.

The rotating pipe structure as shown in Figure 3 consists of a 1 hanger pipe, 2 three-way pipe, 3 main pipe, 4 bent pipe, and 5 nozzle. The hanger pipe is connected with the swivel joint to realize the rotary function of pipeline sealing. The hanger pipe and the three-way pipe are connected by threads which are tightened in the same direction as the rotation of the swivel joint. The three-way pipe, main pipe, and bent pipe are each threaded and sealed for connection and positioned with spot welds.

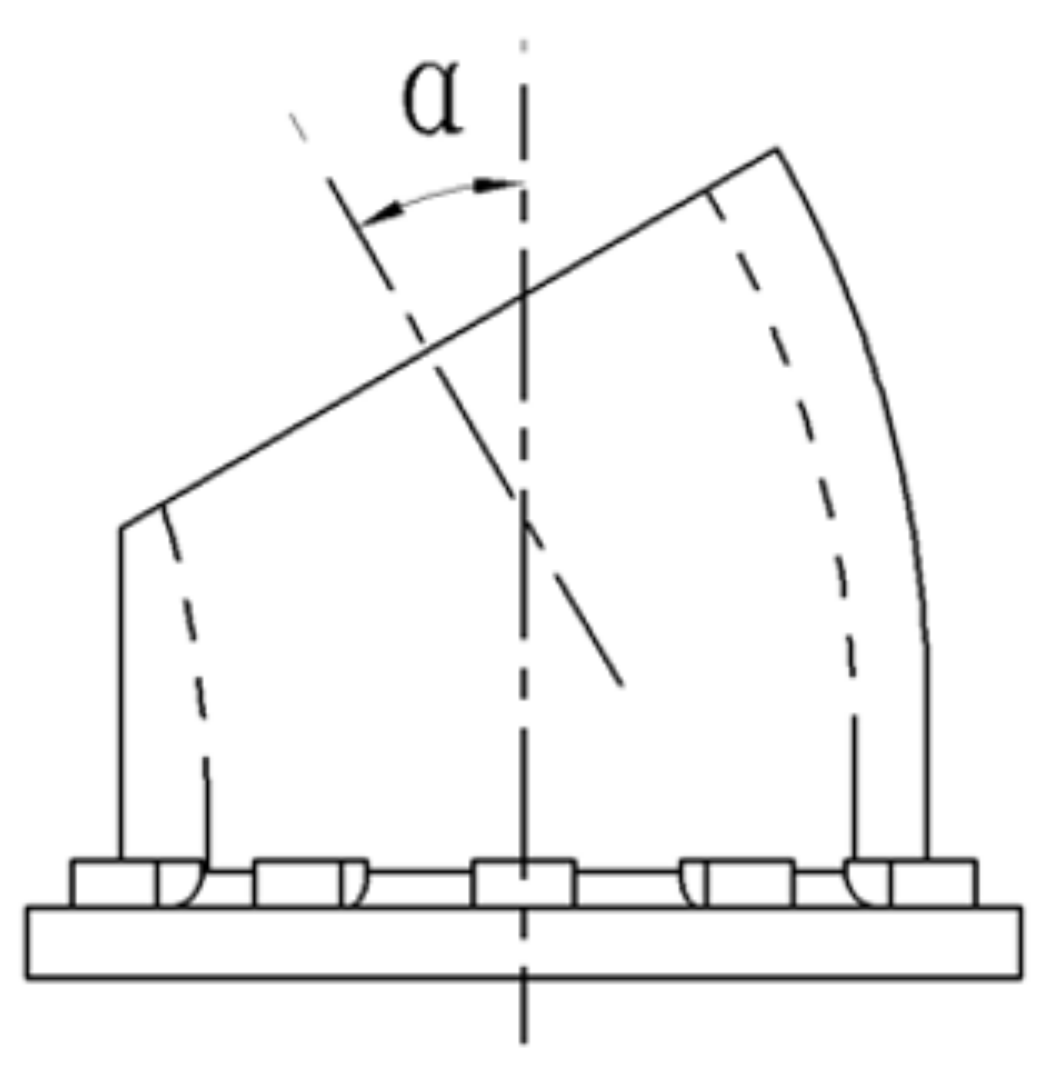
2.3. Nozzle Structure

The nozzle structure is as shown in Figure 4. In order to reduce resistance losses, which was the pipeline flow pressure generated by the nozzle, nozzle structure is designed as a tapering tube structure that the cross-sectional shape and area contract uniformly in transition to the nozzle outlet, maintaining a high flow coefficient and velocity coefficient. In order to analyse the influence of the mounting angle on the rotating line speed, positioning ring, nut, and a separate nozzle are used to adjust the mounting angle. There are 12 positioning slots where the positioning nut contacts the nozzle, and 12 positioning tabs where the nozzle contacts the positioning nut, as shown in Figure 5. Screw the locating ring into the bent pipe of the rotating pipe first, then place the nozzle on the positioning nut and screw it together into the bent pipe of the rotating pipe. By adjusting the position of the positioning ring in the bent pipe and the relative position of the nozzle in the positioning nut, the angle between the nozzle spray direction $F_W$ and the yz plane $\theta$ = 0°, which means that the installation angle $\beta$ = 0°.

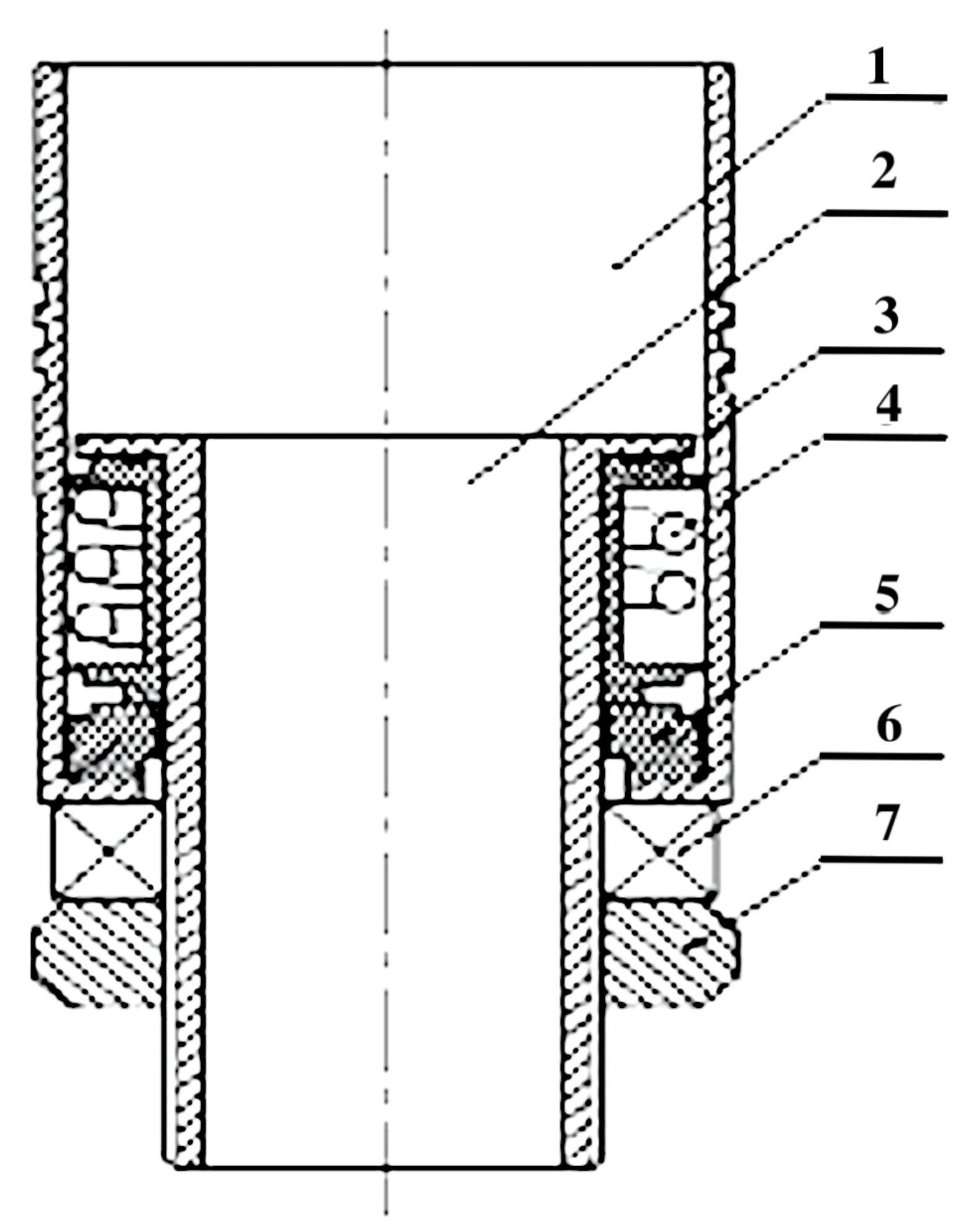
2.4. Swivel Joint Structure

To achieve the function of a rotary seal, the swivel joint is designed as shown in Figure 6. The bottom outer edge of the sleeve of the swivel joint is welded into the center hole of the frame base plate to hold the swivel joint in place. When installing, put the 5 seal, 3 rubber cover, and 2 hanging tube into the 1 casing in order, then put the 6 bearing on the 7 nut, screw the 7 nut into the 2 hanger pipe and tighten it, the tightening direction is the same as the direction of rotation of the rotating pipe. In addition, 4 Spring set in the 3 rubber cover outside, with the 5 seal ring, 3 rubber cover together to form a mechanical 5 seal ring. The contact position between the 3 rubber cover and the 5 seal ring is fixed with a silicon carbide alloy friction ring, respectively, which plays the role of the resistance reduction 5 seal. The three-way pipe of the rotating line is threaded into the hanger pipe, and the thread is tightened in the same direction as the rotating line is working. The water pump discharge pipe is connected to the casing. The mechanical seal has a width of B = 3 mm and an outer diameter of D = 59 mm. The measured static friction angle of the silicon carbide alloy friction ring is 13°, and the static friction coefficient is $\mu$ = 0.23.

3. Key Components Based on Mathematical Model Analysis

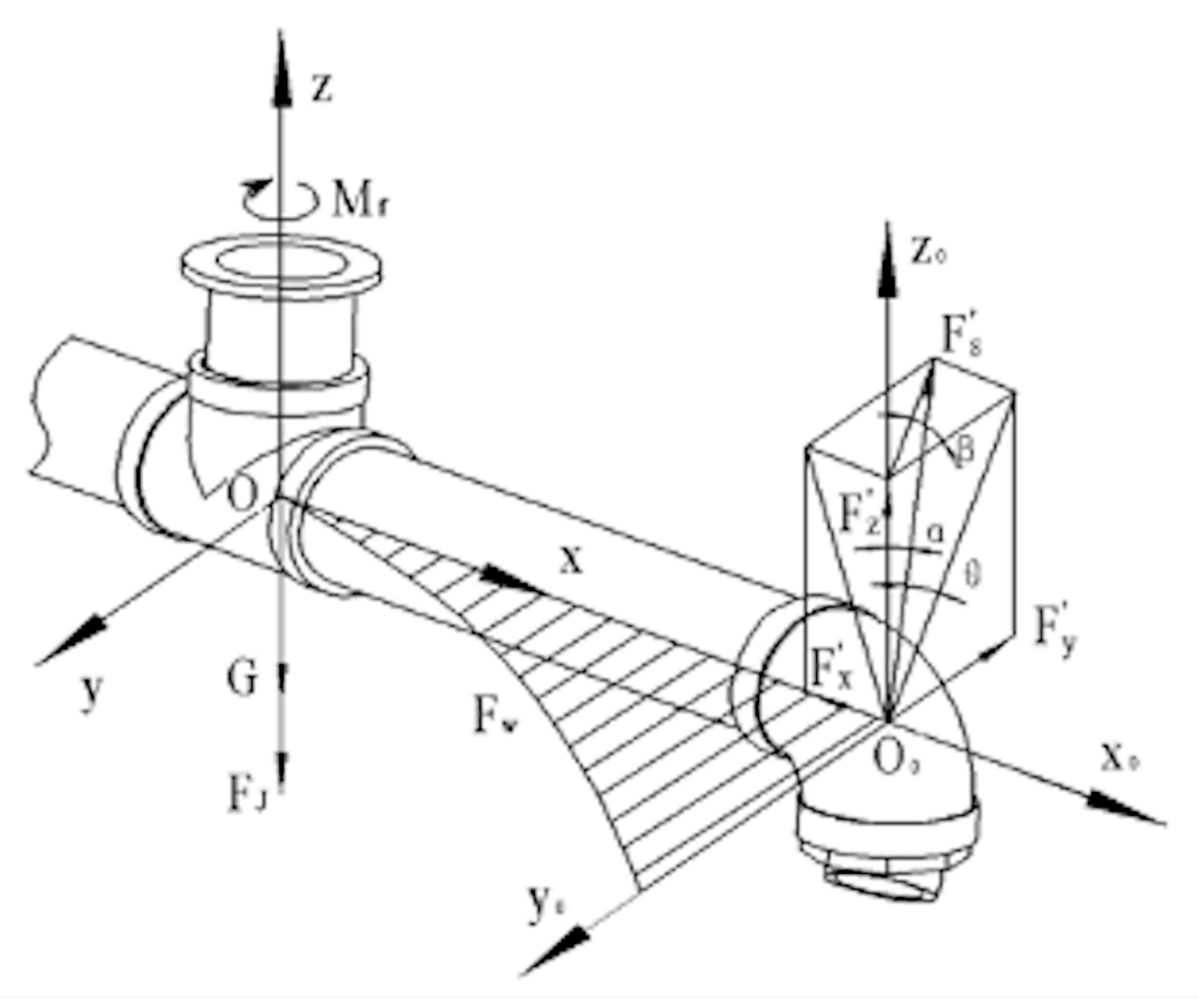
3.1. Force Analysis for Parameter Settings

3.1.1. Nozzle

ProE software was used to draw a model of the rotating pipe. Ignoring the effects of the static water on the nozzle jet, the impact force of jet flow of the nozzle outlet is obtained as shown in Figure 7. $F_S$ is the jet impact force of the nozzle outlet jet, which is decomposed into three components $F_x$, $F_y$, $F_z$ in the coordinate system in Figure 7 according to the direction of the three axes. $\alpha$ is the jet angle, and $\beta$ is the nozzle installation angle.

The jet force at the nozzle outlet is decomposed as:

$$\{\begin{array}{c}{F}_x=F_{S}sin\theta ,\\ F_y=F_{S}sin\alpha cos\beta ,\\ F_z=F_{S}cos\alpha \end{array}$$

(1)

where $F_S$ is the jet impact force. $F_x$, $F_y$, and $F_z$ are the decomposition of the force of $F_S$, respectively.

3.1.2. Rotating Pipe

Due to the small structure of the nozzle, fixed by the thread in the bent pipe inside the rotating pipe, the distance from the nozzle outlet to the inside of the bent pipe is much smaller than the distance from the nozzle to the rotation axis of the rotating pipe, it can be approximated as if the reaction force of the jet impact on the pipe is inside the bent pipe, as shown in Figure 8. When the rotating pipe is working, due to the slow forward speed of the machine, ignore the influence of the resistance of water on the pipe during the forward process, Approximately, the pipe is considered to be rotating at a constant speed around the z-axis with respect to the coordinate system ‘O, X, Y, Z’. The mechanical equilibrium equation of the pipe is:

$$\{\begin{array}{c}\hfill \sum F_x=0,\\ \hfill \sum F_y=0,\\ \hfill \sum F_z=0⟹F_{S}cos\alpha -G-F_J=0\\ \hfill \sum M_z=0⟹l{F}_y-M_w-M_f=0\end{array}$$

(2)

where $F_J$ is the support force of the frame on the rotating pipe, $M_w$ is the resistance dipole moment of the water on the pipe during the rotation of the pipe, and G is the total gravity of the pipe and the water in the pipe. $M_f$ is the torque generated by the frictional resistance of the silicon carbide alloy friction ring of the mechanical seal. l is the distance between the centers of the two nozzles.

In the X-axis direction, the rotating pipe is subjected to the component of the jet reaction force on the X-axis and to the centrifugal force generated by rotation around the axis of rotation, both of which occur in pairs and in opposite directions. In the Y-axis direction, the rotating pipe is subject to the component of the jet reaction force on the Y-axis, the resistance of the water to rotation, and the frictional resistance of the silicon carbide alloy friction ring of the mechanical seal ring inside the swivel joint, and all are force coupled. Both ends of the rotating pipe are subject to the component of the jet reaction force on the Z-axis, the gravity of the rotating pipe and the water in the pipeline, and the support force of the frame on the rotating pipe. The force dipole moment around the Z-axis includes the force dipole moment generated by the component of the reaction force of the jet on the Y-axis, the force dipole moment formed by the damping of the water during the rotation of the rotating pipe, and the torque generated by the frictional resistance of the silicon carbide alloy friction ring of the mechanical seal in the swivel joint.

3.1.3. Friction Ring Torque

The width of the mechanical seal silicon carbide alloy friction ring is B = 3 mm, the outer diameter of the ring is D = 59 mm, the area of the ring $S_h$ = 5.28 × ${10}^{-4}$ m², the static friction angle of the silicon carbide alloy friction ring is 13° and the static friction coefficient is $\mu$ = 0.23. The micro-element area of the friction ring is:

$$\mathit{dA}=\mathit{rdrd}\theta$$

(3)

The torque generated by the friction ring in Equation (5) is:

$$M_f=\int {\int }_{Dh}\mu \frac{F_m}{S_h}{r}^{2}drd\theta {\int }_0^{2\pi }d\theta {\int }_{R_d}^{R_D}\mu \frac{F_m}{S_h}{r}^{2}dr$$

(4)

where $F_m$ is the friction ring preload force, $R_d$ is the inner radius of the friction ring, and $R_D$ is the outer radius of the friction ring. The outer diameter of the compression spring inside the mechanical seal is 70 mm, the wire diameter $d_x$ = 4 mm, the effective number of turns n = 1.5, the shear modulus of the carbon spring steel wire $G_q$ = 78.5 × 103 MPa, with reference to the national standard GB/T 23935-2009 cylindrical spiral spring design spring stiffness coefficient, is:

$$k=\frac{G_q{d}_x^4}{8D_m^{3}n}$$

(5)

where k is the spring stiffness factor, $D_m$ is the spring mid-diameter, and $d_x$ is the spring wire diameterm. The spring stiffness coefficient k = 5.83 N-mm can be calculated from Equation (5). During the installation of the rotating pipe, the nut is screwed into the hanger pipe against the bearing and then screwed $inh$ = 5 mm; at this time, the friction ring preload is equal to the spring force, and the expression is:

$$F_m=k\Delta h$$

(6)

The friction ring preload force $F_m$ = 29.15 N is calculated from Equation (6). The torque of the friction ring on the rotating pipe $M_f$ = 1.9 × ${10}^{-4}$ N·m is obtained by substituting the above calculated parameters into Equation (4).

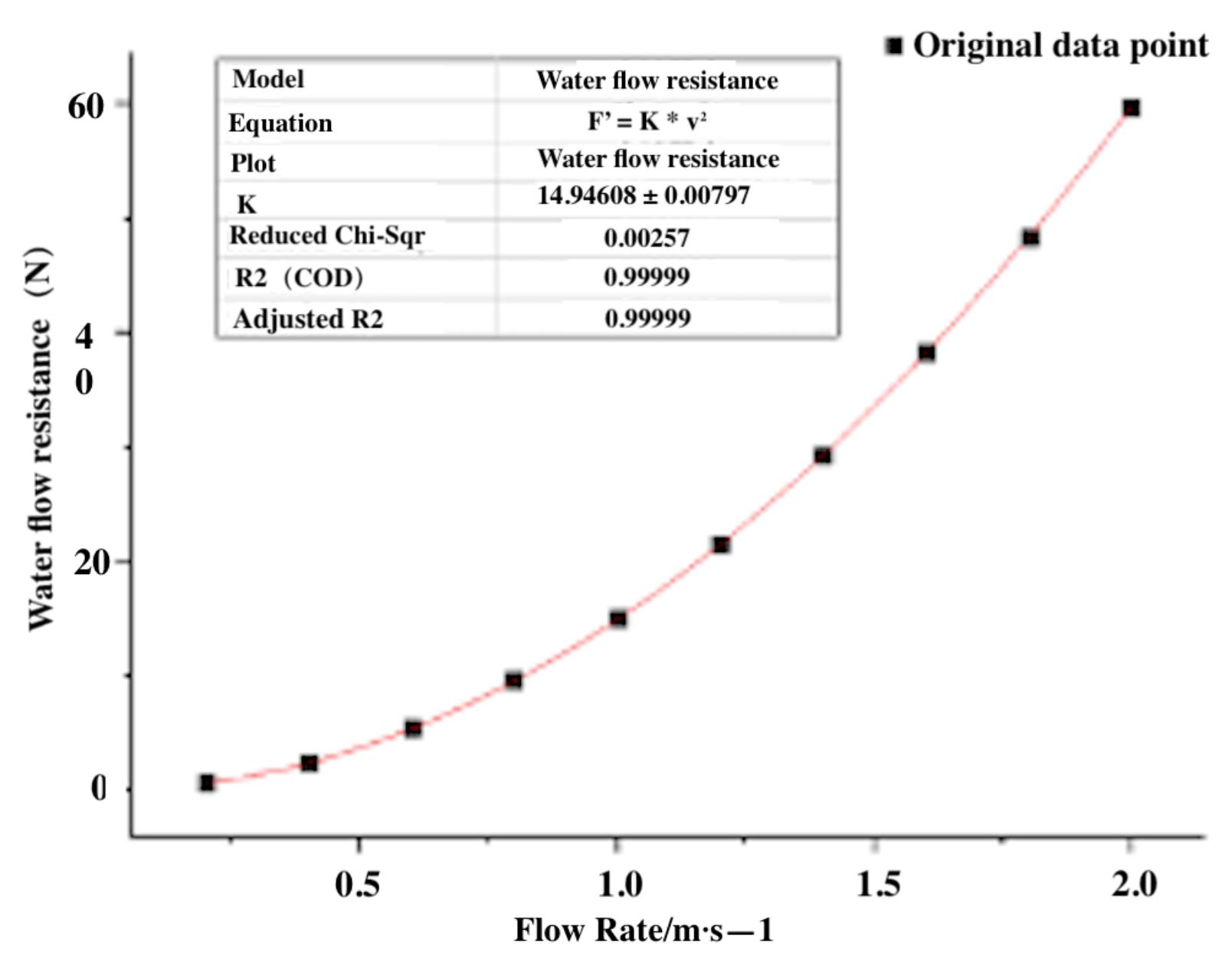
3.1.4. Moment of Resistance of Water Flow

The Fourier model divides the resistance to the motion of a submarine into two parts, one of which is the frictional resistance related to the Reynolds number and the other is the residual resistance related to the Fourier number. As the pipeline cross-section is circular, the contact area with the water in the tangential direction of movement is much smaller than the contact area of the submarine streamline body, the frictional resistance with the water and turbulent disturbance resistance can be ignored, and the water flow resistance is simplified and approximated as air resistance formula can be obtained:

$$F_w^{{}^{″}}=\frac{1}{2}C{\rho }_{w}S{v}^2$$

(7)

where C is the coefficient of resistance of the water. ${\rho }_w$ is the density of water. S is the maximum cross-sectional area of the pipeline perpendicular to the tangential direction of movement. v is the relative velocity of the pipeline and the water. The resistance coefficient is usually an experimental value, and the shape of the windward side, surface roughness. Material properties and other factors, from Formula (7), can be derived from the resistance of water and the square of the relative speed is proportional to the relationship. As the density of water and the maximum cross-sectional area of the pipeline for a fixed value can be incorporated into the resistance coefficient to obtain the rotating pipe in the submerged rotation of the resistance calculation formula for:

$$F_w=K{v}^2$$

(8)

where K is the rotating line resistance coefficient.

In order to analyze the force of the rotating pipeline during its rotation, it is necessary to obtain a mathematical model of the change of the resistance of water to the pipeline with the movement speed. For the convenience of simulation analysis, the rotating pipeline is assumed to be stationary, and the water flow impacts the pipeline perpendicular to the length of the pipeline. CFD simulations are used to analyze the resistance of a half-section pipe at different water flow velocities, when the rotating pipe is at rest, and the water flow is perpendicular to the length of the pipe. Use ProE to model the pipeline. Then, using a mixture of hexahedral and tetrahedral meshing, as shown in Figure 9.

First, the number of grids is 32,634. Then, because there is no time step for the steady-state solution, the k-epsilon standard model is selected in the Viscous Model setting, and the iteration residual convergence standard is set to 0.0001. The number of steps is 1000. In addition, the boundary conditions set the inlet velocity of the flow field to take the jet velocity in

Table 1. Detailed boundary conditions and input parameters.

Flow Rate	Water Flow Resistance
0.2	0.61
0.4	2.42
0.6	5.43
0.8	9.63
1.0	15.01
1.2	21.58
1.4	29.34
1.6	38.28
1.8	48.41
2.0	59.71

, respectively, and the maximum number of iteration steps is 1000. The number of iteration steps is 1000 and the flow field inlet velocity is set as shown in Table 1. The dynamic pressure distribution of the fluid around the pipeline during the simulation is shown in Figure 10, from which it can been seen that the dynamic pressure increases significantly in the inner area of the bent pipe due to the gathering of water and the increase in flow velocity. The dynamic pressure changes to a static pressure against the pipeline when it impacts the pipeline area, and the dynamic pressure becomes smaller. When the water flows over the surface of the pipe, the curved surface effect increases the flow velocity and the dynamic pressure, which then decreases due to energy loss.

The total pressure on the surface of the pipeline corresponding to the flow rate is obtained by running the simulation for each of the 10 flow rates. The pressure is the resistance of the pipeline to water flow, as shown in Table 1.

A graph of the resistance to flow versus flow velocity is shown in Figure 11. From the graph, it can be seen that the relationship between water flow resistance and flow velocity is approximated as a quadratic function. A quadratic regression mathematical model using Origin 2017 is shown in Figure 11. The mathematical model has a correlation coefficient of $R^2$ = 0.999, indicating that we can predict the water flow resistance very well by the water flow velocity.

The coefficient of resistance to the linear motion of the rotating pipe is K’ = 14.95 kg/m. From the figure, the model can be obtained as follows: the total resistance of the section as a function of the velocity of the water flow is:

$$F_w^{{}^{\prime }}=14.95v^2$$

(9)

where $F_w^{{}^{\prime }}$ is the resistance of the water to the linear motion of the half-section pipeline. v is the velocity of the water flow. Approximately, the resistance at each point along the length of the rotating pipe is the same during linear motion, and the total length of the pipe is l; then, the resistance per unit length is equal to 2$F_w^{{}^{\prime }}$/l. During the rotation of the rotating pipe, as the linear velocity v at each point along the length of the pipe is proportional to the distance r from the point to the center of rotation, the resistance micro-element is (2$F_w^{{}^{\prime }}$/l)$dr$, and the moment micro-element is (4$F_w^{{}^{\prime }}$/l)rdr. The linear velocity v = wr, the angular velocity w = $\pi$n/30, n is the rotational speed, and l = 1 m; then, the water flow Moment of resistance during the rotation of the whole rotating pipe is:

$$M_w={\int }_0^{0.5}\frac{K^{{}^{\prime }}{\pi }^2{n}^2}{225}{r}^{3}dr=\frac{K^{{}^{\prime }}{\pi }^2{n}^2}{\mathrm{14,400}}$$

(10)

Substituting K’ = 14.95 kg/m into Equation (10) gives the relationship between moment of resistance of the water flow during rotation of the rotating pipe and the rotational speed as:

$$M_w=0.0102n^2$$

(11)

where n is the speed of the rotating pipe.

3.2. Parametric Analysis Based on Kinematic Analysis

3.2.1. Rotating Pipe Speed

The expression for the component of the reaction force of the jet on the pipe on the y-axis is:

$$F_y^{{}^{\prime }}=F_y=F_{S}sin\alpha cos\beta$$

(12)

The l = 1 m, Formulas (11), (12) and (22) into the fourth equilibrium equation in Formula (2) to obtain the rotating pipe working speed n and pipe nozzle flow $Q_S$, nozzle diameter ds, nozzle jet angle $\alpha$, nozzle installation angle $\beta$ between the mathematical model for:

$$n=\frac{353.3Q_s}{d}\sqrt{sin\alpha cos\beta }$$

(13)

$Q_S$ = 17.5 m³/h, substituted into the Formula (13) to obtain this prototype rotating line working speed n and nozzle diameter ds, nozzle jet angle $\alpha$, nozzle installation angle $\beta$ between the mathematical model for:

$$n=\frac{1.7}{d}\sqrt{sin\alpha cos\beta }$$

(14)

Within the range of values of each parameter, MATLAB is used to plot the spatial four-dimensional mathematical model of the rotating line speed n with the nozzle jet angle $\alpha$, nozzle installation angle $\beta$, and nozzle diameter d, as shown in Figure 12, where the x, y, and z axes represent $\alpha$, $\beta$, and d and the color depth indicates the value of n. The higher speed in the yellow area of the graph shows that the speed increases as the jet angle increases, the installation angle decreases and the nozzle diameter decreases, which is consistent with the function of Equation (14).

The MATLAB program code can be adjusted to change the position of the slices in the diagram to obtain the speed variation law near the corresponding points of the three independent variables, as shown in Figure 13. When a rotary pipe needs to be designed to work at a certain speed, the program can be used to adjust the position of the slices in the diagram to find the range of values of the corresponding three factors at the desired speed, i.e., the process of solving for the three independent variables through the known dependent variable.

3.2.2. Nozzle

The velocity of the nozzle movement during machine operation is decomposed in the relative coordinate system as shown in Figure 14. Where $v_p$ is the linear velocity of the nozzle around the center of rotation, $v_{px}$ and $v_{py}$ are the decomposition of the velocity of $v_p$ on the x- and y-axes, and $v_J$ is the forward velocity of the machine.

The equation of the nozzle trajectory is:

$$\left\{\begin{array}{c}\hfill x=\frac{1}{2}coswt+v_{j}t,\\ \hfill y=\frac{1}{2coswt},\end{array}\right.$$

(15)

From Figure 12, when the nozzle diameter is 17 mm and the jet angle is 45°, the speed is 85 r/min. When the forward speed of the machine is 0.1 m/s, the equation of the nozzle trajectory at this parameter can be obtained by substituting in Equation (18):

$$\left\{\begin{array}{c}\hfill x=0.5sin8.9t+0.1t,\\ \hfill y=0.5cos8.9t,\end{array}\right.$$

(16)

Using MATLAB to draw the nozzle trajectory as shown in Figure 15, where the blue curve and red curve represent the two nozzle trajectories, respectively. From the figure, it can be seen that, on the Y-axis 0 scale, near the horizontal line nozzle trajectory, density is lower; in the 0.5 scale near the horizontal line nozzle trajectory, density is higher, indicating that the root digger travel width edge area of the digging efficiency will be higher than the root digger operation trajectory line area. The area where the root digging operation was completed was cut by the cross-impact of the jets, or by opposite parallel cuts. When the rotating pipe speed increases, the continuous impact time at the same soil location decreases, the jet impact frequency increases, and the discontinuous jet impact facilitates the discharge of broken soil from the crushing pit [19], thus improving the efficiency of the excavation depth. 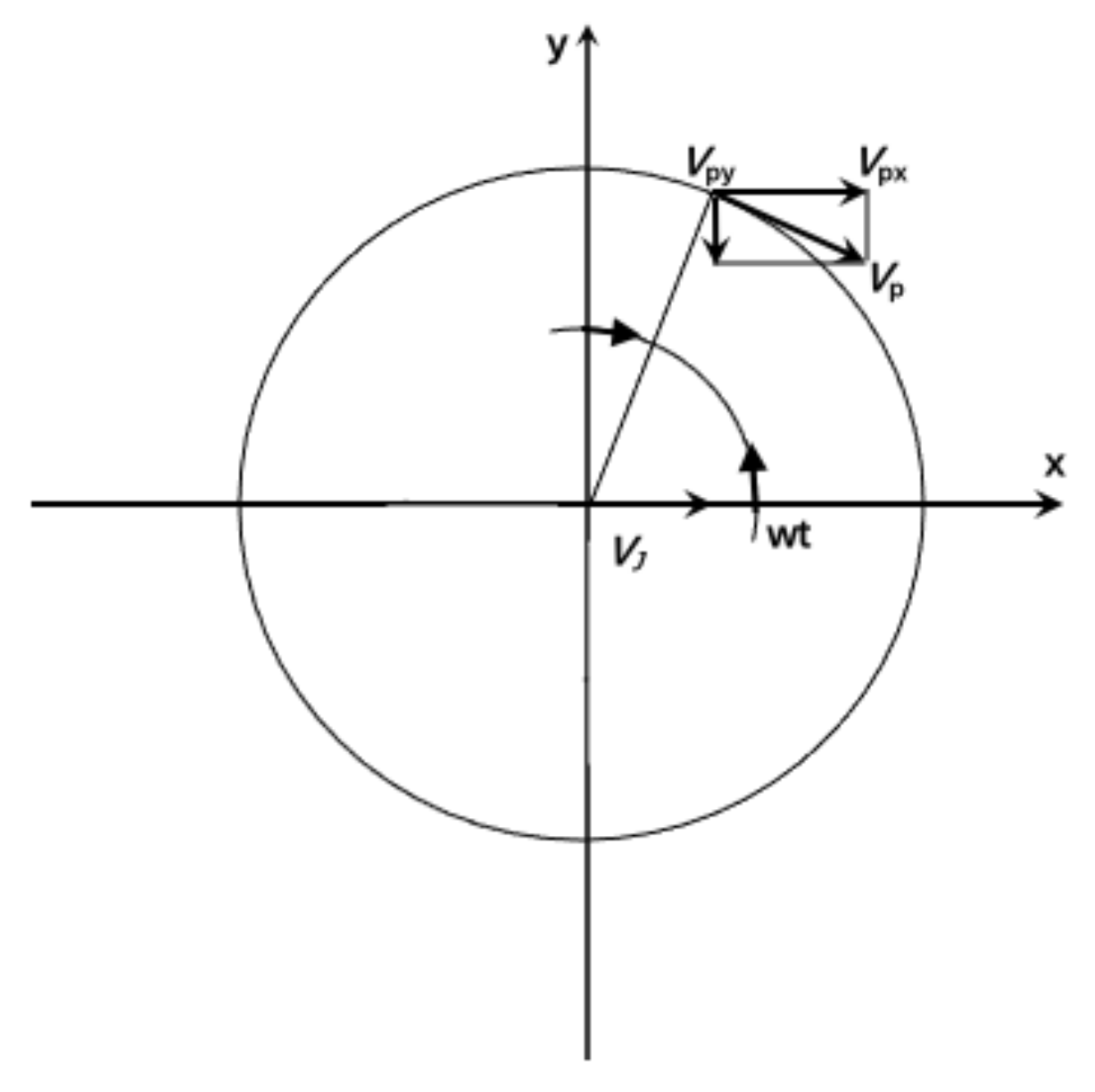Although the jet angle is positively correlated with the rotating pipe speed, increasing the jet angle will reduce the impact pressure of the jet on the soil, which is not conducive to increasing the excavation depth, so the jet angle should not be too large.

3.2.3. Minimum Number of Impacts

The maximum spacing between adjacent blue trajectories and red trajectories in Figure 15 is:

$$\Delta b=\frac{30v_J}{n}$$

(17)

where $v_J$ is the forward speed of the lotus digging machine, and the working speed of the rotating pipeline is n. Based on the trajectory of the nozzle, we obtained the maximum distance between the adjacent blue trajectory and the red trajectory. The radius of the effective range of the jet impact is R. The total minimum number of impacts of the jet on the same point that can be impacted within the excavation width is:

$$c=\frac{4R}{\Delta b}+2$$

(18)

where c is the minimum number of impacts of the jet on the same point that it can impact, taking only the integer part of the result of the calculation, and subtracting 1 from the result for less than even numbers. R is the radius of the effective range of the jet impact. $\Delta$b is the maximum distance between the blue trajectory and the red trajectory. Substituting Equation (17) into Equation (18) gives the relationship between the total minimum number of shocks, the machine’s forward speed and the rotating line speed as:

$$c=\frac{R_n}{7.5v_J}+2$$

(19)

3.2.4. Single Impact Time

From the trajectory of the nozzle in Figure 15, it can be obtained that the minimum time for a single impact of the jet on any point on the trajectory is:

$$T=\frac{120R}{nl\pi }$$

(20)

where T is the single impact time (s); l is the diameter of the rotating pipeline (m); and n is the rotational speed of the rotating pipeline (r/min).

3.3. Kinetic Analysis for Parameter Optimization

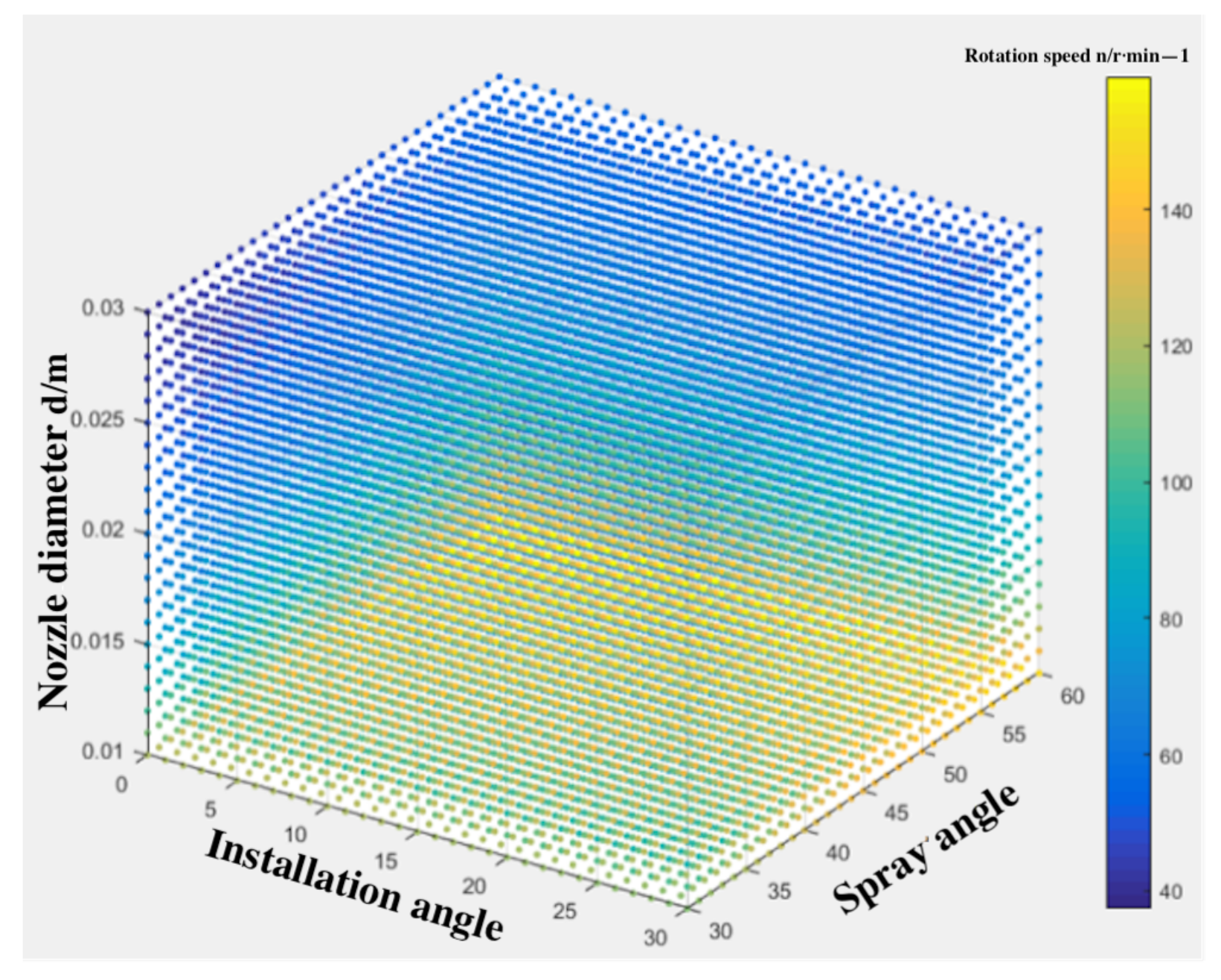
3.3.1. Nozzle Diameter and Jet Angle

With the maximum throttle gear of the water pump and the dredge without the nozzle installed, the ultrasonic flow meter MIK-2000H was used to measure the average flow rate of 35.26 m³/h, which is approximate to the rated flow rate. In addition, the simplicity structure of machine pipeline can ignore the influence of the pipeline on the flow rate. Therefore, approximate operating flow rate of 35 m³/h in maximum throttle gear. According to the relevant literature [19], it is known that the jet velocity is 20 m/s and the jet angle $\alpha$ = 45°. As shown in Figure 16, the excavation depth can reach 400 mm. Since there is a nozzle at each end of the rotating pipe, according to the relationship between flow rate and pipe diameter, the approximate relationship between the jet velocity of a single nozzle and its diameter is:

$$\mathit{d}=\sqrt{\frac{2Q}{V\pi }}$$

(21)

where d for the nozzle diameter; V for the nozzle jet water flow rate; and Q for the pump working flow. According to Formula (21), the nozzle diameter is 17 mm when the jet velocity of 20 m/s.

According to fluid dynamics, the fluid from the nozzle when the impact pressure, that is, the jet, has the momentum per unit time $\rho$Qv, expressed as:

$$F_s=\rho Q_s{v}_s$$

(22)

where F is the jet impact pressure, $\rho$ is the density of the water, $Q_s$ is the nozzle outlet flow rate, $v_s$ is the jet velocity, and the impact pressure of the water jet is the dynamic pressure of the jet, expressed as:

$$P_0=\frac{1}{2}\rho v^2$$

(23)

where $P_0$ is the injection flow pressure, $\rho$ is the fluid density, and v is the fluid flow velocity. When $Q_s$ = 17.5 m³/h, v = 20 m/s, $\rho$ = 1000 kg/m³, from Equations (22) and (23), the impact pressure and impact pressure of 17 mm nozzle outlet are 97.22 N and 0.20 MPa. The jet impact pressure and impact pressure generated by the nozzle are less than those tested in accordance with the relevant [20,21], which was 179 N and 2.32 MPa.

The faster the rotating pipe moves underwater, the greater the resistance, and the greater the energy lost per unit distance, the rotating speed becomes too large to lose the energy of the jet impacting the soil on the resistance of the water, so the rotating speed of the rotating pipe is not the greater, the better. As the friction ring resistance is low, ignore the energy consumed on the friction ring. Approximately, the resistance at each point along the length of the rotating pipe is the same, and the total length of the pipeline is l, and the resistance per unit length is equal to 2$F_w^{{}^{\prime }}$/l. During the rotation of the rotating pipe, as the linear velocity v at each point along the length of the pipeline is proportional to the distance r from the point to the center of rotation, the resistance micro-element is (2$F_w^{{}^{\prime }}$/l)$dr$, the energy micro-element of the jet consumed in one rotation of the rotating pipeline is (4$\pi r{F}_w^{{}^{\prime }}$/l)$dr$, the linear velocity v = $wr$, the angular velocity w = $\pi$n/30, and n is the rotational speed. According to the calculation method of Formula (10), the energy of the jet consumed in one rotation of the whole rotating pipe is:

$$W_w=2{\int }_0^{0.5}\frac{K^{{}^{\prime }}{\pi }^3{n}^2}{225}{r}^{3}dr=\frac{K^{{}^{\prime }}{\pi }^3{n}^2}{7200}$$

(24)

where $W_w$ is the energy consumed by the jet in one revolution of the rotating pipe. Substituting K’ = 14.95 kg/m into Equation (24), the relationship between the energy consumed by the jet and the rotational speed for one rotation of the rotating pipe is:

$$W_W=0.064n^2$$

(25)

where n is the rotational speed of the rotating pipe. From Formula (25), finding the power loss of the pipeline in the water is as follows:

$$P_W=1.07\times {10}^{-6}{n}^3$$

(26)

where $P_w$ is the power loss in the rotation of the rotating pipe. Plot the power loss during the rotation of the rotating pipe as a function of the rotational speed, as shown in Figure 17.

The energy consumption in the working process of the jetting spin type lotus root digging machine is mainly used for impacting the soil. According to the theorem of conservation of energy, when more energy is consumed by the resistance of water, the depth of the jet digging soil in the unit time will be reduced, which is not conducive to the improvement of digging depth and digging efficiency. When the speed is 100 r/min, the impact frequency is calculated to be 3.33 Hz, but the power consumption is 1.07 kw, and the maximum power of the pump is only 4 kw. The adjustable range of the impact frequency is small, and the positive effect of its adjustment on the digging efficiency is small compared to the negative effect of energy loss, and the effect of the impact frequency on the digging effect caused by the rotating pipe can be ignored when considering energy loss.

3.3.2. Optimal Parameter Analysis

The mathematical model obtained from the above mechanical, kinematic, and kinetic analyses is summarized and combined with Equations (14), (19), and (20) to obtain:

$$\left\{\begin{array}{c}\hfill n=\frac{1.7}{d}\sqrt{sin\alpha cos\beta },\\ \hfill c=\frac{R_n}{7.5v_J}+2,\\ \hfill T=\frac{120R}{nl\pi }\end{array}\right.$$

(27)

When the nozzle diameter of 17 mm, the jet angle of 45°, and Formula (27) of a formula is rewritten as:

$$n=84.1\sqrt{cos\beta }$$

(28)

From Formula (28), it can be seen that the larger the nozzle installation angle, the smaller the speed of the pipeline. According to the geometric relationship, it can be seen that the installation angle has a greater impact on the width of the excavation, and the need for the optimal nozzle installation angle through the prototype test can be derived from the optimal speed of the pipeline through Formula (28), and through Formula (26) to determine whether the power consumption is too large. When l = 1 m, the second and third equations of (27) can be combined to obtain the minimum impact time at the same point as:

$$t=Tc=\frac{5.1R^2}{v_J}+\frac{76.4R}{n}$$

(29)

where $v_J$ is the forward speed of the machine and t is the time taken to excavate the depth of the soil at a point location. The optimal rotational speed n of the pipeline, the time t of the depth required to dig a point position of the soil, and the radius R of the effective range of the jet impact can be derived through experiment. From Equation (29), the optimal forward speed $v_J$ of the jetting spin type lotus root digging machine, which can determine the working and structural parameters of the dredger and obtain the power consumed by the water flow, can be obtained. The field pre-test has verified the reliability of the model, and it can carry out the excavation of lotus roots. However, it is still necessary to conduct bench tests on the factors that affect the excavation depth, excavation width and quality of digging lotus roots to find the optimal parameter combination, and improve the jet flow and the digging efficiency of the rotary lotus root digging machine [18].

4. Discussion and Conclusions

This paper provides a detailed description of the structural design of the jetting spin type lotus root digging machine. The parameter levels of the key component nozzles are set according to the factors influencing the depth of the harvested lotus roots and the quality of the harvest, and the jet impact force is calibrated to confirm that no damage is caused to the lotus roots at the chosen level. As a conservative approximation is used for the part of the theory that cannot be explained in this paper, the working and structural parameters derived according to this theory are conservative values, which can provide directions for setting the influencing factors and level arrangements for the field trials of the prototype, so as to obtain the optimal working and structural parameters of the jetting spin type lotus root digging machine.

• This paper provides a detailed description of the structural design of the lotus root digger and explains its operating principles.
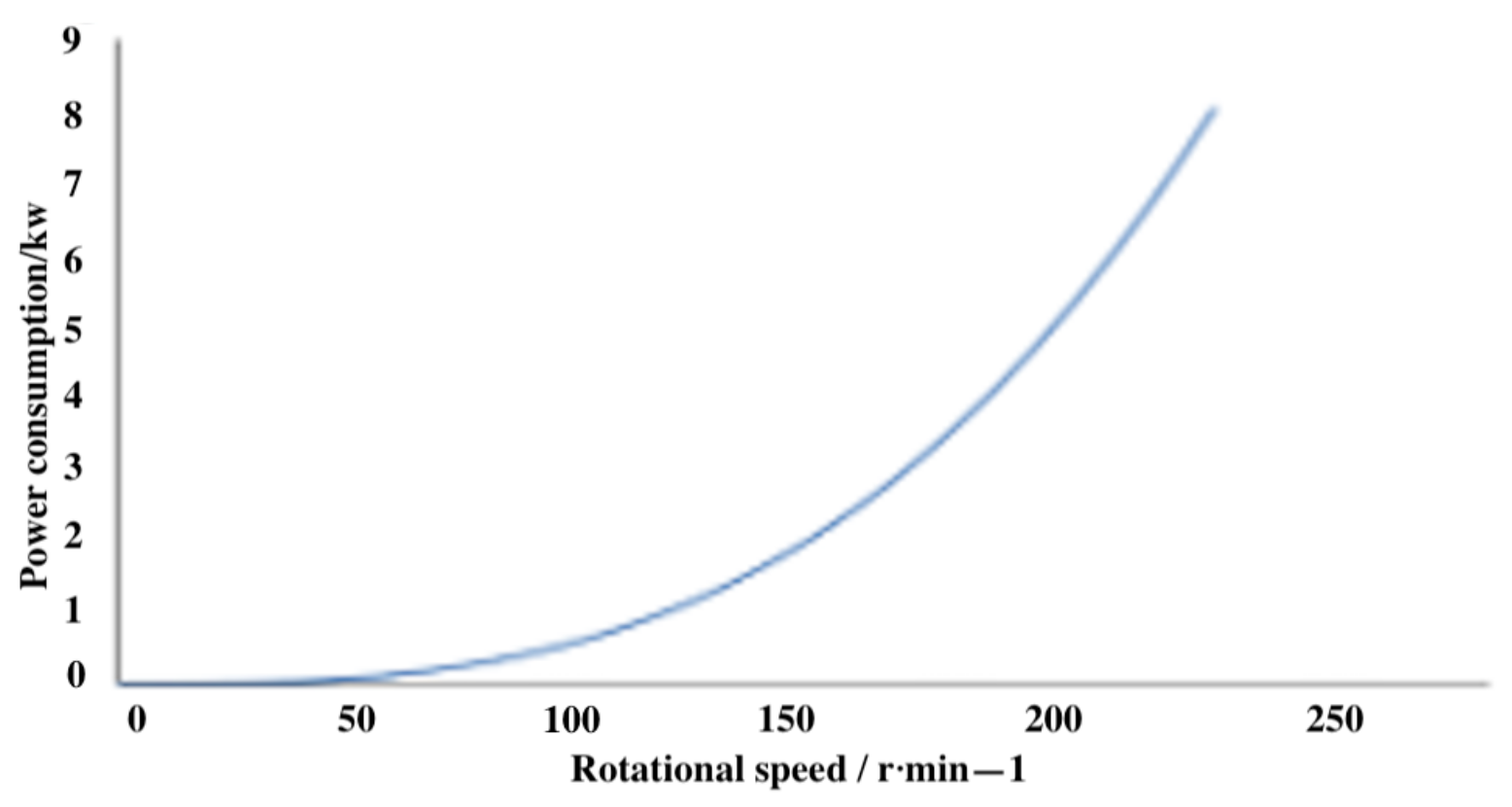
• To build mathematical analysis models for better optimisation of machine parameters, this paper obtains the water flow resistance coefficient during the linear motion of the rotating pipeline combined with CFD simulation analysis through the mechanical analysis of the nozzle and rotating pipe. Then, the mathematical model of rotating pipe speed and nozzle diameter, jet angle, and installation angle were established, and the spatial four-dimensional three-dimensional mathematical model diagram was drawn. The kinematic analysis of the nozzle was used to derive the trajectory of the nozzle. After plotting the trajectory graphs using MATLAB and combining the CFD simulation data for analysis, mathematical models of the maximum number of impacts, and the minimum time of a single impact with the radius of the effective range of the jet impact, the rotating pipe speed and the forward speed of the machine were developed, respectively. Through the analysis of the dynamics of the rotating pipeline, the mathematical model between the power consumed by the rotation of the rotating pipe and the rotational speed is established, and it is concluded that, when the rotational speed is larger, more power is consumed, the adjustable range of the impact frequency is smaller, and its positive effect on the dredging efficiency is adjusted less compared to the negative effect of the energy loss generated, ignoring the effect of the impact frequency caused by the rotating pipe on the dredging effect. The mathematical models of the forward speed of the root digger and the time required for a single point of soil impact, the rotating pipe speed, and the radius of the effective range of the jet impact were derived from a comprehensive analysis, providing a theoretical basis for the adjustment of the operating parameters of the jetting spin type lotus root digging machine.
• The optimum jet angle, nozzle diameter, nozzle installation angle, the time required to excavate the depth of the soil at a certain point, and the radius of the effective range of the jet impact are derived from the prototype tests, and then the mathematical model obtained from the theoretical analysis can be used to determine the forward speed of the jet spin dredge and the power consumed by the water flow. When the jet velocity is 20 m/s, the jet angle $\alpha$ = 45°, and the nozzle diameter is 17 mm°, the excavation depth can reach 4 m, which is greater than the growth depth of most lotus roots. According to the results of data processing, the linear motion resistance coefficient of the rotary pipeline is $K^{\prime }$ = 14.95 kg/m. When the rotation speed is 100 r/min, the impact frequency can be calculated to be 3.33 Hz, but the power consumption is 1.07 KW. Thus, as the soil structure and physical characteristics of the lotus root field vary greatly from region to region, appropriate parameters need to be adjusted for different regions of the lotus root field.
  For joint harvesting of lotus root and large-scale lotus root field harvesting, the following work can be further carried out: Seek new theoretical analysis and simulation research methods to obtain the action mechanism of the moving jet on the soil during the nozzle movement process.