Abstract
In this research, a proportional plus integral plus velocity (PIV) fuzzy gain scheduling flight controller for an octorotor mini-unmanned aerial vehicle is developed. The designed flight controller scheme, with a PIV term, is combined with a fuzzy gain scheduling approach. The tracking controller PIV fuzzy gain scheduling is based on two controllers connected in cascade with a saturation approach. The Newton–Euler equations of motion are applied to obtain a mathematical model for the octorotor mini-unmanned aerial vehicle (mini-UAV). The flight controller approach is applied to obtain coupling moments and forces with interconnected attitude and navigation tracking trajectory. In the design of a flight navigation controller with two layers, the inner layer consists of a PIV fuzzy gain scheduling controller that is applied to the attitude dynamics, obtaining the references for the coupling outer layer PIV fuzzy gain scheduling controller, which manipulates the translational dynamics. The navigation PIV fuzzy gain scheduling controller is saturated for bounding in translational forces to avoid large deviations of commands to Euler angles pitch and roll, and another saturated controller is implemented for the bounded thrust rotor to avoid the excessive angular speed of these rotors. The octorotor mini-UAV flight navigation simulation is performed to validate the tracking control of a sequence of motions in each axis, which is presented as a validation for the proposed control scheme.
1. Introduction
In the last decade, multirotor UAVs have had important developed applications such as agriculture, construction, market, parcel, civil applications, surveillance, research, and rescue missions. However, as the needs of society grow, new challenges and demands for UAV applications also appear. Four-rotor configurations are the most widely used and have many uses; however, given the new demands, these configurations may be limited. Therefore, more robust vehicles with greater fault tolerance and stability are necessary. It is here where eight-rotor configurations called octorotors have been studied. On the other hand, the control techniques that allow vehicles to respond to faults quickly are just as important.
Multi-rotors are designed with different capacities and sizes that depend on the characteristics of the application. In [1], an octorotor UAV with a star-shaped way for radar applications was implemented for vertical take-off and landing, adding disturbance to be controlled with PID and LQR controllers. In other applications such as [2], an octorotor is used for heavy cargo transportation using different kinds of techniques such as magnetic sensor systems. In [3], heavy cargo transportation is applied in the medical field by transporting first-aid kits or external defibrillators. In agriculture [4,5,6], the authors used an octorotor for geolocation and thus detected diseased regions.
For example, in [7], they proposed an orthographic projection based on the Kalman filter to detect disease zones. The configuration of the octorotor that was used allowed a gimbal placed face-down and stability for the orthographic projection method. Furthermore, in [8], technologies for mapping and recollecting data, including thermographic cameras, were used to inspect and detect citrus trees and other types of fruit. Monitoring rivers [9] is another application which was implemented using a high-resolution camera in an octorotor UAV. In [10], an octorotor was developed for night-time visual infrastructure inspection. Here, the octorotor configuration was chosen because of its superiority in terms of payload, stability, and fault tolerance. In [11], a lightweight octocopter was developed for monitoring the indoor environment. The octorotor was designed with a weight of 486 (g), 308 (mm) in width, and 160 (mm) in height to get through narrow spaces in a complex indoor environment. Hover experiments which were conducted demonstrated the high-flying capabilities of the octorotor. Other papers [12,13] have described the advantages of using octorotors when a failure presents in one or more rotors because of unknown forces, since the redundancy of eight rotors possesses the skills to continue the flight without the failed rotor by detecting errors and using a recovery system to change the configuration.
According to the literature, octorotors are UAVs that are currently under research, meaning that there are some unknown dynamics that remain to be studied. For this reason, there exists a need for controllers that can respond to their uncertainty and disturbances. In [14], a controller for a coaxial octorotor with six degrees of freedom was proposed, and the proposed control was designed to respond in the presence of actuator faults. The technique of the control used an approach of a radial base function neural network (RBFNN), fuzzy logic control (FLC), and sliding mode control (SMC), named fault-tolerant control (FTC). The control technique avoids issues of modeling and attenuating the chattering due to the SMC. Moreover, the proposed controller allowed to reduce of the number of rulers of the fuzzy logic. The simulations showed that the FTC guarantees the stability and robustness of the system and reduces the chattering effect to have good tracking in the presence of faults of the octorotor. In [15], another controller with estimation and fault tolerance was designed. The controller presented three fault-tolerant control strategies for the octorotor. The first was a mixing strategy, the second was a robust adaptive sliding mode control, and the third was a new one based on the self-tuning sliding mode of the control system. The experiments for the octorotor were carried out indoors with self-imposed faults in the rotors. The comparison between the techniques showed efficient response fault tolerance results for the three proposed techniques. In [16], a controller based on backstepping with a fast terminal sliding mode was proposed for coaxial octorotor exposure to wind disturbance. The proposed controller works with a new learning technique and extended inverse multi-quadratic radial basis function network that estimates the unmodeled dynamics of the octorotor. The simulations showed improved performance when compared with PID and LQR controllers.
One can find the fuzzy controller among the most innovative techniques, which is used to improve the controllers, specifically the dynamic behavior of the octorotors. In [17], an adaptive fuzzy tracking control combining Lyapunov stability theory and backstepping was proposed. The fuzzy controller was used to estimate the unknown dynamics of the quadrotor; nonlinear disturbance observer was also applied to compensate for external disturbance and an approximation error for the fuzzy controller of the system. Lyapunov stability showed that the quadrotor was stable, and the experimental shows the effectiveness of the proposed controller. In [18], a new adaptative fuzzy terminal sliding mode controller and two proportional and derivative (PD) controllers were proposed. The PD controllers were proposed to determine the quadrotor desired attitude, and the sliding mode was used for the rotation of the motors. Furthermore, two Kalman filters estimated the quadrotor attitude and position. The simulations and implementation showed a good performance of the control for the quadrotor.
In this work, an octorotor mini-UAV is proposed to be used in pipe inspections, surveillance, and coordinated flight as a swarm in closed places. The proposed flight controller for the octorotor mini-UAV is a fuzzy gain scheduling that adapts the PIV controller gains. The dynamic model with the controller is performed using simulation experiments with the Newton–Euler model of the octorotor mini-UAV to validate the proposed system.
Main Contribution
In this work, the implementation of a PIV fuzzy gain scheduling control, integrated with the attitude, altitude, and navigation controllers, is presented, in which the attitude and altitude have saturation functions to avoid exceeding the established limits. In this sense, the rotors use the saturation functions that establish the speed limits for each rotor. The conceptual design of a small-sized UAV is carried out, which is developed based on the 3D print tools using the fused deposition modeling (FDM) technique. The contribution of this work is summarized as follows:
- 1.
- A PIV control with fuzzy gain scheduling is designed for the trajectory tracking of the attitude and navigation of the mini-UAV.
- 2.
- The design of the flight control system is validated by simulations using the Newton–Euler dynamic model of the mini-UAV.
- 3.
- The real parameters of the mini-UAV were obtained through CAD software and 3D-printed parts.
The work was structured as follows: The dynamic equations for the octorotor mini-UAV are presented in Section 2. The PIV controller is designed in Section 3. The gain scheduling controller design was developed in Section 4. The simulation results are shown in Section 5. Finally, the conclusions of this work are presented in Section 6.
2. Dynamic Equations for the Octorotor Mini-UAV
The dynamic model of the octorotor mini-UAV uses the configuration frame north–east–down (NED) for aerospace. The X–axis is coupled in the north direction, the Y–axis is located in the east direction, and the Z–axis is in the direction of the center of the Earth. An Earth-fixed inertial frame is defined as =, and a body frame attached to the center of gravity of the octorotor mini-UAV as = [19,20], as can be seen in Figure 1. In order to formulate the dynamics equation, the Newton–Euler approach is used. The dynamic model is defined as
where describes the position coordinates relative to the inertial frame and describes the rotation coordinates for the octorotor mini-UAV. This is given by an orthogonal rotation matrix parameterized by the Euler angles, where is the roll angle, is the pitch angle, and is the yaw angle, and then, the rotation matrix is defined as
where are cosine and sine operators for each Euler angle, respectively. is the angular velocity vector in , is the translational velocity vector in , is the vertical thrust attached to the body frame considering the rotation speed of each rotor such that , and is the moments acting on the center of gravity of the octorotor mini-UAV. In addition, the canonical basis vectors of are considered; these are represented by ,, and . is the Euler matrix. The term denotes the mass of the octorotor mini-UAV, while contains moments of inertia such that:
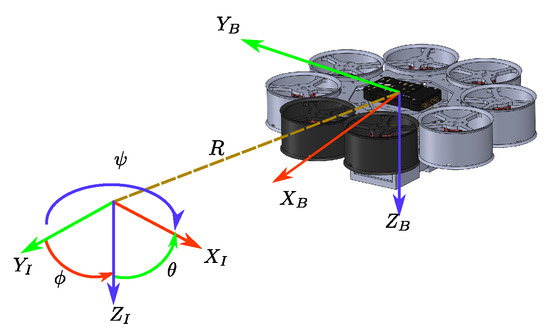
Figure 1.
Reference frames and the direction of rotation of each rotor in the octorotor mini-UAV.
To design the corresponding attitude, altitude and navigation controllers, models (1)–() are used.
3. Flight Controller Design
3.1. Attitude and Altitude Controller
The thrust forces produced by the k-th individual rotor are given by , where is the angular velocity of the k-th rotor, and is the thrust coefficient of the propeller, which can be determined by experimental tests from the measurement of thrust in the steady state.
Considering that the vector represents the moments acting on the octorotor mini-UAV center of gravity and considering the allocation the pair of rotors. For pitch moment actuator, rotors and are parallel to the –axis with a separated angle of (rad) among each rotor. For roll moment , the actuator rotors and are parallel to the –axis. The reactive moment produced by the propeller of each rotor of the octorotor mini-UAV is expressed as with , where is the aerodynamic coefficient of the rotor propeller. The yaw moment must be assigned in the direction of rotation against each pair of rotors (see Figure 2), where the rotors that turn clockwise are positives and the rotors that turn counterclockwise are negative. Consequently, due to those mentioned above, the total thrust and moments applied to the octorotor mini-UAV center of gravity are grouped as follows:
where parameters and are the distance d of the octorotor mini-UAV center of gravity with respect to the axis of rotation of the propellers. The compact expression of the Equation (8) is shown as:
where represents the matrix of the aerodynamic coefficients of the octorotor mini-UAV. Vector is the vector of quadratic rotor speed, and represents the vector that connects the total scalar thrust with the octorotor mini-UAV moments vector. Since the matrix is not square, the inverse matrix is obtained using a pseudo-inverse equation that is expressed as follows
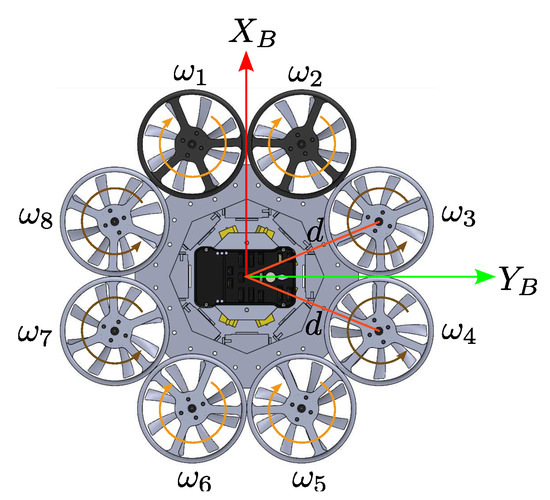
Figure 2.
Reference frames and direction of rotation of each rotor in the octorotor mini-UAV.
Then, the inverse expression of the Equation (9) is shown below.
Thus, the vector of the desired controller variables is obtained, which corresponds to each of the rotors. Below, such a developed matrix expression is shown:
3.1.1. Altitude Controller
The thrust , which is aligned with , is not always in the direction of the inertial frame , and the component of the desired inertial force vector associated with the altitude controller can be calculated in terms of the roll angle and the pitch angle such that
Then, the dynamics of the desired thrust force is proposed for the actuators, with the purpose of complying with the stationary or ascending flight regime, obtaining the following expression
where (rad) and (rad) are constrained to avoid a singularity of altitude compensation, and the desired thrust force is reached by an altitude controller PIV, such that this controller is defined as
where represents the translational position error, represents the desired position, and z is the actual value of the translational position, with both variables in . represents the translational velocity error, where is the desired velocity, and is the actual value of the translational velocity. A saturation is added to improve trajectory tracking with the desired thrust force. The expression of the thrust-saturated controller is shown below.
The PIV controller with thrust compensation is described as follows
3.1.2. Attitude Controller
For the formulation of the attitude control problem, the desired attitude vector is considered, such that giving representing the attitude errors. is the vector containing the desired angles, and are the actual angles. represents the angular velocity error, where vector is the desired angular velocity, and vector is the actual value of the angular velocity. The control problem is strictly the proposal of a controller vector . For attitude control, a PIV controller is proposed. Taking into account the definition established in vector (8), the external moments are rewritten to be expressed in terms of the proposed controller law, as shown below as
A saturation is added to improve the attitude in the torques, and it is expressed below
Then, the developed attitude controller equations are expressed as follows
3.2. Navigation Controller
The attitude controller is integrated into the flight control of the octorotor mini-UAV in such a way that the desired setpoints of the attitude vector are calculated from the translational position controller in the plane and using the reference rotation matrix . To obtain the desired forces of the translational position controller in the plane, a controller of type PIV is proposed as follows
where and represent the translational position error, and represent the desired position, and x, and y are the actual value of the translational position, with both variables in and , respectively. and represent the translational velocity errors, where and are the desired velocities, and and are the actual value of the translational velocities. The equations developed by the navigation controller in the navigation plane are expressed as follows.
The proposed PIV-type navigation controller is linked with the external controller layer by the rotation matrix to generate the desired reference angles and of the attitude controller, in such a way that the following connection between both attitude and translational controllers are obtained.
Equation (26) is proposed for the navigation controller of the octorotor mini-UAV to track the trajectories in the plane .
Mixer Rotor Controllers
As a final step, the control laws corresponding to the motors of the octorotor mini-UAV, considering the mixing matrix (12), are presented as follows
where for . It is necessary to remark that the saturation functions consider the actual limits of the angular velocity of the motors. This saturation function is defined as
where represents the maximum quadratic rotor speed and is the minimum quadratic rotor speed. The complete control scheme and dynamics are represented in a diagram in Figure 3.
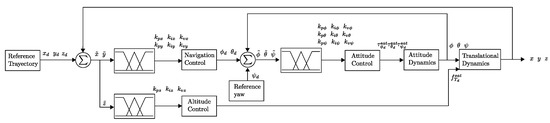
Figure 3.
Diagram of attitude and navigation controllers applied to a dynamic model of an octorotor mini-UAV.
4. Gain Scheduling Controller Design
The PIV controller is widely used due to its fast solution, and some researchers use tuning applications to find the optimal constant gains for the PIV controller. Meanwhile, the gain scheduling combines fuzzy and PIV controllers to autotune the gains in real time. A control strategy using gain scheduling with a PIV controller is proposed for the octorotor mini-UAV. As explained above, the objective of PIV control is to avoid deviations during the dynamic motion. The controller can adjust the gains depending on the error size.
The fuzzy logic controller is connected to the PIV gains of the attitude, altitude, and navigation controller with a total of six fuzzy logic controllers; each fuzzy has a membership function, as is shown in Figure 4.
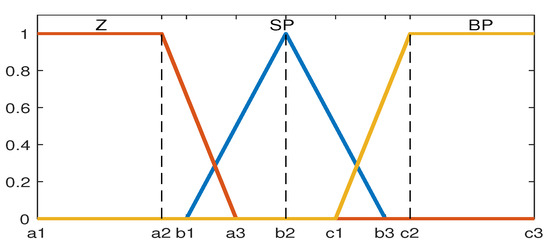
Figure 4.
Membership function for input and output of each controller.
The membership functions have the error and velocity error as inputs while proportional, velocity, and integral gains as outputs. The fuzzy always considers the inputs as positive to determine whether the error is zero (Z), small positive (SP), or big positive (BP) value.
Nine rules are defined in Table 1 by combining the inputs, where and are the input position error and input velocity error, respectively. These rules are set to the six fuzzies in each controller. The Table 2, Table 3, Table 4 and Table 5 are the values for the fuzzy determined by simulating an octorotor mini-UAV using only PIV control to estimate the range of parameters.

Table 1.
Fuzzy rules.

Table 2.
Parameters for roll and pitch in membership function.

Table 3.
Parameters for yaw in membership function.

Table 4.
Parameters for X and Y navigation in membership function.

Table 5.
Parameters for Z altitude in membership function.
5. Flight Controller Simulation
5.1. Parameters of the Octorotor Mini-UAV Controller
The parameters used for the numerical simulations are obtained through the octorotor mini-UAV model in Solidworks. In Table 6, the numerical values of the model parameters are shown.

Table 6.
Parameters of the octorotor mini-UAV.
The parameters used for the saturation are set as follows in Table 7.

Table 7.
Saturation parameters.
5.2. Control Surface
The control surface is produced by the inference logic fuzzy mechanism for a fuzzy PIV attitude controller with programming gains. It is generated with the tuned parameters in Table 2 and Table 3 to compute the variation range of the gain sets (, and ), (, and ) and (, and ) of the attitude controller for roll, pitch, and yaw, (as can be seen in Figure 5). While the control surface is produced by the inference logic fuzzy mechanism for a fuzzy PIV navigation controller with programming gains. It is generated with the tuned parameters in Table 4 and Table 5 to compute the variation range of the gain sets (, and ), (, and ) and (, and ) of navigation and altitude controllers in the X, Y, and Z axes, (see Figure 6). The geometric shape of the control surface (Figure 5 and Figure 6) is the result of the properties that achieve the tuning of fuzzy rules implemented with the Mamdani inference method. It is used to set up the fuzzy PIV controllers with programming gains in the attitude, altitude, and navigation dynamics of the octorotor mini-UAV.
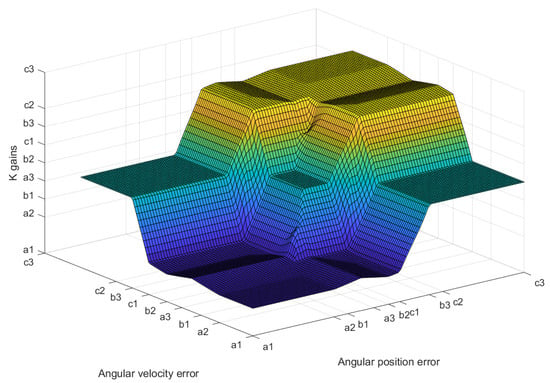
Figure 5.
Attitude control surface.
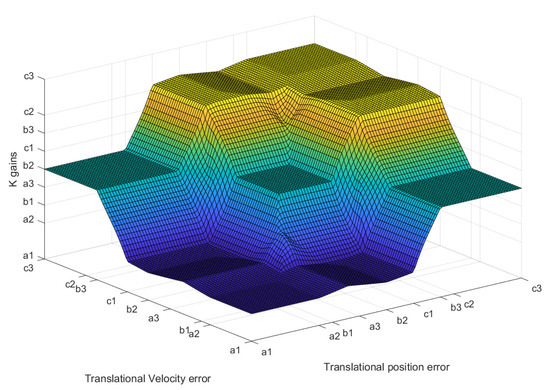
Figure 6.
Translational control surface.
5.3. Trajectory Tracking Navigation
The results of the simulation were obtained using Matlab/Simulink. In previous works, similar algorithms were implemented. In [21], a quadrotor with a two-layer saturated PIV controller was shown. The quadrotor follows an ascending helical trajectory which is decreasing. In [22], an octorotor is proposed using a nonlinear PV plus a linear integral; in this work, the octorotor has a mass of 8 (kg), and its inertial matrix is simplified. The octorotor follows a helical trajectory, which remains constant during time simulation. The octorotor mini-UAV performs a sequence of movements through the axes traveling 1 m in each axis. The sequence is , and the negative part of Z–axis is the take-off. Meanwhile, the positive part is the landing, in the X–axis, and the positive part is the forward movement, and the negative part is the backward movement. Finally, in the Y–axis, the positive part indicates the movement from left to right.
A disturbance is added in Equation (4), such that , where D is the disturbance vector that contains disturbances in each torque. The vector with is a Gauss peak equation acting as a disturbance, where is the height of the peak curve, is the time where the peak is in the center, is the standard deviation, and t is the time, see Figure 7.
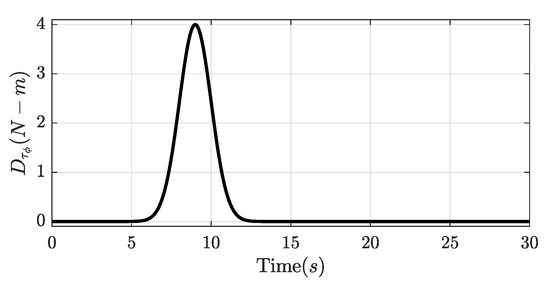
Figure 7.
Disturbance for the desired torque of roll.
In the simulation, Figure 8 shows the tracking of the desired (red line) and actual (black line) trajectories of the octorotor mini-UAV. A disturbance is added to analyze the behavior of the gain scheduling controller that autotunes the gains to recover stability in the octorotor mini-UAV. The following Figure 9 and Figure 10 show the octorotor mini-UAV in attitude, altitude, and navigation behavior. Then, the rotor speed and gains parameters are shown. Finally, the moments and total thrust of the octorotor mini-UAV are presented.
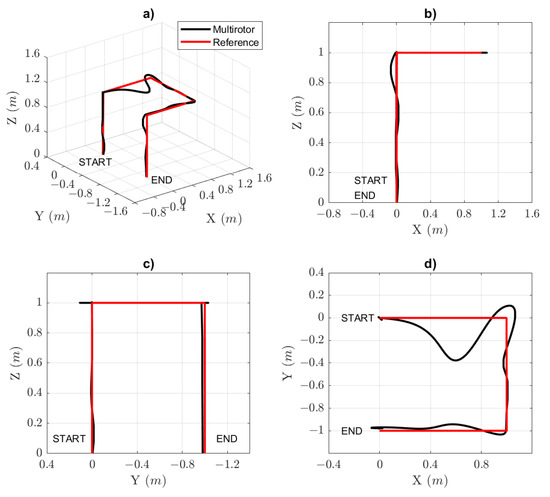
Figure 8.
Trajectory tracking of the octorotor mini-UAV, (a) isometric view, (b) side plane, (c) front plane, and (d) top view.
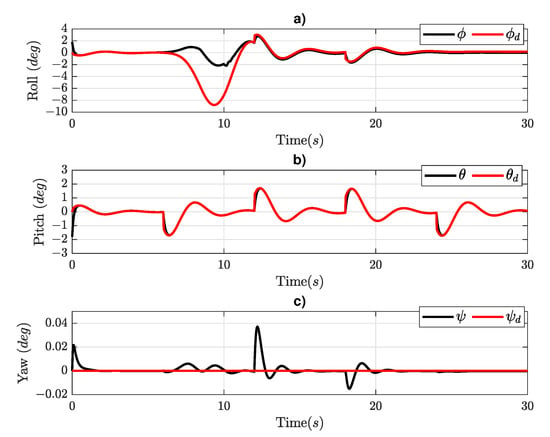
Figure 9.
Euler angle responses in: (a) , (b) , and (c) .
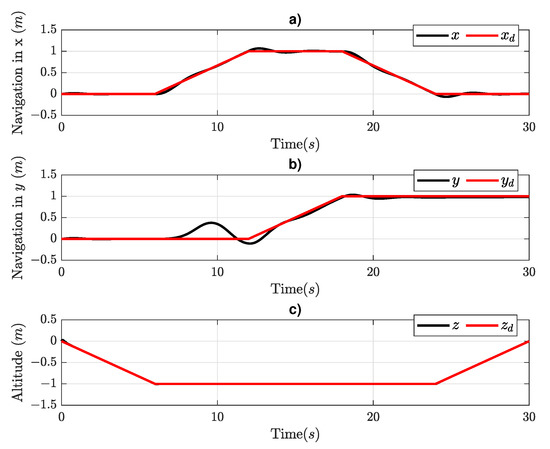
Figure 10.
Translational motion responses in: (a) X–axis, (b) Y–axis, and (c) Z–axis as the altitude.
Figure 9 shows the response of Euler angles; in the roll angle (Figure 9a), the disturbance recalculated the desired value (red line) of the roll angle for a stabilization. While the actual value (black line) continues using less of an angle to recover the trajectory. For the pitch angle (Figure 9b), there is an absence of disturbance due to this simulation considering the disturbance only in which indirectly affects the Y–axis due to the roll angle. There is a small disturbance in the yaw angle (Figure 9c) when the disturbance in the torque is presented at a time of 9 (s), the following two disturbances are related to the change in direction between the X and Y axes at the times of 12 (s) and 18 (s).
Figure 10 shows the sequence of movements in each axis. In the X–axis (Figure 10a), as can be seen, the controller is performs stabilization each time the direction changes due to the attitude controller in . In the Y–axis (Figure 10b), there is a disturbance with a peak at 9 (s) due to the disturbance in . Finally, the Z–axis (Figure 10c) presents rapid stabilization during ascending and descending.
Figure 11 shows the angular velocity in RPM of all rotors, which have a maximum speed limit set to 34,500 (RPM), as obtained in the datasheet of the motor, and a minimum speed limit set to 1000 (RPM), to avoid turning off the rotors. The regulated speed after stabilization is 16,570 (RPM) in each rotor. All rotors are paired in two in the sense that , , , and present a similar behavior with a small difference when the octorotor mini-UAV is changing direction. When the octorotor mini-UAV ascends, the whole rotors are stabilized at 16,570 (RPM), and then, in the X–axis forward direction, rotors and (Figure 11a) increase their speed and and (Figure 11c) decrease their speed. When the octorotor mini-UAV changes direction towards the east, rotors and (Figure 11d) increase their speed and and (Figure 11b) decrease their speed.
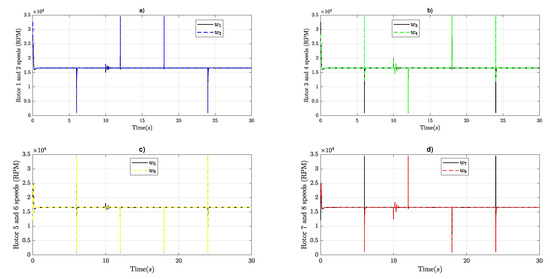
Figure 11.
Rotor speed responses: (a) and , (b) and , (c) and , and (d) and .
Figure 12 shows the gain behavior in the attitude controller. Figure 12a illustrates the gains of controller, where the proportional gain changes by the disturbance set. For each change in direction, the proportional and velocity gains change. The gains of the controller (Figure 12b) present the same behavior when the octorotor mini-UAV changes direction, except that there is no disturbance in . In the controller, the gains (Figure 12c) remain constant due to the desired yaw set to zero.
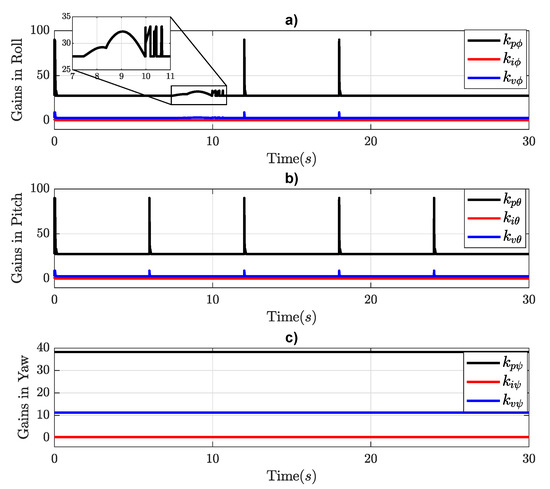
Figure 12.
PIV gain responses in attitude controller: (a) , (b) , and (c) with .
Figure 13 shows the gain behavior in the translation controller. Due to the gain in attitude adjusting, the gains in the translation controller remain constants without changes.
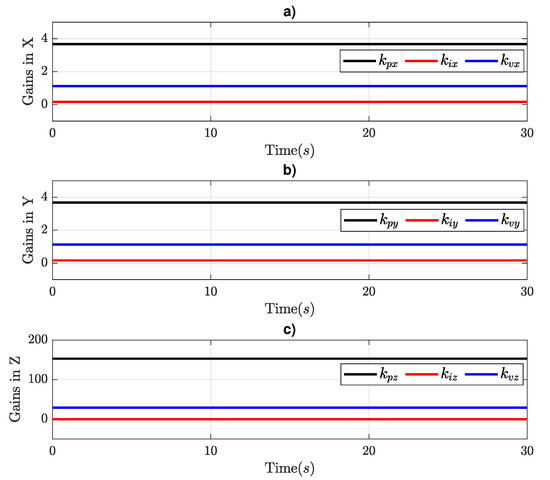
Figure 13.
PIV Gain responses in the translation controller: (a) , (b) , and (c) , with .
Figure 14 shows the total thrust of all rotors in the octorotor mini-UAV. The maximum thrust shown is 22.55 (N) at the beginning, and then the stable thrust is 11.77 (N), which is the minimum to maintain the octorotor mini-UAV hovering during flight. The minimum total thrust shown is 5.45 (N) due to the finalization of ascending and when it starts descending.
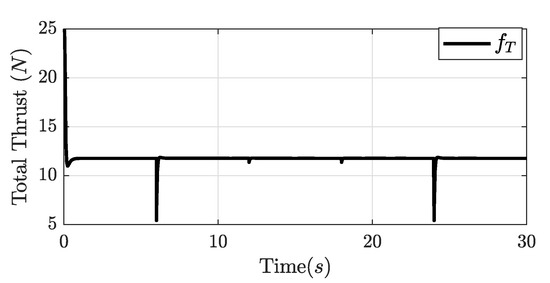
Figure 14.
Response of total thrust of the octorotor mini-UAV.
Figure 15 shows moment actuators in the octorotor mini-UAV, where has the disturbance added at 9 (s) to a disturbated Y–axis as it can be seen in Figure 15a. Then, Figure 15b shows the moment when the octorotor mini-UAV performs the X–axis movements. Then, Figure 15c illustrates the signal with a minimum actuation when the octorotor mini-UAV stops ascending when the octorotor mini-UAV performs the Y–axis movement. Finally, when the octorotor mini-UAV starts descending, these actions affect the yaw angle between and .
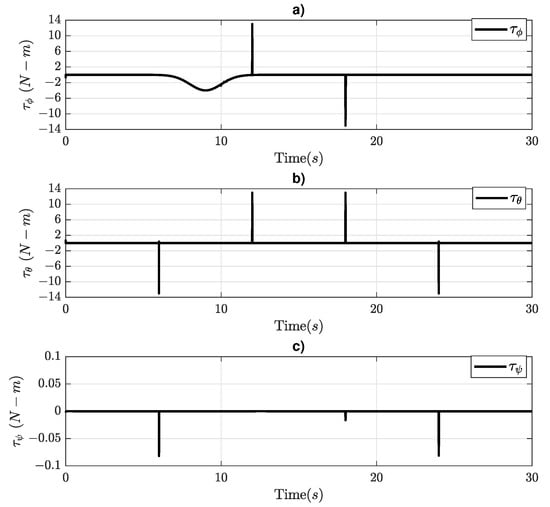
Figure 15.
Response of moments: (a) , (b) , (c) .
5.4. Octorotor Mini-UAV Manufacturing
The octorotor mini-UAV frame was manufactured using the FDM (fused deposition modeling) technique with PLA (polylactide) as the primary material. The 3D printer used was an Ultimaker. Figure 16 shows eight separately printed ducts with two ducts printed using the black PLA to identify the front of the aircraft. The base and top of the fuselage were printed separately due to the volume capacity of Ender 6. Finally, Figure 17 shows the octorotor mini-UAV battery support, which is printed in two parts to avoid future installation problems with the battery.

Figure 16.
Top view of the octorotor mini-UAV manufactured fuselage.

Figure 17.
Bottom view of the octorotor mini-UAV manufactured fuselage.
The electronic power propulsion and avionic system are proposed using eight 2205 Brushless Direct Current (BLDC) motors with 2300 (KV or RPM/V), eight Electronic Speed Controller (ESC) with 30A-S and BLHeli_ S firmware, as well as an eight-blade propeller mounted on each motor. A power distribution board capable of supporting 200 (A) is selected. A PixHawk PX4 ver. 2.4.8 with an STM32F103 processor that works with 160 (MHz), and 256k of RAM is selected. A Turnigy lipo battery with 4000 (mAh), 4S configuration, and a weight of 396 (g) was selected to power up all electronic components.
6. Conclusions
The flight navigation controller PIV fuzzy gain scheduling proposed for the trajectory tracking of the octorotor mini-UAV with attitude inner PIV fuzzy gain scheduling controller was designed. In addition, the PIV fuzzy gain scheduling navigation controller of the octorotor mini-UAV fulfillment a satisfactory performance for tracking trajectories. In effect, it is mentioned that the capacity of the PIV fuzzy gain scheduling flight controller can be tested against heavy cargo transportation and enduring gust wind disturbances. The validation of the attitude and navigation controllers in a closed-loop system with the dynamic model of an octorotor mini-UAV is obtained via numerical simulations. In the simulations, a saturated PIV attitude controller with fuzzy gain scheduling tuning for a fast response was performed. The membership functions of the fuzzy flight controller were tuned on a heuristic procedure to obtain an underdamped response for translational and angular positions with a low overshoot and a fast settling time. For the flight controller tuning procedure, the output membership function of the proportional gain is tuned for fast output response of attitude and navigation positions, then the output membership function of the velocity gain is tuned to reduce the system oscillations; finally, the output membership function of the integral gain is tuned to reduce the steady-state error to a value close to zero. Furthermore, this PIV gain scheduling controller was designed to reject wind gust disturbances fulfilling satisfactory performance of the trajectory tracking responses of the octorotor mini-UAV. Finally, the octorotor mini-UAV fuselage was manufactured using polylactic acid (PLA) material by the fused deposition modeling (FDM) technique, which provides a robust and lightweight platform.
Author Contributions
P.A.T.-B. worked on the mathematical model, controllers, and wrote the first draft. L.E.C.-R. worked on the conceptual design, controllers, and simulation design. M.A.G.-M. worked on the tuning methodology, controller analysis, and the simulation results. E.J.O.-V. proposed the octorotor UAV design, improved the manuscript and supervised the overall project. All authors have read and agreed to the published version of the manuscript.
Funding
This research work is supported by The Technological Institute of La Laguna-TecNM through the award number 14492.22-P. and 10929.21-P.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All research data supporting this study are included in the manuscript.
Acknowledgments
The authors would like to thank The Technological Institute of La Laguna-TecNM and Autonomous University of Nuevo Leon (CIIIA-FIME-UANL).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Makarov, M.; Maniu, C.S.; Tebbani, S.; Hinostroza, I.; Beltrami, M.M.; Kienitz, J.R.; Menegazzi, R.; Moreno, C.S.; Rocheron, T.; Lombarte, J.R. Octorotor UAVs for radar applications: Modeling and analysis for control design. In Proceedings of the 2015 Workshop on Research, Education and Development of Unmanned Aerial Systems (RED-UAS), Cancun, Mexico, 23–25 November 2015; pp. 288–297. [Google Scholar]
- Phelps, G.; Bracken, R.; Spritzer, J.; White, D. Achieving sub-nanoTesla precision in multirotor UAV aeromagnetic surveys. J. Appl. Geophys. 2022, 206, 104779. [Google Scholar] [CrossRef]
- Baumgarten, M.C.; Röper, J.; Hahnenkamp, K.; Thies, K.C. Drones delivering automated external defibrillators—Integrating unmanned aerial systems into the chain of survival: A simulation study in rural Germany. Resuscitation 2022, 172, 139–145. [Google Scholar] [CrossRef] [PubMed]
- Sankey, T.; Donager, J.; McVay, J.; Sankey, J.B. UAV lidar and hyperspectral fusion for forest monitoring in the southwestern USA. Remote Sens. Environ. 2017, 195, 30–43. [Google Scholar] [CrossRef]
- Panagiotidis, D.; Abdollahnejad, A.; Slavik, M. 3D point cloud fusion from UAV and TLS to assess temperate managed forest structures. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102917. [Google Scholar] [CrossRef]
- Garcia, C.A.; Xu, Y. Multitarget geolocation via an agricultural octorotor based on orthographic projection and data association. Proc. Inst. Mech. Eng. Part J. Aerosp. Eng. 2018, 232, 2076–2090. [Google Scholar] [CrossRef]
- Garcia, C.A.; Xu, Y. Target Geolocation for agricultural applications via an Octorotor. IFAC-PapersOnLine 2016, 49, 27–32. [Google Scholar] [CrossRef]
- Donmez, C.; Villi, O.; Berberoglu, S.; Cilek, A. Computer vision-based citrus tree detection in a cultivated environment using UAV imagery. Comput. Electron. Agric. 2021, 187, 106273. [Google Scholar] [CrossRef]
- Rivas Casado, M.; Ballesteros Gonzalez, R.; Kriechbaumer, T.; Veal, A. Automated identification of river hydromorphological features using UAV high resolution aerial imagery. Sensors 2015, 15, 27969–27989. [Google Scholar] [CrossRef] [PubMed]
- Madokoro, H.; Woo, H.; Sato, K.; Shimoi, N. Development of Octo-Rotor UAV Prototype with Night-vision Stereo Camera System Used for Nighttime Visual Inspection. In Proceedings of the 2019 19th International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 15–18 October 2019; pp. 998–1003. [Google Scholar]
- Zhang, B.; Tsuchiya, S.; Lim, H. Development of a Lightweight Octocopter Drone for Monitoring Complex Indoor Environment. In Proceedings of the 2021 6th Asia-Pacific Conference on Intelligent Robot Systems (ACIRS), Tokyo, Japan, 7–9 July 2021; pp. 1–5. [Google Scholar]
- Walter, A.; McKay, M.; Niemiec, R.; Gandhi, F. Trim Analysis of a Classical Octocopter After Single-Rotor Failure. In Proceedings of the 2018 AIAA/IEEE Electric Aircraft Technologies Symposium (EATS), Cincinnati, OH, USA, 9–11 July 2018; pp. 1–20. [Google Scholar]
- Marks, A.; Whidborne, J.F.; Yamamoto, I. Control allocation for fault tolerant control of a VTOL octorotor. In Proceedings of the 2012 UKACC International Conference on Control, Cardiff, UK, 3–5 September 2012; pp. 357–362. [Google Scholar]
- Zeghlache, S.; Mekki, H.; Bouguerra, A.; Djerioui, A. Actuator fault tolerant control using adaptive RBFNN fuzzy sliding mode controller for coaxial octorotor UAV. Isa Trans. 2018, 80, 267–278. [Google Scholar] [CrossRef] [PubMed]
- Hamadi, H.; Lussier, B.; Fantoni, I.; Francis, C.; Shraim, H. Comparative study of self tuning, adaptive and multiplexing FTC strategies for successive failures in an Octorotor UAV. Robot. Auton. Syst. 2020, 133, 103602. [Google Scholar] [CrossRef]
- ul Amin, R.; Inayat, I.; Jun, L.A. Finite time position and heading tracking control of coaxial octorotor based on extended inverse multi-quadratic radial basis function network and external disturbance observer. J. Frankl. Inst. 2019, 356, 4240–4269. [Google Scholar] [CrossRef]
- Li, C.; Wang, Y.; Yang, X. Adaptive fuzzy control of a quadrotor using disturbance observer. Aerosp. Sci. Technol. 2022, 128, 107784. [Google Scholar] [CrossRef]
- Nekoukar, V.; Dehkordi, N.M. Robust path tracking of a quadrotor using adaptive fuzzy terminal sliding mode control. Control. Eng. Pract. 2021, 110, 104763. [Google Scholar] [CrossRef]
- Lozano, R. Unmanned Aerial Vehicles Embedded Control; John Wiley-ISTE Ltd.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Stengel, R.F. Flight Dynamics; Princeton University Press: Princeton, NJ, USA, 2004. [Google Scholar]
- Ollervides-Vazquez, E.J.; Rojo-Rodriguez, E.G.; Rojo-Rodriguez, E.U.; Cabriales-Ramirez, L.E.; Garcia-Salazar, O. Two-layer saturated PID controller for the trajectory tracking of a quadrotor UAV. In Proceedings of the 2020 International Conference on Mechatronics, Electronics and Automotive Engineering (ICMEAE), Cuernavaca, Mexico, 16–21 November 2020; pp. 85–91. [Google Scholar]
- Tellez-Belkotosky, P.A.; Ollervides-Vazquez, E.J.; Rojo-Rodriguez, E.G.; Santillan-Avila, J.L.; Cabriales-Ramirez, L.E.; Gutierrez-Martinez, M.A.; Garcia-Salazar, O. Nonlinear flight navigation controller for an octorotor unmanned aerial vehicle. In Proceedings of the 2021 International Conference on Mechatronics, Electronics and Automotive Engineering (ICMEAE), Cuernavaca, Mexico, 22–26 November 2021; pp. 52–59. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).