PR-Alignment: Multidimensional Adaptive Registration Algorithm Based on Practical Application Scenarios
Abstract
1. Introduction
- Data collection of the scene point cloud is carried out by using the UAV-borne Lidar system, and the point cloud is then preprocessed before being used for analysis. The structure composition and working principle of the point cloud data acquisition system was studied, a calibration experiment for the point cloud data acquisition system was designed and completed, and the internal parameters and relative positional relationship between the color camera and laser radar were determined. An experiment to acquire 3D point clouds of the scene has been completed, and a colored point cloud has been produced. Moreover, for the pre-processing of scene point cloud, the efficient organization of point cloud data is realized based on the data structure of a K–D tree, and an adaptive voxel grid down-sampling method is proposed to ensure a good and stable down-sampling effect. The unreliable outliers are eliminated by statistical filtering, and the point cloud normal vector is estimated based on PCA.
- An algorithm for coarse registration of point clouds based on improved RANSAC is studied. We use NARF and FPFH to detect, describe, and match 3D key points on 3D point clouds, along with the establishment of geometric homonym point pairs. For color images, SIFT is used to detect, describe, and match two-dimensional key points, and their values are obtained through bilinear interpolation, resulting in the establishment of photometric point pairs with the same name. Geometric matching and photometric matching are combined adaptively according to the judgment of the current scene category. Aiming at the deficiency of the traditional RANSAC algorithm, an improved RANSAC algorithm is proposed innovatively, which sets the bias of random sampling and establishes an adaptive hypothesis evaluation method, which shows that the validity and robustness of transformation matrix estimation are improved.
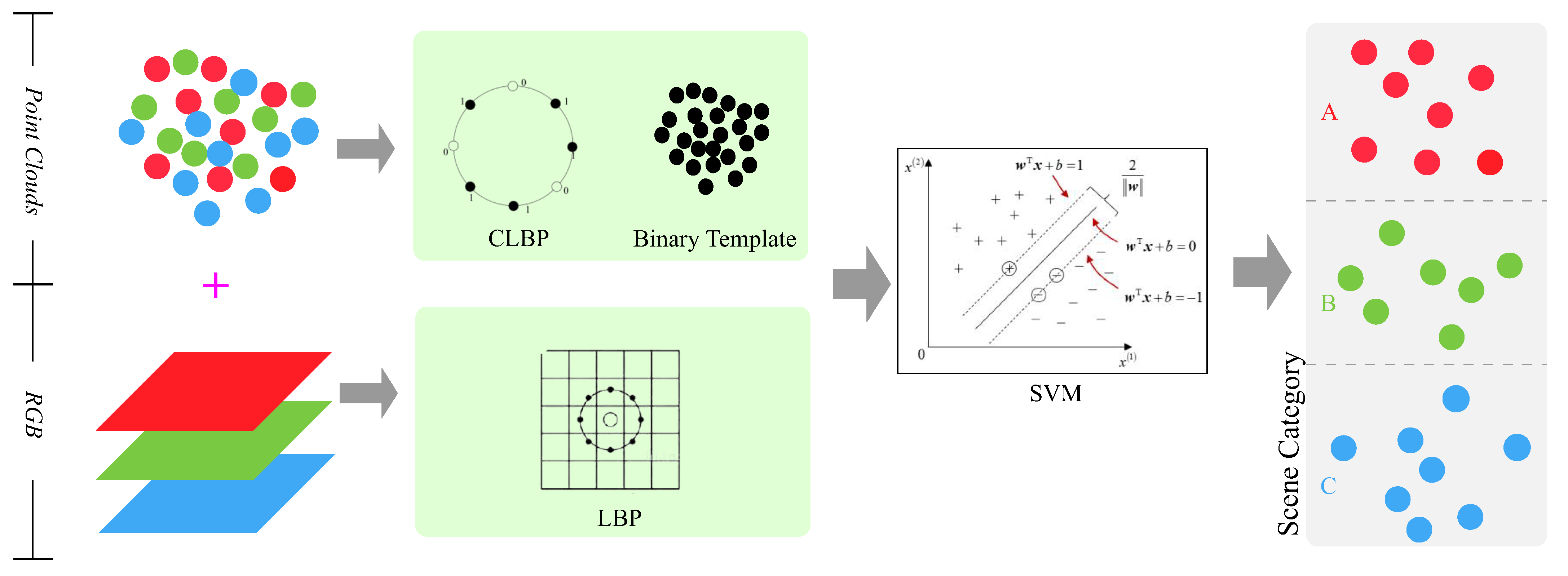
- A scene classification algorithm is studied. A binary validity template is proposed to filter out invalid information from the local description of the luminosity texture features and geometric structure features of the scene by using the LBP and CLBP operators, and the scene feature vector is extracted by computing the normalized statistical histogram of the LBP and CLBP operators. For scene classification, a three-class SVM is used, and the labeled dataset is constructed by using a combination of self-built point cloud data and third-party data.
2. Related Work
3. Methodology
3.1. Overview
3.2. 3D Registration Model
3.3. Adaptive 3D Registration for PR-Alignment
3.3.1. Feature Correspondences
3.3.2. Scene Classification
3.3.3. Random Sampling and Adaptive Evaluation
| Algorithm 1 The pseudocode for the adaptive 3D registration method for PR-Alignment. |
| Require:
Input the mix-and-match point-pair set Ensure: Output the rotation–translation matrix T.
|
- Perform coarse registration on the source point cloud P in order to obtain a new point cloud that needs to be registered. For each point in , find the point qj closest to it in the target point cloud Q as the corresponding point pair .
- Estimate the correspondence between corresponding point pairs in order to calculate the rigid body transformation matrix. Using the transformation matrix, we can obtain the average distance error D between the point in the transformed point cloud and the corresponding point in the target point cloud Q.
- In order to obtain the final rigid body transformation matrix, repeat the above steps until the set error threshold is reached or the maximum number of iterations is reached.
4. Experiments
4.1. Datasets and Experimental Conditions
4.1.1. Datasets
- Self-built datasets. Three-dimensional scanning was conducted at the National Ski Jumping Center and Biathlon Ski Center for the 2022 Beijing Winter Olympics using existing airborne Lidar systems and ground-based Lidar systems (as shown in Figure 7). Laser point cloud data and RGB image sets were included in the collected data. According to the characteristics of the data and the collection environment, we have organized these data into four major categories and eight subcategories, with a total data volume of 43GB. In Table 1, we present the configuration parameters of the acquisition equipment that we used.
- Third-party datasets. Additionally, in order to verify the universality of the method proposed in this paper, we selected the third-party database Semantic 3D for algorithm verification experiments. There are eight semantic classes that cover a wide range of urban outdoor scenes, such as churches, streets, railway tracks, squares, villages, football stadiums, and castles. Approximately four billion hand-labeled points have been evaluated, and the subversions are constantly being updated.
4.1.2. Experimental Conditions
4.2. Evaluation Metrics
4.3. Results and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ICP | Iterative Closest Point |
| PFH | Point Feature Histogram |
| FPFH | Fast Point Feature Histogram |
| 3DSC | Three-dimensional Shape Context |
| T-ICP | T-test-based Iterative Closest Point |
| ICA | Independent Component Analysis |
| LiDAR | Light Detection and Ranging |
| NARF | Normal Aligned Radial Features |
| RGB | Red, Green, Blue |
| 2D and 3D | 2 Dimensions and 3 Dimensions |
| SIFT | Scale Invariant Feature Transform |
| RANSAC | Random Sample Consensus |
| SVD | Singular Value Decomposition |
| UAV | Unmanned Aerial Vehicle |
| RMSE | Root Mean Square Error |
References
- Yu, J.; Zhang, C.; Wang, H.; Zhang, D.; Song, Y.; Xiang, T.; Liu, D.; Cai, W. 3d medical point transformer: Introducing convolution to attention networks for medical point cloud analysis. arXiv 2021, arXiv:2112.04863. [Google Scholar]
- Wang, Q.; Kim, M.K. Applications of 3D point cloud data in the construction industry: A fifteen-year review from 2004 to 2018. Adv. Eng. Inform. 2019, 39, 306–319. [Google Scholar] [CrossRef]
- Yang, S.; Hou, M.; Shaker, A.; Li, S. Modeling and Processing of Smart Point Clouds of Cultural Relics with Complex Geometries. ISPRS Int. J. Geo-Inf. 2021, 10, 617. [Google Scholar] [CrossRef]
- Zheng, S.; Zhou, Y.; Huang, R.; Zhou, L.; Xu, X.; Wang, C. A method of 3D measurement and reconstruction for cultural relics in museums. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 145–149. [Google Scholar] [CrossRef]
- Durupt, A.; Remy, S.; Ducellier, G.; Eynard, B. From a 3D point cloud to an engineering CAD model: A knowledge-product-based approach for reverse engineering. Virtual Phys. Prototyp. 2008, 3, 51–59. [Google Scholar] [CrossRef]
- Urbanic, R.; ElMaraghy, H.; ElMaraghy, W. A reverse engineering methodology for rotary components from point cloud data. Int. J. Adv. Manuf. Technol. 2008, 37, 1146–1167. [Google Scholar] [CrossRef]
- Gupta, P.M.; Pairet, E.; Nascimento, T.; Saska, M. Landing a UAV in harsh winds and turbulent open waters. IEEE Robot. Autom. Lett. 2022, 8, 744–751. [Google Scholar] [CrossRef]
- Giordan, D.; Cignetti, M.; Godone, D.; Wrzesniak, A. Structure from motion multi-source application for landslide characterization and monitoring. Geophys. Res. Abstr. 2019, 21, 2364. [Google Scholar]
- Nguyen, T.; Pham, Q.H.; Le, T.; Pham, T.; Ho, N.; Hua, B.S. Point-set distances for learning representations of 3D point clouds. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10478–10487. [Google Scholar]
- Han, X.F.; Jin, J.S.; Wang, M.J.; Jiang, W.; Gao, L.; Xiao, L. A review of algorithms for filtering the 3D point cloud. Signal Process. Image Commun. 2017, 57, 103–112. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, C.; Zhang, H. Composite Ski-Resort Registration Method Based on Laser Point Cloud Information. Machines 2022, 10, 405. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, C.; Zhang, H. A New Method of Ski Tracks Extraction Based on Laser Intensity Information. Appl. Sci. 2022, 12, 5678. [Google Scholar] [CrossRef]
- Żywanowski, K.; Banaszczyk, A.; Nowicki, M.R.; Komorowski, J. MinkLoc3D-SI: 3D LiDAR place recognition with sparse convolutions, spherical coordinates, and intensity. IEEE Robot. Autom. Lett. 2021, 7, 1079–1086. [Google Scholar] [CrossRef]
- Ćwian, K.; Nowicki, M.R.; Nowak, T.; Skrzypczyński, P. Planar features for accurate laser-based 3-D SLAM in urban environments. In Proceedings of the Advanced, Contemporary Control: Proceedings of KKA 2020—The 20th Polish Control Conference, Łódź, Poland, 22–25 June 2020; pp. 941–953.
- Musil, T.; Petrlík, M.; Saska, M. SphereMap: Dynamic Multi-Layer Graph Structure for Rapid Safety-Aware UAV Planning. IEEE Robot. Autom. Lett. 2022, 7, 11007–11014. [Google Scholar] [CrossRef]
- Petrlík, M.; Krajník, T.; Saska, M. LIDAR-based Stabilization, Navigation and Localization for UAVs Operating in Dark Indoor Environments. In Proceedings of the 2021 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 15–18 June 2021; pp. 243–251. [Google Scholar]
- Grilli, E.; Menna, F.; Remondino, F. A review of point clouds segmentation and classification algorithms. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 339. [Google Scholar] [CrossRef]
- Challis, J.H. A procedure for determining rigid body transformation parameters. J. Biomech. 1995, 28, 733–737. [Google Scholar] [CrossRef]
- Rusinkiewicz, S.; Levoy, M. Efficient variants of the ICP algorithm. In Proceedings of the Third International Conference on 3-D Digital Imaging and Modeling, Quebec City, QC, Canada, 28 May–1 June 2001; pp. 145–152. [Google Scholar]
- Olesik, J.W. Elemental analysis using icp-oes and icp/ms. Anal. Chem. 1991, 63, 12A. [Google Scholar] [CrossRef]
- Eggert, D.W.; Lorusso, A.; Fisher, R.B. Estimating 3-D rigid body transformations: A comparison of four major algorithms. Mach. Vis. Appl. 1997, 9, 272–290. [Google Scholar] [CrossRef]
- Livieratos, L.; Stegger, L.; Bloomfield, P.; Schafers, K.; Bailey, D.; Camici, P. Rigid-body transformation of list-mode projection data for respiratory motion correction in cardiac PET. Phys. Med. Biol. 2005, 50, 3313. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Proceedings of the Sensor Fusion IV: Control Paradigms and Data Structures, Boston, MA, USA, 12–15 November 1991; Volume 1611, pp. 586–606. [Google Scholar]
- Griffiths, D.; Boehm, J. SynthCity: A large scale synthetic point cloud. arXiv 2019, arXiv:1907.04758. [Google Scholar]
- Shen, W.; Ren, Q.; Liu, D.; Zhang, Q. Interpreting representation quality of dnns for 3d point cloud processing. Adv. Neural Inf. Process. Syst. 2021, 34, 8857–8870. [Google Scholar]
- Zhong, J.; Dujovny, M.; Park, H.K.; Perez, E.; Perlin, A.R.; Diaz, F.G. Advances in ICP monitoring techniques. Neurol. Res. 2003, 25, 339–350. [Google Scholar] [CrossRef] [PubMed]
- Deaton, A.; Aten, B. Trying to Understand the PPPs in ICP 2011: Why are the Results so Different? Am. Econ. J. Macroecon. 2017, 9, 243–264. [Google Scholar] [CrossRef]
- Vanhaecke, F.; Vanhoe, H.; Dams, R.; Vandecasteele, C. The use of internal standards in ICP-MS. Talanta 1992, 39, 737–742. [Google Scholar] [CrossRef] [PubMed]
- Sharp, G.C.; Lee, S.W.; Wehe, D.K. ICP registration using invariant features. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 90–102. [Google Scholar] [CrossRef]
- Tyler, G.; Jobin Yvon, S. ICP-OES, ICP-MS and AAS Techniques Compared; ICP Optical Emission Spectroscopy Technical Note; ICP: Taichung, Taiwan, 1995; Volume 5. [Google Scholar]
- Rusu, R.B.; Holzbach, A.; Beetz, M.; Bradski, G. Detecting and segmenting objects for mobile manipulation. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision Workshops, ICCV Workshops, Kyoto, Japan, 29 September–2 October 2009; pp. 47–54. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast point feature histograms (FPFH) for 3D registration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar]
- Guo, Y.; Bennamoun, M.; Sohel, F.; Lu, M.; Wan, J.; Kwok, N.M. A comprehensive performance evaluation of 3D local feature descriptors. Int. J. Comput. Vis. 2016, 116, 66–89. [Google Scholar] [CrossRef]
- Mei, Q.; Wang, F.; Tong, C.; Zhang, J.; Jiang, B.; Xiao, J. PACNet: A High-precision Point Cloud Registration Network Based on Deep Learning. In Proceedings of the 2021 13th International Conference on Wireless Communications and Signal Processing (WCSP), Hunan, China, 20–22 October 2021; pp. 1–5. [Google Scholar]
- Liu, Y.; Li, Y.; Dai, L.; Yang, C.; Wei, L.; Lai, T.; Chen, R. Robust feature matching via advanced neighborhood topology consensus. Neurocomputing 2021, 421, 273–284. [Google Scholar] [CrossRef]
- Zhang, K.; Lu, J.; Lafruit, G. Cross-based local stereo matching using orthogonal integral images. IEEE Trans. Circuits Syst. Video Technol. 2009, 19, 1073–1079. [Google Scholar] [CrossRef]
- Ying, S.; Peng, J.; Du, S.; Qiao, H. A scale stretch method based on ICP for 3D data registration. IEEE Trans. Autom. Sci. Eng. 2009, 6, 559–565. [Google Scholar] [CrossRef]
- Zhao, H.; Tang, M.; Ding, H. HoPPF: A novel local surface descriptor for 3D object recognition. Pattern Recognit. 2020, 103, 107272. [Google Scholar] [CrossRef]
- Liu, C.; Wechsler, H. Independent component analysis of Gabor features for face recognition. IEEE Trans. Neural Netw. 2003, 14, 919–928. [Google Scholar]
- Qi, H.; Li, K.; Shen, Y.; Qu, W. An effective solution for trademark image retrieval by combining shape description and feature matching. Pattern Recognit. 2010, 43, 2017–2027. [Google Scholar] [CrossRef]
- Choy, C.; Dong, W.; Koltun, V. Deep global registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2514–2523. [Google Scholar]
- Gojcic, Z.; Zhou, C.; Wegner, J.D.; Guibas, L.J.; Birdal, T. Learning multiview 3d point cloud registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1759–1769. [Google Scholar]
- Choy, C.; Park, J.; Koltun, V. Fully convolutional geometric features. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 8958–8966. [Google Scholar]
- El Banani, M.; Gao, L.; Johnson, J. Unsupervisedr&r: Unsupervised point cloud registration via differentiable rendering. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 7129–7139. [Google Scholar]
- El Banani, M.; Johnson, J. Bootstrap your own correspondences. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 6433–6442. [Google Scholar]
- Holz, D.; Ichim, A.E.; Tombari, F.; Rusu, R.B.; Behnke, S. Registration with the point cloud library: A modular framework for aligning in 3-D. IEEE Robot. Autom. Mag. 2015, 22, 110–124. [Google Scholar] [CrossRef]
- Kim, H.; Hilton, A. Influence of colour and feature geometry on multi-modal 3d point clouds data registration. In Proceedings of the 2014 2nd International Conference on 3D Vision, Tokyo, Japan, 8–11 December 2014; Volume 1, pp. 202–209. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Marton, Z.C.; Beetz, M. Aligning point cloud views using persistent feature histograms. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3384–3391. [Google Scholar]
- Peng, K.; Chen, X.; Zhou, D.; Liu, Y. 3D reconstruction based on SIFT and Harris feature points. In Proceedings of the 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guilin, China, 13–19 December 2009; pp. 960–964. [Google Scholar]
- Luo, C.; Zhan, J.; Xue, X.; Wang, L.; Ren, R.; Yang, Q. Cosine normalization: Using cosine similarity instead of dot product in neural networks. In Proceedings of the International Conference on Artificial Neural Networks, Rhodes, Greece, 4–7 October 2018; pp. 382–391. [Google Scholar]
- Wang, Y.; Zheng, N.; Bian, Z. A Closed-Form Solution to Planar Feature-Based Registration of LiDAR Point Clouds. ISPRS Int. J. Geo-Inf. 2021, 10, 435. [Google Scholar] [CrossRef]
- Huang, L.; Da, F.; Gai, S. Research on multi-camera calibration and point cloud correction method based on three-dimensional calibration object. Opt. Lasers Eng. 2019, 115, 32–41. [Google Scholar] [CrossRef]
- Aldoma, A.; Marton, Z.C.; Tombari, F.; Wohlkinger, W.; Potthast, C.; Zeisl, B.; Rusu, R.B.; Gedikli, S.; Vincze, M. Tutorial: Point cloud library: Three-dimensional object recognition and 6 dof pose estimation. IEEE Robot. Autom. Mag. 2012, 19, 80–91. [Google Scholar] [CrossRef]
- Haneberg, W.C. Directional roughness profiles from three-dimensional photogrammetric or laser scanner point clouds. In Proceedings of the 1st Canada-US Rock Mechanics Symposium, Vancouver, BC, Canada, 27–31 May 2007. [Google Scholar]
- Vosselman, G.; Gorte, B.G.; Sithole, G.; Rabbani, T. Recognising structure in laser scanner point clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 46, 33–38. [Google Scholar]
- Steder, B.; Rusu, R.B.; Konolige, K.; Burgard, W. NARF: 3D range image features for object recognition. In Proceedings of the Workshop on Defining and Solving Realistic Perception Problems in Personal Robotics at the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Taipei, Taiwan, 18–22 October 2010; Volume 44, p. 2. [Google Scholar]
- Ohkawa, N.; Kokura, K.; Matsu-ura, T.; Obinata, T.; Konishi, Y.; Tamura, T.a. Molecular cloning and characterization of neural activity-related RING finger protein (NARF): A new member of the RBCC family is a candidate for the partner of myosin V. J. Neurochem. 2001, 78, 75–87. [Google Scholar] [CrossRef]
- Marion, B.; Rummel, S.; Anderberg, A. Current–voltage curve translation by bilinear interpolation. Prog. Photovoltaics Res. Appl. 2004, 12, 593–607. [Google Scholar] [CrossRef]
- Hurtik, P.; Madrid, N. Bilinear interpolation over fuzzified images: Enlargement. In Proceedings of the 2015 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Istanbul, Turkey, 2–5 August 2015; pp. 1–8. [Google Scholar]
- Xia, P.; Tahara, T.; Kakue, T.; Awatsuji, Y.; Nishio, K.; Ura, S.; Kubota, T.; Matoba, O. Performance comparison of bilinear interpolation, bicubic interpolation, and B-spline interpolation in parallel phase-shifting digital holography. Opt. Rev. 2013, 20, 193–197. [Google Scholar] [CrossRef]
- Hwang, J.W.; Lee, H.S. Adaptive image interpolation based on local gradient features. IEEE Signal Process. Lett. 2004, 11, 359–362. [Google Scholar] [CrossRef]
- Villota, J.C.P.; da Silva, F.L.; de Souza Jacomini, R.; Costa, A.H.R. Pairwise registration in indoor environments using adaptive combination of 2D and 3D cues. Image Vis. Comput. 2018, 69, 113–124. [Google Scholar] [CrossRef]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for point-cloud shape detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- Agüera-Vega, F.; Agüera-Puntas, M.; Martínez-Carricondo, P.; Mancini, F.; Carvajal, F. Effects of point cloud density, interpolation method and grid size on derived Digital Terrain Model accuracy at micro topography level. Int. J. Remote Sens. 2020, 41, 8281–8299. [Google Scholar] [CrossRef]
- Chen, Z.; Li, J.; Yang, B. A strip adjustment method of UAV-borne lidar point cloud based on DEM features for mountainous area. Sensors 2021, 21, 2782. [Google Scholar] [CrossRef]
- Łępicka, M.; Kornuta, T.; Stefańczyk, M. Utilization of colour in ICP-based point cloud registration. In Proceedings of the 9th International Conference on Computer Recognition Systems CORES, Wroclaw, Poland, 25–27 May 2015; pp. 821–830. [Google Scholar]
- Derpanis, K.G. Overview of the RANSAC Algorithm. Image Rochester NY 2010, 4, 2–3. [Google Scholar]
- Lin, D.; Jarzabek-Rychard, M.; Tong, X.; Maas, H.G. Fusion of thermal imagery with point clouds for building façade thermal attribute mapping. ISPRS J. Photogramm. Remote Sens. 2019, 151, 162–175. [Google Scholar] [CrossRef]
- Magnusson, M.; Lilienthal, A.; Duckett, T. Scan registration for autonomous mining vehicles using 3D-NDT. J. Field Robot. 2007, 24, 803–827. [Google Scholar] [CrossRef]
- Serafin, J.; Grisetti, G. NICP: Dense normal based point cloud registration. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 742–749. [Google Scholar]
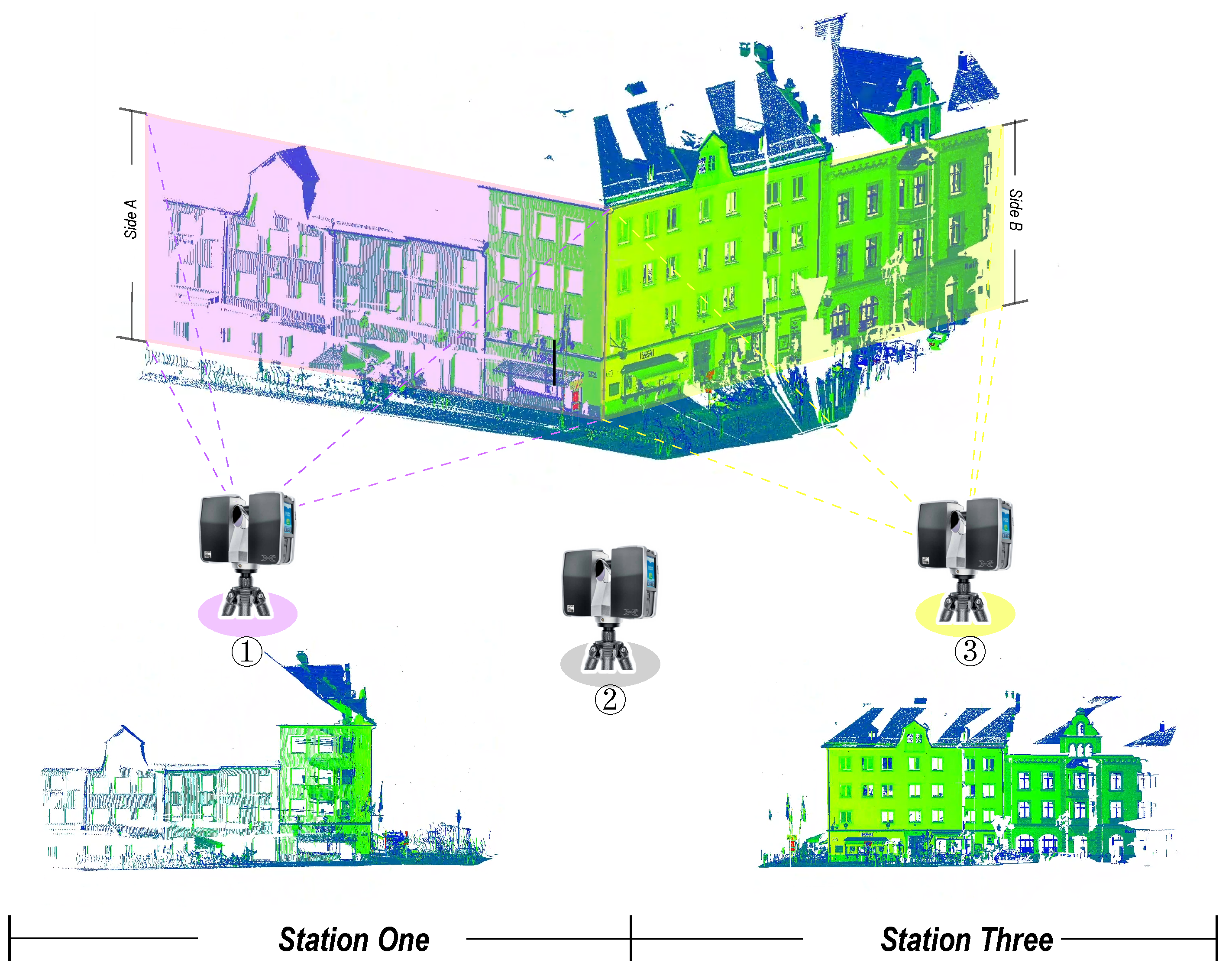
 ) in the point cloud dataset that represent different altitudes; (3) Feature matching point pairs. A mixed feature pair point set is established through geometric matching and photometric matching; (4) Data processing. By optimizing random sampling and evaluation estimation, the RANSAC algorithm finally reaches target registration.
) in the point cloud dataset that represent different altitudes; (3) Feature matching point pairs. A mixed feature pair point set is established through geometric matching and photometric matching; (4) Data processing. By optimizing random sampling and evaluation estimation, the RANSAC algorithm finally reaches target registration.
 ) in the point cloud dataset that represent different altitudes; (3) Feature matching point pairs. A mixed feature pair point set is established through geometric matching and photometric matching; (4) Data processing. By optimizing random sampling and evaluation estimation, the RANSAC algorithm finally reaches target registration.
) in the point cloud dataset that represent different altitudes; (3) Feature matching point pairs. A mixed feature pair point set is established through geometric matching and photometric matching; (4) Data processing. By optimizing random sampling and evaluation estimation, the RANSAC algorithm finally reaches target registration.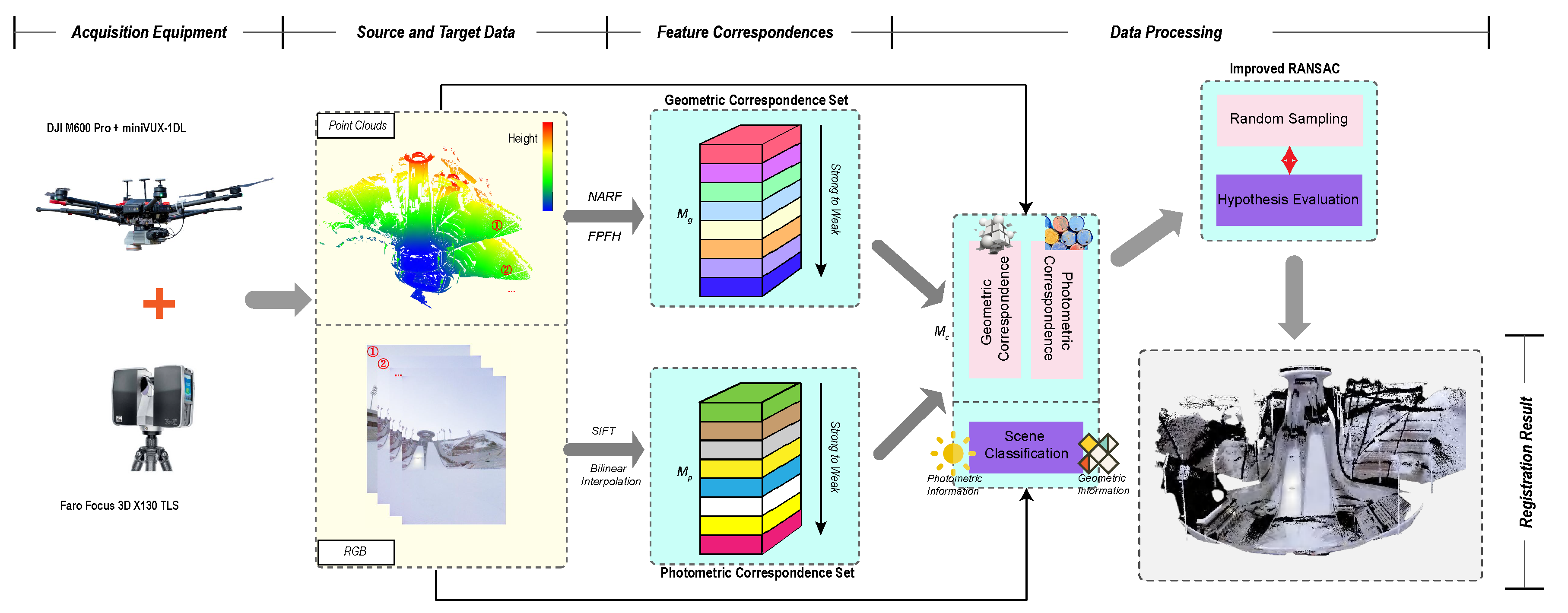
 : Correspondences).
: Correspondences).
 : Correspondences).
: Correspondences).


 ). Moreover, each small sample is displayed sequentially with laser point information and RGB image information. A gradient bar with a changing color based on the height is represented by
). Moreover, each small sample is displayed sequentially with laser point information and RGB image information. A gradient bar with a changing color based on the height is represented by  .
.
 ). Moreover, each small sample is displayed sequentially with laser point information and RGB image information. A gradient bar with a changing color based on the height is represented by
). Moreover, each small sample is displayed sequentially with laser point information and RGB image information. A gradient bar with a changing color based on the height is represented by  .
.


| Category | ULS | TLS |
|---|---|---|
| Model | DJI M600 pro+UAV-1 series | Faro Focus 3D X130 |
| Measuring Distance | 3–1050 m | 0.6–120 m |
| Scan Angle | 360° | 360° (horizontal), 300° (vertical) |
| Measurement Rate | 10–200 lines/s | 976,000 points/s |
| Angular Resolution | 0.006° | 0.009° |
| Accuracy | ±5 mm | ±2 mm |
| Ambient Temperature | −10–+40 °C | −5–+40 °C |
| Wavelength | 1550 nm | 1550 nm |
| Category | Configuration | |
|---|---|---|
| Software | Operating System | Win 11 |
| Point Cloud Processing Library | PCL 1.11.1 | |
| Support Platform | Visual Studio 2019 | |
| Hardware | CPU | Intel(R)Core(TM)i5-9400F |
| Memory | DDR4 32 GB | |
| Graphics Card | Nvidia GTX 1080 Ti 11 GB | |
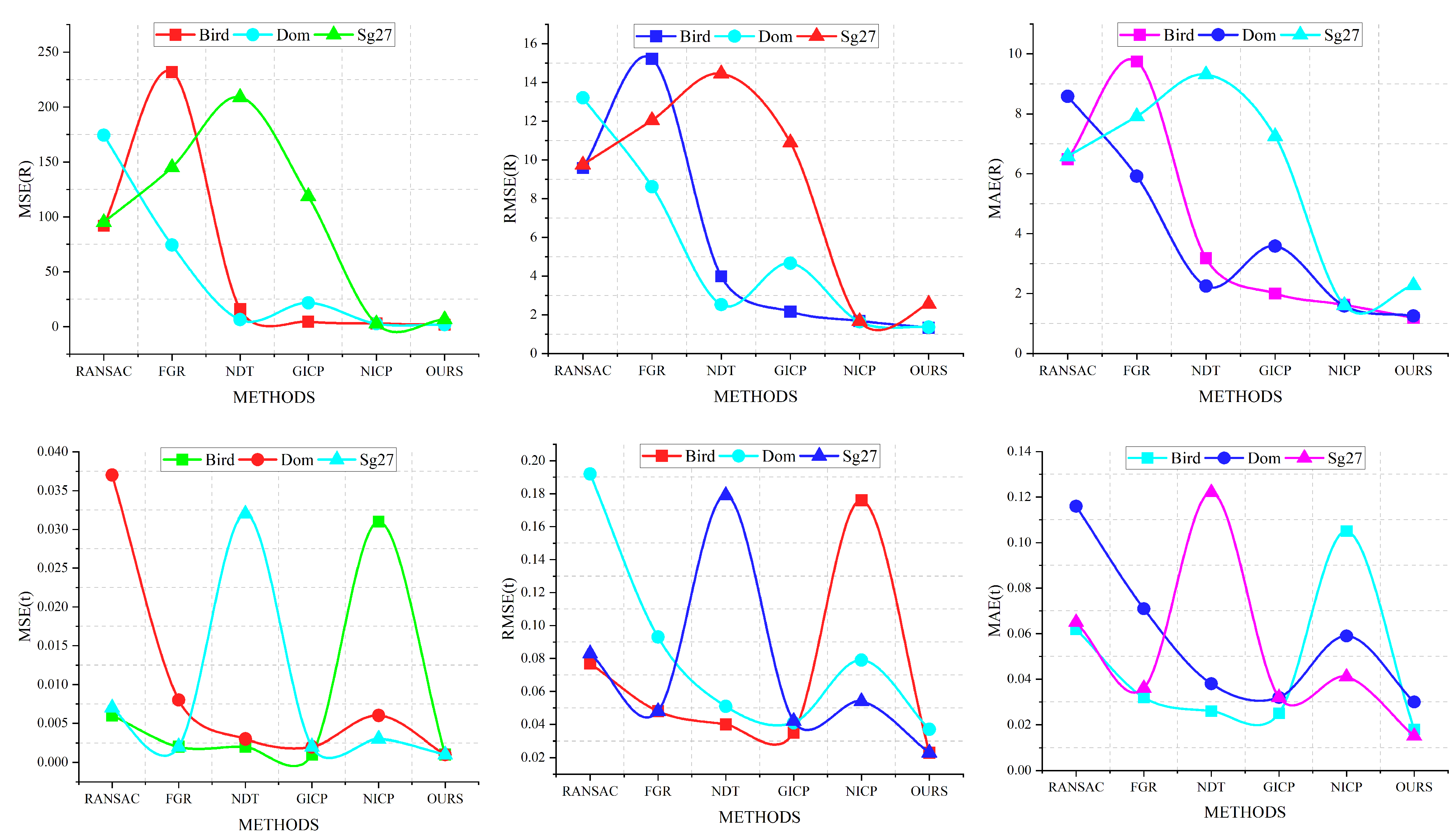
| Methods | MSE(R)↓ | RMSE(R)↓ | MAE(R)↓ | MSE(t) (×)↓ | RMSE(t) (×)↓ | MAE(t) (×)↓ | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bird | Dom | Sg27 | Bird | Dom | Sg27 | Bird | Dom | Sg27 | Bird | Dom | Sg27 | Bird | Dom | Sg27 | Bird | Dom | Sg27 | |
| RANSAC | 91.867 | 174.339 | 95.075 | 9.584 | 13.203 | 9.750 | 6.483 | 8.586 | 6.580 | 0.006 | 0.037 | 0.007 | 0.077 | 0.192 | 0.083 | 0.062 | 0.116 | 0.065 |
| FGR | 231.879 | 74.285 | 145.049 | 15.227 | 8.618 | 12.043 | 9.75 | 5.919 | 7.913 | 0.002 | 0.008 | 0.002 | 0.048 | 0.093 | 0.048 | 0.032 | 0.071 | 0.036 |
| NDT | 15.923 | 6.379 | 208.834 | 3.990 | 2.525 | 14.451 | 3.179 | 2.253 | 9.310 | 0.002 | 0.003 | 0.032 | 0.040 | 0.051 | 0.179 | 0.026 | 0.038 | 0.122 |
| GICP | 4.706 | 21.739 | 118.729 | 2.169 | 4.662 | 10.896 | 2.006 | 3.586 | 7.246 | 0.001 | 0.002 | 0.002 | 0.035 | 0.041 | 0.042 | 0.025 | 0.032 | 0.032 |
| NICP | 2.844 | 2.699 | 2.782 | 1.686 | 1.642 | 1.668 | 1.626 | 1.586 | 1.609 | 0.031 | 0.006 | 0.003 | 0.176 | 0.079 | 0.054 | 0.105 | 0.059 | 0.041 |
| OURS | 1.774 | 1.859 | 6.556 | 1.332 | 1.363 | 2.561 | 1.189 | 1.253 | 2.276 | 0.001 | 0.001 | 0.001 | 0.023 | 0.037 | 0.023 | 0.018 | 0.030 | 0.015 |
| Methods | MSE(R)↓ | RMSE(R)↓ | MAE(R)↓ | MSE(t) (×)↓ | RMSE(t) (×)↓ | MAE(t) (×)↓ | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SJC | CSC | BSC | SJC | CSC | BSC | SJC | CSC | BSC | SJC | CSC | BSC | SJC | CSC | BSC | SJC | CSC | BSC | |
| RANSAC | 148.107 | 76.566 | 47.062 | 12.169 | 8.750 | 6.860 | 7.986 | 5.996 | 4.890 | 0.195 | 0.066 | 0.006 | 4.413 | 2.567 | 0.08 | 1.642 | 0.709 | 0.054 |
| FGR | 41.707 | 134.866 | 32.836 | 6.458 | 11.613 | 5.730 | 4.653 | 7.663 | 4.223 | 0.039 | 8.464 | 0.002 | 1.989 | 29.093 | 0.044 | 0.445 | 2.487 | 0.031 |
| NDT | 17.813 | 2.986 | 16.496 | 4.221 | 1.728 | 4.061 | 3.319 | 1.677 | 3.223 | 0.032 | 0.019 | 0.001 | 1.798 | 1.394 | 0.026 | 0.202 | 0.284 | 0.018 |
| GICP | 2.947 | 34.933 | 2.596 | 1.716 | 5.910 | 1.611 | 1.653 | 4.330 | 1.556 | 0.004 | 0.049 | 0.001 | 0.636 | 2.207 | 0.032 | 0.759 | 0.540 | 0.027 |
| NICP | 9.867 | 1.993 | 63.956 | 3.141 | 1.411 | 7.997 | 2.673 | 1.328 | 5.568 | 0.012 | 0.004 | 0.034 | 1.097 | 0.176 | 0.185 | 0.815 | 0.145 | 0.123 |
| OURS | 1.667 | 1.930 | 2.436 | 1.291 | 1.389 | 1.561 | 1.013 | 1.296 | 1.506 | 0.001 | 0.003 | 0.001 | 0.018 | 0.179 | 0.023 | 0.004 | 0.120 | 0.015 |
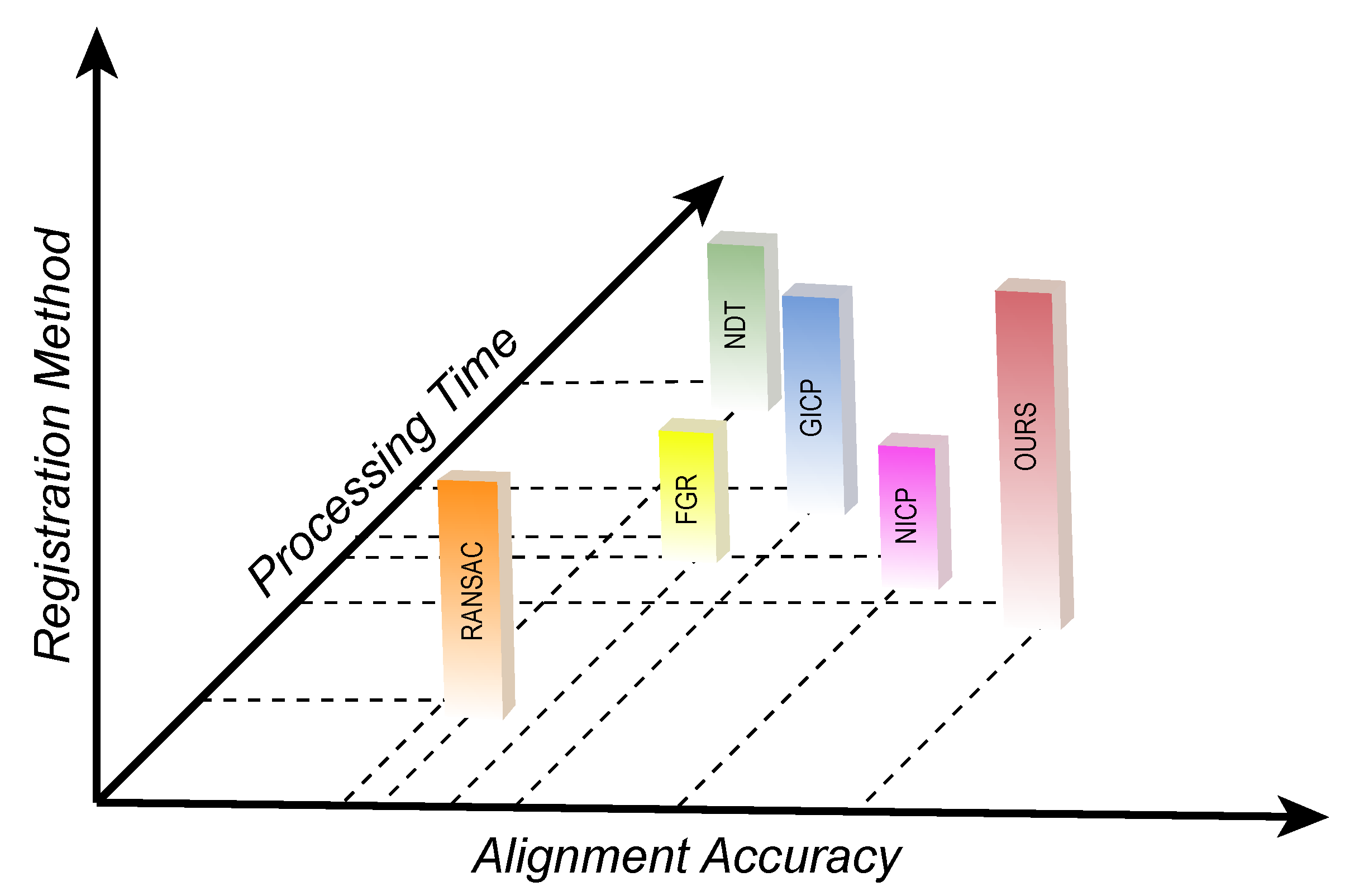
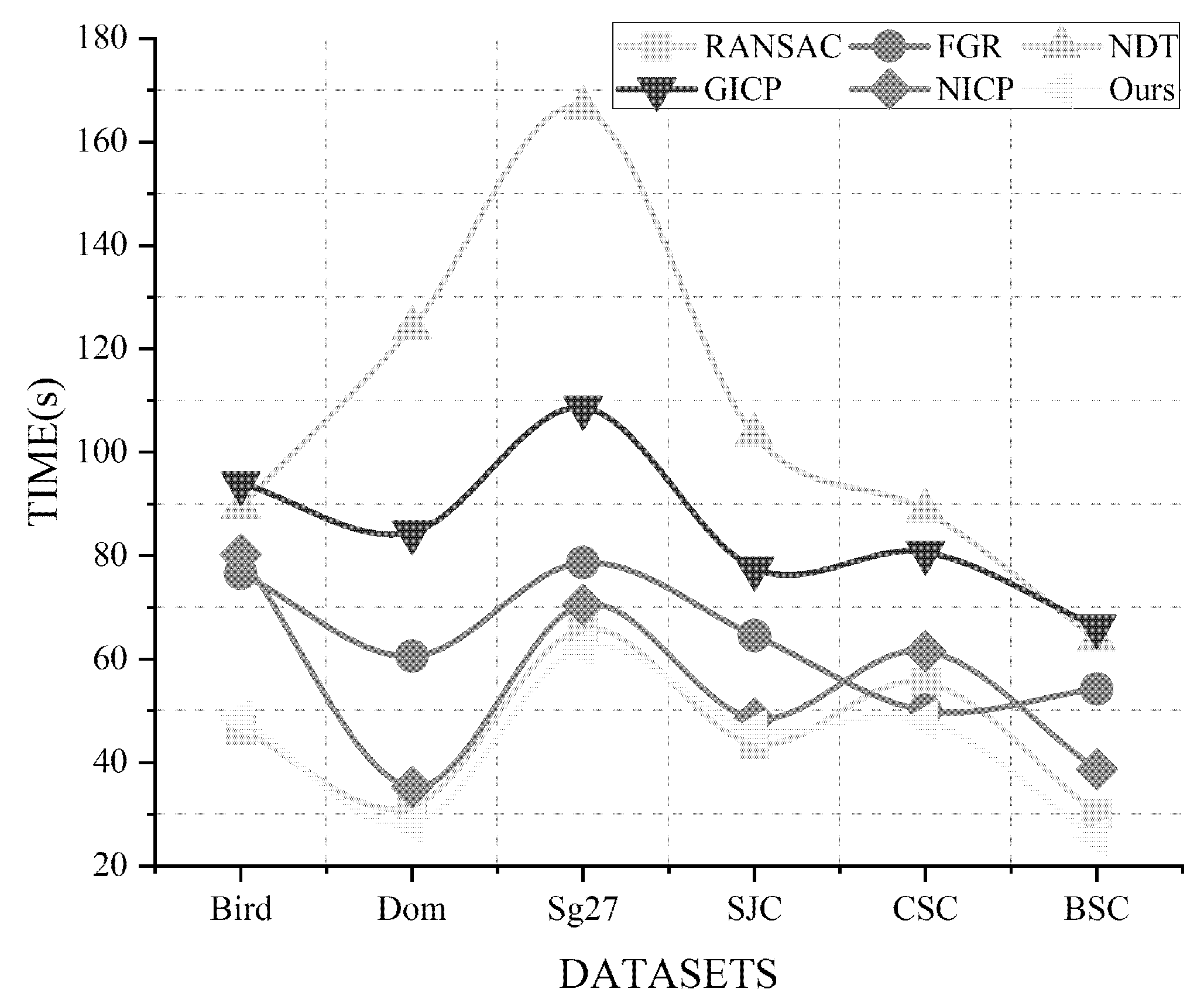
| Methods | Time(s) | |||||
|---|---|---|---|---|---|---|
| Bird | Dom | Sg27 | SJC | CSC | BSC | |
| RANSAC | 46.293 | 31.584 | 65.791 | 43.626 | 55.418 | 30.084 |
| FGR | 76.575 | 60.527 | 78.614 | 64.571 | 50.008 | 54.225 |
| NDT | 89.402 | 124.051 | 166.569 | 103.366 | 88.629 | 63.748 |
| GICP | 94.035 | 84.504 | 108.608 | 77.547 | 80.644 | 66.313 |
| NICP | 80.224 | 35.271 | 70.547 | 48.514 | 61.522 | 38.693 |
| OURS | 48.669 | 28.053 | 62.181 | 46.296 | 48.158 | 25.466 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Zhao, C.; Zhang, H. PR-Alignment: Multidimensional Adaptive Registration Algorithm Based on Practical Application Scenarios. Machines 2023, 11, 254. https://doi.org/10.3390/machines11020254
Wang W, Zhao C, Zhang H. PR-Alignment: Multidimensional Adaptive Registration Algorithm Based on Practical Application Scenarios. Machines. 2023; 11(2):254. https://doi.org/10.3390/machines11020254
Chicago/Turabian StyleWang, Wenxin, Changming Zhao, and Haiyang Zhang. 2023. "PR-Alignment: Multidimensional Adaptive Registration Algorithm Based on Practical Application Scenarios" Machines 11, no. 2: 254. https://doi.org/10.3390/machines11020254
APA StyleWang, W., Zhao, C., & Zhang, H. (2023). PR-Alignment: Multidimensional Adaptive Registration Algorithm Based on Practical Application Scenarios. Machines, 11(2), 254. https://doi.org/10.3390/machines11020254






