A Normalized Terzaghi Model and Time-Step FEA for Predicting the Adsorption of a Cylindrical Object in Subsea Salvage
Abstract
:1. Introduction
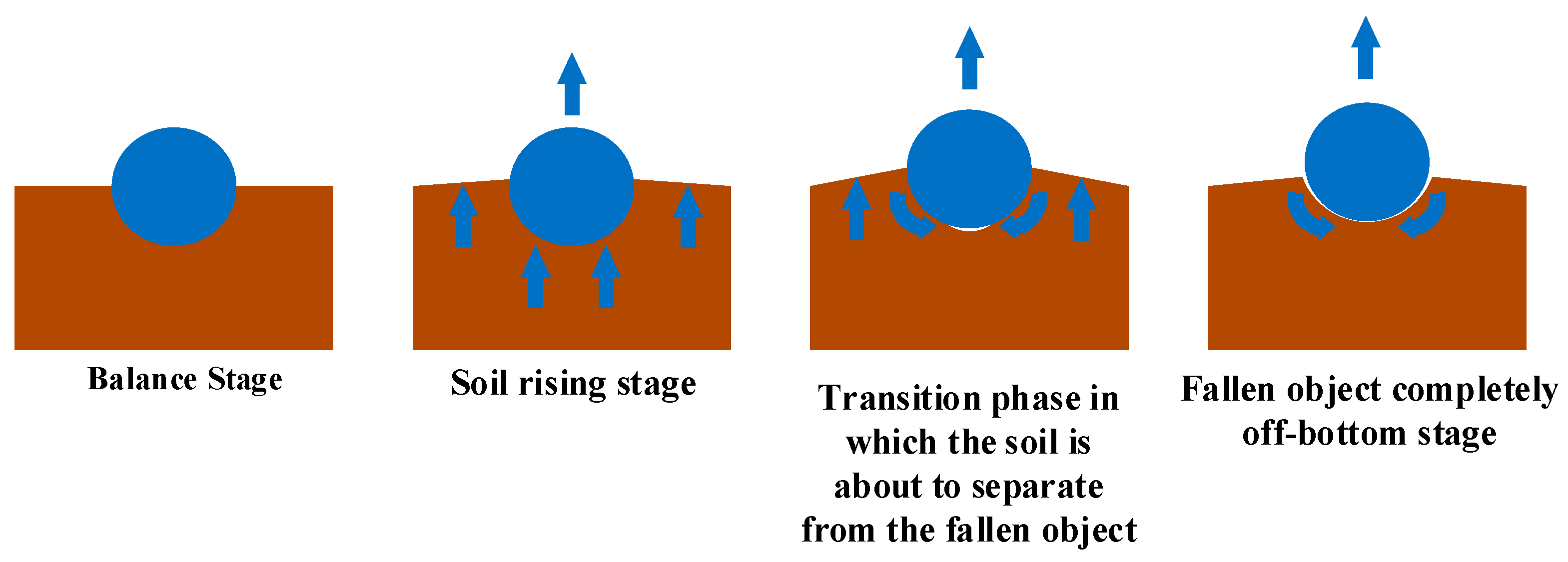
2. The Object and Salvage Process
3. Results of Off-Mud Process Modeling and FEA
3.1. Off-Mud Modelling
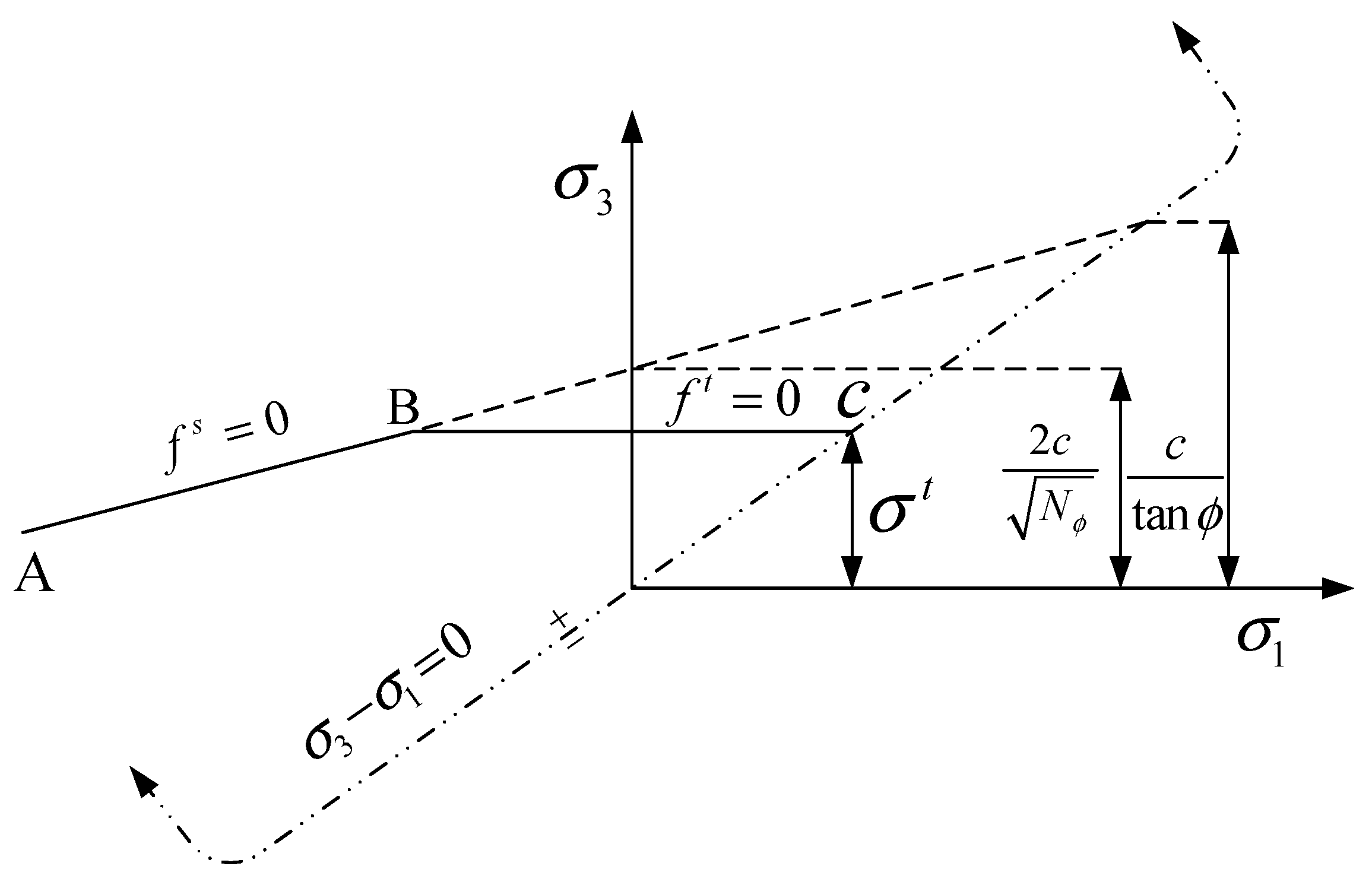
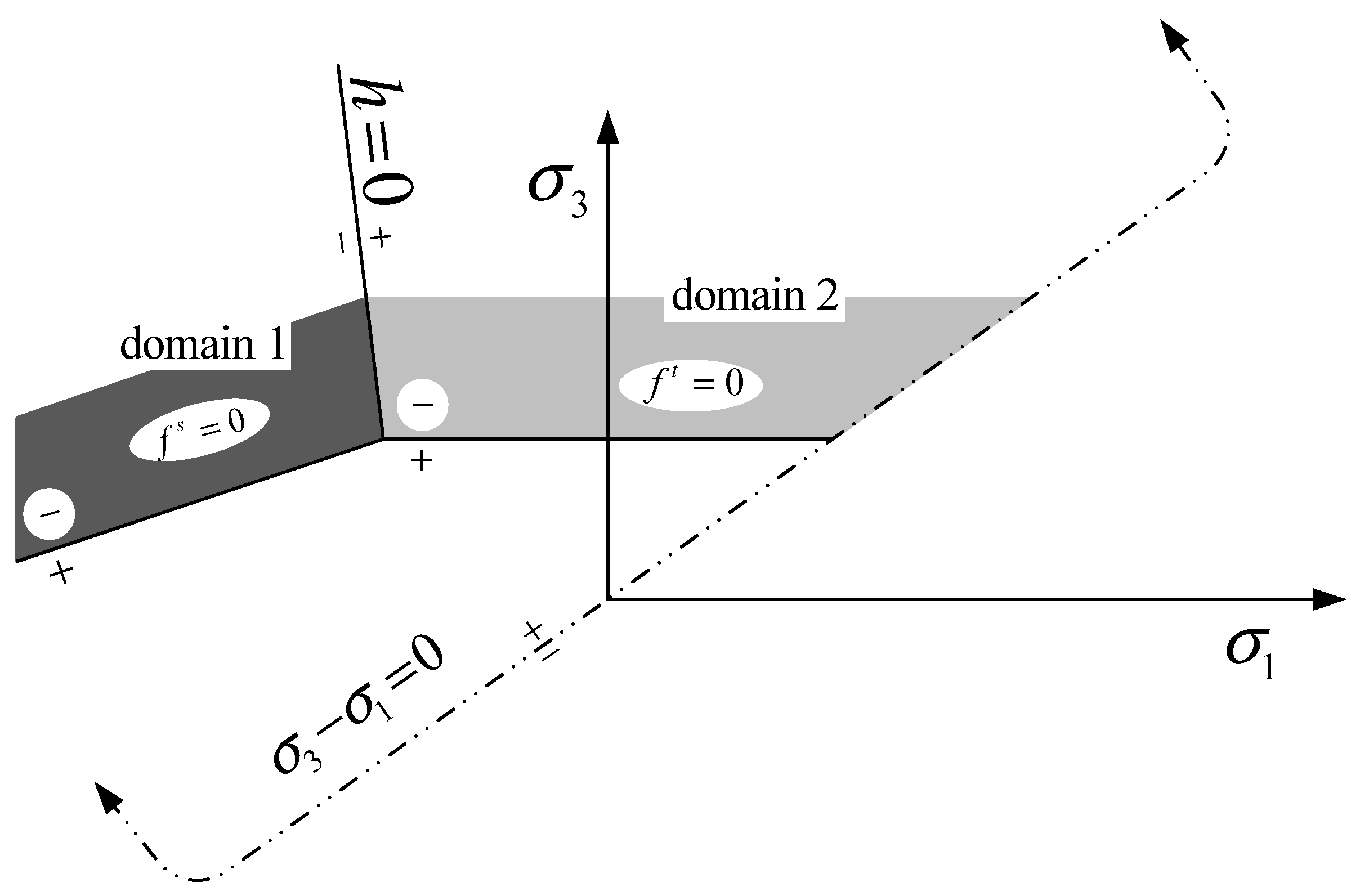
3.1.1. Failure Criterion
3.1.2. Mobility
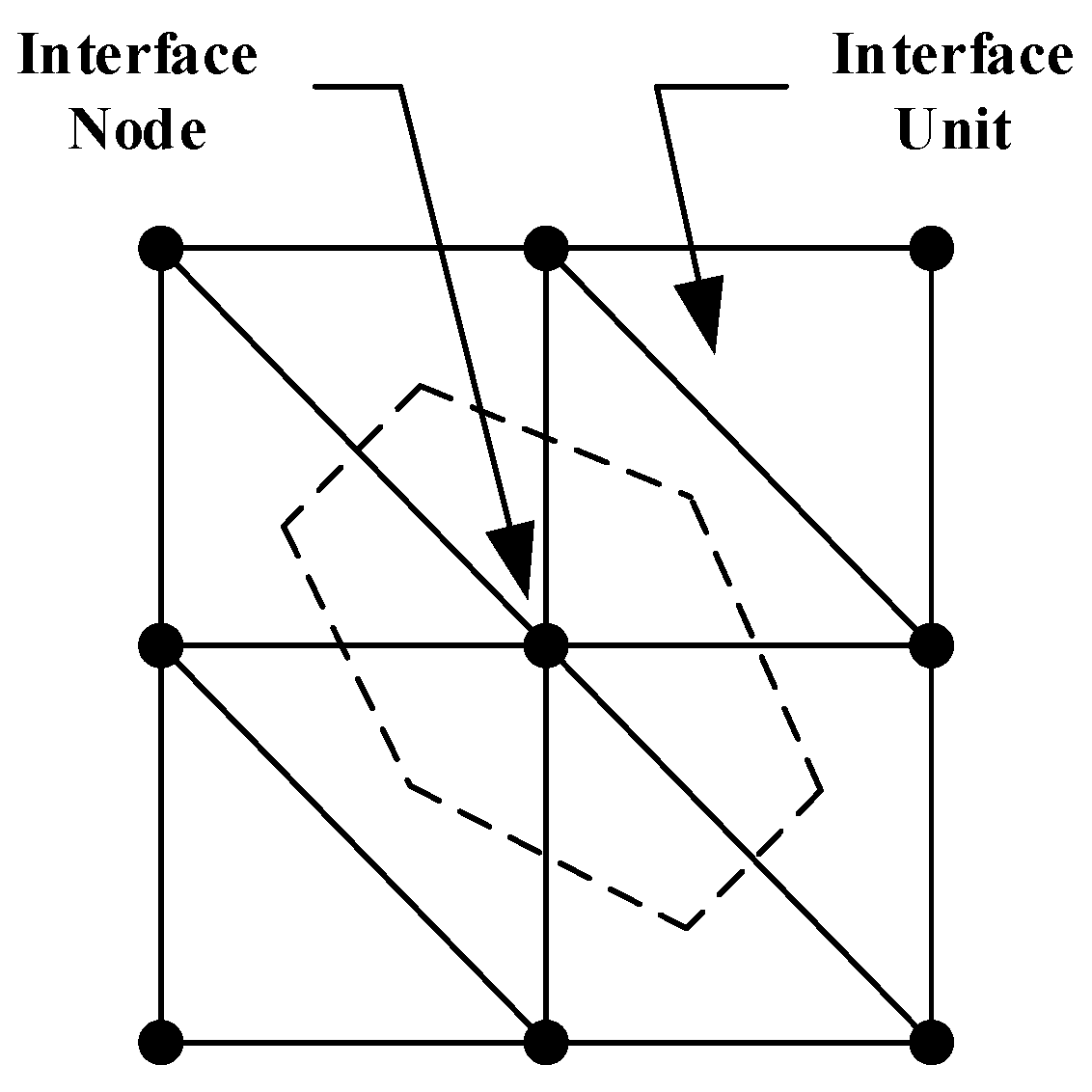
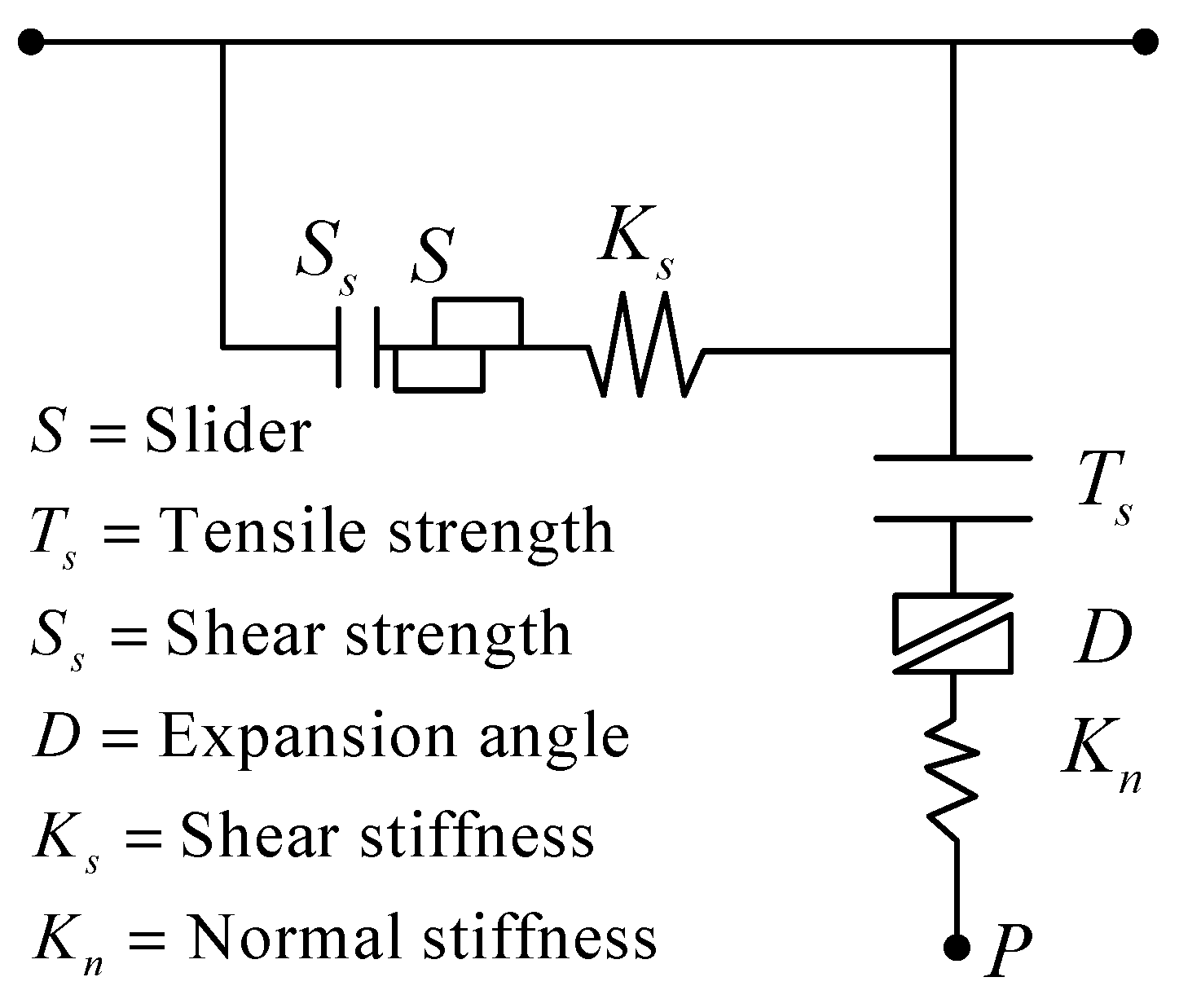
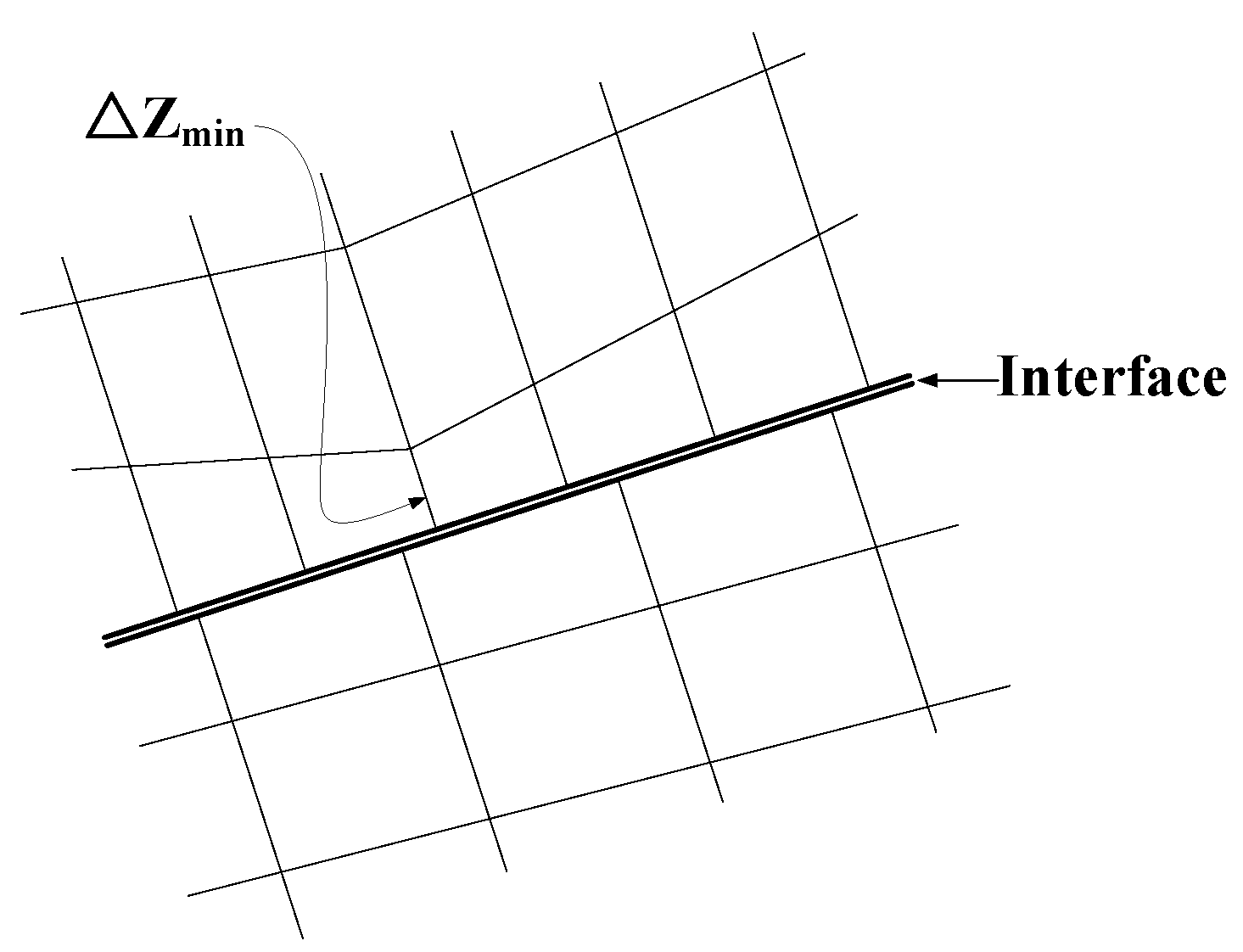
3.1.3. Interface Model
3.1.4. Soil Parameters
3.1.5. Object Parameters
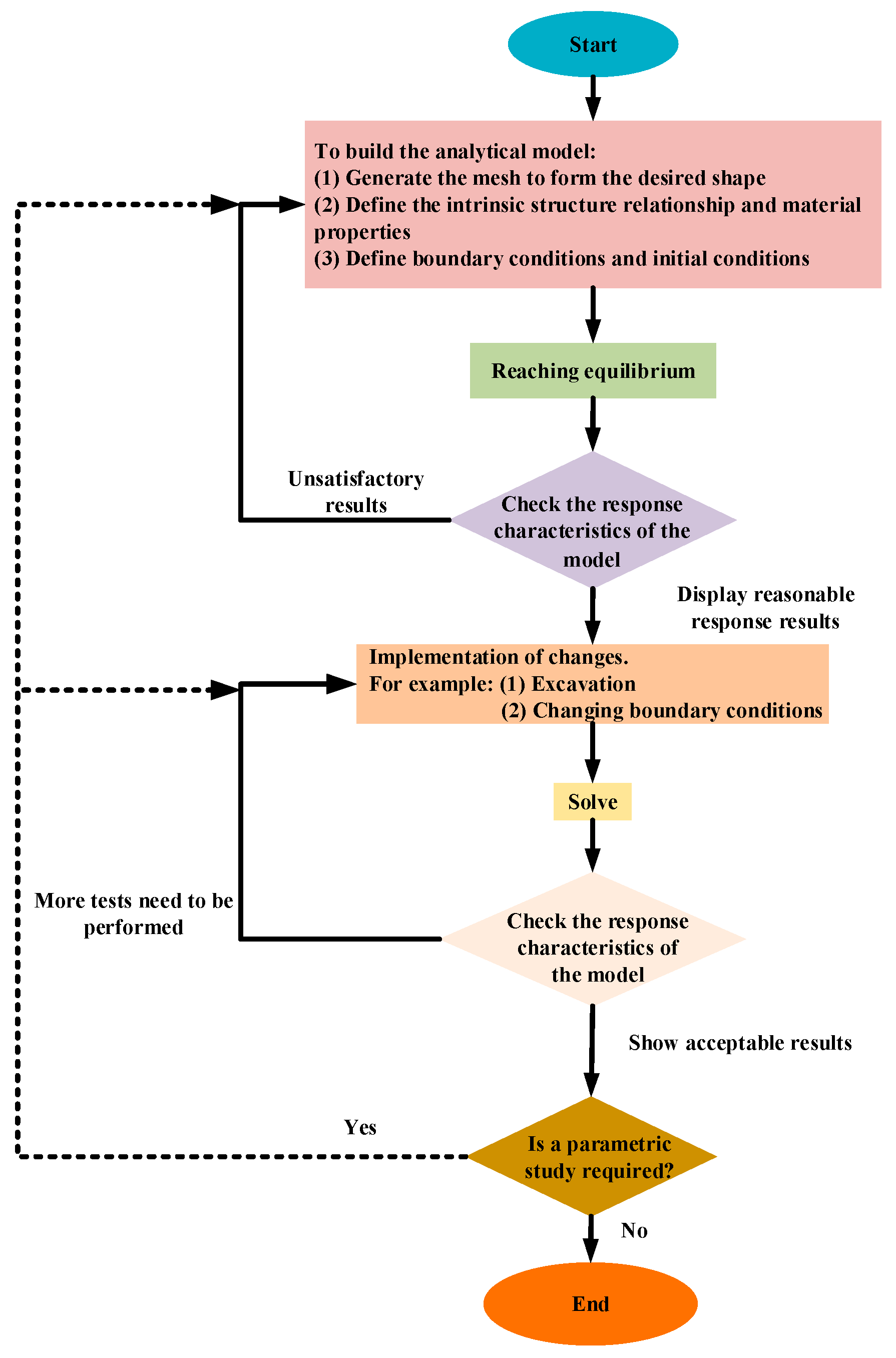
3.2. Finite Element Analysis
- The deformation of the cylindrical structures is not considered;
- The soil is saturated;
- The particles of the soil are incompressible.
Flow Chart of the Simulation
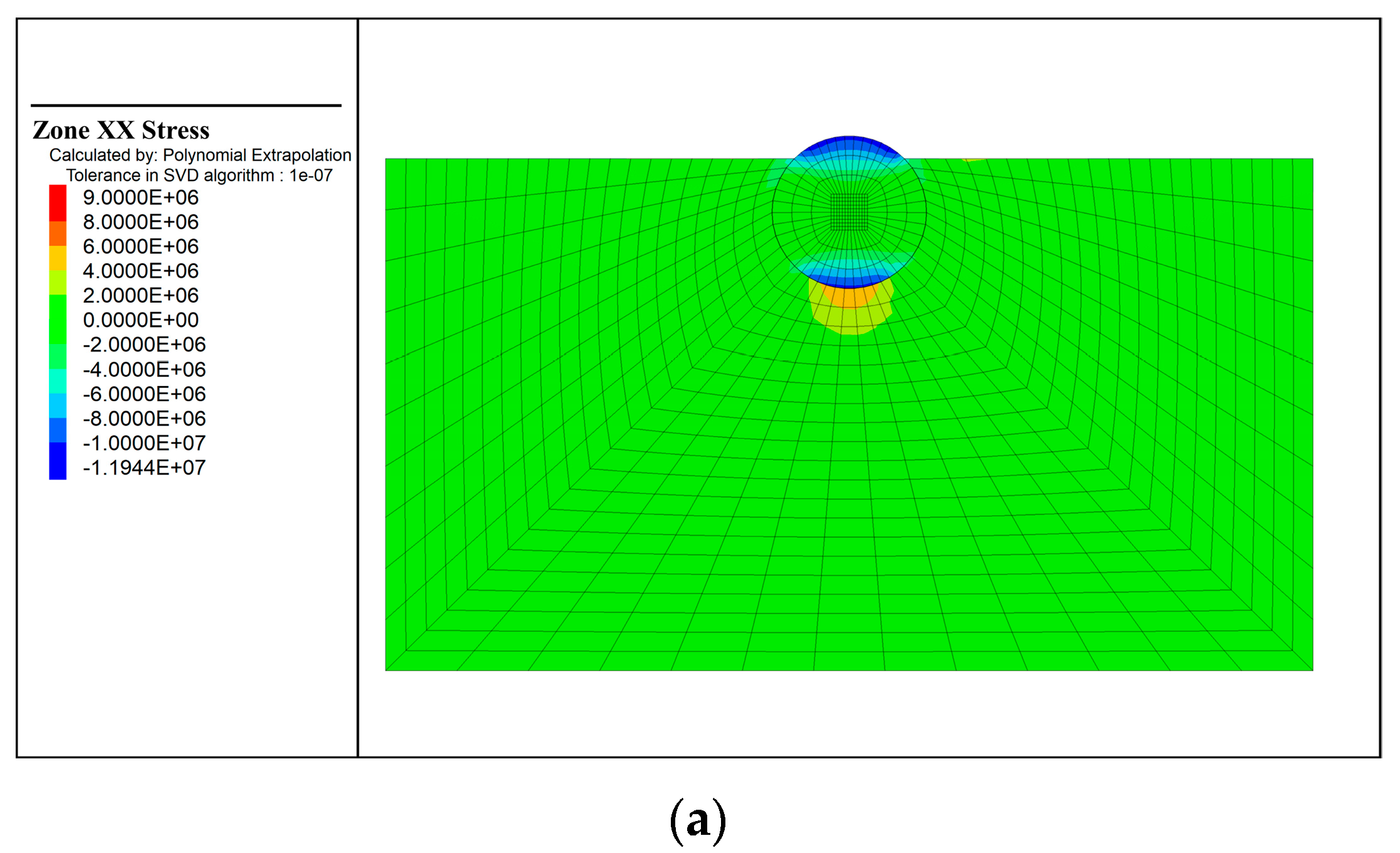
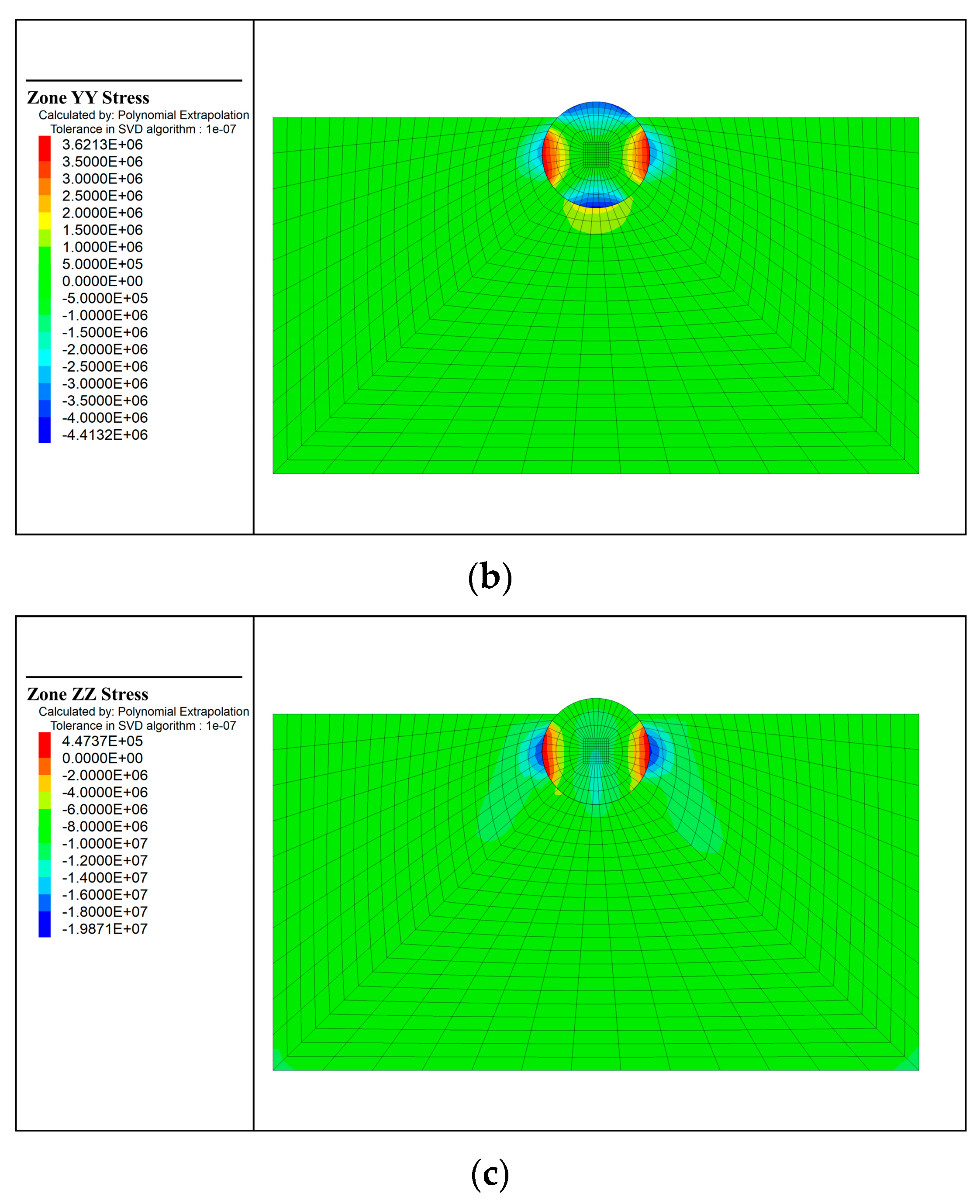
3.3. Initial Stress and Off-Mud Process
3.3.1. Initial Stress
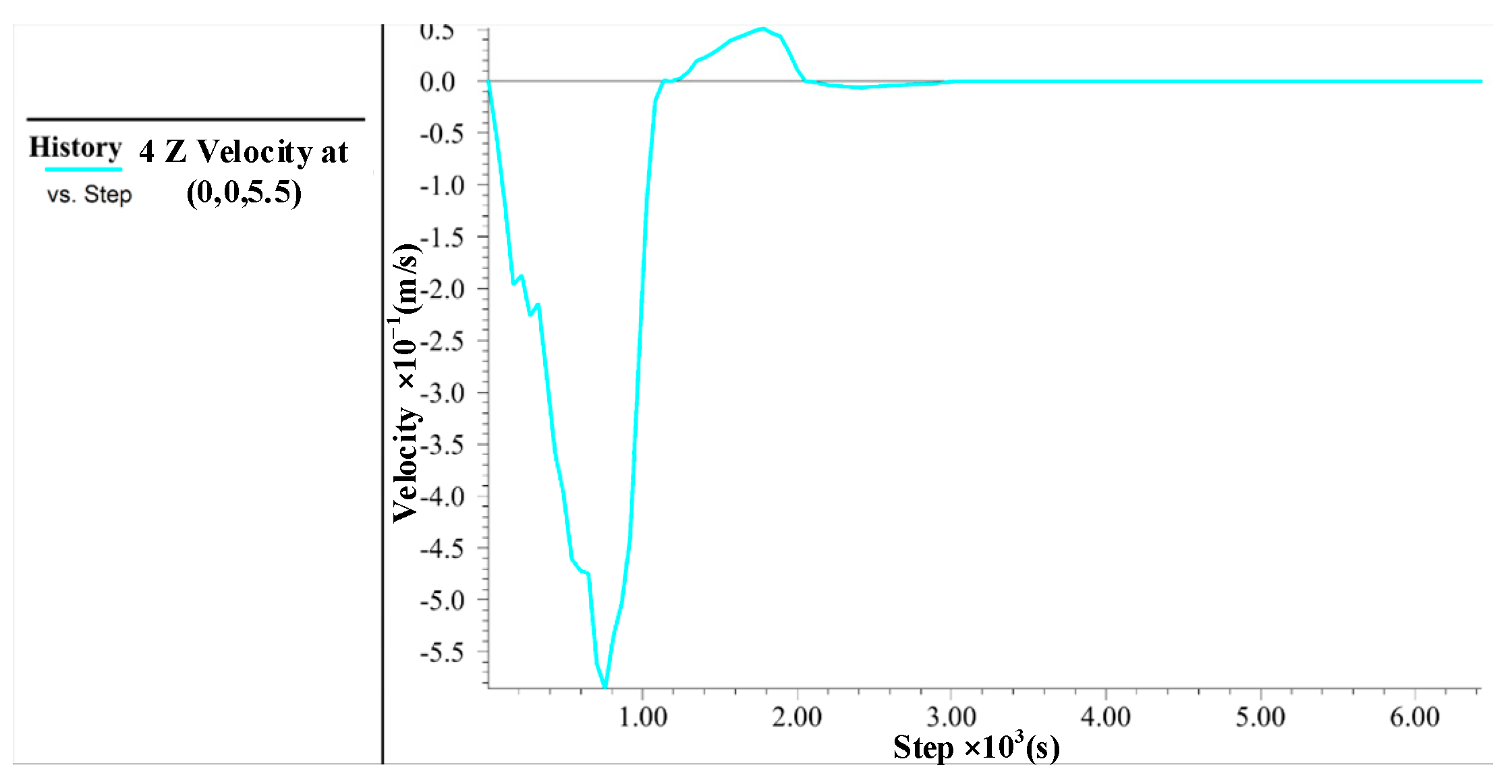
3.3.2. Off-Mud Simulation
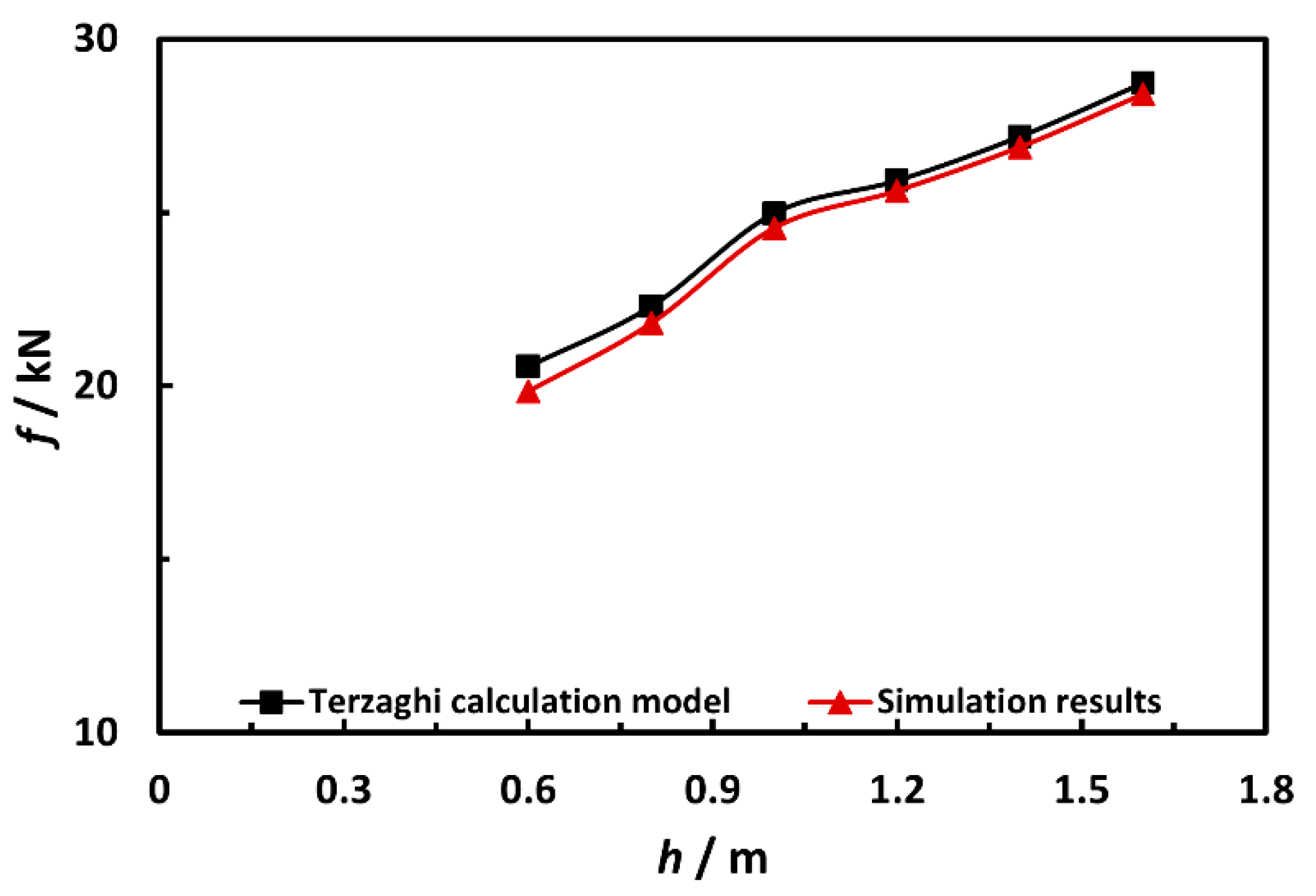
4. Comparison and Modification of the Terzaghi Model
4.1. Comparison with FEA Results
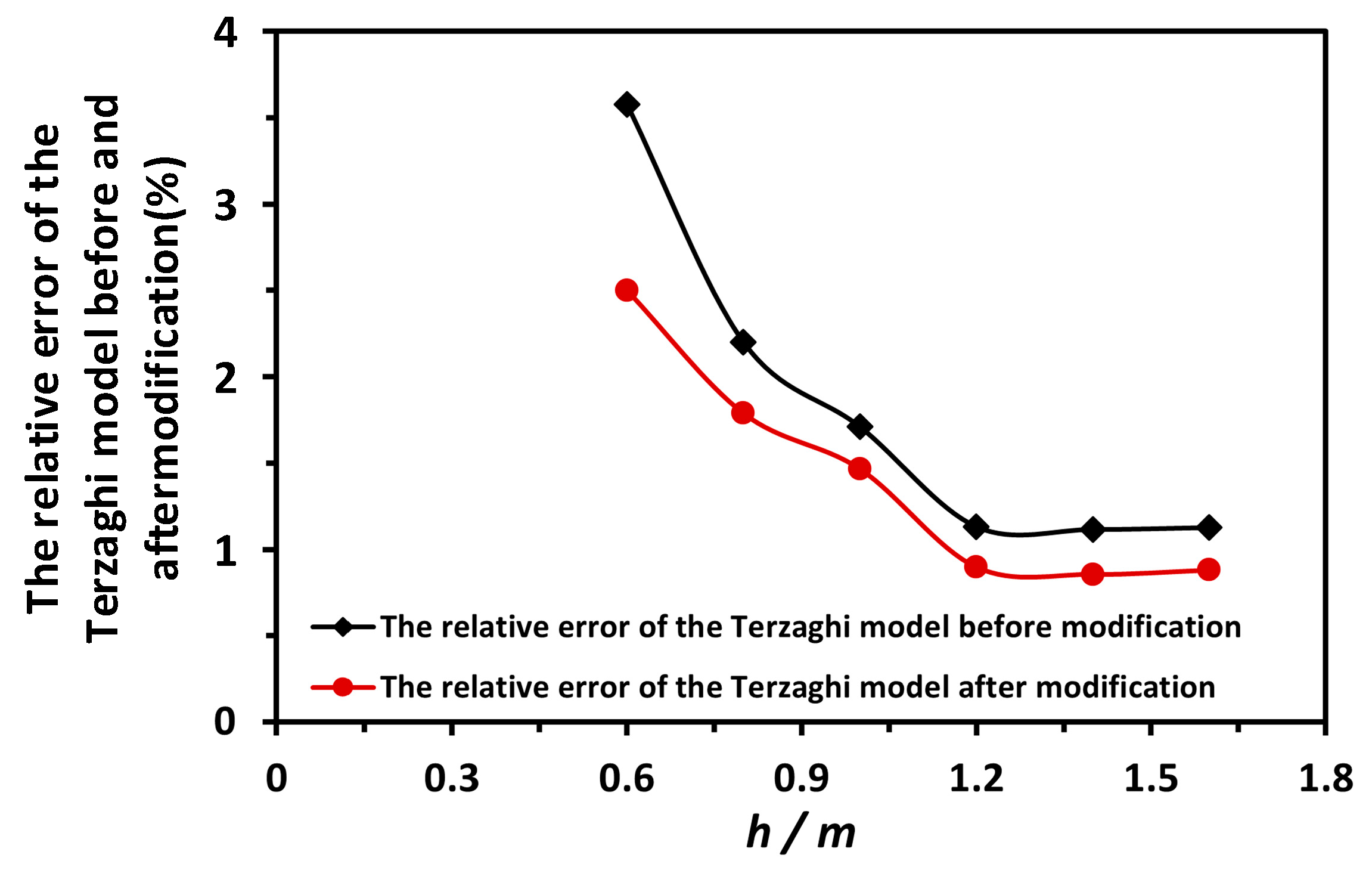
4.2. Normalized Terzaghi Model and Modification
5. Time-Step Analysis
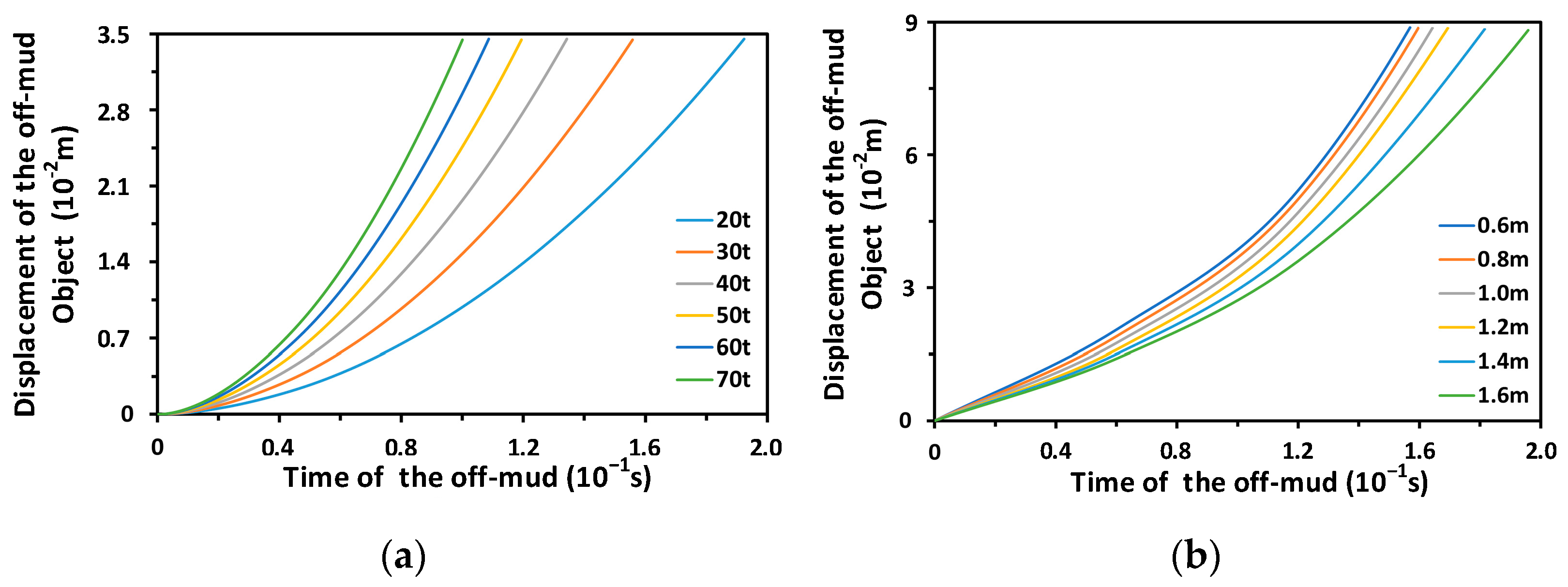
5.1. Effects of Lifting Force and Burial Depth on Critical Displacement
5.2. Effects of Lifting Force and Burial Depth on Displacement
5.3. Effects of Lifting Force and Burial Depth on Velocity
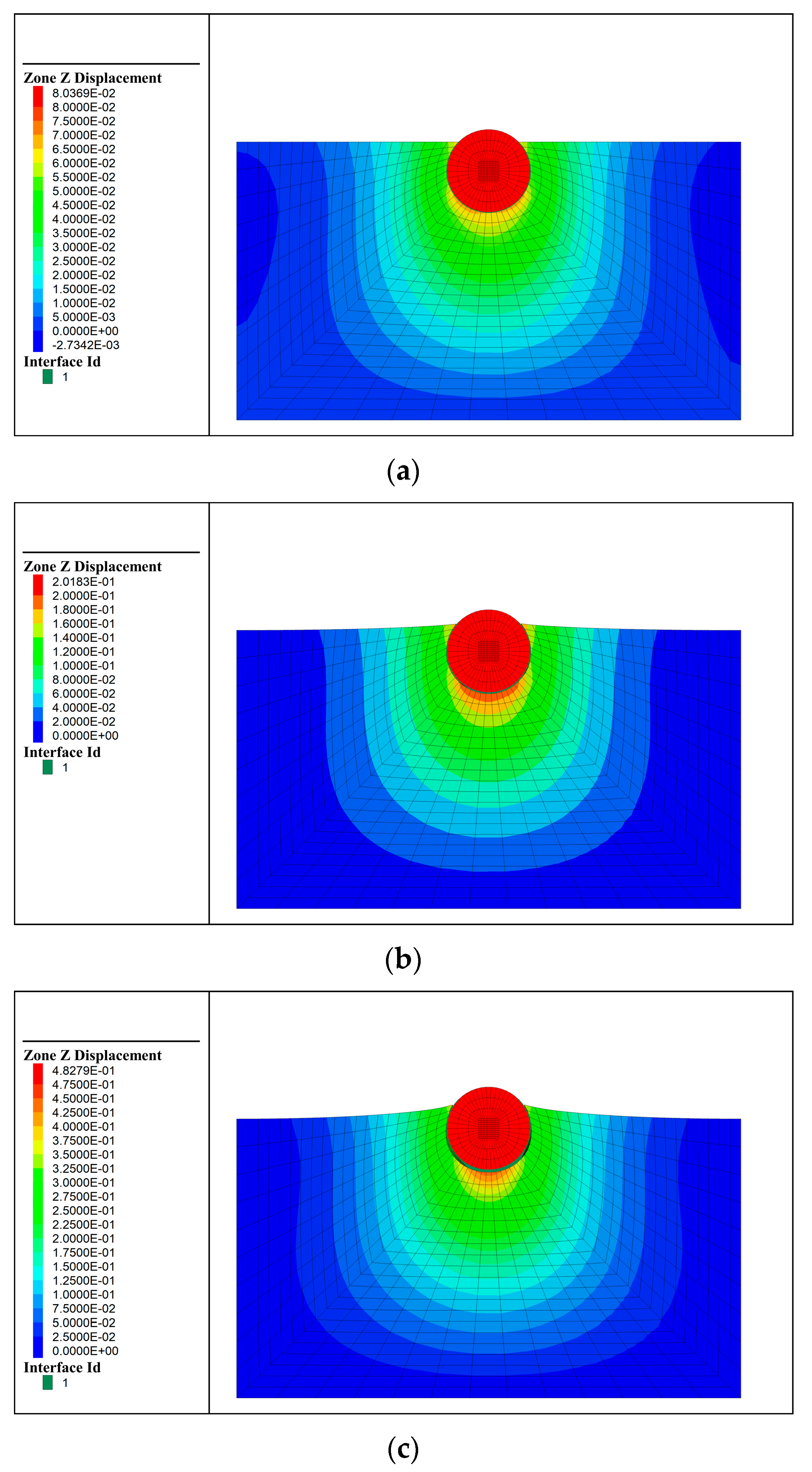
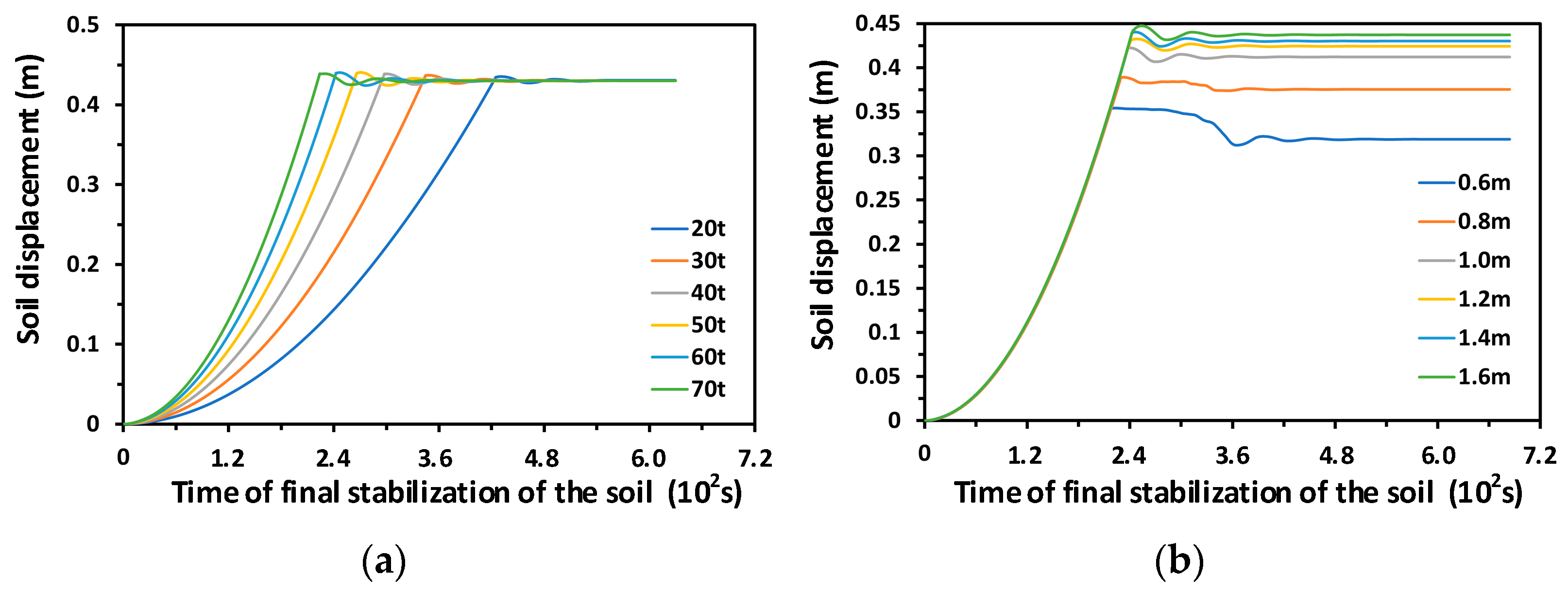
5.4. Effects of Lifting Force and Burial Depth on Soil Displacement
6. Conclusions
- The normalized Terzaghi model can be used to predict the adsorption force in the salvage of cylindrical objects. The maximum relative error is less than 2.49% compared with finite element analysis;
- Time-step finite element analysis can be used to investigate the off-mud process with regard to the effects of the lifting force and burial depth;
- With increased lifting force and the same burial depth, the critical displacement is reduced slightly, soil separation on the bottom of the object occurs earlier, the velocity increases more quickly, soil displacement on the bottom stops increases earlier, and the off-mud process is completed earlier;
- With increased burial depth, the time required for soil separation is considerably increased, the velocity increases more slowly, the maximum soil displacement is increased, and the off-mud process takes longer.
Equation Symbols List
| ,, | The three components of the generalized stress vector. |
| The material constants defined by the shear modulus and bulk modulus. | |
| The material constants defined by the shear modulus and bulk modulus. | |
| ,, | The principal strains. |
| The internal friction angle coefficient. | |
| The angle of the internal friction. | |
| The cohesive force. | |
| The tensile strength. | |
| The expansion angle coefficient. | |
| The expansion angle. | |
| The normal force vector at the time of . | |
| The tangential force at the time of . | |
| The absolute displacement of the interface node penetration into the target surface. | |
| The relative shear displacement increment vector. | |
| The additional normal stress. | |
| The additional tangential stress. | |
| The tangential stiffness of the interface unit. | |
| The normal stiffness of the interface unit. | |
| The area represented by the interface nodes. | |
| The tangential force. | |
| The interface cohesion. | |
| The interface friction angle. | |
| The water pressure. | |
| The bulk modulus. | |
| The shear modulus. | |
| The minimum dimension over the connection area in the normal direction of the interface. | |
| The tangential stiffness. | |
| The normal stiffness. | |
| Young’s modulus. | |
| Poisson’s ratio. | |
| A | The horizontal projection area of the structure. |
| The shear strength of the soil. | |
| The burial depth. | |
| The width of the structure. | |
| The length of the structure. | |
| The contact area of the structure immersed in the soil. | |
| The total surface area of the structure. | |
| β | The nondimensional burial depth. |
| γ | The nondimensional width. |
| λ | The nondimensional burial surface. |
| ψ | The modification coefficient. |
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yan, Y.; Jin, H.; Zhang, Y.; Wang, J.; Guo, J. Statistical analysis of typical ship accidents in past 4 years and review of salvage equipment in China. In Proceedings of the 2019 5th International Conference on Transportation Information and Safety (ICTIS), Liverpool, UK, 14–17 July 2019. [Google Scholar] [CrossRef]
- Drazen, J.C.; Smith, C.R.; Gjerde, K.M.; Haddock, S.H.D.; Carter, G.S.; Choy, C.A.; Clark, M.R.; Dutrieux, P.; Goetze, E.; Hauton, C.; et al. Opinion: Midwater ecosystems must be considered when evaluating environmental risks of deep-sea mining. Proc. Natl. Acad. Sci. USA 2020, 117, 17455–17460. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.; Jung, J.Y.; Park, K.C.; Choi, S.H. Environmental and economic loss analyses of the oil discharge from shipwreck for salvage planning. Mar. Pollut. Bull. 2022, 155, 111142. [Google Scholar] [CrossRef] [PubMed]
- Lee, H. Breakout of partially embedded objects from cohesive seafloor soils. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 29 April 1973. [Google Scholar] [CrossRef]
- Vesic, A.S. Breakout resistance of objects embedded in ocean bottom. J. Soil. Mech. Found. Div. 1971, 97, 1183–1205. [Google Scholar] [CrossRef]
- Ninomiya, K.; Tagaya, K.; Murase, Y. A study on suction breaker and scouring of a submersible offshore structure. In Proceedings of the The Third Annual Offshore Technology Conference, Houston, TX, USA, 18 April 1971; pp. 297–304. [Google Scholar] [CrossRef]
- Ninomiya, K.; Tagaya, K.; Murase, Y. A study on suction breaker and scouring of sit-on-bottom type offshore structure. In Proceedings of the The Fourth Annual Offshore Technology Conference, Houston, TX, USA, 30 April 1972; pp. 869–874. [Google Scholar] [CrossRef]
- Ninomiya, K.; Tagaya, K.; Murase, Y. A study on suction breaker and scouring of bottom-sitting offshore. J. Petrol. Technol. 1973, 25, 279–287. [Google Scholar] [CrossRef]
- Das, B.M. Model tests for uplift capacity of foundations in clay. Soil. Found. 1978, 18, 17–24. [Google Scholar] [CrossRef] [PubMed]
- Das, B.M.; Shin, E.C.; Dass, R.N. Suction force below plate anchors in soft clay. Mar. Georesour. Geotec. 1994, 12, 71–81. [Google Scholar] [CrossRef]
- Das, B.M. Behavior of a shallow plate anchor in clay under sustained loading. Mar. Georesour. Geotec. 1995, 13, 417–428. [Google Scholar] [CrossRef]
- Sawicki, A.; Mierczynski, J. Mechanics of the breakout phenomenon. Comput. Geotech. 2003, 30, 231–243. [Google Scholar] [CrossRef]
- Zhou, X.; Chow, Y.; Leung, C. Numerical modeling of break out process of objects lying on the seabed surface. Comput. Geotech. 2008, 35, 686–702. [Google Scholar] [CrossRef]
- Sui, J. Study on Adsorption Power of Submersible Structure from Sediment. Master’s Thesis, Dalian University of Technology, Dalian, China, 2009. [Google Scholar]
- Hu, Y. Analysis of the Mechanism of Excavation Resistance of Special Shape Falling Object. Master’s Thesis, Harbin Engineering University, Harbin, China, 2018. [Google Scholar]
- Meyerhof, S. Engineering Properties of Nuclear Technical, Report NO.3-699, Report 2; U.S. Army Engineer Water Ways Experiment Station: Vicksburg, MI, USA, 1965. [Google Scholar]
- Qiu, C.; Zhang, Q.; Yan, P.; Ji, Y. Experimental study of adhesion of clay. Rock Soil Mech. 2017, 5, 67–72. [Google Scholar] [CrossRef]
- Jin, G.; Jin, T.; Chen, X.; Zhang, Z.; Luo, D. Experimental Research on Breakout Force of Embeded Objects from Sediments. J. Nav. Acad. Eng. 1998, 3, 49–53. [Google Scholar]
- Han, L.; Jiang, M.; Zhang, R. Experiment Simulation of Absorption Force of Marine Structure Caisson. Port. Eng. Technol. 2009, 46, 43–45. [Google Scholar]
- Fang, T.; Liu, G.; Ye, G.; Pan, S.; Shi, H.X.; Zhang, L. Field Test on Buoyancy Variation of a Subsea Bottom-Supported Foundation Model. J. Mar. Sci. Eng. 2019, 7, 143. [Google Scholar] [CrossRef]
- Karmakar, T.; Sekhar, G.P. Lifting a large object from an anisotropic porous bed. Phys. Fluids 2016, 28, 093601. [Google Scholar] [CrossRef]
- Davie, J.; Sutherland, H. Uplift resistance of cohesive soils. J. Geotech. Eng. Div. 1977, 103, 935–952. [Google Scholar] [CrossRef]
- Cong, X.; Ren, L.; Chen, B. Study on Soil Adhesion Phenomenaby Chemical Adsorption. Trans. Chin. Soc. Agric. Eng. 1996, 12, 40–44. [Google Scholar]
- Michalski, J. Parametric Method Applicable in Calculating Breakout Force and Time for Lifting Axisymmetric Objects from Seabed. Pol. Marit. Res. 2019, 26, 147–152. [Google Scholar] [CrossRef]
- Michalski, J. Parametric Method Applicable in Assessing Breakout Force and Time for Lifting Slender Bodies from Seabed. Pol. Marit. Res. 2020, 27, 69–75. [Google Scholar] [CrossRef]
- FLAC3D Base Commands. Available online: http://docs.itascacg.com/flac3d700/flac3d/docproject/source/flac3dhome.html (accessed on 20 January 2023).
- Chen, Y.; Xu, D. FLAC/FLAC3D Basic and Engineering Examples, 2nd ed.; China Water and Power Press: Beijing, China, 2013; pp. 143–146. [Google Scholar]
- Ma, J.; Yang, G.; Li, T. Study on Breakout Force of Embedded Objects from Seabed. China Offshore Platf. 2007, 2, 16–19. [Google Scholar]





| Cohesion c (Pa) | Friction Angle
(°) | Tangential Stiffness
(Pa) | Normal Stiffness
(Pa) |
|---|---|---|---|
| Density (kg/m3) | Bulk Modulus (Pa) | Shear Modulus (Pa) | Cohesion (kPa) | Friction Angle (°) | Tensile Strength (Pa) |
|---|---|---|---|---|---|
| 1290 |
| Density (kg/m3) | Bulk Modulus (Pa) | Shear Modulus (Pa) | Diameter (m) | Length (Pa) |
|---|---|---|---|---|
| 3002 |
| Length (m) | Width (m) | Height (m) |
|---|---|---|
| 14 | 12 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nan, Y.; Yun, F.; Yao, S.; Liu, M.; Wang, L. A Normalized Terzaghi Model and Time-Step FEA for Predicting the Adsorption of a Cylindrical Object in Subsea Salvage. Machines 2023, 11, 245. https://doi.org/10.3390/machines11020245
Nan Y, Yun F, Yao S, Liu M, Wang L. A Normalized Terzaghi Model and Time-Step FEA for Predicting the Adsorption of a Cylindrical Object in Subsea Salvage. Machines. 2023; 11(2):245. https://doi.org/10.3390/machines11020245
Chicago/Turabian StyleNan, Yibo, Feihong Yun, Shaoming Yao, Ming Liu, and Liquan Wang. 2023. "A Normalized Terzaghi Model and Time-Step FEA for Predicting the Adsorption of a Cylindrical Object in Subsea Salvage" Machines 11, no. 2: 245. https://doi.org/10.3390/machines11020245
APA StyleNan, Y., Yun, F., Yao, S., Liu, M., & Wang, L. (2023). A Normalized Terzaghi Model and Time-Step FEA for Predicting the Adsorption of a Cylindrical Object in Subsea Salvage. Machines, 11(2), 245. https://doi.org/10.3390/machines11020245






