A Multi-Task-Based Deep Multi-Scale Information Fusion Method for Intelligent Diagnosis of Bearing Faults
Abstract
1. Introduction
- A training strategy of task splitting was proposed to achieve fault-type diagnosis and size localization simultaneously. By splitting fault diagnosis multi-tasking into fault size tasks and fault type tasks, the model can flexibly adjust the weights of subtasks to balance the convergence speed. In addition, it can also apply local models of subtasks to other research objects to enhance the models’ robustness while improving the models’ transferability.
- Multi-scale convolution was used for feature extraction to obtain different levels of fault information. This allowed feature extraction of the original data from different perspectives, reducing the limitations of single-scale convolution for feature extraction of time-series data, and making the extracted features more comprehensive and conducive to the following information fusion step.
- A multi-layer attention dynamic weight assignment strategy for multi-scale convolutional neural networks was proposed to weight and fuse the fault features. The system uses the first layer of attention to dynamically weight the feature vectors obtained by convolution at different locations, and the model can assign greater weights to necessary periods. In addition, since the first layer uses multi-scale convolution, the granularity of information obtained by different scale convolution is different. It is also important. Again, the second layer uses attention to weight the information extracted under different information granularity, thus significantly improving the model prediction capability.
- A multi-block model structure was proposed to improve the model’s prediction accuracy. More extensive and complementary features are extracted within each block through feature transfer. At the same time, the model utilizes multi-layer attention to assign weights to elements through dynamic weight assignment and uses parameter sharing to pass the weighted feature matrix to the next block as hidden layer information. To achieve higher latitude of information extraction, the higher the freedom of information extraction, the better the prediction effect.
2. Related Works
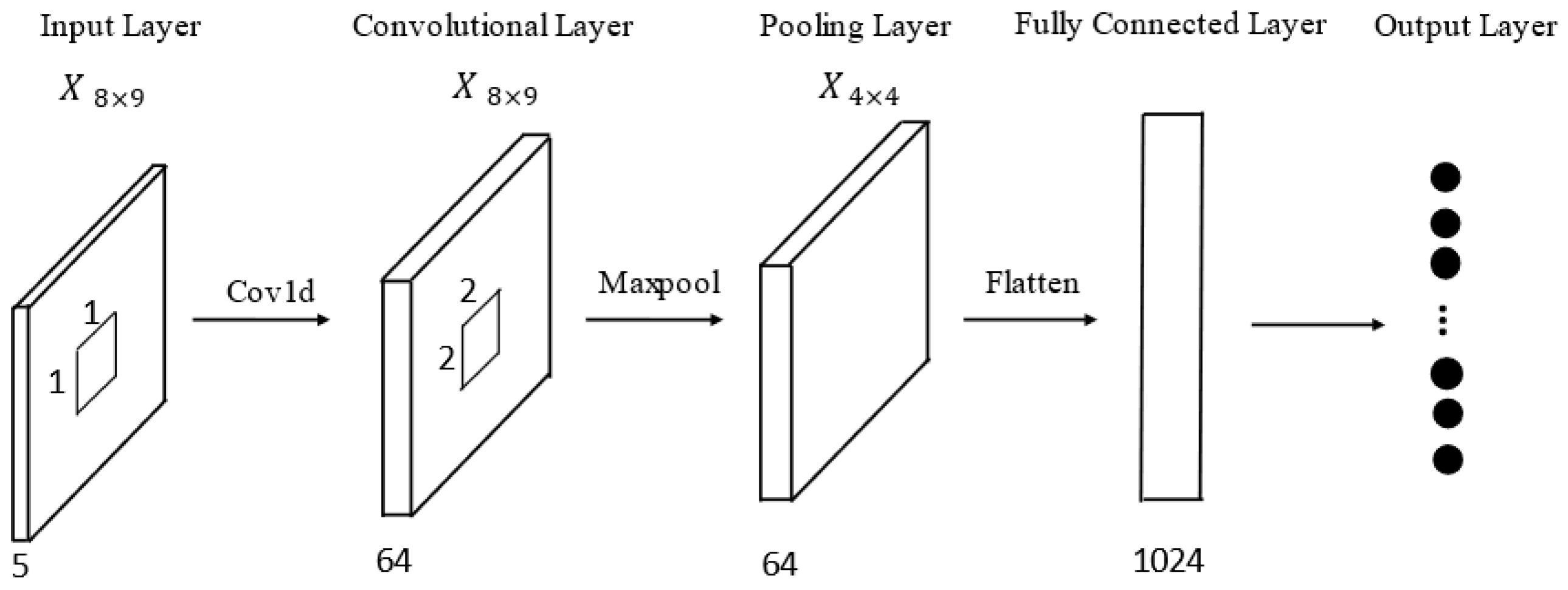
2.1. Convolutional Neural Network
2.2. Batch Normalization
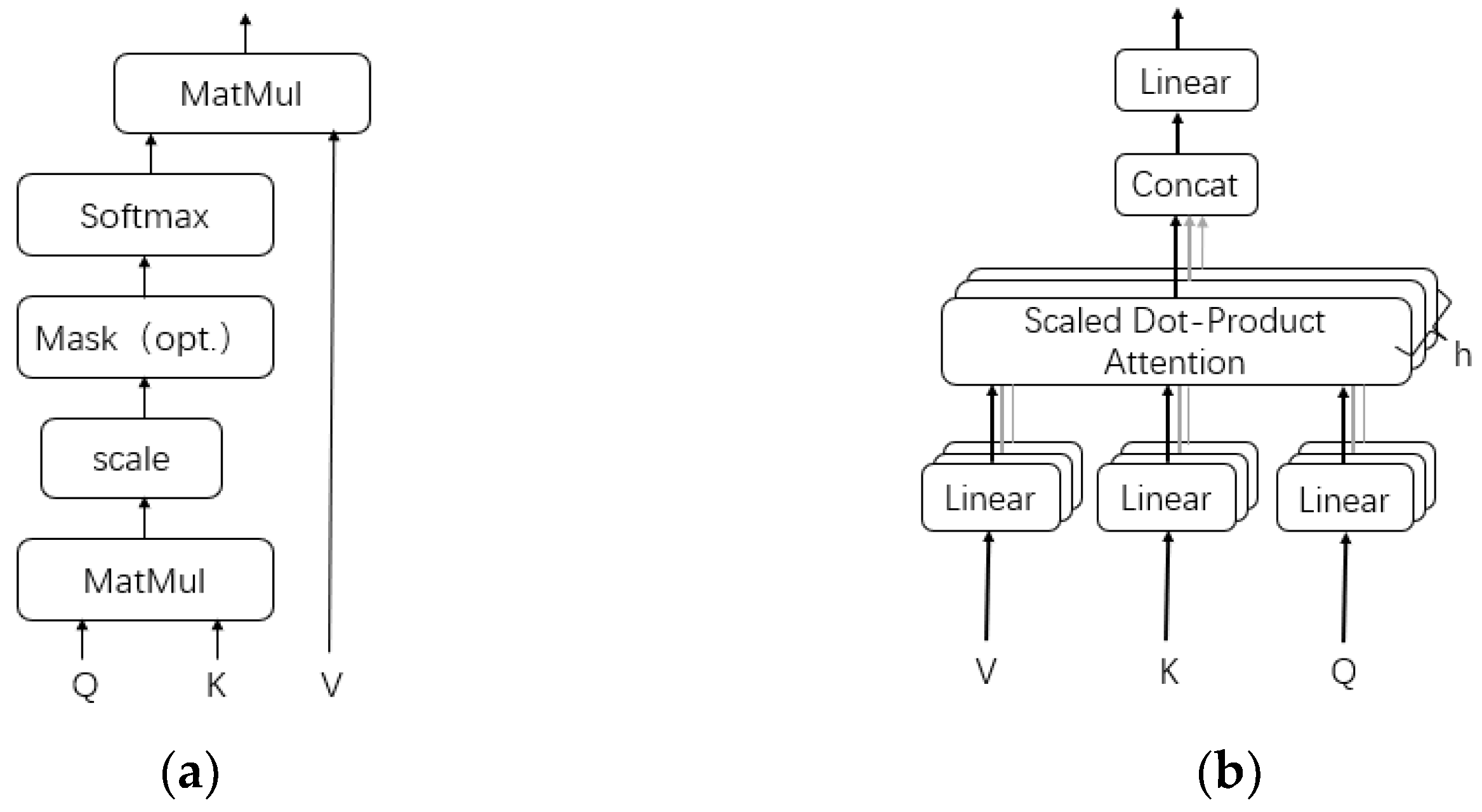
2.3. Attention Mechanism
3. The Proposed Method
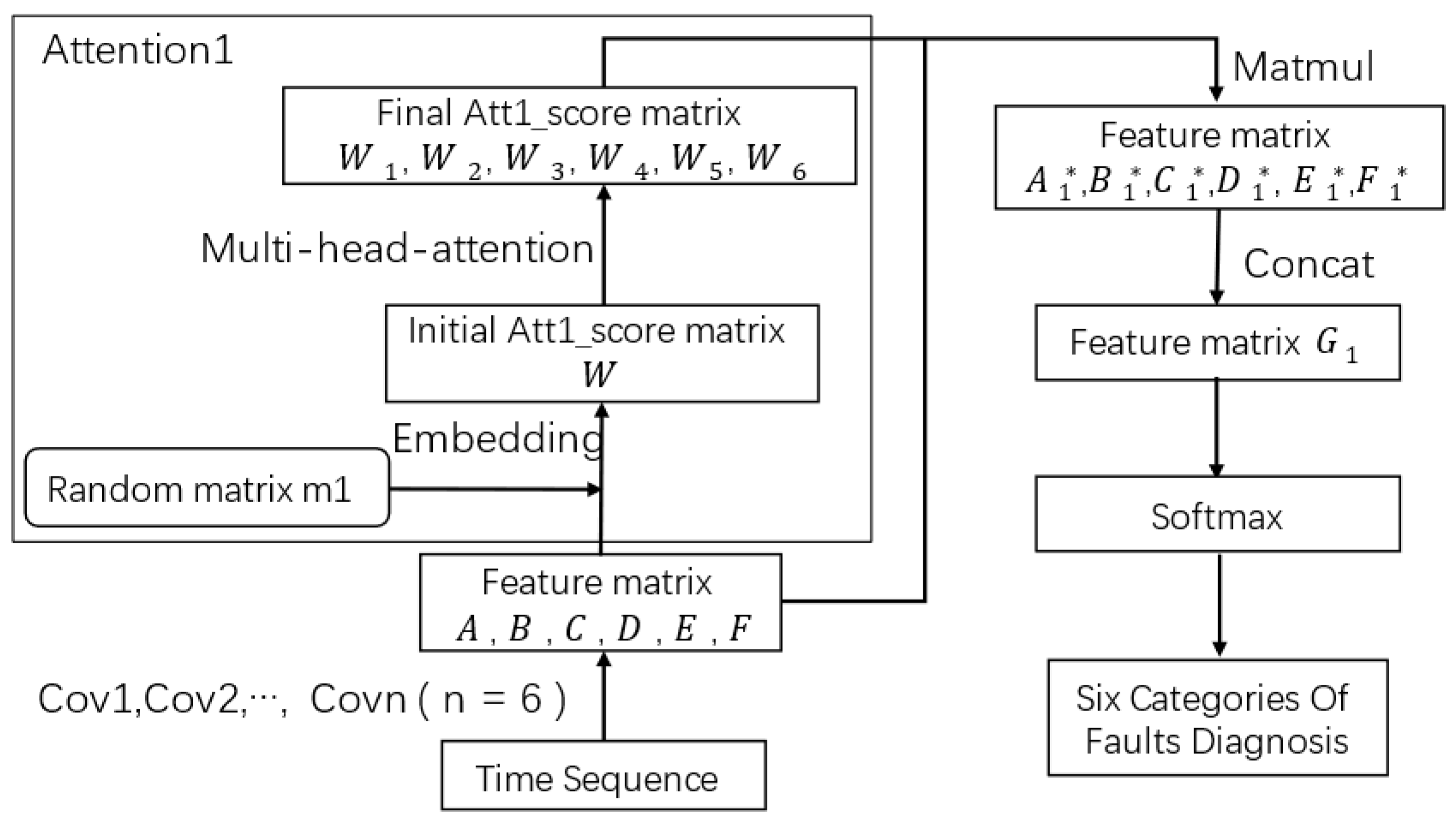
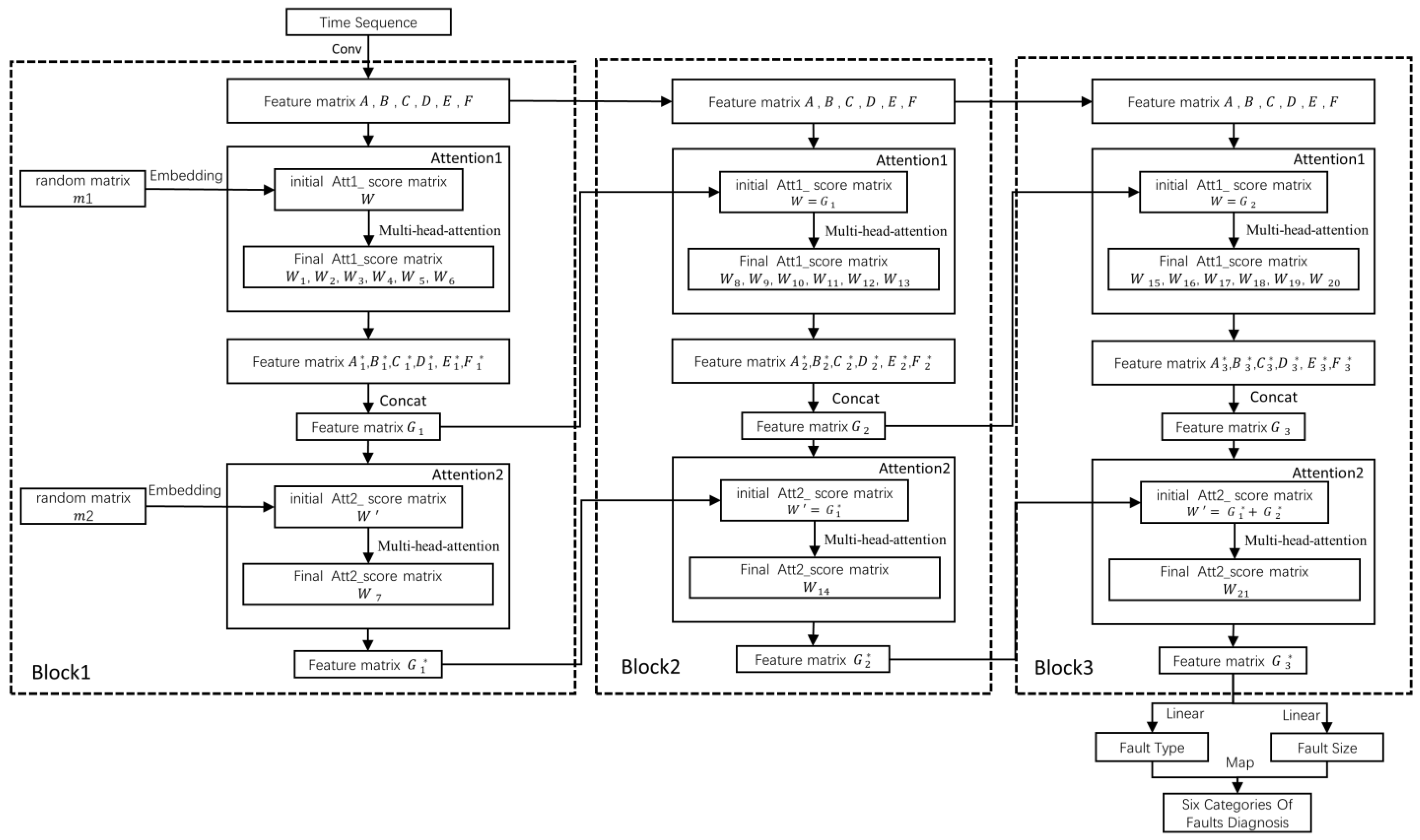
3.1. Feature Extraction Based on Single-Layer Attention
| Algorithm 1: Feature Extraction Based on Single-Layer Attention. |
| Input Parameters: FeatureMatrix (A, B, C, D, E, F); RandomMatrix (m1); HidDim (Dim); Head (h) |
| Result: FeatureMatrix (G1) |
| W = Att1_scoreMatrix (m1) |
| For I in FeatureMatrix (A, B, C, D, E, F); |
| q = Linear (Dim); |
| K = Linear (Dim); |
| v = Linear (Dim); |
| Scale = sqrt (Dim//h) |
| Q = q (I).view (m1.shape [0], −1, h, Dim//h).permute(0, 2, 1, 3); |
| K = k (I).view (m1.shape [0], −1, h, Dim//h).permute(0, 2, 1, 3); |
| V = v (I).view (m1.shape [0], −1, h, Dim//h).permute(0, 2, 1, 3); |
| FinalAtt1_scoreMatrix (W1, W2, W3, W4, W5, W6) = Q * KT/scale; |
| x = matmul (softmax (FinalAtt1_scoreMatrix), V); |
| FeatureMatrix (A1 *, B1 *, C1 *, D1 *, E1 *, F1 *) = x. permute (0, 2, 1, 3).view (m1.shape [0], −1, h * Dim//h); |
| FeatureMatrix (G1) = Concat. FeatureMatrix (A1 *, B1 *, C1 *, D1 *, E1 *, F1 *) |
| end |
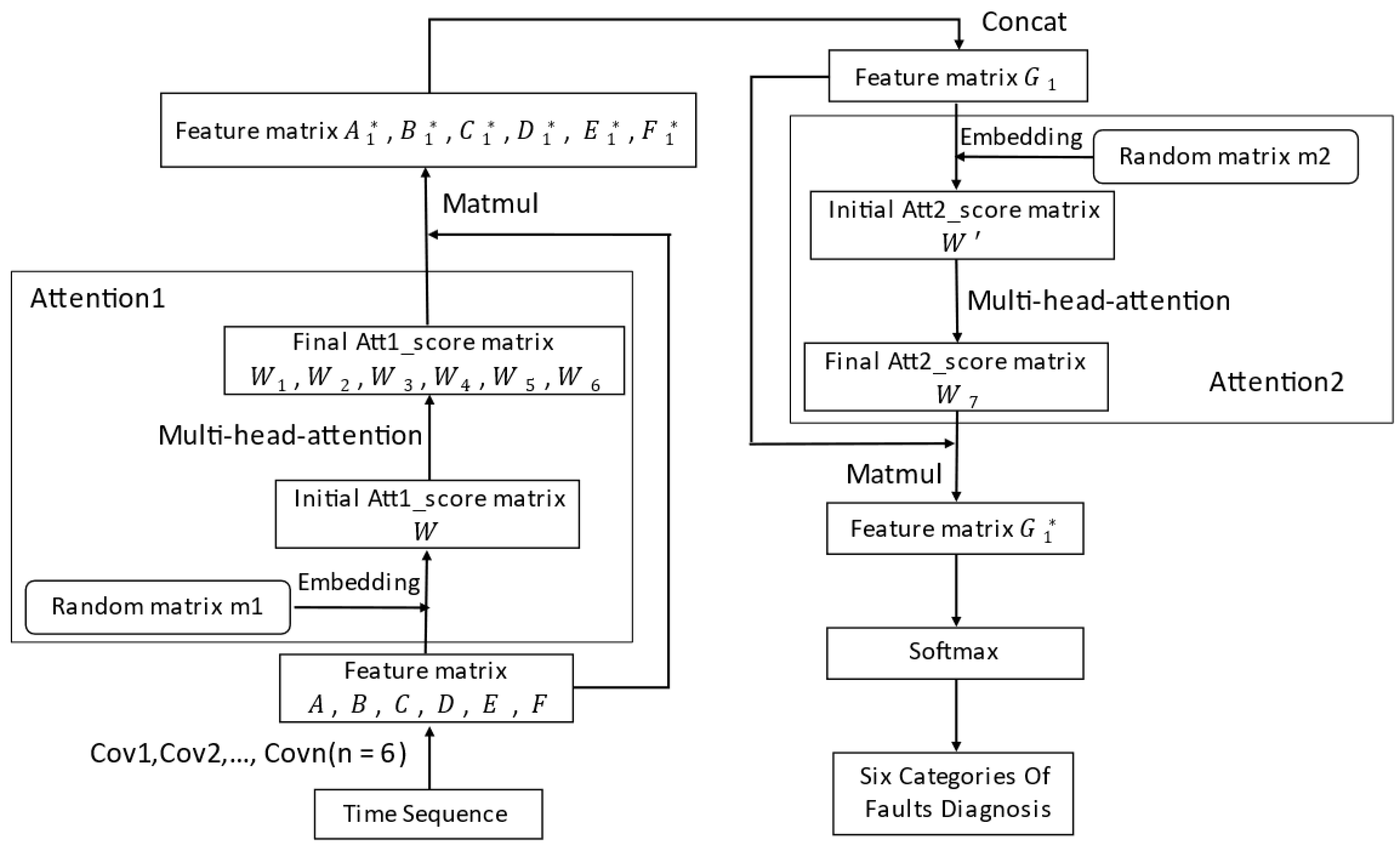
3.2. Feature Fusion Based on Multi-Layer Attention
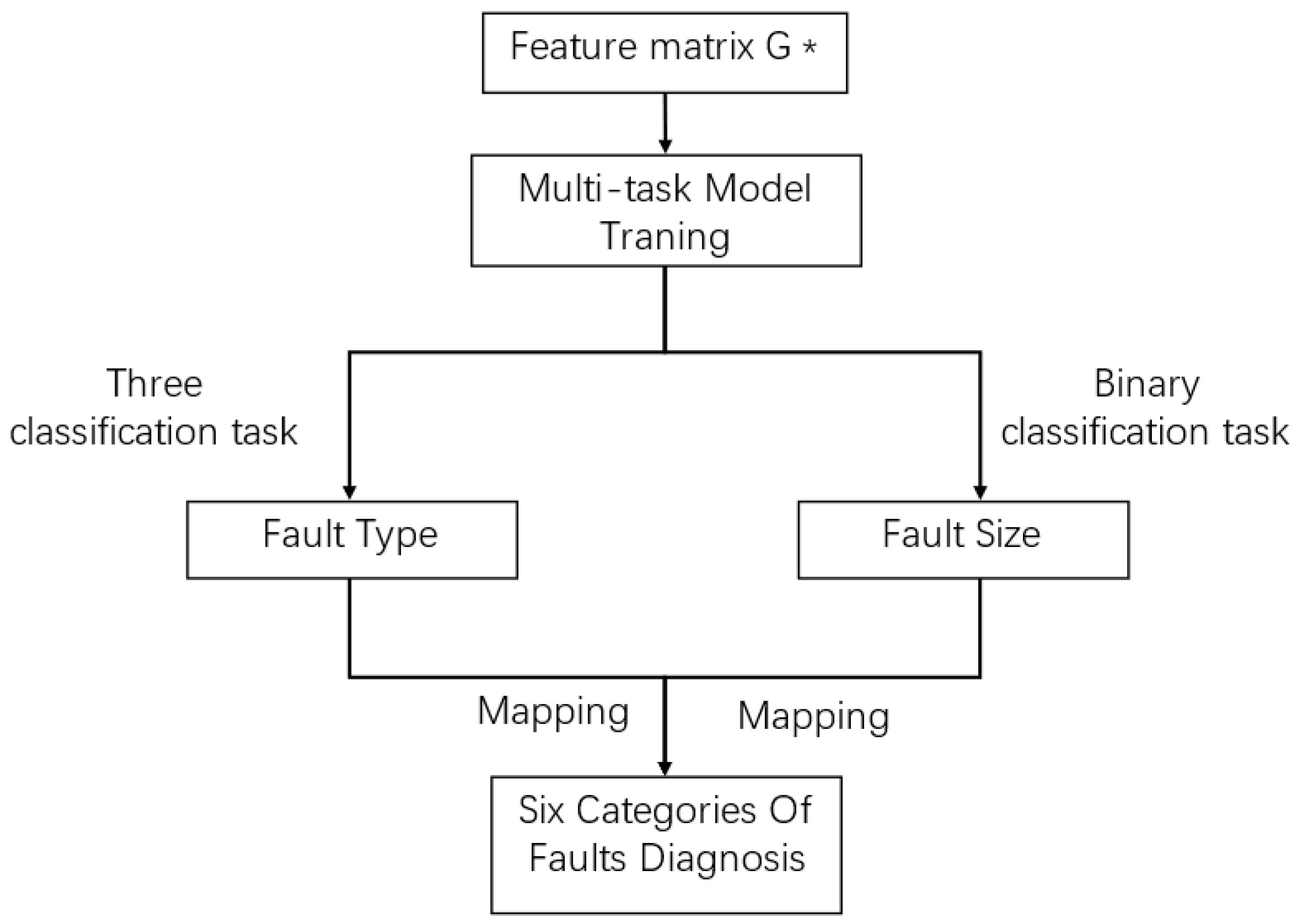
3.3. Multi-Tasking Pattern Classification
3.4. Multi-Block Learning Structure
4. Experimental Verification
4.1. Datasets Introduction
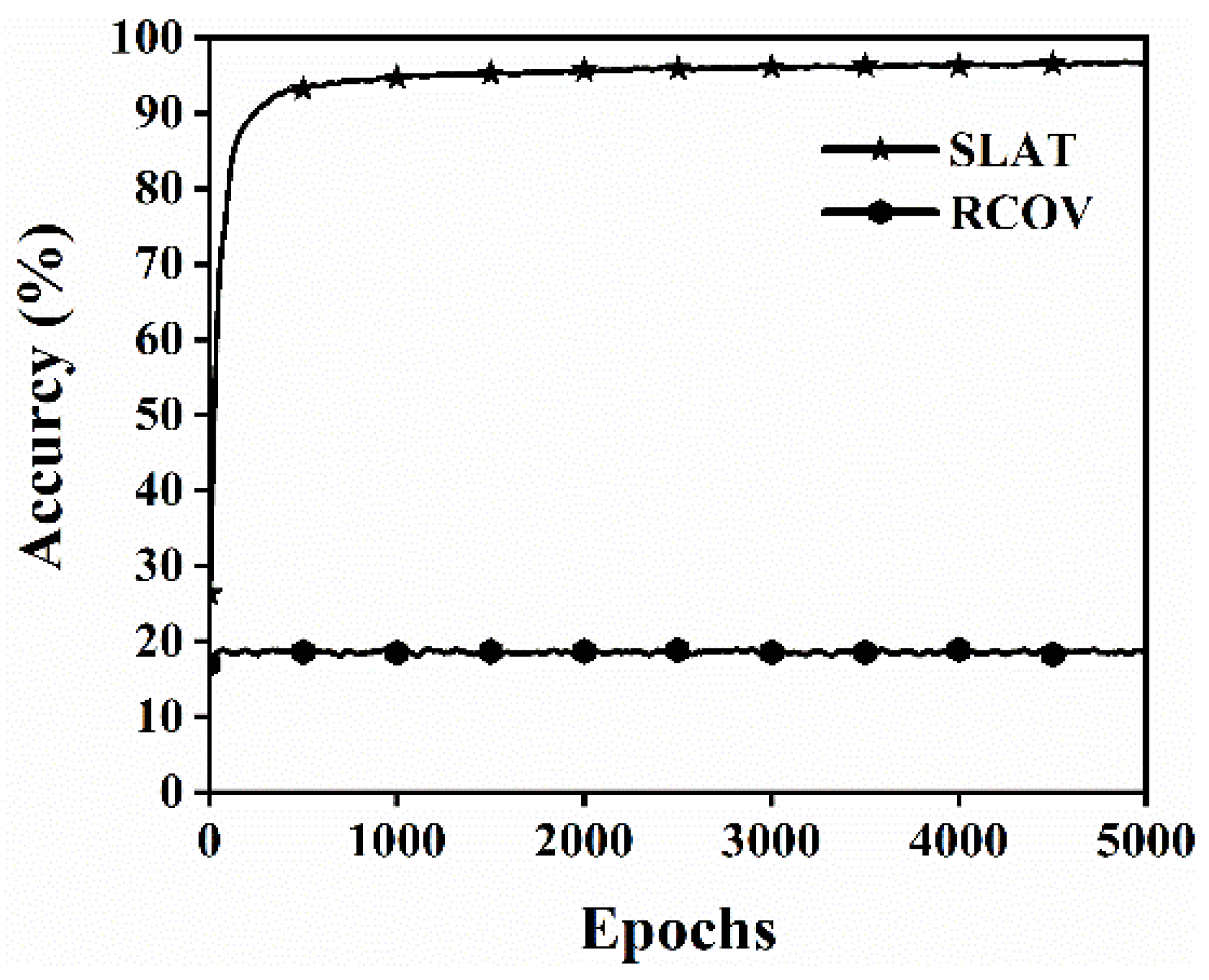
4.2. Ordinary Convolutional Model vs. Single-Layer Attention Convolutional Model
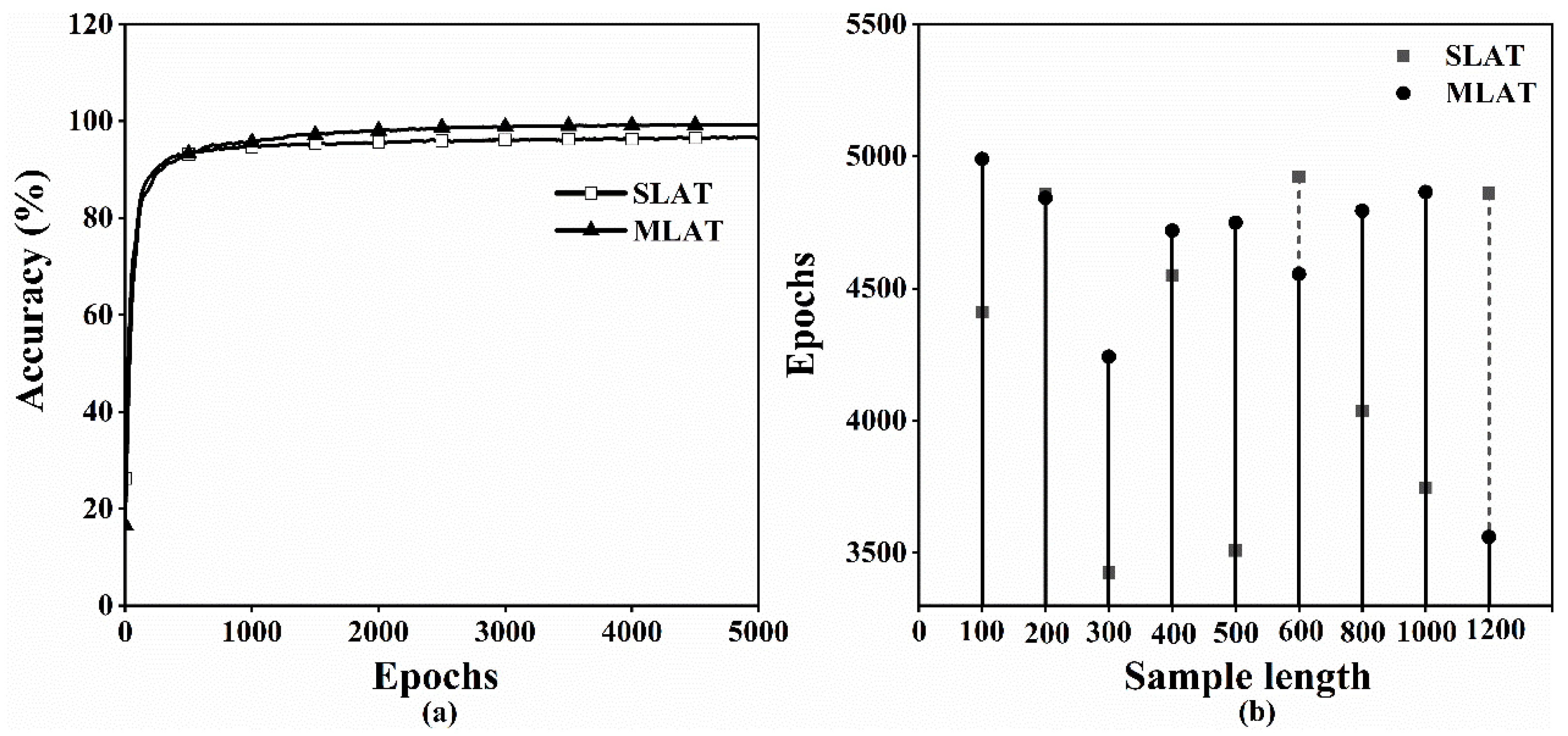
4.3. Comparison of Single-Layer Attention Convolution Model and Multi-Layer Attention Convolution Model
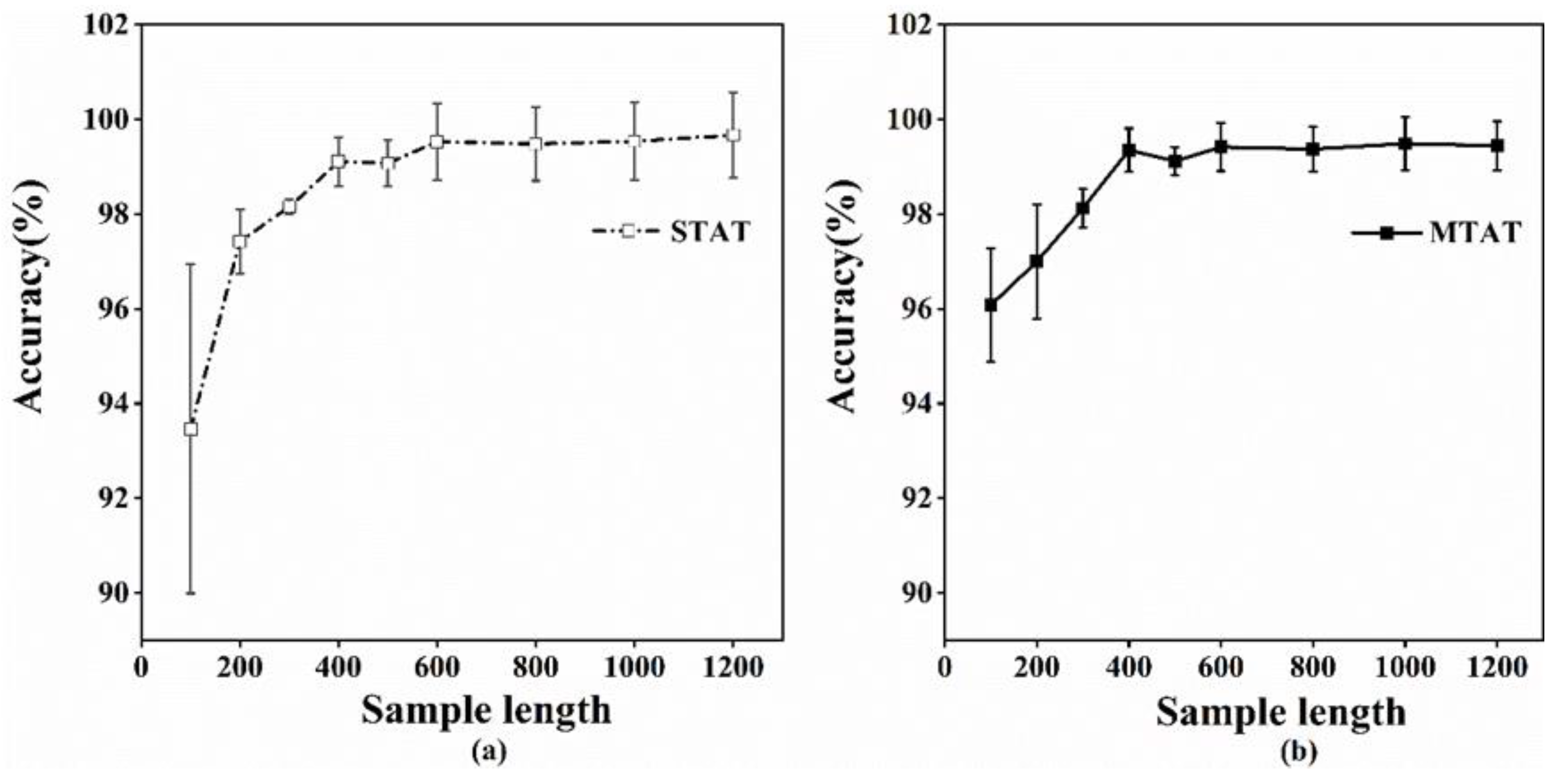
4.4. Single-Task vs. Multi-Task Comparison of Multi-Layer Attention Convolution Models
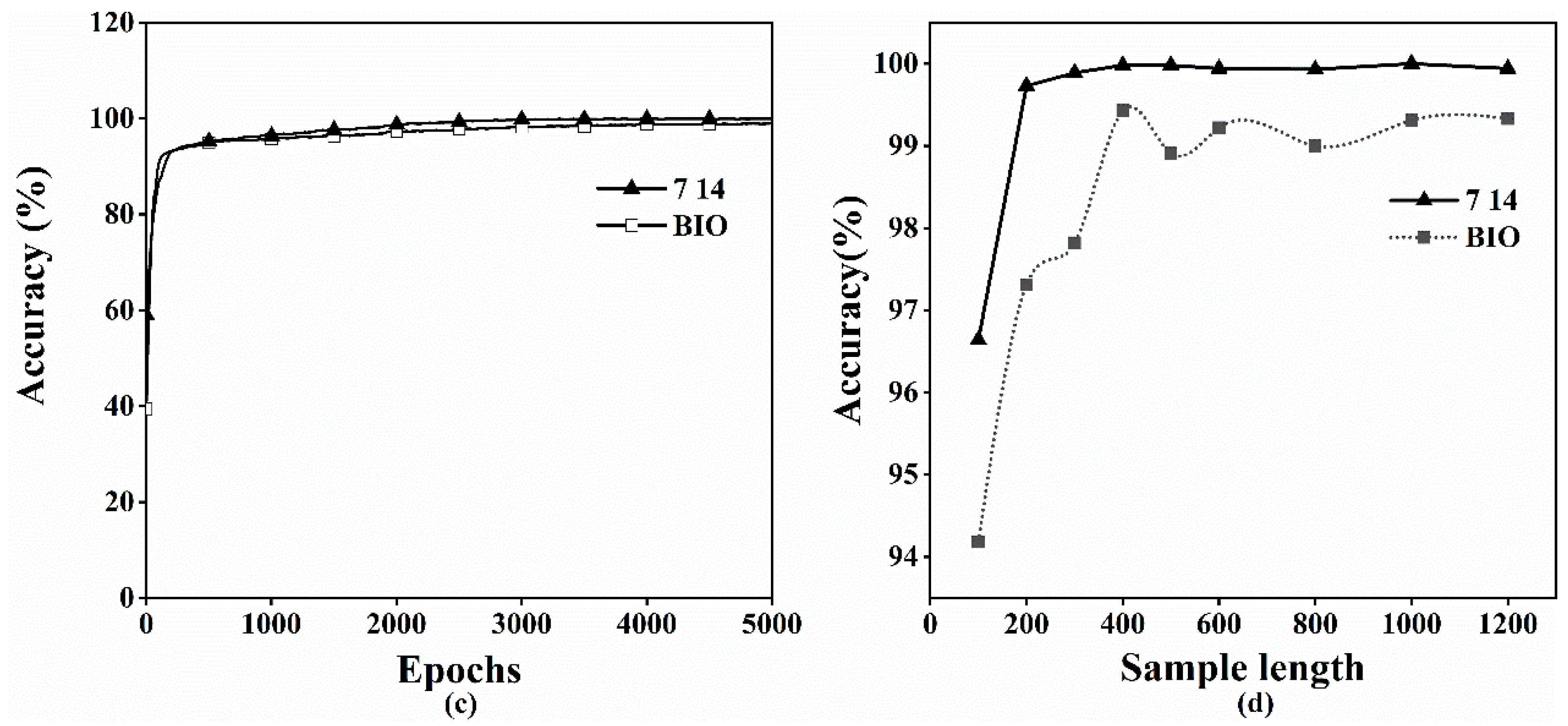
4.5. Multi-Task Single-Block vs. Multi-Block for Multi-Layer Attention Convolutional Models
4.6. Analysis of Multiple Evaluation Indicators of Diagnostic Results
4.7. Comparisons with Other Works
5. Conclusions
- (1)
- The multi-task model splits the fault diagnosis six-task into a fault size dichotomous task and a fault type trichotomous task, simultaneously achieving fault-type diagnosis and size localization. The experimental results show that the model is efficient and transferable, and its robustness and generalization performance is significantly improved.
- (2)
- The multi-layer attention convolution model can weight and fuse bearing fault features. Compared with the standard multi-scale convolutional model and single-layer attention convolutional model, the proposed multi-layer attention convolutional model has significant advantages in fitting speed and classification accuracy.
- (3)
- In the multi-block model structure, each block internally extracts a broader range of complementary features through feature transfer and can obtain more abstract feature information. The experimental results show that the prediction accuracy of the multi-block model structure is significantly improved compared with that of the single-block.
- (4)
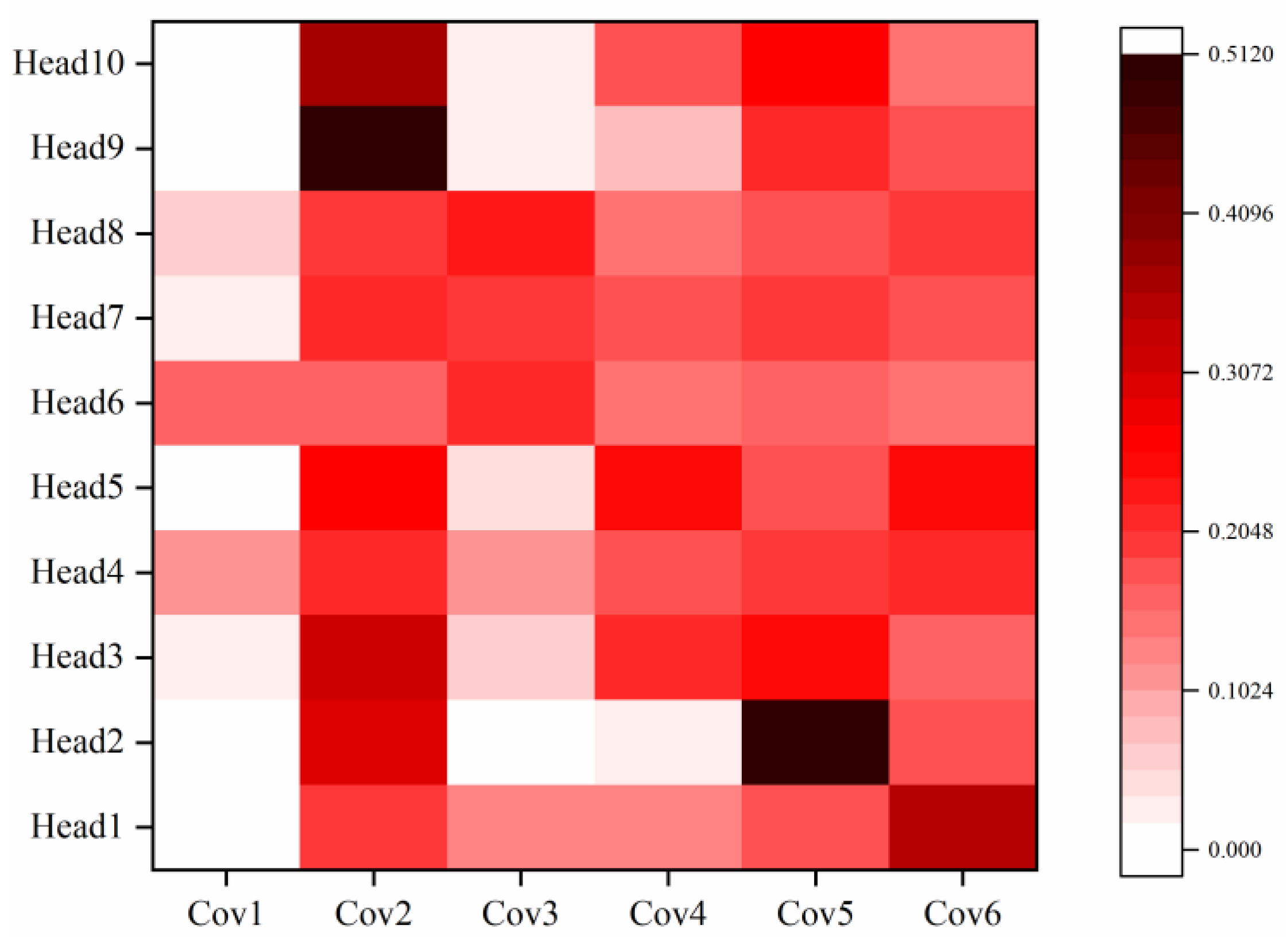
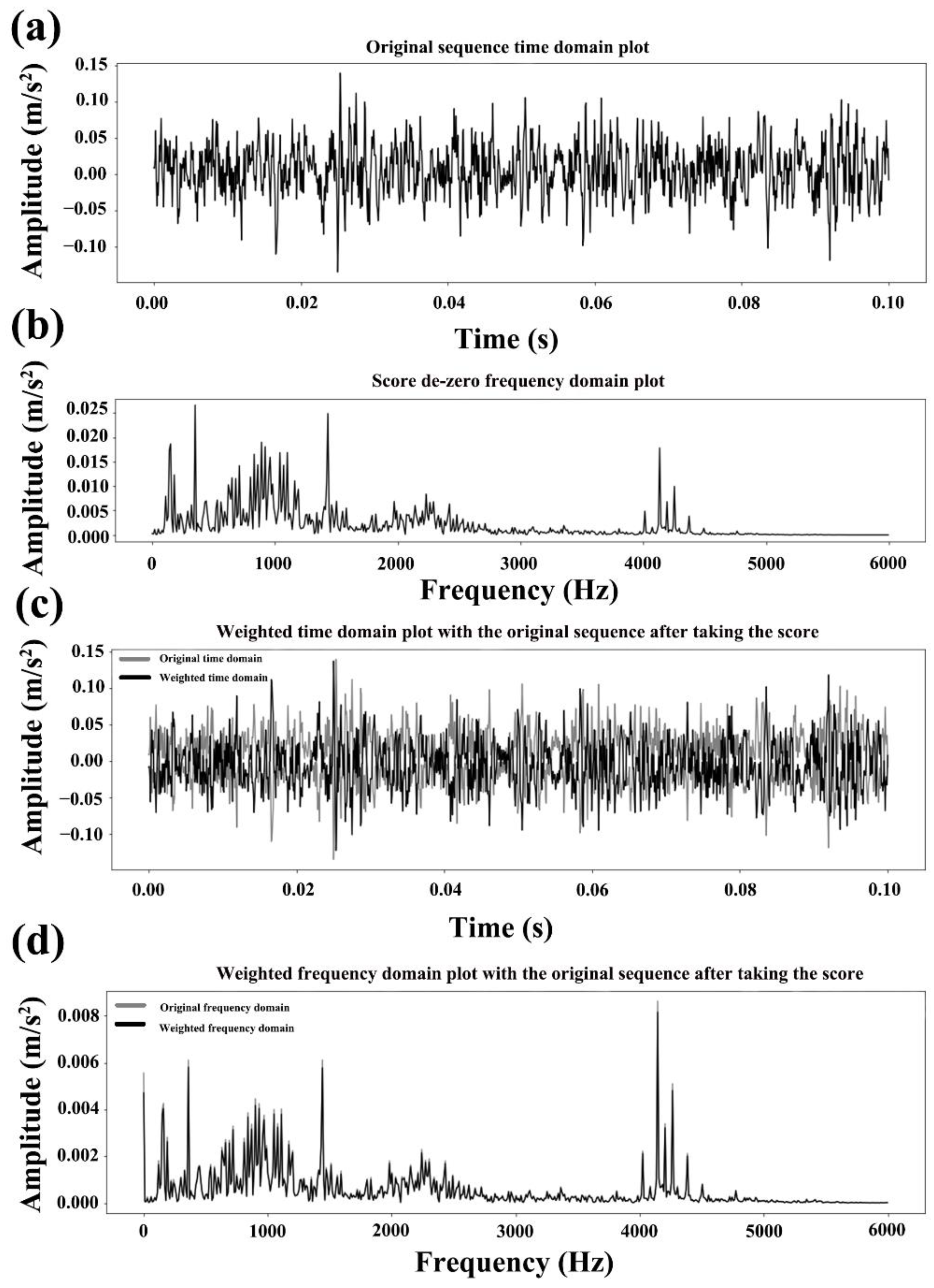
- To improve the interpretability of the model, we verified whether the absolute failure frequency and the model-weighted failure frequency were consistent by reverse weight exploration. The experimental results show that the model’s matching of weights and the search for fault locations were based on the original data and corresponded perfectly to the search results.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, M.; Kang, M.; Tang, B.; Pecht, M. Deep Residual Networks With Dynamically Weighted Wavelet Coefficients for Fault Diagnosis of Planetary Gearboxes. IEEE Trans. Ind. Electron. 2018, 65, 4290–4300. [Google Scholar] [CrossRef]
- Shi, H.T.; Bai, X.T. Model-based uneven loading condition monitoring of full ceramic ball bearings in starved lubrication. Mech. Syst. Signal Process. 2020, 139, 106583. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Zhao, C.; Qu, Y.; He, D. Gear pitting fault diagnosis with mixed operating conditions based on adaptive 1D separable convolution with residual connection. Mech. Syst. Signal Process. 2020, 142, 106740. [Google Scholar] [CrossRef]
- Zhang, Y.; Randall, R.B. Rolling element bearing fault diagnosis based on the combination of genetic algorithms and fast kurtogram. Mech. Syst. Signal Process. 2009, 23, 1509–1517. [Google Scholar] [CrossRef]
- Mao, W.; Feng, W.; Liu, Y.; Zhang, D.; Liang, X. A new deep auto-encoder method with fusing discriminant information for bearing fault diagnosis. Mech. Syst. Signal Process. 2021, 150, 107233. [Google Scholar] [CrossRef]
- Azamfar, M.; Singh, J.; Bravo-Imaz, I.; Lee, J. Multisensor data fusion for gearbox fault diagnosis using 2-D convolutional neural network and motor current signature analysis. Mech. Syst. Signal Process. 2020, 144, 106861. [Google Scholar]
- Xu, G.; Hou, D.; Qi, H.; Bo, L. High-speed train wheel set bearing fault diagnosis and prognostics: A new prognostic model based on extendable useful life. Mech. Syst. Signal Process. 2021, 146, 107050. [Google Scholar] [CrossRef]
- Cui, L.; Huang, J.; Zhang, F.; Chu, F. HVSRMS localization formula and localization law: Localization diagnosis of a ball bearing outer ring fault. Mech. Syst. Signal Process. 2019, 120, 608–629. [Google Scholar] [CrossRef]
- Zhao, X.; Jia, M. A novel unsupervised deep learning network for intelligent fault diagnosis of rotating machinery. Struct. Health Monit. 2019, 19, 1745–1763. [Google Scholar] [CrossRef]
- Cai, B.; Zhao, Y.; Liu, H.; Min, X. A Data-Driven Fault Diagnosis Methodology in Three-Phase Inverters for PMSM Drive Systems. IEEE Trans. Power Electron. 2017, 32, 5590–5600. [Google Scholar] [CrossRef]
- Ming, Z.; Jiang, Z.; Feng, K. Research on variational mode decomposition in rolling bearings fault diagnosis of the multistage centrifugal pump. Mech. Syst. Signal Process. 2017, 93, 460–493. [Google Scholar]
- Liu, H.; Zhang, J.; Cheng, Y.; Lu, C. Fault diagnosis of gearbox using empirical mode decomposition and multi-fractal detrended cross-correlation analysis. J. Sound Vib. 2016, 385, 350–371. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, H.; Zhang, T.Q. Stochastic resonance of coupled time-delayed system with fluctuation of mass and frequency and its application in bearing fault diagnosis. J. Cent. South Univ. 2021, 28, 2931–2946. [Google Scholar] [CrossRef]
- Ma, Y.; Huang, Q.; Zhang, Z.; Cai, D. Application of Multisynchrosqueezing Transform for Subsynchronous Oscillation Detection Using PMU Data. IEEE Trans. Ind. Appl. 2021, 57, 2006–2013. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A New Convolutional Neural Network-Based Data-Driven Fault Diagnosis Method. IEEE Trans. Ind. Electron. 2017, 65, 5990–5998. [Google Scholar] [CrossRef]
- Hu, Z.X.; Wang, Y.; Ge, M.F.; Liu, J. Data-driven Fault Diagnosis Method based on Compressed Sensing and Improved Multi-scale Network. IEEE Trans. Ind. Electron. 2020, 67, 3216–3225. [Google Scholar] [CrossRef]
- Fuan, W.; Hongkai, J.; Haidong, S.; Wenjing, D.; Shuaipeng, W. An adaptive deep convolutional neural network for rolling bearing fault diagnosis. Meas. Sci. Technol. 2017, 28, 095005. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, G.; Li, C.; Chen, Y.; Zhang, Z. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals. Sensors 2017, 17, 425. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, T. Deep convolutional neural network using transfer learning for fault diagnosis. IEEE Access 2021, 9, 43889–43897. [Google Scholar] [CrossRef]
- Kumar, A.; Zhou, Y.; Gandhi, C.; Kumar, R.; Xiang, J. Bearing defect size assessment using wavelet transform based Deep Convolutional Neural Network (DCNN). Alex. Eng. J. 2020, 59, 999–1012. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G.J.N. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Hao, X.; Zhang, G.; Ma, S.J.I.J.o.S.C. Deep learning. Int. J. Semant. Comput. 2016, 10, 417–439. [Google Scholar] [CrossRef]
- Liu, W.; Wen, Y.; Yu, Z.; Yang, M. Large-Margin Softmax Loss for Convolutional Neural Networks. arXiv 2016, arXiv:1612.02295, 137–164. [Google Scholar]
- Li, Y.; Wang, N.; Shi, J.; Liu, J.; Hou, X. Revisiting Batch Normalization For Practical Domain Adaptation. Pattern Recognit. 2016, 80, 3203. [Google Scholar]
- Xu, Z.; Li, C.; Yang, Y. Fault diagnosis of rolling bearings using an Improved Multi-Scale Convolutional Neural Network with Feature Attention mechanism. ISA Trans. 2020, 110, 379–393. [Google Scholar] [CrossRef] [PubMed]
- Lai, T.; Cheng, L.; Wang, D.; Ye, H.; Zhang, W. RMAN: Relational multi-head attention neural network for joint extraction of entities and relations. Appl. Intell. 2021, 52, 3132–3142. [Google Scholar] [CrossRef]
- Hackel, T.; Usvyatsov, M.; Galliani, S.; Wegner, J.D.; Schindler, K. Inference, Learning and Attention Mechanisms that Exploit and Preserve Sparsity in Convolutional Networks. Int. J. Comput. Vis. 2020, 128, 656. [Google Scholar] [CrossRef]
- Wang, H.; Xu, J.; Yan, R.; Sun, C.; Chen, X. Intelligent Bearing Fault Diagnosis Using Multi-Head Attention-Based CNN. Procedia Manuf. 2020, 49, 112–118. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All You Need. Adv. Neural Inf. Process. Syst. 2017, 1–15. [Google Scholar]
- Shao, H.; Xia, M.; Han, G.; Zhang, Y.; Wan, J. Intelligent fault diagnosis of rotor-bearing system under varying working conditions with modified transfer CNN and thermal images. IEEE Trans. Ind. Inform. 2020, 17, 3488–3496. [Google Scholar] [CrossRef]
- Xie, Z.; Chen, J.; Feng, Y.; Zhang, K.; Zhou, Z. End to end multi-task learning with attention for multi-objective fault diagnosis under small sample. J. Manuf. Syst. 2022, 62, 301–316. [Google Scholar] [CrossRef]
- Keskar, N.S.; Socher, R. Improving generalization performance by switching from adam to sgd. arXiv 2017, arXiv:1712.07628. [Google Scholar]
- Zuo, L.; Zhang, L.; Zhang, Z.H.; Luo, X.L.; Liu, Y. A spiking neural network-based approach to bearing fault diagnosis. J. Manuf. Syst. 2021, 61, 714–724. [Google Scholar] [CrossRef]
- Bai, R.X.; Xu, Q.S.; Meng, Z.; Cao, L.X.; Xing, K.S.; Fan, F.J. Rolling bearing fault diagnosis based on multi-channel convolution neural network and multi-scale clipping fusion data augmentation. Measurement 2021, 184, 109885. [Google Scholar] [CrossRef]
- Zhang, F.; Yan, J.; Fu, P.; Wang, J.; Gao, R.X. Ensemble sparse supervised model for bearing fault diagnosis in smart manufacturing. Robot. Comput.-Integr. Manuf. 2020, 65, 101920. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, B.; Yang, T.; Lyu, D.; Gao, W. Multitask Convolutional Neural Network With Information Fusion for Bearing Fault Diagnosis and Localization. IEEE Trans. Ind. Electron. 2020, 67, 8005–8015. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, M.; Li, Y.; Xu, Z.; Wang, J.; Fang, X. A multi-input and multi-task convolutional neural network for fault diagnosis based on bearing vibration signal. IEEE Sens J. 2021, 21, 10946–10956. [Google Scholar] [CrossRef]


| Type of Fault | Outer Ring Fault | Outer Ring Fault | Inner Ring Fault | Inner Ring Fault | Ball Fault | Ball Fault |
|---|---|---|---|---|---|---|
| Fault size | 7 mils | 14 mils | 7 mils | 14 mils | 7 mils | 14 mils |
| Named | O 7 | O 14 | I 7 | I 14 | B_7 | B_14 |
| Sample Length | 100 | 200 | 300 | 400 | 500 | 600 | 800 | 1000 | 1200 |
|---|---|---|---|---|---|---|---|---|---|
| Eval_acc (%) | 73.68 | 84.03 | 89.62 | 93.20 | 94.17 | 95.33 | 96.85 | 96.71 | 97.50 |
| Train_acc (%) | 70.97 | 81.69 | 87.47 | 91.40 | 93.06 | 94.29 | 96.70 | 97.11 | 97.97 |
| Best result epochs | 4410 | 4856 | 3425 | 4550 | 3509 | 4922 | 4037 | 3746 | 4860 |
| 90% of the epochs | - | - | - | 309 | 235 | 204 | 196 | 204 | 223 |
| Sample Length | 100 | 200 | 300 | 400 | 500 | 600 | 800 | 1000 | 1200 |
|---|---|---|---|---|---|---|---|---|---|
| Eval_acc (%) | 93.47 | 97.43 | 98.15 | 99.11 | 99.07 | 99.53 | 99.48 | 99.54 | 99.67 |
| Train_acc (%) | 91.97 | 97.09 | 97.96 | 98.73 | 99.07 | 99.35 | 99.48 | 99.44 | 99.72 |
| Best result epochs | 4990 | 4842 | 4242 | 4719 | 4749 | 4555 | 4794 | 4865 | 3560 |
| 90% of the epochs | 205 | 126 | 116 | 113 | 152 | 141 | 154 | 228 | 252 |
| Sample Length | 100 | 200 | 300 | 400 | 500 | 600 | 800 | 1000 | 1200 |
|---|---|---|---|---|---|---|---|---|---|
| STAT Eval_acc (%) | 93.47 | 97.43 | 98.15 | 99.11 | 99.07 | 99.53 | 99.48 | 99.54 | 99.67 |
| MTAT Eval_acc (%) | 96.08 | 97.00 | 98.13 | 99.35 | 99.12 | 99.42 | 99.37 | 99.49 | 99.44 |
| Sample Length | 100 | 200 | 300 | 400 | 500 | 600 | 800 | 1000 | 1200 |
|---|---|---|---|---|---|---|---|---|---|
| Fault Type Eval_acc (%) | 94.18 | 97.31 | 97.82 | 99.43 | 98.91 | 99.22 | 99.00 | 99.31 | 99.33 |
| Fault Size Eval_acc (%) | 96.64 | 99.73 | 99.89 | 99.98 | 99.98 | 99.94 | 99.93 | 100 | 99.94 |
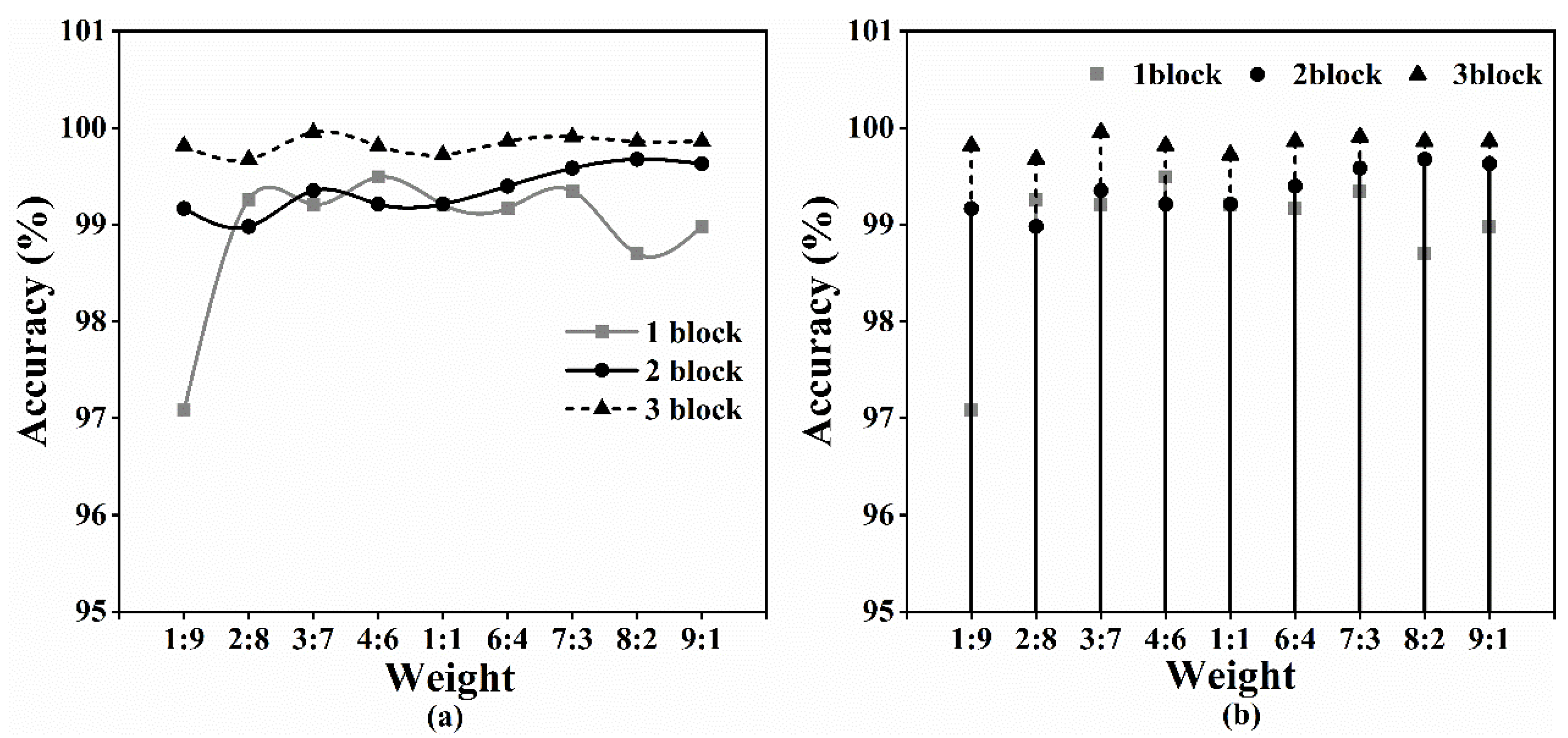
| Weight | 1:9 | 2:8 | 3:7 | 4:6 | 5:5 | 6:4 | 7:3 | 8:2 | 9:1 |
|---|---|---|---|---|---|---|---|---|---|
| 1 block Eval_acc (%) | 97.08 | 99.26 | 99.21 | 99.49 | 99.21 | 99.17 | 99.35 | 98.7 | 98.98 |
| 2 block Eval_acc (%) | 99.17 | 98.98 | 99.35 | 99.21 | 99.21 | 99.40 | 99.58 | 99.68 | 99.63 |
| 3 block Eval_acc (%) | 99.81 | 99.68 | 99.95 | 99.81 | 99.72 | 99.86 | 99.91 | 99.86 | 99.86 |
| Indicators | Precision | ReCall_sn | ReCall_sp | Sacore F1 |
|---|---|---|---|---|
| Minimum value | 0.03 | 0.20 | 0.99 | 0.58 |
| Maximum value | 1 | 1 | 1 | 1 |
| Average value | 0.99 | 0.99 | 1 | 0.99 |
| Methods | Input Type | Classes | Samples Length | Accuracy (%) |
|---|---|---|---|---|
| SNN [33] | Raw signal | Fault classification 4 | 120 | 99.17 |
| SDIAE [5] | Raw signal | Fault classification 9 | 100 | 96.13 |
| MCNN [34] | Raw signal | Fault classification 10 | 110 | 99.7 |
| ESSM [35] | Raw signal | Fault classification 6 | 300 | 96.67 |
| Multi-task CNN [36] | Raw signal | Fault classification 10 | 700 | 96.04 |
| MIMTNet [37] | Raw signal | Fault Size 3 Fault Type 3 | 4425 | 99.96 99.22 |
| MEAT (Our method) | Raw signal | Fault Size 2 Fault Type 3 Mapping Fault classification 6 | 1000 | 100 99.4 99.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, R.; Feng, X.; Wang, T.; Miao, F.; Yu, C. A Multi-Task-Based Deep Multi-Scale Information Fusion Method for Intelligent Diagnosis of Bearing Faults. Machines 2023, 11, 198. https://doi.org/10.3390/machines11020198
Xin R, Feng X, Wang T, Miao F, Yu C. A Multi-Task-Based Deep Multi-Scale Information Fusion Method for Intelligent Diagnosis of Bearing Faults. Machines. 2023; 11(2):198. https://doi.org/10.3390/machines11020198
Chicago/Turabian StyleXin, Ruihao, Xin Feng, Tiantian Wang, Fengbo Miao, and Cuinan Yu. 2023. "A Multi-Task-Based Deep Multi-Scale Information Fusion Method for Intelligent Diagnosis of Bearing Faults" Machines 11, no. 2: 198. https://doi.org/10.3390/machines11020198
APA StyleXin, R., Feng, X., Wang, T., Miao, F., & Yu, C. (2023). A Multi-Task-Based Deep Multi-Scale Information Fusion Method for Intelligent Diagnosis of Bearing Faults. Machines, 11(2), 198. https://doi.org/10.3390/machines11020198






