Rejection of Synchronous Vibrations of AMB System Using Nonlinear Adaptive Control Algorithm with a Novel Frequency Estimator
Abstract
1. Introduction
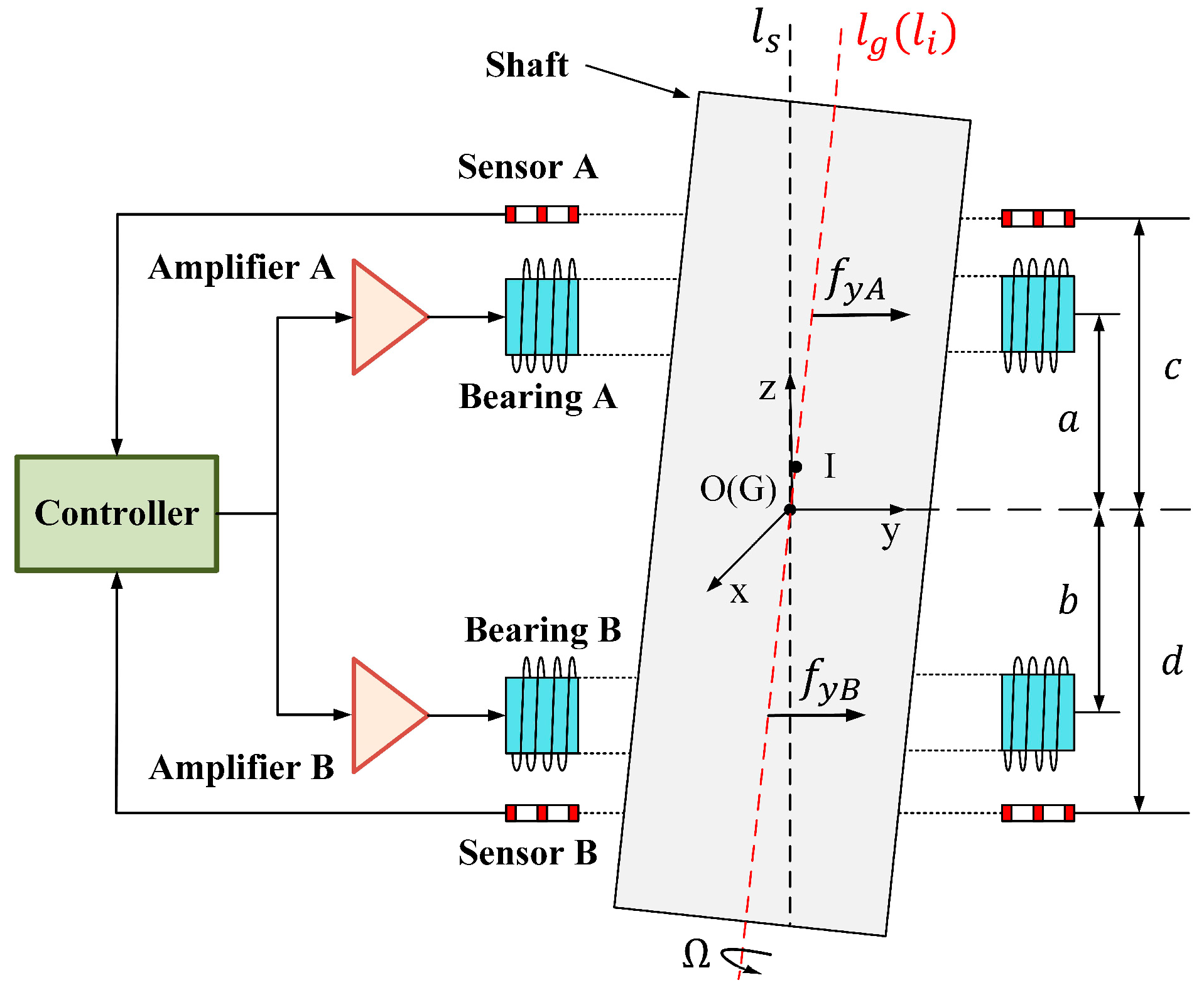
2. Dynamic Model of 4-DOF AMB Rotor System
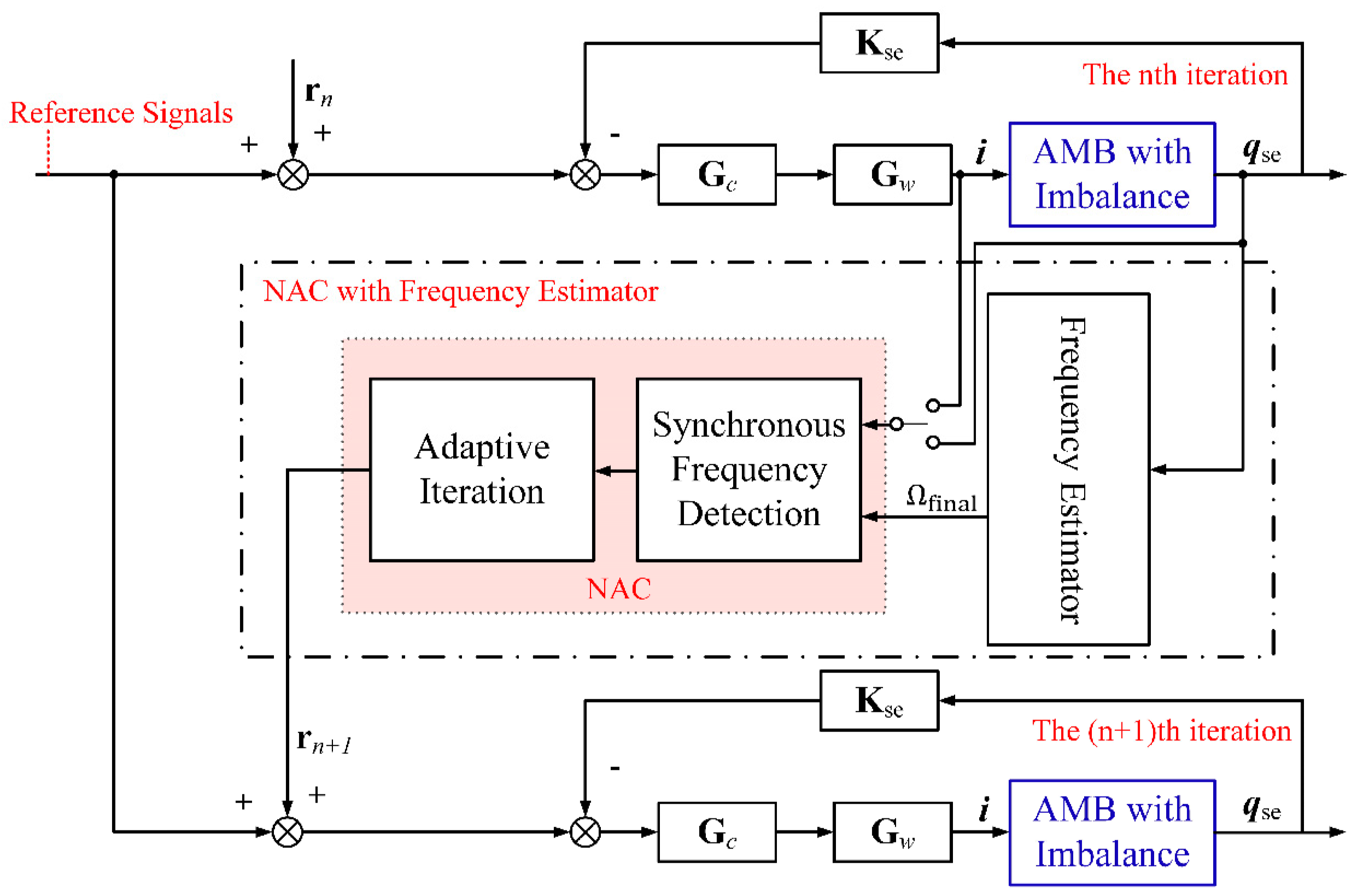
3. Concrete Implementation of NAC Algorithm with the Frequency Estimator
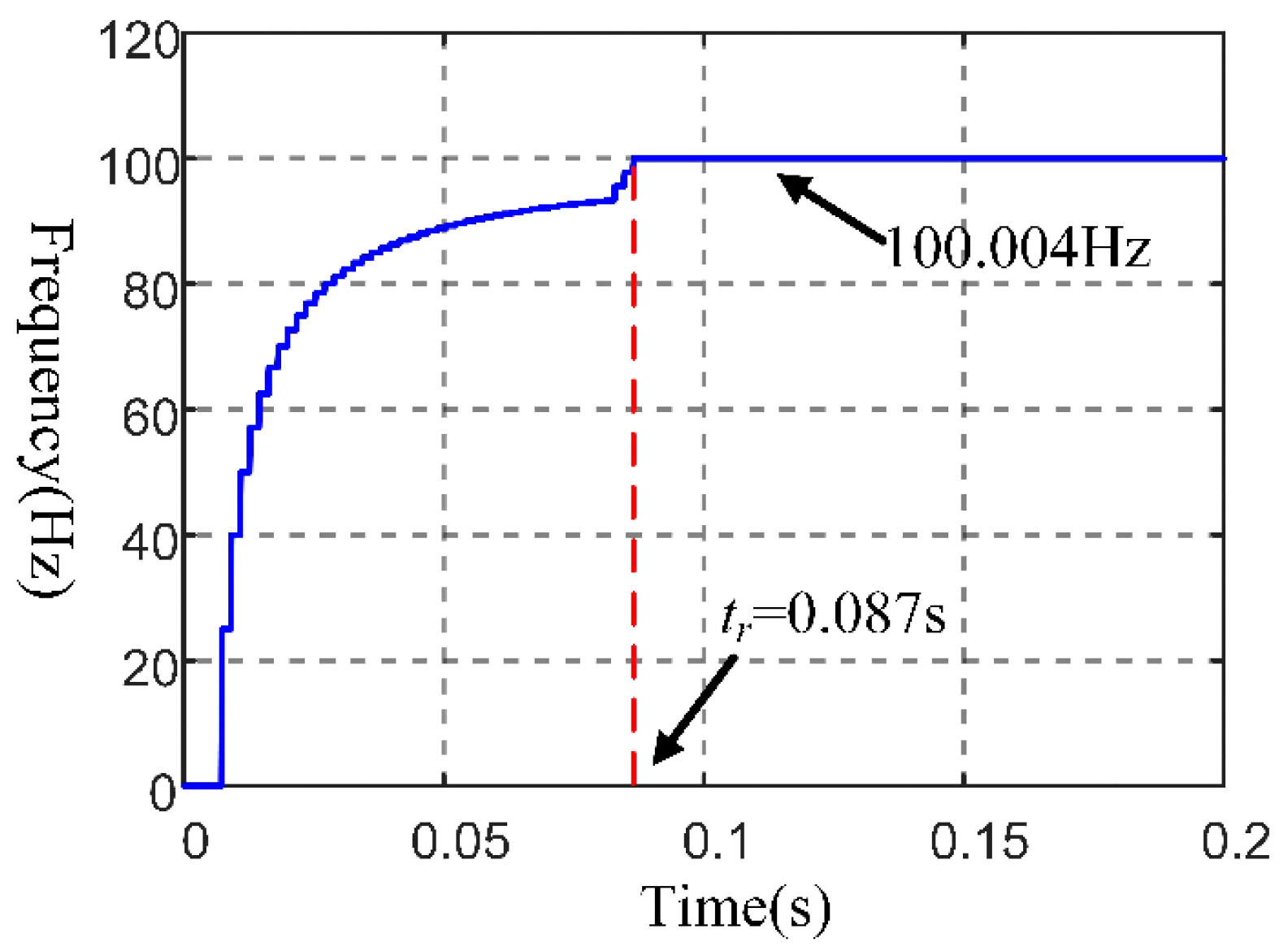
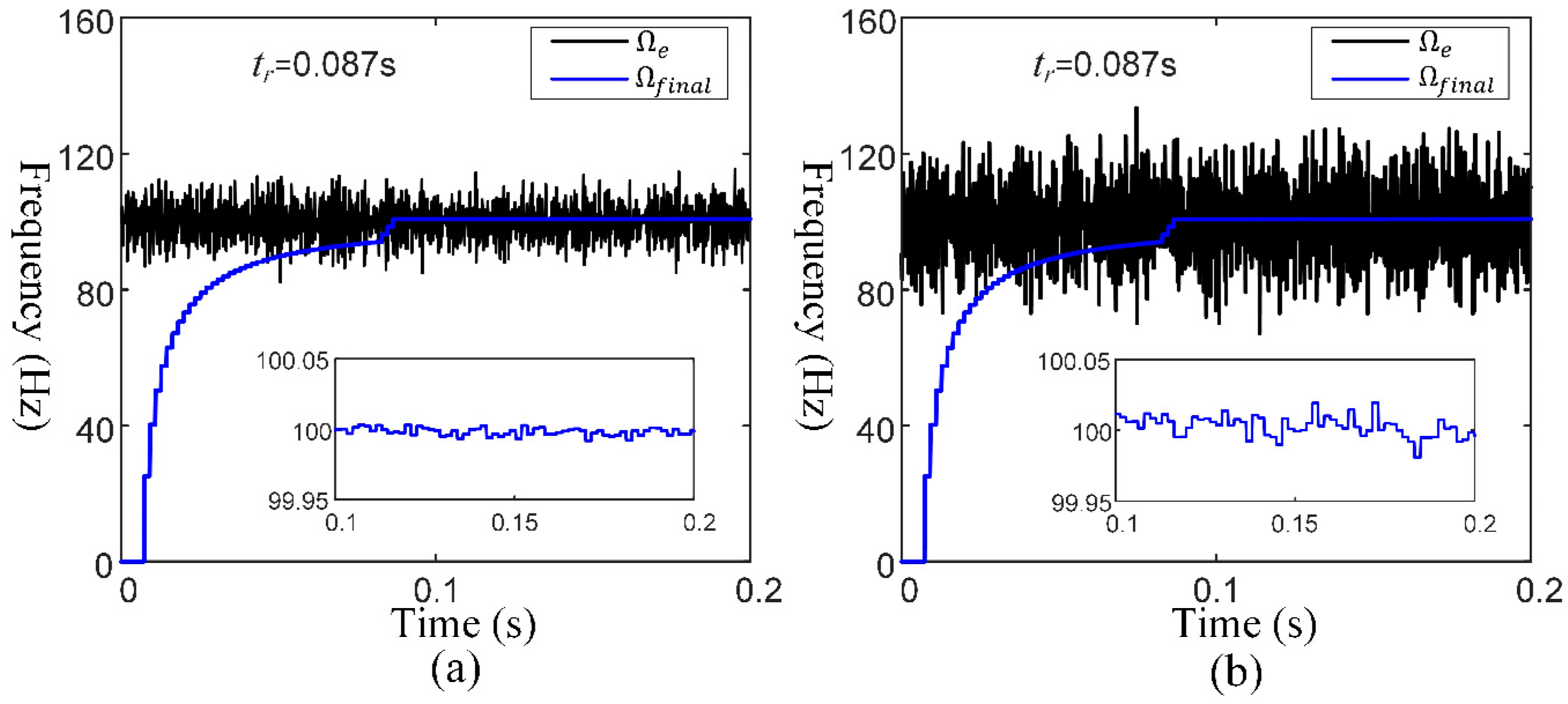
3.1. Frequency Estimator
3.2. NAC Algorithm
3.2.1. Synchronous Frequency Detection
3.2.2. Adaptive Iteration
3.3. Asymptotic Stability of the NAC Algorithm
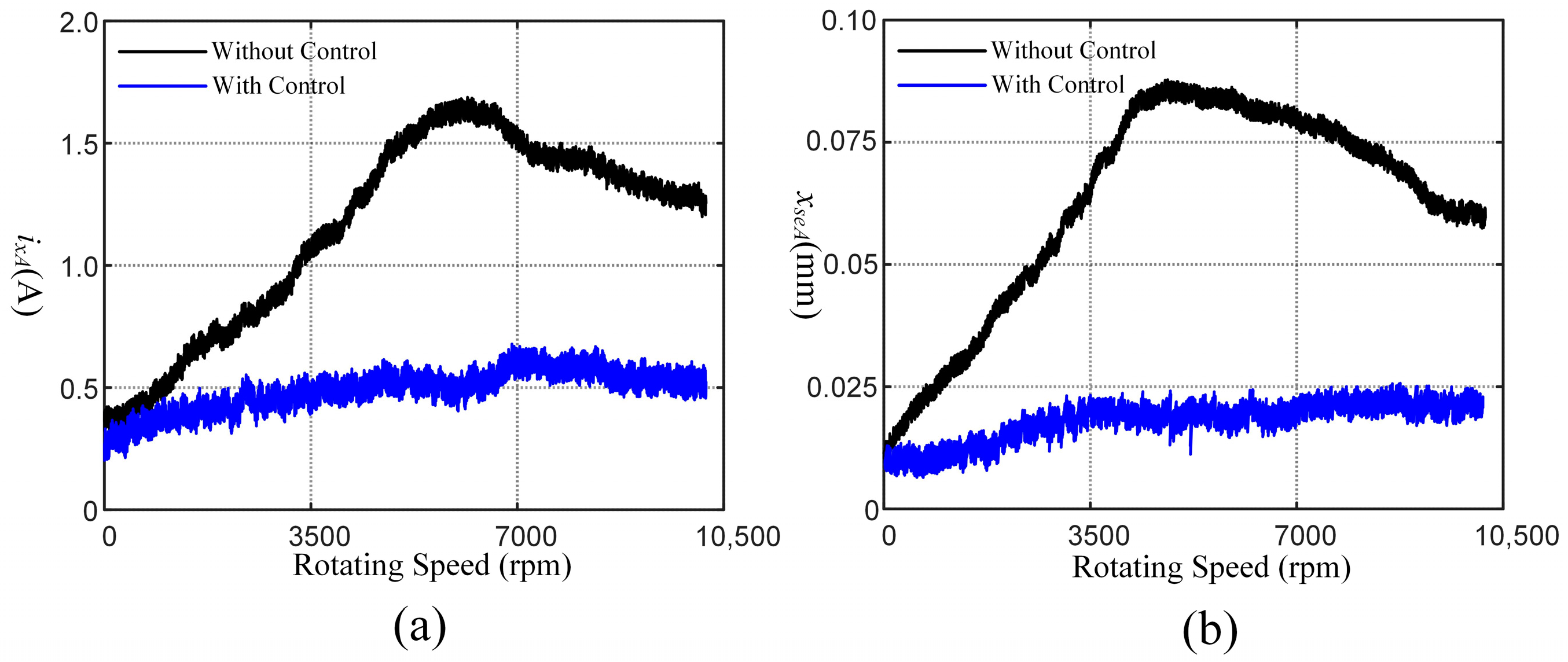
4. Simulation and Experimentation
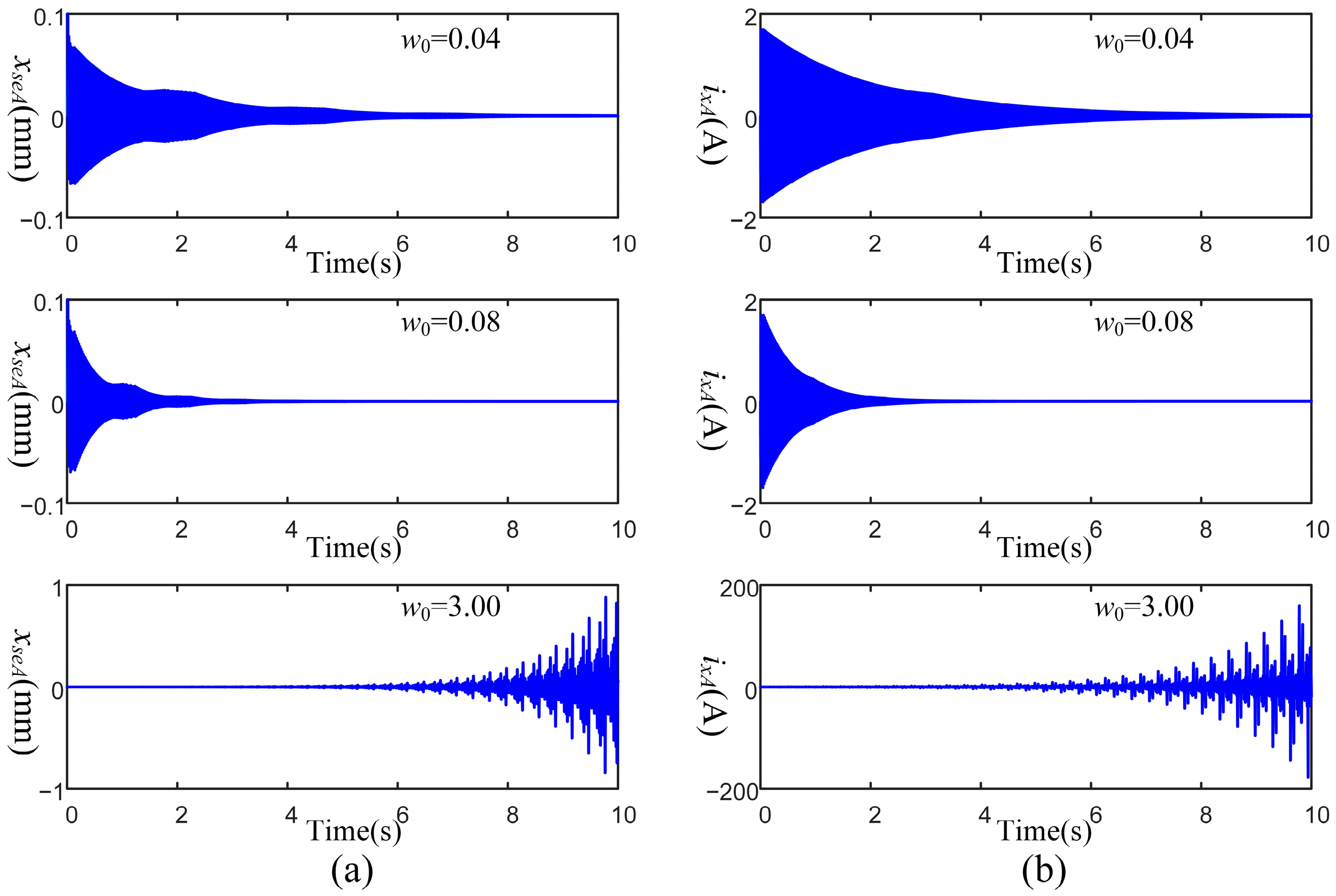
4.1. Simulation
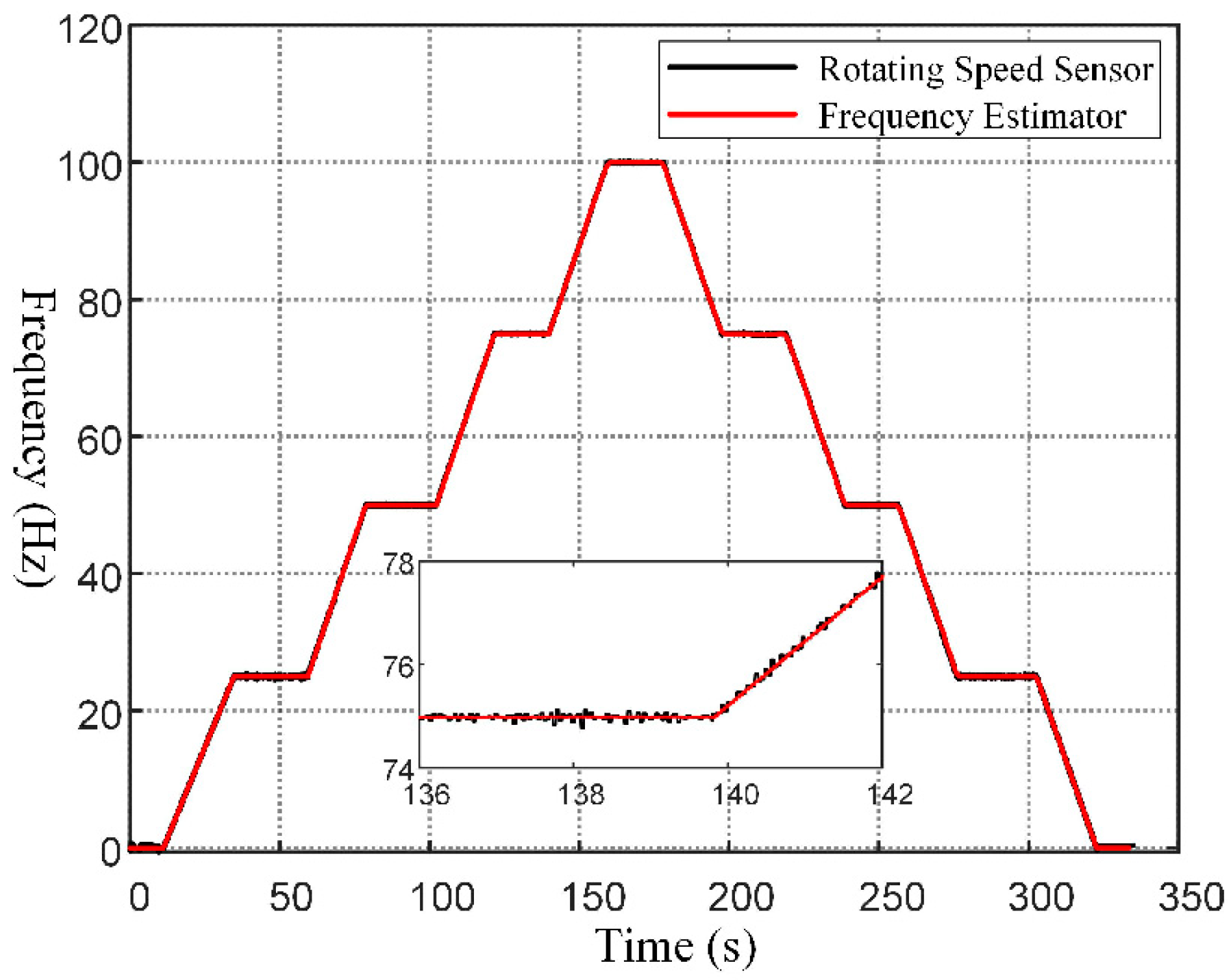
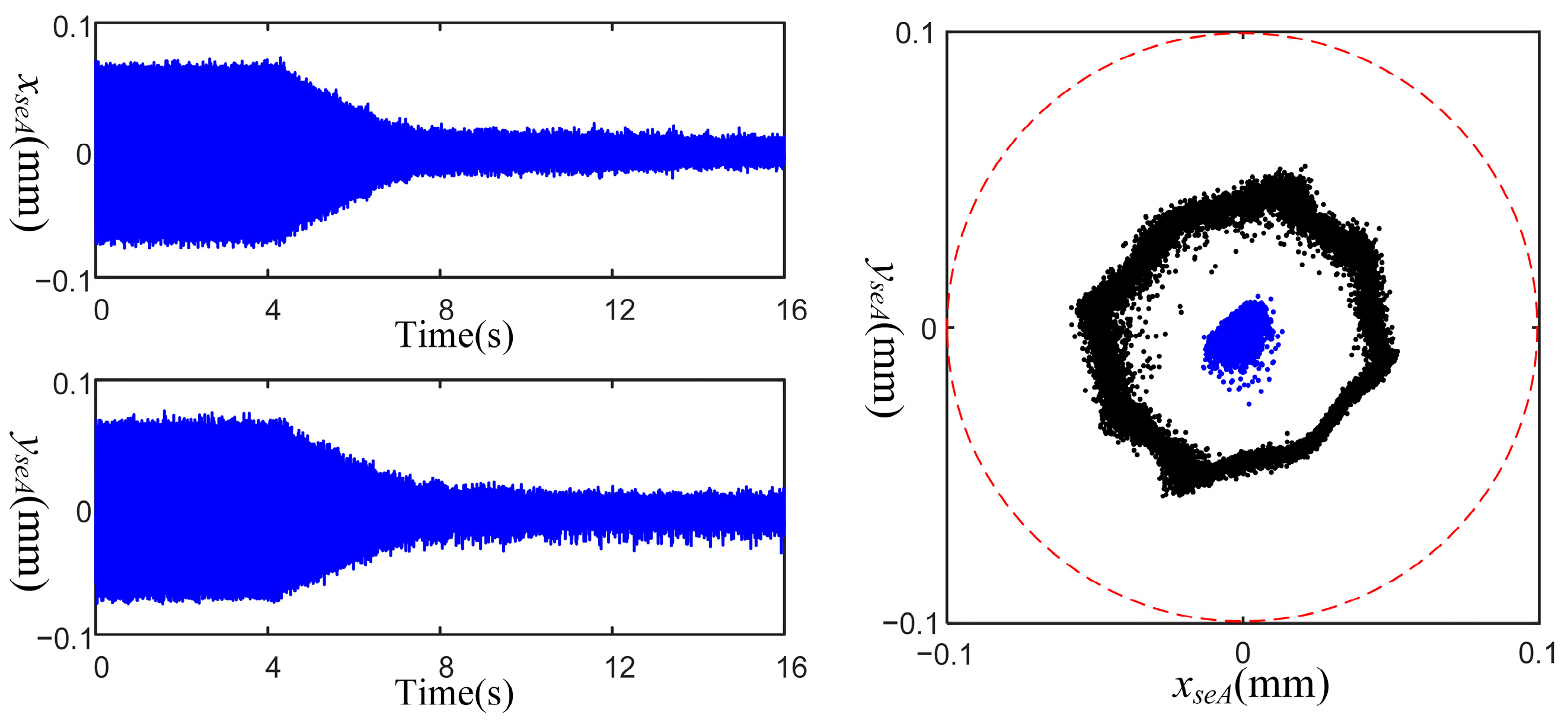
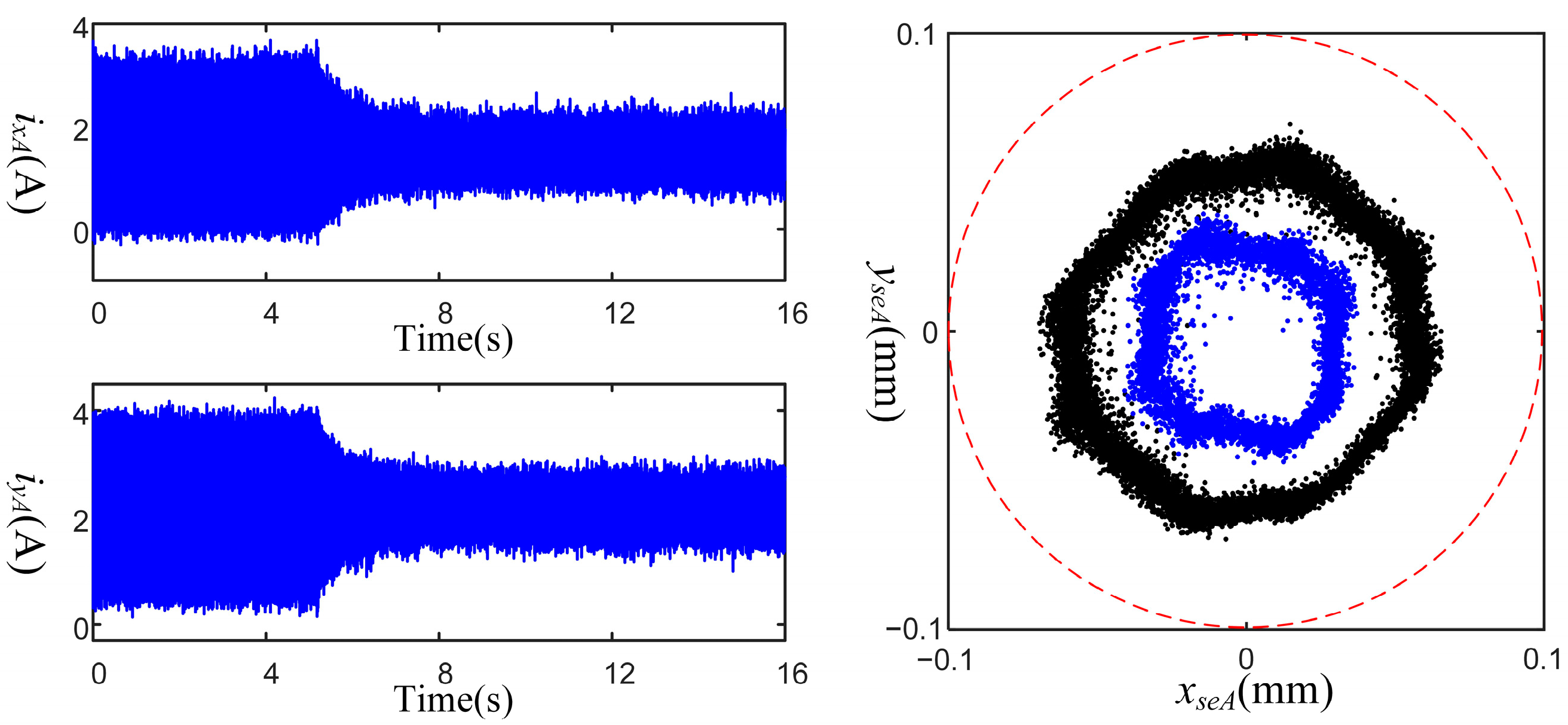
4.2. Experiment
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dai, R.; Zhang, F.G.; Wang, H.J. Characteristics and Key Technical Issues of High-Speed Motors. Chin. J. Turbomach. 2019, 61, 59–66. [Google Scholar]
- Yin, H.; Liu, L. Progress of Active Magnetic Bearings in Compressors and Blowers. Chin. J. Turbomach. 2019, 61, 88–94. [Google Scholar]
- Numanoy, N.; Srisertpol, J. Vibration Reduction of an Overhung Rotor Supported by an Active Magnetic Bearing Using a Decoupling Control System. Machines 2019, 7, 73. [Google Scholar] [CrossRef]
- Zheng, L.; Nie, W.; Xiang, B. Vibration Analysis and Active Control of Rotor Shaft in Magnetically Suspended Air-Blower. Machines 2022, 10, 570. [Google Scholar] [CrossRef]
- Schweitzer, G.; Maslen, E.H. Magnetic Bearings: Theory, Design, and Application to Rotating Machinery; Springer: Berlin, Germany, 2009; pp. 15–36. [Google Scholar]
- Mystkowski, A. Mu-Synthesis for Magnetic Bearings of Flywheel. In PAMM: Proceedings in Applied Mathematics and Mechanics; WILEY-VCH Verlag: Berlin, Germany, 2009. [Google Scholar]
- Mystkowski, A.; Pawluszewicz, E. Nonlinear Position-Flux Zero-Bias Control for AMB System with Disturbance. Appl. Comput. Electrom. 2017, 32, 650–656. [Google Scholar]
- Zhao, Y.; Liu, X.; Yang, G.; Shi, Z.; Zhao, L. Analysis of the Relationship Between the Maximum Bearing Capacity of Axial AMB and the Rotational Speed Based on the Comprehensive Material Strength and Other Factors. Chin. J. Turbomach. 2020, 62, 53–58. [Google Scholar]
- Liu, L.; Wang, Y. On Nonlinear PID Control of Active Electromagnetic Bearing System with Variable Parameters. Chin. J. Turbomach. 2019, 61, 55–60. [Google Scholar]
- Zhao, Y.; Gong, H. Research on Recovery Strategy for the Horizontal AMB Rotor Drop Process. Chin. J. Turbomach. 2020, 62, 38–45. [Google Scholar]
- Chen, S.Y.; Lin, G.J. Robust nonsingular terminal sliding-mode control for nonlinear magnetic bearing system. IEEE Trans. Ind. Electron. 2011, 19, 636–643. [Google Scholar] [CrossRef]
- Chuhmann, T.; Hofmann, W. Improving operational performance of active magnetic bearings using Kalman filter and state feedback control. IEEE Trans. Ind. Electron. 2012, 59, 821–829. [Google Scholar] [CrossRef]
- Beltran-Carbajal, F.; Silva-Navarro, G.; Arias-Montiel, M. Active unbalance control of rotor systems using on-line algebraic identification methods. Asian J. Contr. 2013, 15, 1627–1637. [Google Scholar] [CrossRef]
- Jang, M.J.; Chen, C.L. Sliding mode control for active magnetic bearing system with flexible rotor. J. Franklin I. 2005, 342, 401–419. [Google Scholar] [CrossRef]
- Tung, P.-C.; Tsai, M.-T. Design of model-based unbalance compensator with fuzzy gain tuning mechanism for an active magnetic bearing system. Expert Syst. Appl. 2011, 38, 12861–12868. [Google Scholar] [CrossRef]
- Zheng, S.; Chen, Q.; Ren, H. Active balancing control of AMB-rotor systems using a phase-shift notch filter connected in parallel mode. IEEE Trans. Ind. Electron. 2016, 63, 3777–3785. [Google Scholar] [CrossRef]
- Peng, C.; Zhu, M.; Wang, Y.; Jiang, J. Phase-based video measurement for active vibration suppression performance of the magnetically suspended rotor system. IEEE Trans. Ind. Electron. 2021, 68, 1497–1505. [Google Scholar] [CrossRef]
- Xu, X.; Chen, S.; Zhang, Y. Automatic balancing of AMB systems using plural notch filter and adaptive synchronous compensation. J. Sound Vib. 2016, 374, 29–42. [Google Scholar] [CrossRef]
- Peng, C.; He, J.; Zhu, M.; Deng, Z.; Zhen, Z.; Liu, Q. Optimal synchronous vibration control for magnetically suspended centrifugal compressor. Mech. Syst. Signal Process. 2019, 132, 776–789. [Google Scholar] [CrossRef]
- Peng, C.; Zhu, M. A two-stage synchronous vibration control for magnetically suspended rotor system in the full speed range. IEEE Trans. Ind. Electron. 2020, 67, 480–489. [Google Scholar] [CrossRef]
- Herzog, R.; Buhler, P. Unbalance compensation using generalized notch filters in the multivariable feedback of magnetic bearings. IEEE Trans. Contr. Syst. Technol. 1996, 4, 580–586. [Google Scholar] [CrossRef]
- Vahedforough, E.; Shafai, B. Estimation and rejection of unknown sinusoidal disturbances using a generalized adaptive forced balancing method. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 11–13 July 2007. [Google Scholar]
- Shi, J.; Zmood, R. Synchronous disturbance attenuation in magnetic bearing systems using adaptive compensating signals. Control Eng. Pract. 2004, 12, 283–290. [Google Scholar] [CrossRef]
- Turker, E.; Harvey, A. Improving active magnetic bearing system performance using recursive least square method. In Proceedings of the TENCON 2006—2006 IEEE Region 10 Conference, Hong Kong, China, 14–17 November 2006. [Google Scholar]
- Zhou, J.; Wu, H.; Wang, W.; Hu, Y.; Guo, X.; Song, C. Online unbalance compensation of a maglev rotor with two active magnetic bearings based on the LMS algorithm and the influence coefficient method. Mech. Syst. Signal Process. 2022, 166, 108460. [Google Scholar]
- Jiang, K.; Zhu, C. Unbalance compensation by recursive seeking unbalance mass position in active magnetic bearing rotor system. IEEE Trans. Ind. Electron. 2015, 62, 5655–5664. [Google Scholar]
- Mao, C.; Zhu, C. Unbalance compensation for active magnetic bearing rotor system using a variable step size real-time iterative seeking algorithm. IEEE Trans. Ind. Electron. 2018, 65, 4177–4186. [Google Scholar]
- Gong, L.; Zhu, C. Synchronous vibration control for magnetically suspended rotor system using a variable angle compensation algorithm. IEEE Trans. Ind. Electron. 2021, 68, 6547–6559. [Google Scholar] [CrossRef]
- He, Y.; Shi, L. Unbalance compensation of a full-scale test rig designed for htr-10gt: A frequency-domain approach based on iterative learning control. Sci. Technol. Nucl. Ins. 2017, 2017, 3126738. [Google Scholar] [CrossRef]
- Nonami, K.; Fan, Q.F.; Ueyama, H. Unbalance vibration control of magnetic bearing systems using adaptive algorithm with disturbance frequency estimation. JSME Int. J. 1998, 41, 220–226. [Google Scholar] [CrossRef]
- Yang, R.D.; Pei, W.Z.; Yang, Y.Q.; Deng, Z.Q.; Peng, C. A novel method for rotational speed observation of magnetically suspended high speed motor using quadrature phase-locked-loop. IEEE Sens. J. 2022, 22, 8604–8613. [Google Scholar] [CrossRef]
- Wu, H.T.; Zhou, J.; Zhang, Y.; Han, X.M. Adaptive auto balancing of magnetically suspended rotor based on second order generalized integrator frequency locked loop. Proc. CSEE 2021, 41, 1505–1514. [Google Scholar]
- Chen, Q.; Liu, G.; Han, B.C. Suppression of imbalance vibration in AMB-rotor systems using adaptive frequency estimator. IEEE Trans. Ind. Electron. 2015, 62, 7696–7705. [Google Scholar] [CrossRef]
- Li, J.L.; Liu, G.; Cui, P.L.; Zheng, S.Q. Suppression of harmonic vibration in AMB-rotor systems using double-input adaptive frequency estimator. IEEE Trans. Ind. Electron. 2022, 69, 2986–2995. [Google Scholar] [CrossRef]
- Bodson, M. Rejection of periodic disturbances of unknown and time-varying frequency. Int. J. Adapt. Control Signal Process. 2005, 15, 67–88. [Google Scholar] [CrossRef]




| Parameter | Value | Unit |
|---|---|---|
| 32.45 | kg | |
| 0.88 | kg | |
| 0.05 | kg | |
| −35,428.09 | ||
| 18.35319 | ||
| 30,000 | ||
| 0.41 | m | |
| −0.39 | m | |
| 0.48 | m | |
| −0.47 | m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, X.; Shi, Z.; Mo, N.; Shi, L.; Zheng, Y.; Liu, X. Rejection of Synchronous Vibrations of AMB System Using Nonlinear Adaptive Control Algorithm with a Novel Frequency Estimator. Machines 2023, 11, 188. https://doi.org/10.3390/machines11020188
Bian X, Shi Z, Mo N, Shi L, Zheng Y, Liu X. Rejection of Synchronous Vibrations of AMB System Using Nonlinear Adaptive Control Algorithm with a Novel Frequency Estimator. Machines. 2023; 11(2):188. https://doi.org/10.3390/machines11020188
Chicago/Turabian StyleBian, Xiaoyu, Zhengang Shi, Ni Mo, Lei Shi, Yangbo Zheng, and Xingnan Liu. 2023. "Rejection of Synchronous Vibrations of AMB System Using Nonlinear Adaptive Control Algorithm with a Novel Frequency Estimator" Machines 11, no. 2: 188. https://doi.org/10.3390/machines11020188
APA StyleBian, X., Shi, Z., Mo, N., Shi, L., Zheng, Y., & Liu, X. (2023). Rejection of Synchronous Vibrations of AMB System Using Nonlinear Adaptive Control Algorithm with a Novel Frequency Estimator. Machines, 11(2), 188. https://doi.org/10.3390/machines11020188







