Abstract
Due to the wide spread of robotics technologies in everyday activities, from industrial automation to domestic assisted living applications, cutting-edge techniques such as deep reinforcement learning are intensively investigated with the aim to advance the technological robotics front. The mandatory limitation of power consumption remains an open challenge in contemporary robotics, especially in real-case applications. Spiking neural networks (SNN) constitute an ideal compromise as a strong computational tool with low-power capacities. This paper introduces a spiking neural network actor for a baseline robotic manipulation task using a dual-finger gripper. To achieve that, we used a hybrid deep deterministic policy gradient (DDPG) algorithm designed with a spiking actor and a deep critic network to train the robotic agent. Thus, the agent learns to obtain the optimal policies for the three main tasks of the robotic manipulation approach: target-object reach, grasp, and transfer. The proposed method has one of the main advantages that an SNN possesses, namely, its neuromorphic hardware implementation capacity that results in energy-efficient implementations. The latter accomplishment is highly demonstrated in the evaluation results of the SNN actor since the deep critic network was exploited only during training. Aiming to further display the capabilities of the introduced approach, we compare our model with the well-established DDPG algorithm.
1. Introduction
Models of the cerebral cortex historically served as an inspiration for deep neural networks (DNNs), which, in turn, have produced exceptional results in numerous robotic applications [1,2]. As a representative example, the widely used reinforcement learning (RL) technique enabled researchers and engineers to built robotic agents that could be taught how to complete complicated tasks. Such tasks typically include a trial-and-error scheme, much like a newborn learns how to act and appropriately behave through several attempts and errors [3]. Even in complex challenges, including robots with multiple degrees of freedom (DoF) [4] operating in continuous action spaces, RL, and convolutional neural networks (CNNs) has accomplished outstanding achievements. In spite of their salient performance, DNNs also have numerous inevitable constraints [5]. Typically, the exploitation of such models is accompanied by an expensive demand for computer resources and days of training. As a result, many applications are restricted by these systems, and notably those that cannot be plugged in, such as assisted living robotic systems or aerial robots. Considering the era of the energy crisis, as far as robotic systems are concerned, it is essential to design agents in a power-constrained way [6].
Despite the initial bioinspired origins of DNNs’ design, their implementation significantly diverges from the actual brain’s functionality. That being said, DNNs’ learning process accommodates complex mathematical calculations between neurons [7], while mammalian neurons communicate with spikes [8]. Thanks to the above characteristic, the mammalian brain consumes much less energy compared to artificial neural networks (ANNs) while concurrently excelling at multiple challenging tasks with commendable accuracy. The fact above has driven researchers to design neural networks that were more proximate to biological ones, resulting in the widely known spiking neural networks (SNNs), which are ANNs that communicate with spikes [9]. Taking advantage of the SNN design, the developed algorithms can be implemented in neuromorphic processors, i.e., hardware units that process and store data similarly to neurons and synapses in biological neurons [10]. Such processors running SNNs are more energy-efficient than DNNs, which are commonly implemented in edge graphics processing units (GPUs).
Considering the above, the reader can understand the promising benefits of SNNs’ application in contemporary RL approaches that remain incompatible with neuromorphic hardware solutions. However, their efficient implementation in such RL and robotics applications still faces a wide range of barriers, with sustaining it being an undergoing challenge with many open research questions and gaps for further investigation. Even though SNNs have proven efficacy in the completion of benchmark challenges and databases, they are still lacking in terms of accuracy. Furthermore, due to the nondifferentiable nature of the spikes, no prior knowledge regarding the CNN backpropagation process can be directly adopted in SNNs. To that end, SNNs must often be designed, implemented, and trained from scratch for a specific task despite the existence of competitive DNN-based solutions in the same field. However, complicated systems and training schemes, such as RL ones, could be divided into distinctive subtasks, with each individually addressed by either a DNN or an SNN architecture. An initial realization of the above was recently ascertained in [11], where the deep deterministic policy gradient (DDPG) RL technique was implemented through a combination of the above architectures, concluding in very promising results for robotic navigation tasks. Hence, it is reasonable to conclude that a possible fusion of spiking and deep-learning architectures could benefit the performance of contemporary systems.
Diving into the basic tasks of an efficient robotic application, this paper focuses on the broadly known challenge of robotic-arm object manipulation. More specifically, a 2 DoF robotic arm was considered with a two-finger gripper attached to its wrist. The robotic arm was set to efficiently approach, grasp, and move an orthogonal object placed on a table. To achieve that, we propose the combination of one spiking and one deep neural network for the control of the robotic arm. This approach constitutes an expansion of a previous work of ours [12] where the conceptual framework was presented, but no simulations and experimental results were conducted. Following the above concept, we adopted the DDPG RL approach and implemented a hybrid DDPG version by exploiting a spiking network for the actor and a deep one for the critic. The DDPG technique was used to learn optimal control policies that enabled the robotic arm to efficiently approach, grasp, and move the target object to the desired position. The actor was trained to generate the actions of the arm given the robot’s state, while the critic was responsible for the evaluation of the actor. Since the critic network was deployed only during the training procedure, we ended up with a learning model that was compatible with neuromorphic hardware processors. The overall architecture was compared with that of the well-established DDPG, aiming to assess the efficiency of the proposed hybrid training scheme and the capacity of the spiking actor to control the robotic arm. To that end, the contributions of this paper can be summarized as follows:
- The efficient development of a spiking actor for the box-reach, grasp, and box-transfer approach using a dual finger gripper in 2D space (https://www.youtube.com/watch?v=4XVODJJ6Cs8, accessed on 10 December 2022).
- The implementation of a subgoal training strategy for the RL agent via designing two distinct reward functions, one for the box-reach and one for the box-transfer subtasks, which led to smoother movements of the robotic arm.
- The introduction of a more sophisticated reward function controlled through a designed collinear grasping condition for the box-reach subtask, enabling the robotic arm to attain a proper grasping position before reaching the box.
- Extensive experimental and comparative studies of the proposed subgoal hybrid-DDPG model highly demonstrating its superiority against the classical DDPG and the end-to-end approaches in terms of both performance and time efficiency.
The rest of the paper has the following structure: Section 2 presents contemporary research in the field of RL-based applications for robotic tasks and SNN implementation. Section 3 contains the entire method introduced in the current work. Section 4 demonstrates the experimental study conducted to assess the proposed solution. Section 5 provides a discussion about the obtained results and their importance for energy-efficient robotic manipulation. Lastly, Section 6 concludes with the findings of our study and refers to interesting subjects for future work.
2. Related Work
The ability of an intelligent agent to adjust its movement in unseen environments is a crucial component in robotics research [13]. Thus, techniques enabling robots to empirically learn their behavior through trial-and-error procedures receive evident recognition [3,14,15]. In RL, a set of goals is determined by using a reward function that is realized during the learning procedure as either a positive reward or a negative punishment depending on how well the robot performs regarding the goal. Among a wide range of research areas, robotic manipulation and control are one where RL approaches excel [16,17,18,19]. Although function approximation techniques drove the very first RL achievements in robotics, policy learning RL techniques truly produced a notable change in the field. Hence, instead of working in enormous state-action spaces, policy learning utilizes a smaller policy space, resulting in accelerated convergence time and significantly reduced dimensionality. Recent approaches in the field, such as DDPG [20], employ learning to enable smoother motion planning [21] and collision avoidance [22]. Additionally, studies exploit RL to learn the optimal policies for controlling a gripper equipped with an RGB camera that detects potential occlusions [23]. In general, deep-learning models are built with sophisticated architectures of various trainable layers; thus, they achieve admirable performance in a wide range of applications, even beyond robotics [24,25,26,27]. This is mainly due to their capability to be trained by means of backpropagation optimization algorithms [28,29].
On the other hand, SNNs were initially investigated as biological information models [30] to acquire a better understanding of how the brain works. Researchers have been inspired by the efficiency and accuracy of mammalian movement. The above fact drove researchers to further investigate how brain neurons work and communicate, aiming to develop more energy-efficient and durable algorithms for robotic applications. Thus, research on SNNs began with neuroscientists’ interest and has spread to more areas of study, such as mathematics, computer science, and even physics [31]. Pioneering works in the field demonstrate that SNNs can be utilized to tackle a wide range of modern robotics applications [32,33]. SNNs are the third generation of ANNs and they constitute a result of extended research regarding the learning process and capabilities of the mammalian brain. The early literature revealed that neurons communicate via spikes, i.e., a set of peaks in a cell’s action potential [34]. Due to the nondifferentiable nature of spikes, the learning process in SNNs has become a challenging task. SNNs can be utilized by either converting traditional neural networks into SNNs [35] or developing a more bioinspired learning model. The former technique overcomes the most significant constraint of SNNs, namely, the learning process, but fails to utilize all capabilities of SNNs. The spike-timing-dependent plasticity (STDP) [36] and the ReSuMe [37] learning methods are two of the most common learning rules used in SNNs. Moreover, SpikeProp [38] and Chronotron [39] have been widely exploited, while the spatiotemporal back-propagation (STBP) technique [40] demonstrated a significantly fast inference time. Apart from the learning process, the research community has also focused on numerous biologically inspired neurons. For instance, Hodgkin and Huxley [41], the spike response model (SRM) [42], the Izhikevich neuron model [43], and Leaky integrate-and-fire (LIF) neurons [44] have been frequently employed in many SNNs. Considering the above implementations, LIF neurons have been widely deployed in many mobile robotic applications thanks to their simplicity and effectiveness [45,46].
Nevertheless, the implementation of both DNNs and SNNs has several drawbacks and limitations, as already mentioned in Section 1. For that purpose, a combination of DNNs’ advantages and SNNs’ characteristics could reveal interesting outcomes. To that end, an innovative co-learning model comprising a deep critic network and a spiking actor network was developed for the mapless navigation of a two-wheeled robot [11]. Inspired by this novel work and the promising findings of RL [47], we propose a hybrid DDPG–RL training scheme with a spiking actor for the manipulation of a 2-DoF robotic arm equipped with a 1-DOF gripper. The deployed spiking actor network was trained through the STBP method and is responsible for the generation of optimal policies that control the robotic arm for target reaching, grasping, and movement.
3. Materials and Methods
As was mentioned in Section 1, we designed a 2-DoF robotic arm moving in a 2D space equipped with a ROBOTIQ gripper, i.e., a two-finger gripper. The above design was exploited for a manipulation task as presented in Figure 1. Both of the robot’s joints are prismatic, while the origin was set at the center of the table. The entire experiment was realized using a robot operating system (ROS) and the Gazebo simulator. The first joint () moves horizontally in the range of (−0.45 m, 0.45 m), indicating the table’s width in meters, while the second joint () moves vertically within the range of (0.00, 0.70 m), indicating the table’s height. Thus, the robotic arm’s movements always lie inside the table’s borders. As far as the gripper is concerned, we only controlled the left finger since we implemented a mimic joint Gazebo plugin where the right finger mimicked the exact movement of the left one.
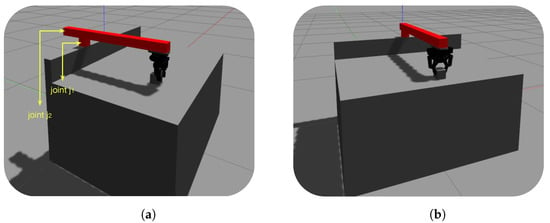
Figure 1.
The 2-DoF robotic arm equipped with a ROBOTIQ dual finger gripper. (a) indicates robot’s joint. (b) indicates the gripper and the target object (box).
Regarding the simulation configurations, the target object was placed randomly within the borders of the table and it was equipped with contact sensors. Subsequently, the agent could detect the object’s position and orientation, the contact between the target object and the table’s surface, and the contact between the target object and the end effector during grasping. We implemented a hybrid actor–critic training approach using the DDPG method to control the robotic system. The employed spiking actor network calculated and provided the agent’s actions, and the deep critic network was responsible for evaluating the actor, as illustrated in Figure 2.
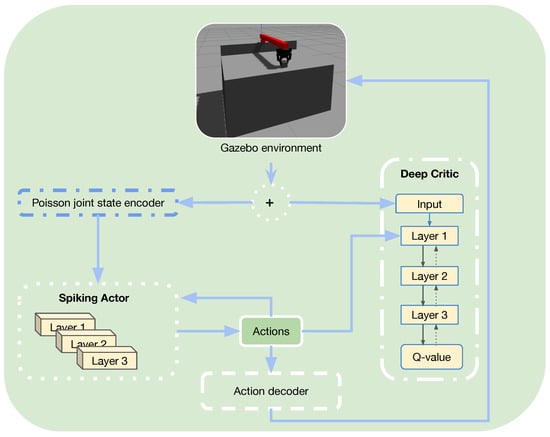
Figure 2.
Actor–critic RL methodology.
We collected the ROS joint messages from the Gazebo environment; then, the joint values were encoded to spikes in order to be fed as input into the spiking actor network. The actor’s network, facilitated by LIF neurons, was trained using the STBP algorithm. Since the STBP method was implemented on an LIF neuron model, we employed a rectangular function for the gradient approximation of a given spike. We trained the actor to generate the optimal actions minimizing the loss function, described as follows:
In other words, given the joints’ state and the actor’s calculated actions, the critic network was trained to maximize the estimated Q values. Thus, the critic was trained to minimize the temporal difference error, similar to [11,48].
As already mentioned, inspired by the way in which the mammalian brain works, we divided the task of reaching, object grasping, and transfer into two individual, self-contained subgoals. Thus, we adopted the implementation of a hierarchical learning scheme. With the aim of updating the actor’s actions, we designed multiple reward functions suitable for each particular subtask, which is analytically described in Section 3.1.
3.1. Box-Reach Learning Scheme
For the hierarchical learning scheme, each individual subgoal was described by its corresponding reward function. The target-object reach task first exploited the reward function described in Algorithm 1. For an efficient grasping position, the robotic arm has to adjust its position on the horizontal axis quite a while before it reaches the object, so as to avoid a possible collision with the object. To that end, aiming to drive the agent to approach the object first in the x axis and then in the y axis, we set two coefficients in the reward function, viz., and , respectively. The value of the coefficient was greater than the value of , resulting in a more elliptical movement, as shown in Figure 3. A further discussion of our findings regarding the adoption of the specific loss reward function is presented in Section 5.
| Algorithm 1 Reward function for the first subgoal of target-object reach. |
Require:, the reward for goal reach. Require:, the distance threshold value for goal reach. Require:, the collision value. Require:, , the target-object’s high value indicating if the end effector would collide with the target object. Require:c, the collinear value as described in (2). Require:, , the current x, y distance, respectively, between the end effector and the target object. Require: and , the previous x, y distance, respectively, between the end effector and the target object. Require: and , distance amplifier for the x, y directions, respectively. Output:R, the reward function.
|
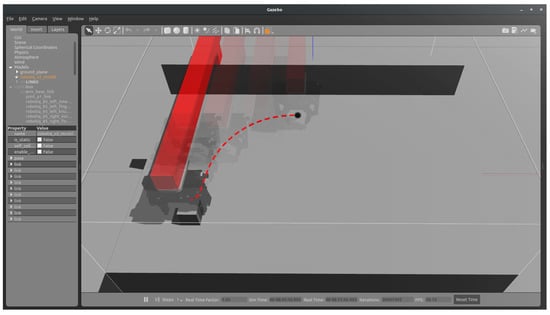
Figure 3.
The elliptical movement of the robotic gripper approaching the target object.
Since the end effector had reached the target object in the y axis, the following task was to approach it with a proper grasping orientation in order to successfully grasp and move it to the target position. In our approach, a proper grasping position requires the left fingertip, the center of mass of the box, and the right fingertip to be collinear, as depicted in Figure 4.
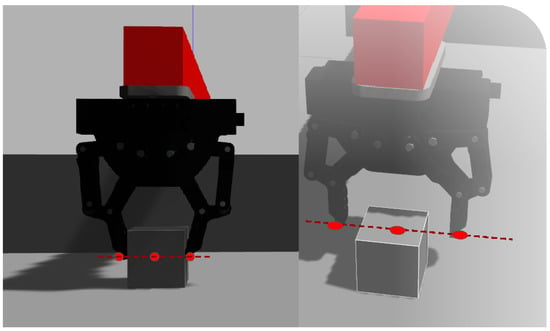
Figure 4.
The frontal and upper views of the three points forming a collinear grasping position.
In order to detect whether the three points were collinear, we calculated the determinant formula of the area of the triangle formed by these three points as follows:
where , are the left finger’s x,y position, , are the left finger’s x,y position, , are the box’s x,y position. In the case where the result c in (2) was zero, the left finger, the box, and the right finger were collinear, indicating that the gripper had reached a proper grasping position.
To that end, given the reward, the collinear value, and the elliptical grasping approach, the agent attempts to predict the joint actions that maximize the total reward. The agent takes as input the state vector:
where are the x- and y-axis distances between the end effector and the target object, are the directions on the x and y axes between the end effector and the target object, c the collinear values described in (2), is the velocity of the end effector at the x direction, is the velocity of the end effector at the y direction, and , are the target object’s x, y positions.
3.2. Box-Transfer Learning Scheme
The next subtask refers to the grasping approach and the movement of the target object to the goal position. Right after the gripper had achieved the collinear grasping position, the gripper was controlled to gradually close its fingers until the contact sensors on the box had published a contact state. Subsequently, while the gripper held the target object, the agent, on the basis of its state vector described in (4), was trained to find the optimal policy to move the target object to the desired goal position. The state vector of the agent was slightly adjusted on the basis of the nature of the task as follows:
where are the distance and the direction between the end effector and the goal position, respectively, is the velocity of the end effector at the x direction, is the velocity of the end effector at the y direction, and are the target object’s x, y positions. Similarly to the state vector, the reward function was also adjusted and redesigned as shown in Algorithm 2:
| Algorithm 2 Reward function for the second subgoal of goal position reach. |
Require:, the reward for goal reach. Require:, the distance threshold value for goal reach. Require:, the collision value. Require:,, the target object’s z value and the value indicating if the end effector collides with the target object, respectively. Require:, the Boolean value from the contact sensor indicating that the gripper holds the target object. Require:, , the current and previous distances, respectively, between the end effector and the goal position. Require:, distance amplifier. Output:R, the reward function.
|
We exploited the same simulation environment for training both subgoal scenarios. The proposed agent was trained by employing only two different starting positions and two final goal positions in the environment. More specifically, we used two critical initial positions at the opposite edges of the table. Moreover, aiming to highlight the efficiency of the introduced algorithm, we trained the agent by also exploiting the classical DDPG adopting the same environment and training configurations. The training procedure lasted 100 episodes in each environment for both the hybrid DDPG with a spiking actor network and the DDPG with a deep actor one.
4. Results
In the current section, we describe the experimental study and the obtained evaluation results regarding the efficiency of the hybrid DDPG in terms of success rate and execution time compared with that of the well-established DDPG approach. The aforementioned evaluation was realized for the target-object reach, grasping, and transfer subtasks. In order to evaluate our model, we designed a similar evaluation environment to the training one.
The evaluation was performed using 10 distinct environments covering different points of the table’s surface. To achieve that, 10 distinct initial positions were sampled from the agent’s available space of movement. Furthermore, in order to capture the agents’ stochasticity and ensure robustness, we repeated the evaluation process for many trials given a specific subtask.
4.1. Box-Reach Subtask
In particular, for the first subtask, defined as a box-reach task, we evaluated the scenario in 10 environments and for 50 trials. Figure 5 illustrates the obtained success rates of the target-object reach task for both the hybrid DDPG and the classical DDPG method. The corresponding execution time of these trials is depicted in Figure 6. Moreover, Table 1 contains the mean value () and the standard deviation () of the 50 runs in the 10 above-mentioned environments. As observed, the proposed spiking actor achieved high success rate values after being trained only with two starting positions. On the other hand, the classical DDPG had a better execution time in the successful trials, but it did not manage to successfully learn to consistently execute the target-object reach task.
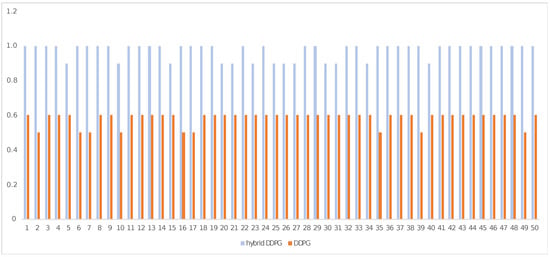
Figure 5.
The average success rate of the hybrid DDPG model vs. the classical DDPG model for 50 trials in 10 different starting and goal positions. Blue bars indicate the hybrid DDPG, while orange bars refer to the classical DDPG.
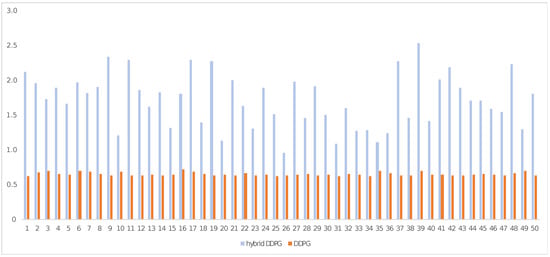
Figure 6.
The average execution time of the hybrid DDPG model vs. the classical DDPG model for 50 trials in 10 different starting and goal positions. Blue bars indicate the hybrid DDPG, while orange bars refer to the classical DDPG.

Table 1.
The mean () and the standard deviation () values of the success rate and the execution time obtained by both the hybrid DDPG and the DDPG for the box-reach subtask after 50 trials in 10 evaluation environments.
To further understand the behavior of the spiking actor, we gathered all 50 repetitions of a specific evaluation environment and projected the robotic arm’s joint positions in the same plot as a heat map. Thus, brighter colors in the heat map correspond to more frequently visited points by the arms joints, while dark ones refer to unvisited positions. To this effect, one can visualize in an aggregated manner the way in which robotic arm attempted to solve the task.
The results of the spiking actor for the hybrid DDPG model for four indicative evaluation scenarios of the box-reach task are presented in Figure 7. Each different subfigure represents a distinct evaluation environment, which means a different set of the robot’s starting pose and the position of the box. Each subfigure includes a heat map and a graph. The heat map displays the evaluation runs of 50 trials, while the graph illustrates 10 robot paths, randomly selected from the corresponding heat map, along with the desired trajectory indicated with a red line. The robot’s starting position can be easily perceived as a small bright dot. Then, the different trajectories of the robotic arm could be visualized with specific mention to several wide regions corresponding to the end effector’s attempts to be properly placed when it was near the box.
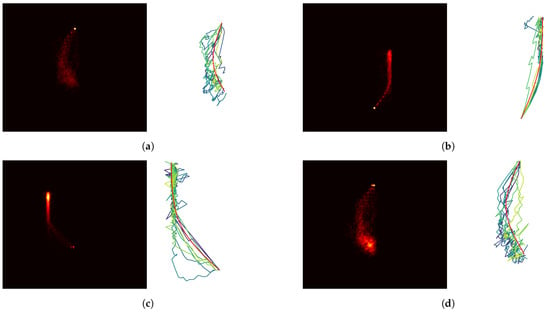
Figure 7.
The obtained results from the hybrid DDPG model with the spiking actor. Each subfigure corresponds to a particular starting pose and target-object position of the robot, along with the path that the agent generated to solve the task. (a–d) Heat map and a graph.The heat map summarizes the evaluation results from 50 trials for the box-reach subtask, while the graph depicts 10 paths randomly selected from the 50 paths of the heat map, along with a red line indicating the desired target path.
However, the most interesting finding in Figure 3 is the clear depiction of the elliptical movement adopted by the agent during evaluation. The agent efficiently learnt to first approach the target object on the x axis and then on the y axis, following the designed reward function presented in Algorithm 1. Having achieved that, the robot’s gripper was able to approach the target object with a proper grasping orientation.
4.2. Box-Transfer Subtask
For the next subtask, called grasping and box transfer, we deployed the second reward function, as described in Algorithm 2. Due to its complexity, for this subtask, we trained our model in four particular starting and goal positions; then, we evaluated 10 different goal positions. The results depicted in Figure 8 indicate the success rate in the task of grasping and box transfer to the desired position. Each column corresponds to the average success rate of a given evaluation trial on 10 environments for the hybrid and conventional DDPG approaches, while each row refers to 1 of the 17 different trials. Accordingly, Figure 9 illustrates the average execution time for the hybrid DDPG and DDPG models. Comparing the results of the two subfigures, we observe that the hybrid DDPG achieved higher accuracy with lower execution time in this particular task compared to the classical DDPG model. Figure 8 shows that, from Trials 13 to 17, the DDPG had extremely low accuracy results. Table 2 shows the mean () and standard deviation () values of the obtained results for the 10 different environments and the 17 trials. The DDPG once again needed more training time or environments to achieve competitive performance. As far as the execution time is concerned, the two models achieved similar results. An improvement regarding the time efficiency of the DDPG could be possibly realized with the exploitation of advanced GPUs and computational engines, but such solutions entail higher computational costs, adding a barrier to mobile applications. However, our method and NNs generally implemented on neuromorphic hardware units efficiently operate with low-power consumption demands in real-time conditions [49,50].
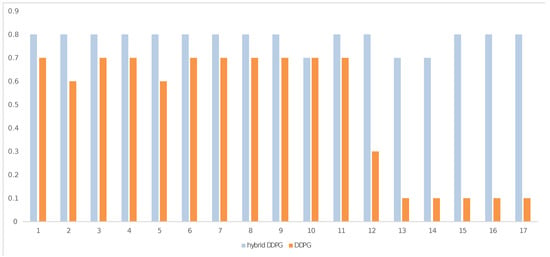
Figure 8.
The average success rate of the hybrid DDPG model vs. the classical DDPG model for 17 trials in 10 different starting and goal positions. Blue bars indicate the hybrid DDPG, while orange bars refer to the classical DDPG.
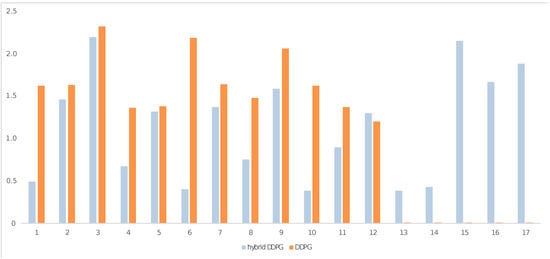
Figure 9.
The average execution time of the hybrid DDPG model vs. the classical DDPG model for 17 trials in 10 different starting and goal positions. Blue bars indicate the hybrid DDPG, while orange bars refer to the classical DDPG.

Table 2.
The mean () and the standard deviation () values of the success rate and the execution time obtained by the hybrid DDPG and the DDPG for the box-transfer subtask after 50 trials in 10 evaluation environments.
Lastly, similarly to the box-transfer subtask, we gathered all 17 repetitions of each specific evaluation environment and projected the robotic arm’s joint positions onto the same plot as that of the heat map. Dark regions in the heat map correspond to unvisited positions, while bright ones refer to frequently visited points by the robotic arm’s joints during the evaluation runs.
Figure 10 illustrates the results of the spiking actor, viz., the hybrid DDPG model, for four indicative evaluation scenarios of the box-transfer task. Each of the four different subfigures represents 17 runs of a distinct evaluation environment, i.e., a specific set of the robot’s starting pose and the position of the box. By comparing Figure 7 and Figure 10, we can detect how the different reward functions affect the produced behavior of the agent. Thus, although the produced actions in Figure 7 followed an obvious elliptical movement, the actions produced by Algorithm 2 clearly differed, following a smoother movement, as depicted in Figure 10.
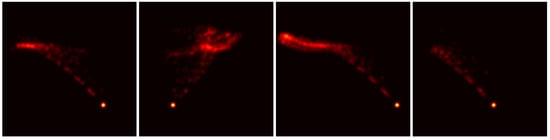
Figure 10.
Results from the hybrid DDPG model with the spiking actor. Each of the subfigures represents a particular robot’s starting position and target-object position along with the path that the agent generated. Each subfigure indicates the results from 17 trials for the box-transfer task.
5. Discussion
In the previous section, we presented the evaluation results obtained from the hybrid DDPG and the DDPG agents. At this stage, we discuss our findings, indicate the benefits and limitations of the introduced hybrid approach, and attempt to provide reasonable explanations and possible extensions.
5.1. Findings of the Box-Reach Subtask
The obtained results of the box-reach subtask demonstrate enhanced performance for the spiking-actor network compared to the deep actor one. As far as the execution time is concerned, the DNN succeeded in reaching the target object at shorter execution times. However, the proposed implementation of the spiking actor trained with the hybrid DDPG scheme was designed to be embedded in neuromorphic hardware units. Thus, thanks to the capacities of neuromorphic hardware processors, the spiking actor has the potential to reach even shorter execution times. Additionally, we developed a modified reward function that promotes elliptical movement for the robotic arm as an attempt to avoid the gripper hitting and shifting the target object before grasping. In particular, the agent was motivated to adjust its horizontal (x-axis) position quite a bit before it reached the target object in order to approach it from a vertical orientation, constituting a suitable grasping orientation for the ROBOTIQ gripper. To that end, we designed the reward function of the first subtask that drove the agent to an elliptical movement in Algorithm 1. The obtained simulation results, highlighted in Figure 3, prove the ability of the designed function to teach the agent to correctly follow such an approaching trajectory, as well as the reasoning of our concept. Figure 7 provides a clear visual depiction of the agent’s adopted behavior. On the other hand, such an approach resulted in a high-dimensional state vector, which might have been reason for the increased execution time of the spiking actor.
5.2. Findings of the Box-Transfer Subtask
Proceeding with the box-transfer subtask, the agent was directed to grasp and move the target object to the desired final position. This task was interconnected with the first task, since in the case that the agent failed to drive the end effector to a proper grasping position during the first subtask, the agent could not proceed with a successful grasping execution in the second subtask. Due to the complexity of the second subtask, we designed a new reward function, as described in Algorithm 2. At that stage, it was not essential for the agent to approach the goal position from a certain axis rather than reach the desired goal position. Thus, for this subtask, we only used the distance and the direction of the end effector towards the goal position, resulting in a more compact state vector. Given the above property of the agent’s state space, the spiking actor achieved not only better accuracy than that of the classical DDPG, but also shorter execution time.
The lower success rates observed in the second subtask compared to the first one are mainly attributed to two main reasons. First, the agent was not able to reach a proper grasping position, which was realized as an error in the second task, where the gripper failed to grasp the object. Second, due to the nature of the environment in the Gazebo simulator, the end effector could not hold the target object for more than 15 s. Thus, in the cases where the agent explored the environment for more than 15 s, the end effector released the object, the contact sensor returned a nonholding state, and the exploration could, thus, not be continued. As a result, the reward function returned a timeout state, and the agent was not capable of sufficiently exploring the available action space. Two possible solutions to the above problem could be tested. First, an increase in the training episodes of the agent would give an opportunity for enhanced exploration; however, the issue of the limited training steps per episode remains, rendering it difficult for the agent to consistently succeed in the task, even in training, if the object is quite far from the goal position. Second, an improved contact sensor or simulation environment could extend the available grasping duration for the agent to explore the space, but it was not essential for our experiments. The above limitation allowed for us to clearly demonstrate the benefits of the spiking actor network, highlighting its superiority in the given challenge.
5.3. End-To-End Learning Scheme
Apart from the discussion regarding the findings of the subtasks during the hierarchical learning scheme, we now present the end-to-end learning scheme that was initially adopted to train both the hybrid and the classical DDPG. In the previous sections, the proposed hierarchical method efficiently taught the agent to reach, grasp, and transfer the target object to the desired goal position. However, before the hierarchical learning scheme, we implemented a spiking DDPG algorithm that tried to learn the optimal policies to perform the two subtasks in an end-to-end manner.
To achieve that, the state vector of the actor network was formed as follows:
where is the distance between the gripper and the box, is the direction between the gripper and the box, is the distance between the box and the target goal position, is the direction between the box and the target goal position, p is the position of the middle point between the two fingers, and u is the velocity of the second joint. Given the state s, the spiking actor was assigned to estimate the robot arm’s actions , where represents the action for the first joint, the action for the second joint, and the action for the end effector. Then, the agent was trained to calculate the optimal policy that maximized the reward function, described as follows:
In the above equation, is the reward for the end goal of the box transfer to the goal position, is the distance threshold value for goal reach, is the previous distance between the target object and goal position, is the distance amplifier, is the collision value, and are the target object’s height and a value indicating if the end effector collides with the target object, respectively, is the Boolean value from the contact sensor indicating that the gripper held the target object, and is the current distance between the end effector and the target object.
However, this approach was unable to solve the ending task of the target-object transfer. To be clearer, in Figure 11, we present the results obtained from the end-to-end learning scheme. The yellow circle indicates the robotic arm’s starting pose, the white box indicates the box’s position and the green circle refers to the desired target position of the box. Figure 11 aggregates the results from 50 trials in 4 different sets of values for the robotic arm’s initial pose, the position of the box, and the desired target position. As one can observe, even in the cases where the network learnt to successfully approach the target object, it subsequently failed to properly grasp it, and was thereby unable to transfer the box to the desired goal position and complete the task. The above observations, after extensive experimentation and trials, drove our research to a hierarchical approach by dividing the entire challenge into two self-contained subtasks as was extensively described in Section 3.

Figure 11.
The obtained result from the end-to-end learning scheme. The yellow circle indicates the robotic arm’s starting pose, the pink box indicates the box’s position, and the green circle refers to the desired goal position.
6. Conclusions
This paper introduced a hybrid DDPG framework for the autonomous planning of energy-efficient robots based on SNNs and a neuromorphic hardware-compatible architecture. The aforementioned system uses a spiking-actor and a deep-critic network to complete object manipulation tasks. To achieve that, the initial challenge was divided into two separate but interconnected subtasks, adopting a hierarchical training scheme. For that purpose, we proposed two different reward functions, each one particularly designed for each subtask, viz., the box-reach and box-transfer tasks.
The aim of the first reward function was to efficiently approach the target object while achieving a proper grasping position. Hence, we suggested a collinear grasping method to control the efficient execution of the first subtask. Due to the high-dimensional state space required by the agent of the first subtask, we designed a more compact reward function, suitable for the second box-transfer subtask. Moreover, we employed a contact sensor at the object to ensure accurate grasping during the training and evaluation process.
We evaluated the efficiency of the proposed hybrid model with that of the classical DDPG approach, which was implemented and tested in the same environment for comparison purposes. Hence, we compared the proposed hybrid DDPG with the spiking actor with the classical DDPG method that exploits a deep actor. The obtained results demonstrate the superiority of our approach in the specific challenge. Moreover, the usage of the deep-critic network only for the training resulted in a compatible model with neuromorphic hardware units. The above fact enables the possibility of deploying such a method in robotics applications, where the demand for quick, transportable, and energy-efficient applications is becoming increasingly important. We further discussed the reasons that drove us to design this hierarchical learning scheme, which lay in the incapacity of the end-to-end learning model to complete the box-transfer task. The latter was also supported by the hierarchical way in which the mammalian brain works.
Considering the above, a further step in our research would be the development of a spiking-actor model that could control a gripper with more than 2 DoF, offering the possibility to grasp multiple deformable objects. As an additional step, we aim to deploy the aforementioned approach to a neuromorphic hardware unit in order to capture the entire operational capacities of SNNs and produce valuable results in real-case scenarios.
Author Contributions
Methodology, K.M.O.; software, K.M.O.; writing–original draft preparation, K.M.O.; writing–review and editing, I.K. and A.G.; supervision, I.K. and A.G. All authors have read and agreed to the published version of the manuscript.
Funding
We acknowledge the support of this work by the project “Study, Design, Development and Implementation of a Holistic System for Upgrading the Quality of Life and Activity of the Elderly” (MIS 5047294), which is implemented under the Action “Support for Regional Excellence”, funded by the Operational Programme “Competitiveness, Entrepreneurship and Innovation” (NSRF 2014–2020) and co-financed by Greece and the European Union (European Regional Development Fund).
Data Availability Statement
In this research, only simulation data have been exploited through the Gazebo simulator and the Robot Operation System (ROS).
Conflicts of Interest
The authors declare no conflict of interest.
References
- An, S.; Zhou, F.; Yang, M.; Zhu, H.; Fu, C.; Tsintotas, K.A. Real-time monocular human depth estimation and segmentation on embedded systems. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 55–62. [Google Scholar]
- Kansizoglou, I.; Misirlis, E.; Tsintotas, K.; Gasteratos, A. Continuous Emotion Recognition for Long-Term Behavior Modeling through Recurrent Neural Networks. Technologies 2022, 10, 59. [Google Scholar] [CrossRef]
- Polydoros, A.S.; Nalpantidis, L. Survey of model-based reinforcement learning: Applications on robotics. J. Intell. Robot. Syst. 2017, 86, 153–173. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, P.; Zheng, C.; Tian, L.; Tian, Y. A deep reinforcement learning strategy combining expert experience guidance for a fruit-picking manipulator. Electronics 2022, 11, 311. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, D.; Zhou, P.; Zhang, T. Model compression and acceleration for deep neural networks: The principles, progress, and challenges. IEEE Signal Process. Mag. 2018, 35, 126–136. [Google Scholar] [CrossRef]
- Mohammadpour, M.; Zeghmi, L.; Kelouwani, S.; Gaudreau, M.A.; Amamou, A.; Graba, M. An Investigation into the Energy-Efficient Motion of Autonomous Wheeled Mobile Robots. Energies 2021, 14, 3517. [Google Scholar] [CrossRef]
- Kansizoglou, I.; Bampis, L.; Gasteratos, A. Do neural network weights account for classes centers? IEEE Trans. Neural Netw. Learn. Syst. 2022, 2022, 1–10. [Google Scholar] [CrossRef]
- Swanson, L.W. Brain Architecture: Understanding the Basic Plan; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Pfeiffer, M.; Pfeil, T. Deep learning with spiking neurons: Opportunities and challenges. Front. Neurosci. 2018, 12, 774. [Google Scholar] [CrossRef]
- Balaji, A.; Das, A.; Wu, Y.; Huynh, K.; Dell’Anna, F.G.; Indiveri, G.; Krichmar, J.L.; Dutt, N.D.; Schaafsma, S.; Catthoor, F. Mapping spiking neural networks to neuromorphic hardware. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2019, 28, 76–86. [Google Scholar] [CrossRef]
- Tang, G.; Kumar, N.; Michmizos, K.P. Reinforcement co-Learning of Deep and Spiking Neural Networks for Energy-Efficient Mapless Navigation with Neuromorphic Hardware. In Proceedings of the IEEE/RSJInternational Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 25–29 October 2020; pp. 6090–6097. [Google Scholar] [CrossRef]
- Oikonomou, K.M.; Kansizoglou, I.; Gasteratos, A. A Framework for Active Vision-Based Robot Planning using Spiking Neural Networks. In Proceedings of the 2022 30th Mediterranean Conference on Control and Automation (MED), Athens, Greece, 1–28 July 2022; pp. 867–871. [Google Scholar]
- Sevastopoulos, C.; Oikonomou, K.M.; Konstantopoulos, S. Improving Traversability Estimation through Autonomous Robot Experimentation. In Proceedings of the International Conference on Computer Vision Systems, Thessaloniki, Greece, 23–25 September 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 175–184. [Google Scholar]
- Dalal, M.; Pathak, D.; Salakhutdinov, R.R. Accelerating robotic reinforcement learning via parameterized action primitives. Adv. Neural Inf. Process. Syst. 2021, 34, 21847–21859. [Google Scholar]
- Kansizoglou, I.; Bampis, L.; Gasteratos, A. An active learning paradigm for online audio-visual emotion recognition. IEEE Trans. Affect. Comput. 2019, 13, 756–768. [Google Scholar] [CrossRef]
- Peters, J.; Schaal, S. Policy gradient methods for robotics. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 2219–2225. [Google Scholar]
- Pastor, P.; Kalakrishnan, M.; Chitta, S.; Theodorou, E.; Schaal, S. Skill learning and task outcome prediction for manipulation. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 3828–3834. [Google Scholar]
- Kober, J.; Bagnell, J.A.; Peters, J. Reinforcement learning in robotics: A survey. Int. J. Robot. Res. 2013, 32, 1238–1274. [Google Scholar] [CrossRef]
- Nguyen, H.; La, H. Review of deep reinforcement learning for robot manipulation. In Proceedings of the 2019 Third IEEE International Conference on Robotic Computing (IRC), Naples, Italy, 25–27 February 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 590–595. [Google Scholar]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 387–395. [Google Scholar]
- Kim, M.; Han, D.K.; Park, J.H.; Kim, J.S. Motion Planning of Robot Manipulators for a Smoother Path Using a Twin Delayed Deep Deterministic Policy Gradient with Hindsight Experience Replay. Appl. Sci. 2020, 10, 575. [Google Scholar] [CrossRef]
- Wen, S.; Chen, J.; Wang, S.; Zhang, H.; Hu, X. Path planning of humanoid arm based on deep deterministic policy gradient. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 1755–1760. [Google Scholar]
- Cheng, R.; Agarwal, A.; Fragkiadaki, K. Reinforcement learning of active vision for manipulating objects under occlusions. In Proceedings of the Conference on Robot Learning, Zurich, Switzerland, 29–31 October 2018; pp. 422–431. [Google Scholar]
- Kamilaris, A.; Prenafeta-Boldú, F.X. Deep learning in agriculture: A survey. Comput. Electron. Agric. 2018, 147, 70–90. [Google Scholar] [CrossRef]
- Kansizoglou, I.; Bampis, L.; Gasteratos, A. Deep feature space: A geometrical perspective. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 6823–6838. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, Y.; Oerlemans, A.; Lao, S.; Wu, S.; Lew, M.S. Deep learning for visual understanding: A review. Neurocomputing 2016, 187, 27–48. [Google Scholar]
- Deng, L.; Yu, D. Deep learning: Methods and applications. Found. Trends Signal Process. 2014, 7, 197–387. [Google Scholar] [CrossRef]
- Hecht-Nielsen, R. Theory of the backpropagation neural network. In Neural Networks for Perception; Elsevier: Amsterdam, The Netherlands, 1992; pp. 65–93. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Gerstner, W.; Kistler, W.M. Spiking Neuron Models: Single Neurons, Populations, Plasticity; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Querlioz, D.; Bichler, O.; Dollfus, P.; Gamrat, C. Immunity to device variations in a spiking neural network with memristive nanodevices. IEEE Trans. Nanotechnol. 2013, 12, 288–295. [Google Scholar] [CrossRef]
- Hagras, H.; Pounds-Cornish, A.; Colley, M.; Callaghan, V.; Clarke, G. Evolving spiking neural network controllers for autonomous robots. In Proceedings of the IEEE International Conference on Robotics and Automation, ICRA ’04, New Orleans, LA, USA, 26 April–1 May 2004; Volume 5, pp. 4620–4626. [Google Scholar] [CrossRef]
- Bouganis, A.; Shanahan, M. Training a spiking neural network to control a 4-DoF robotic arm based on Spike Timing-Dependent Plasticity. In Proceedings of the 2010 International Joint Conference on Neural Networks (IJCNN), Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Nelson, M.; Rinzel, J. The Hodgkin—Huxley Model. In The Book of Genesis; Wm. B. Eerdmans Publishing: Grand Rapids, MI, USA, 1998; pp. 29–49. [Google Scholar]
- Deng, L.; Wu, Y.; Hu, X.; Liang, L.; Ding, Y.; Li, G.; Zhao, G.; Li, P.; Xie, Y. Rethinking the performance comparison between SNNS and ANNS. Neural Netw. 2020, 121, 294–307. [Google Scholar] [CrossRef]
- Caporale, N.; Dan, Y. Spike timing-dependent plasticity: A Hebbian learning rule. Annu. Rev. Neurosci. 2008, 31, 25–46. [Google Scholar] [CrossRef]
- Ponulak, F.; Kasiński, A. Supervised learning in spiking neural networks with ReSuMe: Sequence learning, classification, and spike shifting. Neural Comput. 2010, 22, 467–510. [Google Scholar]
- Bohte, S.M.; Kok, J.N.; La Poutré, J.A. SpikeProp: Backpropagation for networks of spiking neurons. In Proceedings of the ESANN, Bruges, Belgium, 26–28 April 2000; Volume 48, pp. 419–424. [Google Scholar]
- Florian, R.V. The chronotron: A neuron that learns to fire temporally precise spike patterns. PLoS ONE 2012, 7, e40233. [Google Scholar] [CrossRef]
- Wu, Y.; Deng, L.; Li, G.; Zhu, J.; Shi, L. Spatio-temporal backpropagation for training high-performance spiking neural networks. Front. Neurosci. 2018, 12, 331. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500. [Google Scholar]
- Jolivet, R.; Lewis, T.J.; Gerstner, W. The spike response model: A framework to predict neuronal spike trains. In Proceedings of the Artificial Neural Networks and Neural Information Processing, Istanbul, Turkey, 26–29 June 2003; pp. 846–853. [Google Scholar]
- Izhikevich, E.M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef]
- Burkitt, A.N. A review of the integrate-and-fire neuron model: I. Homogeneous synaptic input. Biol. Cybern. 2006, 95, 1–19. [Google Scholar]
- Youssef, I.; Mutlu, M.; Bayat, B.; Crespi, A.; Hauser, S.; Conradt, J.; Bernardino, A.; Ijspeert, A. A Neuro-Inspired Computational Model for a Visually Guided Robotic Lamprey Using Frame and Event Based Cameras. IEEE Robot. Autom. Lett. 2020, 5, 2395–2402. [Google Scholar] [CrossRef]
- Bauer, C.; Milighetti, G.; Yan, W.; Mikut, R. Human-like reflexes for robotic manipulation using leaky integrate-and-fire neurons. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 2572–2577. [Google Scholar] [CrossRef]
- Metta, G.; Sandini, G.; Konczak, J. A developmental approach to sensori-motor coordination in artificial systems. In Proceedings of the International Conference on Systems, Man, and Cybernetics, San Diego, CA, USA, 14 October 1998; Volume 4, pp. 3388–3393. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Ji, Y.; Zhang, Y.; Li, S.; Chi, P.; Jiang, C.; Qu, P.; Xie, Y.; Chen, W. NEUTRAMS: Neural network transformation and co-design under neuromorphic hardware constraints. In Proceedings of the 2016 49th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO), Taipei, Taiwan, 15–19 October 2016; pp. 1–13. [Google Scholar] [CrossRef]
- Davies, M. Lessons from Loihi: Progress in Neuromorphic Computing. In Proceedings of the 2021 Symposium on VLSI Circuits, Kyoto, Japan, 13–19 June 2021; pp. 1–2. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).