Novel Tool Path Generation Method for Pocket Machining Using Sound Field Synthesis Theory

Abstract

Contour parallel tool paths have been proved to be a preferred machining strategy for their advantage of less tool retractions and less sharp turns. The traditional geometrical algorithm-based tool path generation method often makes it hard to simply and simultaneously solve the problems of self-intersection, no residual, and smoothness at the same time due to their contradictions. To address this issue, a contoured parallel tool path generation method for pocket machining is developed in this study. It is based on sound field synthesis theory inspired by the phenomenon of sound wave propagation. Firstly, the simplified medial axis (SMA) tree of the pocket is extracted and the propagation direction of each SMA segment is calculated on account of the geometric characteristics of the pocket boundary. Secondly, the final tool path is obtained through the synthesis of the sound field. Finally, the novel method is verified on five different pockets to generate a contoured parallel milling tool path. After machining these pockets and measuring the machining time, roughness, and cutting force, the experimental results demonstrate that the tool path obtained by the novel method has advantages in improving machining quality and efficiency.

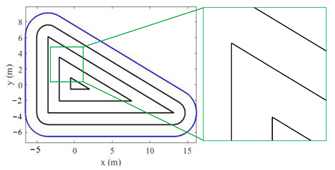
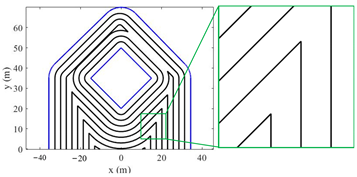
1. Introduction

Aviation structural parts are becoming integrated and lightweight as the development of aviation industry continues, which leads to the design of structures with complex geometric characteristics and puts forward higher requirements on machining quality and efficiency [1]. As one of the most important parts of machining technology, tool path has been widely discussed in the past decades, and many tool path generation strategies for pocket machining have been developed by experts and scholars, which can be roughly divided into direction parallel [2,3] and contour parallel [4,5] tool path generation strategies. Of the two strategies, contour parallel tool paths have been proved to be a preferred machining strategy for their advantage of less tool retractions and less sharp turns [6,7].

The core idea of contour parallel tool path generation is isometric offset based on a given pocket, and the generation strategies can be divided into the following categories according to different principles: the pairwise offset method [8,9,10], Voronoi diagram-based method [11,12,13,14], and pixel-based method [15,16,17,18]. The pairwise offset method usually includes the following steps: Calculate the offset segment of the boundary curve and add arcs on it to form the initial offset curve, detect the intersection points of the initial curve and eliminate both local loops and global loops of it. Choi et al. [8] designed an effective pairwise offset algorithm firstly to generate a tool path for a 2D closed pocket. Lin et al. [9] developed a pairwise offset method to round the inferior corners while generating contour parallel tool paths, which involves residual detection based on Boolean operation. Bahloul et al. [10] established an analytical model for contour parallel tool path generation based on curves of pocket boundary, including a corner residual elimination method and a center residual elimination method. Although the pairwise offset method can generate tool paths directly by initial boundary segment offsetting, it also constantly introduces a certain amount of local and global invalid loops that require further adjustments to rationalize the final tool path, and the generation of additional residuals is usually unavoidable. The Voronoi diagram-based method usually includes the following steps: Calculate two endpoints of the offset segment of the boundary curve, and then calculate the path formed by obtained endpoints based on Voronoi skeleton. Jeong et al. [11] developed a tool path generation method for free-form shaped pockets based on Voronoi diagrams, which can be utilized to generate tool paths in any pocket with quadratic differentiable curve boundary. Lai et al. [12] developed an incremental algorithm based on the Voronoi diagram to calculate the offset distance and minimum passage width in the tool path generation of a pocket. Hinduja et al. [14] developed a linking algorithm for contour-parallel tool paths generation by using the segments on a Voronoi diagram to overcome defects such as being not based on clear geometric principles, non-optimal, and not considering technical factors. The main defect of this method is that the smoothness of the generated tool path is not ideal and the calculation process is complicated. The main idea of the pixel-based method is to decompose the interior region defined by the curve of pocket boundary into pixels, and then generate tool paths through machining simulation. Dhanik et al. [17] developed a tool path generation method based on the boundary formulation of the pocket boundary and fast marching method, in which topological changes and slope discontinuities were dealt with by adding “entropy conditions” to the numerical implementation during the process of offset. Xu et al. [18] developed a tool path generation method based on the digital image method, in which the region within the pocket boundary is converted into a binary image and machining residuals and smoothness are optimized by adjusting the blurring and sharpness parameters of the image. The main advantage of the pixel-based method is that it does not need to calculate the offset segment, and the precision of the offset curve only depends on the mesh dispersion of the region inside the pocket, but this method can only be applied to a closed pocket in principle.

The biggest three problems in tool path generation are self-intersection, sharp corners, and uncut residual. Therefore, a large number of methods have been designed to solve these problems and effectively improve the machining efficiency under the premise of machining quality. Li et al. [19] developed a smooth tool path generation method for pocket machining by using linear interpolation, exponential regularization, and B-spline curve fitting. Xu et al. [20] developed a self-intersection identification and elimination algorithm based on mapping to process offset tool paths for milling operation. Zhou et al. [21] developed a residual regions identification method and a looping tool paths generation method to remove uncut areas left by pocket roughing while make the generated tool paths achieve G1 continuous and progressive radial cutting depths. Chen et al. [22] introduced the central axis (MA) transformation of the pocket and proposed a tool path generation optimization method for pocket machining in order to avoid interference and achieve the highest efficiency. Similarly, Huang et al. [23] developed an improved spiral toolpath generation method based on MA transformation to improve the machining performance. Although the problems of self-intersecting loops, sharp turning, and uncut residual have been well addressed by previous studies, it is important to note that most solutions are not only complicated but also not universal, which makes them potentially invalid on pockets of other type or geometry.

It is undeniable that most tool path generation methods are based on computational geometry, but people often fall into the dilemma of geometric algorithm to find a better solution. However, most geometry-based solutions are prone to result in trouble since the two problems of “smoothness” and “no residual” are usually contradictory and difficult to solve simultaneously. In view of the above questions, the diffusion process of sound waves with time is deeply studied. The research results show that if the sound source of the sound field is properly processed, the ideal steady-state sound field distribution can be obtained. The diffusion process of steady sound field is almost parallel, which is very similar to the geometric shape of the cutting tool path, and the diffusion line is generally smooth and non-intersecting. This can not only match the geometry of the pocket boundary well, but also effectively achieve the goal of smoothness, no self-intersection, and no residual. Therefore, based on the theory of sound field synthesis (SFS), a tool path generation method using the plane wave synthesis of a continuous linear sound source is developed in this study. In order to facilitate readers’ understanding, the theory of SFS utilized in this study is introduced in Section 2; the tool path generation method based on SFS is described in Section 3, including the medial axis transformation of a pocket, the calculation method of step-over, and propagation direction for different geometry. In Section 4, the validity of the developed method is proved by three examples with different geometric characteristics, moreover, the method is experimentally verified in a closed pocket, open pocket, and pocket with an island. Conclusions are summarized in Section 5.

2. The Theory of SFS

In this study, sound field $s_p\left(x,t\right)$ represents the sound pressure, that is, the local pressure deviation from the ambient pressure caused by a sound wave. In the time-frequency domain, $S_p\left(x,\omega \right)$ denotes sound field or sound pressure, $S_{\mathrm{pd}}\left(x,\omega \right)$ is referred to as sound pressure deviation caused by a plane wave sound field, which can be given by

$$S_{\mathrm{pd}}\left(x,\omega \right)={\overline{S}}_{\mathrm{pd}}\left(\omega \right)e^{-i{k}_{\mathrm{pd}}^{T}x}$$

(1)

where $x=\left[x y z\right]$ represents Cartesian coordinates, $k_{\mathrm{pd}}^T=\left[k_{pd,x}{k}_{pd,y}{k}_{pd,z}\right]$ denotes propagation direction, ${\overline{S}}_{\mathrm{pd}}\left(\omega \right)$ denotes time-frequency component.

According to the literature [24], the SFS means that the sound field emitted by individual elementary sound sources is superimposed on an extended domain to form a sound field with given a desired property, which happens to coincide with the generation process of the tool path. The employed elementary sound source is referred as a “secondary source” in the remainder of this study. For the sake of facilitating the mathematical treatment, it can be assumed that the ensemble of the secondary source considered is continuous. Therefore, it will be called the secondary sources distribution (SSD). Similarly, as the distribution considered can be also assumed to enclose the target region expected to synthesize the desired sound field, then the SFS problem can be expressed as

$$S_p\left(x,\omega \right)={\displaystyle \underset{\partial \mathsf{\Omega }}{\oint }D\left(x_0,\omega \right)G\left(x,x_0,\omega \right)dF}\left(x_0\right)$$

(2)

where $\partial \mathsf{\Omega }$ denotes the geometry of the distribution, $\omega$ is the radian frequency, $D\left(x_0,\omega \right)$, $G\left(x,x_0,\omega \right)$, and $dF\left(x_0\right)$ denote the driving function, spatial transfer function, and infinitesimal surface element of the secondary source located at $x_0$, respectively.

$s_p\left(x,t\right)$ can be physically possible as long as the scalar wave equation in the domain of interest is fulfilled. Therefore, considering source-free domains, the wave equation can be expressed as [24]

$${\Delta }^2{S}_P\left(x,t\right)-\frac{1}{v^2}\frac{{\partial }^2{S}_P\left(x,t\right)}{\partial t^2}=0$$

(3)

where $v$ represents the speed of sound, and the scalar differential operator ${\Delta }^2$ can be obtained by using twice the gradient $\Delta$ in Cartesian coordinates, which can be described as follow.

$$\Delta =\frac{\partial }{\partial x}{e}_x+\frac{\partial }{\partial y}{e}_y+\frac{\partial }{\partial z}{e}_z$$

(4)

where $e_i(i=x,y,z)$ represents the unit vector of indexed direction.

Using the temporal Fourier transform, Equation (3) can be obtained as below

$${\Delta }^2{S}_p\left(x,\omega \right)-k^2{S}_p\left(x,\omega \right)=0$$

(5)

where $k$ is termed wavenumber and can be expressed as

$$k=\frac{\omega }{v}$$

(6)

Generally speaking, the solution of a continuous distribution boundary condition in a sound field can be roughly divided into the arbitrary shaped simple connected SSD, spherical SSD, circular SSD, plane SSD, linear SSD, and so on. In this study, by analyzing the possibility and complexity of SFS by using different source distribution schemes in tool path generation, linear SSD is finally selected to SFS.

Based on Equation (2), the SFS problem of linear source distribution can be expressed as

$$S_p\left(x,\omega \right)={\displaystyle {\int }_{-\infty }^{\infty }D\left(x_0,\omega \right)G\left(x-x_0,\omega \right)d{x}_0}$$

(7)

where $x_0={\left[\begin{array}{ccc}{x}_0& 0& 0\end{array}\right]}^T$.

Just as literature [24], the explicit solution for linear SSD can be given as follows:

$$S_p\left(x,\omega \right)=\frac{e^{-i{k}_{\mathrm{pd},y}{y}_{\mathrm{ref}}}}{H_0^{\left(2\right)}\left(k_{\mathrm{pd},\mathrm{y}}{y}_{\mathrm{ref}}\right)}{e}^{-i{k}_{\mathrm{pd},x}x}{H}_0^{\left(2\right)}\left(k_{\mathrm{pd},\mathrm{y}}\sqrt{y^2+z^2}\right)$$

(8)

and it consists with the required sound field for $y=y_{\mathrm{ref}}$ and $z=0$.

Substituting $H_0^{\left(2\right)}\left(z\right)=2/\left(\pi z\right)\exp -i\left(z-\pi /4\right)$ [25] into Equation (8), the approximated synthesized sound field can then be expressed as

$$S_{\mathrm{appr}}\left(x,\omega \right)=\sqrt{\frac{y_{\mathrm{ref}}}{\sqrt{y^2+z^2}}}{e}^{-i{k}_{\mathrm{pd},x}x}{e}^{-i{k}_{\mathrm{pd},y}\sqrt{y^2+z^2}}$$

(9)

which can be used as an option to reduce the amount of computation in the algorithm without a great loss of accuracy.

In order to actually apply the SSD, the SFS systems and milling tool path cannot be of infinite length. Therefore, incorporating a suitable window function $f\left(x_0\right)$ into Equation (7), the sound field $S_{tr}\left(x,\omega \right)$ of a truncated linear source distribution in x-dimension can be expressed as

$$S_{tr}\left(x,\omega \right)={\displaystyle {\int }_{-\infty }^{\infty }f\left(x_0\right)D\left(x_0,\omega \right)G\left(x-x_0,\omega \right)d{x}_0}$$

(10)

Using the convolution theorem, the synthesized sound field ${\overline{S}}_{tr}\left(k_x,y,z,\omega \right)$ can be given by

$$\begin{array}{ll}{\overline{S}}_{tr}\left(k_x,y,z,\omega \right)& =\frac{1}{2\pi }\left(\overline{\omega }\left(k_x\right){\ast }_{k_x}\overline{D}\left(k_x,\omega \right)\right)\overline{G}\left(k_x,y,z,\omega \right)\\ & =\frac{1}{2\pi }{\overline{D}}_{tr}\left(k_x,\omega \right)\overline{G}\left(k_x,y,z,\omega \right)\end{array}$$

(11)

where the symbol ${\ast }_{k_x}$ represents convolution with respect to $k_x$. ${\overline{D}}_{tr}\left(k_x,\omega \right)$ represents the truncated driving function.

The finite extent of an SSD with length L that started at $x=0$ and ended at $x=L$ can be given by a rectangular window function $f_R\left(x\right)$ as

$$f_R\left(x\right)=\mathrm{rect}\left(\frac{x}{L}\right)=\left\{\begin{array}{cc}1& \mathrm{if} 0\le x\le L\\ 0& \mathrm{else}\end{array}\right.$$

(12)

Using the Fourier transformation and Equation (12) can be expressed as

$${\overline{f}}_R\left(k_x\right)=L·\sin \mathrm{c}\left(\frac{k_{x}L}{2}\right)$$

(13)

As can be seen from the above formula, the convolution of $\overline{D}\left(k_x,\omega \right)$ with ${\overline{f}}_R\left(k_x\right)$ is essentially a spatial low pass filtering operation smearing $\overline{D}\left(k_x,\omega \right)$ along the $k_x$ axis. Therefore, the truncated SSD reveals distinctive complex radiation properties. According to Equation (10), the properties of ${\overline{S}}_{tr}\left(k_x,y,z,\omega \right)$ can be directly gained from the performances of ${\overline{D}}_{tr}\left(k_x,\omega \right)$.

3. Universal Tool Path Generation Method

Pocket machining has been widely applied in the aerospace and mold industry. Although almost all commercial CAM packages provide the implementation of traditional strategy, the generated tool path is only based on the idea of geometric bias, which cannot simply and directly guarantee the high efficiency of the generated path. However, machining time is the most concerned evaluation index of tool path in roughing.

In this study, inspired by the phenomenon of sound field fluctuation and diffusion, a rough machining tool path generation method based on SFS is developed. The developed method is not only of great universality, but also has high machining efficiency, which is very suitable for rough machining of pockets. The specific generation method and process will be described in this section.

3.1. Medial Axis Transformation of Pocket

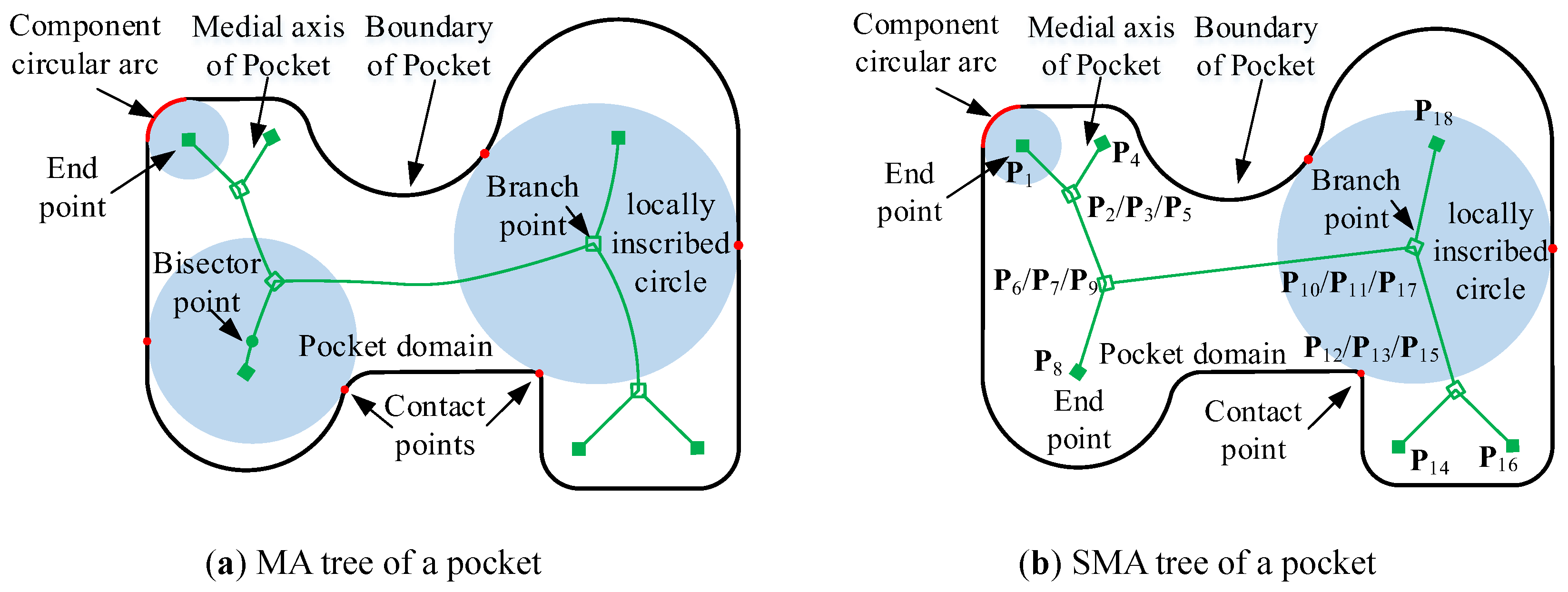
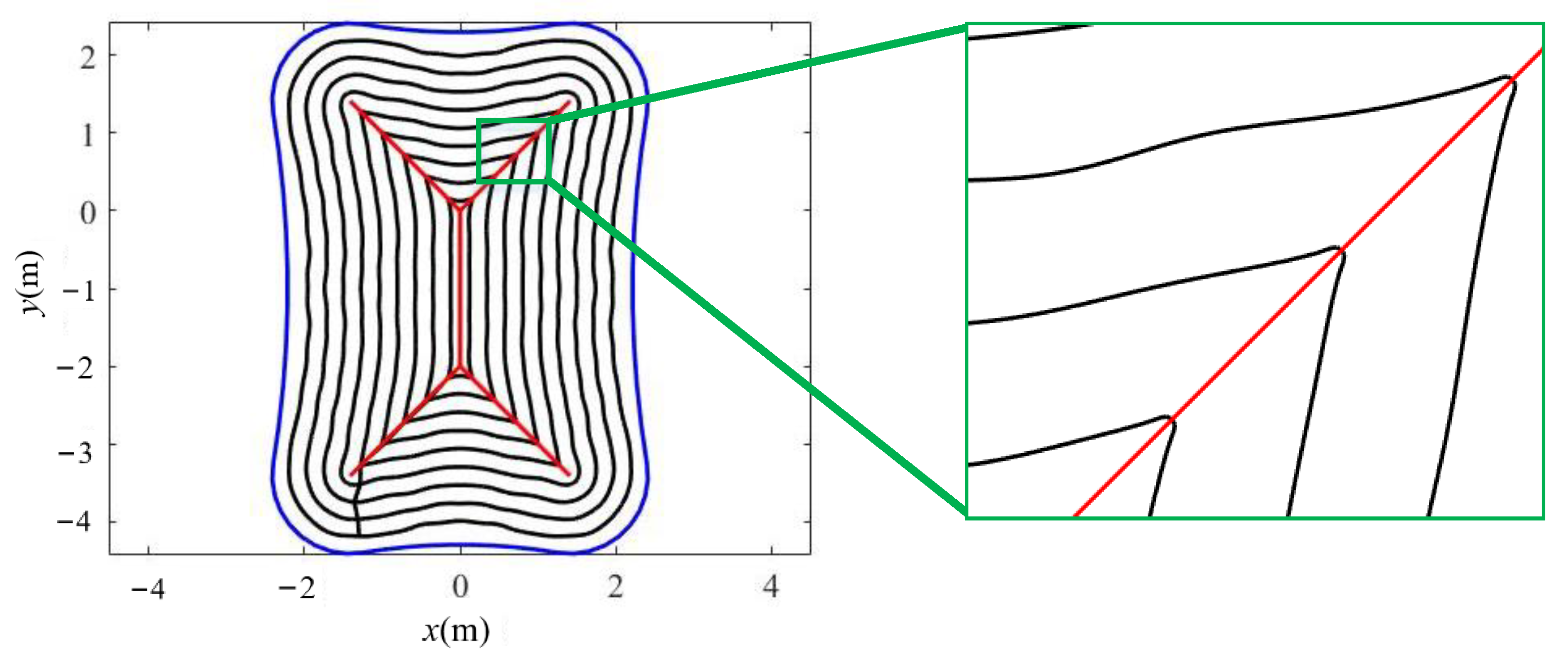
The medial axis transform (MAT) of a pocket is a completed shape descriptor, which is of great importance in describing the boundary of complex pocket [22]. The MAT is based on medial axis (MA) and locally inscribed circles. The MA of the pocket is composed of all the locus of centers of the tangent circles, and it is also called the MA tree, as shown in Figure 1a. The locally inscribed circles are confined to the boundary and can be placed anywhere in the pocket. A detailed description of MA can be found in literature [22], including the definition of the locally inscribed circle, end point, bisector point, and branch point.

It is essential to calculate locally inscribed circles of bisector points accurately and efficiently in the calculation of MAT, and the method used in [22] is directly used in this study. After that, the MAT should be stored in a tree data structure, and several specialized data structures have been developed in the past few years to represent the MA tree. In order to store the MA tree as simply as possible under the premise of application requirements, the strategy proposed in [23] is adopted in this study and some adjustments are made to meet the requirements of the tool path generation method developed in this study.

In this method, complex MA tree structure is transformed into simple closed loop called the MA cycle by a clockwise or counterclockwise traversal strategy. The MA cycle begins at the MA point with the minimum locally tangent circle and visits the branch point more than twice, the bisector points twice, and the end point once.

Even though the MA consists of a series of curves that can be approximated by a series of linear segments, such a complex MA is not needed in the method of tool path generation in this study. Instead, only linear continuous secondary sources combined with the acoustic propagation method is needed to achieve the fitting of the straight line and curve boundary, which will be described in Section 3.3. Therefore, after the calculation of MA, only branch points and end points are needed to construct a simplified MA (SMA), which can be marked as $P_i\left(i=1,2,\cdots ,n\right)$. An example is shown in Figure 1b, linear segments connecting branch points and end points are the simplified MA, which and can be represented by $\overline{P_1{P}_2{P}_3\cdots P_{16}{P}_{17}{P}_{18}}$. The Euclidean distance from $P_i$ to $P_j$ can be expressed as $len\left(P_i,P_j\right)$.

3.2. Step-Over Calculation for Tool Path

The first problem to be solved is to analyze the mapping between the step-over of the tool path and sound field parameters. It is not difficult to see that the mathematical description of the sound field caused by a plane wave in the time–frequency domain is a complex wave, which seems difficult to relate to the step-over. However, only the real part of it is used as the sound field in practical application, and the real part of Equation (1) can be expressed as

$$\Re \left(S_{\mathrm{pd}}\left(x,\omega \right)\right)={\overline{S}}_{\mathrm{pd}}\left(\omega \right)\cos \left(k_{\mathrm{pd}}^{T}x\right)$$

(14)

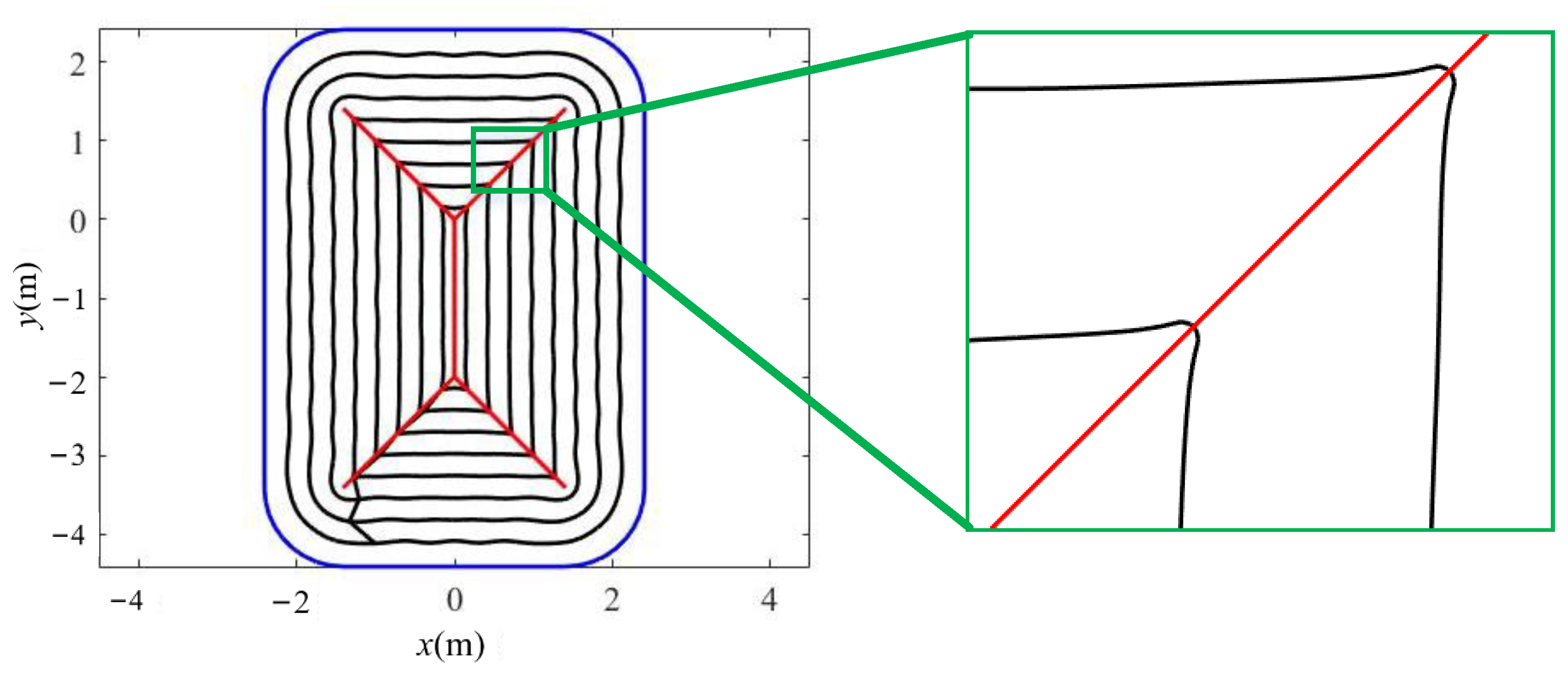
In this study, 2.5-D SFS is utilized in the generation of the tool path, however, if the theory of SFS is used for calculation, it is not difficult conclude that the calculation result is a wave surface by analyzing Equation (14), as shown in Figure 2. It also shows that the diffusion process of the sound field is almost parallel and non-intersecting, which is very similar to the geometry of the cutting tool path.

To handle this problem, the intersection line of the surface and the x-y plane is used as the generated tool path, which means that the step-over between two adjacent tool paths is related to the wave cycle of the sound field and is half of the wave cycle in terms of spatial length. Therefore, the following relationship can be obtained by combining Equations (6) and (14)

$$stepover=\frac{\pi }{k}=\frac{\pi v}{\omega }=\frac{v}{2f}$$

(15)

which means the step-over of the tool path is determined by the time frequency and sound speed of the sound field, meaning that SFS can fully meet the actual needs of tool path generation.

3.3. Propagation Direction Calculation Considering Pocket Boundary Geometry

A SMA tree consisting of linear segments has been constructed in Section 3.1 to generate the tool path by using continuous linear secondary sources. However, the SMA tree cannot reflect the geometric characteristics of the pocket boundary well, but instead only the segmentation of the boundary. Therefore, in order to make the synthesized sound field effectively reflect the geometric characteristics of the pocket boundary, different propagation directions of acoustic waves are studied to realize the matching of the synthetic sound field to different boundary features in this section.

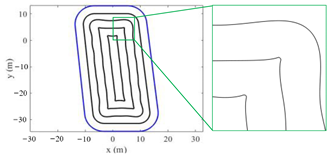
3.3.1. Propagation Direction for Linear Boundary

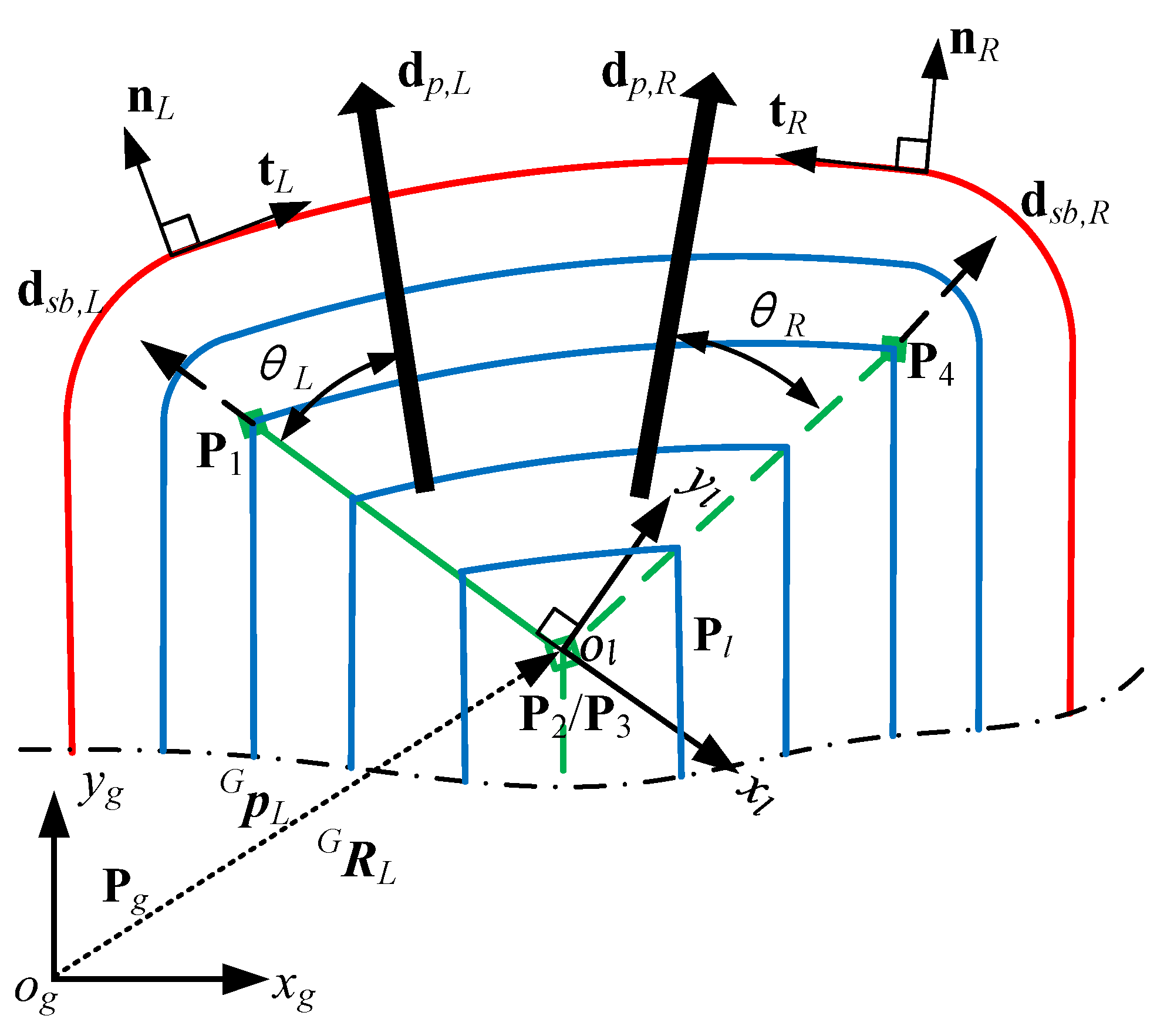
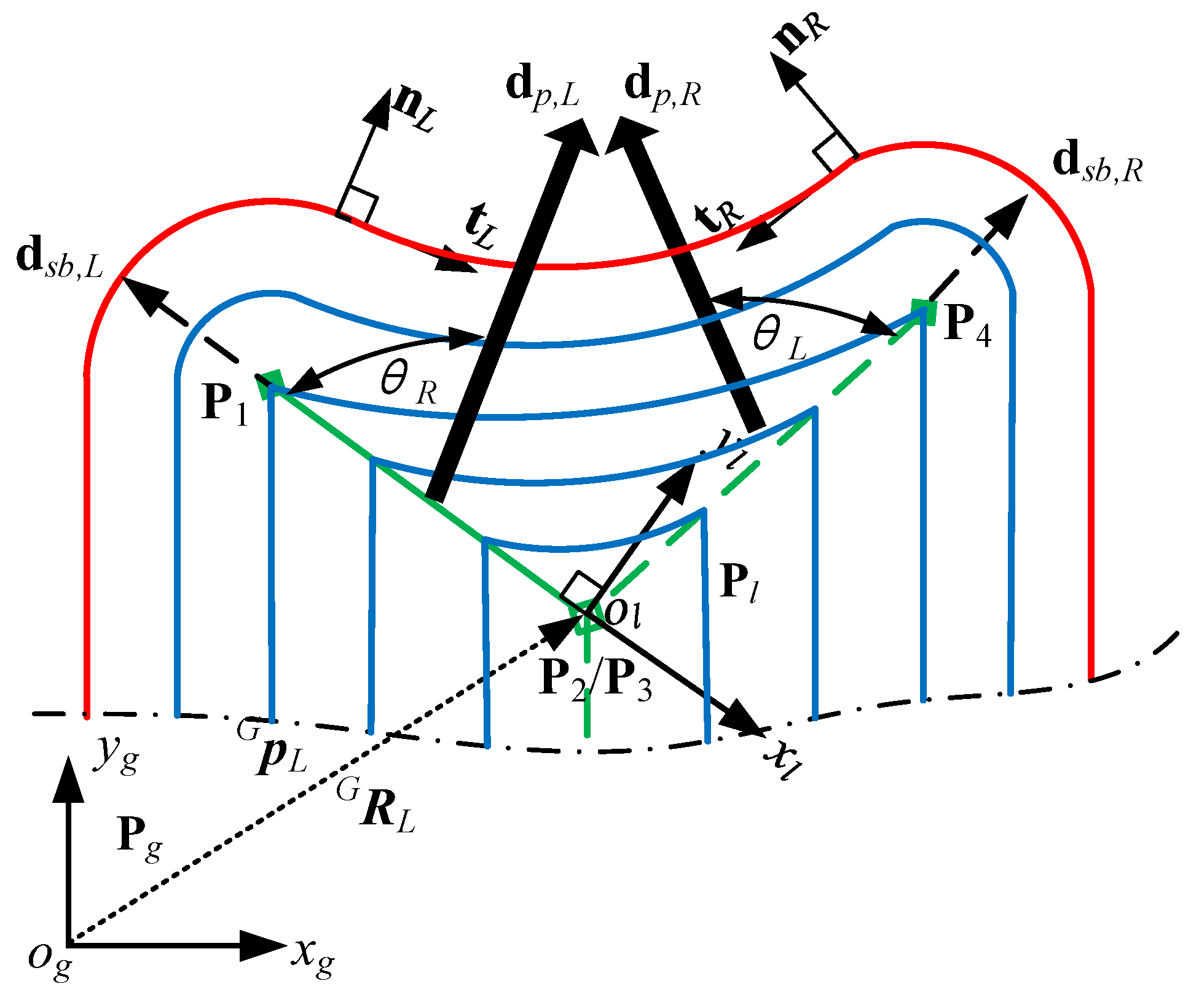
The sound field solution method of linear secondary sources situated along the x-axis and propagating to the y-axis has been described in Section 2, However, in order to use the linear sequences of SMA in Section 3.1 to synthesize the sound field reflecting the comprehensive geometric characteristics of the pocket, the position and attitude of the secondary source must be transformed firstly, including translation and rotation. As shown in Figure 3, the transformation of the secondary source position and attitude is described by taking the SMA $P_1{P}_2$ as an example, where $P_g$ is the global coordinate of the pocket and $P_l$ is the local coordinate of $P_1{P}_2$. The transformation relationship is as follows

$$\left(\begin{array}{c}{P}_l\\ 1\end{array}\right)=\left(\begin{array}{cc}{}^G\mathbf{R}_L& {}^G\mathbf{p}_L\\ 0& 1\end{array}\right)\left(\begin{array}{c}{P}_g\\ 1\end{array}\right)$$

(16)

After the coordinate transformation, the propagation direction of each linear secondary source (segment of SMA) can be calculated in the local coordinates. Taking ${\theta }_L$ to represent the propagation direction of $P_1{P}_2$, and that the propagation direction is along the direction of $y_l$-axis if ${\theta }_L=\pi /2$. In order to meet the needs of different linear boundaries, $d_{pd}$ and $d_{sb}$ are utilized to represent the direction of linear boundary and the direction of the linear SMA, respectively, and then the propagation direction can be expressed as

$${\theta }_L=\pi /2-〈d_{pd},d_{sb}〉$$

(17)

where $〈d_{pd},d_{sb}〉$ denotes the angle between $d_{pd}$ and $d_{sb}$.

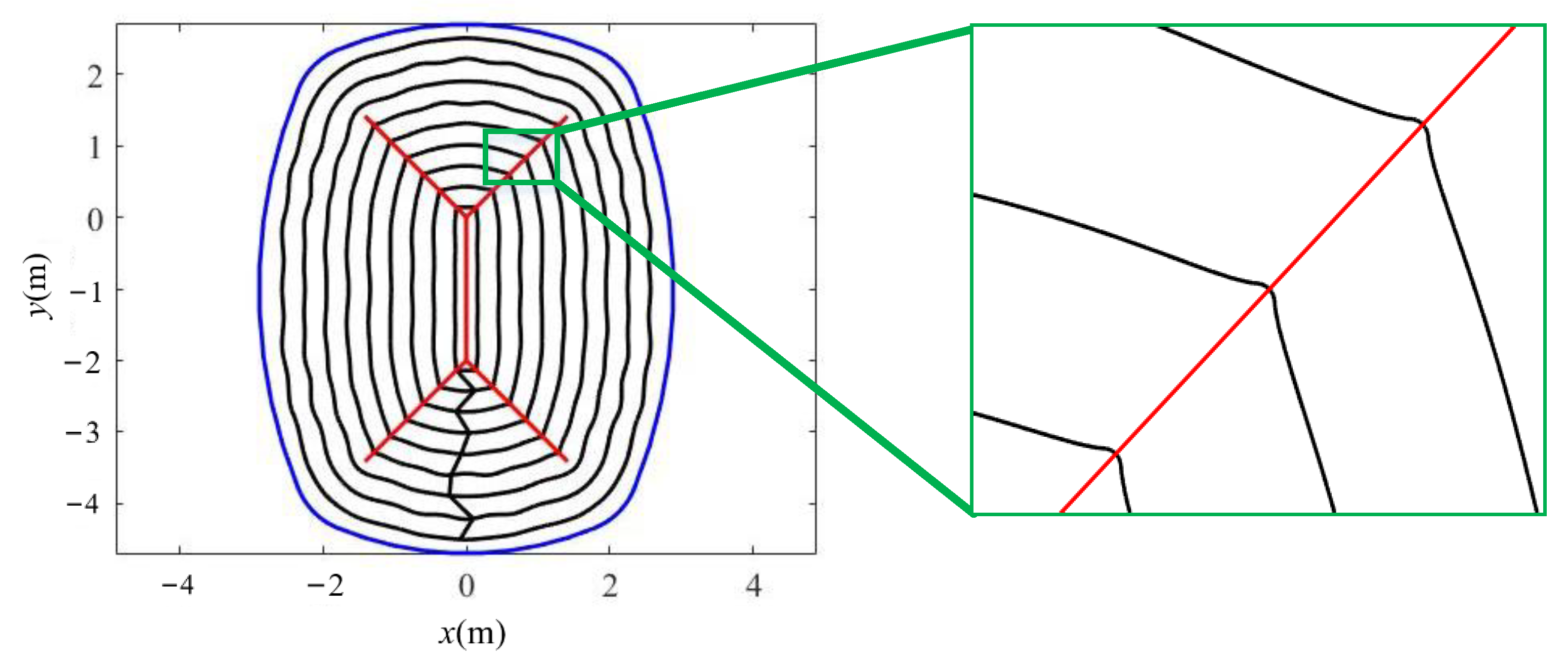
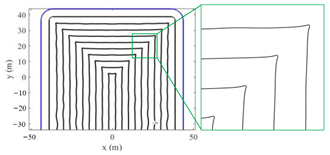
An example of tool path generation based on the abovementioned method is shown in Figure 4; it is not difficult to see the feasibility of the developed method and the advantage of smoothness at the corner.

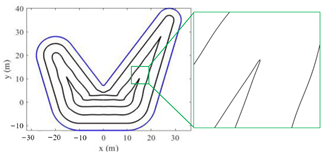
3.3.2. Propagation Direction for Convex Arc Boundary

Analogous to the linear boundary, the propagation direction of each linear secondary source can be calculated in the local coordinates to approximate the convex arc boundary after the coordinate transformation, but the difference is that the approximation of a convex curve requires at least two linear secondary sources, as shown in Figure 5. Taking ${\theta }_L$ and ${\theta }_R$ to represent the propagation direction of $P_1{P}_2$ and $P_3{P}_4$, respectively, to meet the approximation of the convex arc boundary, $d_{sb,L}$ and $d_{sb,R}$ are utilized to represent the direction of linear SMA at the left and right, respectively. The normal vector and tangent vector of convex arc boundary at left and right ends of the curve can be expressed in turn as $n_L$, $t_L$, $n_R$ and $t_R$, respectively, and the calculation of them are not complicated and will not be repeated here. After defining and calculating the above variables, the propagation direction of $P_1{P}_2$ and $P_3{P}_4$ can be expressed as

$$\left\{\begin{array}{l}{\theta }_L=〈t_L,d_{sb,L}〉-\pi /2\\ {\theta }_R=〈t_R,d_{sb,L}〉-\pi /2\end{array}\right.$$

(18)

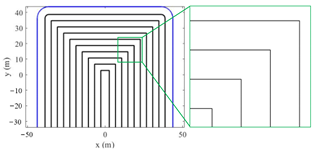
An example is also shown in Figure 6; it is not difficult to see the feasibility of the developed method and the advantage of smoothness at the corner.

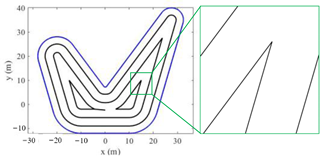
3.3.3. Propagation Direction for Concave Arc Boundary

The same as for the convex arc boundary, the propagation direction of each linear secondary source can be calculated in the local coordinates to approximate concave arc boundary after the coordinate transformation, as shown in Figure 7. Taking ${\theta }_L$ and ${\theta }_R$ to represent the propagation direction of $P_1{P}_2$ and $P_3{P}_4$, respectively, to meet the approximation of convex arc boundary, $d_{sb,L}$ and $d_{sb,R}$ are utilized to represent the direction of linear SMA at the left and right, respectively. The normal vector and tangent vector of convex arc boundary at left and right ends of the curve can be expressed in turn as $n_L$, $t_L$, $n_R$, and $t_R$, and the propagation direction of $P_1{P}_2$ and $P_3{P}_4$ can be expressed as

$$\left\{\begin{array}{l}{\theta }_L=〈t_L,d_{sb,L}〉-\pi /2\\ {\theta }_R=〈t_R,d_{sb,L}〉-\pi /2\end{array}\right.$$

(19)

An example is also shown in Figure 8; it is not difficult to see the feasibility of the developed method and the advantage of smoothness at the corner.

4. Experimental Verification

4.1. Simulation Results

To verify the validity and universality of the developed SFS-based method, five pockets are selected as test cases for tool path generation, including an open pocket (pocket 1), three closed pockets (pockets 2, 3, and 4), and a pocket with an island (pocket 5). At the same time, for the purpose of comparison, tool paths of these five pockets are generated by using famous commercial CAM software NX^® under the same machining parameters, and the generated tool paths are shown in

Table 1. Simulation comparison of tool path generation methods.

	Method	SFS-Based	NX®-Based
No.
1
2
3
4
5

.

It can be seen from Table 1 that the developed tool path generation method can effectively generate tool paths for different pocket types and improve the smoothness of tool paths. In addition, the total length of tool paths obtained by these two methods are also compared in this simulation, and the test results are shown in Figure 9.

As we can see from Figure 9, the length of the tool path generated by using the developed SFS-based method is slightly less than NX^® in two out of five cases and slightly greater than NX^® in the other case. However, this does not mean that the generated path by the developed SFS-based method has no advantage in machining efficiency; because the smooth tool path can effectively reduce the frequent acceleration and deceleration in the process of machining, it is not only beneficial to improve the efficiency, but also to improve the stability and dynamic accuracy of machining, so physical experiments should be carried out.

4.2. Physical Experimental Results

To further verify the above conclusions, physical experiments were carried out on a CNC machine tool, and all five examples in Table 1 were cut on the machine tool. The test system is shown in Figure 10. The machine tool utilized on this experiment is XK-L540, the force sensor is YD-F3220, the data acquisition card is uT3408M, and the data acquisition system is uTekAcqu. Of course, except for the tool path, the tool, fixture, and cutting parameters of the comparison experiment are strictly consistent to ensure the objectivity of the results. To verify the advantages of the developed method in improving the dynamic characteristics of tool paths, cutting forces were measured at the corner of the closed pocket 3 and the open pocket 5 in the machining process, and surface roughness was measured by surface roughness measuring instrument MarSurf PS 10 to verify the advantages of the developed method in improving the machining quality.

Machining time directly reflects the machining efficiency of tool paths. As shown in Figure 11, the machining time of tool paths generated by NX^® and the developed method was recorded in the process of machining and data which are obtained from the machine tool directly. The machining time of the tool path generated by using the developed SFS-based method is slightly less than NX^® in two out of five cases and slightly greater than NX^® in the other two cases, but it does not mean that our developed SFS-based method has no advantage over the tool path generated by NX^® in machining efficiency, because all the tool paths are converted to small line segments in the post-processing stage for the consideration of fair comparison, resulting in the machining time being closely related to the length of the tool path, and the advantage of path smoothness in machining efficiency and quality is not reflected. Therefore, the developed SFS-based tool path generation method can achieve higher machining efficiency and accuracy by the b-spline post-processing strategy, in theory. Of course, from the perspective of statistical data, the total machining time of the developed SFS-based method on all the five pockets is improved by 2.10% compared with NX^®. Therefore, a conclusion can be drawn that the developed SFS-based method has a certain improvement in machining efficiency compared with NX^®.

Not only are the machining times recorded in the cutting process, but the cutting force of closed pocket 3 and the open pocket 5 are also measured. As shown in Figure 12, the relationship between the cutting force and machining time were measured in the sampled corner, where one corner in the tool path of pocket 3 and two corners in the tool path of pocket 5 are sampled, as shown in Figure 12a. It can be seen in Figure 12b that the amplitude and change of cutting force are lower than that of the NX^® due to the developed method produces a smooth transition at the corner, as we can see in Table 1, indicating that the tool path obtained by the developed SFS-based method has better dynamic characteristics compared to NX^®.

Better dynamic performance of tool paths generally means that the machining quality of workpiece is also better, but it cannot be directly concluded that the machining quality of the workpiece machined by using the developed SFS-based method is better. Therefore, the surface roughness of open pockets 1 and 5 are measured after machining to compare the average roughness (Ra), the mean roughness depth (Rz), and the maximum roughness depth (Rmax) of the machined surface. To reduce the measurement error, roughness values were measured at multiple points, and the distribution of measurement points is shown in Figure 13a; average values were measured at each point three times, and then the surface roughness values were averaged at each point, as shown in Figure 13b.

According to the measurement results, compared with the tool path generated by NX^®, the roughness Ra, Rz, and Rmax obtained by using the developed SFS-based method were reduced by 18.94%, 14.32%, and 25.83%, respectively, on pocket 1. For pocket 5, the roughness Ra, Rz, and Rmax obtained by using the developed SFS-based method were reduced by 14.48%, 35.19%, and 16.00%, respectively, which indicated that the developed tool path generation method has obvious advantages in improving machining quality.

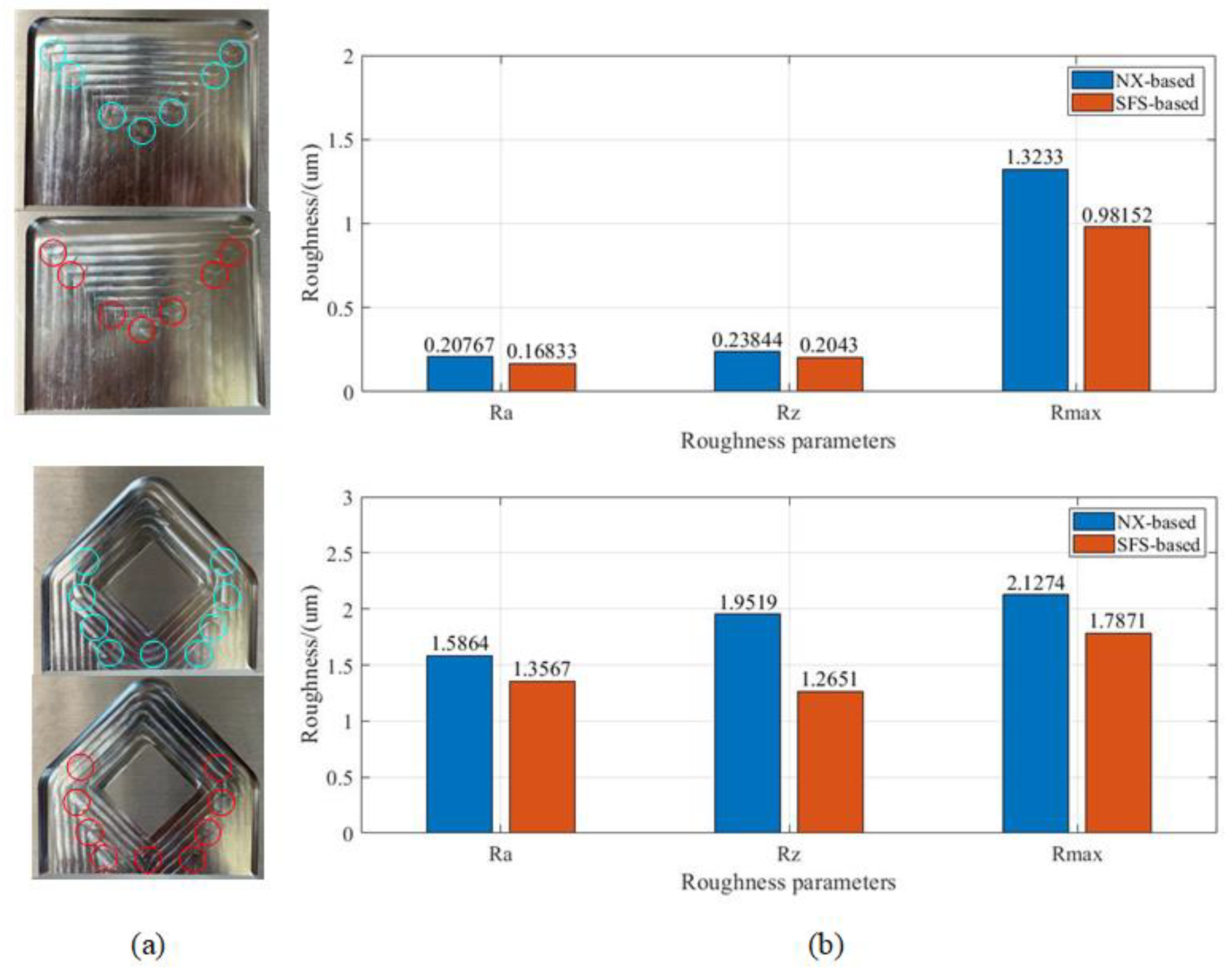
5. Conclusions

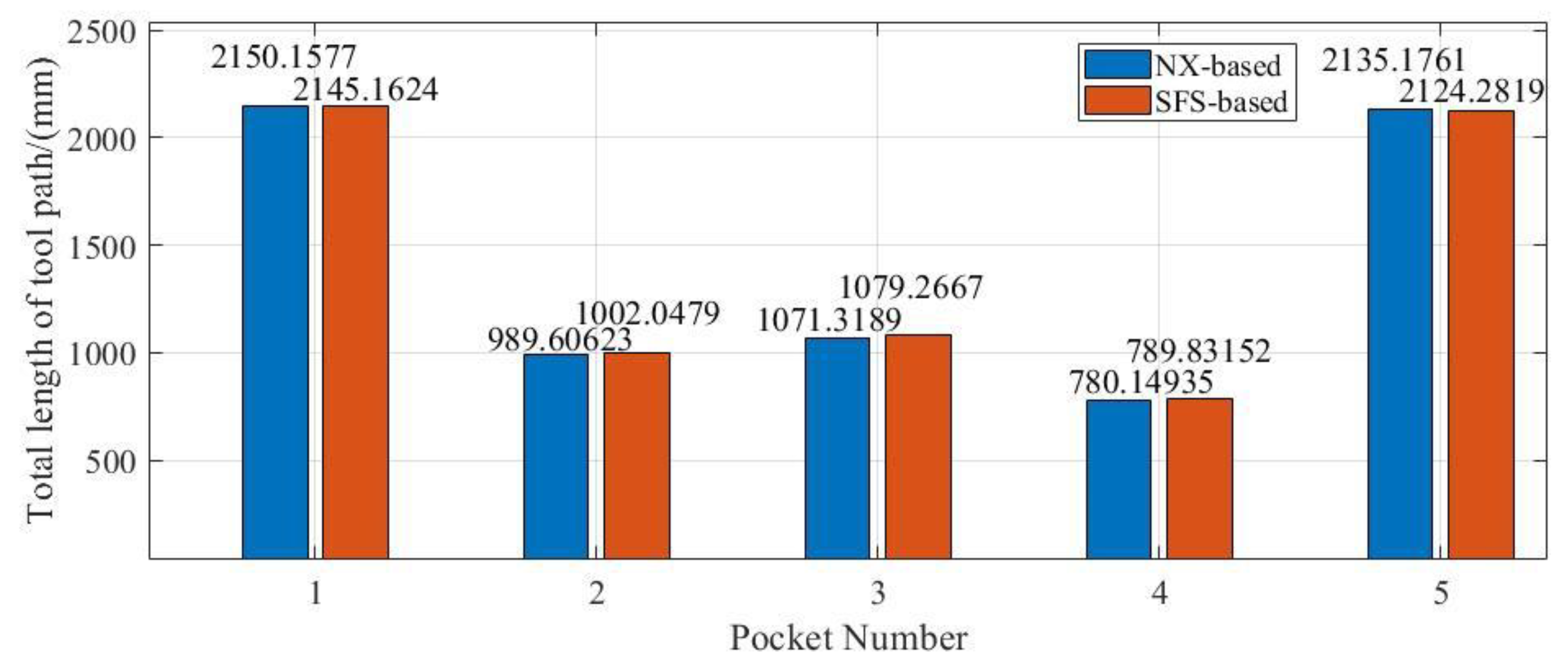
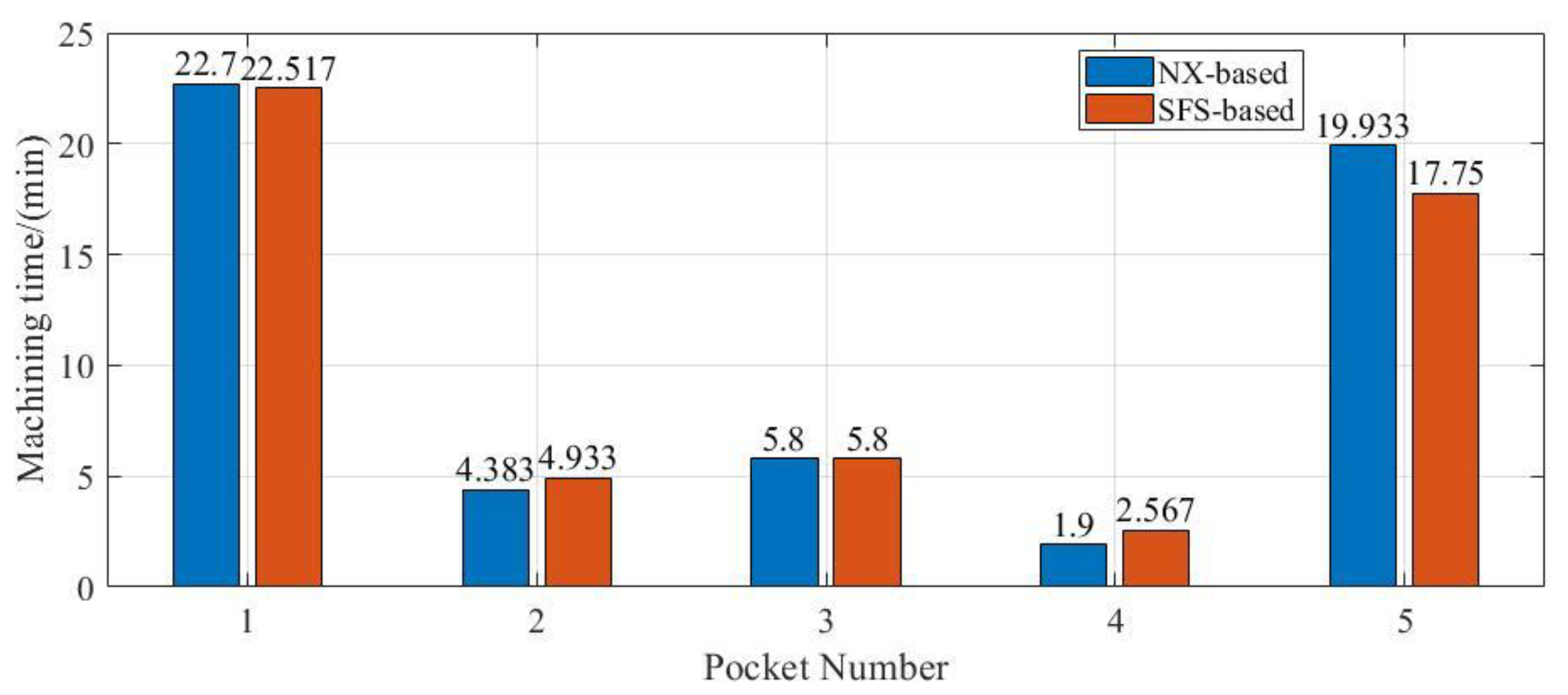
In this paper, a novel contoured parallel tool path generation method is developed. Compared to previous works, the SMA tree of the pocket is extracted in the proposed method and then the propagation direction of each SMA segment is calculated based on the geometric characteristics of the pocket boundary. Moreover, the final tool path is obtained through the synthesis of the sound field, which can not only match the geometry of the pocket boundary well, but also effectively achieves the goal of smoothness, no self-intersection, and no residual. Finally, the experimental results show that the tool path obtained by the developed SFS-based method has better advantages in smoothness, and the cutting force variation range during machining is much smaller, which reflected better dynamic performance. At the same time, the SFS-based method can effectively improve the machining quality and machining efficiency.

There is a research direction that deserves to be investigated in the future. Although this study is aimed at pocket milling, its idea can be extended to the milling of complex surfaces.