Abstract
The increasing use of high-speed machinery leads to a growing demand for efficient balancing methods for flexible rotors. Conventional balancing methods are costly and time-consuming since they require multiple trial runs. For this reason, recent research focuses on model-based balancing methods, which substitute measurements with simulations. This work presents and examines a model-based modal balancing method, which utilizes the Numerical Assembly Technique (NAT) for the in situ balancing of warped rotors with flexible behaviour. NAT is a successive modification of discrete–continuous modelling that leads to analytical harmonic solutions and is very computationally efficient. In this version of NAT, internal damping is also included with a viscoelastic material model using fractional time derivatives. The modal balancing procedure is adapted to handle measurements outside of the critical speeds and the effect of the pre-bend on the rotor. The accuracy of the simulations is shown by comparing measured mode shapes and eigenvalues with values calculated with NAT. Furthermore, the first two modes of a rotor test bed are successfully balanced without trial runs.
1. Introduction
Imbalance and bow are the most common causes of excessive rotor vibrations, which can be harmful to the machinery and its surroundings. Techniques for the balancing of rotors with flexible behaviour, like modal balancing [1] or the influence coefficient method [2], are necessary to reduce imbalance if the operational speed exceeds 70% of the first critical speed [3]. Additional consideration needs to be taken if the rotor is warped due to thermal distortion, gravity sag or mechanical bow. The balancing procedure can be either performed independently or used to compensate for the effects of the bow at certain spin speeds [4]. While the modal balancing method is efficient and accurate up to higher modes, it is necessary to know the mode shapes of the system to calculate the orthogonal weight sets [5]. Orthogonal weight sets can be found either intuitive [6], experimental [7] or with model-based methods [8].
Modern balancing techniques for rotors with flexible behaviour aim to improve upon both traditional methods in various ways. The unified balancing approach combines the advantages of influence coefficient and modal balancing technique [9]. Transient rotor balancing techniques use run-up data to speed up and improve the balancing process [10]. Another approach, often referred to as homologous information fusion technology, is to use multiple types of information besides vibration measurement, for example, flow, pressure and temperature for balancing [11]. Advances were also made in the balancing of non-standard rotors, e.g., warped rotors [12] or rotor-bearing systems with non-linear behaviour [13,14]. The focus of many modern balancing methods is to substitute measurements with simulations. Recent examples of model-based balancing techniques were proposed by Yun et al. [15], Carvalho et al. [16] and Nordmann et al. [17,18].
This paper investigates the application of a model-based modal balancing technique for warped rotors utilising the Numerical Assembly Technique (NAT). NAT is an analytic method used for determining the steady-state harmonic response, mode shapes and eigenvalues of rotor-bearing systems. Upon its introduction in 1999 by Wu and Chou [19,20], it was only capable of solving very simple beam models. Since then, NAT has been extended significantly, especially in the field of rotor dynamics. Chen and Wu [21,22] applied NAT to calculate the natural frequencies of uniform Euler–Bernoulli beams. Lin [23,24] included multiple lumped masses, multiple-pinned supports, and rotary inertias. In their study [25], Wang et al. incorporated the Timoshenko beam theory into NAT and investigated the effects of shear coefficients and slenderness ratios. Yesilce [26,27] studied the effects of axial forces on Timoshenko and Reddy–Bickford beams. NAT was extended to rotating systems in 2014, allowing the calculation of forward and backward whirling speeds [28]. Farghaly [29] utilized NAT to investigate Timoshenko beams on elastic supports and Vaz [30] examined the effects of various material and geometric discontinuities using NAT. Klanner et al. [31] expanded NAT to encompass distributed loading, imbalance, and fractional derivative material damping. Within recent years, Quinz et al. presented a modal balancing technique [32] and an influence coefficient balancing technique [33], where measurements were substituted with NAT simulations.
The main aim of this work is to adjust the modal balancing method based on NAT first presented in [32] to be used under real-world conditions and verify its utility experimentally. The novelty of this work is:
- Investigation of the optimal adaption of the model-based modal balancing procedure for warped rotors.
- Adaption of the procedure to measurements outside of critical speeds.
- Experimental verification of the proposed procedure.
Numerical analyses demonstrate the functionality, experiments are performed on a test bed to compare measured and calculated values and the first two modes of a test setup are balanced with the proposed method.
2. Materials and Methods
In this section, the proposed model-based modal balancing method—where the imbalance responses, eigenvalues and mode shapes are calculated with a simulation of the rotor-bearing system using NAT—is described. Only a vibration measurement of the initial rotor without trial weights is necessary for balancing. As long as the bow of the rotor is significantly smaller than its diameter, it does not influence the accuracy of the NAT simulation but is considered in the subsequent modal balancing process.
2.1. Numerical Assembly Technique
NAT employs a continuum model to derive analytic solutions when imbalance is introduced at discrete points. In the case of distributed imbalances, it also leverages the Fourier extension method to generate semi-analytical results. NAT can be used to accurately balance linear rotor-bearing systems with stepped shafts and multiple disks that are supported on roller bearings [32] or fluid film bearings [33]. It has been shown that the results of state-of-the-art finite element method (FEM) models converge to the results of NAT when the number of nodes is increased [33]. Furthermore, NAT reduces the computational time by a factor of ten compared to FEM [31]. This version of NAT has been improved from the ones described in [32] as Timoshenko beam theory is used instead of the Rayleigh theory and external damping is considered. Additionally, material damping is taken into account by a fractional derivative damping model. For further details on this version of NAT, readers are referred to [34], where it was used for an influence coefficient method.
The space fixed coordinate system, denoted as , is established in accordance with the setup illustrated in Figure 1. In this configuration, x and y are mutually orthogonal and lie in the transverse plane to z, which traverses the undeflected axis of the rotor within its bearings.
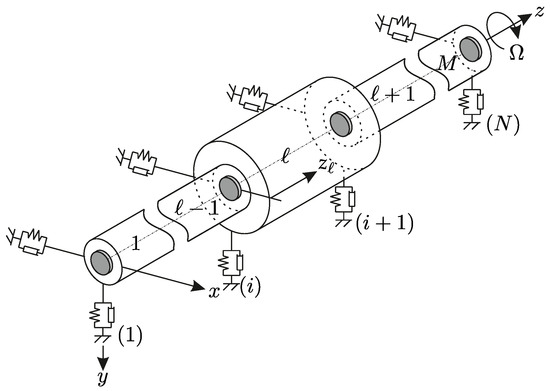
Figure 1.
General rotor problem [33].
Within the framework of NAT, the rotor-bearing system is characterized by N stations connected by segments. These stations correspond to components such as disks, bearings, steps, and the ends of the rotor, whereas the segments correspond to the cylindrical elements interconnecting these stations. Bearings are modelled as spin-speed-independent spring and damper elements, although the spin-speed-dependent behaviour of, e.g., fluid film bearings can also be modelled [33]. Disks are characterized by their mass , mass moments of inertia about the x- and y-axis , mass moment of inertia about the z-axis , amount of eccentricity , and angular position of eccentricity . Segments are defined by the frequency-dependent complex Young’s modulus and shear modulus , density , area of the cross-section , its diametric moment of area about the x- and y-axis , external damping coefficient and the shear correction factor . denotes the spin speed of the system and its whirling speed. When the system is only subjected to imbalance excitation, and are equal. The state of the rotor is defined by the vector consisting of the displacements and , the rotations of the cross-section and , the bending moments and , and the shear forces and . The symbol denotes the Fourier transform of the value •. Due to the fact that the solutions are complex conjugated, only four of the eight resulting differential equations are necessary to describe the system. Therefore only the solutions with the + index are considered.
2.1.1. Characteristic Equations
The Timoshenko beam theory [35] is used together with a fractional derivative damping model developed by Pritz et al. [36] to obtain the characteristic equations of a segment ℓ
with
where , and are the parameters of the fractional derivative material damping model. These are derived by measurements and are available for many commonly used materials [37]. A detailed derivation of the characteristic equations is found in [34].
2.1.2. Homogeneous Solution
To find the homogeneous solution the imbalance excitation is set to zero and solutions of the form of
are assumed. This results in a system of equations
with the non-trivial solutions of k
with
The state of each segment is defined by the matrix equation
where is the homogeneous solution vector, is the state variable matrix, and is the vector of arbitrary constants, which are defined as
and
with
2.1.3. Boundary and Interface Conditions
To yield a unique solution, the governing equations require boundary conditions on the left and right end of the rotor and interface conditions on every station within the rotor. Since solving Equation (1) leads to fourth-order equations, eight boundary or interface conditions are necessary for each segment. The process in which the boundary- and interface conditions are found for different bearing types is described in detail in [33].
2.1.4. Particular Solution
The particular solutions for concentrated imbalances and arbitrarily distributed imbalances are derived utilizing the Fourier extension method [38], Greens function method [39], the residue theorem and Jordan’s lemma [40]. The complete derivation is omitted for the sake of brevity.
2.1.5. Assembly and Solution Procedure
The total solution vector of each rotor segment consists of the homogeneous and the particular solution . A system of linear equations is found by assembling the characteristic equations of each segment with the boundary and interface conditions
where is the system matrix, the right-hand side vector and a vector of unknown constants. The unknown constants can be transformed into the total solution vector , which defines the behaviour of the rotor, using Equation (7). A detailed explanation of the assembly procedure of NAT is found in [31].
2.2. Modal Balancing Method
The proposed method builds on the N plane method, which corrects modal components of unbalance in a progressive way near critical speeds without affecting already balanced modes [1]. To avoid confusion with the index N for the rotor stations, the index P is used for the number of balanced modes in this paper. Modal balancing using NAT was first presented in [32]. The proposed version adds a distinction between balancing speeds and critical speeds, to make it better suited to balance systems under real-world conditions, where critical speeds often can not be reached safely before balancing.
The proposed model-based balancing method is built on three matrices: the measured vibrations of the initial system at the balancing speeds , the calculated vibrations of the system under unit unbalance at the balancing speeds and the calculated vibrations of the system under unit unbalance at the critical speeds . Since and are simulated using NAT, trial runs are avoided and the rotor-bearing system is balanced with a single measurement run of the initial system without additional weights. With this approach, the assembly needs to be dismantled only once to mount the balancing weights, as long as suitable measurement equipment is in place.
Orthogonal balancing weights that only influence a single mode shape are found by multiplying generalised unbalances with a modal matrix . This matrix consists of the relations between rotor displacements at each critical speed and measurement position. The modal matrix is found by making the simulated matrix non-dimensional. This procedure allows us to determine accurate mode shapes, without measuring the unbalanced system at critical speeds, which is often infeasible. A balanced rotor is excited by the unbalance mounted for compensation and its initial unbalance . To achieve perfect balance, both excitations need to cancel each other out and all displacements must vanish
Through modal decomposition, Equation (9) can be divided into one equation for each critical speed
By comparing the measured excitation caused by the unknown initial unbalance to the excitation caused by a unit unbalance calculated with NAT at the same position and spin speed, a general unbalance can be calculated, which quantifies how much each mode shape is excited by the initial unbalance
where p is the index of the critical speed, q is the index of the measurement position and Q is the number of measurement positions. Since there are usually multiple measurement positions available, the surplus information is used to optimise the calculation of the generalised unbalance using the least squares method. Simply mounting the generalised unbalance at the opposite side of the rotor would minimize the vibration of the according mode but at the cost of influencing the vibration of all other modes. To avoid this problem, the generalised unbalances are modified with the modal matrix to generate orthogonal balancing weights
A set of balancing weights is called orthogonal if it balances a single mode without influencing all other considered modes. In theory, if a set of orthogonal balancing weights is mounted for each mode of the system—which means for a continuous system—the system would be perfectly balanced and thus
In practice, it is sufficient to only balance all modes up to the balancing speed and sometimes one or two modes above the critical speed to reach acceptable vibration levels [1].
2.3. Theory of Bow Compensation
There are three classical ways of bow compensation. Nicholas et al. [4] first described these three methods for the Laval rotor. Rao [41], Deepthikumar et al. [12,42], Sanches and Pederiva [43] among others expanded upon these approaches to identify bow and unbalance and balance various rotor-bearing systems. The total excitation of a warped rotor consists of the unbalance excitation and the excitation due to the pre-bend of the shaft. The resulting displacement amplitude of the rotor is referred to as the total whirl, while the displacement caused only by the unbalance is called the net whirl.
Method 1 aims to reduce the total whirl at the balancing speed to zero. The correction unbalance is therefore
This method corresponds to the balancing of a straight rotor and usually takes place when the operator is not aware of the bow of the shaft. Unfortunately, this method leads to the worst results, since the balancing weights not only counteract the unbalance but also the effect of the bow at the balancing speed. This “overbalancing” leads to residual unbalance at every other speed, except the balancing speed, and is especially harmful near the critical speed. The only way to consistently reduce unbalance over the whole frequency range with this approach is to balance at the critical speed, which is in practice often not feasible.
The second method only balances the net whirl and takes the effect of the warped shaft out of the balancing process. This is achieved by deducting the slow roll bow from the vibration measurements at the balancing speed
where is the complex residual bow. This term describes the vector from the journal axis to the geometrical centre of the shaft at a standstill in a specific plane in complex coordinates. For a completely straight rotor, the complex residual bow is 0 at every axial position. The interaction between residual bow , displacement due to unbalance excitation and total displacement is demonstrated in Figure 2.
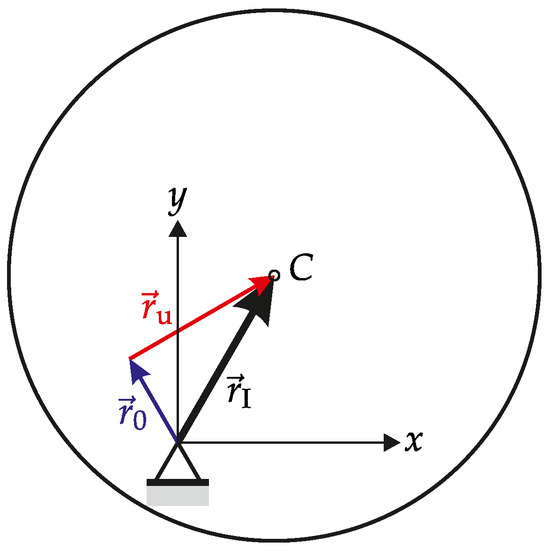
Figure 2.
Residual bow , displacement due to unbalance excitation and total displacement of a warped rotor (inspired by [4]).
The second balancing procedure leads to a very good overall reduction in vibration. Since the vibration amplitude due to the warped shaft is not constant and only approximately corresponds to the slow-roll bow, a certain displacement at the critical speed remains, even with faultless balancing.
The third approach—which is recommended by Nicholas et al. [4]—aims to minimize the total whirl at the critical speed, by measuring the subcritical balancing speed. This is performed by modifying the vibration due to the shaft bow with a factor
where is the balancing speed and is the first critical speed. In theory, this leads to the best reduction in vibration for a warped Laval rotor, where the vibration amplitude never exceeds the slow-roll bow and is even minimized at the first critical speed.
The ideal results of the three balancing methods for warped Laval rotors are summarized in Figure 3.
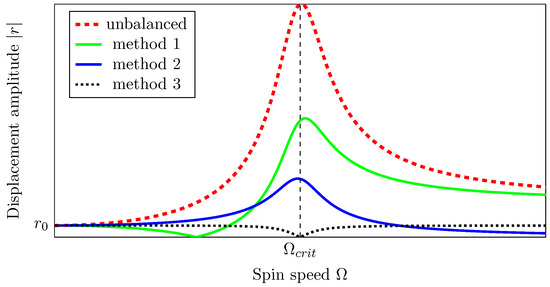
Figure 3.
Ideal results of the balancing methods for a warped Laval rotor (inspired by [4]).
Which of these approaches is optimal for the presented model-based modal balancing method using NAT on a multi-disk rotor-bearing system is investigated in Section 3.4.
3. Results and Discussion
This section provides a detailed description of the rotor-dynamic test bed, its corresponding NAT model, and the experiments conducted. First, the proposed method is demonstrated for a numerical example. After that, the optimal method of bow compensation for the model-based balancing approach is investigated on a one-disk rotor. Then, the proposed balancing technique is applied to balance the first mode and later, the first two modes of the test setup. Furthermore, the eigenvalues and mode shapes are calculated and compared to measurements.
3.1. Test Bed
Figure 4 shows the rotor dynamic test bed of the Institute of Mechanics of the Graz University of Technology.

Figure 4.
Rotordynamic test bed of the Institute of Mechanik of the University of Technology Graz without blast protection.
The elastic shaft, with a maximum diameter of 15 mm, can be mounted with any number of disks and is supported by two roller bearings. Due to the considerably greater stiffness of the supports compared to the isotropic shaft, the anisotropy of the bearing housing is neglected during the balancing process. The shaft is connected to a Kemmerich HM90D-140 P electric motor through a magnetic coupling, with a maximum spin speed of 400 Hz and a power of 6 kW. Due to safety requirements, the whole setup is limited to spin speeds up to 150 Hz, which makes measurements above the second eigenfrequency infeasible. The unbalance response is measured by four Keyence LK-H055 laser displacement measurement systems, with an accuracy of 0.025 and the phase is monitored by an IE5349 inductive sensor manufactured by IFM electronics. The test bed is safeguarded by two safety bearings and blast protection during operation. Five disks of varying weights were mounted onto the shaft, as seen in Figure 5. To maximize the effect of material damping on the rotor-bearing system, external damping was minimized by using roller bearings and no external damping elements.
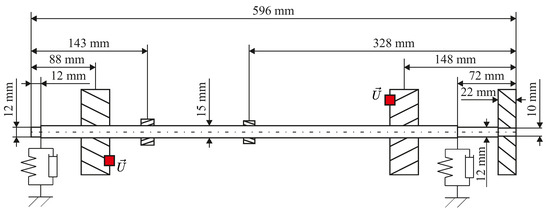
Figure 5.
Setup of the test bed.
The initial rotor is excited by the unbalance caused by manufacturing errors and the bow of the shaft. Table 1 lists the slow-roll bow of the shaft.

Table 1.
Bow of the pre-bent shaft.
Additionally, two unbalance weights are mounted on the disks: 5.57 g at 42.5 mm radius at the 0 position of the first balancing disk at m and the 180 position of the second balancing disk at m. These unbalances excite especially the second mode of the system.
3.2. Rotor Model
First, an NAT simulation of the test bed is generated. The parameters of the stations of this mathematical model are shown in Table 2, where z is the axial position, m the mass of the disks, the angular mass of the disk about the x- and y-axis, the angular mass about the z-axis, the bearing stiffness in x-direction, the bearing stiffness in y-direction and d the damping coefficient of the bearing in both directions.

Table 2.
Stations of the NAT model.
The cylindrical segments of the rotor are represented in the model with the following properties:
- Density: 7700 ;
- Shear modulus: ;
- Shear correction factor: 0.89;
- External damping coefficient: 45 .
The fractional derivative damping parameters are as follows:
- : ;
- : ;
- : .
The Zener material model is also capable of modelling the very low viscoelastic properties of steel [37].
3.3. Numerical Analysis
Before the experimental investigation is carried out, a numerical analysis of the proposed balancing method is presented to show how the procedure works in principle. All calculations for the experiments were conducted on a 3.2 GHz Intel® CoreTM i7-8700 CPU running Windows 10 using MATLABTM R2019a. For the numeric analysis, the rotor bow is neglected. The eigenvalues and Campbell diagram are found with a recursive search algorithm described in [32,33]. As is shown in Figure 6, the first two forward bending modes are calculated to be at 59.107 Hz and 145.48 Hz. These values will later be compared to measurements.
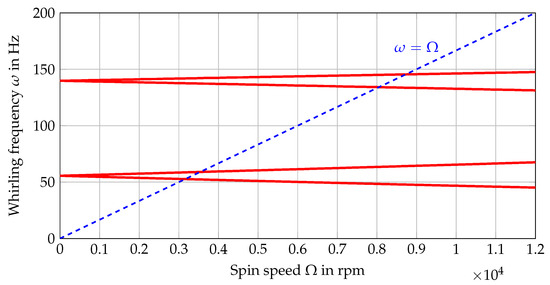
Figure 6.
Campbell diagram.
For the numeric balancing test, a concentrated unbalance at the disk and a distributed eccentricity of the shaft are assumed. The amount of eccentricity of the shaft, shown in Figure 7, is arbitrarily chosen follow to the function
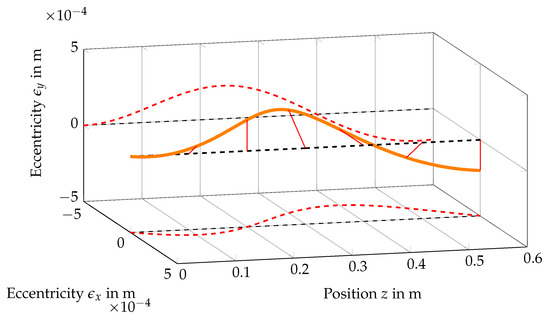
Figure 7.
Distributed eccentricity.
Its direction changes in a corkscrew manner according to
and the eccentricities of the disks are listed in Table 3.

Table 3.
Eccentricity of the disks of the numeric example.
The balancing planes are at position m and m. 50 Hz and 128 Hz are chosen as balancing speeds, which are in the information zone, but not so close to the critical speeds that measurements of an unbalanced system would be unrealistic. The displacements of the unbalanced example are compared to displacements of a system with unit unbalance, mode shapes are calculated and the correction unbalances, shown in Table 4, are found within 0.17 s.

Table 4.
Balancing weights of the numeric example.
The unbalance responses of the balanced and unbalanced system are shown in Figure 8. The amplitude of vibration is measured at the three disks at positions 0.088 m, 0.268 m and 0.448 m. In this paper, the comparisons of vibrational amplitude show always the average amplitude of these three measurement positions. The average reduction in vibration across all balancing planes and measured speeds is 93.43%.
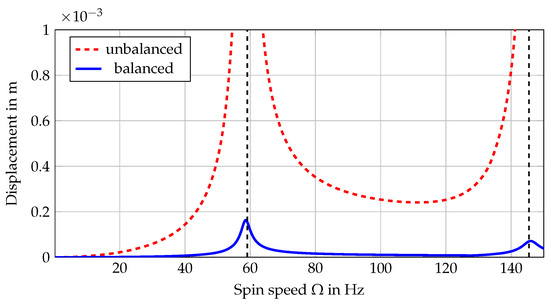
Figure 8.
Balancing success of the numeric example.
In the next steps, the balancing procedure is replicated with an experimental setup. The aim of the experimental investigation is to find out how well the model-based balancing procedure works under the additional challenges of real-world systems like:
- Unknown parameters, especially the influence of the foundation and the coupling.
- Warped shafts.
- Measurement and mounting errors.
3.4. Investigation of Optimal Bow Compensation
Before the testing of the modal balancing procedure on the two disk rotor, the optimal way of compensating for the rotor bow with the model-based balancing method is investigated. The three classical compensation methods by Nicholas et al. [4] are considered. Method 1 minimizes the total displacement at the balancing speed, method 2 minimizes only the unbalance vibration while ignoring the residual bow and method 3 minimizes the total vibration at the first critical speed through measurements at the balancing speed as described in Section 2.3. For this investigation, the test bed described in Section 3.1 is modified so that only a single 2 kg disk is mounted on the middle of the shaft at to make the results comparable to the literature. The balancing weights, mounted at a radius of 42.5 mm, for all three approaches, are shown in Table 5.

Table 5.
Balancing weights of the one disk rotor.
The results of mounting these balancing weights are shown in Figure 9. The measured eigenfrequency matches the eigenfrequency calculated with an NAT of 43.96 Hz very well.
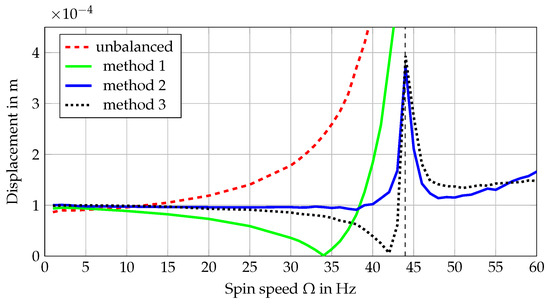
Figure 9.
Practical assessment of the balancing methods for a warped rotor.
Method 1 (and the unbalanced case) did not allow for a safe passage through the first critical speed, which is in line with [4], where the authors advise against the use of the method. Although Nicholas et al. recommend method 3 for single disk systems, method 2 is chosen for the following experiments. As can be seen in Figure 9, small modelling and mounting errors can reduce the efficiency of method 3 significantly. Since the balancing weights calculated with NAT are slightly too big, the minimum total vibration is at 42 Hz instead of 44 Hz. This leads to a rapid increase in vibration amplitude towards the resonance frequency comparable to method 1. Method 3 also only minimizes the total vibration at a specific spin speed and plane at the rotor, which is less useful if multiple disks and modes are balanced, unlike method 2, which circumvents the problem [42].
Therefore, the bow of the shaft is considered as follows for the experimental investigation: the vector of the slow roll bow is deducted from the subcritical vibration measurements according to method 2. The calculated unbalance response to a unit unbalance using NAT remains unchanged. This way, the balancing is performed corresponding to the net whirl instead of the total whirl. At supercritical speeds, the effect of unbalance dominates the influence of the shaft bow [44] and, therefore, the total whirl is used for balancing.
3.5. Balancing of the First Mode of the Multi-Disk System
In the first experimental test of the multi-disk rotor, only the first mode of the system is balanced. The left disk at 0.088 m is chosen as the balancing plane. The unbalanced system cannot reach the first critical speed safely; therefore, 50 Hz is chosen as the balancing speed. As described before, the complex residual bow is deducted from the measured total whirl at 50 Hz to obtain the net whirl. The net whirl is compared to the response to a unit unbalance calculated with NAT at 50 Hz. This leads to a balancing weight of 9.5458 g at a radius of 42.5 mm and the position within a total calculation time of 0.071 s. Mounting this balancing weight reduces the vibration of the first mode significantly as is shown in Figure 10.
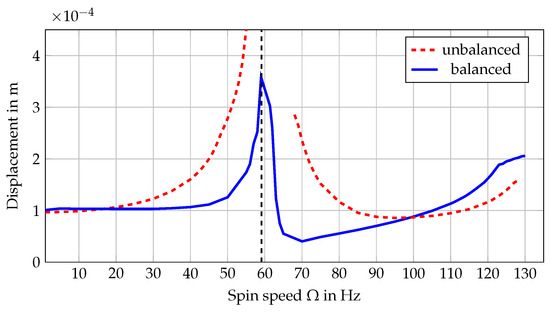
Figure 10.
Balancing success of the first example.
The average amplitude of vibration is reduced by 61.39% at 55 Hz. Since only the first mode is balanced, the amplitude of the second mode is not reduced but even increased. Furthermore, it is observable that the calculated eigenfrequency of 59.107 Hz matches the measured frequency of the highest amplitude well. After balancing, the first critical speed can be transversed safely and the calculated and measured first mode shape is compared. The calculated dimensionless mode shape matches the measurement accurately, as is shown in Figure 11.
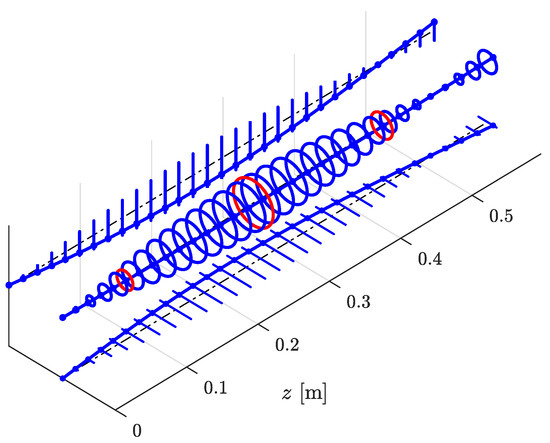
Figure 11.
First mode shape: NAT calculation in blue, measurements in red.
3.6. Balancing of the First and Second Mode of the Multi-Disk System
Even though the balancing weight of the previous example reduces the amplitude of the first mode significantly, it does increase the excitation of the second mode. For this reason, the first two modes are balanced simultaneously in the second example. The slow roll bow and the total whirl of the test bed at 50 Hz and 128 Hz are measured. Comparing these values with values calculated with NAT following the presented model-based modal balancing leads to the balancing weights shown in Table 6. The total calculation time is 0.1042 s.

Table 6.
Balancing weights of the second experimental example.
The calculated balancing weights reduce the vibration of the first two flexural modes of the system significantly, as is shown in Figure 12.
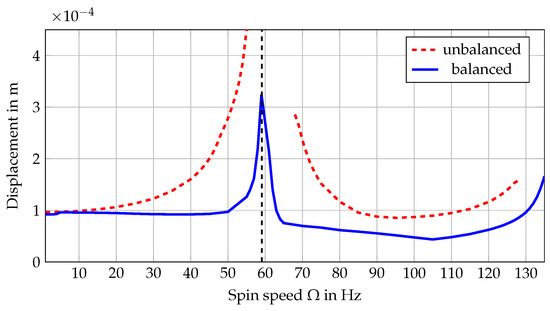
Figure 12.
Balancing success of the second example.
The average amplitude of vibration is reduced by 71.95% at 55 Hz and 45.96% at 128 Hz. The calculated and measured dimensionless second mode shape is compared after balancing, as is shown in Figure 13. As for the first mode shape, the calculation matches the experimental data well.
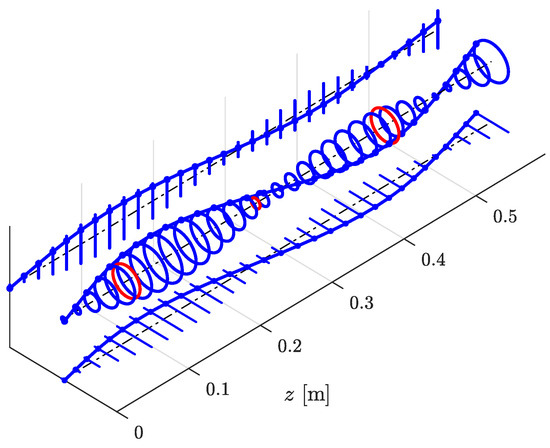
Figure 13.
Second mode shape: NAT calculation in blue, measurements in red.
3.7. Discussion
The experiments show that the proposed simulation and balancing method works for the investigated examples and opens up interesting directions for further research:
- Despite the unknown foundation parameters, the eigenfrequencies were accurately predicted. In this test case, the shaft was substantially more flexible than the bearings and bearing foundations, reducing their influence. Further research could extend NAT with detailed foundation behaviour and investigate systems on elastic supports. Also, the balancing on rotors supported on fluid film bearings using NAT has only been theoretically presented [33], but has not yet been experimentally verified.
- The fractional time derivative damping model depicted the behaviour of the shaft correctly. Since the shaft is made out of steel, which shows very low viscoelastic properties, a less sophisticated material model would suffice. The applied material model in combination with NAT has already been used to calculate eigenfrequencies of strongly viscoelastic materials like Polyvinylchlorid [37], suggesting that the balancing of rotors made out of these materials could also be possible. This should be verified experimentally.
- Although NAT assumes a straight shaft, the vibration amplitudes of the first two modes of a warped rotor were successfully reduced using the presented procedure. Since the pre-bend of the test bed is significantly higher than the usually accepted values for high-speed machinery, it is inferred that a slight bow of the shaft poses no problem for the method.
4. Conclusions
The proposed model-based balancing procedure was numerically and experimentally validated to be effective for an isotropic rotor-bearing system with a warped shaft and low damping. The method is first demonstrated on a numerical example and then verified on a rotor test bed, where the first two modes are balanced without trial runs. The simulation shows high numerical efficiency as the balancing weights of all test cases are calculated in less than a second. The numerical test was conducted under idealized conditions and led to a total reduction in vibration of 93.43%. The experimental tests included common challenges for model-based balancing methods, like unknown foundation parameters and warped shafts, and led to a reduction in vibration amplitude between 45.96% and 71.95%, depending on the spin speed and test setup. Calculated mode shapes and eigenfrequencies match the measured values well, indicating that the proposed simulation method is sufficiently accurate.
Author Contributions
Conceptualization, G.Q.; methodology, G.Q.; software, G.Q., G.Ü. and M.K.; validation, G.Q.; formal analysis, G.Q.; investigation, G.Q.; resources, K.E.; data curation, G.Q.; writing—original draft preparation, G.Q.; writing—review and editing, G.Ü., M.K. and K.E.; visualization, G.Q.; supervision, K.E.; project administration, K.E.; funding acquisition, G.Q. All authors have read and agreed to the published version of the manuscript.
Funding
Supported by TU Graz Open Access Publishing Fund.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this paper are available from the corresponding author upon reasonable request.
Acknowledgments
Open Access Funding by the Graz University of Technology.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FEM | Finite element method |
| NAT | Numerical assembly technique |
| rpm | Rotations per minute |
References
- Bishop, R.E.D.; Gladwell, G.M.L. The Vibration and Balancing of an Unbalanced Flexible Rotor. J. Mech. Eng. Soc. 1959, 1, 66–77. [Google Scholar] [CrossRef]
- Thearle, E.L. Dynamic Balancing of Rotating Machinery in the Field. Trans. ASME 1934, 56, 745–753. [Google Scholar] [CrossRef]
- Tessarzik, J.M.; Badgley, R.H.; Anderson, W.J. Flexible Rotor Balancing by the Exact Point-Speed Influence Coefficient Method. J. Eng. Ind. 1972, 94, 145–158. [Google Scholar] [CrossRef]
- Nicholas, J.C.; Gunter, E.J.; Allaire, P.E. Effect of Residual Shaft Bow on Unbalance Response and Balancing of a Single Mass Flexible Rotor—Part II: Balancing. J. Eng. Power 1976, 98, 171–181. [Google Scholar] [CrossRef]
- Gnielka, P. Modal balancing of flexible rotors without test runs: An experimental investigation. J. Vib. 1982, 90, 152–170. [Google Scholar] [CrossRef]
- Federn, K. Grundlagen Einer Systematischen Schwingungsentstorung Wellenelastischer Rotoren. VDI-Bericht 1957, 24, 9. [Google Scholar]
- Parkinson, A.G.; Bishop, R.E.D. Residual vibration in modal balancing. J. Mech. Eng. Sci. 1965, 7, 33–39. [Google Scholar] [CrossRef]
- Kellenberger, W. Das Wuchten elastischer Rotoren auf zwei allgemeinelastischen Lagern. Brown Boveri Mitteilungen 1967, 54, 603–617. [Google Scholar]
- Darlow, M.; Smalley, A.; Parkinson, A. Demonstration of a unified approach to the balancing of flexible rotors. J. Eng. Power 1981, 103, 101–107. [Google Scholar] [CrossRef]
- Zhao, S.; Ren, W.; Deng, W.; Lu, K.; Yang, Y.; Fu, C. A transient characteristic-based balancing method of rotor system without trail weights. Mech. Syst. Signal Process. 2021, 1487, 107117. [Google Scholar] [CrossRef]
- Goldman, P.; Muszynska, A. Application of full spectrum to rotating machinery diagnostics. Orbit 1999, 20, 17–21. [Google Scholar]
- Deepthikumar, M.B.; Sekhar, A.S.; Srikanthan, M.R. Balancing of flexible rotor with bow using transfer matrix method. J. Vib. Control 2014, 20, 225–240. [Google Scholar] [CrossRef]
- Green, K.; Champneys, A. Bifurcation analysis of an automatic dynamic balancing mechanism for eccentric rotors. J. Sound Vib. 2006, 291, 861–881. [Google Scholar] [CrossRef]
- Nauclér, P.; Söderström, T. Unbalance estimation using linear and nonlinear regression. Automatica 2010, 46, 1752–1761. [Google Scholar] [CrossRef]
- Yun, X.; Mei, X.; Jiang, G.; Hu, Z.; Zhang, Z. Investigation on a no trial weight spray online dynamic balancer. Shock Vib. 2018, 2018, 7021215. [Google Scholar] [CrossRef]
- Carvalho, V.N.; Dourado, A.D.; Rende, B.R.; Cavalini, J.A.A.; Steffen, J.V. Experimental validation of a robust model-based balancing approach. J. Vib. Control 2019, 25, 423–434. [Google Scholar] [CrossRef]
- Nordmann, R.; Knopf, E.; Abrate, B. Numerical analysis of influence coefficients for on-site balancing of flexible rotors. In Proceedings of the 10th International Conference on Rotor Dynamics, Rio de Janeiro, Brazil, 23–27 September 2018; pp. 157–172. [Google Scholar]
- Nordmann, R.; Knopf, E.; Krueger, T. Balancing of flexible rotors by means of calculated influence coefficients. In Proceedings of the SIRM 2021 International Conference on Dynamics of Rotating Machinery, Gdansk, Poland, 17–19 February 2021; pp. 1–13. [Google Scholar]
- Wu, J.-S.; Chou, H.M. A new approach for determining the natural frequency of mode shapes of a uniform beam carrying any number of sprung masses. J. Sound Vib. 1999, 220, 451–468. [Google Scholar] [CrossRef]
- Wu, J.-S.; Chen, D.-W. Free vibration analysis of a Timoshenko beam carrying multiple spring masses by using the numerical assembly technique. Int. J. Numer. Methods Eng. 2001, 50, 1039–1058. [Google Scholar] [CrossRef]
- Chen, D.-W. The exact solutions for the natural frequencies and mode shapes of non-uniform multi-span beamscarrying multiple various concentrated elements. Struct. Eng. Mech. Int. J. 2003, 16, 153–176. [Google Scholar] [CrossRef]
- Chen, D.-W. The exact solutions for free vibration of uniform beams carrying multiple two-degree-of-freedom spring-mass systems. J. Sound Vib. 2006, 295, 342–361. [Google Scholar] [CrossRef]
- Lin, H.-Y.; Tsai, Y.-C. On the natural frequencies and mode shapes of a multi-step beam carrying a number of intermediate lumped masses and rotary inertias. Struct. Eng. Mech. Int. J. 2006, 22, 701–717. [Google Scholar] [CrossRef]
- Lin, H.-Y.; Tsai, Y.-T. Free vibration analysis of a uniform multi-span beam carrying multiple spring-mass systems. J. Sound Vib. 2007, 302, 442–456. [Google Scholar] [CrossRef]
- Wang, J.-R.; Liu, T.-L.; Chen, D.-W. Free vibration analysis of a Timoshenko beam carrying multiple sping mass systems with the effect of shear deformation and rotary inertia. Struct. Eng. Mech. Int. J. 2007, 26, 1–14. [Google Scholar] [CrossRef]
- Yesilce, Y.; Demirdag, O. Effect of axial force on free vibration of Timoshenko multi-span beam carrying multiple spring-mass systems. Int. J. Mech. Sci. 2008, 50, 995–1003. [Google Scholar] [CrossRef]
- Yesilce, Y. Free Vibrations of a Reddy-Bickford Multi-span Beam Carrying Multiple Spring-mass Systems. J. Shock Vib. 2011, 18, 709–726. [Google Scholar] [CrossRef][Green Version]
- Wu, J.-S.; Lin, F.-T.; Shaw, H.-J. Analytical Solution for Whirling Speeds and Mode Shapes of a Distributed-Mass Shaft with Arbitrary Rigid Disks. J. Appl. Mech. 2014, 81, 034503. [Google Scholar] [CrossRef] [PubMed]
- Farghaly, S.H.; El-Sayed, T.A. Exact free vibration of a multi-step Timoshenko beam system with several attachments. Mech. Syst. Signal Process. 2016, 72, 525–546. [Google Scholar] [CrossRef]
- Vaz, J.D.C.; de Lima, J.J., Jr. Vibration anaysis of Euler–Bernoulli beams in multiple steps and different shapes of cross section. J. Vib. Control 2016, 22, 193–204. [Google Scholar] [CrossRef]
- Klanner, M.; Prem, M.S.; Ellermann, K. Steady-state harmonic vibrations of a linear rotor- bearing system with a discontinuous shaft and arbitrarily distributed mass unbalance. In Proceedings of the ISMA2020 International Conference on Noise and Vibration Engineering and USD2020 International Conference on Uncertainty in Structural Dynamics, Leuven, Belgium, 7–9 September 2020; pp. 1257–1272. [Google Scholar]
- Quinz, G.; Prem, M.S.; Klanner, M.; Ellermann, K. Balancing of a linear elastic rotor-bearing system with arbitrarily distributed unbalance using the Numerical Assembly Technique. Bull. Pol. Acad. Sci. Tech. Sci. 2021, 69, e138237. [Google Scholar]
- Quinz, G.; Klanner, M.; Ellermann, K. Balancing of Flexible Rotors Supported on Fluid Film Bearings by Means of Influence Coefficients Calculated by the Numerical Assembly Technique. Energies 2022, 15, 2009. [Google Scholar] [CrossRef]
- Quinz, G.; Überwimmern, G.; Klanner, M.; Ellermann, K. Field balancing of flexible rotors without trial runs using the Numerical Assembly Technique. In Proceedings of the 15th International Conference on Dynamics of Rotating Machinery, Darmstadt, Germany, 22–24 February 2023. [Google Scholar]
- Bauchau, O.A.; Craig, J.I. Structural Analysis—With Applications to Aerospace Structures; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Pritz, T. Analysis of four-parameter fractional derivative model of real solid materials. J. Sound Vib. 1996, 195, 103–115. [Google Scholar] [CrossRef]
- Prem, M.S.; Klanner, M.; Ellermann, K. Model parameter estimation of ball bearings using generalized Polynomial Chaos Expansion. In Proceedings of the SIRM 2021 International Conference on Dynamics of Rotating Machinery, Gdansk, Poland, 17–19 February 2021; pp. 331–340. [Google Scholar]
- Davies, B. Integral Transforms and Their Applications; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2002; Volume 41. [Google Scholar]
- Hayek, S.I. Advanced Mathematical Methods in Science and Engineering; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Mitrinovic, D.S.; Keckic, J.D. The Cauchy Method of Residues: Theory and Applications; Springer Science and Business Media: Berlin/Heidelberg, Germany, 1984; Volume 9. [Google Scholar]
- Rao, J.S. Dynamic analysis of bowed rotors. In Proceedings of the VETOMAC-1 Conference, Bangalore, India, 25–27 October 2000. [Google Scholar]
- Deepthikumar, M.B.; Sekhar, A.S.; Srikanthan, M.R. Modal balancing of flexible rotors with bow and distributed unbalance. J. Sound Vib. 2013, 332, 6216–6233. [Google Scholar] [CrossRef]
- Sanches, F.D.; Dalmazzo, F. Simultaneous identification of unbalance and shaft bow in a two-disk rotor based on correlation analysis and the SEREP model order reduction method. J. Sound Vib. 2018, 433, 230–247. [Google Scholar] [CrossRef]
- Ehrich, F.F. Handbook of Rotordynamics; Krieger Publishing Company: Malabar, FL, USA, 1999. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).