Abstract
Coal has been used as the most commonly energy source for power plants since it is relatively cheap and readily available. Thanks to these benefits, many countries operate coal-fired power plants. However, the combustion of coal in the coal-fired power plant emits pollutants such as sulfur oxides (SOx) and nitrogen oxides (NOx) which are suspected to cause damage to the environment and also be harmful to humans. For this reason, most countries have been strengthening regulations on coal-consuming industries. Therefore, the coal-fired power plant should also follow these regulations. This study focuses on the prediction of harmful emissions when the coal is mixed with high-quality and low-quality coals during combustion in the coal-fired power plant. The emission of SOx and NOx is affected by the mixture ratio between high-quality and low-quality coals so it is very important to decide on the mixture ratio of coals. To decide the coal mixture, it is a prerequisite to predict the amount of SOx and NOx emission during combustion. To do this, this paper develops a deep neural network (DNN) model which can predict SOx and NOx emissions associated with coal properties when coals are mixed. The field data from a coal-fired power plant is used to train the model and it gives mean absolute percentage error (MAPE) of 7.1% and 5.68% for SOx and NOx prediction, respectively.
1. Introduction
Depending on energy sources (i.e., wind, solar, hydroelectric, geothermal, bio, nuclear energy, and so on), various kinds of power plant exist. Among them, the coal-fired power plant is a kind of thermal power station using coal as an energy source. Coal is relatively cheap compared to other fossil fuels and readily obtainable. Therefore, coal-fired power plants are operated in many countries. Coal supplied a third of global electricity generation in 2022 [1]. However, the issue of global warming deters the increase in coal-fired power plants and many countries are planning to replace coal with renewable energies. In spite of much effort, the substitution of the coal-fired power plant with more environmentally friendly energy sources is not easy due to its unignorable benefits. The expected future use of the coal-fired power plant still seems set to continue until the 2040s and economical threats may extend the life of the coal-fired power plant [2].
One of the major hindrances for the use of coal-fired power plants is side effects during coal burning. The combustion of coal is suspected to emit harmful substances causing climate change [3]. Primarily, sulfur oxides (SOx), nitrogen oxides (NOx), and fine dust included in the emission after coal burning are regarded as strong candidates for the cause of global warming [4]. SOx emissions mainly originate from the combustion of sulfur-containing fossil fuels, such as coal and oil, and from certain industrial processes like metal smelting. During combustion, sulfur present in fossil fuels reacts with oxygen to form sulfur dioxide (SO2). The reaction can be represented as:
NOx emissions primarily occur during combustion processes at high temperatures. During high-temperature combustion processes, nitrogen (N2) from the atmosphere reacts with oxygen (O2) to produce NOx. Specifically, this reaction occurs when combustion temperatures exceed 1370 °C (2500 °F), a mechanism also referred to as the “Zeldovich mechanism”. The reaction can be represented as:
In addition, coal burning generates various potential pollutants which represent major causes of respiratory diseases of humans. For these reasons, most countries have strengthened the regulations on coal-consuming industries [5]. Therefore, the coal-fired power plant should meet these regulations and a lot of technologies to reduce harmful emissions to the environment have been applied.
The main component for coal combustion in the coal-fired power plant is the boiler. The boiler converts internal energy of coal into thermal energy through combustion. This energy changes water into steam, which is used to rotate turbines. The rotational energy of the turbines generates electricity. During coal combustion, lots of chemical reactions happen and some pollutant substances are emitted to the environment. The combustion control of coal within the boiler decides how much harmful pollutant is released. Therefore, it is very important to control the combustion of coal within the boiler without sacrificing operation objectives [6] such as calorific value, stability, cost, etc.
There are many factors affecting coal combustion such as coal type, combustion temperature, air intake, coal grinding, and so on [7]. A proper controlling of operation parameters (amount of feeding coal, nozzle angle, boiler feed water, intake air) of the boiler helps to burn coal completely. Even though the operational parameters of boiler are important, a more direct component relation with coal combustion is the coal itself as burning material. More precisely, depending on the quality of coal, the operational parameters should be adjusted. The quality of coal is decided by the constituent substances such as carbon, hydrogen, oxygen, nitrogen, sulfur, and some minerals [8]. The composition of substances varies depending on source country and the location of mines.
From the viewpoint of combustion sources for the coal-fired power plant, coal can be classified into high-heat-capacity coal and low-heat-capacity coal depending on how many calories (i.e., energy) can be generated during combustion. The high-heat-capacity coal has better combustion characteristics so it is expensive. On the contrary, the low-heat-capacity coal can produce fewer calories and emit more harmful pollutants during combustion. However, it is cheaper than the high-heat-capacity coal [9]. Some coal-fired power plants located in developed countries use only high-heat-capacity coal regardless of its high price [10]. It is easy to decide operational parameters to reduce harmful emissions in this case. However, most coal-fired power plants operated in developing or underdeveloped countries use both types of coal as a mixture in order to reduce electricity generation costs. This coal mixture makes the operation of coal-fired power plants difficult. Since each coal has different properties depending on substance composition, the mixture of high-heat-capacity coal and low-heat-capacity coal shows diverse combustion characteristics depending on the ratio of the mixture. The emission also varies after combustion with differently mixed coals. Therefore, it is important to decide a proper mixture ratio between high-heat-capacity coal and low-heat-capacity coal considering their composition. Therefore, the decision on the mixture ratio is important in the coal-fired power plant and there are divisions consisting of specialists to do this.
The decision on the mixture ratio between high-heat-capacity coal and low-heat-capacity coal should consider meeting minimum heating calories, reducing harmful emissions, guaranteeing combustion stability, and so on [11]. Among these considerations, this study focuses on the level of harmful emissions (especially SOx and NOx) after combustion according to various ratios of coal mixture. This paper provides a prediction methodology for harmful emissions such as SOx and NOx since these two chemicals are mostly of interest from the viewpoint of accelerating global warming. An artificial intelligence (AI) model to predict the amount of emitted SOx and NOx depending on coal mixture ratio is developed in this study, which will help operators in coal-fired power plants to find a proper ratio of coal mixture. The proposed method in this study consists of data preprocessing, developing a machine learning model to predict pollutant emissions, and verifying the effectiveness of the prediction model. In the preprocessing step, the available data are defined and the selection of highly related data for prediction of SOx and NOx is performed. The selected data for the development of the prediction model are used as input/output variables. Machine learning algorithms such as the DNN are implemented for the prediction. Various statistical methods such as variable importance and mean absolute percentage error are also used in the evaluation of prediction capability. The feasibility and usefulness of the proposed methodology are proved by the operational data collected from the operated coal-fired power plant in the field. The remainder of this paper is organized as follows: Section 2 reviews the related works in predicting SOx and NOx. Section 3 presents the development of a data analysis-based predictive model approach to predict SOx and NOx in the boiler of the coal-fired power plant. Section 4 provides conclusions and directions of future work.
2. Materials and Methods
This section reviews the previous works related to predicting pollutants such as SOx and NOx in the coal-fired power plant. As described in Section 1, due to the issue of global warming and the strengthening of regulations on industries consuming coal, there has been growing attention towards the development of systems to monitor and control pollutant emissions. As monitoring technology is developing, some prediction methods for the combustion of boilers are now adopted. Several approaches, including experimental studies, mathematical models, and machine learning models, have been proposed over the years to estimate SOx and NOx and other emissions from the coal-fired power plant. Krzywaski et al. [12] proposed a four-layer artificial neural network (ANN) to predict NOx emissions from circulating fluidized bed (CFB) combustors, considering operational parameters, fuel characteristics, and combustion chamber shape. The results obtained by this ANN model achieved a prediction error of ±20% compared to the experimental data. Some results showed results even lower than 1% in predicting NOx emission in CFB boilers. The research of Lv et al. [13] proposed a method based on prior understanding of thermal dynamics and fluid mechanics to conduct simulation experiments. The suggested model in their work is an ensemble-learning paradigm based on a soft fuzzy c-means–least squared vector machine–partial least squares ensemble without membership (SFLPE) and it predicts NOx emissions of coal-fired boilers. The proposed model obtained a training root mean squared error (RMSE) and mean relative error (MRE) of only 15.32 and 3.65%. The RMSE and MRE are reduced to 14.07 and 3.85% in comparison with LSSVM, and the SFLPE obtained a lower prediction error. Krzywanski et al. [14] also developed an ANN model that can predict SO2 emissions from coal combustion in both large- and small-scale boilers using experimental data and simulation. The 8–3–7–1-layered ANN model achieved R2 of 0.9278, mean absolute error of 144.36 (MAE), and MRE of 0.19%. This model demonstrated the capability of neural networks in generalizing the association between SO2 emissions and operational factors. According to this paper, the ANN model, which employs a tangent sigmoid activation function, may be useful in lowering SO2 emissions in CFB combustors. Zhou et al. [15] used support vector regression and an ant colony method to develop a model for forecasting NOx emissions from coal-fired boilers. The research examined the prediction performance and temporal reaction of several models, including a back propagation neural network (BPNN) and general regression neural network (GRNN). The results showed that the support vector regression (SVR) model has the greatest predictive performance and temporal responsiveness. The data used in their study came from an actual power plant. The SVR model demonstrated a promising generalization property by obtaining accuracy of 92% under test data with a relative error of less than 5%. Tang and Zhang [16] developed a framework of a deep belief network and JAYA algorithm to find the best values of boiler efficiency and NOx emissions. The results showed that adjusting control parameters of the combustion system might improve both combustion efficiency and NOx emissions. Tan et al. [17] developed a methodology combining the advanced extreme learning machine (ELM) with harmony search (HS) and optimized the operational parameters of a boiler for the control of NOx emissions in a 700 MW pulverized-coal-fired power plant. The results achieved an MRE of 1.13% which is better than those of the ANN and SVR. The HS optimized operation parameters in reducing NOx emission by 16.5% with the ANN and 19.2% with SVR.
As outlined in previous literature, many studies have attempted to predict and reduce SOx and NOx emissions in coal-fired power plants considering operational parameters and fuel characteristics with various methods. A significant challenge using machine learning (ML) is that most ML models operate as “black boxes”, making it difficult to interpret the relationships between process variables and NOx emissions. For this reason, it is required to find important features in coal combustion to offer better interpretability and transparency. In large and complex systems like coal-fired power plants, the causal relationships between process variables are often incomplete due to factors like high dimensionality, non-linearity, interdependencies, and historical data gaps and the need for prior knowledge [18]. As a result, it becomes essential to adopt methods that do not rely heavily on prior knowledge on processes [19]. By reducing the number of variables, models can be simplified, thus enhancing computational efficiency and preventing overfitting.
Moreover, due to lack of prior research on predicting SOx and NOx based on mixed coal properties, this study focuses on developing a deep neural network (DNN) model for predicting SOx and NOx emissions with emphasis on analyzing the influence of coal properties using feature importance with mixture of coal.
3. Model Development
In the case that the high-heat-capacity coal and the low-heat-capacity coal are mixed with a proper ratio, SOx and NOx emission after combustion can be minimized, meeting several operation constraints such as heat calories, stability, cost, and so on. However, the possible ratio combinations between the high-heat-capacity coal and the low-heat-capacity coal can be diverse and hard to explore. To decide the best mixture ratio [20], it is a prerequisite to know how much SOx and NOx are generated based on the properties of mixed coal. Depending on the prediction, an unsatisfactory mixture ratio can be eliminated in advance, which helps to reduce SOx and NOx. This section describes how the coal properties that affect SOx and NOx emission can be selected and also how SOx and NOx can be predicted depending on various mixture ratios of coals.
3.1. Data Preprocessing
3.1.1. Coal Mixture
The targeted coal-fired power plant in this study burns various kinds of coal which are imported from several countries. Some of them are classified as high-heat-capacity coal and others are low-heat-capacity coal. Since there are multiple course countries, the composition of coals is diverse even within the same type of coal (high-heat-capacity coal or low-heat-capacity coal). From field experience and for economic advantages, four kinds of coal (two high-heat-capacity coals and two low-heat-capacity coals) are mixed for combustion in the targeted coal-fired power plant currently. The combustion of mixed coals should meet required thermal energy and guarantee stability in the boiler during combustion. Figure 1 shows how the coals are mixed in the targeted coal-fired power plant.
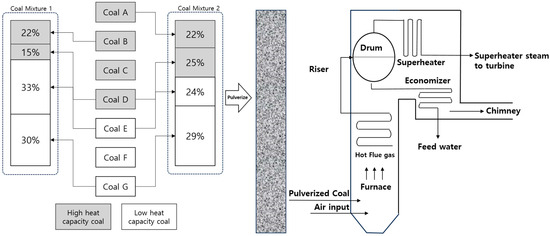
Figure 1.
Coal mixture and combustion in boiler.
To ensure complete combustion and increase surface area, coal needs to be pulverized. The mixed coal is ground by the pulverizer and burned in the boiler to minimize pollutants and to maximize heat energy.
As an energy source of combustion, several properties should be considered and important properties are described in Table 1. Pulverized coal is supplied to the combustion chamber of a boiler and provides heat to the power plant by burning.

Table 1.
Coal properties.
Since four different kinds of coal are mixed (refer Figure 1), the overall characteristics of the coal mixture should be calculated. To do this, the properties of each coal are aggregated by the ratio of each coal and it is regarded as the general properties of the coal mixture. The calculation method is described in the following Equation (3).
In Equation (3), k indicates the index of properties in Table 1. The notation i represents the index of mixed coal. n means the number of coals to be mixed and n is set to 4 in this power plant. Pk represents the kth property value of the mixed coal. pk,i means the kth property value of the ith coal. ri is the mixture ratio of the ith coal. These general properties of the coal mixture are related to SOx and NOx emission when it is combusted.
3.1.2. Feature Selection for AI Model Development
Among several properties in Table 1, some of them can more strongly contribute to the generation of SOx and NOx during coal combustion. Other properties which have less correlation with SOx and NOx emissions may disturb model training and worsen prediction capability. To resolve this problem, feature selection is adopted before prediction model development. The selection of features is carried out by feature importance. Feature importance refers to strategies that compute a score for a particular model and the scores simply describe the “importance” of each feature. A higher score indicates that a specific property will have a greater impact on the model being used to forecast a certain dependent variable [21]. By performing feature selection with feature importance, a model can be more simplified and the training time can be reduced. The feature importance can also help in comprehending and explaining the model.
There are several methods for calculating feature importance. Generally, they can be divided into two categories, namely model agnostic [22] and model dependent [23]. Model-agnostic methods can be applied to any model type without relying on its internal structure, with examples like permutation importance [24], local interpretable model agnostic explanation (LIME) [25], and Shapley additive explanations (SHAP) [26]. In contrast, model-specific methods leverage the internal mechanics of particular models, with techniques such as feature importance for decision trees [27] and coefficient magnitudes for linear models [28]. While model-dependent methods are often faster and tailored to the model’s characteristics, model-agnostic approaches offer broader applicability and flexibility. Breiman et al. [29] presented the permutation feature importance assessment for random forests. Based on this concept, Fisher et al. [30] suggested model dependency, a model-independent variation of the feature importance. As mentioned in Section 2, a huge data set with too many variables affects the capability of the model to perform, so model-agnostic permutation feature importance is adopted in this study to select the most significant variables for the model development. When the values of a feature are permuted, the link between the feature and the actual result of the model can be disrupted. This disruption increases the prediction error of the model and it is measured as the permutation feature importance. The increase in the prediction error of the model after permuting a feature is calculated in order to determine how important it is When changing the value of the feature causes the model error to rise, this feature is considered as important. Otherwise, when changing a feature’s values causes the model error to remain constant, the feature can be disregarded for the prediction and it is unimportant. In this study, feature importance is calculated using extreme gradient boosting (XGBoost) [31] and random forest [29]. XGBoost is an optimized implementation of the gradient boosting algorithm that uses an ensemble of weak decision tree models to gradually improve predictive performance of the model by minimizing the loss function through an iterative process.
Random forest is a bagging ensemble learning model that combines multiple decision trees trained on random subsets of the training data and features. The predictions from these trees are then aggregated through majority voting for classification or averaging for regression, resulting in the final prediction. Figure 2 shows the general architecture of random forest and XGBoost.
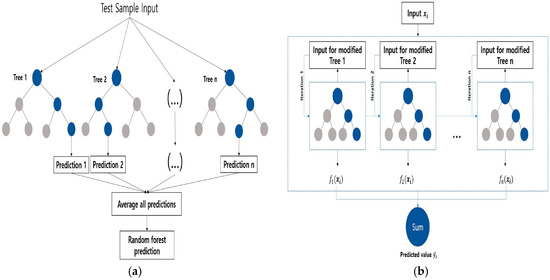
Figure 2.
(a) Schematic diagram of the random forest [32]. (b) Schematic diagram of the XGBoost [33].
Table 2 shows the calculated feature importance for each property through random forest and XGBoost.

Table 2.
Feature importance score.
In this analysis, features with weight higher than 0.1 are considered important, serving as a criterion for identifying the most influential variables in the model. For NOx prediction, XGBoost identifies five variables (volatile matter, calorific value, moisture, SO2, and ignition point). In contrast, random forest identifies four significant variables (volatile matter, calorific value, SO2, and ignition point). For SOx prediction, XGBoost identifies four variables (moisture, SO2, calorific value, and ignition point), while random forest identifies two significant variables (SO2 and calorific value). Upon comparing the calculated feature importance between XGBoost and random forest, it is found that there is not a significant difference in variable importance across the models. Based on the analysis results, it is decided that the DNN model for NOx incorporates volatile matter, calorific value, total moisture, SO2, and ignition point as input variables, while the DNN model for SOx adopts SO2, calorific value, and ignition point.
3.2. Prediction Model Development
3.2.1. Data Collection
The necessary data to develop an AI model are extracted from the field data of the targeted coal-fired power plant which is operated in South Korea. The duration of data collection is 9 months. Since various kinds of data are collected, time synchronization among data is performed. For example, the properties of coal are fixed for 8 h since the coal mixture loaded into the pulverizer lasts 8 h. Until the loaded coal is burned out, other operational data change. On the contrary, emissions of SOx and NOx are monitored every 10 min. Therefore, the average of the measured SOx and NOx values for 8 h is matched to the properties of the coal mixture. After time synchronization, approximately 800 data points are usable. In addition, some sensor errors and facility shutdown reduced the data into 588 data points.
3.2.2. Normalization
To improve prediction capability, it is necessary to perform normalization for selected properties (explained in Section 3.1.2) respectively since the measured value is spread over different ranges. There are several advantages to normalizing data for machine learning models [34], including reducing their learning time and preventing decreases in accuracy caused by heavy computations. In addition, normalization improves the training stability and reduces the influence of the deviations caused by differences in the ranges of variables [35]. In this study, robust scaler normalization is adopted for each property. Results of normalization are represented in Table 3.

Table 3.
Collected data after normalization.
3.2.3. DNN Model
Deep neural networks (DNNs) [36] offer a sophisticated approach to modeling complex non-linear relationships inherent in data. In predicting SOx and NOx emissions, which are vital parameters in environmental science and regulatory compliance, a DNN model can capture intricate patterns and dependencies in the data that might be missed by traditional linear models. By leveraging multiple layers of artificial neurons, DNNs can represent high-level abstractions and interactions among features, making them especially suited for tasks that require recognizing subtle patterns in vast data sets. Selecting a DNN model for SOx and NOx emissions prediction is motivated by the model capacity to handle vast amount of data and its adaptability to various feature scales and types. Given the multifaceted nature of factors influencing emissions, it is crucial to have a model that can adapt and learn from such complexity. A DNN operates by taking input data and passing it through multiple interconnected layers, transforming and processing the data at each stage. This multistage processing allows the model to incrementally abstract and recognize patterns, culminating in an output layer that provides the desired predictions. The model is trained by adjusting its internal weights based on the error of its predictions, using algorithms like backpropagation and optimization techniques such as gradient descent. The structure of the proposed model in this study is illustrated in Figure 3.
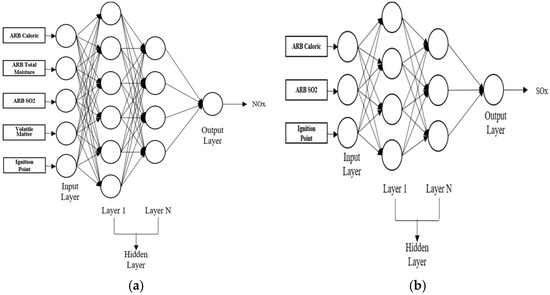
Figure 3.
(a) DNN structure for NOx. (b) DNN structure for SOx.
3.3. Evaluation of Model Performance
3.3.1. Performance Measure
To evaluate the performance of the developed model, mean absolute percentage error (MAPE) and correlation coefficient are used (refer to Equations (4) and (5)). MAPE is commonly used to measure prediction performance. Units of the MAPE are scaled to a percentage from 0% to 100%, and a lower value of MAPE means better performance. To validate the prediction performance of the developed model resulting in the highest performance, the correlation coefficient r of Pearson correlation analysis is used. Correlation analysis is used to infer the relationship between real and predicted values. The range of correlation coefficient is from −1 to 1. When r is close to 0, it means no correlation. In the case of strong correlation, r is more than 0.6 or less than −0.6. The formulae for MAPE and correlation coefficient are as expressed as Equations (4) and (5).
In Equations (4) and (5), Ai denotes the actual emission of SOx and NOx, and Fi represents the predicted emission of SOx and NOx by the model. indicates the mean of A. indicates the mean of F.
3.3.2. Prediction Results
The whole data set is divided into a training data set with 80% of the data and a testing data set with the remaining 20% in order to avoid overfitting. The training set is only used to adjust the parameters of the model, and the testing data set is used with the trained model in order to check whether the model works correctly with the properties of the new coal mixture. Table 4 shows the results of SOx and NOx prediction with the proposed predictive model. As well as DNNs, commonly used conventional predictive models such as XGBoost and random forest are also tested so as to compare with the proposed DNN model.

Table 4.
Prediction results.
According to Table 4, prediction accuracy of the XGBoost algorithm with the following hyperparameters: N_estimators = 50; Learning_rate = 0.08; gamma = 0; subsample = 0.75 and Max_depth = 5, shows the performance with MAPE of 22.65% and 22.63% for SOx and NOx, respectively. Random forest, with the following hyperparameters: N_estimators = 100; Min_samples_leaf = 4; Min_samples_split = 8; and Max_depth = 2, gives the best result with an MAPE of 24.71% and 19.82% for SOx and NOx, respectively. However, XGBoost and random forest do not provide a large variance of performance depending on the hyperparameters of the model. On the other hand, the prediction accuracy of the DNN model for SOx, training with the following hyperparameters: activation function = Relu; layer = (input layer (number of input variables), hidden layer (9, 18, 36, 18, 9, 9), and output layer (1); value in () means number of nodes of each layer); drop out = none; weight initialization = He initialization; optimizer = Adam, gives the best result as MAPE = 7.1%. NOx prediction by the trained DNN model with the following hyperparameters: activation function = Relu; layer = (input layer (number of input variables), hidden layer (15, 30, 60, 30, 15, 5), and output layer (1); value in () means number of nodes of each layer); drop out = none; weight initialization = He initialization; optimizer = Adam, gives the best result, with MAPE = 5.68%. From these results, it is evident that the DNN has the highest accuracy in SOx and NOx emission prediction.
Figure 4a,c shows the residual error between the actual SOx and NOx and the predicted SOx and NOx as a graph. To validate the prediction performance of the predictive model with the highest performance, the correlation coefficient r of Pearson correlation analysis is used. In the DNN model used in this study, the correlation coefficient between the actual and predicted value is r = 0.866 and 0.916 for SOx and NOx, respectively, which means that they have a strong correlation. Figure 4b,d show the correlation between the actual SOx and NOx and the predicted SOx and NOx as a graph.
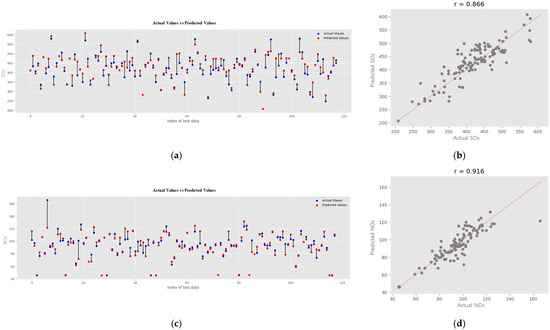
Figure 4.
(a) Residual error plot of real values and predicted values of SOx. (b) Scatter plot of real values and predicted values of SOx. (c) Residual error plot of real values and predicted values of NOx. (d) Scatter plot of real values and predicted values of NOx.
4. Conclusions and Discussion
This study proposed a machine learning model that learns and predicts the levels of pollutants such as SOx and NOx that are emitted depending on mixed coal in the coal-fired power plant. The targeted process includes a boiler which is one of the important machines in coal-fired power plants. In case the machine learning model is able to predict emission of pollutants depending on various mixed coals, the operator can be alert and know in advance the result of the emission of the pollutants before the operation process. Depending on this information, operator can decide on a better coal mixture ratio, which has a huge impact on reducing the emission of pollutants. To achieve this, this study analyzes the importance of variables with permutation feature importance. The selected variables by feature importance are used as input variables in the DNN model. In addition, a robust scaler is adopted to reduce the influence of the deviations caused by the values being measured at different scales.
Some conventional predictive models such as random forest and XGBoost are also adopted to compare prediction performance with the developed DNN model. According to this analysis, the DNN model shows its effectiveness in the experimental results, with a mean absolute percentage error (MAPE) of 7.1% and 5.68% for SOx and NOx, respectively. In addition, to validate the prediction performance of the predictive model with the highest performance, Pearson correlation analysis is used, which give results depicting a high correlation between the real and predicted values. The developed model may be used to estimate emission of SOx and NOx when a new coal is supplied under various combinations of coal. The predictive model is applied to help reduce the emission of pollutants by predicting the emission of SOx and NOx of a boiler using coal properties collected from real operational data of coal-fired power plants. A multitude of factors, including the operational parameters (boiler, air pollution control device, injection condition, and so on), as well as coal properties, significantly influence the levels of SOx and NOx emissions. These operational parameters are automatically set up within specific boundaries predefined by the operators. This automated regulation presents a challenge in modifying operational parameters in a real industry setting, thus introducing a limitation when considering them in the development of our optimization model. Therefore, we only consider coal properties in this study. The next step in this research is to find the best mixture ratio of coal for combustion automatically. Advanced computer methods like search algorithms or learning algorithms could help in achieving this. The authors suggest that future studies should focus on this area.
Author Contributions
Conceptualization, M.S.S., S.-J.K. and J.-H.S.; methodology, M.S.S., S.-J.K. and J.-H.S.; software, M.S.S. and T.K.W.; validation, M.S.S. and J.-H.S.; formal analysis, M.S.S. and T.K.W.; investigation, M.S.S. and D.K.; resources, M.S.S.; data curation, M.S.S. and T.K.W.; writing—original draft preparation, M.S.S.; writing—review and editing, M.S.S., D.K. and J.-H.S.; visualization, M.S.S. and T.K.W.; supervision, S.-J.K. and J.-H.S.; project administration, J.-H.S.; funding acquisition, J.-H.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Ministry of Science and ICT and the National Research Foundation of Korea grant number NRF-2021R1A2C1012796.
Data Availability Statement
The data presented in this study are available on request form the corresponding author. The data are not publicly available due to privacy restrictions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gilbert, A.; Bazilian, M.D.; Gross, S. The Emerging Global Natural Gas Market and the Energy Crisis of 2021–2022; Brookings Report. 2021. Available online: https://www.brookings.edu/wp-content/uploads/2021/12/FP_20211214_global_energy_crisis_gilbert_bazilian_gross.pdf (accessed on 20 November 2023).
- Clark, R.; Zucker, N.; Urpelainen, J. The Future of Coal-Fired Power Generation in Southeast Asia. Renew. Sustain. Energy Rev. 2020, 121, 109650. [Google Scholar] [CrossRef]
- Jiang, K.; Xing, R.; Luo, Z.; Huang, W.; Yi, F.; Men, Y.; Zhao, N.; Chang, Z.; Zhao, J.; Pan, B. Pollutant Emissions from Biomass Burning: A Review on Emission Characteristics, Environmental Impacts, and Research Perspectives. Particuology 2023, 85, 296–309. [Google Scholar] [CrossRef]
- Tiwari, S.; Neha Mishra, N.M. Methods for the Measurement of Air Pollutants. In Air Pollution: SOURCES, Impacts and Controls; CAB International: Wallingford, UK, 2019; pp. 55–78. [Google Scholar]
- Arens, M.; Åhman, M.; Vogl, V. Which Countries Are Prepared to Green Their Coal-Based Steel Industry with Electricity? Reviewing Climate and Energy Policy as Well as the Implementation of Renewable Electricity. Renew. Sustain. Energy Rev. 2021, 143, 110938. [Google Scholar] [CrossRef]
- Liu, C.; Xu, J.; Li, M.; Wang, Q.; Liu, G. The Comprehensive Solution to Decrease Cooling Wall Temperatures of sCO2 Boiler for Coal Fired Power Plant. Energy 2022, 252, 124021. [Google Scholar] [CrossRef]
- Hou, H.; Xie, B.; Cheng, Y. Analysis of Carbon Emissions and Emission Reduction from Coal-Fired Power Plants Based on Dual Carbon Targets. Sustainability 2023, 15, 7369. [Google Scholar] [CrossRef]
- Taha, Y.; Elghali, A.; Derhy, M.; Amrani, M.; Hakkou, R.; Benzaazoua, M. Towards an Integrated Approach for Zero Coal Mine Waste Storage: Solutions Based on Materials Circularity and Sustainable Resource Governance. Miner. Process. Extr. Metall. Rev. 2023, 44, 375–388. [Google Scholar] [CrossRef]
- Kim, Y.; Park, T.; Hong, D. Heating and Emission Characteristics of Briquettes Developed from Spent Coffee Grounds. Environ. Eng. Res. 2022, 27, 210063. [Google Scholar] [CrossRef]
- Zhou, S.; He, H.; Zhang, L.; Zhao, W.; Wang, F. A Data-Driven Method to Monitor Carbon Dioxide Emissions of Coal-Fired Power Plants. Energies 2023, 16, 1646. [Google Scholar] [CrossRef]
- Mollo, M.; Kolesnikov, A.; Makgato, S. Simultaneous Reduction of NOx Emission and SOx Emission Aided by Improved Efficiency of a Once-Through Benson Type Coal Boiler. Energy 2022, 248, 123551. [Google Scholar] [CrossRef]
- Krzywański, J.; Nowak, W. Neurocomputing Approach for the Prediction of NOx Emissions from CFBC in Air-Fired and Oxygen-Enriched Atmospheres. J. Power Technol. 2017, 97, 75–84. [Google Scholar]
- Lv, Y.; Liu, J.; Yang, T.; Zeng, D. A Novel Least Squares Support Vector Machine Ensemble Model for NOx Emission Prediction of a Coal-Fired Boiler. Energy 2013, 55, 319–329. [Google Scholar] [CrossRef]
- Krzywanski, J.; Nowak, W. Artificial Intelligence Treatment of SO2 Emissions from CFBC in Air and Oxygen-Enriched Conditions. J. Energy Eng. 2016, 142, 04015017. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, J.P.; Zheng, L.G.; Wang, C.L.; Cen, K.F. Modeling NOx Emissions from Coal-Fired Utility Boilers Using Support Vector Regression with Ant Colony Optimization. Eng. Appl. Artif. Intell. 2012, 25, 147–158. [Google Scholar] [CrossRef]
- Tang, Z.; Zhang, Z. The Multi-Objective Optimization of Combustion System Operations Based on Deep Data-Driven Models. Energy 2019, 182, 37–47. [Google Scholar] [CrossRef]
- Tan, P.; Xia, J.; Zhang, C.; Fang, Q.; Chen, G. Modeling and Optimization of NOX Emission in a Coal-Fired Power Plant Using Advanced Machine Learning Methods. Energy Procedia 2014, 61, 377–380. [Google Scholar] [CrossRef][Green Version]
- Saito, T.; Fujiwara, K. Causal Analysis of Nitrogen Oxides Emissions Process in Coal-Fired Power Plant with LiNGAM. Front. Anal. Sci. 2023, 3, 1045324. [Google Scholar] [CrossRef]
- Adams, D.; Oh, D.-H.; Kim, D.-W.; Lee, C.-H.; Oh, M. Prediction of SOx–NOx Emission from a Coal-Fired CFB Power Plant with Machine Learning: Plant Data Learned by Deep Neural Network and Least Square Support Vector Machine. J. Clean. Prod. 2020, 270, 122310. [Google Scholar] [CrossRef]
- Ji, B.; Jiang, B.; Yuan, L.; Yu, C.; Zhou, G.; Zhao, Y.; Wang, S.; Wang, X. Experimental and Molecular Dynamics Simulation Study on the Influence of SDS and JFC Composite Ratios on Bituminous Coal Wettability. Process Saf. Environ. Prot. 2023, 174, 473–484. [Google Scholar] [CrossRef]
- Khaire, U.M.; Dhanalakshmi, R. Stability of Feature Selection Algorithm: A Review. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 1060–1073. [Google Scholar] [CrossRef]
- Hadash, S.; Willemsen, M.C.; Snijders, C.; IJsselsteijn, W.A. Improving Understandability of Feature Contributions in Model-Agnostic Explainable AI Tools. In Proceedings of the 2022 CHI Conference on Human Factors in Computing Systems, Orleans, LA, USA, 29 April–5 May 2022; pp. 1–9. [Google Scholar]
- Molnar, C.; König, G.; Bischl, B.; Casalicchio, G. Model-Agnostic Feature Importance and Effects with Dependent Features: A Conditional Subgroup Approach. Data Min. Knowl. Discov. 2023, 1–39. [Google Scholar] [CrossRef]
- Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation Importance: A Corrected Feature Importance Measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef]
- Zafar, M.R.; Khan, N. Deterministic Local Interpretable Model-Agnostic Explanations for Stable Explainability. Mach. Learn. Knowl. Extr. 2021, 3, 525–541. [Google Scholar] [CrossRef]
- Nohara, Y.; Matsumoto, K.; Soejima, H.; Nakashima, N. Explanation of Machine Learning Models Using Improved Shapley Additive Explanation. In Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, New York, NY, USA, 7–10 September 2019; p. 546. [Google Scholar]
- Grabczewski, K.; Jankowski, N. Feature Selection with Decision Tree Criterion. In Proceedings of the Fifth International Conference on Hybrid Intelligent Systems (HIS’05), Rio de Janerio, Brazil, 6–9 November 2005; p. 6. [Google Scholar]
- Su, Y.; Dai, Y.; Zeng, Y.; Wei, C.; Chen, Y.; Ge, F.; Zheng, P.; Zhou, D.; Dral, P.O.; Wang, C. Interpretable Machine Learning of Two-Photon Absorption. Adv. Sci. 2023, 10, 2204902. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Fisher, A.; Rudin, C.; Dominici, F. All Models Are Wrong, but Many Are Useful: Learning a Variable’s Importance by Studying an Entire Class of Prediction Models Simultaneously. J. Mach. Learn. Res. 2019, 20, 1–81. [Google Scholar]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T. Xgboost: Extreme Gradient Boosting. R Package 2015, 1, 1–4. [Google Scholar]
- Sahour, H.; Gholami, V.; Torkaman, J.; Vazifedan, M.; Saeedi, S. Random Forest and Extreme Gradient Boosting Algorithms for Streamflow Modeling Using Vessel Features and Tree-Rings. Environ. Earth Sci. 2021, 80, 747. [Google Scholar] [CrossRef]
- Jiang, J.; Pan, H.; Li, M.; Qian, B.; Lin, X.; Fan, S. Predictive Model for the 5-Year Survival Status of Osteosarcoma Patients Based on the SEER Database and XGBoost Algorithm. Sci. Rep. 2021, 11, 5542. [Google Scholar] [CrossRef]
- Sinsomboonthong, S. Performance Comparison of New Adjusted Min-Max with Decimal Scaling and Statistical Column Normalization Methods for Artificial Neural Network Classification. Int. J. Math. Math. Sci. 2022, 2022, 3584406. [Google Scholar] [CrossRef]
- Liu, Z. A Method of SVM with Normalization in Intrusion Detection. Procedia Environ. Sci. 2011, 11, 256–262. [Google Scholar] [CrossRef]
- Miikkulainen, R.; Liang, J.; Meyerson, E.; Rawal, A.; Fink, D.; Francon, O.; Raju, B.; Shahrzad, H.; Navruzyan, A.; Duffy, N. Evolving Deep Neural Networks. In Artificial Intelligence in the Age of Neural Networks and Brain Computing; Elsevier: Amsterdam, The Netherlands, 2019; pp. 293–312. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).